第2章 弹性力学基本理论
合集下载
第二章 弹性力学的基本理论

2
0 0 0
0 0 0
0
0
0
x (2-18)
y
0 0 0
0
0
z
yz
0 0
0
0
66
zx xy
61
弹性力学简明教程
二、平面问题
平面问题{ 平面应力问题 平面应变问题 1、平面应力问题:
z zx zy 0
xz yz 0
由(2-15)式知:
z
fy
0
(2-4)
xz
x
yz
y
z
z
fz
0
x
0
0
0
y 0
0
0 z
0
z y
z
0
x
x
y x
0
36
y
z yz
zx xy
61
fx fy fz
31
0 31
H P 0
36
61
31
31
(2-6)
弹性力学简明教程
二、空间问题的平衡微分方程
弹性力学简明教程
§2 平衡微分方程
一、平面问题的平衡微分方程
y
y
y
dy
x
fy
yx
yx
y
dy
xy
xy
x
dx
y
xy
dy c dx
fx
yx
x
x
x
dx
o(z)
x y
平衡微分方程:
Fx 0 Fy 0
微元体:厚度为1
平面问题的特点:
一切现象都看作是在一个平面内发生的
Fx 0 Fy 0
Mc 0
2--弹性力学基本理论

yz
zx
• 应变的定义
• 设平行六面体单元,3个轴棱边 :
– 变形前为MA,MB,MC; – 变形后变为M'A',M'B',M'C'
。
x、 y、 z
•正应变(小变形)
•符号规定: 正应变以伸长为正。
•剪应变
•符号规定: 正应变以伸长为正;剪应变以角度变小为正。
材料力学 — 区别与联系 — 弹性力学
y
y
q
q
sx
ͼ 1-1a
x
0
sx x
ͼ 1-1b
材料力学 — 区别与联系 — 弹性力学
ͼ 1-3a ͼ 1-3b
2.1 弹性力学的基本假定
• 连续性假设:物体所占的空间被介 质充满,不考虑材料缺陷,在物体 内的物理量是连续的, 可以采用连续 函数来描述对象。
虽然都从静力学、几何学与物理学三方面进行研究, 但是在建立这三方面条件时,采用了不同的分析方法。 材料力学是对构件的整个截面来建立这些条件的,因而 要常常引用一些截面的变形状况或应力情况的假设。这 样虽然大大简化了数学推演,但是得出的结果往往是近 似的,而不是精确的。而弹性力学是对构件的无限小单 元体来建立这些条件的,因而无须引用那些假设,分析 的方法比较严密,得出的结论也比较精确。所以,我们 可以用弹性力学的解答来估计材料力学解答的精确程度, 并确定它们的适用范围。
当△S 趋近于0,则为P点的面力
•面力分量 •符号规定:与坐标轴方向一致为正,反之为负。 •面力的量纲:[力]/[长度]^2 •列阵表示:Fs={X Y Z}T
集中力
体力与面力都是分布力,集中力则只是作用在一个点
2-弹性力学基本理论

x
1 E
( x
y
)
y
1 E
(
y
x
)
xy
2(1 E
) xy
x
1 2
E
( x
1
y)
y
1 2
E
(
y
1
x
)
xy
2(1 E
) xy
E E (1 2 )
(1 )
弹性力学基础 2.2.5 物理方程
两种平面问题的物理方程写成统一形式。若以应变表示应力 ,则两种平面问题物理方程的统一形式如下
应变特征:如图选取坐标系,以任一横截面为xy面,任一纵线为
z轴。则任一横截面均可视为对称面,有沿z方向的位移
z
x
w0
弹性力学基础 2.2.2平面应变问题
所有各点的位移矢量都平行于x y平面,则
z 0 , zy yz 0 , zx xz 0
因此,平面应变问题只有三个应变分量,仅为x、y的函数, 与z无关,如下
x
yx
y
xy x
Gx
x
x x
dx
T
G Gx Gy
Gy
xy
xy x
dx
y
y
y y
yx
dy
yx y
dy
弹性力学基础 2.2.3 平衡微分方程
x
yx
y
xy x
Gx Gy
x
x x
dx
xy
xy x
dx
y
y
y y
yx
dy
yx y
dy
由 Fx 0 ,得
x
x
yx
y
Gx
0
有限元法基本原理及应用第2章重庆大学龙雪峰

有限元原理及应用
第二章 弹性力学基本理论
3.完全弹性假设。 假设除去引起物体变形的外力之后,物体形状能够完全恢 复,而没有任何残余变形并且假定材料服从胡克定律,即 应力与应变成正比,这样物体在任意瞬时,应变完全取决 于该瞬时所受外力,而与它之前加载的历史无关,与外力 施加顺序也无关。 由材料力学知,物体所受应力未达到比例极限之前,可 近似看作完全弹性体。
有限元原理及应用
第二章 弹性力学基本理论
2.均匀性假设。 假设物体内各处材料的力学性能完全相同,即从物体中任 意取出一个微元体进行分析,都可以使用同一组材料常数。 实际上,物体是由颗粒组成的,不可能是完全均匀的, 但只要颗粒的尺寸远远小于物体的尺寸并且均匀分布,将 物体性能看作各组成部分性能的统计平均量是没问题的。 这里的均匀性假设并不妨碍弹性力学处理由不同材料组成 的弹性体,只要在每一部分都满足均匀性假设即可。
有限元原理及应用
• 2.2.7 主应变 • 由单元体六个应变分量:
第二章 弹性力学基本理论
• 可以求出过该点任意方向线应变和任意两 线段之间角度的改变:
2.7 2.8
式中l、m、n 为过物体内一点P 的线 段PN 的方向余弦, l1、m1、 n1为过P 点 与PN 成θ 角的线段PN1 的方向余弦,θ’ 为物体受力变形后线段PN 与PN1 的夹角, 如图2.5 所示。
有限元原理及应用
第二章 弹性力学基本理论
• 这个极限矢量p 就是物体在截面mn 上的、在P 点所受内力的 集度,即P 点的应力。因为ΔA 是标量,所以p 的方向就是ΔF 的极限方向。 • 对于应力,通常沿截面的法向和切向将应力分解为正应力σ 和切应力τ,如图2.3 所示。应力及其分量的因次是[力][长 度]-2。 • 在物体内的同一点,不同方向的截面上的应力是不同的。过 一点,各截面上应力的大小和方向的总和称为一点的应力状 态。
第二章 固体弹性力学基础

应力定义为:单位面积上所受的内力,是在面力或 体力作用下,物体内部假想面上单位面积上的一对 大小相等、方向相反的力,是作用在该面上力的大 小的度量。
应力也称为胁强(力的强度):应力并不是一个 “力”,因为它的量纲不是力而是单位面积上的力。
应力的方向与作用力的方向相反。
6
2.1 应力分析
16
2、非均匀变形 用物体内部变形 单元体(应变椭 圆)表示非均匀 变形 ——褶皱
17
2.2.3 应变分类
应变---当弹性体受到应力作用后,将发生体积和形 状的变化,即应变。
体积形变----指物体只发生体积变化而无形状变化的 应变。它是受正应力作用的结果。 形状形变-----物体只发生形状的变化。它是剪切应力 作用的结果。 理论力学是研究物体的整体运动。把物体作为一种刚 体,在外力作用下只能产生整体平移和转动。 弹性力学不仅要考虑物体的整体运动,而且要研究物 体内部各质点的相对运动,相对运动是产生应变的必 要条件。
设N为M 邻近点,其向径 为 r dr 。受力后N点位移 到 N ,它的位移向量记 为 u(r dr) 。 N点对M点的相对位移是
z
N (x+dx,y+dy,z+dz)
dr
M (x,y,z)
u (r )
u( r )
u (r dr)
N
u(r dr) u(r)
dx 1。由 (1-9) ds
u e e xx x
同理可求得沿y和z轴上单位长度得伸长值
e e yy
e e zz
v y w z
28
(2)切应变:变形体不仅在三个坐标方向上有相对伸长(或 压缩),而且还会产生旋转,即夹角也会发生变化。(见下图) 假设两个正交线元素 MN和MP。受力后, 相对位移分别是du1 和du2。假设: dx=|MN|=|dr1| dy=|MP|=|dr2| MN、MP的相对位移 du1和du2对可由(11)式求出。
弹性力学-第二章 平面问题基本理论 (徐芝纶第五版)
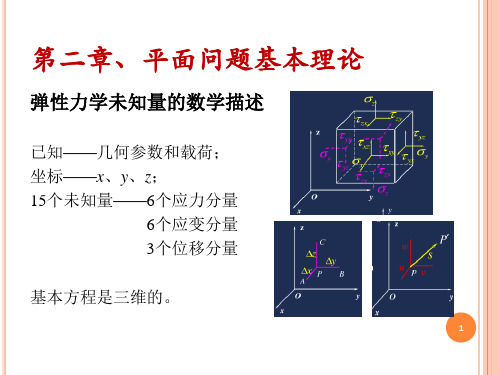
基本方程是二维的。
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
弹性力学第二章平面问题的基本理论

应力边界条件:
在应力约束 面上: 设 面法线与x轴正向夹角
的余玄为l,与y轴正向夹角
的余玄为m。
混合条件:
位移约束与应力约束的组合。
边界条件举例
x
y q
x
y
p
圣维南原理及其应用
圣 维 南 ( Adhémar Jean Claude Barré de Saint-Venant , 1797~1886)原理:如果把物体的一小部分边界上的面力, 变换为分布不同但静力等效的面力(主矢量相同,对于同 一点的主矩也相同),那么近处的应力分布将有显著改变, 但是远处所受的影响可以忽略不计。
— 边界条件
按位移求解平面应力问题(5)
— 小结
按位移求解平面问题需要:
1. 位移分量满足微分方程:
2.边界条件:
按位移求解平面问题(5)
— 举例
x
ρg
y=h y
按位移求解平面问题(6)
— 举例
x
ρg
y=h y
按应力求解平面应力问题(1)
— 用位移表达应变(几何方程)
形变协调方程或相容方程 连续体的形变分量不是相互独立的,它们之间必须满足 相容方程,才能保证真实的位移分量存在。
因此,由 中第一式:
最后得到:
由 中第二式:
常体力情况下的简化(5)
— 平衡方程的解
通解
特解
常体力情况下的简化(6)
— 艾里应力函数表示的相容方程
应力调和方程 代入
得到:
简写为:
常体力情况下的平面问题
常体力情况下的平面问题需要满足:
1.艾里应力函数表示的相容方程:
2.边界条件
3.位移单值条件
弹性力学第二章平面问题的基本理论
在应力约束 面上: 设 面法线与x轴正向夹角
的余玄为l,与y轴正向夹角
的余玄为m。
混合条件:
位移约束与应力约束的组合。
边界条件举例
x
y q
x
y
p
圣维南原理及其应用
圣 维 南 ( Adhémar Jean Claude Barré de Saint-Venant , 1797~1886)原理:如果把物体的一小部分边界上的面力, 变换为分布不同但静力等效的面力(主矢量相同,对于同 一点的主矩也相同),那么近处的应力分布将有显著改变, 但是远处所受的影响可以忽略不计。
— 边界条件
按位移求解平面应力问题(5)
— 小结
按位移求解平面问题需要:
1. 位移分量满足微分方程:
2.边界条件:
按位移求解平面问题(5)
— 举例
x
ρg
y=h y
按位移求解平面问题(6)
— 举例
x
ρg
y=h y
按应力求解平面应力问题(1)
— 用位移表达应变(几何方程)
形变协调方程或相容方程 连续体的形变分量不是相互独立的,它们之间必须满足 相容方程,才能保证真实的位移分量存在。
因此,由 中第一式:
最后得到:
由 中第二式:
常体力情况下的简化(5)
— 平衡方程的解
通解
特解
常体力情况下的简化(6)
— 艾里应力函数表示的相容方程
应力调和方程 代入
得到:
简写为:
常体力情况下的平面问题
常体力情况下的平面问题需要满足:
1.艾里应力函数表示的相容方程:
2.边界条件
3.位移单值条件
弹性力学第二章平面问题的基本理论
第2章 弹性力学的基本知识

(2)均匀性假设:假定物体内各点处材料均相同。
(3)各向同性假设:假定物体内各点处各个方向上的物理性质相同。
(4)完全弹性假设:胡可定律
(5)几何假设——小变形假设: 变形产生的位移与物体的尺 寸相比 ,是微小的。
关于外力、应力、应变和位移的定义
1.外力
体力 (定义)分布在物体体积内的力,如重力、惯性力等。 分为体积力(体力)和表面力(面力)两类。 有限元分析也使用集中力这一概念。
以通过一点的沿坐标正向微分线段的 正应变ε和 切(剪)应变 γ 来表示。 正应变εx ,εy , εz 以伸长为正。
切应变γxy , γyz ,γzx 以直角减小为正, 用弧度表示。 正应变和切应变都是无因次的量 应变列阵 x y z xy yz zx
Tຫໍສະໝຸດ 4. 位移材力研究方法
也考虑这几方面的条件,但不是十分严格的:常常引用近 似的计算假设(如平面 截面假设)来简化问题,并在许多 方面进行了近似的处理。 因此材料力学建立的是近似理论,得出的是近似的解答。 从其精度来看,材力解法只能 适用于杆件形状的结构。
★ 弹塑性力学研究问题的基本方法
在受力物体 内任取一点 (单元体)为 研究对象。
写成矩阵形式:
ε=
σ
ε=φσ 显然: φ=D-1
三、平衡方程
弹性体中任一点满足平衡方程, 在给定边界上满 足应力边界条件。
弹力的研究方法
在体积V内 由微分体的平衡条件,建立平衡微分方程; 由微分线段上应变与位移的几何关系,建立几何方程; 由应力与形变之间的物理关系,建立物理方程; 在边界 S 面上
x
二、物理方程
若弹性体只有单向拉伸或压缩时,根据材料 力学胡克定律:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
u
z
z
z 0
0
0
z
u v
0
w
y
x
3、物理方程(应力与应变之间的关系)
x
1 E
x y z
y
1 E
y z x
•微观上这个假设不成立——宏观假设。
2. 均匀性假设
•——假设弹性物体是由同一类型的均匀材料组成的。 因此物体各个部分的物理性质都是相同的,不随坐标 位置的变化而改变。
•——物体的弹性性质处处都是相同的。
•工程材料,例如混凝土颗粒远远小于物体的几何形 状,并且在物体内部均匀分布,从宏观意义上讲,也 可以视为均匀材料。
——在弹性体的平衡等问题讨论时,可以不考虑因 变形所引起的尺寸变化。
——忽略位移、应变和应力等分量的高阶微量,使 基本方程成为线性的偏微分方程组。
6. 无初始应力假设
——假设物体处于自然状态,即在外界因素作用之前, 物体内部没有应力。
弹性力学求解的应力、位移仅仅是外力、边界约 束或温度改变而产生的。
向或负面上的应力沿坐
x
图1-7
标负向为正。
口诀:正面正向或负面负向的应力为正。
例:应力和面力的符号规定有什么区别?试分别画 出正面和负面上的正应力和正的面力的方向。
Oz
x
y
注意:
弹性力学
材料力学 图1-8
(3)注意弹性力学切应 力符号和材料力学是有 区别的。在图1-8中, 弹性力学里,切应力都 为正,而材料力学中相 邻两面的符号是不同的, 顺时针转动为正。
2.性质:在物体内的同一点,不同截面上的应力是不 同的。
3.应力集度:
r
ΔA面积上的内力的平均集度为: F
r
A
P点的应力为:pr lim F
A0 A
z
B
r
r F
m △A
p
P n
P点的应力分量为 、
--正应力 ---切应力
o
A
y 因次是[力][长度]-2。
图1-4
0
1
1
1
0
D E(1 ) 1 1
x
4.应力分量
应力不仅和点的位置有关,和截面的方位也有关,
不是一般的矢量,而是二阶张量。
zA o
x
C
(1)为了分析一点的应力
状态,在这一点从物体内取出一
个微小的正平行六面体,各面上
B 的应力沿坐标轴的分量称为应力 分量。
P
y 图1-5
在略去体力和高阶微量的情况下, 相互平行的面上的应力大小相等, 方向相反。
0
0
y
uv
A
x
0
0
y
y
x
y x
微分算子矩阵
AT d ----几何方程
• §2-3 弹性力学的基本方程 主要是描述应力、应变、位移及外力间的相互关系
•对于环氧树脂基玻璃纤维复合材料,不能处理为均 匀材料。
3. 各向同性假设
•——假定物体在各个不同的方向上具有相同的物 理性质,这就是说物体的弹性常数将不随坐标方向 的改变而变化。
•当然,像木材、竹子以及纤维增强材料等,属于 各向异性材料。
•——这些材料的研究属于复合材料力学研究的对 象。
4. 完全弹性假设
• 应力
σ (σx σ y τxy )T 。
• 结点位移列阵 δ (ui vi u j v j )T 。
• 结点力列阵 F (Fix Fiy Fjx Fjy )T 。
FEM中应用的方程:
几何方程 ε (u v v u )T。
(a)
x y x y
物理方程
σ Dε,
基本量和基本方程的矩阵表示
采用矩阵表示,可使公式统一、简洁,且 便于编制程序。
本章无特别指明,均表示为平面应力问 题的公式。
基本物理量:
• 体力 • 面力 • 位移函数
f ( fx f y )T 。 f ( fx f y )T 。 d (u(x, y),v(x, y))T。
• 应变
ε (εx εy γxy )T 。
(b)
其中D为弹性矩阵,对于平面应力问题
是
1 μ 0
D
E 1 μ
2
μ
0
1 0
0 。
1 μ 2
(c)
几何方程---位移与应变之间的关系
x
u x
y
v y
xy
u y
v x
x y
xy
x
y
xzy
yz
zx
x
v
y
w z
u
y
v
v
0
0 y 0
y
0
x
w
A
xy
y
x B
n
px
n
py p
N
O
2
P
1
y
N
B
x
将x、y轴分别放在两个主 A 应力的方向
N
N
§2-2 弹性力学的基本假设
•工程问题的复杂性是诸多方面因素组成的。如果不 分主次考虑所有因素,则问题的复杂,数学推导的困 难,将使得问题无法求解。
•根据问题性质,忽略部分暂时不必考虑的因素,提 出一些基本假设。使问题的研究限定在一个可行的范 围。
1、平衡方程 (应力间的关系)
x
x
yx
y
zx
z
fx
0
xy
x
y
y
zy
z
fy
0
xz
x
yz
y
z
z
fz
0
2、几何方程(应变与位移的关系)
u
x
0
x
(2)性质:一般情况下,体力随点的位置不同 而不同,体力是连续分布的。
(3)体力集度:
r
体力的平均集度为: F
V
P点所受体力的集度为:
r
x
f lim F
V 0 V
r
z
△V
r f
F
P
O
y
图1-2
f
的方向就是
r F
的极限方向。
(4)体力分量: 将f 沿三个坐标轴分解,
可得到三个正交的分力:
y
yx
y
yz
y
zx zy z
共六个应力分量。
x
(三)形变(应变)
形变就是形状的改变。物体的形变可以归结为长 度的改变和角度的改变。
C
1.线应变:图1-9中线段
PA、PB、PC每单位长度的伸
缩,即单位伸缩或相对伸缩,
称为线应变。分别用 x 、 y 、
PP
z
1 E
z x y
xy
1 G
xy
yz
1 G
yz
zx
1 G
zx
其中: E为杨氏弹性模量
为泊松比
G为剪切弹性模量 且:G E
2(1 )
因此物理方程可以简写为: D
1
1 1
•——对应一定的温度,如果应力和应变之间存在一 一对应关系,而且这个关系和时间无关,也和变形历 史无关,外力消失后能够恢复原形,称为完全弹性。
•完全弹性分为线性和非线性弹性,弹性力学研究限 于线性的应力与应变关系。
•研究对象的材料弹性常数不随应力或应变的变化而 改变。
5. 小变形假设
——假设在外力或者其他外界因素(如温度等)的 影响下,物体的变形与物体自身几何尺寸相比属于 高阶小量。
vvv f fxi fy j fzk x
z
f
z
r f
r F
△V
fy
fx P
O
y
图1-2
fx、fy、fz 称为物体在P点的体力分量,其 方向与坐标轴正向相同时为正,因次是[力][长 度]-3。(N/m3)方向沿坐标轴为正。
2. 面力 (1)定义:分布在物体表面上 z 的力。如流体压力和接触力。
第二章 有限元法的基本原理
机械与汽车工程学院 School of Mechanical and Automobile Engineering
§2-1 弹性力学中的几个基本概念 (一)外力
按照外力作用的不同分布方式,可分为体 积力和表面力,分别简称体力和面力。 1.体力
(1)定义:所谓体力是分布在物体体积内的 力,如重力和惯性力。
(2)性质:一般情况下,面
