弹性力学 空间问题的基本理论
弹性力学基本理论
15
1.1.3 应变的概念
(a) x方向的线应变
(b) y方向的线应变
(c) xy面内的剪应变
图 1-3 单元体应变的几何描述
在图1-3(a)中，单元体在x方向上有一个的伸长量。微分单元 体棱边的相对变化量就是x方向上的正应变。即
x
u x x
y
u y x
（1.9）
u y y
ux y
相应地，y轴方向的正应变为： x-y 平面内的剪应变：
tan 1
（1.10）
; tan 2
（1.11）
16
1.1.3 应变的概念
因此，剪应变 xy 为
xy
u x 1 2 x y u y
（1.12）
应变分量的矩阵型式
x xy ij yx y zx yy
2 2 Tn n n 2
m A
B T
G
P A
n
o
y
图1-1 物体内任意点处的应力
（1.6）
12
1.1.2 应力的概念 应力状态
在物体内的同一点处，不同方向截面上的应力是不同的。只有 同时给出过该点截面的外法向方向，才能确定物体内该点处此截面 上应力的大小和方向，才能表示这一点的应力状态。
x' ' y z'
=
0 1 0 cos 0 sin
0 x1 sin y1 cos z1
（b）
将第一式代入上式，可得
x ' 1 0 0 cos sin 0 x ' y y 0 cos sin = sin cos 0 z' z 0 sin cos 0 0 1
弹性力学简明教程
弹性简明课程是教育部第十个五年计划的国家计划教科书。
在第二版的基础上，它保留了原有的体系和特征，并根据教学改革的需要和相关的新国家标准进行了修订。
根据从浅到深的原理，本书安排了平面问题的理论和解决方案，空间问题的理论和解决方案以及薄板弯曲的理论。
着重介绍了弹性的数值解，如差分法，变分法和有限元法。
简明课程作为一本介绍性的弹性教科书，着重于基础理论（基础概念，基本方程式和基本解）的阐述和应用，以便学生在掌握基础知识的基础上阅读和应用弹性文献。
理论，并可以初步应用弹性数值解来解决实际工程问题。
主符号表第1章简介1-1弹性的内容1-2弹性的一些基本概念1-3弹性的基本假设第二章平面问题的基本理论2-1平面应力问题和平面应变问题2-2平衡微分方程2-3平面问题中点的应力状态2-4几何方程式刚体位移2-5物理方程式2-6边界条件2-7 Saint Venant原理及其应用2-8通过位移求解平面问题2-9通过应力相容方程求解平面问题2-10在恒力下简化的应力函数练习第三章平面问题的直角坐标解3-1逆解和半逆解多项式解。
3-2矩形梁纯弯曲的计算3-3位移分量3-4均布荷载下的简支梁3-5重力和液压作用下的楔形体第四章平面问题的极坐标解4-1极坐标中的平衡微分方程4-2极坐标中的几何方程和物理方程4-3极坐标中的应力函数和相容性方程4-4应力分量的坐标转换公式4- 5轴对称应力和相应的位移4-6圆环或圆柱体上的压力均匀分布4-7压力通道孔口处的应力集中4-8圆孔4-9边界上的集中力4-10边界上的分布力第5章用差分法和变分法求解平面问题5-1差分公式的推导5-2应力函数的微分分解5-3应力函数的微分分解的例子5-4弹性体的变形势能和外力势能5 -5位移变化方程5-6位移变化方法5-7位移变化方法示例..第6章使用有限元方法解决平面问题。
6-1基本数量和方程的矩阵表示。
6-2有限元方法的概念。
6-3单元的位移模式和解的收敛性。
弹性力学主要内容
1、弹性力学的研究对象、内容及范围弹性力学是研究在外界因素（外力、温度变化）的影响下，处于弹性阶段的物体所产生的应力、应变及位移。
弹性力学的研究对象为一般及复杂形状的构件、实体结构、板、壳等。
2、弹性力学的基本假设（即满足什么样条件的物体是我们在弹性力学中要研究的）（1）均匀性假设即物体是由同一种材料所组成的，在物体内任何部分的材料性质都是相同的。
（用处：物体的弹性参数，如弹性模量E，不会随位置坐标的变化而变化）（2）连续性假设即物体的内部被连续的介质所充满，没有任何孔隙存在。
（用处：弹性体的所用物理量均可用连续的函数去表示）（3）完全弹性假设即当我们撤掉作用于物体的外力后，物体可以恢复到原状，没有任何的残余变形；应力（激励）与应变（响应）之间呈正比关系。
（用处：可以使用线性虎克定律来表示应力与应变的关系）（4）各向同性假设即物体内任意一点处，在各个方向都表现出相同的材料性质。
（用处：物体的弹性参数可以取为常数）（5）小变形假设即在外力的作用下，物体所产生的位移和形变都是微小的。
（用处：可以在某些方程的推导中略去位移和形变的高阶微量）3、弹性力学的基本量表1 直角坐标表示的各种基本量情况4、两类平面问题的概念（1）平面应力问题（应力是平面的；变形是空间的）如图所示薄板，其z 方向的尺寸比其他两个方向上的尺寸小得多；外力和体力都平行于板面，并且沿着板的厚度没有变化，这样的问题称为平面应力问题。
（2）平面应变问题若物体在z 方向的尺寸比在其他两个方向上的尺寸大得多，如图所示很长的坝体，外力及体力沿着z 方向没有变化，则这类问题称为平面应变问题。
（3）两类平面问题的一些特征空间问题的基本未知量共有8个，每个基本未知量仅仅是坐标(),x y 的函数。
表2 两类平面问题的一些特征5、平面问题的基本方程平面问题的基本方程包括：（1）平衡方程；（2）几何方程；（3）物理方程 平面问题的基本量有8个，分别是：3个应力分量：x σ、y σ、xy τ； 3个形变分量：x ε、y ε、xy γ； 2个位移分量：u 、v（1）平衡方程平衡方程描述的是体力分量与应力分量之间的关系0yxx x f x y τσ∂∂++=∂∂； 0xy y y f x yτσ∂∂++=∂∂ 上述平衡方程对于平面应力问题和平面应变问题均适用 （2）几何方程几何方程描述的是形变分量与位移分量之间的关系x uxε∂=∂；y v y ε∂=∂；xy v u x y γ∂∂=+∂∂（3）物理方程物理方程描述的是形变分量与位移分量之间的关系平面应力问题的物理方程为： 平面应变问题的物理方程为：()1x x y E εσμσ=- 211x x y E μμεσσμ⎛⎫-=- ⎪-⎝⎭ ()1y y x E εσμσ=- 211y y x E μμεσσμ⎛⎫-=- ⎪-⎝⎭xy xy γτ= xy xy γτ=6、平面问题的边界条件弹性力学问题的边界条件，简单的说就是用来描述弹性体边界上所受的外部作用。
弹性力学-第7章 空间问题
zx
z
dz
zy
zy
z
dz
z 0
y
y
yx yz
xy
x
yz
yz
y
dy
fz
fy fx
xz
yx
y yx dy
y
y y
dy
zx zy
x
x
x x
dx
z
根椐平衡条件： Fx 0
xz
xzx
x
dx
x
x
x
dx dydz
xdydz
(
yx
yx
x
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdy
zxdxdy
Xdxdydz
0
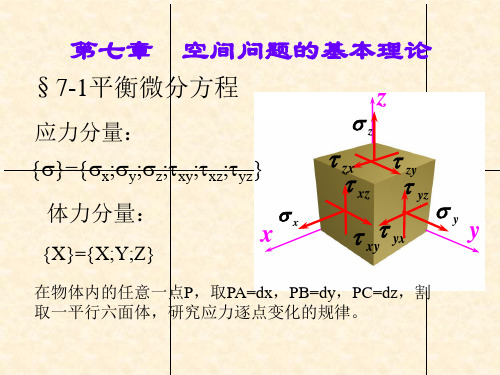
§7-1平衡微分方程
x x
yx y
zx
z
fx
0
xy
y
x
y
zy
z
f y
0
xz yz
x
y
z z fz 0
（7-1）
平面应力问题：
1、平面应力问题z方向应力为零：
0
xz
yz
0
z
2、所有的应力、应变和位移分量均与z无关，仅是x,y的函数。 以上方程可以直接转化为平面应力的平衡方程。
在计算任一平面上的应力时，方向余弦l,m,n可变化，但 均为有限值，故必存在某个平面，其上正应力取得极值。
主平面：正应力取得极值的平面。 主应力：主平面上的正应力。 主方向：主应力的方向，也称应力主向。 在主平面上，正应力取极值、剪应力为零。
二、主应力的确定：
设主平面存在，其外法线为n，
第七章 弹性力学空间问题解答
§7-1 空间问题的基本方程 1. 平衡微分方程方程
2. 几何方程
3. 物理方程
各种弹性常数之间的关系
4. 相容方程
5. 边界条件：
位移边界条件：对于给定的表面Su，其上沿 x，y，z方向给定位移为 ，则
应力边界条件：给定表面上的面力为
• 求解空间问题同样有位移法、应力法和应力函 数法三种方法。
§7-2柱坐标和球坐标系下的基本方程
• 一. 柱坐标系下的基本方程
直角坐标系下，空间一点M的位置由（x,y,z）表示，在柱坐 标系下，空间一点M的位置由（r, q, z）表示。两坐标间的关 系为：
在柱坐标系下的应力分量为
应变分量为 位移分量为
柱坐标表示的基本方程 • 1. 平衡方程
（7-1）
• 2. 几何方程
（7-6）
(2)几何方程：将式（7-5）代入式（7-2），得
（7-7）
(3)物理方程：将式（7-5）代入式（7-4），得
（7-8）
(4)空间轴对称问题位移求解的基本方程
空间轴对称问题共有四个应力分量，两个位移分量。 以位移求解更方便。 将几何方程（7-7）代入物理方程（7-8），得
（7-9）
• 将式（7-9）代入平衡方程（7-6），化简后得
1. 位移法：将几何方程代入物理方程，得到用位移
表示的应力分量，再将应力分量代入平衡方程和应力边 界条件，即得到空间问题的位移法控制方程。
2. 应力法：以应力作为基本未知量。将相容方程用应 力表示——应力控制方程
3. 应力函数法：先引入应力函数，满足微分平衡方
程。 由微分平衡方程得应力函数与应力分量的关系，再将 用应力函数表示的应力分量代入相容方程，得到一组 用应力函数表示的相容方程，即应力函数表示的控制 方程。
第一章 弹性力学的基本理论
学习弹性力学的目的
理解和掌握弹性力学的基本理论、基本概念、基本 方程、基本解法。 能够阅读弹性力学相关文献，并应用已有解法为工 程服务。 能够将所学的弹性力学知识应用于近似解法－变分 法、差分法和有限单元法的理解。 为进一步学习固体力学的其它分支学科打下基础。
v v y dy dy v dy v y dy y
y
同样，可以列出另两个力矩平衡方程。得出
yz zy , zx xz , xy yx
机自学院安全断裂分析研究室
应力张量
是对称的二阶张量
x xy xz yx y yz zx zy z
过一点任意截面上的应力分量，完全由该点的应 力张量唯一地确定。即一点的应力状态是用该点的应 力张量表示的。
机自学院安全断裂分析研究室
弹性力学的发展史 自学
机自学院安全断裂分析研究室
弹性力学中的几个基本概念
外力 体积力：分布在物体体积内的力，如重力和惯性力 表面力：作用在物体表面的力，可以是分布力，也 可以是集中力
z
Q Z V X P
X
z
Q Z F Y P S
F Y
o
Q F V 0 V lim
x
y
o
Q F S 0 S lim
x
y
机自学院安全断裂分析研究室
内力、应力及应力张量
物体在外力的作用下，伴随变形而同时在物体内
产生抵抗变形的力，称为内力。
Ⅱ
F2
F1 — Ⅱ部分物体对Ⅰ部分物体的作用力
F1
F2 — Ⅰ部分物体对Ⅱ部分物体的作用力 F1 和F2 大小相等，方向相反。
2--弹性力学基本理论
yz
zx
• 应变的定义
• 设平行六面体单元，3个轴棱边 ：
– 变形前为MA，MB，MC； – 变形后变为M'A'，M'B'，M'C'
。
x、 y、 z
•正应变（小变形）
•符号规定： 正应变以伸长为正。
•剪应变
•符号规定： 正应变以伸长为正；剪应变以角度变小为正。
材料力学 — 区别与联系 — 弹性力学
y
y
q
q
sx
ͼ 1-1a
x
0
sx x
ͼ 1-1b
材料力学 — 区别与联系 — 弹性力学
ͼ 1-3a ͼ 1-3b
2.1 弹性力学的基本假定
• 连续性假设：物体所占的空间被介 质充满，不考虑材料缺陷，在物体 内的物理量是连续的, 可以采用连续 函数来描述对象。
虽然都从静力学、几何学与物理学三方面进行研究， 但是在建立这三方面条件时，采用了不同的分析方法。 材料力学是对构件的整个截面来建立这些条件的，因而 要常常引用一些截面的变形状况或应力情况的假设。这 样虽然大大简化了数学推演，但是得出的结果往往是近 似的，而不是精确的。而弹性力学是对构件的无限小单 元体来建立这些条件的，因而无须引用那些假设，分析 的方法比较严密，得出的结论也比较精确。所以，我们 可以用弹性力学的解答来估计材料力学解答的精确程度， 并确定它们的适用范围。
当△S 趋近于0，则为P点的面力
•面力分量 •符号规定：与坐标轴方向一致为正，反之为负。 •面力的量纲：[力]/[长度]^2 •列阵表示：Fs={X Y Z}T
集中力
体力与面力都是分布力，集中力则只是作用在一个点
弹性力学-05空间问题的基本理论 第五章(1)
B
dz A
d
O x
P
z
y
r
dr
y
z
O
dz
r rz
r
C Z
zr
P
rz rz dr z dr r
r
Kr
r r dr r
A
d
rd
r
dr
Kr
(r+dr)d
x
r r dr r
F
r
0, （略去四阶以上小量）
r r dzdrd drdzrd r zr dzrdrd dzdrd z K r rddrdz 0
物理方程：
x c11 x c12 y c13 z c14 yz c15 zx c16 xy y c21 x c22 y c23 z c24 yz c25 zx c26 xy z c31 x c32 y c33 z c34 yz c35 zx c36 xy yz c41 x c42 y c43 z c44 yz c45 zx c46 xy zx c51 x c52 y c53 z c54 yz c55 zx c56 xy xy c61 x c62 y c63 z c64 yz c65 zx c66 xy
体积应变 e 、体积应力 Θ 不随体积而变。
用应变表示的物理方程：
E r e r e 2G r 1 1 2 E e e 2G 1 1 2 E z e z e 2G z 1 1 2
式中：E 为材料的弹性模量； 为泊松比。
弹性力学的基本理论及其在实际中的应用
弹性力学的基本理论及其在实际中的应用弹性力学是固体力学学科的分支。
其基本任务是研究弹性体由于外力载荷或者温度改变，物体内部所产生的位移、变形和应力分布等，为解决工程结构的强度，刚度和稳定性问题作准备，但是并不直接作强度和刚度分析。
一．弹性力学的基本规律规律假设弹性力学的研究对象是完全弹性体。
弹性力学所依据的基本规律有三个：变形连续规律、应力-应变关系和运动(或平衡)规律，它们有时被称为弹性力学三大基本规律。
井下工程是复杂多变的，随着工程的进展，巷道的应力情况也在不断的变化，我们研究的不是一个静止的物体，我们要研究的是一个动态的、不断变化的围岩条件。
要研究岩体的弹性问题,必须要给它一个前提,也就是对它的假设,基本假设是弹性力学讨论问题的基础。
没有基本假设任何问题也进行不了.下面简要介绍弹性力学的几个基本假设：1.连续性假设：假设所研究的整个弹性体内部完全由组成物体的介质所充满，各个质点之间不存在任何空袭。
2.均匀性假设：假设弹性物体是由同一类型的均匀材料组成的。
因此物体各个部分的物理性质都是相同的，不随坐标位置的变化而改变。
因此，物体的弹性性质处处是相同的。
3.各向同性假设：假定物体在各个不同的方向上具有相同的物理性质，这就是说物体的弹性常熟将不随坐标方向的改变而变化。
4.完全弹性假设：对应一定的温度，如果应力和应变之间存在一一对应关系，而且这个关系和时间无关，也和变形历史无关，称为完全弹性材料。
5.小变形假设：假设在外力或者其他外界因素（如温度等）的影响下，物体的变形与物体自身几何尺寸相比属于高阶小量。
6.无初始应力的假设：假设物体处于自然状态，即在外界因素（如外力或温度变化等）作用之前，物体内部没有应力。
根据这一假设，弹性力学求解的应力仅仅是外力或温度改变而产生的。
二．下面介绍一下弹性力学基本的解决问题的方法：弹性力学的研究方法主要有数学方法和实验方法，以及二者结合的方法。
数学方法基本上是根据弹性力学的基本方程，对岩体在某种假设的前提下进行弹性分析，从而得出岩体的各种力学参数。
弹性力学 空间问题的基本理论
应力中只有 σ,σ,σz,z, z 0 ;
形变中只有 ,,z,z,
z
0
;
(a)
位移中只有 u ,uz ,
u 0。
弹性力学
精选ppt课件
36
五 轴对称问题的基本方程
平衡微分方程：
F 0, FZ 0,
σ z z
σσ
f
0,
σz z
z
z
fz
0.
(b)
而由 F 0, 得出为σ σ 。
空间问题的应力，形变，位移等15个未 知函数，它们都是(x ,y ,z)的函数。这些函数 在区域V内必须满足3个平衡微分方程，6个 几何方程及6个物理方程，并在边界上满足3 个应力或位移的边界条件。
弹性力学
精选ppt课件
33
第七章 空间问题的基本理论
内容提要
徐芝纶院士(1911-1999)
一、平衡微分方程 二、物体内任一点的应力状态 三、主应力 最大与最小的应力 四、几何方程及物理方程 五、轴对称问题的基本方程 例题
精选ppt课件
39
五 轴对称问题的基本方程 应力用应变表示：
σ 1E(12)，（,,z),
z 2(1E)z.
(e)
其中 zu uuzz。
弹性力学
精选ppt课件
40
五 轴对称问题的基本方程
平衡微分方程弹性力学空间问题的基本理论弹性力学空间问题的基本理论轴向投影力的平衡微分方程可得因为x弹性力学空间问题的基本理论由3个力矩方程得到3个切应力互等定理空间问题的平衡微分方程精确到三阶微量yxxyxzzxzyyz弹性力学一平衡微分方程二物体内任一点的应力状态三主应力最大与最小的应力四几何方程及物理方程五轴对称问题的基本方程例题内容提要弹性力学简明教程第三版徐芝纶院士19111999弹性力学空间问题的基本理论在空间问题中同样需要解决
3001《固体力学》专业综合
（3001）《固体力学》专业综合考试内容:一、结构力学1. 静定与静不定杆系结构内力求解-力法；2. 杆系结构的位移解法（直接刚度法）；3.薄壁工程梁理论；4. 结构力学中的能量原理及其应用。
包括应变能及余应变能、虚功原理、最小位能原理、最小余能原理、卡氏定理、单位载荷定理、叠加原理与位移互等定理。
二、弹性力学1. 平面问题的基本理论。
包括平面问题的平衡微分方程、几何方程、物理方程、及应力函数、逆解法与半逆解法等；2. 平面问题的直角坐标解答。
包括多项式解答、矩形梁的纯弯曲、简支梁受均布荷载等；3. 平面问题的极坐标解答。
包括极坐标中的平衡微分方程、几何方程、物理方程、轴对称应力和相应的位移等；4. 空间问题的基本理论。
包括空间问题的平衡微分方程、主应力与应力主向、几何方程、物理方程、轴对称问题及球对称问题的基本方程等；5. 弹性力学中的变分解法。
弹性体的位移变分方程及最小势能原理，基于最小势能原理的近似解法，应力变分方程及最小余能原理，基于最小余能原理的近似解法。
三、有限元方法及应用1．有限元法中的变分原理。
包括最小位能原理、最小余能原理、广义变分原理、修正变分原理等。
2. 有限元方法的一般性原理和表达格式； 3. 单元和插值函数的构造；4. 等参元和数值积分。
四、结构振动理论1．单自由度系统自由振动。
包括能量法，无阻尼自由振动，有阻尼衰减振动。
2.单自由度系统强迫振动。
包括简谐激励下的响应，强迫振动的复指数解法，频响函数与频域分析。
3.多自由度系统的振动。
包括拉格朗日方程，实模态分析，复模态分析，假设模态法。
参考书目：1. 结构力学基础，黄其青，王生楠编，西安：西北工业大学出版社2. 飞行器结构力学，王生楠主编，西安：西北工业大学出版社3. 弹性力学，吴家龙编著，北京：高等教育出版社4. 有限元法中的变分原理，王生楠编，西安：西北工业大学出版社5. 有限单元法王勖成编著，北京：清华大学出版社，20036. 振动理论及应用方同，薛璞著，西安：西北工业大学出版社。
四、 弹性力学有限元法基本原理(三)
该单元位移模式及其形函数的构造可采用根据形函数性质直接
构造插值函数的方法。或从对应的二维单元进行推广，再用形
函数性质进行验证。 • 为了突破这类单元几何上的限制，得到实用的单元，必须引
入等参变换。
第二节 等参单元
• 问题的提出
从前面介绍的各种二、三维单元看出，这些单元可能有两个方面 的约束： 第一是单元的精度，显然单元的节点数越多，单元精度越高。因 此在这一点上，矩形单元优于简单三角形单元，六面体单元优于四面 体单元； 第二是单元几何上的限制。单独使用矩形或长方体单元都不能 模拟任意形状几何体，且网格中单元大小无法过渡。所有上述单元
n
n
n
n
•
显然，只要形函数满足性质 满足。
N
i 1
n
i
1 ，等参单元的完备性就得到
六、等参单元力学特性分析
• 等参单元特性分析的所有公式的导出原理与前面介绍的其它单元相同。
•
等参单元的形函数矩阵、应变矩阵、应力矩阵均用自然坐标描述。应变 矩阵中涉及到形函数对总体x,y,z坐标求导数时，须进行坐标变换。
•
该单元在母单元中的位移模式为包含完全二次式的不完全三次多项式。
插值基函数可以用形函数性质直接构造。对应图中局部节点编号，8个节 点形函数为：
1 (1 i )(1 i )( i i 1)(i 1,2,3,4) 4 1 N i (1 2 )(1 i )( i 5,6) 2 1 N i (1 2 )(1 i )(i 7,8) 2 Ni
一、等参单元的概念
• 图4-3为一个4节点任意四边形单元（Q4），单元有8个自由度。将矩 形单元放松为4节点任意四边形单元将带来许多好处。 • 但在建立单元位移模式时产生了新的问题：
弹性力学第七章 主应力
（7-3）
p2
2 n
2 n
px2
p
2 y
pz2
2 n
px2
p
2 y
pz2
2 n
（7-4）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－2 物体内一点的应力状态
如果ABC是边界面，px, py , pz 成为面力分量
fx, fy, fz
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－5 轴对称问题的基本方程
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－5 轴对称问题的基本方程
轴对称问题： 在空间问题中，如果弹性体的几何形状、约束情况，以及所受的外
力作用，都是对称于某一轴（通过这个轴的任一平面都是对称面），则 所有的应力、变形和位移也就对称于这一轴。轴对称问题的弹性体的形 状一般为是圆柱或半空间。
( x
1)
m1 l1
yx
n1 l1
zx
0
xy
m1 l1
( y
1)
n1 l1
zy
0
可以求得 m1 , n1 的比值，再利用 l 2 m2 n2 1 求出：
l1 l1
l1
1
2
2
1
m1 l1
n1 l1
同样也可以求出其他主应力的方向余弦。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
E
（7－13）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－4 几何方程及物理方程
弹性力学的基本理论及其在实际中的应用
弹性力学的基本理论及其在实际中的应用弹性力学是固体力学学科的分支。
其基本任务是研究弹性体由于外力载荷或者温度改变，物体内部所产生的位移、变形和应力分布等，为解决工程结构的强度，刚度和稳定性问题作准备，但是并不直接作强度和刚度分析。
一．弹性力学的基本规律规律假设弹性力学的研究对象是完全弹性体。
弹性力学所依据的基本规律有三个：变形连续规律、应力-应变关系和运动(或平衡)规律，它们有时被称为弹性力学三大基本规律。
井下工程是复杂多变的，随着工程的进展，巷道的应力情况也在不断的变化，我们研究的不是一个静止的物体，我们要研究的是一个动态的、不断变化的围岩条件。
要研究岩体的弹性问题,必须要给它一个前提,也就是对它的假设,基本假设是弹性力学讨论问题的基础。
没有基本假设任何问题也进行不了.下面简要介绍弹性力学的几个基本假设：1.连续性假设：假设所研究的整个弹性体内部完全由组成物体的介质所充满，各个质点之间不存在任何空袭。
2.均匀性假设：假设弹性物体是由同一类型的均匀材料组成的。
因此物体各个部分的物理性质都是相同的，不随坐标位置的变化而改变。
因此，物体的弹性性质处处是相同的。
3.各向同性假设：假定物体在各个不同的方向上具有相同的物理性质，这就是说物体的弹性常熟将不随坐标方向的改变而变化。
4.完全弹性假设：对应一定的温度，如果应力和应变之间存在一一对应关系，而且这个关系和时间无关，也和变形历史无关，称为完全弹性材料。
5.小变形假设：假设在外力或者其他外界因素（如温度等）的影响下，物体的变形与物体自身几何尺寸相比属于高阶小量。
6.无初始应力的假设：假设物体处于自然状态，即在外界因素（如外力或温度变化等）作用之前，物体内部没有应力。
根据这一假设，弹性力学求解的应力仅仅是外力或温度改变而产生的。
二．下面介绍一下弹性力学基本的解决问题的方法：弹性力学的研究方法主要有数学方法和实验方法，以及二者结合的方法。
数学方法基本上是根据弹性力学的基本方程，对岩体在某种假设的前提下进行弹性分析，从而得出岩体的各种力学参数。
弹性力学：09 空间问题的解答
4. 位移势函数的引用 (对应于无旋位移场)
为简单起见，不计体力
(
G)
x
G2u
Fx
0
(
G)
y
G2v
Fy
0
1 2u 0 1 2 x
1 2v 0 1 2 y
(
G)
z
G2w
Fz
0
1 2w 0 1 2 z
现假设位移是有势的，即：位移在某一方向
的分量可以用位移势函数ψ（x,y,z)在该方向的
问题描述： 设有半空间体，其比重为p，在水平边界面上
受均布压力q的作用，试用位移法求位移分量和应力分量。
并假设在z = h 处w =0。
q
1. 由于任意铅直平面都是对称面，假设
u 0,v 0, w w(z) (1)
x
R
y
z
e u v w d w e 0, e 0, e d2 w (2) z x y z d z x y z d z2
通过与平面问题 及极坐标中同样的分 析，可见，由径向位 移引起的形变分量为：
由于对称，各点
环向位移为零，由径
向位移产生的应变为
u
,
u
,
z
u z
1. 轴对称问题和球对称问题的基本方程
由轴向位移w产生的 应变为
z
w z
,
z
w
迭加得到几何方程
u
,
u
z
w, z
z
u z
w
1. 轴对称问题和球对称问题的基本方程
在球对称问题中，应力、应变、位移等分 量都只是径向坐标ρ的函数。
球对称问题
1. 轴对称问题和球对称问题的基本方程
《弹性力学与有限元》第1章弹性力学的基础知识
（五）小应变位移假设 物体在外加因素作用下，物体变形产生的位移与物体尺寸相比极其微小，因 而应变分量和转角均远小于 1。这样，在建立物体变形后的平衡方程时，可以不 考虑由于变形引起的物体尺寸和位置的变化；在建立几何方程和物理方程时，可 以略去应变、转角的二次幂或二次乘积以上的项，使得到的基本方程是线性偏微 分方程组。这个假设又称为几何线性的假设。
物体的弹性性质是客观存在的，人类很早就可以利用物体的弹性性质了，比 如在树枝上荡漾，古代的弓箭等等。
了解掌握弹性物体的客观规律，并形成弹性力学这样一门学科，则经过了三 个发展时期：
弹性力学的发展初期。17 世纪开始，主要是通过实践，尤其是通过实验来 探索弹性力学的基本规律。英国的胡克和法国的马略特于 1680 年分别独立地提 出了弹性体的变形和所受外力成正比的定律，后被称为胡克定律。牛顿于 1687 年确立了力学三定律，奠定了力学的发展基础。
《弹性力学与有限元》
第 1 章 弹性力学的基础知识
第 1 章 弹性力学的基础知识
弹性力学(Elastic Mechanics)是固体力学的重要分支，它研究弹性物体在外力 和其它外界因素作用下产生的变形和内力，也称为弹性理论。它是材料力学、结 构力学、塑性力学和某些交叉学科的基础，广泛应用于建筑、机械、化工、航天 等工程领域。
材料力学的研究对象主要是杆状构件（一维弹性杆件），而且常采用一些关 于变形的近似假设，如“平面截面”的假设等等，使得计算简化。
而弹性力学的分析方法在一开始并不考虑平面截面的假设，而是从变形连续 性的观念出发列出几何方程，所谓变形连续性是指在变形前的连续物体在变形后 仍保持连续，物体的任一部分及单元体均保持连续。在保持变形连续的情况下， 平面界面变形以后可能不再保持平面，
弹性力学复习思考题
第二章平面问题的基本理(1) 两类平面问题的特点？(几何、受力、应力、应变等)。
(2) 试列出两类平面问题的基本方程，并比较它们的异同。
(3) 在建立平面问题基本方程(平衡方程、几何方程)时，作了哪些近似简化处理？其作用是什么？(4) 位移分量与应变分量的关系如何？是否有位移就有应变？(5) 已知位移分量可唯一确定其形变分量，反过来是否也能唯一确定？需要什么条件？(6) 已知一点的应力分量，如何求任意斜截面的应力、主应力、主方向？(7) 什么是线应变(正应变)、剪应变(切应变、角应变)？如何由一点应变分量求任意方向的线应变、主应变、主应变方向？(8) 平面应力与平面应变问题的物理方程有何关系？(9) 边界条件有哪两类？如何列写？第四章平面问题的极坐标解(1 )极坐标解答适用的问题结构的几何形状(?圆环、圆筒、圆弧形曲杆、楔形体、半无限平面体等)(2) 极坐标下弹性力学平面问题的基本方程？平衡微分方程、几何方程、物理方程、边界条件方程)(3) 极坐标下弹性力学平面问题的相容方程？用应变表示的、用应力函数表示的相容方程等)(4) 极坐标下应力分量与应力函数间关(5) 极坐标下弹性力学平面问题边界条件的列写？(6) 极坐标下轴对称问题应力函数、应力分量、位移分量的特点？(7) 圆弧形曲梁问题应力函数、应力分量、位移分量的确定？(如何利用材料力学中曲梁横截面应力推出应力函数的形式？)(8) 楔形体在力偶、集中力、边界分布力作用下，应力函数、应力分量、位移分量的确定？(10) 何为圣维南原理？其要点是什么？圣维南原理的作用是什么？如何利用圣维南原理列写边界条件？(11) 弹性力学问题为超静定问题，试说明之。
(12) 弹性力学问题按位移求解的基本方程有哪些？(13) 弹性力学平面问题的变形协调方程有哪些形式？各自的使用条件是什么？(14) 按应力求解弹性力学问题，为什么除了满足平衡方程、边界条件外，还必须满足变形协调方程(相容方程)？而按位移求解为什么不需要满足变形协调方程？(15 )应力分量满足平衡方程、相容方程、边界条件，是否就是问题的正确解？为什么？(16) 常体力情况下，如何将体力转化为面力？其意义如何？(17) 何为逆解法？何为半逆解法？(18) Airy应力函数在边界上值的物理意义是什么？应力函数的导数：_________ 在边界上值的物理意义是什么？x ' y (9 )半无限平面体在边界上作用力偶、集中力、分布力下，应力函数、应力分量、位移分量的确定？(10) 圆孔附近应力集中问题应力函数、应力分量、位移分量的确(11) 定加法的应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以 x , y , z 坐标具有对等性，其方程也必然具有对等性。
弹性力学 空间问题的基本理论 5
一 平衡微分方程
由3个力矩方程得到3个切应力互等定理， y z zy
zx x z xy yx
空间问题的平衡微分方程精确到三阶 微量 (d xd yd z )。
四、几何方程及物理方程
徐芝纶院士(1911-1999)
五、轴对称问题的基本方程 例题
弹性力学简明教程(第三版)
四 几何方程及物理方程
空间问题的几何方程，可以从平面问 题推广得出：
u x x
xy
v u x y
v y y
zx
u w z x
空间问题的基本理论
弹性力学 空间问题的基本理论 10
二 物体内任一点的应力状态 2. 求 p (σ n , n ) 将 p ( px , p y , pz ) 向法向 n投影，即得
σ n lp x mpy np z
l 2σ x m2σ y n2σ z 2mn yz 2nl zx 2lm xy . (b)
w z z
(a)
yz
w v y z
26
弹性力学
四 几何方程及物理方程 从几何方程同样可得出形变与位移 之间的关系： ⑴ 若位移确定，则形变完全确定。
从数学上看，由位移函数求导数是 完全确定的，故形变完全确定。
弹性力学
空间问题的基本理论
27
四 几何方程及物理方程 ⑵ 若形变确定，则位移不完全确定。
弹性力学
空间问题的基本理论
21
三 主应力 最大与最小的应力
式(g)中的各式，左边是不随坐标选择
而变的；而右边各项虽与坐标的选择有关，
但其和也应与坐标选择无关。 所以分别称 Θ1,Θ2 ,Θ3 为第一、二、
三应力不变量。这些不变量常用于塑性力 学之中。
弹性力学 空间问题的基本理论 22
三 主应力 最大与最小的应力
一 平衡微分方程
在空间问题中，应力、形变和位移等基
本知函数共有15个，且均为x,y,z的函数。
空间问题的基本方程，边界条件，以
及按位移求解和按应力求解的方法，都是
与平面问题相似的。因此，许多问题可以
从平面问题推广得到。
弹性力学
空间问题的基本理论
3
一 平衡微分方程
取出微小的平行六面体， d v d x d y d z，
弹性力学
空间问题的基本理论
8
二 物体内任一点的应力状态 斜面的全应力p 可表示为两种分量形式： p沿坐标向分量：
p ( px , p y , pz ).
p沿法向和切向分量：
p (σ n , n ).
弹性力学 空间问题的基本理论 9
二 物体内任一点的应力状态
1. 求 p ( px , p y , p z )
由形变求位移，要通过积分，会出现待定的 函数。若 x yz 0 ( x, y , z )，还存在对应的位 移分量，为：
u u0 y z z y,
( x, y, z; u, v, w). (b)
u0 , v0 , w0 --沿x , y , z 向的刚体平移；
x , y , z --绕x , y , z轴的刚体转动。
考虑方向余弦关系式，有
l m n 1.
2 2 2
(b)
结论：式(a) , (b)是求主应力及其方 向余弦的方程。
弹性力学 空间问题的基本理论 15
三 主应力 最大与最小的应力
2. 求主应力 σ
将式(a)改写为：
(σ x σ )l yx m zx n 0, xy l (σ y σ )m zy n 0, xz l yz m (σ z σ )n 0。
代入 p x , p y , p z , 得到：
弹性力学 空间问题的基本理论 14
三 主应力 最大与最小的应力
lσ x m yx n zx lσ , mσ y n zy l xy mσ , nσ z l xz m yz nσ .
(a)
d xd y d z
(1 x )(1 y )(1 z ) 1
x y z.
(d)
其中由于小变形假定，略去了形变的2、3次幂。
弹性力学 空间问题的基本理论 30
四 几何方程及物理方程
空间问题的物理方程
可表示为两种形式： ⑴ 应变用应力表示，用于按应力求解方法：
弹性力学 空间问题的基本理论 16
三 主应力 最大与最小的应力
上式是求解 l , m , n 的齐次代数方程。由于l , m , n不全为0，所以其系数行列式必须为零，得
σ x σ
xy xz
σ y σ
yx yz
σ z σ
zx zy 0,
展开，即得求主应力的方程,
σ (σ x σ y σ z )σ (σ yσ z σ zσ x σ xσ y )σ
1 x (σ x σ y σ z ), E
yz
弹性力学
2(1 ) yz , E
空间问题的基本理论
( x ,y ,z ).
(e)
31
四 几何方程及物理方程 ⑵ 应力用应变表示，用于按位移求解方法：
E x ( x ), 1 1 2
l1
1 m1 2 n1 2 1 ( ) ( ) l1 l1
.
(e)
再求出 m1 及 n1 。
4. 一点至少存在着三个互相垂直的主应力
σ1 ,σ 2 ,σ 3 （证明见书上）。
弹性力学 空间问题的基本理论 19
三 主应力 最大与最小的应力 5.应力不变量 若从式(c) 求出三个主应力 σ1 ,σ 2 ,σ 3 ， 则式(c)也可以用根式方程表示为，
取出如图的包含斜面 的微分四面体，斜面面积 为ds, 则x面，y面和z面的 面积分别为lds,mds,nds。 由四面体的力平衡条件可得
px l x m xy n zx p y m y n zy l xy pz n z l xz m yz
弹性力学
空间问题的基本理论
6
第七章
内容提要
空间问题的基本理论
一、平衡微分方程 二、物体内任一点的应力状态 三、主应力 最大与最小的应力
四、几何方程及物理方程
徐芝纶院士(1911-1999)
五、轴对称问题的基本方程 例题
弹性力学简明教程(第三版)
二 物体内任一点的应力状态
在空间问题中，同样需要解决：由直 角坐标的应力分量 σ x … yz …，来求出斜 面(法线为 n ）上的应力。
四、几何方程及物理方程
徐芝纶院士(1911-1999)
五、轴对称问题的基本方程 例题
弹性力学简明教程(第三版)
三 主应力 最大与最小的应力 1.假设 n 面(l , m , n)为主面，则此斜面上
n 0 , p σ n σ.
斜面上沿坐标向的应力分量为：
p x l , p y m , p z n .
考虑其平衡条件:
F 0, F 0, F 0; M 0,
x
y
z
x
M M
y
0,
z
0.
空间问题的基本理论 4
弹性力学
一 平衡微分方程
由x 轴向投影力的平衡微分方程可得
x yx zx fx 0 y z x y zy xy fy 0 z x y xz yz z fz 0 x y z
由 得
弹性力学
2 2 2 2 p 2 px p2 p σ y z n n,
2 2 2 2 2 n px py pz σn .
(c)
11
空间问题 在 sσ 上的应力边界条件 设在 sσ 边界上，给定了面力分量 f x , f y , f z , 则可将微分四面体移动到边界点上，并使斜 面与边界重合。斜面应力分量 ( p x , p y , pz ) 应 代之为面力分量 ( f x , f y , f z ) ，从而得出空间 问题的应力边界条件:
合肥工业大学本科生教学
《弹性力学》
第七章 空间问题的基本理论
主讲教师：袁海平 (副教授、博士后)
第七章
内容提要
空间问题的基本理论
一、平衡微分方程 二、物体内任一点的应力状态 三、主应力 最大与最小的应力
四、几何方程及物理方程
徐芝纶院士(1911-1999)
五、轴对称问题的基本方程 例题
弹性力学简明教程(第三版)
(l x m xy n zx ) s f x (m y n zy l xy ) s f y (n z l xz m yz ) s f z
弹性力学 空间问题的基本理论 12
第七章
内容提要
空间问题的基本理论
一、平衡微分方程 二、物体内任一点的应力状态 三、主应力 最大与最小的应力
σ1 σ 3 . (5) 最大和最小切应力为 2
设 σ1 σ 2 σ3
，作用于通过中间
主应力、并且“平分最大和最小正应
力的夹角”的平面上。
弹性力学 空间问题的基本理论 24
第七章
内容提要
空间问题的基本理论
一、平衡微分方程 二、物体内任一点的应力状态 三、主应力 最大与最小的应力
m1 n1 yx zx (σ x σ1 ) 0, l1 l1 m1 n1 (σ y σ1 ) zy xy 0. l1 l1