第七章 刚体的平面运动—new1
刚体的平面平行运动
1.刚体的平面平行运动
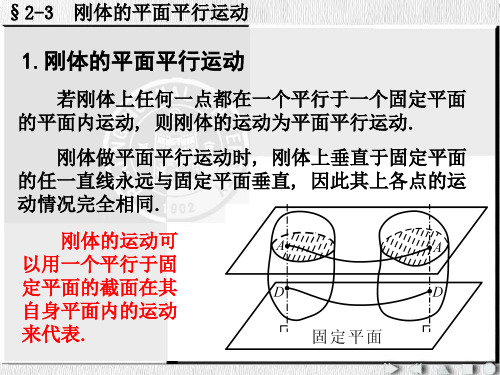
若刚体上任何一点都在一个平行于一个固定平面 的平面内运动, 则刚体的运动为平面平行运动.
刚体做平面平行运动时, 刚体上垂直于固定平面 的任一直线永远与固定平面垂直, 因此其上各点的运 动情况完全相同.
刚体的运动可 以用一个平行于固 定平面的截面在其 自身平面内的运动 来代表.
2l
u2
l
u2
aB
cos
j
l 2 cos2
cos
j
l cos3
j
30
aB
(8u 2
3
3l) j
aB sin a1
(u 2 sin
l 2 cos3 )k
§2-3 刚体的平面平行运动
A为瞬心,还可以利用瞬心法求 vP
vP AP
例题2
____
AP 2R sin
2
(1)用瞬心法求
vB
u
k
u
k
AC l cos
vB CB u tanj
vP
2R sin
2
§2-3 刚体的平面平行运动
§2-3 刚体的平面平行运动
2.刚体平面平行运动的基点描述法
(1)在刚体上任取一确定点 A(xA, yA) 为基点, 作过基点的定线和动线.
再用从定线到动线的角度 即可确
定刚体的位置.
s3
(2)刚体的平面平行运动可以 分解为随基点的平动和绕基点 的转动.
基点不同, 则平动不同, 但是 绕基点的转动是相同的.
7刚体的平面运动

7刚体的平面运动半径为R的车轮沿直线轨道作无滑动的滚动,如图所示。
已知轮心A在图示瞬时的速度为vA及加速度为aA。
求该瞬时车轮边缘上瞬心C的加速度aC.AvACaAAvACwAaA解:轮A作平面运动,C为其瞬心.AwAaAaAaAaCatCAanCA在图示的平面机构中,O1A=AB=2l,O2B=l,摇杆O1A以匀角速度w1绕轴O1转动。
图示瞬时,A、B两点的连线水平,两摇杆O1A、O2B方向平行,且q=600。
试求矩形板D的角加速度a1和摇杆O2B的角加速度a2。
O2O1ABqqw1D解:杆O1A、O2B作定轴转动,矩形板AB为瞬时平动。
vAvBw2。
O2O1ABqqw1aAatBAaABxy。
O2O1ABθθw1aAatBanBx方向投影:y方向投影得:A为基点,B点的加速度:图示的曲柄连杆机构中,已知连杆AB长1m,曲柄OA长0.2m,以匀角速度w=10rad/s绕轴O转动。
求在图示位置时滑块B的加速度和连杆AB的角加速度。
OAB45°w45°解:杆OA定轴转动,滑块B平动,杆AB作平面运动,速度瞬心I。
vAvBI?ABOAB45°w45°xyaABOAB45°45°waAaBanBAatBAA为基点,点B的加速度的矢量式:y方向投影:x方向投影:rROBlAvAC图示瞬时滑块A以匀速度vA=12cm/s沿水平直槽向左运动,并通过连杆AB带动轮B沿圆弧轨道作无滑动的滚动。
已知轮B的半径为r=2cm,圆弧轨道的半径为R=5cm,滑块A 离圆弧轨道中心O的距离为l=4cm。
求该瞬时连杆AB,以及轮B 的角加速度。
C?BO?BvBOBAvA解:滑块A作平动,杆AB瞬时平动、轮B作平面运动。
轮B的速度瞬心为C。
B点的轨迹圆周运动,角速度:y方向投影:x方向投影:A为基点,B点的加速度:轮B的角加速度:求导:CwBaBaCatBanBBatBCanBCxyCaABaBOOBAatBatBAanB半径为r的圆轮在一静止曲面上作只滚不滑的运动,图示瞬时,曲面的曲率半径为R,轮心O的速度为vO,切向加速度为ato,试求圆轮边缘上A、B、C三点的加速度。
平面运动刚体上各点的速度

vA
ωAB
C1
n v A OA OA 30 1.5 m/s
vB vC
ωBC
C2
点C1为杆AB的速度瞬心 vA AB 7.16rad/s AC1
vB BC1 AB 2.72 m/s vB 5.13rad/s 点C2为杆BC的速度瞬心 BC BC2
vB vBA vA
ω
A
B
取点A为动点,则点B的速度为
vB v A vBA
其中
vA
v BA AB
13
方向垂直AB。
7.2
平面运动刚体上各点的速度(基点法)
例:半径为R的车轮,沿直线轨道作无滑动的滚动。已知 轮轴以匀速v0前进。求轮缘上A、B、C、D各点的速度。
vA vO vAO vO vBO
取点A为基点,则点B速度
vB
vBA
vB v A vBA
v AB vA vB sin 45 sin(90 ) sin(45 )
l sin r sin 45
作速度图,得
vA vB sin( 45 ) 162 cm/s cos v AB 1 v A AB sin 45 0.714 rad/s l l cos
θ
vCB vB vC
再取点B为基点,则点C的速度
vC vB vCB
vBA vB
vA
ωABC
2 练习:7-3 vB rO 2 1 vCB BC ABC 2r O rO 2 2 2 vC vB vCB 2vB vCB cos 45
10 rO 2 vB sin 135 arcsin 18 26' vC 19
第七章 刚体的简单运动

第7 章刚体的简单运动❒刚体的平行移动❒刚体绕定轴的转动❒转动刚体内各点和速度和加速度❒速度和加速度的矢量表示❒结论与讨论平移的实例平移的实例A Bo 1o 2特征:如果在物体内任取一直线,在运动过程中这条直线始终与它的最初位置平行,这种运动称为平行移动,简称平动或移动。
直线平动:如果刚体上各点的运动轨迹为直线曲线平动:如果刚体上各点的运动轨迹为曲线ABA 1B 1B 2B 3B 4A 2A 3A 4Or Ar BABA B +=r r 常矢量-AB ★刚体平动时,其上各点的轨迹的形状完全一样。
A B v v =AB a a =★刚体平动时,其上各点的轨迹的形状相同;在每一瞬时,各点的速度相同,加速度也相同。
刚体的平动可归结为研究刚体内任一点的运动。
例题1已知:OA =l ;ϕ=ωt 求:T 型杆的速度和加速度ϕOABC解:T 型杆作平动,建立图示坐标系,取M 点为研究tl l x M ωϕsin sin ==tl dt dx v MM ωωcos ==tl dtdv a M M ωωsin 2-==xM已知:OA=O1B=l;O1A杆的角速度ω和角加速度α。
1求:C点的运动轨迹、速度和加速度。
解:板运动过程中,其上任意直线始终平行于它的初始位置。
因此,板作平移。
1、运动轨迹C点的运动轨迹与A、B两点的运动轨迹形状相同,即以O点为圆心l为半径的圆弧线。
2、速度v C = v A =v B = ωl3、加速度42ωα+=l 22)()(n CC A C a a a a +==τ22)()(n AA a a +=τ222)()(l l ωα+=已知:O 1A =O 1B =l ;O 1A 杆的角速度ω和角加速度α。
求:C 点的运动轨迹、速度和加速度。
A §7-2 刚体绕定轴的转动z三维定轴转动刚体ϕ特征:如刚体在运动时,其上有两点保持不动。
ϕ=f (t )B刚体转动的运动方程刚体转动的角速度刚体转动的角加速度dtd ϕω=22dtd dt d ϕωα==讨论(1)匀速转动ω=常量ϕ=ϕ0+ ωt30602n n ππω==(2)匀变速转动α=常量ϕαωωαωϕϕαωω221202200=-++=+=tt t§7-3 刚体内各点的速度和加速度M 0MORϕωS =R ϕωϕR dtd R dt dS v ===vR ——转动半径vOω★转动刚体内任一点的速度的大小,等于刚体的角速度与该点到轴线的垂直距离的乘积,它的方向沿圆周的切线而指向转动的一方。
理论力学课件07第七章-刚体的简单运动PPT课件

26n03n01n0(rad) /s
α与方向一致为加速转动, α与 方向相反为减速转动。
3.匀速转动和匀变速转动 当 =常数,为匀速转动;当α =常数,为匀变速转动。
常用公式
0 t
0
t
1t2
精选2பைடு நூலகம்
与点的运动相类似。
9
§7-3 转动刚体内各点的速度和加速度
一、速度
z
S R
v
dS dt
Rddt
2avr2
av 2 r2
av2
2 r3
精选
17
(例2)
升降机装置由半径R=50cm的鼓轮带动,被升降物体M 的运动方程为x=5t2(t:时间,秒;x:高度,米),求: (1)鼓轮的角速度和角加速度; (2)任一时刻轮缘上一点的全加速度大的大小。
解: (1) 轮缘上任一点的速度和切向加速度分别为:
1
4
公式,有:
3
i12
n1 n2
Z2 Z1
n1
i 34
n3 n4
Z4 Z3
两式相乘,得:
精选
25
n1n3 Z2Z4
n2n4
Z1Z3
因 n2= n3 ,所以有:
i14 n n 1 4Z Z 2 1Z Z 3 4131 6 1 3 22 2 1 8.4 2
n4in 1141 14 2 .450 117(r/min)
③
ω α
θ a3
精选
12
〔例1〕画点的速度和加速度
试画出图中刚体上M、N两点在图示位置时的速度和
加速度。 (O 1 A O 2 B , O 1 O 2 A)B
ω为常数 αα
精选
13
第七章 刚体

29
(3)经某段时间后,有
2 v 0, 0 v0 0 R 3 3v0 该阶段的末态为 1 0 , v1 0 2R
vB
R
平面平行运动 在每一个点部位对应的运动平面上 瞬心是一个点 由两点速度确定瞬心的位置
B
A
vA
刚体的任意运动 瞬心是一条线----瞬时转动轴 平动刚体的瞬心
23
例 两个质量同为m、半径同为R匀质实心滑轮,用不可伸长轻绳
连接,定滑轮可无摩擦的转动。将系统从静止释放,求下面滑 轮的平动加速度。
支持力
3 cos 2 6 cos 4 3(cos 1) 2 1 N mg mac mg mg 0 2 2 2 2 (1 3 sin ) (1 3 sin )
杆的下端不会跳离地面
33
例 物体落地为什么会翻转?
设刚体落地速度v0 与光滑地面的碰撞是弹性的 质心运动 刚体转动
P2
P0
d
vc
Nt m(v0 vc )
C
Nt d I
c
N
1 2 1 1 2 2 mvc I c mv0 机械能守恒 2 2 2
2
P1
I c md 2md vc v , v 2 0 2 0 I c md I c md
P0点速度反向
v vc d v0
34
思考题
两个质量比为 4:1 的小球用长 l 的轻质细杆相连, 重球在上,与竖直方向成300的夹角自由落下,下端 轻球触地前的速度为v0,碰撞为弹性碰撞。试求细杆 落地前能翻转成竖直的条件。
§7.1刚体运动的描述
mac
刚体的总质量 质心加速度
刚体所受的外力矢量和
上页 下页 返回 结束
第七章 刚体力学
[例题3]一圆盘形均质飞轮质量为m=5.0kg,半径为 r=0.15m,转速为n=400r/min.飞轮作匀速转动.飞轮质心 距转轴d=0.001m,求飞轮作用于轴承的压力.计入飞轮 质量但不考虑飞轮重量(这意味着仅计算由于飞轮的转
第七章 刚体力学
取图参中考rij点表O示质元i指向质 元j的矢量,
由平dd动rtj 定 d义drtirijr为j 恒r矢ivj量rij
vi
d2rj d2ri dt 2 dt 2
a j ai
O
rj
ri
rij
结论:刚体平动时,其上各点具有相同的速度、加速
度及相同的轨迹.可用一个质点的运动代替刚体的运
Δt0 Δt dt
可正可负, 当与 同号时,转动加快,异号时减慢.
上页 下页 返回 结束
第七章 刚体力学
(5)刚体定轴转动运动方程
d (t)dt
t
0 0 (t )dt
匀速转动 =常量
0 t
d (t)dt
t
0
(t )dt
0
匀变速转动 =常量
0 t
0
t
1 t 2
2
2 02 2( 0)
V
V
R xπ(R2 x2 )dx
0
πR3 2 / 3
3R 8
R
x O x dx
z
由对称性得
yc zc 0
上页 下页 返回 结束
第七章 刚体力学
[例题2] 在半径为R的均质等厚大圆板的一侧挖掉半径为
R/2的小圆板,大小圆板相切,如图所示.求余下部分的质心.
07刚体的简单运动PPT优秀课件
转动半径与刚体角速度的 乘积 方向:沿着轨迹的切线方向 (即 与转动半径R垂直) ,指
向与一致
参见动画:定轴转动
参见动画:转动速度分布
12
3. 点的加速度
切向加速度
大小:at=R 转动半径与刚体转动的角加速度的乘积 方向:沿着轨迹的切线方向,指向与 一致
法向加速度
大小:an= R 2
vM = vA = vB , aM = aA = aB 又点A 在半径为l的圆弧上运动。如以最低点O为起点,规定弧坐标s向右
为正,则A点的运动方程为
sA
ll0s
inπt 4
vAd dst π 4l0c
oπst 4
at
ddvt 1π26l0s
inπt 4
an
v2 l
1π26l02co2sπ4t
5
例题
0
0
2
φ0
v (m/s)
π 4
l
0 (水平向右)
0
at (m/s2)
0
π2 16
l 0
an (m/s2)
π2 16
l
2 0
(铅直向上)
0
6
第2节 刚体绕定轴的转动
1.定义
刚体运动时,体内有一条直线保持不动,而整个刚 体绕此直线旋转,则称刚体作定轴转动。
参见动画:主轴
参见动画:定轴转动
不动直线称为转轴(轴线、轴)
单位:弧度/秒2(rad/s2)
角速度矢量
=k = k
9
参见动画:角速度矢量a
5. 几种特殊运动
Байду номын сангаас
匀速转动
常数 0 t
匀变速转动
7、第七章刚体的基本运动
vM a O α an
at M
因为物体 A 与轮缘上 M 点的 运动不同,前者作直线平移, 而后者随滑轮作圆周运动 ,因 此,两者的速度和加速度都不 完全相同。由于细绳不能伸长, 物体 A 与 M 点的速度大小相等, A 的加速度与 M 点切向加速度的 大小也相等,于是有
v A vM 0.36 m s-1
A
vM r 0.36 m s-1
加速度的两个分量
vM at
at r 0.36 m s
φ
M
-2
aM
O α
an r 0.648 m s
2
-2
an ω
总加速度 aM 的大小和方向
aM at an 0.741 m s-2
2 2
A
tan 2 0.556,
两式相除:
O
φ
a
tg 60 2 3 2 d 3 2 dt
d d dt d
d 3 2 d d 3d d 3d
0
0
3 2
0e
3
§7-4 轮系的传动比
ω1
ω2 r2
v r11 r22
传动比: ω1 r1
r1
v
r2 ω2
1 r2 i12 2 r1
1 R2 z2 i12 2 R1 z1
概念题 1)转动刚体的角加速度为正时,则刚体 (1)越转越快 (2)越转越慢 (3)不一定 2)两齿轮啮合时: 接触点的速度 (1)相等;(2)不相等;(3)不一定
d dt
t 0, 0 0 t
匀变速运动,ε=常数 d t 0, 0 0
第七章 刚体力学
(二)刚体的定轴转动 1.各点运动的特点
在自己的转动平面内作圆周运动 2.描述的物理量 任一质点圆周运动的线 量和角量的关系 r r
简化
加速 z
r
an r an at r at r
细棒势能 质点势能
M l
o
2
0 m
两式联 立得解
25
例2 已知:细棒如图 求:任意位置时,轴给细棒的作用力
解:设任意位置时,细棒角速度为
设轴给细棒的作用力为 Fn Ft 作细棒受力图 F n
o
Mg
o
c
M l
26
Ft
Fn
o
o
c
M l
Ft
Mg
Fn Mg cos Macn
Ft Mg sin Mact l l 2 act acn 2 2
碰撞过程中系统对o 点 的合力矩为 M 0 即,
0 m
所以,系统对o点的角动量守恒。
L1 L2
1 2 m0l Ml m l2 3
1
24
过程2 质点、细棒上摆 系统中包括地球, 只有保守内力作功,所以机械能守恒。 设细棒处于最低点为势能零点
11 2 2 2 Ml m l 23 1 Mgl1 cos m gl1 cos 2
第七章 刚体力学
1
基本方法:
质点系运动定理
加 刚体特性 刚体定轴转动的
动能定理
平动:动量定理
F mac
角动量定理
可以解决刚体的一般运动(平动加转动)
2
