安徽省全椒中学2017-2018学年高一上学期期中考试数学试卷 (word版含答案)

合集下载

安徽省宣城市2017-2018学年高一上学期期中数学试卷(普通班) Word版含解析

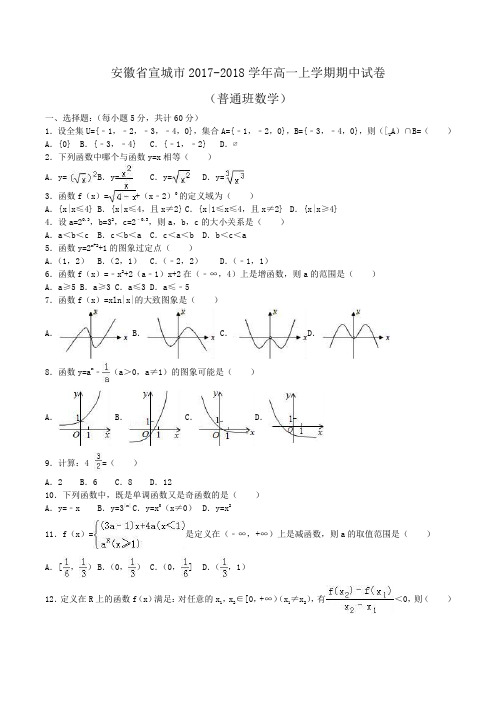
安徽省宣城市2017-2018学年高一上学期期中试卷（普通班数学）一、选择题：（每小题5分，共计60分）1．设全集U={﹣1，﹣2，﹣3，﹣4，0}，集合A={﹣1，﹣2，0}，B={﹣3，﹣4，0}，则（∁U A ）∩B=（）A ．{0}B ．{﹣3，﹣4}C ．{﹣1，﹣2}D ．∅2．下列函数中哪个与函数y=x 相等（）A ．y=B ．y=C ．y=D ．y=3．函数f （x ）=+（x ﹣2）0的定义域为（）A ．{x|x ≤4}B ．{x|x ≤4，且x ≠2}C ．{x|1≤x ≤4，且x ≠2}D ．{x|x ≥4}4．设a=20.3，b=32，c=2﹣0.3，则a ，b ，c 的大小关系是（）A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．b ＜c ＜a5．函数y=2x+2+1的图象过定点（）A ．（1，2）B ．（2，1）C ．（﹣2，2）D ．（﹣1，1）6．函数f （x ）=﹣x 2+2（a ﹣1）x+2在（﹣∞，4）上是增函数，则a 的范围是（）A ．a ≥5B ．a ≥3C ．a ≤3D ．a ≤﹣57．函数f （x ）=xln|x|的大致图象是（）A ．B ．C ．D ．8．函数y=a x ﹣（a ＞0，a ≠1）的图象可能是（）A ．B ．C ．D ．9．计算：4=（）A ．2B ．6C ．8D ．1210．下列函数中，既是单调函数又是奇函数的是（）A ．y=﹣xB ．y=3|x|C ．y=x 0（x ≠0）D ．y=x 211．f （x ）=是定义在（﹣∞，+∞）上是减函数，则a 的取值范围是（）A ．[，）B ．（0，）C ．（0，]D ．（，1）12．定义在R 上的函数f （x ）满足：对任意的x 1，x 2∈[0，+∞）（x 1≠x 2），有＜0，则（）A．f（3）＜f（2）＜f（4）B．f（1）＜f（2）＜f（3）C．f（2）＜f（1）＜f（3）D．f（3）＜f（1）＜f（0）二、填空题：本大题共4小题，每小题5分，共20分．13．写出函数y=﹣（x﹣1）2单调增区间．14．若f（x）=+2 求f（9）= ．15．若函数f（x）满足f（x）+2f（）=3x（x≠0），则f（x）= ．16．已知函数f（x）=，则 f（f（2））= ．三、解答题（共6小题，出必要的文字说明，解题过程和演算步骤）17．（1）证明函数f（x）=x3﹣1，是增函数．（2）判断函数g（x）=e x﹣e﹣x的奇偶性，并证明．18．设全集u={1，2，3，4，5，6，7，8，9}，集合A={1，2，3，4，5，6}，B={4，5，6，7，8}（1）求A∩B（2）求A∪B（3）求∁u A∪∁uB（4）求∁uA∩B．19．（1）化简9×64÷30（2）化简（）×36÷3﹣3（2）化简（a＞0）20．（1）求函数f（x）=的值域（2）求函数f（x）=x2+4x﹣1的值域（3）求函数f（x）=x+的值域．21．解不等式：23x﹣1＜2解不等式：a＜a（a＞0且a≠1）22．已知f（x）是定义在区间[﹣1，1]上的奇函数，且f（1）=1，且f（x）是增函数．（1）解不等式f（x+）+f（x﹣1）＜0（2）若f（x）≤t2﹣2at+1对所有x∈[﹣1，1]、a∈[﹣1，1]恒成立，求实数t的取值范围．安徽省宣城市2017-2018学年高一上学期期中试卷（普通班数学）参考答案与试题解析一、选择题：（每小题5分，共计60分）1．设全集U={﹣1，﹣2，﹣3，﹣4，0}，集合A={﹣1，﹣2，0}，B={﹣3，﹣4，0}，则（∁UA）∩B=（）A．{0} B．{﹣3，﹣4} C．{﹣1，﹣2} D．∅【考点】交、并、补集的混合运算．【分析】先计算集合CU A，再计算（CUA）∩B．【解答】解：∵A={﹣1，﹣2，0}，B={﹣3，﹣4，0}，∴CUA={﹣3，﹣4}，∴（CUA）∩B={﹣3，﹣4}．故答案选B．2．下列函数中哪个与函数y=x相等（）A．y=B．y=C．y=D．y=【考点】判断两个函数是否为同一函数．【分析】确定函数的三要素是：定义域、对应法则和值域，据此可判断出答案．【解答】解：A．y=的定义域是{x|x≥0}，而函数y=x的定义域R，故不是同一函数．B．y=的定义域是{x|x≠0}，而函数y=x的定义域R，故不是同一函数．C．y==|x|与y=x的对应法则、值域皆不同，故不是同一函数．D．y==x与y=x是同一函数．故选：D．3．函数f（x）=+（x﹣2）0的定义域为（）A．{x|x≤4} B．{x|x≤4，且x≠2} C．{x|1≤x≤4，且x≠2} D．{x|x≥4}【考点】函数的定义域及其求法．【分析】根据二次根式的性质以及指数幂的性质求出函数的定义域即可．【解答】解：由题意得：，解得：x≤4且x≠2，故函数的定义域是{x|x≤4且x≠2}，故选：B．4．设a=20.3，b=32，c=2﹣0.3，则a，b，c的大小关系是（）A．a＜b＜c B．c＜b＜a C．c＜a＜b D．b＜c＜a【考点】指数函数的图象与性质．【分析】根据指数函数的性质判断a，c，根据a，b的范围判断a，b的大小即可．【解答】解：∵c=2﹣0.3＜1＜a=20.3＜2＜b=32∴c＜a＜b，故选：C．5．函数y=2x+2+1的图象过定点（）A．（1，2）B．（2，1）C．（﹣2，2）D．（﹣1，1）【考点】指数函数的图象变换．【分析】利用指数函数y=2x的图象的平移变换，得出函数y=2x+2+1的图象过的定点．或者由任意非零实数a，均满足a0=1计算出函数y=2x+2+1的图象过的定点．【解答】解法一：令x+2=0，得x=﹣2，当x=﹣2时，y=2°+1=1+1=2；故函数图象过定点（﹣2，2）故选C．解法二：∵指数函数y=2x的图象向左平移2个单位，再向上平移1个单位，得到函数y=2x+2+1．∴由指数函数y=2x过定点（0，1）得函数y=2x+2+1过定点（﹣2，2）故选C．解法三：代点验证法．选项A，若x=1，代入函数y=2x+2+1=9≠2，即该函数图象不过点（1，2）．选项B，若x=2，代入函数y=2x+2+1=17≠1，即该函数图象不过点（2，1）．选项C，若x=﹣2，代入函数y=2x+2+1=2，即该函数图象过点（﹣2，2）．选项D，若x=﹣1，代入函数y=2x+2+1=3≠1，即该函数图象不过点（﹣1，1）．故选C．6．函数f（x）=﹣x2+2（a﹣1）x+2在（﹣∞，4）上是增函数，则a的范围是（）A．a≥5 B．a≥3 C．a≤3 D．a≤﹣5【考点】函数单调性的性质．【分析】先将函数f（x）=﹣x2+2（a﹣1）x+2转化为：y=﹣（x﹣a+1）2﹣2a+3+a2明确其对称轴，再由函数在（﹣∞，4）上单调递增，则对称轴在区间的右侧求解．【解答】解：函数f（x）=﹣x2+2（a﹣1）x+2∴其对称轴为：x=a﹣1又∵函数在（﹣∞，4）上单调递增∴a﹣1≥4即a≥5故选A7．函数f（x）=xln|x|的大致图象是（）A． B． C．D．【考点】函数的图象．【分析】由于f（﹣x）=﹣f（x），得出f（x）是奇函数，其图象关于原点对称，由图象排除C，D，利用导数研究根据函数的单调性质，又可排除选项B，从而得出正确选项．【解答】解：∵函数f（x）=xln|x|，可得f（﹣x）=﹣f（x），f（x）是奇函数，其图象关于原点对称，排除C，D，又f′（x）=lnx+1，令f′（x）＞0得：x＞，得出函数f（x）在（，+∞）上是增函数，排除B，故选A8．函数y=a x﹣（a＞0，a≠1）的图象可能是（）A． B． C．D．【考点】函数的图象．【分析】讨论a与1的大小，根据函数的单调性，以及函数恒过的定点进行判定即可．【解答】解：函数y=a x﹣（a＞0，a≠1）的图象可以看成把函数y=a x的图象向下平移个单位得到的．当a＞1时，函数y=a x﹣在R上是增函数，且图象过点（﹣1，0），故排除A，B．当1＞a＞0时，函数y=a x﹣在R上是减函数，且图象过点（﹣1，0），故排除C，故选D．9．计算：4=（）A．2 B．6 C．8 D．12【考点】根式与分数指数幂的互化及其化简运算．【分析】根据幂的运算法则进行化简，即可得出结果．【解答】解： ===23=8．故选：C．10．下列函数中，既是单调函数又是奇函数的是（）A ．y=﹣xB ．y=3|x|C ．y=x 0（x ≠0）D ．y=x 2【考点】二次函数的性质；函数单调性的判断与证明；函数奇偶性的判断；分段函数的应用．【分析】分析给定四个函数的单调性和奇偶性，可得答案．【解答】解：y=﹣x 是减函数，且是奇函数，y=3|x|=是偶函数；幂函数y=x 0=1（x ≠0）是偶函数；二次函数y=x 2是偶函数；故选：A ．11．f （x ）=是定义在（﹣∞，+∞）上是减函数，则a 的取值范围是（）A ．[，）B ．（0，）C ．（0，]D ．（，1）【考点】分段函数的应用．【分析】由题意根据函数的单调性可得列出不等式组，由此求得a 的范围．【解答】解：由题意可得，求得≤a ＜，故选：A ．12．定义在R 上的函数f （x ）满足：对任意的x 1，x 2∈[0，+∞）（x 1≠x 2），有＜0，则（）A ．f （3）＜f （2）＜f （4）B ．f （1）＜f （2）＜f （3）C ．f （2）＜f （1）＜f （3）D ．f （3）＜f （1）＜f （0）【考点】函数单调性的性质．【分析】根据函数单调性的等价条件，即可到底结论．【解答】解：若对任意的x 1，x 2∈[0，+∞）（x 1≠x 2），有＜0，则函数f （x ）满足在[0，+∞）上单调递减，则f （3）＜f （1）＜f （0），故选：D ．二、填空题：本大题共4小题，每小题5分，共20分．13．写出函数y=﹣（x ﹣1）2单调增区间（﹣∞，1] ．【考点】二次函数的性质；函数的单调性及单调区间．【分析】根据函数的解析式，分析函数的图象和性质，进而可得答案．【解答】解：函数y=﹣（x ﹣1）2的图象是开口朝下，且以直线x=1为对称轴的抛物线，故函数y=﹣（x﹣1）2单调增区间为（﹣∞，1]，故答案为：（﹣∞，1]．14．若f（x）=+2 求f（9）= 5 ．【考点】函数的值．【分析】利用函数性质直接求解．【解答】解：∵f（x）=+2，∴f（9）==5．故答案为：5．15．若函数f（x）满足f（x）+2f（）=3x（x≠0），则f（x）= ﹣x+（x≠0）．【考点】函数解析式的求解及常用方法．【分析】由题意得到方程组解出f（x）即可．【解答】解：∵f（x）+2f（）=3x①令x=，则f（）+2f（x）=②，①﹣2×②得：﹣3f（x）=3x﹣，∴f（x）=﹣x+，故答案为：﹣x+（x≠0）．16．已知函数f（x）=，则 f（f（2））= ．【考点】函数的值．【分析】利用分段函数的定义分别计算f（2），f（f（2））即可得出．【解答】解：f（2）=2﹣4=﹣2，f（﹣2）=3﹣2=，即 f（f（2））=．故答案为：．三、解答题（共6小题，出必要的文字说明，解题过程和演算步骤）17．（1）证明函数f（x）=x3﹣1，是增函数．（2）判断函数g（x）=e x﹣e﹣x的奇偶性，并证明．【考点】函数单调性的判断与证明；函数奇偶性的判断．【分析】（1）导数法根据已知中函数的解析式，求出函数导函数的解析式，进而根据在（﹣∞，+∞）上f′（x）≥0恒成立，得到函数f（x）=x3﹣1在（﹣∞，+∞）上是增函数．（2）利用奇函数的定义即可判断．【解答】（1）证明：∵f（x）=x3﹣1，∴f′（x）=3x2，∴在（﹣∞，+∞）上f′（x）≥0恒成立∴函数f（x）=x3﹣1在（﹣∞，+∞）上是增函数．（2）解：函数的定义域为R，∵g（﹣x）=e﹣x﹣e x=﹣（e x﹣e﹣x）=﹣g（x），∴函数g（x）=e x﹣e﹣x是奇函数．18．设全集u={1，2，3，4，5，6，7，8，9}，集合A={1，2，3，4，5，6}，B={4，5，6，7，8} （1）求A∩B（2）求A∪B（3）求∁u A∪∁uB（4）求∁uA∩B．【考点】交、并、补集的混合运算．【分析】根据交集、并集与补集的定义进行计算即可．【解答】解：（1）集合A={1，2，3，4，5，6}，B={4，5，6，7，8}，∴A∩B={4，5，6}；（2）A∪B={1，2，3，4，5，6，7，8}；（3）由全集u={1，2，3，4，5，6，7，8，9}，∁u A={7，8，9}，∁uB={1，2，3，9}，∴（∁u A）∪（∁uB）={1，2，3，7，8，9}；（4）∁uA∩B={7，8}．19．（1）化简9×64÷30（2）化简（）×36÷3﹣3（2）化简（a＞0）【考点】有理数指数幂的化简求值．【分析】分别根据有理数数指数幂的运算性质计算即可．【解答】解：（1）原式=×÷1=27×2=54，（2）原式=×÷=××27=，（3）原式==20．（1）求函数f（x）=的值域（2）求函数f（x）=x2+4x﹣1的值域（3）求函数f（x）=x+的值域．【考点】函数的值域．【分析】（1）利用反比例性质求解值域即可．（2）根据二次函数的性质求解值域即可．（3）换元法转化为二次函数，利用二次函数的性质求解值域即可．【解答】解：（1）函数f（x）=，∵x﹣1≠0，∴f（x）≠0故得函数函数f（x）=的值域为（﹣∞，0）∪（0，+∞）．（2）函数f（x）=x2+4x﹣1，根据二次函数的性质可知：开口向上，对称轴x=﹣2．当x=﹣2时，函数y取得最小值为﹣5；故得函数f（x）=x2+4x﹣1的值域为[﹣5，+∞）．（3）函数f（x）=x+，设t=，（t≥0），则x=t2﹣1．∴函数f（x）=x+转化为g（t）═t2﹣1+t，（t≥0）根据二次函数的性质可知：函数g（t）开口向上，对称轴t=﹣．∵t≥0，∴当x=0时，函数y取得最小值为﹣1；故得函数g（t）═t2﹣1+t的值域为[﹣1，+∞），即函数f（x）=x+的值域为[﹣1，+∞）．21．解不等式：23x﹣1＜2解不等式：a＜a（a＞0且a≠1）【考点】指、对数不等式的解法．【分析】（1）直接利用指数函数的性质化指数不等式为一元一次不等式求解；（2）对a分类，然后利用指数函数的性质化指数不等式为一元二次不等式求解．【解答】解：（1）由23x﹣1＜2，得3x﹣1＜1，即x＜．∴不等式23x﹣1＜2的解集为{x|x＜}；（2）当a＞1时，由a＜a，得3x2+3x﹣1＜3x2+3，解得x＜，∴不等式a＜a的解集为{x|x＜}；当0＜a＜1时，由a＜a，得3x2+3x﹣1＞3x2+3，解得x＞，∴不等式a＜a的解集为{x|x＞}．22．已知f（x）是定义在区间[﹣1，1]上的奇函数，且f（1）=1，且f（x）是增函数．（1）解不等式f（x+）+f（x﹣1）＜0（2）若f（x）≤t2﹣2at+1对所有x∈[﹣1，1]、a∈[﹣1，1]恒成立，求实数t的取值范围．【考点】奇偶性与单调性的综合；函数恒成立问题．【分析】（1）由即可求得不等式f（x+）+f（x﹣1）＜0的解集；=f（1）=1，将问题转化为：t2﹣2at+1≥1对a∈[﹣1，1]恒成立，构造函数f（a）=（3）先求得f（x）max﹣2ta+t2，则f（a）≥0对a∈[﹣1，1]恒成立，解关于t的不等式组即可．【解答】解：（1）∵f（x）在区间[﹣1，1]上是增函数且f（x+）＜f（1﹣x），∴，∴0≤x＜，∴解集为：{x|0≤x＜}；=f（1）=1．（2）f（x）maxf（x）≤t2﹣2at+1对所有x∈[﹣1，1]恒成立，则t2﹣2at+1≥1对a∈[﹣1，1]恒成立，构造函数f（a）=﹣2ta+t2，则f（a）≥0对a∈[﹣1，1]恒成立，∴或或t=0，解得：t≤﹣2或t=0或t≥2．。

2017-2018学年高一上学期期中考试数学试卷

第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，满分60分，每题四个选项中只有一项是符合题目要求的）1、设集合{|4},{1,2},{2,3}U x N x A B ，则()()U U C A C B =( )(A){0,4}(B){4}(C) {1,2,3}(D)2、下列函数中，既是偶函数，又在)0,(上为减函数的是( )(A)x y 2(B)x y (C)2x y (D)||lg x y 3、已知函数122x y ，当自变量]1,0[x 时，因变量y 的取值范围为( )(A)]2,1[(B)]1,0[(C)]3,2[(D)]2,0[4、已知函数x x x f 3)(，则函数)1(x f 的定义域为( )(A)1,4x x x (B)1,2x x x (C)0,2x x x (D)1,4x x x 5、函数1()1x a f x a x (0a 且1a )的图象恒经过定点( )(A)(1,1)(B)(1,2)(C)(1,3)(D)(0,2)6、用二分法求方程x x 2)1ln(的近似解时，可以取的一个区间是( )(A)(1,2)(B)(2,)e (C)(3,4)(D)(0,1)7、函数223()log ()f x x x 的单调减区间为( )(A) 1(,)2(B) 1(,1)2(C) 1(,)2(D) 1(0,)28、设集合(,),0A x y x R y ，B R ，点(,)x y 在映射:f A B 的作用下的象是2x y ，则对于B 中的数5，与之对应的A 中的元素不．可能．．是( )(A)(1,3)(B)2(log 3,2)(C)(0,5)(D)(2,1)9、在平面直角坐标下，函数21()22x xf x x x 的图象( )(A) 关于x 轴对称(B) 关于y 轴对称(C) 关于原点对称(D) 关于直线y x 轴对称。

高中数学复习提升高一数学期中测试卷

2017-2018学年高一数学期中考试卷（本卷共有三个大题，满分150分，考试时间120分钟）第I 卷（60分）一、选择题：（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设全集R U =，集合{}02A x x =<≤， {}1B x x =<，则集合A B ⋃=（） A. ()2,+∞ B. [)2,+∞ C. (],2-∞ D. (],1-∞2．设集合M ＝{0，1，2，3}，N ＝{x|x 2－3x ＋2≤0}，则M ∩N 等于（） A ．{1} B ．{2} C ．{0，1} D ．{1，2} 3．函数x x f 2-1)(=的定义域是（）A.(,0]-∞B.[0,)+∞C.】，（21-∞ D.(,)-∞+∞ 4．已知13x x-+=，则1122x x -+值为（）A .3B .5C .5±D . 5-5．若函数()(0,1)xf x a a a -=>≠是定义域为R 的增函数，则函数()()log 1a f x x =+的图象大致是（）6.函数 ()245f x x x =-+在区间[]0,m 上的最大值为5，最小值为1，则m 的取值范围是（） A ．),2[+∞ B ．[]24， C ．（]2,∞- D ．[]02， 7.已知函数f （x ）=221,1{,1xx x ax x +<+≥ ，若f[f （0）]=4a ，则实数a 等于（） A. B. C. 2 D. 98.已知实数 221311log 3,,log 330a b c ⎛⎫=== ⎪⎝⎭，则,,a b c 的大小关系是（）A. a b c >>B. a c b >>C. c a b >>D. c b a >> 9．函数213()log 6()f x x x =--的单调递增区间是（）A ．),21[+∞-B ．]21,(--∞C ．1(3,]2--D ．)2,21[-10．幂函数8622)44()(+-+-=m m x m m x f 在（0，+∞）为减函数，则m 的值为（）A ． 1或3B ． 1C ．3D ． 2 11．已知)(x f 是偶函数，且在（﹣∞，0]上是减函数，若)9()3(122-≥--f f x x ，则x 的取值范围是（）A ．（﹣∞，﹣1]∪[23，+∞） B ．（﹣∞，﹣23]∪[1，+∞） C ．[﹣1，23] D ．[﹣23，1] 12.设奇函数]1,1[)(-在x f 上是单调函数，且,1)1(-=-f 若函数12)(2+-≤at t x f 对所有的]1,1[-∈x 都成立，当]1,1[-∈a 时，则t 的取值范围是（）A ．22≤≤-tB ．2121≤≤-t C ．2,2,0t t t ≥≤-=或或 D ．11022t t t ≥≤-=,或,或第II 卷（90分）二、填空题（本大题共4小题，每小题5分，共20分．）13．集合(]2,1=A ，集合{}a x x B <=，满足A ≠⊂B ，则实数a 的范围是_______________ 14．幂函数)(x f 的图象过点1(4,)2，那么(16)f 的值为．15．已知函数log a y x =(0,1)a a >≠的图象经过点1(2,)2，则其反函数的解析式y = ． 16．设()f x 是定义在R 上的偶函数，对任意的x ∈R ，都有)2()2(+=-x f x f ，且当[2,0]x ∈-时，1()12xf x ⎛⎫=- ⎪⎝⎭，若关于x 的方程()log (2)0a f x x -+=()1a >在区间（-2,6）内恰有三个不同实根，则实数a 的取值范围是 .三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．（本小题满分10分）计算下列各式的值：（1）2103439)41()2(4)161(-+-⋅---（2）3log 333558log 932log 2log 2-+-18．（12分）．已知二次函数()f x 的图像过A （-1,0）,B(3,0),C(1,8)。

安徽省马鞍山市2017-2018学年高一上学期期中素质测试数学试题(精品解析)

安徽省马鞍山市2017―2018学年度第一学期期中素质测试数学必修①考生注意：本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共22小题，满分100分．请在答题卡上答题．第Ⅰ卷（选择题，共36分）一、选择题：本题共12小题，每小题3分，共36分，每小题所给的四个选项中只有一个是正确的，请将正确答案的代号在答题卡上用2B铅笔涂黑．1.已知，，等于（）A. B. C. D.【答案】D【解析】由题意可知，，故选D。

2.已知，则满足条件的集合的个数是（）A. B. C. D.【答案】C【解析】由题意可知，，所以满足要求的集合有，故选C。

3.下列函数中与函数是同一函数的是（）A. B. C. D.【答案】D【解析】函数相等必须满足定义域相同和解析式相同，A、B解析式不同，C定义域不同，故选D。

4.函数，的图象如图所示，则函数的所有单调递减区间为（）A. B.C. D.【答案】C 【解析】有图可知，在和两个区间单调递减，故选C 。

5.下列函数为幂函数的是（）A. B.C.D.【答案】A 【解析】由幂函数的定义可知，选A 。

6.函数的零点是（）A.B.C.D.【答案】C 【解析】，解得或，故选C 。

7.化简（）A.B.C.D.【答案】A 【解析】，故选A 。

8.已知，则的大小关系是（）A. B.C.D.【答案】A【解析】，，，所以，故选A。

9.已知，则（）A. B. 1 C. 2 D. 3【答案】B【解析】当，即时，得，故选B。

点睛：函数解析式中特别强调整体思想的应用，在本题中，将条件函数研究对象整体，得，再带入条件函数，就可以解得的值。

在函数的解析式相关题型中，整体思想的应用非常广泛，学会灵活应用。

10.某商场将彩电的售价先按进价提高，然后“八折优惠”，结果每台彩电利润为360元，那么彩电的进价是（）A. B. C. D.【答案】C【解析】设进价为元，得，解得，故选C。

11.已知函数是定义在上的偶函数，当时，恒成立，设，则的大小关系为（）A. B. C. D.【答案】D【解析】是偶函数，得关于对称，又由题意可知，在上单调递减，又，则，，故选D。

【精品】2018年安徽省滁州市全椒县城东中学高一上学期期中数学试卷

2017-2018学年安徽省滁州市全椒县城东中学高一（上）期中数学试卷一、选择题：本题共12题，每小题5分，共计60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知集合M={x|﹣3＜x＜1}，N={﹣3，﹣2，﹣1，0，1}，则M∩N 等于（）A．{﹣2，﹣1，0，1}B．{﹣3，﹣2，﹣1，0}C．{﹣2，﹣1，0}D．{﹣3，﹣2，﹣1}2．（5分）下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（）A．y= B．y=5x C．y=﹣x2+1 D．y=lg|x|3．（5分）下列哪组中的两个函数是同一函数（）A．与y=x B．与y=xC．与D．与4．（5分）设函数f（x）=，则f（f（3））=（）A．B．3 C．D．5．（5分）若函数f（x）满足f（3x+2）=9x+8，则f（x）的解析式是（）A．f（x）=3x+2 B．f（x）=9x+8C．f（x）=﹣3x﹣4 D．f（x）=3x+2或f（x）=﹣3x﹣46．（5分）已知函数f（x）的定义域为（﹣1，0），则函数f（2x+1）的定义域为（）A．（﹣1，1）B．C．（﹣1，0）D．7．（5分）设函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣3x+k （k为常数），则f（﹣1）=（）A．2 B．1 C．﹣2 D．﹣18．（5分）函数y=（x＞0）的值域为（）A．（﹣，+∞）B．（﹣1，2）C．{y|y≠2}D．{y|y＞2}9．（5分）函数y=a x﹣a（a＞0，a≠1）的图象可能是（）A．B． C．D．10．（5分）已知函数f（x）是定义在区间[0，+∞）上的增函数，则满足f（2x ﹣1）＜f（）的x的取值范围是（）A．（，）B．[，）C．（，）D．[，）11．（5分）设函数f（x）是定义在R上的奇函数，且∀x∈∈R，f（x）=f（x+4）．当x∈∈（﹣2，0）时，f（x）=2x，则f（2015）﹣f（2013）的值为（）A．﹣ B．0 C．D．112．（5分）已知函数是R上的增函数，则实数k的取值范围为（）A．（1，+∞）B． C．（﹣∞，1）D．二、填空题：本题共4题，每小题5分，共计20分.13．（5分）函数是幂函数，实数m的值为．14．（5分）从集合A到集合B的映射f：x→x2+1，若A={﹣2，﹣1，0，1，2}，则B中至少有个元素．15．（5分）设x0是函数f（x）=2x+x的零点，且x0∈（k，k+1），k∈Z，则k=．16．（5分）已知函数f（x）=．若a＜b＜c且f（a）=f（b）=f（c），则（ab+2）c的取值范围是．三.解答题，共6小题，共计70分，解答应写出必要的证明过程或演算步骤. 17．（10分）（1）÷；（2）2lg5+lg8+lg5•lg20+（lg2）2．18．（12分）已知A={x|x2+4x=0}，B={x|x2+2（a+1）x+a2﹣1=0}，其中a∈R，如果A∩B=B，求实数a的取值范围．19．（12分）某投资公司计划投资A、B两种金融产品，根据市场调查与预测，A 产品的利润y与投资量x成正比例，其关系如图1，B产品的利润y与投资量x 的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）（1）分别将A、B两产品的利润表示为投资量的函数关系式；（2）该公司已有10万元资金，并全部投入A、B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？20．（12分）已知函数f（x）=2ax+（a∈R）．（1）当时，试判断f（x）在（0，1]上的单调性并用定义证明你的结论；（2）对于任意的x∈（0，1]，使得f（x）≥6恒成立，求实数a的取值范围．21．（12分）已知函数的值域为集合A，关于x的不等式的解集为B，集合，集合D={x|m+1≤x ＜2m﹣1}（m＞0）（1）若A∪B=B，求实数a的取值范围；（2）若D⊆C，求实数m的取值范围．22．（12分）对于函数f1（x）、f2（x）、h（x），如果存在实数a，b使得h（x）=a•f1（x）+bf2（x），那么称h（x）为f1（x）、f2（x）的和谐函数．（1）已知函数f1（x）=x﹣1，f2（x）=3x+1，h（x）=2x+2，试判断h（x）是否为f1（x）、f2（x）的和谐函数？并说明理由；（2）已知h（x）为函数f 1（x）=log3x，f2（x）=x的和谐函数，其中a=2，b=1，若方程h（9x）+t•h（3x）=0在x∈[3，9]上有解，求实数t的取值范围．2017-2018学年安徽省滁州市全椒县城东中学高一（上）期中数学试卷参考答案与试题解析一、选择题：本题共12题，每小题5分，共计60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知集合M={x|﹣3＜x＜1}，N={﹣3，﹣2，﹣1，0，1}，则M∩N 等于（）A．{﹣2，﹣1，0，1}B．{﹣3，﹣2，﹣1，0}C．{﹣2，﹣1，0}D．{﹣3，﹣2，﹣1}【解答】解：M={x|﹣3＜x＜1}，N={﹣3，﹣2，﹣1，0，1}，则M∩N={x|﹣3＜x＜1}∩{﹣3，﹣2，﹣1，0，1}={﹣2，﹣1，0}．故选：C．2．（5分）下列函数中，既是偶函数又在区间（0，+∞）上单调递减的是（）A．y= B．y=5x C．y=﹣x2+1 D．y=lg|x|【解答】解：由于y=是奇函数，不满足题意，排除A；由于y=5x是非奇非偶的函数，不满足题意，排除B；由于函数y=﹣x2+1是偶函数，且满足在（0，+∞）上是单调递减函数，C满足条件；由于y=lg|x|是偶函数，但在区间（0，+∞）上是单调递增，排除D．故选：C．3．（5分）下列哪组中的两个函数是同一函数（）A．与y=x B．与y=xC．与D．与【解答】解：A、y=x与y=的定义域不同，故不是同一函数．B、=x与y=x的对应关系相同，定义域为R，故是同一函数．C、f与的定义域不同，故不是同一函数．D、与具的定义域不同，故不是同一函数．故选：B．4．（5分）设函数f（x）=，则f（f（3））=（）A．B．3 C．D．【解答】解：函数f（x）=，则f（3）=，∴f（f（3））=f（）=+1=，故选：D．5．（5分）若函数f（x）满足f（3x+2）=9x+8，则f（x）的解析式是（）A．f（x）=3x+2 B．f（x）=9x+8C．f（x）=﹣3x﹣4 D．f（x）=3x+2或f（x）=﹣3x﹣4【解答】解：令3x+2=t，则x=，故f（t）=3（t﹣2）+8=3t+2，故f（x）=3x+2，故选：A．6．（5分）已知函数f（x）的定义域为（﹣1，0），则函数f（2x+1）的定义域为（）A．（﹣1，1）B．C．（﹣1，0）D．【解答】解：∵原函数的定义域为（﹣1，0），∴﹣1＜2x+1＜0，解得﹣1＜x＜﹣．∴则函数f（2x+1）的定义域为．故选：B．7．（5分）设函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=2x﹣3x+k （k为常数），则f（﹣1）=（）A．2 B．1 C．﹣2 D．﹣1【解答】解：∵f（x）为定义在R上的奇函数；∴f（0）=1﹣0+k=0；∴k=﹣1；∴x≥0时，f（x）=2x﹣3x﹣1；∴f（﹣1）=﹣f（1）=﹣（2﹣3﹣1）=2．故选：A．8．（5分）函数y=（x＞0）的值域为（）A．（﹣，+∞）B．（﹣1，2）C．{y|y≠2}D．{y|y＞2}【解答】解：y==2﹣．∵x＞0，∴x+1＞1，∴0＜＜1，∴﹣1＜2﹣＜2．∴函数y=（x＞0）的值域为（﹣1，2）．故选：B．9．（5分）函数y=a x﹣a（a＞0，a≠1）的图象可能是（）A．B． C．D．【解答】解：由于当x=1时，y=0，即函数y=a x﹣a 的图象过点（1，0），故排除A、B、D．故选：C．10．（5分）已知函数f（x）是定义在区间[0，+∞）上的增函数，则满足f（2x ﹣1）＜f（）的x的取值范围是（）A．（，）B．[，）C．（，）D．[，）【解答】解：∵函数f（x）是定义在区间[0，+∞）上的增函数，则满足f（2x ﹣1）＜f（），∴0≤2x﹣1＜，解得≤x＜，故选：D．11．（5分）设函数f（x）是定义在R上的奇函数，且∀x∈∈R，f（x）=f（x+4）．当x∈∈（﹣2，0）时，f（x）=2x，则f（2015）﹣f（2013）的值为（）A．﹣ B．0 C．D．1【解答】解：∀x∈∈R，f（x）=f（x+4）可得周期T=4，f（2015）﹣f（2013）=f（﹣1+4×504）﹣f（1+4×503）=f（﹣1）﹣f（1），由f（x）是定义在R上的奇函数，则f（﹣1）﹣f（1）=2f（﹣1），由于x∈（﹣2，0）时，f（x）=2x，则f（﹣1）=2﹣1=，即有f（2015）﹣f（2013）=2×=1．故选：D．12．（5分）已知函数是R上的增函数，则实数k的取值范围为（）A．（1，+∞）B． C．（﹣∞，1）D．【解答】解：∵函数f（x）为增函数，∴满足，解得≤k＜1，故选：D．二、填空题：本题共4题，每小题5分，共计20分.13．（5分）函数是幂函数，实数m的值为2或﹣1．【解答】解：函数是幂函数，可得m2﹣m﹣1=1，解得m=2或﹣1，即有y=x﹣1和y=x2均为幂函数．故答案为：2或﹣1．14．（5分）从集合A到集合B的映射f：x→x2+1，若A={﹣2，﹣1，0，1，2}，则B中至少有3个元素．【解答】解：当x=±1时，x2+1=1+1=2，当x=±2时，x2+1=4+1=5，当x=0时，x2+1=0+1=1，故B中至少有1，2，5三个元素，故答案为：315．（5分）设x0是函数f（x）=2x+x的零点，且x0∈（k，k+1），k∈Z，则k=﹣1．【解答】解：∵f（x）=2x+x，∴函数f（x）为增函数，f（0）=1＞0，f（﹣1）=＜0，满足f（0）f（﹣1）＜0，则在（﹣1，0）内函数f（x）存在一个零点，即x0∈（﹣1，0），∵x0∈（k，k+1），∴k=﹣1，故答案为：﹣116．（5分）已知函数f（x）=．若a＜b＜c且f（a）=f（b）=f（c），则（ab+2）c的取值范围是（27，81）．【解答】解：由a＜b＜c，根据已知画出函数图象：∵f（a）=f（b）=f（c），∴﹣log3a=log3b=﹣c+4，∴log3（ab）=0，0＜﹣c+4＜1，解得ab=1，3＜c＜4，∴（ab+2）c=3c∈（27，81）．故答案为：（27，81）．三.解答题，共6小题，共计70分，解答应写出必要的证明过程或演算步骤. 17．（10分）（1）÷；（2）2lg5+lg8+lg5•lg20+（lg2）2．【解答】解：（1）=（2）原式=lg25+lg4（1﹣lg2）（1+lg2）+lg2=lg25+lg4+1﹣lg22+lg22=lg100+1=3或：原式==2（lg5+lg2）+lg5•（lg5+2lg2）+（lg2）2=2+（lg5）2+2lg5•lg2+（lg2）2=2+（lg5+lg2）2=318．（12分）已知A={x|x2+4x=0}，B={x|x2+2（a+1）x+a2﹣1=0}，其中a∈R，如果A∩B=B，求实数a的取值范围．【解答】解：A={x|x2+4x=0}={0，﹣4}，B={x|x2+2（a+1）x+a2﹣1=0}，A∩B=B，可得B⊆A，（1）当B=∅时，△=4（a+1）2﹣4（a2﹣1）＜0，解得a＜﹣1．（2）当B={0}或{﹣4}时，即B⊆A时，△=4（a+1）2﹣4（a2﹣1）=0，解得a=﹣1，此时B={0}，满足B⊆A．（3）当B={0，﹣4}时，，解得a=1．综上所述，实数a的取值范围是a=1或者a≤﹣1．19．（12分）某投资公司计划投资A、B两种金融产品，根据市场调查与预测，A 产品的利润y与投资量x成正比例，其关系如图1，B产品的利润y与投资量x 的算术平方根成正比例，其关系如图2，（注：利润与投资量单位：万元）（1）分别将A、B两产品的利润表示为投资量的函数关系式；（2）该公司已有10万元资金，并全部投入A、B两种产品中，问：怎样分配这10万元投资，才能使公司获得最大利润？其最大利润为多少万元？【解答】解：（1）设投资为x万元，A产品的利润为f（x）万元，B产品的利润为g（x）万元．由题意设f（x）=k 1x，．由图知，∴又g（4）=1.6，∴．从而，（8分）（2）设A产品投入x万元，则B产品投入10﹣x万元，设企业利润为y万元．（0≤x≤10）令，则=当t=2时，，此时x=10﹣4=6（15分）答：当A产品投入6万元，则B产品投入4万元时，该企业获得最大利润，利润为2.8万元．（16分）20．（12分）已知函数f（x）=2ax+（a∈R）．（1）当时，试判断f（x）在（0，1]上的单调性并用定义证明你的结论；（2）对于任意的x∈（0，1]，使得f（x）≥6恒成立，求实数a的取值范围．【解答】解：（1）∵∴f（x）在（0，1]上的单调递减…（2分）证明：取任意的x1，x2，且0＜x1＜x2≤1∵0＜x1＜x2≤1，∴x1﹣x2＜0，0＜x1x2＜1得f（x1）﹣f（x2）＞0所以f（x）在（0，1]上的单调递减…（8分）（2）由f（x）≥6在（0，1]上恒成立，∴2ax+≥6 恒成立即…（14分）21．（12分）已知函数的值域为集合A，关于x的不等式的解集为B，集合，集合D={x|m+1≤x ＜2m﹣1}（m＞0）（1）若A∪B=B，求实数a的取值范围；（2）若D⊆C，求实数m的取值范围．【解答】解：（1）因为f（x）在[，4]上，单调递增，∵f（）==﹣2，f（4）=log44=1，所以，A=[﹣2，1]．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）又由关于x的不等式可得（2）﹣3x﹣a＞2x，﹣3x﹣a＞x，即x＜﹣，所以，B=（﹣∞，﹣）．﹣﹣﹣﹣﹣（4分）又A∪B=B，∴A⊆B．﹣﹣﹣﹣﹣﹣﹣﹣（5分）所以，﹣＞1，a＜﹣4，即实数a的取值范围为（﹣∞，﹣4）．﹣﹣﹣﹣﹣﹣﹣（6分）（2）因为，所以有，所以﹣1＜x≤5，所以，C=（﹣1，5]，﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）对于集合D={x|m+1≤x＜2m﹣1}（m＞0），若D⊆C，有：①当m+1≥2m﹣1时，即0＜m≤2时，D=∅，满足D⊆C．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）②当m+1＜2m﹣1 时，即m＞2时，D≠∅，所以有：，解得﹣2＜m ≤3，又m＞2，2＜m≤3．﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）综上：由①②可得：实m的取值范围为（0，3]．﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）22．（12分）对于函数f1（x）、f2（x）、h（x），如果存在实数a，b使得h（x）=a•f1（x）+bf2（x），那么称h（x）为f1（x）、f2（x）的和谐函数．（1）已知函数f1（x）=x﹣1，f2（x）=3x+1，h（x）=2x+2，试判断h（x）是否为f1（x）、f2（x）的和谐函数？并说明理由；（2）已知h（x）为函数f 1（x）=log3x，f2（x）=x的和谐函数，其中a=2，b=1，若方程h（9x）+t•h（3x）=0在x∈[3，9]上有解，求实数t的取值范围．【解答】解：（1）h（x）是f1（x）、f2（x）的和谐函数，因为存在a=﹣1，b=1使h（x）=﹣f1（x）+f2（x）…2分设h（x）=af 1（x）+bf2（x），则2x+2=a（x﹣1）+b（3x+1），所以，所以h（x）是f1（x）、f2（x）的和谐函数．…6分（2）解法一：依题意，由方程在x∈[3，9]上有解，即log3（9x）+t•log3（3x）=0在x∈[3，9]上有解，化简得：2+log3x+t（1+log3x）=0…10分设m=log3x，x∈[3，9]，则m∈[1，2]，即（1+m）•t+（t+2）=0原问题可以转化关于m的方程（1+t）m+（t+2）=0在m∈[1，2]上有解，令g（m）=（1+t）m+（t+2）…13分由题意得：g（1）•g（2）≤0，解得．综上：…16分（2）解法二：log3（9x）+t•log3（3x）=0，化简得：2+log3x+t（1+log3x）=0 (10)分因为x∈[3，9]，所以（1+log3x）∈[2，3]，原式可转化为方程在x∈[3，9]区间上有解即求函数在x∈[3，9]的值域…12分令，因为 2≤1+log 3x ≤3由反比例函数性质可得，函数g （x ）的值域为所以实数t的取值范围．…16分．赠送：初中数学几何模型举例【模型四】几何最值模型：图形特征：P ABl运用举例：1. △ABC 中，AB =6，AC =8，BC =10，P 为边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，M 为AP 的中点，则MF 的最小值为MFEB2.如图，在边长为6的菱形ABCD 中，∠BAD ＝60°，E 为AB 的中点，F 为AC 上一动点，则EF +BF 的最小值为_________。

安徽省滁州市2017-2018学年高一上学期期末考试数学试题(word版含答案)

滁州市2017-2018学年第一学期高一期末考试数学试卷第Ⅰ卷（选择题共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合{}{}1,2,4,1,2,3A B ==，则A B = （）A ．{}3,4B ．{}1,2C ．{}2,3,4D ．{}123,4，，2. 已知角α的始边是x 轴的正半轴，终边经过点()3,4-，且4si n 5α=，则t a n α=（） A ．43-B ．34-C ．43D ．343. 计算：114333122x x x -⎛⎫+= ⎪⎝⎭（）A ． 3B ． 2C ．2x +D ．12x +4. 已知向量()()3,2,2,a b x ==，若a b ⊥ ，则23a b -= （）A ．．9 C. 13 D ．5. 若幂函数()af x x =的图象过点()4,2，则满足()11f x ->的实数x 的取值范围是（）A ．()0,1B ．()2,+∞ C. ()1,1- D ．(),2-∞ 6.函数()()1sin cos 32f x x x ππ⎛⎫=++- ⎪⎝⎭的最大值是（） A ．43 B ．23 C. 1 D ．137.下列函数是奇函数，且在()0,+∞上是增函数的是（）A ．21x y x +=B ．21x y x-= C. 22x x y -=+ D ．lg 1y x =+8. 若3sin 4α=，α是第二象限角，则sin 24πα⎛⎫-= ⎪⎝⎭（）A ．16．16- C. 16 D ．116-9.函数33x y x =+的零点为0x ，则（） A ．031,4x ⎛⎫∈--⎪⎝⎭ B ．031,42x ⎛⎫∈-- ⎪⎝⎭ C. 011,24x ⎛⎫∈-- ⎪⎝⎭ D ．01,04x ⎛⎫∈- ⎪⎝⎭10. 在平行四边形ABCD 中，E 是CD 中点，F 是BE 中点，若AF mAB nAD =+，则（）A ．31,42m n == B ．13,44m n == C. 11,22m n == D ．13,24m n ==11.曲线1:sin C y x =，曲线2:cos2C y x =，下列说法正确的是（） A ．将1C 上所有点横坐标扩大到原来的2倍，纵坐标不变，再将所得曲线向左平移4π个单位，得到2C B ．将1C 上所有点横坐标缩小到原来的12，纵坐标不变，再将所得曲线向左平移4π个单位，得到2C C. 将1C 上所有点横坐标扩大到原来的2倍，纵坐标不变，再将所得曲线向左平移2π个单位，得到2C D ．将1C 上所有点横坐标缩小到原来的12，纵坐标不变，再将所得曲线向左平移2π个单位，得到2C 12.若不等式()2log 14x a x +≥对任意的()0,x ∈+∞恒成立，则a 的取值范围是（） A ．(],0-∞ B ．1,4⎛⎤-∞ ⎥⎝⎦ C. [)0,+∞ D ．1,4⎡⎫+∞⎪⎢⎣⎭第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上.13.若cos 2sin cos ααα=+，则tan 2α= ．14. ()()4log 1,01,0x x f x x x ⎧+≥=⎨-<⎩，则()()11f f -+= ．15.若函数()2231y x a x =+-+在[]1,3是单调函数，则实数a 的取值范围是．16.已知函数()()2cos 06f x x πωω⎛⎫=-> ⎪⎝⎭在区间2,63ππ⎡⎤⎢⎥⎣⎦内单调递减，则ω的最大值为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.已知集合{}{}{}|2318,|215,|1A x x B x x C x x a x a =≤-≤=-<=≤≥+或．（1）求,A B A B ；（2）若()R C C A ⊆，求实数a 的取值范围．18.已知向量()([]cos ,sin ,,0,a x x b x π==∈．（1）若a 与b共线，求x 的值；（2）记()f x a b =，求()f x 的最大值和最小值，及相应的x 的值．19.已知函数()31x f x x a+=+的图象过点()1,4-．（1）若()210f x =，求实数x 的值；（2）当[]5,1x ∈-时，求函数()f x 的取值范围． 20.函数()()cos 20,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示．（1）求,,A ωϕ的值；（2）求图中,a b 的值及函数()f x 的递增区间．21.已知,αβ都是锐角，()14sin ,sin 235ααβ=-=．（1）求cos β的值；（2）求()sin αβ-的值．22. 已知函数()3131x x f x +=-．（1）求证：()f x 是奇函数；（2）判断()f x 的单调性，并证明；（3）已知关于t 的不等式()()222310f t t f t -++--<恒成立，求实数t 的取值范围．试卷答案一、选择题1-5: DADCB 6-10:BBCCA 11、12：BD二、填空题13. 13-14. 52 15. 31,,22⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭16.1 三、解答题17.解：{}{}|13,|3A x x B x x =≤≤=<，（1）{}{}|13,|3A B x x A B x x =≤<=≤ ；（2）∵{}|,1C x x a x a =≤≥+或，∴{}|1R C C x a x a =<<+， ∵()R C C A ⊆，∴113a a ≥⎧⎨+≤⎩，∴[]1,2a ∈．18.解：（1）∵a 与bsin 0x x -=，∴tan x =[]0,x π∈，∴3x π=；（2）()cos 2sin 6f x a b x x x π⎛⎫===+ ⎪⎝⎭ ，∵[]0,x π∈，∴7,666x πππ⎡⎤+∈⎢⎥⎣⎦，∴1sin 126x π⎛⎫-≤+≤ ⎪⎝⎭，∴()12f x -≤≤，当62x ππ+=即3x π=时，()f x 取得最大值2；当766x ππ+=，即x π=时，()f x 取得最小值-1．19.解：（1）()1141f a==-+，∴2a =-， ()222223110,3110202x f x x x x +==+=--，∴22721,3x x ==，∴x = （2）()()3273173222x x f x x x x -++===+---，显然()f x 在[)2,+∞与(),2-∞上都是减函数， ∵[](]5,1,2-⊆-∞，∴()f x 在[]5,1-上是减函数， ∵()()77532,13471f f -=+==+=---，∴()[]4,2f x ∈-． 20.解：（1）由图知2452,23123A T πππω⎛⎫===+ ⎪⎝⎭，∴1ω=，∴()()2cos 2f x x ϕ=+，又52,0312f f ππ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭， ∴5cos 1,cos 036ππϕϕ2⎛⎫⎛⎫-+=-+= ⎪ ⎪⎝⎭⎝⎭，且2πϕ<，∴3πϕ=-；（2）由（1）知()2cos 23f x x π⎛⎫=-⎪⎝⎭，由512a T ππ-==， ∴()7,02cos 1123a b f ππ⎛⎫=-==-= ⎪⎝⎭，由()2223k x k k Z ππππ-≤-≤∈得()36k x k k Z ππππ-≤≤+∈，∴()f x 的单调增区间为(),36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦． 21.解：因为,αβ都是锐角()14sin ,sin 235ααβ=-=，所以cos 3α==，且()30,2,cos 24225πππααβαβ<<-<-<-=，所以227sin 22sin cos 2cos sin 99αααααα===-=，（1）()()()21cos cos 22cos 2cos 2sin 2sin 215βααβααβααβ+=--=-+-=⎡⎤⎣⎦；（2）()()()()3sin sin 2sin 2cos cos 2sin 15αβαβααβααβα-=--=---=⎡⎤⎣⎦． 22．（1）证明：由310x-≠，得0x ≠，∵()()31133113x xxxf x f x --++-===---， ∴()f x 是奇函数；（2）解：()f x 的单调减区间为(),0-∞与()0,+∞没有增区间，设120x x <<，则()()()()()()()21121221121212121212233313133313331313131313131x x x x x x x x x x x x x x x x xx f x f x --+++----++-=-==------ ．∵120x x <<，∴21331x x>>， ∴2112330,31,310x x x x->-->，∴()()120f x f x ->，∴()()12f x f x >， ∴()f x 在()0,+∞上是减函数，同理，()f x 在(),0-∞上也是减函数；（3）()f x 是奇函数，∴()()2211f t f t --=-+，∴()()222310f t t f t -++--<化为()()22231f t t f t -+<+，又()()22223120,10,t t t t f x -+=-+>+>在()0,+∞上是减函数，∴22231t t t -+>+，∴1t <，即(),1t ∈-∞．。

2023-2024学年安徽省高一(上)期中数学试卷【答案版】

2023-2024学年安徽省高一（上）期中数学试卷一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合M ＝{﹣1，0，1}，集合N ＝{x ∈R |x 2＝2x }，则M ∩N ＝（） A ．{0，1}B ．{﹣1，0}C ．{0}D ．∅2．已知命题p ：∃x ∈R ，4x ＞x 4，则¬p 是（） A ．∃x ∈R ，4x ≤x 4 B ．∀x ∈R ，4x ＜x 4C ．∀x ∈R ，4x ＞x 4D ．∀x ∈R ，4x ≤x 43．若α是β的必要不充分条件，γ是β的充要条件，则γ是α的（） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件4．已知幂函数f （x ）＝x α（α∈Z ），具有如下性质：f 2（1）+f 2（﹣1）＝2[f （1）+f （﹣1）﹣1]，则f （x ）是（） A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．是非奇非偶函数5．函数f(x)={x +3，x ≤0√x ，x ＞0，且f （a ﹣3）＝f （a +2）（a ∈R ），则f （a ）＝（）A ．2B ．1C ．√2D ．06．已知实数a ，b ，c 满足3×2a ﹣2b +1＝0，且a ＝c +x 2﹣x +1（x ∈R ），则a ，b ，c 的大小关系是（） A ．a ＞b ＞cB ．b ＞a ＞cC ．a ＞c ＞bD ．c ＞b ＞a7．水池有两个相同的进水口和一个出水口，每个口进出的速度如图甲乙所示．某天零点到六点该水池的蓄水量如图丙所示（至少打开一个水口）．给出以下三个论断：①零点到三点只进水不出水；②三点到四点不进水只出水；③四点到六点不进水也不出水．其中正确论断的序号是（）A ．①②B ．②③C ．①③D ．①8．设函数f(x)=√ax 2+bx +c （a ，b ，c ∈R ，且a ＜0）的定义域为D ，若所有点（s ，f （t ））（s ，t ∈D ）构成一个正方形区域，则a ＝（） A ．﹣4B ．﹣5C ．﹣6D ．﹣8二、选择题：本题共4小题，每小题5分，共20分。

安徽省滁州市2017-2018学年高一上学期期末考试数学试题 Word版含解析

滁州市2017-2018学年第一学期高一期末考试数学试卷第Ⅰ卷（选择题共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合，则（）A. B. C. D.【答案】D2. 已知角的始边是轴的正半轴，终边经过点，且，则（）A. B. C. D.【答案】A【解析】依题意可知，故.3. 计算：（）A. 3B. 2C.D.【答案】D【解析】原式.5. 若幂函数的图象过点，则满足的实数的取值范围是（）A. B. C. D.【答案】B【解析】依题意有，，.6. 函数的最大值是（）A. B. C. 1 D.【答案】B【解析】，故最大值为.7. 下列函数是奇函数，且在上是增函数的是（）A. B. C. D.【答案】B【解析】选项为偶函数，选项为非奇非偶函数.选项在为减函数，在为增函数.选项在上为增函数，符合题意.【点睛】本题主要考查函数的奇偶性和单调性.判断函数的奇偶性，首先判断函数的定义域是否关于原点对称，选项定义域显然不关于原点对称，故为非奇非偶函数.然后计算，化简后看等于还是.函数的单调性中是对钩函数，在不是递增函数.8.9. 函数的零点为，则（）A. B. C. D.【答案】C【解析】，，故函数的零点在区间.11. 曲线，曲线，下列说法正确的是（）A. 将上所有点横坐标扩大到原来的2倍，纵坐标不变，再将所得曲线向左平移个单位，得到B. 将上所有点横坐标缩小到原来的，纵坐标不变，再将所得曲线向左平移个单位，得到C. 将上所有点横坐标扩大到原来的2倍，纵坐标不变，再将所得曲线向左平移个单位，得到D. 将上所有点横坐标缩小到原来的，纵坐标不变，再将所得曲线向左平移个单位，得到【答案】B【解析】由于，故首先横坐标缩小到原来得到，再向左平移个单位得到.故选.12. 若不等式对任意的恒成立，则的取值范围是（）A. B. C. D.【答案】D【解析】当时，原不等式化为，不恒成立，排除，故选.第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上.13.14. ，则__________．【答案】【解析】，，故原式.15. 若函数在是单调函数，则实数的取值范围是__________．【答案】【解析】由于函数为二次函数，对称轴为，只需对称轴不在区间上即可，即或，解得.【点睛】本题主要考查二次函数单调区间的知识.对于二次函数来说，它的单调区间主要由开口方向和对称轴来决定.当开口向上时，左减右增，当开口向下是，左增右减.本题中由于题目只需要区间上的单调函数，不需要递增还是递减，故只需对称轴不在给定区间内即可.16.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知集合．（1）求；（2）若，求实数的取值范围．【答案】（1）；（2）【解析】【试题分析】（1）首先求得，由此求得的值.（2），由于，故，解得.【试题解析】解：，（1）；（2）∵，∴，∵，∴，∴．18.19. 已知函数的图象过点．（1）若，求实数的值；（2）当时，求函数的取值范围．【答案】（1）（2）【解析】【试题分析】（1）将点代入函数，由此求得的值，进而得出的表达式.解方程，可求得实数的值.（2）将分离常数，得到，它在上为减函数，在区间端点取得最小值和最大值.由此求得函数的值域.【试题解析】解：（1），∴，，∴，∴；（2），显然在与上都是减函数，∵，∴在上是减函数，∵，∴．20. 函数的部分图象如图所示．（1）求的值；（2）求图中的值及函数的递增区间．【答案】（1）（2）【解析】【试题分析】（1）根据图像最大值求得,根据可求得，在根据图像上一个点，可求得的值.（2）利用求出，利用周期为可求得的值.将代入余弦函数的单调递增区间，求得的范围即函数的递增区间.【试题解析】解：（1）由图知，∴，∴，又，∴，且，∴；（2）由（1）知，由，∴，由得，∴的单调增区间为．21.22. 已知函数．（1）求证：是奇函数；（2）判断的单调性，并证明；（3）已知关于的不等式恒成立，求实数的取值范围．【答案】（1）见解析（2）见解析（2）【解析】【试题分析】（1）定义域为关于原点对称，判断故函数为奇函数.（2）函数在定义域的两个区间上都是减函数.利用定义法，计算，由此判断出函数的单调性.（3）根据函数的单调性和奇偶性，将原不等式转化为即，解不等式得.【点睛】本题主要考查函数奇偶性的判断，考查利用定义法求函数单调性，考查利用函数的奇偶性和单调性求参数的取值范围.判断函数的奇偶性首先要求出函数的定义域，看定义域是否关于原点对称，然后再判断与的关系，进而判断函数的奇偶性.定义法判断函数的单调性，需计算的值来判断.【试题解析】（1）证明：由，得，∵，∴是奇函数；（2）解：的单调减区间为与没有增区间，设，则．∵，∴，∴，∴，∴，∴在上是减函数，同理，在上也是减函数；（3）是奇函数，∴，∴化为，又在上是减函数，∴，∴，即．。

2023-2024学年安徽省滁州市高一(上)期中数学试卷【答案版】

2023-2024学年安徽省滁州市高一（上）期中数学试卷一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求. 1．已知集合A＝{﹣3，﹣2，0，2}，B＝{x||x﹣1|＜2}，则A∩B＝（）A．{﹣2，0}B．{0，2}C．{﹣2，2}D．{﹣2，0，2}2．如图，f：A→B表示从集合A到集合B的函数，若f（a）＝2，则a的值为（）A．1B．2C．1或2D．33．“一切分数都是有理数”的否定是（）A．一切分数都不是有理数B．一切分数不都是有理数C．有些分数不是有理数D．有些分数是有理数4．现有下列函数：①y＝x3；②y＝4x2；③y＝x5+1；④y＝（x﹣1）2；⑤y＝x，其中幂函数的个数为（）A．4B．3C．2D．15．对于实数a，b，c，下列命题为真命题的是（）A．若a＞b，则1a ＜1bB．若a＞b，则ac2＞bc2C．若a3＞b3，则a＞b D．若|a|＞|b|，则a＞b6．已知函数f（x）为R上的奇函数，当x＜0时，f（x）＝x+2，则f（0）+f（3）＝（）A．﹣3B．﹣1C．1D．37．若x，y为实数，则“x2+y2+4x+3≤0”是“（x+4）（x+3）≥0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件8．设f(x)=|x+1x −a|(a∈R)，记f（x）在区间[12，4]上的最大值为M（a），则M（a）的最小值为（）A．0B．98C．158D．2二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．9．下列关系正确的是（）A．a∈{a，b，c}B．∅∈{0}C．{0，1}⫋N D．√2∈Q10．下列结论正确的是（）A ．当x ≥0时，x +1+1x+1≥2 B ．当x ＞0时，√x ≥2 C ．x +1x的最小值为2D ．√x 2+21√x 2+2的最小值为211．对于给定的实数a ，关于实数x 的不等式a （x ﹣a ）（ax +a ）≥0的解集不可能为（） A ．∅B ．{x |a ≤x ≤﹣1}C ．{x |x ≤a 或x ≥﹣1}D ．R12．函数y ＝f （x ）是定义域为R 的奇函数，且对于任意的x 1≠x 2，都有f(x 1)−f(x 2)x 1−x 2＞1成立．若f （m ）＞m ，则实数m 的取值可以是（） A ．﹣1B ．0C ．1D ．2三、填空题：本题共4小题，每小题5分，共20分．13．已知集合M ＝{3，2a }，N ＝{a +1，3}，若M ⊆N ，则a ＝． 14．已知f(xx+1)=x ﹣1，则f （x ）＝． 15．已知函数f(x)=x+13−2x 的值域是[1，2]，那么函数f （x ）的定义域是． 16．若x ＞0，y ＞0，x 2+y 2＝xy （x 2y 2+2），则1x+1y 的最小值为．四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17．（10分）已知集合A ＝{x |1≤x ＜6}，B ＝{x |2＜x ＜9}，C ＝{x |x ＜a }．（1）求A ∪B ；（2）若A ∩C ≠∅，求a 的取值范围．18．（12分）已知p ：√x −1≤1，q ：﹣1≤x ≤a ．（1）若q 是p 的必要不充分条件，求实数a 的取值范围；（2）若a ＝1，且p ，q 至少有一个成立，求x 的取值范围． 19．（12分）已知函数f(x)={−x −3，x ＜0，x 2−2x ，x ≥0.（1）求f （1），f （f （﹣6））的值；（2）在给定的坐标系中，画出f （x ）的图象（无需列表）；（3）根据（2）中的图象，写出f （x ）的单调区间和值域．20．（12分）已知函数f(x)=x+bax2+1是定义域为（﹣1，1）的奇函数，且f(12)=25．（1）求实数a，b的值；（2）判断函数f（x）在（﹣1，1）上的单调性并给出证明；（3）解关于t的不等式f（t+1）+f（2t）＜0．21．（12分）已知不等式（1+k）x≤k2+k+4，其中x，k∈R．（1）若x＝3，解上述关于k的不等式；（2）若不等式对∀k∈[﹣4，+∞）恒成立，求x的取值范围．22．（12分）某生活超市经销某种蔬菜，经预测从上架开始的第n（n∈N*且n≤5）天，该蔬菜每天销量（单位：kg）为100﹣10|n﹣3|．已知该种蔬菜进货价格是3元/kg，销售价格是5元/kg，该超市每天销售剩余的该种蔬菜可以全部以2元/kg的价格处理掉．若该生活超市每天都购进该种蔬菜xkg（80≤x≤100），从上架开始的5天内销售该种蔬菜的总利润为f（x）元．（1）求f（x）的解析式；（2）若从上架开始的5天内，记该种蔬菜按5元售价销售的总销量与总进货量之比为Q，设g（x）＝f（x）（1﹣Q）（80≤x≤90），求g（x）的最大值与最小值．2023-2024学年安徽省滁州市高一（上）期中数学试卷参考答案与试题解析一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合题目要求. 1．已知集合A＝{﹣3，﹣2，0，2}，B＝{x||x﹣1|＜2}，则A∩B＝（）A．{﹣2，0}B．{0，2}C．{﹣2，2}D．{﹣2，0，2}解：A＝{﹣3，﹣2，0，2}，B＝{x||x﹣1|＜2}＝{x|﹣1＜x＜3}，所以A∩B＝{0，2}．故选：B．2．如图，f：A→B表示从集合A到集合B的函数，若f（a）＝2，则a的值为（）A．1B．2C．1或2D．3解：观察图，f（a）＝2，则a＝1或2．故选C．3．“一切分数都是有理数”的否定是（）A．一切分数都不是有理数B．一切分数不都是有理数C．有些分数不是有理数D．有些分数是有理数解：根据题意，“一切分数都是有理数”是全称量词命题，则其否定是“有些分数不是有理数”．故选：C．4．现有下列函数：①y＝x3；②y＝4x2；③y＝x5+1；④y＝（x﹣1）2；⑤y＝x，其中幂函数的个数为（）A．4B．3C．2D．1解：根据幂函数的定义，①y＝x3和⑤y＝x是幂函数，其余的不是幂函数．故选：C．5．对于实数a，b，c，下列命题为真命题的是（）A．若a＞b，则1a ＜1bB．若a＞b，则ac2＞bc2C．若a3＞b3，则a＞b D．若|a|＞|b|，则a＞b 解：当a＝1，b＝﹣1时，A显然错误；当c＝0时，B显然错误；因为y＝x3在R上单调递增，若a3＞b3，则一定有a＞b，C正确；当a＝﹣2，b＝1时，D显然错误．故选：C．6．已知函数f（x）为R上的奇函数，当x＜0时，f（x）＝x+2，则f（0）+f（3）＝（）A．﹣3B．﹣1C．1D．3解：因为函数f（x）为R上的奇函数，当x＜0 时，f（x）＝x+2，所以f（3）＝﹣f（﹣3）＝﹣（﹣3+2）＝1．而f（0）＝0，所以f（0）+f（3）＝1．故选：C．7．若x，y为实数，则“x2+y2+4x+3≤0”是“（x+4）（x+3）≥0”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解：易知y2≥0，因为x2+y2+4x+3≤0，则x2+4x+3≤0，解得﹣3≤x≤﹣1，所以x+3≥0，x+4＞0，即（x+4）（x+3）≥0成立，充分性成立；若（x+4）（x+3）≥0，取x＝0，此时x2+y2+4x+3≤0不成立，故必要性不成立．故选：A．8．设f(x)=|x+1x −a|(a∈R)，记f（x）在区间[12，4]上的最大值为M（a），则M（a）的最小值为（）A．0B．98C．158D．2解：设g(x)=x+1x−a，x∈[12，4]，则g（x）在[12，1]上单调递减，在[1，4]上单调递增，且g(12)=52−a，g(1)=2−a，g(4)=174−a，所以M（a）是|52−a|，|2−a|，|174−a|三者中的较大者，如图：M（a）表示的函数图象为图中粗线部分，且M(a)={174−a，a≤258a−2，a＞258，所以当a=258时，M（a）的最小值为98．故选：B．二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．9．下列关系正确的是（）A．a∈{a，b，c}B．∅∈{0}C．{0，1}⫋N D．√2∈Q解：对于A，因为a是集合{a，b，c}中的元素，所以a∈{a，b，c}，所以选项A正确；对于B，因为⌀是任何集合的子集，所以⌀⊆{0}，所以选项B错误；对于C，因为N中含有元素0，1，而且还有其他元素，所以{0，1}⫋N，所以选项C正确；对于D，因为√2是无理数，而Q是有理数集，所以√2∉Q，所以选项D错误．故选：AC．10．下列结论正确的是（）A．当x≥0时，x+1+1x+1≥2B．当x＞0时，√x≥2C．x+1x 的最小值为2D．√x2+21√x2+2的最小值为2解：A：当x≥0时，x+1+1x+1≥2√(x+1)⋅(1x+1)=2，当且仅当x+1=1x+1时，即x＝0时等号成立，正确；B：当x＞0时，√x =√x+√x≥2√√x⋅√x=2，当且仅当√x=1√x时，即x＝1时等号成立，正确；C：当x＜0时，C显然错误；D：因为√x2+2+1√x2+2≥2√√x2+2⋅1√x2+2=2，当且仅当√x2+2=1√x2+2时，此时x2+2＝1无实数解，故取不到等号，不正确．故选：AB．11．对于给定的实数a，关于实数x的不等式a（x﹣a）（ax+a）≥0的解集不可能为（）A．∅B．{x|a≤x≤﹣1}C．{x|x≤a或x≥﹣1}D．R解：a（x﹣a）（ax+a）≥0，则a2（x﹣a）（x+1）≥0，当a＝0时，不等式的解集为R，当a≠0时，不等式变形为（x﹣a）（x+1）≥0，方程（x﹣a）（x+1）＝0的根为x＝a或x＝﹣1，当a＜﹣1时，不等式的解集为{x|x≤a或x≥﹣1}，当a＝﹣1时，不等式的解集为R，当a ＞﹣1且a ≠0时，不等式的解集为{x |x ≤﹣1或x ≥a }，故AB 错误，CD 正确．故选：AB ．12．函数y ＝f （x ）是定义域为R 的奇函数，且对于任意的x 1≠x 2，都有f(x 1)−f(x 2)x 1−x 2＞1成立．若f （m ）＞m ，则实数m 的取值可以是（） A ．﹣1B ．0C ．1D ．2解：因为对于任意的x 1≠x 2，都有f(x 1)−f(x 2)x 1−x 2＞1，当x 1＞x 2时f （x 1）﹣f （x 2）＞x 1﹣x 2，即f （x 1）﹣x 1＞f （x 2）﹣x 2，当x 1＜x 2时f （x 1）﹣f （x 2）＜x 1﹣x 2，即f （x 1）﹣x 1＜f （x 2）﹣x 2，即g （x ）＝f （x ）﹣x 在定义域R 上单调递增，又y ＝f （x ）是定义域为R 的奇函数，所以f （0）＝0，所以g （0）＝f （0）﹣0＝0，若f （m ）＞m ，即f （m ）﹣m ＞0，即g （m ）＞g （0），所以m ＞0．故选：CD ．三、填空题：本题共4小题，每小题5分，共20分．13．已知集合M ＝{3，2a }，N ＝{a +1，3}，若M ⊆N ，则a ＝ 1 ．解：由于集合M ＝{3，2a }，N ＝{a +1，3}，M ⊆N ，所以 2a ＝a +1，即 a ＝1，从而得到 M ＝{3，2}，N ＝{2，3}，满足条件M ⊆N ．故答案为：1． 14．已知f(xx+1)=x ﹣1，则f （x ）＝ 2x−11−x （x ≠1）．解：∵f(xx+1)=x ﹣1，令t =xx+1，则x =t1−t ， ∵t =x x+1=x+1−1x+1=1−1x+1，∴t ≠1， ∴f （t ）=t 1−t −1=2t−11−t （t ≠1），即f （x ）=2x−11−x（x ≠1）．故答案为：f （x ）=2x−11−x（x ≠1）． 15．已知函数f(x)=x+13−2x 的值域是[1，2]，那么函数f （x ）的定义域是 [23，1] ．解：f(x)=x+13−2x =12(53−2x −1)，由1≤f （x ）≤2得3≤53−2x ≤5，即1≤3−2x ≤53，解得23≤x ≤1，所以f （x ）的定义域是[23，1]．故答案为：[23，1]．16．若x ＞0，y ＞0，x 2+y 2＝xy （x 2y 2+2），则1x+1y的最小值为 2 ．解：由x 2+y 2＝xy （x 2y 2+2），可得（x ﹣y ）2＝（xy ）3，两边同除以（xy ）2得（1y−1x）2＝xy ，又因为 (1x +1y )2=(1y −1x )2+4⋅1xy =xy +4xy ≥2√xy ⋅4xy =4，当且仅当xy =4xy ，即{x =2+√2y =2−√3或{x =2−√2y =2+√2时等号成立，所以1x+1y≥√4=2．故答案为：2．四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. 17．（10分）已知集合A ＝{x |1≤x ＜6}，B ＝{x |2＜x ＜9}，C ＝{x |x ＜a }．（1）求A ∪B ；（2）若A ∩C ≠∅，求a 的取值范围．解：（1）因为A ＝{x |1≤x ＜6}，B ＝{x |2＜x ＜9}，所以A ∪B ＝{x |1≤x ＜9}；（2）因为A ＝{x |1≤x ＜6}，C ＝{x |x ＜a }且A ∩C ≠∅，所以a ＞1，即a 的取值范围为{a |a ＞1}．18．（12分）已知p ：√x −1≤1，q ：﹣1≤x ≤a ．（1）若q 是p 的必要不充分条件，求实数a 的取值范围；（2）若a ＝1，且p ，q 至少有一个成立，求x 的取值范围．解：（1）设A ={x|√x −1≤1}={x|1≤x ≤2}，B ＝{x |﹣1≤x ≤a }，因为q 是p 的必要不充分条件，所以A 是B 的真子集，则a ≥2，所以实数a 的取值范围为[2，+∞）．（2）当a ＝1时，p ：1≤x ≤2，q ：﹣1≤x ≤1，考虑“p ，q 至少有一个成立”的对立面：p ，q 均不成立，此时{x ＜1或x ＞2，x ＜−1或x ＞1，，解得x ＜﹣1或x ＞2，故p ，q 至少有一个成立时，x 的取值范围为[﹣1，2]． 19．（12分）已知函数f(x)={−x −3，x ＜0，x 2−2x ，x ≥0.（1）求f （1），f （f （﹣6））的值；（2）在给定的坐标系中，画出f （x ）的图象（无需列表）；（3）根据（2）中的图象，写出f（x）的单调区间和值域．解：（1）f（1）＝12﹣2×1＝﹣1；f（﹣6）＝﹣（﹣6）﹣3＝3，f（f（﹣6））＝f（3）＝32﹣2×3＝3．（2）由题意，得函数f（x）的图象如下：（3）函数f（x）的单调减区间为（﹣∞，0），（0，1）；单调增区间为（1，+∞）．函数f（x）的值域为（﹣3，+∞）．20．（12分）已知函数f(x)=x+bax2+1是定义域为（﹣1，1）的奇函数，且f(12)=25．（1）求实数a，b的值；（2）判断函数f（x）在（﹣1，1）上的单调性并给出证明；（3）解关于t的不等式f（t+1）+f（2t）＜0．解：（1）函数f(x)=x+bax2+1定义在（﹣1，1）上的奇函数，且f(12)=25，∴f（﹣x）＝﹣f（x），∴−x+ba(−x)2+1=−x+bax2+1，即﹣x+b＝﹣x﹣b，故b＝0，又f(12)=25，即12a×14+1=25，解得a＝1，即a＝1，b＝0．（2）由（1）可得f(x)=x1+x2，f(x)=x1+x2在（﹣1，1）上单调递增，证明如下：在（﹣1，1）上任取x1，x2，不妨令x1＜x2，则 f(x 1)−f(x 2)=x 11+x 12−x 21+x 22=(x 1−x 2)(1−x 1x 2)(1+x 12)(1+x 22)， ∵﹣1＜x 1＜x 2＜1，∴x 1−x 2＜0，1−x 1x 2＞0，1+x 12＞0，1+x 22＞0，∴f （x 1）﹣f （x 2）＜0，∴f （x 1）＜f （x 2）， ∴函数f （x ）在（﹣1，1）上单调递增．（3）由f （t +1）+f （2t ）＜0可得f （t +1）＜﹣f （2t ）＝f （﹣2t ），故{−1＜t +1＜1−1＜2t ＜1t +1＜−2t，解得−12＜t ＜−13，故关于t 的不等式f （t +1）+f （2t ）＜0的解集为(−12，−13)． 21．（12分）已知不等式（1+k ）x ≤k 2+k +4，其中x ，k ∈R ．（1）若x ＝3，解上述关于k 的不等式；（2）若不等式对∀k ∈[﹣4，+∞）恒成立，求x 的取值范围．解：（1）若x ＝3，则不等式（1+k ）x ≤k 2+k +4变形为k 2﹣2k +1≥0，即（k ﹣1）2≥0，解得k ∈R ，故不等式的解集为R ；（2）不等式（1+k ）x ≤k 2+k +4对∀k ∈[﹣4，+∞）恒成立，当k ＝﹣1时，0≤（﹣1）2+（﹣1）+4，即0≤4，x ∈R ；当k ＞﹣1时，x ≤k 2+k+41+k 恒成立，∵k 2+k+41+k=k +4k+1=k +1+4k+1−1≥2√(k +1)⋅4k+1−1＝3，当且仅当k +1=4k+1，即k ＝1时，等号成立， ∴x ≤3；当﹣4≤k ＜﹣1时，x ≥k 2+k+41+k 恒成立，∵k 2+k+41+k=k +4k+1=k +1+4k+1−1＝﹣[﹣（k +1）+4−(k+1)]﹣1≤﹣5，当且仅当k ＝﹣3时，等号成立， ∴x ≥﹣5．综上，x 的取值范围为[﹣5，3]．22．（12分）某生活超市经销某种蔬菜，经预测从上架开始的第n （n ∈N *且n ≤5）天，该蔬菜每天销量（单位：kg ）为100﹣10|n ﹣3|．已知该种蔬菜进货价格是3元/kg ，销售价格是5元/kg ，该超市每天销售剩余的该种蔬菜可以全部以2元/kg 的价格处理掉．若该生活超市每天都购进该种蔬菜xkg （80≤x ≤100），从上架开始的5天内销售该种蔬菜的总利润为f （x ）元．第11页（共11页）（1）求f （x ）的解析式；（2）若从上架开始的5天内，记该种蔬菜按5元售价销售的总销量与总进货量之比为Q ，设g （x ）＝f （x ）（1﹣Q ）（80≤x ≤90），求g （x ）的最大值与最小值．解：（1）由第n 天销量为100﹣10|n ﹣3|kg ，可得前5天销量依次为80kg ，90kg ，100kg ，90kg ，80kg ，当80≤x ≤90时，可得f （x ）＝2×80×2﹣1×（x ﹣80）×2+4x +2x ＝4x +480；当90＜x ≤100时，可得f （x ）＝2×80×2﹣1×（x ﹣80）×2+2×90×2﹣1×（x ﹣90）×2+2x ＝﹣2x +1020，所以f （x ）的解析式为f(x)={4x +480，80≤x ≤90−2x +1020，90＜x ≤100．（2）从上架开始的5天内该种蔬菜的总进货量为5xkg ，当80≤x ≤90时，Q =160+3x 5x ，可得1−Q =2x−1605x 则g(x)=(2x−160)(4x+480)5x =85x −15360x+64，因为y =85x 与y =−15360x+64在[80，90]上都是增函数，所以g （x ）在[80，90]上是增函数，所以g(x)max =g(90)=1123，g （x ）min ＝g （80）＝0．。

2017-2018学年度高一上学期期中考试数学试卷(含答案)

2017-2018学年度高一上学期期中考试数学(总分150) 时间:120分钟一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1. 设集合}1,0,1{-=M ，{}1,0,2-=N ，则N M ⋂＝( )A ．{－1,0,1}B ．{0,1}C ．{1}D ．{0} 2. 函数)13lg(13)(2++-=x xx x f 的定义域是( )A ．),31(+∞-B ．)1,31(- C. )31,31(- D.)31,(--∞3. 设221(1),()log (1).x x f x x x ⎧+≤=⎨>⎩ 则(1)(4)f f += ( )A. 5B. 6C. 7D. 8 4.判断下列各组中的两个函数是同一函数的为（）A ．3)5)(3(1+-+=x x x y ，52-=x y ；B ．x x f =)(，2)(x x g =；C．()f x =()F x = D ．1()|25|f x x =-, 2()25f x x =- 5．()2333)2(ππ-+-的值为（）A.5B. 52-πC. 1-D.π25-6.如果集合A={x |a x 2＋2x ＋1=0}中只有一个元素，则a 的值是（） A ．0 B ．0 或1 C ．1 D ．不能确定7、已知幂函数()y f x =的图象过⎛ ⎝⎭，则它的一个单调递减区间是（） A.),2(+∞ B ．(),0-∞ C ．(),-∞+∞ D ．[)0,+∞8. 方程330x x --=的实数解落在的区间是（）A ．[1,0]-B ．[0,1]C ．[1,2] D.[2,3] 9．若2()2(1)2f x x a x =+-+在(,4]-∞上是减函数，则a 的取值范围是（） A ．(,3]-∞- B ．[3,)-+∞ C ．(,5]-∞D ．[3,)+∞10. 函数121()3xf x x ⎛⎫=- ⎪⎝⎭的零点个数为A ．3B ．2C ．1D ．011.函数与（）在同一坐标系中的图像只可能是( ）12.若函数()y f x =定义域为R ，且满足f (－x )＝－f (x )，当a ∈(－∞，0], b ∈(－∞，0]时,总有()()0f a f b a b->-(a ≠b )，若f (m ＋1)＞f (2)，则实数m 的取值范围是( )A ．－3≤m ≤1B ．m ＞1C ．－3＜m ＜1D ．m ＜－3或m ＞1二、填空题：请把答案填在题中横线上（本大题共4个小题，每小题5分，共20分）13.已知f (x )是定义在R 上的奇函数,当x >0时,f (x)=1+,则f (-2)=14.函数32+=-x a y （a >0且a ≠1）的图象必经过点 15.函数)2(log 22+=x y 的值域为 .16．关于函数f(x)＝lg 21x x＋(x>0，x ∈R)，下列命题正确的是____ ____．(填序号)①函数y ＝f(x)的图象关于y 轴对称； ②在区间(－∞，0)上，函数y ＝f(x)是减函数； ③函数y ＝f(x)的最小值为lg2；④在区间(1，＋∞)上，函数y ＝f(x)是增函数．x a y =x y alog -=1,0≠>a a 且三、解答题（本大题共6小题，满分70分，解答题写出必要的文字说明、推演步骤）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

全椒中学2017－2018学年度第一学期期中考试高一数学试卷一、选择题：（每题5分，共60分，每题有且只有一个答案）1. 三条直线两两相交，可确定的平面个数是( )A. 1B. 1或3C. 1或2D. 3【答案】B【解析】空间两两相交的三条直线，如果交于一点，可以确定的平面个数是1个或3个，如果交于不共线的三点，可以确定的平面个数是1个．∴空间两两相交的三条直线，可以确定的平面个数是1或3．故选：B ．2. 已知直线和圆相切，则三条边长分别为|a|，|b|，|c|的三角形( )A. 是锐角三角形B. 是直角三角形C. 是钝角三角形D. 不存在【答案】B【解析】试题分析：直线（）与圆相切，则圆心到直线的距离等于圆的半径，即，，所以三角形为直角三角形.考点：圆的切线；3. 点M(x0,y0)是圆x2+y2=a2 (a>0)内不为圆心的一点，则直线x0x+y0y=a2与该圆的位置关系是（）A. 相切B. 相交C. 相离D. 相切或相交【答案】C【解析】试题分析：圆心到直线的距离，即圆心到直线的距离大于圆的半径，故可知直线与圆的位置关系是相离．故选C.考点：点到直线的距离.4. 命题：（1）夹在两平行平面间的两个几何体，被一个平行于这两个平面的平面所截，若截面积相等，则这两个几何体的体积相等；（2）直棱柱和圆柱侧面展开图都是矩形；（3）斜棱柱的体积等于与它的一条侧棱垂直的截面面积乘以它的任一条侧棱；（4）平行六面体的对角线交于一点，且互相平分；其中正确的个数是( )A. 4个B. 3个C. 2个D. 1个【答案】A【解析】对于（1），根据祖暅原理：“夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等”，正确；对于（2），直棱柱和圆柱的侧面展开图都是矩形，正确；对于（3），斜棱柱的体积等于与它的一条侧棱垂直的截面面积乘以它的一条侧棱，正确；对于（4），平行六面体的任意两条对角线所在的四边形是平行四边形，所以这两条对角线交于一点，且互相平分，正确；综上，正确命题是（1）（2）（3）（4），共4个．故选：A．5. 在△ABC中，若则 ( )A. B. C. D.【答案】B【解析】, , ,,则，选B .6. 与直线2x+y－1=0关于点（1，0）对称的直线方程是（）A. 2x+y－3=0B. 2x+y+3=0C. x+2y+3=0D. x+2y－3=0【答案】A【解析】在所求直线上取点（x，y），关于点（1，0）对称的点的坐标为（a，b），则...............7. 设地球半径为R，在北纬30°圈上有甲、乙两地，它们的经度差为120°，那么这两地间的纬线之长为（）A. πRB. πRC. πRD. 2πR【答案】A【解析】如图所示，设球心为O，北纬30°圈所在的小圆圆心为Q，甲、乙两地分别对应A、B两点，连接QO、QA、QB、OA、OB，则OQ⊥平面QAB，∠OAQ=30°，∠AQB=120°=在Rt△OAQ中，OA=R，可得AQ=OAcos∠OAQ=Rcos30°=R在圆Q中，A、B的经度差为120°，∴弧AB的长为×R=πR故选A8. 圆x2+2x+y2+4y-3=0上到直线x+y+1=0的距离为的点共有（）A. 1个B. 2个C. 3个D. 4个【答案】C【解析】方程化为圆心为，半径为；圆心到直线的距离为。

所以圆上到直线的距离为的点共有3个。

故选C9. 中，若，则形状必为（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 以上答案均有可能【答案】C【解析】∵sinA＜cosB，∴sinA＜sin∵0＜A＜，<<∴0＜A＜∴0＜A+B＜∴C＞∴△ABC为钝角三角形故选C．点睛：本题考查三角形形状的判定，考查了诱导公式，考查正弦函数的单调性，属于基础题．10. 如图是一个几何体的三视图，则这个几何体的体积是（）A. 27B. 30C. 33D. 36【答案】B【解析】解：根据已知中的三视图可知该几何体由一个正方体和一个正四棱锥组成其中正方体的棱长为3，故V正方体=3×3×3=27下四棱锥的底面棱长为3，高为1，故V正四棱锥=×3×3×1=3故这个几何体的体积V=27+3=30 故选B．11. 关于“斜二测”直观图的画法，下列说法中正确的是（）A. 等腰三角形的直观图仍为等腰三角形；B. 圆的直观图仍为圆；C. 正方形的直观图为平行四边形；D. 梯形的直观图不是梯形.【答案】C【解析】根据斜二侧画法画水平放置的平面图形时的画法原则，可得：等腰三角形的直观图不再是等腰三角形，圆的直观图不为圆；正方形的直观图是平行四边形，梯形的直观图还是梯形，故选：C点睛：本题考查的知识点是斜二侧画法，熟练掌握斜二侧画法的作图步骤及实质是解答的关键．12. 已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（）A. 1B.C.D. 2【答案】C【解析】试题分析：设两圆的圆心分别为、，球心为，公共弦为，其中点为，则为矩形，于是对角线，而，∴，故选C．考点：球的表面积和体积.视频二．填空题：每小题4分，共16分.13. 空间两点P1（4，1，9）、P2（2，4，3）的距离|P1P2|=______________.【答案】7【解析】故答案为714. 有一块直角三角板ABC，=30°，=90°，BC边贴于桌面上，当三角板和桌面成45°角时，AB边与桌面所成的角的正弦值是________________.【答案】故答案为15. 如图所示，在单位正方体ABCD-A1B1C1D1的对角线A1B 上存在一点P，使得AP＋D1P最短，则AP＋D1P的最小值为________.【答案】【解析】如图所示，把对角面A1C绕A1B旋转至A1BC′D1′，使其与△AA1B在同一平面上，连接AD1′，则AD1′=为所求的最小值．故答案为16. 已知定点A(0，1),点B在直线x+y=0上运动，当线段AB最短时，点B的坐标是___________________.【答案】B(-，)【解析】定点A（0，1），点B在直线x+y=0上运动，当线段AB最短时，就是直线AB和直线x+y=0垂直，AB的方程为：y-1=x，它与x+y=0联立解得x=-，，y＝所以B的坐标是(-，)故答案为(-，)点睛：本题考查点到直线的距离垂线段最短，由两线垂直写直线方程并求直线交点的问题，注意计算的准确性.三．解答题：本大题共6小题，解答应写出文字说明、证明过程或演算步骤.17. 在△ABC中，角A、B、C所对的边分别为a、b、c，且（1）判断△ABC的形状，并加以证明；（2）当c = 1时，求△ABC周长的最大值.【答案】(1)见解析；（2）ABC周长的最大值为.【解析】试题分析：（1）由可得：即cosA=，即b=c×cosA由余弦定理得：∴c2=a2+b2即得三角形形状（2）由（1）知△ABC为直角三角形，c为斜边，当c=1时设另两直角边长分别为a，b，则a2+b2=1∵∴△ABC周长=1+a+b即得△ABC周长的最大值.试题解析：（1）原式可得：即cosA=即b=c×cosA由余弦定理得：∴c2=a2+b2即△ABC为直角三角形（2）由（1）知△ABC为直角三角形，c为斜边当c=1时设另两直角边长分别为a，ba2+b2=1∵∴△ABC周长=1+a+b当且仅当a=b即△ABC为等腰直角三角形时取等号.∴△ABC周长的最大值为18. 已知曲线C：x2+y2-2x-4y+m=0（1）当m为何值时，曲线C表示圆；（2）若曲线C与直线x+2y-4=0交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值。

【答案】（1）m<5；（2）m=.【解析】试题分析：（1）由二元二次方程表示圆的条件D2+E2-4F大于0列出关于m的不等式，求出不等式的解集即可得到m的取值范围；（2）设出曲线与直线的交点M和N的坐标，联立曲线C与直线的方程，消去y后得到关于x的一元二次方程，利用韦达定理表示出两根之和与两根之积，然后由OM与ON垂直得到M和N横坐标之积与纵坐标之积的和为0，由直线方程化为横坐标的关系式，把表示出的两根之和与两根之积代入即可求出m的值．试题解析：（1）由D2+E2-4F=4+16-4m=20-4m>0，得m<5（2）设M(x1,y1),N(x2,y2)，由OM⊥ON得x1x2+ y1y2=0.将直线方程x+2y-4=0与曲线C：x2+y2-2x-4y+m=0联立并消去y得5x2-8x+4m-16=0，由韦达定理得x1+x2=①,x1x2=②，=64-20（4m-16）=384-80m﹥0﹥所以m﹤4又由x+2y-4=0得y= (4-x),∴x1x2+y1y2=x1x2+(4-x1)· (4-x2)= x1x2-( x1+x2)+4=0.将①、②代入得m=,满足﹥ 0.19. 如图，球面上有四个点P、A、B、C，如果PA，PB，PC两两互相垂直，且PA=PB=PC=a，求这个球的表面积。

【答案】S球=4πR2=3πa2【解析】如题图，设过A、B、C三点的球的截面圆半径为r，圆心为O′，球心到该圆面的距离为d，在三棱锥PABC中，∵PA、PB、PC两两垂直，PA＝PB＝PC＝a，∴AB＝AC＝BC＝a，且点P在△ABC内的射影是△ABC的中心O′，由正弦定理，得＝2r，∴r＝ a.又根据球的截面圆性质，有OO′⊥平面ABC，而PO′⊥平面ABC，∴P、O、O′三点共线，球的半径R＝.又PO′＝＝＝a，∴OO′＝R－a＝d＝，∴＝R2－，解得R＝ a.∴S球＝4πR2＝3πa2.20. 自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程.【答案】3x+4y+3=0或4x+3y+3=0。

【解析】试题分析：已知圆关于轴的对称圆的方程为2分如图所示．可设光线所在直线方程为， 4分∵直线与圆相切，∴圆心到直线的距离＝， 6分解得或. 10分∴光线所在直线的方程为或.…12分考点：点关于直线的对称点；直线与圆的位置关系；点到直线的距离公式。

点评：本题也可以这样做：求出点关于x轴的对称点，则反射光线一定过点，由此设出直线方程，利用直线与圆相切求出即可。

在设直线方程的点斜式时，要注意讨论直线的斜率是否存在。

21. 如图，在底面是菱形的四棱锥P—ABCD中，∠ABC=60°，PA=AC=a，PB=PD=，点E是PD的中点.（Ⅰ）求证：PA⊥平面ABCD；（Ⅱ）求二面角E—AC—D的大小；（Ⅲ）求点P到平面EAC的距离.【答案】（1）见解析；（2）；（3）.【解析】试题分析：（I）证明PA⊥AB，PA⊥AD，AB、AD是平面ABCD内的两条相交直线，即可证明PA⊥平面ABCD；（Ⅱ）如图，建立空间直角坐标系A—xyz,,求出平面EAC的法向量为，平面的法向量为，即得二面角大小（Ⅲ）由（II）问得，点P平面EAC的距离代入计算即得解.试题解析：（Ⅰ）证明：因为底面ABCD是菱形，∠ABC=60°所以AB=AD=AC=a，在△PAB中，可证PA2+AB2=2a2 = PB2∴PA⊥AB.同理，PA⊥AD，所以PA⊥平面ABCD.（II）如图，建立空间直角坐标系A—xyz设平面EAC的法向量为，，，又平面ACD的法向量为，即二面角E—AC—D的大小为；（III）点P平面EAC的距离。