保守力做功和势能变化的关系
静电力做功和电势能的关系

静电力做功和电势能的关系静电力是指由于电荷之间的相互作用而产生的力。
当两个带电体之间存在电荷差异时,它们之间就会产生静电力。
而静电力在物理学中是一种保守力,意味着它可以通过做功来改变电荷之间的位置关系。
静电力的大小与电荷之间的距离和电荷的大小有关。
根据库仑定律,两个电荷之间的静电力与它们的电荷量成正比,与它们之间的距离的平方成反比。
当两个电荷之间的距离越近,静电力就越大;当电荷量越大,静电力也越大。
当一个电荷受到静电力作用而沿某个方向移动时,静电力就对它做了功。
功是物理学中描述能量转化的概念,它表示力对物体的作用所产生的能量转移。
在这种情况下,静电力通过对电荷的作用使其具有了动能或势能。
电势能是指电荷由于位置而具有的能量。
在静电场中,电荷具有电势能,这是由于它与其他电荷之间的静电力相互作用所导致的。
当电荷从一个位置移动到另一个位置时,它的电势能会发生改变。
在静电场中,电势能的改变与电荷的移动路径无关,只与电荷的初始位置和最终位置有关。
根据电势能的定义,当电荷受到静电力作用而沿着力的方向移动时,它的电势能会减小。
换句话说,静电力对电荷做了负功,将电势能转化为了动能。
反之,当电荷受到静电力作用而与力的方向相反移动时,它的电势能会增加。
这时,静电力对电荷做了正功,将动能转化为了电势能。
总结起来,静电力对电荷做功,改变了电荷的位置关系,使其具有了动能或势能。
静电力和电势能之间的关系可以通过考虑电荷之间的相互作用和电荷的移动来理解。
静电力是一种保守力,它对电荷做的功可以转化为电势能,反之亦然。
这种关系在静电场中起着重要的作用,有助于我们理解电荷之间的相互作用和能量转化的过程。
值得注意的是,静电力做的功和电势能的改变是相互关联的,它们之间存在着数学上的联系。
具体来说,静电力做的功等于电势能的负改变。
这是由于功和电势能都是标量,且它们之间的关系可以通过数学公式来描述。
然而,为了遵守要求,本文不提供公式和具体计算方法。
物理题目

1、简述静电平衡条件。
答案:导体达到静电平衡时,导体内部的任意处的电场强度为零;导体表面电场强度的方向都与导体面垂直。
或:导体内部场强为零;导体为等势体;净电荷分布在导体的外表面;3、电介质的极化现象和导体的静电感应现象有什么区别?答案:导体的静电感应是导体中的自由电荷在外电场作用下作定向运动形成,最终达到静电平衡,这时,导体内部电场强度处处为零,净电荷分布在导体表面;电介质的极化是在外电场的作用下,束缚电荷重新取向或正负电荷中心不重合(位移极化),最终在电介质表面出现极化电荷(不均匀的电介质内部还会出现极化体电荷),介质内部场强减小。
4、什么是感应电荷?什么是极化电荷?答案:在外电场力作用下,金属导体中自由电子发生宏观定向漂移运动,最终在导体外表面停留下来的电荷,称为感应电荷;电介质中,在外电场作用下分子的正负电荷中心发生微小位移或重新取向,在介质表面所产生的电荷,称为极化电荷;7、简述电介质的极化和导体的静电感应现象达到稳定后,对于导体和电介质它们的电场、电势、电荷分布有什么区别?答案:对于导体:体内电场处处为零;整个导体为等势体;净电荷分布在外表面; 对于电介质,体内电场小于外电场;体内和体表面都有极化电荷分布;8、何谓电容?或:电容是反映什么的物理量?答案:导体的一个重要性质——具有容纳电荷的本领。
(或:反映导体可以容纳电荷本领的物理量,称为电容。
)5、电荷在磁场中运动时,磁力是否对它做功? 为什么?答:不作功,因为磁力和电荷位移方向成直角2 简述动生电动势和感生电动势答:由于回路所围面积的变化或面积取向变化而引起的感应电动势称为动生电动势。
由于磁感强度变化而引起的感应电动势称为感生电动势。
5 简述感应电场于静电场的区别?答:⎰⎰==⋅s v q dv ds D ρ dS tB l E s L ⋅∂∂-=⋅⎰⎰d0d =⋅⎰S S B dS t D j l H s l ⋅⎪⎭⎫ ⎝⎛∂∂+=⋅⎰⎰d 10、全电流安培环路定理答:磁场强度沿任意闭合回路的积分等于穿过闭合回路围成的曲面的全电流s d t D j l d H s e ∙⎪⎪⎭⎫ ⎝⎛∂∂+=∙⎰⎰ 10、质点运动中平均速度和平均速率有何区别? 在什么情况下平均速度和平均速率的大小相等? 答:平均速度是总位移除以总时间,而平均速率是总路径长度除以总时间。
势能

作功只与质点的始末位置有关,而与具体路径无关的力称为 保守力(例如重力、万有引力和弹性力等) conservative force ;
若物体沿acbda闭合路径运动一周时,保守力所作的功为:
W
F
dr
F
dr
F
dr
0
l
acb
bda
F
dr
F
dr
bda
acb
a c
potential energy
M
ox
x
图2
ra
a
rrF ddmrr dr
rb
图3
b
有关势能的几点说明
a) 势能是状态的函数
Ep mgz
Ep
Ep Ep (x, y, z)
Ep
1 2
kx 2
Ep
G
Mm r
Ep
Ep
r
O
z
O
重力势能曲线
z 0, Ep 0
x
O
弹性势能曲线
x 0, Ep 0
引力势能曲线
d
F
dr
0
l
b
即:物体沿任意闭合路径运动一周,保守力对它所作的功为零。
凡是做功不仅与质点的始末位置有关,而且与具体路径有关的力 称为非保守力(例如摩擦力等) nonconservative force
保守力做功的特点——仅与始末位置有关 势能:与物体间相对位置有关的做功本领,用Ep表示。
设Ep和Ep0分别表示保守体系在末位置和初始位置时的势能, 则它们之间的保守力所做的功与势能的关系可表示为
Ep
0 mgdz mg z
z
(2) 弹性势能 elastic potential energy
大学物理第六讲 势能、功能原理、机械能守恒 (1)

弹力的功与路径无关
2
万有引力的功
mM ˆ F G 2 r r dA F ds F cos ds
设M相对 于m静止.
ds dr m
b
a
F
Fds cos Fdr mM G 2 dr r
Aab dA
a b
ra
r
M
rb
一对相互作用力 的功只决定于两 者间的相对位移.
得
s
s+
m2 g
a
v
g 2 [( L l02 ) ( L l0 )2 ] L
18
例:宇宙速度 第一宇宙速度 ●物体绕地球作圆周运动所需的最小速度 此时
GM v mg m 2 m R R
2 1
GM v1 7.9km/s R
M和R分别为地球质量和半径。
19
第二宇宙速度
黑洞是大质量恒星在一定条件下演化的结果。恒星通过其内 部的热核反应不断燃烧演化。若恒星晚期经过质量抛失后所剩 余的质量大于3倍太阳质量,则就具备了坍缩为黑洞可能性。
坍缩核质量小于1.4倍太阳质量—白矮星;2-3倍太阳质量—中子星。
21
太阳属于小质量恒星, 不可能演化为黑洞。根据太阳的质量 条件,推算出太阳晚期演化的结局是白矮星(质量在1至8倍太 阳质量的孤立恒星也是如此)。
mM mM Aab ( G ) ( G ) ra rb
末
3
◎万有引力的功与路径无关。 初
摩擦力的功
A f r dS N dS
L L
mgds mgL
L
与路径相关
结论:
◎重力、弹力、万 有引力做功与路径 无关; ◎摩擦力做功与路 径有关。
保守力和势能
一对力所作的总功的只取决于两质点的相对运动;
一对力做功的代数和与参考系的选择无关;
5
什么条件下, 一对内力做功为零?
v
m
M
f
s s
C
f
v
N
C
N
Af Af 0
作用点无相对位移
AN AN 0
相互作用力与相对位移垂直
6
功的大小与参照系有关
功的单位为焦耳 功率(power) 功率:单位时间内力对物体所作的功 平均功率
yb ya
W mgdy mg( yb ya ) mg( ya yb )
重力是保守力。重力的功等于重力势能增量 的负值。重力势能以地面为零势能点。
y dy a p o
12
dr dx
W mg( yb ya ) =-EP 为势能增量
dr
b
EP mgdy mg(0 y) mgy
P
C
y
R
.
o
m
F
解:
F F0 xi F0 yj
r
x
0
dr dxi dyj
2R
r xi yj
2 A F d r F0 x d x F0 y d y 2F0 R
0 0
8
练习2 如图 M =2kg , k =200N m , s = 0.2m , g ≈ 10ms
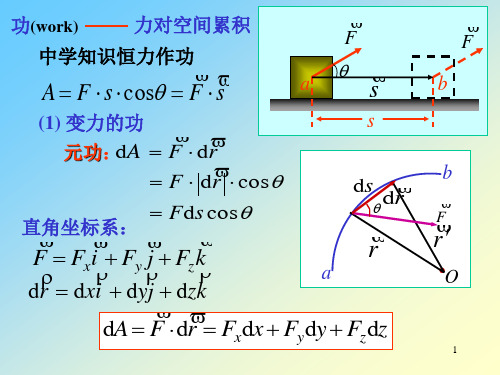
功(work)
力对空间累积
中学知识恒力作功
F
a
F
A F s cos F s
s
s
ds
dr
保守力与非保守力及势能

§3.6 保守力与非保守力、势能
3. 三种势能函数:
(1) 重力势能:
y y
E p ( y ) F重 d r
(0)
( mg ) ˆ j dy ˆ j
y
( y) 0
o
Ep( y )
mg
E p ( y ) mgy
即:势能零点正上方重力 势能为正,下方为负。
E p ( y ) mgy
m?????epr?f引?drf引mrrorep?0??mm????g2er?drerrreprmmepr?gorrmmepr?gr即
Chapter 3. 守恒定律
§3.6 保守力与非保守力、势能
§3.6 保守力与非保守力、势能
·1 ·
Chapter 3.力,其势能函数为何不同?它们
有何内在关系? 3. 若选地表为万有引力势能零点,则 引力势能表达式如何?
?
( The end ) ·7 ·
Chapter 3. 守恒定律
§3.6 保守力与非保守力、势能
归纳:
1.重力势能: E p ( y ) mgy
1 2 2. 弹性势能: E p ( x ) kx 2
Ep( y )
1 E p ( x ) kx 2 2
o
x
·5 ·
Chapter 3. 守恒定律
§3.6 保守力与非保守力、势能
(3) 万有引力势能:
M
F引 m
E p ( r ) F引 d r
(r )
( )
o
r
Ep( ) 0
Mm ˆ r dr e ˆr ( G 2 )e r r
2. 势能函数选取应遵从的原则:
4-4保守力与非保守力-势能(2024版)

o X0
解:重力势能为: (以o点为重力
势能零点,以向
Ep重力
o
mg dx
下为x正向)
P
ox
P
x
0 mgdx
mgx
弹性势能为: (以o点为弹性势能零点)
E p弹性
o F dx
P
x
Fdx
0
x
0 k( x x0 )dx
4 – 4 保守力与非保守力 势能
E p重 力 mgx
Fx Fz 0
A r2 F dr r1
x
mg y2 dy y1
mg y1 y2
A m gh
4 – 4 保守力与非保守力 势能
y2
y2
A Fzdy (mg)dy mg( y1 y2 )
y1
y1
重力作功的特点:
(1)与质点经过的路径无关; (2) 沿任意闭合路径一周重力作功必为零; (3)质点上升重力作负功。
4 – 4 保守力与非保守力 势能
例:如图半径为R的1/4凹圆柱面M放在光滑水平面上,小球m从
静止开始沿圆面从顶端无摩擦下落,小球从水平方向飞离大物体 时速度 v ,求重力所做的功和内力所做的功
解:重力只对小球做功 A重力 mgR
V
m
R v
水平方向无外力,系统 保持水平方向动量守恒:
mv MV 0
Gmemh Re2
Gmemh2 Re3
mgh mg h2 Re
(
Gme Re2
g)
mgh ( Re h)
即引力势能在地面附近可用重力势能来替代。
4 – 4 保守力与非保守力 势能
例、 倔强系数为K的弹簧,上端固定,下端悬挂重物。当弹簧 伸长x0时,重物在O处达到平衡。现取重物在O处时各种势能均 为零,则当 m 偏离O点x时,系统的重力势能为多少?系统的弹 性势能为多少?系统的总势能为多少?
一个保守力作的功等于势能的减少吗

第20卷第5期大 学 物 理Vo l.20N o.52001年5月COL L EGE PHYSICS M ay.2001收稿日期:2000-06-26作者简介:高炳坤(1936 ),男,河南清丰人,清华大学物理系教授.一个保守力作的功等于势能的减少吗高炳坤(清华大学物理系,北京 100084)摘要:通过实例说明一个保守力作的功,在一般情况下并不等于势能的减少,一对保守力作的功才等于势能的减少.关键词:保守力;作功;势能减少中图分类号:O 313 文献标识码:A 文章编号:1000 0712(2001)05 0019 02 常听到这种说法:保守力作的功等于势能的减少.这种说法是含混的,因为它未指明,究竟是一个保守力作的功还是一对保守力作的功.本文来讨论这个问题.1 弹簧的势能如图1所示,一原长为l 0的弹簧系二小球,置于水平地面上,并振动起来.弹簧对球1的作用力为f 1,对球2的作用力为f 2,f 1和f 2为一对弹性保守力.设在地面上沿弹簧的纵向为坐标x ,坐标原点O 可任意选,则有图1f 1=k [(x 2-x 1)-l 0]i f 2=-k [(x 2-x 1)-l 0]if 1和f 2作的元功分别为d A 1=f 1 d s 1=k [(x 2-x 1)-l 0]i d x 1i =k[(x 2-x 1)-l 0]d x 1d A 2=f 2 d s 2=-k [(x 2-x 1)-l 0]i d x 2i =-k [(x 2-x 1)-l 0]d x 2所以 d A 1+d A 2=-k [(x 2-x 1)-l 0]d (x 2-x 1)=-k [(x 2-x 1)-l 0]d [(x 2-x 1)-l 0)]= -d12k [(x 2-x 1)-l 0]2=-d 12k l 2(1)式中的 l 为弹簧的形变量,12k l 2为弹簧的势能.因 l 与参考系无关,故式(1)对任何参考系都成立.式(1)表明:一对弹性保守力作的功等于弹簧势能的减少,但一个弹性保守力作的功却不等于弹簧势能的减少.这是一般的规律.也有特殊的情况,如图2所示,用钉子把球1钉在地面上,在地面参考系中,f 1便不作功了,即d A 1=0,故式(1)变成图2d A 2=-d12k l 2(2)式(2)表明:一个弹性保守力(f 2)作的功就等于弹簧势能的减少.但必须强调:式(2)仅对f 1不作功的参考系才成立;对沿弹簧的纵向相对地面运动的参考系,f 1便作功了,这时,式(2)就回归为式(1).教科书中常见的情形是弹簧的一端系在墙上,另一端系一小球,且将坐标x 的原点O 取在离墙l 0处,如图3所示.图3与图2是类似的:图3中的f 即图2中的f 2,f 作的元功d A 即d A 2,且x = l ;至于图2中的f 1,由于它在地面参考系中不作功,故在图3中就干脆不画出来.显然,图3是地面参考系中的一种特定的情况,对此特定情况式(2)成d A =-d12kx 2(3)式(3)是极其特殊的,但却是经常见到的.这大概就是形成!一个保守力作的功就等于势能的减少∀这种说法的原因吧.图3至于弹簧的势能是内势能还是外势能,这要看如何选择系统.在图1中,若选!二球和弹簧∀为系统,则弹簧的势能便是内势能;若选!球2和弹簧∀为系统,则弹簧的势能也是内势能;若单独选!球2∀为系统,则弹簧的势能便是外势能了.无论把弹簧的势能视为内势能还是外势能,必须牢记:势能的改变是与一对保守力作的功相对应的.2 重力势能如图4所示,一质量为m 的小球,在地面附近沿竖直方向运动,它受到地球的吸引力(也称重力)为m g,它对地球的吸引力为-m g ;-m g 本应作用在地心上,为方便起见,今将其平移到了地面上的P 点.为了看清一对保守力m g 和-m g 与重力势能mgh 的关系,特选相对地面以速度u 运动的物体为参考系,并在此参考系上建立坐标y ,这样就有:d A 1=m g d s 1=-mg j d y j =-mg d y d A 2=-m g d s 2=mg j d y P j =mg d y P d A 1+d A 2=-mg d (y -y P )=-d (mgh)(4)式(4)表明:一对保守力(m g 和-m g)作的功等于重力势能(mgh)的减少,但一个保守力作的功却不等于重力势能的减少.这是普遍的规律.教科书中常见的情况是:选地面为参考系,这样-m g 便不作功了,只有m g 作功,其元功记作d A ,因此式(4)就变成图4d A =-d(mgh)(5)式(5)表明:一个保守力(m g)作的功就等于重力势能的减少.但必须强调:式(5)是特殊情况,它仅在-m g不作功的参考系中才成立.从本质上看,重力势能mgh 是与一对保守力m g 和-m g 相伴的,而m g 和-m g 是属于!小球和地球∀这个系统的,故重力势能应是!小球和地球∀共有的.但对地面这个特殊的参考系,由于只有m g 作功,故也可以说重力势能是属于小球的,这仅是一种通俗的说法而已.弹簧的势能12k l 2就不同了,它有单独的载体 弹簧.究竟应该把重力势能视为内势能还是外势能,这也要看如何选择系统.若把!小球和地球∀选为系统,则重力势能便是内势能;若单把!小球∀选为系统,则重力势能便是外势能了.系统的保守内力作的功等于内势能的减少,这是大家熟知的.需要强调的是:一般情况下,系统的外保守力作的功并不等于外势能的减少.但特殊情况下可有例外,因保守力总是成对的,外保守力也必有伴侣(外保守力作用在系统上,其伴侣则作用在外界上),当其伴侣不作功时,外保守力作的功才等于系统的外势能的减少.参考文献:[1] 张三慧.大学物理学 第一册:力学[M ].第2版.北京:清华大学出版社,1999.[2] 周衍柏.理论力学教程[M ].北京:高等教育出版社,1984.(下转30页)的谱线,但是所选光源的谱线至少要有3条,以便比对,并同时确定仪器的调整是否被破坏.3 半定量分析方法介绍有了以上标准铁谱,拍摄样本光谱时就不需要同时拍摄铁谱,只需同时拍摄标记光源的光谱即可.在计算机上,通过放大或缩小样本光谱,使样本光谱上的标记光谱与标准铁谱上的标记光谱对准,就可以使用铁谱计算样本的谱线波长了.以测量氢的光谱为例,介绍分析方法的使用.使用图1的方法拍摄氢的光谱,同时拍摄汞灯的光谱.在计算机上使铁谱和氢谱的标记对准.见图3.然后用铁谱比对氢谱.数据见表1.图3 汞标记氢谱表1 用铁谱比对氢谱得到的氢波长实测波长/nm 486.13434.05410.47理论值/nm486.08434.00410.13由表1可知,使用标记标准铁谱比对样本光谱进行半定量分析是一个很好的方法.同时,也可以在计算机上读出光谱某一谱线的灰度,从而确定样本中的某一元素的相对含量.本项目的实验是在WSL -0.5#型小型棱镜摄谱仪上完成的.参考文献:[1] 刘书声.现代光学手册[M ].北京:北京出版社,1993.624,643.[2] 吴思诚,王祖铨.近代物理实验∃[M ].北京:北京大学出版社,1986.87,99.A simple way of semi quantitative spectral analysiswith a small prism spectrographZHAO Hui 1,SHI Heng yong 1,ZHAO Xin 2,CHANG Xiao qi1(1.Department of Physics,Anshan T eachers Colleg e,Anshan,L iaoning,114005,China;2.Anshan Bro adcast &T elev ision Device Gr oup,Anshan,L iaoning,114012,China)Abstract:A method for m aking the standard iron spectra and processing the sample by means of a CCD industry camera and a small prism spectrog raph is ing this w ay,we do not need to photog raph the iron spectra every time,so the sem i quantitative spectral analysis is much simplified.Key words:prism spectrograph;spectral analysis;CCD(上接20页)Is the work done by a conservative force equalto the decrease of potential energyGAO Bing kun(Department of Physics,T singhua U niversity ,Beijing ,100084,China)Abstract :The w ork done by a pare of conservative forces is equal to the decrease of potential ener g y and in general,the w ork done by one force in this pare does not equal to the decrease of the potential energy.Key words :conservative force;w ork;decrease of potential energy。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保守力做功和势能变化的关系
保守力做功和势能变化的关系是一个基本的物理原理,它描述了一个物体在受到保守力作用下,其势能的变化与所受的保守力所做的功之间的关系。
首先,我们来定义保守力。
保守力是一个与路径无关的力,它只与物体的位置有关。
这意味着,如果一个物体沿着一个闭合回路运动,受到的保守力所做的总功为零。
常见的保守力有重力和弹性力。
当一个物体受到保守力作用时,它的势能会发生变化。
势能是描述物体位置所具有的能量。
根据势能的定义,势能的变化可以通过将物体从一个位置移动到另一个位置时保守力所做的功来计算。
根据物体在保守力作用下的势能变化,我们可以得出以下关系:
势能变化 = -保守力所做的功
这个关系可以解释为,当保守力对物体做正功时,物体的势能减少;反之,当保守力对物体做负功时,物体的势能增加。
这个关系也可以用数学公式来表示。
假设物体在从位置A移动到位置B时,保守力所做的功为W_AB,物体在位置A的势能为U_A,位置B
的势能为U_B,则势能变化为:
ΔU = U_B - U_A = -W_AB
其中,ΔU表示势能变化。
需要注意的是,这个关系只适用于保守力。
非保守力所做的功不能简单地与势能变化相联系。
非保守力所做的功还需要考虑其他能量转化形式,比如热能、摩擦力等。
总结起来,保守力做功和势能变化之间存在着简单的关系。
势能变化等于保守力所做的功的负值。
这个关系对于理解物体在保守力作用下的运动和能量转化非常重要。
