高等数学上册课件
合集下载
高等数学(第二版)上册课件:导数概念

右极限都存在且相等,因此有:
定理2.2 函数 f (x) 在点 x0 处可导
左导数 f(x0 )和右
导数 f(x0 ) 都存在且相等 .
例 2.1.4 讨论函数 f (x) x 在 x 0 处的可导性 .
解
lim f (0 h) f (0) lim h 1
h0
h
h h0
lim f (0 h) f (0) lim h 1
y x3 的切线方程.
解
设切点为 x0 , y0 曲线 y x3 在点 x0 , y0
处的切线斜率为 k1, 直线的斜率为 k2 则:
| k1
y
x x0
3x02 ,
k2
1 27
而 k1. k2 1, 得 x0 3 则切点为 3, 27 或 3, 27
切线方程为
27x y 54 0 或 27x y 54 0
从高速到低速,最后速度减为0 . 这个过程每一时刻的汽车
的速度都不相同,如何求某时刻 t0汽车的瞬时速度呢?
设汽车所经过的路程s是时间t的函数:s s t ,
任取接近于 t0 的时刻 t0 t ,则汽车在这段
时间内所经过的路程为
s s(t0 t) s(t0 )
而汽车在这段时间内的平均速度为
当自变量 x 在 x 0 处取得增量 x (点 x0 x 仍在该
邻域内),相应地函数取得增量 y f ( x0 x) f ( x0 )
.
如果 y 与 x 之比当 x 0 时的极限存在,
则称函数 y f ( x) 在点 x 0 处可导,并称这个极限值
即
f
(x0 )
lim
x0
f
解 当 x 由1变到 1 x 时,函数相应的增量为
第一章《高等数学(上册)》课件

高等数学
01 函数 02 极限 03 无穷小与无穷大 04 极限的运算 05 两个重要极限 06 无穷小的比较 07 函数的连续与
间断点
08 初等函数的连 续性
高等数学
01 函数 02 极限 03 无穷小与无穷大 04 极限的运算 05 两个重要极限 06 无穷小的比较 07 函数的连续与
间断点
图 1-1
图 1-2
高等数学
01 函数 02 极限 03 无穷小与无穷大 04 极限的运算 05 两个重要极限 06 无穷小的比较 07 函数的连续与
间断点
08 初等函数的连 续性
高等数学
01 函数 02 极限 03 无穷小与无穷大 04 极限的运算 05 两个重要极限 06 无穷小的比较 07 函数的连续与
间断点
08 初等函数的连 续性
高等数学
01 函数 02 极限 03 无穷小与无穷大 04 极限的运算 05 两个重要极限 06 无穷小的比较 07 函数的连续与
间断点
08 初等函数的连 续性
16世纪末期,为适应生产实践的需要,人 们开始对各种变化过程中量与量之间的关系进行 研究,于是产生了函数的概念.函数既是现代数 学中最重要的基本概念之一,也是高等数学的主 要研究对象.极限是微积分学的理论基础,极限 方法是高等数学中研究问题的一种基本方法.本 章将着重介绍有关函数、极限和连续的基础知识 及基本方法.
间断点
08 初等函数的连 续性
高等数学
01 函数 02 极限 03 无穷小与无穷大 04 极限的运算 05 两个重要极限 06 无穷小的比较 07 函数的连续与
间断点
08 初等函数的连 续性
在平面直角坐标系中,偶函数的图形是关于y轴对称 的,如图1-1所示;奇函数的图形是关于原点对称的,如 图1-2所示.
高等数学上期末复习资料大全ppt课件.ppt

,
其中系数A1、B1、C1与A2、B2、C2不成比例.
考虑三元一次方程:
A1xB1yC1zD1(A2xB2 yC2zD2)0,
即
(A1A2)x(B1B2)y(C1C1)zD1D20,
其中为任意常数.
上述方程表示通过定直线L的所有平面的全体, 称为平面
束.
1. 函数的极值问题 第一步 利用必要条件在定义域内找驻点.
如对二元函数 z f (x, y), 即解方程组
f f
x yBiblioteka (x, (x,y) y)
0 0
第二步 利用充分条件 判别驻点是否为极值点 .
2. 函数的条件极值问题
(1) 简单问题用代入法
(2) 一般问题用拉格朗日乘数法
例20 要设计一个容量为 V0 的长方体开口水箱, 试问
水箱长、宽、高等于多少时所用材料最省?
直线
x4 5
y
3 2
z 1
x4
5
y
3
2
y3, 2
z. 1
2x 5y 23
y
2z
3
0.
0,
设通过直线L 的平面方程为:2x 5y 23 ( y 2z 3) 0,
将x=3,y=1,z=-2代入上式,得 11.
再将
11
4 代入上式得所求平面方程:
4
8x 9y 2z 59 0.
z y
Fy Fz
xz y xexz
.
导时,将方程 F(x,y,z)=0中x,y,z 视作独立变量.
解法2 利用隐函数求导
方程两端关于x求偏导,得 方程两端关于y求偏导,得
z
x
y y
ze xz xexz
高等数学上册第六章课件.ppt

(2 , 2)
4
AdA ( y 4 12 y 2 ) d y
2
18
(8 , 4)
x
第二节 定积分在几何中的应用
例
求由摆线
的一拱与 x 轴所围平面图形的面积 .
解
2π
dAA
ydx 0 a (1 cos t ) a (1 cos t ) d t
a
2
4a
X -型绕x轴旋转所围成的立体的体积:
y 2 ( x)
b
b
Vx π ( x)dx π ( x)dx
a
b
2
2
a
2
1
2
2
y 1 ( x)
π [2 ( x) 1 ( x)]dx
a
a
bx
Y-型绕y轴旋转所围成的立体的体积:
d
Vy π [ g g ]dy
2
5 3 1 π
32π a sin u du 32π a 5π 2 a3
0
6 4 2 2
3
2
6
3
第二节 定积分在几何中的应用
y
x x2 ( y )
2a
绕 y 轴旋转而成的体积为
π
π a 2 (t sin t ) 2 a sin t d t
2π
o
πa
πa
4 2 2
2
所围图形的
(利用对称性)
d
o
2a x
第二节 定积分在几何中的应用
心形线(外摆线的一种)
2
2
2
x y ax a x y
2
即 r a(1 cos )
4
AdA ( y 4 12 y 2 ) d y
2
18
(8 , 4)
x
第二节 定积分在几何中的应用
例
求由摆线
的一拱与 x 轴所围平面图形的面积 .
解
2π
dAA
ydx 0 a (1 cos t ) a (1 cos t ) d t
a
2
4a
X -型绕x轴旋转所围成的立体的体积:
y 2 ( x)
b
b
Vx π ( x)dx π ( x)dx
a
b
2
2
a
2
1
2
2
y 1 ( x)
π [2 ( x) 1 ( x)]dx
a
a
bx
Y-型绕y轴旋转所围成的立体的体积:
d
Vy π [ g g ]dy
2
5 3 1 π
32π a sin u du 32π a 5π 2 a3
0
6 4 2 2
3
2
6
3
第二节 定积分在几何中的应用
y
x x2 ( y )
2a
绕 y 轴旋转而成的体积为
π
π a 2 (t sin t ) 2 a sin t d t
2π
o
πa
πa
4 2 2
2
所围图形的
(利用对称性)
d
o
2a x
第二节 定积分在几何中的应用
心形线(外摆线的一种)
2
2
2
x y ax a x y
2
即 r a(1 cos )
高等数学上册第七章课件.ppt
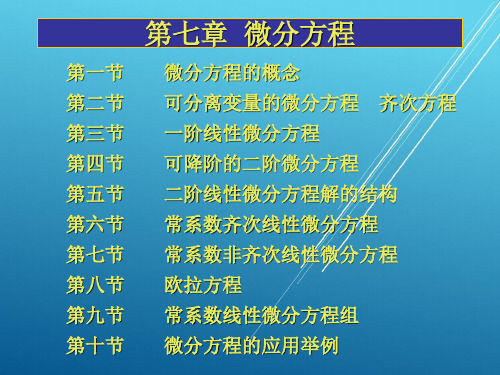
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
高等数学-第1章课件

x x0
三、函数极限的性质
第三节 极限的运算
一、极限的运算法则
法则1 法则2
x x0
lim[ f ( x) g ( x)] lim f ( x) lim g ( x) A B
x x0 x x0 x x0 x x0
x x0
lim[ f ( x ) g ( x )] lim f ( x ) lim g ( x ) A B
第 一 章 函 数 ︑ 极 限 与 连 续
目录
第一节 函数
第二节 极限
第三节 极限的运算 第四节 无穷小与无穷大 第五节 函数的间断性与连续点 第六节 初等函数的连续性
第一节 函数
一、集合、区间与邻域
1.集合
集合(简称集)是具有某种共同性质的事物的全 体,组成集合的单一事物称为该集合的元素。
有限集合 有限个元素构成 北京户籍人口
° a
• a •
a°Leabharlann a3.邻域设 x0, δ R, 其中δ > 0,以 x0为中心,以δ 为半径,长为 2δ的
开区间. 即
( x0 , x0 ) { x x x0 , 0}
称为点 x0 的 δ 邻域 , 记为U(x0 , δ ).
2
x0
x0
x0
集合的运算及关系
由所有属于集合A或属于集合B的元 并集 素所组成的集合,称为集合A与B的 并集 交集 差集 由属于集合A且属于集合B的所有元 素组成的集合,称为A与B的交集
由所有属于集合A 而不属于集合B 的 元素组成的集合
A∪B A∪B={x|x∈A,或 x∈B}
A∩B A-B
A∩B={x|x∈A,且 x∈B} A-B={x|x∈A,且 xB}
三、函数极限的性质
第三节 极限的运算
一、极限的运算法则
法则1 法则2
x x0
lim[ f ( x) g ( x)] lim f ( x) lim g ( x) A B
x x0 x x0 x x0 x x0
x x0
lim[ f ( x ) g ( x )] lim f ( x ) lim g ( x ) A B
第 一 章 函 数 ︑ 极 限 与 连 续
目录
第一节 函数
第二节 极限
第三节 极限的运算 第四节 无穷小与无穷大 第五节 函数的间断性与连续点 第六节 初等函数的连续性
第一节 函数
一、集合、区间与邻域
1.集合
集合(简称集)是具有某种共同性质的事物的全 体,组成集合的单一事物称为该集合的元素。
有限集合 有限个元素构成 北京户籍人口
° a
• a •
a°Leabharlann a3.邻域设 x0, δ R, 其中δ > 0,以 x0为中心,以δ 为半径,长为 2δ的
开区间. 即
( x0 , x0 ) { x x x0 , 0}
称为点 x0 的 δ 邻域 , 记为U(x0 , δ ).
2
x0
x0
x0
集合的运算及关系
由所有属于集合A或属于集合B的元 并集 素所组成的集合,称为集合A与B的 并集 交集 差集 由属于集合A且属于集合B的所有元 素组成的集合,称为A与B的交集
由所有属于集合A 而不属于集合B 的 元素组成的集合
A∪B A∪B={x|x∈A,或 x∈B}
A∩B A-B
A∩B={x|x∈A,且 x∈B} A-B={x|x∈A,且 xB}
高等数学上2_课件1.ppt

FFn1
1, F2 Fn1
1 Fn2
,
n2
写出来为
1,1,2,3,5,8,13,….
例 2.3
bn
Fn Fn1
1, 1 , 2 , 3 , 5 , 8 , 13 , . 2 3 5 8 13 21
bn 是按“大—小—大—小…”依次交错排列的,这
样的数列称振荡数列.显然 bn 是有界的,非单调的.
2
等来代替.
2.1.2 数列极限的概念
●关于数列极限的 N 定义,通过以上几个例子,读 者已有初步认识,再作以下几点注释以便加强.
(2) N 的相应性 一般地, N 随 的变小而变大,
因此有时为强调 N 是依赖 的,也把 N 写作 N ( ) .但这并
不意味 N 是由 唯一确定的.比如对给定的 ,当 N 100 时, n N 便有 xn a 成立,则取 N 101或更大时, n N 时必有 xn a .求 N 的目的在于证实 N 的存在
的项的值随 n 增大而增大,且无限增大. ●若当 n 无限增大时, xn 无限趋向于常数 a ,则说,
当 n 趋于无穷大时,xn 以 a 为极限.
记作
lim
n
xn
a
或
x
a
, (n
)
2.1.2 数列极限的概念
●做定量分析
1n
对例 2.4 中 xn f (n) 1 n
n N 随 n 无限增
大而无限接近 1 的过程做定量分析:
n
它是一个有界的
xn
≤
3
2 振荡数列,图像如图
2.2.
我们会发现,随着 n 的无限增大, xn 以 1 为平衡位置振
荡,而振幅越来越小,并且可以任意的小,即 xn 无限接
高等数学上2_课件2.ppt

达标后的函数值:
f (x) A
2.2.2 x趋于有限值x0时函数的极限
●至此,我们用 N ”、“ X ”、“ ” 的语言定 义了七种极限, 下面将列表类比对照.
极限形式: 接近程度指标:
lim f (x) A
x
实现时刻:
X
实现时刻后的自变量: x X
达标后的函数值:
f (x) A
定义 2.2
*在定义 2.2 中, 将“ f (x) 在 b, 上有定义”换作 “ f (x) 在 , a上有定义;将“ x X ”换作“ x X ”
lim
x
f
(x)
A或
f
(x)
A(x
)
.
2.2.1 x趋于无穷大时函数的极限
定义 2.3 设 f (x) 在 , a b, (a ≤b) 上有定义,A
推 论 若 在 x0 的 某 去 心 邻 域 内 f (x) ≥ 0 ( 或
f
(
x)
≤
0
)且
lim
xx0
f
(x)
A ,则 A≥0 ( A≤0 ).
2.2.3 函数极限的性质
● 在 2.2.1,2.2.2 中我们共列举了六种类型的极限:
(1)
lim
x
f
(x) ;
(2)
lim
x
f
(x) ;
(3)
lim
2.2.1 x趋于无穷大时函数的极限
自变量 x 趋向于无穷大有下面三种方式: x ,表示 x 沿 x 轴无限向右推进,趋于正无穷大; x ,表示 x 沿 x 轴无限向左推进,趋于负无穷大; x ,表示 x 沿 x 轴无限向任何一方推进,即 x 趋于 .
