一种基于傅氏算法的高精度测频方法
一种高精度单频信号频率估计算法

一种高精度单频信号频率估计算法刘建林;陈兵【摘要】根据离散傅里叶变换(DFT)理论和其系数的特点,提出了一种信号离散傅里叶变换系数来构造频率修正项的单频信号频率估计算法.算法利用峰值及前后1个位置的DFT变换系数得到频率修正项的初始值,再迭代计算修正后峰值前后位置的DFT系数来得到频率修正项的精细值.理论分析和仿真结果表明,算法在低信噪比下具有好的频率估计精度并能减少迭代次数.【期刊名称】《无线电工程》【年(卷),期】2011(041)004【总页数】3页(P26-28)【关键词】频率估计;离散傅里叶变换;傅里叶系数【作者】刘建林;陈兵【作者单位】中国电子科技集团公司第五十四研究所,河北石家庄,050081;中国电子科技集团公司第五十四研究所,河北石家庄,050081【正文语种】中文【中图分类】TN971.+10 引言频率估计是信号参数估计中的经典问题,目前国内外已经提出了不少方法,其估计方法主要分为以自回归法等典型方法的参数估计[1]和以周期图法等典型方法的非参数估计[2,3]2类。
短数据、高精度的快速频率估计是倍受电子战领域专家学者的关注。
文章提出了一种先利用峰值前后3个DFT系数得到频率修正项的初值,再迭代计算修正后峰值前后位置DFT系数来得到频率修正项的精细值的频率估计新算法。
仿真分析验证了算法能够快速、高精度估计单频信号的频率,比常规插值迭代算法所需迭代次数要少,有利于工程实现。
1 频率估计算法1.1 信号模型假设离散复单频信号模型为:式中,A、fc和φ分别为复信号的幅度、载频和初相;v(n)为零均值,方差为σ2的加性高斯白噪声;fs为采样频率;N为信号长度。
1.2 初值估计信号的DFT系数为:式中,I为幅度谱的峰值位置;δ为信号真实峰值位置与I的偏差值,即,且有为噪声的DFT系数。
暂不考虑噪声影响,且 N较大时,I-1、I和I+1处的幅度谱可推导得到:当|X(I+1)|>|X(I-1)|时,即0<δ≤0.5,信号真实频率位于I和I+1之间,有式中,^δ0为估计出来的频率修正项初值。
基于局部频谱连续细化的高精度频率估计算法

对有限长信号的频率进行实时精确估计在雷达 & 通讯等领域有着十分重要的应用价值 # 在全数字化多普 勒导航雷达中 # 是整个系统达到实时性要求和保证测速精度的关键 ,
)!&( 目前有多种频率估计算法 ’ # 但是这些算法 都 不 同 程 度 地 存 在 算 法 复 杂 & 计 算 量 大& 噪声抑制差的问
3
!# 9$8
+8"
# % <$ 7 Q ! + RS " !! !" $ 9 # 9 ! @ I 9 9$ " ;#
+ : :
# $ T
第 ) 期 !!!!!!!!!!! 李 ! 鹏等 " 基于局部频谱连续细化的高精度频率估计算法
! %
这时 9 是一个连续的频率 ! 频域的分辨率也已不受 3 的限制 , 采用式 " # 进行细化 ! 这样又一次滤 除 了 噪 声 并 只 在 小 范 围 内 进 行 细 化 ! 提 高 了 效 率! 大大降低了运算 T 量! 而且细化密度可以任意设定 , 在用改进的算法进行细化时 ! 细化范围可以从大到小 ! 细化密度可以从低到 高地逐级往下进行 , 该算法实现过程中尤其需要注意两次 窗 函 数 的 选 取 $ 经 仿 真 验 证! 矩形窗实现简单完全可达到精度要 求, 所以在两次窗函数的选取中都选择长度不同的矩形窗 , 同时 ! 矩形窗函数长度的确定要注意以下两点 $ " 第一次加窗时 ! 为了尽可能地滤除其他频率分量 和高 斯白噪 声 ! 要在 包 含 所 需 频 率 成 分 的 前 提 下 ! $# 尽量减小窗函数的长度 , " 第二次加窗即选取细化密度时 ! 只有当其细化参数选取恰当时 ! 才能达到最理想的效果 , 一方面 ! 细 %# 化区间要小 ! 且细化密度不能太小 ! 以使 运 算 量 尽 量 地 小 % 另 一 方 面! 细化区间太小有可能丢失部分有用信 息! 而细化密度不够细致又达不到细化目的 ! 导致估计精度降低 ,
基于全波傅氏算法的微机继电保护

大 多 数 微 机 保 护 算 法 的计 算 可 视 为 对 若 直 接 利 用 全 波 傅 氏算 法 计 算 n次 谐 交 流 信 号 中参 数 的 估 算 过 程 , 算 法 性 能 波 分 量 , : 对 得 的 评 价 也 取 决 于 其 是 否 能 在 较 短 数 据 窗 中 , 信 号 的 若 干 采 样 值 中 获 得 基 波 分 量 从 a = )o( cs () 4 或 某 次 谐 波分 量 的 精 确 估计 值 …。 目前广 泛 采 用 全 波 傅 氏算 法 和 最 小 二 乘 算法 作为 电 其中 : 力系 统微 机 保 护 提 取 基波 分 量 的 算法 【。 2 全 J 误差 。 l I l 1 Ⅳ 波傅 氏算法能滤 除所有整次 谐波分量 , 且 ¨ 脚 ∑ ∑ 。 。 稳 定 性 好 , 响 应 速 度 较 慢 [。 际 输 入 的 但 3实 J 3改进全波傅 氏算 法仿真计 算 耻 信 号 由于 混 有 衰 减 直 流 分 量 和 复杂 的谐 波 I 为 了验 证 本 改进 全l 傅 氏 算 法 的 正 确 波 成分将 产生畸变 , 如果 此 时 仍 利 用 傅 氏算 性 和 精 度 , 如下 仿 真计 算 , 输 入信 号为 : 作 设 () 6 法 计 算 , 精 度 必然 受 到 影 响 。 文 提 出 了 其 本 S ’ l 』 i) 0 e +6 s ( t O ) ( =10 t 0 i r +6 。 + n_  ̄ 种 改 进 算 法 , 在 未 知 衰 减 时 间 常 数 的 能 由式 ( ) 式 () 5和 6 可知 , / 才 是 真 正要 求 5 s (t +4 。+3 s (a +3 。+8 s (a ) t n 0 i 2o 5) 0 i 3 r 0 ) 0 i 4 r n t n n 情 况 下 对 衰 减 直 流 分 量 进 行 补 偿 , 论 上 理 的 值 , n 是 由衰 减直 流 分 量 造 成 的 误 差 。 A (3 1) 能 够 完 全 滤 除衰 减 直 流 分 量 。 每 基 频 周 期 采样 3 点 , 6 取 =00 s, . 4 用 2改进全波傅氏算法 1原始傅 氏算法的研 究 本 文 中 的 改 进 全 波 傅 氏 算 法 进 行 仿 真 计 下 面 对 由 衰 减 直 流 分 量 造 成 的 误 差 算 , 果 如表 1 傅 氏 算 法 的 基 本 思 想 源 于 傅 立 叶 级 结 所示 。 Aa 进 行分 析 : 由式 ( ) 得 : 5可 数, 该算 法 假 设 输 入信 号 为 一 周 期 性 函数 由表 中 结 果 可 知 , 改 进 全 波 傅 氏算 此 信号, 即输 入 信 号 中 除 基 频 分 量 外 , 只包 含 法 能 够 完 全 滤 除 衰 减 直 流 分 量 , 而 得 出 从 恒 定 的 直 流 和 各 种 整 次 谐 波 分 量 , 电流 以 基波 和各次谐波精确 的幅值和相 角。 以 上 改 进 全 波 傅 氏算 法 的 流 程 图 如 图 信号为例 , 输入信号表示 为: 设
基于DFT的高精度相量测量的新算法

基于DFT的高精度相量测量的新算法
王超;汪芳宗
【期刊名称】《电测与仪表》
【年(卷),期】2009(046)006
【摘要】在传统的离散傅里叶算法的基础上提出了一种新的相量测量算法.首先,对纯基波信号,该算法利用2个数据窗的DFT变换数据推导出了一个关于频率偏移的方程,解此方程后可以求出基波信号的频率、幅值及相位的精确解,在推导过程中无任何近似误差,有效减小计算量的同时提高了测量的精确性;接着,为了提高谐波情况下测量的精度,利用采样起点间隔半个信号周期的DFT变换数据进行谱泄漏抵消;然后用前面的方法进行相量测量,通过跟踪采样频率,进而再次测量;最后,分别对存在谐波和噪声的情况进行了仿真.结果表明,该算法在各种情况下具有测量精度高的优点.【总页数】5页(P13-16,20)
【作者】王超;汪芳宗
【作者单位】三峡大学,电气信息学院,湖北,宜昌,443002;三峡大学,电气信息学院,湖北,宜昌,443002
【正文语种】中文
【中图分类】TM934
【相关文献】
1.基于改进DFT的电力系统同步相量测量算法研究 [J], 金涛;陈毅阳;段小华;唐晓艳
2.基于DFT的同步相量相角测量改进算法研究 [J], 唐晓艳
3.基于频率测量值的相量及电气量的DFT修正算法 [J], 袁石良;董杰;徐志强;宋美杰
4.高频采样下基于DFT的配电网相量测量算法研究 [J], 周治国;王毅;张华良
5.基于高精度测频的修正DFT相量及功率测量算法 [J], 谢运华;赵庆生;郭贺宏;张学军
因版权原因,仅展示原文概要,查看原文内容请购买。
一种频域相位差分测频算法

一种频域相位差分测频算法
戴猛;陈叶明
【期刊名称】《电子测量技术》
【年(卷),期】2015(0)1
【摘要】提出一种新的基于频域的相位差分法,能通过多次等比延时的FFT变换,得到多个时间点相位信息,再利用前后各时间点的相位关系来消除相位模糊的问题;定量分析了FFT计算点数和变换次数以及环境的信噪比3种因素,对测频性能的影响,并得出测量误差的理论表达式。
通过大量仿真结果表明,该方法的测量精度受FFT 的计算点数和环境信噪比影响较小,而受FFT变换次数影响较大;因此该算法不仅稳定性好、测量精度高、对环境的依赖很低,而且计算量较小、便于硬件实现。
【总页数】4页(P25-28)
【关键词】相位差分;相位模糊;测频精度
【作者】戴猛;陈叶明
【作者单位】南京电子技术研究所
【正文语种】中文
【中图分类】TN911.7
【相关文献】
1.一种新的跳频通信体制——载波序列差分相位跳频 [J], 赵荣黎
2.一种稳健的基于解卷叠的相位差分瞬时测频方法 [J], 宋云朝;万群;毛祺;刘刚
3.基于正交频分复用的频域差分幅度相位调制 [J], 束锋;吴乐南
4.数字瞬时测频——相位推算法测频 [J], 胡来招
5.加权相位差分测频算法及其工程应用 [J], 王晓君;安国臣;张秀清
因版权原因,仅展示原文概要,查看原文内容请购买。
提高测频、测周测量精度的方法
提高测频、测周测量精度的方法时间和频率是电子技术中两个重要的基本参数,其他许多电参量的测量方法、测量结果都与时间和频率有着十分密切的联系。
并且,在所有的物理量中,时间和频率具有最高的精度和稳定度,故在实际工作中,也常常把一些非电量或其他电量转换成频率(或时间)进行测量。
因此,寻找方法提高测量频率和测量周期的准确度是十分必要的。
课堂中介绍的主要有两种方法,其一是减少测频量化误差,即增加测量时间(主门时间)的方法;其二是减小侧周量化误差,即采用多周期测量法,在这里不再赘述。
此外,为了提高测量的准确度,比较常用的方法还有游标法、内插法、平均测量技术、多周期同步测量法、相检宽带测频技术以及量化时沿法。
下面分别来进行介绍。
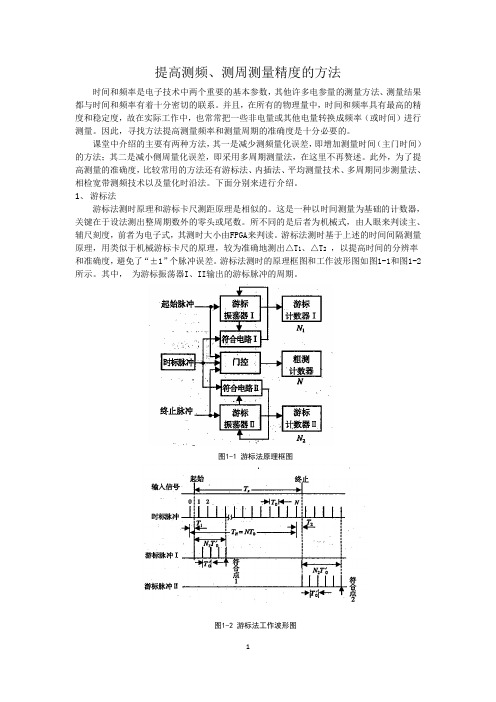
1、游标法游标法测时原理和游标卡尺测距原理是相似的。
这是一种以时间测量为基础的计数器,关键在于设法测出整周期数外的零头或尾数。
所不同的是后者为机械式,由人眼来判读主、辅尺刻度,前者为电子式,其测时大小由FPGA来判读。
游标法测时基于上述的时间间隔测量原理,用类似于机械游标卡尺的原理,较为准确地测出△T1、△T2,以提高时间的分辨率和准确度,避免了“±1”个脉冲误差。
游标法测时的原理框图和工作波形图如图1-1和图1-2所示。
其中,为游标振荡器I、II输出的游标脉冲的周期。
图1-1 游标法原理框图图1-2 游标法工作波形图下面结合上面的原理框图和波形图来说明这种测量方案。
由图可知,被测时间的精确值应为21T T T T N x +-= (1.1)两时钟信号周期差为'00T T T -=∆ (1.2)首先,从被测信号中提取其实脉冲和终止脉冲。
在起始脉冲作用下,使游标振荡器I 输出游标脉冲I,并由游标计数器I 计数,当记到游标脉冲恰好赶上主时标脉冲时(符合点1),此时若游标计数器I 的计数值为N 1,则有)'(0011T T N T -= (1.3)同样,在终止脉冲作用下,当游标计数器II 记录的游标脉冲恰好赶上主时钟脉冲时(符合点2),符合电路II 输出一个脉冲使游标震荡器停止发送游标脉冲II ,若游标计数器II 的计数值为N 2,则)'(0022T T N T -= (1.4)由上面(5.1)(5.2)(5.3)和(5.4)四个式子可以推导)')(()'()'(002100020010T T N N NT T T N T T N NT T x ---=-+--= (1.5)由此可见,游标法的计数分辨力'00T T T -=∆,它比粗测计数器的分辨力0T 和游标计数器的分辨力'0T 都要高得多。
一种高精度快速频率测量方法
一种高精度快速频率测量方法
周增建;王海
【期刊名称】《电子质量》
【年(卷),期】2009(000)005
【摘要】文中研究了一种基于多重自相关的Hilbert变换频率估计算法,利用正弦信号的特性,进行多重自相关运算,有效的提高信噪比,结合Hilbert变换对信号的频率进行估计,从而提高了频率测量的准确度,实验结果表明了该方法具有很好的抗噪能力,能有效的对信号的频率进行估计,比传统的直接Hilbert估计算法精度要高2-3个数量级.
【总页数】3页(P19-21)
【作者】周增建;王海
【作者单位】西安电子科技大学测控技术与仪器系,陕西,西安,710071;西安电子科技大学测控技术与仪器系,陕西,西安,710071
【正文语种】中文
【中图分类】TN911
【相关文献】
1.一种低信噪比正弦信号高精度频率测量方法 [J], 谭超;邾玢鑫
2.一种基于DSP的高精度频率测量方法 [J], 钱时祥;江炜宁;周增建;王海;周渭
3.一种新的快速高精度频率测量方法 [J], 李建林;张仲超
4.一种新的快速高精度频率测量方法 [J], 燕作祥
5.基于αβ变换的快速高精度频率测量方法 [J], 马骁;宋新利;罗伟强;丁镭
因版权原因,仅展示原文概要,查看原文内容请购买。
基于FPGA的一种测频方法的研究
基于FPGA的一种测频方法的研究【摘要】频率信号,因其较强的抗干扰能力以及其易于传输的特性,使得其在实际工程中应用很广泛[1]。
因此,频率信号已经成为当今电子领域里和工程项目中最主要的测量参数之一。
频率的测量方法有很多种,采用电子计数器对频率进行测量是测频的最常用也是最重要的方式之一[2]。
电子计数器有很多优点,如测量精度高、测量迅速、方便使用以及易于实现频率测量过程中的自动化等。
本文将介绍用频率计采用多周期同步测频法测频以及其Verilog HDL的实现。
【关键词】测频方法;FPGA;Verilog HDL;仿真引言频率的测量是电子技术领域中最基本的参数测量之一。
直接测频法为常用的频率测量方法之一,其测量精度很难达到要求,存在较大局限性,因此其在实际应用中使用的较少。
而多周期同步测频法具有测量精度高的优点,并且结合现场可编程门阵列(FPGA,FieldProgrammableGate Array)具有集成度高、可靠性高以及高速的特点,使得频率的测量范围能够达到0.IHz~100MHz,且测量的误差较小[3]。
频率测量分两种情况。
一种是高频信号的测量,需要采用计数测频法,测量过程中需要对初始信号分频,并且要依据频率信号的大致范围来选择计数周期,计数周期随着信号频率的高低而变化,信号的频率越高对应的计数周期越短[4]。
这种做法的目的是为了避免出现测量错误,而这种测量错误出现的根源在于计数值过大且超出计数器允许的最大计数值。
而计时测周法则适用于对低频信号的测量,即便原始信号为低频信号,也要对其进行分频,然后选择适当的高频时钟,高频时钟要由所测信号的大概频率范围来选择。
一、系统软件设计相对于硬件电路,软件设计能适合的信号频率范围更广。
当设计的信号的频率范围变得更高时,需要对硬件电路进行改善,但是软件仍然可以继续使用。
依据上述原因,软件设计时选择的信号的频率范围为:1Hz~20MHz。
如图1所示,软件系统分为分频、计数测频、控制以及计数测周4个模块,其中计数测频模块和计数测周模块都属于计数模块。
FMCW雷达快速高精度测距算法
FMCW雷达快速高精度测距算法FMCW(Frequency-Modulated Continuous Wave)是一种基于连续波的雷达测距技术,由于其快速高精度的特点,在许多领域得到广泛应用。
本文将介绍FMCW雷达的原理,并详细阐述其快速高精度测距算法。
FMCW雷达通过发射一种连续频率变化的信号,并接收到反射回来的信号来实现测距。
它的测距原理是利用多普勒效应,当发射的信号遇到靠近的目标物体时,其频率会发生微小的改变,通过测量频率变化的大小,可以确定目标物体到雷达的距离。
快速高精度测距的关键在于频率变化的控制和信号的处理。
首先,为了实现快速测距,需要快速而准确地控制信号的频率变化。
通常采用锁相环(Phase Locked Loop)技术实现,通过与输入参考信号进行相位比较,产生一个错误信号,然后通过调整本振频率来消除错误信号,从而实现精确的频率变化控制。
接下来是信号的处理,FMCW雷达接收到的信号是一系列的连续波形,需要对这些波形进行处理以获取目标物体的距离信息。
常用的处理算法是快速傅里叶变换(FFT),通过对接收到的信号进行频谱分析,可以得到不同频率的成分,进而确定目标物体的距离。
在进行测距之前,需要进行一些预处理工作,例如去除杂散信号、消除信号的幅度变化等,以提高测距的精度。
同时,还需要注意参考信号与接收信号之间的相位差,这些因素都会影响测距的准确度。
除了以上基本的测距原理和处理方法,还有一些额外的技术可以提高FMCW雷达的测距性能。
例如,使用多通道接收器可以降低误差,并提高系统的鲁棒性。
同时,还可以结合其他传感器,例如惯性测量单元(Inertial Measurement Unit,简称IMU)来实现更精确的测距结果。
总之,FMCW雷达是一种快速高精度测距的技术,其原理是基于多普勒效应实现的。
通过对信号的频率变化进行控制和信号的处理,可以实现对目标物体的精确测距。
同时,还可以通过一些额外的技术手段来进一步提高测距的准确性和稳定性。
傅里叶变换FFT算法的介绍及其在微机继电保护中的应用
傅里叶变换FFT算法的介绍及其在微机继电保护中的应用摘要:传统的微机继电保护算法中 ,一般使用梯形算法来计算周期信号的直流分量和各次谐波的系数 ,此方法计算比较复杂。
本文提出了一种基于 FFT 的算法。
该算法利用 FFT 可以由输入序列直接计算出输入信号的直流分量和各次谐波的幅值和相角的特点 ,大大简化了谐波分析的计算。
与梯形算法相比 ,该算法具有精度高、计算量小、更易在数字信号处理器上实现等优点。
因而可以取代梯形算法来计算谐波系数。
针对 FFT计算 ,还介绍了正弦信号采样频率的选择方法。
关键字:傅里叶算法; FFT; 谐波分析;微机继电保护。
The Introduction of Fourier algorithm based on FFT inModif ied model of power meteringAbstract: In microcomputer relay protection of traditional algorithm, coefficient of DC component generally use the trapezoidal algorithm to calculate the periodic signal and harmonic,and this method is very complex. This paper presents an algorithm based on FFT. The algorithm makes use of the FFT and it can be calculated directly from the input sequence characteristics of amplitude and phase of the DC component of the input signal and harmonic, greatly simplifies the calculation of harmonic analysis. Compared with the trapezoidal algorithm, this algorithm has high precision, small computation, easily realized in digital signal processor. So that you can replace trapezoidal algorithm to calculate the harmonic coefficient. For the FFT calculation, the selection method of sine signal sampling frequency is also presented. Keywords: Fourier algorithm;FFT;harmonic analysis;Modif ied model of power metering.一、傅立叶变换FFT算法简介:计算离散傅里叶变换的一种快速算法,简称FFT。
