广东佛山市高明区2016-2017学年高二数学下学期第4周练习试题 理
广东省佛山市高明区第一中学2016-2017学年高二数学下学期:第二周测含答案

高二下学期数学理科第二周周五测试题一、选择题1.在空间直角坐标系中,点M 的坐标是(4,7,6),则点M 关于y 轴的对称点坐标为( )A .(4,0,6)B .(4,7,6)--C .(4,0,6)--D .(4,7,0)-2.在空间直角坐标系中,()()()4,1,9,10,1,6,2,4,3A B C -,则ABC ∆为 ( )A .等边三角形B .等腰直角三角形C 。
钝角三角形D .锐角三角形3.若向量a 、b 满足()()2,1,2,4,3,2a b a b +=---=--,则a b ⋅等于( )A .5B .5-C .7D .7-4.已知(1,0,2),(6,0,2),,λλ=+=a b a b 则λ的值为 A.15 B.5 C 。
15- D.5- 5.如图所示,已知空间四边形OABC ,其对角线为OB ,AC ,M 、N 分别为OA 、BC 的中点,点G 在线段MN 上,且2MG GN =,若OG xOA yOB zOC =++,则x y z +-= ( )D .1 A .16 B .23 C 。
566.设平面α的一个法向量为1(1,2,2)=-n ,平面β的一个法向量为2(2,4,)k =--n ,若αβ∥,则k =A .2B .4-C .2-D .4 7.如图,在直三棱柱111ABC A B C -中,∠ACB =90°,AA 1=2,AC =BC =1,则异面直线A 1B 与AC所成角的余弦值是( )A 。
65 B. 64 C 。
63 D. 668.已知A (4,1,3),B(2,3,1),C (3,7,-5),点P (x ,-1,3)在平面ABC 内,则x 的值为( )A 。
-4B 。
1 C.10 D.11题目 1 2 3 4 5 6 7 8 答案二、填空题9.已知{},,i j k 为单位正交基底,且3,232a i j k b i j k =-++=--,则向量2a b -的坐标是_____________。
广东省佛山市高明区第一中学2016-2017学年高二数学下

高二周六数学测试理科卷(2017年2月18日)一.选择题(每小题5分共计60分)1.已知双曲线22:13y E x -=的左焦点为F ,直线2x =与双曲线E 相交于A ,B 两点,则ABF △的面积为( )A.12B.24C.D.2.若双曲线22221x y a b-= )A.2y x =±B.y =C.12y x =± D.y = 3.圆22(3)(3)9x y -+-=上到直线34110x y +-=的距离等于1的点有() A .1个 B .2个 C .3个 D .4个 4.设命题2:,2n p n N n ∃∈>,则p ⌝为( )A .2,2n n n ∀∈>B .2,2n n n ∃∈≤C .2,2n n n ∀∈≤D .2,2n n n ∃∈=5.已知命题:p 若x y >,则x y -<-;命题:q 若x y <,则22x y >;在下列题中:(1)p q ∧;(2)p q ∨;(3)()p q ∧⌝;(4)()p q ⌝∨,真命题是( )A .(1)(3)B .(1)(4)C .(2)(3)D .(2)(4) 6.设0,0a b >>,则“x a >,且y b >”是“x y a b +>+且xy ab >”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件7.已知椭圆()222:10525x y C b b+=<<的长轴长、短轴长、焦距成等差数列,则该椭圆的方程是( )A .221254x y += B .221259x y += C. 2212516x y += D .22125x y += 8.过抛物线24y x =的焦点F 作直线l 与其交于,A B 两点,若4AF =,则BF =( ) A .2 B .43C .23D .1 9.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为( )A .B .C .D .10.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体. 它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣和(牟和)在一起的方形伞(方盖). 其直观图如下左图,图中四边形是为体现其直观性所作的辅助线. 其实际直观图中四边形不存在,当正视图和侧视图完全相同时,它的的正视图和俯视图分别可能是( )A .b a ,B .c a , C. b c , D .d b ,11.将半径为1的圆分割成面积之比为1:2:3的三个扇形作为三个圆锥的侧面,设这三个圆锥底面半径依次为1r ,2r ,3r ,那么123r r r ++的值为( )A .12B .2C .1 12.若椭圆221369x y +=的弦被点()4,2平分,则此弦所在直线的斜率为( )A .2B .-2C .13 D .12- 二.填空题(每小题5分共计20分)13.如图,在河的一侧有一塔12CD m =,河宽3BC m =,另一侧有点,4A AB m =,则点A 与塔顶D 的距离AD =_________.14.圆锥的侧面积与过轴的截面积之比为π2,则母线与轴的夹角大小为 15.已知(1,1,)a t t t =--,(3,,)b t t =,则a b -的最小值 16.将一块边长为6cm 的正方形纸片,先按如图(1)所示的阴影部分裁去四个全等的等腰三角形,然后将剩余部分沿虚线折叠并拼成一个正四棱锥模型(底面是正VABCD方形,从顶点向底面作垂线,垂足是底面中心的四棱锥),将该四棱锥如图(2)放置,若其正视图为正三角形,则其体积为 3cm .三.解答题(本大题50分)17. (本题12分)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC -A 1B 1C 1中, AC =AA 1=2AB =2,∠BAC =90°,点D 是侧棱CC 1延长线上一点, EF 是平面ABD 与平面A 1B 1C 1的交线.(1)求证:EF ⊥A 1C ;(2)当直线BD 与平面ABC 所成角的正弦值为31414时,求三棱锥D -EFC 1的体积.18. (本题12分)在四棱锥V ABCD -中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD .(I) 证明:AB ⊥平面VAD ; (II)求二面角A VD B --的余弦值.19.(本题12分)已知椭圆()222210x y a b a b+=>>的离心率e =,以上顶点和右焦点为直径端点的圆与直线20x y +-=相切. (Ⅰ)求椭圆的标准方程;(Ⅱ)对于直线:l y x m =+和点()0,3Q ,是否椭圆C 上存在不同的两点A 与B 关于直线l 对称,且332QA QB ⋅=,若存在实数m 的值,若不存在,说明理由.20.(本题14分)如图,抛物线21:8C y x =与双曲线()22222:10,0x y C a b a b-=>>有公共焦点2F ,点A 是曲线12,C C在第一象限的交点,且25AF =. (Ⅰ)求双曲线2C 的方程;(Ⅱ)以1F 为圆心的圆M 与双曲线2C 的一条渐近线相切,圆()22:21N x y -+=.已知点(P ,过点P 作互相垂直且分别与圆M 、圆N 相交的直线1l 和2l ,设被圆M 截得的弦长为s ,2l 被圆N 截得的弦长为t .试探索ts 是否为定值?请说明理由.高二周六数学测试理科卷(2017年2月18日)答案:选择题(每小题5分共计60分):填空题:(每小题5分共计20分) 13.【答案】1314.【答案】315.16.【答案】三.解答题(本大题50分)17.【解答】:(1)证明:依题意,有平面ABC ∥平面A 1B 1C 1,又平面ABC ∩平面ABD =AB ,平面A 1B 1C 1∩平面ABD =EF , ∴EF ∥AB .∵三棱柱ABC -A 1B 1C 1为直三棱柱,且∠BAC =90°, ∴AB ⊥AA 1,AB ⊥AC .而AA 1∩AC =A ,∴AB ⊥平面ACC 1A 1. 又A 1C ⊂平面ACC 1A 1,∴AB ⊥A 1C .∴EF ⊥A 1C . ……………………………5分 (2)设直线BD 与平面ABC 所成的角为θ,∵直线BD 与平面ABC 所成角的正弦值为31414,∴tan θ=35,又BC =AB 2+AC 2|=5, ∴CD =3,DC 1=1,FC 1=DC 1tan ∠DFC 1=135=53,EF =13,EC 1=23.又S △EFC 1=12×23×13=19,∴VD -EFC 1=13×19×1=127.……………………………12分18. 【解答】:(Ⅰ)因为平面VAD ⊥平面ABCD ,平面VAD ∩平面ABCD=AD , 又AB 在平面ABCD 内,AD ⊥AB ,所以AB ⊥平面VAD. ……………………………5分 (Ⅱ)由(Ⅰ)知AD ⊥AB ,AB ⊥AV.依题意设AB=AD=AV=1,所以设VD 的中点为E,连结AE 、BE ,则AE ⊥VD ,BE ⊥VD , 所以∠AEB 是面VDA 与面VDB 所成二面角的平面角. 又AE=2,BE=2,所以cos ∠AEB=371372+-. (方法二) (Ⅰ)同方法一.(Ⅱ)设AD 的中点为O ,连结VO ,则VO ⊥底面ABCD. 又设正方形边长为1,建立空间直角坐标系如图所示. 则,A(12,0,0),B(12,1,0),D( 12,0,0), V(0,0,2); 13(0,1,0),(,1,),(1,1,0)2AB VB BD ==--=--由(Ⅰ)知m =(0,1,0)-是平面VAD 的法向量.设(1,,)n y z=是平面VDB 的法向量,则1,10,(1,,)(,1,0,(1,1,20,(1,,)(1,1,0)0,y n VB y z n z n BD y z =-⎧⎧⎧∙=∙=⎪⎪⎪⇒⇒⇒=-⎨⎨⎨=∙=⎪⎪⎪⎩∙--=⎩⎩∴(0,1,0)(1,1,cos ,m n -⋅-<>==, ∴求二面角A VD B --的余弦值是7…………………………12分 19.【解答】(1)由已知条件可知,圆心是(,22c b ),半径是2a,圆心到直线20x y +-=的距离为半径2a,则可得方程组:2222ac a a b c⎧⎪⎪=⎪⎪⎪=⎨⎪=+⎪⎪⎪⎪⎩解得11c b a ⎧=⎪=⎨⎪=⎩,因此,所求椭圆的标准方程是2212x y +=.………………………………………5分(2)设AB 直线为AB :y x n =-+,则A ,B 两点的坐标由方程组确定212y x n x y =-+⎧⎪⎨+=⎪⎩,化简得2234220x nx n -+-=,则有21212422,33n n x x x x -+==, 1212122()()()23ny y x n x n x x n +=-++-+=-++=, 22121212122()()()3n y y x n x n x x n x x n -=-+-+=-++=所以AB 中点坐标为(2,33n n )在直线:l y x m =+上,有233n nm =+,得30n m +=; 又11223233(,3)(,3)QA QB x y x y ==--⋅--121212323()93x x y y y y =+-++ 22322222393333n n n --=+-+ 2230n n --=,解得:3n =或1n =-,当3n =时,代入2234220x nx n -+-=无解,当1n =-时,代入2234220x nx n -+-=有解,此时,13m =, 因此存在实数13m =满足条件。
广东省佛山市高明区第一中学2016-2017学年高二下学期

高二文科周五测试(4)命题人:高二文科数学备课组 2017.3.3一、选择题:本大题共10小题,每小题5分,满分50分 1.已知集合{}{}213,4,P x R x Q x R x=∈≤≤=∈≥则()RPQ =ð( )A.[]2,3B.(]2,3-C.[)1,2D.(][),21,-∞-+∞2.已知平面向量()()1,2,2,,ab k ==-若a 与b 共线,则a b+=( )A.5B.3.在ABC ∆中,内角A,B,C 所对的边分别为a,b,c,则""a b =是"cos cos "a B b A =的( )A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件 4.函数()23x f x =-的零点所在区间为( )A.()1,0-B.()0,1C.()1,2D.()2,35.一空间几何体的三视图如图所示,该几何体的体积为12+3π,则正视图与侧视图中 的值为( )A.5B.4C.3D.26.设n S 是等差数列{}n a 的前n 项和,1532,3a a a ==,则9S =( ) A.-72 B. -54 C.54 D.727.已知互相垂直的平面,αβ交于直线l ,若直线m ,n 满足//,m n αβ⊥,则( ) A.//m l B. //m n C.n l ⊥ D.m n ⊥8.函数4cos xyx e=-(e 为自然对数的底数)的图象可能是( )9.若曲线32:22C y x ax ax =-+上任一点处的切线的倾斜角都是锐角,那么整数a 的值等于( )A.-2B.0C.1D.-1 10.已知,x y R ∈,且0x y >>,则( )A.110x y-> B. sin sin 0x y -> C.11022xy⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭D.ln ln 0x y +> 11.为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(10分制)的频率分布直方图如图所示,假设得分值的中位数为c m ,众数为0m ,平均数为x , 则( )A.0c m m x ==B. 0c m m x =<C.0c m m x <<D. 0c m m x <<12.若函数()3241f x x mx mx =+-+在区间()1,2-上有两个极值点,则实数m 的取值范围是( ) A.1,02⎛⎫- ⎪⎝⎭ B.1,+2⎛⎫∞ ⎪⎝⎭ C.10,2⎛⎫ ⎪⎝⎭ D.1,2⎛⎫-∞ ⎪⎝⎭答题卡姓名________ 班级_________学号_________分数_________ 一、选择题(每小题5分,共60分)二、填空题:(本大题共4小题,每小题5分,满分20分) 13.曲线()223f x x x =-在点()()1,1f 处的切线方程为____________________.14. 设p 在[]0,5上随机取值,则关于x 的方程210x px ++=有实数根的概率为____________.15.已知双曲线2222:1x y C a b-=的左顶点为A ,右焦点为F ,点()0,B b ,且0BA BF =,则双曲线C 的离心率为___________________________.16.已知过点()2,4的直线l 被圆22:2450C x y x y +---=截得的弦长为6,则直线l 的方程为_________________________________.BDACCB CACCDC 20x y --=;35;2;2034100x x y -=-+=或。
-数学-高二-广东省佛山市高明区一中2016-2017学年高二下第四周静校练习数学(文)试题

高明一中高二文科下学期数学周日静校训练(4)高二__________班、姓名________、分数___________一、选择题(共3个小题,每小题5分,满分15分)1.已知函数()3239f x x ax x =++-在3x =-处取得极值,则a =( )A .2 B.3 C.4 D. 52.已知函数3227f x x ax bx a a 在1x 处取得极大值10,则a b的值为( ) 2.3A .2B C.2或23D.不存在 3.已知函数()321f x x ax x =-+--在R 上是单调函数,则实数a 的取值范围是( ) .,33,A .3,3B .,33,C .3,3D二、填空题(本题共3小题,每小题5分,满分15分)4.函数()ln f x x x =的单调递减区间是_________ .5.若函数23k k h x x x 在1,上是增函数,则实数k 的取值范围是________.6.下图是yf x 的导函数的图象,对于下列四个判断: (1)f x 在3,1上是增函数. (2)1x是f x 的极小值点. (3)f x 在2,4上是减函数,在1,2上是增函数. (4)2x 是f x 的极小值点. 其中正确的序号为______________.三、解答题(10分)7.已知函数3233.f xx ax bx (1)若f x 在1x 处取得极值,求a,b 的值. (2)若f x 的图象与直线1210x y 相切于点1,11,求a,b 的值. (3)在(2)的条件下,求函数f x 的单调区间.DAD 10,e 2,; (2)(3) 7.10,1;21,3;3,1,3,,1,3a b a b 增区间:减区间:。
广东省佛山市高明区高二数学下学期第4周练习试题理
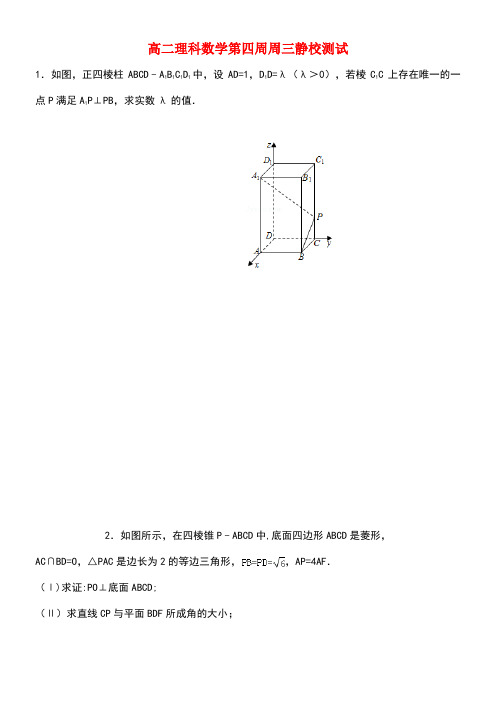
高二理科数学第四周周三静校测试1.如图,正四棱柱ABCD﹣A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在唯一的一点P满足A1P⊥PB,求实数λ的值.2.如图所示,在四棱锥P﹣ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,,AP=4AF.(Ⅰ)求证:PO⊥底面ABCD;(Ⅱ)求直线CP与平面BDF所成角的大小;(Ⅲ)在线段PB上是否存在一点M,使得CM∥平面BDF?如果存在,求的值,如果不存在,请说明理由.高二理科数学第四周周三静校测试答案1。
解:如图,以点D为原点O,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系O﹣xyz,则D(0,0,0),B(1,1,0),A1(1,0,λ),设P(0,1,x),其中x∈[0,λ],因为A1P⊥PB,所以,即(﹣1,1,x﹣λ)•(﹣1,0,x)=0,化简得x2﹣λx+1=0,x∈[0,λ],由点P(0,1,x)的唯一性知方程x2﹣λx+1=0只有唯一解,所以,判别式△=λ2﹣4=0,且λ>0,解得λ=2.2.(Ⅰ)证明:因为底面ABCD是菱形,AC∩BD=O,所以O为AC,BD中点.﹣﹣﹣﹣﹣﹣﹣1分)又因为PA=PC,PB=PD,所以PO⊥AC,PO⊥BD,﹣﹣﹣﹣﹣﹣(3分)所以PO⊥底面ABCD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(Ⅱ)解:由底面ABCD是菱形可得AC⊥BD,又由(Ⅰ)可知PO⊥AC,PO⊥BD.如图,以O为原点建立空间直角坐标系O﹣xyz.由△PAC是边长为2的等边三角形,,可得.所以.﹣﹣﹣﹣(5分)所以,.由已知可得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)设平面BDF的法向量为=(x,y,z),则令x=1,则,所以=(1,0,﹣).﹣﹣﹣﹣﹣﹣﹣﹣(8分)因为cos=﹣,﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)所以直线CP与平面BDF所成角的正弦值为,所以直线CP与平面BDF所成角的大小为30°﹣﹣﹣﹣﹣﹣﹣﹣(10分)(Ⅲ)解:设=λ(0≤λ≤1),则.﹣﹣﹣﹣﹣﹣(11分)若使CM∥平面BDF,需且仅需=0且CM⊄平面BDF,﹣﹣﹣(12分)解得,﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)所以在线段PB上存在一点M,使得CM∥平面BDF.此时=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
广东省佛山市高明区第一中学2016-2017学年高二国庆假期数学(理)试题 含答案

高二理科数学国庆作业一、选择题(每小题5分,共60分)1.函数()sin 2cos 2f x x x =-的最小正周期是( ). A.π2B.πC.2πD.4π2.[2014·郑州质检]要得到函数y =cos2x 的图象,只需将函数y =sin2x 的图象沿x 轴( )A 。
向右平移4π个单位 B 。
向左平移4π个单位C 。
向右平移8π个单位 D 。
向左平移8π个单位3.向量、的夹角为60°,且,,则等于( )A 。
1 B. C 。
D 。
2 4.已知(,3)a x =,(3,1)b =,且//a b , 则x 等于 ( )A .-1B .-9C .9D .1 5.某市有大型超市200家、中型超市400家、小型超市1400家,为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )A. 70家B.50家 C 。
20家 D.10家6.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积( )A .313cm B .323cm C .343cmD .383cm7.若在区间[]0,2中随机地取两个数,则这两个数中较小的数大于32的概率是( )A。
31B。
32C。
94 D.918.公比为2的等比数列{}na的各项都是正数,且16113=⋅aa,则=5a()A。
1 B.2 C.4 D。
89.公差不为零的等差数列{}na的前n项和为n S.若4a 是37a a与的等比中项, 832S=,则10S等于()A.18 B.24 C.60 D.90 10.给出下列命题:(1)垂直于同一直线的两直线平行。
(2)同平行于一平面的两直线平行。
(3)同平行于一直线的两直线平行. (4)平面内不相交的两直线平行。
其中正确的命题个数是( )A.1 B.2 C.3 D.411.如图,在正方体1111ABCD A B C D-中,异面直线1A D与1D C所成的角为()A.30B.45C.60D.9012.根据右边框图,对大于2的整数N,得出数列的通项公式是()A.2na n= B.2(1)na n=-C。
高二年级下学期 经典数学周测卷及答案详解
2017年高二年级下学期数学周测试卷及答案详解(答案附后) 姓名: 班级: 学号: 得分:一、填空题(请把正确的答案写在题后的横线上,每小题5分,共80分)1.若z =4+3i ,则z |z |= ;2.已知f (x )为偶函数,当x ≤0时,f (x )=e -x -1-x ,则曲线y =f (x )在点(1,2)处的切线方程是 .3.若tan θ=-13,则cos 2θ= ;4..小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M ,I ,N 中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是 ;5.直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为 ;6.已知θ是第四象限角,且sin ⎝⎛⎭⎫θ+π4=35,则tan ⎝⎛⎭⎫θ-π4=________. 7.设直线y =x +2a 与圆C :x 2+y 2-2ay -2=0相交于A ,B 两点,若|AB |=23,则圆C 的面积为__________.8.设F 为抛物线C :y 2=4x 的焦点,曲线y =kx (k >0)与C 交于点P ,PF ⊥x 轴,则k =__________.9.若x ,y 满足约束条件⎩⎪⎨⎪⎧x -y +1≥0,x +y -3≥0,x -3≤0,则z =x -2y 的最小值为__________.10.若的内角所对的边分别为,已知,且,则等于__________.11.在Rt △ABC 中,∠ACB=90°,=, =2,则 = .12.设函数f (x )=是(﹣∞,+∞)上的增函数,那么实数k的取值范围为 . 13.已知二次曲线+=1,则当m ∈[﹣2,﹣1]时,该曲线的离心率e 的取值范围是 .14.过抛物线y 2=4x 的焦点作一条直线交抛物线于A ,B 两点,若线段AB 的中点M 的横坐标为2,则|AB |等于 . 15.设为单位向量,①若为平面内的某个向量,则=||•;②若与平ABC ∆,,A B C ,,a b c 2sin 23sin b A a B =2c b =ab行,则=||•;③若与平行且||=1,则=.上述命题中,假命题个数是 .16.若数列{a n }的首项a 1=2,且;令b n =log 3(a n +1),则b 1+b 2+b 3+…+b 100= .二、解答题(20分)17.已知f (x )=x 2﹣ax +lnx ,a ∈R .(1)若a=0,求函数y=f (x )在点(1,f (1))处的切线方程; (2)若函数f (x )在[,1]上是增函数,求实数a 的取值范围;(3)令g (x )=x 2﹣f (x ),x ∈(0,e ](e 是自然对数的底数);求当实数a 等于多少时,可以使函数g (x )取得最小值为3.2017年高二年级下学期数学周测试卷参考答案1.【解答】先求出z 与|z |,再计算z |z |.∵z =4+3i ,∴z =4-3i ,|z |=42+32=5,∴z|z |=4-3i 5=45-35i. 2.【解答】首先求出x >0时函数的解析式,再由导数的几何意义求出切线的斜率,最后由点斜式得切线方程.设x >0,则-x <0,f (-x )=e x -1+x .∵f (x )为偶函数,∴f (-x )=f (x ),∴f (x )=e x -1+x .∵当x >0时,f ′(x )=e x -1+1,∴f ′(1)=e 1-1+1=1+1=2.∴曲线y =f (x )在点(1,2)处的切线方程为y -2=2(x -1),即2x -y =0. 答案:2x -y =03.【解答】解析:先利用二倍角公式展开,再进行“1”的代换,转化为关于tan θ的关系式进行求解.∵cos 2θ=cos 2θ-sin 2θcos 2θ+sin 2θ=1-tan 2θ1+tan 2θ,又∵tan θ=-13,∴cos 2θ=1-191+19=45.4.【解答】解析:根据古典概型的概率公式求解.∵Ω={(M,1),(M,2),(M,3),(M,4),(M,5),(I,1),(I,2),(I,3),(I,4),(I,5),(N,1),(N,2),(N,3),(N,4),(N,5)},∴事件总数有15种.∵正确的开机密码只有1种,∴P =115.5.【解答】解析:利用椭圆的几何性质列方程求离心率.不妨设直线l 经过椭圆的一个顶点B (0,b )和一个焦点F (c,0),则直线l 的方程为x c +yb =1,即bx +cy -bc =0.由题意知|-bc |b 2+c 2=14×2b ,解得c a =12,即e =12. 6.【解答】解析:将θ-π4转化为⎝⎛⎭⎫θ+π4-π2. 由题意知sin ⎝⎛⎭⎫θ+π4=35,θ是第四象限角,所以cos ⎝⎛⎭⎫θ+π4>0,所以cos ⎝⎛⎭⎫θ+π4=1-sin 2⎝⎛⎭⎫θ+π4=45. tan ⎝⎛⎭⎫θ-π4=tan ⎝⎛⎭⎫θ+π4-π2=-1tan ⎝⎛⎭⎫θ+π4=-cos ⎝⎛⎭⎫θ+π4sin ⎝⎛⎭⎫θ+π4=-4535=-43. 7.【解答】解析:利用圆的弦长、弦心距、圆的半径之间的关系及勾股定理列方程求解.圆C :x 2+y 2-2ay -2=0化为标准方程是C :x 2+(y -a )2=a 2+2,所以圆心C (0,a ),半径r =a 2+2.|AB |=23,点C 到直线y =x +2a 即x -y +2a =0的距离d =|0-a +2a |2,由勾股定理得⎝⎛⎭⎫2322+⎝ ⎛⎭⎪⎫|0-a +2a |22=a 2+2,解得a 2=2, 所以r =2,所以圆C 的面积为π×22=4π.8.【解答】解析:根据抛物线的方程求出焦点坐标,利用PF ⊥x 轴,知点P ,F 的横坐标相等,再根据点P 在曲线y =kx上求出k .∵y 2=4x ,∴F (1,0).又∵曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,∴P (1,2).将点P (1,2)的坐标代入y =kx(k >0)得k =2.9.【解答】解析:作出不等式组表示的可行域,利用数形结合思想求解. 不等式组⎩⎪⎨⎪⎧x -y +1≥0,x +y -3≥0,x -3≤0表示的可行域如图阴影部分所示.由z =x -2y 得y =12x -12z .平移直线y =12x ,易知经过点A (3,4)时,z 有最小值,最小值为z =3-2×4=-510.【解答】试题分析:由得,得2sin 23sin b A a B =4sin sin cos 3sin sin B A A A B =,又.∴,则11.【解答】解:如图,∵∠ACB=90°,=, =2,则=2=∙=→→CA CB12.【解答】解:∵f (x )=是(﹣∞,+∞)上的增函数,∴,解得k ≤﹣1或1≤k ≤2,则实数k 的取值范围是(﹣∞,﹣1]∪[1,2], 故答案为:(﹣∞,﹣1]∪[1,2].13.【解答】解:由当m ∈[﹣2,﹣1]时,二次曲线为双曲线, 双曲线+=1即为﹣=1,且a 2=4,b 2=﹣m ,则c 2=4﹣m ,即有,14.【解答】解:由抛物线y 2=4x 可得p=2. 设A (x 1,y 1),B (x 2,y 2).∵线段AB 的中点M 的横坐标为2,∴x 1+x 2=2×2=4. ∵直线AB 过焦点F ,∴|AB |=x 1+x 2+p=4+2=6.15.【解答】解:对于①,向量是既有大小又有方向的量, =||•的模相同,但方向不一定相同,∴①是假命题; 对于②,若与平行时,与方向有两种情况,一是同向,二是反向,反向时=﹣||•,∴②是假命题;3cos 4A =2c b =22222cos 2a b c b A b =+-=2a b =对于③,若与平行且||=1时,与方向有两种情况,一是同向,二是反向,反向时=﹣,∴③是假命题;综上,上述命题中,假命题的个数是3.16.【解答】解:∵数列{a n}的首项a1=2,且,+1=3(a n+1),a1+1=3,∴a n+1∴{a n+1}是首项为3,公比为3的等比数列,∴,∴b n=log3(a n+1)==n,∴b1+b2+b3+…+b100=1+2+3+…+100==5050.故答案为:5050.17.【解答】解:(1)a=0时,f(x)=x2+lnx,x>0∴f′(x)=2x+,∴f′(1)=3,f(1)=1,∴数y=f(x)在点(1,f(1))处的切线方程为3x﹣y﹣2=0,(2)函数f(x)在[,1]上是增函数,∴f′(x)=2x﹣a+≥0,在[,1]上恒成立,即a≤2x+,在[,1]上恒成立,令h(x)=2x+≥2=2,当且仅当x=时,取等号,∴a≤2,∴a的取值范围为(﹣∞,2](3)g(x)=x2﹣f(x)=ax﹣lnx,x∈(0,e].∴g′(x)=a﹣=(0<x≤e),①当a≤0时,g(x)在(0,e]上单调递减,g(x)min=g(e)=ae﹣1=3,解得a=(舍去);②当a>0且<e时,即a>,g(x)在(0,)上单调递减,在(,e]上单调递增,∴g(x)min=g()=1+lna=3,解得a=e2,满足条件;③当a>0,且≥e时,即0<a≤,g(x)在(0,e]上单调递减,g(x)min=g (e)=ae﹣1=3,解得a=(舍去);综上,存在实数a=e2,使得当x∈(0,e]时,g(x)有最小值3.。
广东省佛山市高明区高二数学下学期第一次大考试题 文
2016—2017学年第二学期高二第一次大考文科数学试题一、选择题(下列各小题的四个答案中只有一个是正确的,请把唯一正确答案的代号填涂在答题卡的相应表格中,共12个小题,每小题5分,满分60分。
)1.已知全集{}1234567U =,,,,,,,{}245A =,,,{}1357B =,,,,则()UA B =ðA .{}5B .{}24,C. {}25, D .{}2456,,,2.已知cos 33παα⎛⎫+=- ⎪⎝⎭为锐角),则sin α=A B .3. 0x <“”是ln(1)0x +<“”的 A.充分不必要条件 B.必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 4.设m 、n 是两条不同的直线, α、β是两个不同的平面,下列命题正确的是A.若m ⊥α,n ⊥β,且α⊥β,则m ⊥nB.若m //α,n //β,且α//β,则m //nC.若m ⊥α,n ⊂β,且m ⊥n ,则α⊥βD.若m ⊂α,n ⊂α,且m //β,n //β,则α//β 5.我国古代数学算经十书之一的《九章算术》有一衰分问题:今有北乡八千一百人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,则北乡遣A. 104人B. 108人C. 112人D. 120人6.已知双曲线()22104x y m m-=>,则m 的值为 A.7 B. 8 C. 9 D. 10 7.下列四个结论:①若0x >,则sin x x >恒成立;②命题“若sin 0x x -=,则0x =”的逆否命题为“若0x ≠,则sin 0x x -≠”; ③“命题p q ∧为真”是“命题p q ∨为真”的充分不必要条件; ④命题“x R ∀∈,ln 0x x ->”的否定是“0x R ∃∈,00ln 0x x -<”. 其中正确结论的个数是A .1个B .2个C .3个D .4个8.已知变量x ,y 满足线性约束条件⎪⎩⎪⎨⎧≥++≥+-≤-+0102023y x y x y x ,则目标函数y x z -=21的最小值为A .45-B .2C .2-D .4139.一个四面体的三视图如右图所示,则该四面体的表面积是A.11+C.2+D.10.已知圆()224x a y ++=截直线40x y --=所得的弦的长度为,则a 等于A. ±B. 6C. 2或6D. 2-或-611.四面体ABCD 的四个顶点都在球O 的球面上,2AB AD CD ===,BD =BD CD ⊥,平面ABD ⊥平面BCD ,则球O 的体积为A.C.2D.2π 12. 若()f x 是定义在(0 )+∞,上的单调函数,且对任意2(0)[()log ]3x f f x x ∈+∞-=,,,则方程()()2f x f x '-=的解所在区间是ABC .(1 2),D .(2 3),二、填空题(把答案填在答题卡相应的空格中,共4个小题,每小题5分,满分20分。
广东省佛山市高明区第一中学2016-2017学年高二下学期第一周基础练习数学(文)试题含答案
高明一中高二文科数学周五基础训练(20170210)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确的答案代号写在后面的答题卡上.1.若双曲线的焦点为(0,4)和(0,4-),虚轴长为43,则双曲线的方程为A .221412x y -=B .221412y x -=C .221124x y -=D .221124y x -=2.某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是A .203B .163C .86π-D .83π-3.数列{a n }中,如果na =3n (n =1,2,3,…) ,那么这个数列是A .公差为2的等差数列B .公差为3的等差数列C .首项为3的等比数列D .首项为1的等比数列4. 计算下列几个式子,①35tan 25tan 335tan 25tan ++,②2 (sin35cos25+sin55cos65), ③15tan 115tan 1-+结果为3的是俯视图侧视图正视图A 。
①② B. ①③ C 。
①②③ D. ②③5.设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是 A. 若l m ⊥,m α⊂,则l α⊥ B 。
若l α⊥,l m //,则m α⊥ C 。
若l α//,m α⊂,则l m // D 。
若l α//,m α//,则l m //6.直线32-=x y 与双曲线1222=-y x 相交于B A ,两点,则AB=A .574 B .257C .357D .4577. 如图,在正方体ABCD —A 1B 1C 1D 1中,BC 1与平面BB 1D 1D 所成角为A 。
30°B 。
45°C 。
60°D 。
120°8.点D C B A ,,,均在同一球面上,且AB 、AC 、AD 两两垂直,且,1=AB ,2=AC3=AD,则该球的表面积为A .7πB .14πC .27πD .3147π高明一中高二文科数学周五基础训练答题卡学号 、姓名 、分数 一、选择题:二、填空题:(每小题5分,满分40分)9.在平面直角坐标系中,若角α的终边落在射线(0)y x x =≥上,则tan α=。
广东省佛山市高明区高二数学下学期第1周练习试题理
第一周高二理科数学静校测试1. (本小题满分14分)如图5,已知等腰直角三角形RBC ,其中∠RBC =90º,2==BC RB .点A 、D 分别是RB 、RC 的中点,现将△RAD 沿着边AD 折起到△PAD 位置,使PA ⊥AB ,连结PB 、PC .(1)求证:BC ⊥PB ;(2)求二面角P CD A --的平面角的余弦值.2.(本小题满分14分)如图,△ABC 的外接圆⊙O 的半径为5,CD ⊥⊙O 所在的平面,BE //CD,CD=4,BC=2,且BE=1,21cos 21AEB ∠=. (1)求证:平面ADC ⊥平面BCDE ;O A BE D C(2)求几何体ABCDE的体积;(3)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为27?若存在,确定点M的位置,若不存在,请说明理由。
第一周高二理科数学静校测试答案18. 解:(1)∵点A 、D 分别是RB 、RC 的中点, ∴BC AD BC AD 21,//=。
…… 2分 ∴∠RBC RAD PAD ∠=∠==90º。
∴AD PA ⊥.∴ BC PA ⊥, ∵A AB PA AB BC =⊥ ,,∴BC ⊥平面PAB 。
…… 4分∵⊂PB 平面PAB ,∴PB BC ⊥. …… 6分(2)法1:取RD 的中点F ,连结AF 、PF .∵1==AD RA ,∴RC AF ⊥。
∵AD AP AR AP ⊥⊥,,∴⊥AP 平面RBC 。
∵⊂RC 平面RBC ,∴AP RC ⊥. …… 8分∵,A AP AF = ∴⊥RC 平面PAF 。
∵⊂PF 平面PAF ,∴PF RC ⊥。
∴∠AFP 是二面角P CD A --的平面角. ……10分在Rt △RAD 中, 22212122=+==AD RA RD AF , 在Rt △PAF 中, 2622=+=AF PA PF , 332622cos ===∠PF AF AFP 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二理科数学第四周周三静校测试
1.如图,正四棱柱ABCD﹣A1B1C1D1中,设AD=1,D1D=λ(λ>0),若棱C1C上存在唯一的一点P满足A1P⊥PB,求实数λ的值.
2.如图所示,在四棱锥P﹣ABCD中,底面四边形ABCD是菱形,
AC∩BD=O,△PAC是边长为2的等边三角形,,AP=4AF.
(Ⅰ)求证:PO⊥底面ABCD;
(Ⅱ)求直线CP与平面BDF所成角的大小;
(Ⅲ)在线段PB上是否存在一点M,使得CM∥平面BDF?如果存在,求的值,如果不存
在,请说明理由.
高二理科数学第四周周三静校测试答案
1.解:如图,以点D为原点O,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系O﹣xyz,则D(0,0,0),B(1,1,0),A1(1,0,λ),
设P(0,1,x),其中x∈[0,λ],
因为A1P⊥PB,
所以,即(﹣1,1,x﹣λ)•(﹣1,0,x)=0,
化简得x2﹣λx+1=0,x∈[0,λ],
由点P(0,1,x)的唯一性知方程x2﹣λx+1=0只有唯一解,
所以,判别式△=λ2﹣4=0,且λ>0,
解得λ=2.
2.(Ⅰ)证明:因为底面ABCD是菱形,AC∩BD=O,
所以O为AC,BD中点.﹣﹣﹣﹣﹣﹣﹣1分)
又因为PA=PC,PB=PD,所以PO⊥AC,PO⊥BD,﹣﹣﹣﹣﹣﹣(3分)
所以PO⊥底面ABCD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)
(Ⅱ)解:由底面ABCD是菱形可得AC⊥BD,
又由(Ⅰ)可知PO⊥AC,PO⊥BD.
如图,以O为原点建立空间直角坐标系O﹣xyz.
由△PAC是边长为2的等边三角形,,
可得.
所以.﹣﹣﹣﹣(5分)所以,.
由已知可得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)
设平面BDF的法向量为=(x,y,z),则
令x=1,则,所以=(1,0,﹣).﹣﹣﹣﹣﹣﹣﹣﹣(8分)
因为cos=﹣,﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)
所以直线CP与平面BDF所成角的正弦值为,
所以直线CP与平面BDF所成角的大小为30°﹣﹣﹣﹣﹣﹣﹣﹣(10分)
(Ⅲ)解:设=λ(0≤λ≤1),则.﹣﹣﹣﹣﹣﹣(11分)
若使CM∥平面BDF,需且仅需=0且CM⊄平面BDF,﹣﹣﹣(12分)
解得,﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)
所以在线段PB上存在一点M,使得CM∥平面BDF.
此时=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)。
