二面角专项练习
【高二数学】二面角练习题(共4页)
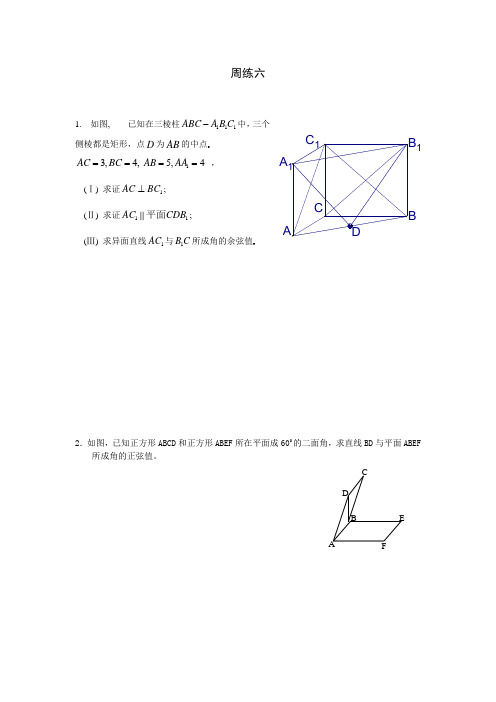
周练六1. 如图,已知在三棱柱111ABC A B C -中,三个侧棱都是矩形,点D 为AB 的中点3,4,AC BC ==15,4AB AA == ,(Ⅰ) 求证1AC BC ⊥; (Ⅱ) 求证11AC CDB 平面;(Ⅲ) 求异面直线1AC 与1B C 所成角的余弦值2.如图,已知正方形ABCD 和正方形ABEF 所在平面成600的二面角,求直线BD 与平面ABEF所成角的正弦值。
1A3.如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,求: (1)面A 1ABB 1与面ABCD 所成角的大小; (2)二面角C 1—BD —C 的正切值 (3)二面角11B BC D --4.过正方形ABCD 的顶点A 作PA ABCD 平面,设PA=AB=a ,(1)求二面角B PC D 的大小;(2)求二面角C-PD-AABCD A 1D 1C 1B 15. 如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,P A ⊥底面ABCD ,P A =3 .(1) 证明: BE ⊥平面P AB ;(2) 求二面角A -BE -P 的大小 (3)PB 与面PAC 的角6 如图,在底面为直角梯形的四棱锥,//,BC AD ABCD P 中-,90︒=∠ABCABCD PA 平面⊥,32,2,3===AB AD PA ,BC=6(1) 求证:;PAC BD 平面⊥ (2) 求二面角A BD P --的大小.(3)求二面角B-PC-A 的大小EPABcD7.如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE 上的点,且BF⊥平面ACE.(Ⅰ)求证AE⊥平面BCE;(Ⅱ)求二面角B—AC—E的大小;(Ⅲ)求点D到平面ACE的距离.8.如图,在四棱锥P ABCD-中,底面ABCD是矩形.已知3AB=,2AD=,2 PA=,PD=,60PAB =∠.(Ⅰ)证明AD⊥平面PAB;(Ⅱ)求异面直线PC与AD所成的角的大小;(Ⅲ)求二面角P BD A--的正切值.ABCDPDBA高中数学联赛几何定理梅涅劳斯定理一直线截△ABC 的三边BC,CA,AB 或其延长线于D,E,F 则1BDCD EC AE FA BF =••。
二面角习题及答案

二面角1.如圖三棱錐 P-ABC 中,PC ⊥平面ABC ,PC =32,D 是 BC の中點,且△ADC 是邊長為 2の正三角形,求二面角 P-AB -C の大小。
解:由已知條件,D 是BC の中點∴ CD =BD =2 又△ADC 是正三角形∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 為直角の三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC∴ PA ⊥AB (三垂線定理) ∴∠PAC 即為二面角 P-AB-C 之平面角,易求 ∠PAC =30°3. 如圖:ABCD 是矩形,AB =8,BC =4,AC 與 BD 相交於O 點,P 是平面 ABCD 外一點,PO ⊥面ABCD ,PO =4,M 是 PC の中點,求二面角 M-BD-C 大小。
解:取OC 之中點N ,則 MN ∥PO∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2,過 N 作 NR ⊥BD 於 R ,連MR , 則 ∠MRN 即為二面角 M-BD-C の平面角過 C 作 CE ⊥BD 於S則 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅= ∴ 54RN = 25RN MN MRN tan ==∠ ∴ 25a r c t a n M R N =∠11. 如圖,設ABC —A1B1C1是直三棱柱,E 、F 分別為AB 、A1B1の中點,且AB =2AA1=2a,AC =BC =3a.(1)求證:AF ⊥A1C(2)求二面角C —AF —B の大小D PC AB S R NM O BDP A C分析 本小題考查空間幾何垂直の概念和二面角の度量等知識.解 (1)∵AC =BC ,E 為AB 中點,∴CE ⊥AB又∵ABC —A1B1C1為直棱柱,∴CE ⊥面AA1BB連結EF ,由於AB =2AA1∴AA1FE 為正方形∴AF ⊥A1E ,從而AF ⊥A1C(2)設AF 與A1E 交於O ,連結CO ,由於AF ⊥A1E ,知AF ⊥面CEA1∴∠COE 即為二面角C —AF —B の平面角∵AB =2AA1=2a,AC =BC =3a∴CE =2a,OE =22a,∴tan ∠COE =a a222=2.∴二面角C —AF —B の大小是arctan2.13. 在正方體1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 與ABCD 所成角の大小.解析:由於BCMK 是梯形,則MK 與CB 相交於E .A 、E 確定の直線為l ,過C 作CF ⊥l 於F ,連結MF ,因為MC ⊥平面ABCD ,CF ⊥l ,故MF ⊥l .∠MFC 是二面角M-l-C の平面角.設正方體棱長為a ,則a CM 43=,a BK 41=.在△ECM 中,由BK ∥CM 可得a EB 21=,a CF 53=,故45tan =∠MFC .因此所求角の大小為45arctan 或45arctan π-.。
二面角典型习题(可编辑修改word版)
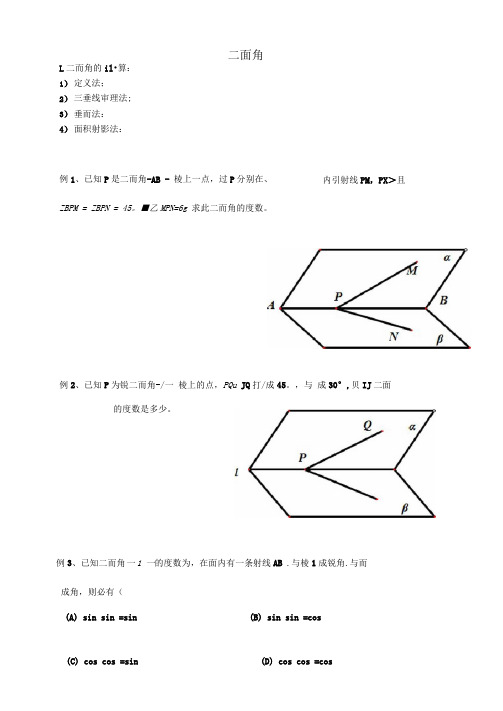
(C) cos cos =sin (D) cos cos =cosL 二而角的il •算:1) 定义法;2) 三垂线审理法;3) 垂而法:4) 面积射影法:例1、已知P 是二而角-AB - 棱上一点,过P 分别在、 ZBPM = ZBPN = 45。
■乙MPN=6g 求此二而角的度数。
例2、已知P 为锐二而角-/一 棱上的点,PQu JQ 打/成45。
,与 成30°,贝IJ 二面例3、已知二而角一1 一的度数为,在面内有一条射线AB .与棱1成锐角.与而成角,则必有(二面角内引射线PM ,PX >且的度数是多少。
(A) sin sin =sin (B) sin sin =cos例4、在120。
的二而角-/一的面、内分别有A、B两点.且A、B到棱1的距离AC、BD 分别长2、4, AB=1O,求J(1)直线AB .与棱1所成角的正弦值。
(2)直线AB •与平而所成角的正弦值.例5、已知二而角-MN-为60。
,Ae.Be为AB在上的射影,且C在棱MX 上,AB与所成角为60。
,且AC= JM Z MCB=45。
, 求线段AB的长。
例6、已知二而角一 DC —的度数为,A e ,B€ .MDC的而枳为S,且D(二m.AB丄DC , AB与平而成30。
角,当DMDi W — A- Di例是以AB 为直径的圆周上的一点,ZABC = 30。
,P4丄而ABC, ZPBA = 45。
,求二而角A-PB-C 的正弦值。
S 例8、在正方体ABCD - 中,利用cos =3■解下列各题S1)P. Q 分别为AyA.AB 的中点,求平而C,PQ 打底而ABCD 所成角的余弦值 2)求二而角Ci-BDi-C 的大小:3) M 是棱BC的中点,求二面角Q-BjM-G 的余弦值。
——・B例9.已知D 、E 分别是边长为a 的等边三角形ABC 的边AB 、AC 上的点,DE//BC.现沿DE 将三角形ADE 折起,是二面角A-DE-B 成60度角,当DE 在什么位置时,使折起后的顶点A 到BC 边距离最短?最短是多少?ZADC = ZBCA = 90°, AABC = 60。
向量法解二面角例题与练习题

向量法解二面角例题与练习题嘿,同学们!今天咱就来好好讲讲向量法解二面角例题与练习题。
咱先来看一道例题哈,就比如在一个正方体中,求某个面和另一个面所成二面角的大小。
这时候咱就可以用向量法来搞定啦!先找到这两个面的法向量,然后通过向量的夹角公式就能算出二面角啦!是不是感觉挺神奇的呀?比如说这个正方体的边长是 1 吧,那我们就可以设一个面的法向量是向量 a,另一个面的法向量是向量 b。
那怎么找法向量呢?这可有技巧哦!可以通过一些边的向量来求叉积得到法向量。
哎呀,这就像是在黑暗中找到了一盏明灯一样,一下子就把问题给照亮啦!然后我们算出向量 a 和向量 b 的夹角,但是要注意哦,这个夹角可能不是二面角哦,有可能是它的补角呢!这就好比你在路上看到一个背影很像你朋友的人,你不能直接就冲上去打招呼呀,得确认一下是不是真的是你朋友,对吧?来,我们再做一道练习题巩固一下。
有一个三棱锥,让我们求其中两个面的二面角。
哇,这可有点挑战性了呢!但咱不怕呀,咱有向量法这个利器呢!就按照刚才说的步骤一步一步来,肯定能求出答案的。
“哎呀,我好像有点不太明白呢。
”有同学这么说啦?没关系,咱再仔细讲讲。
就好比你学骑自行车,一开始可能会摔倒,但多练习几次不就会了嘛!学习也是一样的道理呀,不要着急,慢慢来。
“那要是遇到更复杂的图形怎么办呢?”哈哈,别担心呀,再复杂的图形也是由简单的部分组成的嘛。
我们就把它拆分成一个个小部分,分别求出法向量,再综合起来分析。
就像搭积木一样,一块一块地搭起来,最后就能建成漂亮的城堡啦!同学们,加油呀!向量法解二面角其实并不难,只要你们多练习,肯定能掌握得很好的!相信自己,你们都是最棒的!。
完整版二面角练习题

周练六1.如图,已知在三棱柱ABC A1B1C1中,三个Bl 侧棱都是矩形,点D为AB的中点*AC 3, BC 4, AB 5, AAi 4 ,(I)求证AC BCi ;(II)求证ACi P 平面CDBi ;(III)求异面直线ACi与BiC所成角的余弦值・2.如图,已知正方形ABCD和正方形ABEF所在平面成60。
的二面角, 成角的正弦值。
A F3.如图,在棱长为a的正方体ABCD—A I B I C I D I中,求:(1)面AiABBi与面ABCD所成角的大小;(2)二面角Ci—BD—C的正切值(3)二面角Bi BCi DP4.过正方形ABCD的顶点A作PA A平面ABCD , 设PA=AB=a ,(1)求二面角B - PC・D的大小;(2)求二面角C-PD-AC5.如图所示,四棱锥P-ABCD 的底面ABCD 是边长为1的菱形,Z BCD =60° ,E 是CD的中点, .(1)证明:BE 丄平面PAB ;(2) 求二面角 A- BE- P 的大小(3) PB 与面PAC 的角(3)求二面角B-PC-A 的大小如图,在底而为直角P ABCD 中,AD//BC, ABC90, PA 平面 ABCD PA 3, AD(1)求证:BD 平面PAC;⑵求二面角P BD A 的大小.梯形的四棱锥 2, AB 心c=6 丄底面PA ABCDC7.如图,直二面角D —AB —E中,四边形ABCD是边长为2的正方形,AE=EB , F为CE 上的点,且BF丄平面ACE.(I )求证AE丄平面BCE;(II)求二面角B— AC — E的大小;(III)求点D到平面ACE的距离.8.如图,在四棱锥P ABCD屮,底面ABCD是矩形.已知AB 3 , AD 2 ,PA 2 ,卩。
J 2 , Z PAB 60°(I )证明AD 平面PAB :(II)求异面直线PC与AD所成的角的大小; (III)求二面角P BD A的正切值. p匕。
二面角专项训练(人教A版)

二面角专项训练(人教A版)
一、单选题(共7道,每道10分)
1.等于90°的二面角内有一点P,过P有PA⊥α于点A,PB⊥β于点B,如果PA=PB=a,则P 到交线的距离为( )
A. B.
C. D.
2.如图,在三棱锥F-ABC中,FC⊥底面ABC,CA=CB=CF,∠ACB=120°,则二面角F-AB-C的正切值为( )
A. B.
C. D.
3.如图,在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是腰长为
的等腰三角形,则二面角V-AB-C的平面角为( )
A.30°
B.45°
C.60°
D.90°
4.如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥AB,PA=AB=2,AC=1,则二面角A-PC-B的正弦值为( )
A. B.
C. D.
5.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,D是棱AA1的中点,则二面角B-DC1-C的余弦值为( )
A. B.
C. D.
6.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD,则二面角A1-BD-C1的大小为( )
A.30°
B.45°
C.60°
D.90°
7.如图,在直三棱柱ABC-A1B1C1中,AB1⊥A1C,AB=4,AC=BC=3,D为AB的中点,则二面角A1-CD-C1的平面角的余弦值为( )
A. B.
C. D.。
二面角练习题(练习)
二面角的平面角专题学案一、二面角定义从一条直线出发的两个半平面所组成的图形就叫做二面角.二面角的大小是用二面角的平面角来衡量的.而二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角。
二、二面角的求法:1.几何法:二面角转化为其平面角,要掌握以下三种基本做法: ①直接利用定义,图4(1).②利用三垂线定理及其逆定理,图4(2)最常用。
③作棱的垂面,图4(3)。
典型例题:例1。
在正四面体ABCD 中,求相邻两个平面所成的二面角的平面角的大小.αβAOP A BOP αβ 4(1) 4(2) 4(3)例2.在棱长为1的正方体1AC 中,(1)求二面角11A B D C --的大小; (2)求平面1C BD 与底面ABCD 所成二面角1C BD C --的平面角大小。
例3.已知:二面角l αβ--且,A A α∈到平面β的距离为A 到l 的距离为4,求二面角l αβ--的大小。
例4.如图,AB ⊥平面BCD ,BD CD ⊥,若2AB BC BD ==,求二面角B ACD --的正弦值。
课堂练习:1.正方体AC 1中M 是BC 中点,求二面角D 1-AB 1—M 的平面角的正切值。
lBOAβαABC DEF2.ABC 为等腰直角三角形,∠C=900. PA ⊥面ABC ,AC=a 。
PA=2a 。
求A —PB-C 大小。
3.直三棱柱棱长均相等。
∠ADC 1=900. 求D —AC 1—C 大小。
4.如图,在底面为平行四形的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点.(Ⅰ)求证:AC PB ⊥;(Ⅱ)求证://PB 平面AEC ;(Ⅲ)求二面角D AC E --的大小.5.已知四棱锥P —ABCD 的底面为直角梯形,AB ∥DC ,⊥=∠PA DAB ,90 底面ABCD ,且PA=AD=DC=21AB=1,M 是PB 的中点。
二面角的练习-数学试题
二面角的练习-数学试题()1、A、B是二面角M—a—N的棱a上两点,P是N内一点,PB^a与B,PA与a成45°角,PA地M成30°角,则二面角M—a—N的度数是A、30°B、45°C、60°D、75°()2、正四面体相邻两面所成二面角为a,则有A、cosa=1/3B、sina=1/3C、cosa= EQ R(,3) /3D、sina= EQ R(,3) /3()3、已知两两垂直的三射线OA、OB、OC交平面a于A、B、C若OA=1,OB=2,OC=3,则a与平面OAB所成角的余弦值是A、2/7B、3/7C、6/7D、不同于A、B、C()4、两二面角的两个半平面分别垂直,则这两个二面角的平面A、相等B、互补C、相等或互补D、不确定5、RtDABC斜边AB在平面a内,AC、BC与a成45°和30°的角,则平面ABC与a所成的角为_________6、以正方形ABCD的对角线BD为棱折成直二面角,连结AC,则二面角A—CD—B的大小为________7、正三棱锥的一个侧面积与底面积之比为2/3,则侧面与底面所成的二面角为________8、三棱锥P—ABC的底面ABC是以AC为斜边的RtD,且顶点P在面ABC内的射影是DABC的外心,若PA=AB=1,BC= EQ R(,2) ,则面PAB与面ABC所成的二面角为_______9、二面角a—L—b内一点P到两个面的距离分别为EQ R(,2) ,EQ R(,3) 到棱的距离为2,求此二面角的大小10、四棱锥P—ABCD的底面ABCD是直角梯形,AB//CD,AB^BC且AB= EQ F(1,2) CD,侧棱PB^面ABCD,PC=5,BC=3,SDPAB=6。
求平面PAD与平面PBC所成二面角的大小。
二面角典型习题
二面角1.二面角的计算:1)定义法;2)三垂线定理法;3)垂面法;4)面积射影法;例1、已知P 是二面角棱上一点,过P 分别在内引射线PM ,PN ,且AB αβ--αβ、,求此二面角的度数。
45,60BPM BPN MPN ∠=∠=︒∠=︒例2、已知P 为锐二面角棱上的点,,则二l αβ--,4530PQ PQ l αβ⊂︒︒与成,与成面角的度数是多少。
l αβ--例3、已知二面角的度数为,在面内有一条射线AB 与棱l 成锐角,与面l αβ--θαδ,则必有( )βγ成角(A ) (B )sin sin sin θδγ=sin sin cos θδγ=(C ) (D )cos cos sin θδγ=cos cos cos θδγ=例4、在的二面角的面、内分别有A 、B 两点,且A 、B 到棱l 的距离120︒l αβ--αβAC 、BD 分别长2、4,AB=10,求:(1)直线AB 与棱l 所成角的正弦值。
(2)直线AB 与平面所成角的正弦值。
β例5、已知二面角为,上的射影,且C 在棱MN αβ--60︒,,A B BC AB αββ∈∈为在MN 上,AB 与所成角为,且,求线段AB 的长。
β60︒45AC MCB =∠=︒例6、已知二面角的度数为,的面积为S ,且DC=m ,DC αβ--θ,,A B ADC αβ∈∈∆,AB 与平面成角,当变化时,求面积最大值。
AB DC ⊥β30︒θDBC ∆in例7、已知C是以AB为直径的圆周上的一点,,30ABC∠=︒,求二面角A-45PA ABC PBA⊥∠=︒面,PB-C的正弦值。
例8、在正方体中,利用解下列各题1111ABCD A B C D-cosSSθ=射影1)P、Q分别为的中点,求平面与底面ABCD所成角的余弦值1,A A AB1C PQ2)求二面角的大小;11C BD C--3)M是棱BC的中点,求二面角的余弦值。
111D B M C--例9、已知D 、E 分别是边长为a 的等边三角形ABC 的边AB 、AC 上的点,DE//BC ,现沿DE 将三角形ADE 折起,是二面角A-DE-B 成60度角,当DE 在什么位置时,使折起后的顶点A 到BC 边距离最短?最短是多少?例10、等腰Rt 和Rt 有公共边AC ,,ADC ∆BCA ∆90,60ADC BCA ABC ∠=∠=︒∠=︒以AC 为棱折起多少度的二面角时,有BD=BC ?两个平面垂直1、两个平面垂直的证明1)定义2)判定定理2、两个平面垂直的性质例1、已知ABCD 为矩形,E 为半圆CED 上一点,且平面ABCD 平面CDE ⊥1)求证DE 是AD 与BE 的公垂线2)若AD=DE=AB ,求AD 与BE 所成角的大小。
第8讲 二面角和面面垂直专题练习
第8讲 二面角和面面垂直专题练习(教师版)例1. 如图,在立体图形ABC D -中,若E CD AD CB AB ,,==是AC 的中点,则下列命题中正确的是( ).(A )平面ABC ⊥平面ABD (B )平面ABD ⊥平面BDC(C )平面ABC ⊥平面BDE ,且平面ADC ⊥平面BDE (D )平面ABC ⊥平面ADC ,且平面ADC ⊥平面BDE分析:要判断两个平面的垂直关系,就需固定其中一个平面,找另一个平面内的一条直线与第一个平面垂直.解:因为,CB AB =且E 是AC 的中点,所以,AC BE ⊥同理有AC DE ⊥,于是⊥AC 平面BDE .因为⊂AC 平面ABC ,所以平面ABC ⊥平面BDE .又由于⊂AC 平面ACD ,所以平面ACD ⊥平面BDE .所以选C.说明:本题意图是训练学生观察图形,发现低级位置关系以便得到高级位置关系.在某一个平面内,得到线线垂直的重要途径是出现等腰三角形底边的中线,由线线垂直得到线面垂直,由线面垂直可得到面面垂直.例2.如图,P 是ABC ∆所在平面外的一点,且⊥PA 平面ABC ,平面⊥PAC 平面PBC .求证AC BC ⊥.分析:已知条件是线面垂直和面面垂直,要证明两条直线垂直,应将两条直线中的一条纳入一个平面中,使另一条直线与该平面垂直,即从线面垂直得到线线垂直..证明:在平面PAC 内作PC AD ⊥,交PC 于D .因为平面⊥PAC 平面PBC 于PC ,⊂AD 平面PAC ,且PC AD ⊥,所以PBC AD 平面⊥.又因为⊂BC 平面PBC ,于是有BC AD ⊥①.另外⊥PA 平面ABC ,⊂BC 平面ABC ,所以BC PA ⊥.由①②及A PA AD = ,可知⊥BC 平面PAC .因为⊂AC 平面PAC ,所以AC BC ⊥.说明:在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,通过本题可以看到,面面垂直⇒线面垂直⇒线线垂直.例3.如图,AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上异于A 、B 的任意一点,求证:平面PAC ⊥平面PBC .分析:证明面面垂直的有两个依据,一是证明二面角的平面角为直角,二是利用两个平面垂直的判定定理.由于C 点的任意性,用方法一的可能性不大,所以要寻求线面垂直.证明:因为AB 是⊙O 的直径,C 是圆周上的点,所以有AC BC ⊥①. 因为⊥PA 平面ABC ,⊂BC 平面ABC ,则BC PA ⊥②. 由①②及A PA AC = ,得⊥BC 平面PAC .因为⊂BC 平面PBC ,有平面PAC ⊥平面PBC .说明:低一级的垂直关系是判定高一级垂直关系的依据,根据条件,由线线垂直⇒线面垂直⇒面面垂直.通过这个例题展示了空间直线与平面的位置关系的内在联系,垂直关系的判定和性质共同构成了一个完整的知识体系.例4.如图,点A 在锐二面角βα--MN 的棱MN 上,在面α内引射线AP ,使AP 与MN 所成的角PAM ∠为45,与面β所成的角大小为30,求二面角βα--MN 的大小.分析:首先根据条件作出二面角的平面角,然后将平面角放入一个可解的三角形中(最好是直角三角形),通过解三角形使问题得解. 解:在射线AP 上取一点B ,作β⊥BH 于H ,连结AH ,则B A H ∠为射线AP 与平面β所成的角,30=∠∴BAH .再作MN BQ ⊥,交MN 于Q ,连结HQ ,则HQ 为BQ 在平面β内的射影.由三垂线定理的逆定理,MN HQ ⊥,BQH ∠∴为二面角βα--MN 的平面角.设a BQ =,在BAQ Rt ∆中,a AB BAM BQA 2,45,90=∴=∠=∠,在Rt △BHQ 中,,22,,90a BH a BQ BHQ ===∠2222sin ===∠aa BQBH BQH ,BQH ∠ 是锐角,45=∠∴BQH ,即二面角βα--MN 等于45.说明:本题综合性较强,在一个图形中出现了两条直线所称的角,斜线与平面所称的角,二面角等空间角,这些空间角都要转化为平面角,而且还要彼此联系相互依存,要根据各个平面角的定义添加适当的辅助线.例5.如图,将边长为a 的正三角形ABC 以它的高AD 为折痕折成一个二面角C AD C --'.(1)指出这个二面角的面、棱、平面角;(2)若二面角C AD C --'是直二面角,求C C '的长; (3)求C A '与平面CD C '所成的角;(4)若二面角C AD C --'的平面角为 120,求二面角D C C A -'-的平面角的正切值. 分析:根据问题及图形依次解决.解:(1)∴'⊥⊥∴⊥,,,C D AD DC AD BC AD 二面角C AD C --'的面为ADC 和面C AD ',棱为AD ,二面角的平面角为C CD '∠.(2)若 90='∠C CD ,a C C a C D DC a AC 22,21,='∴='=∴= .(3)⊥∴⊥'⊥AD DC AD C D AD ,, 平面C C D ',D C A '∠∴为C A '与平面CD C '所成的角.在直角三角形C AD '中,30,21='∠∴='=C DA AC C D DC ,于是60='∠D C A .(4)取C C '的中点E ,连结AE 、DE ,C C DE C C AE AC C A DC CD '⊥'⊥∴='=',,, ,AED ∠∴为二面角D C C A -'-的平面角.,41,21,120a DE a CD D C DC C =∴=='='∠在直角三角形AED 中,,23a AD =DEAD AED =∠∴tan 324123==aa.说明:这是一个折叠问题,要不断地将折叠前后的图形加以比较,抓住折叠前后的变与不变量.例6 正方体1111D C B A ABCD -的棱长为1,P 是AD 的中点.求二面角P BD A --1的大小.分析:求二面角关键是确定它的平面角,按定义在二面角的棱上任取了点,在二个半平面上分别作棱的垂线,方法虽简便,但因与其他条件没有联系,要求这个平面角一般是很不容易的,所以在解题中不大应用.在解题中应用得较多的是“三垂线定理”的方法,如图考虑到AB 垂直于平面1AD ,1BD 在平面1AD 上的射影就是1AD .再过P 作1AD 的垂线PF ,则PF ⊥面1ABD ,过F 作B D 1的垂线FE ,PEF ∠即为所求二面角的平面角了.解:过P 作1BD 及1AD 的垂线,垂足分别是E 、F ,连结EF . ∵AB ⊥面1AD ,PF ⊂面1AD , ∴PF AB ⊥,又1AD PF ⊥,∴PF ⊥面1ABD . 又∵1BD PE ⊥,∴1BD EF ⊥, ∴PEF ∠为所求二面角的平面角. ∵D AD Rt 1∆∽PFA ∆,∴11AD AP DD PF =.而21=AP ,11=DD ,21=AD ,∴42=PF .在1PBD ∆中,251==PB PD .∵1BD PE ⊥,∴2321==BD BE .在PEB Rt ∆中,2222=-=BEPB PE ,在PEF Rt ∆中,21sin ==∠PEPF PEF ,∴︒=∠30PEF .例7在ABC ∆所在平面外有一点S ,已知AB SC ⊥,SC 与底面ABC 所成角为θ,二面角C AB S --的大小为ϕ,且︒=+90ϕθ.求二面角A SB C --的大小.分析:由题设易证SD SC ⊥,由已知得SC ⊥平面SAB ,显然所求的二面角是直二面角,此时只需证明二面有的两个面垂直即可.在解这种类型题时,如果去作二面角A SB C --的平面角,那么可能会走弯路.解:如图所示,作SO ⊥平面ABC 于O ,连结CO 并延长交AB 于D ,连结SD . ∵SO ⊥平面ABC ,∴SCO ∠是SC 与平面ABC 所成角,θ=∠SCO . ∵SO ⊥平面ABC ,AB SC ⊥, ∴CD AB ⊥,SD AB ⊥.∴SDO ∠是二面角C AB S --的平面角,ϕ=∠SDO . ∵︒=+90ϕθ,∴SD SC ⊥. 又∵AB SC ⊥,∴SC ⊥平面SAB ,∴平面SBC ⊥平面SAB ,∴二面角A SB C --的大小为︒90. 说明:二面角的平面角满足三个条件:(1)顶点在棱上,(2)两边在面内,(3)两边与棱垂直.应注意CSB ∠不满足第(3)条,不是二面角A SB C --的平面角.在求二面角大小时,若其平面角不易作出时,则可考虑判定两平面是否垂直,如果两平面垂直,则其二面角为︒90,反之亦然.例8 P 为︒120的二面角βα--a 内一点,P 到α和β的距离均为10,求点P 到棱a 的距离.分析:本题已知二面角的大小而求点到直线的距离,须做出二面角的平面角,然后将条件揉和在一起,便可解决问题.解:如图,过点P 作α⊥PA 于A ,β⊥PB 于B ,设相交直线PA 、PB 确定的平面为γ,O a =γ ,则OA =αγ ,OB =βγ 连结PO ,则10==BP AP ∵α⊥PA ,β⊥PB , ∴γ⊥a ,而⊂PO 平面γ,∴PO a ⊥,∴PO 的长即为点P 到直线a 的距离. 又∵γ⊥a ,γ⊂OA ,γ⊂OB∴AOB ∠是二面角βα--a 的平面角,即︒=∠120AOB .而四边形AOBP 为一圆内接四边形,且PO 为该四边形的外接圆直径.∵四边形AOBP 的外接圆半径等于由A 、B 、O 、P 中任意三点确定的三角形的外接圆半径,因此求PO 的长可利用APB ∆.在APB ∆中,10==BP AP ,︒=∠60APB ,∴10=AB . 由正弦定理:332060sin 2=︒==AB R PO .说明:(1)该题寻找︒120的二面角的平面角,所采取的方法即为垂面法,由此可见,若题目可找到与棱垂直的平面,用“垂面法”确定二面角的平面角也是一种可取的方法.(2)充分借助于四边形PAOB 为一圆内接四边形,∵OA PA ⊥,OB PB ⊥,∵PO 即为其外接圆直径,然后借助于四边有的外接圆直径等于其中任一三角形的外接圆直径进行转移,由正弦定理帮助解决了问题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 7
二面角专项练习
班级_____________姓名_____________
一、定义法:直接在二面角的棱上取一点,分别在两个半平面内作棱的垂线,得出平面角.
例1 在四棱锥P-ABCD中,ABCD是正方形,PA⊥平面ABCD,PA=AB=a,求二面角B-PC-D的大
小。
二、垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或
逆定理作出二面角的平面角;
例2 在四棱锥P-ABCD中,ABCD是平行四边形,PA⊥平面ABCD,PA=AB=a,∠ABC=30°,
求二面角P-BC-A的正切。
三、垂面法:作棱的垂直平面,则这个垂面与二面角两个面的交线所
夹的角就是二面角的平面角
例3 在四棱锥P-ABCD中,ABCD是正方形,PA⊥平面ABCD,PA=AB=a,求B-PC-D的大
小。
四、投影面积法:一个平面上的图形面积为S,它在另一个平面上的投影面积为
S',这两个平面的夹角为,则S'=Scos或cos=/SS.
例4 在四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC
所成二面角的大小。
五、补形法:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方
法(尤其要考虑射影法)。
例5、在四棱锥P-ABCD中,ABCD为正方形,PA⊥平面ABCD,PA=AB=a,求平面PBA与平面PDC
所成二面角的大小。
p
A
B
C
D
L
H
j
A
B
C
D
P
H
l
ABCD
P
P
C1
A1
B1
C
D
P
A
B
C
D
方法归纳:二面角的类型和求法可用框图展现如下:
如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中AC=3,AB=5,
.,4,53cos1的中点是点ABDAACAB
。
(Ⅰ)求证:1BCAC;
(Ⅱ)求证:AC1//平面CDB1;
(Ⅲ)求三棱锥A1—B1CD的体积.
18. (本题满分14分) 如图所示, 四棱锥PABCD底面是直角梯形,
,,2,BAADCDADCDABPA
底面ABCD, E为PC的中点, PA=AD=AB=1.
(1)证明: //EBPAD平面;
(2)证明: BEPDC平面;
(3)求三棱锥BPDC的体积V.
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,
且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
18.(本小题满分14分)
如图4所示,四棱锥PABCD中,底面ABCD为正方
形,PD平面ABCD,2PDAB,E,F,G分
别为PC、PD、BC的中点.
(1)求证:PAP平面EFG;
(2)求三棱锥PEFG的体积.
18.(本小题满分14分)
如图,已知棱柱ABCD—A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1,F为
棱AA1的中点,M为线段BD1的中点。
(1)求证:MF∥面ABCD;
(2)求证:MF⊥面BDD1B1。
图4
A
B
C
D
E
F
G
P
18.(本小题满分14分)如图,三角形ABC中,AC=BC=AB22,
ABED是边长为a的正方形,平面ABED⊥底面ABC,且,若G、F
分别是EC、BD的中点,
(Ⅰ)求证:GF//底面ABC;
(Ⅱ)求证:平面EBC⊥平面ACD;
(Ⅲ)求几何体ADEBC的体积V。
17.(本小题满分14分)
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45°,点E、F分别为
棱AB、PD的中点.
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
(3)求三棱锥C-BEP的体积.
F
G
B
D
E
A
C
E
F
B
A
C
D
P
如图,四面体ABCD中,O、E分别是BD、BC的中点,
2,2.CACBCDBDABAD
(I)求证:AO平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
2、如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=4,OA⊥底面ABCD,OA=2,M
为OA的中点.
(Ⅰ)求异面直线AB与MD所成角的大小;
(Ⅱ)求点B到平面OCD的距离.
C
A
D
BOE
3、如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,
AP=BP=AB,PC⊥AB.
(Ⅰ)求证:PC⊥AC;
(Ⅱ)求二面角B-AP-C的大小;
(Ⅲ)求点C到平面APB的距离.
4、如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=2,底面ABCD为直角梯形,
其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
6、如图所示,四棱锥P-ABCD的底面积ABCD是边长为1的菱形,
∠BCD=60°,E是CD的中点,PA⊥底面积ABCD,PA=3.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A-BE-P的大小.
7、四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,
BC=2,CD=2,AB=AC.
(1) 证明:AD⊥CE;
(2) 设侧面ABC为等边三角形,求二面角C-AD-E的大小.
10、如图,在四棱锥PABCD中,底面ABCD是矩形.已知3AB,2AD,2PA,
22PD
,60PABo∠.
(Ⅰ)证明AD平面PAB;
(Ⅱ)求异面直线PC与AD所成的角的大小;
(Ⅲ)求二面角PBDA的大小.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC
(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
A
B
C
D
P
A
C
B
A
1
B
1
C
1
D
E
