陀螺仪随机漂移
mems陀螺仪指标

MEMS陀螺仪可以通过许多指标进行评估。
以下是一些常见的指标:
1.测量范围:是指陀螺仪可以测量的最大旋转速率或最大旋转角度。
它通常以度/秒为单位表示。
2.灵敏度:是指陀螺仪输出的每个单位(即每个度/秒)的电压或数字输入,通常以mV/度/秒或LSB/deg/sec为单位。
3.漂移:是指陀螺仪在没有旋转或运动时产生的电压或数字变化。
它通常以度/小时或度/秒为单位表示。
4.零偏:是指陀螺仪输出的电压或数字值,即使在没有旋转或运动的情况下,也会存在一些偏差。
它通常以度/秒为单位表示。
5.频率响应:是指陀螺仪对旋转速率变化的响应时间,它通常以Hz为单位表示。
6.噪声:是指陀螺仪输出的随机变化,通常以mV或LSB为单位表示。
噪声越低,陀螺仪的性能越好。
7.温度漂移和灵敏度漂移:是指陀螺仪在不同温度下的输出变化程度,它通常以度/小时或度/秒为单位表示。
这些指标可以帮助评估MEMS陀螺仪的性能,在选择和设计陀螺仪时非常重要。
陀螺仪理论及应用

第二节 自由陀螺的视运动及其应用
一、 自由陀螺的视运动
将自由陀螺放在地球的北极,并使转子轴水平, 将自由陀螺放在地球的北极,并使转子轴水平,这时转子轴与 地球极轴互相垂直。 地球极轴互相垂直。站在地球北极上的观察者就会看到陀螺的 自转轴自东向西转动(从上方看H轴顺时针方向旋转),并且 自转轴自东向西转动(从上方看H轴顺时针方向旋转),并且 ), 转动周期与地球自转周期相同,即每24小时旋转一周。 24小时旋转一周 转动周期与地球自转周期相同,即每24小时旋转一周。
陀螺相对动参考系的运动
哈尔滨工程大学自动化学院
刘繁明
前面,我们都是假定陀螺直接安装在惯性基座上,建 前面,我们都是假定陀螺直接安装在惯性基座上, 立了以绕内、外环的转角为广义坐标的运动微分方程, 立了以绕内、外环的转角为广义坐标的运动微分方程,讨 论陀螺在外力矩作用下相对惯性空间的运动规律,但是, 论陀螺在外力矩作用下相对惯性空间的运动规律,但是, 如果计及地球的自转, 如果计及地球的自转,并且考虑实际的陀螺仪总是安装在 运动物体如飞机、舰船上, 运动物体如飞机、舰船上,那么绝对静止的基座是不存在 在这种情况下, 的。在这种情况下,我们就不仅要了解陀螺相对惯性空间 的运动规律, 的运动规律,更重要的是要了解陀螺相对运动基座的运动 规律,进而掌握飞行器、舰船运动的各种参数。 规律,进而掌握飞行器、舰船运动的各种参数。 根据一般运动学原理, 根据一般运动学原理,我们把陀螺相对惯性空间的运 动看成两种运动, 动看成两种运动,即运动基座相对惯性空间的牵连运动和 陀螺相对运动基座的相对运动的合成, 陀螺相对运动基座的相对运动的合成,所以在讨论实际陀 螺的运动时,不仅要考虑陀螺本身的运动情况, 螺的运动时,不仅要考虑陀螺本身的运动情况,还必须要 考虑基座的运动。例如, 考虑基座的运动。例如,当利用安装在载体内的陀螺仪来 测量载体的航向和姿态时, 测量载体的航向和姿态时,就必须考虑载体相对地球的运 以及地球相对惯性空间的运动。 动,以及地球相对惯性空间的运动。
陀螺仪角度随机游走定义

陀螺仪角度随机游走定义
陀螺仪角度随机游走是指陀螺仪在没有外界干扰的情况下,其角度随机变化的
性质。
陀螺仪是一种测量和检测物体旋转姿态的装置,在惯性导航系统、航空航天等领域有着广泛的应用。
陀螺仪内部的转子通过陀螺效应来感应旋转角度,这种效应是指当陀螺仪在一
定速度旋转时,会产生一个力矩,使其保持固定的旋转轴。
然而,在没有外界干扰的情况下,陀螺仪的旋转轴并不总是能保持在一个特定的方向上。
陀螺仪角度随机游走是由于微小的不均匀性和噪音引起的。
陀螺仪内部的各种
元件、材料和电路都存在微小的不均匀性,这些不均匀性会导致转子受到微小的扰动。
而同时,环境中的噪音也会对陀螺仪产生影响。
这些微小的扰动和噪音导致了陀螺仪角度的随机变化。
陀螺仪角度随机游走在实际应用中需要进行补偿和校正。
由于随机游走的性质,陀螺仪在长时间的使用中角度会逐渐偏离真实值。
为了解决这个问题,需要利用其他传感器或者算法来校正陀螺仪的角度,以确保其测量结果的准确性。
总之,陀螺仪角度随机游走是由于微小的不均匀性和噪音引起的陀螺仪角度随
机变化现象。
在实际应用中,需要进行补偿和校正,以确保陀螺仪测量结果的准确性。
陀螺仪高精度寻北方法

陀螺仪⾼精度寻北⽅法 ⼈们普遍认为是1850年法国的物理学家莱昂·傅科(J.Foucault)为了研究地球⾃转,发明了陀螺仪。
那个时代的陀螺仪可以理解成把⼀个⾼速旋转的陀螺放到⼀个万向⽀架上⾯,这样因为陀螺在⾼速旋转时保持稳定,⼈们就可以通过陀螺的⽅向来辨认⽅向,确定姿态,计算⾓速度。
⼀、陀螺仪的发明 陀螺仪先后被⽤在航海上和航空上,因为飞机飞在空中,是⽆法像地⾯⼀样靠⾁眼辨认⽅向的,危险性极⾼,所以陀螺仪迅速得到了应⽤,成为飞⾏仪表的核⼼。
到了第⼆次世界⼤战,德国⼈搞了飞弹去炸英国,从德国飞到英国,千⾥迢迢怎么让飞弹能击中⽬标呢?于是,德国⼈搞出来惯性制导系统。
惯性制导系统采⽤⽤陀螺仪确定⽅向和⾓速度,⽤加速度计测试加速度,然后控制飞⾏姿态,争取让飞弹落到想去的地⽅。
⼆战时候,计算机和仪器的精度都是不太够的,所以德国的飞弹偏差很⼤,想要炸伦敦,结果炸得到处都是,让英国⼈恐慌了⼀阵。
不过,从此以后,以陀螺仪为核⼼的惯性制导系统就被⼴泛应⽤于航空航天,今天的导弹⾥⾯依然有这套东西,⽽随着需求的刺激,陀螺仪也在不断进化。
⼆、陀螺仪的进化 最早的陀螺仪都是机械式的,⾥⾯真有⾼速旋转的陀螺,⽽机械的东西对加⼯精度有很⾼的要求,还怕震动,因此机械陀螺仪为基础的导航系统精度⼀直都不太⾼。
于是,⼈们开始寻找更好的办法,利⽤物理学上的进步,发展出激光陀螺仪,光纤陀螺仪,以及微机电陀螺仪(MEMS)。
这些东西虽然还叫陀螺仪,但是它们的原理和传统的机械陀螺仪已经完全是两码事了。
光纤陀螺仪利⽤的是萨格纳克(Sagnac)效应,通过光传播的特性,测量光程差计算出旋转的⾓速度,起到陀螺仪的作⽤,替代陀螺仪的功能。
激光陀螺仪也是通过算光程差计算⾓速度,替代陀螺仪。
微机电陀螺仪则是利⽤物理学的科⾥奥利⼒,在内部产⽣微⼩的电容变化,然后测量电容,计算出⾓速度,替代陀螺仪。
iPhone和我们的智能⼿机⾥⾯所⽤的陀螺仪,就是微机电陀螺仪(MEMS)。
自动驾驶基础(六十七)--惯性测量单元(IMU)十三

自动驾驶基础(六十七)--惯性测量单元(IMU)十三MEMS陀螺仪的重要参数包括:量程(动态范围)DYNANMIC RANGE,分辨率(Resolution)、零角速度输出(零位输出)、灵敏度(Sensitivity)。
这些参数是评判MEMS陀螺仪性能好坏的重要标志,同时也决定陀螺仪的应用环境。
下面我们把MEMS陀螺仪的主要性能参数列出来,并做简单介绍:·量程(动态范围) DYNAMIC RANGE陀螺仪的量程通常以正、反方向输入角速率的最大值来表示,比如:+/-300 degree/sec。
该值越大表示陀螺仪敏感角速率的能力越强,在此输入角速率范围内,陀螺仪刻度因子非线性度能满足规定要求,通常陀螺仪的量程是可以配置的。
·灵敏度(分辨率)SENSORTIVITY RESOLUTION灵敏度(分辨率)表示在规定的输入角速率下能感知的最小输入角速率的增量,比如:0.05 degree/sec/LSB。
一般而言MEMS陀螺仪的测量范围越大,灵敏度会相应降低。
分辨率是指陀螺仪能检测的最小角速度,该参数与零角速度输出其实是由陀螺仪的白噪声决定。
•零角速度输出(零位输出)ZERO OUTPUTMEMS陀螺仪的误差主要包括零位误差和动态误差,一般重点对零位误差做处理。
零位误差又分为零值偏移误差和随机漂移误差,目前对MEMS陀螺仪零位误差的估算方法主要包括1σ和Allan方差两种方法。
1σ方法得到的是误差的总体指标,Allan方差分析法可以对误差的各种成分进行有效的分析。
目前对零值偏移误差的补偿方法比较简单,一般采用在静态条件下测定零值偏移常量,在应用中通常采用对其一次性的零值偏移补偿的方法。
在陀螺仪长时间工作以及外界环境发生变化条件下,零值偏移量并非恒定值,所以这种简单的零值偏移误差补偿方法存在很大的缺陷。
对陀螺仪的随机漂移误差补偿,目前常采用Kalman滤波的方法,因这种方法具有较好的实时性得到了广泛的引用,但是Kalman滤波法要求信号必须是平稳时间序列,且要知道信号的激励噪声和观测噪声的方差。
基于ARIMA模型的陀螺随机误差分析
稳 的随 机 过 程 , 需要 做 下 述 平 稳 化 处 理 。对 A I Ap q 进 R M (, ,
行差分平稳处理 , 即对序列 进行 d阶差 分 , 也 使之成为如下
的平稳时间序列【 3 】 :
20 5 50 0 70 5 1o 00 l5 10 20 50 1 5 2 0 70 00
E up n n fc r g T c n l g . 1 2 0 q i me t Ma u a t n e h o o y No 1 , 0 8 i
要 确定 d的值 , 以通过 自相关函数来判断 。 可 如果 d次差
计。 将式 ( ) 1拆分为 p阶 自回归模型部分 和 q阶滑动平均模 型 部分。阶 自回归模型如下 :
来 消 除 随 机 噪声 , 高 陀 螺精 度 。 提
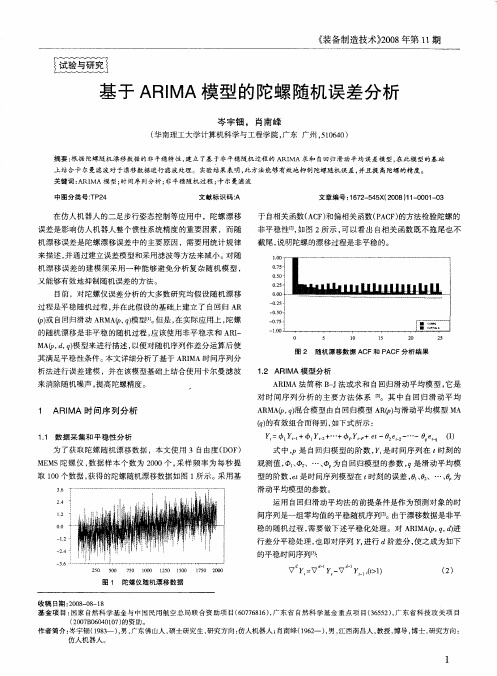
图 2 随 机 漂 移 数 据 AC F和 P CF分 析 结 果 A
12 RI . A MA模 型分 析
A I A法简称 B J RM — 法或求和 自回归滑动平均模 型 , 它是 对 时 间序列分析 的主要 方法 体系 I 2 】 。其 中 自回归 滑动平 均
《 装备制造技术}0 8 20 年第 l 期 1
陌磊
基 于 ARI MA模 型 的 陀螺 随机 误差 分 析
岑宇钿 , 肖南峰
( 华南理工大学计 算机科学 与工程学院 , 广东 广州 ,1 60 504 )
摘 要 : 据 陀螺 随机 漂移 数 据 的 非 平稳 特 性 , 立 了基 于 非 平稳 随机 过 程 的 A MA 求和 自回 归滑 动 平 均 误 差 模 型 , 此 模 型 的基 础 根 建 RI 在
于 自相 关 函数 ( C ) 偏相 关 函数 ( A F 的方 法 检 验 陀 螺 的 A F和 PC )
陀螺仪卡尔曼滤波漂移
陀螺仪卡尔曼滤波漂移
卡尔曼滤波是一种在各种系统估计和控制系统应用中广泛使用的先进算法,其中包括陀螺仪。
然而,当使用卡尔曼滤波对陀螺仪数据进行处理时,可能会遇到一个常见的问题——漂移。
这种漂移现象通常是由于陀螺仪内部的物理特性导致的,例如热效应、非理想因素等,这些因素可能导致陀螺仪读数的长期偏差,进而严重影响其准确性。
为了解决这个问题,我们可以采取一些方法来减小陀螺仪的漂移。
首先,可以采用更精确的陀螺仪技术来提高测量值的准确性。
其次,可以在系统中使用其他传感器,如加速度计和磁力计等,来辅助姿态估计,以减少对陀螺仪数据的依赖。
此外,还可以通过校准和补偿技术来减小陀螺仪的漂移。
这些方法的应用可以有效地提高姿态估计的准确性,从而解决卡尔曼滤波在处理陀螺仪数据时遇到的问题。
虽然卡尔曼滤波可以用于处理陀螺仪数据,但是由于陀螺仪可能存在的漂移问题,需要采取一些有效的措施来减小其影响。
一种陀螺仪零点漂移的校准方法与流程
一种陀螺仪零点漂移的校准方法与流程
陀螺仪的零点漂移是指在无旋转状态下,陀螺仪输出的角速度不能为0的现象。
为了纠正和校准陀螺仪的零点漂移,可以采用以下方法和流程:
1. 初始化:打开陀螺仪并连接到电脑或微控制器等设备上。
2. 数据采集:将陀螺仪固定在静止状态下,保持一段时间(如30秒),期间采集陀螺仪输出的角速度数据。
3. 分析数据:将采集到的角速度数据进行分析,计算平均值。
4. 判断零点漂移:将平均值与零点漂移阈值进行比较,判断陀螺仪是否存在零点漂移现象。
5. 校准零点漂移:如果判断陀螺仪存在零点漂移,则进行校准。
校准方法可以采用两种方式:
a. 软件校准:在软件层面上对陀螺仪的输出进行校准,通过
对输出值进行偏移修正,使得零点漂移降低或消除。
校准方法可以根据陀螺仪的具体型号和驱动程序提供的接口进行选择。
b. 硬件校准:通过物理操作对陀螺仪进行校准。
一种常用的
方法是将陀螺仪放置在温度恒定的环境中,并保持静止。
在此过程中,通过传感器测量温度和角速度,并根据预先制定的模型对零点漂移进行估计和校准。
6. 校验校准效果:校准完成后,可以重新采集陀螺仪输出的角速度数据,并进行分析和比较,以验证校准效果。
陀螺仪的零点漂移校准是一个迭代的过程,可能需要多次尝试和调整参数来优化校准效果。
在实际应用中,可以根据具体需求和设备要求来选择适合的校准方法和流程。
陀螺角度随机游走系数和陀螺噪声单位转换-概述说明以及解释
陀螺角度随机游走系数和陀螺噪声单位转换-概述说明以及解释1.引言1.1 概述概述:陀螺角度随机游走系数和陀螺噪声单位转换是陀螺仪在导航、飞行控制等领域中非常重要的参数和技术。
随机游走系数是描述陀螺仪输出信号随机漂移的一个重要指标,而噪声单位转换则是将陀螺噪声从一种单位转换为另一种单位,以方便分析和应用。
本文将从背景介绍、定义和计算方法、噪声的来源和特点、单位转换的原理和方法等方面系统地介绍陀螺角度随机游走系数和陀螺噪声单位转换的相关知识,希望能够帮助读者更好地理解和应用这些技术。
1.2文章结构1.2 文章结构本文将分为三个主要部分:引言、正文和结论。
在引言部分,将介绍本文研究的背景和意义,以及文章的结构安排。
在正文部分,将分为两个小节:陀螺角度随机游走系数和陀螺噪声单位转换。
在陀螺角度随机游走系数部分,将首先介绍背景知识,然后详细解释游走系数的定义和计算方法。
在陀螺噪声单位转换部分,将探讨噪声的来源和特点,然后深入讨论单位转换的原理和方法。
在结论部分,将总结陀螺角度随机游走系数和陀螺噪声单位转换的研究成果,分析它们对陀螺的影响及应用。
1.3 目的本文的主要目的是探讨陀螺角度随机游走系数和陀螺噪声单位转换的相关理论和方法。
通过对陀螺角度随机游走系数的背景介绍和计算方法的详细论述,希望读者能够更深入地了解陀螺在实际应用中的角度变化规律。
同时,对陀螺噪声单位转换的原理和方法进行讨论,旨在帮助读者更好地理解陀螺噪声的特点以及如何进行单位转换以满足实际需求。
通过本文的研究,可以为陀螺在导航、航空航天等领域的应用提供理论支持和技术参考,进一步提高陀螺系统的性能和精度,促进相关领域的发展和进步。
希望读者通过阅读本文,能够深入了解陀螺技术的前沿发展动态,拓宽视野,提升专业水平。
2.正文2.1 陀螺角度随机游走系数2.1.1 背景介绍陀螺角度随机游走系数是描述陀螺仪在姿态估计中的误差漂移情况的重要参数之一。
在惯性导航系统中,陀螺角度随机游走系数表示了陀螺仪输出角度随机误差的增长速率。
微机电陀螺随机漂移建模与卡尔曼滤波
微机电陀螺随机漂移建模与卡尔曼滤波
杨庆辉;杜红英;陈雄;周长省
【期刊名称】《计算机仿真》
【年(卷),期】2015(032)003
【摘要】微机电系统(MEMS)陀螺精度较低,严重影响制导火箭弹惯导系统的精度.为了减小MEMS陀螺的随机漂移,提高其精度使其满足简易制导火箭弹的精度要求,需要对陀螺信号进行滤波,MEMS陀螺随机漂移建模与补偿是其中的难点.针对上述问题,提出采用自回归移动平均(ARMA)分析的方法建立MEMS陀螺随机漂移模型,然后基于此模型对随机漂移信号进行卡尔曼(Kalman)滤波.对某MEMS陀螺在静止条件下的观测信号的滤波效果表明,ARMA模型拟合度高,能准确描述MEMS陀螺随机漂移特性;Kalman滤波方法能有效减小随机漂移误差,提高MEMS陀螺的精度,对提高简易制导火箭弹的精度具有一定的参考价值.
【总页数】5页(P68-72)
【作者】杨庆辉;杜红英;陈雄;周长省
【作者单位】南京理工大学机械工程学院,江苏南京210094;晋西工业集团有限责任公司技术中心,山西太原030027;南京理工大学机械工程学院,江苏南京210094;南京理工大学机械工程学院,江苏南京210094
【正文语种】中文
【中图分类】TJ765.4
【相关文献】
1.微机电系统陀螺仪随机漂移误差建模与滤波研究 [J], 宋吉磊;吴训忠;郭铃
2.光纤陀螺随机漂移建模与卡尔曼滤波器设计 [J], 李辉;谷宏强;李洪儒
3.基于ARMA模型和狼群算法的陀螺随机漂移建模研究 [J], 来凌红
4.卡尔曼滤波在陀螺仪随机漂移中的应用 [J], 陆芳;刘俊
5.基于时间序列分析的MEMS陀螺仪随机漂移建模研究 [J], 包书怡;袁心仪因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
万俊 潘鸿飞 杨柏军
(辽宁葫芦岛 91851 部队 125001)
摘要:导弹控制系统中,陀螺精度是系统精度的重要指标之一,而陀螺仪随 机漂移是影响陀螺精度的重要误差源,因而研究陀螺仪随机漂移对提高陀螺精度 有着重要意义。本文在统计分析的基础上提出了用固定方位力矩反馈法测取陀螺 仪的随机漂移,并简述了利用平稳时间法建立其数学模型的过程,对研究陀螺仪 随机漂移具有重要的参考价值。
陀螺仪随机漂移是衡量陀螺精度的最重要指标之一,它实际上是 一个随机过程。
根据随机过程的定义,陀螺仪随机漂移随机过程 x(t)可以被看成 是由依赖于时间 t 的这一族随机变量所构成的总体,因而可以借助数 理统计方法通过对大量漂移数据的统计分析,来寻求它的统计特性。
①概率分布函数(概率密度函数)---提供随机过程中各种取值 的概率特性,它可以给陀螺随机漂移以完整的描述。
AR(1)模型自相关函数为:
R(τ ) = σ 2e−β τ
⒁
式中: σ 2 为一阶马尔科夫过程的方差
β为反相关时间(β=1/τR,τR 为相关时间) 一阶马尔科夫过程自相关函数的离散形式可写为:
RK = σ 2e− β∆t K
⒂
Δt 为采样周期
同样,自相关系数的离散形式可写为:
ρK
= RK σ2
= e−β∆t K
可利用平稳时间法建立其误差模型。首先确定所要拟合的线性模型的
类别和阶数,其次估计模型参数并进行适用性检验,如发现潜周期分
量,应提取其中较大的潜周期分量,最后对去除了趋势项和潜周期分
量的残差序列进行正态性检验。
③当残差序列仍然是非平稳时间序列,则应进行差分处理,使之
成为平稳时间序列,然后再利用平稳时间法建立其误差模型。
KEY WORDS: Gyro drift, Smooth processing,Time sequence analysis method
0 引言 现代惯性系统对陀螺仪精度的要求越来越高,因而对陀螺仪随机
漂移的研究就显得越来越重要。本文从陀螺仪随机漂移的测取方法入
1
手,提出了用固定方位力矩反馈法测取陀螺仪的随机漂移,在此基础 上对陀螺随机漂移进行了理论分析,并详细探讨了陀螺仪漂移数学模 型的建立。 1 陀螺仪随机漂移的概述及其数学概率基础
⎟⎞2 ⎠
⑴
该方程实际上是有偏估计,也可写成无偏估计,则公式可写为:
∑ Λ
σ=
1 N −1
N i=1
⎜⎛ ⎝
Xi
−
Λ
µ
⎟⎞2 ⎠
⑵
当样本数 N 很大时,(N-1)与 N 的差别很小,两式计算结果近
似相等。
3 数学模型的建立
3.1 建模步骤
导弹控制系统中,可以利用卡尔曼滤波降低陀螺随机漂移对系统
精度的影响,但首先应建立陀螺随机漂移的数学模型,建模步骤大致
②均值函数和方差函数---提供随机过程中幅值方面的基本信 息,是从幅域来描述陀螺随机漂移的统计特性。
③自相关函数(自协方差函数)---反映随机过程中两个不同时 刻之间的相关度,是从时域来描述陀螺随机漂移的统计特性。
④自功率频谱密度函数---反映随机过程的平均功率按频率分布 的密度,是从频域来描述陀螺随机漂移的统计特性。
N=km,把漂移数据序列分成 k 个等时间区间的子样(子序列),每个
子样的数据个数相同,均为 m。顺序分别计算每个子样的均值μi 和
方差
α
2 i
(i=1,2,…,k),计算各子样的均方值:
ϕi2
=
ui2
+
α
2 i
(i=1,2,…,k )
⑶
则该子样均方值序列的中值为:
4
∑ = ϕ
2 0
1k k i−1
现的白噪声组成),按照尤尔概念,有色噪声序列可以看作是白噪声
序列经过成形滤波器变换得到的。
设{xt}表示观测到的时间序列,{ωt}表示白噪声序列,对时间序 列{xt}构造数学模型就是以白噪声{ωt}为输入,经过一个实时变换的 滤波器之后,得出时间序列{xt}的输出三者之间的关系。实际工程中, 平稳时间序列{xt}的线性模型通常可以表示成以下三种形式:滑动平 均模型 MA 模型,自回归模型 AR 模型,自回归滑动平均模型 ARMA
⑾
如果残差序列{xt}还是非平稳数据序列(主要是随机游动造成的),
一般采取差分的方法来处理,只需经过一阶差分,即可化为平稳时间
序列,对时间序列{xt}作一阶差分,
Δxt=xt-xt-1(t≥2)
⑿
对于含有趋势项的非平稳时间序列,也可直接利用差分处理,如果趋
势项中只含常数项和一次项,经过一阶差分即可使之平稳化;如果趋
验的首要问题,它是用来判别数据序列是否具有不随时间变化推移而
变化的统计特性。
平稳性检验的方法一般采用非参数检验法。非参数检验法是在未
知子样分布抽样情况下的检验方法。该方法是以轮次数这个统计量来
度量漂移数据序列与平稳随机序列之间的差异,以检验平稳性假设是
否成立。
假设随机过程 X(t)的现实序列足够长,即 N 取值足够大,令
势项中还含有二次项,则经过二阶差分就可使之平稳化。
3.3 利用时间序列分析法对平稳化的残差序列建立数学模型
时间序列分析是一种时域分析法,它不仅仅研究过程的确定性
变化,而且更着重于研究过程的随机性变化,它直接利用随机时间序
列来建立差分方程,把一个高度相关的平稳随机时间序列表示成一种
数字递推的形式(即看作是由各时刻相关的随机时间序列和各时刻出
模型。
本文着重讨论自回归模型 AR 模型(自回归模型, p 代表 AR 模型
的阶数),适用于动力调谐陀螺仪,以一阶自回归模型 AR(1)为例,其
6
结构式为:
xt = b1xt-1+ωt
⒀
该模型代表“一阶马尔科夫”过程的平稳随机过程,这种随机过
程的特点是:随机过程在 t 时刻的观测值 xt 仅与相邻的前一时刻(t-1) 时刻的观测值 xt-1 存在相关性。
立。
“平稳性假设”是否成立,是在显著性水平α(一般取 0.05)
之下作出的,判别置信度为 1-α(当α取 0.05 置信度为为 95%)。
实际工程中,陀螺漂移测试所得到的数据序列可能是非平稳随机
序列,对于此类序列则应设法去掉其中的有规律部分和趋势项以实现
数据的平稳化处理。
对于一个非平稳时间序列{yt},可以看成由一个确定性的趋势项
以上是描述陀螺仪随机漂移过程中的几个重要统计特征函数,均 值反映了随机过程在各个时刻取值的分布中心;方差反映了随机过程 在各个时刻取值相对均值的离散程度;自相关函数反映了随机过程在 两个不同时刻取值之间的相关程度;自功率频谱密度函数反映了随机 过程的平均功率按频率分布的密度。
上述描述平稳随机过程统计特性的数学估计式只对平稳正态随 机过程才适用;如果含有趋势项随机漂移数据序列,必须经过平稳化 处理才可应用上述数学估计式进行计算。 2 陀螺仪随机漂移率的测取
X t − X t −1 = − β∆tX t −1 + ωt
⒆
如此一来,我们就可以把离散差分方程化为连续型微分方程,对
上式两边同时除以Δt 并取极限,则为:
7
lim X t
∆t →0
− X t −1 ∆t
=
lX t −1 ∆t
+
ωt
•
⇒ X (t ) = − β ( X )t + ω(t )
⒃
由 AR(1)模型的性质可知 Rt = b1Rt-1,带入上式可得自回归系数的
表达式:
b1 = e − β∆t
⒄
则,AR(1)模型的表达式:
X t = e−β∆t X t−1 + ωt
⒅
把 e−β∆t 展开级数,并忽略二阶及二阶以上的小量,则得:
X t = (1− β∆t )X t−1 + ωt ⇒
ϕ i2
⑷
把它作为真实均方值的估计值。如果陀螺漂移数据序列是平稳随
机序列,每个子样均方值 相对与子样均方值中值 的变化是随机
的,不应存在共同的确定趋势项。子样均方值序列中
ϕ
2 i
≥
ϕ
2 0
(记为
“+”号)的子样数为
k1
和 ϕ i2
<ϕ
2 0
(记为“-”号)的子样数为
k2
应相
等,都应等于 k/2,
n=k1=k2=k/2
随机漂移率是衡量陀螺仪精度的最重要指标,在一定的测试条件 下,陀螺漂移率是指在某一均值水平上随时间作无规律变化的随机变 量,其均值μ代表了系统性漂移,而随机漂移则以均方根值或标准偏 差σ来表示,陀螺仪漂移随机过程满足各态遍历性条件时,随机漂移 的数学估计为:
∑ Λ
σ
=
1 N
N i=1
⎜⎝⎛
Xi
−
Λ
µ
如下:
①对陀螺漂移测试所得到的样本数据序列(随机时间序列)进行
统计检验。首先进行平稳性检验,如发现为非平稳的随机时间序列,
3
应提取其中确定性的趋势项,其次进行周期性检验,如发现潜周期分
量,应提取其中能量较大的潜周期分量,最后对除了趋势项和潜周期
分量的残差序列进行正态性检验。
②如果经过检验的陀螺漂移数据的残差序列是平稳时间序列,则
关键词: 陀螺漂移;平稳化处理;时间序列分析法
Measurement of Random Drift of Gyro and Establishment of Mathematical Model
ABSTRACT : The precision of gyro is one of the most important points to decide precision of missile control system and it is mostly effected by the gyro random drift.On basis of statistics analysis, the fixed-azimuths-moment feedback method for measurement of random drift is put forward in the paper, and the mathematical model is established by means of stabilization time method,with greatreference to study of gyro random drift。
