5第五章现代谱估计解析
合集下载
现代信号处置最大熵谱估计

M k 1
Ak2
1
2
exp[
j(k m)]dk
M
Ak2 exp[ j(k m)] k 1
(5.5.2)
假如c(n)与u(n)时互不有关旳,则x(n)旳自有关函数为:
M
R(m) Ak2 exp[ j(k m)] u (m) k 1
x(n)旳功率谱为:
m 0,1, , p(5.5.3)
假设:信号 x n是由M个复正弦信号加白噪声构成,即:
M
x n Ak e j(knk ) u(n) c n u n k 1
(5.5.1)
式中:k是[- , ]内均匀分布的零均值随机变量, u(n)为白噪声,A k 和k 为常数
c(n) 旳自有关函数为:
R '(m) E[c(n)c*(n m)]
当代数字信号处理
第五章 功率谱估计
内容摘要
• 5.1 概述 • 5.2 经典谱估计旳基本措施
5.2.1 周期图 5.2.2 有关图 • 5.3 功率谱估计旳参数模型法 5.3.1 AR谱估计旳有关函数法
5.3.2 AR参数谱估计与最佳线性预测器旳关系 5.3.3 Levinson-Durbin算法 5.3.4 Burg算法 5.3.5 AR谱估计旳性质 5.3.6 MA谱估计、ARMA谱估计 5.4 最大熵谱分析 5.5 特征分解法谱估计 5.5.1 Pisarenko谐波分解与有关矩阵旳特征分解 5.5.2 基于信号子空间旳频率估计及功率谱估计
☆ N维高斯分布:
p( x1 ,
x2 ,,
xN
)
(2
)N
/2
det
R(N )
1/ 2
exp
1 2
X
第一部分_谱分析与谱估计(3)

x(n) = ∑ bk e(n − k ) + e(n)
k =1
q
(5-9)
42
测试信号分析与处理 —— 现代谱估计
q
H ( z ) = B( z ) = 1 + ∑ bk z − k
k =1
(5-10)
S xx (ω ) = σ 1 + ∑ bk e
2 k =1
q
2 − jω k
(5-11)
(5-9)式称为 q 阶滑动平均(Moving-Average)模型,简称为 MA(q)模型。 MA 过程与 AR 过程不同,它是过程{e(t)} 的现在和有限范围内过去值的线性组合,所 以 e(n)只影响 x(n)的 q 个未来值。 如果时间间隔小于 q 的 x(n)中所包含的 e(n)已经全部更新, 时滞超过 q 的两个 x(n)是不相关的。 也就是说, MA 过程的自相关函数, 当|m|>q 时 Rxx(m)=0。 关于这点,我们以后还会分析。另外,由于{x(n)}是由互不相关的{e(n)}的线性组合,所以, {x(n)}是平稳的,而不论参数 bk 的取值如何。 (3)ak,bk ( k=1,2,…,p 或 q )不全为零,则(5-1b)式给定的模型称为自回归滑动平均模型, 简称为 ARMA (p,q)模型。是一个既有极点,又有零点的模型。显然,更一般的平稳随机过 程是用这种具有(p 阶)自回归和 (q 阶) 滑动平均模型来描述, AR 或 MA 过程都只是 ARMA 过程的特殊情况。 由于(5-1)式中,是用线性差分方程描述了{x(n)}和{e(n)}两个序列在不同时刻之间的 线性关系,因而是一种线性时间序列模型。 模型(5-3)式还常常写成如下更广泛的线性时间序列形式: Φ ( B) xt = θ ( B )et (5-12) 式中:
5谱估计(概述和经典法)分解

xx (m)Ex(n) x (n m)
N 1 jm Pxx () Pxx () lim x(n) x (n m) e N 2 N 1 m n N
1 N jn j ( n m ) lim x(n)e x (n m)e N 2 N 1 n N m
N 1 n 0 2
1 ˆ Pxx ( ) N
x(n)e
jn
1 2 X N ( ) N
进行功率谱估计(不通过自相关函数的估计)
将已知数据序列的傅立叶 变换的模的平方除以序列 长度作为功率谱的估计
计算效率高 频率分辨率低
1
• 研究现状
经典谱估计:
引
言
固有缺陷:原因:“加窗效应” 频率分辨率低 原因:加窗截取,认为窗以外的数据为零。
1
引
言
• 功率谱估计的应用
在信号处理的许多场所,要求预先知道信号
的功率谱密度(或自相关函数)。
常常利用功率谱估计来得到线性系统的参数
估计。
从宽带噪声中检测窄带信号。
• 功率谱估计的应用
谱估计的分辨率可以粗略地定义为能够分辨出的 二个分立的谱分量间的最小频率间隙(距)。 例如:有一个随机信号,它包括二个频率相差1Hz振 幅相等的正弦波以及加性白噪声(白色噪声的方差是 正弦波功率的10%)。
N
2
功率谱的 真实值
2
才有意义
N 1 j n Pxx ( ) lim E x ( n ) e N 2 N 1 n N
1
• 谱分析
引
言
用有限的N个样本数据来估计平稳随机过 程的功率谱密度。
《现代谱估计》课件

周期图平均法
将多个周期的频谱进行平均, 降低噪声对频谱估计的影响。
移动平均法
对信号进行滑动平均,减小高 频部分的噪声。
核方法
利用核函数对信号进行平滑处 理,提高频谱估计的精度。
参数谱估计方法
1
基于自相关函数的方法
通过自相关函数计算信号的频谱,适用于具有明显周期性的信号。
2
基于协方差函数的方法
利用Байду номын сангаас号的协方差函数进行频谱估计,适用于具有随机性的信号。
《现代谱估计》PPT课件
现代谱估计PPT课件
概述
谱估计是一种用于分析信号频谱特征的方法。它可以帮助我们了解信号的频率分布和功率,对信号处理和通信 系统设计具有重要意义。
经典谱估计方法
周期图法
通过离散傅里叶变换来计算信号的频谱。
快速傅里叶变换法
利用傅里叶变换的性质,高效计算信号的频谱。
非参数谱估计方法
谱估计在信号处理、通信系统 设计等领域具有广泛应用,对 于优化系统性能至关重要。
利用最小二乘法进行频谱估计,得到更准确 的频谱估计结果。
2 最大熵谱估计法
通过最大熵原理寻找最平滑的频谱估计。
3 光滑谱估计法
利用光滑函数对信号进行频谱估计,减少估 计结果的噪声。
4 自适应谱估计法
根据信号的特性调整谱估计方法,得到更好 的估计结果。
谱估计算法的评价指标
均方误差
衡量估计结果与真实频谱之间的差距。
3
基于线性预测模型的方法
利用线性预测模型对信号进行建模,从而估计信号的谱。
噪声下的谱估计问题
白噪声下的问题
白噪声对频谱估计的影响较小, 但会增加估计的方差。
彩色噪声下的问题
第五章 线谱估计

器权矢量的估计。
ˆ 如果在 [ , ] 内改变 ,画出 P MVDR ( ) 曲线。在 i , i 1, 2, , K 处的信号和噪声都被
滤波器抑制,曲线会出现很低的幅度;当 i , i 1, 2, , K 时,频率为 i 的信号可以无失 真地通过滤波器,因此曲线呈现出一个峰值。 在上面 MVDR 线谱估计方法的推导中,涉及了横向滤波器,但在进行信号频率估计时,无需构 建滤波器,而直接计算式(5.1.13)就可以得到复正弦信号的线谱。 应该指出,上面的 PMVDR (e ) 被称为最小方差谱,它并不是功率谱,它描述了信号功率谱的相 对强度。 Capon 提出的 MVDR 线谱估计方法的谱估计分辨率不高于基于 AR 模型的功率谱估计方法。
其中,矩阵 R
M M
(5.1.6)
为矢量 x(n) 的 M 维自相关矩阵,即
r (1) r (0) r (1) r (0) R E x(n)x H (n) r (1 M ) r (2 M )
r ( M 1) r ( M 2) r (0)
根据式(5.1.9),求其梯度 J (w ) ,并令其为零,有
(5.1.9)
J (w ) 2Rw 2a(e j ) 0
考虑到自相关矩阵 R 是非奇异的,所以有
(5.1.10)
w R 1a(e j )
将其代入到约束条件 w a(e ) 1 中,并考虑 R 的共轭对称性,可得
x(n) k e jk n v(n)
k 1
K
(5.1.1)
其中, v(n) 是零均值,方差 为加性白噪声, k 和 k 分别是第 k 个复正弦信号复幅度和角频率,
ˆ 如果在 [ , ] 内改变 ,画出 P MVDR ( ) 曲线。在 i , i 1, 2, , K 处的信号和噪声都被
滤波器抑制,曲线会出现很低的幅度;当 i , i 1, 2, , K 时,频率为 i 的信号可以无失 真地通过滤波器,因此曲线呈现出一个峰值。 在上面 MVDR 线谱估计方法的推导中,涉及了横向滤波器,但在进行信号频率估计时,无需构 建滤波器,而直接计算式(5.1.13)就可以得到复正弦信号的线谱。 应该指出,上面的 PMVDR (e ) 被称为最小方差谱,它并不是功率谱,它描述了信号功率谱的相 对强度。 Capon 提出的 MVDR 线谱估计方法的谱估计分辨率不高于基于 AR 模型的功率谱估计方法。
其中,矩阵 R
M M
(5.1.6)
为矢量 x(n) 的 M 维自相关矩阵,即
r (1) r (0) r (1) r (0) R E x(n)x H (n) r (1 M ) r (2 M )
r ( M 1) r ( M 2) r (0)
根据式(5.1.9),求其梯度 J (w ) ,并令其为零,有
(5.1.9)
J (w ) 2Rw 2a(e j ) 0
考虑到自相关矩阵 R 是非奇异的,所以有
(5.1.10)
w R 1a(e j )
将其代入到约束条件 w a(e ) 1 中,并考虑 R 的共轭对称性,可得
x(n) k e jk n v(n)
k 1
K
(5.1.1)
其中, v(n) 是零均值,方差 为加性白噪声, k 和 k 分别是第 k 个复正弦信号复幅度和角频率,
DSP-第五章 谱估计
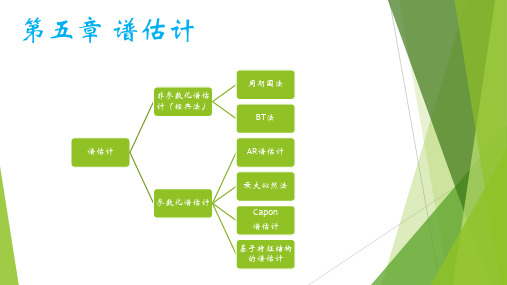
������=1
������
������
������ ������ = − ������������������ ������ − ������ + ������ ������ + ������������������(������ − ������)
������=1
������=1
自回归模型(AutoRegressive)方法
第五章 谱估计
谱估计
非参数化谱估 计(经典法)
参数化谱估计
周期图法
BT法
AR谱估计
最大似然法 Capon 谱估计
基于特征结构 的谱估计
两种自相关函数的估计方法
优选
经典谱估计之BT法(相关图法)
数据
估计自相 关
FT
谱估计
经典谱估计之周期图法
数据
加矩形窗
FT
平方求平均
傅里叶变换
对周期图法的改进1:窗口处理法
Levinson-Durbin递推算法
AR模型阶数选择
三种阶数确定准则
Burg递归算法
在求解Lenvinson递推的时候,需要知道自相关序列。我们只能从随机序列中计 算。若序列长度较短,自相关的估计误差就会偏大。为解决上述问题,Burg提出 利用观察数据直接计算AR模型参数,用以克服以上问题。
������ ������=1
������������
������−������
差分方程
������ ������
=−
������ ������=1
������������
������
������ − ������
+ω(n)
������
第5章频域统计参数估计-谱估计

– 现代谱估计的优点:谱分辨率高,平滑性好 – 现代谱估计的缺点:计算复杂
第5章频域统计参数估计-谱估计
功率谱估计:经典谱估计与现代谱估计
谱估计就是从无限长随机序列中截取一段数据(加窗)来分 析。而问题的真正要害:如何看待截取数据以外的那无限长 数据序列,因为统计特性是以足够大的数据窗为前提的。
经典法:侧重于如何处理已经截得的那段数据上,很多技 巧表现在如何选择合适的窗,周期图法(直接法)默认为窗 外数据是窗内数据的周期重复;相关法(间接法)默认为数 据窗外的数据一概为零,延迟窗外的数据也一概为零,这显 然都是不符合实际的,这就导致经典谱估计的分辨率低,质 量差。
1)波束形成器
第5章计参数估计-谱估计
第5章频域统计参数估计-谱估计
证明:
第5章频域统计参数估计-谱估计
2)信号子空间与噪声子空间
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
证明:
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
ai
3)ARMA模型的MA阶数q确定
第5章频域统计参数估计-谱估计
4)ARMA模型的MA参数bi估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
5.2.2 最大熵谱估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
3)基本MUSIC法
第5章频域统计参数估计-谱估计
4)改进方法1—求根的MUSIC法
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
5)改进方法2
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
功率谱估计:经典谱估计与现代谱估计
谱估计就是从无限长随机序列中截取一段数据(加窗)来分 析。而问题的真正要害:如何看待截取数据以外的那无限长 数据序列,因为统计特性是以足够大的数据窗为前提的。
经典法:侧重于如何处理已经截得的那段数据上,很多技 巧表现在如何选择合适的窗,周期图法(直接法)默认为窗 外数据是窗内数据的周期重复;相关法(间接法)默认为数 据窗外的数据一概为零,延迟窗外的数据也一概为零,这显 然都是不符合实际的,这就导致经典谱估计的分辨率低,质 量差。
1)波束形成器
第5章计参数估计-谱估计
第5章频域统计参数估计-谱估计
证明:
第5章频域统计参数估计-谱估计
2)信号子空间与噪声子空间
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
证明:
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
ai
3)ARMA模型的MA阶数q确定
第5章频域统计参数估计-谱估计
4)ARMA模型的MA参数bi估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
5.2.2 最大熵谱估计
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
3)基本MUSIC法
第5章频域统计参数估计-谱估计
4)改进方法1—求根的MUSIC法
第5章频域统计参数估计-谱估计
第5章频域统计参数估计-谱估计
5)改进方法2
第5章频域统计参数估计-谱估计
第五章谱估计

2 ( 2k )..( 5 30 )
lim E[ I N ( )] ( )...(5 31) 渐进无偏差
2 sin N 4 估计方差: Var[ I N ( )] x 1 ..( 5 32 ) N sin
E
x(t ) dt (5 1)
2
则x(t)的连续傅氏变换存在,由下式给出:
X( f )
E
x (t ) exp( j 2ft )dt (5 2)
2
根据Parseval能量定理,有:
14:56
x(t ) dt
X ( f ) df (5 3)
d (n) x(n)d (n k ) x(n k ) (5 15 )
功率谱的估计可写成:
jn j ( n k ) d (n) x(n)e d (n k ) x(n k )e n n
关(协方差)函数为: ( k )
若有:
k
E x(n ) x(n k ) (5 8)
( k )
(5 9 )
jk ( ) ( k ) e (5 10 ) 则功率谱密度为: k ( ) 是以0对称,周期为2。反变换为:
定义:长度为N的实平稳随机信号序列
x N ,0 n N 1
的周期图为: I ( ) 1 X ( ) 2 , (5 26) N N
式中
X N ( )
jn x ( n ) e DFT n 0
N 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1967年以后为现代谱估计阶段,是基于非线性的谱分析。 包括各种模型参数法,熵谱法及最小方差法,与奇异值/特 征值分解处理的非参数法等。 当数据序列较长时,经典谱估计有较好的性能,但对于 短序列,经典谱估计存在分辨率不高等致命弱点。现代谱 估计具有优良性能,为经典法所不及。
现代谱估计的主要方法有:
N
2
时间序列由角频率0的正弦信号与噪声叠加而成。 则周期图(寻找数据的隐周期性即频率)在0 处会出 现峰值。通过计算周期图。由各峰值可显示出正弦频 率信号。
1930年,维纳-辛钦定理,证明自相关函数和功率谱互 为傅立叶变换,建立了使用傅氏方法处理随机过程的 理论体系。谱分析的第二步。
1958年,布莱克曼(Blackman)和图基(Tukey)经典论 文“由通信工程观点对功率谱的测量”给出用维纳相关法 从抽样序列得到功率谱的实现方法——BT法。其性能与窗 函数选择有关。周期图和BT法称为经典谱估计方法。(且 是线性估计方法)。 上述方法的最大问题是由于数据截断(或开窗)带来的 频率泄漏。弱信号的主瓣很容易被强信号的旁瓣所淹没。 对于短序列这一情况尤为突出。
p x
5.2 AR模型参量法
模型参量法的基本思想是根据所研究信号的先验知 识,对信号窗外的数据作出某种比较合理的假设(外 推或预测)。具体步骤为: 1、选择一个好的模型。 输入为 n 或 t 或白噪声情况下,使输出等于所 研究的信号,至少也是对该信号的一个近似。AR, MA, ARMA及谐波信号模型。 2、利用已知的自相关函数或数据求模型参数。 3、利用求出的模型参数估计该信号的功率谱。
1971年,范登博斯证明,最大熵谱分析I法与AR 模型参量法等效。因此也将该法列为模型参量法谱估 计。 1979年,美国海军实验室绍尔(Shore)提出最 q x 小交叉熵谱分析I法。 H p, q q x ln dx
以后又有最大熵谱分析II法、最小交叉熵谱分析II 法、最大熵分析拓广、最小交叉熵分析拓广、多信号 交叉熵谱分析等,已可独立成为现代谱估计的重要组 成部分。 4、多谱(高阶谱)与多维谱估计 通常的谱估计或功率谱估计,只包含振幅信息。 但许多实际问题需要相位信息。这种情况可考虑使用 多谱(高阶谱)——高阶累积量的多维傅氏变换。 5、自适应谱估计和鲁棒估计
递推求解的方法。
设p-1阶AR参量矩阵方程为:
rxx (1) rxx ( p 1) 1 2 rxx (0) p 1 a r (1) r (0) r ( p 2) xx xx xx p 1,1 0 a r ( p 1) r ( p 2) r (0) 0 xx xx xx p 1, p 1
第五章 现代谱估计
主要内容:
5.1 5.2 5.3 5.4 5.5 谱估计的发展 AR模型参数法 最大熵谱估计 最大似然谱功率估计 谐波分解模型
5.1 谱估计的发展
19世纪末舒斯特(Schuster)周期图 1 S x1e j x2 e j 2 ... xN e jN
1、模型参量谱估计——可得到高分辨率的谱估计。而 这取决于假定模型对观察数据的适配能力。 2、非参量谱估计 不用有限参数描述的信号模型,直接由自相关延 迟序列得到。高信噪比下不如模型法,但在低信噪比 下,模型参量谱估计的分辨率大为下降。 1973年,皮萨伦科(Pisarenko)提出特征矢量 法,开辟了基于自相关矩阵或数据矩阵进行特征分解 的非参量谱估计。 3、熵谱估计 1967年,伯格提出最大熵谱分析法。其方法是对 已知延迟点上的自相关函数不加修改,而是对未知延 迟点上的自相关函数按信息论中的最大熵外推而得。
p AR ( f )
(3)
2
1 ak exp( j k )
k 1 p 2
(4)
5.2.2 莱文森-德宾(Levinson-Durbin)算法
2 2 { a , },{ a , a , 此算法是以 1,1 1 2,1 2,2 2 }
2 {ap1,1, ap1,2 ,, ap1, p1, p 1}
xx
l 1
l xx
取k=0,1,2,…,p,可得矩阵表达为:
rxx (0) rxx (1) rxx ( p) 1 2 a rxx (0) rxx ( p 1) 1 0 rxx (1) a r ( p ) r ( p 1) r (0) 0 p xx xx xx
* rxx k E ห้องสมุดไป่ตู้ x x nk n
p E al xn k l n k xn l 1
al rxx k l E x nk n l 1 p al rxx k l , k 0 l 1 (2) p a r k l 2 , k 0 l xx l 1 p 此式(2)可简写成: r (k ) a r (k l ) k p
5.2.1 5.2.2 5.2.3 5.2.4
尤拉-沃克(Yule-Walker)方程 莱文森-德宾(Levison-Durbin)算法 BURG 算法 AR模型阶数的判定
5.2.1 尤拉-沃克(Yule-Walker)方程
AR(p)模型
xn al xn l n
l 1
p
(1)
现代谱估计的主要方法有:
N
2
时间序列由角频率0的正弦信号与噪声叠加而成。 则周期图(寻找数据的隐周期性即频率)在0 处会出 现峰值。通过计算周期图。由各峰值可显示出正弦频 率信号。
1930年,维纳-辛钦定理,证明自相关函数和功率谱互 为傅立叶变换,建立了使用傅氏方法处理随机过程的 理论体系。谱分析的第二步。
1958年,布莱克曼(Blackman)和图基(Tukey)经典论 文“由通信工程观点对功率谱的测量”给出用维纳相关法 从抽样序列得到功率谱的实现方法——BT法。其性能与窗 函数选择有关。周期图和BT法称为经典谱估计方法。(且 是线性估计方法)。 上述方法的最大问题是由于数据截断(或开窗)带来的 频率泄漏。弱信号的主瓣很容易被强信号的旁瓣所淹没。 对于短序列这一情况尤为突出。
p x
5.2 AR模型参量法
模型参量法的基本思想是根据所研究信号的先验知 识,对信号窗外的数据作出某种比较合理的假设(外 推或预测)。具体步骤为: 1、选择一个好的模型。 输入为 n 或 t 或白噪声情况下,使输出等于所 研究的信号,至少也是对该信号的一个近似。AR, MA, ARMA及谐波信号模型。 2、利用已知的自相关函数或数据求模型参数。 3、利用求出的模型参数估计该信号的功率谱。
1971年,范登博斯证明,最大熵谱分析I法与AR 模型参量法等效。因此也将该法列为模型参量法谱估 计。 1979年,美国海军实验室绍尔(Shore)提出最 q x 小交叉熵谱分析I法。 H p, q q x ln dx
以后又有最大熵谱分析II法、最小交叉熵谱分析II 法、最大熵分析拓广、最小交叉熵分析拓广、多信号 交叉熵谱分析等,已可独立成为现代谱估计的重要组 成部分。 4、多谱(高阶谱)与多维谱估计 通常的谱估计或功率谱估计,只包含振幅信息。 但许多实际问题需要相位信息。这种情况可考虑使用 多谱(高阶谱)——高阶累积量的多维傅氏变换。 5、自适应谱估计和鲁棒估计
递推求解的方法。
设p-1阶AR参量矩阵方程为:
rxx (1) rxx ( p 1) 1 2 rxx (0) p 1 a r (1) r (0) r ( p 2) xx xx xx p 1,1 0 a r ( p 1) r ( p 2) r (0) 0 xx xx xx p 1, p 1
第五章 现代谱估计
主要内容:
5.1 5.2 5.3 5.4 5.5 谱估计的发展 AR模型参数法 最大熵谱估计 最大似然谱功率估计 谐波分解模型
5.1 谱估计的发展
19世纪末舒斯特(Schuster)周期图 1 S x1e j x2 e j 2 ... xN e jN
1、模型参量谱估计——可得到高分辨率的谱估计。而 这取决于假定模型对观察数据的适配能力。 2、非参量谱估计 不用有限参数描述的信号模型,直接由自相关延 迟序列得到。高信噪比下不如模型法,但在低信噪比 下,模型参量谱估计的分辨率大为下降。 1973年,皮萨伦科(Pisarenko)提出特征矢量 法,开辟了基于自相关矩阵或数据矩阵进行特征分解 的非参量谱估计。 3、熵谱估计 1967年,伯格提出最大熵谱分析法。其方法是对 已知延迟点上的自相关函数不加修改,而是对未知延 迟点上的自相关函数按信息论中的最大熵外推而得。
p AR ( f )
(3)
2
1 ak exp( j k )
k 1 p 2
(4)
5.2.2 莱文森-德宾(Levinson-Durbin)算法
2 2 { a , },{ a , a , 此算法是以 1,1 1 2,1 2,2 2 }
2 {ap1,1, ap1,2 ,, ap1, p1, p 1}
xx
l 1
l xx
取k=0,1,2,…,p,可得矩阵表达为:
rxx (0) rxx (1) rxx ( p) 1 2 a rxx (0) rxx ( p 1) 1 0 rxx (1) a r ( p ) r ( p 1) r (0) 0 p xx xx xx
* rxx k E ห้องสมุดไป่ตู้ x x nk n
p E al xn k l n k xn l 1
al rxx k l E x nk n l 1 p al rxx k l , k 0 l 1 (2) p a r k l 2 , k 0 l xx l 1 p 此式(2)可简写成: r (k ) a r (k l ) k p
5.2.1 5.2.2 5.2.3 5.2.4
尤拉-沃克(Yule-Walker)方程 莱文森-德宾(Levison-Durbin)算法 BURG 算法 AR模型阶数的判定
5.2.1 尤拉-沃克(Yule-Walker)方程
AR(p)模型
xn al xn l n
l 1
p
(1)
