中考数学压轴题(二)动点问题(2)(20200424154543)

合集下载

2020年九年级数学三轮冲刺复习培优练习：《二次函数动点综合压轴》(二)

2020年九年级数学三轮冲刺复习培优练习：《二次函数动点综合压轴》（二）1．如图，抛物线y＝﹣x2+bx+c与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l：y＝kx+n与y轴交于点C，与抛物线y＝﹣x2+bx+c的另一个交点为D，已知A（﹣1，0），D（5，﹣6），P点为抛物线y＝﹣x2+bx+c上一动点（不与A、D重合）．（1）直接写出抛物线和直线l的解析式；（2）当点P在直线l上方的抛物线上时，连接PA、PD，①当△PAD的面积最大时，P点的坐标是；②当AB平分∠DAP时，求线段PA的长．（3）设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，直接写出点M的坐标；若不存在，请说明理由．2．如图，抛物线y＝﹣x2+bx+c的图象与x轴交于A、B两点（点A在点B的左边），与y 轴交于点C，点D为抛物线的顶点．点A坐标的为（﹣3，0），点C的坐标为（0，3）．（Ⅰ）求抛物线的解析式；（Ⅱ）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；（Ⅲ）在（Ⅱ）的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y 轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG＝2DQ，求点F的坐标．3．已知：二次函数y＝x2﹣2mx﹣m2+4m﹣2的对称轴为l，抛物线与y轴交于点C，顶点为D．（1）判断抛物线与x轴的交点情况；（2）如图1，当m＝1时，点P为第一象限内抛物线上一点，且△PCD是以PD为腰的等腰三角形，求点P的坐标；（3）如图2，直线y＝mx和抛物线交于点A、B两点，与l交于点M，且MO＝MB，点Q（x0，y）在抛物线上，当m＞1时，h+12≤﹣my2﹣6my时，求h的最大值．4．已知点P（2，﹣3）在抛物线L：y＝ax2﹣2ax+a+k（a，k均为常数，且a≠0）上，L交y轴于点C，连接CP．（1）用a表示k，并求L的对称轴及L与y轴的交点坐标；（2）当L经过（3，3）时，求此时L的表达式及其顶点坐标；（3）横、纵坐标都是整数的点叫做整点．如图，当a＜0时，若L在点C，P之间的部分与线段CP所围成的区域内（不含边界）恰有4个整点，求a的取值范围；（4）点M（x1，y1），N（x2，y2）是L上的两点，若t≤x1≤t+1，当x2≥3时，均有y1≥y2，直接写出t的取值范围．5．如图①，直线y＝﹣x﹣3分别与x轴、y轴交于点B，C，抛物线y＝ax2+bx+c经过B，C 两点，且与x轴的另一交点为A（1，0）．（1）求抛物线的函数解析式；（2）如图①，点P在第三象限内的抛物线上．①连接AC，PB，PC，当四边形ABPC的面积最大时，求点P的坐标；②在①的条件下，G为x轴上一点，当PG+AG取得最小值时，求点G的坐标；（3）如图②，Q为x轴下方抛物线上任意一点，D是抛物线的对称轴与x轴的交点，直线AQ，BQ分别交抛物线的对称轴于点M，N．问：DM+DN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．6．如图，抛物线y＝ax2﹣3ax+4（a＜0）与x轴交于A、B两点，与y轴交于点C，直线y ＝m，交抛物线于D、E两点．（1）当a＝﹣时，求A，B两点的坐标；（2）当m＝2，DE＝4时，求抛物线的解析式；（3）当a＝﹣1时，方程ax2﹣3ax+4＝m在﹣6≤x＜4的范围内有实数解，请直接写出m 的取值范围：．7．如图1所示，抛物线与x轴交于A、B两点，与y轴交于点C，已知C点坐标为（0，4），抛物线的顶点的横坐标为，点P是第四象限内抛物线上的动点，四边形OPAQ是平行四边形，设点P的横坐标为m．（1）求抛物线的解析式；（2）求使△APC的面积为整数的P点的个数；（3）当点P在抛物线上运动时，四边形OPAQ可能是正方形吗？若可能，请求出点P的坐标，若不可能，请说明理由；（4）在点Q随点P运动的过程中，当点Q恰好落在直线AC上时，则称点Q为“和谐点”，如图（2）所示，请直接写出当Q为“和谐点”的横坐标的值．8．如图，一条抛物线与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C（0，3），D为抛物线的顶点，点P在x轴上．（1）求抛物线解析式；（2）若∠PCB＝∠CBD，求点P的坐标；（3）过点P作直线l∥AC交抛物线于Q，是否存在以点A，P，Q，C为顶点的四边形是平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由；（4）坐标平面内一点M到点B的距离为1个单位，求DM+OM的最小值．9．在四边形OABC中，AB∥OC，BC⊥x轴于C，A（1，﹣1），B（3，﹣1），动点P从O点出发，沿x轴正方向以3个单位/秒的速度运动．过P作PQ⊥OA于Q．设P点运动的时间为t秒（0＜t＜），△OPQ与四边形OABC重叠的面积为S．（1）求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标；（2）用含t的代数式表示P、Q两点的坐标；（3）将△OPQ绕P点逆时针旋转90°，是否存在t，使得△OPQ的顶点O或Q落在抛物线上？若存在，直接写出t的值；若不存在，请说明理由；（4）求S与t的函数解析式；10．如图所示，抛物线y＝ax2+bx+4的顶点坐标为（3，），与y轴交于点A．过点A作AB∥x轴，交抛物线于点B，点C是第四象限的抛物线上的一个动点，过点C作y轴的平行线，交直线AB于点D．（1）求抛物线的函数表达式；（2）若点E在y轴的负半轴上，且AE＝AD，直线CE交抛物线y＝ax2+bx+4于点F．①求点F的坐标；②过点D作DG⊥CE于点G，连接OD、ED，当∠ODE＝∠CDG时，求直线DG的函数表达式．参考答案1．解：（1）将点A、D的坐标代入直线表达式得：，解得：，故直线l的表达式为：y＝﹣x﹣1，将点A、D的坐标代入抛物线表达式，同理可得抛物线的表达式为：y＝﹣x2+3x+4；（2）当△PAD的面积最大时，P点到直线AD的距离就最大．∴P点在与直线AD平行且与抛物线相切的直线上，即P点是这两个图象的唯一的交点，设P点坐标为（x，y），由题意得，，∴x2﹣4x+m﹣4＝0，∵直线y＝﹣x+m与抛物线只有一个交点，∴△＝42+4（m﹣4）＝0，∴m＝8，∴x2﹣4x+4＝0，∴x1＝x2＝2，∴代入抛物线的解析式得y＝﹣4+6+4＝6，∴P（2，6）；故答案为：（2，6）．②过点P作PE⊥x轴于点E，∵y＝﹣x﹣1，∴A（﹣1，0），C（0，﹣1），∴OA＝OC，∵∠AOC＝90°，∴∠CAB＝45°，∴当AB平分∠DAP时，∠BAP＝∠DAB，则∠BAP＝45°，∴△PEA是等腰直角三角形，∴PE＝EA，设P点坐标为（m，n），由题意得，m+1＝﹣m2+3m+4，∴m1＝3，m2＝﹣1（舍去），∴PE＝EA＝4，∴PA＝4．（3）NC＝5，①当NC是平行四边形的一条边时，设点P坐标为（x，﹣x2+3x+4）、则点M（x，﹣x﹣1），由题意得：|y M﹣y P|＝5，即：|﹣x2+3x+4+x+1|＝5，解得：x＝2±或0或4（舍去0），则点M坐标为（2+，﹣3﹣）或（2﹣，﹣3+）或（4，﹣5）；②当NC是平行四边形的对角线时，则NC的中点坐标为（0，），设点P坐标为（m，﹣m2+3m+4）、则点M（n，﹣n﹣1），N、C，M、P为顶点的四边形为平行四边形，则NC的中点即为PM中点，即：m+n＝0，2＝，解得：m＝0（舍去）或m＝4，故点M（﹣4，3）；故点M的坐标为：（2+，﹣3﹣）或（2﹣，﹣3+）或（4，﹣5）或（﹣4，3）．2．解：（Ⅰ）依题意解得∴抛物线的解析式y＝﹣x2﹣2x+3；（Ⅱ）∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，∴抛物线的对称轴是直线x＝﹣1，设M（x，0），P（x，﹣x2﹣2x+3），其中﹣3＜x＜﹣1，∵P、Q关于直线x＝﹣1对称，设Q的横坐标为a，则a﹣（﹣1）＝﹣1﹣x，∴a＝﹣2﹣x，∴Q（﹣2﹣x，﹣x2﹣2x+3），∴MP＝﹣x2﹣2x+3，PQ＝﹣2﹣x﹣x＝﹣2﹣2x，∴周长d＝2（﹣2﹣2x﹣x2﹣2x+3）＝﹣2x2﹣8x+2＝﹣2（x+2）2+10，当x＝﹣2时，d取最大值，此时，M（﹣2，0），∴AM＝﹣2﹣（﹣3）＝1，设直线AC的解析式为y＝kx+b，则，解得，∴设直线AC的解析式为y＝x+3，将x＝﹣2代入y＝x+3，得y＝1，∴E（﹣2，1），∴EM＝1，∴；（Ⅲ）由（Ⅱ）知，当矩形PMNQ的周长最大时，x＝﹣2，此时点Q（0，3），与点C重合，∴OQ＝3，∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，∴D（﹣1，4），如图，过D作DK⊥y轴于K，则DK ＝1，OK ＝4，∴QK ＝OK ﹣OQ ＝4﹣3＝1，∴△DKQ 是等腰直角三角形，∴DQ ＝DK ＝， ∴，设F （m ，﹣m 2﹣2m +3），则G （m ，m +3），FG ＝m +3﹣（﹣m 2﹣2m +3）＝m 2+3m ，∴m 2+3m ＝4，解得m 1＝﹣4，m 2＝1，当m ＝﹣4时，﹣m 2﹣2m +3＝﹣5，当m ＝1时，﹣m 2﹣2m +3＝0，∴点F （﹣4，﹣5）或（1，0）．3．解：（1）针对于二次函数y ＝x 2﹣2mx ﹣m 2+4m ﹣2，令y ＝0，则x 2﹣2mx ﹣m 2+4m ﹣2＝0，∴△＝（﹣2m ）2﹣4×1×（﹣m 2+4m ﹣2）＝4m 2+4m 2﹣16m +8＝8（m ﹣1）2≥0， ∴抛物线与x 轴必有交点，即当m ＝1时，有一个交点，当m ≠1时，有两个交点；（2）当m ＝1时，抛物线的解析式为y ＝x 2﹣2x +1＝（x ﹣1）2①，∴C （0，1），D （1，0），∵△PCD 是以PD 为腰的等腰三角形，如图1，①当PC ＝PD 时，点P 是CD 的垂直平分线上，∵C （0，1），D （1，0），∴OC ＝OD ＝1，∴CD 的垂直平分线的解析式为y ＝x ②，联立①②解得，或，∴点P 的坐标为（，）或（，），②当PD ＝CD 时，点D 是CP 的垂直平分线上，∴点P 的纵坐标为1，则x 2﹣2x +1＝1，∴x ＝0或x ＝2，∴P （2，1），即满足条件的点P 的坐标为（，）或（，）或（2，1）；（3）∵二次函数y ＝x 2﹣2mx ﹣m 2+4m ﹣2的对称轴为l ，∴抛物线的对称轴l 为x ＝m ，∴点M 的横坐标为m ，∵点M 在直线y ＝mx 上，∴M （m ，m 2），∵MO ＝MB ，∴点B （2m ，m 2），将点B （2m ，m 2）代入二次函数y ＝x 2﹣2mx ﹣m 2+4m ﹣2得，m 2＝4m 2﹣4m 2﹣m 2+4m ﹣2， ∴m ＝1或m ＝，∵m ＞1，∴m ＝，∴抛物线的解析式为y ＝x 2﹣x +＝（x ﹣）2﹣， ∵点Q （x 0，y 0）在抛物线上，∴y 0＝（x 0﹣）2﹣，∴﹣my 02﹣6my 0＝﹣m （y 02+6y 0）＝﹣[（y 0+3）2﹣9]＝﹣[（x 0﹣）2﹣+3]2+12＝﹣[（x﹣）2+]2+12，∵h+12≤﹣my02﹣6my，∴h≤﹣[（x﹣）2+]2，当x0＝时，h最大＝﹣．4．解：解：（1）∵点P（2，﹣3）在抛物线L：y＝ax2﹣2ax+a+k（a，k均为常数且a≠0）上，∴﹣3＝4a﹣4a+a+k，∴k＝﹣3﹣a；抛物线L的对称轴为直线x＝﹣＝1，即x＝1；（2）∵L经过点（3，3），∴9a﹣6a+a+k＝3，∵k＝﹣3﹣a，∴a＝2，k＝﹣5∴L的表达式为y＝2x2﹣4x﹣3；∵y＝2（x﹣1）2﹣5，∴顶点坐标为（1，﹣5）；（3）顶点坐标（1，﹣a﹣3），∵在点C，P之间的部分与线段CP所围成的区域内（不含边界）恰有5个整点，∴2＜﹣a﹣3≤3，∴﹣6≤a＜﹣5；（4）当a＞0时，t≥3或t+1≤﹣1，∴t≥3或t≤﹣2；观察图象，此时有不符合条件的点使y1≥y2，故此情况舍去；当a＜0时，t+1≤3且t≥﹣1，∴﹣1≤t≤2；综上所述，﹣1≤t≤2；5．解：（1）在y＝﹣x﹣3中，令x＝0，得y＝﹣3；令y＝0，得x＝﹣3．∴B（﹣3，0），C（0，﹣3）．设抛物线的函数解析式为y＝a（x+3）（x﹣1）．将点C（0，﹣3）代入，得a＝1．∴抛物线的函数解析式为y＝x2+2x﹣3；（2）①如图1，过点P作PE⊥x轴于点E，交BC于点F．设点P的坐标为（t，t2+2t﹣3），则点F的坐标为（t，﹣t﹣3）．∴PF＝﹣t﹣3﹣（t2+2t﹣3）＝﹣t2﹣3t．∴S 四边形ABPC ＝S △BPC +S △ABC ＝PF •OB +AB •OC ＝（﹣t 2﹣3t ）+6＝． ∵＜0，∴当t ＝时，S 四边形ABPC 取得最大值．∴此时点P 的坐标为；②如图2，在y 轴上取一点Q （0，），作直线AQ ，过点G 作GT ⊥AQ 于T ，连接PG在Rt △AOQ 中，AQ ＝＝＝， ∴sin ∠OAQ ＝＝， ∴GT ＝AG •， ∴PG +AG ＝PG +GT ，根据垂线段最短，可知当P ，G ，T 共线，且PT ⊥AQ 时，PG +AG 的值最小， ∵直线AQ 的解析式为y ＝﹣x +，又∵PT ⊥AQ ，∴直线PT 的解析式为y ＝2x ﹣，∴G （，0）．（3）DM +DN 是定值．如图3，过点Q 作QH ⊥x 轴于点H ．∵ND⊥x轴，∴QH∥ND．∴△BQH∽△BND，△AMD∽△AQH．∴，．设点Q的坐标为（k，k2+2k﹣3），则HQ＝﹣k2﹣2k+3，BH＝3+k，AH＝1﹣k．∵D是抛物线的对称轴与x轴的交点，∴AD＝BD＝2．∴，．∴DN＝2﹣2k，DM＝2k+6．∴DM+DN＝2k+6+2﹣2k＝8．∴DM+DN是定值，该定值为8．6．解：（1）当a＝﹣时，令y＝﹣x2﹣3×（﹣）x+4＝0，解得：x＝5或﹣2，故点A、B的坐标分别为（5，0）、（﹣2，0）；（2）函数的对称轴为x＝，∵DE＝4，m＝2，故点D（，2），将点D的坐标代入y＝ax2﹣3ax+4并解得：a＝﹣，故抛物线的表达式为：y＝﹣x2+x+4；（3）当a＝﹣1时，y＝﹣x2+3x+4，令y＝0，则x＝﹣6或4，当x＝﹣6时，y＝﹣x2+3x+4＝﹣50，函数的对称轴为x＝，则顶点坐标为（，），当﹣6≤x＜4时，﹣50≤y≤，故m的取值范围为：﹣50≤m≤，故答案为：﹣50≤m≤．7．解：（1）抛物线与y轴交于点C，顶点的横坐标为，则，解得，故抛物线的抛物线为：y＝x2﹣x+4；（2）对于y＝x2﹣x+4，令y＝0，则x＝1或6，故点B、A的坐标分别为（1，0）、（6，0）；如图，过点P作PH∥y轴交AC于点H，由点A、C的坐标得，直线AC的表达式为：y＝﹣x+4①，设点P（x，x2﹣x+4），则点H（x，﹣x+4），△APC的面积S＝S△PHA +S△PHC＝×PH×OA＝×6×（﹣x+4﹣x2+x﹣4）＝﹣2x2+12（1＜x＜6），当x＝1时，S＝10，当x＝6时，S＝0，故使△APC的面积为整数的P点的个数为9个；（3）当四边形OPAQ是正方形时，点P只能在x轴的下方，此时OAP为等腰直角三角形，设点P（x，y），则x+y＝0，即y＝x2﹣x+4＝﹣x，解得：x＝或4，故点P的坐标为（，﹣）或（4，﹣4）；（4）设点P（m，m2﹣m+4），为点A（6，0），设直线AP的表达式为：y＝kx+t，同理可得，直线AP的表达式为：y＝（m﹣1）（x﹣6），∵AP∥OQ，则AP和OQ表达式中的k值相同，故直线OQ的表达式为：y＝（m﹣1）x②，联立①②并解得：x＝，则点Q（，4﹣），∵四边形OPAQ是平行四边形，则AO的中点即为PQ的中点，则m+＝6，解得：m＝3，则＝3，故Q的横坐标的值为3．8．解：（1）∵抛物线与x轴交于A（﹣1，0），B（3，0）两点，∴设此抛物线的解析式为y＝a（x+1）（x﹣3），将点C（0，3）代入，得a＝﹣1，∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3；（2）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴顶点D（1，4），设直线DB解析式为y＝kx+b，将D（1，4），B（3，0）代入得，解得：，∴直线DB解析式为y＝﹣2x+6，①如图1，当点P在点B左侧时，∵∠PCB＝∠CBD，∴CP∥BD，设直线CP解析式为y＝﹣2x+m，将C（0，3）代入，得m＝3，∴直线CP解析式y＝﹣2x+3，当y＝0时，x＝，∴P（，0）；②如图2，当点P在点B右侧时，作点P关于直线BC的对称点N，延长CN交x轴于点P'，此时∠P'CB＝∠CBD，∵C（0，3），B（3，0），∴OC＝OB，∴△OBC为等腰直角三角形，∴∠CPB＝45°，∴∠NBC＝45°，∴△PBN为等腰直角三角形，∴NB＝PB＝3﹣＝，∴N（3，）；设直线CN的解析式为：y＝nx+t，将C（0，3），N（3，）代入直线CN解析式y＝nx+t得，解得，∴直线CN解析式为y＝﹣x+3，当y＝0时，x＝6，∴P'（6，0），综上所述，点P坐标为（，0）或（6，0）．（3）①如图3，当四边形APQC为平行四边形时，∴CQ∥AP，CQ＝AP，∵y C＝3，∴y Q＝3，令﹣x2+2x+3＝3，解得：x1＝0，x2＝2，∴Q（2，3），②如图4，当四边形AQPC为平行四边形时，AC∥PQ，AC＝PQ，∴y C﹣y A＝y P﹣y Q＝3，∵y P＝0，∴y Q＝﹣3，令﹣x2+2x+3＝﹣3，解得，x1＝1+，x2＝1﹣，∴Q1（1+，﹣3），Q2（1﹣，﹣3），综上所述，点Q的坐标为Q（2，3）或（1+，﹣3）或（1﹣，﹣3）．（4）∵点M到点B的距离为1个单位，∴点M在以点B为圆心，半径为1的圆上运动，如图5，在x轴上作点E（，0），连接BM、EM、DE，∴BE＝OB﹣OE＝3﹣＝，∵BM＝1，∴，∵∠MBE＝∠OBM，∴△MBE∽△OBM，∴，∴ME＝OM，∴DM+OM＝DM+ME，∴当点D、M、E在同一直线上时，DM+OM＝DM+ME＝DE最短，∵D（1，4），∴DE＝＝，∴DM+OM的最小值为．9．解：（1）∵抛物线过点A（1，﹣1），B（3，﹣1），∴抛物线的对称轴为直线x＝2，∴抛物线与x轴的另一个交点坐标为（4，0），设抛物线的解析式为y＝ax（x﹣4），把A（1，﹣1）代入得a•1•（﹣3）＝﹣1，解得a＝，∴抛物线的解析式为y＝x（x﹣4），即y＝x2﹣x；∵y＝（x﹣2）2﹣，∴顶点M的坐标为（2，﹣）；（2）作QN⊥x轴于N，AH⊥x轴于H，如图1，∵A（﹣1，1），∴OH＝AH＝1，∴△AOH为等腰直角三角形，∴△ONQ为等腰直角三角形，∴QN＝ON＝NP＝OP＝，∴P（3t，0），Q（t，﹣t）；（3）存在．△OPQ 绕P 点逆时针旋转90°得到△O ′PQ ′，如图2，作Q ′K ⊥x 轴于K ，∠QPQ ′＝90°，PO ′⊥x 轴，PO ′＝PO ＝3t ，PQ ′＝PQ ＝t ，则O ′（3t ，﹣3t ）；∵∠KPQ ′＝90°﹣∠OPQ ＝45°，∵△PQ ′K 为等腰三角形，∴PK ＝Q ′k ＝t ，∴Q ′（t ，﹣t ），当O ′（3t ，﹣3t ）落在抛物线上时，﹣3t ＝•9t 2﹣•3t ，解得t 1＝0，t 2＝；当Q ′（t ，﹣t ）落在抛物线上时，﹣t ＝•t 2﹣•t ，解得t 1＝0，t 2＝；综上所述，当t 为或时，使得△OPQ 的顶点O 或Q 落在抛物线上；（4）当0＜t ≤时，如图1，S ＝•3t •t ＝t 2；当＜t ≤1时，如图3，PQ 交AB 于E 点，S ＝S △POQ ﹣S △AEQ ＝•t •3t ﹣•（t ﹣1）•2（t ﹣1）＝3t ﹣1；当1＜t ＜，如图4，PQ 交AB 于E 点，交BC 于F 点，∵△POQ 为等腰直角三角形，∴∠CPF ＝45°，∴△PCF 为等腰直角三角形，∴PC ＝CF ＝3t ﹣3，∴BF ＝1﹣（3t ﹣3）＝4﹣3t ，∴S △BEF ＝（4﹣3t ）2＝t 2﹣12t +8，∴S ＝S 梯形OABC ﹣S △BEF ＝•（2+3）•1﹣（t 2﹣12t +8，）＝﹣t 2+12t ﹣．10．解：（1）∵抛物线y ＝ax 2+bx +4的顶点坐标为（3，）， ∴y ＝a （x ﹣3）2+＝ax 2﹣6ax +9a +， ∴9a +＝4， ∴a ＝﹣，∴抛物线解析式为y ＝﹣x 2+x +4；（2）如图1，设C（m，﹣m2+m+4）；∵AD＝AE，AD∥x轴，CD∥y轴，∴AD＝AE＝m，∵OA＝4，∴OE＝m﹣4，∵点E在y轴的负半轴上，∴E（0，4﹣m），设CE的解析式为：y＝kx+b，则，解得，∴CE的解析式为：y＝（﹣）x+4﹣m，解法一：∴﹣x2+x+4＝（﹣）x+4﹣m，∴﹣x2+（m﹣1）x+m＝0，x2+（4﹣m）x﹣4m＝0，（x+4）（x﹣m）＝0，x 1＝﹣4，x2＝m，∴定点F（﹣4，﹣6）；解法二：CE的解析式为：y＝（﹣）x+4﹣m＝（﹣x﹣1）m+x+4，由画图可知：F是直线CE上的定点，∴﹣x﹣1＝0，∴x＝﹣4，∴定点F（﹣4，﹣6）；②如图2，过E作EH⊥CD于H，交DG于Q，连接OQ，由①知：OE＝m﹣4，∵∠DAE＝∠ADH＝∠EHD＝90°，AD＝AE，∴四边形AEHD是正方形，∴∠EDH＝45°，AD＝AE＝DH＝EH，∵∠ODE＝∠CDG，∴∠ODE+∠EDQ＝∠EDQ+∠CDG＝45°，即∠ODQ＝45°，∴∠ADO+∠CDG＝45°，在OA的延长线上取AP＝QH，连接PD，∵∠PAD＝∠QHD＝90°，AD＝DH，∴△PAD≌△QHD（SAS），∴PD＝DQ，∠ADP＝∠CDG，AP＝QH，∴∠ADP+∠ADO＝45°＝∠ODQ，∵OD＝OD，∴△PDO≌△QDO（SAS），∴OP＝OQ，∵EH＝DH，∠EHC＝∠DHQ，∠GEH＝∠CDG，∴△EHC≌△DHQ（ASA），∴CH＝QH＝﹣（m﹣4）＝＝AP，∴OQ＝OP＝4+，∵OE＝m﹣4，EQ＝EH﹣QH＝m﹣（）＝﹣m，在Rt△OEQ中，由勾股定理得：OE2+EQ2＝OQ2，∴（m﹣4）2+（﹣）2＝（4+）2，m3﹣10m2﹣24m＝0，解得：m1＝0（舍），m2＝12，m3＝﹣2（舍），∴D（12，4），Q（6，﹣8），设直线DG的解析式为：y＝kx+b，则，解得，∴直线DG的函数表达式为：y＝2x﹣20．。

中考数学压轴题动点

中考专题动点问题详细分层解析(一)所谓“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题•关键：动中求静•专题一：建立动点问题的函数解析式函数揭示了运动变化过程中量与量之间的变化规律，是初中数学的重要内容•动点问题反映的是一种函数思想，由于某一个点或某图形的有条件地运动变化，引起未知量与已知量间的一种变化关系，这种变化关系就是动点问题中的函数关系•那么，我们怎样建立这种函数解析式呢？下面结合中考试题举例分析•一、应用勾股定理建立函数解析式例1如图1,在半径为6,圆心角为90°的扇形OABI勺弧AB上，有一个动点P,PH丄0A, 垂足为H,△ OPH的重心为G.(1) 当点P在弧AB上运动时,线段GO GP GH中,有无长度保持不变的线段？如果有,请指出这样的线段，并求出相应的长度•⑵设PH x,GP y,求y关于x的函数解析式，并写出函数的定义域(即自变量x的取值范围)•(3)如果△ PGH是等腰三角形，试求出线段PH的长•解：(1)当点P在弧AB上运动时,0P保持不变,于是线段GOGP、GH中，有长度保持不变的线段，这条线段是2 2 1GH壬NH= 0P=2.图13 3 2(3) △ PGH是等腰三角形有三种可能情况：①GP=PH^, 1 36 3x2x,解得x ,6 •经检验,x .6是原方程的根,且符合题意•3②GP=GHtf, 1 - 36 3x22,解得x 0.经检验,x 0是原方程的根，但不符合题意•3③PH=G W, x 2.综上所述，如果△ PGH是等腰三角形,那么线段PH的长为..6或2.、应用比例式建立函数解析式例2如图2,在厶ABC中,AB=AC=1点D,E在直线BC上运动•设BD=x,CE=y •(1) 如果/ BAC=30 , / DAE=105 ,试确定y与x之间的函数解析式;(2) 如果/ BAC的度数为，/ DAE的度数为，当，满足怎样的关系式时,(1)中y与x之间的函数解析式还成立？试说明理由•71 此时,△A0C 勺面积y =4 --综上所述,当O O 与O A 相切时,△ AOC 勺面积为例 3(2005 年•上海)如图 3(1),在厶 ABC 中, Z ABC=90 ,AB=4,BC=3.点O是边AC 上的一个动点，以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E. 作EP 丄ED,交射线AB 于点P,交射线CB 于点F.(1)求证：△ AD 0A AEP. B O H⑵设OA=x ,AP=y,求y 关于x 的函数解析式,并写出它的定义域.图8(3)当BF=1时，求线段AP 的长.、应用求图形面积的方法建立函数关系式例3如图,在厶ABC 中, / BAC=90 ,AB=AC=2 V2 , O A 的半径为 1.若点0在BC 边上运动(与点B C 不重合),设BO=x , △ AOC 的面积为y.(1)求y 关于x 的函数解析式，并写出函数的定义域.⑵ 以点O 为圆心,BO 长为半径作圆O,求当O O 与O A 相切时,△ AOC 勺面积.解:(1)过点A 作AHIBC,垂足为H.vZ BAC=90 ,AB=AC=2 一 2 , /. BC=4,AH=~ BC=2. 2--OC=4-x . 1 S AOC — OC AH , - - y 2(2)①当O O 与O A 外切时,4). 在 Rt △ AOH 中 ,OA=x 1 ,OH=2 x,二(x 1)2 22 (2 x)2. 解得x 7 17此时,△ AOC 的面积y=4 - 一6 6②当O 0与O A 内切时,在 Rt △ AOH^ ,OA=x 1 ,OH=x 2,二(x 1)2 22 (x 2)2. 解得x17十1 或一. 6 2 AC C 图2 3(1 E 0 ABDE O3(2)中考专题 --- 动点问题（二）所谓“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题•关键：动中求静• 专题二：动态几何型压轴题动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

【中考数学压轴题专题突破02】二次函数中的动点问题

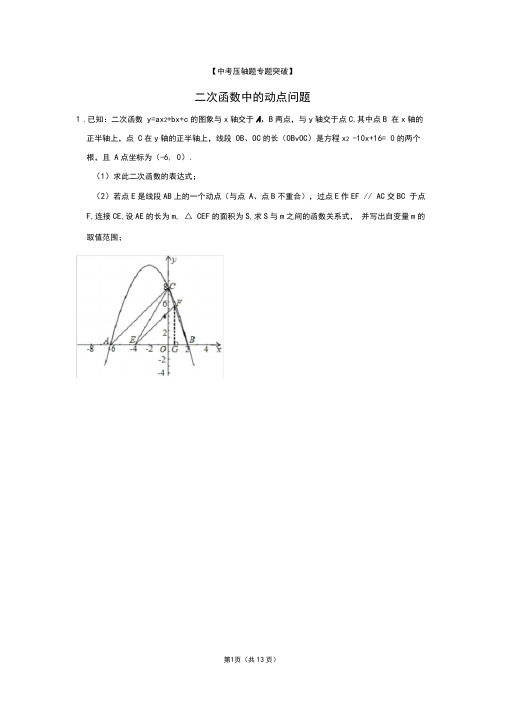
【中考压轴题专题突破】二次函数中的动点问题1.已知：二次函数y=ax2+bx+c的图象与x轴交于A、B两点，与y轴交于点C,其中点B 在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OBvOC）是方程x2 -10x+16= 0的两个根，且A点坐标为（-6, 0）.（1）求此二次函数的表达式；（2）若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF // AC交BC 于点F,连接CE,设AE的长为m, △ CEF的面积为S,求S与m之间的函数关系式，并写出自变量m的取值范围；2.如图是二次函数y= ( x+m) 2+k的图象，其顶点坐标为M (1, -4).(1)求出图象与x轴的交点A, B的坐标；(2)在二次函数的图象上是否存在点P,使S APAB=—S；AMAB?若存在，求出P点的坐标，4若不存在，请说明理由；(3)点C在x轴上一动点，以BC为边作正方形BCDE ,正方形BCDE还有一个顶点(除点B外)在抛物线上，请写出满足条件的点E的坐标；(4)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b与此图象至少有三个公共点时，请直接写出b的取值范围是 .即圄2 邺3.如图，二次函数图象的顶点为坐标系原点O,且经过点A (3, 3), 一次函数的图象经过点A和点B (6, 0).(1)求二次函数与一次函数的解析式；(2)如果一次函数图象与y轴相交于点C,点D在线段AC上，与y轴平行的直线DE 与二次函数图象相交于点巳/ CDO = / OED ,求点D的坐标；(3)当点D在直线AC上的一个动点时，以点O、C、D、E为顶点的四边形能成为平行四边形吗？请说明理由.4.如图，二次函数y=ax2+bx+c (a^0)的图象与x轴交于A (- 3, 0)、B (1, 0 与y轴相交点C (0,近).(1)求该二次函数解析式；(2)连接AC、BC,点M、N分别是线段AB、BC上的动点，且始终满足BM = 接MN.①将4BMN沿MN翻折，B点能恰好落在AC边上的P处吗？若能，请判断四边形的形状并求出PN的长；若不能，请说明理由.②将^ BMN沿MN翻折，B点能恰好落在此抛物线上吗？若能，请直接写出此时于MN的对称点Q的坐标；若不能，请说明理由.两点,BN,连BMPNB点关5.如图，在平面直角坐标系中，抛物线y=』!x2-2F3x-代与x轴交于A、B两点（点3 3（1）判断△ ABC的形状，并说明理由;（2）如图（1）,点P为直线BC下方的二次函数图象上的一个动点（点P与B、C不重合），过点p作Y轴的平行线交X轴于点E.当△ PBC面积的最大值时，点F为线段BC 一点（不与点BC重合），连接EF,动点G从点E出发，沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒2工3个单位的速度运动到点C后停止，当点F的坐标| 3是多少时，点G在整个运动过程中用时最少？（3）如图2,将4ACO沿射线CB方向以每秒个单位的速度平移，记平移后的△ ACO 为AA l C l O l连接AA1,直线AA1交抛物线与点M,设平移的时间为t秒，当^ AMC 1为等腰三角形时，求t的值.6.如图，二次函数y=—x2+bx- -的图象与x轴交于点A (-3, 0)和点B,以AB为边在2 2x轴上方作正方形ABCD ,点P是x轴上一动点，连接DP ,过点P作DP的垂线与y轴交于点E.(1)b=;点D的坐标：;(2)线段AO上是否存在点P (点P不与A、。

2020年广东中考数学压轴题：动点

2020年广东省中考数学压轴题：动点问题如图1，抛物线经过点A (4，0)、B （1，0)、C （0，－2）三点．（1）求此抛物线的解析式；（2）P 是抛物线上的一个动点，过P 作PM ⊥x 轴，垂足为M ，是否存在点P ，使得以A 、P 、M 为顶点的三角形与△OAC 相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；（3）在直线AC 上方的抛物线是有一点D ，使得△DCA 的面积最大，求出点D 的坐标．,图1 满分解答（1）因为抛物线与x 轴交于A (4，0)、B （1，0)两点，设抛物线的解析式为)4)(1(--=x x a y ，代入点C 的坐标（0，－2），解得21-=a ．所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y ．（2）设点P 的坐标为))4)(1(21,(---x x x ． ①如图2，当点P 在x 轴上方时，1＜x ＜4，)4)(1(21---=x x PM ，x AM -=4．如果2==CO AO PM AM ，那么24)4)(1(21=----xx x ．解得5=x 不合题意．如果21==CO AO PM AM ，那么214)4)(1(21=----x x x ．解得2=x ．此时点P 的坐标为（2，1）．②如图3，当点P 在点A 的右侧时，x ＞4，)4)(1(21--=x x PM ，4-=x AM ．解方程24)4)(1(21=---x x x ，得5=x ．此时点P 的坐标为)2,5(-．解方程214)4)(1(21=---x x x ，得2=x 不合题意．③如图4，当点P 在点B 的左侧时，x ＜1，)4)(1(21--=x x PM ，x AM -=4．解方程24)4)(1(21=---xx x ，得3-=x ．此时点P 的坐标为)14,3(--．解方程214)4)(1(21=---x x x ，得0=x ．此时点P 与点O 重合，不合题意．综上所述，符合条件的点P 的坐标为（2，1）或)14,3(--或)2,5(-．图2 图3 图4（3）如图5，过点D 作x 轴的垂线交AC 于E ．直线AC 的解析式为221-=x y ．设点D 的横坐标为m )41(<<m ，那么点D 的坐标为)22521,(2-+-m m m ，点E 的坐标为)221,(-m m ．所以)221()22521(2---+-=m m m DE m m 2212+-=．因此4)221(212⨯+-=∆m m S DAC m m 42+-=4)2(2+--=m ．当2=m 时，△DCA 的面积最大，此时点D 的坐标为（2，1）．图5 图6。

2020中考数学压轴题之动点之等腰三角形

动点之等腰三角形编者语：动态几何形成的存在性问题是动态几何中的基本类型，包括等腰（边）三角形存在问题；直角三角形存在问题；平行四边形存在问题；矩形、菱形、正方形存在问题；梯形存在问题（不考）；全等三角形存在问题；相似三角形存在问题；其它存在问题等在中考压轴题中，线动形成的等腰三角形存在性问题的重点和难点在于应用分类思想和数形结合的思想准确地进行分类。

※解决方法：解直角三角形，相似辅助的做法：✍作等腰三角形的高✍向其余边作垂线构成全等。

1.勾股定理。

（辅助线✍）2.锐角三角函数。

（辅助线✍）3.两个角的相似比较常见。

（辅助线✍）典型例题：1.如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．（1）当x= ▲s时，DE⊥AB；（2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；（3）当△BEF为等腰三角形时，求x的值．2.如图，抛物线2323y x x 63-=与x 轴交于点A ，将线段OA 绕点O 逆时针旋转1200至OB 的位置. （1）证明：点B 在抛物线上;（2）在此抛物线的对称轴上，是否存在点P ，使得以点P 、O 、B 为顶点的三角形是等腰三角形？若存在，求点P 的坐标；若不存在，说明理由．典型例题答案：1.解：（1）232 （2分）（2 ）（3）2.解：（2）等腰三角形练习题2.如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P（0,m）是线段OC上一动点（C点除外）,直线PM交AB的延长线于点D.⑴求点D的坐标（用含m的代数式表示）⑵当△APD是等腰三角形时,求m的值。

2023中考数学-压轴专题训练之动点问题(含答案)

中考数学压轴专题训练之动点问题1. 如图1，在平面直角坐标系中，四边形OABC 各顶点的坐标分别为O (0，0)，A (3，33)，B (9，53)，C (14，0)．动点P 与Q 同时从O 点出发，运动时间为t 秒，点P 沿OC 方向以1单位长度/秒的速度向点C 运动，点Q 沿折线OA －AB －BC 运动，在OA ，AB ，BC 上运动的速度分别为3，3，52(单位长度/秒)．当P ，Q 中的一点到达C 点时，两点同时停止运动． (1)求AB 所在直线的函数表达式．(2)如图2，当点Q 在AB 上运动时，求△CPQ 的面积S 关于t 的函数表达式及S 的最大值．(3)在P ，Q 的运动过程中，若线段PQ 的垂直平分线经过四边形OABC 的顶点，求相应的t 值．图1 图21. 【答案】【思维教练】(1)设一次函数解析式，将已知点A 、B 的坐标值代入求解即可；(2)S△CPQ＝12·CP ·Q y ，CP ＝14－t ，点Q 在AB 上，Q y 即为当x ＝t 时的y 值，代入化简得出S 与t 的函数关系式，化为顶点式得出最值；(3)垂直平分线过顶点需以时间为临界点分情况讨论，当Q 在OA 上时，过点C ；当Q 在AB 上时，过点A ；当Q 在BC 上时，过点C 和点B ，再列方程并求解．解图1解：(1)把A(3，33)，B(9，53)代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧3k ＋b ＝33，9k ＋b ＝53，解得⎩⎨⎧k ＝33，b ＝23，∴y＝33x＋23；(3分)(2)在△PQC中，PC＝14－t，∵OA＝32＋（33）2＝6且Q在OA上速度为3单位长度/s，AB＝62＋（23）2＝43且Q点在AB上的速度为3单位长度/s，∴Q在OA上时的横坐标为t，Q在AB上时的横坐标为32 t，PC边上的高线长为33t＋2 3.(6分)所以S＝12(14－t)(32t＋23)＝－34t2＋532t＋143(2≤t≤6)．当t＝5时，S有最大值为8134.(7分)解图2(3)①当0＜t≤2时，线段PQ的中垂线经过点C(如解图1)．可得方程(332t)2＋(14－32t)2＝(14－t)2.解得t1＝74，t2＝0(舍去)，此时t＝74.(8分)解图3②当2＜t≤6时，线段PQ的中垂线经过点A(如解图2)．可得方程(33)2＋(t－3)2＝[3(t－2)]2.解得t1＝3＋572，∵t2＝3－572(舍去)，此时t＝3＋572.③当6＜t≤10时，(1)线段PQ的中垂线经过点C(如解图3)．可得方程14－t＝25－52t，解得t＝223.(10分)解图4(2)线段PQ的中垂线经过点B(如解图4)．可得方程(53)2＋(t－9)2＝[52(t－6)]2.解得t1＝38＋2027，t2＝38－2027(舍去)．此时t＝38＋2027.(11分)综上所述，t的值为74，3＋572，223，38＋2027.(12分)【难点突破】解决本题的关键点在于对PQ的垂直平分线过四边形顶点的情况进行分类讨论，在不同阶段列方程求解．2. 如图，抛物线y=-x2+bx+c与x轴交于A，B两点(A在B的左侧)，与y轴交于点N，过A点的直线l:y=kx+n与y轴交于点C，与抛物线y=-x2+bx+c的另一个交点为D，已知A(-1，0)，D(5，-6)，P点为抛物线y=-x2+bx+c上一动点(不与A，D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值;(3)设M为直线l上的点，探究是否存在点M，使得以点N，C，M，P为顶点的四边形为平行四边形.若存在，求出点M的坐标;若不存在，请说明理由.2. 【答案】[分析] (1)将点A，D的坐标分别代入直线表达式、抛物线的表达式，即可求解;(2)设出P点坐标，用参数表示PE，PF的长，利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况，分别求解即可.解:(1)将点A，D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A，D的坐标代入抛物线表达式，得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1，∴C(0，-1)，则直线l与x轴的夹角为45°，即∠OAC=45°，∵PE∥x轴，∴∠PEF=∠OAC=45°.又∵PF∥y轴，∴∠EPF=90°，∴∠EFP=45°.则PE=PF.设点P坐标为(x，-x2+3x+4)，则点F(x，-x-1)，∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18，∵-2<0，∴当x=2时，PE+PF有最大值，其最大值为18.(3)由题意知N(0，4)，C(0，-1)，∴NC=5，①当NC是平行四边形的一条边时，有NC∥PM，NC=PM.设点P坐标为(x，-x2+3x+4)，则点M的坐标为(x，-x-1)，∴|y M-y P|=5，即|-x2+3x+4+x+1|=5，解得x=2±或x=0或x=4(舍去x=0)，则点M坐标为(2+，-3-)或(2-，-3+)或(4，-5);②当NC是平行四边形的对角线时，线段NC与PM互相平分.由题意，NC的中点坐标为0，，设点P坐标为(m，-m2+3m+4)，则点M(n'，-n'-1)，∴0==，解得:n'=0或-4(舍去n'=0)，故点M(-4，3).综上所述，存在点M，使得以N，C，M，P为顶点的四边形为平行四边形，点M 的坐标分别为:(2+，-3-)，(2-，-3+)，(4，-5)，(-4，3).3. 如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c经过A(－2, －4 )、O(0, 0)、B(2, 0)三点．（1）求抛物线y＝ax2＋bx＋c的解析式；（2）若点M 是该抛物线对称轴上的一点，求AM ＋OM 的最小值．3. 【答案】（1）212y x x =-+。

2020年广东省中考数学压轴题：动点

2020年广东省中考数学压轴题：动点问题例：如图1，已知抛物线211(1)444b y x b x =-++（b 是实数且b ＞2）与x 轴的正半轴分别交于点A 、B （点A 位于点B 是左侧），与y 轴的正半轴交于点C ．（1）点B 的坐标为______，点C 的坐标为__________（用含b 的代数式表示）；（2）请你探索在第一象限内是否存在点P ，使得四边形PCOB 的面积等于2b ，且△PBC 是以点P 为直角顶点的等腰直角三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）请你进一步探索在第一象限内是否存在点Q ，使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q 的坐标；如果不存在，请说明理由．图1满分解答（1）B 的坐标为(b , 0)，点C 的坐标为(0,4b )．（2）如图2，过点P 作PD ⊥x 轴，PE ⊥y 轴，垂足分别为D 、E ，那么△PDB ≌△PEC ．因此PD ＝PE ．设点P 的坐标为(x, x)．如图3，联结OP ．所以S 四边形PCOB ＝S △PCO ＋S △PBO ＝1152428b x b x bx ⨯⋅+⨯⋅=＝2b ．解得165x =．所以点P 的坐标为(1616,55)．图2 图3（3）由2111(1)(1)()4444b y x b x x x b =-++=--，得A (1, 0)，OA ＝1． ①如图4，以OA 、OC 为邻边构造矩形OAQC ，那么△OQC ≌△QOA ．当BA QA QA OA=，即2QA BA OA =⋅时，△BQA ∽△QOA ．所以2()14b b =-．解得8b =±Q 为(1,2．②如图5，以OC为直径的圆与直线x＝1交于点Q，那么∠OQC＝90°。

因此△OCQ∽△QOA．当BA QAQA OA=时，△BQA∽△QOA．此时∠OQB＝90°．所以C、Q、B三点共线．因此BO QACO OA=，即14b QAb=．解得4QA=．此时Q(1,4)．图4 图5。

中考数学压轴题(动点).doc

中考数学压轴题总结（动点）（一）因动点产生的相似三角形问题例1,已知抛物线的方程Cl： y =-丄（X+2）（X-/H）伽＞0）与X轴交于点B、C,与y m 轴交于点£,且点B在点C的左侧.（1）若抛物线C1过点M（2,2）,求实数加的值；（2）在（1）的条件下，求△BCE的面积；（3）在（1）的条件下，在抛物线的对称轴上找一点H,使得BH+EH最小，求出点H 的坐标；（4）在第四象限内，抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与ABCE相似？若存在，求加的值；若不存在，请说明理由.思路点拨1.第（3）题是典型的“牛喝水”问题，当H落在线段EC上时，BH+EH最小.2.第（4）题的解题策略是：先分两种情况画直线BF,作ZCBF=ZEBC=45° ,或者作BFHEC.再用含加的式子表示点F的坐标.然后根据夹角相等，两边对应成比例列关于m的方程.满分解答（1）将M（2, 2）代入y = 一~ （兀+2）（兀-加）,得2 = -■ x4（2-/w）.解得加=4.m tn（2）当加=4 时,y =—丄（兀+2）（兀一4） = --x2+-兀+ 2・所以C（4,0）,E（0,2）・4 4 2所以S HBCE=—BC-OE = — x6x2 = 6*2 2（3）如图2,抛物线的对称轴是直线兀=1,当H落在线段EC上时，BH+EH最小. 设对称轴与兀轴的交点为P，那么竺=竺.CP CO因此HL = l.解得HP 丄所以点H的坐标为（1,丄）・3 4 2 2（4）®如图3,过点B作EC的平行线交抛物线于F,过点F作FF丄x轴于F.由于ZBCE=ZFBC,所以当£色=竺，即BC2=CE BF吋，/XBCEs'FBC.CB BF设点F 的坐标为(兀,-丄(x + 2)(x -〃?)) m解得x=m+2.所以F (加+2,0).由 BC —CE BF,得（加 + 2严=+ 4%（加+ 勺+ 4 m②如图4,作ZCBF=45°交抛物线于F,过点F 作FF 丄x 轴于F, 由于ZEBC=ZCBF,所以匹=—,即 BC 2= BE BF 时，HBCEs^BFC. BC BF在 RtABFF 中,由 FF=BF,得丄（x + 2）（x-m ） = x+2 .m解得 x=2m.所以 F （2加,0）・所以 BF'=2加+2, BF = ^2（2m+2）.由 BC2 = BE BF,得(m+2)2=2y/2x^2(2m+2).解得血= 2±2血. 综合①、②，符合题意的加为2 + 2A /2 .例2,抛物线经过点人(4, 0)、B (1, 0)、C (0, -2)三点.(1) 求此抛物线的解析式；(2) P 是抛物线上的一个动点，过P 作PM 丄兀轴，垂足为M,是否存在点P,使得以 A 、P 、M 为顶点的三角形与相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由；(3) 在直线AC 上方的抛物线是有一点D,使得△DC4的面积最大，求出点D 的坐标.由算唱由耳旦 CE BF"2 + 4 V m 2 +4 BF所以= 虽症 m 得思路点拨1. 已知抛物线与兀轴的两个交点，用待定系数法求解析式时，设交点式比较简便.2. 数形结合，用解析式表示图彖上点的坐标，用点的坐标表示线段的长.3. 按照两条直角边对应成比例，分两种情况列方程.4. 把△DCA 可以分割为共底的两个三角形，高的和等于0A.满分解答(1 )因为抛物线与x 轴交于A(4, 0)、B (1, 0)两点，设抛物线的解析式为 y = tz(x-l)(x-4),代入点C 的坐标(0, -2),解得G =-丄.所以抛物线的解析式为1 1 9 5y =——(兀一 1)(兀一 4)=——兀一 +-X-2. 2 2 2(2)设点P 的坐标为(匕一丄(兀_1)(兀_4))・ 2① 如图2,当点P 在兀轴上方时，1＜兀＜4, PM =-!(%-l)(x-4) , AM = 4-x.此时点P 的坐标为(2, 1).② 如图3,当点户在点A 的右侧时，兀〉4, PM =l(x-l)(x-4) , AM =x-4.解方程 ------------- =2,得兀=5.此时点P 的坐标为(5-2).x-4-(x-l)(x-4)解方程 -------------- 得x = 2不合题意.x-4 2解方程 =2,得x = -3.此时点P 的坐标为(一3厂14)・—(x-l)(x-4) |解方程 -------------- =-,得x = 0.此时点P 与点O 重合，不合题意.4-x 2综上所述,符合条件的点P 的坐标为(2, 1)或(-3-14)或(5,—2).那么一"解得心不合题意.PM CO(3)如图5,过点D 作兀轴的垂线交AC 于E.直线AC 的解析式为y = *兀一2.设点£>的横坐标为m (1 < m < 4),那么点D 的坐标为(加，-丄m 2 + —m-2),点E 的 2 211 95 1 1 9 坐标为(•所以 DE =(——m" (— m - 2)=——+ 2m . 2 2 22 2 当m = 2时，△DC4的面积最大，此时点D 的坐标为(2, 1).(二) 因动点产生的等腰三角形问题例3,抛物线y =aj?+bx+c 经过A(—1,0)、B(3,0)、C(0,3)三点,直线/是抛物线的对称轴.(1) 求抛物线的函数关系式；(2) 设点P 是直线/上的一个动点，当△〃C 的周长最小时，求点P 的坐标；(3) 在直线/上是否存在点M,使△MAC 为等腰三角形，若存在，直接写出所有符合条件的点M 的坐标；若不存在，请说明理由・因此S2AC*( 一却+2心—3+4.思路点拨1.第(2)题是典型的“牛喝水”问题，点P在线段BC上吋的周长最小.2.第(3)题分三种情况列方程讨论等腰三角形的存在性.满分解答(1)因为抛物线与x轴交于A(T,0)、3(3,0)两点，设心+1)9—3),代入点C(0,3),得一3a=3.解得a= — {.所以抛物线的函数关系式是y = —(兀+1)(兀一3) = —疋+ 2兀+3.(2)如图2,抛物线的对称轴是直线x=\.当点P落在线段BC上时，PA + PC最小，△必C的周长最小. 设抛物线的对称轴与x轴的交点为H.由BO=CO,得PH=BH=2.BO CO所以点P的坐标为(1,2).图2(3)点M 的坐标为(1,1)、(1,乔)、(1,-亦)或(1,0).考点伸畏第(3)题的解题过程是这样的：设点M的坐标为(1,加)・在△MAC 屮，AC2=10, MC*2=1+伽一3几A/A2=4+w2.①如图3,当MA=MC时，M^=MC2.解方程4+/«2= 1+(/??-3)2,得m=\.此时点M的坐标为(1, 1).②如图4,当AM=AC时，AM—AC2.解方程4+//=10,得m = 土氏・此时点M的坐标为(1,舲)或(1,_衙).③如图5,当CM=CA时，CM2 = CA2.解方程1 +(加一3尸=10,得加=0或6. 当M(l,6)时，M、A、C三点共线，所以此时符合条件的点M的坐标为(1,0).例4,点人在x轴上，04=4,将线段04绕点O顺时针旋转120°至0B的位置.(I )求点B的坐标；(2)求经过A、0、B的抛物线的解析式；(3)在此抛物线的对称轴上，是否存在点P，使得以点P、0、3为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，请说明理rh.图11.用代数法探求等腰三角形分三步：先分类，按腰相等分三种情况；再根据两点间的距离公式列方程；然后解方程并检验.2.本题中等腰三角形的角度特殊，三种情况的点P重合在一起.满分解签(1)如图2,过点B作BC丄y轴，垂足为C.在RtAOBC 中，ZBOC=30° , 0B=4,所以B C=2, OC = 2x/3 .所以点B的坐标为(-2,-2石).(2)因为抛物线与x轴交于0、A(4,0),设抛物线的解析式为y=ox(x—4), 代入点B(_2,—2Q), -2^3 =x(-6).解得a = _週.6所以抛物线的解析式为尸一血班—4) = -¥〒+苹兀.(3)抛物线的对称轴是直线x=2,设点P的坐标为(2,)，).①当0P=0B=4 时，0尸=16.所以4+/=16.解得y = ±2y/3.当P在(2,2>/3)吋，B、0、P三点共线(如图2).②当BP=BO=4 时，B 尸=16.所以42+(y+2>/3)2=16.解得y]=y2=-2y[3 -③当PB=PO 时，PB2=PO2.所以42+(^ + 2>/3)2=22 + /.解得y = -2y/3 ・综合①、②、③，点P的坐标为(2,-2巧)，如图2所示.考盍伸駄如图3,在本题中，设抛物线的顶点为D,那么△DO4与△O4B是两个相似的等腰三角形.由y = 心_4)= -逅(兀-2尸+迹，得抛物线的顶点为D(2,6 6 3因此tan ADO A = - •所以ZDOA = 30° , ZOD4=120° .3(三)因动点产生的直角三角形问题例5：在平面直角坐标系屮，反比例函数与二次函数y=k^+x~\)的图象交于点A(1,Q 和点B(—l, — Q・(1)当k=~2时，求反比例函数的解析式；(2)要使反比例函数与二次函数都是y随x增大而增大，求£应满足的条件以及兀的取值范围；(3)设二次函数的图象的顶点为0当△AB0是以AB为斜边的直角三角形时，求R 的值. 思路点拨1.由点A(1,Q或点B(T, — k)的坐标可以知道，反比例函数的解析式就是y =-.题目x中的比都是一致的.2.由点A(1Q或点的坐标还可以知道，A、B关于原点0对称，以AB为直径的圆的圆心就是0.3.根据直径所对的圆周角是直角，当0落在OO上是，ZBQ是以AB为直径的直角三角形. 满分解答(1)因为反比例函数的图象过点A(1,Q,所以反比例函数的解析式是y = ±.当k=~2吋，反比例函数的解析式是y .X(2)在反比例惭数y =-中，如果y随x增大而增大,X那么k<0.当£V0时，抛物线的开口向下，在对称轴左侧，y随兀增大而增大.抛物线y =饥？ +兀+ 1）=比（兀+丄尸-汶的对称轴是直线2 4丄・图1 2所以当后0且x v -*时，反比例函数与二次函数都是y随兀增大而增大.（3）抛物线的顶点Q的坐标是（一丄，一丄灯，A、B关于原点O中心对称，2 4当OQ=OA = OB时，△ABQ是以AB为直径的直角三角形.由o（22=OA2,得冷y +（一討2才+疋解得k. =-73 （如图2）, =--73 （如图3）.3- 3考盍伸爰如图4,已知经过原点0的两条直线AB与CD分别与双曲线y=- （Q0）交于A、B X和C、D,那么A3与CD互相平分，所以四边形ACBD是平行四边形.问平行四边形ABCD能否成为矩形？能否成为正方形？如图5,当4、C关于直线〉=兀对称时，AB与CD互相平分且相等，四边形ABCD是矩形.因为A、C可以无限接近坐标系但是不能落在坐标轴上，所以0A与0C无法垂直，因此四边形ABCD不能成为正方形.例6,已知抛物线y=x 2+hx+c 与x 轴交于A 、B 两点(点A 在点B 左侧)，与y 轴交于点C(0, -3),对称轴是直线x=l,直线BC 与抛物线的对称轴交于点D.(1) 求抛物线的函数表达式；(2) 求直线BC 的函数表达式； (3) 点E 为y 轴上一动点，CE 的垂直平分线交CE ■于点F,交抛物线于P 、Q 两点, 且点P 在第三彖限.① 当线段PQ = ^AB 时，求tanZCED 的值；② 当以C 、D 、E 为顶点的三角形是直角三角形时，请直接写出点P 的坐标.温馨提示：考生可以根据第(3)问的题意，在图中补岀图形，以便作答.思路点拨1. 第(1)、(2)题用待定系数法求解析式，它们的结果直接影响后续的解题.2. 第(3)题的关键是求点E 的坐标，反复用到数形结合，注意y 轴负半轴上的点的纵坐标的符号与线段长的关系.3. 根据C 、D 的坐标，可以知道直角三角形CDE 是等腰直角三角形，这样写点E 的坐标就简单了.满分解签(1) 设抛物线的函数表达式为y = (X -1)2+/2,代入点C(0, —3),得n = -4.所以抛物线的函数表达式为y = (x-l)2-4 = x 2-2x-3.(2) 由『=X 2-2X -3 = (X +1)(X -3)，知 A(—l, 0), B(3, 0).设直线 BC 的函数表达a 7, . _ n式为y = kx + b.代入点B(3, 0)和点C(0, -3),得J" '解得k = l, b = -3.所以 b = —3.直线BC 的函数表达式为y = x-3 . (3) ①因为43=4,所以PQ = ^AB = 3 -因为P 、Q 关于直线兀=1对称，所以点P 7 5 5FC = OC — OF = 3 ——=-，EC = 2FC = ~-4 4 2进而得到OE = OC — EC = 3—2 =丄，点E 的坐标为(0, —丄•2 2 I 2丿的横坐标为冷于是得到点P 的坐标为冷日点F 的坐标为0,-fj •所以直线BC:y = x-3与抛物线的对称轴x=l的交点D的坐标为(1, 一2).过点D作丄y轴，垂足为H.在RtAED/7 中，DH=1, EH = 0H-0E = 2-丄=。

动点问题(中考数学压轴)

动点问题（中考数学压轴）一、解答题(共1道，每道100分)1.如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上．直线CB的表达式为，点A、D的坐标分别为（－4，0），（0，4）．动点P自A点出发，在AB上匀速运动．动点Q自点B出发，在折线BCD上匀速运动，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P运动t（秒）时，△OPQ 的面积为S（不能构成△OPQ的动点除外）．（1）求出点B、C的坐标；（2）求S随t变化的函数关系式；（3）当t为何值时S有最大值？并求出最大值．答案：解：（1）把y＝4代入，得x＝1.∴C点的坐标为（1，4）.当y＝0时，，∴x＝4.∴点B坐标为（4，0）.（2）作CM⊥AB于M，则CM＝4，BM＝3.∴.∴sin∠ABC＝＝.①0＜t＜4时，作QN⊥OB于N，则QN＝BQ·sin∠ABC＝t.∴S＝OP·QN＝（4－t）×t＝（0＜t＜4）.②当4＜t≤5时，（如备用图1），连接QO，QP，作QN⊥OB于N.同理可得QN＝t.∴S＝OP·QN＝×（t－4）×t.＝（4＜t≤5）.③当5＜t≤6时，（如备用图2），连接QO，QP.S＝×OP×OD＝（t－4）×4＝2t－8（5＜t≤6）.（3）①在0＜t＜4时，当t＝＝2时，S最大＝＝.②4＜t≤5时，对于抛物线S＝，当t＝－＝2时，S最小＝＝－.∴抛物线S＝的顶点为（2，－）.∴在4＜t≤5时，S随t的增大而增大.∴当t＝5时，S最大＝＝2. ③在5＜t≤6时，在S＝2t－8中，∵2＞0，∴S随t的增大而增大. ∴当t＝6时，S最大＝2×6－8＝4. ∴综合三种情况，当t＝6时，S取得最大值，最大值是4. （说明：（3）中的②也可以省略，但需要说明：在（2）中的②与③的△OPQ，③中的底边OP和高CD都大于②中的底边OP和高.所以③中的△OPQ面积一定大于②中的△OPQ的面积.）解题思路：（1）把y=4代入，求得x的值，则可得点C的坐标，把y=0代入，求得x的值，即可得点B的坐标；（2）作CM⊥AB于M，则可求得CM与BM的值，求得∠ABC的正弦值，然后分别从0＜t＜4时，当4＜t≤5时与当5＜t≤6时去分析求解即可求得答案；（3）在（2）的情况下求S的最大值，然后比较即可求得答案. 试题难度：三颗星知识点：中考压轴之动点问题。

(完整word版)苏教版中考数学压轴题动点问题

.本资料本源于?七彩教育网运动变化型问题专题复习【考点导航】运动变化题是指以三角形、四边形、圆等几何图形为载体，设计动向变化，并对变化过程中陪同着的等量关系、变量关系、图形的特别状态、图形间的特别关系等进行观察研究的一类问题，这类试题信息量大，题目灵便多变，有较强的选拔功能，是近来几年来中考数学试题的热点题型之一，常以压轴题的面目出现．解决此类问题需要运用运动和变化的见解，掌握运动和变化的全过程，动中取静，静中求动，抓住变化过程中的特别状况，建立方程、不等式、函数模型．【答题锦囊】例 1 如图在 Rt △中，∠ ＝ 90°，＝ 12，＝ 16，动点P从点A出发沿边向点C以每秒 3 个单位ABC C AC BC AC长的速度运动，动点 Q从点 C出发沿 CB边向点 B 以每秒4个单位长的速度运动． P， Q分别从点 A， C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ关于直线 PQ对称的图形是△ PDQ．设运动时间为 t 〔秒〕．（1〕设四边形PCQD的面积为y，求y与t的函数关系式；（2〕t为何值时，四边形PQBA是梯形？（3〕可否存在时辰t，使得PD∥AB？假设存在，求出t的值；假设不存在，请说明原由；〔 4〕经过观察、画图或折纸等方法，猜想可否存在时辰t ，使得 PD⊥ AB？假设存在，请估计t 的值在括号中的哪个时间段内〔0≤t≤ 1； 1＜t≤ 2； 2＜t≤ 3；3＜t≤ 4〕；假设不存在，请简要说明原由．AAPPDDCQ B C Q M B图 1例２如图 2，直角梯形ABCD 中， AB ∥CD ，∠ A=90 0， AB=6 ，AD=4 ，DC=3→ D→ C→ B 方向搬动，动点Q 从点A出发，在AB边上搬动．设点P 搬动的行程为线段 PQ 均分梯形 ABCD 的周长．〔 1〕求y与x的函数关系式，并求出x， y 的取值范围；〔 2〕当 PQ∥ AC 时，求x，y的值；〔 3〕当P不在 BC 边上时，线段 PQ 可否均分梯形 ABCD 的面积？假设能，求出此时由．D C DCPPEＢA Q BＡQ图 2.例 3如图3，在平面直角坐标系中，以坐标原点O 为圆心， 2 为半径画⊙ O， P 是⊙ O 上一动点，且 P 在第一象限内，过点P 作⊙ O 的切线与x轴订交于点 A，与y轴订交于点 B.(1)点 P 在运动时，线段AB 的长度也在发生变化，请写出线段AB 长度的最小值，并说明原由；(2)在⊙ O 上可否存在一点Q，使得以 Q、O、 A、 P 为极点的四边形时平行四边形？假设存在，央求出Q 点的坐标；假设不存在，请说明原由 .yBPO Ax图 3例４如图 7①，一张三角形纸片 ABC，∠ ACB=90° ,AC=8,BC=6. 沿斜边 AB的中线 CD 和BC2 D 2两个三角形〔如图7②所示〕 . 将纸片AC1D1沿直线D2B〔 AB〕方向平素来线上〕，当点D1于点 B 重合时，停止平移 . 在平移过程中，C D与2交于点 E,1 1BCF、 P.⑴当 AC1D1平移到如图7③所示的地址时，猜想图中的D1E 与 D2 F 的数量关⑵设平移距离 D2 D1为 x ， AC1D1与BC2 D2重叠局部面积为y ，请写出 y 与量的取值范围；⑶关于〔 2〕中的结论可否存在这样的x 的值，使重叠局部的面积等于原ABC 面值；假设不存在，请说明原由.CC1C2FBA D1D2AD2D1BA D B①②③.图 7【中考展望】⒈如图 8①，有两个形状完满相同的直角三角形ABC和 EFG叠放在一起〔点 A 与点 E 重合〕， AC＝ 8cm，BC＝ 6cm，∠ C＝ 90°， EG＝ 4cm，∠ EGF＝ 90°， O是△ EFG斜边上的中点．如图 8②，假设整个△ EFG从图①的地址出发，以1cm/s 的速度沿射线AB 方向平移，在△EFG 平移的同时，点 P 从△ EFG的极点 G出发，以 1cm/s 的速度在直角边GF上向点 F 运动，当点P 到达点 F 时，点 P 停止运动，△EFG也随之停止平移．设运动时间为x〔 s〕， FG的延长线交AC 于 H，四边形OAHP的面积为y〔 cm2) 〔不考虑点 P 与 G、F 重合的状况〕．〔 1〕当 x 为何值时， OP∥ AC ?〔 2〕求 y 与 x 之间的函数关系式，并确定自变量x 的取值范围．〔 3〕可否存在某一时辰，使四边形OAHP面积与△ ABC面积的比为13∶ 24？假设存在，求出 x 的值；假设不存在，说明原由．〔参照数据：1142＝ 12996， 1152＝13225， 1162＝ 13456 或 4. 42＝19. 36， 4. 52＝ 20. 25， 4. 62＝ 21. 16〕⒉如图 9，在平面直角坐标系中，两个函数y=x ，y1x 6 的图象交于点A．2向以每秒 1 个单位的速度运动，作 PQ//x 轴交直线 BC 于点 Q，以 PQ 为一边向下作正方形重叠局部的面积为 S．（1〕求点 A 的坐标．（2〕试求出点 P 在线段 OA 上运动时， S 与运动时间 t〔秒〕的关系式．〔 3〕在〔 2〕的条件下， S 可否有最大值？假设有，求出 t 为何值时， S 有最大值，并说明原由．〔 4〕假设点 P 经过点 A 后连续按原方向、原速度运动，当正方形PQMN 和OA 动时间 t 满足的条件是__________．图 9图8⒊如图 10, 平面直角坐标系中 , 直线AB与x轴 , y轴分别交于A(3,0), B(0, 3 ) 两点 , , 点C为线段AB上的一动点 , 过点C作CD⊥x轴于点D.(1)求直线 AB的剖析式;(2)假设 S梯形OBCD＝4 3,求点 C的坐标;3(3) 在第一象限内可否存在点P,使得以 P,O,B 为极点的三角形与△OBA相似.假设存在,央求出所有吻合条件的点P的坐标;假设不存在,请说明原由.图 10⒋如图11，在锐角△ABC中，BC9 ， AH BC 于点 H ，且 AH 6，点 D 过点 D 作 DE ∥ BC ，交 AC 于点 E ．设△ ADE 的高 AF 为x(0x 6) ，以DE 得的△ A DE 与梯形 DBCE 重叠局部的面积记为y 〔点 A 关于 DE 的对称点 A 落在〔 1〕分别求出当0x ≤ 3 与3 x 6时，y与 x 的函数关系式；〔 2〕当x取何值时，y 的值最大？最大值是多少？ADFEAB H CB图 11⒌如图 12，在ABC 中，∠C=900，AC=4cm，BC=5cm，点D在BC上，且CD=3cm，现有两个动点P、Q 分别从点 A 和点 B 同时出发，其中点P 以 1cm/s 的速度，沿AC 向终点 C 搬动；点Q 以的速度沿BC 向终点 C 搬动．过点P 作 PE∥BC 交 AD 于点 E，连接 EQ．设动点运动时间为x 秒．（1〕用含 x 的代数式表示 AE 、DE 的长度；（2〕当点 Q 在 BD 〔不包括点 B、 D〕上搬动时，设EDQ的面积为y(cm2)，求y与月份x的函数关系式，并写出自变量 x 的取值范围；〔 3〕当x为何值时，EDQ 为直角三角形．APEB Q D C图 12⒍如图 13，在平面直角坐标系中，点A(0，4 3) ，点B在 x 正半轴上，且∠AB 上从点 A 向点 B 以每秒3 个单位的速度运动，设运动时间为t秒．在 x 轴上取两点求直线AB的剖析式；〔 2〕求等边△PMN的边长〔用t的代数式表示〕，并求出当等边△PMN的极点t的值；〔 3〕若是取OB的中点D，以OD为边在Rt△AOB内部作如图 14 所示的矩形OD 上．设等边△ PMN 和矩形 ODCE 重叠局部的面积为 S ，央求出当 0 ≤ t ≤ 2 秒时 S S的最大值．y yA P ACEM O N B x O D图13图14⒎如图15，Rt △ ABC中， CAB30o，BC 5．过点A作AE⊥AB，且AE15BE交AC于，连接点 P ．（1〕求PA的长；（2〕以点A为圆心，AP为半径作⊙ A，试判断BE与⊙ A可否相切，并说明原由；（3〕如图 16，过点C作CD⊥AE，垂足为D．以点A为圆心，r为半径作⊙ A；以点C为圆心，R为半径作⊙ C．假设r和R 的大小是可变化的，并且在变化过程中保持⊙A和⊙相切，且使 D 点在⊙A的内部， B 点在⊙AC ．．的外面，求r和R的变化范围．E E8.抛物线 y ax 2 bx c ，经过点A〔0，5〕和点B〔3，2〕（1〕求抛物线的剖析式；〔 2〕现有一半径为1，圆心 P 在抛物线上运动的动圆，问⊙P 在运动过程中，可否状况？假设存在，央求出圆心P的坐标；假设不存在，请说明原由；〔 3〕假设⊙ Q的半径为r ，点 Q在抛物线上、⊙Q与两坐PCＤCPA B A B图15图16⒐如图 17，在平面直角坐标系中，点P 从点 A 开始沿 x 轴向点 O以 1cm／ s 的速度搬动，点Q从点 O开始沿 y轴向点 B 以 2cm／ s 的速度搬动，且OA=6cm， OB=12cm.若是 P， Q分别从 A，O同时出发 .⑴设△ POQ的面积等于 y, 运动时间为 x，写出 y 与 x 之间的函数关系，并求出头积的最大值；终点时，所有运动即停止 ) ．设 P、 Q同时出发并t 秒．⑵几秒后△ POQ与△ AOB相似；⑶几秒后以 PQ为直径的圆与直线AB相切 .Q图 186O Ax。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ABCO 是菱形，且
∠ AOC=60 °，点 B 的坐标是 (0,8 3) ，点 P 从点 C 开始以每秒 1 个单位长度的速度在线段
CB 上向点 B 移动，同时，点 Q 从点 O 开始以每秒 a（1≤ a≤ 3 ）个单位长度的速度沿射线
OA 方向移动，设 t (0 t 8) 秒后，直线 PQ 交 OB 于点 D.
（ 1）求直线 BC 的解析式；
（ 2 ）若动点 P 在线段 OA 上移动，当 t 为何值时，四边形 OPDC 的面积是梯形 COAB 面积
2
的？
7
（ 3 ）动点 P 从点 O 出发，沿折线
OABD 的路线移动过程中，设
△OPD 的面积为 S ，请
直接写出 S 与 t 的函数关系式，并指出自变量 t 的取值范围；
⑶在抛物线的对称轴上找一点 M，使 | AM MC |的值最大，求出点 M的坐标。
提示：第（ 2 ）问按直角位置分类讨论后画出图形 ---- ① P 为直角顶点 AE 为斜边时，以 AE
为直径画圆与 x 轴交点即为所求点 P，②A 为直角顶点时，过点 A 作 AE 垂线交 x 轴于点 P，
③ E 为直角顶点时，作法同②；
从 B 点出发沿 BC 方向运动，设运动时间为 t( s)( 0 t 2) ，连结 EF，当 t 为何值时， △ BEF
为直角三角形．注意：第（ 3 ）问按直角位置分类讨论
3、（ 2009 重庆綦江）如图，已知抛物线 y a( x 1)2 3 3( a 0) 经过点 A( 2， 0) ，抛
物线的顶点为 D ，过 O 作射线 OM ∥ AD ．过顶点 D 平行于 x 轴的直线交射线 OM 于点 C ， B 在 x 轴正半轴上，连结 BC ．
秒；
（ 3）求 y 与 x 之间的函数关系式．
D
C
提示：第 (3) 问按
P
高相等的两个三角形
AQ
点 Q 到拐点时间 B、C 所有时间分段分类；提醒 ----B 面积比等于底边的比。
5、（ 2009 年哈尔滨）如图 1，在平面直角坐标系中，点 O 是坐标原点，四边形 ABCO 是菱
形，点 A 的坐标为（ 3， 4），点 C 在 x 轴的正半轴上，直线 AC 交 y 轴于点 M，AB 边交 y
学习必备
欢迎下载
(2) 当 t 为何值时， AB∥DF； (3) 设四边形 AEFD的面积为 S． ①求 S 关于 t 的函数关系式；
②若一抛物线 y=x 2+mx经过动点 E，当 S<2 3 时，求 m的取值范围 ( 写出答案即可 ) ．
注意：发现特殊性， DE ∥OA 7 、（ 07 黄冈）已知：如图，在平面直角坐标系中，四边形
第（ 3 ）问，三角形两边之差小于第三边，那么等于第三边时差值最大。
10、（ 2009 年兰州）如图①，正方形 ABCD中，点 A、B的坐标分别为（ 0，10），（ 8，4），点 C在第一象限．动点 P 在正方形 ABCD的边上，从点 A 出发沿 A→ B→ C→D匀速运动，同时动点 Q以相同速度在 x 轴正半轴上运动，当 P 点到达 D点时，两点同时停止运动，设运动的时间为 t 秒． (1) 当 P 点在边 AB上运动时，点 Q的横坐标 x （长度单位）关于运动时间 t （秒）的函数图象如图②所示，请写出点 Q开始运动时的坐标及点 P 运动速度； (2) 求正方形边长及顶点 C的坐标； (3) 在（ 1）中当 t 为何值时，△ OPQ的面积最大，并求此时 P 点的坐标； (4) 如果点 P、 Q保持原速度不变，当点 P 沿 A→ B→ C→ D匀速运动时， OP与 PQ能否相等，若能，写出所有符合条件的 t 的值；若不能，请说明理由．
（ 1）求该抛物线的解析式；
（ 2）若动点 P 从点 O 出发，以每秒 1 个长度单位的速度沿射线 OM 运动，设点 P 运动的
时间为 t( s) ．问当 t 为何值时，四边形 DAOP 分别为平行四边形？直角梯形？等腰梯形？
（ 3）若 OC OB ，动点 P 和动点 Q 分别从点 O 和点 B 同时出发，分别以每秒 1 个长度单
Q ，使得以 B， N， Q 为项点
的三角形与 △ ABC 相似？如果存在，请求出点 Q 的坐标；如果不存在，请说明理由．
y
C
P
N
A
MO B
x
提示：第（ 2 ）问发现
特殊角∠CAB=30 °,∠CBA=60 °
特殊图形四边形 BNPM 为菱形；
第(3) 问注意到△ ABC 为直角三角形后，按直角位置对应分类；先画出与△ ABC 相似的
学习必备
欢迎下载
一、三角形边上动点
1、（ 2009 年齐齐哈尔市）直线 y
3 x 6 与坐标轴分别交于 A、B 两点，动点 P、 Q 同时 4
从 O 点出发，同时到达 A 点，运动停止．点 Q 沿线段 OA 运动，速度为每秒 1 个单位长
度，点 P 沿路线 O → B → A 运动．（ 1）直接写出 A、B 两点的坐标；
（ 3）在（ 2）的条件下，当 t 为何值时，∠ MPB 与∠ BCO 互为余角，并求此时直线 OP 与
直线 AC 所夹锐角的正切值．
y
A HB M
y
A
HB
O
Cx
图（ 1）
MOCx来自图（ 2）注意：第（ 2 ）问按点 P 到拐点 B 所用时间分段分类；
第（ 3 ）问发现∠ MBC=90 °，∠BCO 与∠ABM 互余，画出点 P 运动过程中，
当△OPQ 面积最大时，四边形 BCPQ 的面积最小。
二、
特殊四边形边上动点
4、（ 2009 年吉林省）如图所示，菱形
ABCD 的边长为 6 厘米， B 60°．从初始时刻开
始，点 P 、 Q 同时从 A 点出发，点 P 以 1 厘米 /秒的速度沿 A C B 的方向运动，点 Q
以 2 厘米 /秒的速度沿 A B C D 的方向运动，当点 Q 运动到 D 点时， P 、 Q 两点
三、
直线上动点
8、（2009 年湖南长沙）如图，二次函数
y ax2 bx c（ a 0 ）的图象与 x 轴交于 A、 B
两点，与 y 轴相交于点 C ．连结 AC、 BC，A、C 两点的坐标分别为 A( 3，0) 、 C (0， 3) ，
且当 x 4 和 x 2 时二次函数的函数值 y 相等．
（ 1）求实数 a， b，c 的值；
时 , 点 Q 也同时停止运动 ,线段 OC, PQ 相交于点
D,过点 D 作 DE∥OA ,交 CA 于点 E,射线 QE 交 x
轴于点 F．设动点 P,Q 移动的时间为 t(单位 :秒)
(1) 求 A,B,C 三点的坐标和抛物线的顶点的坐标 ;
(2) 当 t 为何值时 , 四边形 PQCA 为平行四边形 ?请写出计算过程 ;
知线段身份不同分类 ----- ① OP 为边、 OQ 为边，② OP 为边、 OQ 为对角线，③ OP
为对角线、 OQ 为边。然后画出各类的图形，根据图形性质求顶点坐标。
2、（ 2009 年衡阳市）
C
C
C
F
F
A
O
A
E
BD
O
B
A
O EB
图（ 1）
图（ 2）
图（ 3）
学习必备
欢迎下载
如图， AB 是⊙ O 的直径，弦 BC=2cm ， ∠ ABC=60 o．（ 1）求⊙ O 的直径；（ 2）若 D 是 AB 延长线上一点，连结 CD，当 BD 长为多少时， CD 与⊙ O 相切；（ 3）若动点 E 以 2cm/s 的速度从 A 点出发沿着 AB 方向运动，同时动点 F 以 1cm/s 的速度
(3) 当 0 ＜ t＜ 9 时 ,△PQF 的面积是否总为定值 ?若是 ,求出此定值 , 2
(4) 当 t 为何值时 , △PQF 为等腰三角形 ?请写出解答过程．
提示：第（ 3）问用相似比的代换，
得 PF=OA（定值）。
第（ 4）问按哪两边相等分类讨论
若不是 ,请说明理由 ;
学习必备
欢迎下载
① PQ=PF,②PQ=FQ,③QF=PF.
y B
P C
D
A
Q
x O
学习必备
欢迎下载
8 、（ 08 黄冈）已知：如图，在直角梯形 COAB 中， OC ∥ AB ，以 O 为原点建立平面直角
坐标系， A， B，C 三点的坐标分别为 A(8，0)， B (8，10) ， C (0，4) ，点 D 为线段 BC 的中点，
动点 P 从点 O 出发，以每秒 1 个单位的速度，沿折线 OABD 的路线移动，移动的时间为 t 秒．
位和 2 个长度单位的速度沿 OC 和 BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为 t (s) ，连接 PQ ，当 t 为何值时，四边形 BCPQ 的面积最小？
并求出最小值及此时 PQ 的长．
y
M
D
C
P
A O
Q Bx
注意：发现并充分运用特殊角∠ DAB=60 °
△BNQ ，再判断是否在对称轴上。
9 、（ 2009 眉山）如图，已知直线
1 y x 1 与 y 轴交于点 A，与 x 轴交于点 D，抛物线
2
学习必备
欢迎下载
y 1 x2 bx c 与直线交于 2
⑴求该抛物线的解析式；
A、E 两点，与
x 轴交于 B、 C 两点，且
B点坐标为
(1 ， 0) 。
⑵动点 P 在 x 轴上移动，当△ PAE是直角三角形时，求点 P 的坐标 P。
轴于点 H．
（ 1）求直线 AC 的解析式；