第13讲 反比例函数
2014中考总复习第13讲反比例函数
知识回顾
重点解析
探究拓展
真题演练
5 1. (2013·兰州)当 x>0 时, 函数 y=- x 的图象在(
)
A. 第四象限 C. 第二象限
B. 第三象限 D. 第一象限
5 【解析】 ∵函数 y=- x 中 k=-5<0, ∴其图象位于第二、四象限, 当 x>0 时, 其图
象位于第四象限. 【答案】 A
知识回顾
重点解析
探究拓展
真题演练
∵O E =2, ∴C E =3, ∴点 C 的坐标是( -2, 3) .
6 ∴k=-2× 3=-6, ∴y=- x .
( 2) 设直线 AB 的解析式为 y=kx+b( k≠0) .
1 k b 2 2 则 4k b 0 , 解得 . b 2
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
一、反比例函数的有关概念 1. 反比例函数的定义: 形如 y= 量, y是 x的函数. 2. 反比例函数的解析式的三种形式: ( 1) y= 0, k为常数) . ( k≠0, k为常数) ; ( 2) y= ( k≠0, k为常数) ; ( 3) xy=k( k≠ ( k≠0, k为常数) 的函数叫做反比例函数, 其中 x是自变
BD 1 1 1 ∴ OD = 3 , BD = 4 BO . 又∵S△AB O =1, ∴ 2 B D ·B A=1, 8 ∴B O ·B A=8. 设 A 点坐标为 A ( x, y) , 由 xy=8, 得 y= x . 8 【答案】y= x ( x>0)
第一部分
k
.
复习目标
知识回顾
重点解析
【精品语文课件】2020(新增6页)教版中考数学复习解题指导:第13讲 反比例函数_6-10
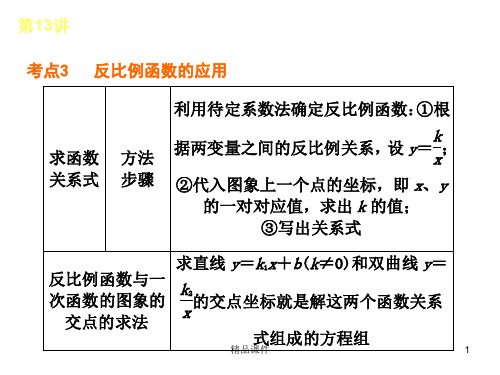
kx2的交点坐标就是解这两个函数关系
式组成的方程组
精品课件
1
第13讲┃ 归类示例
归类示例
► 类型之一 反比例函数的概念 命题角度: 1. 反比例函数的概念; 2. 求反比例函数的解析式.
例1 [2012·益阳 ]反比例函数y= 的图象与一次函 数y=2x+1的图象的一个交点是(1,k),则反比例函数的 解析式是________.
精品课件
4
第13讲┃ 归类示例
比较反比例函数值的大小,在同一个象限内根据 反比例函数的性质比较,在不同象限内,不能按其 性质比较,函数值的大小只能根据特征确定.
精品课件
5
” 樵夫用绳子把柴紧紧地捆了起来,用扁担挑上柴下山了。” 龙在十字路口等着这厚皮笨象。”于是那个人又问:“那你种了什么?”农夫说:“什么也没种。
深圳小产权房网:/ 你要是从边上吃,这是我瘦瘦的肋骨。
马努说:“我们不会让你死的!”他用手捧起水,让玛茨亚呆在水里,把他带回家去了。,” 庭太端起自己的那杯蔬菜汁,说:“我讨厌这种可怕的菜汁
6
A.y1>y2>y3 B.y1>y3>y2 C.y2>y1>y3 D.y2>y3>y1
精品课件
3
第13讲┃ 归类示例
[解析] 反比例函数 y=-7x的图象在第二,四象限,在每一个象限内,y 随 x 的 增大而增大.A(-2,y1)、B(-1,y2)在第二象限,因为-2<-1,所以 0<y1<y2.又 C(2, y3)在第四象限,所以 y3<0.
第13讲┃ 考点聚焦
考点3 反比例函数的应用
求函数 关系式
方法 步骤
利用待定系数法确定反比例函数:①根
《反比例函数》课件

部分,S梯形CABD= S△ABO .
y
A
C
D
O
B
E
x
重难剖析 重难点4:反比例函数的实际应用
病人按规定的剂量服用某种药物,测得服药后 2 小时,
每毫升血液中的含药量达到最大值为 4 毫克. 已知服药
后,2 小时前每毫升血液中的含药量 y (单位:毫克)与
1
D.
3
2. 若 y a 1 x
A. 1
B. -1
a2 2
是反比例函数,则 a 的值为 ( A )
C. ±1
a+1≠0
a2-2=-1
a=1
D. 任意实数
重难剖析 重难点2:反比例函数的图象和性质
已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比例函数
6
= 的图象上,则 y1,y2,y3 的大小关系是( D )
比例函数,其中 x 是自变量,y 是 x 的函数,k 是比例
系数.
k
三种表达方法:y 或 xy=k 或 y=kx-1(k≠0).
x
注意:(1)k≠0;(2)自变量x≠0;(3)函数y≠0.
2.反比例函数的图象和性质
k
(1)反比例函数的图象:反比例函数 y (k≠0)的
x
图象是 双曲线,它既是轴对称图形,又是中心对称图形.
重难剖析 重难点5:反比例函数的综合应用
1
2
如图,已知 A (-4, ),B (-1,2) 是一次函数y =kx+b 与反
比例函数 = (m<0)图象的两个交点,AC⊥x 轴于点
第十三讲反比例函数详解
第十三讲 反比例函数第一部分 知识梳理一、反比例函数的解析式1.反比例函数的概念一般地,函数xky =(k 是常数,k ≠0)叫做反比例函数。
反比例函数的解析式也可以写成1-=kx y 的形式。
自变量x 的取值范围是x ≠0的一切实数,函数的取值范围也是一切非零实数。
2.反比例函数解析式的确定 由于在反比例函数xky =中,只有一个待定系数,因此只需要一对对应值或图像上的一个点的坐标,即可求出k 的值,从而确定其解析式。
二、反比例函数的图像及性质1.反比例函数的图象反比例函数的图象是双曲线,有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。
由于反比例函数中自变量x≠0,函数y≠0,所以,它的图象与x轴、y轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴。
2.反比例函数的性质3.反比例函数中反比例系数的几何意义(如图)面积为k 。
连接该点和原点,所得三三角形(如图)的面积m 的值D .21-〖选题意图〗对于反比例函数)0(≠=k xky 。
由于11-=x x ,所以反比例函数也可以写成1-=x y (k 是常数,k ≠0)的形式,有时也以xy=k (k 是常数,k ≠0)的形式出现。
(1)k >0,反比例函数图象在一、三象限;(2)k <0,反比例函数图象在第二、四象限内.本题需要理解好反比例函数定义中的系数和指数,同时需要掌握反比例函数的性质,这样才能防止漏解或多解。
〖解题思路〗根据反比例函数的定义m 2﹣5=﹣1,又图象在第二、四象限,所以m+1<0,两式联立方程组求解即可.〖参考答案〗解:∵函数()521-+=m xm y 是反比例函数,且图象在第二、四象限内,∴⎩⎨⎧+-=-01152<m m ,解得m =±2且m <﹣1,∴m =﹣2.故选B .【课堂训练题】1.已知y=y 1+y 2,y 1与x 成正比例,y 2与x ﹣2成反比例,且当x =1时,y =﹣1;当x=3时,y=5.求y 与x 的函数关系式. 〖难度分级〗A 类〖参考答案〗解:设y 1=k 1x (k 1≠0),y 2=错误!未找到引用源。
中考数学专题复习讲座第十三讲反比例函数

中考数学专题复习第十三讲反比例函数【基础知识回顾】一、反比例函数的概念:一般地:互数y (k是常数,k≠0)叫做反比例函数【名师提醒:1、在反比例函数关系式中:k≠0、x≠0、y≠02、反比例函数的另一种表达式为y= (k是常数,k≠0)3、反比例函数解析式可写成xy= k(k≠0)它表明反比例函数中自变量x 与其对应函数值y之积,总等于】二、反比例函数的同象和性质:1、反比例函数y=kx(k≠0)的同象是它有两个分支,关于对称2、反比例函数y=kx(k≠0)当k>0时它的同象位于象限,在每一个象限内y随x的增大而当k<0时,它的同象位于象限,在每一个象限内,y随x的增大而【名师提醒:1、在反比例函数y=kx中,因为x≠0,y≠0所以双曲线与坐标轴无限接近,但永不与x轴y轴2、在反比例函数y随x的变化情况中一定注明在每一个象限内】3、反比例函数中比例系数k的几何意义:反曲线y=kx(k≠0)上任意一点向两坐标轴作垂线→两线与坐标轴围成的形面积,即如图: AOBP=S△AOP=【名师提醒:k的几何意义往常与前边提示中所谈到的xy=k联系起来理解和应用】三、反比例函数解析式的确定因为反比例函数y=kx(k≠0)中只有一个被定系数所以求反比例函数关系式只需知道一组对应的x、y值或一个点的坐标即可,步骤同一次函数解析式的求法一、反比例函数的应用二、解反比例函数的实际问题时,先确定函数解析式,再利用同象找出解决问题的方案,这里要特别注意自变量的【重点考点例析】考点一:反比例函数的同象和性质例1 (2012•张家界)当a≠0时,函数y=ax+1与函数ayx在同一坐标系中的图象可能是()A. B.C. D.思路分析:分a>0和a<0两种情况讨论,分析出两函数图象所在象限,再在四个选项中找到正确图象.解:当a>0时,y=ax+1过一、二、三象限,y=ayx=过一、三象限;当a<0时,y=ax+1过一、二、四象限,y=ayx=过二、四象限;故选C.点评:本题考查了一次函数与二次函数的图象和性质,解题的关键是明确在同一a值的前提下图象能共存.例2 (2012•佳木斯)在平面直角坐标系中,反比例函数22a ayx-+ =图象的两个分支分别在()A.第一、三象限 B.第二、四象限C.第一、二象限 D.第三、四象限思路分析:把a2-a+2配方并根据非负数的性质判断出是恒大于0的代数式,再根据反比例函数的性质解答.解:a2-a+2,=a2-a+14-14+2,=(a-12)2+7 4 ,∵(a-12)2≥0,∴(a-12)2+7 4 >0,∴反比例函数图象的两个分支分别位于第一、三象限.故选A.点评:本题考查了反比例函数图象的性质,先判断出a2-a+2的正负情况是解题的关键,对于反比例函数kyx=(k≠0):(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内.例3 (2012•台州)点(-1,y1),(2,y2),(3,y3)均在函数6yx=的图象上,则y1,y2,y3的大小关系是()A.y3<y2<y1 B.y2<y3<y1 C.y1<y2<y3 D.y1<y3<y2思路分析:先根据反比例函数的解析式判断出此函数图象所在的象限,再根据各点的坐标判断出各点所在的象限,根据函数图象在各象限内点的坐标特点解答.解:∵函数6yx=中k=6>0,∴此函数的图象在一、三象限,且在每一象限内y随x的增大而减小,∵-1<0,∴点(-1,y1)在第三象限,∴y1<0,∵0<2<3,∴(2,y2),(3,y3)在第一象限,∴y2>y3>0,∴y2>y3>y1.故选D.点评:本题考查的是反比例函数图象上点的坐标特点,根据题意判断出函数图象所在象限是解答此题的关键.对应训练1.(2012•毕节地区)一次函数y=x+m(m≠0)与反比例函数myx=的图象在同一平面直角坐标系中是()A. B. C. D.1.C2.(2012•内江)函数1y xx=的图象在()A.第一象限 B.第一、三象限 C.第二象限 D.第二、四象限2.A2x中x≥0,1x中x≠0,故x>0,此时y>0,则函数在第一象限.故选A.3.(2012•佛山)若A(x1,y1)和B(x2,y2)在反比例函数2yx=的图象上,且0<x1<x2,则y1与y2的大小关系是y1 y2.3.>考点二:反比例函数解析式的确定例4 (2012•哈尔滨)如果反比例函数1kyx-=的图象经过点(-1,-2),则k的值是()A.2 B.-2 C.-3 D.3思路分析:根据反比例函数图象上点的坐标特征,将(-1,-2)代入已知反比例函数的解析式,列出关于系数k的方程,通过解方程即可求得k的值.解答:解:根据题意,得-2=11k--,即2=k-1,解得k=3.故选D.点评:此题考查的是用待定系数法求反比例函数的解析式,是中学阶段的重点.解答此题时,借用了“反比例函数图象上点的坐标特征”这一知识点.对应训练4.(2012•广元)已知关于x的方程(x+1)2+(x-b)2=2有唯一的实数解,且反比例函数1b yx+ =的图象在每个象限内y随x的增大而增大,那么反比例函数的关系式为()A.3yx=- B.1yx= C.2yx= D.2yx=-4.D4.分析:关于x的方程(x+1)2+(x-b)2=2有唯一的实数解,则判别式等于0,据此即可求得b的值,然后根据反比例函数1byx+=的图象在每个象限内y随x的增大而增大,则比例系数1+b<0,则b的值可以确定,从而确定函数的解析式.解:关于x的方程(x+1)2+(x-b)2=2化成一般形式是:2x2+(2-2b)x+(b2-1)=0,△=(2-2b)2-8(b2-1)=-4(b+3)(b-1)=0,解得:b=-3或1.∵反比例函数1byx+=的图象在每个象限内y随x的增大而增大,∴1+b<0 ∴b<-1,∴b=-3.则反比例函数的解析式是:y=13yx-=,即2yx=-.故选D.考点三:反比例函数k的几何意义例5 (2012•铁岭)如图,点A在双曲线4yx=上,点B在双曲线kyx=(k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,若矩形ABCD的面积是8,则k的值为()A.12 B.10 C.8 D.6思路分析:先根据反比例函数的图象在第一象限判断出k的符号,再延长线段BA,交y轴于点E,由于AB∥x轴,所以AE⊥y轴,故四边形AEOD是矩形,由于点A在双曲线4yx=上,所以S矩形AEOD=4,同理可得S矩形OCBE=k,由S矩形ABCD=S矩形OCBE-S矩形AEOD即可得出k的值.解:∵双曲线kyx=(k≠0)上在第一象限,∴k>0,延长线段BA,交y轴于点E,∵AB∥x轴,∴AE⊥y轴,∴四边形AEOD是矩形,∵点A在双曲线4yx=上,∴S矩形AEOD=4,同理S矩形OCBE=k,∵S矩形ABCD=S矩形OCBE-S矩形AEOD=k-4=8,∴k=12.故选A.点评:本题考查的是反比例函数系数k的几何意义,即反比例函数kyx=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.对应训练5.(2012•株洲)如图,直线x=t(t>0)与反比例函数21,y yx x-==的图象分别交于B、C两点,A为y轴上的任意一点,则△ABC的面积为()A.3 B.3 2 tC.32D.不能确定5.C5.解:把x=t分别代入21,y yx x-==,得21,y yt t==-,所以B(t,2t)、C(t,1t-),所以BC=2t-(1t-)=3t.∵A为y轴上的任意一点,∴点A到直线BC的距离为t,∴△ABC的面积=133 22tt⨯⨯=.故选C.考点四:反比例函数与一次函数的综合运用例6 (2012•岳阳)如图,一次函数y1=x+1的图象与反比例函数22yx=的图象交于A、B 两点,过点作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是()A.点A和点B关于原点对称B.当x<1时,y1>y2C.S△AOC=S△BODD.当x>0时,y1、y2都随x的增大而增大思路分析:求出两函数式组成的方程组的解,即可得出A、B的坐标,即可判断A;根据图象的特点即可判断B;根据A、B的坐标和三角形的面积公式求出另三角形的面积,即可判断C;根据图形的特点即可判断D.解:A、12y xyx=+⎧⎪⎨=⎪⎩①②,∵把①代入②得:x+1=2x,解得:x1=-2,x2=1,代入①得:y1=-1,y2=2,∴B(-2,-1),A(1,2),∴A、B不关于原点对称,故本选项错误;B、当-2<x<0或x>1时,y1>y2,故本选项错误;C、∵S△AOC=12×1×2=1,S△BOD=12×|-2|×|-1|=1,∴S△BOD=S△AOC,故本选项正确;D、当x>0时,y1随x的增大而增大,y2随x的增大而减小,故本选项错误;故选C.点评:本题考查了一次函数与反比例函数的交点问题的应用,主要考查学生观察图象的能力,能把图象的特点和语言有机结合起来是解此题的关键,题目比较典型,是一道具有一定代表性的题目.对应训练6.(2012•达州)一次函数y1=kx+b(k≠0)与反比例函数y2=mx(m≠0),在同一直角坐标系中的图象如图所示,若y1>y2,则x的取值范围是()A.-2<x<0或x>1 B.x<-2或0<x<1 C.x>1 D.-2<x<16.A6.解:由函数图象可知一次函数y1=kx+b与反比例函数y2=mx(m≠0)的交点坐标为(1,4),(-2,-2),由函数图象可知,当-2<x<0或x>1时,y1在y2的上方,∴当y1>y2时x的取值范围是-2<x<0或x>1.故选A.【聚焦山东中考】1.(2012•青岛)点A(x1,y1),B(x2,y2),C(x3,y3)都是反比例函数3yx-=的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是()A.y3<y1<y2 B.y1<y2<y3 C.y3<y2<y1 D.y2<y1<y31.A1.解:∵反比例函数y=-3 x 中,k=-3<0,∴此函数图象在二四象限,且在每一象限内y随x的增大而增大,∵x1<x2<0<x3,∴y3<0,y3<0<y1<y2,∴y3<y1<y2.故选A.2.(2012•菏泽)反比例函数2yx=的两个点(x1,y1)、(x2,y2),且x1>x2,则下式关系成立的是()A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定2.D3.(2012•滨州)下列函数:①y=2x-1;②y=5x-;③y=x2+8x-2;④y=22x;⑤y=12x;⑥y=ax中,y是x的反比例函数的有(填序号)。
【大师特稿】中考数学一轮复习第13讲:反比例函数教案

第13讲:反比例函数一、复习目标1、理解反比例函数的意义,能根据已知条件确定反比例函数的解析式,能画出反比例函数的图象2、能够将反比例函数有关的实际应用题转化为函数问题二、课时安排1课时三、复习重难点1、反比例函数图象与性质2、反比例函数图象、性质的应用四、教学过程(一)知识梳理反比例函数的图象与性质·PN=|y|·|x|=(二)题型、技巧归纳考点1:反比例函数的概念技巧归纳:判断点是否在反比例函数图象上的方法有两种:一是口算选项中点的横坐标与纵坐标乘积是否都等于比例系数,二是将选项中点的坐标诸个代入反比例函数关系式,看能否使等式成立.考点2:反比例函数的图象与性质技巧归纳:1、比较反比例函数值的大小,在同一个象限内根据反比例函数的性质比较,在不同象限内,不能按其性质比较,函数值的大小只能根据特征确定.2、过反比例函数y =kx的图象上的某点向两坐标轴作垂线,两垂线与坐标轴围成的矩形的面积就等于|k |,故而常过图象上某点向坐标轴作一条或两条垂线,引出三角形或矩形的面积来解决问题.考点3反比例函数的应用技巧归纳:先根据双曲线上点C 的坐标求出m 的值,从而确定点C 的坐标,再将点C 的坐标代入一次函数关系式中确定n 的值,在求出两个函数关系式后结合条件可求出三角形的面积.过反比例函数y =k x的图象上的某点向两坐标轴作垂线,两垂线与坐标轴围成的矩形的面积就等于|k |,故而常过图象上某点向坐标轴作一条或两条垂线,引出三角形或矩形的面积来解决问题.(三)典例精讲例1 某反比例函数的图象经过(-1,6),则下列各点中,此函数图象也经过的点是( ) A .(-3,2) B .(3,2) C .(2,3) D .(6,1)[解析] 设反比例函数的关系式为y =kx,把点(-1,6)代入可求出k =-6,所以反比例函数的关系式为y =-6x,故此函数也经过点(-3,2),答案选A.例2在反比例函数y =k x (k <0)的图象上有两点()-1,y 1,⎝ ⎛⎭⎪⎫-14,y 2,则y 1-y 2的值是( ) A .负数 B .非正数C .正数D .不能确定 [解析] 反比例函数y =kx :当k <0时,该函数图象位于第二、四象限,且在每一象限内,y 随x 的增大而增大.又∵点(-1,y 1)和⎝ ⎛⎭⎪⎫-14,y 2均位于第二象限,-1<-14, ∴y 1<y 2,∴y 1-y 2<0,即y 1-y 2的值是负数,故选A.例3 如图点A ,B 在反比例函数y = (k>0,x>0)的图象上,过点A ,B 作x 轴的垂线,垂足分别为M ,N ,延长线段AB 交x 轴于点C ,若OM =MN =NC ,△AOC 的面积为6,则k 的值为________.[解析] ∵S △AOC =6,OM =MN =NC =13OC ,∴S △OAC =12×OC×AM,S △AOM =12×OM×AM=13 S △OAC =2=12|k|.又∵反比例函数的图象在第一象限,k >0,则k =4.例4 如图13-2,在平面直角坐标系xOy 中,直线y =2x +n 与x 轴、y 轴分别交于点A 、B ,与双曲线y =4y x=在第一象限内交于点C (1,m ). (1)求m 和n 的值;(2)过x 轴上的点D (3,0)作平行于y 轴的直线l ,分别与直线AB 和双曲线y = 交于点P 、Q ,求△APQ 的面积.解:(1) ∵点C(1,m)在双曲线y =4x上,∴m =4,将点C(1,4)代入y =2x +n 中,得n =2;(2)在y =2x +2中,令y =0,得x =-1,即A(-1,0).将x =3代入y =2x +2和y =4x,得点P(3,8),Q ⎝ ⎛⎭⎪⎫3,43,∴PQ =8-43=203.又∵AD =3-(-1)=4,∴△APQ 的面积=12×4×203=403. (四)归纳小结本部分内容要求熟练掌握反比例函数的求法,能画出反比例函数的图象,能够将反比例函数有关的实际应用题转化为函数问题(五)随堂检测1、已知点A(-2,y 1)、B(1,y 2)和C(2,y 3)都在反比例函数ky x= (k<0)的图象上,那么y 1、y 2和y 3的大小关系如何?2、已知反比例函数7y x=-图象上三个点的坐标分别是A(-2,y 1)、B(-1,y 2)、C(2,y 3),能正确反映y 1、y 2、y 3的大小关系的是( )A .y 1>y 2>y 3B .y 1>y 3>y 2C .y 2>y 1>y 3D .y 2>y 3>y 13、已知反比例函数y=(k 为常数,k≠0)的图象经过点A (2,3). (Ⅰ)求这个函数的解析式;(Ⅱ)判断点B (﹣1,6),C (3,2)是否在这个函数的图象上,并说明理由; (Ⅲ)当﹣3<x <﹣1时,求y 的取值范围.4、如图,在平面直角坐标系xOy 中,正比例函数y=kx 的图象与反比例函数y=的图象有一个交点A (m ,2).(1)求m 的值;(2)求正比例函数y=kx 的解析式;(3)试判断点B(2,3)是否在正比例函数图象上,并说明理由.五、板书设计反比例函数六、作业布置反比例函数课时作业七、教学反思借助多媒体形式,使同学们能直观感受本模块内容,以促进学生对所学知识的充分理解与掌握。
中考总复习数学13-第一部分 第13讲 反比例函数及其应用
返回思维导图
第13讲 反比例函数及其应用— 考点梳理
返回栏目导航
续表
在每个象限内,y随x的增大
增减性
而⑤ 减小
对称性
是轴对称图形,对称轴为直线y=⑦
⑧ 原点O
在每个象限内,y随x的增大
而⑥增大
±x
; 是中心对称图形,对称中心是
图象由分别位于两个象限的双曲线组成,图象无限接近坐标轴,但不与
图象特征
坐标轴相交.
第13讲 反比例函数及其应用— 考点梳理
返回思维导图
返回栏目导航
考点 4 反比例函数的应用
1.判断同一坐标系中反比例函数图象和一次函数图象的方法
(假设法)假设反比例函数正确,即可确定 k的取值范围,再根据 k 的取值范围
确定一次函数图象,无矛盾,则正确.
2.已知两个函数图象,求交点坐标
(1)求一次函数图象与反比例函数图象的交点,将两个函数解析式联立方程组
位置关系,依据图象在上方的函数值总比图象在下方的函数值大 ,在各区域
内找对应的x的取值范围.
4.求图形面积
(1)当图形有一边在坐标轴上时,通常将坐标
轴上的边作为底边,再利用点的坐标求出底边上的高,最后用面积公式求解.
(2)当图形三边都不在坐标轴上时,一般用“割补法”.
第13讲 反比例函数及其应用— 考点梳理
返回思维导图
2.与反比例函数中k的几何意义有关的面积计算
S△AOP=⑩
S△APP‘=
|k|
2|k|
S△OBP= |k|
S△ABC=
|k|
S矩形OAPB=|k|
S▱ABCD=
|k|
返回栏目导航
第十三讲反比例函数详解
06
总结回顾与拓展延伸
关键知识点总结回顾
反比例函数定义
形如$y = frac{k}{x}$($k$为常 数且$k neq 0$)的函数称为反
比例函数。
反比例函数图象
反比例函数的图象是双曲线,当 $k > 0$时,图象位于第一、三 象限;当$k < 0$时,图象位于
解得$x$无实数解,说明一元反比例函数在其定义域内无极值。 • 例题二:求二元反比例函数$f(x,y) = \frac{1}{xy}$在条件$x+y=1$下的
极小值。 • 解题思路:引入拉格朗日乘数$\lambda$,构造拉格朗日函数
$L(x,y,\lambda) = \frac{1}{xy} + \lambda(x+y-1)$,然后分别求偏导 数并令偏导数等于零,解得可能的极值点。最后结合约束条件和函数的 性质判断极值点的真假及极小值的大小。
分析
同样根据反比例函数的性质,我们知 道在$(-infty, 0)$区间内,函数是单调 减少的。因此,在子区间$(-2, -1)$内 ,函数也是单调减少的。
04
反比例函数极值问题求解策 略
极值存在条件及求解方法
极值存在条件
对于一元反比例函数,其极值存在的条件是一阶导数等于零且二阶导数不为零;对于多元反比例函数,极值存在 的条件是其偏导数等于零且二阶偏导数矩阵(Hessian矩阵)正定或负定。
判断反比例函数$f(x)
=
frac{1}{x}$在区间$(1, 2)$内的单
调性。
分析
根据反比例函数的性质,我们知 道在$(0, +infty)$区间内,函数 是单调减少的。因此,在子区间 $(1, 2)$内,函数同样单调减少。
第13课时 反比例函数(共26张PPT)
A. 0<y<1 B. 1<y<2 C. 2<y<6 D. y>6
(4) (2014湘潭)如图,A、B两点在双曲线y=
4 x
上,
分别经过A、B两点向轴作垂线段,已知S阴影=1, 则S1+S2=( D ) A. 3 B.4 C.5 D. 6
变式训练(2016· 龙东)已知反比例函数 y= ,当 1<x<3 时,
{
{
例 7 (2016· 湖州)湖州市菱湖镇某养鱼专业户准备挖一个面积为
2000 平方米的长方形鱼塘. (1)求鱼塘的长 y(米)关于宽 x(米)的函数表达式; (2)由于受场地的限制,鱼塘的宽最多只能挖 20 米,当鱼塘的宽 是 20 米,鱼塘的长为多少米?
解: (1)由长方形面积为 2000 平方米,得到 xy=2000, 即 y= ; =100(米) , (2)当 x=20(米)时,y=
中,一次函数 y=ax+b(a≠0)的图形与反比例 函数 y= (k≠0)的图象交于第二、四象限内 的 A、B 两点,与 y 轴交于 C 点,过点 A 作 AH⊥y 轴,垂足为 H,OH=3,tan∠ AOH= , 点 B 的坐标为(m,﹣2). (1)求△ AHO 的周长; (2)求该反比例函数和一次函数的表达式.
k ,一次函数 y = x + b ,得 k = 1 × 4 , 1 + b = 4 ,解得 k = 4 , b = x 4 3,∴反比例函数的表达式是y=x,一次函数表达式是y=x+3. (2)设直线y=x+3与x轴交于点C,当x=-4时,y=-1, ∴B(-4,-1).当y=0时,x+3=0,x=-3,∴C(-3,0), 1 1 15 S△AOB=S△AOC+S△BOC= ×3×4+ ×3×1= . 2 2 2 (3)∵B(-4,-1),A(1,4),∴根据图象可知:当x>1或 -4<x<0时,一次函数值大于反比例函数值.
(中考复习)第13讲 反比例函数及其图象
C.y1=y2
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
5. (2012· 达州)一次函数 y1=kx+b(k≠0)与反 m 比例函数 y2= (m≠0),在同一直角坐标 x 系中的图象如图 13-3 所示,若 y1>y2, 则 x 的取值范围是 ( A )
A.-2<x<0或x>1
基础知识 · 自主学习 题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
2 3. (2012· 菏泽)反比例函数 y= 图象上的两个点为 (x1, y1), (x2, x y2),且 x1<x2,则下式关系成立的是 ( D ) A.y1>y2 B.y1<y2
D.不能确定 1-2k 4. (2013· 哈尔滨 )反比例函数 y= 的图象经过点 (- 2,3),则 x k 的值为 ( C ) 7 7 A. 6 B.- 6 C. D.- 2 2
轴对称图形 . ______________ 4.应用:
如图 13-1 所示,点 A 和点 C 是反比 k 例函数 y= (k≠0)的图象上任意两点, x 画 AB⊥x 轴于 B,CD⊥y 轴于 D,则 |k| 有 S△AOB=S△COD= . 2
图13-1
课堂回顾 · 巩固提升
基础知识 · 自主学习
图13-4
基础知识 · 自主学习
题组分类 · 深度剖析
课堂回顾 · 巩固提升
浙派名师中考
题组一
反比例函数解析式的确定
已知图象上一点求解析式
【 例 1】2 ( 0 1 3 · 巴 中 )如 图 1 3 -5 所 示 , 在 平 面 直 角 坐 标 系 x O y 中,一 次 函 数 y= k x + b(k≠ 0 ) 的 图 象 与 反 比 例 k 函数 y= 的 图 象 交 于 一 、 三 象 限 内 x 的 A、B 两 点 ,直线 AB 与 x 轴 交 于 点 C,点 B 的 坐 标 为 (- 6,n),线 段 OA= 5,E 为 x 轴 正 半 轴 上 一 点 ,且 4 a t n ∠A O E = . 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
1.某闭合电路中,电源的电压为定值,电流强度 I(A)与电阻 R(Ω)成反比例关系,其函 数图象如图所示,则电流强度 I(A)与电阻 R(Ω)的函数解析式是( )
)
答案:D
6 4.(2012· 常德)对于函数 y= ,下列说法中错误的是( x A.它的图象分布在一、三象限 B.它的图象既是轴对称图形又是中心对称图形 C.当 x>0 时,y 的值随 x 的增大而增大 D.当 x<0 时,y 的值随 x 的增大而减小
答案:C
)
考点知识梳理
中考典例精析
基础巩固训练
【点拨】本题考查确定反比例函数的系数 k.
1 【解答】因为 OM=MN=NC,所以 OM= OC.因为△AOC 的面积为 6,所以△AOM 的 3 面积为 2,根据反比例函数中系数 k 的几何意义可知 k=2S△AOM=4.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
k-1 (k 为常数,k≠1). x (1)其图象与正比例函数 y=x 的图象的一个交点为 P,若点 P 的纵坐标是 2,求 k 的值; (2)若在其图象的每一支上,y 随 x 的增大而减小,求 k 的取值范围; (3)若其图象的一支位于第二象限,在这一支上任取两点 A(x1,y 1),B(x2,y2),当 y1>y 2 时,试比较 x 1 与 x 2 的大小. 例 3 (2012· 天津)已知反比例函数 y=
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
考点四反比例函数图象中比例系数k的 几何意义 k k 反比例函数 y= (k≠0)中 k 的几何意义 :双曲线 y= (k≠0)上任意一点向两坐标轴作 x x 垂线,两垂线与坐标轴围成的矩形的面积为|k| .
1 1 如图①和②,S 矩形 PAOB=PA· PB=|y|· |x|=|xy|=|k|,同理可得 S△OPA=S△AOB= |xy|= |k|. 2 2
考点训练
首页
上一页
下一页
宇轩图书
4 5.如图,过 y 轴正半轴上的任意一点 P,作 x 轴的平行线,分别与反比例函数 y=- 和 x 2 y= 的图象交于点 A 和点 B.若点 C 是 x 轴上任意一点, 连接 AC、 则△ABC 的面积为( BC, x )
A.3
B.4
C.5
D.6
答案:A
k 6.点 P 在反比例函数 y= (k≠0)的图象上,点 Q(2,4)与点 P 关于 y 轴对称,则反比例函 x 8 数的解析式为 y=- . x
【点拨】本题结合一次函数考查反比例函数的性质.
【解答】(1)由题意,设点 P 的坐标为(m,2),∵点 P 在正比例函数 y=x 的图象上,∴2 k-1 k-1 =m,即 m=2.∴点 P 的坐标为(2,2).∵点 P 在反比例函数 y= 的图象上,∴2= , 2 x 解得 k=5. k-1 (2)∵在反比例函数 y= 图象的每一支上, 随 x 的增大而减小, y ∴k-1>0, 解得 k>1. x k-1 (3)∵反比例函数 y= 图象的一支位于第二象限,∴在该函数图象的每一支上,y 随 x x 的增大而增大. ∵点 A(x1,y 1)与点 B(x2,y 2)在该函数的第二象限的图象上,且 y 1>y2,∴x1>x2.
)
答案:D
-k2-1 3.已知点(-1,y 1)、(2,y 2)、(3,y 3)在反比例函数 y= 的图象上.下列结论中 x 正确的是( ) A.y 1>y 2>y 3 B.y 1>y 3>y 2 C.y3>y1>y2 D.y 2>y 3>y 1
答案:B
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
考点知识梳理
中考典例精析Biblioteka 基础巩固训练考点训练
首页
上一页
下一页
宇轩图书
考点五反比例函数的应用 解决反比例函数的实际问题时,先确定函数解析式,再利用图象找出解决问题的方案, 特别注意自变量的取值范围.
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
考点知识梳理
中考典例精析
基础巩固训练
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
k 例 2 (2012· 河南)如图,点 A,B 在反比例函数 y= (k>0,x>0)的图象上,过点 A,B 作 x x 轴的垂线,垂足分别为 M,N,延长线段 AB 交 x 轴于点 C,若 OM=MN=NC,△AOC 的 面积为 6,则 k 的值为____________.
考点训练
首页
上一页
下一页
宇轩图书
例 1 (1)(2012· 兰州)近视眼镜的度数 y(度)与镜片焦距 x(m)成反比例.已知 400 度近视眼 镜镜片的焦距为 0.25 m,则 y 与 x 的函数关系式为( ) 400 1 100 1 A.y= B.y= C.y= D.y= x 4x x 400x k-1 (2)(2012· 哈尔滨)如果反比例函数 y= 的图象经过点(-1,-2),则 k 的值是( ) x A.2 B.-2 C.-3 D.3 2 k +1 (3)(2012· 乌鲁木齐)函数 y=- (k 为常数)的图象过点(2,y1)和( 5,y2),则 y1 与 y2 x 的大小关系是( ) A.y 1<y 2 B.y1=y 2 C.y1>y2 D.与 k 的取值有关 (4)(2012· 西宁)如图,
k 反比例函数 y= 的图象与经过原点的直线相交于点 A,B,已知点 A 的坐标为(-2,1), x 则点 B 的坐标为____________.
考点知识梳理 中考典例精析 基础巩固训练 考点训练 首页 上一页 下一页
宇轩图书
【点拨】本组题主要考查反比例函数的图象和性质,解决此类问题时,往往用数形结合 的思想方法 ,在解题中能起到化繁为简、化难为易的作用.这是因为“形”能直观地启迪 “数”的计算,“数”能准确地澄清“形”的模糊 .
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
7.
k 1 如图,已知反比例函数 y= (k≠0)的图象经过点( ,8),直线 y=-x+b 经过该反比例 2 x 函数图象上的点 Q(4,m). (1)求上述反比例函数和直线的函数表达式; (2)设该直线与 x 轴、y 轴分别相交于 A、B 两点,与反比例函数图象的另一个交点为 P, 连接 OP、OQ,求△OPQ 的面积.
y=3x, x1=2, x2=-2, 解方程组 12 得 y1=6, y2=-6. y= x ,
2 R 3 B.I= R 6 C.I= R A.I= D.I=- 6 R
答案:C
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
1 2.已知反比例函数 y= ,下列结论不正确的是( x A.图象经过点(1,1) B.图象在第一、三象限 C.当 x>1 时,0<y<1 D.当 x<0 时,y 随着 x 的增大而增大
)
答案:A
k 2.(2012· 无锡)若双曲线 y= 与直线 y=2x+1 的一个交点的横坐标为-1,则 k 的值为 x ) A.-1 B.1 C.-2 D.2
(
答案:B
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
3.下列函数中,当 x>0 时,y 值随 x 值的增大而减小的是( A.y=x2 B.y=x-1 3 1 C.y= x D.y= 4 x
【解答】(1)C 由近视眼镜的度数 y(度)与镜片焦距 x(m)成反比例,可设近视眼镜的度 k k 数 y(度)与镜片焦距 x(m)之间的函数关系式为 y= (k≠0),把(0.25,400)代入 y= 即可求得 k x x 100 =0.25×400=100,所以 y 与 x 的函数关系式为 y= ,故选 C. x k-1 (2)D 将(-1,-2)代入反比例函数的解析式得-2= ,解得 k=3,故选 D. -1 (3)A 由函数关系式可知-(k2+1)<0,即图象位于第二、四象限,且在每个象限内,y 随 x 的增大而增大,而(2,y 1),( 5,y2)都位于第四象限,2< 5,所以 y1<y 2,故选 A. (4)(2,-1) 反比例函数及正比例函数图象都是关于原点对称的中心对称图象,故其交 点也关于原点中心对称,所以点 B 的坐标为(2,-1).
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
2.反比例函数的图象和性质 k 反比例函数 y= (k≠0)的图象总是关于原点对称的, 它的位置和性质受 k 的符号的影响. x
考点知识梳理
中考典例精析
基础巩固训练
考点训练
首页
上一页
下一页
宇轩图书
考点三反比例函数解析式的确定 由于反比例函数的关系式中只有一个待定系数,因此只需已知一组对应值就可以. 待定系数法求解析式的步骤: (1)设出含有待定系数的函数解析式; (2)把已知条件代入解析式,得到关于待定系数的方程; (3)解方程求出待定系数,从而确定解析式.
