第二章 拉伸压缩3--强度条件和变形计算
材料力学(机械类)第二章 轴向拉伸与压缩

二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1
轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下,杆件伸长 (简称拉伸) 轴向压缩——轴力作用下,杆件缩短 (简称压缩)
2
拉、压的特点:
1.两端受力——沿轴线,大小相等,方向相反 2. 变形—— 沿轴线
3
§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN,求刚索的应力和 C点的垂直位移。 (刚索的 E =177GPa,设横梁ABCD为刚梁)
16
§2-4
材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。
现在要研究材料的整个力学性能(应力 —— 应变):
从受力很小
破坏
理论上——用简单描述复杂
工程上——为(材料组成的)构件当好医生
17
一、 低碳钢拉伸时的力学性能 (含碳量<0.3%的碳素钢)
力均匀分布于横截面上,σ等于常量。于是有:
N d A d A A
A A
得应力:
N A
F
FN
σ
10
例题2-2
A 1
45°
C
2
机械设计基础第2章拉伸与压缩

x
轴பைடு நூலகம்将杆件从位置坐标为x的C截面处截开。
由BC受力图建立平衡方程:
Fx 0
FN F qx 0
(0≤x≤2)
FN F qx 4 2 x
由轴力FN的表达式可知,轴力FN与横截面位置坐标x成线性关系,轴力 图为一斜直线。当x=0时,FN=4 kN;当x=2m时,FN=8 kN。画出轴力 图如图所示,FN.max=8 kN,发生在截面A上。 .
知h=25mm,h0=10mm,b=20mm。求杆内最大正应力。 解: (1)计算轴力。用截面法 求得各截面上的轴力均为
FN F 20 kN
(2) 计算最大正应力。 开槽部分的横截面面积为
A (h h0 )b (25 10) 20 300mm 则杆件内的最大正应力 max为
解:(1)计算D端 支座反力。由整体受力 图建立平衡方程:
Fx 0
FD F1 F2 F3 0
FD F2 F3 F1 14kN
(2)分段计算轴力 将杆件分为三段。用截面法截取如图b,c,d所示的研究对象,分 别用FN1、FN2、FN3替代另一段对研究对象的作用,一般可先假设 为拉力,由平衡方程分别求得:
第三节 应力的概念 拉(压)杆横截面上的应力
一、应力的概念:杆件的强度不仅取决于内力的大 小,还与构件截面的面积有关,即与内力在截面上 的分布密度有关。单位面积上的内力称为应力。 应力:正应力σ 切应力τ 应力的单位:1Pa=1N/m2 1GPa=109Pa 帕-Pa 千帕-kPa 兆帕-MPa 吉帕-GPa 1kPa=103Pa=1kN/m2 1MPa=106Pa=1N/mm2
第二章 拉压3

P 133.5 kN
显然,与前一种方法解出的 P = 97.1 kN 不同。
为什么? 哪一种方法不正确? 错在哪里?
第二种方法不正确。 两杆中的内力,并不一定
同时达到最大允许轴力。
14
§2. 8 轴向拉伸或压缩时的变形
l 直杆轴向拉压时变形的特点
1. 轴向变形
轴向变形量
l l1 l
下面建立变形与力之间的关系
3 许用应力与安全系数
u 塑性材料
[] s
ns
u 脆性材料
[] b
nb
ns 塑性材料的 安全系数
nb 脆性材料的 安全系数
3
3 许用应力与安全系数
u 塑性材料 [] s
ns
l 安全系数的确定
u 脆性材料 [] b
nb
u 材料素质(质量、均匀性、塑性、脆性); u 载荷情况(峰值载荷、动静、不可预见性); u 构件简化过程和计算方法的精确度; u 零件的重要性、制造维修的难易程度; u 减轻重量(飞机、手提设备等)。
73.2 MPa
[ ] 160MPa
(3) 计算杆的变形
BC杆变形 l1
BB1
FN1l1 EA1
0.86103
m
24
(3) 计算杆的变形
BC杆变形
l1
BB1
FN1l1 0.86103m EA1
BD杆变形 l2 DB 2m
l2
BB2
FN 2l2 EA2
P1 154.5 kN
0.732P 113.1 kN
(2) N2 A2 [ ] 50.3 kN
0.518P 50.3 kN
第2章、杆件的变形和强度分析.
计
1.轴向拉伸和压缩变形;2.剪切变形;
算
3.扭转变形;4.弯曲变形。
两种或两种以上的基本变形组合而成的,称为组 合变形。
2.1 变形体静力学分析基础
杆
1.轴向拉伸和压缩变形;
件
的
变
形
及
强
度
3.扭转变形
计
算
2.剪切变形; 4.弯曲变形。
2.2 杆件的内力分析
杆 件
内力的概念: 内力是指构件内部两相邻部分之间的
及
强
度
计
算
2.3 轴向拉伸与压缩变形
杆 推断:杆件在变形过程中横截面始终保持为平面。进一步可 件 推断:轴力在横截面上的分布是均匀的,且方向垂直于横截 的 面。得出横截面的正应力σ计算公式为:
变
mn
形 及 强 度
σ= FN
A
MPa
F
mn
F
计
算 FN 表示横截面轴力(N) F
A 表示横截面面积(mm2)
2.3 轴向拉伸与压缩变形
杆 件
轴力: 拉(压)杆的内力。
的
用截面法求内力:截、弃、
m
变
代、平
F
F
形 及
由平衡方程可求出轴力 的大小 :
强
m
度 计
FN F
F
FN
算
规定:FN的方向离开截面为
F`N
F
正(受拉),指向截面为负(受
压)。
2.3 轴向拉伸与压缩变形
杆 件
截面法是求内力最基本的方法。 选在外力作用点处的截面上。
的应力下工作,且变形很小,故可近似地认
为符合虎克定律。通常以割线Oa的斜率作为
材料力学2-第二章拉伸、压缩与剪切
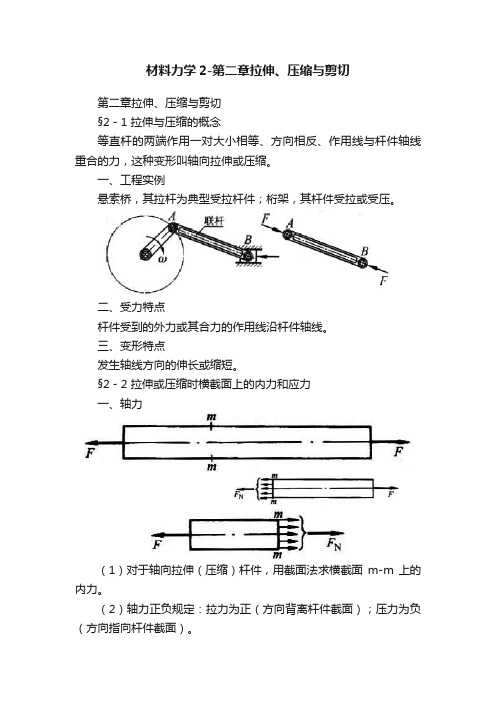
材料力学2-第二章拉伸、压缩与剪切第二章拉伸、压缩与剪切§2-1 拉伸与压缩的概念等直杆的两端作用一对大小相等、方向相反、作用线与杆件轴线重合的力,这种变形叫轴向拉伸或压缩。
一、工程实例悬索桥,其拉杆为典型受拉杆件;桁架,其杆件受拉或受压。
二、受力特点杆件受到的外力或其合力的作用线沿杆件轴线。
三、变形特点发生轴线方向的伸长或缩短。
§2-2 拉伸或压缩时横截面上的内力和应力一、轴力(1)对于轴向拉伸(压缩)杆件,用截面法求横截面m-m上的内力。
(2)轴力正负规定:拉力为正(方向背离杆件截面);压力为负(方向指向杆件截面)。
二、轴力图(1)轴力图:轴力沿轴线方向变化的图形,横坐标表示横截面位置,纵坐标表示轴力的大小和方向。
(2)轴力图作用:通过它可以快速而准确地判断出最大内力值及其作用截面所在位置,这样的截面称为危险截面。
轴向拉(压)变形中的内力图称为轴力图,表示轴力沿杆件轴线方向变化的情况。
(3)作下图所示杆件的轴力图三、横截面上的应力(1)平面假设:变形前原为平面的横截面,变形后仍保持为平面且仍垂直于轴线,只是各横截面间发生沿杆轴的相对平移。
通过对称性原理,平面假设可得以证明。
(2)由平面假设可得,两截面间所有纵向纤维变形相同,且横截面上有正应力无切应力。
(3)由材料的均匀连续性假设,可知所有纵向纤维的力学性能相同。
所以,轴向拉压时,横截面上只有正应力,且均匀分布。
即 N AF dA A σσ==? ANF =σ ,(2-1)为拉(压)杆横截面上的正应力计算公式。
正应力的正负号与轴力正负号相同,拉应力为正,压应力为负。
当轴力与横截面的尺寸沿轴线变化时,只要变化缓慢,外力与轴线重合,外力与轴线重合,如左图,式(2-1)也可使用。
这时某一横截面上的正应力为()()x A x x N F =)(σ (2-2)例题一等直杆受力情况如图a 所示,试作杆的轴力图。
解:(1)先求约束力直杆受力如图b 所示,由杆的平衡方程0F =∑x 得()k Nk N RA F =+-=50104020 (2)求杆中各段轴力AB 段:沿任意截面1-1将杆截开,取左段为研究对象,1-1截面上的轴力为N1F ,设N1F 为正,由左段的平衡方程0F =∑x 得:σ()x σ0F F RA N1=-, N1RA F F 20kN ==BC 段:沿任意截面2-2将杆截开,取左段为研究对象,设轴力N2F 为正,由左段的平衡方程0F =∑x 得:N2RA F F kN 0-+=50, N2F 0kN =-3 结果为负,说明N2F 的指向与所设方向相反,实为压力。
第二章-拉伸和压缩-PPT课件
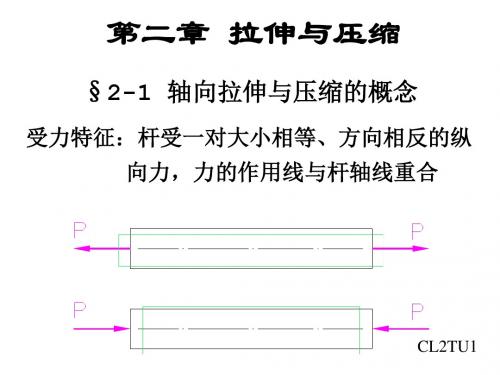
式中: max 称为最大工作应力
[ ] 称为材料的许用应力
根据上述强度条件,可以进行三种类型 的强度计算: 一、校核杆的强度 已知Nmax、A、[σ],验算构件是否满足 强度条件
二、设计截面 已知Nmax、[σ],根据强度条件,求A 三、确定许可载荷
已知A、[σ],根据强度条件,求Nmax
例1:一直径d=14mm的圆杆,许用应力
[σ]=170MPa,受轴向拉力P=2.5kN作 用,试校核此杆是否满足强度条件。
解:
N 2 . 51 0 m a x 1 6 2 M P a < [ ] m a x A 2 6 1 4 1 0 4
3
满足强度条件。
例2:图示三角形托架,其杆AB是由两根
等边角钢组成。已知P=75kN, [σ]=160MPa, 试选择等边角钢的型号。
N 1 0 k N 1
N 5 k N 2
N 2 0 k N 3
CL2TU3
N 1 10 kN N 2 5 kN N 3 20 kN
§2-3 轴向拉伸或压缩杆件的应力
一、横截面上的应力
N P
CL2TU2
平面假设:变形前为平面的横截面变形后 仍为平面
N A
或
E
μ称为横向变形系数或泊松(Poisson)比
l
Pl l EA
N(x) dl dx EA(x)
N(x) l d x EA ( x ) l
x
N ( x)
dx
N ( x)
dx
CL2TU7
M 0 , 得 :NP 7 5 k N 解:由 C A B
3
第02章 拉伸压缩、剪切
第二章拉伸、压缩与剪切§2-1 轴向拉压的概念及实例§2-2 轴向拉压的内力§2-3 应力及强度条件§2-4 材料在拉伸和压缩时的力学性能§2-5 拉压杆的变形计算§2-6 拉压超静定问题§2-7 剪切与挤压1§2-1轴向拉压的概念及实例一、工程实例234三、变形特点二、受力特点四、计算简图FFFF轴向压缩轴向拉伸外力的合力作用线与杆的轴线重合。
沿轴向伸长或缩短。
5mmFF一、求内力设一等直杆在两端轴向拉力F 的作用下处于平衡,欲求杆件横截面m -m 上的内力.§2–2轴向拉压的内力在求内力的截面m-m 处,假想地将杆截为两部分.取左部分部分作为研究对象。
弃去部分对研究对象的作用以截开面上的内力代替,合力为FN 。
mmF F N1、截面法求内力(1)截开mmF F (2)代替67对研究对象列平衡方程F N = F式中:F N 为杆件任一横截面m -m 上的内力.与杆的轴线重合,即垂直于横截面并通过其形心,称为轴力。
(3)平衡mm FFm mFF N若取右侧为研究对象,则在截开面上的轴力与部分左侧上的轴力数值相等而指向相反.mmF FmmF F NmFmNF′892.轴力符号的规定mFFm mFF NmFm(1)若轴力的方向背离截面,则规定为正的,称为拉力。
(2)若轴力的方向指向截面,则规定为负的,称为压力。
NF ′以拉为正m10二、轴力图用平行于杆轴线的坐标表示横截面的位置,用垂直于杆轴线的坐标表示横截面上的轴力数值,从而绘出表示轴力与横截面位置关系的图线,称为轴力图。
将正的轴力画在x 轴上侧,负的画在x 轴下侧.xF NOFFF ⊕11例题1一等直杆其受力情况如图所示,作杆的轴力图。
CABD 600300500400E40kN55kN 25kN 20kN12CABD 600300500400E40kN55kN 25kN 20kN CABDE40kN 55kN 25kN 20kN F R A解: 求支座反力202555400R =+−+−−=∑A xF FkN10R =A F13求AB 段内的轴力F R A F N1CABDE40kN 55kN 25kN 20kN F R A1R 1N =−A F F )()kN (10R 1N ++==A F F14求BC 段内的轴力F R A40kNF N220kN CABDE40kN 55kN 25kN F R A2040R 2N =−−A F F )()kN (5040R 2N ++=+=A F F15F N3求CD 段内的轴力20kN25kNCABDE40kN55kN 25kN20kN F R A3020253=+−−N F )()kN (53N −−=F16求DE 段内的轴力20kNF N440kN55kN 25kN20kN F R A4)((kN)204N ++=F CABDE17F N1=10kN (拉力)F N2=50kN (拉力)F N3= -5kN (压力)F N4=20kN (拉力)发生在BC 段内任一横截面上5010520++CABD 600300500400E40kN55kN 25kN 20kN (kN)50Nmax =F185kN8kN4kN1kNO练习:作图示杆的轴力图。
材料力学-2-拉伸与压缩杆件的应力变形分析与强度计算
FN
+
-
FN
第2章 拉伸与压缩杆件的应力变形分析与强度计算
轴力与轴力图
绘制轴力图的方法与步骤如下:
首先,确定作用在杆件上的外载荷与约束力; 其次,根据杆件上作用的载荷以及约束力,轴力图的分段点: 在有集中力作用处即为轴力图的分段点; 第三,应用截面法,用假想截面从控制面处将杆件截开,在 截开的截面上,画出未知轴力,并假设为正方向;对截开的部分 杆件建立平衡方程,确定轴力的大小与正负:产生拉伸变形的轴 力为正,产生压缩变形的轴力为负; 最后,建立 FN- x坐标系,将所求得的轴力值标在坐标系中, 画出轴力图。
第2章 拉伸与压缩杆件的应力变形分析与强度计算
拉、压杆件横截面上的应力
2.计算直杆横截面上绝对 值最大的正应力
横截面上绝对值最大的正 应力将发生在轴力绝对值最大 的横截面,或者横截面面积最 小的横截面上。本例中,AD段 轴力最大;BC段横截面面积最 小。所以,最大正应力将发生 在这两段杆的横截面上:
拉、压杆件横截面上的应力
在很多情形下,杆件在轴力作用下产生均匀的伸长或缩 短变形,因此,根据材料均匀性的假定,杆件横截面上的应 力均匀分布,这时横截面上的正应力为 FN A 其中FN——横截面上的轴力,由截面法求得;A——横截面面 积。
第2章 拉伸与压缩杆件的应力变形分析与强度计算
拉、压杆件横截面上的应力
轴力与轴力图
FA
A
B" B l l
F1
FN B' '
B" B
F1
3. 应用截面法求控制面上的轴力 用 假 想 截面 分 别 从 控 制 面 A 、 B' 、B"、C处将杆截开,假设横截 面上的轴力均为正方向(拉力), 并考察截开后下面部分的平衡,求 得各截面上的轴力:
工程力学 第二章 轴向拉伸与压缩.
2 sin ( 2 cos 1 )ctg 3.9 103 m
B1 B B1 B3 B3 B
B B
B B12 B1 B 2 4.45 10 3 m
[例2-11] 薄壁管壁厚为,求壁厚变化和直径变化D。
解:1)求横截面上的正应力
dx
N ( x) l dx EA( x) l
例[2-4] 图示杆,1段为直径 d1=20mm的圆杆,2 段为边长a=25mm的方杆,3段为直径d3=12mm的圆杆。 已知2段杆内的应力σ 2=-30MPa,E=210GPa,求整个 杆的伸长△L
解: P 2 A2
30 25 18.75KN
N 1l Pl l1 l2 EA 2 EA cos l1 Pl cos 2 EA
[例2-8]求图示结构结点A 的垂直位移和水平位移。
解:
N1 P, N 2 0
Pl l1 , l2 0 EA Pl y l1 EA
N1
N2
Pl x l1ctg ctg EA
F
FN
FN F
F
F
CL2TU2
2.实验现象:
平截面假设
截面变形前后一直保持为平面,两个平行的截面之 间的纤维伸长相同。 3.平面假设:变形前为平面的横截面变形后仍为平面。 4.应力的计算 轴力垂直于横截面,所以其应力也仅仅是正应力。按 胡克定律:变形与力成正比。同一截面上各点变形相 同,其应力必然也相同。 FN (2-1) A 式中: A横截面的面积;FN该截面的轴力。 应力的符号:拉应力为正值应力,压缩应力为负 值应力。
1. 截面法的三个步骤 切: 代: 平:
F F F F
材料力学 第二章拉伸、压缩与剪切
根据轴力图可以显示各段轴力的大小以及各段的变形是拉伸或压缩
9
§2-2 轴向拉伸或压缩时横截面上的内力与应力
2.应力
轴力的大小并不能用来判断杆件是否有足够的强度,如:
F
F
F
F
细杆先被拉断,说明拉杆的强度不仅与轴力的大小有关,还 与拉杆的的横截面有关,所以必须用横截面上的应力来度量 杆件的受力程度。
3
§2-1 轴向拉伸与压缩的概念与实例
1.轴向拉伸与压缩的实例
2.拉伸压缩动画示范
5
§2-1 轴向拉伸与压缩的概念与实例
3.拉伸与压缩的受力特点
作用于杆件上的外力合力的作用线与杆件的轴 线重合,杆件变形是沿轴线方向伸长或缩短的。
6
§2-2 轴向拉伸或压缩时横截面上的内力与应 力
F1 FN1 0 FN1 F1 2.62 KN (压力)
F1 F2 FN2 0 FN2 F1 F2 1.32KN(压力)
FN 2 F3 0 FN 2 F3 1.32 KN (压力)
8
§2-2 轴向拉伸或压缩时横截面上的内力与应力
轴力图:用平行于杆件轴线的坐标表示横截面的位置, 用垂直于杆件轴线的坐标表示横截面上轴力的数值,从 而绘出表示轴力沿杆轴变化规律的图线。
铸铁压缩时,仍在较小在变形下
突然破裂,破坏断面的法线与轴
线大致成45°角。表明沿斜截面
相对错动而破坏。抗压强度约比
抗拉强度高4-5倍。
24
§2-7 失效、安全因数和强度计算
一、失效 构件因强度、刚度、稳定性等原因不能正常工作。 强度条件引起的失效: 脆性材料制成的构件在拉应力下,当变形很小时就突然断裂; 塑性材料制成的构件在拉断之前已经出现塑性变形,由于不 能保持原有的形状和尺寸,它已经不能正常工作。断裂与出现 塑性变形统称为失效。
