位移法
位移法的基本原理

位移法的基本原理位移法是物理学中一种常用的求解方法,可以用来分析物体在空间中的运动。
它的基本原理是通过观察物体在一段时间内的位移,来推导出物体的速度和加速度等运动信息。
位移法的基本原理可以通过以下几个步骤来理解和应用:1. 观察物体的位移:位移是指物体在某段时间内从一个位置移动到另一个位置的距离。
在位移法中,我们需要观察物体在一段时间内的位移情况,可以通过测量物体的起始位置和结束位置来计算位移的大小和方向。
2. 计算物体的平均速度:在位移法中,我们可以利用物体的位移和时间来计算物体的平均速度。
平均速度是指物体在某段时间内的位移与时间的比值,可以用公式v=Δx/Δt来表示,其中v表示平均速度,Δx表示位移,Δt表示时间。
通过计算平均速度,我们可以获得物体在某段时间内的平均速度信息。
3. 推导物体的瞬时速度:瞬时速度是指物体在某一时刻的速度。
在位移法中,我们可以利用物体的平均速度和时间间隔的缩小来逼近物体的瞬时速度。
当时间间隔趋近于0时,平均速度就可以无限接近瞬时速度。
因此,我们可以通过计算物体在时间间隔趋近于0时的平均速度来推导物体的瞬时速度。
4. 求解物体的加速度:加速度是指物体在某一时刻的速度变化率。
在位移法中,我们可以通过物体的瞬时速度和时间的变化率来求解物体的加速度。
加速度可以用公式a=Δv/Δt来表示,其中a表示加速度,Δv表示速度的变化量,Δt表示时间的变化量。
通过计算加速度,我们可以获得物体在某一时刻的加速度信息。
5. 应用位移法分析运动问题:通过以上步骤,我们可以利用位移法来分析物体的运动问题。
例如,我们可以根据物体的位移和时间来计算物体的速度;根据物体的速度和时间来计算物体的加速度;根据物体的加速度和时间来计算物体的位移等。
通过位移法,我们可以得到物体在不同时间点的运动信息,从而对物体的运动进行更详细和准确的描述。
位移法是一种基于观察物体位移的方法,通过计算物体的位移、速度和加速度等参数来分析物体的运动。
结构力学-位移法的典型方程及计算步骤
(e)
依题意可知并根据叠加原理上述条件可写为:
R1=R11+R12+R1P=r11 Z1+r12 Z2+R1P=0 R2=R21+R22+R2P=r21 Z1+r22 Z2+R2P=0
上述方程称为位移法基本方程,也称为位移法的典型方程。
为了求出典型方程的系数和自由项,可借助于表10-1,绘出基本
结构图,如下图10-7a,b, 和c所示。然后求出各系数和自由项。
r11 1 3i 4i
r12 6i1 0
R1P PL1 0
l
8
Z1=1
4i 1
2
6i 1l
2
Z2=1 1
2
3i M
3 2i 4
(a)
6i 3 l
3i 4 l
(b)
p
MP
PL 3
4
8
(C)
T10-7
1
2
r21 1
2
r22 1
6i l
0
12i
L2
3i
P
L2
2
2
R2P
0
系数和自由项可分为两类,分别由力矩平衡方程 M1=O求得为:
0
6 2 6 9 12 2 11 l Z1 l 2 Z2 16 P 0
Z1 0.02218 Pl Z2 0.02859 Pl 2
M M1Z1 M 2Z2 M P
转到下一节
者的原理有所不同。
§10-7 有侧移的斜柱刚架
B
B’
C’ C
C”
C
A
D
O A,D
B 结点位移图
O为极点,各结点位移前的位置
位移法基本概念

基本概念
F
A
B
C
D
E
BV
CV
D
E
G
解:由图可见,只有AB杆及CD杆有杆端相对侧移 -ΔBV 及ΔCV 。E端为弹簧铰,所以,刚结点有D和E。但是,因为CD杆旳刚 度无限大,ΔCV与D结点旳转角有关。
所以,构造有三个位移法变量:θE 、ΔBV 、ΔCV (或D结点 转角θD)
基本思绪
基本概念
三、位移法旳基本思绪---------先修改,后复原。
[举例]
基本概念
例题6
B
A
B
C
A
D
解:三根杆件,A支座为弹簧铰,有约束能力,也可产生转角, 但不可发生水平及竖向位移。C支座有约束能力,但可产生竖向 位移。
所以,位移法变量有:A、B处旳转角θA及θB ,C处旳竖向 位移Δ,共三个位移法变量。 BC杆有侧移Δ,D处无转角,C截面旳转角不作为位移法变量。
C
B
B
A 1.位移法变量:θB 2.修改旳措施
基本思绪
基本概念
1)在B结点附加刚臂,设想刚臂旳作用只是阻止结点B旳转动, 各杆旳弯矩不能相互传递。
2)求杆端弯矩。因为各杆旳弯矩不能相互 传递。所以AB杆与BC杆旳弯矩可独自求 解。即,对弯矩而言,BC杆等价于一端 固定,另一端铰支旳超静定杆;而AB杆
[举例]
基本概念
例题8 D
E
EI
F
EI
D
E
EI
EI1 EI
A B
C
F
F
解:①这是具有无限刚性杆旳构造,BD杆没有变形,只有刚体 侧移,设弦转角为θ。则因为结点E刚结点旳特征,三杆端在E 点保持相同旳转角,从而,结点E旳转角也为θ ②由结点E旳侧移方向垂直BE杆轴线,所以,ΔD =ΔE =ΔF =ΔH 与θ有关,不是独立旳变量。 ③至于弹簧支座,对变形没有影响,只与构造旳受力有关。
结构力学上第8章 位移法

(非独立角位移) l FQBA
M AB M BA
F 3i A 3i M AB l 0
3、一端固 FQAB
A
B1
B
l
F M AB i A i B M AB F M BA i A i B M BA
(非独立线位移)
q B EI C L
Z1
q B
EI C
Z2 4i
Z1=1
EI A 原结构
L
=
Z2=1
EI A qL2 8 基本体系
=
3i
M1图×Z1 2i
+
6EI L2 6EI M2图×Z2 L2
+
qL2 8 MP图
在M1、M2、MP三个 图中的附加刚臂和链杆 中一定有约束反力产生, 而三个图中的反力加起 来应等于零。
M
q
应用以上三组转角位移方程,即可求出三种基本的单跨超 静定梁的杆端弯矩表达式,汇总如下:
F 1)两端固定梁 M AB 4i A 2i B 6i M AB
M BA
l F 2i A 4i B 6i M BA l
2)一端固定另一端铰支梁
F M AB 3i A 3i M AB l M BA 0 3)一端固定另一端定向支承梁 F M AB i A i B M AB
3
2
1
结点转角的数目:7个
独立结点线位移的数目:3个
D
E
A
B
C
C
D
刚架结构,有两个刚结点D、E, 故有两个角位移,结点线位移由铰 结体系来判断,W=3×4-2×6=0, 铰结体系几何不变,无结点线位移。
A
B
位移法

F B 端为铰支座固端弯矩 M AB 由上式得: F M BA F F 铰 支 M AB M AB (c) 2 B 端为滑动支座:q B FQBA 0
P M A 0 FQBAl M AB M BA M A 0
把式(a) 、(b)代入上式,得:
D F F P 6iq A 12i M AB M BA M A P M AB M BA M A l FQBA 0 l l F F P 6iq Al M ABl M BAl M A l 1 l F F P D q Al ( M AB M BA M A ) (d) 12i 2 12i
§8-3 无侧移刚架的计算
1、无侧移刚架基本未知量的判定:
其位移法基本未知量数目
结构上刚结点的独立角位移数 等于结构上的自由刚结点数 。
(a)
1 D E 2 C F
A
(b)
B
D
EA=
C
1 C
B
1 A
2 B
A
(c)
(d)
说明:
1)强调位移法基本未知量是结 构中自由结点上的独立结点位移。 结点上的独立角位移是自由刚结 点上的角位移。
(2) B 端为铰支座
式(8-5)中
M BA 0
,得:
D M AB 4iq A 2iq B 6i L D 0 2iq A 4iq B 6i L
整理上式得:
M AB
D 3iABq A 3i L
(8-9)
(3) B 端为滑动支座
代入(8-5)式,得:
D 1 qA 式(8-6)中 q B FQAB FQBA 0 ,得: L 2
(8-10)
位移法的知识点总结

位移法的知识点总结一、基本原理1. 位移法的基本原理位移法是以位移为基本变量进行分析的一种结构分析方法。
它的基本原理是根据结构受力状态和边界条件,通过对结构各部分的变形进行分析,推导出结构的位移场。
根据结构力学的基本原理,结构的受力和变形是密切相关的,因此通过分析结构的位移场,可以获得结构的受力分布和变形情况,为结构的设计和分析提供重要参考。
2. 位移的重要性在结构力学中,位移是描述结构变形的基本形式之一,它直接反映了结构受力的情况。
在进行结构分析时,通常可以通过计算结构的位移场来获得结构的受力分布和变形情况。
因此,位移是结构分析的重要变量,在位移法中被广泛应用。
3. 位移法的实质位移法的实质是通过假设结构各部分的变形是线性的,即受到外力作用后,结构的变形与受力成线性关系。
这一假设是位移法能够简化结构分析的基础,使得结构分析更加方便和实用。
二、应用范围1. 适用范围位移法适用于各种类型的结构,包括梁、柱、板、桁架、壳体等。
它可以用于解决结构在受力作用下的位移和变形问题,对于复杂结构的受力分析和设计具有广泛的适用性。
2. 适用条件位移法的应用条件包括结构受力状态和边界条件的明确,结构各部分的变形可线性假设,结构受力和变形之间存在较强的相关性等。
在满足这些条件的情况下,位移法可以有效地用于解决各种结构受力和变形问题。
三、操作步骤1. 结构建模首先需要对结构进行建模,确定结构的几何形状、受力条件和边界条件等。
通过建模可以获得结构的刚度矩阵和载荷向量,为后续的分析提供基础数据。
2. 变形分析根据结构的刚度矩阵和载荷向量,可以建立结构的位移方程。
通过对位移方程进行分析,可以获得结构的位移场,揭示结构受力和变形的关系。
3. 反演求解根据结构的位移场,可以反演求解结构的受力分布和变形情况。
通过求解可以获得结构各部分的受力情况,评估结构的受力状况和安全性。
4. 结果分析最后需要对求解结果进行分析,评估结构的受力和变形情况。
第六章位移法
第六章位移法一、几个值得注意的问题1、位移法的适用条件(1)位移法既可以求解超静定结构,也可以求解静定结构;正,顺时针为负。
4柱顶有相同的水平线位移。
(图中的-=50。
B 点以6-1-17 用位移法计算某一结构后,当荷载改变了,这应重新计算位移法基本方程式中的全部系数和自由项。
( )6-1-18 图6-1-5所示结构对称,荷载为反对称,用位移法计算时结点位移基本未知量最少可取为2个。
( )图6-1-56-1-19 位移法典型方程的右端项一定为零。
()6-1-20 用位移法求解结构内力时如果PR一定为零。
()M图为零,则自由项1P6-1-21 结构按位移法计算时,其典型方程的数目与结点位移数目相等。
()6-1-22 位移法未知量的数目与结构的超静定次数有关。
( )6-1-23 位移法的基本结构为超静定结构。
( )6-1-24 位移法是以某些结点位移作为基本未知数,先求位移,再据此推求内力的一种结构分析的方法。
()6-1-26 图6-1-7所示结构的位移法基本体系,其典型方程系数k为20,图中括号内数字为线刚度。
11()6-1-306-1-31 超静定结构中杆端弯矩只取决于杆端位移。
()6-1-32 位移法中的固端弯矩是当其基本未知量为零时由外界因素所产生的杆端弯矩。
()6-1-33 图6-1-12a对称结构可简化为图(b)来计算。
()6-1-34 位移法中角位移未知量的数目恒等于刚结点数。
()q,线位移未知量为_______。
图6-2-26-2-3 图6-2-3所示结构位移法基本方程的系数k11= __________EI/l。
A.18;B. 16;C.15;D.17。
A.附加约束i发生Z i=1时在附加约束i上产生的反力或反力矩;B.附加约束i发生Z i=1时在附加约束j上产生的反力或反力矩;C.附加约束j发生Z j=1时在附加约束i上产生的反力或反力矩;D.附加约束j发生Z j=1时在附加约束j上产生的反力或反力矩。
位移法
位
移
法
5.1位移法基本概念 5.1位移法基本概念
在计算超静定结构时,可设法求出结构中 在计算超静定结构时, 的某些位移, 的某些位移,通过位移与内力之间确定的 对应关系,求出相应的内力, 对应关系,求出相应的内力,从而对超静 定结构进行计算, 定结构进行计算,这种计算超静定结构的 方法叫 位移法 。
位移法中采用增加附加约束,以限制原结构的结点 位移法中采用增加附加约束, 位移而得到的新结构,称为位移法的基本结构 位移而得到的新结构,称为位移法的基本结构 ● 在刚结点处附加刚臂,只限制刚结点的角位 移,不限制 在刚结点处附加刚臂, 点线位移,用符号“▼” “▼”表示刚臂 结 点线位移,用符号“▼”表示刚臂 对应于独立的结点线位移用附加链杆,只限制结点线位移。 ● 对应于独立的结点线位移用附加链杆,只限制结点线位移。
5.4 位移法典型方程
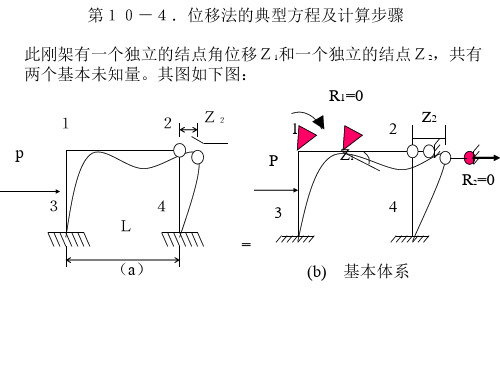
图(a)中刚架在刚结点B 中刚架在刚结点B 有一个独立角位移, 有一个独立角位移,编号 Z1;另外结点A 为Z1;另外结点A、B、C 有一个独立水平线位移, 有一个独立水平线位移, 编号为Z2, 编号为Z2,基本未知量和 基本结构见图( 基本结构见图(b)。
a图
b图
基本结构在外荷载q 基本结构在外荷载 单独作用下引起的弯 矩图,记为M 矩图,记为 P图,见 )。它引起附 图(C)。它引起附 )。 加刚臂和附加链杆的 反力矩和反力, 反力矩和反力,分别 用R1P、R2P(图C) 、 ) 基本结构在Z1=1及 基本结构在Z1=1及 Z2=1单独作用下产 Z2=1单独作用下产 生的弯矩图, 生的弯矩图,称为 单位弯矩图( 单位弯矩图(d、e )。用r11、r21、 图)。用r11、r21、 r12、r22表示在相应 r12、r22表示在相应 的附加约束中产生 的反力矩及反力。 的反力矩及反力。
位移法基本概念
8 — 1 位移法基本概念一. 位移法的基本概念1. 位移发育力法的比较:1〉力法把多余约束力选为基本未知量,位移法把节点位移选为基本未知量。
2〉力法是把超静定结构拆成静定结构,再由静定结构构过渡到超静定结构。
位移法是将结构拆成单个杆件,再由杆件过渡到结构。
3〉力法是从静定结构为出发点,位移法是以杆件位出发点。
EI =M AB 2 B B EI=M Q C22〉荷载作用产生德杆端变矩称为固端变矩8P =M BA F 8P -=M AB F3〉转角与荷载共同作用产生的杆端变矩:P +EI =M B BA 814Q (1)B B EI=M Q C 4 (2)82P-EI =M B AB Q (3)B B EI=M Q C 22 (4)4〉如何求B Q ?取结点B 平衡。
0,0=M +M =MB BA B∑C40481=EI+P +EI B B Q QEI+P -=B )(322 Q 将B Q 代入式(1)(2)(3)(4)式求得B A B B BA M M M M C C ,,,18—2 位移法的基本未知量一.未知量:1>刚结点的角位移;2>刚结点的线位移。
二.刚结点角位移未知量的确定:c.∆产生的杆端变矩:∆-=M ∆-=M BA ABi i 6''',6''' d.荷载作用产生的固端变矩:8,8 P =M P -=M BA BA FFe.据叠 加原理的杆端变矩:P ∆B A ...Q Q 共同作用产生的杆端变矩。
转角位移方程:Fi iQ iQ BA B A BA M +∆-+=M642 Fi iQ iQ AB B A AB M +∆-+=M624 2. 一端固定一端铰支的梁: F iiQ AB A AB M +∆-=M3δ 0=M BA.这是位移各杆刚度取相对值,计算方便。
EI =1 解:1.未知量:∆B ,,C ϕϕ3. 转角位移方程——杆端变矩 816203832⨯+=+=M B BAB BA BA ϕϕ q iC C C C Ci i q ϕϕϕϕ2412252024122++⨯-=++-=M B B B B BA BB c CBC CB CB CBi i q ϕϕϕϕ2412252024122++⨯=++=M BC C CD CD i ϕϕ33==M∆⨯-⨯=∆-=M B BE BE B BE 443643464ϕϕ i i BE∆⨯-⨯=∆-=M B BE B BE EB 443643262ϕϕ i i∆⨯-⨯=∆-=M B 621621464ϕϕCF CF C CF CF i i ∆⨯-⨯=∆-=M 621621262B CF CF C CF FC i i ϕϕ∆,C0=M BC07.1125.12=-∆-+B C ϕϕ=M+M+M即:BA BC CBMKNCD.18.14-=M ; MKN.5=MBE; MKN.59.3=MEB。
第8章_位移法
k11
MP
3i
3
1
k11 4i 3i 7i
4i
将以上两式代入基本方程,得:
kR1111
4i
1
2
3Pl 7i Z1 16 0
1=Z1
Z1=
3i 1
3Pl Z1 112i
3
2i
M1
4、根据叠加原理作最后弯矩图
M M1Z1 MP
3Pl Z1 112i
3Pl 28
1
2
11Pl 56
3
3Pl 56
1
M 2
X2=1 1/l
l 3EI
X1
l 6EI
X2
l
A
l 6EI
X1
l 3EI
X2
l
B
A
fA
X1
fB
令 i EI l 线刚度
X1
4i A
2iB
6i l
X1=1
X2
2i A
4iB
6i l
1
M AB
4i A
2i B
6i l
M BA
2i A
4i B
6i l
M 1
M 2
X2=1
VAB
M AB
M BA l
C
D
C
D
1
C
D
A
B
A
B
1
试确定图示结构的独立线位移数
4
0
3、位移法的基本未知数
n n nl
例:确定结构按位移法求解的基本未知数
n 4 n n nl 4 2 6
nl 2
思考:确定结构按位移法求解的基本未知数
n n nl 6 2 8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A θA θB
B Δ
可由两端固定的等截面梁转角位移方程推出:
6i M AB 4i A 2i B AB l 6i ----两端固定的等截面梁转角位移方程 M BA 2i A 4i B AB l
因为B端为铰支, 可由MBA = 0,可得:
1 3 B A AB 2 l
位移法:以某些结点位移基本未知量
用力法求解,有6个未知数。 用位移法求解,未知数=
?个。
5.力法与位移法的适用范围:
力 法: 超静定结构
位移法:超静定结构,也可用于静定结构。 一般用于结点较少而杆件较多的刚架。
位移法正负号规定
★杆端角位移、杆两端相对线位移(侧移)Δ :顺时针为正 ★ 杆端弯矩:绕杆端顺时针为正、绕结点逆时针为正
剪力:以绕隔离体顺时针转动为正。
三、位移法的基本解题思路
例:要求用位移法计算图示刚架?
Z1 Z1
为了使问题简化,作如下 计算假定:
对于受弯杆件,
1.略去其轴向变形和剪 切变形的影响;
2.设发生的弯曲变形是 微小的。 即认为受弯直杆之间的距离在变形后保持不变
由此可知,结点1只有角位移Z1,而无线位移。因 此,汇交于结点1的两杆杆端也应有同样的转角Z1。
M2
X2=1
两端固定等截面梁的杆端弯 矩的一般计算公式,通常也称 为转角位移方程
Δ
1/ l 1/ l
两端固定的等截面梁
A θA θB
B Δ
Δ AB M AB 4iθ A 2iθ B 6i L M 2iθ 4iθ 6i Δ AB BA A B L
FQAB FQBA
B B
3i
1
0 0
l
3i
l
3i
l2
A
θ=1
B
i
-i
0
mAB
二、由外部荷载求固端反力矩
q
EI l
q EI l mBA
mAB
ql 2 8
ql 2 mBA 8
» 在已知荷载及杆端位移的共同作用下的杆端力
6i 一般公式(转角位移方程): M AB 4i A 2i B m AB M BA l 6i 2i A 4i B mBA l
FP B
l/2
FP B
l/ 2
l/ 2
§8-3 位移法的基本未知量和基本结构
一、位移法的基本未知量----独立的结点位移(角位移和线位移) 两个假定: 1.略去受弯杆件的轴向变形和剪切变形影响; 2. 发生的弯曲变形是微小的。
即认为受弯直杆之间的距离在变形前后保持不变
1.无侧移结构
1
----基本未知量为所有刚结点的转角
F F M AB M BA ——固端弯矩。(两端固定的梁在荷 载、温度变化的作用下的杆端弯矩)
两端固定的等截面梁转角位移方程:
一端固定、另一端铰支的等截面梁转角位移方程:
一端固定、另一端定向滑动支座的等截面梁转角位移方程:
F M AB iθ A M AB F M i θ M A BA BA
θA
A
B
将上式θB 代入MAB式可得:
M AB 3i 3i A l
---- 一端固定、另一端铰支的等截面梁转角位移方程
常见的单位杆端位移引起的杆端弯矩和剪力
单跨超静定梁
A A
MAB
B B
MBA
QAB= QBA
θ=1
4i
6i l
2i
6i l
6i
12i
3i
l
l2
1
A
A
θ=1
A θA
X1
B θB Δ
X2
EI 令i , 称为杆件的线刚度 l 6i X 1 4i A 2i B AB l 6i X 2 2i A 4i B AB l
X1=1
1
M1
1
用M AB代替X1,M BA代替X 2,可得
6i M AB 4i A 2i B AB l 6i M BA 2i A 4i B AB l
11
1 l 2 l 22 EI 2 3 3EI 1 l 1 l 21 EI 2 3 6 EI
X1
X1=1
12
1C
1
M1
M2
X2=1
AB ( ) 2C l
1
1/ l
弦转角
β
AB
Δ
1/ l
l l AB X1 X2 A 3EI 6 EI l l l AB X1 X2 B 6 EI 3EI l
M AB M BA L
6iθ A 6iθ B Δ AB FQAB L L 12i 2 L 6iθ A 6iθ B Δ AB F 12i QBA L L L2
如何计算一端固定、另一端铰支等截面梁的转角位移方程? θA
⑴ 解出单跨超静定梁在常见外部因素作用下 的内力。
⑵ 确定以哪些结点的哪些位移为基本未知量。
⑶ 如何建立一般情形下的基本方程。
§8-2 等截面直杆的转角位移方程
θA
ΔAB
X2
一、由杆端位移计算杆端弯矩与剪力 A 先用力法求解单跨超静定梁
B
θB
11 X 1 12 X 2 1C A 21 X 1 22 X 2 2C B
R1P
P
基本结构
此时附加刚臂中产生了反力矩R1P,反力矩规定以顺时 针为正。
Z1
R1P
P
Z1
基本结构
于是,基本结构与原结构就发生了差别,表现为:
1.由于加了约束,使结点1不能转动,而原来是能 转动的。 2.由于加了约束,产生了约束反力矩,而原来是 没有这个约束反力矩的。
为了消除基本结构与原
R11
程
Байду номын сангаасM
1
0 ,求出 :
7 EI r11 l
M1
1 R1P Pl 8
Pl 8
P
Pl 8
MP图
r11
7 EI l
1 R1P Pl 8
r11Z1 R1P 0
Pl 2 Z1 56EI
将这些结果代入位移法基 本方程中后解方程,即得
最后,根据叠加原理 M M P M 1 Z1 ,即可求出最后弯 矩图 。
Z1
结构的差别,在结点 1 的附
加约束上人为地加上一个外
力矩 R11,迫使结点 1 正好转
动了一个转角 Z1,于是变形
复原到原先给定的结构。
结点1正好转动一个转角Z1时,所加的附加约束不再 起作用,其数学表达式为:
R1=0
即在外荷载和应有的转角Z1共同作用于基本结构时, 附加约束反力矩等于零。 根据叠加原理,共同作用等于单独作用的叠加:
单跨超静定梁在梁端1、柱顶1处分别转动单位角位移(即
Z1=1 )时的弯矩图及在外荷载单独作用下的弯矩图。
画出各单跨超静定梁在梁端1、柱顶1处分别转动单位 角位移(即Z1=1 )时的弯矩图
r11 Z1=1
M1
画出各单跨超静定梁在外荷载单独作用下的弯矩图
R1P
1
P
Pl 8
P
Pl 8
MP图
A
现取 M 1 图、MP图中的结点1为隔离体,由力矩平衡方
Z1
整个刚架的变形只要用角 位移Z1来描述,如果能设法 求得转角Z1,即可求出刚架 的内力。
Z1
为了求出Z1值,可先对原结构作一些修改
1
1
B
基本结构
A
这样,原结构就被改造成两个单跨超静定梁: 其中: 1B是两端固定梁; 1A是一端固定、另一端铰结的梁。
在基本结构上加上原来的 力P,由于附加刚臂不允许结 点1转动,此时只有梁lB发生 变形,梁1A则不变形。
2. 回顾力法的解题思路
先求多余未知力 结构内力
结构位移
具体解题过程:
超静定结构 拆成基本结构 加上某些条件
位移条件(力法典型方程)
3. 反推位移法的解题思路
先求某些结点位移 结构内力
具体解题过程:
结 构 拆成单根杆件 的组合体
1.杆端位移协调条件
2.结点平衡条件
加上某些条件
4.力法与位移法最基本的区别:基本未知量不同 力法:以多余未知力基本未知量
q
ql2/3 B A ql2/6
F M AB ql 2 / 3 F M BA ql 2 / 6
ql B A B
A
l
F FQ AB ql F FQ BA 0
A
FP B l/2
l/2
3FPl/8 A FP l/8
F M AB 3FP l / 8 F M BA FP l / 8
FP
B
A
B
F FQ AB FP F FQ BA 0
小
结
1 计算形常数时常见的几种单跨超静定梁
1 A
B A B 1
1 A
A
B
B
1
1 A B
2 计算载常数时常见的几种单跨超静定梁
q
A B A
表 8-1 等直梁杆端 弯矩和剪力。P181 FP B
l/2
l/2
q A B A l/2 q A l B A
q A B
ql2/8 A B
5ql/8 A
B 3ql/8
M
F AB
ql / 8
2
F FQ AB 5ql / 8 F FQ BA 3ql / 8
FP
3FP l/16 B A B A
