非饱和土剑桥模型的基本框架
剑桥模型

1.剑桥模型(Cam-clay Model )剑桥模型是由英国剑桥大学Roscoe 等于1963年提出的,这个模型基于正常固结土和超固结土试样的排水和不排水三轴实验基础上,提出了土体临界状态的概念,并在实验基础上,再引入加工硬化原理和能量方程,提出剑桥模型。
这个模型从试验和理论上较好的阐明了土体弹塑性变形特征,尤其考虑了土的塑性体积变形,因而一般认为,剑桥模型的问世,标志着土本构理论发展的新阶段的开始。
(1) 剑桥模型。
剑桥模型基于传统塑性位势理论,采用单屈服面和关联流动法则屈服面形式也不是基于大量的实验而提出的假设,而是依据能量理论提出的。
依据能量方程,外力做功dW 一部分转化为弹性能e dW ,另一部分转化为耗散能(或称塑性能)p dW ,因而有dW =e dW +p dW(1-154) e dW =e eV qd d p γε+' (1-155)p pV p qd d p dW γε+'= (1-156)剑桥模型中,由各向等压固结实验中回弹曲线确定弹性体积变形p p d e k d eV ''+=1ε (1-157)式中,k 为膨胀指数,即 p In e '-回弹曲线的斜率。
同时,假设弹性剪切变形为零,即0=e d γ (1-158)则弹性能 p d ekp p d k dW e '+=''=1υ (1-159)剑桥模型中还建立如下的能量方程,即塑性能等于由于摩擦产生的能量耗散,则有 p p p V d p qd d p γνγε'=+'- (1-160)式中第一项改用负号,是因为p V d ε取以压为正。
代入式(1-161)⎪⎭⎪⎬⎫==ij pij p d s d d λεεθθσ (1-161) 并考虑式(1-158),则有γγγνd p M d p M d p dW p p p '='='= (1-162) 式中,M 为q p '-'平面上的破坏线的斜率,即ϕϕ'-'=sin 3sin 6M (1-163) 式中ϕ'为土体有效摩擦角。
高等土力学题目汇总

高等土力学题目汇总 Modified by JACK on the afternoon of December 26, 2020一、填空题1.饱和土体上的总应力由土骨架承担的 有效应力 和由孔隙承担的孔隙水压力组成,土的强度及变形都是由土的有效应力决定的。
2.莱特邓肯屈服准则在常规三轴压缩实验中,当φ=0°时它在π平面上的屈服与破坏轨迹趋近于一个圆;当φ=90°时,它退化为一个正三角形。
由于在各向等压σ1=σ2=σ3时I 13I 3=27,所以K f >27是必要条件,因为静水压力下不会引起材料破坏。
3. 东海风力发电桩基础有8根。
4.通过现场观测与试验研究,目前认为波浪引起的自由场海床土体响应的机制主要取决于海床中孔隙水压力的产生方式。
孔隙水压力产生方式有两种:超孔隙水压力的累积(残余孔隙水压力)、循环变化的振荡孔隙水压力5.目前计算固结沉降的方法有( )、( )、( )及( )。
答案:弹性理论法、工程实用法、经验法、数值计算法。
6.根据莫尔—库伦破坏准则,理想状态下剪破面与大主应力面的夹角为( )。
答案:45°+φ/27.土的三种固结状态:欠固结、超固结、正常固结。
8.硬化材料持续受力达到屈服状态后的变化过程:屈服 硬化 破坏9.相对密实度计算公式I D = e max −ee max −e min 。
10.静力贯入试验的贯入速率一般为 2 cm/s 。
11用一种非常密实的砂土试样进行常规三轴排水压缩试验,围压为 100kPa 和3900kPa ,用这两个试验的莫尔圆的包线确定强度参数有什么不同?答:当围压由100kPa 增加到3900kPa 时,内摩擦角会大幅度降低。
12.塑性应力应变关系分为_____理论和_____________理论两种增量(流动)、全量(形变)13.三轴剪切试验依据排水情况不同可分为()、()、()答案:不固结不排水剪、固结不排水剪、固结排水剪。
高等土力学思考题与概念题

⾼等⼟⼒学思考题与概念题⾼等⼟⼒学思考题与概念题公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]思考题第⼀章:1.对于砂⼟,在以下三轴排⽔试验中,哪些试验在量测试样体变时应考虑膜嵌⼊(membrane penetration)的影响HC, CTC, CTE, RTC, RTE, 以及平均主应⼒为常数的TC TE 试验。
2.对于砂⼟,在常规三轴固结不排⽔(CU)压缩试验中,围压为常数,其膜嵌⼊(membrane penetration)效应对于试验量侧的孔隙⽔压⼒有没有影响,为什么对于常规三轴固结排⽔试验对于试验有⽆影响3.对于砂⼟,在常规三轴固结不排⽔(CU)压缩试验中,围压为常数,其膜嵌⼊(membrane penetration)效应对于试验的不排⽔强度有没有影响,4.在周期荷载作⽤下饱和砂⼟的动强度d (或d )如何表⽰定性绘出在同样围压3,不同初始固结⽐1/3下的动强度曲线。
5.在⼀定围压下,对⼩于、等于和⼤于临界孔隙⽐e cr 密度条件下的砂⼟试样进⾏固结不排⽔三轴试验时,破坏时的膜嵌⼊对于量侧的孔隙⽔压⼒有何影响对其固结不排⽔强度有什么影响(⽆影响、偏⼤还是偏⼩)6.在⼟⼯离⼼模型试验中进⾏固结试验,如果模型⽐尺为100,达到同样固结度,模型与原型相⽐,固结时间为多少7.举出三种⼟⼯原位测试的⽅法,说明其⼯作原理、得到的指标和⽤途。
8.对于粗颗粒⼟料,在室内三轴试验中常⽤哪些⽅法模拟各有什么优缺点9.真三轴试验仪器有什么问题影响试验结果⽤改制的真三轴试验仪进⾏试验,其应⼒范围有何限制10.在饱和⼟三轴试验中,孔压系数A 和B 反映⼟的什么性质如何提⾼孔压系数B 11.在p, q 坐标、,坐标和在平⾯坐标下画出下⾯⼏种三轴试验的应⼒路径(标出应⼒路径的斜率)。
(1) CTC (常规三轴压缩试验)(2) p =常数,b==常数,真三轴试验;(3) RTE (减压的三轴伸长试验)。
非饱和土土力学(新)

传统(经典)土力学的局限
1、传统土力学理论都是针对饱和土建立的,对非饱和土无能为力,只
能称之为饱和土力学
两相介质(固体和液体)
只涉及土的变形,不考虑水量的变化(因为对饱和土
v w)
唯一应力状态变量——有效应力
用总应力或有效应力分析
pw
传统(经典)土力学的局限
一屈服面模型。
* p0 p0 ms n[e / patm 1]
吸力的影响
200
吸力 s(kPa)
150 100 50 0 0 50 100 150 200 250 300 净平均应力 p(kPa)
LC屈服面
s
s * p p0 ms n e pat 1
Ri (1 sin )( 1 3 ) 3 ua m 2 0 Et patm[1 ] ( K m1s)( ) b 2(c s f tan ) cos 2( 3 ua ) sin patm
Kt Kt0 m2 s
起始模量、体积模量、土骨架和水量变化都与吸力有关
修正SSCC 含水率4.8% 含水率15.2% 含水率25.4% 未修正SSCC 饱和试样
'
10 20 30
饱和破坏包络线 40 50 60
和及非饱和时,其摩擦
角变化不大,主要是粘 聚力随含水量在变化。 明确了粘聚力的物理含 义。
-50
-40
-30
-20
-10 0 -20 -40
n '(kPa)
未修正SSCC曲线
-60 -80 修正SSCC曲线 -100
(ua uw)(kPa)
) tan ( ua ) tan ( s
剑桥模型推导
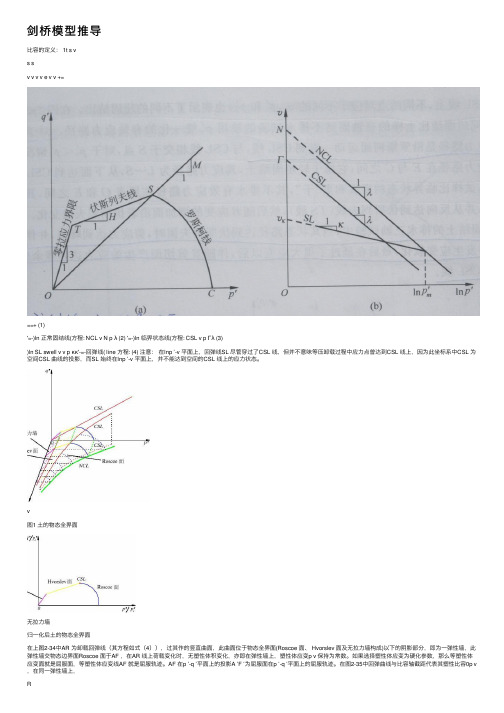
剑桥模型推导⽐容的定义: 1t s vs sv v v v e v v +===+ (1)'=-)ln 正常固结线(⽅程: NCL v N p λ (2) '=-)ln 临界状态线(⽅程: CSL v p Γλ (3))ln SL swell v v p κκ'-=-回弹线( line ⽅程: (4) 注意:在lnp ’-v 平⾯上,回弹线SL 尽管穿过了CSL 线,但并不意味等压卸载过程中应⼒点曾达到CSL 线上,因为此坐标系中CSL 为空间CSL 曲线的投影,⽽SL 始终在lnp ’-v 平⾯上,并不能达到空间的CSL 线上的应⼒状态。
v图1 ⼟的物态全界⾯⽆拉⼒墙归⼀化后⼟的物态全界⾯在上图2-34中AR 为卸载回弹线(其⽅程如式(4)),过其作的竖直曲⾯,此曲⾯位于物态全界⾯(Roscoe ⾯、 Hvorslev ⾯及⽆拉⼒墙构成)以下的阴影部分,即为⼀弹性墙,此弹性墙交物态边界⾯Roscoe ⾯于AF ,在AR 线上荷载变化时,⽆塑性体积变化,亦即在弹性墙上,塑性体应变p v 保持为常数。
如果选择塑性体应变为硬化参数,那么等塑性体应变⾯就是屈服⾯,等塑性体应变线AF 就是屈服轨迹。
AF 在p ’-q ’平⾯上的投影A ’F ’为屈服⾯在p ’-q ’平⾯上的屈服轨迹。
在图2-35中回弹曲线与⽐容轴截距代表其塑性⽐容0p v ,在同⼀弹性墙上,R或同⼀屈服线上,弹性墙的塑性⽐容0const p p v v ==,也就是说其塑性体应变p v ε为常数。
剑桥模型基于传统塑性位势理论,采⽤单屈服⾯和相关联流动法则。
屈服⾯形式(⽅程) A ’F ’不是基于试验⽽提出的,上⾯已根据物理意义在⼏何上表⽰出屈服⾯A ’F ’ ,但还⽆法⽤数学表达式表⽰,剑桥模型是依据能量理论得出的其屈服⾯⽅程,实质上是⼀种假设。
依据能量⽅程,外⼒(荷载)做功dW ⼀部分转化为变形体的弹性变形能e dW (可储存在变形体内,外⼒或荷载卸除时,可完全释放出来),另⼀部分转化为耗散能(或称塑性变形能,外⼒或荷载卸除时,不能再释放出来)p dW ,因⽽有e p dW dW dW =+ (5)两种变形能可表⽰如下:e e e v s dW p d q d εε''=+ (6) p p p v s dW p d q d εε''=+ (7)关于弹塑性变形能,Roscoe 作了如下的假设:(1) 假定⼀切剪切应变都是不可恢复的, 亦即⽆弹性剪应变, 只有不可恢复的塑性剪应变(总剪应变等于塑性剪应变)0e s d ε= (8) p s s d d εε= (9)(2)假定弹性体应变可从各向等压固结试验中所得的回弹曲线求取,即由式(4)可得e dp dv pκ'=-' (10) 11e e vdv dp d e e p κε'=-='++ (11) 1e e v dW p d dp eκε''==+ (12)故:1p e v v v v dp d d d d e p κεεεε'=-=-'+ (13)(3)假定全部耗散能(塑性变形能)等于由摩擦产⽣的能量耗散, 即:p p p s s dW p d Mp d µεε''== (14)式中 µ为内摩擦系数, 其值等于p ’-q ’平⾯上临界状态线CSL 的斜率M63s i n s i n M ??'='- (三轴压缩) (15)或 63s i n s i n M ??'='+ (三轴伸长) (16)所以1e p p s dW dW dW dp Mp d eκε''=+=++ (17)⽽单位体积的⼟在p ’,q ’应⼒作⽤下如产⽣应变v d ε和s d ε, 变形能为v s dW p d q d εε''=+ (18)则由式(17)和式(18)可得能量⽅程:1pv s s p dq d d p M p deκεεε''''+=++ (19) 于是 ()1p v s dp p d Mp q d e p κεε'??'''-=- ?'+?? 将式(13)代⼊上式, 则()p p v s p d Mp q d εε'''=-或 p v ps d q M M d p εηε'=-=-' (20) 式(20)实际表⽰了流动法则, 即表⽰了塑性应变增量在p ’-q ’平⾯上的⽅向, 与这⼀⽅向正交的轨迹就是在这个平⾯上⼟的屈服轨迹(相适应的流动法则),如图2-34所⽰.设此屈服轨迹的⽅程为:()0,,f p q H ''= (21)则0f f fdf dp dq dH p q H''=++='' (22) 因为在同⼀屈服⾯上硬化参数为常数, 所以0dH =, 则0f fdf dp dq p q ??''=+=''(23) 根据相适应流动法则p v fd d p ελ='(24)p s fd d q ελ='(25) 将以上两式代⼊式(23),则得0p p v s dp d dq d εε''+= (26) 将式(20)代⼊上式,则得0dq q M dp p ''-+=''(27) 将此微分⽅程变换可得到20()Mq dp Mp dq dp Mp p '''''-++=''积分得到ln q p C Mp ''+='(28) 式中 C 为积分常数. 利⽤p ’轴上起始各向等压固结试验点A, 对应0p p ''=, 0q '=代⼊上式,则得 0ln C p '=, 将之代⼊式(28), 则得得到湿粘⼟(正常固结和轻超固结⼟)的屈服轨迹⽅程为00ln p q f M p p ''=-=''(29) 其在p ’-q ’平⾯上的形状如图2-34和图2-35(a)所⽰, 像⼀个”帽⼦”, 是⼦弹头形,以0p '为硬化参数.由于NCL 上每⼀个0p '都对应于⼀个0p v (或p v ε), 所以实际上这⼀模型是以塑性体应变p v ε为硬化参数.对于重超固结⼟, 可得到类似的屈服⾯, 只是对应的0p '不同. 空间⽆拉⼒墙的⽅程为3q p ''= 03e x p M h v p h Γλ--??'≤≤-(30) Hvoslev ⾯的⽅程为()e x p ()vq h p M h Γλ-''=+- (31)式中 h 为Hvoslev 线的斜率. 空间Roscoe ⾯的⽅程为:(l n )Mp q N v p λλκ'''=--- (32)由湿粘⼟对应0p p ''=, 0v v =的不排⽔试验路径在p ’-q ’平⾯上的投影或归⼀化的Roscoe ⾯, 由式(2)得00ln v v N p λ'==- (33) 将式(33)代⼊式(32),则得对应不排试验路径在p ’-q ’平⾯上的⽅程为00ln p q Mp p λλκ''-=''- (34)也为指弹头形, 但显然此不排⽔路径与屈服轨迹并不重合, 不排⽔路径在屈服轨迹以外.剑桥模型增量型应⼒-应变本构关系将式(32)微分, 可得()dv dq dp dp Mp p λκλη??-'''=--+??''?? (35) 因由式(11)知 ()1v d v e d ε=-+ 所以 ()()111/v dp M d dq dp dp dq e Mp p e Mp λκλλκλεηηλκ'--??''''=-+=-+ '''++- (36) ⼜因 q p η'=', dq d dp p p ηη''=-'' (37) 于是 11v dp d d e M p λκεηλ'??-=+??'+??(38) 将式(38)代⼊能量⽅程(19), 可得()1s dq d dp e Mp M λκεη'??-'=+??'+-?(39) 于是剑桥模型的弹塑性矩阵可表⽰为:()1111v s M d dp d e Mp dq M ληελκλκεη??-??'--??=''+-?? (40) 修正剑桥模型:1965年, 英国剑桥⼤学的Burland 采⽤了⼀种新的能量⽅程形式, 得到了修正剑桥模型.他建议以下式代替式(14) p dW =(41)即假定总的塑性变形能等于塑性体变能和由摩擦耗散能的算术平⽅根,以之代替式(19)右边第⼆项, 则p p v s p d q d εε''=即p v ps d q d p εε'='pv p sd d εηε+=故可得:222p v ps d M d εηεη-= (42) 此即修正剑桥模型的流动法则. 将其代⼊式(26), 得到2202dq M dp ηη'-+='在p ’-q ’平⾯上的屈服轨迹⽅程为222c p M p M η'='+ (43a) 或 222c p M p M η'='+ (43b) 或 ()()22020q p p p M''''+-=(43c) 或 220002122///p p q p Mp'''-+= ? ?''(43b)即为椭圆⽅程. 其顶点在q Mp ''=线上, 以0()p v p ε'为硬化参数, 即000()()()p p v v H p p p H εε'''=== 因为001+??'= ?-??exp p v e p ελκ.其增量型应⼒-应变关系为 ()22121v d dp d e M p ηηελκλη'??=-+??'++??2222221s d dp d e M M p λκηηηεηη'??-=+ ?'+-+??于是修正剑桥模型的弹塑性矩阵可表⽰为:()()()()()222222122121v s M d dp d dq e M p M ληηεηλκηλκεηηη??+??-'-??-=''++-?然⽽, 有限元等数值计算中, 常按如下⼀般弹塑性矩阵式{}{}{}{}Te ee e e pepQ D D D Q d A D D D D d d d φσσφσσσεεε-????????????+????? -????????=??==来表⽰, 由等塑性硬化规律0()p v H H p ε'== 有: p v H QA H pφε=-按相适应的流动法则0p p v v p H A H p p p φφφφεε'=-=-' ⽽屈服⾯和加载⾯()()2220q Q p p p Mφ''''==+-= 0p p v v p H A H p p p φφφφεε'=-=-''' ()()()()()()()()23000000012121exp p v i p e p p p e p p e A p ελκλκλκ''''''+-+-+??== ?'---??。
10分钟认识剑桥模型

10分钟认识剑桥模型王川第一节:认识“临界状态”首先,大家一定接受以下两张图(无数实验已经证明过):图1 摩尔库伦强度理论图2 土的压实曲线(e为孔隙比,p’为有效应力)那么,如果把τ换成偏应力q(其中q=σ1-σ3),把σ换成平均主应力p(其中p=(σ1+2σ3)/3,p’表示其有效应力),就得到三轴实验中的p-q曲线:图3 p-q曲线土样的体积由固体颗粒和空隙组成,由于固体颗粒不可压缩,故土样体积的变化完全取决于空隙的变化,即土样体积v和孔隙率e描述的物理意义等价。
那么,将图2中e替换为v,就得到v-logp曲线:图4 v-logp曲线与图1和图2一样,图3和图4同样经历了无数实验的验证,属于“事实”。
基于图3和图4的定量分析以及实验观察,可以得出一个结论,这个结论就是临界状态(critical state):无论土样的初始状态和经历的应力路径如何,在剪切的最终阶段,只有剪应变在持续增加,而土样所受的有效应力和体积趋于不变。
临界状态由图3和图4同时确定,因此图3和图4中的曲线也叫临界状态线CSL (Critical State Line)。
将临界状态现象翻译成数学语言:(1)体积不变对应于,为p’引起的体积的改变;(2)剪应变在变对应于,为q引起的剪应变;(3)有效应力不变等价于q与p’的比值为常量。
若令在一般情况下,有(被叫做应力比),则可以定义临界状态下的应力比:(被叫做临界状态应力比)。
从图3中能看出,M为常量,即“有效应力不变”。
◆第二节:剑桥模型假设(1)所有的剪应变都不可恢复,即(为弹性剪应变),(为塑性剪应变)。
(2)假定塑性变性能增量可表示为:(这一假设看不懂没关系,继续往后看)。
(3)相关联流动法则:(与塑性力学中关联流动一致)。
◆第三节:剑桥模型推导从能量角度推导屈服函数:应变能的增量等于主应力p’和偏应力q所做的功,即(式1)因为:(此处用了假设1)所以:(式2)(此处用了假设2)由式1和式2得:(式3)根据(假设1),整理式3得:d为剪胀系数,表示塑性应变的方向(因为d体现了与的相对大小,与塑性力学中流动法则表达得意义一致);为剪胀方程。
非饱和土水力全耦合模型与数值模拟方法研究
非饱和土水力全耦合模型与数值模拟方法研究无论是300m级高坝,还是高陡边坡、大型地下工程建设,均无一例外地涉及复杂赋存环境下岩土体渗流、变形与稳定控制问题。
岩土体渗流与变形的耦合作用以及多场多相耦合过程既是近30年来国际岩土力学领域的前沿研究热点,也是大型水利水电工程、深部岩体工程、核废料地质处置工程等建设中迫切需要解决的关键科学技术难题。
本文以非饱和土为主要研究对象,以土体细观结构及其演化为基础,紧密围绕非饱和土水力耦合机理的量化描述、耦合过程的精细模拟、耦合效应的工程控制这一核心科学问题,重点开展了非饱和土水力全耦合本构模型及数值模拟方法等内容的研究。
主要研究成果如下:(1)建立了考虑颗粒黏结效应的非饱和土弹塑性本构模型大量研究表明,非饱和状态下土体颗粒间的黏结效应对其变形具有显著影响。
采用单位接触面积上弯液面引起的黏结力,定义了黏结因子这一具有严格物理意义的独立变量,用以表征颗粒黏结效应对非饱和土力学特性的影响。
基于试验成果,建立了黏结因子与孔隙比的内在联系,推导了加载一湿陷屈服方程,并在修正剑桥模型的框架下建立了三轴应力状态下非饱和土的弹塑性本构模型。
与经典的巴塞罗那模型(Barcelona Basic Model, BBM)相比,该模型仅采用单一屈服面(BBM有2个),模型参数较少(8个,较BBM少4个参数),且物理意义明确,均可通过常规试验确定。
试验验证结果表明,该模型不仅具备BBM模型所有的描述能力,还能够描述脱湿引起的弹塑性变形等复杂力学特性。
(2)建立了考虑变形效应的土水特性与渗透特性演化模型在水力耦合过程中,土体变形及孔隙分布演化对其土水特性具有显著影响。
尽管土体孔隙分布的演化模式较为复杂,但试验研究表明,土体在变形过程中,孔隙分布的基本形态未发生显著变化、统计分布特征基本不变。
以参考状态孔隙分布函数为基础,经平移和缩放给岀了变形条件下土体的孔隙分布函数,进而建立了考虑变形和滞回效应的土水特征曲线模型。
非饱和土剑桥模型的基本框架
非饱和土剑桥模型的基本框架
范秋雁
【期刊名称】《岩土力学》
【年(卷),期】1996(17)3
【摘要】分析了用有效应力原理和用两个应力变量建立非饱和土力学理论的区别与联系,借助于有效应力原理将饱和土的剑桥模型推广到非饱和土,并与现有的几种弹塑性模型作了对比分析。
【总页数】7页(P8-14)
【关键词】非饱和土;吸力;剑桥模型;框架;土力学
【作者】范秋雁
【作者单位】广西大学土木系
【正文语种】中文
【中图分类】TU43
【相关文献】
1.基于非饱和土压强度计算模型的土湿吸力物理模型试验分析 [J], 王鑫
2.非饱和土双应力变量广义土水特征曲线模型验证 [J], 程明书;李贤;汪时机;王晓琪;胡东旭;胡嫚
3.非饱和土双应力变量广义土水特征曲线理论模型构建 [J], 汪时机;程明书;李贤;王晓琪;毛新;杨惠迪
4.基于非饱和土压强度计算模型的水利工程土湿吸力计算 [J], 姜巽
5.冻融循环下非饱和膨胀土一维土柱模型试验研究 [J], 崔郁雪;杨忠年;时伟;凌贤长;涂志斌
因版权原因,仅展示原文概要,查看原文内容请购买。
非饱和土土力学(新)
温度
3 ua 200kPa
u a u w 100 kPa
15℃ 30℃ 45℃ 60℃
温度的影响
非饱和土土力学理论
4、非饱和土的应力应变关系及本构模型
(1)弹性模型
Fredlund和Morganstern(1976)、Fredlund(1979)提出了基于双应力变量 ( u a ) 和 (ua u w ) 的弹性应力应变关系:
强度分析:
固结变形分析:
传统(经典)土力学的局限
3、现有土工试验仪器主要是针对饱和土设计的
① 试验数据按饱和土相关理论来整理,不符合实际情况 。 ② 不能测负孔隙水压力。 ③ 未考虑气相影响。
单轴压缩
三轴压缩
非饱和土土力学理论
非饱和土物质组成:固体、气体和液体
固体
液体
气体
n
Vpores Vtotal
固结本构方程
Mechanical constitutive law
q w k grad( pw w z)
d v m dp
1 dp K
pw 1 p k 2 pw wm t 3 t
3-D consolidation
传统(经典)土力学的局限
2、固结变形和强度分析中有效应力的表现形式是不一致的
Vliquid Vgas Vtotal
Sl
Vliquid Vpores
Vliquid Vliquid Vgas
饱和度
1 Sg
空隙度
非饱和土土力学理论
非饱和土为固、液、气相及收缩膜组成的四相介质
非饱和土土力学理论
存在一个新的应力状态变量:吸力
剑桥模型1
剑桥模型1958 - 1963 年间,英国剑桥大学的Roscoe 等根据正常固结粘土和弱超固结粘土的三轴试验,提出的剑桥粘土的本构模型,他们将“帽子”屈服准则、正交流动准则和加工硬化规律系统地应用于Cam 模型之中,并提出了临界状态线、状态边界面、弹性墙等一系列物理概念,构成了第一个比较完整的土塑性模型。
Roscoc 和Burland 又进一步修正了剑桥模型,认为剑桥模型的屈服面轨迹应为椭圆,给出了现在众所周知的修正剑桥模型。
试验证明,对于正常固结粘土和弱固结的饱和重塑粘土,孔隙比e 与外力p ,q 之间存在有唯一的关系,且不随应力路径而发生变化。
该模型试图描述室内试验所观察到的现象,即从某一初始状态开始加载直到最终维持塑性常体积变形的临界状态,其基本组成如下:(1)在(e ,p)平面中,存在一条曲线,在正常固结粘性土中的所有应力遵循此路径,这被称为正常固结线(NCL)。
这条线提供了体积硬化规则,可以被广义化为一般应力条件。
(2)在(e ,p ,q )空间中存在一条线,所有的残余状态都遵循此路径,而与实验类别和初始条件无关。
这条线与(e ,p)平面中的正常固结线平行,在此线上,剪切变形发生而没有体积变形发生。
(3)从固结排水和不排水实验中所得到的应力路径位于唯一的状态面,通称为Roscoe 面。
事实上,在不排水路径中,土随着塑性体积应变的发展而硬化。
其中,体积应变的弹性和塑性应变增量之和保持常数。
Roscoe 面价值在于给出了屈服面类型的一个选择依据。
模型基于对临界状态线、相关联塑性理论中屈服面与固结定律的假定。
该模型假定:①屈服只与应力球量p 和应力偏量q 两个应力分量有关,与第三应力不变量无关;②采用塑性体应变硬化规律,以p v ε为硬化参数;③假定塑性变形符合相关联的流动法则,即g(σ)=f(σ);④假定变形消耗的功,即塑性功为 p s p Mpd dW ε= (1)式中:M =q /P ; p s d ε为塑性偏应变增量。
