2013-2014-1微积分test
AP物理学实战练习题(2013年版)—— 电势潜能、电容性与相关基本微积分知识说明书

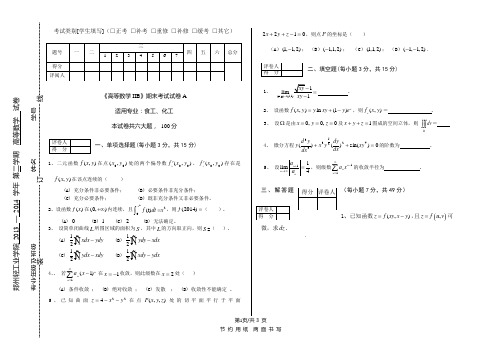
1µF6µF 5µF12Vdielectric-Q+Q +2Q (+r , 0)(-r , 0)(0, +r )OPart II. Free Response10.The electric potential diagram above shows equipotentials for a 2-dimensional region of space.a.At which point—A, B, C, D, or E—would an electron have the highest electric potentialenergy? Briefly explain your answer.b.In which general direction does the electric field point in this diagram? Briefly explain youranswer.c.Based on the equipotentials, draw a sketch on the diagram above of the electric field,including at least five field lines.d.At which point—A, B, C, D, or E—is the magnitude of the electric field the greatest? Brieflyjustify your answer.e. A proton is released from rest at point C. Qualitatively describe the proton’s subsequent:i.direction of motionii.speediii.accelerationf.For the proton in part e, calculate its velocity after having moved through a potentialdifference of 10 V.+q –q 0.01 m0.50 m0.50 m–q +qe Gauss’s Law to determine the magnitude of the electric field between the plates.c.Calculate the electric potential V between the two plates.d.Calculate the capacitance of this capacitor.AP Physics Practice Test: Potential, Capacitance κ=2.00A dielectric of is now inserted between the isolated plates while the same amount of charge Qremains on each plate.e.Calculate the new capacitance of the system with the dielectric between the plates.f.The electric field strength between the plates has (check one): ____ increased____ decreased____ remained the sameg.The electric potential between the plates has (check one): ____ increased____ decreased____ remained the sameh.The energy stored in the capacitor has (check one): ____ increased____ decreased____ remained the samei.How would your answers to f , g, and h change if the dielectric had been inserted while thevoltage supply was still connected to the capacitor? Explain.–Qba +Qc r +E –E c b ac.Calculate the magnitude of the difference in electric potential V between the two spheres.d.Calculate the capacitance of this conducting-sphere system.e.The spheres are discharged, and then connected to a source of electric potential of magnitude2V. Calculate how much Work must be done to fully charge the capacitor under these new conditions.-Q+Q +2Q (+r , 0) (-r , 0) (0, +r ) O9. The correct answer is a . The electric potential, or energy per unit charge, represents the amount ofenergy per unit charge it takes to move a test particle from infinitely far away to a given location. For apoint charge, the absolute potential is calculated using for each charge, and the electricpotential at a given location is simply the sum of the individual potentials for each charge in the vicinity:V =kQrV =V +Q +V +2Q +V −Q∑V =k (+Q )r +k (+2Q )r +k (−Q )r =2kQr. Field lines become more closely spaced there.The proton accelerates in the same direction of field, ie, towards upper left of diagram.The proton has a speed that increases over time; the electric field applies a force to it, causing it to accelerate.The proton’s acceleration increases as it moves into an area with an increasingly strong electricfield.This is a conservation of energy problem, with the field doing Work on the charge to increase its kinetic energy. Here, we can look at the change in electric potential energy and see how that converts to kinetic−Ki =12mv2−0=2(1.60e−19C)(10V)(1.67e−27kg)=4.38e4m/s– +– +–Q ba+Qcr +E –E c b aBecause only the magnitude of the potential was requested, is also acceptable.d. Using the definition of capacitance:Note that capacitance formula must use (b – a ) in denominator to produce positive result, because capacitance is always positive.e. Potential has doubled, and because Q = VC , the charge on the capacitor has doubled as well.kQ 1a −1b "#$%&'C =Q V =Q kQ 1a −1b #$&'=1k ab b −a "#$%&'U =12QV =122Q ()2kQ ab b −a "#$%&'=2kQ 2ab b −a "#$%&'。
2013-2014高数IIB试卷A
第1页/共3 页 考试类别[学生填写](□正考 □补考 □重修 □补修 □缓考 □其它)《高等数学IIB 》期末考试试卷A适用专业:食工、化工 本试卷共六大题, 100分一、单项选择题(每小题3分,共15分)1、二元函数),(y x f 在点),(00y x 处的两个偏导数),(00y xf x ',),(00y x f y '存在是),(y x f 在该点连续的( )(A) 充分条件非必要条件; (B) 必要条件非充分条件;(C) 充分必要条件; (D) 既非充分条件又非必要条件。
2、设函数()f x 在(0,)+∞内连续,且22(t)x f dt x =⎰,则(2014)f =( ).(A) 0 (B) 1 (C) 2 (D) 无法确定。
3、 设简单闭曲线L 所围区域的面积为S ,其中L 的方向取正向,则S =( ). (A)12L xdx ydy -⎰Ñ (B) 12L ydy xdx -⎰Ñ (C) 12L ydx xdy -⎰Ñ (D) 12L xdy ydx -⎰Ñ4、、 若∑∞=-1)1(n n nx a在1-=x 收敛,则此级数在2=x 处( )(A) 条件收敛 ; (B) 绝对收敛 ; (C) 发散 ; (D) 收敛性不能确定 。
5、已知曲面224yx z --=在点(,,)P x y z 处的切平面平行于平面0122=-++z y x ,则点P 的坐标是( )(A )(1,1,2)-; (B )(1,1,2)-; (C )(1,1,2); (D )(1,1,2)--.二、填空题(每小题3分,共15分)1、 (x,y)(1,1)lim→= .2、 设函数(,)ln (1)xf x y y xy y e =+-,则(,)x f x y = .3、 设Ω是由0,0,0x y z ===及1x y z ++=围成的空间立体,则dv Ω⎰⎰⎰=4、 微分方程0)sin()()(4225333=++xy dx dy y x dxy d y 的阶数为 .5、 设11lim 4n n na a +→∞=,则级数11n n n a x ∞-=∑的收敛半径为 .三、解答题(每小题7分,共49分)1、 已知函数(,)z f xy x y =-,且(),z f u v =可微,求dz ..线 订 装郑州轻工业学 2013 — 2014 学年 第二学期 高等数学 试卷专业年级及班级 姓名 学号第2页/共3 页2、交换积分次序10xydx dy y⎰⎰,并求其值.3、计算曲线积分⎰,其中L 为ln y x =上点(1,0)与点(,1)e 间的弧段.4、计算2 2Ly dx xydy +⎰,其中L :2y x =从()0,0O 到()1,1A .5. 判定级数2123n n n n ∞=∑的敛散性..6.计算二重积分()22Dx y dxdy +⎰⎰,其中D :221x y +≤.7.求微分方程56x y y y e '''-+=通解第3页/共3 页四、解答题(本题9分)求幂级数2121n n x n +∞=+∑的收敛域及和函数五、应用题(本题满分9分)计算由曲面22x y z +=与2z =所围成立体的体积.六、证明题(本题满分3分)设函数()f x 在[0,1]上连续, 证明1112001()()[()]2xdx f x f y dy f x dx =⎰⎰⎰.线订装第4页/共3 页。
2014高考数学一轮汇总训练《积分与微积分基本定理》理新人教A版

第十四节定积分与微积分基本定理[备考方向要明了]考什么怎么考1.了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念.2.了解微积分基本定理的含义. 1.考查形式多为选择题或填空题.2.考查简单定积分的求解.如2012年江西T11等.3.考查曲边梯形面积的求解.如2012年湖北T3,山东T15,上海T13等.4.与几何概型相结合考查.如2012年福建T6等.[归纳·知识整合]1.定积分(1)定积分的相关概念在∫b a f(x)d x中,a,b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,f(x)叫做被积函数,x叫做积分变量,f(x)d x叫做被积式.(2)定积分的几何意义①当函数f(x)在区间[a,b]上恒为正时,定积分∫b a f(x)d x的几何意义是由直线x=a,x=b(a≠b),y=0和曲线y=f(x)所围成的曲边梯形的面积(左图中阴影部分).②一般情况下,定积分∫b a f(x)d x的几何意义是介于x轴、曲线f(x)以及直线x=a,x =b之间的曲边梯形面积的代数和(右上图中阴影所示),其中在x轴上方的面积等于该区间上的积分值,在x轴下方的面积等于该区间上积分值的相反数.(3)定积分的基本性质①∫b a kf(x)d x=k∫b a f(x)d x.②∫b a [f 1(x )±f 2(x )]d x =∫b a f 1(x )d x ±∫ba f 2(x )d x . ③∫b a f (x )d x =∫c a f (x )d x +∫bc f (x )d x .[探究] 1.若积分变量为t ,则∫b a f (x )d x 与∫ba f (t )d t 是否相等?提示:相等.2.一个函数的导数是唯一的,反过来导函数的原函数唯一吗?提示:一个函数的导数是唯一的,而导函数的原函数则有无穷多个,这些原函数之间都相差一个常数,在利用微积分基本定理求定积分时,只要找到被积函数的一个原函数即可,并且一般使用不含常数的原函数,这样有利于计算.3.定积分∫ba [f (x )-g (x )]d x (f (x )>g (x ))的几何意义是什么?提示:由直线x =a ,x =b 和曲线y =f (x ),y =g (x )所围成的曲边梯形的面积. 2.微积分基本定理如果f (x )是区间[a ,b ]上的连续函数,并且F ′(x )=f (x ),那么∫ba f (x )d x =F (b )-F (a ),这个结论叫做微积分基本定理,又叫做牛顿—莱布尼兹公式.为了方便,常把F (b )-F (a )F (x )|ba ,即 ∫b a f (x )d x =F (x )|ba =F (b )-F (a ).[自测·牛刀小试]1.∫421xd x 等于( )A .2ln 2B .-2ln 2C .-ln 2D .ln 2解析:选D ∫421xd x =ln x |42=ln 4-ln 2=ln 2.2.(教材习题改编)一质点运动时速度和时间的关系为V (t )=t 2-t +2,质点作直线运动,则此物体在时间[1,2]内的位移为( )A.176B.143C.136D.116解析:选A S =∫21(t 2-t +2)d t =⎝⎛⎪⎪⎪⎭⎪⎫13t 3-12t 2+2t 21=176. 3.(教材习题改编)直线x =0,x =2,y =0与曲线y =x 2所围成的曲边梯形的面积为________.解析:∫20x 2d x =13x 3 |20=83.答案:834.(教材改编题)∫101-x 2d x =________.解析:由定积分的几何意义可知,∫101-x 2d x 表示单位圆x 2+y 2=1在第一象限内部分的面积,所以∫101-x 2d x =14π.答案:14π5.由曲线y =1x ,直线y =-x +52所围成的封闭图形的面积为________.解析:作出图象如图所示.解方程组可得交点为A ⎝ ⎛⎭⎪⎫12,2,B ⎝ ⎛⎭⎪⎫2,12,所以阴影部分的面积,212⎰⎝⎛ -x +52- ⎭⎪⎫1xd x =⎝ ⎛⎭⎪⎫-12x 2+52x -ln x 212=158-2ln 2. 答案:158-2ln 2利用微积分基本定理求定积分[例1] 利用微积分基本定理求下列定积分:(1)∫21(x 2+2x +1)d x ;(2)∫π0(sin x -cos x )d x ;(3)∫20x (x +1)d x ;(4)∫21⎝ ⎛⎭⎪⎫e 2x+1x d x ;(5)20π⎰sin 2x2d x .[自主解答] (1)∫21(x 2+2x +1)d x =∫21x 2d x +∫212x d x +∫211d x =x 33|21+x 2 |21+x |21=193. (2)∫π0(sin x -cos x )d x=∫π0sin x d x -∫π0cos x d x =(-cos x ) |π0-sin x |π0=2.(3)∫20x (x +1)d x =∫20(x 2+x )d x=∫20x 2d x +∫20x d x =13x 3 |20+12x 2 |20=⎝ ⎛⎭⎪⎫13×23-0+⎝ ⎛⎭⎪⎫12×22-0=143. (4)∫21⎝ ⎛⎭⎪⎫e 2x +1x d x =∫21e 2x d x +∫211xd x=12e 2x |21+ln x |21=12e 4-12e 2+ln 2-ln 1 =12e 4-12e 2+ln 2. (5)20π⎰sin 2x2d x =20π⎰⎝ ⎛⎭⎪⎫12-12cos x d x =20π⎰12d x -1220π⎰cos x d x=12x 20π-12sin x 20π=π4-12=π-24. ———————————————————求定积分的一般步骤计算一些简单的定积分,解题的步骤是:(1)把被积函数变形为幂函数、正弦函数、余弦函数、指数函数与常数的积的和或差; (2)把定积分用定积分性质变形为求被积函数为上述函数的定积分; (3)分别用求导公式找到一个相应的原函数; (4)利用牛顿—莱布尼兹公式求出各个定积分的值; (5)计算原始定积分的值.1.求下列定积分:(1)∫20|x -1|d x ;(2)20π⎰1-sin 2x d x .解:(1)|x -1|=⎩⎪⎨⎪⎧1-x , x ∈[0,1x -1, x ∈[1,2]故∫20|x -1|d x =∫10(1-x )d x +∫21(x -1)d x=⎝ ⎛⎭⎪⎫x -x 22 |10+⎝ ⎛⎭⎪⎫x 22-x |21=12+12=1.(2) 2π⎰1-sin 2x d x=2π⎰|sin x-cos x|d x=4π⎰ (cos x-sin x)d x+24ππ⎰ (sin x-cos x)d x=(sin x+cos x)4π+(-cos x-sin x) 24ππ=2-1+(-1+2)=22-2.利用定积分的几何意义求定积分[例2] ∫10-x2+2x d x=________.[自主解答] ∫10-x2+2x d x表示y=-x2+2x与x=0,x=1及y=0所围成的图形的面积.由y=-x2+2x得(x-1)2+y2=1(y≥0),又∵0≤x≤1,∴y=-x2+2x与x=0,x=1及y=0所围成的图形为14个圆,其面积为π4.∴∫10-x2+2x d x=π4.在本例中,改变积分上限,求∫20-x2+2x d x的值.解:∫20-x2+2x d x表示圆(x-1)2+y2=1在第一象限内部分的面积,即半圆的面积,所以∫20-x2+2x d x=π2.———————————————————利用几何意义求定积分的方法(1)当被积函数较为复杂,定积分很难直接求出时,可考虑用定积分的几何意义求定积分.(2)利用定积分的几何意义,可通过图形中面积的大小关系来比较定积分值的大小.2.(2013·福建模拟)已知函数f (x )=∫x0(cos t -sin t )d t (x >0),则f (x )的最大值为________.解析:因为f (x )=∫x02sin ⎝ ⎛⎭⎪⎫π4-t d t=2cos ⎝⎛⎭⎪⎫π4-t |x 0=2cos ⎝ ⎛⎭⎪⎫π4-x -2cos π4=sin x +cos x -1=2sin ⎝ ⎛⎭⎪⎫x +π4-1≤2-1,当且仅当sin ⎝⎛⎭⎪⎫x +π4=1时,等号成立.答案:2-1利用定积分求平面图形的面积[例3] (2012·山东高考)由曲线y =x ,直线y =x -2及y 轴所围成的图形的面积为( )A.103 B .4 C.163D .6[自主解答] 由y =x 及y =x -2可得,x =4,即两曲线交于点(4,2).由定积分的几何意义可知,由y =x 及y =x -2及y 轴所围成的封闭图形面积为∫40(x -x +2)d x =⎝ ⎛⎭⎪⎫23x 32-12x 2+2x |40=163. [答案] C若将“y =x -2”改为“y =-x +2”,将“y 轴”改为“x 轴”,如何求解? 解:如图所示,由y =x 及y =-x +2可得x =1.由定积分的几何意义可知,由y =x ,y =-x +2及x 轴所围成的封闭图形的面积为∫2f (x )d x =∫10x d x +∫21(-x +2)d x =23x 32 |10+⎝⎛⎭⎪⎫2x -x 22 |21 =76.——————————————————— 利用定积分求曲边梯形面积的步骤(1)画出曲线的草图.(2)借助图形,确定被积函数,求出交点坐标,确定积分的上、下限. (3)将“曲边梯形”的面积表示成若干个定积分的和或差. (4)计算定积分,写出答案.3.(2013·郑州模拟)如图,曲线y =x 2和直线x =0,x =1,y =14所围成的图形(阴影部分)的面积为( )A.23 B.13 C.12D.14解析:选D 由⎩⎪⎨⎪⎧y =14,y =x 2⇒x =12或x =-12(舍),所以阴影部分面积 S =120⎰⎝ ⎛⎭⎪⎫14-x 2d x +112⎰⎝⎛⎭⎪⎫x 2-14d x =⎝ ⎛⎭⎪⎫14x -13x 3120+⎝ ⎛⎭⎪⎫13x 3-14x 112=14. 定积分在物理中的应用[例4] 列车以72 km/h 的速度行驶,当制动时列车获得加速度a =-0.4 m/s 2,问列车应在进站前多长时间,以及离车站多远处开始制动?[自主解答] a =-0.4 m/s 2,v 0=72 km/h =20 m/s. 设t s 后的速度为v ,则v =20-0.4t . 令v =0,即20-0.4 t =0得t =50 (s). 设列车由开始制动到停止所走过的路程为s , 则s =∫500v d t =∫500(20-0.4t )d t =(20t -0.2t 2) |50=20×50-0.2×502=500(m),即列车应在进站前50 s 和进站前500 m 处开始制动. ———————————————————1.变速直线运动问题如果做变速直线运动的物体的速度v 关于时间t 的函数是v =v (t )(v (t )≥0),那么物体从时刻t =a 到t =b 所经过的路程为∫ba v (t )d t ;如果做变速直线运动的物体的速度v 关于时间t 的函数是v =v (t )(v (t )≤0),那么物体从时刻t =a 到t =b 所经过的路程为-∫bav (t )d t .2.变力做功问题物体在变力F (x )的作用下,沿与力F (x )相同方向从x =a 到x =b 所做的功为∫ba F (x )d x .4.一物体在力F (x )=⎩⎪⎨⎪⎧10 0≤x ≤23x +4 x >2(单位:N)的作用下沿与力F (x )相同的方向运动了4米,力F (x )做功为( )A .44 JB .46 JC .48 JD .50 J解析:选B 力F (x )做功为∫2010d x +∫42(3x +4)d x=10x |20+⎝⎛⎪⎪⎪⎭⎪⎫32x 2+4x 42 =20+26=46.1个定理——微积分基本定理由微积分基本定理可知求定积分的关键是求导函数的原函数,由此可知,求导与积分是互为逆运算.3条性质——定积分的性质 (1)常数可提到积分号外; (2)和差的积分等于积分的和差; (3)积分可分段进行.3个注意——定积分的计算应注意的问题(1)若积分式子中有几个不同的参数,则必须分清谁是积分变量; (2)定积分式子中隐含的条件是积分上限不小于积分下限; (3)面积非负, 而定积分的结果可以为负.易误警示——利用定积分求平面图形的面积的易错点[典例] (2012·上海高考)已知函数y =f (x )的图象是折线段ABC ,其中A (0,0),B ⎝ ⎛⎭⎪⎫12,5,C (1,0).函数y =xf (x )(0≤x ≤1)的图象与x 轴围成的图形的面积为________.[解析] 由题意可得 f (x )=⎩⎪⎨⎪⎧10x ,0≤x ≤12,10-10x ,12<x ≤1,所以y =xf (x )=⎩⎪⎨⎪⎧10x 2,0≤x ≤12,10x -10x 2,12<x ≤1,与x 轴围成图形的面积为120⎰10x 2d x +112⎰(10x -10x 2)d x =103x3120+⎝⎛⎭⎪⎫5x 2-103x 3112=54. [答案] 54[易误辨析]1.本题易写错图形面积与定积分间的关系而导致解题错误.2.本题易弄错积分上、下限而导致解题错误,实质是解析几何的相关知识和运算能力不够致错.3.解决利用定积分求平面图形的面积问题时,应处理好以下两个问题: (1)熟悉常见曲线,能够正确作出图形,求出曲线交点,必要时能正确分割图形; (2)准确确定被积函数和积分变量. [变式训练]1.由曲线y =x 2,y =x 3围成的封闭图形面积为( ) A.112B.14 C.13D.712解析:选A 由⎩⎪⎨⎪⎧y =x 2,y =x 3,得x =0或x =1,由图易知封闭图形的面积=∫10(x 2-x 3)d x=13-14=112.2.(2012·山东高考)设a >0.若曲线y =x 与直线x =a ,y =0所围成封闭图形的面积为a 2,则a =________.解析:由题意∫a 0x d x =a 2. 又⎝ ⎛⎭⎪⎫23x 32′=x ,即23x 32 |a 0=a 2,即23a 32=a 2.所以a =49. 答案:49一、选择题(本大题共6小题,每小题5分,共30分) 1.∫e11+ln xxd x =( )A .ln x +12ln 2xB.2e -1C.32D.12解析:选C ∫e 11+ln x x d x =⎝ ⎛⎭⎪⎫ln x +ln 2x 2e 1=32. 2.(2012·湖北高考)已知二次函数y =f (x )的图象如图所示,则它与x 轴所围图形的面积为( )A.2π5B.43C.32D.π2解析:选 B 由题中图象易知f (x )=-x 2+1,则所求面积为2∫10(-x 2+1)d x =2⎝ ⎛⎭⎪⎫-x 33+x 10=43.3.设函数f (x )=ax 2+b (a ≠0),若∫30f (x )d x =3f (x 0),则x 0等于( )A .±1 B. 2 C .± 3D .2解析:选C ∫30f (x )d x =∫30(ax 2+b )d x =⎝ ⎛⎭⎪⎫13ax 3+bx 30=9a +3b ,则9a +3b =3(ax 20+b ), 即x 20=3,x 0=± 3.4.设f (x )=⎩⎪⎨⎪⎧x 2, x ∈[0,1],2-x , x ∈1,2],则∫20f (x )d x =( ) A.34 B.45 C.56D .不存在解析:选C 如图.∫20f (x )d x =∫10x 2d x +∫21(2-x )d x=13x 3 |10+⎝ ⎛⎭⎪⎫2x -12x 2 |21=13+⎝ ⎛⎭⎪⎫4-2-2+12=56. 5.以初速度40 m/s 竖直向上抛一物体,t 秒时刻的速度v =40-10t 2,则此物体达到最高时的高度为( )A.1603 m B.803 m C.403m D.203m 解析:选A v =40-10t 2=0,t =2,∫20(40-10t 2)d t =⎝⎛⎭⎪⎫40t -103t 3 |20=40×2-103×8=1603 (m).6.(2013·青岛模拟)由直线x =-π3,x =π3,y =0与曲线y =cos x 所围成的封闭图形的面积为( )A.12 B .1C.32D. 3解析:选D 结合函数图象可得所求的面积是定积分33ππ-⎰cos x d x =sin x33ππ-=32-⎝ ⎛⎭⎪⎫-32= 3. 二、填空题(本大题共3小题,每小题5分,共15分)7.设a =∫π0sin x d x ,则曲线y =f (x )=xa x+ax -2在点(1,f (1))处的切线的斜率为________.解析:∵a =∫π0sin x d x =(-cos x ) |π0=2,∴y =x ·2x+2x -2. ∴y ′=2x+x ·2xln 2+2.∴曲线在点(1,f (1))处的切线的斜率k =y ′|x =1=4+2ln 2. 答案:4+2ln 28.在等比数列{a n }中,首项a 1=23,a 4=∫41(1+2x )d x ,则该数列的前5项之和S 5等于________.解析:a 4=∫41(1+2x )d x =(x +x 2) |41=18,因为数列{a n }是等比数列,故18=23q 3,解得q =3,所以S 5=231-351-3=2423. 答案:24239.(2013·孝感模拟)已知a ∈⎣⎢⎡⎦⎥⎤0,π2,则当∫a0(cos x -sin x )d x 取最大值时,a =________.解析:∫a 0(cos x -sin x )d x =(sin x +cos x ) |a=sin a +cos a -1=2sin ⎝⎛⎭⎪⎫a +π4-1,∵a ∈⎣⎢⎡⎦⎥⎤0,π2,∴当a =π4时,2sin ⎝⎛⎭⎪⎫a +π4-1取最大值.答案:π4三、解答题(本大题共3小题,每小题12分,共36分) 10.计算下列定积分: (1)20π⎰sin 2x d x ;(2)∫32⎝ ⎛⎭⎪⎫x +1x 2d x ;(3)120⎰e 2xd x .解:(1)20π⎰sin 2x d x =20π⎰1-cos 2x2d x =⎝ ⎛⎭⎪⎫12x -14sin 2x 20π=⎝⎛⎭⎪⎫π4-14sin π-0=π4.(2)∫32⎝ ⎛⎭⎪⎫x +1x 2d x =∫32⎝⎛⎭⎪⎫x +1x+2d x =⎝ ⎛⎭⎪⎫12x 2+2x +ln x |32 =⎝ ⎛⎭⎪⎫92+6+ln 3-(2+4+ln 2) =92+ln 3-ln 2=92+ln 32. (3)120⎰e 2xd x =12e2x120=12e -12. 11.如图所示,直线y =kx 分抛物线y =x -x 2与x 轴所围图形为面积相等的两部分,求k 的值.解:抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1, 所以,抛物线与x 轴所围图形的面积 S =∫1(x -x 2)d x =⎝ ⎛⎭⎪⎫x 22-13x 3 |10=16. 又⎩⎪⎨⎪⎧y =x -x 2,y =kx ,由此可得,抛物线y =x -x 2与y =kx 两交点的横坐标为x 3=0,x 4=1-k ,所以,S2=∫1-k 0(x -x 2-kx )d x=⎝⎛⎭⎪⎫1-k 2x 2-13x 3 |1-k 0=16(1-k )3.又知S =16,所以(1-k )3=12,于是k =1- 312=1-342.12.如图,设点P 从原点沿曲线y =x 2向点A (2,4)移动,直线OP 与曲线y =x 2围成图形的面积为S 1,直线OP 与曲线y =x 2及直线x =2围成图形的面积为S 2,若S 1=S 2,求点P 的坐标.解:设直线OP 的方程为y =kx ,点P 的坐标为(x ,y ), 则∫x0(kx -x 2)d x =∫2x (x 2-kx )d x ,即⎝ ⎛⎭⎪⎫12kx 2-13x 3 |x 0=⎝ ⎛⎭⎪⎫13x 3-12kx 2|2x, 解得12kx 2-13x 3=83-2k -⎝ ⎛⎭⎪⎫13x 3-12kx 2,解得k =43,即直线OP 的方程为y =43x ,所以点P 的坐标为⎝ ⎛⎭⎪⎫43,169.1.一物体做变速直线运动,其v -t 曲线如图所示,则该物体在12s ~6 s 间的运动路程为________. 解析:由题图可知,v (t )=⎩⎪⎨⎪⎧2t 0≤t ≤1,2 1≤t ≤3,13t +1 3≤t ≤6,因此该物体在12s ~6 s 间运动的路程为s =612⎰v (t )d t =112⎰2t d t +∫312d t +∫63⎝ ⎛⎭⎪⎫13t +1d t=t2112+2t |31+⎝ ⎛⎭⎪⎫16t 2+t |63=494(m).答案:494m2.计算下列定积分: (1)31-⎰(3x 2-2x +1)d x ;(2)∫e 1⎝ ⎛⎭⎪⎫x +1x +1x 2d x .解:(1)31-⎰(3x 2-2x +1)d x =(x 3-x 2+x )31-=24.(2)∫e 1⎝ ⎛⎭⎪⎫x +1x +1x 2d x =∫e 1x d x +∫e 11x d x +∫e 11x 2d x =12x 2 |e 1+ln x |e 1-1x |e1=12(e 2-1)+(ln e -ln 1)-⎝ ⎛⎭⎪⎫1e -11=12e 2-1e +32. 3.求曲线y =x ,y =2-x ,y =-13x 所围成图形的面积.解:由⎩⎨⎧y =x ,y =2-x ,得交点A (1,1);由⎩⎪⎨⎪⎧y =2-x ,y =-13x ,得交点B (3,-1).故所求面积S =∫10⎝ ⎛⎭⎪⎫x +13x d x +∫31⎝ ⎛⎭⎪⎫2-x +13x d x=⎝ ⎛⎭⎪⎫23x 32+16x 2 |10+⎝ ⎛⎭⎪⎫2x -13x 2 |31=23+16+43=136. 4.某技术监督局对一家颗粒输送仪生产厂进行产品质量检测时,得到了下面的资料:这家颗粒输送仪生产厂生产的颗粒输送仪,其运动规律属于变速直线运动,且速度v (单位:m/s)与时间t (单位:s)满足函数关系式v (t )=⎩⎪⎨⎪⎧t 20≤t ≤10,4t +60 10<t ≤20,140 20<t ≤60.某公司拟购买一台颗粒输送仪,要求1 min 行驶的路程超过7 673 m ,问这家颗粒输送仪生产厂生产的颗粒输送仪能否被列入拟挑选的对象之一?解:由变速直线运动的路程公式,可得s =∫100t 2d t +∫2010(4t +60)d t +∫6020140d t=13t 3 |100+(2t 2+60t ) |2010+140t |6020 =7 133 13(m)<7 676(m).∴这家颗粒输送仪生产厂生产的颗粒输送仪不能被列入拟挑选的对象之一.六招破解函数最值及巧用数形结合求参数问题一、六招破解函数最值问题函数最值问题一直是高考的一个重要的热点问题,在高考中占有极其重要的地位.为了让大家能够更加系统、全面地掌握函数最值问题的解决方法,下面就其问题的常用解法,分类浅析如下:1.配方法配方法是求二次函数最值的基本方法,如函数F (x )=af (x )2+bf (x )+c (a ≠0)的最值问题,可以考虑用配方法.[例1] 已知函数y =(e x -a )2+(e -x -a )2(a ∈R ,a ≠0),求函数y 的最小值. [解] y =(e x -a )2+(e -x -a )2=(e x +e -x )2-2a (e x +e -x )+2a 2-2. 令t =e x +e -x ,则f (t )=t 2-2at +2a 2-2.因为t ≥2,所以f (t )=t 2-2at +2a 2-2=(t -a )2+a 2-2的定义域为[2,+∞). 因为抛物线y =f (t )的对称轴为t =a ,所以当a ≤2且a ≠0时,y min =f (2)=2(a -1)2; 当a >2时,y min =f (a )=a 2-2.[点评] 利用二次函数的性质求最值,要特别注意自变量的取值范围,同时还要注意对称轴与区间的相对位置关系.如本题化为含参数的二次函数后,求解最值时要注意区分对称轴与定义域的位置关系,然后再根据不同情况分类解决.2.换元法换元法是指通过引入一个或几个新的变量,来替换原来的某些变量(或代数式),以便使问题得以解决的一种数学方法.在学习中,常常使用的换元法有两类,即代数换元和三角换元,我们可以根据具体问题及题目形式灵活选择换元的方法,以便将复杂的函数最值问题转化为简单的函数最值问题.如可用三角换元解决形如a 2+b 2=1及部分根式函数形式的最值问题.[例2] 设a ,b ∈R ,a 2+2b 2=6,则a +b 的最小值是________.[解析] 因为a ,b ∈R ,a 2+2b 2=6,所以令a =6cos α,2b =6sin α,α∈R . 则a +b =6cos α+3sin α=3sin(α+φ),所以a +b 的最小值是-3. [答案] -3[点评] 在用换元法时,要特别注意换元后新元的取值范围.如本题换元后中间变量α∈R ,这是由条件a ,b ∈R 得到的.3.不等式法利用不等式法求解函数最值,主要是指运用基本不等式及其变形公式来解决函数最值问题的一种方法.常常使用的基本不等式有以下几种:a 2+b 2≥2ab (a ,b 为实数),a +b2≥ab (a ≥0,b ≥0),ab ≤⎝ ⎛⎭⎪⎫a +b 22≤a 2+b 22(a ,b 为实数).[例3] 函数f (x )=1x +41-x (0<x <1)的最小值为________.[解析] f (x )=1x +41-x =1-x +4x x 1-x =3x +1-x 2+x ,令t =3x +1,则x =t -13,t ∈(1,4),f (x )变为g (t )=t-⎝ ⎛⎭⎪⎫t -132+t -13=t -19t 2+59t -49=9t -t 2+5t -4=9-⎝ ⎛⎭⎪⎫t +4t +5,因为t ∈(1,4),所以5>t +4t≥4,0<-⎝ ⎛⎭⎪⎫t +4t +5≤1,9-⎝ ⎛⎭⎪⎫t +4t +5≥9,所以f (x )的最小值为9.[答案] 9[点评] 利用基本不等式法求解最值的关键在于确定定值,求解时应注意两个方面的问题:一是检验基本不等式成立的三个条件——“一正、二定、三相等”,灵活利用符号的变化转化为正数的最值问题解决;二是要注意函数解析式的灵活变形,通过“拆”、“添”或“减”等方法“凑”出常数.对于条件最值问题,应首先考虑常数的代换,将函数解析式乘以“1”构造基本不等式.4.函数单调性法先确定函数在给定区间上的单调性,然后依据单调性求函数的最值.这种利用函数单调性求最值的方法就是函数单调性法.这种方法在高考中是必考的,多在解答题中的某一问出现.[例4] 已知函数f (x )=x ln x ,则函数f (x )在[t ,t +2](t >0)上的最小值为________.[解析] 因为f ′(x )=ln x +1,所以当x ∈⎝ ⎛⎭⎪⎫0,1e 时,f ′(x )<0,f (x )单调递减; 当x ∈⎝ ⎛⎭⎪⎫1e ,+∞时,f ′(x )>0,f (x )单调递增. ①当0<t <t +2<1e时,t 无解;②当0<t <1e <t +2,即0<t <1e 时,f (x )min =f ⎝ ⎛⎭⎪⎫1e =-1e ; ③当1e ≤t <t +2,即t ≥1e时,f (x )在[t ,t +2]上单调递增,f (x )min =f (t )=t ln t .所以f (x )min=⎩⎪⎨⎪⎧ -1e ,0<t <1e ,t ln t ,t ≥1e.[答案] f (x )min=⎩⎪⎨⎪⎧-1e ,0<t <1e ,t ln t ,t ≥1e[点评] 本题是函数在不定区间上的最值问题,因此区间的位置要全部考虑到,不要遗漏.5.导数法设函数f (x )在区间[a ,b ]上连续,在区间(a ,b )内可导,则f (x )在[a ,b ]上的最大值和最小值应为f (x )在(a ,b )内的各极值与f (a ),f (b )中的最大值和最小值.利用这种方法求函数最值的方法就是导数法.[例5] 函数f (x )=x 3-3x +1在闭区间[-3,0]上的最大值,最小值分别是________,________.[解析] 因为f ′(x )=3x 2-3,所以令f ′(x )=0,得x =-1(舍正).又f (-3)=-17,f (-1)=3,f (0)=1,易得,f (x )的最大值为3,最小值为-17. [答案] 3 -17[点评] (1)利用导数法求函数最值的三个步骤:一是求函数在(a ,b )内的极值,二是求函数在区间端点的函数值f (a ),f (b ),三是比较上述极值与区间端点函数值的大小,即得函数的最值.(2)函数的最大值点及最小值点必在以下各点中取得,导数为零的点,导数不存在的点及区间端点.6.数形结合法数形结合法是指利用函数所表示的几何意义,借助几何方法及函数的图象求函数最值的一种常用的方法.这种方法借助几何意义,以形助数,不仅可以简捷地解决问题,还可以避免诸多失误,是我们开阔思路、正确解题、提高能力的一种重要途径.[例6] 对a ,b ∈R ,记max|a ,b |=⎩⎪⎨⎪⎧a ,a ≥b ,b ,a <b ,函数f (x )=max||x +1|,|x -2||(x∈R )的最小值是________.[解析] 由|x +1|≥|x -2|,得(x +1)2≥(x -2)2,解得x ≥12.所以f (x )=⎩⎪⎨⎪⎧|x +1|,x ≥12,|x -2|,x <12,其图象如图所示.由图形,易知当x =12时,函数有最小值,所以f (x )min =f ⎝ ⎛⎭⎪⎫12=⎪⎪⎪⎪⎪⎪12+1=32.[答案] 32[点评] 用数形结合的方法求解函数最值问题,其关键是发现条件中所隐含的几何意义,利用这个几何意义,就可以画出图形,从而借助图形直观地解决问题.如将本题化为分段函数的最值问题后,可以用分段求解函数最值的方法去解.二、巧用数形结合妙解3类求参数问题数形结合就是根据数学问题的条件与结论的内在联系,既要分析问题的代数含义,又要揭示其几何意义,把“数”与“形”巧妙地结合起来,并利用“结合”寻找解题的思路,使问题得到圆满解决,数形结合是根据数量与图形之间的对应关系,通过数与形的互相转化来解决问题的一种重要思想方法.通过“以形助数,以数辅形”把复杂问题简单化,抽象问题具体化,充分利用形的直观性和数的严谨性来思考问题,拓展了思路,这就是数形结合的核心价值.通过以下三个方面体会数形结合思想的运用.1.通过基本函数模型及变式的图象求参数的取值范围或值 [例1] 已知函数f (x )=⎩⎪⎨⎪⎧|lg x |,0<x ≤10,-12x +6,x >10,若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则abc 的取值范围是( )A .(1,10)B .(5,6)C .(10,12)D .(20,24)[解析] 画出函数f (x )的图象,再画出直线y =d (0<d <1),如图所示,直观上知0<a <1,1<b <10,10<c <12,再由|lg a |=|lg b |,得-lg a =lg b ,从而得ab =1,则10<abc <12.[答案] C[点评] 通过图形可以发现a ,b ,c 所在的区间,再把绝对值符号去掉,就能发现ab =1,这样利用数形结合就可把问题化难为易了.2.通过函数的零点与方程的解的相互关系求函数零点和方程的解及参数的范围 [例2] 已知m ∈R ,函数f (x )=x 2+2(m 2+1)x +7,g (x )=-(2m 2-m +2)x +m . (1)设函数p (x )=f (x )+g (x ).如果p (x )=0在区间(1,5)内有解但无重根,求实数m 的取值范围;(2)设函数h (x )=⎩⎪⎨⎪⎧fx ,x ≥0,gx ,x <0,是否存在m ,对于任意非零实数a ,总存在唯一非零实数b (b ≠a ),使得h (a )=h (b )成立?若存在,求m 的值;若不存在,请说明理由.[解] (1)因为p (x )=f (x )+g (x )=x 2+mx +7+m ,令p (x )=0,① 因为方程①在(1,5)内有实数解,且没有重根, 由p (x )=0,得m =-x 2+7x +1=-x +12-2x +1+8x +1=2-(x +1)-8x +1, 因为1<x <5,令t =x +1,则2<t <6,如图所示,所以-163<m ≤2-4 2.当m =2-42时,p (x )=0有两个相等的根, 所以实数m 的取值范围是-163<m <2-4 2. (2)由题意,得当x ≥0时,h (x )=x 2+2(m 2+1)x +7,h (x )在区间[0,+∞)上单调递增; 当x <0时,h (x )=-(2m 2-m +2)x +m ,h (x )在区间(-∞,0)上单调递减. 记A ={h (x )|x ≥0},B ={h (x )|x <0},则A =[7,+∞),B =(m ,+∞).(ⅰ)若∀a >0时,如图(1)知,由于h (x )在(0,+∞)上是增函数,若存在非零实数b (b ≠a ),使得h (a )=h (b ),则b <0,且A ⊆B ,即m ≤7;(ⅱ)若∀a <0时,如图(2)知,由于h (x )在(-∞,0)上是减函数,若存在非零实数b (b ≠a ),使得h (a )=h (b ),则b >0,且B ⊆A ,即m ≥7.综合(ⅰ)(ⅱ),知所求m =7.现在证明充要性:①必要性:由求解过程知必要性成立;②充分性:当m =7时,A =B ,对于∀a ≠0,则∃b (b ≠a ,且ab <0),使得h (a )=h (b ).[点评] 第(1)问含有参数的二次方程或分式方程在区间(1,5)内有解且无重根,纯粹从数的角度去理解是相当困难的,通过分离变量,把方程化归为函数m =-x 2+7x +1(1<x <5),再通过换元画出函数的图象,方程在区间内有解的条件就非常容易得出了.第(2)问的解题思路也是在“形”指点下进行的,对于∀a >0,存在b ≠a ,使得h (a )=h (b )的条件是m ≤7;反过来,对于∀a <0,存在b ≠a ,使得h (a )=h (b )的条件是m ≥7.3.通过圆或圆锥曲线的部分图形与函数图象的关系来求参数的范围[例3] 如果函数y =1+4-x 2(|x |≤2)的图象与函数y =k (x -2)+4的图象有两个交点,那么实数k 的取值范围是________.[解析] 函数y =1+4-x 2的值域为[1,3],将y -1=4-x 2两边平方,得x 2+(y -1)2=4,考虑到函数的值域,函数y =1+4-x 2的图象是以(0,1)为圆心,2为半径的上半圆,半圆的端点为点A (-2,1)和点B (2,1);函数y =k (x -2)+4是过定点P (2,4)的直线.画出两函数的图象如图所示,易得实数k 的范围是⎝ ⎛⎦⎥⎤512,34.[答案] ⎝ ⎛⎦⎥⎤512,34 [点评] 函数y =1+4-x 2的图象是半圆,像这样由圆或圆锥曲线的部分图形构成的函数图象,在基本初等函数中没有涉及,应该把它和对勾函数y=x+1x作为“基本初等函数”来掌握.典例3的等价命题是方程式4-x2=3+k(x-2)在[-2,2]上有两个不同的实根,求实数k的取值范围.。
2013-2014高等数学A(1)_A卷答案

π
六 (7 分) 求由曲线 y = arcsin x (0 ≤ x ≤ 1) , y = 绕 y 轴旋转的旋转体体积. 解: Vy = π
∫
π 2
0
sin ydy = π ∫
2
π 2
0
2 1 − cos 2 y 1 ⎡1 ⎤2 π . dy = π ⎢ y − sin 2 y ⎥ = 2 4 ⎣2 ⎦0 4
−1 0
−1
−1
0
t 0 dt = [t − 2 ln(2 + t ) ]−1 = 1 − 2 ln 2 . 2+t
三、计算下列各题. (每小题 6 分,满分 24 分) 1.
∫ x( x
1
2
+ 1)
dx . (拆项) 解: ∫
1 1 x dx = ∫ ( − 2 )dx = ln | x | − ln( x 2 + 1) + C . x( x + 1) x x +1 2
x − 1 ln x = 0 ; f (1) = 0 ;
因 f (1 ) = f (1 ) = f (1) ,故 f ( x) 在 x = 1 处连续. (2) f −′(1) = lim −
x →1
−
+
−1 − ln x f ( x) − f (1) 1 − x ln x x = lim = = = 0; lim lim 1 x →1− x →1− x −1 x −1 1 − x x →1− − 2 1 −x
∫
四 (7 分) 试分析函数 f ( x ) = | x − 1| ln x , ( x > 0) 在 x = 1 处的连续性和可导性(说明理由). 解:(1) f (1 ) = lim f ( x) = 1 − x ln x = 0 ; f (1 ) = lim f ( x) = − +
2013-2014-1线性代数(本科)A卷答案

武汉科技大学2013-2014-1线性代数期末试卷(本科A)解答与参考评分标准一、单项选择题(本大题共6小题,每小题4分,共24分)1. 设A 是n 阶可逆方阵,则T B A A =-是( D ).A.正交矩阵;B.对称矩阵;C.可逆矩阵;D.反对称矩阵. 2. 向量组12,,,m ααα线性无关,则下列结论不正确的是( B ).A. 12,,,m ααα的秩为m ;B. 12,,,m ααα的极大无关组不唯一C. 12,,,m ααα中任意两个向量的分量不对应成比例;D. 12,,,m ααα中任意一个向量都不能由其余1m -个向量线性表示.3. 行列式33332222(1)(2)(3)(1)(2)(3)1231111a a a a a a a a aa a a ---------的值为( A ).A .12; B. 11; C. 13; D. 14.4.设A 为n 阶方阵,()3r A n =- ,且123,,a a a 是0Ax =的三个线性无关的解向量,则0Ax =的基础解系为( A ).A .122331,,a a a a a a +++;B .213213,,a a a a a a ---;C .21321312,,2a a a a a a ---; D .1233213,,2a a a a a a a ++---.5. 下列不是方阵A 可逆的充要条件的是( C )A. A 的行向量组线性无关;B. A 的列向量组线性无关;C. 零为A 的特征值;D. 非齐次线性方程组Ax b =有唯一解.6.非齐次线性方程组Ax b =中未知量个数为n ,方程个数为m ,系数矩阵A 的秩为r ,则( A ).A.r m =时,方程组Ax b =有解;B. r n =时,方程组Ax b =有唯一解;C.m n =时,方程组Ax b =有唯一解;D. r n <时,方程组Ax b =有无穷多解.二、填空题(本大题共6小题,每小题4分,共24分)7.A 为3阶方阵,且1A =-,则1*(2)A A --=____278____;8. 若121210021A -⎛⎫⎪=- ⎪ ⎪-⎝⎭,则1A -= 101212423⎛⎫⎪⎪ ⎪⎝⎭;9. 01010000A x ⎛⎫ ⎪=-⎪ ⎪⎝⎭,当 1± 时,矩阵A 为正交矩阵;10. 向量组123(2,4,2),(1,2,1),(3,5,2)ααα==---=的秩为 2 ;11. 已知3阶矩阵A 与3维列向量x 满足323A x Ax A x =-,且向量组2,,x Ax A x 线性无关,记 ()2,,P x Ax A x =,若有AP PB =,则B =000103011⎛⎫⎪ ⎪ ⎪-⎝⎭;12. 已知20132013001335100010242010100111001A -⎛⎫⎛⎫⎛⎫ ⎪⎪⎪=--- ⎪⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,00020002B λ⎛⎫⎪= ⎪ ⎪⎝⎭,且A 相似于B ,则λ= 6.三、解答题(本大题共4个小题,第13、14、15题,每小题10分,第16题12分,共42分)13. 计算行列式1122100000000011111n n n a a a a D a a +--=-。
2013-2014(2)高数A2(A卷)

2013-2014(2)高数A2(A 卷)一、填空题(每空3分,共18分):12:2332:43___1_6_.x y z x y z λλππ++=-+=1.设平面平行,则=与2______..yz z x x y ∂==∂∂2设则二阶混合偏导数,223.:1,______.DD x y +≤=则二重积分设区域223()______Ly x x y ds =+=⎰4.设L 为上从点(0,0)到点(1,3)的一段直线,则对弧长的曲线积分1 _______?1.n n q q ∞=∑5.当且仅当的值满足条件时,比级数收敛等 _________.x y dy e dx-=6.微分方程的通解是 二、单项选择题(请把下列各题答案的序号填入括号内,每空3分,共18分):221.1xoy x y x -=面上的曲线绕轴旋转所得旋转曲面的方程为_______.222()1;A x y z ++=; 222()1;B x y z -+= 222()1;C x y z +-=222() 1.D x y z --= ()23,,1_____1_.1x t y t z t ===--在点,,2.曲线处的法平面方程是()2360;A x y z --+= ()2340;B x y z -++=()2360;C x y z -++= ()2340.D x y z --+=2223_______.).1(x y z f x y z dV ΩΩ++=⎰⎰⎰设是由球面及三个坐标面围成的在第一卦限的那部分空间闭区域,则将三重积分化为三次积分,正确的结,,果是100()();A dx f x y z dz ⎰⎰⎰,,100()();B dx f x y z dz ⎰⎰⎰,,1000()();C dx f x y z dz ⎰⎰⎰,,1000()().D dx f x y z dz ⎰⎰⎰,,2322_4.(2sin )(cos )______.L x y mx y dx x x y y dy L m ++=++⎰已知对坐标的曲线积分在全平面内与路径无关,为平面上任一曲线,则常数()1;A ()2;B ()3;C ()4.D05.2n n n a x x ∞==∑如果幂级数在处收敛,则下列结论正确的是______.()||2A x <时级数当绝对收敛; ()||2B x <时级数当条件收敛;()||2C x >当时级数发散; ()D 以上结论都不对.226.56(1)______.xy y y x x e y *'''-+=-+=二阶常系数非齐次线性微分方程的特解形式可设为 2();A ax bx c ++ 22()();x B ax bx c e ++ 322()();x C ax bx cx e ++4322()().x D ax bx cx e ++,.(,)z y z z z z x y z x ydz x e -∂∂=+=∂∂8三(分)、设函数由方程所确定,求偏导数及全微分 2241(,).ax byx y z x y e a b ++-+=8四(分)、设二元函数在点(1,1)处取得极值,求、的值 2111.xy xI dx ye dy I =⎰⎰8五(分)、交换二次积分的积分次序,并求出的值 22(2)(2)(0,0)(1,1)(0,1)(1,0)Lx xy dx y xy dy -+-⎰8六(分)、计算对坐标的曲线积分其中积分路径L 是以为顶点的正方形区域的取正向的整,、、、个边界.1()(2)(1)(3).f x x x x =-++8七(分)、将函数展开成关于的幂级数,并指出其收敛区间 13(,.1)1n nnn x n ∞=-+∑9123八(分)、设有幂级数()求其收敛半径;()指出其收敛区间;()讨论幂级数在收敛区间端点处的敛散性,并确定其收敛域.24202424x x x y y y e y y y y y y e y y y e '''-+='''-+='''-+='''-+=9123九(分)、设有二阶常系数非齐次线性微分求()求对应的常系数齐次线性微分方程的通解;()求的一个特解;()求的通解.23(2)(3)32610.z x z y x y z -=-++-=6十(分)、证明曲面上任一点处的法线都平行于平面。
【山东专用】2014届高考数学(理)一轮复习专题集训《定积分与微积分基本定理》1Word版含解析
定积分与微积分基本定理(时间:35分钟 分值:80分)基础热身1.∫π20(x -sin x)d x 等于( )A .π24-1B .π28-1 C .π28 D .π28+1 2.下列各命题中,不正确的是( )A .若f(x)是连续的奇函数,则⎠⎛-aa f(x)d x =0B .若f(x)是连续的偶函数,则⎠⎛-aaf(x)d x =2⎠⎛0a f (x )d xC .若f(x)在[a ,b]上连续且恒正,则⎠⎛ab f(x)d x>0D .若f(x)在[a ,b]上连续,且⎠⎛ab f(x)d x>0,则f(x)在[a ,b]上恒正3.设函数f(x)=⎩⎪⎨⎪⎧x 2,0≤x<1,1,1<x ≤2,则定积分⎠⎛02f(x)d x =( )A .83B .2C .43D .134.曲线y =x 3与直线y =x 所围成图形的面积为( ) A .13 B .12 C .1 D .2能力提升5.[2013·湖南卷] 由直线x =-π3,x =π3,y =0与曲线y =cos x 所围成的封闭图形的面积为( )A .12B .1C .32D . 3 6.由曲线y =x 2,y =x 3围成的封闭图形面积为( ) A .112 B .14 C .13 D .7127.如果1 N 的力能拉长弹簧1 cm ,为了将弹簧拉长6 cm ,所耗费的功为( ) A .0.18 J B .0.26 J C .0.12 J D .0.28 J8.若y =⎠⎛0x (sin t +cos t sin t)d t ,则y 的最大值是( )A .1B .2C .-72D .09.[2013·东北名校二模] ⎠⎛01⎝⎛⎭⎫8π1-x 2+6x 2d x =________.10.[2013·陕西卷] 设f(x)=⎩⎪⎨⎪⎧lg x ,x>0,x +⎠⎛0a 3t 2d t ,x ≤0,若f(f(1))=1,则a =________.11.[2013·漳州模拟] 由曲线y =2x 2,直线y =-4x -2,直线x =1围成的封闭图形的面积为________.12.(13分)计算下列定积分:(1)⎠⎛03π1-cos 2x d x ;(2)⎠⎛011x 2+3x +2d x ;(3)⎠⎛12⎝⎛⎭⎫x -1x 2d x ;(4)⎠⎛01()e x -e -x 2d x.难点突破13.(12分)已知点P 在曲线y =x 2-1上,它的横坐标为a(a>0),由点P 作曲线y =x 2的切线PQ(Q 为切点).(1)求切线PQ 的方程;(2)求证:由上述切线与y =x 2所围成图形的面积S 与a 无关.课时作业(十六)【基础热身】1.B [解析] ∫π20(x -sin x)d x =⎪⎪⎝⎛⎭⎫12x 2+cos x π20=π28-1.2.D [解析] 根据定积分的几何意义可得.3.C [解析] ⎠⎛02f (x )d x =⎠⎛01x 2d x +⎠⎛121d x =13x 3 ⎪⎪⎪ )10+x⎪⎪⎪ )21=43. 4.B [解析] 如图,所围图形面积A =2⎠⎛01(x -x 3)d x =2⎝⎛⎭⎫12x 2-14x 4⎪⎪⎪10=2⎝⎛⎭⎫12-14-0=12.【能力提升】5.D [解析] 根据定积分的简单应用的相关知识可得到:由直线x =-π3,x =π3,y =0与曲线y =cos x 所围成的封闭图形的面积为:S =⎪⎪⎪⎪∫π3-π3cos x d x = )⎪⎪⎪ )sin x⎪⎪⎪ )π3-π3⎪⎪⎪ )=⎪⎪⎪⎪sin π3-sin ⎝⎛⎭⎫-π3=3, 故选D .6.A [解析] 由⎩⎪⎨⎪⎧y =x 2,y =x 3得交点为(0,0),(1,1).所以所求图形的面积S =⎠⎛01(x 2-x 3)d x =⎝⎛⎭⎫13x 3-14x 4⎪⎪⎪10=13-14=112.7.A [解析] 由物理知识F =kx 知,1=0.01k ,∴k =100,则W =⎠⎛0.06100x d x =50x2⎪⎪⎪ )0.060=0.18(J ).8.B [解析] y =⎠⎛0x(sin t +cos t ·sin t)d t =⎠⎛0xsin t d t +12⎠⎛0x sin 2t d t =(-cos t)⎪⎪⎪ )x 0+12⎝⎛⎭⎫-12cos 2t⎪⎪⎪ )x0 =-cos x +1-14cos 2x +14=-12(cos x +1)2+2,故当cos x =-1时,y max =2.9.4 [解析] 根据定积分的性质⎠⎛01⎝⎛⎭⎫8π1-x 2+6x 2d x =8π⎠⎛011-x 2d x +2⎠⎛013x 2d x =8π×π4+2×x 3⎪⎪⎪ )10=4. 10.1 [解析] 由f(x)=⎩⎪⎨⎪⎧lg x , x>0,x +⎠⎛0a 3t 2d t , x ≤0得f(x)=⎩⎪⎨⎪⎧lg x , x>0,x +a 3, x ≤0,f(1)=lg 1=0, f(f(1))=f(0)=a 3=1,∴a =1. 11.163[解析] 联立直线方程与抛物线方程得x 2+2x +1=0,解得x =-1,即直线y =-4x -2为抛物线y =2x 2的一条切线(如图),因此所求的面积为定积分⎠⎛-11(2x 2+4x +2)d x =23(x+1)3⎪⎪⎪ )1-1=163.12.解:(1)⎠⎛3π1-cos 2x d x =⎠⎛3π2sin 2x d x =2⎠⎛3π⎪⎪⎪ )sin x⎪⎪⎪ )d x =2⎠⎛0πsin x d x -2⎠⎛π2πsin x d x +2⎠⎛2π3πsin x d x=-2cos x ⎪⎪⎪ )π0+2cos x ⎪⎪⎪ )2ππ-2cos x⎪⎪⎪ )3π2π=22+22+22=6 2.(2)⎠⎛011x 2+3x +2d x =⎠⎛011x +1-1x +2d x =ln (x +1)-ln (x +2)⎪⎪⎪ )10=(ln 2-ln 3)-(ln 1-ln 2)=2ln 2-ln 3.(3)⎠⎛12⎝⎛⎭⎫x -1x 2d x =⎠⎛12⎝⎛⎭⎫x -2+1x d x =⎠⎛12x d x -2⎠⎛121d x +⎠⎛121xd x =12x 2 ⎪⎪⎪ )21-2x ⎪⎪⎪ )21+ln x⎪⎪⎪ )21=⎝⎛⎭⎫2-12-(4-2)+(ln 2-ln 1)=ln 2-12. (4)⎠⎛01(e x-e -x)d x =⎠⎛01(e x +e -x )′d x =(e x +e -x)⎪⎪⎪ )10=e +1e -2. 【难点突破】13.解:(1)点P 的坐标为(a ,a 2-1), 设切点Q 的坐标为(x ,x 2),由k PQ =a 2-1-x 2a -x 及y′=2x 知a 2-1-x 2a -x=2x ,解得x =a +1或x =a -1.所以所求的切线方程为2(a +1)x -y -(a +1)2=0或2(a -1)x -y -(a -1)2=0.(2)S =⎠⎛a -1a [x 2-2(a -1)x +(a -1)2]d x +⎠⎛aa +1[x 2-2(a +1)x +(a +1)2]d x =23.故所围成的图形面积S =23,此为与a 无关的一个常数.。
高等数学A(一)2013-2014(B)
第 1 页 共 6 页上 海 海 事 大 学 试 卷2013 — 2014 学年第一学期期末考试《 高等数学A (一)》(B 卷) (本次考试不能使用计算器)班级 学号 姓名 总分一、单项选择题(在每个小题四个备选答案中选出一个正确答案,填在题末的括号中) (本大题分5小题, 每小题2分, 共10分)1、当x →0时,()2cos 1x -是sin 2x 的 ( )。
(A)高阶无穷小; (B)同阶无穷小;但不等价; (C)等价无穷小; (D)低阶无穷小xx D x x x x C x x x x e B x x e A y x x e y 222222csc sec cot csc tan sec cot csc tan sec 11csc sec 11csc sec arctan 2++++++++-='-+=. .. .)(,则、设 也无水平渐近线无铅直渐近线又有水平渐近线,有铅直渐近线无水平渐近线)有铅直渐近线无铅直渐近线,有水平渐近线)渐近线的正确结论是(、关于曲线,)(,)(,(,)(1cos 32D C B A xxy +=⎰⎰⎰-=⎥⎦⎤⎢⎣⎡-202022sin 2)( 0)(sin )(sin )(sin 224ππππππxdxD C xdxB xdx A x x y 、 、 、 、 )轴围成图形的面积为(与上的曲线,、在--------------------------------------------------------------------------------------装订线------------------------------------------------------------------------------------第 2 页 共 6 页5、曲面22y x z +-=是( )(A )zox 平面上曲线z x =绕z 轴旋转而成的旋转曲面;(B )zoy 平面上曲线y z -=绕z 轴旋转而成的旋转曲面; (C )zox 平面上曲线z x =绕x 轴旋转而成的旋转曲面; (D )zoy 平面上曲线y z -=绕y 轴旋转而成的旋转曲面.二、填空题(将正确答案填在横线上) (本大题分4小题, 每小题4分, 共16分)1、处的法线方程为曲线在设曲线方程为1,sin sin 122=⎪⎩⎪⎨⎧+=++=x tt y tt x 2、='⋅⋅+⎰x x f x f x x xx f d )()( , sin 1sin )(则的一个原函数为已知3、设a b c ,,均为非零向量,且a b c b c a c a b =⨯=⨯=⨯,,b ++=4、⎰-=223_______________cos ππxdx三 计算题(必须有解题过程,否则不给分) (本大题分10小题,每题6分,共 60分)1、之值。
2013-2014学年高二数学配套课件4.5.4《微积分基本定理》(湘教版选修2-2)
即13a+b2+c=0.
③
联立①②③,得 a=3,b=-4,c=1,
∴f(x)=3x2-4x+1.
点评 利用定积分求参数的问题,主要是利 用求定积分的基本方法,列出方程组求解.
2.已知 f(a)=1(2ax2-a2x)dx,求 f(a)的最大值. 0
解
∵012ax2-a2xdx=23ax3-12a2x210=23a-12a2,
4.利用微积分基本定理求定积分bf(x)dx的关键是找出满足
a
F′(x)=f(x)的函数F(x),通常,我们可以运用基本初等函数 的求导公式和导数的四则运算法则从反方向上求出F(x). 常用的基本初等函数f(x)和它的一个原函数F(x)如下: (1)若f(x)=c(c为常数),则F(x)=cx; (2)若f(x)=xn(n≠-1),则F(x)=n+1 1·xn+1; (3)若f(x)=1x,则F(x)=ln x(x>0);
自主探究
1.f(x)的原函数唯一吗? 提示 不一定.如F(x)+c,c可以是任意一个 常数,也就是原函数可能有无穷多个.
2.当a=b时,bf(x)dx的值是多少?
a
提示 0
预习测评
1.π(sin 2x-cos x)dx的值为 0
A.1
B.0
( ).
C.2
D.-2
解析
π(sin 2x-cos x)dx=
2.微积分基本定理的直观理解
画出[a,b]上的函数y=F(x)的曲线,设f(x)是F(x)的导数,取
分点:a=x0<x1<x2<…<xn-1<xn=b. 记xk+1-xk=Δxk,显然有
n-1
F(b)-F(a)= (F(xk+1)-F(xk))
高数1-2 2013-2014 B
高数1-2 13-14 A一、选择题(每题3分,24分)1. z =,则dz =2.函数()23,22y f x y xy x =++ 在点()1,1M - 处的最大方向导数为3. 方程2sin z x y z =+ 确定了函数(),z z x y = ,则zx∂=∂ 4. 曲面2232z x y =+ 在点()1,1,0 处的切平面方程为 5. 交换二次积分()2220,yyI dy f x y dx =⎰⎰的积分次序,得I =6. 微分方程30y y '''+=的通解为7. 幂级数2nn x ∞=-的收敛域为8. 设L 为圆周22x y ax += ,则22Lx y ds +=⎰二、选择题1. 曲线2cos sin x t t =+ ,()sin 1cos y t t =- ,cos z t =- 在点2t π=处的切线方程为( )A. 11111x y z --==- B. 11111x y z--==- C. 11111x y z --==-- D. 11111x y z--==- 2. 二元函数(),z f x y =在点()00,x y 处偏导数存在是函数在该点可微分的( ) A. 必要条件 B. 充分条件 C. 充要条件 D. 既非充分也非必要 3. 设(){}22,1,0,0D x y xy x y =+≤≥≥ ,(),f x y 在D 上连续,则下列四个二次积分中与二重积分(),D f x y d σ⎰⎰ 相等的是( )A. ()100,dx f x y dy ⎰B.()0,f x y dyC.()11,dx f x y dy ⎰⎰D. ()1,dx f x y dy ⎰4. 下列级数中绝对收敛的是( )A. ()111nn nn ∞=-+∑ B.()1111nn n ∞=-+∑C. 11nn ∞=-D.11nn ∞=-三. 解答题1. 求函数()23,434f x y x y x y =++-+的极值,并说明是极大值还是极小值?(7分)2. 设函数2,y z f x y x ⎛⎫=+ ⎪⎝⎭,其中f 具有二阶连续偏导数,求z x ∂∂,2z x y ∂∂∂.(7分)3. 利用极坐标计算二重积分22x y De d σ+⎰⎰,其中D 是圆形闭区域:224x y +≤ .(7分)4. 将函数()()ln 3f x x =+ 展开成1x -的幂级数,并写出可展区间.(7分)5. 求微分方程()22cos xy y x '+=的通解. (7分)6. 求微分方程51025xy y y xe '''-+=的通解. (8分)7. 计算曲线积分()()sin cos xxLey b x y dx e y ax dy ⎡⎤-++-⎣⎦⎰,其中,a b 均为正常数,L为从点()2,0A a 沿曲线y =到原点()0,0O 的有向弧段.(8分)8. 计算曲面积分()()I x y dxdy y z xdydz ∑=-+-⎰⎰,其中∑为柱面221x y += 及 0,3z z == 围成的空间区域Ω 的整个边界曲面的外侧. (8分)四. 证明题:可微函数()f x 满足:()()111xf x f xt dt =-⎰ ()0t > ,证明:()21112f x x ⎛⎫=+ ⎪⎝⎭(5分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题 得分
1. 函数()fx在0xx处连续是可导的(B ).
A 充分条件 B 必要条件 C 充要条件 D 无关条件
2. 下列极限等于1的是(C ).
A 1limsinxxx B 11limsinxxx C 01limsinxxx D sinlimxxx
3. 0x时,23sinxx是x的( C ).
A 低阶无穷小 B 高阶无穷小
C 等价无穷小 D 同阶非等价无穷小
4. 0sin()sin44limttt=( B ).
A 2 B 22 C 12 D 2
5. 下列曲线既有水平渐近线又有垂直渐近线的是( b ).
A sinxyx B )11ln(xy C 211xyx D 2exy
6. 已知20tan(1cos)lim2ln(12)(1e)xxaxbxcxd 22(0)ac, 则( ).
A 4bd B 4bd C 4ac D 4ac
二、填空题 得分
7.2332lim23xxxx__2分之一______ .
8. 设函数212,0,(),0,xxfxax且()fx无间断点,则a .
9. 2ln(1)yx在[1,3]上的最大值 LN10 .
10. 设某函数的需求量Q关于价格的函数为4ePQ,3P时的
需求价格弹性为—四分之三 ,其经济意义是
三、计算题 得分
11. 设方程sin()ln(1)ln1xyxy确定函数()yyx, 求.y
12.利用微分求arcsin0.5002的近似值.
13.求极限 30(e1)2(e1)limsinxxxxx
14. 设2(2)e,xyx求(8).y
15. 讨论函数13()3fxxx的单调区间、极值、凹凸区间和拐点坐标.
四、应用题 得分
16. 某商品的需求函数是143Px,企业的总成本是2()5Cxxx,
(1)若每单位商品向企业征收税款t,试求企业的最大利润;
(2)试求政府可能的最大税收。
五、证明题 得分
17试证:当0x时,
2
ln(1)2xxx
.
一、选择题 得 分
二、 填空题 得 分
7.2332lim23xxxx____12____ .
8. 设函数212,0,(),0,xxfxax且()fx无间断点,则a 0 .
9. 2ln(1)yx在[1,3]上的最大值 ln9 .
10. 设某函数的需求量Q关于价格的函数为4PQe,3P时的需求价格弹性
为____3/4 或 -3/4___,其经济意义是____。
三、解答题 得 分
11. 设方程sin()ln(1)ln1xyxy确定函数()yyx, 求.y
解: 对方程两边分别对x求导,得:
1()cos()01yyxyxyxy
1
cos()11cos()yxyxyxxyy
12. 利用微分求arcsin0.5002的近似值.
解:用微分代替函数值增量,有
arcsin0.5002arcsin0.5arcsin(0.5)0.00020.00043/3
因此
arcsin0.5002/60.00043/2
题号
1 2 3 4 5 6
选项 B D C B B D
13. 求极限 30(1)2(1)limsinxxxxeex
解 原式sin~30(1)2(1)limxxxxxxeex
00
00
2
001limlim366xxxxxxeexexx
14. 设2(2),xyxe求(8).y
解:由公式()()()0()nnkknknkuvCuv
令22,xuxve,有
(8)02128882(2)22(1658)xxx
x
yCxeCxeCeexx
15. 讨论函数13()3fxxx的单调区间、极值、凹凸区间和拐点坐标.
解25332()1()()01,3fxxfxxfxx由得
0()xfx时不存在
x
,1
1
(-1,0) 0 (0,1) 1
(1,)
)(xf
+ 0 — 不存在 — 0 +
)(xf
— — — 不存在 + + +
()fx
极大 拐点 极小
2)1(2)1(0)0(fff
(),11,,1,1fx在与上单调增加在上单调减少
1x
时有极大值2
,1x
有极小值2
f ( x
) 在0,上是凸的,在,0上是凹的,
拐点为(0,0)。
四、 应用题 得 分
16. 某商品的需求函数是143Px,企业的总成本是2()5Cxxx,(1)若
每单位商品向企业征收税款t,试求企业的最大利润;(2)试求政府可能的
最大税收。
解:(1)收益 2()143RxxPxx,
税收 ()Txtx
利润 222()()()()14354(9)LxRxCxTxxxxxtxxtx
令()890Lxxt
得 98tx
又 ()1/80Lx
所以商家获得最大利润为2(9)/16Lt
(2)取得最大利润时的税收为
2
9()8ttTxtx
令 9208tT
得4.5t,又
0.250T
所以4.5t时,政府税收总额最大81/32
五、证明题 得 分
17. 证明不等式:当0x时,2ln(1)2xxx.
证明: 2ln12xfxxx设
2
110011x
fxxfxx则且
x当>0时 fx>0,所以fx单调增加
x当>0时 fx>00f,即 2ln(1)2xxx
证毕。
