高一数学第一讲任意角和弧度制练习题(1)
高一数学训练习题参考答案

数学必修(4)同步练习参考答案§1.1任意角和弧度制一、CDDCBA二、7.{x|x=k•3600+1800, k∈Z}, {x|x=k•1800+450,k∈Z} ; 8.-345°; 9. ;10.第二或第四象限, 第一或第二象限或终边在y轴的正半轴上三、11.{ α|α=k•3600+1200或α=k•3600+3000, k∈Z } -60° 120°12.由7θ=θ+k•360°,得θ=k•60°(k∈Z)∴θ=60°,120°,180°,240°,300°13.∵l=20-2r,∴S= lr= (20-2r)•r=-r2+10r=-(r-5)2+25∴当半径r=5 cm时,扇形的面积最大为25 cm2,此时,α= = =2(rad)14.A点2分钟转过2θ,且π<2θ<π,14分钟后回到原位,∴14θ=2kπ,θ= ,且 <θ< π,∴θ= π或π§1.2.1 任意角的三角函数一、CCDBCD二、7.一、三; 8. 0 ; 9. 或π; 10.二、四三、11.[2kπ, 2kπ,+ ( k∈Z)12.13.∵sinθ= - ,∴角θ终边与单位圆的交点(cosθ,sinθ)=( ,- )又∵P(-2, y)是角θ终边上一点, ∴cosθ<0,∴cosθ= - .14.略.§1.2.2同角三角函数的基本关系式一、BCDBBA二、7. ; 8.0; 9. ; 10.三、11.12.原式= - ==sinx+cosx13.左边=tan2θ-sin2θ= -sin2θ=sin2θ• =sin2θ• =sin2θ•tan2θ=右边14.(1)当m=0时, α=kπ, k∈Z ,cosα=±1, tanα=0(2)当|m|=1时, α=kπ+ , k∈Z ,cosα=0, tanα=0不存在(3)当0<|m|<1时,若α在第一或第四象限,则cosα= tanα= ;若α在第二或第三象限,则cosα=- tanα=- .§1.3 三角函数的诱导公式一、BBCCBC二、7. ; 8.1 ; 9.1 ; 10.三、11. 112. f(θ)= = =cosθ-1∴f( )=cos -1=-13.∵cos(α+β)=1, ∴α+β=2kπ, k∈Z. ∴cos(2α+β)= cos(α+α+β)= cos(π+α)=- cosα= - .14. 由已知条件得:sinα= sinβ①, cos α=- cosβ②,两式推出sinα= ,因为α∈(- , ),所以α= 或- ;回代②,注意到β∈(0,π),均解出β= ,于是存在α= ,β= 或α=- ,β= ,使两等式同时成立。
2020年人教A版高中数学必修第一册5.1 任意角及弧度制(解析版)
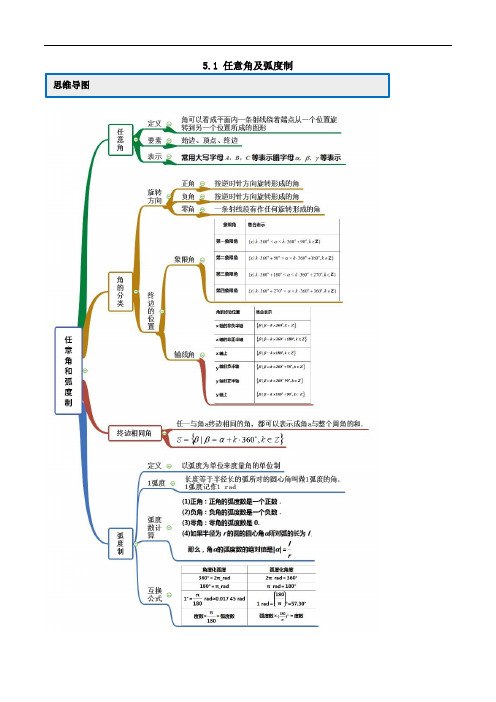
5.1 任意角及弧度制运用一 基础概念理解【例1】(2019·湖南高一期末)下列说法正确的是( ) A.小于90︒的角是锐角B.钝角是第二象限的角C.第二象限的角大于第一象限的角D.若角α与角β的终边相同,则,απβ=+∈k k Z 【答案】B【解析】A :负角不是锐角,比如“30-︒”的角,故错误; B :钝角范围是“90180α︒<<︒”,是第二象限的角,故正确; C :第二象限角取“91︒”,第一象限角取“361︒”,故错误; D :当角α与角β的终边相同,则2,k k Z απβ=+∈.故选:B. 【触类旁通】1.已知A ={第一象限角},B ={锐角},C ={小于90°的角},那么A ,B ,C 的关系是( ) A.B =A ∩C B.B ∪C =C C.A ⊆B ∩C D.A =B =C【答案】B【解析】∵A ={第一象限角}={α|k ⋅360∘<α<k ⋅360∘+90∘,k ∈Z};B ={锐角}={α|0∘<α<90∘};C ={小于90°的角}={α|α<90∘}.∴B ∪C ={小于90°的角}=C ,即B ⊂C ,且B ⊂A ,则B 不一定等于A ∩C ,A 不一定是C 的子集,三集合不一定相等, 由集合间的关系可得B ∪C =C .故选B .运用二 终边相同的角【例2】(1)如果α=−21∘,那么与终边相同的角可以表示为 A.{β|β=k ⋅360∘+21∘,k ∈Z } B.{β|β=k ⋅360∘−21∘,k ∈Z } C.{β|β=k ⋅180∘+21∘,k ∈Z }D.{β|β=k ⋅180∘−21∘,k ∈Z } (2)终边在直线y =-x 上的所有角的集合是( )A .{α|α=k ·360°+135°,k ∈Z}B .{α|α=k ·360°-45°,k ∈Z}C .{α|α=k ·180°+225°,k ∈Z}D .{α|α=k ·180°-45°,k ∈Z}(3)(2019春•南京期中)若角α=m•360°+60°,β=k•360°+120°,(m,k∈Z),则角α与β的终边的位置关系是()A.重合B.关于原点对称C.关于x轴对称D.关于y轴对称【答案】(1)B(2)D(3)D【解析】根据终边相同的角相差360∘的整数倍,故与角α有相同终边的角为k⋅360∘+α(k∈Z),所以α=−21∘,表示为k⋅360∘−21∘(k∈Z),故选B.(2)直线y=﹣x过原点,它是第二、四象限角的平分线所在的直线,故在0°~360°范围内终边在直线y=﹣x上的角有两个:135°,315°.因此,终边在直线y=﹣x上的角的集合S={α|α=135°+k•360°,k∈Z}∪{α|α=315°+k•360°,k∈Z}={α|α=135°+2k•180°,k∈Z}∪{α|α=135°+(2k+1)•180°,k∈Z}={α|α=135°+k•180°,k∈Z}.或者表示为S={α|α=k·180°-45°,k∈Z}.故选:D.(3)α的终边和60°的终边相同,β的终边与120°终边相同,∵180°﹣120°=60°∴角α与β的终边的位置关系是关于y轴对称,故选:D.【触类旁通】1.与角-1 560°终边相同的角的集合中,最小正角是________,最大负角是________.【答案】240°-120°【解析】根据终边相同的角相差360°的整数倍,故与﹣1560°终边相同的角可表示为:{α|α=k•360°﹣1560°,k∈Z}.则当k=4时,α=4×360°﹣1560°=﹣120°,此时为最大的负角.当k=5时,α=5×360°﹣1560°=240°,此时为最小的正角.故答案为:240°,﹣120°2.(2018春•武功县期中)下列各组角中,终边相同的角是()A.﹣398°,1042°B.﹣398°,142°C.﹣398°,38°D.142°,1042°【答案】A【解析】由题意,﹣398°=322°﹣2×360°,1042°=322°+2×360°,142°,38°;这四个角中,终边相同的角是﹣398°和1042°.故选:A.3.已知α=﹣30°,若α与β的终边关于直线x﹣y=0对称,则β=;若α与β的终边关于y轴对称,则β=;若α与β的终边关于x轴对称,则β=.【答案】见解析【解析】如图,设α=﹣30°所在终边为OA,则关于直线x﹣y=0对称的角β的终边为OB,终边在OB上的最小正角为120°,故β=120°+k•360°,k∈Z;关于y轴对称的角β的终边为OC,终边在OC上的最小正角为210°,故β=210°+k•360°,k∈Z;关于x轴对称的角β的终边为OD,终边在OD上的最小正角为30°,故β=30°+k•360°,k∈Z.故答案为:120°+k •360°,k ∈Z ;210°+k •360°,k ∈Z ;30°+k •360°,k ∈Z .运用三 角所在象限【例3】(1)(2019·湖南高一期末)179︒是() A .第一象限角B .第二象限角C .第三象限角D .第四象限角(2)(2019春•北碚区校级期中)已知α为第二象限角,则所在的象限是( ) A .第一或第二象限 B .第二或第三象限 C .第一或第三象限 D .第二或第四象限【答案】(1)B (2)C【解析】(1)1791801︒︒︒=-,所以179︒表示第二象限角,故选B . (2)∵α是第二象限角,∴k •360°+90°<α<k •360°+180°,k ∈Z , 则k •180°+45°<<k •180°+90°,k ∈Z ,令k =2n ,n ∈Z 有n •360°+45°<<n •360°+90°,n ∈Z ;在一象限;k =2n +1,n ∈z ,有n •360°+225°<<n •360°+270°,n ∈Z ;在三象限;故选:C .【触类旁通】1.(2018•徐汇区校级模拟)若α是第二象限的角,则的终边所在位置不可能是( ) A .第一象限 B .第二象限 C .第三象限D .笫象限【答案】C【解析】∵α是第二象限角,∴90°+k •360°<α<180°+k •360°,k ∈Z . 则30°+k •120°<<60°+k •120°,k ∈Z .当k =0时,30°<<60°,α为第一象限角;2α3α当k =1时,150°<<180°,α为第二象限角;当k =2时,270°<<300°,α为第四象限角.由上可知,的终边所在位置不可能是第三象限角.故选:C .2.(2019秋•宜城市校级月考)如果α是第三象限角,则是( )A .第一象限角B .第一或第二象限角C .第一或第三象限角D .第二或第四象限角【答案】C【解析】∵α是第三象限角,∴180°+k •360°<α<270°+k •360°,k ∈Z , ∴﹣135°﹣k •180°<﹣<﹣90°﹣k •180°,∴﹣是第一或第三象限角.故选:C .运用四 弧度制的理解【例4】(2019春•历城区校级月考)下列命题中,真命题的是( ) A .1弧度是一度的圆心角所对的弧 B .1弧度是长度为半径的弧 C .1弧度是一度的弧与一度的角之和D .1弧度是长度等于半径长的弧所对的圆心角的大小 【答案】D【解析】根据弧度的定义知:长度等于半径长的弧所对的圆心角叫做1弧度的角. 故选:D .2α-【触类旁通】1.(2019春•静安区期末)下列选项中,错误的是( ) A .“度”与“弧度”是度量角的两种不同的度量单位B .一度的角是周角的,一弧度的角是周角的 C .根据弧度的定义,180度一定等于π弧度D .不论是用角度制还是弧度制度量角,它们与圆的半径长短有关 【答案】D【解析】“度”与“弧度”是度量角的两种不同的度量单位,判断正确;一度的角是周角的,一弧度的角是周角的,满足两种角的度量定义,正确; 根据弧度的定义,180度一定等于π弧度,满足两种角的度量关系,正确; 不论是用角度制还是弧度制度量角,它们与圆的半径长短有关,不正确;故选:D .运用五 角度与弧度的转化【例5-1】(2019春•微山县校级月考)将下列弧度转化为角度:角度化为弧度: (1)12π= ; (2)136π= ;(3)512π-= . (4)36︒= rad ;(5)105-︒= rad . 【答案】:15°,390°,﹣75°,.【解析】∵π=180°, ∴;;;36°=36×;.【例5-2】(2019·榆林市第二中学高一期末)下列各角与3π终边相同的角是( ) A .43π B .53π C .43π-D .53π-【答案】D 【解析】与3π终边相同的角可表示为()23k k Z πβπ=+∈,当1k =-时,53πβ=- 136012π136012π故选D【触类旁通】1.1 920°的角化为弧度数为( )A.163B.323C.163π D.323π【答案】D【解析】∵1°=π180rad ,∴1 920°=1 920×π180rad =323π rad.2.(2019·上海市三林中学高一月考)与角136π终边相同的最小正角大小是_________ 【答案】6π 【解析】所有与角136π终边相同的角是α =132,6k k Z ππ+∈ ,令1k =- 即得到最小的正角,即6π。
高一数学任意角和弧度制和任意角的三角函数试题

高一数学任意角和弧度制和任意角的三角函数试题1.化为弧度是( )A.B.C.D.【答案】B【解析】本题角度化为弧度,变换规则是度数乘以,,故选B.【考点】弧度与角度的互化.2.是第( )象限角.A.一B.二C.三D.四【答案】C【解析】本题主要考查三角函数终边相同的角.由得出终边在第三象限,故选C.【考点】终边相同的角的表示.3.已知角的终边过点(-5,12),则=________.【答案】【解析】.【考点】任意角的三角函数的定义.4.与终边相同的最小正角是.【答案】【解析】因为与终边相同的角是所以当时,与终边相同的最小正角是【考点】与终边相同的角5.与60°角终边相同的角的集合可以表示为( )A.{|=k·360°+,k Z}B.{|=2k+60°,k Z}C.{|=k·180°+60°,k Z}D.{|=2k+,k Z}【答案】D【解析】A,B把弧度制与角度制混在了一起,不规范,而C,应为=k·360°+60°,D正确.【考点】终边相同的角的集合.6.已知是第一象限的角,那么是()A.第一象限角B.第二象限角C.第一或第二象限角D.第一或第三象限角【答案】D【解析】∵α的取值范围(k∈Z)∴的取值范围是(k∈Z),分类讨论①当k="2n+1" (其中n∈Z)时的取值范围是即属于第三象限角.②当k=2n(其中n∈Z)时的取值范围是即属于第一象限角.故答案为:D.【考点】象限角、轴线角.7.设,,,则( )A.B.C.D.【答案】D【解析】因为,所以<;因为,所以>,<,,所以b<a<c.故答案为:D.【考点】三角函数值.8.计算:= ;【答案】1【解析】原式=【考点】三角函数值的计算9.一个扇形的周长是6,该扇形的中心角是1弧度,该扇形的面积是_______.【答案】【解析】设该扇形的半径、弧长分别为,则依题意有,从中解得,从而.【考点】1.扇形的弧长公式;2.扇形的面积公式.10.已知角的顶点在坐标原点,始边在轴的正半轴,终边经过点,则【答案】-.【解析】由题意可得 x=-1,y=,r2=x2+y2=4,r=2,故cosa==-.【考点】任意角的三角函数的定义.11.已知圆中一段弧长正好等于该圆的外切正三角形的边长,那么这段弧所对的圆心角的弧度数为 ( )A.B.C.D.2【答案】D【解析】根据题意,由于设圆的半径为r,则可知,圆中一段弧长正好等于该圆的外切正三角形的边长,可知圆心到三角形不边长的距离为r,利用30得三角函数知可知,正三角形得边长得的长度为2r,那么利用弧长公式可知,弧度数等于弧长除以半径即为2,故选D.【考点】弧度数的问题点评:解决的关键是根据弧长公式,利用圆的半径来得到弧度数,属于基础题。
高中数学新教材必修第一册第五章 三角函数 5.1 任意角和弧度制(南开题库详解)

第五章三角函数 5.1 任意角和弧度制一、选择题(共60小题;共300分)1. 下列结论正确的是A. 终边相同的角一定相等B. 轴上的角均可表示为C. 第一象限的角都是锐角D. 钝角一定是第二象限的角2. 如果,,则是A. 第一或第三象限角B. 第一或第二象限角C. 第二或第四象限角D. 第三或第四象限角3. 已知角,的终边相同,那么的终边在A. 轴非负半轴上B. 轴非负半轴上C. 轴非正半轴上D. 轴非正半轴上4. 在半径不等的两个圆内,弧度的圆心角A. 所对弧长相等B. 所对的弦长相等C. 所对弧长等于各自半径D. 所对弦长等于各自半径5. 下列四个选项中,与角终边相同的角是A. B. C. D.6. 与的终边相同的角是A. B. C. D.7. 下列命题正确的是A. 第一象限角一定不是负角B. 小于的角一定是锐角C. 钝角一定是第二象限角D. 终边相同的角一定相等8. 若是第二象限角,则是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角9. 的弧度数是A. B. C. D.10. 已知一个扇形的圆心角的弧度数为,则该扇形的弧长与半径的比等于A. B. C. D.11. 半径为,中心角为的弧长为A. B. C. D.12. 下列各组角中,终边相同的是A. 与,B. 与,C. 与,D. 与,13. 一个扇形的圆心角为,半径为,则此扇形的面积为A. B. C. D.14. 与角终边相同的角是A. B. C. D.15. 圆弧长度等于圆弧所在圆的内接正三角形的边长,则圆弧所对圆心角的弧度数为A. B. C. D.16. 集合中,各角的终边都在A. 轴正半轴上B. 轴正半轴上C. 轴或轴上D. 轴正半轴或轴正半轴上17. 已知扇形的半径为,周长为,则扇形的圆心角等于A. B. C. D.18. 设集合,,那么A. B. C. D.19. 把表示成的形式,使最小的的值是A. B. C. D.20. 设小于的角,锐角,第一象限的角,小于但不小于的角,那么有A. B.C. D.21. 已知为第二象限角,则所在的象限是A. 第一或第二象限B. 第二或第三象限C. 第一或第三象限D. 第二或第四象限22. 下列命题正确的是A. 第一象限角一定不是负角B. 小于的角一定是锐角C. 钝角一定是第二象限角D. 终边相同的角一定相等23. 将表的分针拨快分钟,则分针旋转过程中形成的角的弧度数是A. B. C. D.24. 将化为弧度为A. B. C. D.25. 是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角26. 对于始边相同的角,下列命题正确的是A. 第一象限角必定为锐角B. 终边相同的角必定相等C. 相等的角,其终边位置必定相同D. 不相等的角,其终边位置必定不同27. 已知扇形的周长为,圆心角为弧度,则该扇形的面积为A. B. C. D.28. 下列选项中叙述正确的是A. 三角形的内角是第一象限角或第二象限角B. 锐角是第一象限的角C. 第二象限的角比第一象限的角大D. 终边不同的角同一三角函数值不相等29. 与角的终边相同的角是A. B. C. D.30. 角的终边所在的象限是A. 第一象限B. 第二象限C. 第三象限D. 第四象限31. ,则的终边在A. 第一象限B. 第二象限C. 第三象限D. 第四象限32. 已知集合,,则等于A.B.C.D. 或33. 将分针拨慢分钟,则分钟转过的弧度数是A. B. C. D.34. 下列说法正确的是A. 第二象限的角比第一象限的角大B. 若,则C. 三角形的内角是第一象限角或第二象限角D. 不论用角度制还是弧度制度量一个角,它们与扇形所对应的半径的大小无关35. 时钟经过一小时,时针转过了A. B. C. D.36. 若一扇形的圆心角为,半径为,则扇形的面积为A. B. C. D.37. 时钟经过一小时,时针转过了A. B. C. D.38. 已知第一象限角,锐角,小于的角,那么,,之间的关系是A. B. C. D.39. 周长为,圆心角为的扇形面积为A. B. C. D.40. 已知扇形的圆心角为,半径等于,则扇形的弧长为A. B. C. D.41. 在单位圆中,面积为的扇形所对的弧长为A. B. C. D.42. 集合中的角的终边所在的范围(阴影部分)是A. B.C. D.43. 已知扇形的周长是,面积是,则扇形的圆心角的弧度数是A. 或B.C.D.44. 给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论用角度制还是用弧度制度量一个角,它们与扇形所对半径的大小无关;④若,则与的终边相同;⑤若,则是第二或第三象限的角.其中正确命题的个数是A. B. C. D.45. 已知扇形的周长为,圆心角为弧度,则该扇形的面积为A. B. C. D.46. 已知弧度的圆心角所对的弦长为,则这个圆心角所对的弧长是A. B. C. D.47. 一圆内切于圆心角为,半径为的扇形,则该圆的面积与扇形面积之比为A. B. C. D.48. 中心角为的扇形,它的弧长为,则三角形的内切圆半径为A. B. C. D.49. 若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为A. B. C. D.50. 设集合,,那么A. B. C. D.51. 下列结论中错误的是A. 若,则B. 若是第二象限角,则为第一象限或第三象限角C. 若角的终边过点,则D. 若扇形的周长为,半径为,则其中心角的大小为弧度52. 若角和角的终边关于轴对称,则角可以用角表示为A. B.C. D.53. 若角和角的终边关于轴对称,则角可以用角表示为A. B.C. D.54. 设,下列终边相同的角是A. 与B. 与C. 与D. 与55. 在一块顶角为,腰长为的等腰三角形钢板废料中裁剪扇形,现有如图所示两种方案,则A. 方案一中扇形的周长更长B. 方案二中扇形的周长更长C. 方案一中扇形的面积更大D. 方案二中扇形的面积更大56. 已知第一象限角,锐角,小于的角,那么,,关系是A. B. C. D.57. 设集合,集合,则.A. B. C. D.58. 下列命题中正确的是A. 若,则是第一或第三象限角B. 若,则C. 若,则与的终边相同D. 若角的终边在坐标轴上,则,59. 已知,则是A. 第一象限或第二象限的角B. 第二象限或第四象限的角C. 第一象限或第三象限的角D. 第二象限或第三象限的角60. 若是第二象限角,那么和都不是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角二、填空题(共30小题;共150分)61. 若角,则角的终边在第象限.62. 与角终边相同的角的集合是,它们中最小的正角是,最大的负角是,它们是第象限角.63. 某蒸汽机上的飞轮直径为,每分钟按顺时针方向旋转转,则飞轮每秒钟转过的弧度数是;轮周上的一点每秒钟经过的弧长为.64. 设,且角的终边与角的终边相同,则.65. 如图所示,用集合表示终边在阴影部分的角的集合为.66. 已知扇形的半径为,圆心角为弧度,则该扇形的面积为.67. 有下列四个结论:①角和的终边重合,则,;②角和的终边关于原点对称,则,;③角和的终边关于轴对称,则,;④角和的终边关于轴对称,则,.其中正确的有.(填序号)68. 若是第四象限,则是第象限角.69. 如果把化为(,)的形式,那么,.70. 已知角的终边经过点,且为第三象限角,则的取值范围是.71. 在集合中,属于区间的角的集合是.72. 终边与角的终边互相垂直的角的集合是.73. 若角的终边与角的终边关于直线对称,且,则.74. 已知扇形的面积为,扇形圆心角的弧度数是,那么扇形的周长为.75. 巳知一扇形的圆心角,那么此扇形的面积与其内切圆的面积之比为.76. 如图,已知扇形的圆心角为,半径为,则扇形中所含弓形的面积是.77. 已知扇形的周长为,那么当扇形的半径为时,扇形的面积最大.78. 已知圆心角为的扇形的弧长为,则它的内切圆半径是.79. 若某扇形的面积是,它的周长是,则该扇形圆心角的弧度数为.80. 若圆弧长度等于该圆内接正方形的边长,则其圆心角的弧度数是.81. 若将时钟拨慢,则时针转了;若将时钟拨快,则分针转了.82. 下列说法:①终边相同的角一定相等;②第二象限角大于第一象限角;③的角是第一象限角;④小于的角是钝角,直角或锐角.⑤弧度是的圆心角所对的弧;⑥弧度是长度等于半径的圆弧所对圆心角;⑦弧度等于.其中正确的序号为(把正确的序号都写出来).83. 给出下列命题:第二象限角大于第一象限角;三角形的内角是第一象限角或第二象限角;不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关;若,则与的终边相同;若,则是第二或第三象限的角.其中不正确的命题是.84. 若扇形的圆心角为,弧长为,则扇形的半径为.85. 如图,点,,是圆上的点,且,,则劣弧的长为.86. ()终边在直线上的角的集合是.()若角的终边与角的终边相同,则在内终边与角的终边相同的角的个数为.87. 用弧度制表示终边在直线上的角的集合是.88. 有下列四个结论:①角和角的终边重合,则,;②角和角的终边关于原点对称,则,;③角和角的终边关于轴对称,则,;④角和角的终边关于轴对称,则,.其中正确的有.(填序号)89. 圆的半径为,为圆周上一点,现将如图放置的边长为的正方形(实线所示,正方形的顶点与点重合)沿圆周逆时针滚动,点第一次回到点的位置,则点走过的路径的长度为.90. 如图,在平面直角坐标系中,一单位圆的圆心的初始位置在,此时圆上一点的位置在,圆在轴上沿正向滚动.当圆滚动到圆心位于时,的坐标为.三、解答题(共10小题;共130分)91. 已知,若的终边与角的终边重合,求角.92. 试求出终边在如图所示阴影区域内的角的集合.93. 已知,求,并指出的终边位置.94. 今天是周日,那天后是周几?过多少天是周二?在数轴上表达:如图,周二是那些天?如何统一表达?95. (1)写出与下列各角终边相同的角的集合,并把中适合不等式的元素写出来:①;②(2)试写出终边在直线上的角的集合,并把中适合不等式的元素写出来.96. 已知扇形的圆心角是,半径是,弧长为.(1)若,,求扇形的面积;(2)若扇形的周长为,求扇形面积的最大值,并求此时扇形圆心角的弧度数.97. 如图,动点,从点出发,沿着圆周做匀速运动.点按逆时针方向每秒转,点按顺时针方向每秒转,求点,第一次相遇时所用的时间及点,各自走过的弧长.98. 己知弦长为,它所对的圆心角,求所夹的扇形面积以及所对的弓形的周长.99. 设是第二象限角,试比较,,的大小.100. 如图,在扇形中,,弧长为,求此扇形内切圆的面积.答案第一部分1. D2. A3. A4. C5. C6. D7. C8. A9. A10. C11. D12. D13. A 【解析】因为扇形的圆心角为,半径为,所以扇形的面积.14. D15. C16. C17. B18. B19. C20. D21. C22. C23. C 【解析】将表的分针拨快应按顺时针方向旋转,为负角.故A、B不正确,又因为拨快分钟,故转过的角的大小应为圆周的 .故所求角的弧度数为 .24. B25. B26. C27. A 【解析】设扇形的弧长为,扇形所在圆的半径为,由题意得解得.扇形28. B29. A30. C【解析】由,知角和角终边相同,在第三象限.31. C32. D33. C【解析】钟表的指针按顺时针方向转动,角为负角..36. B 【解析】,所以扇形37. B 【解析】钟表的指针按顺时针方向转动,角为负角.38. A39. A40. A41. B42. C 【解析】当时,;当时,,应选C.43. A44. A 【解析】由于第一象限角不小于第二象限角,故①错;当三角形的内角为时,其既不是第一象限角,也不是第二象限角,故②错;③正确;由于,但与的终边不相同,故④错;当,时既不是第二象限角,又不是第三象限角,故⑤错.综上可知只有③正确.45. A【解析】由题意得解得所以.46. C 【解析】由题设,圆弧的半径,所以圆心角所对的弧长.47. B48. B49. D 【解析】如图,等边三角形是半径为的圆的内接三角形,则线段所对的圆心角,作,垂足为,在中,,,所以,,所以,由弧长公式得.50. B51. C52. B53. B【解析】因为为顶角为,腰长为的等腰三角形,所以,,,所以方案一中扇形的周长,方案二中扇形的周长,方案一中扇形的面积,方案二中扇形的面积.56. B 【解析】因为第一象限角,小于的角,锐角,所以.集合57. D 【解析】集合,所以.58. D 【解析】当时,,但不是第一或第三象限角,所以A不正确;当,时,,所以B不正确;当,时,,但是与的终边不相同,所以C不正确;D 正确.59. C 【解析】提示:由已知,所以,即.故是第一象限或第三象限的角.60. B【解析】因为是第二象限角,所以,,所以,,所以是第一或第三象限角,而是第三象限角,所以是第四象限角.第二部分61. 二62. ;,;,;,三63. ,64.65.【解析】由题图知,终边落在射线上的角为,以为终边的角与角的终边相同,所以终边落在图中阴影部分的角的集合为.66.【解析】根据扇形的弧长公式可得,根据扇形的面积公式可得.67. ①②③④68. 三69. 略,略70.71.72. 略73.74.【解析】设扇形的半径为,则,所以,所以扇形的周长为.75.【解析】设扇形的半径为,内切圆的半径为,则,即.又扇,内切圆,所以扇内切圆.76.【解析】因为扇形(),(),所以弓形扇形().77.【解析】设扇形的圆心角为,半径为,扇形的弧长.因为,,所以扇形当时,扇形的面积最大.78.【解析】如图,设内切圆半径为,则扇形的半径为,扇形弧长,解得.79.【解析】设扇形的半径为,弧长为,由题意知解得所以扇形的圆心角的弧度数为.80.【解析】设圆半径为,则圆内接正方形的对角线长为,所以正方形边长为,所以圆心角的弧度数是.81. ,【解析】将时针拨慢,时针按逆时针方向转动,转过的是正角,转过的度数为.将时针拨快,分针按顺时针方向转动,转过的是负角,转过的度数为.82. ⑥【解析】(1)明确各种角的定义,逐一判断即可.对于①,终边相同的角不一定相等,终边相同的角有无数多个,它们相差的整数倍,故①是错误的;对于②,角是第一象限角,角是第二象限角,,所以②错误;对于③,的角是指的角,其中角不是任何象限的角,为轴线角,故③错误;对于④,小于的角指满足的角,其中也包括负角和零角,故④错误.(2)弧度角的定义:把长度等于半径长的弧所对的圆心角叫做弧度的角.由此可知,只有⑥正确.⑤⑦错误.83.【解析】由于第一象限角不小于第二象限角,故错;当三角形的内角为时,其既不是第一象限角,也不是第二象限角,故错;正确;由于,但与的终边不相同,故错;当,时既不是第二象限角,又不是第三象限角,故错.综上可知只有正确.84.【解析】由,解得.85.【解析】.86. ,【解析】()在内终边在直线上的角为,所以终边在直线上的角的集合为.()因为,所以,依题意,,所以,所以=,即在内与角的终边相同的角为,,共三个.87.【解析】,,,解得,又,故,,,角为,,.88. ①②③④89. .【解析】每次转动一个边长时,圆心角转过,正方形有边,所以需要转动次,回到起点.在这次中,半径为的次,半径为的次,半径为的次,点走过的路径的长度= + = .90.【解析】设,,由题意知劣弧长为,由于圆的半径为,所以.设,则,,所以的坐标为.第三部分91. 略92. 因为,所以终边在题图所示阴影区域内的角的集合为.93. 略94. 略.95. (1)①,其中适合不等式的元素为:,,;②,其中适合不等式的元素为:,,.(2)终边在直线上的角的集合其中适合不等式的元素为:,.96. (1).(2)由题意知,即,,当时,的最大值为,当时,,.即扇形面积的最大值为,此时扇形圆心角的弧度数为.97. ,得秒,走过的弧长为,走过的弧长为.98. ();().99. 因为是第二象限角,所以,,所以,,所以是第一或第三象限角(如图阴影部分).结合单位圆上的三角函数线可得,(i)当是第一象限角时,,,,从而得;(ii)当是第三象限角时,,,,从而得.综上,当是第一象限角,即,时,;当是第三象限角,即,时,.100. 设扇形的半径为,其内切圆的半径为,由已知得,.又因为,所以.所以内切圆的面积为.。
高一数学任意角和弧度制和任意角的三角函数试题

高一数学任意角和弧度制和任意角的三角函数试题1.已知角的终边经过点,则.【答案】【解析】由题意可得:,所以.【考点】任意角三角函数的定义.2.半径为1m的圆中,60°的圆心角所对的弧的长度为()m.A.B.C.60D.1【答案】B【解析】因为60°=又根据弧长计算公式L=故选B.【考点】扇形的弧长计算公式.3.下列命题正确的是 ( )A.小于的角一定是锐角B.终边相同的角一定相等C.终边落在直线上的角可以表示为,D.若,则角的正切值等于角的正切值【答案】D【解析】小于的角可以是锐角、零角及负角,故错;终边相同的角相差的整数倍,故错;终边落在直线上的角可以表示为,故错;正确.故选D.【考点】三角函数的概念的应用.4.一个半径大于2的扇形,其周长,面积,求这个扇形的半径和圆心角的弧度数.【答案】,【解析】由题设条件给出周长,面积,因为扇形周长由两半径和弧长组成,故可列出方程,再结合扇形面积公式:,可解得半径,从而求得圆心角试题解析:由得:将上式代入得(舍去)【考点】扇形的面积公式和弧长公式.5. sin480°等于().A.B.C.D.【答案】D.【解析】因为,所以选D.【考点】诱导公式,特殊角的三角函数值.6.一扇形的中心角为2,对应的弧长为4,则此扇形的面积为().A.1B.2C.4D.8【答案】C【解析】,,则扇形的面积.【考点】扇形的弧长与面积公式.7.半径为3,中心角为120o的扇形面积为().A.B.C.D.【答案】B【解析】,.【考点】扇形面积公式.8.如图,在直角坐标系中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是().A.(cosθ,sinθ)B.(-cosθ,sinθ)C.(sinθ,cosθ)D.(-sinθ,cosθ)【答案】A【解析】设,则,由任意角的三角函数定义得:,即.【考点】任意角的三角函数定义.9.如果有意义,那么的取值范围是()A.B.C.D.【答案】B【解析】∵,∴,即,∴.【考点】三角函数的取值范围.10. 2400化成弧度制是()A.B.C.D.【答案】C【解析】本题考查度与弧度的互化,利用公式弧度,可得.【考点】度与弧度的互化.11.设,,,则( )A.B.C.D.【答案】D【解析】因为,所以<;因为,所以>,<,,所以b<a<c.故答案为:D.【考点】三角函数值.12.已知点是角终边上一点,且,则的值为()A.5B.C.4D.【答案】D【解析】由两点间距离公式知点P到原点的距离=,有三角函数定义知==<0,故<0,平方解得=4(舍)或=4.由题知=,∴==<0,∴<0,解得=-4,故选D.【考点】任意角的三角函数定义13.设角的终边上有一点,则的值是( )A.B.C.或D.1【答案】A【解析】由三角函数的定义可知,所以,选A.【考点】任意角的三角函数.14.已知角是第二象限角,角的终边经过点,且,则()A.B.C.D.【答案】D【解析】由角的终边经过点与,可得,解得或,而是第二象限角,所以,故,所以,故选答案D.【考点】任意角的三角函数.15.是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角【答案】C【解析】因为第一象限角的范围为;第二象限角的范围为;第三象限角的范围为;第四象限角的范围为;是第三象限角,故选C.【考点】象限角的概念.16.比较大小:(用“”,“”或“”连接).【答案】>.【解析】在单位圆中,做出锐角1的正切线、正弦线、余弦线,观察他们的长度,发现正切线最长,余弦线最短,故有 tan1>sin1>cos1>0.【考点】三角函数线.17.已知角的终边过,则= .【答案】【解析】根据题意,由于角的终边过,那么可知,该点的,则可知该点的正切值为,结合角的范围可知,的值为,故答案为。
高中数学新教材必修第一册第五章 三角函数 5.1 任意角和弧度制(南开题库含详解)

第五章三角函数 5.1 任意角和弧度制一、选择题(共40小题;共200分)1. 下列四个选项中,与角终边相同的角是A. B. C. D.2. 已知一个扇形的圆心角的弧度数为,则该扇形的弧长与半径的比等于A. B. C. D.3. 的弧度数是A. B. C. D.4. 与的终边相同的角是A. B. C. D.5. 把表示成的形式,使最小的的值是A. B. C. D.6. 与角的终边相同的角是A. B. C. D.7. 将化为弧度为A. B. C. D.8. 是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角9. 一个扇形的圆心角为,半径为,则此扇形的面积为A. B. C. D.10. 已知为第二象限角,则所在的象限是A. 第一或第二象限B. 第二或第三象限C. 第一或第三象限D. 第二或第四象限11. 在单位圆中,面积为的扇形所对的弧长为A. B. C. D.12. 与角终边相同的角是A. B. C. D.13. 下列说法正确的是A. 第二象限的角比第一象限的角大B. 若,则C. 三角形的内角是第一象限角或第二象限角14. 将分针拨慢分钟,则分钟转过的弧度数是A. B. C. D.15. 已知扇形的周长为,圆心角为弧度,则该扇形的面积为A. B. C. D.16. 已知集合,,则等于A.B.C.D. 或17. ,则的终边在A. 第一象限B. 第二象限C. 第三象限D. 第四象限18. 圆弧长度等于圆弧所在圆的内接正三角形的边长,则圆弧所对圆心角的弧度数为A. B. C. D.19. 时钟经过一小时,时针转过了A. B. C. D.20. 集合中的角的终边所在的范围(阴影部分)是A. B.C. D.21. 下列命题中:①小于的角是锐角,②第二象限角是钝角,③终边相同的角相等,④若与有相同的终边,则必有,正确的个数是A. B. C. D.22. 时钟经过一小时,时针转过了A. B. C. D.23. 设小于的角,锐角,第一象限的角,小于但不小于的角,那么有A. B.C. D.A. 轴正半轴上B. 轴正半轴上C. 轴或轴上D. 轴正半轴或轴正半轴上25. 已知扇形的半径为,周长为,则扇形的圆心角等于A. B. C. D.26. 设集合,,那么A. B. C. D.27. 若一扇形的圆心角为,半径为,则扇形的面积为A. B. C. D.28. 已知扇形的周长为,圆心角为弧度,则该扇形的面积为A. B. C. D.29. 下列结论中错误的是A. 若,则B. 若是第二象限角,则为第一象限或第三象限角C. 若角的终边过点,则D. 若扇形的周长为,半径为,则其中心角的大小为弧度30. 给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论用角度制还是用弧度制度量一个角,它们与扇形所对半径的大小无关;④若,则与的终边相同;⑤若,则是第二或第三象限的角.其中正确命题的个数是A. B. C. D.31. 设集合,集合,则.A. B. C. D.32. 若是第二象限角,那么和都不是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角33. 若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为A. B. C. D.34. 设集合,,那么A. B. C. D.35. 已知扇形的周长是,面积是,则扇形的圆心角的弧度数是A. 或B.C.D.36. 若角和角的终边关于轴对称,则角可以用角表示为A. B.C. D.37. 若角和角的终边关于轴对称,则角可以用角表示为A. B.C. D.38. 设,下列终边相同的角是A. 与B. 与C. 与D. 与39. 中心角为的扇形,它的弧长为,则三角形的内切圆半径为A. B. C. D.40. 一圆内切于圆心角为,半径为的扇形,则该圆的面积与扇形面积之比为A. B. C. D.二、填空题(共40小题;共200分)41. 若是第三象限的角,则是第象限角.42. 若角,则角的终边在第象限.43. 如图,射线绕顶点顺时针旋转到,再逆时针旋转到达,则的度数为.44. 将化为弧度为.45. 若是第四象限,则是第象限角.46. 已知扇形的半径为,圆心角为弧度,则该扇形的面积为.47. 已知角的终边经过点,且为第三象限角,则的取值范围是.48. 若扇形的中心角为,则扇形的内切圆的面积与扇形面积之比为.49. 终边与角的终边互相垂直的角的集合是.50. 某蒸汽机上的飞轮直径为,每分钟按顺时针方向旋转转,则飞轮每秒钟转过的弧度数是;轮周上的一点每秒钟经过的弧长为.51. 与角终边相同的角的集合是,它们中最小的正角是,最大的负角是,它们是第象限角.52. 的角化为角度制的结果为,的角化为弧度制的结果为.53. 已知扇形的周长为,圆心角为弧度,则该扇形的面积为.54. 设,且角的终边与角的终边相同,则.55. 如图所示,用集合表示终边在阴影部分的角的集合为.56. 已知,的终边所在的象限是.57. 有下列四个结论:①角和的终边重合,则,;②角和的终边关于原点对称,则,;③角和的终边关于轴对称,则,;④角和的终边关于轴对称,则,.其中正确的有.(填序号)58. 如果把化为(,)的形式,那么,.59. 在集合中,属于区间的角的集合是.60. 若圆弧长度等于该圆内接正方形的边长,则其圆心角的弧度数是.61. 把写成的形式为.62. 已知圆心角为的扇形的弧长为,则它的内切圆半径是.63. 如图,点,,是圆上的点,且,,则劣弧的长为.64. 如图,已知扇形的圆心角为,半径为,则扇形中所含弓形的面积是.65. 若将时钟拨慢,则时针转了;若将时钟拨快,则分针转了.66. 已知扇形的面积为,扇形圆心角的弧度数是,那么扇形的周长为.68. 巳知一扇形的圆心角,那么此扇形的面积与其内切圆的面积之比为.69. 下列说法:①终边相同的角一定相等;②第二象限角大于第一象限角;③的角是第一象限角;④小于的角是钝角,直角或锐角.⑤弧度是的圆心角所对的弧;⑥弧度是长度等于半径的圆弧所对圆心角;⑦弧度等于.其中正确的序号为(把正确的序号都写出来).70. 给出下列命题:第二象限角大于第一象限角;三角形的内角是第一象限角或第二象限角;不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关;若,则与的终边相同;若,则是第二或第三象限的角.其中不正确的命题是.71. 若扇形的圆心角为,弧长为,则扇形的半径为.72. ()终边在直线上的角的集合是.()若角的终边与角的终边相同,则在内终边与角的终边相同的角的个数为.73. 若角的终边与角的终边关于直线对称,且,则.74. 有下列四个结论:①角和角的终边重合,则,;②角和角的终边关于原点对称,则,;③角和角的终边关于轴对称,则,;④角和角的终边关于轴对称,则,.其中正确的有.(填序号)75. 扇形的周长为,若这个扇形的面积为,则圆心角的大小为 .76. 已知扇形的周长为,那么当扇形的半径为时,扇形的面积最大.77. 若某扇形的面积是,它的周长是,则该扇形圆心角的弧度数为.78. 如图,在平面直角坐标系中,一单位圆的圆心的初始位置在,此时圆上一点的位置在,圆在轴上沿正向滚动.当圆滚动到圆心位于时,的坐标为.79. 圆的半径为,为圆周上一点,现将如图放置的边长为的正方形(实线所示,正方形的顶点和点重合)沿着圆周顺时针滚动,经过若干次滚动,点第一次回到点的位置,则点走过的路径的长度为.80. 圆的半径为,为圆周上一点,现将如图放置的边长为的正方形(实线所示,正方形的顶点与点重合)沿圆周逆时针滚动,点第一次回到点的位置,则点走过的路径的长度为.三、解答题(共20小题;共260分)81. 将集合中的角(角度制)在数轴上表达出来,并表示出第一象限角,锐角,负角的区间.82. 今天是周日,那天后是周几?过多少天是周二?在数轴上表达:如图,周二是那些天?如何统一表达?83. 已知角的终边与的终边相同,求在内与终边相同的角.84. 已知,若的终边与角的终边重合,求角.85. 用弧度制表达.写出终边在下列阴影部分内的角的集合(含边界).(1)(2)86. 已知,求,并指出的终边位置.87. 集合,,试确定集合与之间的关系.88. (1)写出与下列各角终边相同的角的集合,并把中适合不等式的元素写出来:①;②(2)试写出终边在直线上的角的集合,并把中适合不等式的元素写出来.89. 试求出终边在如图所示阴影区域内的角的集合.90. 如图,三棱锥内接于一个圆锥(有公共顶点和底面,侧棱与圆锥母线重合).已知,,,,(1)求圆锥的侧面积及侧面展开图的中心角;(2)求经过圆锥的侧面到点的最短距离.91. 如图,动点,从点出发,沿着圆周做匀速运动.点按逆时针方向每秒转,点按顺时针方向每秒转,求点,第一次相遇时所用的时间及点,各自走过的弧长.92. 请回答下列问题:(1)设,,用弧度制表示它们,并指出它们各自所在的象限.(2)设,,用角度制表示它们,并在~的范围内找出终边相同的所有角.93. 己知弦长为,它所对的圆心角,求所夹的扇形面积以及所对的弓形的周长.94. 已知是第二象限的角,求,是第几象限的角.95. 设是第二象限角,试比较,,的大小.96. 如图,在扇形中,,弧长为,求此扇形内切圆的面积.97. 如图所示,点在半径为且圆心在原点的圆上,.点从点出发,依逆时针方向匀速地沿圆周旋转,已知在内转过的角度为,经过到达第三象限,经过后又回到出发点,求,并判断其是第几象限角.98. 已知扇形的圆心角是,半径是,弧长为.(1)若,,求扇形的面积;(2)若扇形的周长为,求扇形面积的最大值,并求此时扇形圆心角的弧度数.99. (1)已知扇形的周长为,面积为,求扇形的圆心角的弧度数.(2)已知扇形的周长为,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?100. 如图,一个扇形的周长为,问它的圆心角取何值时,扇形的面积最大?并求出最大值.答案第一部分1. C2. C3. A4. D5. C6. A7. B8. B9. A 【解析】因为扇形的圆心角为,半径为,所以扇形的面积.10. C11. B12. D13. D14. C15. A【解析】设扇形的弧长为,扇形所在圆的半径为,由题意得解得.扇形16. D17. C18. C19. B 【解析】钟表的指针按顺时针方向转动,角为负角.20. C【解析】当时,;当时,,应选C.21. B22. B 【解析】钟表的指针按顺时针方向转动,角为负角.23. D24. C25. B26. B.27. B 【解析】,所以扇形28. A 【解析】由题意得解得所以.29. C30. A【解析】由于第一象限角不小于第二象限角,故①错;当三角形的内角为时,其既不是第一象限角,也不是第二象限角,故②错;③正确;由于,但与的终边不相同,故④错;当,时既不是第二象限角,又不是第三象限角,故⑤错.综上可知只有③正确.集合31. D 【解析】集合,所以.32. B 【解析】因为是第二象限角,所以,,所以,,所以是第一或第三象限角,而是第三象限角,所以是第四象限角.33. D 【解析】如图,等边三角形是半径为的圆的内接三角形,则线段所对的圆心角,作,垂足为,在中,,,所以,,所以,由弧长公式得.34. B35. A36. B37. B38. A39. B40. B第二部分41. 四42. 二43.44.45. 三46.【解析】根据扇形的弧长公式可得,根据扇形的面积公式可得.47.48.49. 略50. ,51. ;,;,;,三52. ,53.【解析】设扇形的半径为,所以,,所以,扇形的弧长为,半径为,扇形的面积为.54.55.【解析】由题图知,终边落在射线上的角为,以为终边的角与角的终边相同,所以终边落在图中阴影部分的角的集合为.56. 一、二象限57. ①②③④58. 略,略59.60.【解析】设圆半径为,则圆内接正方形的对角线长为,所以正方形边长为,所以圆心角的弧度数是.61.62.【解析】如图,设内切圆半径为,则扇形的半径为,扇形弧长,解得.63.【解析】.64.【解析】因为扇形(),(),所以弓形扇形().65. ,【解析】将时针拨慢,时针按逆时针方向转动,转过的是正角,转过的度数为.将时针拨快,分针按顺时针方向转动,转过的是负角,转过的度数为.66.【解析】设扇形的半径为,则,所以,所以扇形的周长为.67.【解析】,,,解得,又,故,,,角为,,.68.【解析】设扇形的半径为,内切圆的半径为,则,即.又扇,内切圆,所以扇内切圆.69. ⑥【解析】(1)明确各种角的定义,逐一判断即可.对于①,终边相同的角不一定相等,终边相同的角有无数多个,它们相差的整数倍,故①是错误的;对于②,角是第一象限角,角是第二象限角,,所以②错误;对于③,的角是指的角,其中角不是任何象限的角,为轴线角,故③错误;对于④,小于的角指满足的角,其中也包括负角和零角,故④错误.(2)弧度角的定义:把长度等于半径长的弧所对的圆心角叫做弧度的角.由此可知,只有⑥正确.⑤⑦错误.70.【解析】由于第一象限角不小于第二象限角,故错;当三角形的内角为时,其既不是第一象限角,也不是第二象限角,故错;正确;由于,但与的终边不相同,故错;当,时既不是第二象限角,又不是第三象限角,故错.综上可知只有正确.71.【解析】由,解得.72. ,【解析】()在内终边在直线上的角为,所以终边在直线上的角的集合为.()因为,所以,依题意,,所以,所以=,即在内与角的终边相同的角为,,共三个.73.74. ①②③④75. 或76.【解析】设扇形的圆心角为,半径为,扇形的弧长.因为,,所以扇形当时,扇形的面积最大.77.【解析】设扇形的半径为,弧长为,由题意知解得所以扇形的圆心角的弧度数为.78.【解析】设,,由题意知劣弧长为,由于圆的半径为,所以.设,则,,所以的坐标为.79.【解析】由题意知,圆的半径,正方形的边长.由图可知,以正方形的边为弦时所对的圆心角为.正方形在圆上滚动时点的顺序依次为如图所示.当点首次回到点的位置时,正方形滚动了圈共次.设第次滚动,点的路程为,则;;;,因此,点所走过的路径的长度为.80. .【解析】每次转动一个边长时,圆心角转过,正方形有边,所以需要转动次,回到起点.在这次中,半径为的次,半径为的次,半径为的次,点走过的路径的长度= + = .第三部分81. 略.82. 略.83. 略84. 略85. (1)略.(2)略.86. 略87. 因为集合表示终边在四个象限的角平分线上角的集合,集合表示终边在坐标轴上(为偶数时)和四个象限的角平分线上(为奇数时)的角的集合,所以.88. (1)①,其中适合不等式的元素为:,,;②,其中适合不等式的元素为:,,.(2)终边在直线上的角的集合其中适合不等式的元素为:,.89. 因为,所以终边在题图所示阴影区域内的角的集合为.90. (1)因为,,,所以为底面圆的直径侧.圆锥的侧面展开图是一个扇形,设此扇形的中心角为,弧长为,则,所以,所以.(2)沿着圆锥的侧棱展开,在展开图中,,,.91. ,得秒,走过的弧长为,走过的弧长为.92. (1),所以在第二象限;,所以在第一象限.(2),与它终边相同的角可表示为,,由,得,所以,,即在~的范围内与终边相同的角是,.同理,在~范围内与终边相同的角是.93. ();().94. ①因为为第二象限角,则,,所以,,所以是第三或第四象限角,以及终边落在轴的非正半轴上的角.②,.令,则,所以为第一象限角.令,则,所以为第二象限角.令,则,所以为第四象限角.所以是第一或第二或第四象限角.95. 因为是第二象限角,所以,,所以,,所以是第一或第三象限角(如图阴影部分).结合单位圆上的三角函数线可得,(i)当是第一象限角时,,,,从而得;(ii)当是第三象限角时,,,,从而得.综上,当是第一象限角,即,时,;当是第三象限角,即,时,.96. 设扇形的半径为,其内切圆的半径为,由已知得,.又因为,所以.所以内切圆的面积为.97. 由题意,有.所以.又,即,所以,且所以或.故或.易知,故当,是第一象限角;当,是第二象限角.98. (1).(2)由题意知,即,,当时,的最大值为,当时,,.即扇形面积的最大值为,此时扇形圆心角的弧度数为.99. (1)设扇形的圆心角的弧度数为,弧长为,半径为.由题意得:解得:,当时,,此时(舍)当时,,此时,∴扇形圆心角的弧度数是.(2)设扇形的圆心角为,半径为,弧长为,面积为,.所以当时,扇形的面积最大,这个最大值是,此时.当它的半径和圆心角分别取和弧度时,才能使扇形的面积最大,最大面积是.100. 设扇形的半径为,则周长,所以..因为,当且仅当,即时等号成立.此时,所以当时,取得最大值为.。
高一数学任意角和弧度制和任意角的三角函数试题答案及解析

高一数学任意角和弧度制和任意角的三角函数试题答案及解析1.若为第三象限,则的值为()A.B.C.D.【答案】B【解析】因为为第三象限,所以.因此,故选择B.【考点】同角三角函数基本关系及三角函数符号.2.下列各式中,值为的是A.B.C.D.【答案】D【解析】;;;.【考点】二倍角的正弦、余弦、正切公式.3.已知扇形半径为8, 弧长为12, 则中心角为弧度, 扇形面积是【答案】.【解析】圆心角;由扇形的面积公式得.【考点】扇形的面积公式及圆心角的计算.4.是第( )象限角.A.一B.二C.三D.四【答案】C【解析】本题主要考查三角函数终边相同的角.由得出终边在第三象限,故选C.【考点】终边相同的角的表示.5.已知角的终边上有一点(1,2),则的值为( ).A.B.C.D.–2【答案】A【解析】角的终边过,,.【考点】任意角三角函数的定义.6.已知点P()在第三象限,则角在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】由已知得,即,则角在第二象限。
【考点】(1)三角函数值符号的判断;(2)象限角的判断。
7. 2400化成弧度制是()A.B.C.D.【答案】C【解析】本题考查度与弧度的互化,利用公式弧度,可得.【考点】度与弧度的互化.8.的值是()A.B.C.D.【答案】C【解析】.任意角的三角函数值可利用诱导公将角化为锐角的三角函数值求得.【考点】诱导公式,特殊角的三角函数值.9.若,且,则角的终边所在的象限是().A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】因为,又因为,所以,所以角的终边所在象限是第四象限,故选D.【考点】1、三角函数值的符号;2、二倍角的正弦.10.设为第四象限角,其终边上的一个点是,且,求和.【答案】;.【解析】利用余弦函数的定义求得,再利用正弦函数的定义即可求得的值与的值.∵为第四象限角,∴,∴,∴,∴,∴=,∴,.【考点】任意角的三角函数的定义.11.将120o化为弧度为()A.B.C.D.【答案】B【解析】,故.【考点】弧度制与角度的相互转化.12.下列角中终边与330°相同的角是()A.30°B.-30°C.630°D.-630°【答案】B【解析】与330°终边相同的角可写为,当时,可得-30°.【考点】终边相同的角之间的关系.13.的值()A.小于B.大于C.等于D.不存在【答案】A【解析】因为,所以,从而,选A.【考点】任意角的三角函数.14.圆心角为弧度,半径为6的扇形的面积为 .【答案】【解析】扇形面积公式,即(必须为弧度制).【考点】扇形面积公式.15.比较大小:(用“”,“”或“”连接).【答案】>.【解析】在单位圆中,做出锐角1的正切线、正弦线、余弦线,观察他们的长度,发现正切线最长,余弦线最短,故有 tan1>sin1>cos1>0.【考点】三角函数线.16.已知【答案】【解析】由已知得,又因为,所以,而,故答案为.【考点】1.诱导函数;2.特殊角的三角函数值.17.一钟表的分针长5 cm,经过40分钟后,分针外端点转过的弧长是________cm【答案】【解析】分针每60分钟转一周,故每分钟转过的弧度数是,分针经40分钟,分针的端点所转过的角的弧度数为2π×=,代入弧长公式l=αr,得出分针的端点所转过的长为×5=(cm).故答案为:。
任意角和弧度制+同步练习- 高一上学期数学人教A版(2019)必修第一册

5.1任意角与弧度制一、单选题1.某班级举行“变废为宝”手工活动,某学生用扇形纸壳裁成扇环(如图1)后,制成了简易笔筒(如图2)的侧面,在它的轴截面ABCD 中 ,10cm AB AD ==,15cm CD =,则原扇形纸壳中扇形的圆心角为( )A.π3 B .π2 C .π4D .π62.已知扇形的周长为8cm ,圆心角为2rad ,则此扇形的面积是( ) A .22cmB .24cmC .26cmD .28cm3.半径为2的圆上长度为4的圆弧所对的圆心角是( ) A .1B .2C .4D .84.中国传统折扇可看作是从一个圆面中剪下的扇形环(扇形环是一个圆环被扇形截得的一部分)制作而成.若一把折扇完全打开时,其扇形环扇面尺寸(单位:cm )如图所示,则该扇面的面积为( )A .22700cmB .23500cm C .24300cmD .24800cm5.我国古代数学著作《九章算术》中记载:“今有宛田,下周三十步,径十六步,问为田几何?”译成现代汉语其意思为:有一块扇形田,弧长30步,其所在圆的直径是16步,问这块田的面积为多少?( )A .240平方步B .120平方步C .80平方步D .60平方步6.已知A = {第二象限角},B ={钝角},C ={大于90°的角},那么,,A B C 关系是( )A .B AC =⋂ B . C C =B ∪ C . A C ⊆D . A B C ==7.已知扇形的周长是6cm ,则扇形面积最大时,扇形的中心角的弧度数是( ) A .2B .1C .12D .38.在[0,2π]上,与π5-终边相同的角是( )A .π5B .4π5C .6π5D .9π5二、多选题9.已知某扇形的弧长为3π,圆心角为12,则( )A .该扇形的半径为6πB .该扇形的周长为9πC .该扇形的面积为9πD .该扇形的面积为29π10.下列说法正确的有( )A .若一个扇形弧长的值与面积的值都是5,则这个扇形圆心角的大小是52B .已知346x y ==,则212+=x yC .函数1()x f x x在其定义域上单调递减 D .若幂函数()21()1kf x k k x +=+-的图象过点12,2⎛⎫ ⎪⎝⎭,则1k =11.下列说法中正确的是( )A .π180-=-︒B .第一象限角都是锐角C .在半径为2的圆中,π6弧度的圆心角所对的弧长为π3D .终边在直线y x =-上的角的集合是π2,Z 4k k ααπ⎧⎫=-∈⎨⎬⎩⎭三、填空题12.已知圆心角为32的扇形,其周长为21,则该扇形的半径为 ,该扇形的面积为 .13.半径为2的圆中,π7的圆心角所对的弧的长度是 .14.若扇形的周长为40cm ,面积为2100cm ,则它的圆心角的弧度数为 .四、解答题15.已知角α的终边在第四象限,确定下列各角终边所在的象限:(1)2α; (2)3α;16.某农户计划围建一块扇形的菜地,已知该农户围建菜地的篱笆的长度为24米. (1)若该扇形菜地的圆心角为4弧度,求该扇形菜地的面积;(2)当该扇形菜地的圆心角为何值时,菜地的面积最大,最大值是多少?17.已知扇形的半径2r cm =,周长为π43C cm ⎛⎫=+ ⎪⎝⎭,(1)求扇形的面积;(2)在区间[]0,4π上求出与此扇形的圆心角α终边相同的角.18.已知一扇形的圆心角为()02παα<<,所在圆的半径R . (1)当π,43R α==,求其弧所在弓形的面积. (2)若该扇形的面积为4S =,当它的圆心角和半径取何值时,该扇形的周长C 最小?最小值是多少?19.用弧度制分别表示每个图中顶点在原点、始边重合于x 轴的非负半轴、终边落在阴影部分内(包括边界)的角的集合.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角的概念和弧度制测试题
1.下列命题中的真命题是
( )
A .圆心角为1弧度的扇形的弧长都相等
B .第一象限的角是锐角
C .第二象限的角比第一象限的角大
D .角α是第四象限角的充要条件是2k π-
2
π
<α<2k π(k ∈Z) 2.已知A={第一象限角},B={锐角},C={小于90°的角},那么A 、B 、C 关系是 ( )
A .B=A ∩C
B .B ∪C=C
C .A ⊂C
D .A=B=C 3.下列各组角中,终边相同的角是
( )
A .π2
k 与)(2
Z k k ∈+
π
π
B .)(3
k 3Z k k ∈±
ππ
π与
C .ππ)14()12(±+k k 与 )(Z k ∈
D .)(6
6Z k k k ∈±+π
πππ与
4.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是 ( )
A .2
B .
1
sin 2
C .1sin 2
D .2sin
5.一钟表的分针长10 cm ,经过35分钟,分针的端点所转过的长为:
( )
A .70 cm
B .
670 cm C .(3425-3
π)cm D .
3π35 cm 6.若90°<-α<180°,则180°-α与α的终边 ( )
A .关于x 轴对称
B .关于y 轴对称
C .关于原点对称
D .以上都不对 7.将分针拔快15分钟,则分针转过的弧度数是
( )
A .
4
π
B .-
4
π C .
2
π D .-
2
π 8.角α的终边上有一点P (a ,|a |),a ∈R 且a ≠0,则sinα值为
( )
A .22-
B .2
2
C .1
D .
22或2
2
- 9.一个半径为R 的扇形,它的周长为4R ,则这个扇形所含弓形的面积为 ( )
A .
2)1cos 1sin 2(21
R ⋅- B .
1cos 1sin 2
12
⋅R
C .22
1R
D .2
21cos 1sin R R ⋅⋅-
二、填空题:
10.已知一扇形在圆的半径为10cm ,扇形的周长是45cm ,那么这个扇形的圆心角为 弧度.
11.与-1050°终边相同的最小正角是 . 12.若角α是第四象限角,则
2
α
角的终边在 . ≠
三、计算题 14.在半径为12 cm 的扇形中, 其弧长为5π cm, 中心角为θ. 求θ的大小(用角度制表示).
15 (1)将下列角化成0
360()k k Z α⨯+∈的形式: ①0300 ② 0
1125 ③
0660-
(2)将下列角进行角度与弧度的换算:① 0330 ② 0
900 ④ 23
π-
16,已知一扇形的圆心角是α,所在圆半径是R 。
(1) 若α=600
,R =10cm,求扇形的弧长及该弧所在的弓形面积。
(2) 若扇形的周长是一定值C (C>0),当α是多少弧度时,该扇形有最大面积?
任意角的三角函数测试题
一、选择题
1.有下列命题:
①终边相同的角的三角函数值相同; ②同名三角函数的值相同的角也相同;
③终边不相同,它们的同名三角函数值一定不相同; ④不相等的角,同名三角函数值也不相同. 其中正确的个数是( )
A.0
B.1
C.2
D.3 2.若角α、β的终边关于y 轴对称,则下列等式成立的是( )
A.sin α=sin β
B.cos α=cos β
C.tan α=tan β
D.cot α=cot β 3.角α的终边上有一点P (a ,a ),a ∈R ,a ≠0,则sin α的值是( ) A.22 B.-22 C. 22或-22
D.1
4.若x x sin |sin |+|cos |cos x x +x
x tan |tan |=-1,则角x 一定不是( )
A.第四象限角
B.第三象限角
C.第二象限角
D.第一象限角 5.sin2·cos3·tan4的值( ) A.小于0 B.大于0 C.等于0 D.不存在
6.若θ是第二象限角,则( )
A.sin
2
θ
>0 B.cos
2
θ
<0 C.tan
2
θ
>0 D.cot
2
θ
<0 二、填空题
7.若角α的终边经过P (-3,b ),且cos α=-
5
3
,则b =_________,sin α=_________. 8.在(0,2π)内满足x 2cos =-cos x 的x 的取值范围是_________.
9.已知角α的终边在直线y =-3x 上,则10sin α+3cos α=_________.
10.已知点P (tan α,cos α)在第三象限,则角α的终边在第_________象限.
三、解答题
11,计算
=-
65sin π ,=413cos π ,=43sin π ,=-3
2sin π
, 12.
(1)若点(6,)P t 是角α终边上的一点,且满足0t >,3
cos 5
α=,求sin α,tan α的值
(2)已知角α的终边上有一点(3,4)(0)P t t t -≠,求sin α,cos α,tan α的值; 【知识聚焦】 1、任意角
(1)角概念的推广:①按旋转方向不同分为正角、负角、零角;②按终边位置不同分为象限角和轴线角。
(2)终边相同的角:终边与角α相同的角可写成0
360()k k Z α⨯+∈。
(3)象限角及其集合表示:
象限角 象限角的集合表示
第一象限角的集合 {α|2k π<α<2k π+2
π
,k ∈Z} 第二象限角的集合 {α|2k π+
2
π
<α<2k π+π,k ∈Z} 第三象限角的集合 {α|2k π+π<α<2k π+32
π
,k ∈Z}
第四象限角的集合
{α|2k π+32
π
<α<2k π+2π,k ∈Z}
2、弧度制
(1)1弧度的角:长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad 表示。
(2)角α的弧度数:如果半径为r 的圆的圆心角α所对弧的长为l ,那么角α的弧度数的绝对值是|α|=l /r.
(3)角度与弧度的换算:①0
180π=; ②0
1180
rad π
=; ③0
1801()rad π
=.
(4)弧长、扇形面积的公式:扇形的弧长l r α=⋅,则扇形的面积为21
122
S l r r α=⋅=⋅
3、任意角的三角函数 三角函数
正弦
余弦
正切
定义
设α是一个任意角,它的终边上有一点
(,)P x y , P 到原点O 的距离为r ,那么
y
r
叫做α的正弦,记作:sin α
x
r 叫做α的余弦,
记作:cos α y
x
叫做α的正切,
记作:tan α
各象限 符号
Ⅰ + + + Ⅱ + - - Ⅲ - - + Ⅳ -
+
-
记忆口诀 一正,二正弦,三切,四余弦
终边相同角三角函数值 (k ∈Z)(公式一)
sin(α+k ·2π)=sin α
cos(α+k ·2π)=cos α
tan(α+k ·2π)=tan α
4、同角三角函数的基本关系
(1)平方关系:2
2
sin cos 1αα+=;(2)商数关系:
sin tan cos α
αα= 注:同角并不拘泥于角的形式,如:22sin
cos 122αα+=,sin 3tan 3cos3ααα
=都成立。
