基于抽取与重构的瞬时频率估计算法

合集下载

基于WVD的雷达信号瞬时频率提取方法研究

第１期
张静，等：基于ＷＶＤ的雷达信号瞬时频率提取方法研究
３９
Ｊ一∞ Ｊ一∞
ＩＩｏ－（ｘ，ｙ）ａ（一）ｅｆ２。ｄｙｄｘ
Ｃ
∞ Ｊ一∞ Ｃ
多不同类型的时频分布．虽然Ｗｉｇｎｅｒ — Ｖｉｌｌｅ分布具有许多期望的优良数学性质而倍受学界推崇，
之一．
雷达回波中的多普勒频率是目标的重要信息，它描述了目标径向运动的情况．瞬时频率可以
更好地反映信号频率随时间的变化情况，本文分析了噪声情况下多普勒信号的能量谱分布，将ＷＶＤ用于雷达回波信号的瞬时频率提取，并比较
鲁东大学学报（自然科学版）
ＬｕｄｏｎｇＵｎｉｖｅｒｓｉｔｙＪｏｕｎａｒｌ（ＮａｔｕｒａｌＳｃｉｅｎｃｅＥｄｉｔｉｏｎ）
基于ＷＶＤ的雷达信号瞬时频率提取方法研究
信号由于呈现较强的非平稳特性，传统方法对其难以实现有效的信噪分离．时频分析是近年来兴起的用于非平稳信号分
速．由于实际目标不可能是单独的理想点，通常把尺寸远小于脉冲宽度所对应长度的目标近似为 “ 点”目标．实际目标可视为众多散射点的集合，因而接收信号应为多个子回波的叠加．由于子回波问的延迟时间差远小于脉冲包络的宽度，因而接收信号可以近似看成具有相同包络的载波叠加ｊ．假设目标为二维的，目标的散射分布函数为Ｏｒ（，Ｙ），雷达射线与轴重合，则在距离处，一小段Ａｘ（设Ａｘ一０）的目标切片散射系数

基于WVD的调频引信瞬时频率估计算法

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

基于二维DFT的多分量信号瞬时频率估计方法

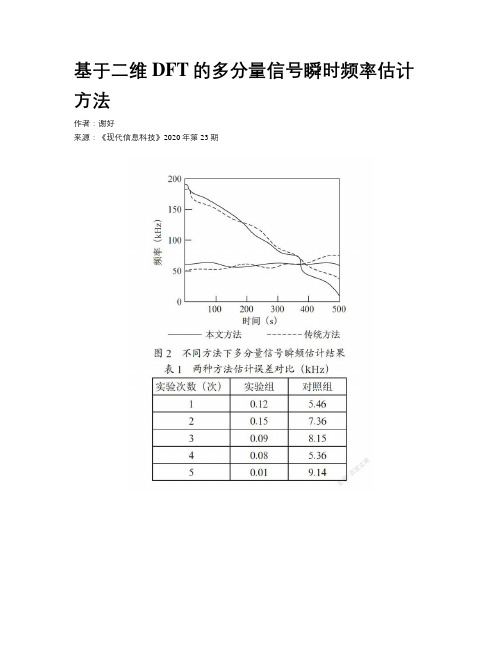
基于二维DFT的多分量信号瞬时频率估计方法作者：***来源：《现代信息科技》2020年第23期摘要：在进行多分量信号瞬时频率估计时，存在较大误差，为此提出基于二维DFT的多分量信号瞬时频率估计方法。

首先通过建立多分量信号模型获取到多分量信号瞬时频率的相参特性，然后利用二维DFT技术对多分量信号脉冲特性进行变换，最后利用加权均值的方法求出多分量信号瞬时频率，以此完成基于二维DFT的多分量信号瞬时频率估计。

经实验证明，设计方法估计误差小于传统方法。

关键词：二维DFT;多分量信号;瞬时频率;估计中图分类号：TN911.72 文献标识码：A 文章编号：2096-4706（2020）23-0058-03Instantaneous Frequency Estimation Method of Multicomponent Signals Based on Two-Dimensional DFTXIE Hao（Henan University，Kaifeng 475004，China）Abstract：There is a big deviation in the instantaneous frequency estimation of multicomponent signals，so a method of instantaneous frequency estimation of multicomponent signals based on two-dimensional DFT is proposed. Firstly，the coherent characteristics of the instantaneous frequency of the multicomponent signal are obtained by establishing the multicomponent signal model. Then，the pulse characteristics of the multicomponent signal are transformed by using the two-dimensional DFT technology. Finally，the instantaneous frequency of the multicomponent signal is obtained by using the weighted average method，so as to complete the instantaneous frequency estimation of the multicomponent signal based on the two-dimensional DFT. The experimental results show that the estimation error of the design method is smaller than that of the traditional method.Keywords：two-dimensional DFT;multicomponent signal;instantaneous frequency;estimation0 引言瞬時频率是电子信号处理中最常用的一个术语，传统的瞬时频率概念是指电子信号傅立叶参数瞬时发生的变化，从根本上是指电子信号在某一瞬间的总体表征。

基于瞬时频率估计与Vold-Kalman滤波的铣削颤振识别

基于瞬时频率估计与Vold-Kalman滤波的铣削颤振识别汪晓姗;彭志科;陈是扦【摘要】颤振严重制约了高速铣削加工效率.动态铣削力信号具有非线性、非平稳的特点,常规的信号分解方法难以处理该类信号.提出了一种基于瞬时频率估计和Vold-Kalman滤波的多分量信号分解方法,并运用该信号分解方法识别颤振.基于频谱集中性指标估计信号的瞬时频率参数;用Vold-Kalman滤波器提取对应参数的各信号分量;由于颤振时铣削力信号的能量分布在频域发生变化,由此引入能量熵的定义.采用分解得到的子信号能量熵变化来识别颤振.实验分析表明该方法有效可行.【期刊名称】《振动与冲击》【年(卷),期】2018(037)016【总页数】7页(P70-76)【关键词】铣削;颤振;频谱集中性指标;Vold-Kalman滤波;能量分布【作者】汪晓姗;彭志科;陈是扦【作者单位】上海交通大学机械系统与振动国家重点实验室,上海200240;上海交通大学机械系统与振动国家重点实验室,上海200240;上海交通大学机械系统与振动国家重点实验室,上海200240【正文语种】中文【中图分类】TH17;TP181颤振是金属加工中出现的自激振动，严重制约了加工精度和加工效率。

随着机床加工柔性化的日益发展，要求加工能对不同的工件在不同的条件下进行，因此不能从根本上杜绝颤振。

近年来，于英华等[1-2]很多国内外学者开始着力于研究颤振的在线监测和预报控制。

铣削颤振的形成是一个孕育的过程，在颤振早期，监测系统抢先把铣削过程即将发生颤振的预兆先通报给控制系统，是实现颤振预报的关键。

各种各样的传感信号可以被用来采集颤振信号，比如动态铣削力信号[3-4]，加速度信号[5]，力矩信号[6]等。

Kuljanic等[7]提出了利用多传感器来监测识别颤振，这种方法提高了颤振监测的精确性和鲁棒性；Tansel等[8]通过铣削位移信号的谐波分量来监测颤振；Tarng等[9]在发生颤振时切削力信号在的频谱上的窄带特性来预测颤振。

基于改进时频分析方法的雷达信号瞬时频率估计

ｅｕｎｙｄｓｂｔｎｏｅｎｉｅｉｓｐｒｓｅｙａｏｔｇｔ — ｅｕｎｙｅｅｇｎｅｒ — ｅ．Ｓｍｕｔｅｕｌ，ｔｅｔａｍｅｆｑｅｃｉｔｕｉｆｔｏｓｓｕｐｅｓｄｂｄｐｉｉｆｑｅｃｎｒｙｉｔｇａｒｉｒｏｈｎｍｅｒ
一
种混合的时频分析方法，而后采用多样本信号时频能量累积的方法，进一步抑制噪声在时频面上的分布；然后
以时频分布峰值在信号自项时频聚集区域的分布概率为准则，计算出时频分布的数据窗长，并根据该窗长得到ＩＦ的初始估计；最后依据初始ＩＦ，采用交叉置信区间算法对时频分布峰值进行检测，得到信号的瞬时频率估计值。文中对ＳＭ、ＬＭ和ＦＫ信号的ＩＦＦＳＦ估计进行了研究，并与ＷＶＤ峰值检测法和时频分布一阶矩法进行了比
（．解放军信息工程大学信息工程学院，河南郑州４００；．６９６部队，河北廊坊０５０）１５０２２１０６０１
摘
要：瞬时频率估计（ｎｔｎｎｏｓｒｑｅｃ，Ｉ）ＩｓｔｅｕｅｕｎｙＦ在雷达信号处理中有着重要的研究意义，时频分布峰值检测ａａＦ
２ｎｔ１０，ａｇｎｂｉ６０１ｈｎ）．Ｕｉ６９６ＬｎｆｇＨｅｅ０５０，Ｃｉａａ
Ａｓｒｃ：Ｉｓｎａｅｕｅｕｎｙ（ＦｓｍａｏａｒａｓｎｉａａｉａｐｏｅｓｇｅｅｔｇｔｅｐａｆｂｔｔａｎｔｔｏｓｑｅｃＩ）ｅｔｔｎｈｓｇｅｔｉａｔｉｒｄｒｇｌｒｃｓｉ．Ｄｔｃｎｅｋｏａｎｒｆｉｉｇｌｙｎｓｎｎｉｈ

基于小波脊的瞬时频率提取技术研究

基于小波脊的瞬时频率提取技术研究摘要：多普勒测速仪测量信号的频率反映着被测物体的速度信息，对测量信号进行瞬时频率提取是速度测量的关键技术之一。

针对这一问题，论文以0~40MHz正弦变化的多普信号为例研究了基于小波脊的瞬时频率提取方法，探讨了小波中心频率和带宽、算法迭代精度、信号比等对瞬时频率提取精度影响，并最终给出了保证算法精度的条件。

关键词：小波脊；瞬时频率；多普勒；信噪比引言激光多普勒测速仪是利用激光的多普勒效应进行速度测量的装置，已广泛应用于各种物体速度的测量。

由于物体的运动速度与多普勒频移信号的瞬时频率密切相关，因此瞬时频率的估计成为激光多普勒测速的关键技术之一。

瞬时频率作为非平稳信号的重要参数，成为非平稳信号分析中的一项重要工作。

瞬时频率的估计方法包括短时傅里叶变换、经验模态分析、局部均值分解、Hilbert-Huang变换、小波脊等。

其中基于小波脊的瞬时频率提取算法得到了广泛应用。

然而目前的文献大都围绕小波脊的提取算法展开，很少有文献探讨参数设置对提取精度的影响。

本文以Morlet小波为例，对频率从0~40MHz正弦变化的多普勒信号提取瞬时频率，探讨参数设置对频率提取结果的影响，给出保证瞬时频率提取精度的条件。

1基于小波脊的瞬时频率提取原理Morlet小波是一种单频复正弦调制高斯波，与多普勒信号具有一定的相似性，且在时域和频域都具有很好的局部性，因此比较适合用来处理多普勒信号。

Morlet小波函数g（t）和多普勒信号s（t）分别表如下：2小波参数的影响分析小波函数的可变参数主要包括中心频率和带宽。

中心频率对应的是小波的时域波形的中心位置，而带宽对应波形的幅度和宽度。

当小波带宽增加时，时域波形被拉宽压扁，而频域的波形被挤压成瘦窄状，因此更适合用来分析低频信号；反之，当小波的带宽减小时，更适合用来分析高频信号。

为了分析小波参数的影响，以频率0~30MHz正弦变化的信号作为待估计信号进行仿真分析。

按频率抽取的FFT算法课件

高效性
按频率抽取的FFT算法相较于其他 FFT算法，具有更快的计算速度和更低的计算复杂度。
广泛应用
按频率抽取的FFT算法被广泛应用于信号处理、图像处理、语音识别等领域。
04
CATALOGUE
fft算法实现细节
算法的步骤和流程
确定输入数据长度
根据需要确定输入数据的长度，通常为2的幂次方。
执行蝶形操作
02
CATALOGUE
fft算法基础知识
fft的基本概念
FFT是快速傅里叶变换的简称，它是一种高效计算离散傅里叶变换（DFT ）及其逆变换的算法。
FFT的基本思想是通过旋转因子和对称性来减少DFT计算的复杂度，从而快速计算出频域表示。
离散傅里叶变换（dft）
DFT是信号处理中的基本工具，它通过将时域信号转换到频域，提供了一种分析信号频率成分的方法。
算法的基本原理
1 2
傅里叶变换与反变换
傅里叶变换是一种将时域信号转化为频域信号的方法，而按频率抽取的FFT算法是基于傅里叶变换的一种高效计算方法。
离散傅里叶一组样本信号进行傅里叶变换，可以得到每个频率分量的幅度和相位。
3
快速傅里叶变换（FFT）
FFT是一种高效计算DFT的方法，其采用了一种称为“蝶形运算”的算法结构，减少了计算复杂度。
使用并行计算
利用并行计算技术，如多线程或多进程，加速算法的执行过程。
05
CATALOGUE
实验与验证
数据准备与实验设计
数据来源
选取了真实的电网信号数据，包括频率、相位、幅值等参数，用于模拟和验证FFT算法。
实验设计
针对电网信号数据，采用按频率抽取的FFT 算法进行频谱分析，并对结果进行比较和验证。

一种新的估计瞬时频率的方法-经验包络法

一种新的估计瞬时频率的方法-经验包络法郑近德，程军圣，杨宇【摘要】常用的求取瞬时频率的方法，希尔伯特变换，会出现无法解释的负频率和明显的端点效应。

标准希尔伯特变换克服了希尔伯特变换出现负频率的缺点，但仍然有端点效应。

为了避免希尔伯特变换，基于信号的经验调幅调频分解，论文提出了一种新的求取瞬时频率的方法—经验包络法（empirical envelope method，简称EE）。

经验包络法本质上是先通过经验调幅调频分解获取纯调频信号，然后对其求导，再对求导的结果进行经验调幅调频分解，提取出包络信号，便可获得原信号的瞬时频率。

首先给出了经验调幅调频分解的详细过程，然后给出了经验包络法的原理和具体步骤，最后采用仿真信号将经验包络法与希尔伯特变换、标准希尔伯特变换和反余弦法进行了对比，分析结果表明了经验包络法的优越性。

【期刊名称】振动与冲击【年(卷),期】2012(031)017【总页数】5【关键词】瞬时频率；经验调幅调频分解；标准希尔伯特变换；反余弦法；经验包络法频率在信号处理、通信、物理学等领域都是一个很重要的概念，它是刻画波形的周期性质和振荡模式的一种属性。

频率在物理上定义为周期的倒数，据此定义，如果要定义频率，必须有一个完整的波形才能有周期。

然而对一些平稳或非平稳信号而言，不存在固定的周期，但它却有一定的振荡模式，其频率随时间不断变化，传统的频率的定义所具有的物理意义无法明确地描述其频率瞬变现象。

因此，需要一个类似于频率的物理量来反映和刻画信号这一性质。

于是相关学者提出了瞬时频率的概念。

Carson等提出了瞬时频率的概念，并对其定义进行了详细研究。

Gabor［1］给出了解析信号的概念，Ville等［2］提出了现在普遍接受的一般实信号的瞬时频率（instantaneous frequency，简称IF）的定义。

即，实信号的瞬时频率定义为该信号所对应的解析信号的相位函数关于时间的导数。

其中，解析信号是基于希尔伯特变换而定义的。

一种新的线性调频信号的瞬时频率估计方法

一种新的线性调频信号的瞬时频率估计方法
崔华
【期刊名称】《计算机应用研究》
【年(卷),期】2008(25)8
【摘要】基于HHT(Hilbert-Huang transformation)是一种能分解出信号的任何频率分量的主成分分析法以及线性调频信号(LFM)的瞬时频率是关于时间的直线,将LFM 信号先作HHT得到其瞬时频率,然后利用该瞬时频率中间部分的时频点作最小二乘(LSM)直线拟合.这种改进的LSM直线拟合方法不仅剔除了HHT固有的边界效应在瞬时频率斜线两端产生的高频谐波,从而有效地抑制了这种边界效应对瞬时频率估计的影响,而且直接得到了较为准确的LFM 信号的瞬时频率参数估计值.与通过改变HHT算法来减小HHT边界效应的方法相比,该方法更有效、更简单易行.仿真结果表明,该方法较小波脊频率提取法更具优越性.
【总页数】3页(P2532-2533,2536)
【作者】崔华
【作者单位】西安电子科技大学,理学院,西安,710071
【正文语种】中文
【中图分类】TP393
【相关文献】
1.基于正负斜率线性调频脉冲信号的一种新的测速方法 [J], 康丽艳;苏涛;牛亚莉
2.一种新的混合线性调频雷达信号识别方法 [J], 李楠;曲长文;苏峰;平殿发
3.一种新的线性调频信号数字产生方法 [J], 黄洪全;方方;万永伦;苏仔建
4.一种新的基于分数阶Fourier变换的线性调频信号的参数估计方法 [J], 陈蓉;汪一鸣
5.一种基于新误差标准的ANF线性调频信号参数估计方法 [J], 赵红梅;崔艳
因版权原因，仅展示原文概要，查看原文内容请购买。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

ＡｓａｔｄｉｖｈｔＧｕｓｎｎｉ（ＷＧｂｔｃ：ＡｄｔｅｗｉａｓｉｏｓＡＮ）ｃａｎｌａｒｒｓｎｌｉｓｎａｅｕｅｕｎｙｐｏａｉｔｒｉｅａｅｈｎｅｃｒｅｉａｎｔｔｏｓ￣ｑｅｃｒｂｂｌｙｉｇａｎｉ
ｒｕＦ。如果在后续的处理中能够剔除这些虚假瞬时频ｉｓ）ｏＩ率，那么对于提高多载波信号瞬时频率的估计性能是非常有利的。
率』。利用Ｇｂｒａｏ的平均测度，ｉｅ证明了信号谱的平Ｖｌｌ
均频率等于瞬时频率的时间平均。但是Ｖｌ并没有进一ｉｅｌ步推导与瞬时频率相对应的瞬时谱的表达式或者瞬时频率
ｒｑｅｃｓｉｉｌｏｈｉｒｓｎｅａｄｔｅｐｒｒｎｅｏｅａｇｒｈｉｎｌｚｄｉｅａｌｈｌ — ｆｅｕｎｙｅｔｔｎａｇｒｔｍｓｐｅｅｔｄ，ｎｈｅｏｍａｃｆｈｌｏｉｍｓａａｙｅｎｄｔｉＴｅｍｕｔｍａｏｉｆｔｔ．ｉｃｒｉｒｓｇａａｌｇｓｒｓｉｓａｔｎｏｓ￣ｅｕｎｙａｉｓｎｒｌｏａａｙｅｎｈｉｔｆｒｌｆｔｅａｒｉｎｓｍｐｉｅｅｎｔｎａｅｕｅｌｎｉｑｅｃｌｉｇａｅａｓｎｌｚｄａｄｔｅｌｏｍｕａｏｈａｍｉｉｓａｔｎｏｓｆｑｅｃｌｓｎｓｄｒｅ．ｅｃｒｅｔｅｓｏｎｔｎａｅｕｎｔｎａｅｕｅｕｎｙａｉｉｇｉｅｉｄＴｈｏｒｃｎｓｆｉｓａｔｎｏｓ￣ｑｅｃｆｔｅｐｏａｉｔｅｓｔｒａｖｅｕｎｙｏｒｂｂｌｙｄｎｉｈｉｙｄｓｒｕｉｎｉｖｒｉｄ，ｈｏｇｈｎｅＣｒｉｌｔｎｉｉｔｓｅｆｔｂｏｉｅｔｒｕｈｔｅＭｏｔ — ａｌｓｍｕａｉ．ｏｏ
１０４
传感器与微系统（ｒｎｄｃｒｎｃｏｙｔｍＴｃｎｌｉ）ＴａｓｕｅｄＭｉｓｓｅｈｏｇｅａｒｅｏｓ
２１０２年第３卷第４期１
基于抽取与重构的瞬时频率估计算法
司伟建，蒋鹏
（尔滨工程大学信息与通信工程学院，龙江哈尔滨１００）哈黑５０１
摘
要：研究了在ＡＮ信道中载波信号采样序列瞬时频率的概率密度分布模型，ＷＧ并通过假设检验验证
该分布模型。分析了不同采样速率和信噪比对瞬时频率概率密度分布的影响，根据该分析结论提出了一
种基于抽取与重构的瞬时频率的估计算法，并且对该算法的性能进行了详细的分析；还对多载波信号采样序列瞬时频率产生混叠以至无法分辨的情况进行分析，推导了瞬时频率完全混叠时的极限公式。最后并通过蒙特一卡罗仿真验证了提出的瞬时频率的概率密度分布的正确性。
上，出了一种基于抽取与重构的瞬时频率的估计算法，提该
算法具有与差分运算相似的瞬时频率概率密度分布，据根分布模型的参数可知，该算法能够极大地提高单载波信号瞬时频率的估计性能。对于多载波信号，算法同样能够该
提高瞬时频率的估计性能，是在提高估计性能的同时存但在错误的瞬时频率现象，文称其为虚假瞬时频率（ｐ — 本ｓｕ
（）ｄｓｉｕｉｎｆｎｔｎｏｄｆｒｎｐｗｅ＝．７ｂｉｒｂｔｃｉｆｉｅｅｔｈｎｘＯ０５ｔｏｕｏ
＝ｐ＝ＳＮ，／ｏ
图１Ｋ。不同时ＦＫ信号载波频率的概率密度分布曲线ＰＳ
ＦｉＣｕｖｆｐｒｂｂｌｙｄｎｉｉｔｉｕｔｎｏＫａｄｅｇ１ｒｅｏｏａｉｔｅｓｔｄｓｒｂｉｆＦＳｃｒｒｉｙｏｓｇａｒｑｅｃｎｒｄｆｅｅｔＫｎｐｉｎｌｆｅｕｎｙｕｄｅｉｒｎａｄ
关键词：ＡＮ信道；ＷＧ载波信号；瞬时频率；ｏｅｉ分布；ＶｎＭｓｓ概率密度分布
中图分类号：Ｔ１Ｎ９１文献标识码：Ａ文章编号：１０－７７２１）４０４－３００９８（０２０－１０－０
Ｉｌｔａｎｔｎｅｕｓｌｑｕｅｙｅｎｍａ』ｎ ’ ｏｉｈｍｅ１０ｎｓａｏｒｅ一ｎｃＳ ● Ｊｎ０ａｒｔ ● ｌｇ・’ ・０ｂａｓｄｎ
ｅｔａｔｏｎｄｒｃｎｓｒｃｉｎｘｒｃｉｎａｅ０ｔｕｔ０
ＳＷｅｊｎＪＮｅｇＩｉｉ，ＩＧＰｎ－ａＡ
（ｃｏｌｆｎｏｍａｉｎａｄＣｍｍｕｉｔｎＥｇｅｒｇＨａｂｎＥｇｅｒｇＵｉｒｉ，ｒｉ５０１ＣｉａＳｈｏｆｒｔｎｏｏＩｏｎｃｉｎｉｅｉ，ｒｉｎｉｅｎｎｖｓｙＨａｂｎ１００，ｈｎ）ａｏｎｎｎｉｅｔ
Ａｃｏｄｉｇｔｈｅｃｎｃｕｉｎｆｔｎｌｓｓ，ｔｄａｅｎｅｔａｔｏｎｅｏｓｒｃｉｎｏｈｎｔｎａｏｃｒｎｏｔｏｌｓｏｓｏｈｅａａｙｉａｍｅｈｏｂｓｄｏｘｒｃｉｎａｄｒｃｎｔｕｔｏｆｔｅｉｓａｔｎｅｕｓ
Ｏ
本文提出了载波信号差分运算得到的瞬时频率分布服
从ＶｎＭｉｓｏｓ分布的假设，ｅ且该分布的参数与载波频率，采
样频率和信噪比有关，表达式如式（）３和式（）４所示
＝ቤተ መጻሕፍቲ ባይዱ
角频率／ａ＿ｒｄｓ
２／，，ｆ
（）３
（）４
（）＝．５Ｐ不同时的分布函数ｂＫ０７，０
ｄｆｅｅｔｓｍｐｉｇｒｔａｄＳＲｎｉｓａｔｎｏｓｆｅｕｎｙｐｏａｉｔｆｄｎｉｄｓｒｕｉｎｉｎｌｚｄｉｒｎａｌａｅｎＮｏｎｔｎａｅｕｑｅｃｒｂｂｌｙｏｅｓｔｉｔｂｔｓａａｙｅ．ｆｎｒｉｙｉｏ
在方向数据统计理论中ＶｎＭｉｓｏｓ分布（，）圆ｅ。ｋ在上分布中占有重要的作用，其密度函数为
ｇＯｇ，（；ｏ）。，（）１
２
＼
档褂
其中，（・为修正的第一类零阶Ｂｓｅ函数，０）ｅｓｌ
１（，０ｋ＝
辨。因此，为了能够分辨２个瞬时频率，噪比Ｐ应大于Ｐ信ｐ —－ｃｓ２Ａ／）１ｏ（— Ｆｆｗ
，
对于ＭＦＫ这类多载波信号而言，Ｓ瞬时频率的分布是
关于２／，ｆ对称的多峰分布。其中每一个峰均符合ＶｎｏＭｉｓｓ分布，ｅ相应的＝２ｒ ±ｎＦ）ｆ，中，Ｆ为载波１（Ａ／ｓ其 △ 频率间隔，２ｍ～１／ｍ为调制阶数。ｎ＝（（）２；
一
Ｎｑｉ采样定理，ｙｕｓｔ即采样频率不低于信号最高频率的２倍，因此，（）式３总能满足。在［，叮）０２『区间或者［一盯，）区
间。
定时，当信噪比恶化时，２个瞬时频率将部分混叠在一起，而当信噪比在Ｐ时，Ｓ ≤ｐＦＫ信号的２个瞬时频率将无法分
ｒ＝Ｏ
角频率／ｄＳｒ・ａ（ｐ１，不同时的分布函数ａ＝０Ｋ）
（］ｉｒｕｉｎｆｎｔｎｏｄｆｅｅｔｅｐ０ａｄｓｉｔｃｉｆｉｒｎｗｈｎ＝１ｔｂｏｕｏＫ
００２．１０００．１００８．０
志（，
收稿日期：０２０－３２１－２２
基金项目：国家重点基础研究发展计划（９３计划） “７” 资助项目（１９０００— ）６３３１１１１
第４期
１瞬时频率的概率密度分布
司伟建，：等基于抽取与重构的瞬时频率估计算法
１１４
且式（）。中和的取值有如下约定：１／．ｔ
依余弦函数的性质，Ｍ（ｏｒｋ＝Ｍ（。）为克有／＋叮，）ｚ／－ｋ，ｘ
服由此带来的不确定性，约定００叮，。 ≤ ＜２丁＞Ｏ
嚣０６ｌ００
槲００４．０娶００．２０
ｄｎｉｙｄｓｒｂｕｉｎｍｏｅｓｔｄｉｄ，ｎｄｔｅｉｔｉｕｉｎｍｏｅｓｖｒｆｅｂｈｐｔｓｓｔｔ．Ｔｈｅｅｆｃｆｅｓｔｉｔｉｔｏｄｌｉｓｕｅａｈｄｓｒｂｔｏｄｌｉｅｉｉｄｙｙｏｈｅｉｅｓｉｎｇｆｅｔｏ
通信领域的信号识别、跟踪估计等。
瞬时频率的定义最早是由ＣｒｏＲ与ＦｙＴＣ提ａｎＪｓｒ出，ｉｅＧｂｒＶｌ将ａｏ提出的解析信号与Ｃｒｎ及Ｆｙ的工作ｌａｓｏｒ结合起来将瞬时频率定义为解析信号的相位导数。Ｖｌｉｅｌ提到，由于瞬时频率是时变的，以，所应该存在有与瞬时频率相对应的瞬时谱，并且该瞬时谱的平均频率即为瞬时频