(寒假总动员)2020年高三数学寒假作业 专题14 椭圆、双曲线、抛物线(背)
【2020届】高考数学圆锥曲线专题复习:圆锥曲线(椭圆-双曲线-抛物线)的定义、方程和性质知识总结
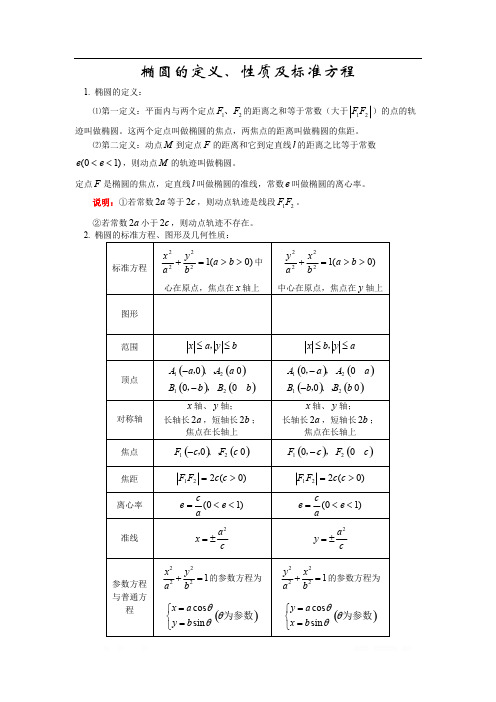
椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点的距离之和等于常数(大于)的点的轨12F F 、12F F 迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点到定点的距离和它到定直线的距离之比等于常数M F l ,则动点的轨迹叫做椭圆。
)10(<<e e M 定点是椭圆的焦点,定直线叫做椭圆的准线,常数叫做椭圆的离心率。
F l e 说明:①若常数等于,则动点轨迹是线段。
2a 2c 12F F ②若常数小于,则动点轨迹不存在。
2a 2c 2. 椭圆的标准方程、图形及几何性质:标准方程中)0(12222>>=+b a by a x 心在原点,焦点在轴上x )0(12222>>=+b a bx a y 中心在原点,焦点在轴上y 图形范围x a y b≤≤,x b y a≤≤,顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴轴、轴;x y 长轴长,短轴长;2a 2b 焦点在长轴上轴、轴;x y 长轴长,短轴长;2a 2b 焦点在长轴上焦点()()1200F c F c -,、,()()1200F c F c -,、,焦距)0(221>=c c F F )0(221>=c c F F 离心率)10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程的参数方程为22221x y a b+=()cos sin x a y b θθθ=⎧⎨=⎩为参数的参数方程为22221y x a b+=()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
2020高考文科数学专用专题能力训练:椭圆、双曲线、抛物线含解析

������ = ������(������-������), 由{������ = 1 ������2 消去 y,整理得:x2-4kx+4kt=0,
4
由于直线 PA 与抛物线相切,得 k=t.
因此,点 A 的坐标为(2t,t2).
设圆 C2 的圆心为 D(0,1),点 B 的坐标为(x0,y0),由题意知:点 B,O 关于直线 PD 对称,
(2)由(1)知|AP|=t·√1 + ������2和直线 PA 的方程 tx-y-t2=0.
点 B 到直线 PA 的距离是 d=√1������+2������2. 设△PAB 的面积为 S(t),
所以 S(t)=12|AP|·d=������23. 10.解 (1)设 M 的坐标为(x,y),当 x=-1 时,直线 MA 的斜率不存在;
(1)求点 A,B 的坐标; (2)求△PAB 的面积.
2 / 10
注:直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物 线相切,称该公共点为切点.
10.如图,动点 M 与两定点 A(-1,0),B(1,0)构成△MAB,且直线 MA,MB 的斜率之积为 4,设动 点 M 的轨迹为 C.
对于方程①,其判别式 Δ=(-2m)2-4×3(-m2-4)=16m2+48>0,
而当 1 或-1 为方程①的根时,m 的值为-1 或 1.
结合题设(m>0)可知,m>0,且 m≠1.
设 Q,R 的坐标分别为(xQ,yQ),(xR,yR),
A.������2 − ������2=1
B.������2 − ������2=1
4 12
12 4
C.������32-y2=1
(寒假总动员)2020年高三数学寒假作业专题14椭圆、双曲线、抛物线(练)(含解析)

(寒假总动员)2020年高三数学寒假作业 专题14椭圆、双曲线、抛物线(练)x 22y (含解析)1•已知椭圆E: 2 a b 2 1(a b 0) 的右焦点为F (3,0),过点 F 的直线交 E 于A , B 两点•若AB 的中点坐标为 (1, 1) ?则 E 的方程为 ()2 22 2 2 22 2xy1x y1 x y 1X y 1 A. 45 36B .4527C . 27 18D . 18 9【答案】D 【解析】笙二竺+匸空“ 原丸二1二上工空亠Z 剜得工丄 W,得 ab' 花—芒 a i': - v ; a 1 S a 2ff :=18i fe :=9)故选几施 1.W3中皿的关系;乩点差法的应用.2•定义:曲线C 上的点到直线1的距离的最小值称为曲线C 到直线1的距离,已知曲线C 1:y' x a到直线1:x2y 0的距离为「5,则实数a 的值为()【答案】D 【解析】试题分忻2设平行于M^r r-2i =0_E 的直践黄工一邛十刚二0,gpw =±5,由Higx-2v + w = 0^曲块C\相切.-■龙一2丘一加+翊二CL— 2^/^—2玄+拥=0,由A =】一4『-A +栩)=°得1 + 2口一叨=0 ,①当酬=哎时,d = 2» (检验得不満定亲冲,舍去)②当删二一5时,立二一3,选D.试题分析;由设月(禺』)卫帀・门)、代丄椭圆中得,两式相减得A. 3 或 3B. 2 或 3C.2D. 3F 1H考点:平行直线,直线与曲线相切,一元二次方程的根的判别式2b 2 1(a 0,b 0)的右焦点,若双曲线C 的渐近线与圆【解析】试题分析;扇如双曲箜的渐近塢亩稈为V- ±-,町血土妙丛又風』:(r-c); + v :=-mt 为 a4【解祈】试題分析:设椭园的焦点斤(-亡』》,兀仁Q.由壬倉可知民冏线方程为二-写=1,其酣近线方程为 c iT=±-JC ,又双曲线的两条渐近趺与橢创的煌点构飞的四边形恰酋正方形,所以由瞞园的对除性知双曲线C的斯近绽方程為F 二士口即方二G 所以宀辰"石戲椭圆的离心率为也.肴擦2双曲线、椭圆的性质.瞞圆的离尤苗刘求法.3.已知F (c,°)是双曲线M : (x c)24相切,则双曲线的离心率为(B. 、2C. 33 2D. 2半径5 且双曲线匸的渐近戍与圆・滸启理得即肿7可執二空23考点:收曲缕的性质.直线与囿的位置穴系,欢也的离心駁4.已知双曲线的顶点与焦点分别是椭圆 2 2M 古1(a b 0)的焦点和顶点,若双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,则椭圆的离心率为( 1A. 3【答案】B. 2C. 3_2D. 2)5•已知两个正数a, b的等差中项是92,一个等比中项是 2 5,且a2 by _ xb,则抛物线 a 的焦点坐标为( )51 1 c、2(,0)(-,0)(匚,0)(-,0)A. 16B.5C. 5rD. 5【着案】B【解析】N + 占=9’4盂题分析:依题意::= 20,解得口二境ir=4r ' J方程九工*=一二小7=6二其定点ffi] \a>h ~色标为(--.0),选B・皆点:等差中项,等比中项.抛物线的性质.二、填空题6•与抛物线y 8x相切的倾斜角为135的直线1与X轴和y轴的焦点分别为A和B,记过A、B两点的最小圆为C •(I)则圆C的方程是;(n)圆C截抛物线'8x的准线所得的弦长为1):是£PA8当"0时【解析】V = —br试题分析!( I )谡直线r 的方程対丁二-X 十乩 麻立方程绢消去工整理得L 十蚤-甜 严—8^越―2Q ),风Q —2),过小P 两点的最小團町一叨为审它的鳳 其片程为(>亠1『十(丁十1)(II )依题意,抛物^y :=8^Bfg^^:Z].Y=-l 由(1)切囚C 的圆心対(―人―1),其圆系到准鏡的距离为1-于是所载得的弦长为丄J 而 M = 2.肴点,;直线与拋物録的位置关系,團的方程,直线截園所得的弦按计算.|PA|27•抛物线y 8x的焦点为F ,点(x,y )为该抛物线上的动点,,又已知点A ( 2,0),则|PF|的取值范围【解析】述题分析:由抛物线的定义可得|W 二 K, X | PA |=7(-V-2)-+V -=^ + 2):+8JC )当且仅当K =・卩:V = 2时取等务・于是K+?44Ng,综上所述二皂 的母值范围是[i=JT] + PF普点;拋物统的定久 最值问题,基本不等式.T 直统2抛物线相切,则△二S : -4其(-$防二0,解得b:直徙r 的方程为工十二o’从而 【答宪】[1.71] 当“0时,1—X'++ 4三•解答题2 2 2C :x y b 相切于点 M (X 。
椭圆双曲线抛物线 高考数学专题复习精细高效梳理(附详解)
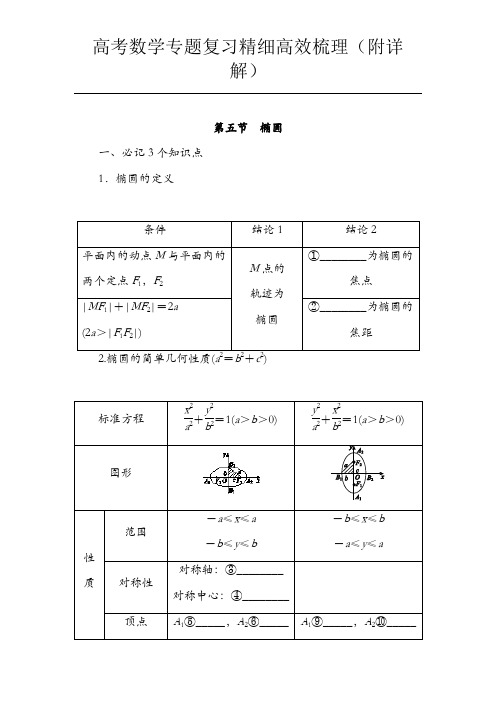
第五节椭圆一、必记3个知识点1.椭圆的定义-a≤x≤a(1)设椭圆x 2a 2+y 2b2=1(a >b >0)上任意一点P (x ,y ),则当x =0时,|OP |有最小值b ,这时,P 在短轴端点处;当x =±a 时,|OP |有最大值a ,这时,P 在长轴端点处.(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a 是斜边长,a 2=b 2+c 2.(3)已知过焦点F 1的弦AB ,则△ABF 2的周长为4a .(4)若P 为椭圆上任一点,F 为其焦点,则a -c ≤|PF |≤a +c .二、必明3个易误点1.椭圆的定义中易忽视2a >|F 1F 2|这一条件,当2a =|F 1F 2|其轨迹为线段F 1F 2,当2a <|F 1F 2|不存在轨迹.2.求椭圆的标准方程时易忽视判断焦点的位置,而直接设方程为x 2a 2+y 2b 2=1(a >b >0). 3.注意椭圆的范围,在设椭圆x 2a 2+y 2b 2=1(a >b >0)上点的坐标为P (x ,y )时,则|x |≤a ,这往往在求与点P 有关的最值问题中特别有用,也是容易被忽略而导致求最值错误的原因.三、技法1. 求椭圆标准方程的2种常用方法(1)直接求出a ,c 来求解e .通过已知条件列方程组,解出a ,c 的值.(2)构造a ,c 的齐次式,解出e .由已知条件得出关于a ,c 的二元齐次方程,然后转化为关于离心率e 的一元二次方程求解.(3)通过取特殊值或特殊位置,求出离心率.提醒:在解关于离心率e 的二次方程时,要注意利用椭圆的离心率e ∈(0,1)进行根的取舍,否则将产生增根.3. 求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析,即使画不出图形,思考时也要联想到一个图形.(2)椭圆的范围或最值问题常常涉及一些不等式.例如,-a ≤x ≤a ,-b ≤y ≤b,0<e <1,在求椭圆的相关量的范围时,要注意应用这些不等关系.(3)最值问题,将所求列出表达式,构造基本不等式或利用函数单调性求解.4. 判断直线与椭圆位置关系的四个步骤第一步:确定直线与椭圆的方程.第二步:联立直线方程与椭圆方程.第三步:消元得出关于x (或y )的一元二次方程.第四步:当Δ>0时,直线与椭圆相交;当Δ=0时,直线与椭圆相切;当Δ<0时,直线与椭圆相离.5.直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A (x 1,y 1),B (x 2,y 2),则|AB |=(1+k 2)[(x 1+x 2)2-4x 1x 2]= ⎝ ⎛⎭⎪⎪⎫1+1k 2[(y 1+y 2)2-4y 1y 2](k 为直线斜率).参考答案①F1,F2②|F1F2| ③x轴,y轴④坐标原点⑤(-a,0) ⑥(a,0) ⑦(0,-b) ⑧(0,b) ⑨(0,-a) ⑩(0,a) ⑪(-b,0) ⑫(b,0) ⑬2a⑭2b⑮2c⑯(0,1) ⑰c2=a2-b2第六节双曲线一、必记3个知识点1.双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|=2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线.这两个定点叫做双曲线的②________,两焦点间的距离叫做③________.(2)集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.(ⅰ)当④________________时,M点的轨迹是双曲线;(ⅱ)当⑤________________时,M点的轨迹是两条射线;(ⅲ)当⑥________________时,M点不存在.2.双曲线的标准方程和几何性质⑧________ x∈R3.双曲线中的4个常用结论(1)双曲线为等轴双曲线⇔双曲线的离心率e=2⇔双曲线的两条渐近线互相垂直.(2)渐近线的斜率与双曲线的焦点位置的关系:当焦点在x轴上时,渐近线斜率为±ba,当焦点在y轴上时,渐近线斜率为±ab.(3)渐近线与离心率.x2 a2-y2b2=1(a>0,b>0)的一条渐近线的斜率为ba=e2-1.(4)若P为双曲线上一点,F为其对应焦点,则|PF|≥c-a.二、必明4个易误点1.双曲线的定义中易忽视2a<|F1F2|这一条件.若2a=|F1F2|,则轨迹是以F1,F2为端点的两条射线,若2a>|F1F2|则轨迹不存在.2.双曲线的标准方程中对a,b的要求只是a>0,b>0,易误认为与椭圆标准方程中a,b的要求相同.若a>b>0,则双曲线的离心率e∈(1,2);若a=b>0,则双曲线的离心率e=2;若0<a<b,则双曲线的离心率e> 2.3.注意区分双曲线中的a,b,c大小关系与椭圆a,b,c关系,在椭圆中a2=b2+c2,而在双曲线中c2=a2+b2.4.易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x轴上,渐近线斜率为±b a ,当焦点在y 轴上,渐近线斜率为±a b.三、技法1. 双曲线定义的应用 (1)判定满足某条件的平面内动点的轨迹是否为双曲线,进而根据要求可求出曲线方程;(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立|PF 1|与|PF 2|的关系.[注意] 在应用双曲线定义时,要注意定义中的条件,搞清所求轨迹是双曲线,还是双曲线的一支,若是双曲线的一支,则需确定是哪一支.2. 求双曲线标准方程的一般方法(1)待定系数法:设出双曲线方程的标准形式,根据已知条件,列出参数a ,b ,c 的方程并求出a ,b ,c 的值.与双曲线x 2a 2-y 2b2=1有相同渐近线时,可设所求双曲线方程为:x 2a 2-y 2b 2=λ(λ≠0). (2)定义法:依定义得出距离之差的等量关系式,求出a 的值,由定点位置确定c 的值.3. 求双曲线离心率或其范围的方法(1)求a ,b ,c 的值,由c 2a 2=a 2+b 2a 2=1+b 2a2直接求e .(2)列出含有a ,b ,c 的齐次方程(或不等式),借助于b 2=c 2-a 2消去b ,然后转化成关于e 的方程(或不等式)求解.4.求双曲线的渐近线方程的方法求双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线的方法是令x 2a 2-y 2b 2=0,即得两渐近线方程为:x a ±y b=0.参考答案①之差的绝对值 ②焦点 ③焦距 ④2a <|F 1F 2| ⑤2a =|F 1F 2| ⑥2a >|F 1F 2|⑦x ≥a 或x ≤-a ⑧y ≥a 或y ≤-a ⑨x 轴,y 轴 ⑩坐标原点 ⑪x 轴,y 轴⑫坐标原点 ⑬(-a,0) ⑭(a,0) ⑮(0,-a ) ⑯(0,a ) ⑰y =±b a x ⑱y =±a bx ⑲c a ⑳ a 2+b 2 ○212a ○222b ○23a 2+b 2第七节抛物线一、必记2个知识点1.抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________设AB 是过抛物线y 2=2px (p >0)的焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则(1)x 1x 2=p 24,y 1y 2=-p 2. (2)弦长|AB |=x 1+x 2+p =2p sin 2α(α为弦AB 的倾斜角). (3)以弦AB 为直径的圆与准线相切.(4)通径:过焦点且垂直于对称轴的弦,长等于2p .二、必明2个易误点1.抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与直线垂直的直线.2.抛物线标准方程中参数p 易忽视,只有p >0,才能证明其几何意义是焦点F 到准线l 的距离,否则无几何意义.三、技法1. 应用抛物线定义的2个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P (x ,y )到焦点F 的距离|PF |=|x |+p 2或|PF |=|y |+p 2. 2. 求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法,因为未知数只有p ,所以只需一个条件确定p 值即可.(2)因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.3.确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化为标准方程.(2)要结合图形分析,灵活运用平面几何的性质以图助解.4. 解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时,一般用“点差法”求解.参考答案①相等 ②y 2=-2px (p >0) ③x 2=-2py (p >0) ④x 2=2py (p >0) ⑤x 轴 ⑥y 轴⑦F (-p 2,0) ⑧F (0,-p 2) ⑨F (0,p 2) ⑩e =1 ⑪x =-p 2 ⑫y =-p 2 ⑬-y 0+p 2⑭y 0+p 2⑮y ≤0 ⑯y ≥0。
(寒假总动员)2018-2019年秋年高三数学寒假作业 专题14 椭圆、双曲线、抛物线(练)(含解析)

(寒假总动员)2015年高三数学寒假作业专题14 椭圆、双曲线、抛物线(练)(含解析)1.已知椭圆)0(1:2222>>=+babyaxE的右焦点为)0,3(F,过点F的直线交E于A,B两点.若AB的中点坐标为)1,1(-,则E的方程为()A.1364522=+yxB.1274522=+yxC.1182722=+yxD.191822=+yx2.定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线1:C y x a=+到直线:20l x y-=的距离为5,则实数a的值为()A.3或3-B.2或3-C.2D.3-考点:平行直线,直线与曲线相切,一元二次方程的根的判别式.3.已知)0,(c F 是双曲线)0,0(1:2222>>=-b a b y a x C 的右焦点,若双曲线C 的渐近线与圆4)(:222c y c x M =+-相切,则双曲线的离心率为( )A.332 B.2 C.3 D. 2234.已知双曲线的顶点与焦点分别是椭圆)0(12222>>=+b a b y a x 的焦点和顶点,若双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,则椭圆的离心率为( )A. 31B.21C.33D.225.已知两个正数a ,b 的等差中项是92,一个等比中项是25,且a b >,则抛物线2b y xa =-的焦点坐标为( )A.5(,0)16-B.1(,0)5-C.1(,0)5D.2(,0)5-二、填空题6.与抛物线x y 82=相切的倾斜角为135 的直线l 与x 轴和y 轴的焦点分别为A 和B ,记过A 、B 两点的最小圆为C .(Ⅰ)则圆C 的方程是 ;(Ⅱ)圆C 截抛物线x y 82=的准线所得的弦长为. 7.抛物线x y 82=的焦点为F ,点),(y x 为该抛物线上的动点,,又已知点)0,2(-A ,则||||PF PA 的取值范围是 .三.解答题8.已知椭圆)0(1:2222>>=+b a b y a x E 的右焦点F ,y 轴右侧的点A 在椭圆E 上运动,直线MA 与圆222:b y x C =+相切于点),(00y x M .(Ⅰ)求直线MA 的方程; (Ⅱ)求证:||||AM AF +为定值.。
(寒假总动员)2020年高三数学寒假作业 专题14 椭圆、双曲线、抛物线(测)(含解析)

(寒假总动员)2020年高三数学寒假作业 专题14 椭圆、双曲线、抛物线(测)(含解析)时间:45分钟 满分:100分 一、选择题(每小题5分,共50分)1.(2020年高考新课标全国卷理科4)设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点,P 为直线32ax =上一点,∆21F PF 是底角为30o的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34()D 45【答案】C【解析】∆21F PF 是底角为30o的等腰三角形221332()224c PF F F a c c e a ⇒==-=⇔==. 2.(2020年高考新课标全国卷理科8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,43AB =;则C 的实轴长为( )()A 2 ()B 22 ()C 4 ()D 83. (2020年高考福建卷理科8)双曲线22214x y b-=的右焦点与抛物线x y 122=的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )A .5B .24C .3D .54.(2020年高考浙江卷理科8)如图,F1,F2分别是双曲线C:22221x ya b-=(a,b>0)的左右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是A.23B.6C.2 D.35.(2020年高考山东卷理科10)已知椭圆C:的离心率为,双曲线x²-y²=1的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为6.(2020年高考安徽卷理科9)过抛物线24y x =的焦点F 的直线交抛物线于,A B 两点,点O 是原点,若3AF =,则AOB ∆的面积为( )()A 22 ()B 2 ()C 322()D 227. (2020年高考湖南卷理科5)已知双曲线C :22x a -22y b=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为( )A .220x -25y =1 B.25x -220y =1 C.280x -220y =1D.220x -280y =18. (2020年高考四川卷理科8)已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y 。
高考数学专题复习《椭圆、双曲线、抛物线》突破解析
第2讲 椭圆、双曲线、抛物线【要点提炼】考点一 椭圆、双曲线、抛物线的定义与标准方程1.圆锥曲线的定义(1)椭圆:|PF 1|+|PF 2|=2a(2a>|F 1F 2|).(2)双曲线:||PF 1|-|PF 2||=2a(0<2a<|F 1F 2|).(3)抛物线:|PF|=|PM|,l 为抛物线的准线,点F 不在定直线l 上,PM ⊥l 于点M.2.求圆锥曲线标准方程“先定型,后计算”所谓“定型”,就是确定曲线焦点所在的坐标轴的位置;所谓“计算”,就是指利用待定系数法求出方程中的a 2,b 2,p 的值.【热点突破】【典例】1 (1)(2020·广州四校模拟)若椭圆x 2a 2+y 2b 2=1(其中a>b>0)的离心率为35,两焦点分别为F 1,F 2,M 为椭圆上一点,且△F 1F 2M 的周长为16,则椭圆C 的方程为( )A.x 216+y 225=1 B.x 225+y 29=1C.x 29+y 225=1 D.x 225+y 216=1【答案】 D【解析】 椭圆x 2a 2+y 2b 2=1(其中a>b>0)的两焦点分别为F 1,F 2,M 为椭圆上一点,且△F 1F 2M的周长为16,可得2a +2c =16,椭圆x 2a 2+y 2b 2=1(其中a>b>0)的离心率为35,可得c a =35,解得a =5,c =3,则b =4,所以椭圆C 的方程为x 225+y 216=1.(2)(2020·全国Ⅰ)设F 1,F 2是双曲线C :x 2-y 23=1的两个焦点,O 为坐标原点,点P 在C 上且|OP|=2,则△PF 1F 2的面积为( )A.72 B .3 C.52 D .2【答案】 B【解析】 方法一 由题意知a =1,b =3,c =2,F 1(-2,0),F 2(2,0),如图,因为|OF 1|=|OF 2|=|OP|=2,所以点P 在以F 1F 2为直径的圆上,故PF 1⊥PF 2,则|PF 1|2+|PF 2|2=(2c)2=16.由双曲线的定义知||PF 1|-|PF 2||=2a =2,所以|PF 1|2+|PF 2|2-2|PF 1||PF 2|=4,所以|PF 1||PF 2|=6,所以△PF 1F 2的面积为12|PF 1||PF 2|=3.方法二 由双曲线的方程可知,双曲线的焦点F 1,F 2在x 轴上,且|F 1F 2|=21+3=4.设点P 的坐标为(x 0,y 0),则Error!解得|y 0|=32.所以△PF 1F 2的面积为12|F 1F 2|·|y 0|=12×4×32=3.易错提醒 求圆锥曲线的标准方程时的常见错误双曲线的定义中忽略“绝对值”致错;椭圆与双曲线中参数的关系式弄混,椭圆中的关系式为a 2=b 2+c 2,双曲线中的关系式为c 2=a 2+b 2;圆锥曲线方程确定时还要注意焦点位置.【拓展训练】1 (1)设抛物线C :y 2=2px(p>0)的焦点为F ,点M 在C 上,|MF|=5.若以MF 为直径的圆过点(0,2),则C 的方程为( )A .y 2=4x 或y 2=8x B .y 2=2x 或y 2=8x C .y 2=4x 或y 2=16x D .y 2=2x 或y 2=16x【答案】 C【解析】 方法一 因为以MF 为直径的圆过点(0,2),所以点M 在第一象限.由|MF|=x M +p 2=5,得x M =5-p2,即M (5-p2,2p (5-p2)).从而以MF 为直径的圆的圆心N 的坐标为(52,122p (5-p2)).因为点N 的横坐标恰好等于圆的半径,所以圆与y 轴相切于点(0,2),从而2=122p (5-p2),即p 2-10p +16=0,解得p =2或p =8,所以抛物线方程为y 2=4x 或y 2=16x.方法二 由已知得抛物线的焦点F (p2,0),设点A(0,2),点M(x 0,y 0),则A F → =(p 2,-2),A M →=(y 202p ,y 0-2).由已知,得A F → ·A M →=0,即y 20-8y 0+16=0,解得y 0=4,M (8p,4).由|MF|=5,得(8p -p2)2+16=5.又因为p>0,解得p =2或p =8,所以抛物线C 的方程为y 2=4x 或y 2=16x.(2)已知椭圆C :x 2m +y 2m -4=1(m>4)的右焦点为F ,点A(-2,2)为椭圆C 内一点,若椭圆C上存在一点P ,使得|PA|+|PF|=8,则实数m 的取值范围是( )A .(6+25,25] B .[9,25]C .(6+25,20]D .[3,5]【答案】 A【解析】 椭圆C :x 2m +y 2m -4=1(m>4)的右焦点F 的坐标为(2,0).设左焦点为F ′,则F ′(-2,0).由椭圆的定义可得2m =|PF|+|PF ′|,即|PF ′|=2m -|PF|,可得|PA|-|PF ′|=|PA|+|PF|-2m =8-2m .由||PA|-|PF ′||≤|AF ′|=2,可得-2≤8-2m ≤2,解得3≤m ≤5,所以9≤m ≤25.①又点A 在椭圆内,所以4m +4m -4<1(m>4),所以8m -16<m(m -4)(m>4),解得m<6-25(舍)或m>6+25.②由①②得6+25<m ≤25,故选A.【要点提炼】考点二 圆锥曲线的几何性质1.求离心率通常有两种方法(1)求出a ,c ,代入公式e =ca.(2)根据条件建立关于a ,b ,c 的齐次式,消去b 后,转化为关于e 的方程或不等式,即可求得e 的值或取值范围.2.与双曲线x 2a 2-y 2b 2=1(a>0,b>0)共渐近线bx±ay =0的双曲线方程为x 2a 2-y 2b 2=λ(λ≠0).【热点突破】【典例】2 (1)设F 1,F 2分别是椭圆E :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,过F 2的直线交椭圆于A ,B 两点,且A F 1→ ·A F 2→ =0,A F 2→ =2F 2B →,则椭圆E 的离心率为( )A.23 B.34 C.53 D.74【答案】 C【解析】 ∵A F 2→ =2F 2B →,设|BF 2|=x ,则|AF 2|=2x ,∴|AF 1|=2a -2x ,|BF 1|=2a -x ,∵A F 1→ ·A F 2→=0,∴AF 1⊥AF 2,在Rt △AF 1B 中,有(2a -2x)2+(3x)2=(2a -x)2,解得x =a3,∴|AF 2|=2a3,|AF 1|=4a3,在Rt △AF 1F 2中,有(4a 3)2+(2a 3)2=(2c)2,整理得c 2a 2=59,∴e =c a =53.(2)(2020·莆田市第一联盟体联考)已知直线l :y =x -1与抛物线y 2=4x 相交于A ,B 两点,M 是AB 的中点,则点M 到抛物线准线的距离为( )A.72 B .4 C .7 D .8【答案】 B【解析】 由题意可知直线y =x -1过抛物线y 2=4x 的焦点(1,0),如图,AA ′,BB ′,MM ′都和准线垂直,并且垂足分别是A ′,B ′,M ′,由图象可知|MM ′|=12(|AA ′|+|BB ′|),根据抛物线的定义可知|AA ′|+|BB ′|=|AB|,∴|MM ′|=12|AB|,联立Error!得x 2-6x +1=0,设A ,B 两点的坐标为(x 1,y 1),(x 2,y 2),x 1+x 2=6,∴|AB|=x 1+x 2+2=8,∴|MM ′|=4.二级结论 抛物线的有关性质:已知抛物线y 2=2px(p>0)的焦点为F ,直线l 过点F 且与抛物线交于两点A(x 1,y 1),B(x 2,y 2),则(1)|AB|=x 1+x 2+p =2ps i n 2α(α为直线l 的倾斜角).(2)以AB 为直径的圆与抛物线的准线相切.(3)1|A F |+1|B F |=2p .【拓展训练】2 (1)已知F 是抛物线C :y 2=2px(p>0)的焦点,抛物线C 的准线与双曲线Γ:x 2a 2-y 2b 2=1(a>0,b>0)的两条渐近线交于A ,B 两点,若△ABF 为等边三角形,则Γ的离心率e 等于( )A.32B.233C.217D.213【答案】 D【解析】 抛物线的焦点坐标为(p 2,0),准线方程为x =-p 2,联立抛物线的准线方程与双曲线的渐近线方程得Error!解得y =±p b 2a ,可得|AB|=p ba,由△ABF 为等边三角形,可得p =32·p ba ,即有b a =23,则e =ca=1+b 2a 2=1+43=213.(2)已知抛物线C :y 2=2px(p>0)的焦点为F ,点M(x 0,22)(x 0>p 2)是抛物线C 上一点,圆M与线段MF 相交于点A ,且被直线x =p2截得的弦长为3|MA|,若|M A ||A F |=2,则|AF|等于( )A.32 B .1 C .2 D .3【答案】 B【解析】 如图所示,由题意知,|MF|=x 0+p2.∵圆M 与线段MF 相交于点A ,且被直线x =p2截得的弦长为3|MA|,∴|MA|=2|DM|=2(x 0-p2).∵|M A ||A F |=2,∴|MF|=32|MA|,∴x 0=p.又∵点M(x 0,22)在抛物线上,∴2p 2=8,又∵p>0,∴p =2.∴|MA|=2(x 0-p2)=2,∴|AF|=1.【要点提炼】考点三 直线与圆锥曲线的位置关系解决直线与椭圆的位置关系问题,经常利用设而不求的方法,解题要点如下:(1)设直线与椭圆的交点坐标为A(x 1,y 1),B(x 2,y 2);(2)联立直线的方程与椭圆的方程;(3)消元得到关于x 或y 的一元二次方程;(4)利用根与系数的关系设而不求;(5)把题干中的条件转化为含有x 1+x 2,x 1x 2或y 1+y 2,y 1y 2的式子,进而求解即可.【热点突破】【典例】3 (2020·全国Ⅲ)已知椭圆C :x 225+y 2m 2=1(0<m<5)的离心率为154,A ,B 分别为C 的左、右顶点.(1)求C 的方程;(2)若点P 在C 上,点Q 在直线x =6上,且|BP|=|BQ|,BP ⊥BQ ,求△APQ 的面积.【解析】解 (1)由题设可得25-m 25=154,得m 2=2516,所以C 的方程为x 225+y 22516=1.(2)设P(x P ,y P ),Q(6,y Q ),根据对称性可设y Q >0,由题意知y P >0.由已知可得B(5,0),直线BP 的方程为y =-1y Q(x -5),所以|BP|=y P1+y 2Q,|BQ|=1+y 2Q .因为|BP|=|BQ|,所以y P =1.将y P =1代入C 的方程,解得x P =3或-3.由直线BP 的方程得y Q =2或8,所以点P ,Q 的坐标分别为P 1(3,1),Q 1(6,2);P 2(-3,1),Q 2(6,8).所以|P 1Q 1|=10,直线P 1Q 1的方程为y =13x ,点A(-5,0)到直线P 1Q 1的距离为102,故△AP 1Q 1的面积为12×102×10=52;|P 2Q 2|=130,直线P 2Q 2的方程为y =79x +103,点A 到直线P 2Q 2的距离为13026,故△AP 2Q 2的面积为12×13026×130=52.综上,△APQ 的面积为52.规律方法 解决直线与圆锥曲线位置关系的注意点(1)注意使用圆锥曲线的定义.(2)引入参数,注意构建直线与圆锥曲线的方程组.(3)注意用好圆锥曲线的几何性质.(4)注意几何关系和代数关系之间的转化.【拓展训练】3 (1)(2019·全国Ⅰ)已知椭圆C 的焦点为F 1(-1,0),F 2(1,0),过F 2的直线与C 交于A ,B 两点.若|AF 2|=2|F 2B|,|AB|=|BF 1|,则C 的方程为( )A.x 22+y 2=1 B.x 23+y 22=1C.x 24+y 23=1 D.x 25+y 24=1【答案】 B【解析】 由题意设椭圆的方程为x 2a 2+y 2b 2=1(a>b>0),连接F 1A ,令|F 2B|=m ,则|AF 2|=2m ,|BF 1|=3m.由椭圆的定义知,4m =2a ,得m =a2,故|F 2A|=a =|F 1A|,则点A 为椭圆C 的上顶点或下顶点.令∠OAF 2=θ(O 为坐标原点),则sin θ=ca =1a .在等腰三角形ABF 1中,cos2θ= 2m 2+ 3m 2- 3m 22×2m ·3m =13,因为cos 2θ=1-2sin 2θ,所以13=1-2(1a)2,得a 2=3.又c 2=1,所以b 2=a 2-c 2=2,椭圆C 的方程为x 23+y 22=1.(2)设F 为抛物线y 2=2px(p>0)的焦点,斜率为k(k>0)的直线过F 交抛物线于A ,B 两点,若|FA|=3|FB|,则直线AB 的斜率为( )A.12B.1 C.2 D.3【答案】 D【解析】 假设A在第一象限,如图,过A,B分别向抛物线的准线作垂线,垂足分别为D,E,过A作EB的垂线,垂足为C,则四边形ADEC为矩形,由抛物线定义可知|AD|=|AF|,|BE|=|BF|,又∵|FA|=3|FB|,∴|AD|=|CE|=3|BE|,即B为CE 的三等分点,设|BF|=m,则|BC|=2m,|AF|=3m,|AB|=4m,即|AC|=|A B|2-|B C|2=16m2-4m2=23m,则tan∠ABC=|A C||B C|=23m2m=3,即直线AB的斜率k=3.专题训练一、单项选择题1.(2020·福州模拟)已知双曲线x2a2-y2b2=1(a>0,b>0)的渐近线方程为y=±23x,则此双曲线的离心率为( )A.134B.132C.133D.134【答案】 C【解析】 因为双曲线x2a2-y2b2=1(a>0,b>0)的渐近线方程为y=±23x,所以ba=23,所以双曲线的离心率e=ca=1+(b a)2=1+(23)2=133.2.(2020·全国Ⅰ)已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p等于( )A.2 B.3 C.6 D.9【答案】 C【解析】 设A(x,y),由抛物线的定义知,点A到准线的距离为12,即x+p2=12.又因为点A到y轴的距离为9,即x=9,所以9+p2=12,解得p=6.3.已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,左、右顶点分别为M,N,过F2的直线l交C于A,B两点(异于M,N),△AF1B的周长为43,且直线AM与AN的斜率之积为-23,则C的方程为( )A.x212+y28=1 B.x212+y24=1C.x23+y22=1 D.x23+y2=1【答案】 C【解析】 由△AF1B的周长为43,可知|AF 1|+|AF 2|+|BF 1|+|BF 2|=4a =43,解得a =3,则M (-3,0),N(3,0).设点A(x 0,y 0)(x 0≠±3),由直线AM 与AN 的斜率之积为-23,可得y 0x 0+3·y 0x 0-3=-23,即y 20=-23(x 20-3),①又x 203+y 20b 2=1,所以y 20=b 2(1-x 203),②由①②解得b 2=2.所以C 的方程为x 23+y 22=1.4.设F 为双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ|=|OF|,则C 的离心率为( )A.2 B.3 C .2 D.5【答案】 A【解析】 如图,由题意,知以OF 为直径的圆的方程为(x -c2)2+y 2=c 24,①将x 2+y 2=a 2记为②式,①-②得x =a 2c,则以OF 为直径的圆与圆x 2+y 2=a 2的公共弦所在直线的方程为x =a 2c,所以|PQ|=2a 2-(a 2c)2.由|PQ|=|OF|,得2a 2-(a 2c )2=c ,整理得c 4-4a 2c 2+4a 4=0,即e 4-4e 2+4=0,解得e =2.5.(2020·潍坊模拟)已知点P 为双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)右支上一点,F 1,F 2分别为C 的左、右焦点,直线PF 1与C 的一条渐近线垂直,垂足为H ,若|PF 1|=4|HF 1|,则该双曲线的离心率为( )A.153 B.213 C.53 D.73【答案】 C【解析】 如图,取PF 1的中点M ,连接MF 2.由条件可知|HF 1|=14|PF 1|=12|MF 1|,∵O 是F 1F 2的中点,∴OH ∥MF 2,又∵OH ⊥PF 1,∴MF 2⊥PF 1,∴|F 1F 2|=|PF 2|=2c.根据双曲线的定义可知|PF 1|=2a +2c ,∴|HF1|=a+c 2,直线PF1的方程是y=ab(x+c),即ax-by+ac=0,原点到直线PF1的距离|OH|=|a c|a2+b2=a,∴在△OHF1中,a2+(a+c2)2=c2,整理为3c2-2ac-5a2=0,即3e2-2e-5=0,解得e=53或e=-1(舍).二、多项选择题6.(2020·新高考全国Ⅰ)已知曲线C:mx2+ny2=1.( ) A.若m>n>0,则C是椭圆,其焦点在y轴上B.若m=n>0,则C是圆,其半径为nC.若mn<0,则C是双曲线,其渐近线方程为y=±-m n xD.若m=0,n>0,则C是两条直线【答案】 ACD【解析】 对于A,当m>n>0时,有1n>1m>0,方程化为x21m+y21n=1,表示焦点在y轴上的椭圆,故A正确.对于B,当m=n>0时,方程化为x2+y2=1n,表示半径为1n的圆,故B错误.对于C,当m>0,n<0时,方程化为x21m-y2-1n=1,表示焦点在x轴上的双曲线,其中a=1m,b =-1n ,渐近线方程为y =±-m nx ;当m<0,n>0时,方程化为y 21n -x 2-1m =1,表示焦点在y 轴上的双曲线,其中a =1n ,b =-1m ,渐近线方程为y =±-mn x ,故C 正确.对于D ,当m =0,n>0时,方程化为y =±1n,表示两条平行于x 轴的直线,故D 正确.7.已知双曲线C 过点(3,2)且渐近线为y =±33x ,则下列结论正确的是( )A .C 的方程为x 23-y 2=1B .C 的离心率为3C .曲线y =e x -2-1经过C 的一个焦点D .直线x -2y -1=0与C 有两个公共点【答案】 AC【解析】 因为渐近线方程为y =±33x ,所以可设双曲线方程为x 29-y 23=λ,代入点(3,2),得λ=13,所以双曲线方程为x 23-y 2=1,选项A 正确;该双曲线的离心率为233,选项B 不正确;双曲线的焦点为(±2,0),曲线y =e x -2-1经过双曲线的焦点(2,0),选项C 正确;把x =2y +1代入双曲线方程,得y 2-22y +2=0,解得y =2,故直线x -2y -1=0与曲线C 只有一个公共点,选项D 不正确.8.已知抛物线C :y 2=2px(p>0)的焦点为F ,直线l 的斜率为3且经过点F ,直线l 与抛物线C 交于A ,B 两点(点A 在第一象限),与抛物线的准线交于点D.若|AF|=8,则下列结论正确的是( )A .p =4 B.D F → =F A →C .|BD|=2|BF|D .|BF|=4【答案】 ABC【解析】 如图所示,分别过点A ,B 作准线的垂线,垂足分别为E ,M ,连接EF.抛物线C 的准线交x 轴于点P ,则|PF|=p ,由于直线l 的斜率为3,则其倾斜角为60°.又AE ∥x 轴,∴∠EAF =60°,由抛物线的定义可知,|AE|=|AF|,则△AEF 为等边三角形,∴∠EFP =∠AEF =60°,则∠PEF =30°,∴|AF|=|EF|=2|PF|=2p =8,解得p =4,故A 正确;∵|AE|=|EF|=2|PF|,PF ∥AE ,∴F 为线段AD 的中点,则D F → =F A →,故B 正确;∵∠DAE =60°,∴∠ADE =30°,∴|BD|=2|BM|=2|BF|(抛物线定义),故C 正确;∵|BD|=2|BF|,∴|BF|=13|DF|=13|AF|=83,故D 错误.三、填空题9.(2019·全国Ⅲ)设F 1,F 2为椭圆C :x 236+y 220=1的两个焦点,M 为C 上一点且在第一象限.若△MF 1F 2为等腰三角形,则M 的坐标为________.【答案】 (3,15)【解析】 不妨令F 1,F 2分别为椭圆C 的左、右焦点,根据题意可知c =36-20=4.因为△MF 1F 2为等腰三角形,所以易知|F 1M|=2c =8,所以|F 2M|=2a -8=4.设M(x ,y),则Error!得Error!所以M 的坐标为(3,15).10.(2020·全国Ⅰ)已知F 为双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的右焦点,A 为C 的右顶点,B 为C 上的点,且BF 垂直于x 轴.若AB 的斜率为3,则C 的离心率为________.【答案】 2【解析】 如图,A(a,0).由BF ⊥x 轴且AB 的斜率为3,知点B 在第一象限,且B (c ,b 2a ),则k AB =b 2a -0c -a =3,即b 2=3ac -3a 2.又∵c 2=a 2+b 2,即b 2=c 2-a 2,∴c 2-3ac +2a 2=0,∴e 2-3e +2=0.解得e =2或e =1(舍去).故e =2.11.设双曲线mx 2+ny 2=1的一个焦点与抛物线y =18x 2的焦点相同,离心率为2,则抛物线的焦点到双曲线的一条渐近线的距离为________.【答案】 3【解析】 ∵抛物线x 2=8y 的焦点为(0,2),∴mx 2+ny 2=1的一个焦点为(0,2),∴焦点在y 轴上,∴a 2=1n ,b 2=-1m,c =2.根据双曲线三个参数的关系得到4=a 2+b 2=1n -1m,又离心率为2,即41n =4,解得n =1,m =-13,∴此双曲线的方程为y 2-x 23=1,则双曲线的一条渐近线方程为x -3y =0,则抛物线的焦点(0,2)到双曲线的一条渐近线的距离为d =|23|1+3=3.12.如图,抛物线C 1:y 2=2px 和圆C 2:(x -p 2)2+y 2=p 24,其中p>0,直线l 经过C 1的焦点,依次交C 1,C 2于A ,D ,B ,C 四点,则A B → ·C D → 的值为________.【答案】 p 24【解析】 易知A B → ·C D →=|AB|·|CD|,圆C 2的圆心即为抛物线C 1的焦点F ,当直线l 的斜率不存在时,l 的方程为x =p 2,所以A (p 2,p ),B (p 2,p 2),C (p 2,-p 2),D (p 2,-p ),|A B →|=|C D → |=p 2,所以A B → ·C D → =p 2·p 2=p 24;当直线l 的斜率存在时,设A(x 1,y 1),D(x 2,y 2),则|AB|=|FA|-|FB|=x 1+p 2-p2=x 1,同理|CD|=x 2,设l 的方程为y =k (x -p 2),由Error!可得k 2x 2-(pk 2+2p)x +k 2p 24=0,则A B → ·C D → =|AB|·|CD|=x 1·x 2=p 24.综上,A B → ·C D →=p 24.四、解答题13.(2020·全国Ⅱ)已知椭圆C 1:x 2a 2+y 2b 2=1(a>b>0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD|=43|AB|.(1)求C 1的离心率;(2)设M 是C 1与C 2的公共点,若|MF|=5,求C 1与C 2的标准方程.【解析】解 (1)由已知可设C 2的方程为y 2=4cx ,其中c =a 2-b 2.不妨设A ,C 在第一象限,由题设得A ,B 的纵坐标分别为b 2a ,-b 2a;C ,D 的纵坐标分别为2c ,-2c ,故|AB|=2b 2a ,|CD|=4c.由|CD|=43|AB|得4c =8b 23a,即3×ca=2-2(ca )2,解得ca =-2(舍去),ca =12.所以C 1的离心率为12.(2)由(1)知a =2c ,b =3c ,故C 1:x 24c 2+y 23c 2=1.设M(x 0,y 0),则x 204c 2+y 203c 2=1,y 20=4cx 0,故x 204c 2+4x 03c=1.①由于C 2的准线为x =-c ,所以|MF|=x 0+c ,而|MF|=5,故x 0=5-c ,代入①得 5-c 24c 2+4 5-c 3c=1,即c 2-2c -3=0,解得c =-1(舍去),c =3.所以C 1的标准方程为x 236+y 227=1,C 2的标准方程为y 2=12x.14.已知点F 为抛物线E :y 2=2px(p>0)的焦点,点A(2,m)在抛物线E 上,且到原点的距离为23.(1)求抛物线E 的方程;(2)已知点G(-1,0),延长AF 交抛物线于点B ,证明:以点F 为圆心且与直线GA 相切的圆必与直线GB 相切.【解析】(1)解 由题意可得Error!解得p =2,所以抛物线E 的方程为y 2=4x.(2)证明 设以点F 为圆心且与直线GA 相切的圆的半径为r.因为点A(2,m)在抛物线E :y 2=4x 上,所以m =±22,由抛物线的对称性,不妨取A(2,22).由A(2,22),F(1,0)可得直线AF 的方程为y =22(x -1),联立Error!得2x 2-5x +2=0,解得x =2或x =12,从而B (12,-2).所以直线GB 的方程为22x +3y +22=0,易知直线GA 的方程为22x -3y +22=0,从而r=|22+22|8+9=4217.因为点F到直线GB的距离d=|22+22|8+9=4217=r,所以以点F为圆心且与直线GA相切的圆必与直线GB相切.。
2020年高考数学(文)二轮复习命题考点串讲系列-专题14 椭圆、双曲线、抛物线(含答案解析)
2020年高考数学(文)二轮复习命题考点串讲系列-专题14 椭圆、双曲线与抛物线1、考情解读1.以客观题形式考查圆锥曲线的标准方程、圆锥曲线的定义、离心率、焦点弦长问题、双曲线的渐近线等,可能会与数列、三角函数、平面向量、不等式结合命题,若与立体几何结合,会在定值、最值、定义角度命题.2.每年必考一个大题,相对较难,且往往为压轴题,具有较高的区分度.平面向量的介入,增加了本部分高考命题的广度与深度,成为近几年高考命题的一大亮点,备受命题者的青睐,本部分还经常结合函数、方程、不等式、数列、三角等知识结合进行综合考查.2、重点知识梳理一、椭圆、双曲线、抛物线的定义及几何性质椭圆双曲线抛物线定义|PF1|+|PF2|=2a(2a>|F1F2|)||PF1|-|PF2||=2a(2a<|F1F2|)定点F和定直线l,点F不在直线l上,P到l距离为d,|PF|=d标准方程焦点在x轴上x2a2+y2b2=1(a>b>0)焦点在x轴上x2a2-y2b2=1(a>0,b>0)焦点在x轴正半轴上y2=2px(p>0)图象几何性质范围|x|≤a,|y|≤b |x|≥a,y∈R x≥0,y∈R 顶点(±a,0),(0,±b)(±a,0)(0,0)对称性关于x轴、y轴和原点对称关于x轴对称焦点(±c,0)⎝⎛⎭⎫p2,0轴 长轴长2a ,短轴长2b 实轴长2a ,虚轴长2b 离心率 e =c a=1-b2a2(0<e<1)e =c a=1+b2a2(e>1)e =1 准线x =-p 2通径 |AB |=2b 2a|AB |=2p渐近线y =±b ax【误区警示】1.求椭圆、双曲线方程时,注意椭圆中c 2=a 2+b 2,双曲线中c 2=a 2-b 2的区别. 2.注意焦点在x 轴上与y 轴上的双曲线的渐近线方程的区别.3.平行于双曲线渐近线的直线与双曲线有且仅有一个交点;平行于抛物线的轴的直线与抛物线有且仅有一个交点.3、高频考点突破考点1 椭圆的定义及其方程例1.【2017课标3,文11】已知椭圆C :22221x y a b +=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A .63B .33C .23D .13【答案】A【变式探究】【2016高考浙江文数】已知椭圆C 1:22x m +y 2=1(m >1)与双曲线C 2:22x n–y 2=1(n >0)的焦点重合,e 1,e 2分别为C 1,C 2的离心率,则( )A .m >n 且e 1e 2>1B .m >n 且e 1e 2<1C .m <n 且e 1e 2>1D .m <n 且e 1e 2<1 【答案】A【解析】由题意知2211m n -=+,即222m n =+,由于m >1,n >0,可得m >n ,又22212222222111111()(1)(1)(1)(1)2m n e e m n m n n n -+=⋅=-+=-++=42422112n n n n++>+ ,故121e e >.故选A .【变式探究】已知椭圆E :x 2a 2+y 2b 2=1(a >b >0)的右焦点为F (3,0),过点F 的直线交E 于A ,B 两点.若AB 的中点坐标为(1,-1),则E 的方程为( )A.x 245+y 236=1 B.x 236+y 227=1 C.x 227+y 218=1 D.x 218+y 29=1【答案】D考点2 椭圆的几何性质例2.【2017浙江,2】椭圆22194x y +=的离心率是A 13B 5C .23D .59【答案】B 【解析】94533e -==B .【变式探究】【2016高考新课标3文数】已知O为坐标原点,F是椭圆C:22221(0) x ya bab+=>>的左焦点,,A B分别为C的左,右顶点.P为C上一点,且PF x⊥轴.过点A的直线l与线段PF 交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为()(A)13(B)12(C)23(D)34【答案】A【变式探究】(2015·北京,19)已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为22,点P(0,1)和点A(m,n)(m≠0)都在椭圆C上,直线P A交x轴于点M.(1)求椭圆C的方程,并求点M的坐标(用m,n表示);(2)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.解(1)由题意得⎩⎪⎨⎪⎧b=1,ca=22,a2=b2+c2解得a2=2,故椭圆C的方程为x22+y2=1.|x M ||x N |.因为x M =m 1-n ,x N =m 1+n,m 22+n 2=1.所以y 2Q =|x M ||x N |=m 21-n 2=2.所以y Q =2或y Q =- 2.故在y 轴上存在点Q ,使得∠OQM =∠ONQ ,点Q 的坐标为(0,2)或 (0,-2).考点3 双曲线的定义及标准方程例3.【2017课表1,文5】已知F 是双曲线C :1322=-y x 的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为A .13B .1 2C .2 3D .3 2【答案】D【解析】由2224c a b =+=得2c =,所以()2,0F ,将2x =代入2213y x -=,得3y =±,所以3PF =,又点A 的坐标是(1,3),故△APF 的面积为()1332122⨯⨯-=,选D .【变式探究】【2016高考天津文数】已知双曲线2224=1x y b-(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点,四边形的ABCD 的面积为2b ,则双曲线的方程为( )(A )22443=1y x -(B )22344=1y x -(C )2224=1x y b -(D )2224=11x y -【答案】D【变式探究】(2015·福建,3)若双曲线E :x 29-y 216=1的左、右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|=3,则|PF 2|等于( )A .11B .9C .5D .3【答案】B【解析】由双曲线定义||PF 2|-|PF 1||=2a ,∵|PF 1|=3,∴P 在左支上,∵a =3,∴|PF 2|-|PF 1|=6,∴|PF 2|=9,故选B.考点4 双曲线的几何性质例4.【2017课标II ,文5】若1a >,则双曲线2221x y a-=的离心率的取值范围是A. (2,)+∞B. (2,2)C. (1,2)D. (1,2) 【答案】C【解析】由题意222222111c a e a a a+===+,因为1a >,所以21112a <+<,则12e <<,故选C.【变式探究】【2016高考新课标1卷】已知方程222213x y m n m n-=+-表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( )(A )()1,3- (B )()1,3- (C )()0,3 (D )()0,3 【答案】A【解析】由题意知:双曲线的焦点在x 轴上,所以2234m n m n ++-=,解得21m =,因为方程22113x y n n -=+-表示双曲线,所以1030n n +>⎧⎨->⎩,解得13n n >-⎧⎨<⎩,所以n 的取值范围是()1,3-,故选A .【变式探究】(2015·新课标全国Ⅱ,11)已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为( )A. 5 B .2 C. 3 D. 2 【答案】D考点5 抛物线的定义及方程例5.【2017山东,文15】在平面直角坐标系xOy 中,双曲线22221(00)x y a b a b-=>>, 的右支与焦点为F 的抛物线22(0)x py p =>交于A ,B 两点,若|AF |+|BF |=4|OF |,则该双曲线的渐近线方程为 .【答案】22y x =±【解析】42A B A B AF BF OF y y p p y y p ∴+=∴++=⇒+=由抛物线方程与双曲线方程联立得2222222102A B y py pb y y p a b b a a-+-=∴+==⇒=因此该双曲线的渐近线方程为22y x =±【变式探究】【2016年高考四川文数】设O 为坐标原点,P 是以F 为焦点的抛物线22(p 0)y px => 上任意一点,M 是线段PF 上的点,且PM =2MF ,则直线OM 的斜率的最大值为( )(A 3 (B )23(C )22 (D )1 【答案】C【解析】设()()22,2,,P pt pt M x y (不妨设0t >),则212,2.,23p FP pt pt FM FP ⎛⎫=-=⎪⎝⎭u u u r u u u u r u u u r Q()222max 22,,21121223633,,122212221,,22332OM OM p p p p p x t x t t k t k pt pt t t t y y t ⎧⎧-=-=+⎪⎪⎪⎪∴∴∴==≤==∴=⎨⎨+⎪⎪+==⎪⎪⎩⎩当且仅当时取等号,,故选C.【变式探究】过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,O 为坐标原点,若|AF |=3,则△AOB 的面积为( )A.22B. 2C.322D .2 2【答案】C考点6 抛物线的几何性质例6.【2016高考新课标1卷】以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E 两点.已知|AB |=42,|DE|=25,则C 的焦点到准线的距离为(A)2 (B)4 (C)6 (D)8 【答案】B【变式探究】(2015·天津,6)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线过点(2,3) ,且双曲线的一个焦点在抛物线y 2=47x 的准线上,则双曲线的方程为( )A.x 221-y 228=1 B.x 228-y 221=1 C.x 23-y 24=1 D.x 24-y 23=1【答案】D【解析】双曲线x 2a 2-y 2b 2=1的渐近线方程为y =±b a x ,又渐近线过点(2,3),所以2ba =3,即2b =3a ,①抛物线y 2=47x 的准线方程为x =-7,由已知,得a 2+b 2=7,即a 2+b 2=7②, 联立①②解得a 2=4,b 2=3,所求双曲线的方程为x 24-y 23=1,选D.4、真题感悟(2014-2017年)1.【2017课表1,文5】已知F 是双曲线C :1322=-y x 的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为A .13B .1 2C .2 3D .3 2【答案】D2.【2017课标II ,文5】若1a >,则双曲线2221x y a-=的离心率的取值范围是A. )+∞B. 2)C.D. (1,2) 【答案】C【解析】由题意222222111c a e a a a+===+,因为1a >,所以21112a <+<,则1e <<故选C.3.【2017浙江,2】椭圆22194x y +=的离心率是A B C .23D .59【答案】B【解析】e ==B .4.【2017课标II ,文12】过抛物线2:4C y x =的焦点F ,且斜率为3的直线交C 于点M (M 在x 轴上方),l 为C 的准线,点N 在l 上且MN l ⊥,则M 到直线NF 的距离为A.5B.22C. 23D. 33 【答案】C5.【2017课标1,文12】设A 、B 是椭圆C :2213x y m +=长轴的两个端点,若C 上存在点M 满足∠AMB =120°,则m 的取值范围是A .(0,1][9,)+∞UB .(0,3][9,)+∞UC .(0,1][4,)+∞UD .(0,3][4,)+∞U【答案】A6.【2017课标3,文11】已知椭圆C :22221x y a b +=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A 6B .3 C 2D .13【答案】A【解析】以线段12A A 为直径的圆的圆心为坐标原点()0,0,半径为r a =,圆的方程为222x y a +=,直线20bx ay ab -+=与圆相切,所以圆心到直线的距离等于半径,即22d a a b==+,整理可得223a b =,即()2223,a a c =-即2223a c =,从而22223c e a ==,则椭圆的离心率c e a ===故选A.7.【2017天津,文5】已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为(A )221412x y -=(B )221124x y -=(C )2213x y -=(D )2213y x -=【答案】D8.【2017北京,文10】若双曲线221y x m-=m =__________.【答案】2【解析】221,a b m == ,所以1c a ==,解得2m = . 9.【2017山东,文15】在平面直角坐标系xOy 中,双曲线22221(00)x y a b a b-=>>, 的右支与焦点为F 的抛物线22(0)x py p =>交于A ,B 两点,若|AF |+|BF |=4|OF |,则该双曲线的渐近线方程为 .【答案】y x = 【解析】42A B A B AF BF OF y y p p y y p ∴+=∴++=⇒+=由抛物线方程与双曲线方程联立得222222210A B y py pb y y p a b a a-+-=∴+==⇒=因此该双曲线的渐近线方程为2y x =±10.【2017课标3,文14】双曲线22219x y a -=(a >0)的一条渐近线方程为35y x =,则a = .【答案】5【解析】由双曲线的标准方程可得渐近线方程为:3y x a=± ,结合题意可得:5a =.学%科网11.【2017江苏,8】 在平面直角坐标系xOy 中,双曲线2213x y -=的右准线与它的两条渐近线分别交于点P ,Q ,其焦点是12,F F ,则四边形12F PF Q 的面积是 .【答案】2312.【2017课标1,文20】设A ,B 为曲线C :y =24x 上两点,A 与B 的横坐标之和为4.(1)求直线AB 的斜率;(2)设M 为曲线C 上一点,C 在M 处的切线与直线AB 平行,且AM ⊥BM ,求直线AB 的方程.【答案】(1)1; (2)7y x =+. 【解析】解:(1)设A (x 1,y 1),B (x 2,y 2),则12x x ≠, 2114x y =, 2224x y =,x 1+x 2=4,于是直线AB 的斜率12121214y y x x k x x -+===-. (2)由24x y =,得'2xy =.设M (x 3,y 3),由题设知312x =,解得32x =,于是M (2,1). 设直线AB 的方程为y x m =+,故线段AB 的中点为N (2,2+m ),|MN |=|m +1|.将y x m =+代入24x y =得2440x x m --=.当()1610m ∆=+>,即1m >-时, 1,2221x m =±+从而()12||=2421AB x m -=+. 由题设知2AB MN =,即()()42121m m +=+,解得7m =. 所以直线AB 的方程为7y x =+.13.【2017课标II ,文20】设O 为坐标原点,动点M 在椭圆C 上,过M作x 轴的垂线,垂足为N ,点P 满足2NP NM =u u u r u u u u r(1)求点P 的轨迹方程;(2)设点Q 在直线3x =-上,且1OP PQ ⋅=u u u r u u u r.证明过点P 且垂直于OQ 的直线l 过C 的左焦点F.【答案】(1)(2)见解析14.【2017山东,文21】(本小题满分14分)在平面直角坐标系xOy 中,已知椭圆C :22221x y a b+=(a >b >0)的离心率为22,椭圆C 截直线y =1所得线段的长度为22.(Ⅰ)求椭圆C 的方程;(Ⅱ)动直线l :y =kx +m (m ≠0)交椭圆C 于A ,B 两点,交y 轴于点M .点N 是M 关于O 的对称点,圆N 的半径为|NO |. 设D 为AB 的中点,DE ,DF 与圆N 分别相切于点E ,F ,求∠EDF 的最小值.【答案】(Ⅰ) 22142x y +=.(II) 3π. 【解析】因为NF m =, 所以()()()2422222224318312121k k ND k NFkk+++==+++.令283,3t k t =+≥,故21214t k ++=, 所以()222161611112ND tNFt t t=+=++++ . 令1y t t =+,所以211y t'=-.当3t ≥时, 0y '>,从而1y t t=+在[)3,+∞上单调递增,因此1103t t +≥,等号当且仅当3t =时成立,此时0k =,所以22134ND NF≤+=,由(*)得 22m -<<且0m ≠.故12NFND ≥,设2EDF θ∠=,则1sin 2NF ND θ=≥ ,所以θ的最小值为π6,从而EDF ∠的最小值为π3,此时直线L 的斜率是0. 综上所述:当0k =, ()()2,00,2m ∈-⋃时, EDF ∠取到最小值π3.15.【2017北京,文19】已知椭圆C 的两个顶点分别为A (−2,0),B(2,0),焦点在x 轴上,离心率为3. (Ⅰ)求椭圆C 的方程;(Ⅱ)点D 为x 轴上一点,过D 作x 轴的垂线交椭圆C 于不同的两点M ,N ,过D 作AM 的垂线交BN 于点E .求证:△BDE 与△BDN 的面积之比为4:5.【答案】(Ⅰ)2214x y += ;(Ⅱ)详见解析.16.【2017江苏,17】 如图,在平面直角坐标系xOy 中,椭圆2222:1(0)x y E a b a b+=>>的左、右焦点分别为1F , 2F ,离心率为12,两准线之间的距离为8.点P 在椭圆E 上,且位于第一象限,过点1F 作 直线1PF 的垂线1l ,过点2F 作直线2PF 的垂线2l .(1)求椭圆E 的标准方程;(2)若直线E 的交点Q 在椭圆E 上,求点P 的坐标.【答案】(1)22143x y +=(2)4737) 【解析】1. 【2016高考新课标1卷】已知方程222213x y m n m n-=+-表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( )(A )()1,3- (B )(3- (C )()0,3 (D )(3 【答案】AF 1 ⋅O⋅F 2xy(第17题)【解析】由题意知:双曲线的焦点在x 轴上,所以2234m n m n ++-=,解得21m =,因为方程22113x y n n -=+-表示双曲线,所以1030n n +>⎧⎨->⎩,解得13n n >-⎧⎨<⎩,所以n 的取值范围是()1,3-,故选A .2.【2016年高考四川文数】设O 为坐标原点,P 是以F 为焦点的抛物线22(p 0)y px => 上任意一点,M 是线段PF 上的点,且PM =2MF ,则直线OM 的斜率的最大值为( )(A(B )23(C(D )1 【答案】C3.【2016高考新课标2文数】已知12,F F 是双曲线2222:1x y E a b-=的左,右焦点,点M 在E上,1MF 与x 轴垂直,211sin 3MF F ∠=,则E 的离心率为( )(A(B )32(C(D )2【答案】A【解析】因为1MF 垂直于x 轴,所以2212,2b b MF MF a a a ==+,因为211sin 3MF F ∠=,即2122132b MF ab MF a a==+,化简得b a=,故双曲线离心率e ==.选A. 4.【2016高考浙江文数】已知椭圆C 1:22x m +y 2=1(m >1)与双曲线C 2:22x n–y 2=1(n >0)的焦点重合,e 1,e 2分别为C 1,C 2的离心率,则( )A .m >n 且e 1e 2>1B .m >n 且e 1e 2<1C .m <n 且e 1e 2>1D .m <n 且e 1e 2<1 【答案】A5.【2016高考浙江文数】若抛物线y 2=4x 上的点M 到焦点的距离为10,则M 到y 轴的距离是_______.【答案】9【解析】1109M M x x +=⇒=6.【2016高考新课标1卷】以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E 两点.已知|AB |=42,|DE|=25,则C 的焦点到准线的距离为(A)2 (B)4 (C)6 (D)8 【答案】B【解析】如图,设抛物线方程为22y px =,,AB DE 交x 轴于,C F 点,则22AC =,即A 点纵坐标为22,则A 点横坐标为4p ,即4OC p=,由勾股定理知2222DF OF DO r +==, 2222AC OC AO r +==,即22224(5)()(22)()2p p+=+,解得4p =,即C 的焦点到准线的距离为4,故选B.7.【2016高考新课标3文数】已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,,A B 分别为C 的左,右顶点.P 为C 上一点,且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E .若直线BM 经过OE 的中点,则C 的离心率为( )(A)13(B )12(C )23(D )34【答案】A8.【2016高考天津文数】已知双曲线2224=1x y b-(b >0),以原点为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点,四边形的ABCD 的面积为2b ,则双曲线的方程为( )(A )22443=1y x -(B )22344=1y x -(C )2224=1x y b -(D )2224=11x y -【答案】D【解析】根据对称性,不妨设A 在第一象限,(,)A x y ,∴22224444224x x y b bb y x y b ⎧=⎧+=⎪+⎪⎪⇒⎨⎨=⎪⎪=⋅⎩⎪+⎩, ∴221612422b b xy b b =⋅=⇒=+,故双曲线的方程为221412x y -=,故选D. 9.【2016高考江苏卷】如图,在平面直角坐标系xOy 中,F 是椭圆22221()x y a b a b+=>>0 的右焦点,直线2by =与椭圆交于,B C 两点,且90BFC ∠=o ,则该椭圆的离心率是 .【答案】6 【解析】由题意得33(,),C(,),22b b B a a -,因此2222236()()032.2b c a c a e -+=⇒=⇒= 10.【2016高考天津文数】设抛物线222x pt y pt⎧=⎨=⎩,(t 为参数,p >0)的焦点为F ,准线为l .过抛物线上一点A 作l 的垂线,垂足为B .设C (72p ,0),AF 与BC 相交于点E .若|CF |=2|AF |,且△ACE 的面积为p 的值为_________.11.【2016高考山东文数】已知双曲线E :22221x y a b -= (a >0,b >0),若矩形ABCD的四个顶点在E 上,AB ,CD 的中点为E 的两个焦点,且2|AB |=3|BC |,则E 的离心率是______.【答案】2【解析】假设点A 在第一象限,点B 在第二象限,则2b A(c,)a ,2b B(c,)a -,所以22b |AB |a =,|BC |2c =,由2AB 3BC =,222c a b =+得离心率e 2=或1e 2=-(舍去),所以E 的离心率为2.12.【2016年高考北京文数】双曲线22221x y a b-=(0a >,0b >)的渐近线为正方形OABC 的边OA ,OC 所在的直线,点B 为该双曲线的焦点,若正方形OABC 的边长为2,则a =_______________.【答案】213.【2016高考江苏卷】在平面直角坐标系xOy 中,双曲线22173x y -=的焦距是__________.【答案】【解析】222227,3,7310,2a b c a b c c ==∴=+=+=∴=∴=Q 焦距为2c故答案应填:14.【2016高考山东文数】(本小题满分14分)平面直角坐标系xOy 中,椭圆C :()222210x y a b a b+=>> E :22x y =的焦点F 是C 的一个顶点(I )求椭圆C 的方程;(II )设P 是E 上的动点,且位于第一象限,E 在点P 处的切线l 与C 交与不同的两点A ,B ,线段AB 的中点为D ,直线OD 与过P 且垂直于x 轴的直线交于点M .(i )求证:点M 在定直线上;(ii )直线l 与y 轴交于点G ,记PFG △的面积为1S ,PDM △的面积为2S,求12S S的最大值及取得最大值时点P 的坐标.【答案】(Ⅰ)1422=+y x ;(Ⅱ)(i )见解析;(ii )12S S 的最大值为49,此时点P 的坐标为)41,22(【解析】 令122+=m t ,则211)1)(12(2221++-=+-=tt t t t S S , 当211=t ,即2=t 时,21S S 取得最大值49,此时22=m ,满足0∆>,所以点P 的坐标为)41,22(,因此12SS 的最大值为49,此时点P 的坐标为)41,22(. 15.【2016高考江苏卷】(本小题满分10分)如图,在平面直角坐标系xOy 中,已知直线:20l x y --=,抛物线2:y 2(0)C px p => (1)若直线l 过抛物线C 的焦点,求抛物线C 的方程; (2)已知抛物线C 上存在关于直线l 对称的相异两点P 和Q . ①求证:线段PQ 的中点坐标为(2,).p p --;②求p 的取值范围.【答案】(1)x y 82=(2)①详见解析,②)34,0(【解析】因此,线段PQ 的中点坐标为(2,).p p -- ②因为(2,).M p p --在直线y x b =-+上 所以(2)p p b -=--+,即22.b p =-由①知20p b +>,于是2(22)0p p +->,所以4.3p <因此p 的取值范围为4(0,).316.【2016高考天津文数】(本小题满分14分)设椭圆13222=+y a x (3>a )的右焦点为F ,右顶点为A ,已知||3||1||1FA e OA OF =+,其中O 为原点,e 为椭圆的离心率.(Ⅰ)求椭圆的方程;(Ⅱ)设过点A 的直线l 与椭圆交于点B (B 不在x 轴上),垂直于l 的直线与l 交于点M ,与y 轴交于点H ,若HF BF ⊥,且MOA MAO ∠≤∠,求直线的l 斜率的取值范围.【答案】(Ⅰ)22143x y +=(Ⅱ)),46[]46,(+∞--∞Y 【解析】(Ⅰ)解:设(,0)F c ,由113||||||e OF OA FA +=,即113()c c a a a c +=-,可得2223a c c -=,又2223a c b -==,所以21c =,因此24a =,所以椭圆的方程为22143x y +=.因此直线MH 的方程为kk x k y 124912-+-=.设),(M M y x M ,由方程组⎪⎩⎪⎨⎧-=-+-=)2(124912x k y k k x k y 消去y ,解得)1(1292022++=k k x M . 在MAO △中,||||MO MA MAO MOA ≤⇔∠≤∠,即2222)2(M M M M y x y x +≤+-,化简得1≥M x ,即1)1(1292022≥++k k ,解得46-≤k 或46≥k . 所以,直线l 的斜率的取值范围为),46[]46,(+∞--∞Y . 17.【2016高考新课标3文数】已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于,A B 两点,交C 的准线于P Q ,两点.(I )若F 在线段AB 上,R 是PQ 的中点,证明AR FQ P ;(II )若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程. 【答案】(Ⅰ)见解析;(Ⅱ)21y x =-.【解析】由题设)0,21(F .设b y l a y l ==:,:21,则0≠ab ,且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---. 记过B A ,两点的直线为l ,则l 的方程为0)(2=++-ab y b a x . .....3分 (Ⅰ)由于F 在线段AB 上,故01=+ab . 记AR 的斜率为1k ,FQ 的斜率为2k ,则222111k b aaba ab a b a a b a k =-=-==--=+-=, 所以AR FQ P . ......5分 (Ⅱ)设l 与x 轴的交点为)0,(1x D , 则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211ba x ab -=--,所以01=x (舍去),11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与x 轴不垂直时,由DE AB k k =可得)1(12≠-=+x x y b a .而yba=+2,所以)1(12≠-=xxy.当AB与x轴垂直时,E与D重合,所以,所求轨迹方程为12-=xy. ....12分18.【2016高考浙江文数】(本题满分15分)如图,设椭圆2221xya+=(a>1).(I)求直线y=kx+1被椭圆截得的线段长(用a、k表示);(II)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.【答案】(I)2222211a kka k⋅++;(II)22e<≤.【解析】(Ⅰ)设直线1y kx=+被椭圆截得的线段为AP,由22211y kxxya=+⎧⎪⎨+=⎪⎩得()2222120a k x a kx++=,故1x=,222221a kxa k=-+.因此22212222111a kAP k x x ka k=+-=⋅++.(Ⅱ)假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q,满足AP AQ=.记直线AP,AQ的斜率分别为1k,2k,且1k,2k>,12k k≠.由(Ⅰ)知,22 11121a k kAP+=,2222221a k kAQ+=,故22221122122121a k k a k k++=,所以()()22222222121212120k k k k a a k k⎡⎤-+++-=⎣⎦.由于12k k≠,1k,2k>得()2222221212120k k a a k k+++-=,19.【2016高考新课标2文数】已知椭圆:E2213x yt+=的焦点在x轴上,A是E的左顶点,斜率为(0)k k>的直线交E于,A M两点,点N在E上,MA NA⊥.(Ⅰ)当4,||||t AM AN==时,求AMN∆的面积;(Ⅱ)当2AM AN=时,求k的取值范围.【答案】(Ⅰ)14449;(Ⅱ))32,2.【解析】(Ⅰ)设()11,M x y,则由题意知1y>,当4t=时,E的方程为22143x y+=,()2,0A-.由已知及椭圆的对称性知,直线AM的倾斜角为4π.因此直线AM的方程为2y x=+.20.【2016年高考北京文数】(本小题14分)已知椭圆C:22221+= x ya b (0a b>>)的离心率为3,(,0)A a,(0,)B b,(0,0)O,OAB∆的面积为1.(1)求椭圆C的方程;(2)设P的椭圆C上一点,直线PA与y轴交于点M,直线PB与x轴交于点N.求证:BMAN⋅为定值.【答案】(1)2214xy+=;(2)详见解析.令0=y ,得100--=y x x N ,从而12200-+=-=y x x AN N . 所以221120000-+⋅-+=⋅x y y x BM AN228844224844400000000000000002020+--+--=+--+--++=y x y x y x y x y x y x y x y x y x4=.当00=x 时,10-=y ,,2,2==AN BM 所以4=⋅BM AN . 综上,BM AN ⋅为定值.21.【2016年高考四川文数】(本小题满分13分)已知椭圆E:22221(0) x ya ba b+=>>的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线:3l y x=-+与椭圆E有且只有一个公共点T.(Ⅰ)求椭圆E的方程及点T的坐标;(Ⅱ)设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l 交于点P.证明:存在常数λ,使得2PT PA PBλ=⋅,并求λ的值.【答案】(Ⅰ)22163x y+=,点T坐标为(2,1);(Ⅱ)45λ=.所以P点坐标为(222,133m m-+),2289PT m=.设点A,B的坐标分别为1122(,)(,)A x yB x y,.由方程组2216312x yy x m⎧+=⎪⎪⎨⎪=+⎪⎩,,可得2234(412)0x mx m++-=.②方程②的判别式为2=16(92)m ∆-,由>0∆,解得323222m -<<. 由②得212124412=,33m m x x x x -+-=. 所以221112252(2)(1)23323m m mPA x y x =--++-=-- , 同理252223m PB x =--, 所以12522(2)(2)433m mPA PB x x ⋅=---- 21212522(2)(2)()433m mx x x x =---++ 225224412(2)(2)()43333m m m m -=----+ 2109m =.故存在常数45λ=,使得2PT PA PB λ=⋅. 22. 【2016高考上海文数】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.双曲线2221(0)y x b b-=>的左、右焦点分别为12F F 、,直线l 过2F 且与双曲线交于A B、两点。
(寒假总动员)2019年高三数学寒假作业 专题14 椭圆、双曲线、抛物线(练)(含解析)
(寒假总动员)2015年高三数学寒假作业专题14 椭圆、双曲线、抛物线(练)(含解析)1.已知椭圆)0(1:2222>>=+babyaxE的右焦点为)0,3(F,过点F的直线交E于A,B两点.若AB的中点坐标为)1,1(-,则E的方程为()A.1364522=+yxB.1274522=+yxC.1182722=+yxD.191822=+yx2.定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线1:C y x a=+到直线:20l x y-=的距离为5,则实数a的值为()A.3或3-B.2或3-C.2D.3-考点:平行直线,直线与曲线相切,一元二次方程的根的判别式.3.已知)0,(c F 是双曲线)0,0(1:2222>>=-b a b y a x C 的右焦点,若双曲线C 的渐近线与圆4)(:222c y c x M =+-相切,则双曲线的离心率为( )A.332 B.2 C.3 D. 2234.已知双曲线的顶点与焦点分别是椭圆)0(12222>>=+b a b y a x 的焦点和顶点,若双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,则椭圆的离心率为( )A. 31B.21C.33D.225.已知两个正数a ,b 的等差中项是92,一个等比中项是25,且a b >,则抛物线2b y xa =-的焦点坐标为( )A.5(,0)16-B.1(,0)5-C.1(,0)5D.2(,0)5-二、填空题6.与抛物线x y 82=相切的倾斜角为135 的直线l 与x 轴和y 轴的焦点分别为A 和B ,记过A 、B 两点的最小圆为C .(Ⅰ)则圆C 的方程是 ;(Ⅱ)圆C 截抛物线x y 82=的准线所得的弦长为. 7.抛物线x y 82=的焦点为F ,点),(y x 为该抛物线上的动点,,又已知点)0,2(-A ,则||||PF PA 的取值范围是 .三.解答题8.已知椭圆)0(1:2222>>=+b a b y a x E 的右焦点F ,y 轴右侧的点A 在椭圆E 上运动,直线MA 与圆222:b y x C =+相切于点),(00y x M .(Ⅰ)求直线MA 的方程; (Ⅱ)求证:||||AM AF +为定值.。
2020年高考数学(文科)二轮复习押题特训专题14 椭圆、双曲线与抛物线(含答案解析)
2020年高考数学(文科)二轮复习押题特训专题14 椭圆、双曲线与抛物线1.已知双曲线x2a2-y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,以F1,F2为直径的圆与双曲线渐近线的一个交点为(3,4),则此双曲线的方程为()A.x216-y29=1 B.x23-y24=1C.x29-y216=1 D.x24-y23=1【答案】C2.椭圆x212+y23=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的()A.7倍B.5倍C.4倍D.3倍【答案】A【解析】由题设知F1(-3,0),F2(3,0),如图,∵线段PF1的中点M在y轴上,∴可设P(3,b),把P(3,b)代入椭圆x212+y23=1,得b2=34.∴|PF1|=36+34=732,|PF2|=0+34=32.∴|PF1||PF2|=73232=7.故选A.3.已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|=( )A .2B .4C .6D .8 【答案】B4.设F 1,F 2分别是双曲线C :x 2a 2-y 2b 2=1的左、右焦点,点P ⎝ ⎛⎭⎪⎫62,22在此双曲线上,且PF 1⊥PF 2,则双曲线C 的离心率等于( )A.22B. 2C. 3D.62 【答案】B【解析】根据已知条件得: ⎩⎪⎨⎪⎧32a 2-12b2=1,⎝ ⎛⎭⎪⎫62+c 2+12+⎝ ⎛⎭⎪⎫62-c 2+12=4c 2, 即⎩⎪⎨⎪⎧3a 2-1c 2-a 2=2,c 2=2, ∴解得a =1,c = 2.∴双曲线C 的离心率e =ca = 2.故选B.5.已知抛物线C 的顶点是椭圆x 24+y 23=1的中心,焦点与该椭圆的右焦点F 2重合,若抛物线C 与该椭圆在第一象限的交点为P ,椭圆的左焦点为F 1,则|PF 1|=( )A.23B.73C.53 D .2 【答案】B【解析】由椭圆的方程可得a 2=4,b 2=3,∴c =a 2-b 2=1,故椭圆的右焦点F 2为(1,0),即抛物线C 的焦点为(1,0),∴p2=1,∴p =2,∴2p =4,∴抛物线C 的方程为y 2=4x ,联立⎩⎪⎨⎪⎧x 24+y 23=1,y 2=4x .解得⎩⎪⎨⎪⎧x =23,y =263或⎩⎪⎨⎪⎧x =23,y =-263,∵P 为第一象限的点,∴P ⎝ ⎛⎭⎪⎫23,263, ∴|PF 2|=1+23=53,∴|PF 1|=2a -|PF 2|=4-53=73,故选B.6.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左顶点与抛物线y 2=2px (p >0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )A .2 3B .2 5C .4 3D .4 5 【答案】B7.抛物线y 2=4x 的焦点为F ,准线为l ,经过F 且斜率为3的直线与抛物线在x 轴上方的部分相交于点A ,AK ⊥l ,垂足为K ,则△AKF 的面积是( )A .4B .3 3C .4 3D .8 【答案】C【解析】∵y 2=4x ,∴F (1,0),l :x =-1,过焦点F 且斜率为3的直线l 1:y =3(x -1),与y 2=4x 联立,解得x =3或x =13(舍),故A (3,23),∴AK =4,∴S △AKF =12×4×23=4 3.故选C.8.已知直线y =k (x +1)(k >0)与抛物线C :y 2=4x 相交于A ,B 两点,F 为抛物线C 的焦点,若||F A =2||FB ,则k =( )A.13B.223C.23D.23 【答案】B【解析】设A ,B 的纵坐标分别为y 1,y 2, 由||F A =2||FB 得y 1=2y 2(如图).9.设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),右焦点为F (c ,0)(c >0),方程ax 2+bx -c =0的两实根分别为x 1,x 2,则P (x 1,x 2)( )A .必在圆x 2+y 2=2内B .必在圆x 2+y 2=2外C .必在圆x 2+y 2=1外D .必在圆x 2+y 2=1与圆x 2+y 2=2形成的圆环之间 【答案】D【解析】椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),右焦点为F (c ,0)(c >0),方程ax 2+bx -c =0的两实根分别为x 1和x 2,则x 1+x 2=-b a ,x 1·x 2=-ca ,x 21+x 22=(x 1+x 2)2-2x 1·x 2=b 2a2+2ac a2>a 2+c 2a2=1+e 2,因为0<e <1, 即0<e 2<1. 所以1<e 2+1<2,所以x 21+x 22>1,又b 2a 2+2ac a 2<b 2+a 2+c 2a 2=2,所以1<x 21+x 22<2,即点P 在圆x 2+y 2=1与x 2+y 2=2形成的圆环之间.故选D.10.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,右顶点为A ,抛物线y 2=158(a +c )x 与椭圆交于B ,C 两点,若四边形ABFC 是菱形,则椭圆的离心率等于( )A.158B.415C.23D.12 【答案】D11.过曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的左焦点F 1作曲线C 2:x 2+y 2=a 2的切线,设切点为M ,直线F 1M 交曲线C 3:y 2=2px (p >0)于点N ,其中曲线C 1与C 3有一个共同的焦点,若|MF 1|=|MN |,则曲线C 1的离心率为( )A. 5B.5-1C.5+1D.5+12 【答案】D12.已知F 1,F 2分别是双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,过点F 2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ,若点M 在以线段F 1F 2为直径的圆外,则双曲线离心率的取值范围是( )A .(1,2)B .(2,3)C .(3,2)D .(2,+∞) 【答案】D 【解析】如图所示,过点F 2(c ,0)且与渐近线y =b a x 平行的直线为y =b a (x -c ),与另一条渐近线y =-ba x 联立得⎩⎪⎨⎪⎧y =b a (x -c ),y =-b a x ,解得⎩⎪⎨⎪⎧x =c 2,y =-bc2a ,即点M ⎝ ⎛⎭⎪⎫c2,-bc 2a . ∴|OM |=⎝ ⎛⎭⎪⎫c 22+⎝ ⎛⎭⎪⎫-bc 2a 2 =c21+⎝ ⎛⎭⎪⎫b a 2. ∵点M 在以线段F 1F 2为直径的圆外, ∴|OM |>c , 即c 21+⎝ ⎛⎭⎪⎫b a 2>c , 得1+⎝ ⎛⎭⎪⎫b a 2>2. ∴双曲线离心率e =ca =1+⎝ ⎛⎭⎪⎫b a 2>2. 故双曲线离心率的取值范围是(2,+∞).故选D.13.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F ,由F 向其渐近线引垂线,垂足为P ,若线段PF 的中点在此双曲线上,则此双曲线的离心率为________.【答案】 214.已知F 1,F 2分别是双曲线3x 2-y 2=3a 2(a >0)的左、右焦点,P 是抛物线y 2=8ax 与双曲线的一个交点,若|PF 1|+|PF 2|=12,则抛物线的准线方程为________.【答案】x =-2【解析】将双曲线方程化为标准方程得x 2a 2-y 23a 2=1,抛物线的准线为x =-2a , 联立⎩⎪⎨⎪⎧x 2a 2-y 23a 2=1,y 2=8ax ,解得x =3a ,即点P 的横坐标为3a . 而由⎩⎨⎧|PF 1|+|PF 2|=12,|PF 1|-|PF 2|=2a解得|PF 2|=6-a ,∴|PF 2|=3a +2a =6-a ,解得a =1, ∴抛物线的准线方程为x =-2.15.设椭圆中心在坐标原点,A (2,0),B (0,1)是它的两个顶点,直线y =kx (k >0)与线段AB 相交于点D ,与椭圆相交于E ,F 两点.若ED→=6DF →,则k 的值为________.【答案】23或3816.在平面直角坐标系xOy 中,已知点A 在椭圆x 225+y 29=1上,点P 满足AP →=(λ-1)OA →(λ∈R ),且OA →·OP→=72,则线段OP 在x 轴上的投影长度的最大值为________.【答案】1517.已知抛物线C :y 2=2px (p >0)的焦点为F (1,0),抛物线E :x 2=2py 的焦点为M . (1)若过点M 的直线l 与抛物线C 有且只有一个交点,求直线l 的方程; (2)若直线MF 与抛物线C 交于A ,B 两点,求△OAB 的面积.解:(1)由题意得抛物线C :y 2=2px (p >0)的焦点为F (1,0),抛物线E :x 2=2py 的焦点为M ,所以p =2,M (0,1),①当直线l 的斜率不存在时,x =0,满足题意;②当直线l 的斜率存在时,设方程为y =kx +1,代入y 2=4x ,得k 2x 2+(2k -4)x +1=0,当k =0时,x =14,满足题意,直线l 的方程为y =1;当k ≠0时,Δ=(2k -4)2-4k 2=0,所以k =1,方程为y =x +1,综上可得,直线l 的方程为x =0或y =1或y =x +1.(2)结合(1)知抛物线C 的方程为y 2=4x ,直线MF 的方程为y =-x +1, 联立⎩⎨⎧y 2=4x ,y =-x +1,得y 2+4y -4=0,设A (x 1,y 1),B (x 2,y 2), 则y 1+y 2=-4,y 1y 2=-4, 所以|y 1-y 2|=42,所以S △OAB =12|OF ||y 1-y 2|=2 2.18.如图,已知椭圆C 的中心在原点,其一个焦点与抛物线y 2=46x 的焦点相同,又椭圆C 上有一点M (2,1),直线l 平行于OM 且与椭圆C 交于A ,B 两点,连接MA ,MB .(1)求椭圆C 的方程;(2)当MA ,MB 与x 轴所构成的三角形是以x 轴上所在线段为底边的等腰三角形时,求直线l 在y 轴上截距的取值范围.联立⎩⎪⎨⎪⎧y =12x +m ,x 28+y 22=1消去y 得x 2+2mx +2m 2-4=0,∴Δ=(2m )2-4(2m 2-4)=4(4-m 2)>0, ∴m 的取值范围是{m |-2<m <2,且m ≠0}, 设MA ,MB 的斜率分别为k 1,k 2, ∴k 1+k 2=0,则A (x 1,y 1),B (x 2,y 2),则k 1=y 1-1x 1-2,k 2=y 2-1x 2-2,x 1x 2=2m 2-4,x 1+x 2=-2m , ∴k 1+k 2=y 1-1x 1-2+y 2-1x 2-2=(y 1-1)(x 2-2)+(y 2-1)(x 1-2)(x 1-2)(x 2-2)=⎝ ⎛⎭⎪⎫12x 1+m -1(x 2-2)+⎝ ⎛⎭⎪⎫12x 2+m -1(x 1-2)(x 1-2)(x 2-2)=x 1x 2+(m -2)(x 1+x 2)-4(m -1)(x 1-2)(x 2-2)=2m 2-4-2m 2+4m -4m +4(x 1-2)(x 2-2)=0,故MA ,MB 与x 轴始终围成等腰三角形时,∴直线l 在y 轴上的截距m 的取值范围是{m |-2<m <2,且m ≠0}.19.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点分别为F 1(-1,0),F 2(1,0),且椭圆C 经过点P ⎝ ⎛⎭⎪⎫43,13.(1)求椭圆C 的离心率;(2)设过点A (0,2)的直线l 与椭圆C 交于M ,N 两点,点Q 是线段MN 上的点,且2|AQ |2=1|AM |2+1|AN |2,求点Q 的轨迹方程.因为M ,N 在直线l 上,可设点M ,N 的坐标分别为(x 1,kx 1+2),(x 2,kx 2+2),则|AM |2=(1+k 2)x 21,|AN |2=(1+k 2)x 22.又|AQ |2=x 2+(y -2)2=(1+k 2)x 2. 由2|AQ |2=1|AM |2+1|AN |2,得2(1+k 2)x 2=1(1+k 2)x 21+1(1+k 2)x 22, 即2x 2=1x 21+1x 22=(x 1+x 2)2-2x 1x 2x 21x 22.① 将y =kx +2代入x 22+y 2=1中,得(2k 2+1)x 2+8kx +6=0.②由Δ=(8k )2-4×(2k 2+1)×6>0,得k 2>32.20.如图,已知M (x 0,y 0)是椭圆C :x 26+y 23=1上的任一点,从原点O 向圆M :(x -x 0)2+(y -y 0)2=2作两条切线,分别交椭圆于点P ,Q .(1)若直线OP ,OQ 的斜率存在,并记为k 1,k 2,求证:k 1k 2为定值;(2)试问|OP |2+|OQ |2是否为定值?若是,求出该值;若不是,说明理由.联立⎩⎪⎨⎪⎧y =k 1x ,x 26+y 23=1,解得⎩⎪⎨⎪⎧x 21=61+2k 21,y 21=6k 211+2k 21,所以x 21+y 21=6(1+k 21)1+2k 21,同理得x 22+y 22=6(1+k 22)1+2k 22,又因为k 1k 2=-12,所以|OP |2+|OQ |2=x 21+y 21+x 22+y 22 =6(1+k 21)1+2k 21+6(1+k 22)1+2k 22 =6(1+k 21)1+2k 21+6⎣⎢⎡⎦⎥⎤1+⎝ ⎛⎭⎪⎫-12k 121+2⎝ ⎛⎭⎪⎫-12k 12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(寒假总动员)2020年高三数学寒假作业专题14 椭圆、双曲线、抛物线(背)
1.椭圆的定义
在平面内与两定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
2.椭圆的标准方程和几何性质
标准方程x2
a2+
y2
b2=1(a>b>0)
y2
a2+
x2
b2=1
(a>b>0)
图形
性质范围
-a≤x≤a
-b≤y≤b
-b≤x≤b
-a≤y≤a
对称性对称轴:坐标轴;对称中心:原点
顶点
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a)
B1(-b,0),B2(b,0)
轴长轴A1A2的长为2a;短轴B1B2的长为2b
焦距|F1F2|=2c
离心率e=
c
a∈(0,1)
3.双曲线的定义
平面内动点P与两个定点F1,F2(|F1F2|=2c>0)的距离之差的绝对值为常数2a(2a<2c),则点P的轨迹叫双曲线.这两个定点叫双曲线的焦点,两焦点间的距离叫焦距.
4.双曲线的标准方程和几何性质
标准方程x2
a2-
y2
b2=1(a>0,b>0)
y2
a2-
x2
b2=1(a>0,b>0)
性质范围x≥a或x≤-a,y∈R x∈R,y≤-a或y≥a
对称性对称轴:坐标轴;对称中心:原点
顶点A1(-a,0),A2(a,0) A1(0,-a),A2(0,a)
渐近线y=±
b
a x y=±
a
b x
离心率e=
c
a,e∈(1,+∞),其中c=a2+b2
实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫做双曲线的虚轴,
它的长|B1B2|=2b;a叫做双曲线的半实轴长,b叫做双曲线的半虚轴长
a,b,c的关
系
c2=a2+b2(c>a>0,c>b>0)
5.抛物线的定义
(1)平面内与一个定点F和一条定直线l(F∉l)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
(2)其数学表达式:|MF|=d(其中d为点M到准线的距离).
图形
标准方程y2=2px (p>0)
y2=-2p
x(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
p的几何意义:焦点F到准线l的距离
续表
性质顶点O(0,0)
对称轴y=0 x=0
焦点F⎝⎛⎭⎫
p
2,0F⎝
⎛
⎭
⎫
-
p
2,0F⎝
⎛
⎭
⎫
0,
p
2F⎝
⎛
⎭
⎫
0,-
p
2离心率e=1
准线方程x=-
p
2x=
p
2y=-
p
2y=
p
2
范围x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R 开口方向向右向左向上向下。
