结构力学第二章几何组成分析(典型例题)
02结构的几何组成分析--习题

静定结构 无多余约束几何不变体系
二、无多余约束几何不变体系的组成规则有三个: 无多余约束几何不变体系的组成规则有三个:
①三刚片规则 三刚片用不在一直线上的三个铰两两相连。 三刚片用不在一直线上的三个铰两两相连。 ②两刚片规则 两刚片用一个铰和一根不通过此铰的链杆或 不全平行也不交于一点的三根链杆连接。 不全平行也不交于一点的三根链杆连接。 一刚片和一个点用不共线的两根链杆连接。 ③二元体规则 一刚片和一个点用不共线的两根链杆连接。
无法显示图像。计算机可能没有足够的内存以打开该图像,也可能是该图像已 损坏。请重新启动计算机,然后重新打开该文件。如果仍然显示红色 “x”,则 可能需要删除该图像,然后重新将其插入。
结构力学电子教程
2 结构的几何组成分析 (c)
2.5 分析所示体系的几何构造。 分析所示体系的几何构造。 (a) (b)
结构力学电子教程
2 结构的几何组成分析 2.5
2.4
【解】
【解】
结论: 结论:无多余约束的几何 不变体系。 不变体系。 2.6 【解】 I
结论: 结论:有1个多余约束的几 个多余约束的几 何不变体系。 何不变体系。
III
II 结论:无多余约 结论: 束的几何不变体 系。
无法显示图像。计算机可能没有足够的内存以打开该图像,也可能是该图像已 损坏。请重新启动计算机,然后重新打开该文件。如果仍然显示红色 “x”,则 可能需要删除该图像,然后重新将其插入。
无法显示图像。计算机可能没有足够的内存以打开该图像,也可能是该图像已 损坏。请重新启动计算机,然后重新打开该文件。如果仍然显示红色 “x”,则 可能需要删除该图像,然后重新将其插入。
结构力学电子教程
2 结构的几何组成分析
结构力学-体系的几何组成分析

第二章 体系的几何组成分析
第一节 体系几何组成的定义和分析目的
1、体系几何组成的定义
在忽略变形的前提下,在某种外力作用下,若体系不 能保证其形状或位置不变,则该体系称为几何可变体系。
FP
FP
3 / 40
第二章 体系的几何组成分析 第一节 体系几何组成的定义和分析目的
1、体系几何组成的定义
第二节 自由度和约束的概念
体系自由度数 S 等于零是体系几何不变的充分条件 复杂体系的必要约束往往不易直观判定。 W > 0 表明体系存在自由度,肯定是几何可变体系。 W = 0 表明体系的约束数正好等于部件总自由度数,是
体系不变的必要条件,而非必要条件,如无多余 约束,体系是静定结构。 W < 0 表明体系的约束数多于部件总自由度数,必有多余 约束,如为几何不变体系,则体系是超静定结构。
a、研究结构正确的连接方式,确保所设计的结构能 承受荷载,维持平衡,不至于发生刚体运动。
b、了解结构各部分之间的组成关系,有助于改善和 提高结构的性能。
c、在结构计算时,可根据其几何组成情况,选择适 当的计算方法;分析其组成顺序,寻找简便的求解途 径。
7 / 40
第二章 体系的几何组成分析
第二节 自由度和约束的概念
单约束 仅连接两个刚片的约束.
单铰
1个单铰 = 2个约束 = 2个的单链杆。
虚铰——在运动中虚铰的位置不定,这 是虚铰和实铰的区别。通常我们研究的 是指定位置处的瞬时运动,因此,虚铰 和实铰所起的作用是相同的都是相对转 动中心。
10 / 40
第二章 体系的几何组成分析 第二节 自由度和约束的概念
1、体系的自由度 2、约束 所谓约束即能限制体系运动的装置。
结构工程师结构力学几何组成分析例题
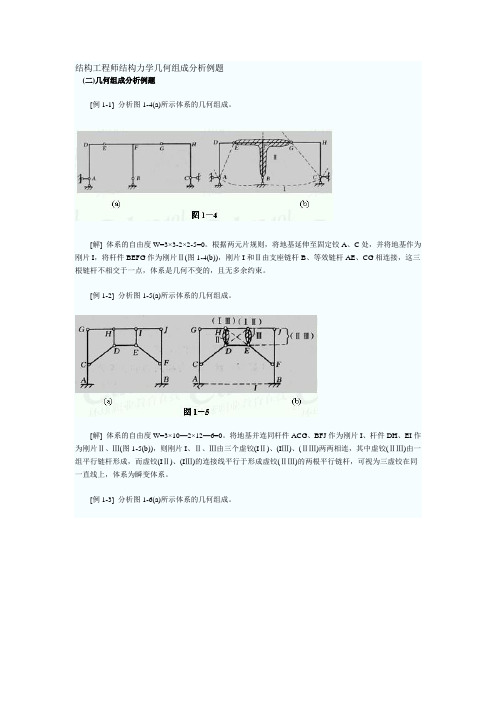
结构工程师结构力学几何组成分析例题(二)几何组成分析例题[例1-1] 分析图1-4(a)所示体系的几何组成。
[解] 体系的自由度W=3×3-2×2-5=0。
根据两元片规则,将地基延伸至固定铰A、C处,并将地基作为刚片I,将杆件BEFG作为刚片Ⅱ(图1-4(b)),刚片I和Ⅱ由支座链杆B、等效链杆AE、CG相连接,这三根链杆不相交于一点,体系是几何不变的,且无多余约束。
[例1-2] 分析图1-5(a)所示体系的几何组成。
[解] 体系的自由度W=3×10—2×12—6=0。
将地基并连同杆件ACG、BFJ作为刚片I、杆件DH、EI作为刚片Ⅱ、Ⅲ(图1-5(b)),则刚片I、Ⅱ、Ⅲ由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,其中虚铰(ⅡⅢ)由一组平行链杆形成,而虚铰(IⅡ)、(IⅢ)的连接线平行于形成虚铰(ⅡⅢ)的两根平行链杆,可视为三虚铰在同一直线上,体系为瞬变体系。
[例1-3] 分析图1-6(a)所示体系的几何组成。
[解] 体系的自由度W=3×8—2×10-4=0。
根据两元片规则,将地基延伸至固定铰A处,并将地基作为刚片I,将CEF作为等效刚片Ⅱ,DB杆作为刚片Ⅲ,这三个刚片由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,如图1-6(b)所示。
因形成无穷远处的两个虚铰(IⅢ)、(ⅡⅢ)的两组平行链杆不相互平行,故体系是无多余约束的几何不变体。
[例1-4] 分析图1-7(a)所示体系的几何组成。
[解] 体系的自由度W=3×9—2×12—3=0。
根据一元片规则,去除图1-7(a)所示体系的一元片,得图1-7(b)所示体系。
再将杆件AB、CE、DF分别作为刚片I、Ⅱ、ⅡⅢ,这三个刚片由三组平行链杆形成的三个无穷远处的虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,根据三刚片连接规则,体系为无多余约束的几何可变体系(无穷远处的三个点在一广义直线上)。
结构力学

二、几何组成分析的目的
(1)判别体系是否几何不变; (2)按什么规律组成一个几何不变体系; (3)区分结构是静定的还是超静定的。
返回
§2-2 刚片、约束、体系自由度 和计算自由度
一、体系自由度的定义:
体系自由度:体系的独立运动方式数,或确定体系位置所需的独立坐标数。 例如:平面内一个点有2个自由度,一个刚片有3个自由度。
在某一瞬间可以产生微小运动的体系,称为瞬变体系,它是可变体系 的一种特殊情况。
FN
瞬变体系在工程中不能采用。
FP 2 Sin
如果一个几何可变体系可以发生大位移,则称为常变体系。
法则Ⅱ: 两刚片法则,两刚片用不完全 相交于一点且不完全平行的三 根连杆连接而成的体系,是几 何不变而无多余约束的。
两刚片以一铰及不通过该铰的一个链杆相联,构成几何不变体系。
法则Ⅲ:三刚片六连杆法则,三刚片之间用六连杆彼 此两两相连接,六连杆所组成的三个铰不在 同一条直线上,则所组成的体系是几何不变 而无多余约束的。
讨论
虚铰在无穷远的情形
二元体的概念
二元体的定义:从任意基础上用不共线的两根连杆形成一个 新结点的装置。
2.结论:给定体系为几何不变无多余约束体系。
返回
例六
试分析图示体系是否为几何不变系
解:1.几何组成分析 去除二元体 刚片Ⅰ、Ⅱ、Ⅲ符合三刚片法则。
2.结论:给定体系为几何不变无多余约束体系
返回
例七 试分析图示体系是否为几何不变体系
解:1.几何组成分析 ABEF与基础之间符合两刚片法则,组成新刚片Ⅲ 在刚片Ⅲ上增加一个二元体形成新节点G,由二元体的性质知 体系仍为几何不变,看作刚片Ⅳ CDHI看作刚片Ⅴ,刚片Ⅳ、Ⅴ之间三根连杆交于点D。 2.结论:该体系为几何瞬变体系。
结构力学第二章 平面体系的几何组成分析

不完全铰节点 1个单铰
13/73
2-1 几何构造分析的几个概念
四、约束 两个互不相连的刚片,若用刚结点连接, 则两者被连为一体成为一个刚片,自由 度由6减少为3。 一个单刚结点相当于3个约束。 单刚结点
三个互不相连的刚片,若用刚结点连接, 自由度由9减少为3。
由此类推:
复刚节点
连接 n 个刚片的复刚结点,它相当于n-1 个单刚结点或3(n- 1)个约束。
A A
1 B
2 C B
1
3
2 C
B 1
A 2
C
几何可变 几何不变 有多余约束
几何不变 无多余约束
规律1 一个刚片与一个点用两根链杆相连,且三个铰不在同一 直线上,则组成几何不变的整体,并且没有多余约束。
23/73
2-2 平面几何不变体系的组成规律
二、两个刚片之间的联结方式
A 2 B I 3 C
A II B I 3 C
16/73
2-1 几何构造分析的几个概念
六、瞬变体系
B 1
I II A
2
I
C
A
II
1 B
2 C
两根链杆彼此共线 1、从微小运动的角度看,这是一个可变体系。 左图两圆弧相切,A点可作微小运动; 右图两圆弧相交,A点被完全固定。
17/73
2-1 几何构造分析的几个概念
六、瞬变体系
B 1
I II A
2
I A 1 B C 2 D
在体系运动的过程中,瞬铰的位臵随之变 化。 用瞬铰替换对应的两个链杆约束,这种约 束的等效变换只适用于瞬时微小运动。
20/73
2-1 几何构造分析的几个概念
八、无穷远处的瞬铰
结构力学 第二章 几何组成分析(典型例题)
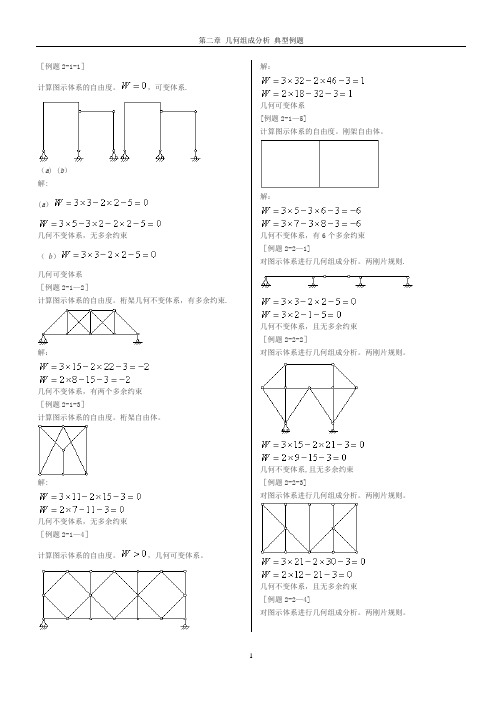
[例题2-1-1]计算图示体系的自由度。
,可变体系.(a) (b)解:(a)几何不变体系,无多余约束(b )几何可变体系[例题2-1—2]计算图示体系的自由度。
桁架几何不变体系,有多余约束. 解:几何不变体系,有两个多余约束[例题2-1-3]计算图示体系的自由度。
桁架自由体。
解:几何不变体系,无多余约束[例题2-1—4]计算图示体系的自由度。
,几何可变体系。
解:几何可变体系[例题2-1—5]计算图示体系的自由度。
刚架自由体。
解:几何不变体系,有6个多余约束[例题2-2—1]对图示体系进行几何组成分析。
两刚片规则.几何不变体系,且无多余约束[例题2-2-2]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束[例题2-2-3]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束[例题2-2—4]对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,有一个多余约束[例题2—2—5]对图示体系进行几何组成分析.二元体规则.几何不变体系,且无多余约束[例题2-2—6]对图示体系进行几何组成分析.两刚片规则,三刚片规则.几何不变体系,且无多余约束[例题2-2-7]对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-2-8]对图示体系进行几何组成分析.三刚片规则.几何不变体系,且无多余约束[例题2-3-1]对图示体系进行几何组成分析.两刚片规则。
几何瞬变体系[例题2—3—2]对图示体系进行几何组成分析。
两刚片规则。
几何瞬变体系[例题2-3-3]对图示体系进行几何组成分析。
三刚片规则。
几何瞬变体系[例题2—3-4]对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-3-5]对图示体系进行几何组成分析.三刚片规则.几何不变体系,且无多余约束[例题2-3—6]对图示体系进行几何组成分析。
二元体规则,三刚片规则.几何瞬变体系[例题2-3-7]对图示体系进行几何组成分析。
02-2结构力学第二章 平面体系的几何组成分析-作业答案汇总
38 3 2 29 3 3
3个单铰结点, 3个折算为2个单铰结点的复铰结点
支杆
b3
11/73
(II III) 刚片II
(I II)
刚片III
几何不变且无多余约束
j9 单链杆:12根 复链杆:2根 折算为6根单链杆
W 2 j b 29 12 6 0
5/73
【作业1】分析图示体系的几何构造
图3
【作业1】分析图示体系的几何构造
图4
先考察如图所示结构
∞(II III)
9/73
【作业2】求图示系统的计算自由度
刚片 m 1 单刚结点 g 4 铰结点 h 0 支杆 b 3
内部无多余约束刚片
W 3m 3g 2h b
31 3 4 3 12
10/73
【作业2】求图示系统的计算自由度
刚片 m 8
单刚结点 g 2
W 3m 3g 2h b
铰结点 h 9
刚片 m 14 单铰链结点 h 18
刚片II
刚片III
(I II)
(I III) 刚片I
瞬变体系
其中折算为2个单铰结点的 复铰结点有6个
∞(II III)
其中折算为3个单铰结点的 复铰结点有2个 单刚结点 2个 g 2 和基础相连的支杆 0个 b 0
W 3m 3g 2h b
314 3 2 218 0
∞(II III)
刚片II (I II) (I III) 刚片III
刚片I
几何不变且无多余约束
(I II) 刚片II (I III) 刚片III
刚片I
几何不变且无多余约束
7/73
【作业2】求图示系统的计算自由度
图1 并进行几何构造分析
结构力学
第二章 结构的几何组成分析(一)单项选择题1.三刚片组成无多余约束的几何不变体系,其连接方式是 【 B 】A .以任意的三个铰相连B .以不在一条线上的三个铰相连C .以三对平行链杆相连D .以三个无穷远处的虚铰相连2.从一个无多余约束几何不变体系上去除二元体得到的新体系为 【 A 】 A .无多余约束的几何不变体系 B .有多余约束的几何不变体系 C .常变体系 D .瞬变体系3.静定结构的几何组成是 【 C 】 A .瞬变体系 B .常变体系C .无多余约束的几何不变体系D .有多余约束的几何不变体系4.图示体系属于 【 D 】 A .无多余约束的几何不变体系 B .有多余约束的几何不变体系 C .瞬变体系 D .常变体系5.图示体系是 【 B 】 A .瞬变体系 B .常变体系C .无多余约束的几何不变体系D .有多余约束的几何不变体系 (二)填空题6.连接4个刚片的复铰相当于 6 个约束。
7.不能起到减少自由度作用的约束称为 多余约束 。
8.将三刚片组成无多余约束的几何不变体系,必要的约束数目是 6 。
9.在一个几何不变体系上加二元体后的新体系为 几何不变体系 。
题4图题5图10.图示体系的几何组成是 无多与约束的几何不变体系 。
(三)分析题11~15.对图示体系进行几何组成分析(要写出分析过程)。
解:11.撤除支座约束,剩余部分为刚片Ⅰ和Ⅱ用既不完全平行又不完全相交的三根链杆1、2、3相连,故原体系为无多余约束的几何不变体系12题解:.撤除支座约束,去除二元体C -A -D 、C -B -E ,剩余部分为刚片Ⅰ(CDE )和Ⅱ(FGH )用既不完全平行又不完全相交的三根链杆1、2、3相连,故原体系为无多余约束的几何不变体系。
AB CDEF GH题12图AB CDEF题11图题10图CDEF 答11图ⅠⅡ123CDE F GH12313题解;.撤除支座约束,去除二元体D -C -E ,剩余部分为两刚片(杆AF 和BF )用两平行链杆相连,故原体系为有一个自由度的几何可变体系。
结构力学二(第二章)
4
B
B 杆通过铰 瞬变体系 瞬 变 体 系
瞬 变 体 系
常 变 体 系
郑州大学土木工程学院
5
规则四、一点与一刚片用两 根不共线的链杆相联,组成无多 余约束的几何不变体系。
1
A
A
2
B
C
两根共线的链杆联一点 瞬变体系
两根不共线的链杆联 结一点称为二元体。
在一体系上增加(或减去)二元体不改变原体系的机 动性,也不改变原体系的自由度。
郑州大学土木工程学院
2
3、约束:在体系内部加入的减少自由度的装置。 ⑴单链杆:仅在两处与其它物体用铰相连,不论其形状和 铰的位置如何。 一根链杆可以减少体系一个自由度,相当于一个约束。 多余约束:不减少体系自由度的约束。 注意:多余约束将影响结构的受力与变形。 ⑵单铰: 联结 两个 刚片的铰。 一个单铰可减少体系两个自由度相当于两个约束。 ⑶虚铰(瞬铰) 联结两刚片的两根不共线的链杆相当于一个单铰即瞬铰。 ⑷复铰(重铰)联结三个或三个以上刚片的铰 联结n个刚片的复铰相当于n-1个单铰,相当于 2(n-1)个约束! ⑸刚性连接——固定支座、刚节点 一个刚性连接可减少体系三个自由度相当于三个约束。
郑州大学土木工程学院
8
1-4、瞬变体系在一般荷载作用下 (C ) A 产生很小的内力 B 不产生内力 C 产生很大的内力 D 不存在静力解答 1-5、从一个无多余约束的几何不变体系上去除二元体后得到 的新体系是 (A ) A 无多余约束的几何不变体系 B 有多余约束的几何不变体系 C 几何可变体系 D 几何瞬变体系 1-6、图示体系是什么体系? (C ) A 无多余约束的几何不变体系 Ⅲ B A B 有多余约束的几何不变体系 C C 几何可变体系 Ⅱ Ⅰ D 几何瞬变体系
结构力学第四讲平面体系的几何组成分析
平行,则该体系为瞬变体系。
第二章 平面体系的几何组成分析 课堂练习1 :
结论:无多余约束几何不变体系
结论:几何可变体系
结论:有3个多余约束 的几何不变体系
第二章 平面(2)体系的几何组成分析
(3)
五、课后练习:试对图示体系进行几何组成分析:
(1)
(1)
(1)
(2) ((22)) (2)
(2)
(3) (3)
§2-5 几何组成与静定性的关系
一、几何可变体系:一般无静力解答。 二、无多余联系的几何不变体系:静力解答唯一确定。 三、几何瞬变体系:其平衡方程或者没有有限值解答, 或在特殊情况下,解答不确定。 四、具有多余联系的几何不变体系:静力解答有无穷 多组解。
体系的几何组成与静定性的关系: 1、无多余约束的几何不变体系是静定结构; 2、有多余约束的几何不变体系是超静定结构; 3、几何可变体系不能作为结构使用。
第二章 平面体系的几何组成分析
练习:
刚片的等效替换
CC
FF
BB
EE
GG
C
II
B
F O(2,3)
G
E
III
AA
瞬变
DD
HH
A(1,2)
D(1,3)
I
题7-1(12)图
将地基视为刚片I;刚片II、III由平行的链杆BE、CF连
接,形成无穷远的虚铰, I、II刚片由A铰、 I、III刚片
由D铰连接。A、B的连线与形成无穷远虚铰的链杆相互
答案: (1)几何不变体系,有4个多余约束。 (2)几何不变体系,有6个多余约束。 (3)几何不变体系,有3个多余约束。 (4)几何不变体系,有2个多余约束。 (5)几何不变体系,有6个多余约束。 (6)几何不变体系,无多余约束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[例题2-1-1]
计算图示体系的自由度。
,可变体系。
(a)(b )
解:
(a)
几何不变体系,无多余约束
(b)
几何可变体系
[例题2-1-2
]
计算图示体系的自由度。
桁架几何不变体系,有多余约束。
解:
几何不变体系,有两个多余约束
[例题2-1-3]
计算图示体系的自由度。
桁架自由体。
解:
几何不变体系,无多余约束
[例题2-1-4]
计算图示体系的自由度。
,几何可变体系。
解:
几何可变体系
[例题2-1-5]
计算图示体系的自由度。
刚架自由体。
解:
几何不变体系,有6个多余约束
[例题2-2-1
]
对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束
[例题2-2-2]
对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束
[例题
2-2-3]
对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,且无多余约束
[例题2-2-4]
对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,有一个多余约束
[例题2-2-5]
对图示体系进行几何组成分析。
二元体规则。
几何不变体系,且无多余约束
[例题2-2-6]
对图示体系进行几何组成分析。
两刚片规则,三刚片规则。
几何不变体系,且无多余约束
[例题2-2-7]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-2-8]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-1]
对图示体系进行几何组成分析。
两刚片规则。
几何瞬变体系
[例题2-3-2]
对图示体系进行几何组成分析。
两刚片规则。
几何瞬变体系
[例题2-3-3]
对图示体系进行几何组成分析。
三刚片规则。
几何瞬变体系
[例题2-3-4]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束[例题2-3-5]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-6]
对图示体系进行几何组成分析。
二元体规则,三刚片规则。
几何瞬变体系
[例题2-3-7]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-8]
对图示体系进行几何组成分析。
二元体规则,三刚片规则。
几何瞬变体系
[例题2-3-9]
对图示体系进行几何组成分析。
二元体规则,三刚片规则。
几何瞬变体系
[例题2-3-10]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-11]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-12]
对图示体系进行几何组成分析。
三刚片规则。
几何瞬变体系[例题2-3-13]
对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,有一个多余约束
[例题2-3-14]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-15]
对图示体系进行几何组成分析。
两刚片规则,三刚片规则。
几何不变体系,且无多余约束
[例题2-3-16]
对图示体系进行几何组成分析。
三刚片规则。
几何不变体系,且无多余约束
[例题2-3-17]
对图示体系进行几何组成分析。
两刚片规则。
几何不变体系,有一个多余约束。
