2机械控制工程基础第二章答案
机械控制工程基础第二章2可编辑全文

ms2
1 Cs
K
R-L-C无源电路网络的传递函数
LC
d2 dt 2
uo
(t)
RC
d dt
uo
(t)
uo
(t)
ui
(t)
所有初始条件均为零时,其拉氏变换为:
LCs2Uo (s) RCsUo (s) Uo (s) Ui (s)
G(s)
Uo (s) Ui (s)
LCs2
1 RCs
1
几点结论 ✓ 传递函数是复数s域中的系统数学模型,
线性微分方程
拉氏变换
象函数
解 代 数 方 程
象函数的 代数方程
拉氏变换法求解线性微分方程的过程
➢例 设系统微分方程为:
d
2 xo (t) dt 2
5
dxo (t) dt
ቤተ መጻሕፍቲ ባይዱ
6xo
(t)
xi
(t)
若xi (t) =1(t),初始条件为0,试求xo(t)。
解:对微分方程左边进行拉氏变换(微分定理):
L
X(s), x(t) 信号线
信号引出点(线)
表示信号引出或测量的位置和传递方向。
同一信号线上引出的信号,其性质、大小完全一样。
X(s)
X(s)
X(s)
X(s)
X(s)
X(s)
引出线
函数方框(环节) 传递函数的图解表示。
X1(s) G(s) X2(s)
函数方框
函数方框具有运算功能,即:
X2(s) = G(s)X1(s)
dn dt n
xo (t)
a1
d n1 dt n1
xo (t)
an 1
d dt
控制工程基础第二章参考答案

第二章 参考答案2-1 (1) 不是 (2) 是 (3) 不是 (4) 不是 2-2 (a))()()(3)(2222t u t u dtt du RC dt t u d C R i o o o =++ (b) )()()()()()()()(2211222121222111222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (c ) )()()()()()(33221312221t u R dtt du C R R t u R R dt t du C R R R R R i i o o +=++++(d))()()()()()()()(1211222121211211222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (e))()()()()()()()(221222121211222222121t u dtt du R C C dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (f) )()()()()()()(22121221t u R dtt du L t u R R dt t du L C R R dt t u d CL R i i oo o +=++++ 2-3 (a) )]()([)()()(23213121t u R dtt du C R R t u R dt t du C R R R R i i o o +=++-(b) )()()()(4141232022213210t u R R t u R R dt t du C R R R dt t u d C C R R R R i o o o -=++ (c))]()()([)(32321t u R R dtt du C R R t u R i i o ++=-(d) )()()()()(221122212121t u dt t du C R C R dt t u d C C R R dt t du C R i i i o +++=- (e) )()()()(2412222142t u dtt du C R C R dt t u d C C R R o o o +++ )}()(])([)({21213224223221432132t u dtt du R R C C R R C R dt t u d R R C C R R R R R R i i i +++++++=- 2-4 (a) dt t dx f dt t dx f f dt t x d m i o o )()()()(12122=++ (b) dt t dx f k t x k k dt t dx f k k i o o )()()()(12121=++ (c) )()()()()(121t x k dt t dx f t x k k dt t dx f i i o o +=++ (d) )()()()()()(112121t x k dtt dx f t x k k dt t dx f f i i o o +=+++2-5 (a))(1)()()()(1)()()(2112212221211*********t u C C dt t du C R C R dt t u d R R t u C C dt t du C R C R C R dt t u d R R i i i o o o +++=++++ (b))()()()()()()()(2112212221211211212221t x k k dtt dx k f k f dt t x d f f t x k k dt t dx k f k f k f dt t x d f f i i i o o o +++=++++ 由(a)(b)两式可以看出两系统具有相同形式的微分方程,所以(a)和(b)是相似系统。
重庆大学机械控制工程习题参考答案 第二章

习题五
题型:填空题
习题三
题型:填空题
题目:
F s
1 s
的拉氏反变换为
。
分析与提示:此为基本函数。
答案: f t 1
习题四
题型:填空题
题目:
F s
s
1
a
的拉氏反变换为
。
分析与提示:此为基本函数。
答案: f t eat
习题五
题型:填空题
题目:
F s
1 Ts 1
的拉氏反变换为
式称为系统的
。
分析与提示:数学模型是定量地描述系统的动态性能,揭示系统的结构、参数与动态性
能之间的数学表达式。
答案:数学模型
习题五
题型:填空题
题目:线性系统满足两个重要性质,分别为:
、
。
分析与提示:线性系统满足叠加性和均匀性。
答案:叠加性;均匀性
第二节(2)
习题一 题型:单项选择题 题目:线性系统与非线性系统的根本区别在于( )。 A、线性系统有外加输入,非线性系统无外加输入 B、线性系统无外加输入,非线性系统有外加输入 C、线性系统满足迭加原理,非线性系统不满足迭加原理 D、线性系统不满足迭加原理,非线性系统满足迭加原理 分析与提示:数学模型表达式是线性的系统称为线性系统,满足叠加性和均匀性。 答案:C
题型:填空题
题目:函数 f t eat 的拉氏变换 L[f(t)]=
。
分析与提示:拉氏变换定义式可得,且 f(t)为基本函数。
1
答案:
sa
习题四 题型:单项选择题
题目:若 f t t 2e2t ,则 L[ f (t)] =( )。
控制工程基础第2章答案
第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
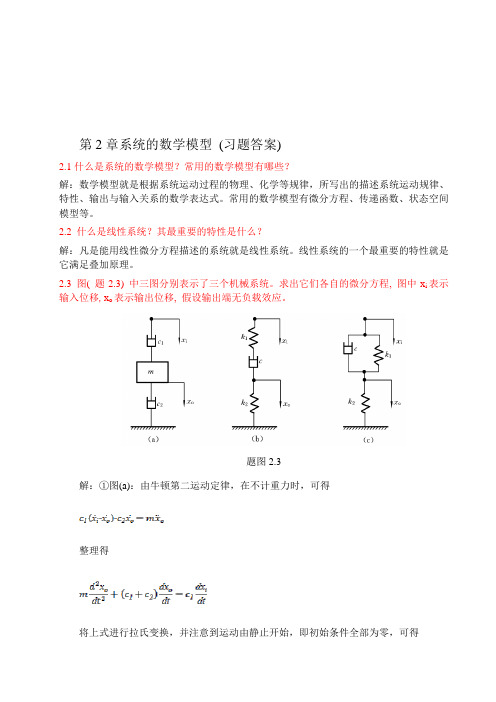
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-u )tfC)+-+-f)(a )(b )(c )(d R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
机械工程控制基础答案(第七版)

机械工程控制基础答案(第七版)第一章:控制系统的基本概念1.1 什么是控制系统?控制系统是由各种组件和部件组成的工程系统,它们通过传递信号和信息来控制和调节系统的运行状态。
1.2 控制系统的分类控制系统可以根据输入和输出信号的性质分为连续时间控制系统和离散时间控制系统。
1.3 控制系统的组成控制系统主要由输入部分、执行部分和输出部分组成。
输入部分负责接收输入信号,执行部分负责根据输入信号执行相应的操作,输出部分负责输出结果。
1.4 控制系统的闭环与开环闭环控制系统是指系统的输出信号可以作为输入信号的一部分进行反馈控制,而开环控制系统是指系统的输出信号不会作为输入信号的一部分进行反馈控制。
1.5 控制系统的性能指标控制系统的性能指标包括稳定性、快速性、准确性和鲁棒性等。
第二章:传输函数与信号流图2.1 传输函数的定义传输函数描述了控制系统中输入和输出之间的关系。
它可以通过系统的微分方程和拉普拉斯变换来求得。
2.2 传输函数的性质传输函数具有线性、时不变和因果性等性质。
2.3 信号流图的表示信号流图是用于描述控制系统的一种图形表示方法,它由节点和支路组成。
节点表示系统的状态,支路表示信号的传递。
2.4 信号流图的简化信号流图可以通过串联、并联、反馈和转移等操作进行简化和求解。
第三章:经典控制系统设计3.1 一阶惯性环节的控制系统设计一阶惯性环节的控制系统设计主要包括根轨迹法和频率响应法。
根轨迹法通过绘制根轨迹来设计控制系统的参数,频率响应法通过频率特性来设计控制系统的参数。
3.2 二阶惯性环节的控制系统设计二阶惯性环节的控制系统设计主要包括模拟法和频率法。
模拟法通过模拟计算来设计控制系统的参数,频率法通过频率特性来设计控制系统的参数。
3.3 控制系统的稳定性分析与设计控制系统的稳定性是指系统在受到干扰时能够保持稳定的状态。
稳定性分析和设计是控制系统设计中的重要内容。
3.4 控制系统的性能分析与设计控制系统的性能包括快速性、准确性和鲁棒性等方面。
机械控制第二章答案

第二章作业 (一)1、解:列复阻抗方程,根据电阻分压:秒秒5.0,1,1)(1)(111)()(22211121212212122111222212====+++++++=++++=C R T C R T s C R T T s T T s T T s T T R s C s C R sC R s U s U 整理得:)(]1)([)(]1)([12122122121221s U s T T s T T s U s C R T T s T T +++=++++变换得:)()()()()()()()(11212122122212122221t u dt t du T T dtt u d T T t u dt t du T T C R dt t u d T T +++=++++ )()(5.1)(5.0)()(6.1)(5.01121222222t u dt t du dt t u d t u dt t du dt t u d ++=++ 2、解:以弹簧不变形时为静态工作点,列微分方程得:⎩⎨⎧−−−+−+=−−−−+=)(')()](')('[)]()([)('')](')('[)]()([)()(''2222211211222211211111t y B t y K t y t y B t y t y K g M t y M t y t y B t y t y K g M t f t y M 令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=)(')(')()()(2121t y t y t y t y t X⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+−+−+−+−=g g M t f t X M B B M B M K K M K M B M B M K M Kt X 1222212212111111111)(10010000)(10000100)(' 以不受)(t f 力,有重力作用下静止状态为静态工作点,列微分方程得:⎩⎨⎧−−−+−=−−−−=)(')()](')('[)]()([)('')](')('[)]()([)()(''22222112112221121111t y B t y K t y t y B t y t y K t y M t y t y B t y t y K t f t y M 相应的状态方程为:1222212212111111111)(0100)(10000100)('M t f t X M B B M B M K K M K M B M B M K M Kt X ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+−+−+−+−= 3、解:传递函数定义为零初始条件下的拉氏变换,所以s 就是一个微分算子: (1) )()('3)(6)('5)(2)()2()3(t u t u t y t y t y t y +=+++ )()(3)(6)(5)(2)(23s U s sU s Y s sY s Y s s Y s +=+++,得: 65213)(23++++=s s s s s G(2) )(8)(3)('6)(10)()2()4(t u t y t y t y t y =+++ 36108)(24+++=s s s s G(3) )(2)('5)(3)(5)(')(2)(0)2()3(t u t u d y t y t y t y t y t +=++++∫ττ352)25()(234+++++=s s s s s s s G (4) )(2)()()('3)(''2τ−+=++t u t u t y t y t y 13221)(2+++=−s s e s G sτ4、解:⎩⎨⎧+=−+++=++)(')()()()('3)('')()()(3)('2)(''12211221211t u t u t y t y t y t y t u t u t y t y t y L 变换得⎪⎩⎪⎨⎧+=−+++=++)()()()()(3)()()()(3)(2)(1221122212112s sU s U s Y s Y s sY s Y s s U s U s Y s sY s Y s ,用消元法或矩阵变换解方程: ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−++)()(111)()(11332212122s U s U s s Y s Y s s s s ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−++=⎥⎦⎤⎢⎣⎡−)()(11111332)()(2112221s U s U s s s s s s Y s Y =⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−−−+−−−−−−+)()(1132413311212122322234s U s U s s s s s s s s s s s s 传递函数矩阵: ⎥⎦⎤⎢⎣⎡−−−−+−−−−−−+=113241331121)(22322234s s s s s s s s s s s s s G8、解:(1))(5)(4)('3)(''2)()3(t u t y t y t y t y =+++L 变换得:4325)()(5)(4)(3)(2)(2323+++==+++s s s s G s U s Y s sY s Y s s Y s ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−−=234100010A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100B []005=C 状态方程为:⎩⎨⎧=+=)()()()()('t Cx t y t Bu t Ax t x(2))()('2)(''3)(2)()('2)(''3)(4)3()3(t u t u t u t u t y t y t y t y +++=+++L 变换得:12341232)()()(2)(3)(2)()(2)(3)(423232323++++++=+++=+++s s s s s s s G s U s sU s U s s U s s Y s sY s Y s s Y s化成标准形式:41214381418321)(232++++++=s s s s s s G ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−−−=432141100010A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100B ⎥⎦⎤⎢⎣⎡=834181C 21=D 状态方程为:⎩⎨⎧+=+=)()()()()()('t Du t Cx t y t Bu t Ax t x 也可以采用能观标准型。
机械控制工程基础习题集

《机械控制工程基础》习题及解答目录第1章绪论第2章控制系统的数学模型第3章控制系统的时域分析第4章控制系统的频域分析第5章控制系统的性能分析第6章控制系统的综合校正第7章模拟考试题型及分值分布第1章绪论一、选择填空题1。
开环控制系统在其控制器和被控对象间只有(正向作用).P2A。
反馈作用 B.前馈作用 C。
正向作用 D。
反向作用2.闭环控制系统的主反馈取自(被控对象输出端)。
P3A.给定输入端B.干扰输入端 C。
控制器输出端 D。
系统输出端3。
闭环系统在其控制器和被控对象之间有(反向作用)。
P3A.反馈作用B.前馈作用 C。
正向作用 D.反向作用A。
输入量 B。
输出量 C。
反馈量 D。
干扰量4.自动控制系统的控制调节过程是以偏差消除(偏差的过程)。
P2-3A。
偏差的过程 B。
输入量的过程 C.干扰量的过程 D.稳态量的过程5.一般情况下开环控制系统是(稳定系统)。
P2A.不稳定系统B.稳定系统 C。
时域系统 D。
频域系统6.闭环控制系统除具有开环控制系统所有的环节外,还必须有(B)。
p5A.给定环节B.比较环节 C。
放大环节 D.执行环节7.闭环控制系统必须通过(C)。
p3A.输入量前馈参与控制 B。
干扰量前馈参与控制C。
输出量反馈到输入端参与控制 D。
输出量局部反馈参与控制8.随动系统要求系统的输出信号能跟随(C的变化)。
P6A。
反馈信号 B。
干扰信号 C。
输入信号 D。
模拟信号9。
若反馈信号与原系统输入信号的方向相反则为(负反馈)。
P3A。
局部反馈 B。
主反馈 C.正反馈 D.负反馈10.输出量对系统的控制作用没有影响的控制系统是(开环控制系统)。
P2A。
开环控制系统 B。
闭环控制系统 C.反馈控制系统 D.非线性控制系统11。
自动控制系统的反馈环节中一般具有( B )。
p5A。
.给定元件 B.检测元件 C.放大元件 D.执行元件12. 控制系统的稳态误差反映了系统的〔B 〕p8A. 快速性B.准确性C. 稳定性 D。
机械工程控制基础第二版答案
Mavis际何1.2.」解在進祗屮恒苗15内ftJSitr 需妥械挖晴,因此*lfi 凰箱为捜控制对SL 恒諷鞘的实环 狙度为彼控制量{農姣的幕吕扯人设为TJUh 希衆的恒卫甬的退度为杲址的输人扯f 拾定 值),说力T,(TC )ilW 艇电阻逐的穗出功卑为按制It :百危温材啟热*为季址対武功竟*怛宦籀的诅决蹇i6蛤宝的电压信号«,和热电沼输出的电医倍号Hf 之何的阳垄旳」岭控 制的■当工⑴时rtfl此时束(f 不工作,恆温鶴的期嵐限持在斡卽制凰嵐上"当拥■界丙累引刘曙内认度变化时,當差憤号比一u’HD.嗚差館电圧和功聿放大 后,隹电机的荐連和特向担塞在雙,井逋过传谕装覺葩动雷Ek 器的动陋去*当温世脅高0,谕魅 養沟著隕少电it 的方向移动,反直协丈电疥,直科越度达到绘定曲为止*據證控制方厲田如国 <W I. 2. b )^,习题与解答11札城工程控制论的研究对東和任务星卄农?鴛机裁工棺揑制址宴质上是科究机械工魅中广戈系境的功力学何範山毎览盪・它爲究 的呈机植工糧技术中的广文系竦在一定曲并界聂件(即甬人空殖励,包括外加世期勻挣加干〔和了解时整制岳址的早申要京. 二、本章重点门)学台搭* sb 茁烷总论的祀贞分折广义恳址帕动蕊特性"佶也戒■理翳倩息反槪的含2 童加作用.铝)章惺植制泵紀的赴本槪倉.墓專炎蜀、基审如堆特T.fne :理’煌制牲解丟瓊用柜団》三,就隶难点rJl«W.«Wf.&W.S :15M#ffi 方 n 图帥临刪.M I I 匪也烛木眷如UEH 讯I, 1,)膚 示.为丁际聘矣®的陷!f.由刃挖开关議通或 斷幵牡皿外辟能电孰.在便H!热水耐,水霸屮 址岀痕朮井杯克冷水、.沆说齧该窑册工牛原理 非奁出眾炕的力軽Hi,M 在电热朮黠瓶筑中,水箱肉的木ifl 需 罢拧甘"即木艳为長桂对Jt.水的辛薛奮厦壬SA<C )i 辑A *为皿P 昭镇的ifi 蘆I 给定伍、.设肖 ^■/CJrifaf &tlE|jft*4注人冷水咬水紀轨嵌并界因甫惶水箱内*翌下烽猊肖裁来旋的l.!S T 找,耳r.(r )=r,cc )e?.+Lffi 的实尿水诅轻巒迫元件检幡.并持宾对观盘妹牝成相应的电 價号"与辺艳开头两光段定的估号进行弍较而得魁的備东为輩,此时电加叢甜不工作,忒科中 的朮惶廉祥牲需宝的诅鹰匕‘呀使用煦水井辻人冷水比,朮汨卩悔"此肘rjCKTCC ).*! 慎追*为平帀Tiflis 开关:Eft.于址电匣陀:通,电.制鎭界厅的农水珂内的朮进打加轴”使朮迅 上冲.直到r.cv )"7-i { CJ 时为止.泵屿检M 方征国IUF (^ !. i.to 所示.MUxITm '那I .I ."电匹玄”月枢皿^1.2 EF («J-2-0^-恒10箱脸釦更揑制系堺.试分折过伞尿蜒的自动同田过軽井说 明眩个系婕的输出IL 输人址、"魁ii 和扰动fit 咨是fl 么:扰)作用下.从丟荻的-定的切船狀$出笈,所蛉力的山鮎内部的国韦怦性(即由乐絲的结构士娄 數严决琏的特性)所决宦的整冲动态肝费研究裝一系烧观其输从输出=者之司的诟态娄系.从系貌.骗人.输岀三吾豈同皆关系峦誥,規誓已如茶件与城晞问题眉不同•机城工程12对 论的任费可C (舟舟以下五方面:⑴巳知乘如城人求聶嶽的曲出,即系城幷析问4S ; ("己知采纹利系境的理想域%.谊打附.4即曲优控抽间題: 轄}巳期曹人和理犯增起,设奸昴抚.即蛊忧谡计甸薊I<4)^出已曲,琳定杀境,以识刖检人或箱人中的有关侣熄,此即注渡可療相闷赴r(5)系址時塔人和输出已知,求系娠的堆种与摻救,即茶址窮识局题,12卄直拦内辰慣?旳f 卜公说内反愦毘使Plt£系娩纷蹩!(杂的£要原因?解rtfifflfift 在乘境内克亦曾的各E 自然世成的刘乱它.王娶由義就内部各亍元1?之向的 内:帳區快恳咬円娜各晏®[之间的内庄联盒其澤咅对船址的动态舟性有非常章 规的电*h iTri 机枝義歩存崔的内反俳惊况千差万别.错煤賀杂,因此使科林戦系晓轴緊复决*13试分析妇田<i L S.aljff 示系统的内反愷情况.fflf« t-3.n ) 轟茨的方柢用玛晁 1 A+(X J —— /(/) ⑴«t]J| + Af(j| — TjJ 十 Jt]JT| = 0⑵由(1》有«JX* +环吧=f{t) T 妬町⑶由⑵有«|T| * 傀十 *」工| = k,.T,⑷若Ki At )为系SE 的藕人*,卄为爲蔬的甫出*则呆蜒的割力学方程可用国(■遞 1. 3.町所电ta^fi示的方电1?1表示.显烘•该系蛻寻任内皈恨.14试分析fcffi<6i.4,s )所示机tiin 工过聚的内反血悄况.解 当刀具战名止进给量,进行切削时.在切削过柱屮产生切制力介.而建机慮-工秤產貌旋 的实乐讲绪心此时口=』一八建而瓦於购貝切制力的变代・如曲韬环.便 得切用过悍为一十动态历押.具有一些动态特世*耳过程可用番(超i.4.bJ 所示的方(£图曲示.15什么是外反》!?为ft ■么莊进行反簾悴制?M 外反撫見1S 人们为了达到一定的目的•有意如人的反IS •闭环捽制系统的工作是荃于 系疣的实除输出与参舎傳人何的■誌之上的.在系炊存厲扰动的宿况E.dttiBfttt 会出3L 进行适当的反谕控制正*?«&«岀这HWg.ff 力图城尔这科岛能•币最终使側《1差为系.事 实上•反倔控JK 仅仅需为无袪预计的扰动而没计•因为对可以M 知的找为•总可以存系址中加 以校正.1・6试分析以下例子枣師些見人为楚利用反说抄制•以达利預期指你的白动控制孩置・ 仃)荚汽机的沟連系竦〈歩阳刁題1.12)><2>«HJI«ft 中并嚴的电«;(3)电冰無曲恒IS 系 统M4〉家用全自动洸衣机°« <1).(3)为反饿应制系境《2)・Q )不是反集控利系统’详畑分折请養冬习越1・12和 习Gi.io 的鮮答・17在下刿这些捋坡运动的才程中・都存在估@的伶输•并利用反《!来进冇枠制•试加以 说明. d )人册自行车;《2)人驾狡九车。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题2.1 什么是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,x o 表示系统输出,x i 表示系统输入,哪些是线性系统? (1) x x x x x ioooo222=++ (2) x tx x xiooo222=++ (3)x x x x io222oo=++ (4) x tx x x xiooo222o=++ 解: 凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系统。
2.2 图(题2.2)中三同分别表示了三个机械系统。
求出它们各自的微分方程,图中x i 表示输入位移,x o 表示输出位移,假设输出端无负载效应。
图(题2.2) 解: (1)对图(a)所示系统,由牛顿定律有xm x c x x c ioo2o1)(=-- 即x c x c c xm i121oo )(=++ (2)对图(b)所示系统,引入一中间变量x,并由牛顿定律有)1()()(1x xc k x x oi-=- )2()(2x k x xc oo=-消除中间变量有x ck x k k xk k c io121o21)(=-- (3)对图(c)所示系统,由牛顿定律有 x k x x k x xc ooioi21)()(=-+-即x k x c x k k xc iioo121)(+=++ 2.3求出图(题2.3)所示电系统的微分方程。
图(题2.3)解:(1)对图(a)所示系统,设i 1为流过R 1的电流,i 为总电流,则有⎰+=idt Ci R u o122i R u u o i 11=-dti i Cu u oi)(111⎰-=-消除中间变量,并化简有u R C u CC R R uR C u R C u C C R R u R C iiiooo12211221222121211)()1(1+++=-+++(2)对图(b)所示系统,设i 为电流,则有⎰++=idtC i R u u oi111⎰+=i R idt Cu o221 消除中间变量,并化简有u Cu R u C C u R R iioo2221211)11()(+=+++2.4 求图(题2.4)所示机械系统的微分方程。
图中M 为输入转矩,C m 为圆周阻尼,J 为转动惯量。
解:设系统输入为M (即),输出θ(即),分别对圆盘和质块进行动力学分析,列写动力学方程如下:)(x R Rk C J M m-++=θθθxc x m x R k +=-)(θ 消除中间变量x,即可得到系统动力学方程KM M c Mm C R c k KJ c C km R cJ mC mJ mmm++=++-++++ θθθθ)(22)()()4(2.5 输出y(t)与输入x(t)的关系为y(t)= 2x(t)+0.5x 3(t)。
(1)求当工作点为x o =0,x o =1,x o =2时相应的稳态时输出值; (2)在这些工作点处作小偏差线性化模型,并以对工作的偏差来定义x 和y ,写出新的线性化模型。
解: (1) 将 x o =0,x o =1,x o =2分别代入y(t)= 2x(t)+0.5x 3(t)中,即当工作点为xo=0,xo=1,xo=2时相应的稳态输出值分别为0=y o,5.20=y , 8=y o。
(2) 根据非线性系统线性化的方法有,在工作点)(,y x oo附近,将非线性函数展开成泰勒级数,并略去高阶项得xx x x y y x x oooo∇•=+++=∇+|)5.12(5.0223∴ xx y xx o∇•=+=∇|)5.12(2若令x x∇=,y y∇=有x x y )5.12(20+=当工作点为0=x o 时,xx x y 2)5.12(20=+=当工作点为1=x o 时, xx x y 5.3)5.12(20=+=当工作点为2=x o 时,x x x y 8)5.12(20=+=2.6已知滑阀节流口流量方程式为ρpcwx Qv2=,式中.Q 为通过节流阀流口的流量;p 为节流阀流口的前后油压差;x v 为节流阀的位移量;c 为疏量系数;w 为节流口面积梯度;ρ为油密度。
试以Q 与p 为变量(即将Q 作为P 的函数)将节流阀流量方程线性化。
解:利用小偏差线性化的概念,将函数Q=F(x v ,p)在预定工作点F(x o ,p o )处按泰勒级数展开为+∇•÷∇•∂∂+=∂∂p p x x p x x F p x F Q o vo PFv o vo vo vo ),()(),()(),(消除高阶项,有pp x x p x x F p x F Q o vo PFv o vo vo vo ∇•+∇•∂∂+=∂∂),()(),()(),(∴),(),(p x F p x F Q o vo v -=∇),(),()(),()(),(p x F p p x x p x x F p x F o vo o vo PFv o vo vo vo -∇•+∇•∂∂+=∂∂pp x x p x x F o vo PFv o vo v∇•+∇•∂∂=∂∂),()(),()(若令)(p x x F K ovo v,|)(1∂∂=,)(p x F K o vo ,|)p (2∂∂=, pKx K Qv∇•∇•∇+=21将上式改写为增量方程的形式pK x K Q v••+=212.7 已知系统的动力学方程如下,试写出它们的传递函数Y(s)/R(s)。
(1))(2)()(500)(50)(15)(t r t r t y t y t y t y+=+++(2))(5.0)(25)(5t r t yt y =+ (3))(5.0)(25)(t r t yt y =+ (4))(4)(4)(6)(3)(t r dt t y t y t yt y=+++⎰解:根据传递函数的定义,求系统的传递函数,只需将其动力学方程两边分别在零初始条件下进行拉式变换,然后求Y(s)/R(s)。
(1))(2)()(500)(50)(15)(223s sR s R s s Y s sY s Y s s Y s +=+++ ∴ 50050152)(/)(222++++=s s s ss s R s Y(2))(5.0)(25)(52s sR s sY s Y s =+∴ss ss R s Y 2555.0)(/)(2+=(3))(5.0)(25)(2s R s SY S Y s =+∴ ss s R S Y 255.0)(/)(2+=(4))(4)(14)(6)(3)(2s Y s Y ss Y S sY s Y s =+++∴ 4634)(/)(23+++=s s s ss R s Y2.8 如图(题2.8)为汽车或摩托车悬浮系统简化的物理模型,试以位移x 为输入量,位移y 为输出量,求系统的传递函数Y(s)/X(s)。
2.9 试分析当反馈环节H(s)=1,前向通道传递函数G(s)分别为惯性环节、微分环节、积分环节时,输入、输出的闭环传递函数。
解:由于惯性环节、微分环节、积分环节的传递函数分别为1)(+=Ts K s G ,Ts s G =)(,s K s G =)(,而闭环传递函数为)()(1)()(s H s G s G s G B •±=,则(1)当反馈环节H(s)=1,前向通道传递函数G(s)为惯性环节时,K Ts K Ts K Ts Ks H s G s G s G B±+=+±+=•±=1111)()(1)()((2)当反馈环节H(s)=1,前向通道传递函数G(s)为微分环节时,TsTs s H s G s G s G B ±=•±=1)()(1)()((3)当反馈环节H(s)=1,前向通道传递函数G(s)为积分环节时,K s K sK s Ks H s G s G s G B ±=±=•±=1)()(1)()(2.10 证明图(题2.10)与图(题2.3(a )所示系统是相似系统(即证明两系统的传递函数具有相同形式)。
解:对题2.4(a)系统,可列出相应的方程。
)1(122⎰+=idtCR u o)2(11iR u u oi=-)3()(111dti i Cu u oi⎰-=-对以上三式分别作Laplce 别换,并注意到初始条件为零,即0)0()0(0)0()0(21====II II则)(4)()1()()()(2222s I sC R sC s I s I R s U O+=+= )(5)()()(1s I R S U s U iOi=- )(6)()()()(11sC s I s C s I S U s U Oi-=- sC 11)5(⨯,得)7()()()(111110s I sC R s U s U sC i=-⎥⎦⎤⎢⎣⎡R ⨯)6(1, 得 )8()()()()(111111s I sC R s C s I R s U s U R i -=-⎥⎦⎤⎢⎣⎡)8()7(+, 得)()()()1(11110s I sC R s U s U R sC i=-+⎥⎦⎤⎢⎣⎡即 )(1)(1)()(11111111s I C R R s I sC R s C s C R s U s U Oi+=+⨯=-则 )9()(1)()(1110s I C R R s U s U i ++=将(4)式中的)(0s U 代入(9)式 )(1)()1()(11122s I C R R s I sC R s U i +++=)()11(11122s I sC R R s C R +++=再用(4)式与上式相比以消去)(s I ,即得电系统的传递函数为)())1(1()()1()()()(111222210s I s C R R s C R s I s C R s U s U s G ++++==)1(111112222s C R R s C R sC R ++++=而本题中,引入中间变量x,依动力学知识有cx x c x x k x x o i i)-()()-(12o2=-+x k c x xi =-11o)(对上二式分别进行拉式变换有[]scs X s X s s X sc s X X k O ii12)()()(X -)()(02-=+-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡sc k s X s c s X +=1101)()(消除)(s X 有sk c c s k c s k c s c k s c k s c k s c k s X s X s G i 11122221111222201)()()(++++=++++==比较两系统的传递函数有Ck 221⇔Ck 111⇔R c22⇔ R c 11⇔故这两个系统为相似系统。
