求下图所示系统的传递函数
控制工程基础试卷2015补考复习
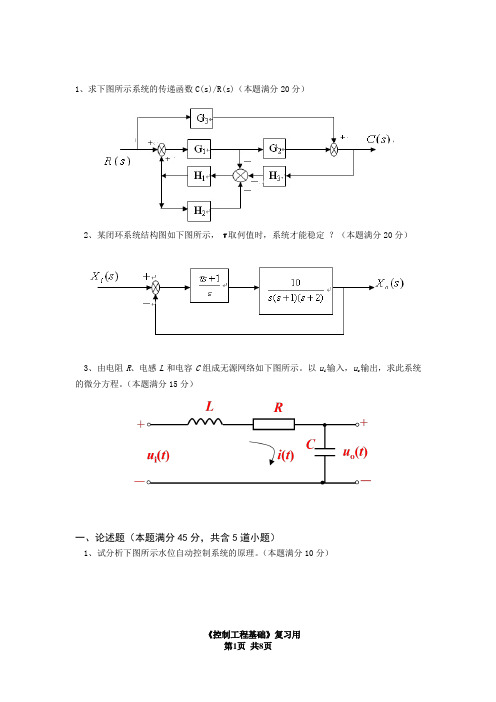
1、求下图所示系统的传递函数C(s)/R(s)(本题满分20分)2、某闭环系统结构图如下图所示,τ取何值时,系统才能稳定?(本题满分20分)3、由电阻R、电感L和电容C组成无源网络如下图所示。
以u i输入,u o输出,求此系统的微分方程。
(本题满分15分)一、论述题(本题满分45分,共含5道小题)1、试分析下图所示水位自动控制系统的原理。
(本题满分10分)《控制工程基础》复习用《控制工程基础》复习用2、写出如何利用梅森(Mason )公式得到系统传递函数。
(本题满分10分)3、求取无源网络或电子调节器的传递函数,采用阻抗法求取更为方便。
写出下表中列出的电阻、电容和电感的阻抗的微分方程与传递函数。
(本题满分10分)4、对控制系统的“稳”的要求,具体是什么含义?对系统的“准”的要求,含义又是什么? (本题满分5分)5、解释闭环控制系统中比较元件、校正元件、执行元件、被控对象(或过程)的含义。
(本题满分10分)1、求系统传递函数C(s)/R(s)(本题满分10分)系统的开环传递函数成为闭环传递函数为2、化简如下所示系统框图,求化简后的传递函数2n2n n ()(2)f G s s s K sωζωω=++《控制工程基础》复习用求系统传递函数C(s)/R(s)(本题满分15分)2、系统结构图如图所示,τ取何值时,系统才能稳定 ?(本题满分10分)3、已知1[()]()(1)L f t F s s s ==+, 试求lim ()t f t ->∞。
(本题满分8分)解:1()(1)sF s s =+的极点位于左半s 平面,所以极限存在。
用终值定理 :001lim ()()lim ()limlim 1(1)1t s s s s f t f sF s s s s ->∞->->->=∞====++4、一个由弹簧-质量-阻尼器组成的机械平移系统如图所示。
m 为物体质量,k 为弹簧系数,f 为粘性阻尼系数,外力F(t)为输入量,位移x(t)为输出量。
自动控制原理考试试题及答案(整理版)
自动控制原理考试复习题整理1.开环、闭环系统的最主要区别是()。
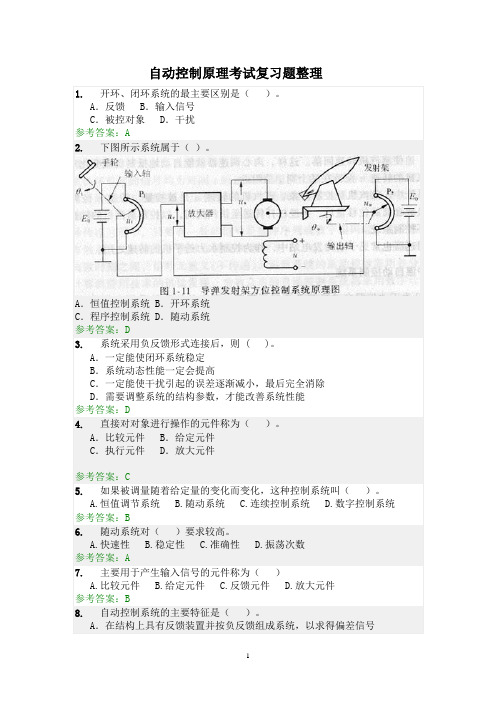
A.反馈 B.输入信号C.被控对象 D.干扰参考答案:A2.下图所示系统属于()。
A.恒值控制系统 B.开环系统C.程序控制系统 D.随动系统参考答案:D3.系统采用负反馈形式连接后,则 ( )。
A.一定能使闭环系统稳定B.系统动态性能一定会提高C.一定能使干扰引起的误差逐渐减小,最后完全消除D.需要调整系统的结构参数,才能改善系统性能参考答案:D4.直接对对象进行操作的元件称为()。
A.比较元件 B.给定元件C.执行元件 D.放大元件参考答案:C5.如果被调量随着给定量的变化而变化,这种控制系统叫()。
A.恒值调节系统B.随动系统C.连续控制系统D.数字控制系统参考答案:B6.随动系统对()要求较高。
A.快速性B.稳定性C.准确性D.振荡次数参考答案:A7.主要用于产生输入信号的元件称为()A.比较元件B.给定元件C.反馈元件D.放大元件参考答案:B8.自动控制系统的主要特征是()。
A.在结构上具有反馈装置并按负反馈组成系统,以求得偏差信号B.由偏差产生控制作用以便纠正偏差C.控制的目的是减少或消除偏差D.系统开环参考答案:ABC9.自动控制系统按输入信号特征可分为()。
A.恒值控制系统 B.程序控制系统C.线性系统 D.随动系统参考答案:ABD10.自动控制系统按描述元件的动态方程分()。
A.随动系统 B.恒值控制系统C.线性系统 D.非线性系统参考答案:CD11.自动控制系统的基本要求()。
A.稳定性 B.快速性C.准确性 D.安全性参考答案:ABC12.人工控制与自动控制系统最大的区别在于控制过程中是否有人参与。
()参考答案:√第二章控制系统的教学模型1.下图所示电路的微分方程是()。
A.B.C.D.参考答案:A2.下图所示电路的传递函数是()。
A.B.C.D.参考答案:A3.关于传递函数,错误的说法是()。
A 传递函数只适用于线性定常系统;B 传递函数不仅取决于系统的结构参数,给定输入和扰动对传递函数也有影响;C 传递函数一般是为复变量s的真分式;D 闭环传递函数的极点决定了系统的稳定性。
第二章传递函数习题与答案

第二章习题课一. 求图示系统结构图的传递函数)()(s R s C ,)()(s N s C ,)()(s R s E ,)()(s N s E 。
二.T 型网络如下图所示,试绘出其动态结构图,并求出传递函数)()(s U s U i o 。
1i三.系统的微分方程组为)()()(1t c t r t x -=)()()(21121t x t x k dtt dx T -=)()()(323t c k t x t x -=)()()(322t x k t c dtt dc T =+式中32121,,,,k k k T T 均为正的常数,系统的输入量为)(t r ,输出量为)(t c ,试画出动态结构图,并求)()(s R s C 。
四.求下图所示系统的传递函数。
五.用结构图化简法求系统传递函数)()(s R s Y 。
)(s六.系统动态结构图如图所示,试确定系统的闭环传递函数)()(s R s C第二章习题课一. 求图示系统结构图的传递函数)()(s R s C ,)()(s N s C ,)()(s R s E ,)()(s N s E 。
1、求)()(s R s C )1(1)1()()(5412152545421G G H G G G G G G G G GG s R s C -++--=2、求)()(s N s C))1)(1()1)(()()(5221545432G G H G G G G G G G G s N s C ++--+=)1(11)()(5412152545254G G H G G G G G G G G G G s R s E -++-+-=)1(1))(1()()(5412152543254G G H G G G G G G G G G G H s N s E -++-+--=二.T 型网络如下图所示,试绘出其动态结构图,并求出传递函数)()(s U s U i o 。
自动控制原理典型习题(含答案)

自动控制原理习题一、(20分)试用结构图等效化简求下图所示系统的传递函数)()(s R s C 。
解:所以:32132213211)()(G G G G G G G G G G s R s C +++= 二.(10分)已知系统特征方程为06363234=++++s s s s ,判断该系统的稳定性,若闭环系统不稳定,四.(121m -=222K K-0=1K ⇒=,s = 所以当1K >时系统稳定,临界状态下的震荡频率为ω五.(20分)某最小相角系统的开环对数幅频特性如下图所示。
要求(1) 写出系统开环传递函数; (2) 利用相角裕度判断系统的稳定性;(3) 将其对数幅频特性向右平移十倍频程,试讨论对系统性能的影响。
解(1)由题图可以写出系统开环传递函数如下:(2)系统的开环相频特性为截止频率1101.0=⨯=c ω相角裕度:︒=+︒=85.2)(180c ωϕγ故系统稳定。
(3)将其对数幅频特性向右平移十倍频程后,可得系统新的开环传递函数其截止频率10101==c c ωω而相角裕度︒=+︒=85.2)(18011c ωϕγγ= 故系统稳定性不变。
由时域指标估算公式可得)11(4.016.0-+=σoo=o o 1σ(1(2(2)121)(=s G 2函数。
1、的输出量不会对系统的控制量产生影响。
开环控制结构简单、成本较低、系统控制精度取决于系统元部件、抗干扰能力较差。
(2分)2、根轨迹简称为根迹,它是开环系统某一参数从零变到无穷时,闭环特征方程式的根在s 平面上变化的轨迹。
(3分)系统根轨迹起始于开环极点,终至于开环零点。
(2分)二、看图回答问题(每小题10分,共20分)1、解:结论:稳定(2分)理由:由题意知系统位于s 右半平面的开环极点数0=P ,且系统有一个积分环节,故补画半径为无穷大,圆心角为2122πππ-=⨯-=-v 的圆弧,则奈奎斯特曲线如图1示,(3分)由图可知系统奈奎斯特曲线包围(-1,j0)点的圈数为000=-=-=-+N N N ,(3分)由奈奎斯特稳定判据,则系统位于s 右半平面的闭环极点数02=-=N P Z ,(2分)故闭环系统稳定。
《控制工程基础》习题集(浓缩24页)

第一部分:单选题1.自动控制系统的反馈环节中必须具有[ ] a.给定元件 b .检测元件 c .放大元件 d .执行元件2. 在直流电动机的电枢回路中,以电流为输出,电压为输入,两者之间的传递函数是[ ] a .比例环节 b .积分环节 c .惯性环节 d .微分环节3. 如果系统不稳定,则系统 [ ]a.不能工作 b .可以工作,但稳态误差很大c .可以工作,但过渡过程时间很长d .可以正常工作4. 在转速、电流双闭环调速系统中,速度调节器通常采用[ ]调节器。
a .比例 b .比例积分 c .比例微分 d .比例积分微分5.单位阶跃函数1(t)的拉氏变换式L[1(t)]为[ ]:a .S b. S 1c. 21Sd. S 26. 在直流电动机的电枢回路中,以电流为输出,电压为输入,两者之间的传递函数是[ ] A .比例环节 B .积分环节 C .惯性环节 D .微分环节 7.如果系统不稳定,则系统 [ ]A. 不能工作 B .可以工作,但稳态误差很大C .可以工作,但过渡过程时间很长D .可以正常工作8. 已知串联校正网络(最小相位环节)的渐近对数幅频特性如下图所示。
试判断该环节的相位特性是[ ]:[ ]调节器。
[ ]:C. 相位滞后-超前D. 相位超前-滞后12. 开环增益K 增加,系统的稳定性( ):A .变好 B. 变坏 C. 不变 D. 不一定13. 开环传递函数的积分环节v 增加,系统的稳定性( ):A .变好 B. 变坏 C. 不变 D. 不一定14. 已知 f(t)=0.5t+1,其L[f(t)]=( ):A .S+0.5S 2 B. 0.5S 2 C. S S1212 D. S 2115.自动控制系统的反馈环节中必须具有( ):A.给定元件 B .检测元件 C .放大元件 D .执行元件16.PD 调节器是一种( )校正装置。
A .相位超前 B. 相位滞后 C. 相位滞后-超前 D. 相位超前-滞后17.已知最小相位系统的开环对数幅频特性曲线的渐近线如下图所示,试确定其开环增益K ( )。
《自动控制原理》第二章传递函数
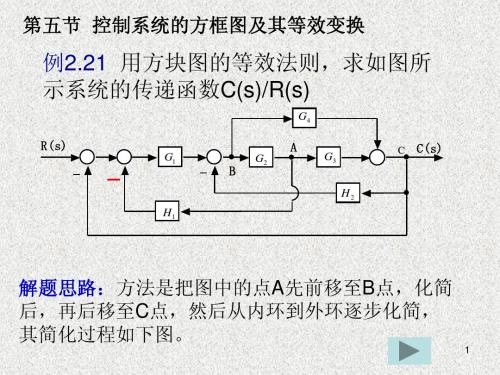
G2 ( s ) N ( s) 1 + G1 ( s)G 2 ( s) H ( s)
∑ C ( s ) = Φ ( s) R( s) + Φ ( s) N ( s) =
G2 ( s )[G1 ( s) R ( s) + N ( s )] 1 + G1 ( s)G 2 ( s ) H ( s)
20
N ( s)
14
例2.23
R(s)
G4 G1 A G3 H2 H1
C
p1 = G1G2G3
_
-
B
G2
C (s)
∆1 = 1
L1 = −G1 G 2 H 1
p2 = G1G4
∆2 = 1
L2 = − G 2 G 3 H 2 L3 = −G 1 G 2 G3
L4 = − G 4 H 2
注意:回路 注意: 找不全是最 大的问题
5
1 R 1 G1 -1 1 G2 -1 1 G3 -1 K C
1
-1
•前向通路:开始于输入节点,沿支路箭头方向,每个节点 前向通路:开始于输入节点,沿支路箭头方向, 前向通路 只经过一次,最终到达输出节点的通路称之前向通路。 只经过一次,最终到达输出节点的通路称之前向通路。 •回路:起点和终点在同一节点,并与其它节点相遇仅一次的通路。 回路:起点和终点在同一节点,并与其它节点相遇仅一次的通路。 回路 •回路中所有支路的乘积称为回路增益。 回路中所有支路的乘积称为回路增益。 回路中所有支路的乘积称为回路增益 •不接触回路:回路之间没有公共节点时, 不接触回路:回路之间没有公共节点时, 不接触回路 不接触回路。 这种回路叫做 不接触回路。 •在信号流图中,可以有两个或两个以上不接触回路。 在信号流图中, 在信号流图中 可以有两个或两个以上不接触回路。
例1某系统的结构图如图所示试求系统的传递函数
所以 则Gs 分母的常数项应为零。
设 则闭环系统传递函数为
Gs
k s as2 bs c
ห้องสมุดไป่ตู้
s
Gs k 3 1 Gs as bs2 cs k
14
特征方程式为
as3 bs2 cs k s 3 4s 2 6s 10 0
1 s
C s
2
(a)
s
s2
Rs
k
B
1 s
s 1
s
A
1 s
C s
(a)
s
s 1
s
s2
Rs
k
1 s
s 1
s
1 s
C s
k
3
(b)
s
s 1
s
s2
Rs
k
1 s
s 1
s
1 s
C s
k
(b)
s 1
总复习题
C s 例1.某系统的结构图如图所示。试求系统的传递函数 Rs
。
s
s2
Rs
k
1 s
A
s 1
s
1 s
C s
结构图
1
1.解:
Rs
s
s2
k
1 s
A
s 1
s
1 s
C s
结构图
s
自动控制原理试卷及答案
1《自动控制原理》试卷(A 卷)一、 用运算放大器组成的有源电网络如图所示,试采用复数阻抗法写出它的传递函数。
(10分)(1图 )(3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、试用梅逊增益公式求图中系统的闭环传递函数。
(写出步骤)(10分)四、控制系统的结构如图所示,设 r(t ) = t ⋅ 1(t ) ,p (t ) = 1(t )定义e (t ) = r(t ))(t y -,试求系统的稳态误差。
(10分)(4图)五、试确定题图所示系统参数K 和ξ的稳定域。
(写步骤)(10分)(5图)六、设单位反馈控制系统的开环传递函数为(1) 绘制根轨迹,并加以简要说明。
(2) 当系统的阻尼振荡频率s rad /1d =ω时试确定闭环主导极点的值与相应的增益值。
(15分)七、最小相位系统的开环对数幅频特性的渐近线如图所示,确定系统的开环传递函数。
(10分)八、已知最小相位系统校正前后系统的折线对数幅频特性如图所示,其中Lo(ω)为校正前特性,L开(ω)为校正后特性。
(1)试作出校正装置的对数幅频特性Lc(ω)(折线);(2)试写出校正装置的传递函数Gc(s);(3)计算校正后系统的相位裕度γ。
(15分)cp为s右半平面上的开环根的个数,v为开九、设开环系统的奈氏曲线如下图所示,其中,环积分环节的个数,试判别闭环系统的稳定性。
(10分)(a)(b)2《自动控制原理》试卷(B 卷)一、 求下图所示系统的传递函数)(/)(0s U s U i 。
(10分)(1图) (3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、系统的信号流图如图所示,求输出C (S )的表达式。
机械工程控制基础题库2
第二章1. 在转速、电流双闭环调速系统中,速度调节器通常采用[ B ]调节器。
a.比例 b.比例积分c.比例微分 d.比例积分微分2. 在直流电动机的电枢回路中,以电流为输出,电压为输入,两者之间的传递函数是[ A ]A.比例环节 B.积分环节C.惯性环节 D.微分环节3. 在转速、电流双闭环调速系统中,速度调节器通常采用[ B ]调节器。
A.比例 B.比例积分C.比例微分 D.比例积分微分4. 振荡环节的传递函数为( a )。
A. ωn /(S2+2ξωn S+1) (0<ξ<1) ;B. ωn /(S2+2ξωn S+1) (ξ=1);5.函数b + ce-at(t≥0)的拉氏变换是( c )。
A、bS + c/(S+1) ;B、 bS – c/(S+a) ;C、 b/S + c/(S+a) ;D、 b/S + c/(S-a)6.某机械平移系统如图所示,则其传递函数的极点数P 为( )。
A. 3 ; B. 4 ; C.5 ; D. 67. cos2t 的拉普拉斯变换式是 〔 〕 A. S 1B.442+SC.42+S SD. 21S8. 已知 f(t)=0.5t+1,其L[f(t)]=( ): A .S+0.5S 2 B. 0.5S 2 C.S S1212+ D. S 21 9.下列函数既可用初值定理求其初值又可用终值定理求其终值的为:( )。
A. 5/(S 2+25);B.5/(S 2+16);C. 1/(S-2);D.1/(S+2)10.函数b + ce -at (t ≥0)的拉氏变换是( )。
A 、 bS + c/(S+1) ;B 、bS – c/(S+a) ;C 、b/S + c/(S+a) ;D 、b/S + c/(S-a)11.振荡环节的传递函数为( )。
A.ωn /(S 2+2ξωn S+1) (0<ξ<1) ;B.ωn /(S 2+2ξωn S+1)(ξ=1);C. T 2/(T 2S 2+2ξTS+1) (0<ξ<1) ;D.1/[S (TS+1)]12.下列函数既可用初值定理求其初值又可用终值定理求其终值的为:( )。
自动控制原理 吴怀宇 课后习题 第二章
第二章2-1试求下图所示电路的微分方程和传递函数。
解:(a )根据电路定律,列写出方程组:001L i R c L R C di L u u dtu R i i dt Ci i i ⋅+==⋅==+⎰ 消除中间变量可得微分方程:20002i d u du L L C u u dt R dt⋅⋅+⋅+= 对上式两边取拉氏变换得:2000()()()()i L L C U s s U s s U s U s R⋅⋅⋅+⋅⋅+= 传递函数为022()1()()1i U s R G s L U s R Ls LCRs s LCs R ===++++ (b)根据电路定律,列写出方程组:12011()i i u i R R idt C u u i R =++-=⎰消除中间变量可得微分方程:121012i R R R u u idt R R C+=-⎰ 对上式两边取拉氏变换得:2012()(1)()(1)i U s R Cs U s R Cs R Cs +=++ 传递函数为0212()1()()1i U s R Cs G s U s R Cs R Cs+==++2—3求下图所示运算放大器构成的电路的传递函数.解:(a )由图(a ),利用等效复数阻抗的方法得22111(s)1(s)()1o i R U R Cs Cs G U s R R Cs ++==-=-+ (b )由图(b ),利用等效复数阻抗的方法得222121211221211111(s)()1(s)1()1o i R U C s R R C C s R C R C s G U s R C s R C sR C s ++++==-=-+ 2—5试简化下图中各系统结构图,并求传递函数()()C s R s 。
2-6试求下图所示系统的传递函数11()()C s R s ,21()()C s R s ,12()()C s R s 及22()()C s R s 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、求下图所示系统的传递函数)(/)(0s U s U i 。
(10分) )1()()(3132320+++-=CS R R R R CS R R s U s U i 一、控制系统方块图如图所示:
(1)当a =0时,求系统的阻尼比ξ,无阻尼自振频率n ω和单位斜坡函数输入时的稳态误差;
(2)当ξ=0.7时,试确定系统中的a 值和单位斜坡函数输入时系统的稳态误差;
系统的开环传函为
s
a s s G )82(8)(2++=闭环传函为8)82(8)()(2+++=s a s s R s Y 25.0 83.2 36.0===ss n e ωξ4 25.0==ss e a
设某控制系统的开环传递函数为
)
22()(2++=s s s k s G 试绘制参量k 由0变至∞时的根轨迹图,并求开环增益临界值。
(15分)
1)j p j p p --=+-==110
321 2)πππϕσ3
5,,332=-=a a (10分) 3)ω=j 2±,c k =4,开环增益临界值为K=2
设某系统的特征方程为23)(2
34+--+=s s s s s D ,试求该系统的特征根。
列劳斯表如下 000022
0112311
23
4
s s s s ---(4分)
得辅助方程为0222=+-s ,解得1,
121-==s s (4分) 最后得1,243=-=s s
设某控制系统的开环传递函数为
)()(s H s G =)10016()12.0(752+++s s s s 试绘制该系统的Bode 图,并确定剪切频率c ω的值
剪切频率为s rad c /75.0=ω
某系统的结构图和Nyquist 图如图(a)和(b)所示,图中
2)1(1)(+=s s s G 23
)
1()(+=s s s H 试判断闭环系统稳定性,并决定闭环特征方程正实部根的个数。
(16分)
解:由系统方框图求得内环传递函数为:
s
s s s s s s H s G s G +++++=+23452
474)1()()(1)((3分) 内环的特征方程:04742345=++++s s s s s (1分)
由Routh 稳定判据:
01:0
310:
16:
044:
171:
01234s s s s s
七、设某二阶非线性系统方框图如图所示,其中 4 , 2.0 , 2.00===K M e 及s T 1=,试画出输入信号)(12)(t t r ⋅=时系统相轨迹的大致图形,设系统原处于静止状态。
(16分)
解:根据饱和非线性特性,相平面可分成三个区域,运动方程分别为
区)
(区)
(区)
(III 2.0 08.0II 2.0 08.0I 2.0|| 04-<=-+>=++<=++e e e e e e e e e e (9分)
相轨迹大致图形为
(7分)
什么是闭环主导极点?
所有闭环极点距离虚轴最近的极点 周围没有闭环零点 而其他闭环极点又远离虚轴这样的极点为闭环极点
对自动控制系统的基本要求有哪些?时域中的动态性能指标有哪些?
要求:准确性 快速性 稳定性 指标: 延迟时间td 上开时间tr 峰值时间tp 调节时间ts 超调&%
什么是参量根轨迹?
随着开环传递函数种某一参数的变化 这一参数出去开环增益 闭环极点在S 平面的变化轨迹成为参量根轨迹
设控制系统(图) 若要求系统在单位斜坡输入信号作用时,位置输出稳态误差ess (正无穷)≤0.
1、 常见的建立数学模型的方法有哪几种?各有什么特点?
2、 PD 属于什么性质的校正?它具有什么特点?
3、 幅值裕度,相位裕度各是如何定义的?
4、 举例说明什么是闭环系统?它具有什么特点?
1、有以下三种:
1. 机理分析法:机理明确,应用面广,但需要对象特性清晰
2. 实验测试法:
不需要对象特性清晰,只要有输入输出数据即可,但适用面受限
3. 以上两种方法的结合
通常是机理分析确定结构,实验测试法确定参数,发挥了各自的优点,克
服了相应的缺点
2、 超前校正。
可以提高系统的快速性,改善稳定性。
3、 |
)()(|1`g g g jw H jw G K = , 。
180)()(-=∠g g jw H jw G 1|)()(| ),()(180)=∠+=c c c c c jw H jw G jw H jw G w 。
(γ
4、 既有前项通道,又有反馈通道,输出信号对输入信号有影响。
存在系统稳定性问题。
(例子任意)
系统如图2所示
求:
(1))
()()(s E s Y s G == (2))()()(s R s C s =φ=1
1)(0+==TS S G T S
设单位反馈系统的开环传递函数为
1
2 )1()(23++++=s s s s K s G α 若系统以2rad/s 频率持续振荡,试确定相应的K 和α值
五、(10分)
理想PID 算式为:
)1
(dt
de T edt T e K P D I P ⎰++=, 试推导出离散PID 的增量式算式。
(1))()()()()()(21s H s G s G s E s Y s G ==
(2))
()()(1)()()()()(2121s H s G s G s G s G s R s C s +==ϕ 四、(15分)
2=K ,75.0=α ,可以利用Routh 判据或其它方法解答 五))2((211---+-++-=∆n n n s
D n I s n n c n e e e T T e T T e e K P 二、 某控制系统的方框图如图所示,欲保证阻尼比ξ=0.7和响应单位斜坡函数的稳态误差为
ss e =0.25,试确定系统参数K 、τ。
(15分)
二、解:s
τK s K s G k )2()(2++= (2分) K
s τK s K s R s C +++=)2()()(2 (2分) K
s τK s s τK s s R s E +++++=)2()2()()(22 (2分) 25.02=+=K
K e ss τ,(2分) K n =ω,τξωK n +=22 (4分) 综合上面的式子,得
31=
=τ
K
.
36
.0
,
186。
