长方体正方体思维训练(含答案)(最新整理)
最新苏教版六年级数学同步思维训练(上册)

第一讲:长方体和正方体的表面积同学们,我们已经知道长方体(或正方体)6个面的总面积,叫做它的表面积。
在实际生产和生活中,有时不需要计算6个面的总面积,只需要计算某几个面的总面积,解题时需要根据具体情况思考要求哪几个面的面积和,再进行计算。
解答这类问题,不仅需要我们具备较扎实的基础知识和观察能力、作图能力和空间想象能力,还要掌握一些解题的方法和技巧。
例题1:小明和妈妈一起给奶奶买了一份礼物,营业员阿姨用一个长30厘米、宽20厘米、高10厘米的长方体盒子装好,并用彩带捆扎起来(打结处的彩带长15厘米),一共需彩带多少厘米?【思路点拨】要求彩带的长度,应该将这些彩带分类整理。
这段彩带包括了打结的15厘米,高有4段,共32厘米,长宽各有2段,共有30×2+20×2=100厘米。
最后只要将这些彩带的长度相加即可。
想一想:还有别的解法吗?例题2:用5个相同的立方体,粘接成一个长方体,总棱长84厘米。
这个长方体的表面积是多少?【思路点拨】要求长方体的表面积的关键是求出长方体的长、宽、高;由于这个长方体是有立方体粘接成,若立方体棱长是a,那么长方体的长和高都是a,宽等于5a;根据题意,得4a×2+5a×4=84,a=3,表面积=a×a×2+5a×a×4=3×3×2+3×15×4=198(平方厘米)例题3:一个立方体增高2厘米(这样底面不变)后,得到一个长方体。
长方体的表面积比原来立方体的表面积增加了96平方厘米。
原来立方体表面积是多少平方厘米?现在长方体的表面积是多少?【思路点拨】长方体比立方体表面积增加了96平方厘米,就是增加了侧面的面积,即4个相等的长方形面积,这个长方形的宽是2厘米,长96÷4÷2=12厘米,长就是立方体的棱长。
立方体的表面积是:12×12×6=864(平方厘米)长方体的表面积是:864+96=960(平方厘米)想一想:还有别的解法吗?1、小明给教师买了一个教师节礼物,他用一个长方体纸盒装礼物,长方体纸盒长35厘米、宽20厘米、高8厘米把它用彩绳包扎起来,打结处需要20厘米(如图),一共需要彩绳多少厘米?2、一个长方体的长是6厘米,宽和高都是2厘米。
小学数学四年级升五年级《思维训练》题(长方形和正方形)
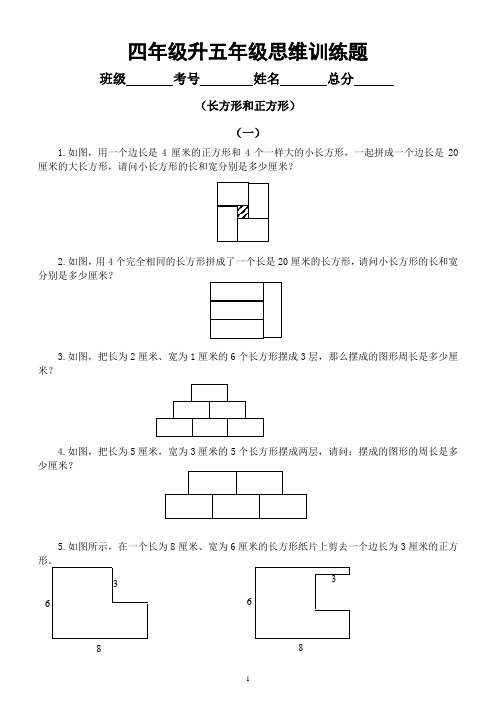
四年级升五年级思维训练题班级 考号 姓名 总分(长方形和正方形)(一)1.如图,用一个边长是4厘米的正方形和4个一样大的小长方形,一起拼成一个边长是20厘米的大长方形,请问小长方形的长和宽分别是多少厘米?2.如图,用4个完全相同的长方形拼成了一个长是20厘米的长方形,请问小长方形的长和宽分别是多少厘米?3.如图,把长为2厘米、宽为1厘米的6个长方形摆成3层,那么摆成的图形周长是多少厘米?4.如图,把长为5厘米,宽为3厘米的5个长方形摆成两层,请问:摆成的图形的周长是多少厘米?5.如图所示,在一个长为8厘米、宽为6厘米的长方形纸片上剪去一个边长为3厘米的正方(1)如果剪去的正方形在右上角,那么剩下的图形周长是多少厘米?(2)如果剪去的正方形在右边,那么剩下的图形周长是多少厘米?6.如图所示,在一个边长为6厘米的正方形纸片上减去一个长3厘米、宽2厘米的长方形,那么剩下的图形的周长是多少厘米?7.如图,这个多边形任意相邻的两条边都互相垂直,那么这个多边形的周长是多少?8.如图,这个多边形任意相邻的两条边都互相垂直,那么这个多边形的周长是多少?9.如图所示,一个边长10厘米的正方形纸片,被横着剪了一刀,竖着剪了两刀,分成了6个小长方形纸片,这6个小长方形纸片的周长总和等于多少厘米?6 2 3 8 3 4 110如图,在一个长方形中有一块阴影部分,如果阴影部分恰好是正方形,那么图中大长方形的周长是多少厘米?6厘米9厘米11.如图,用4个完全相同的长方形拼成了一个边长是40厘米的正方形,请问小正方形的长和宽分别是多少厘米?12.如图所示,把长为4厘米、宽为2厘米的3个长方形摆成两层,请问:摆成的图形的周长是多少厘米?13.如图所示,在一个边长为4厘米的正方形纸片上剪去一个边长为1厘米的正方形,那么剩下的图形的周长是多少厘米?14.如图所示,其中任意相邻的两条边都互相垂直,请问:这个图形的周长是多少?15.一块边长为30厘米的正方形蛋糕,横着切2刀,竖着切2刀,分成了9个小长方形,这9块小长方形蛋糕的周长总和为多少厘米?(二)1.有一块长方形的土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是一个正方形,周围是草坪,草坪的面积是多少平方米?(单位:米)2.如下图,有一个长方形的市民广场,长100米,宽80米。
【北师大版】五年级数学下册--第二单元《长方体(一)》--知识点+思维导图+针对性训练
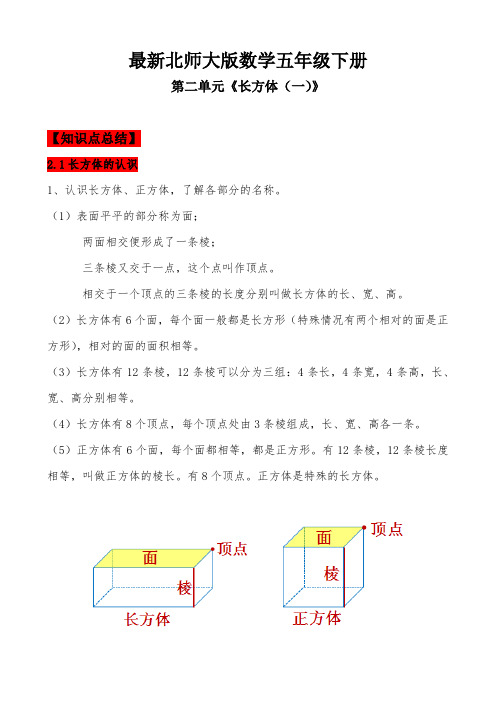
最新北师大版数学五年级下册第二单元《长方体(一)》【知识点总结】2.1长方体的认识1、认识长方体、正方体,了解各部分的名称。
(1)表面平平的部分称为面;两面相交便形成了一条棱;三条棱又交于一点,这个点叫作顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
(2)长方体有6个面,每个面一般都是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等。
(3)长方体有12条棱,12条棱可以分为三组:4条长,4条宽,4条高,长、宽、高分别相等。
(4)长方体有8个顶点,每个顶点处由3条棱组成,长、宽、高各一条。
(5)正方体有6个面,每个面都相等,都是正方形。
有12条棱,12条棱长度相等,叫做正方体的棱长。
有8个顶点。
正方体是特殊的长方体。
2、长方体、正方体各自的特点。
3、长方体的棱长总和=(长+宽+高)×4,或者是长×4+宽×4+高×4正方体的棱长总和=棱长×122.2展开与折叠正方体的展开图,一共11种。
第一类,中间四连方,两侧各一个,共六种。
第二类,中间三连方,两侧各有一、二个,共三种。
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
注意:“田”字型与“凹”字型的是错误的。
2.3长方体的表面积1、表面积的意义:是指六个面的面积之和。
2、长方体表面积的计算方法:长方体上面(或下面)的面积=长×宽长方体前面(或后面)的面积=长×高长方体左面(或右面)的面积=宽×高长方体的表面积=长×宽×2+长×高×2 +宽×高×2,用字母表示为:S长 = a×b×2+ a×h×2 +b×h×2或者,长方体的表面积=(长×宽+长×高 +宽×高)×2,用字母表示为:S长 = (a×b+ a×h +b×h)×23、正方体表面积的计算方法:正方体每个面的面积=棱长×棱长。
思维训练第4周(含答案)

第4周最大公因数思维导航:几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数。
我们可以把自然数a、b的最大公因数记作(a、b),如果(a、b)=1,则a和b互质。
求几个数的最大公因数可以用分解质因数和短除法等方法。
第一天:1、一张长方形的纸,长7分米5厘米,宽6分米。
现在要把它裁成一块块正方形,而且正方形边长为整厘米数,有几种裁法?如果要使裁得的正方形面积最大,可以裁多少块?2、将一块长80米、宽60米的长方形土地划分成面积相等的小正方形,小正方形的面积最大是多少?第二天:3、一个长方体木块的长是4分米5厘米、宽3分米6厘米、高2分米4厘米。
要把它切成大小相等的正方体木块,不许有剩余,求所切正方体木块的棱长最长是多少厘米?4、有50个梨,75个橘子和100个苹果,要把这些水果平均分给儿个小组,并且每个小组分得的三种水果的个数也相同,最多可以分给几个小组?第三天:5、有三根钢管,它们的长度分别是240厘米、200厘米和480 厘米,如果把它们截成同样长的小段,每小段最长可以是多少厘米?6、工人加工了三批零件,每加工一批零件,除了王师傅比其他工人多加工若干个外,其他工人加工的都同样多。
已知他们第一批共加工2100个,其中王师傅比每个工人多加工7个;第二批加工1800 个,其中王师傅比每个工人多加工6个;第三批加工1600个,其中王师傅比每个工人多加工13个。
这批工人最多有多少人?第四天:7、有336支铅笔,252块橡皮,210个文具盒,用这些文具,最多可以分成多少份同样的礼物?在每份礼物中,铅笔、橡皮、文具盒各有多少?8、甲数是36,甲、乙两数的最小公倍数是288,最大公约数是4,乙数是多少?第五天:9、用一张长1072毫米、宽469毫米的长方形纸,剪成面积相等的正方形,并且最后没有剩余,这些正方形的边长最长是多少?10、求568和1065的最大公约数。
(建议用辗转相除法)第4周最大公因数答案IL 9a。
小学数学总复习-立体图形思维训练题(含答案)

小学数学总复习-立体图形班级:姓名:分数:基础练习1、填空(1)把圆柱的侧面沿高展开,一般可以得到(长方)形,这个图形的长相当于(底面圆周长),宽相当于(高)。
(2)用一根铁丝焊接成一个长10厘米、宽3厘米、高2厘米的长方体框架,至少需要铁丝( 60 )厘米。
(3)一个长方体最多可以有( 2 )个面是正方形,最多可有( 8 )条棱长相等。
(4)做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求它的(表面积),罐头盒周围贴商标纸,求商标纸的面积是求它的(侧面积)。
(5)做一只圆柱形通风管要用多少铁皮,是求它的(侧面积)。
(6)一个正方体的底面周长是8分米,它的表面积是(24平方分米),体积是(8立方分米)。
(7)圆锥的体积是100立方米,高是10米,它的底面积是(30 )平方米。
(8)一个圆柱和圆锥的体积相等,底面积也相等,圆柱高6厘米,圆锥高( 18 )厘米。
(9)圆柱与圆锥的高之比是3:2,底面半径比是4:3,那么圆柱与圆锥的体积比是(8:1)。
分析:半径之比为4:3,则底面积之比为16π:9π=16:9圆柱体积=16*3=48圆锥体积=9*2*(1/3)=6圆柱和圆锥的体积之比是48/6=8/1拓展练习1、一个正方体所有棱长的和是72厘米,它的表面积是多少平方厘米?棱长=72/12=6CM,表面积=6*6*6=216平方厘米2、一个长方体所有棱长的和是96厘米,长、宽、高的比是3:2:1,它的体积是多少立方厘米?长+宽+高=96÷4=24厘米;长=24×3÷(3+2+1)=12厘米;宽=24×2÷(3+2+1)=8厘米;3、小明要糊一个长方体募捐箱,但忘了箱子的长,宽,高,只记得是框架是用一根36分米的铁丝做成的,而且长、宽、高都是整分米数,他至少要买多少红纸才能保证够用?36/4=9(长方体框架由4条长、4条宽及4条高组成)也即长宽高的和为9表面积最小,长宽高尽可能接近。
小学数学总复习-立体图形思维训练题(含答案)

小学数学总复习-立体图形班级:姓名:分数:基础练习1、填空(1)把圆柱的侧面沿高展开,一般可以得到(长方)形,这个图形的长相当于(底面圆周长),宽相当于(高)。
(2)用一根铁丝焊接成一个长10厘米、宽3厘米、高2厘米的长方体框架,至少需要铁丝( 60 )厘米。
(3)一个长方体最多可以有( 2 )个面是正方形,最多可有( 8 )条棱长相等。
(4)做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求它的(表面积),罐头盒周围贴商标纸,求商标纸的面积是求它的(侧面积)。
(5)做一只圆柱形通风管要用多少铁皮,是求它的(侧面积)。
(6)一个正方体的底面周长是8分米,它的表面积是(24平方分米),体积是(8立方分米)。
(7)圆锥的体积是100立方米,高是10米,它的底面积是(30 )平方米。
(8)一个圆柱和圆锥的体积相等,底面积也相等,圆柱高6厘米,圆锥高( 18 )厘米。
(9)圆柱与圆锥的高之比是3:2,底面半径比是4:3,那么圆柱与圆锥的体积比是(8:1)。
分析:半径之比为4:3,则底面积之比为16π:9π=16:9圆柱体积=16*3=48圆锥体积=9*2*(1/3)=6圆柱和圆锥的体积之比是48/6=8/1拓展练习1、一个正方体所有棱长的和是72厘米,它的表面积是多少平方厘米?棱长=72/12=6CM,表面积=6*6*6=216平方厘米2、一个长方体所有棱长的和是96厘米,长、宽、高的比是3:2:1,它的体积是多少立方厘米?长+宽+高=96÷4=24厘米;长=24×3÷(3+2+1)=12厘米;宽=24×2÷(3+2+1)=8厘米;3、小明要糊一个长方体募捐箱,但忘了箱子的长,宽,高,只记得是框架是用一根36分米的铁丝做成的,而且长、宽、高都是整分米数,他至少要买多少红纸才能保证够用?36/4=9(长方体框架由4条长、4条宽及4条高组成)也即长宽高的和为9表面积最小,长宽高尽可能接近。
人教版数学三年级上册长方形、正方形周长思维训练
1、长方形和正方形的边有什么特点?
长方形的对边相等
正方形的四条边都相等
2、长方形和正方形的周长怎么求?
长方形的周长= (长+宽)×2 正方形的周长= 边长×4
3、计算下面图形的周长。
10米
20米
8厘米
(20+10)×2=60(米) (8+5)×2=26(厘米)
9厘米
5×4=20(厘米)
(7+3+6)×2=32(厘米)
求下面图形的周 长
5 厘 米 5厘米
1
2
3 1
2
3
(单位:米)
周长是
20厘米 。
周长是
24米
。
蚂蚁回家——上下左右相等
例2:小蚂蚁沿着下面的图形找食物,它如果绕着 这个图形走一圈,一共要走多少厘米?
2 3
4
8
4
向上:8+4=12(厘米) 向下: 12(厘米) 向右:3+4+2=9(厘米) 向左: 9(厘米)
a
a
a+b=10(厘米、平移——转化为规则图形 2、蚂蚁回家——上下左右相等
3、等量代换——整体思想
A
(12+9)×2=42(厘米)
答:一共要走42厘米。
求下面图形的周 长。
1
2
(单位:厘米)
2
5
15 10 25
7
3 5 10
30
周长是 18厘米 。 周长是 42厘米 。 周长是 150厘米 。
等量代换——整体思想
例3:如图,在一个长为10厘米的长方形上截下 最大的正方形 一个最大的正方形,求剩下的图形的周长。 (单位:厘 米) a 10 b
1、长(正)方体专题训练(一)-答案
长方体与正方体训练一答案
(基本公式及情境辨识)
一、基本公式
1、棱长总和:所有棱的长度和。
(长度单位)
表面积:长方体(正方体)6个面的总面积。
(面积单位)体积:物体所占空间的大小。
(体积单位)
2、基本公式
长方体上(下)面面积计算公式:长×宽
长方体前(后)面面积计算公式:长×高
长方体左(右)面面积计算公式:宽×高
二、情境辨识。
在括号内填出问题所求的是“棱长总和”或“表面积”或“体积”或“容积”
1、一个长方体框架长8厘米,宽6厘米,高4厘米,
(1)做这个框架共要用多少厘米铁丝,是求长方体(棱长总和),
(2)在表面贴上塑料板,共要用多少塑料板是求(表面积),
(3)这个盒子有多少立方厘米是求(体积)
(4)在里面能盛多少升水是求(容积)
2、游泳池占空间大小时候求它的(体积),蓄水多少时指它的(容积)
3、长(正)方体表面贴包装纸是求它的(表面积)
如果在棱上粘贴胶带,是求它的(棱长总和)
4、空调(布衣柜)换布罩是求它的(棱长总和),不考虑少面。
5、长方体土坑内的土是指它的(体积)
6、制作长方体邮箱的铁皮是指它的(表面积)
7、正方体鱼缸的玻璃是指它的(表面积)不考虑少面。
盛水多少是指它的(容积)
8、通风管(烟囱)的铁皮是指它的(表面积)不考虑少面。
长方体正方体 练习题含答案
长方体正方体练习题1、长、宽、高分别为30cm、30cm、20cm的小纸箱,在所有的棱上粘上一圈胶带,至少需要多长的胶带?(30+30+20)×4=320(cm)答:至少需要320厘米的胶带。
2、五一劳动节,工人叔叔要在工人俱乐部的四周装上彩灯(地面的四边不装),已知工人俱乐部长90m,宽55m,高22m,工人叔叔至少需要多长的彩灯线?(90+55)×2+20×4=370(m)3、要做一个长2.2m、宽40cm、高80cm的玻璃柜台,现在要在柜台各边都安上角铁,至少需要多少米的角铁?40厘米=0.4米,80厘米=0.8米,(2.2+0.4+0.8)×4=13.6(米)答:至少需要13.6米的角铁。
4、一个长方体的饼干盒,长10cm,宽6cm,高12cm,如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?(10×12+6×12)×2=384(平方厘米)答:这张商标纸的面积至少有384平方厘米。
5、把一个棱长46cm的正方体纸箱的各面都贴上红纸,将它作为给希望小学捐款的“爱心箱”。
(1)他们至少需要多少平方厘米的红纸?(2)如果只在棱上粘贴胶带纸,一卷长4.5m的胶带纸够用吗?(1)46×46×6=12696(平方厘米)答:他们至少需要12696平方厘米的红纸。
(2)46cm=0.46m0.46×12=5.52(m)5.52>4.5答:一卷长4.5m的胶带纸不够用。
6、玻璃鱼缸的形状是正方体,棱长3dm,制作这个鱼缸时至少需要玻璃多少平方分米?(上面没有盖)3×3×5=45(平方分米)答:制作这个鱼缸时至少需要玻璃45平方分米。
7、一个长方体礼品盒,棱长1.5dm,如果包装这个礼品盒的用纸是其表面积的1.5倍,至少需要多少平方分米的包装纸?6×1.22×1.5=12.96(平方分米)答:至少要用12.96平方分米的包装纸。
华二小五班-思维训练1 长方体与正方体
思维训练1 长方体与正方体【Did you know】长方体和正方体的特征,长方体和正方体的表面积、体积计算。
已知长方体的高分别为a,b,c,则它的表面积是:它的体积是已知正方体的棱长为a,则它的表面积是它的体积是【Try it out】1.一个长方体,前面和上面的面积之和是209平方厘米,这个长方体的长、宽、高以厘米为单位都是质数,这个长方体的体积和表面积各是多少?2.在一个长15分米,宽12分米的长方体水箱中,有10分米深的水,如果在水中沉入一个棱长为30厘米的正方体铁块,那么,水箱中水深多少分米?3.一个长方体容器内装满水,现在有大、中、小三个铁球,第一次把小球沉入水中;第二次把小球取出,把中球沉入水中;第三次把中球取出,把小球和大球一起沉入水中。
已知每次从容器中溢出水量的情况:第二次是第一次的3倍,第三次是第一次的2.5倍。
问:大球的体积是小球的多少倍?4.一个长方体容器的底面是一个边长为60厘米的正方形,容器里直立着一个高1米,底面边长15厘米的长方体铁块,这时容器里的水深0.5米,如果把铁块取出,容器里水深多少厘米?【Exercise】1.一个长方体棱长总和是48厘米,已知长是宽的1.5倍,宽是高的2倍,求这个长方体的体积。
2.用2100个棱长是1厘米的正方体木块堆成一个实心的长方体,已知长方体的高是10厘米,并且长和宽都大于高,这个长方体的长和宽各是多少厘米?3.在一个长20分米,宽15分米的长方体容器中,有20分米深的水。
现在在水中沉入一个棱长30厘米的正方体铁块,这时容器中水深多少分米?4.把一个长9厘米,宽7厘米,高3厘米的长方体铁块和一块棱长5厘米的正方体铁块熔铸成一个底面积是20平方厘米的长方体。
求这个长方体的高。
5.有一块长方形的铁皮,长30厘米,宽20厘米,在这块铁皮的四角各剪下一个边长为2厘米的小正方形,然后制成一个无盖的长方体盒子(1)求这个盒子的容积;(2)做这个盒子拱了多少平方厘米的铁皮?。
