理论力学第5章 点的复合运动分析
理论力学-5-运动学基础

ds =v =s dt
dv at s dt
an
v
2
a a a
2 τ
2 n
5.1 点的运动学
自然轴系
自然轴系
当运动轨迹为空间曲线时,弧坐标系中所得 到的结论同样成立,只需将弧坐标系扩展为自然 轴系。
5.1 点的运动学
自然轴系P-TNB
B(副法线) N(主法线)
0
dτ n d
5.1 点的运动学
τ vτ av
τ
弧坐标法
τ ?
ds =v =s dt
dτ dτ d ds dt d ds dt
dτ n d
d 1 曲率 ds
a at an at τ an n
速度方向的变化率 法向加速度
xA OC CM R
M
即
CM v0t R R
v0t x OC AM sin v t R sin 0 R 于是M点的运动方程为: vt y AC AM cos R R cos 0 R
5.1 点的运动学
v0t x OC AM sin v t R sin 0 R vt y AC AM cos R R cos 0 R
切线方向的单位矢量为t ,则有 r ds lim τ =v = s t 0 s dt t指向弧坐标s增加的方向。 动点的速度为
τ v vτ s
速度方向
速度大小
5.1 点的运动学
弧坐标法
加速度
dτ dτ d ds dt d ds dt dτ d 1 ds 曲率 ? =v =s ds d dt τ
理论力学答案第5章点的复合运动分析
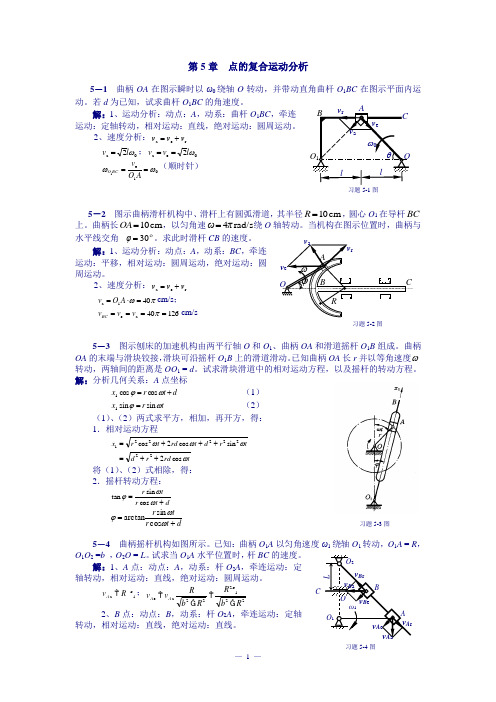
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
浅析复合运动点的速度和加速度分析

1 点的复合运动点或者物体只相对于一个参考系的运动为简单运动;反之,点或者物体相对于多个参考系的运动为复合运动。
在工程或者实际生活中,复合运动实例很常见,一般研究方法是相对于两个参考系为最简单复合运动的单元运动来分析,然后再用叠加原理依次解决工程实际问题。
分析复合运动前,参考系确定是关键。
为研究方便,本文将研究对象的点看成是动点,且只有两个参考系的简单复合运动的情况。
动点相对于静止不动的参考系称为静参考系,简称静系;另一个参考系是相对于静系运动的坐标系称为动参考系,简称动系。
自此,动点、动系以及静系三个确定复合运动的基本参数的已基本确定,这对后续相关分析至关重要。
在研究点的合成运动时,动点相对于静系和动系以及静系和动系之间会产生三种运动,这三种运动都可以用平行四边形法则或者三角形法则来确定,且思路清晰,复合运动就变得简单了。
三种运动分别是指动点相对于静系的运动为绝对运动、动点相对于动系的运动为相对运动以及动系相对于静系的运动为牵连运动。
其中,绝对运动用a表示,相对运动用r 表示,牵连运动用e表示。
用平行四边形法则或者三角形法则分析合成运动时,绝对运动为法则中的“合”,而其他两个运动就是法则中“分”。
因此,法则满足“分”首尾相接,“合”为首尾相接中的起点到终点的方位;掌握了这个基本方法,解决多数工程实际问题就游刃有余了。
例如,曲柄滑块机构如图1所示,曲柄长r,倾角为θ为60°,图示瞬时φ=60,曲柄的角速度ω,角加速度为α,分析此时滑道BCDE的速度和加速度。
速度和加速度分析都可用平行四边形法则和三角形法A作为动点,地面作为O(静系)v a、a a;动点相对于滑道BCDE(动系)的移动为相对运动,则速度、加速度分别为v r、a r;滑道BCDE(动系)相对于地面(静系)的左右移动就为牵连运动,则速度、加速度分别为v e、a e。
依据上述分析,要计算滑道BCDE的速度和加速度,其实就是计算系统的牵连速度、牵连加速度v e、a e。
论点的复合运动中动点、动系的选择原则和方法

论点的复合运动中动点、动系的选择原则和方法1引言理论力学是机械、土木类专业的专业基础课。
包括静力学、运动学和动力学三大部分。
运动学是从几何角度研究物体运动轨迹、运动方程、速度和加速度,而不考虑引起物体运动的物理原因。
其中点的合成运动是运动学的重点内容。
此部分内容题目多样,解题方法灵活,并且具有趣味性,完成一道题目时很有成就感。
当然也是让学生感到没有思路、无从下手的部分,普遍反映难度较大,也是测验、考核过程中丢分比较多的部分,问题的关键是无法正确的选取动点和动系。
本文从典型例题出发,介绍了点的合成运动中动点和动系的选取原则,可以帮助学生理清思路,提高点的合成运动的解题能力。
2点的合成运动概述在日常生活中,会经常遇到这样的情况。
当我们站在不同的参考物上,观察同一个物体的运动,发现物体所呈现的运动形式是不一样的。
举个最常见的例子,如图1。
人站在一辆沿直线匀速行驶的公共汽车上,以地面为参考物,观察人的运动,人在作匀速直线运动。
而以公共汽车为参考物,则人静止的。
可见,人的运动形式依选取的参考物不同而不同。
再引申一个例子,如图2。
沿直线轨道滚动的车轮,研究其轮缘上任意一点M的运动。
对于地面来说,点M的轨迹是旋轮线,而对于车厢来说,点M的轨迹则是一个圆。
车轮上的点M是沿旋轮线运动,是一种比较复杂复杂的运动形式,但是以车厢作为参考体,则点M相对于车厢的运动是简单的定轴转动,车厢相对于地面的运动是简单的平移。
轮缘上一点M的运动就可以看成为两个简单运动的合成,即点M相对于车厢作圆周运动,同时车厢相对地面作平移。
于是得到了合成运动的定义,即相对于某一参考体的运动可由相对于其他参考体的几个运动组合而成,称这种运动为合成运动。
3一点二系三运动研究点的合成运动,确定一个动点,选择定参考系和动参考系两个坐标系,分析动点的绝对运动、相对运动和牵连运动是首要任务。
3.1两个参考坐标系研究点的合成运动,总要涉及两个参考坐标系。
(1)定参考系建立在固定参考物上的坐标系,简称定系。
理论力学点的合成运动

例 8-4 曲柄OA以匀角速度 w绕O轴转动,其上
套有小环 M,而小环 M又在固定的大圆环上运动,大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时,小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解:(1)选择动点及 动系: 小环M为动点,动系固连在 OA上。
(2)分析三种运动:绝 对运动为圆周运动,相对运 动为沿OA的直线运动,牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中,设 Oxyz为定系,Oxyz为动系且作平
动,M为动点。动点M在动系中的坐标为 x、y 、z, 动系单位矢量为 i、 j、k。动系平动,i、j、k 的
Oxyz 作某种运动,在瞬时t,动系连同相对轨迹AB在
定系中的I位置,动点则在曲线 AB
上的 M 点。经过时间间 隔 t ,动系运动到定系 中的II位置,动点运动到
点 M。 如果在动系上观
察点M 的运动,则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶,雨滴 以速度 v2 铅直下落,试求雨滴相对于汽车的速度。
v1
解: 因为雨滴相对运动的汽车有运动,所以本题 为点的合成运动问题,可应用点的速度合成定理求解。
理论力学第5章 点的一般运动与刚体的基本运动

基础部分——运动学第5 章点的一般运动与刚体的基本运动一、运动学的研究对象及任务点刚体zz几何性质z合成分解例1例2例3例4例5例6二、学习运动学的目的三、运动学的分析方法矢量工具数值求解工具四、具体内容第5章点的一般运动与刚体的基本运动点的运动的矢量法点的运动的直角坐标法点的运动的弧坐标法一、运动方程二、轨迹三、点的速度O)(t r )(t t Δ+r vMM ′位矢四、点的加速度点的运动的矢量法一、运动方程点的运动的直角坐标法O rMxy z)(zy,x,xyz二、轨迹方程三、点的速度四、点的加速度AB点的运动的弧坐标法运动轨迹原点O 一、运动方程sMO)(−)(+正方向弧坐标s二、自然轴系主法线n 切线τ,指副法线b思考:共同点不同点)(t r M O三、点的速度⋅lim ⋅st s d d d d r⋅τ⋅=v tsv d d =)(t t Δ+r vM ′sΔO)(−)(+r Δτ四、点的加速度速度大小随时间的变化率方向ττa 22t d d d d tst v ==22t d d d d tst v a ==z切向tas t ΔΔ⋅→Δτ0lim⋅速度方向随时间的变化率z法向n a sΔΔτs ΔΔϕsd d ϕ→方向?n2n2taa +全t 讨论:加速减速[例5-1]纯滚动解:(1)运动方程运动方程=x =y (2)速度22yxv v +t ωcos 22−(3)切向、法向加速度思考:如何求速度投影加速度投影全加速度22a a yx +法向加速度2t2aa −曲率半径(4)运动方程(弧坐标)如何取弧坐标的原点?讨论:Array纯滚动速度为零加速度不为零5-4-1 平行移动(平移)任一直线z形状相同z速度相同z加速度相同5-4-2 定轴转动=矢量表示:=右手规则滑动矢量αωαkz线速度v(弧坐标法)Rv ω=Rna ta αta 方向?z加速度aRa α=t Ra 2n ω=2n2t aa +42ωα+t a α思考:过轴的任一条直线上θαθrωv ×=ααt a rαa ×=t na vωa ×=nr ωr×=td d αααx ′y ′z ′1O i ′j ′k ′rωv ×=[例5-2]解:r ω=+d d r tω−=avtr R +=22ππ[思考题]j i i k ⎜+′⎟⎜′⋅+′⎟′⋅提示:5-5-1 注意区别几组公式5-5-2 描述点的运动的其它方法点的一般运动与刚体基本运动点的一般运动刚体基本运动矢量法直角坐标法弧坐标法其它方法平移定轴转动5-5-3 本章知识结构框图补充:轮系的传动比一、齿轮传动z速度z 切向加速度外啮合内啮合=两齿轮之传动比:21=1 2112R R i ==ωω2112ωω=i 22211±=±=±=正号內啮合负号外啮合11±=外啮合转向推广:二、带轮(链轮)传动二、带轮(链轮)传动z z 皮带与带轮间无相对滑动。
点的合成运动

点的合成运动
在此之前,我们研究点的运动时,都是相对于某 一个参考系(定系)而言。但在有些问题中,往往需 要同时在两个不同的参考系中来描述同一点的运动, 而其中一个参考系相对于另一参考系也在运动。
为此,引入动点,动系,定系。并研究同一动点 相对 于两个不同参考系的运动之间的关系。
2013年8月6日
计算有何影响?
2013年8月6日
理论力学CAI
20
选择方法一
动系
动点
2013年8月6日
理论力学CAI
21
选择方法二
动系
动点
2013年8月6日
理论力学CAI
22
动点、动系和定系的选择原则
1. 动点是个确定的点。
2. 动点与动系必须分别选在两个不同的物体上,动点
与动系间有相对运动。
3. 动点相对动系的相对运动轨迹易于直观判断。
例题
已知:AB匀角速度转动。 求:M在导槽EF及BC中运动的速度与加速度。
E
B
C M
A
l F D
2013年8月6日
理论力学CAI
35
y
vB
B
ve
M
E
vM
C
速度分析:
x 动点—M点 动系—BC杆
A
vr
D
l
F
ve = vB = l
v M = ve v r
y : vM = ve sin = l sin x : 0 = vr ve cos
相对轨迹,相对速度vr,相对加速度ar。
2013年8月6日 理论力学CAI
7
牵连运动(entangled motion) :
《理论力学》(范钦珊)习题解答第2篇第46章.doc

(b)第2篇 工程运动学基础第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环 A的运动规律。
解:Rv a a 2ns in ==θ,θs in 2R v a =θθt an co s d d 2tR v a tv a ===,⎰⎰=t v v t R v v 02d t an 1d 0θ t v R R v t s v 00t an t an d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0t an t an ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324t t y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2ar cco s 213ar cs i n y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π== t,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮A习题4-1图习题4-2图习题4-3图e e -t (c)e e -t υ (b)R t R +υ (a)习题4-6图以匀角速度ω转动,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题2
y´ x´
解: 1. 运动分析
动点:小环P; 动系:固连于OBC;
绝对运动:沿OA固定直线; 相对运动:沿BC杆直线; 牵连运动:绕O定轴转动。
例题2
x´
解 :2. 速度分析
va =ve+ vr
y´
vr va
ve
其中 va、ve、vr方向如图; ve =OP· =0.2×0.5=0.1m/s;于是式 中只有va、vr二者大小未知。从 而由速度平行四边形解得小环P 的速度
z z x
P
y
r
r
y
x O P,P1
r1
P1
速度合成定理
z x P, P1
P y
r
r
r1
P1
r r1 r
r1 r r lim lim lim t 0 t t 0 t t 0 t
va vr ve
va vr ve
5.3 牵连运动为平移时点的加速度合成定理
点的合成运动中,加速度之间的关系比较复杂,
因此,我们由简单到复杂,先分析动系作平移的情形
。即先研究牵连运动为平动时的加速度合成定理,然 后再介绍牵连运动为转动时的加速度合成定理。
设O´x´y´z´为平移参考系,由于 x´、y´、z´各轴方向不变,可使与 定坐标轴x、y、z分别平行。
5.1 点的复合运动的几个基本概念
两种参考系 三种运动与三种速度和加速度
两种参考系
定参考系
动参考系
一般工程问题中,通常将固连在地球或相对 地球不动的架构上的坐标系,称为定参考系(fixed reference system ) , 简称定系,以坐标系 Oxyz 表示; 固定在其它相对于地球运动的参考体上的坐标系称 为动参考系(moving reference system),简称动 系,以坐标系O'x'y'z'表示。
牵连运动为转动时加速度合成定理的证明
设动系 O′x′y′z′ 以角速度矢 绕定轴 Oz( Oxyz为定系)转动,角加速度矢 为。动点P的相对矢径、相对速度和 相对加速度可以表示为
r x i y j z k
i y j z k vr x
理论力学
西安航空学院
赵银燕 教授
西安航空学院机械学院力学基础部 范钦珊教育与教学工作室
回顾 第4章 运动分析基础
4.1 点的运动学 4.2 刚体的简单运动 4.3 结论与讨论
第5章 点的复合运动分析
由于运动的相对性,在不同的参考系中,对于同一动点, 其运动方程、速度和加速度是不相同的。许多力学问题中,常 常需要研究一点在不同参考系中的运动量(速度和加速度)的相 互关系。 本章将用定、动两种参考系,描述同一动点的运动;分析 两种结果之间的相互关系,建立点的速度合成定理和加速度合 成定理。
i j k ar x y z
i y j z k vr x
i j k ar x y z
利用点的速度合成定理
va ve vr
以及因为牵连运动为平移而 得到的
v e vO i y j z k v a v O x
aa
由平行四边形法则,得 aCD ae sin 0.346m/s
第5章 点的复合运动分析
5.1 点的复合运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论 5.6 参考例题分析
va 3ve 0.173m / s
此外,还可求得vr=2 ve=0.2m/s
第5章 点的复合运动分析
5.1 点的复合运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论 5.6 参考例题分析
关于速度合成定理的讨论
牵连运动与牵连速度-牵连运动是刚体(动 系)的运动;牵连速度是固连在动系上的刚体上 一点(与动点相重合的点)的速度(在定系的绝对 速度)。
速度合成定理为平面矢量式,由此可以写出 两个分量式,用于求解两个未知量。
例 题
例 题 1
铰接四边形
O1A=O2B=100mm, O1O2=AB, 杆O1A以等角速度 ω=2rad/s绕轴 O1转动。 AB杆上有一套筒C,此 套筒与杆CD相铰接,机构的各部 件都在同一铅垂平面内。 试求:当 =60°时,CD杆的 速度。
分析3种运动的实例
主梁不动时 定参考系? 动参考系? 绝对运动? 相对运动? 牵连运动?
分析3种运动的实例
定参考系?
动参考系? 绝对运动?
相对运动?
牵连运动?
第5章 点的复合运动分析
5.1 点的复合运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论 5.6 参考例题分析
5.4 牵连运动为转动时点的 加速度合成定理 科氏加速度
z’ x’
y’r
r1
P
r
回顾 4.2 刚体的简单运动
va vr ve
i y j z k vr x
aP
1、刚体平移运动,动 坐标系固连在刚体上:
A r B r
a A aB
P, P1
夹持在车床三爪卡盘上的圆 柱体工件与切削车刀。卡盘—工 件绕轴转动,车刀向左作直线平 移。若以刀尖 P 点为动点作为研 究对象,则可以卡盘—工件为动 系 O´x´y´z´ , 而 以 车 床 床 身 (固连于地球)为定系Oxyz分析 动点P的运动。
三种运动与三种速度和加速度
动点(研究对象)相对于定系 的运动,称为动点的绝对运动 ( absolute motion )。动点刀尖 P 点 的绝对运动为水平直线(绝对轨迹) 运动。 动点相对于定系的运动速度和 加速度,分别称为动点的绝对速度 ( absolute velocity )和绝对加速度 (absolute acceleration),分别用符 号va和aa表示。
动点相对于动系的运动,称为 动点的相对运动(relativemotion)。 动点刀尖上P点的相对运动是在工件 圆柱面上的螺旋线(相对轨迹)运 动。 动点相对于动系的运动速度和 加速度,分别称为动点的相对速度 (relative velocity)和相对加速度 (relative acceleration),分别用符 号vr和ar表示。
5.2 点的速度合成定理
动系与定系 三种运动轨迹 速度合成定理 关于速度合成定理的讨论 例题
动系与定系
刚体(用刚体上在定系中运动的曲线表示)
z x z y x O t 瞬时
y
t+ t 瞬时
三种运动轨迹
刚体在定系中运动,动系固结在刚体上。 刚体在定系中或平移或转动 动点P沿着刚体上的曲线运动。 P1点-动系上与动点重合的点。
绝对速度 相对速度 牵连速度
此即为速度合成定理( theorem for composition of velocities),即动点的绝对速度等于其牵连速度与相对 速度的矢量和。 由于没有对绝对运动和相对运动轨迹形状作任何限 制,也没有对牵连运动为何种刚体运动作限制,因此 本定理对各种运动都是适用的。
P1
aa ae ar
2、刚体定轴转动:
d vP dr dω rP ω P dt dt dt
v P ω rP
1
1
α rP ω ( ω rP )
t n aP aP
相对速度对时间求导数时,因为动系的转动,多出动系 坐标单位矢量对时间的导数项。 牵连速度对时间求导数时,因为动系的转动,多出牵连 点的绝对速度项,该绝对速度项中含有相对速度,因此 有了相对速度的求导,因此同样多出了出动系坐标单位 矢量对时间的导数项。 因此,不能用牵连加速度和相对加速度的和表示最后的 加速度。
点的运动复合是运动分析方法的重要内容,在工程运动 分析中有着广泛的应用;同时可为相对运动动力学提供运动分 析的理论基础;点的运动复合的分析方法还可推广应用于分析 刚体的复合运动。本章是“工程运动学” 篇的重点内容。
第5章 点的复合运动分析
5.1 点的复合运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论 5.6 参考例题分析
例题3
y´ 解:1. 运动分析 动点:CD上的C点; 动系:固连于AB杆。
x´
绝对运动:上下直线运动; 相对运动:沿AB直线运动; 牵连运动:平面运动,平面内曲线 平移。
例题3
y´
ae φ ar
解:2.加速度分析:
aa ae ar
其中由于动系作平移,故动 系AB杆上各点的加速度相同, x´ 因此动系AB杆上与动点套筒C 相重合点C1(图中未示出)的 加速度即牵连加速度: ae=aA , aA=O1A 2=0.4 m/s2
y´
例 题 1
解:1. 运动分析
x´ 动点:CD上的C点; 动系:固连于AB杆。
绝对运动:上下直线运动; 相对运动:沿AB直线运动; 牵连运动:动系做平面运动,牵连 点与A点运动一致。
y´
例 题 1
x´
解:2.速度分析
va =ve+ vr
ve=vA=O1A× =0.2m/s, ve垂直O1A;
aO
这就是牵连运动为平移时点的加速度合成定理:当牵连运 动为平移时,动点在某瞬时的绝对加速度等于该瞬时它的牵连
