连续函数离散化matlab程序
matlab离散数据积分

matlab实现离散数据积分
在MATLAB中,离散数据积分可以通过数值积分方法来实现。
MATLAB提供了一些内置函数来计算数值积分,如integral 函数。
下面是一个示例代码,展示如何在MATLAB中实现离散数据积分:
在上面的示例中,我们首先生成了一组离散数据,其中x表示输入数据,y表示输出数据。
然后,我们使用MATLAB内置的integral函数来计算离散数据的积分。
integral函数接受一个函数句柄和积分的范围作为参数。
在示例中,我们将y(x)作为函数句柄传递给integral函数,表示要根据输出数据y和输入数据x计算积分。
积分的范围是1到5,即从x=1到x=5。
运行上述代码后,将输出计算得到的积分结果。
请注意,这只是一个简单的示例,演示了如何在MATLAB中实现离散数据积分。
对于更复杂的情况,您可能需要使用其他数值积分方法或自定义函数来计算积分。
连续传递函数离散化的方法与原理

目录第一章模拟化设计基础 1 第一节步骤 1 第二节在MATLAB中离散化 3 第三节延时e-Ts环节的处理 5 第四节控制函数分类 6 第二章离散化算法10 摘要10 比较11 第一节冲击响应不变法(imp,无保持器直接z变换法) 11 第二节阶跃响应不变法(zoh,零阶保持器z变换法) 11 第三节斜坡响应不变法(foh,一阶保持器z变换法) 11 第四节后向差分近似法12 第五节前向差分近似法14 第六节双线性近似法(tustin) 15 第七节预畸双线性法(prevarp) 17 第八节零极点匹配法(matched) 18 第三章时域化算法19 第一节直接算法1—双中间变量向后递推19 第二节直接算法2—双中间变量向前递推20 第三节直接算法3—单中间变量向后递推21 第四节直接算法4—单中间变量向前递推(简约快速算法) 21 第五节串联算法22 第六节并联算法23 第四章数字PID控制算法24 第一节微分方程和差分方程25 第二节不完全微分25 第三节参数选择26 第四节c51框架27 第五章保持器33 第一节零阶保持器33 第二节一阶保持器30 附录两种一阶离散化方法的结果的比较31第一章 模拟化设计基础数字控制系统的设计有两条道路,一是模拟化设计,一是直接数字设计。
如果已经有成熟的模拟控制器,可以节省很多时间和部分试验费用,只要将模拟控制器离散化即可投入应用。
如果模拟控制器还不存在,可以利用已有的模拟系统的设计经验,先设计出模拟控制器,再进行离散化。
将模拟控制器离散化,如果用手工进行,计算量比较大。
借助数学软件MATLAB 控制工具箱,可以轻松地完成所需要的全部计算步骤。
如果需要的话,还可以使用MATLAB 的SIMULINK 工具箱,进行模拟仿真。
第一节 步骤步骤1 模拟控制器的处理在数字控制系统中,总是有传输特性为零阶保持器的数模转换器(DAC ),因此,如果模拟控制器尚未设计,则应以下图的方式设计模拟控制器,即在对象前面加上一个零阶保持器,形成一个新对象Ts 1e G s s ()--,然后针对这个新对象求模拟控制器D(s)。
连续传递函数离散化的方法及原理

目录第一章模拟化设计根底1第一节步骤1第二节在MATLAB中离散化 3 第三节延时e-Ts环节的处理 5 第四节控制函数分类 6 第二章离散化算法10摘要10比拟11第一节冲击响应不变法(imp,无保持器直接z变换法) 11 第二节阶跃响应不变法(zoh,零阶保持器z变换法)11第三节斜坡响应不变法(foh,一阶保持器z变换法) 11 第四节后向差分近似法12 第五节前向差分近似法14 第六节双线性近似法(tustin) 15 第七节预畸双线性法(prevarp) 17 第八节零极点匹配法(matched)18第三章时域化算法19第一节直接算法1—双中间变量向后递推19 第二节直接算法2—双中间变量向前递推20第三节直接算法3—单中间变量向后递推21 第四节直接算法4—单中间变量向前递推(简约快速算法) 21 第五节串联算法22 第六节并联算法23 第四章数字PID控制算法24 第一节微分方程和差分方程25 第二节不完全微分25 第三节参数选择26 第四节c51框架27第五章保持器33第一节零阶保持器33第二节一阶保持器30附录两种一阶离散化方法的结果的比拟31第一章 模拟化设计根底数字控制系统的设计有两条道路,一是模拟化设计,一是直接数字设计。
如果已经有成熟的模拟控制器,可以节省很多时间和局部试验费用,只要将模拟控制器离散化即可投入应用。
如果模拟控制器还不存在,可以利用已有的模拟系统的设计经历,先设计出模拟控制器,再进展离散化。
将模拟控制器离散化,如果用手工进展,计算量比拟大。
借助数学软件MATLAB 控制工具箱,可以轻松地完成所需要的全部计算步骤。
如果需要的话,还可以使用MATLAB 的SIMULINK 工具箱,进展模拟仿真。
第一节 步骤步骤1 模拟控制器的处理在数字控制系统中,总是有传输特性为零阶保持器的数模转换器〔DAC 〕,因此,如果模拟控制器尚未设计,那么应以下列图的方式设计模拟控制器,即在对象前面加上一个零阶保持器,形成一个新对象Ts 1e G s s ()--,然后针对这个新对象求模拟控制器D(s)。
离散系统的MATLAB的实现
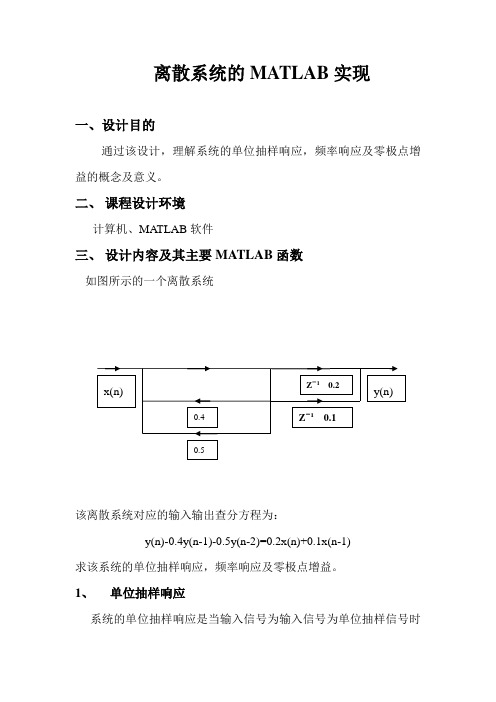
离散系统的MATLAB实现一、设计目的通过该设计,理解系统的单位抽样响应,频率响应及零极点增益的概念及意义。
二、课程设计环境计算机、MATLAB软件三、设计内容及其主要MATLAB函数如图所示的一个离散系统该离散系统对应的输入输出查分方程为:y(n)-0.4y(n-1)-0.5y(n-2)=0.2x(n)+0.1x(n-1)求该系统的单位抽样响应,频率响应及零极点增益。
1、单位抽样响应系统的单位抽样响应是当输入信号为输入信号为单位抽样信号时系统的输出响应。
MATLAB 中有两个函数可以计算系统的单位抽样响应:filter 函数和impz 函数。
1)filter 函数filter 函数是利用递归滤波器或非递归滤波器对数据进行滤波。
因为一个离散系统可以看做一个滤波器。
系统的输出就是输入经过滤波器滤波的结果。
filter 函数的格式为:y=filter (b ,a ,x )此函数是对由a 和b 组成的系统对输入进行滤波,如果输入为单位抽样信号)(n δ,那么输出就是系统的单位抽样响应。
2) impz 函数impz 函数的格式为:impz (b ,a )可直接给出系统的单位抽样响应。
2、频率响应e jw )(H由向量a 和b 组成的系统的频率响应为∑∑=-=-+=H N k jwkMr jwrjweee k a r b 10)(1)()(MATLAB 中的freqz 函数使用基于FFT 的算法来计算由向量a 和b 组成的系统的频率响应。
其一般用法为:【h ,f 】=freqz (b ,a ,n ,Fs )其中向量a 和b 由离散系统决定,Fs 为采样频率,在【0,2Fs】频率范围内选取n 个频率点,并记录在f 中。
由于freqz 函数是从用基2的FFT算法,n常取2的幂次方,这样可以提高运算速度。
3、零极点增益利用MATLAB中roots的函数可求得系统的零、极点,从而得到系统的零极点增益表示。
其一般用法为:zr=roots(b)zp=roots(a)四、设计报告要求1、按题目要求进行设计,写出设计报告,给出源程序。
matlab表现离散型数据的函数

matlab表现离散型数据的函数在MATLAB中有很多不同的函数可以用来描述和展示离散型数据。
这些函数可以用于统计分析、数据可视化以及模拟等应用。
下面我会介绍几个常用的MATLAB函数,来展示离散型数据的表现。
一、histogram函数histogram函数可以用来绘制直方图,用于展示离散型数据的分布情况。
直方图将数据分成一系列的柱子,每个柱子表示一定范围内的数据频数。
在MATLAB 中,我们可以使用histogram函数来计算和绘制直方图,如下所示:matlabdata = [1,2,3,4,4,4,5,5,5,5]; % 一组离散型数据histogram(data);运行上述代码后,MATLAB会自动计算数据的频数,并绘制出直方图。
二、bar函数bar函数可以用来绘制柱状图,也适合展示离散型数据的分布情况。
与直方图不同,柱状图的柱子宽度是一样的,并且通常是水平或垂直排列。
在MATLAB中,我们可以使用bar函数来计算和绘制柱状图,如下所示:matlabdata = [1,2,3,4,4,4,5,5,5,5]; % 一组离散型数据unique_data = unique(data); % 获取去重后的离散型数据counts = histcounts(data, unique_data); % 计算每个数据值的频数bar(unique_data, counts);上述代码中,我们先使用unique函数来获取去重后的离散型数据值,并使用histcounts函数来计算每个数据值的频数,然后将这些频数作为柱状图的高度绘制出来。
三、boxplot函数boxplot函数可以用来绘制箱线图,用于展示离散型数据的分布情况和离群点。
箱线图主要展示了数据的中位数、上下四分位数以及上下边界。
在MATLAB中,我们可以使用boxplot函数来绘制箱线图,如下所示:matlabdata = [1,2,3,4,4,4,5,5,5,5]; % 一组离散型数据boxplot(data);运行上述代码后,MATLAB会自动计算出箱线图的各个参数,并将其绘制出来。
matlab对离散数据积分计算

matlab对离散数据积分计算
Matlab是一款功能强大的计算机软件,它能够对离散数据进行积分计算,帮助用户更加轻松地实现复杂的数学计算。
Matlab提供了强大的积分计算功能,可以实现对离散数据的积分计算。
用户可以通过Matlab提供的函数,将离散数据转换为连续函数,然后使用Matlab提供的积分计算函数,对这些连续函数进行积分计算。
首先,用户可以使用Matlab提供的拟合函数,将离散数据拟合成连续函数。
例如,用户可以使用Matlab的polyfit函数,将离散数据拟合成一元多项式函数,用户也可以使用Matlab的spline函数,将离散数据拟合成样条函数。
然后,用户可以使用Matlab提供的积分计算函数,对这些连续函数进行积分计算。
例如,用户可以使用Matlab提供的integral函数,计算某个函数在一定区间内的积分值。
此外,用户还可以使用Matlab提供的intgral2函数,计算某个函数在二维区间内的积分值。
此外,Matlab还提供了多种高级的积分计算函数,可以帮助用户更轻松地完成复杂的积分计算。
例如,用户可以使用Matlab提供的quadgk函数,计算复杂函数在一定区间内的积分值;用户还可以使用Matlab提供的dblquadgk函数,计算复杂函数在二维区间内的积分值。
总之,Matlab能够实现对离散数据进行积分计算,用户可以使用其强大的积分计算功能,更加轻松地实现复杂的数学计算。
matlab 离散转化为公式

Matlab是一种高级技术计算语言和交互式环境,广泛用于工程、科学和数学领域。
在Matlab中,离散转换是指将连续的时间信号或连续的空间信号转化为离散的时间或离散的空间信号。
离散转换有许多种形式,包括傅立叶变换、离散傅立叶变换、z变换等,在Matlab中,我们可以使用相应的函数来进行离散转换,并将其表示为数学公式。
1. 傅立叶变换傅立叶变换是将一个时间函数或空间函数转换为频率函数的过程。
在Matlab中,我们可以使用fft函数来进行离散傅立叶变换。
假设我们有一个离散时间信号x,我们可以使用以下公式来表示其离散傅立叶变换:X(k) = Σ(x(n) * e^(-j*2πnk/N))其中,X(k)表示频率域上的离散信号,x(n)表示时域上的离散信号,N 表示信号的长度,k表示频率的索引,j表示虚数单位。
2. 离散傅立叶变换离散傅立叶变换是离散时间信号的傅立叶变换,其变换公式与连续信号的傅立叶变换类似,但在离散域内进行。
在Matlab中,我们同样可以使用fft函数来进行离散傅立叶变换。
假设我们有一个离散时间信号x,我们可以使用以下公式来表示其离散傅立叶变换:X(k) = Σ(x(n) * W^(-kn))其中,X(k)表示频率域上的离散信号,x(n)表示时域上的离散信号,N 表示信号的长度,k表示频率的索引,W表示旋转因子。
3. z变换z变换是离散时间信号的复平面变换,其用途广泛,包括系统分析、数字滤波器设计等。
在Matlab中,我们可以使用ztrans函数来进行z 变换。
假设我们有一个离散时间信号x,我们可以使用以下公式来表示其z变换:X(z) = Σ(x(n) * z^(-n))其中,X(z)表示复平面域上的离散信号,x(n)表示时域上的离散信号,n表示离散时间的索引,z表示复变量。
Matlab提供了丰富的离散转换函数和工具,能够帮助工程师和科学家对离散信号进行快速而准确的分析和处理。
通过将离散信号转化为数学公式,我们能够更好地理解信号的特性和行为,为后续的信号处理和系统设计提供有力支持。
(完整版)连续时间信号和离散时间信号在MATLAB中的绘制

南京信息工程大学实验(实习)报告实验(实习)名称实验一实验(实习)日期 2019年3月19 指导教师院专业年级班次姓名学号一、实验目的(1)学会使用MA TLAB产生常见的连续时间信号和离散时间信号;(2)学会使用MA TLAB完成一些信号的基本运算;(3)熟悉MATLAB的基本操作,以及一些基本函数的使用,为后续的实验奠定基础。
二、实验内容1.利用MATLAB绘制单位冲击信号,单位阶跃信号,指数信号,单位矩形信号,抽样信号,正弦信号(分别取不同周期)(1)单位冲击信号代码:T=1000;t=linspace(0,10,T);t1=linspace(-5,5,T);f1=stepfun(t1,-1/T)-stepfun(t1,1/T);plot(t1,f1);grid on;axis([-5 5 -1 2])xlabel('t');ylabel('c(t)');title('单位冲击信号');(2)单位阶跃信号T=1000;t=linspace(-5,5,T);f1=stepfun(t,0);plot(t,f1);grid on;axis([-5 5 -1 2]);xlabel('t');ylabel('u(t)');title('单位阶跃信号');(3)指数信号T=1000;t=linspace(-5,5,T);xe=exp(t);subplot(2,1,1);plot(t,xe);grid on;axis([-5 3 -0.5 20]); xlabel('t');ylabel('x(t)');title('指数信号1');subplot(2,1,2);xe=exp(-t);plot(t,xe);grid on;axis([-3 3 -0.5 20]); xlabel('t');ylabel('x(-t)');title('指数信号2');(4)单位矩形信号T=1000;t=linspace(-5,5,T);xt=rectpuls(t,1);plot(t,xt);grid on;axis([-2 2 -0.5 1.5]); xlabel('t');ylabel('x(t)');title('单位矩形信号');(5)抽样信号T=10000;t=linspace(-100,100,T);xt=sinc(t/pi);plot(t,xt);grid on;axis([-100 100 -0.3 1.1]);(6)正弦信号w=100;T=12000;t=linspace(-1,10,T);xt=sin(w*t);subplot(3,1,1);plot(t,xt);grid on;axis([-0.2 0.2 -1.5 1.5]); xlabel('t');ylabel('x(t)');title('w=100');w2=50;T=12000;t=linspace(-1,10,T);xe=sin(w2*t);subplot(3,1,2);plot(t,xe);grid on;axis([-0.2 0.2 -1.5 1.5]); xlabel('t');ylabel('x(t)');title('w=50');w3=200;T=12000;t=linspace(-1,10,T);xr=sin(w3*t);subplot(3,1,3);plot(t,xr);grid on;axis([-0.2 0.2 -1.5 1.5]); xlabel('t');ylabel('x(t)');title('w=200');2.利用MATLAB绘制单位冲击序列,单位阶跃序列,实指数序列(1)单位冲击序列n=50;x=zeros(1,n);x(1)=1;xn=0:n-1;stem(xn,x);grid on;axis([-1 25 0 1.2]);xlabel('n');ylabel('c(n)');title('单位冲击序列');(2)单位阶跃序列n=50;x=ones(1,n);xn=0:n-1;stem(xn,x);grid on;axis([-5 25 0 1.2]);xlabel('n');ylabel('u(n)');title('µ¥Î»½×Ô¾ÐòÁÐ');(3)实指数序列n=0:20;a1=2;a2=-2;a3=0.5;a4=-0.5;xn1=a1.^n;xn2=a2.^n;xn3=a3.^n;xn4=a4.^n;subplot(2,2,1);stem(xn1);grid on;axis([0 20 0 600000]);xlabel('n');ylabel('xn1(n)');title('实指数序列xn1(n)[a>1]');subplot(2,2,2);stem(xn2);grid on;axis([0 20 -150000 300000]); xlabel('n');ylabel('xn2(n)');title('实指数序列xn2(n)[a<-1]');subplot(2,2,3);stem(xn3);grid on;axis([0 20 0 1.3]);xlabel('n');ylabel('xn3(n)');title('实指数序列xn3(n)[1>a>0]');subplot(2,2,4);stem(xn4);grid on;axis([0 20 -0.7 1.3]);xlabel('n');ylabel('xn4(n)');title('实指数序列xn4(n)[0>a>-1]');3.讨论题:已知连续信号x(t)=cos(πt),当抽样间隔分别取T=0.08, 0.16,和0.24时所对应的离散余弦信号的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续函数离散化matlab程序
连续函数离散化是在数值分析和科学计算中常常用到的一种技术。
离
散化的目的是为了将连续函数转化为离散点的数据,以便在计算机程
序中进行计算和处理。
在 MATLAB 中,我们可以使用一些内置函数来
实现连续函数的离散化。
1. 离散化的概念
离散化是将连续函数转化成离散点的数据。
我们可以将其想象成将一
条曲线在数轴上映射成若干个点,每个点代表函数在该点处的函数值。
在实际的计算中,离散化不仅可以提高计算效率,还可以让我们将连
续函数以表格的形式展示出来,使得我们更容易进行分析和处理。
2. 样条插值
样条插值是一种常用的连续函数离散化方法,在 MATLAB 中可以使用spline 函数实现。
该函数可以根据一组已知的数据点(也就是离散的点),生成一个插值函数。
之后,我们就可以使用该插值函数来计算
任意点处的函数值,并对其进行分析和处理。
3. 离散变量的生成
离散化的第一步是生成函数在某一区间内的离散变量。
MATLAB 中的linspace 函数可以帮助我们生成等间距的离散点。
例如,下面的代码
可以生成一个包含 100 个离散点的行向量 x:
```matlab
x = linspace(0, 1, 100);
```
这个代码使用了 linspace 函数,第一个参数是区间的起点,第二个参数是区间的终点,第三个参数是离散点的个数。
在这个例子中,代码生成了一个从 0 到 1 的区间,并且将该区间等分成了 100 个离散点。
4. 进行样条插值
一旦我们生成了离散变量,我们就可以使用 MATLAB 中的 spline 函数来进行样条插值。
下面的代码演示了如何生成一个样条插值函数:
```matlab
y = sin(2 * pi * x);
pp = spline(x, y);
```
这段代码中,我们使用了 spline 函数,它的第一个参数是离散点的横坐标 x,第二个参数是离散点的纵坐标 y。
函数返回一个插值函数pp,我们可以使用该插值函数对任意点进行估算。
例如,我们可以使用以下代码计算插值函数在 0.25 处的函数值:
```matlab
val = ppval(pp, 0.25);
```
其中,ppval 函数的第一个参数是插值函数 pp,第二个参数是要计算函数值的点。
5. 结论
通过本文我们了解了连续函数离散化的方法和流程。
在 MATLAB 中,
我们可以使用内置的函数 spline 和 ppval 来实现样条插值和对函数值的计算。
离散化的使用可以提高计算和处理的效率,也可以帮助我们更好地进行数据分析和理解。
