数据结构7
数据结构课后习题答案第七章
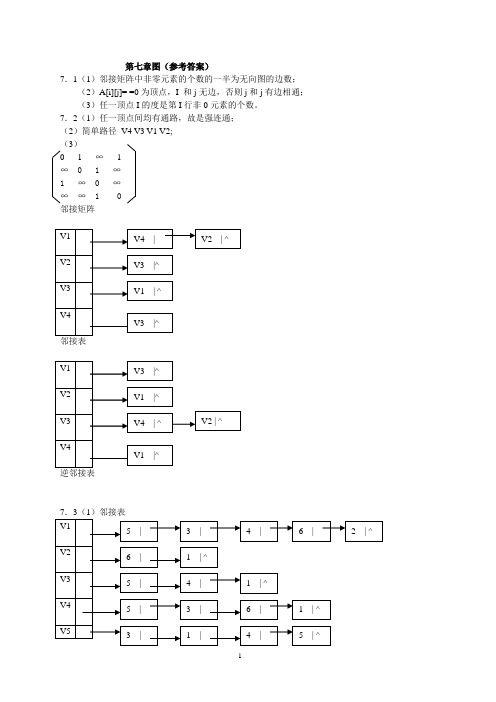
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
数据结构-7顺序查找与二分查找

i=m+1=8,j=8, m=(i+j)/2=8。 r[m]>k : 在左半部分继续查找。
i=8, j=m-1=7 ,
i>j: 查找失败
存储结构
key info 0 1 k1 2 k2 3 k3
…………
n kn
typedef struct { keytype key; ………….
} elemtype;
分块有序表的结构可以分为两部分: 1、线性表本身是顺序存储结构 2、再建立一个索引表,线性表中每个子表建立一个索引节点
。索引节点包括两部分:一是数据域,一是指针域。数据域存 放对应子表中的最大元素值,指针域用于指示子表第一个元素 的在整个表中序号。
分块查找
template<class T> struct indnode {
key=32
d (1) 27
i=1
d (2) 36
i=2
d (3) 32i=3 Nhomakorabead (4) 18
此时d(i)=key,数组中的第3个位置
如果输入查找的元素值key=22
d (1) 27 i=1
d (2) 36 i=2
d (3) 32 i=3
d (4) 18
i=4 i=5 此时i等于5,超过数组中元素个数,找不到
T key; int k; };
上图查找过程:首先查找索引表,确定查找的子表,然后再相应的子表中 应顺序表查找法查找。
• int blksearch(record r[],index idx[],keytype key)
•{
• int i=0,j;
• while(i<idxN)
•{
• if(key<=idx[i].key){
数据结构第7章-答案

一、单选题C01、在一个图中,所有顶点的度数之和等于图的边数的倍。
A)1/2 B)1 C)2 D)4B02、在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。
A)1/2 B)1 C)2 D)4B03、有8个结点的无向图最多有条边。
A)14 B)28 C)56 D)112C04、有8个结点的无向连通图最少有条边。
A)5 B)6 C)7 D)8C05、有8个结点的有向完全图有条边。
A)14 B)28 C)56 D)112B06、用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A)栈 B)队列 C)树 D)图A07、用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A)栈 B)队列 C)树 D)图A08、一个含n个顶点和e条弧的有向图以邻接矩阵表示法为存储结构,则计算该有向图中某个顶点出度的时间复杂度为。
A)O(n) B)O(e) C)O(n+e) D)O(n2)C09、已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是。
A)0 2 4 3 1 5 6 B)0 1 3 6 5 4 2 C)0 1 3 4 2 5 6 D)0 3 6 1 5 4 2B10、已知图的邻接矩阵同上题,根据算法,则从顶点0出发,按广度优先遍历的结点序列是。
A)0 2 4 3 6 5 1 B)0 1 2 3 4 6 5 C)0 4 2 3 1 5 6 D)0 1 3 4 2 5 6D11、已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是。
A)0 1 3 2 B)0 2 3 1 C)0 3 2 1 D)0 1 2 3A12、已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是。
A)0 3 2 1 B)0 1 2 3 C)0 1 3 2 D)0 3 1 2A13、图的深度优先遍历类似于二叉树的。
A)先序遍历 B)中序遍历 C)后序遍历 D)层次遍历D14、图的广度优先遍历类似于二叉树的。
数据结构第七章课后习题答案 (1)

7_1对于图题7.1(P235)的无向图,给出:(1)表示该图的邻接矩阵。
(2)表示该图的邻接表。
(3)图中每个顶点的度。
解:(1)邻接矩阵:0111000100110010010101110111010100100110010001110(2)邻接表:1:2----3----4----NULL;2: 1----4----5----NULL;3: 1----4----6----NULL;4: 1----2----3----5----6----7----NULL;5: 2----4----7----NULL;6: 3----4----7----NULL;7: 4----5----6----NULL;(3)图中每个顶点的度分别为:3,3,3,6,3,3,3。
7_2对于图题7.1的无向图,给出:(1)从顶点1出发,按深度优先搜索法遍历图时所得到的顶点序(2)从顶点1出发,按广度优先法搜索法遍历图时所得到的顶点序列。
(1)DFS法:存储结构:本题采用邻接表作为图的存储结构,邻接表中的各个链表的结点形式由类型L_NODE规定,而各个链表的头指针存放在数组head中。
数组e中的元素e[0],e[1],…..,e[m-1]给出图中的m条边,e中结点形式由类型E_NODE规定。
visit[i]数组用来表示顶点i是否被访问过。
遍历前置visit各元素为0,若顶点i被访问过,则置visit[i]为1.算法分析:首先访问出发顶点v.接着,选择一个与v相邻接且未被访问过的的顶点w访问之,再从w 开始进行深度优先搜索。
每当到达一个其所有相邻接的顶点都被访问过的顶点,就从最后访问的顶点开始,依次退回到尚有邻接顶点未曾访问过的顶点u,并从u开始进行深度优先搜索。
这个过程进行到所有顶点都被访问过,或从任何一个已访问过的顶点出发,再也无法到达未曾访问过的顶点,则搜索过程就结束。
另一方面,先建立一个相应的具有n个顶点,m条边的无向图的邻接表。
数据结构-第7章图答案

7.3 图的遍历 从图中某个顶点出发游历图,访遍图中其余顶点, 并且使图中的每个顶点仅被访问一次的过程。 一、深度优先搜索 从图中某个顶点V0 出发,访问此顶点,然后依次 从V0的各个未被访问的邻接点出发深度优先搜索遍 历图,直至图中所有和V0有路径相通的顶点都被访 问到,若此时图中尚有顶点未被访问,则另选图中 一个未曾被访问的顶点作起始点,重复上述过程, 直至图中所有顶点都被访问到为止。
void BFSTraverse(Graph G, Status (*Visit)(int v)) { // 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组 visited。 for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; InitQueue(Q); // 置空的辅助队列Q for ( v=0; v<G.vexnum; ++v ) if ( !visited[v]) { // v尚未访问 EnQueue(Q, v); // v入队列 while (!QueueEmpty(Q)) { DeQueue(Q, u); // 队头元素出队并置为u visited[u] = TRUE; Visit(u); // 访问u for ( w=FirstAdjVex(G, u); w!=0; w=NextAdjVex(G, u, w) ) if ( ! visited[w]) EnQueue(Q, w); // u的尚未访问的邻接顶点w入队列Q
4。邻接多重表
边结点
mark ivex
顶点结点
ilink
jvex
jlink
info
data
firstedge
#define MAX_VERTEX_NUM 20 typedef emnu {unvisited, visited} VisitIf; typedef struct Ebox { VisitIf mark; // 访问标记 int ivex, jvex; // 该边依附的两个顶点的位置 struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条 边 InfoType *info; // 该边信息指针 } EBox; typedef struct VexBox { VertexType data; EBox *firstedge; // 指向第一条依附该顶点的边 } VexBox; typedef struct { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; // 无向图的当前顶点数和边数 } AMLGraph;
《数据结构》第 7 章 图

v3
v4 v5 v4
v3
v5 v4
v3
v5 v4
v3
v5 v4
v3
v5
注
一个图可以有许多棵不同的生成树。 所有生成树具有以下共同特点: 生成树的顶点个数与图的顶点个数相同; 生成树是图的极小连通子图; 一个有 n 个顶点的连通图的生成树有 n-1 条边; 生成树中任意两个顶点间的路径是唯一的; 在生成树中再加一条边必然形成回路。 含 n 个顶点 n-1 条边的图不一定是生成树。
A1 = {< v1, v2>, < v1, v3>, < v3, v4>, < v4, v1>} v1 v2
有向图
v3
v4
制作:计算机科学与技术学院 徐振中
数据结构 边:若 <v, w>∈VR 必有<w, v>∈VR,则以 无序对 (v, w) 代表这两个有序对,表示 v 和 w 之 间的一条边,此时的图称为无向图。 G2 = (V2, E2) V2 = {v1, v2, v3, v4, v5}
第七章 图
E2 = {(v1, v2), (v1, v4), (v2, v3), (v2, v5) , (v3, v4), (v3, v5)} v1
G2
v3
v2
无向图
v4
v5
制作:计算机科学与技术学院 徐振中
数据结构
第七章 图
例:两个城市 A 和 B ,如果 A 和 B 之间的连线的涵义是 表示两个城市的距离,则<A, B> 和 <B, A> 是相同的, 用 (A, B) 表示。 如果 A 和 B 之间的连线的涵义是表示两城市之 间人口流动的情况,则 <A, B> 和 <B, A> 是不同的。 北京 <北京,上海> (北京,上海) <上海,北京> <北京,上海> 北京 上海 上海
数据结构(朱战立)章 (7)
7.1 树
7.1.1 树的定义 树是由n(n≥0)个结点构成的集合。 n=0的树称为空树;
对n>0的树T有: (1) 有一个特殊的结点称为根结点, 根结点没有前驱结点;
3
(2) 当n>1时, 除根结点外其他结点被分成m(m>0)个互不相 交的集合T1, T2,…, Tm, 其中每一个集合Ti(1≤i≤m)本身又 是一棵结构和树类同的子树。
10
7.1.2 树的表示方法 树的表示方法主要有三种, 分别用于不同的用途。 1. 直观表示法 图7 - 1就是一棵以直观表示法表示的树。 树的直观表示法
主要用于直观描述树的逻辑结构。 2. 形式化表示法 树的形式化表示法主要用于树的理论描述。 树的形式化表
示法定义树T为T=(D,R),其中D为树T中结点的集合, R为树T 中结点之间关系的集合。 当树T为空树时D=∅; 当树T不为空树 时有
5ቤተ መጻሕፍቲ ባይዱ
下面介绍树的其他一些常用术语。 结点: 由数据元素和构造数据元素之间关系的指针组成。 例如, 在图7 - 1(a)中有1个结点, 图7 - 1(b)中有12个结点。 结点的度: 结点所拥有的子树的个数称为该结点的度。 例 如, 在图7 - 1(b)中结点A的度为3, 结点B的度为2, 结点J的 度为0。 叶结点: 度为0的结点称为叶结点, 叶结点也称作终端结 点。 例如, 在图7 - 1(b)中结点J,F,K,L,H,I均为叶结点。
6
分支结点: 度不为0的结点称为分支结点, 分支结点也称 作非终端结点。 显然, 一棵树中除叶结点外的所有结点都是分 支结点。
孩子结点: 树中一个结点的子树的根结点称作这个结点的 孩子结点。 例如, 在图7 - 1(b) 中结点B,C,D是结点A的孩 子结点。 孩子结点也称作后继结点。
数据结构第7章排序
7.2.1 冒泡排序
• 排序过程 – 将第一个和第二个元素的关键字进行比较,若为逆序 ,则将两个元素互换;接着比较第二个和第三个元素 的关键字,依次类推,直至最后两个元素的完成比较 ,这称为第一趟冒泡排序。第一趟排序分划出一组元 素个数为n-1的待排序列和一个关键字最大的元素。 – 第i趟对前n - i + 1个的元素进行类似的排序操作,得到 一组元素个数为n - i的待排序列和一个(在前n-i+1个元 素中)关键字最大的元素。 – 这样不断分划直至一趟分划时无元素互换为止。
34 28 81 79 63 28 34 81 79 63 28 34 79 81 63
第一趟
28 34 79 63 81
第二趟
28 34 63 79 81
初始
7.2.1 冒泡排序
• 冒泡排序算法
template<class ElemType> void BubbleSort(ElemType data[], int n) { int lastSwapIndex = n - 1; //用于记录最后一次交换的元素下标 int i, j; for (i = lastSwapIndex; i > 0;i = lastSwapIndex){ lastSwapIndex = 0; for (j = 0; j < i; j++) if (data[j] > data[j + 1]){ Swap(data[j],data[j + 1]); lastSwapIndex = j; } } }
数 据 结 构
第7章 排序
概述
• 什么是排序? – 排序是计算机内经常进行的一种操作,其目的是将一 组“无序”的元素序列调整为“有序”的元素序列。 – 假设含n个记录的序列为{ R1, R2, …, Rn },其相应的 关键字序列为 { K1, K2, …,Kn }。这些关键字相互之 间可以进行比较,即在它们之间存在着这样一个关系 : Kp1≤Kp2≤…≤Kpn (或≥) 按此关系将上面记录序列重新排列为: { Rp1, Rp2, …,Rpn } 的操作称作排序。
数据结构第七章 排序
name 张涛 赵亮
冯博远 王强 李燕
7.2
基本原理
插入排序
每次将一个待排序的对象,按其关键字大小, 插入到前面已经排序好的一组对象的适当位臵上, 直到对象全部插入为止。
直接插入排序(Insert Sort)
希尔排序(Shell Sort)
7.2.1
直接插入排序
R[1]---R[i-1]
08 08
16 16
第三次
08
16
21
25* 25
49
希尔排序中d(间隔量)的取法 Shell最初的方案是 d= n/2, d=d/2, 直到d=1; Knuth的方案是d= d/3+1;
其它方案有:都取奇数为好;d互质为好 等等。
希尔排序的稳定性
如序列: 21 25 排序后为:08 16
R[0]有两个作用:
其一: 进入查找循环之前,保存 R[i] 的副本,使之不至 于因记录的后移而丢失R[i]中的内容; 其二: 在 while 循环时,“监视”下标变量 j 是否越界, 一旦越界(j<0),R[0]自动控制while循环的结束, 从而 避免了在while 循环内的每一次都要检测 j 是否越界( 即 省略了循环条件j>=0)。 因此,把 R[0] 称为“监视哨”。
第七章 排 序
本章内容
排序的概念和有关知识
常用的几种排序方法的基本思想、排序过 程和算法实现 各种排序算法的时间复杂度分析
学生成绩表
学号 姓名 高数 英语 总分
005 010 002
018 004
Chen Lin Gao Hong Wang Na
ZhangYang Zhao Pen
84 69 90
数据结构第七章--图(严蔚敏版)
8个顶点的无向图最多有 条边且该图为连通图 个顶点的无向图最多有28条边且该图为连通图 个顶点的无向图最多有 连通无向图构成条件:边 顶点数 顶点数-1)/2 顶点数*(顶点数 连通无向图构成条件 边=顶点数 顶点数 顶点数>=1,所以该函数存在单调递增的单值反 顶点数 所以该函数存在单调递增的单值反 函数,所以边与顶点为增函数关系 所以28个条边 函数 所以边与顶点为增函数关系 所以 个条边 的连通无向图顶点数最少为8个 所以28条边的 的连通无向图顶点数最少为 个 所以 条边的 非连通无向图为9个 加入一个孤立点 加入一个孤立点) 非连通无向图为 个(加入一个孤立点
28
无向图的邻接矩阵为对称矩阵
2011-10-13
7.2
图的存储结构
Wij 若< vi,vj > 或<vj,v i > ∈E(G)
若G是网(有权图),邻接矩阵定义为 是网(有权图), ),邻接矩阵定义为
A [ i,j ] = , 0或 ∞
如图: 如图:
V1
若其它
V2
3 4
2
V3
2011-10-13
C
A
B
D 2011-10-13 (a )
3
Königsberg七桥问题
• Königsberg七桥问题就是说,能否从某点出发 通过每桥恰好一次回到原地?
C
C
A B
.
A D
B
D (a)
2011-10-13
(b)
4
第七章 图
7.1 图的定义 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径
2011-10-13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
插入和删除弧 InsertArc(&G, v, w) // 在G中增添弧<v,w>,若G 是无向的,则还增添对称弧<w,v> DeleteArc(&G, v, w) //在G中删除弧<v,w>,若G 是无向的,则还删除对称弧<w,v> 遍历 DFSTraverse(G, v, Visit())//从顶点v起深度优先 遍历图G,并对每个顶点调用函数Visit一次且仅 一次 BFSTraverse(G, v, Visit())//从顶点v起广度优先 遍历图G,并对每个顶点调用函数Visit一次且仅 一次
无向图的邻接矩阵是对称的; 顶点i 的度=第 i 行 (列) 中1 的个数; 完全图的邻接矩阵中,对角元素为0,其余全1
数据结构
2016-12-15
Page ‹#›
7.2 图的存储结构
例2 表示有向图的邻接矩阵 顶点表 邻接矩阵 v3 v4 A.Edge = ( v1 v2 v3 v4 ) 0 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 v1 v2 v3 v4
数据结构
1 3 2
2016-12-15 Page ‹#›
4
3
7.1 图的定义和术语
例:判断下列4种图形各属什么类型?
无向 完全图
无向图(树)
有向图
有向 完全图
n(n-1)/2 条边来自n(n-1) 条边G1的顶点集合为V(G1)={0,1,2,3} 边集合为E(G1)={(0,1),(0,2),(0,3),(1,2),(1,3),(2,3)}
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
邻接点 若 (u, v) 是 E(G) 中的一条边,则称 u 与 v 互为邻接 顶点 弧头和弧尾 有向边<u, v>称为弧,边的始点u 叫弧尾,终点v 叫 弧头 度 顶点v 的度是与它相关联的边的条数。记作TD(v)。 在有向图中, 顶点的度等于该顶点的入度与出度之和 入度和出度 顶点 v 的入度是以 v 为终点的有向边的条数, 记作 ID(v); 顶点 v 的出度是以 v 为始点的有向边的条数, 记作 OD(v)
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
由于“弧”是有方向的,因此称由顶点集和弧集构成的 图为有向图 例如: G1 = (V1, VR1) A B C D E
其中 V1={A, B, C, D, E} VR1={<A,B>, <A,E>, <B,C>, <C,D>, <D,B>, <D,A>, <E,C> }
B
C
A
D
F
E
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
图的术语 图:记为 G=( V, E ) 其中:V 是G 的顶点集合,是有穷非空集;E 是G 的边集合,是有穷集 当E(G)为空时,图G还存在,但此时图G只有顶点而 没有边 有向图 图G中的每条边都是有方向的 v1
第7章 图
重点 图的数组表示法 图的邻接表存储表示 图的深度优先搜索、广度优先搜索 最短路径
数据结构
2016-12-15
Page ‹#›
第7章 图
难点 关键路径
数据结构
2016-12-15
Page ‹#›
第7章 图
学习要点 掌握图的基本概念和术语。 掌握用邻接矩阵和邻接表的方法描述图的存储结构。 理解并掌握深度优先搜索和广度优先搜索算法实现图的 遍历的算法。 能够用C语言根据深度优先搜索和广度优先搜索算法编 写具体程序 理解最小生成树的Prim和Kruskal算法。 能够用C语言根据Prim和Kruskal算法编写具体程序。 掌握拓扑排序,关键路径的思路和算法。 理解最短路径的Dijkstra算法和Floyd算法。
有向图的生成森林 若干棵生成树的集合,含全部顶点,但构成这些树 的边或弧是最少的
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
图的抽象数据类型 ADT Graph { 数据对象V:V是具有相同特性的数据元素的集合,称 为顶点集 数据关系 R:R={VR};VR={<v,w>|v,w∈V 且 P(v,w), <v,w>表示从v到w的弧,谓词P(v,w)定义 了弧<v,w>的意义或信息} 基本操作P: }ADT Graph
如果在生成树上添加1条边,必定构成一个环。
若图中有n个顶点,却少于n-1条边,必为非连通图
数据结构
Page ‹#›
2016-12-15
7.1 图的定义和术语
有向树 如果一个有向图恰有一个顶点的入度为0,其余顶点 的入度均为1,则是一棵有向树
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
数据结构
2016-12-15 Page ‹#›
7.1 图的定义和术语
观察下图的度 v2 v3 v4 v4 v5 v3 v4 v2
v1
v1
一般的,如果顶点vi的度记为TD(vi),那么n个顶 点e条边或弧的图满足如下关系
1 n e TD(vi ) 2 i 1
数据结构
2016-12-15 Page ‹#›
连通分量 非连通图的极大连通子图叫做连通分量
A C F D G I J L 数据结构 E H B A C F B
D
G I
E
H K
K
J M
2016-12-15
L
Page ‹#›
M
7.1 图的定义和术语
强连通图 在有向图中, 若对于每一对顶点vi和vj, 都存在一条从 vi到vj和从vj到vi的路径, 则称此图是强连通图 强连通分量 非强连通图的极大强连通子图叫做强连通分量 v1 v2 v1 v2
数据结构
2016-12-15
Page ‹#›
7.2 图的存储结构
例1 表示无向图的邻接矩阵 v1 v2 顶点表 邻接矩阵 A.Edge = v5 ( v1 v2 v3 v4 v5 )
A
v3
v4 v4
0 1 0 1 0
1 0 1 0 1
0 1 0 1 1
1 0 1 0 1
0 1 1 1 0
v1 v2 v3 v4 v5
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
回路 若路径上第一个顶点 v1 与最后一个顶点vm 重合, 则称这样的路径为回路或环
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
带权图 即边上带权的图。其中权是指每条边可以标上具有 某种含义的数值(即与边相关的数),也叫网络
数据结构
2016-12-15 Page ‹#›
7.2 图的存储结构
图的特点 非线性结构(m :n) 如果用顺序存储结构比较难,因为图多个顶点,无序可 言,无法仅以顶点坐标表达相互关系 但可用数组描述元素间关系 --- 邻接矩阵 可以采用链式存储结构 --- 多重链表 邻接表 十字链表 邻接多重表 各种表示法成立的原则:存入电脑后能惟一复原
v2
v3
数据结构
2016-12-15
v4
Page ‹#›
7.1 图的定义和术语
无向图 图G中的每条边都是无方向的 v1 v2
v3
v4 v4 v5
完全图 图G任意两个顶点都有一条边相连接
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
若 n 个顶点的有向图有n(n-1) 条边, 称为有向完全图 证明:若是有向完全图,则n个顶点中的每个顶点都 有一条弧指向其它n-1个顶点, 因此总边数=n(n-1) 若 n 个顶点的无向图有 n(n-1)/2 条边, 称为无向完全图 证明:可以直接推论出无向完全图的边数——因为 无方向,两弧合并为一边,所以边数减半,总边数 为n(n-1)/2 1 2 4
数据结构
2016-12-15 Page ‹#›
7.1 图的定义和术语
稀疏图 边较少的图。通常边数远少于nlogn 稠密图 边很多的图 无向图中,边数接近n(n-1)/2 有向图中,边数接近n(n-1) 子图 设有两个图 G=(V, E) 和 G’=(V’, E’)。 若 V’ V 且 E’ E, 则称 图G’ 是图G 的子图
数据结构
2016-12-15 Page ‹#›
7.1 图的定义和术语
图的结构定义 图是由一个顶点集 V 和一个弧(VR)集 R构成的数据结构。 Graph = (V, R ) 其中,VR={<v,w>| v,w∈V 且 P(v,w)} <v,w>表示从 v 到 w 的一条弧,并称 v 为弧尾,w 为弧头。 谓词 P(v,w) 定义了弧 <v,w>的意义或信息。
数据结构
2016-12-15
Page ‹#›
7.1 图的定义和术语
对邻接点的操作 FirstAdjVex(G, v)// 返回 v 的“第一个邻接点” 。 若该顶点在 G 中没有邻接点,则返回“空” NextAdjVex(G, v, w)// 返回 v 的邻接点w的(相对 于 w 的) “下一个邻接点”。若 w 是 v 的最后一 个邻接点,则返回“空” 插入或删除顶点 InsertVex(&G, v)//在图G中增添新顶点v DeleteVex(&G, v) // 删除G中顶点v及其相关的弧
