多面体与旋转体
第八讲多面体及旋转体(一)

第八讲多面体与旋转体(一)知识要求本章内容包括多面体和旋转体中常见的柱、锥、台、球的概念、性质、直观图、展开图的画法以及有关侧面积、体积的计算等.它是考查空间想象能力和逻辑思维能力及其运算能力的重要载体.高考试题中,立体几何试题的分值一般占20%左右,题量一般是五个,选择题、填空题、解答题的比例是3︰1︰1.立体几何试题大多以多面体和旋转体为载体,融线面关系于几何体中,融推理论证于几何量的计算中,融逻辑思维能力、空间想象能力于运算中.从近年高考立体几何试题中,可以发现以多面体和旋转体为载体设计的题目一般占25分左右,是立体几何试题分值的75%以上.涉及多面体或旋转体中有关元素的位置判定,数量的计算或最值的计算常常是以选择题或填空题的形式出现,涉及柱、锥、台体中的线面关系、面面关系的判定及运用于面积或体积的计算大多以中等难度的解答题的形式出现,而在面积或体积的计算中又侧重于体积.近年高考涉及多面体与旋转体的命题改革有所创新与突破,其主要特点是:①注意考查学生的想象、判断、推理与计算的综合能力素质,融推理与运算于一体;②注意对非常规空间几何图形的数量关系和位置关系的考查;③改变了选择题和填空题形式单一的弊端,拓宽了填空题的考查功能,采用多选、多填及开放性等形式,富有挑战性和探索性,体现高考“稳中有变”的思想.对柱、锥、台,会从复杂的空间图形中找出反映几何体特征的平面图形如:直角三角形、直角梯形,寻找有关的几何元素的位置关系,数量关系,并注意几种特殊四棱柱的联系与区别,重视平行于底面的截面的有关性质,树立“还台为锥”的思想,空间问题平面化的思想如:截面、展开图、平移、旋转、射影,应用整体思想、方程思想的策略.对多面体与旋转体的体积问题,应以公式法为基础并注意利用化归与转化思想,即①转移法(利用祖暅原理,把所求几何体的体积转化为与它等底、等高的几何体的体积),②分割求和法,③补形求差法,④换底等积法,沟通有关元素之间的联系,从而完成计算或证明.对多面体与旋转体的表面积除直接利用公式外,还可采用“化整为零”各个击破的策略,并熟悉直截面,轴截面的特性,通过展开图,将空间面积转化为平面面积来处理.解决折叠问题时,要将折叠前后的两个图形对照考察,弄清所涉及的元素在折叠前后的数量关系或位置关系.要计算柱、锥、台表面上两点的最短距离,可采用侧面展开图或全面展开图,化曲折为直.对简单多面体、旋转体的“切”“接”问题,一般是通过选择能够包含各元素间的关系的一个截面(多为轴截面),转化为平面图形或采用“等积法”来解决.应特别注意截面图形与直观图的联系,并注意两者构成元素的异同.对面积、体积的最值问题,一般转化为函数的最值问题加以解决,比较常用的方法是利用均值不等式.综合应用,关键在于沟通几何、代数、三角知识的联系,达到对知识的进一步理解、深化、升华.典型例题 例1.(2001福建)设长方体的三条棱长分别为a 、b 、c ,若长方体所有棱的长度之和为24,一条对角线长度为5,体积为2,则a 1+b 1+c1等于……………………………………( ) A .114 B .411 C .211 D .112 【分析】根据题意可得三个方程,从而求出a ,b ,c ,但计算量太大.若对a 1+b 1+c1变形可得a 1+b 1+c 1=abc ca bc ab ++,故只需求出ab +bc +ca ,从而利用整体思想求解. 【解】由题设,知⎪⎪⎩⎪⎪⎨⎧==++=++.2524)(4222abc c b a c b a∵ (a +b +c )2=a 2+b 2+c 2+2(ab +bc +ca ),∴ 2)212(=25+2(ab +bc +ca ), ∴ ab +bc +ac =211. 从而a 1+b 1+c 1=abc ca bc ab ++=411, 故选B .【点评】本题考查长方体的对角线公式,体积公式.在解题过程中,常对a 、b 、c 设而不求,利用恒等式,整体思想避开繁琐的计算过程,而直接得出结论.若长方体的对角线与交于同一点的三条棱分别成角α、β、γ,则cos 2 α+cos 2 β+cos 2 γ=1,若长方体的对角线与交于同一点的三个面分别成角α、β、γ,则cos 2 α+cos 2 β+cos 2 γ=2,在解题中的应用也应给予重视.例2.已知正三棱柱ABC—A1B1C1,过一面对角线AB1且与另一面对角线BC1平行的平面交上底面A1B1C1的一边A1C1于点D.①确定D点的位置,并证明你的结论;②证明平面AB1D⊥平面AA1D;③若AB=6,AA1=4,求直线BC1与平面AB1D的距离;④若AB︰A1A=k,问是否存在k,使平面AB1D与平面AB1A1所成角的大小为45°?若存在请求出k,若不存在请说明理由.【分析】①要证线面平行,须证线线平行,故可通过补形进行平移.②要证面面垂直,须证线面垂直.③要求线面距离可通过线面平行转化为点面距离.④对探索性性问题,不妨假设存在,然后求解或推理论证.【解】①将正三棱柱ABC—A1B1C1补成直平行六面体ABCE—A1B1C1E1,从而有AE1∥BC1,∴BC1∥面AB1E1.∴面AB1E1为所求平面,此时面AB1E1与A1C1交于D.又A1B1C1E1为平行四边形,∴D为A1C1中点.(或先猜D为A1C1中点,然后予以证明).②连结AD,由直平行六面体定义知AA1⊥面A1B1C1E1,∴AA1⊥B1D,又A1B1C1E1为菱形,∴B1D⊥A1C1,∴ B 1D ⊥面AA 1D ,又 B 1D ⊂面AB 1D ,∴ 面AB 1D ⊥面AA 1D .③∵ BC 1∥平面AB 1D ,∴ 只要求C 1 到平面AB 1D 的距离.又 A 1D =DC 1 故只要求A 1 到面AB 1D 的距离即可.由②,知面AB 1D ⊥面AA 1D ,所以过A 1 作AM ⊥AD ,则A 1M ⊥平面AB 1D .∴ A 1M 为所求.由A 1D ·AA 1=A 1M ·AD ,得:A 1M =512. (或由D AB C V 11-=D C B A V 11-,D C B S 11∆=293,1ADB S ∆=2153,得C 1 到平面AB 1D 的距离为512). ④过D 作DG ⊥A 1B 1 于G ,则DG ⊥面A 1B 1BA ;过G 作GH ⊥AB 1 于H ,连DH ,则DH ⊥AB 1,∴ ∠DHG 为A 1—AB 1—D 的平面角,若∠DHG =45°,设AA 1=a ,则AB =ka ,DG =43ka . ∵ AA 1︰AB 1=GH ︰GB 1, ∴ GH =1432+k ka . ∵ DG =GH ,∴ k =2.∴ 存在k =2,使平面AB 1D 与平面AB 1A 1 所成角的大小为45°.【点评】本题以正三棱柱为载体,考查了线线、线面、面面的位置关系以及距离、角、体积等问题.补形法、等积法是常用技巧,开放性问题是近年高考热点,应予重视.一般地利用三棱锥等积法寻找底面上的高,常将一个底面的顶点选在多面体的同一表面上.例3.各棱长都等于2的斜三棱柱ABC—A1B1C1中,侧面ABB1A1垂直于底面.①问侧棱与底面所成角为多少时,能使B1C⊥AC1;②在①的条件下求此三棱柱的侧面积.【分析】①取AB中点D,设BC1 B1C=O,则DO∥AC1要证B1C⊥AC1只需证DO ⊥B1C又O为B1C中点,∴只需证B1D=DC=3,在△B1BD中由余弦定理可得:∠B1BD=60°,又面B1BAA1⊥底面,∴∠B1BA为侧棱与底面所成角.故可猜测当侧棱与底面成角为60°时,B1C⊥AC1.②棱柱侧面积有两种解法,一是判断各侧面的形状,各个击破,再求各侧面的面积之和,二是求其直截面周长与侧棱长的乘积.【解】①当侧棱与底面成角为60°时,能使B1C⊥AC1.事实上,作B1D⊥AB于D.∵面ABB1A1⊥底面ABC,∴B1D⊥平面ABC.∴∠B1BD为侧棱与底面所成角.∴∠B1BD=60°.又BD=B1E cos 60°=1,∴D为AB中点.∴CD=3.又B1D=3,∴CD=B1D.又O为B1C中点,∴DO⊥B1C而AC1∥DO.∴AC1⊥B1C(或证B1C⊥面ABC1).② 在侧面ABB 1A 1 中11A ABB S 平行四边形=2·2·si n 60°=4×23=23, 在△B 1CD 中,CD =3=B 1D ,∴ B 1C =6.又 BCC 1B 1 为菱形,∴ BC 1=2 BO =222)26(2-=10, 又 AB ⊥面B 1CD ,∴ AB ⊥DO ,又 DO ∥AC 1,∴ AC 1⊥AB .在Rt △ABC 1中,AC 1=222)10(-=6.∴ 11B BCC S 平行四边形=C C AA S 11平行四边形=2110·6=15. ∴ S 侧=11A ABB S 平行四边形+211B BCC S 平行四边形=2(3+15).【点评】① 条件探索型命题,解题时要善于从所给的题断出发,逆向追索,逐步探寻出应具备的条件,然后予以证明.S 棱柱侧=C 直截面×l ,V 棱柱=S 直截面×l ,其中l 为侧棱长.例4.三棱锥P —ABC 中,侧棱P A ⊥底面ABC ,H 是A 在平面PBC 上的射影.① 若H 是△PBC 的重心,则在此三棱锥的棱所在直线中与AC 垂直的直线有几条?② 若H 是△PBC 的重心,且△ABC 是边长为2的正三角形,求二面角P —BC —A 的大小.【分析】① 充分利用线线垂直与线面垂直的相互关系进行挖掘与探求.② 二面角问题关键是“作”“证”“算”,本题关键要利用重心性质及方程思想进行求解.【解】① P A ⊥平面ABC ,AC ⊂平面ABC ,∴ P A ⊥AC ,AH ⊥平面PBC ,CH ⊥PB .∴ AC ⊥PB .∴ AC ⊥平面ABC .又 AB 平面P AB ,∴ AC ⊥AB .故与AC 垂直的直线有P A 、PB 、AB 三条.② 若H 是重心,连结PH 交BC 于D ,可设PH =2 x ,HD =x ,由AB =2,可知AD =3,于是有(3)2=x ·(2 x +x ),则x =1,∴ PD =3.又 D 是BC 的中点,∴ AD ⊥BC .∴ PD ⊥BC .∴ ∠PDA 是二面角P —BC —A 的平面角.由cos ∠PDA =PD AD =33得∠PDA =arc cos 33即为所求. 【点评】① 结论探索型命题,解题时要充分利用已知条件或图形的特征进行全面、透彻分析,从而推理、发现、获取结论.② 要正确区分三棱锥的顶点在底面上的射影何时是底面三角形的外心、内心、重心、中心.例5.棱锥被平行于底面的平面所截,当截面分别平分棱锥的侧棱,侧面积和体积时,相应的截面面积依次为S 1、S 2、S 3,则…………………………………………………………( ) A .S 1<S 2<S 3 B .S 3<S 2<S 1 C .S 2<S 1<S 3 D .S 1<S 3<S 2【分析】棱锥被平行于底面的平面所截,若顶点到截面的距离与顶点到底面的距离之比为k ,则它们对应棱长的比等于k ,底面积(侧面积、全面积)的比等于k 2,体积比等于k 3.【解】设棱锥的底面积为S ,高为h ,以截面为底面的棱锥的高分别为h 1、h 2、h 3,则21S S =21h h ,S S 2=h h 2,SS 3=h h 3 由题意,得 h h 1=21,21)(h h =21,23)(hh =21∴ 21S S =21,S S 2=21,SS 3=321. ∵ 21<21<321, ∴ S 1<S 2<S 3.故选A .【点评】① 对于台体平行于底面的截面,可补台为锥,再利用有关比例性质便可解决.② 棱台中平行于底面的截面及上、下底面面积分别为S 0、S 1、S 2 截面与上下底面的距离之比为m ︰n 时,则0S =nm S n S m ++12,特别地当m =n 时,为中截面公式. ③ 圆台的上下底面半径分别为r 、R ,作平行于底面的截面分别平分圆台的侧棱、侧面积,体积时,若截面分母线(自上到下)的比为m ︰n ,中截面半径为x ,则可利用性质“mrx -=n x R -”,得到相应的截面半径分别为2r R +,222r R +,3332r R +. 例6.一个正三棱台的上、下底面边长分别为3 cm 和6 cm ,高是23cm .求三棱台的① 侧棱长;② 斜高;③ 侧棱与底面所成的角的正切值;④ 侧面与底面所成的角;⑤ 侧面积.【分析】利用图中的直角三角形与直角梯形进行求解.【解】如图,设O 1,O 分别是上、下底面中心,则O 1O =23cm , 连结A 1O 1 并延长交B 1C 1 于D 1,连结AO 并延长交BC 于D ,过A 1 作A 1F ⊥AD 于F ,作D 1E ⊥AD 于E .① 在Rt △A 1AF 中,A 1F =23cm ,AF =AO -A 1O 1=33(6-3)=3(cm ), 所以AA 1=212F A AF +=221(cm ). ② 在Rt △D 1DE 中, D 1E =23,DE =DO -D 1O =63(6-3)=23(cm ), 所以斜边上的高 D 1D =221DE E D +=22)23()23(+=3(cm ). ③ 因为A 1F ⊥底面ABC ,所以∠A 1AF 为侧棱与底面所成的角,所以tan ∠A 1AF =AF F A 1=323=23. ④ 因为D 1D ⊥BC ,AD ⊥BC ,所以∠D 1DA 为侧面与底面所成二面角的平面角,tan ∠D 1DA =DE E D 1=2323=3 所以∠D 1DA =60°.(或还台为锥,设棱锥的高为h ,利用OA =2 OD ,得tan ∠D 1DE =OD h =OAh 2=2 tan ∠A 1AF =3). ⑤ S 侧=21(3×3+3×6)×3=2273(cm 2) (或利用S 侧=︒-60cos 上下S S =2(S 下-S 上)=243(62-32 )=2273). 【点评】对正棱锥、正棱台的问题可转化为直角三角形问题,使高、斜高、斜高在底面上的射影,侧棱、侧棱在底面上的射影,底面边长之半,边心距,外接圆半径及侧棱和底面所成角,侧面和底面所成的二面角等元素转化为直角三角形的边和角,还台为锥有利于整体上把握本章内容和公式.对正棱锥、正棱台,若侧面与底面所成角为α,则可利用公式:S 正棱锥侧=αcos 底S ,S 正棱台侧=αcos 上下S S -(适合选择、填空). 基础练习一、选择题1.设M ={正四棱柱},N ={长方体},P ={直四棱柱},Q ={正方体}则这四个集合的关系是……………………………………………………………………( ) A .P ⊂N ⊂M ⊂Q B .Q ⊂M ⊂N ⊂PC .P ⊂M ⊂N ⊂QD .Q ⊂N ⊂M ⊂P2.如果三棱锥S —ABC 的底面是不等边三角形,侧面与底面所成二面角都相等,且顶点S 在底面的射影O 在△ABC 内,那么O 是三角形的……………………( ) A .垂心 B .重心 C .外心 D .内心3.台体中一个平行于底面的截面把台体分成上、下两部分,若台体的上底面积,截面面积,下底面积之比为1︰4︰9,那么截面把台成分成上、下两部分的体积比为( ) A .278 B .197 C .135 D .53 4.一个圆锥的轴截面的顶角为120°,过顶点的截面的最大值是4,那么此圆锥的侧面积是………………………………………………………………………………( ) A .23π B .43π C .63π D .83π5.夹在两平行平面间的圆锥、球、圆柱在平面内的射影是等圆,那么它们的体积之比是…………………………………………………………………………………( ) A .1︰2︰3 B .2︰3︰6 C .4︰6︰9 D .1︰2︰46.圆台的侧面积是它的内切球表面积的34倍,则圆台母线和底面所成角的大小是( ) A .30° B .45° C .60° D .75°7.设地球半径为R ,在北纬45°圈上A 、B 两地的经度分别为东经165°和西经105°,则A 、B 两地间的球面距离是…………………………………………………( ) A .R B .42π R C .2πR D .3πR 8.在轴截面是直角三角形的圆锥内,有一个体积最大的内接圆柱,则内接圆柱的体积与圆锥的体积的比值为…………………………………………………………( )A .83B .94C .73D .21 9.将边长为a 的正方形ABCD 沿对角线AC 折起,使得BD =a ,则三棱锥D —ABC的体积为…………………………………………………………………………( )A .b a 3B .123aC .123a 3D .122a 3 10.平行四边形两邻边的长为a 和b ,当它分别绕边a 、b 旋转一周后,所形成的几何体的体积之比为………………………………………………………………( ) A .a b B .b a C .3)(a b D .3)(ba 11.如图三棱台ABC —A 1B 1C 1 中,已知S △ABC =S 1,111C B A S =S 2,高为h ,则四面体ACB 1C 1 的体积为………………………………………………………………( )A .3h 21S S B .31S 1h C .31S 2h D .3h (S 1+S 2+21S S ) 12.有三个球一个球内切于正方体的各个面,一球内切正方体各条棱,另一球过正方体的各顶点,则这三球面积比是…………………………………………………( ) A .1︰2︰3 B .1︰2︰3 C .1︰22︰33 D .1︰4︰9二、填空题13.斜三棱柱ABC —A 1B 1C 1 的一个侧面的面积为S ,这个侧面与它对棱的距离为a ,则这个棱柱的体积是______________.14.若正棱台上下底面及侧面的面积比为4︰9︰10,则侧面与底面所成的角大小为________.15.圆锥母线长为3,底面半径为1 cm ,底面圆周上有一点A ,由A 点出发绕圆锥一周回到A 点的最短路线长等于_________________.16.一个正六棱锥,底面边长为2,高为1,则过两条侧棱所作的截面中,最大的截面积等于______________.17.如图是一个正方体的展开图,在原正方体中有以下命题:① AB 与EF 所在直线平行;② AB 与CD 所在直线异面;③ MN 与BF 所在直线成60°角;④ MN 与CD 所在直线互相垂直.其中正确命题的序号是____________(注:把你认为正确的命题都填上)18.若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积的值是_____________(只需写出一个可能的值).三、解答题19.正三棱台ABC —A ′B ′C ′上、下底面的边长分别为1 cm 和3 cm ,高是36cm . ① 证明AA ′⊥平面BCC ′B ′;② 求正三棱台ABC —A ′B ′C ′的侧面积.20.把半径为R 的圆面剪去一个扇形,设剩下的扇形圆心角为α,将其作为一个圆锥的侧面围成一个圆锥.问α 为多大时,圆锥的体积最大?最大值为多少?21.如图所示四面体ABCD 中,已知AB =m ,CD =n ,还需要知道哪些条件(条件个数应最少)就可以求出四面体ABCD 的体积,并说明理由.参考答案基础练习一、选择题 1.B 2.D 3.B 4.B 5.A 6.C7.D 8.B 9.D 10.A 11.A 12.A二、填空题13.21aS 14.60° 15.33 16.6 17.②④ 18.611或1214或1211三、解答题19.① 提示:还台为锥;② 6.20.α=326π;V =2763π R 3.21.提示:以BD 、DC 为邻边作□BDCE ,利用三棱锥换底等积法得须两个条件得:AB 与CD 的距离h 及所成角θ.。
认识多面体和旋转体

课题: 6.1.1 认识多面体和旋转
【教学目标】
了解多面体和旋转体的基本概念,认识多面体的面、棱、顶点、对角线及旋转体的轴和母线;通过学习认识空间几何体的结构特征,提高学生的归纳总结能力,培养学生由具体到抽象,由一般到特殊的思想方法。
【教学重点】
多面体和旋转体的有关概念
【教学难点】
多面体和旋转体的基本概念,初步形成空间想象力
【教学方法】
观察演示探究
【教学过程】
教学
环节教学内容师生活动二次修改
导入
PPT展示:在现实生活中,我们周围存在着很多
形状各异的几何体,让学生观察它们的结构特点
圆形的方形的,多面的,旋转的都有
教师展示图形,并
分析这些图形的结构特
点,学生认真观察,并
回答老师提出的问题:
这些图形各有什么特
点?
估计学生认识到:方的,
圆的,有尖的等多面体
教师分析所展示图形并
板书多面体。
最新认识多面体与旋转体教案
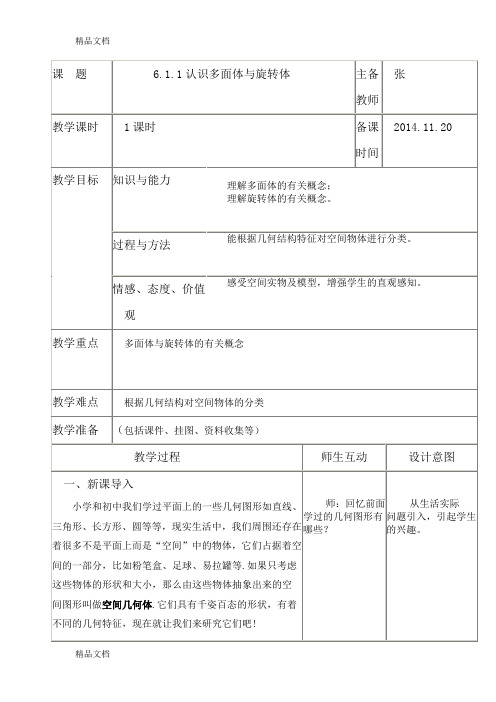
二、探索新知
探究1:多面体的相关概念
新知1:由若干个平面围成的几何体几何体叫做多面体.围成每个多面体的多边形叫做多面体的面,如面ABCD ; 两个面的公共边叫多面体的棱,如棱AB ;棱和棱的公共点叫多面体的顶点,如顶点A .连结不在同一平面上的两个顶点的线段叫做多面体的对角线,
具体如下图所示:
生回答问题,教师总结。
面 顶
点
棱
A B 'C 'D 'A 'C B
目,
探究2:旋转体的相关概念
生回答问题,教师
总结。
新知2:
由一条平面曲线绕一条定直线旋转所形成的曲面叫
旋转面,封闭的旋转面围成的几何体叫做旋转体,这条定
直线叫旋转体的轴.这条曲线叫做旋转体的母线。
如下图
的旋转体:
目,。
第二章多面体与旋转体 几何体求积复习

高中立体几何教案第二章多面体与旋转体几何体求积复习课教案教学目标1.使学生能熟练地掌握和运用简单多面体和旋转体的求积(面积和体积)公式;2.进一步培养学生研究空间问题的转化能力;3.要求学生在掌握好解多面体和旋转体问题基本方法的基础上,注意方程思想、割补思想和等积变换思想的指导作用,以期提高综合运算能力;4.通过对典型例题的分析,培养学生一题多解的发散性思维能力.教学重点和难点本节课的教学重点是突出元素度量关系的分析,加强综合运算的规律与方法的指导.教学难点是诱导学生分析几何体的空间结构,并根据题目中所给几何体的结构特点,去揭示元素之间的内在联系.教学设计过程一、复习讨论师:研究简单几何体的求积运算问题是立体几何第二章的中心议题,也是以后我们日常生活中经常要接触到的问题.今天,我们在复习旧知识的基础上,进一步总结运算规律,寻找解决问题的办法.(板书课题)师:请同学们一起来回忆多面体和旋转体的求积(侧面积和体积)公式.(放幻灯片,引导学生回忆,学生口答公式,最后给出正确答案.)(注:其中C,C'及S,S'分别为正棱台上、下底面周长和面积,h,h'分别为多面体的高和斜高,r,r'分别为圆台的上、下底面半径,l为母线长,R为球的半径)师:为了能使用公式,我们还必须要先求出公式中所需的几何体基本元素的数值大小.那么,在柱、锥、台、球的性质中,哪些性质较多地集中了它们基本元素(如:侧棱、高、斜高、母线等)间的相互关系?(幻灯分别打出棱柱、圆柱、棱锥、圆锥、棱台、圆台和球的示意图,帮助同学们寻找和归纳.讨论后,再请几位同学上讲台,边指图边报告讨论结果)生甲:在棱柱中,可以通过侧面和过不相邻的两条侧棱的截面即为对角面来把棱柱中的基本元素纳入同一平面.生乙:在正棱锥中,有2个特征直角三角形起到了把锥体中的基本元素联系在一起的作用.它们是:由棱锥的高、斜高和斜高在底面上的射影所组成的直角三角形(如图Rt △SOD);由棱锥的高、侧棱和侧棱在底面上的射影组成的直角三角形(如图Rt△SOA).生丙:(补充)棱锥中,Rt△SAD和Rt△OAD也有一样的作用.生丁:因为棱台是由平行于棱锥底面的平面截棱锥而得到的,所以在正棱台中有3个特征直角梯形和1个直角三角形(如图:O1,O2为上、下底面中心,O1E⊥A1B1,O2F ⊥AB,直角梯形有O1O2FE,O1O2AA1,A1EFA,直角三角形是△O2FA)生:在旋转体中是它们的轴截面.师:(归纳与讲评)刚才几位同学的发言都很好.无论是多面体,还是旋转体,它们的基本元素往往都集中在几个特征直角三角形、几个特征直角梯形、平行四边形和圆中,掌握了这一规律,我们在以后的解题过程中,只要抓住具体问题的特点,根据基本关系的分析,就可以把空间问题转化为解各个具体的三角形、梯形、平行四边形或圆了.二、课堂练习,例题分析例1 (1)正四棱台的两个底面的边长分别为a和b(a>b),侧棱和底面的夹角为2,则它的侧面积是______.(2)圆台上、下底面半径分别为r,R,平行于底面的截面把圆台分成侧面积相等的两个部分,则以此截面为底面,圆台所在的圆锥的顶点为顶点的圆锥与该圆台的体积比为______.(教学手段采用先练习,教师巡视,后讲评的方法)研究第(2)小题.师:我们还能否采用第(1)小题的方法“缺什么,求什么”吗?生:此题中的未知待求元素太多,根本没法直接求出其中的一个元素.师:那该怎么办?生:可以试一试设未知数,列方程求解.师:设什么?如何列方程?生:平行于底面的截面是个关键.我想设此截面半径为x.以r,x分别为上下底面圆半径的圆台的母线为l1,以r,R为上下底面圆半径的圆台的母线为l,先求出x.在圆台的轴截面中,做A2B⊥AO交A1O1于B1,那么△A2A1B1∽△A2AB,依题意可得师:大家可以看到这三道题都是对单个的多面体或旋转体的求积计算.下面,我们转入对比较复杂的由多面体和旋转体复合放置在一起的“组合体”的研究.例2 一个正方体所有的顶点都在球面上,如果这个球的体积为V,求正方体的棱长.师:首先;我们怎样把这类问题转化为平面图形的计算?(同学们较少接触到此类问题,还需继续启发引导)师:在旋转体中它的主要元素的关系集中在轴截面中,球的主要元素在它的大圆中;而正方体的主要元素关系在各个侧面及对角面上,我们能否做一个截面,使得二者兼顾?师:过正方体一个面作截面行吗?生:(讨论)不行.因为这样截得的是球的小圆.师:由对称性可知,正方体的中心一定就是球的中心,要得大圆必须过球心作截面,过球心作一个平行于正方体一个面的截面行吗?生:(讨论)也不行,因为这样截得的正方体的截面四个顶点不在大圆上.师:我们希望截得的正方体的截面的顶点在大圆上,那么这个截面应是正方体的什么截面?生:对角面.师:好,这样正方体的截面是一个什么平面图形?生:矩形.师:球与正方体的基本元素间取得了什么联系?生:正方体的对角线,恰是球的直径.师:大家可以看到这三道题都是对单个的多面体或旋转体的求积计算.下面,我们转入对比较复杂的由多面体和旋转体复合放置在一起的“组合体”的研究.例2 一个正方体所有的顶点都在球面上,如果这个球的体积为V,求正方体的棱长.师:首先;我们怎样把这类问题转化为平面图形的计算?(同学们较少接触到此类问题,还需继续启发引导)师:在旋转体中它的主要元素的关系集中在轴截面中,球的主要元素在它的大圆中;而正方体的主要元素关系在各个侧面及对角面上,我们能否做一个截面,使得二者兼顾?师:过正方体一个面作截面行吗?生:(讨论)不行.因为这样截得的是球的小圆.师:由对称性可知,正方体的中心一定就是球的中心,要得大圆必须过球心作截面,过球心作一个平行于正方体一个面的截面行吗?生:(讨论)也不行,因为这样截得的正方体的截面四个顶点不在大圆上.师:我们希望截得的正方体的截面的顶点在大圆上,那么这个截面应是正方体的什么截面?生:对角面.师:好,这样正方体的截面是一个什么平面图形?生:矩形.师:球与正方体的基本元素间取得了什么联系?生:正方体的对角线,恰是球的直径.已知球的体积为V,则如何消去中间量R是解题的关键.(请同学口述解答)三、小结我们通过对前几道例题的分析和讨论,已经总结得到了一些解题规律,它们是:(打幻灯)(1)解决多面体和旋转体的计算间题,可根据题目的具体特点,采用不同的方法,对于待求元素少的问题,可根据公式,采用“缺什么,找什么;要什么,求什么”的方法,抓住数量关系集中的平面,通过分析逐层求得,对于待求元素多的问题,可根据数量关系采用“设未知数、列方程”的方法.(2)对于多面体和旋转体复合放置的一类组合体的求积问题,关键要抓住“接”点与“切”点的位置,适当地选择截面.师:下面,请同学们继续开动脑筋,看看通过对例3的分析研究,还会给咱们带来一些什么新思路.例3 已知:在三棱锥P-ABC中,PA⊥BC,PA=BC=l,PA,BC的公垂线ED=h.四、作业1.一个圆台的母线长为5cm,两底面半径比为2∶5,侧面展开图的圆心角为216°.求这个圆台的侧面积和体积.(侧面积:35π;体积:52π)2.正四棱柱的对角线长为9,全面积为144.求它的底面边长和侧棱长.(底面边长为4,侧棱长为7;底面边长为6,侧棱长为3)3.长方体一个顶点上三条棱长分别为3、4、5,且它的八个顶点都在同一球面上.求这个球的表面积.(50π)4.四面体S-ABC中,M,N,P,Q分别为棱SB,SC,AC,AB的中点.(1)求证:M,N,P,Q四点共面;(2)求平面MNPQ把四面体分成的两部分的体积比.(1∶1)5.已知斜三棱柱的一个侧面积为S,此侧面与相对侧棱间的距离为a.求斜三棱柱的体积.课堂教学设计说明几何体的求积(面积和体积)问题,是历年高考中的重点考查内容之一.而学生对这一章知识的认识经常只停留在简单代公式计算的程度上.所以,他们往往忽视对几何体空间结构的认真分析,缺乏总结综合运算规律的学习环节,这样就达不到借助对具体几何体的研究来进一步培养学生空间想象能力的目的了.因此,教师应及时指导学生分析几何体的结构特点,帮助学生总结运算方法.这节课的目的就在于①巩固学生已有的求积运算方法“缺什么,找什么,要什么,求什么”(抓问题基本元素间关系);②诱导学生自己发现当要研究的问题中未知量及其数量关系较多时,可以利用方程的思想求解(提供学生一种常用的解题思维方法);③培养学生解决问题的应变能力——割补法与等积变换法在求积中的运用.这三点正是我安排的几个例题各想达到的目的.另外,例2要求学生认真分析组合体的结构特点.这节课应放在复习完基本概念之后再使用.补充说明近年来,求积问题的高考试题主要考查三个方面内容,一类是求几何体的侧面积、全面积和体积;一类是已知几何体的面积或体积求它的高、斜高、半径等,还有一类是求几何体的面积或体积的最值问题,针对高一学生的能力情况,应由易到难,不易一步到位.建议这个课题的复习课再安排1~2节.。
多面体与旋转体 高二数学(沪教版2020必修第三册)

与平面上的正多边形类似,在空间中可以考虑正多面体.如果一个 多面体的所有面都是全等的正三角形或正多边形,每个顶点聚集的 棱的条数都相等,这个多面体就叫做正多面体(regularp olyhedron).图113 1给出了五种不同的正多体.事 实上,用本节“课后阅读”中所介绍多面体的欧拉定理,可以验证 只有这五种正多面体.
旋转面是大学空间解析几何课程中的 内容之一.我们这里只关注最简单的 情况:一条直线a绕同一平面内的另
一条直线l旋转一周所形成的曲面: 圆柱面或圆锥面.当直线a与直线l平 行时,得到的是圆柱面;当直线a与 直线l相交(但不垂直)时,得到的 是圆锥面(图1133).直线a称
为圆柱面或圆锥面的母线.在圆锥面
课本练习
1.我国古代数学著作《九章算术》中研究过一种叫“鳖(biē)臑 (nào)”的几何体(见《九章算术》卷第五“商功”之一六),它 指的是由四个直角三角形围成的四面体.用你学过的立体几何知识说 明这种四面体确实存在
如图,先作一个底面为直角三角形的直棱柱AEF—BDC,其中∠BCD 是直角。 用平面ACD截此直三棱柱,则几何体A-BCD就是满足要求的“鳖臑”,这是 因为AB⊥平面BCD,所以△ABD、△ABC是直角三角形;又已知∠BCD为直 角,所以△BCD是直角三角形;最后,由CD⊥平面ABCF,推出CD⊥CA,即 ∠ACD为直角,所以△ACD是直角三角形。这样几何体A—BCD的四个面都是 直角三角形,即它是一个“鳖臑”。
我们迄今所见的多面体(如棱柱、棱锥、正多面体等)都是简单多 面体.但要构造一个非简单多面体也不难.如图11-3-4,这是 一个中间有一个长方体空洞的十六面体,往这样的橡胶多面体充气, 得到的是一个游泳圈,而不是球.算一算,对于图11- 3- 4的 多面体,V+F-E等于多少.
高中数学中的多面体和旋转体

多面体和旋转体是高中数学中的重要概念,它们在几何学中起着重要的作用。
本篇文章将介绍多面体和旋转体的基本概念、性质以及它们在实际生活中的应用。
一、多面体多面体是指由若干个平面多边形围合而成的三维几何体。
每个面都是一个平面多边形,并且相邻两个面的公共边是相交于一点的。
多面体分为凸多面体和凹多面体,如果一个多面体的任何一个面都在另一个面的外部,则这个多面体是凸多面体;否则,这个多面体是凹多面体。
1. 多面体的性质(1)多面体的顶点数V和面数F之间有如下关系:V = F + E - 3,其中E表示边数。
这个公式称为欧拉公式。
(2)多面体的棱数E和面数F之间有如下关系:E = 3F - E - F,这个公式称为欧拉-斯图姆定理。
(3)多面体的对角线数D和面数F之间有如下关系:D = 2F - 4,这个公式称为拉格朗日定理。
2. 多面体的应用(1)多面体在计算机图形学中有着广泛的应用,例如,计算机生成的三维图形通常都是由许多平面多边形构成的。
(2)多面体在机械制造中也有着重要的应用,例如,制造凸轮、齿轮等零件时需要使用凸多面体或凹多面体的概念。
二、旋转体旋转体是指由一条平面曲线绕着它所在的平面内的一条定直线旋转所生成的立体。
曲线称为旋转体的母线,定直线称为旋转体的轴。
1. 旋转体的性质(1)如果一个旋转体的底面是一个圆,则这个旋转体一定是圆柱或圆锥;如果这个圆的半径等于旋转体的底面半径,则这个旋转体是圆柱;否则,这个旋转体是圆锥。
(2)如果一个旋转体的底面是一个椭圆或其他平面曲线,则这个旋转体一定是圆台或球;如果这个椭圆或其他平面曲线是旋转体的底面半径的倍数,则这个旋转体是圆台;否则,这个旋转体是球。
2. 旋转体的应用(1)旋转体在建筑工程中有着广泛的应用,例如,圆柱形和球形建筑物的外壳是由旋转体的概念构成的。
(2)旋转体在油管和通风管道的设计中也有着重要的应用。
认识多面体和旋转体课件
体积计算
对于多面体,体积可以通过计算各个 面的体积之和得到。对于旋转体,体 积可以通过计算底面圆的体积或整个 旋转体的体积得到。
角度和弧度的计算
角度计算
在多面体中,角度可以通过测量各个 面之间的夹角得到。在旋转体中,角 度可以用来描述旋转体的旋转角度。
弧度计算
在旋转体中,弧度可以用来描述旋转 体的旋转程度,通常用于旋转轴的角 度测量。
旋转体的建模
旋转体的建模可以使用旋转几何公式进行,例如圆柱和圆锥可以使用旋转面的几何公式进行建模。
建模方法的比较和选择
01 02
精度和复杂性
使用CAD软件进行建模可以获得高精度的模型,但需要一定的技能和经 验。而使用数学公式进行建模可以创建相对简单的模型,但对于复杂模 型可能不够精确。
适用范围
CAD软件适用于各种类型的多面体和旋转体建模,而数学公式适用于某 些特定类型的模型,例如正多面体和旋转体。
在科学研究和教学中的应用
多面体和旋转体的科学研究价值
多面体和旋转体的研究涉及到几何学、拓扑学、物理学等多个学科领域,对于推动数学 和科学的发展具有重要意义。
多面体和旋转体的教学价值
在数学和工程学科的教学中,多面体和旋转体是重要的教学素材,有助于培养学生的空 间思维、几何直觉和解决实际问题的能力。
THANKS
该直线称为旋转轴, 平面图形称为旋转面 。
旋转体的分类
根据旋转面的形状,旋转体可以 分为圆柱、圆锥、圆台等类型。
根据旋转轴的方向,旋转体可以 分为正轴和斜轴两类。
根据旋转轴与旋转面的关系,旋 转体可以分为直纹和单叶两类。
旋转体的性质
旋转体的侧面是曲面,其展开 后是平面图形。
旋转体的体积和表面积与旋转 面和旋转轴的形状、大小和位 置有关。
《多面体旋转体》PPT课件
27
棱锥的分类:按底面多边形的边数
分别称底面是三角形,四边形,五边形……的 棱锥为三棱锥,四棱锥,五棱锥……
正棱锥:
底面是正多边形,顶点在底面上的射影是底面正 多边形的中心的棱锥叫正棱锥。
整理ppt
28
正棱锥性质 : (1)正棱锥的各侧棱相等, (2)各侧面是全等的等腰三角形, (3)各等腰三角形底边上的高相等, (4)侧棱和底面所成角相等,侧面与底面所 成角相等,相邻两侧面所成角相等。
侧面
侧棱
整理ppt
底面
10
思考3:下列多面体都是棱柱吗?如何在 名称上区分这些棱柱?如何用符号表示?
D1 C1
E1
A1
B1
D E
A
C
B D1
A1
D
C1 B1
C B
A1
A
C1
B1 C
D1 A1
C1 B1
D
C
B
A
整理ppt
A
B
11
思考4:棱柱上、下两个底面的形状大小 如何?各侧面的形状如何?
两底面是全等的多边形,
整理ppt
2
(一):空间几何体的类型
思考1:观察下列图片,你知道这图片在 几何中分别叫什么名称吗?
整理ppt
3
整理ppt
4
思考2:如果将这些几何体进行适当分类, 你认为可以分成那几种类型?
思考3:图(2)(5)(7)(9)(13) (14)(15)(16)有何共同特点?这 些几何体可以统一叫什么名称?
每个侧面都是全等的矩形的四棱柱整理整理pptppt2323整理整理pptppt2424整理整理pptppt2525侧面顶点底面多边形面叫做棱锥的底面有公共顶点的各三角形面叫做棱锥的侧面相邻侧面的公共边叫做棱锥的侧棱各侧面的公共顶点叫做棱锥的顶点
多面体和旋转体
第二章多面体和旋转体一多面体§2.1 棱柱一、素质教育目标(一)知识教学点1、棱柱的概念及性质。
2、平等六面体,长方体的概念及长方体的性质。
3、直棱柱直观图的画法4、棱柱侧面积的计算(二)能力训练点1、在学习棱住概念和性质过程中,努力提高学生的观察、抽象和概括能力。
2、通过直棱柱直观图的画法的教学,进一步提高学生的作图和识图能力。
3、通过直棱柱侧面积公式的教学,进一步增强学生把空间形转化为平面图形的意识,使学生进一步掌握化归的数学思想和方法,以提高学生分析问题、解决问题的能力。
(三)德育渗透点1、棱柱概念的形成,是从特殊到一般、具体到抽象的过程;通过教学使学生初步认识辩证唯物主义认识论的观点。
2、通过四面体、平行六面体、直平行六面体、长方体、正方体之间相互关系的教学,使学生树立普遍联系的唯物主义观点。
3、通过运用侧面积公式计算生产实践中具体零件的面积,使学生懂得数学对工、农业生产的意义,激励学生努力学好数学,将来为祖国的“四化”建设做出更大的贡献。
二、教学重点、难点、疑点及解决办法1、教学重点:理解棱柱的概念,掌握棱柱的性质及直棱柱侧面积公式,能利用性质及侧面积公式解决有关问题。
2、教学难点:直棱柱直观图的画法3、教学疑点:直棱柱的判断,注意引导学生严格按定义三、课时安排本课题建议安排3课时四、教与学过程设计第一课时节棱柱的概念及性质(一)引入将画有图2-1、图2-2、图2-3的小黑板挂出师:今天这一节课我们学习棱柱的概念和性质(给出课题),以上三个图形所表示的模型均为棱柱,下面我们一起来研究它们的共同特点。
(二)棱柱及有关概念的定义师:大家注意到图2-1到图2-3所表示的几何本均由一些面围成,而面与面之间有交线,因此可以从“面”和“线”两个角度去找它们的特点,先观察图2-1。
(1)首先看面:从面和面的关系及面的开头引导学生讨论,得出结论;有两个面互相平行,其余各面为四边形。
(2)再看线:从线与线之间的引导学生得出结论:每相邻两个四边形的公共边都互相平行。
1.1.1棱柱、棱锥、棱台的结构特征
(二)棱柱,棱锥,棱台 棱柱,棱锥,
1.棱柱:有两个面互相平行,其余各面都是四 .棱柱:有两个面互相平行, 边形, 边形,并且每相邻两个四边形的公共边都互相 平行, 平行,由这些面所围成的几何体叫做棱柱.
顶点 侧面 底面
用表示底面各顶点表示棱柱. 用表示底面各顶点表示棱柱.
侧棱 按底面多边形的边数分为三棱柱,四棱柱,五棱柱… 按底面多边形的边数分为三棱柱,四棱柱,五棱柱
3.棱台:用一个平行于棱锥底面的平面去截棱锥, 棱台:用一个平行于棱锥底面的平面去截棱锥, 底面与截面之间的部分叫做棱台. 底面与截面之间的部分叫做棱台.
上底面
棱台用表示底 面各顶点的字 母表示. 母表示.
按底面多边形的边 数为三棱台, 数为三棱台,四棱 五棱台…. 台,五棱台
下底面
棱柱,棱锥, 棱柱,棱锥,棱台的结构特征比较
上底面
下底面Biblioteka 棱台和圆台统称为台体. 棱台和圆台统称为台体. 台体
球的结构特征
球:以半圆的直径所在的直线为旋转轴,半圆 以半圆的直径所在的直线为旋转轴, 面旋转一周形成的几何体叫做球体 球体. 面旋转一周形成的几何体叫做球体.
球心
A
直径
O
C
大圆
B
圆柱,圆锥,圆台, 圆柱,圆锥,圆台,球的结构特征比较
问题2 与其他多面体相比,图片中的多面体 问题2:与其他多面体相比,图片中的多面体(14), , (15)有什么样的共同特征? 有什么样的共同特征? 有什么样的共同特征
思考:长方体被截去一部分, 思考:长方体被截去一部分,剩下的部分 是棱柱吗? 是棱柱吗?
A D E H G C F B
2.棱锥:有一个面是多边形,其余各面都 .棱锥:有一个面是多边形, 是有一个公共顶点的三角形, 是有一个公共顶点的三角形,由这些面所围 成的几何体叫做棱锥.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
· · · · ·
E D B C
底
棱柱的性质
E’ F’ A’ D’ B’
C’
有两个面互相平行, (1)底面互相平行。 其余各面都是四边形, (2)侧面是平行四边形。 并且每相邻两个面的公 共边都平行。
底 面
E A
侧面
D C B
顶点
侧棱 F
棱柱的分类
E’ F’ A’ D’ B’ C’
思考:倾斜后 的几何体还是 柱体吗?
2、思考:有一个面是多边形,其余各面都是 三角形的立体图形一定是棱锥吗?
课堂小结
空间几何体
多面体
旋转体
棱 柱
棱 台
棱 锥
圆 柱
圆 台
圆 锥
球 体
C1
A1 C
C1
B1
A1 B1 E
E1
D1 C1
D
C
A
B
A
B
A B
C
D
课堂练习题
问题1:有两个面互相平行,其余各面都
是四边形的几何体是棱柱吗?
答:不一定是
观察下面的几何体,哪些是棱柱?
(1)
(
√
)
(
×
(2)
)
(
(3)
√
)
(
(4)
×
)
(
√
(5)
)
(
×
(6)
(7)
) (
×
)
探究发现
观察下列多面体,有什么相同点?
金字塔 商贸大厦 盒子 鱼缸
方便面桶 地球 冰激凌 可乐瓶
观察下列物体的形状和大小,试给出相应的空 由若干平面多边形围成的几何体叫做多面体 间几何体,说说它们的共同特征。
由一个平面图形绕它所在的平面 观察下列物体的形状和大小,试 内的一条定直线旋转所成的封闭几何 给出相应的空间几何体,说说有它们 体叫做旋转体. 的共同特征。
球:以半圆的直径所在的直线为旋转轴, 半圆面旋转一周形成的几何体叫做球体, 简称球。 其中半圆的圆心叫做球的球心,半圆的 半径叫做球的半径,半圆的直径叫做球 的直径。 球的表示方法:用表示球心的字母O表 示,如课本图1.1-8中的球表示为球O。
思考题:3.用一个平面去截球体得到的截面 是什么图形? 性质3:用一个平面去截球体得到的截面是一个 圆。
底 面
E
侧棱 F
D
C
A
侧面
B
顶点
棱柱的分类
1、按侧棱是否和底面垂直分类:
棱柱 斜棱柱 直棱柱 正棱柱
棱柱的分类
其它直棱柱
2、按底面多边形边数分类: 三棱柱、四棱柱、 五棱柱、·· ·· ··
棱柱的表示
平行的两底面多边形的字母表示棱柱,如:棱柱 ABCDE- A1B1C1D1E1 D1 A1 B1
直角梯形
分别以矩形、直角三角形的直角边、 直角梯形垂直于底边的腰所在的直线为旋
转轴,其余各边旋转而成的曲面所围成的
几何体, 分别叫做圆柱,圆锥,圆台。
圆柱
圆锥
圆台
圆柱
O1 A
圆锥
S
圆台
O1 A
O
B
O
A
O
B
轴
高
底面
侧面
母线Leabharlann 思考题:1.平行于圆柱,圆锥,圆台的底面的 截面是什么图形? 2.过圆柱,圆锥,圆台的旋转轴的截 面是什么图形? 性质1:平行于底面的截面都是圆。 性质2:过轴的截面(轴截面)分别是的矩 形,等腰三角形,等腰梯形。
有一个面是多边形,其余各面都是有一个公 共顶点的三角形。
棱锥的概念及表示
S
顶点
有一个面是多 边形,其余各面都 是有一个公共顶点 侧棱 的三角形。
A
侧面
D C 底面
B
棱锥的表示方法;如:S-ABCD
棱锥的分类
分类标准:底面多边形的边数
三棱锥
四棱锥
五棱锥
六棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面 的射影是底面中心,这样的棱锥叫做正棱锥。
棱柱的概 念
有两个面互相平行, 其余各面都是四边形, 并且每相邻两个面的公 共边都平行。
E’ F’ A’
D’ B’
C’
E
D
F
A B
C
棱柱的概念
侧面与底面的 公共顶点叫 做棱柱的 顶点
· A’ · 两个互相 · · ·
D’ C’ B’ 平行的面 叫做棱柱 的底
E’
底
其余各面叫做 两个面的 棱柱的侧面 公共边叫做 相邻侧面的 棱柱的棱 公共边叫做 棱柱的侧棱 A
在日常生活和生产实践中,我们常常遇到这 样一类几何体(geometric solid),它是由几 个平面相交而围成的封闭的或者由一个平面图形 绕着一条与它同在一个平面内、且不通过该平面 图形内部的定直线旋转一周所形成的封闭的几何 体,前者如方砖、盒子、金字塔等,后者如球体、 桶装方便面盒子等。这些几何体在我们的生活中 处处可见。 今天我们就一起走进这美妙的几何体世界中, 从科学的角度来体验和研究其中的奥妙。
空间几何体的定义: 如果只考虑物体的形状和大小,而不考虑 其它因素,那么这些由物体抽象出来的空间图 形就叫做空间几何体
空间几何体的分类: 1.多面体:由若干平面多边形围成的几何体 2.旋转体:由一个平面图形绕它所在的平面内的 一条定直线旋转所成的封闭几何体
O1
A
S
O1
A
O
矩 形
B
O
A O
B
直角三角形
棱台的概念及表示
用一个平行于棱锥底 面的平面去截棱锥,底面 与截面之间的部分是棱 台. A’ 棱台的表示方法:用平行的两底 面多边形的字母表示棱台, A 1B1C1D1 如: ABCD- A
D’ D B’
C’ C
B
正棱台 : 由正棱锥截的的棱台
课堂练习
1、思考:有两个面平行,其余各面都是平行四 边形所围体一定是棱柱吗?
