中考数学难点突破与经典模型精讲练相似三角形中的旋转型相似模型(解析版)

合集下载

相似三角形重难点模型(五大模型)(解析版)

相似三角形重难点模型(五大模型)【题型01：(双)A字型相似】【题型02：(双)8型相似】【题型03：母子型相似】【题型04：旋转相似】【题型05：K字型相似】【题型01：(双)A字型相似】1.如图，在△ABC中，BC=12，高AD=6，正方形EFGH一边在BC上，点E,F分别在AB,AC上，AD交EF于点N，求AN的长．【答案】2【分析】设正方形EFGH的边长EF=EH=x，易证四边形EHDN是矩形，则DN=x，根据正方形的性质得出EF∥BC，推出△AEF∽△ABC，根据相似三角形的性质计算即可得解．【详解】解：设正方形EFGH的边长EF=EH=x，∵四边形EFGH是正方形，∴∠HEF=∠EHG=90°,EF∥BC，∴△AEF∽△ABC，∵AD是△ABC的高，∴∠HDN=90°，∴四边形EHDN是矩形，∴DN=EH=x，∵△AEF∽△ABC，∴AN AD =EFBC(相似三角形对应边上的高的比等于相似比)，∵BC=12,AD=6，∴AN=6-x，∴6-x6=x 12，解得：x=4，∴AN=6-x=6-4=2．【点睛】本题考查了相似三角形的判定和性质，矩形的判定和性质．解题的关键是掌握相似三角形的判定和性质，矩形的判定和性质的运用，注意：矩形的对边相等且平行，相似三角形的对应高的比等于相似比．2.如图，光源P 在水平横杆AB 的上方，照射横杆AB 得到它在平地上的影子为CD (点P 、A 、C 在一条直线上，点P 、B 、D 在一条直线上)，不难发现AB ⎳CD ．已知AB =1.5m ，CD =4.5m ，点P 到横杆AB 的距离是1m ，则点P 到地面的距离等于m ．【答案】3【分析】作PF ⊥CD 于点F ，利用AB ∥CD ，推导△P AB ∽△PCD ，再利用相似三角形对应高之比是相似比求解即可．【详解】解：如图，过点P 作PF ⊥CD 于点F ，交AB 于点E ，∵AB ∥CD ，∴△P AB ∽△PCD ，PE ⊥AB ，∵△P AB ∽△PCD ，∴AB CD =PE PF ，(相似三角形对应高之比是相似比)即：1.54.5=1PF，解得PF =3．故答案为：3．【点睛】本题考查相似三角形的判定与性质，掌握相似三角形对应高之比是相似比是解题的关键．3.如图，在Rt △ABC 中，∠ACB =90°，∠BAC =60°，AC =6，AD 平分∠BAC ，交边BC 于点D ，过点D 作CA 的平行线，交边AB 于点E ．(1)求线段DE 的长；(2)取线段AD 的中点M ，连接BM ，交线段DE 于点F ，延长线段BM 交边AC 于点G ，求EF DF的值．【答案】(1)4(2)23【分析】(1)根据平行线分线段成比例定理，列出比例式求解即可；(2)根据平行线分线段成比例定理，列出比例式求解即可．【详解】(1)解：∵AD 平分∠BAC ，∠BAC =60°，∴∠DAC =30°，在Rt △ACD 中，∠ACD =90°，∠DAC =30°，AC =6，∴CD =23，在Rt △ACB 中，∠ACB =90°，∠BAC =60°，AC =6，∴BC =63，∴BD =BC -CD =43，∵DE ∥CA ，∴DE CA=BD BC =23，∴DE =4；(2)解：如图．∵点M 是线段AD 的中点，∴DM =AM ，∵DE ∥CA ，∴DF AG =DM AM．∴DF =AG ．∵DE ∥CA ，∴EF AG =BF BG ，BF BG =BD BC ．∴EF AG=BD BC ．∵BD =43，BC =63，DF =AG ，∴EF DF=23．【点睛】考查了平行线分线段成比例定理，注意线段之间的对应关系．4.如图，△ABD 中，∠A =90°，AB =6cm ，AD =12cm ．某一时刻，动点M 从点A 出发沿AB 方向以1cm/s 的速度向点B 匀速运动；同时，动点N 从点D 出发沿DA 方向以2cm/s 的速度向点A 匀速运动，运动的时间为ts ．(1)求t 为何值时，△AMN 的面积是△ABD 面积的29；(2)当以点A ，M ，N 为顶点的三角形与△ABD 相似时，求t 值．【答案】(1)t 1=4，t 2=2；(2)t =3或245【分析】(1)由题意得DN =2t (cm )，AN =(12-2t )cm ，AM =tcm ，根据三角形的面积公式列出方程可求出答案；(2)分两种情况，由相似三角形的判定列出方程可求出t的值．【详解】解：(1)由题意得DN=2t(cm)，AN=(12-2t)cm，AM=tcm，∴△AMN的面积=12AN•AM=12×(12-2t)×t=6t-t2，∵∠A=90°，AB=6cm，AD=12cm∴△ABD的面积为12AB•AD=12×6×12=36，∵△AMN的面积是△ABD面积的29，∴6t-t2=29×36，∴t2-6t+8=0，解得t1=4，t2=2，答：经过4秒或2秒，△AMN的面积是△ABD面积的2 9；(2)由题意得DN=2t(cm)，AN=(12-2t)cm，AM=tcm，若△AMN∽△ABD，则有AMAB=ANAD，即t6=12-2t12，解得t=3，若△AMN∽△ADB，则有AMAD=ANAB，即t12=12-2t6，解得t=24 5，答：当t=3或245时，以A、M、N为顶点的三角形与△ABD相似．【点睛】本题考查了相似三角形的判定，直角三角形的性质和一元二次方程的应用，正确进行分类讨论是解题的关键．【题型02：(双)8型相似】5.已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE=AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．(1)求证：△BND∽△CNM；(2)如果AD2=AB•AF，求证：CM•AB=DM•CN．【答案】(1)见解析；(2)见解析【分析】(1)利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；(2)先利用AD 2=AB •AF 可证明△ADB ∽△AFD ，则∠1=∠F ，再根据平行线的性质得∠F =∠4，∠2=∠3，所以∠3=∠4，加上∠NMC =∠CMD ，于是可判断△MNC ∽△MCD ，所以MC ：MD =CN ：CD ，然后利用CD =AB 和比例的性质即可得到结论．【详解】证明：(1)∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD ，而BE =AB ，∴BE =CD ，而BE ∥CD ，∴四边形BECD 为平行四边形，∴BD ∥CE ，∵CM ∥DB ，∴△BND ∽△CNM ；(2)∵AD 2=AB •AF ，∴AD ：AB =AF ：AD ，而∠DAB =∠FAD ，∴△ADB ∽△AFD ，∴∠1=∠F ，∵CD ∥AF ，BD ∥CE ，∴∠F =∠4，∠2=∠3，∴∠3=∠4，而∠NMC =∠CMD ，∴△MNC ∽△MCD ，∴MC ：MD =CN ：CD ，∴MC •CD =MD •CN ，而CD =AB ，∴CM •AB =DM •CN ．【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．6.如图，在平行四边形ABCD 中，点E 是AD 上一点，AE =2ED ，连接BE 交AC 于点G ，延长BE 交CD 的延长线于点F ，则BG GF 的值为()A.23B.12C.13D.34【答案】A【分析】本题考查了相似三角形的判定与性质，平行四边形的性质，解决本题的关键是利用平行四边形的性质对边平行而构建相似三角形．先根据平行四边形的性质得到AB ∥CD ，则可判断△ABG ∽△CFG ，△ABE ∽△DFE ，于是根据相似三角形的性质和AE =2ED 即可得结果．【详解】解：∵四边形ABCD 为平行四边形，∴AB ∥CD ，∴△ABG ∽△CFG ，∴BG GF =AB CF∵△ABE ∽△DFE ，∴AE DE =AB DF，∵AE =2ED ，∴AB =2DF ，∴AB CF =23，∴BG GF=23．故选：A ．7.如图1，在四边形ABDE 中，∠ABC =∠BDE ，点C 在边BD 上，且AC ∥DE ，AB ∥CE ，点F 在边AC 上，且AF =CE ，连接BF ,DF ，DF 交CE 于点G ．(1)求证：BF =DF ；(2)如图2，若∠ACE =∠CDF ，求证：CE ⋅CF =BF ⋅DG ；(3)如图3，若延长BF 恰好经过点E ，求BC CD的值．【答案】(1)见解析(2)见解析(3)1+52【分析】(1)证明△ABF ≌△CAE ，得出BF =AE ，证明四边形AFDE 为平行四边形，得出AE =DF ，则可得出结论；(2)证明△FCG ∽△FDC ，得出CF DF =GF CF ，证明△FCG ∽△DEG ，得GF DG =CF DE ，则得出结论；(3)证明△ABF ∽△CEF ，得出AB CE =AF CF，设AB =x ,AF =CE =m ，解方程求出x ，则可得出答案．【详解】(1)∵AC∥DE,AB∥CE∴∠BDE=∠ACB,∠ABC=∠DCE,∠BAC=∠ACE ∵∠ABC=∠BDE∴∠ABC=∠BDE=∠ACB=∠DCE∴AB=AC,CE=DE在△ABF和△CAE中，又∵AF=CE∠BAC=∠ACE AB=AC∴△ABF≌△CAE(SAS)∴BF=AE∵CE=DE,AF=CE∴AF=DE∵AF=DE,AC∥DE∴四边形AFDE为平行四边形∴AE=DF∴BF=DF(2)∵∠CFG=∠CFD ∠ACE=∠CDF∴△FCG∽△FDC∴CF DF =GF CF又∵AC∥DE∴△FCG∽△DEG∴GF DG =CFDE，即GFCF=DGDE∴CF DF =DGDE．又∵DE=CE,DF=BF∴CF BF =DGCE，即CE⋅CF=BF⋅DG(3)∵∠ABC=∠DCE ∠ACB=∠EDC∴△ABC∽△ECD∴BC CD =AB CE∵AB∥CE，∴△ABF∽△CEF∴AB CE =AF CF∴AB⋅CF=AF⋅CE．设AB=x,AF=CE=m，则有x(x-m)=m2解得x=1+52m(负值舍去)∴BC CD =ABCE=1+52【点睛】本题考查了相似三角形的判定和性质、全等三角形的判定和性质、平行四边形的性质，利用相似三角形的判定和性质是本题解题的关键．8.如图1，在矩形ABCO 中，OA =8，OC =6，D ，E 分别是AB ，BC 上一点，AD =2，CE =3，OE 与CD 相交于点F ．(1)求证：OE ⊥CD ；(2)如图2，点G 是CD 的中点，延长OG 交BC 于H ，求CH 的长．【答案】(1)见解析；(2)CH 的长为6．【分析】(1)根据四边形ABCO 是矩形，可得OA =BC =8，OC =AB =6，根据勾股定理可得OE 和CP 的长，进而得EF 和CF 的长，再根据勾股定理的逆定理即可得OE ⊥CD ；(2)在Rt △CBD 中，CB =8，BD =AB -AD =6-2=4，根据勾股定理可得CD =45，根据点G 是CD 的中点，可得CG =DG =25，所以得点G 是CP 的三等分点，根据OA ∥BC ，对应边成比例即可求出CH 的长．【详解】(1)∵四边形ABCO 是矩形，∴OA =BC =8，OC =AB =6，在Rt △OCE 中，CE =3，∴OE =OC 2+CE 2=62+32=35，∵AB ∥OC ，即AD ∥OC ，且AD =2，∴AD OC =P A PO ，∴26=P A P A +8，∴P A =4，∴PO =P A +OA =12，∴在Rt △OPC 中，OC =6，∴CP =OC 2+PO 2=62+122=65，∵OA ∥BC ，即OP ∥CE ，∴CE OP =EF OF =CF PF ，∴EF OF=CF PF =312=14，∴EF =15OE =355，CF =15CP =655，∵355 2+655 2=95+365=9，∴EF 2+CF 2=CE 2，∴△CEF 是直角三角形，∴∠CFE=90°，∴OE⊥CD；(2)在Rt△CBD中，CB=8，BD=AB-AD=6-2=4，根据勾股定理，得CD=CB2+BD2=82+42=45，∵点G是CD的中点，∴CG=DG=25，由(1)知：CP=65，∴DP=CP-CD=25，∴点G是CP的三等分点，∵OA∥BC，即OP∥CH，∴CH OP =CG GP，∴CH12=12，∴CH=6．答：CH的长为6．【点睛】本题考查了矩形的性质、勾股定理及其逆定理的应用、相似三角形的判定与性质以及平行线分线段成比例定理，解决本题的关键是掌握矩形的性质．【题型03：母子型相似】9.【典例3】如图1，∠C=90，BC=6，tan B=43，点M从点B出发以每秒1个单位长度的速度向点C运动，点N同时从点C出发以每秒2个单位长度的速度向点A运动，当一点到达终点时，另一点也停止运动．(1)求AB的长．(2)当以点M、C、N为顶点的三角形与△ABC相似时，求t的值．(3)如图2，将本题改为点M从点B出发以每秒3个单位长度的速度在BA上向点A运动，点N同时从点A出发向点C运动，其速度是每秒2个单位长度，其它条件不变，求当t为何值时，△MNA为等腰三角形．【答案】(1)10(2)t=125或t=1811时，以点M、C、N为顶点的三角形与△ABC相似(3)t=2或t=4017或t=5031时，△MNA为等腰三角形【分析】(1)根据三角函数解得即可；(2)分①当△MCN ∽△BCA 时和②当△MCN ∽△ACB 时，两种情况利用相似三角形的性质解答即可；(3)分①当AM =AN 时，②当AM =MN 时，③当MN =AN 时，三种情况，利用等腰三角形的性质得出比例解答即可．【详解】(1)解：∵∠C =90°,BC =6,tan B =43∴AC =8∴AB =BC 2+AC 2=62+82=10(2)解：解：①当△MCN ∽△BCA 时，∴MC BC =CN CA ，即6-t 6=2t 8，解得：t =125，②当△MCN ∽△ACB 时，∵MC AC =CN BC ，即6-t 8=2t 6，解得：t =1811，综上所述，t =125或t =1811时，以点M 、C 、N 为顶点的三角形与△ABC 相似，(3)解：①如图3，当AM =AN 时，10-3t =2t ，解得：t =2，②如图4，当AM =MN 时，过点M 作MD ⊥AC 于D ，则∠ADM =90°，AM =MN =10-3t ，AD =12AN =t ，∵∠ACB =90°，∴MD ∥BC ，∴△AMD ∽△ABC ，∴AM AB =AD AC ，即10-3t 10=t 8，解得：t =4017，③如图5，当MN =AN 时，过点N 作ND ⊥AB 于D ，则∠ADN =∠ACB =90°，AD =DM =12AM =12(10-3t )，∵∠A =∠A ，∴△ADN ∽△ACB ，∴AD AC =AN AB ，即12(10-3t )8=2t 10，解得：t =5031，综上所述，t =2或t =4017或t =5031时，△MNA 为等腰三角形【点睛】本题考查考查了相似三角形的判定与性质、等腰三角形的性质，已知正切求边长，解题的关键是掌握辅助线的作法，数形结合，分类讨论思想的应用．10.如图，在△ABC 中，D 是BC 上的点，E 是AD 上一点，且AB AC=AD CE ，∠BAD =∠ECA ．(1)求证：AC 2=BC •CD ；(2)若AD 是△ABC 的中线，求CE AC 的值．【答案】(1)证明见解析；(2)22【分析】(1)首先利用相似三角形的判定得出△BAD ∽△ACE △，得∠B =∠EAC ，进而求出△ABC ∽△DAC ，再利用相似三角形的性质得出答案即可；(2)由△BAD ∽△ACE 可证∠CDE =∠CED ，进而得出CD =CE ，再由(1)可证AC =2CD ，由此即可得出线段之间关系．【详解】(1)证明：∵AB AC =AD CE ，∠BAD =∠ECA ，∴ΔBAD ∽ΔACE ，∴∠B =∠EAC ，∵∠ACB =∠DCA ，∴△ABC ∽△DAC ，∴AC CD =BC AC，∴AC 2=BC ·CD ．(2)解：∵△BAD ∽△ACE ，∴∠BDA =∠AEC ，∴∠CDE =∠CED ，∴CD =CE ，∵AD 是△ABC 的中线，∴BC =2BD =2CD ，∴AC 2=BC ·CD =2CD 2，即：AC =2CD ，∴CE AC =CD 2CD=22．【点睛】此题主要考查了相似三角形的判定与性质以及重心的性质等知识，根据已知得出△BAD ∽△ACE 是解题关键．11.如果两个相似三角形的对应边存在2倍关系，则称这两个相似三角形互为母子三角形．(1)如果△DEF 与△ABC 互为母子三角形，则DE AB 的值可能为()A.2B.12C.2或12(2)已知：如图1，△ABC 中，AD 是∠BAC 的角平分线，AB =2AD , ∠ADE =∠B ．求证：△ABD 与△ADE 互为母子三角形．(3)如图2，△ABC 中，AD 是中线，过射线CA 上点E 作EG ⎳BC ，交射线DA 于点G ，连结BE ，射线BE 与射线DA 交于点F ，若△AGE 与△ADC 互为母子三角形．求AG GF的值．【答案】(1)C ；(2)见解析；(3)AG GF=13或3．【分析】(1)根据互为母子三角形的定义即可得出结论；(2)根据两角对应相等两三角形相似得出△ABD ∽△ADE ，再根据AB =2AD 从而得出结论；(3)根据题意画出图形，分当G ,E 分别在线段AD ,AC 上时和当G ,E 分别在射线DA ,CA 上时两种情况加以讨论；【详解】(1)∵△DEF 与△ABC 互为母子三角形，∴DEAB=12或2故选：C(2)∵AD 是∠BAC 的角平分线，∴∠BAD =∠CAD ，∵∠ADE =∠B ，∴△ABD ∽△ADE ．又∵AB =2AD ，∴△ABD 与△ADE 互为母子三角形．(3)如图，当G ,E 分别在线段AD ,AC 上时，∵△AGE 与△ADC 互为母子三角形，∴CD GE =AD AG=2，∴AG =DG ，∵AD 是中线，∴BD =CD ，又∵GE ⎳BC ，∴△GEF ∽△DBF ．∴DF GF =DB GE =CD GE=2，∴DG =3GF ，∴AG GF=3．如图，当G ,E 分别在射线DA ,CA 上时，∵△AGE 与△ADC 互为母子三角形，∴CD GE =AD AG =2，∴AG =12AD =13DG ，∵AD 是中线，∴BD =CD ，又∵GE ⎳BC ，∴△GEF ∽△DBF ．∴DF GF =DB GE =CD GE=2，∴DG =GF ，∴AG GF =13．综上所述，AG GF =13或3【点睛】本题主要考查了相似三角形的判定与性质、分类讨论的数学思想以及接受与理解新生事物的能力．准确理解题设条件中互为母子三角形的定义是正确解题的先决条件，在分析与解决问题的过程中，要考虑全面，进行分类讨论，避免漏解．12.如图1，AB =AC =2CD ，DC ∥AB ，将△ACD 绕点C 逆时针旋转得到△FCE ，使点D 落在AC 的点E 处，AB 与CF 相交于点O ，AB 与EF 相交于点G ，连接BF ．(1)求证：△ABE ≌△CAD ；(2)求证：AC ∥FB ；(3)若点D，E，F在同一条直线上，如图2，求ABBC的值．(温馨提示：请用简洁的方式表示角)【答案】(1)见解析(2)见解析(3)2【分析】(1)根据旋转变换的性质得到旋转前后两个三角形全等，从而得到CE=CD，根据AC=2CD，就能得到AE=CD，然后利用平行可以得到内错角相等，最后加上AB=AC，就可以通过边角边证明两个三角形全等．(2)根据旋转和第一小题的结论，可以得到BE=FE，然后用等角对等边即可得到∠EFB=∠EBF，又可以从前面的两个全等中得到∠EFC=∠EBA，∠OAC=∠OCA从而得到∠OFB=∠OBF，那么△ACO和△BOF就是顶角互为对顶角的一组等腰三角形，所以就能得到底角相等，即∠CAO=∠FOB，那么内错角相等，两直线平行即可证结论．(3)根据D，E，F在同一条直线上，可以证明△AEG和△CED全等，即可得到AG=12AB，那么EG就是中位线，则EG∥CB，加上第二小题结论就能得到四边形BCEF是平行四边形，那么BC=AD，然后通过三角形外角的性质，可以证得∠ADE=∠ACD，就能证△ACD和△ADE是一组子母型相似，然后根据相似比可得最终答案．【详解】(1)解：∵将△ACD绕点C逆时针旋转得到△FCE，∴△FCE≌△ACD，∴CE=CD，∵AC=2CD，∴AC=2CE，∴AE=AC-CE=2CE-CE=CE=CD，∵DC∥AB∴∠DCA=∠EAB，在△ABE和△CAD中，∵AE=CD∠EAB=∠DCA AB=CA，∴△ABE≌△CAD SAS．(2)解：由(1)得BE=AD，∠ABE=∠CAD，∵△CEF≌△CDA，∴FE=AD，∠EFC=∠DAC，∴BE=FE，∠EFC=∠EBA，∴∠EFB=∠EBF，∵∠OFB=∠EFB-∠EFC，∠OBF=∠EBF-∠EBA，∴∠OFB=∠OBF，∵∠ECF=∠DCA，∴∠OAC=∠OCA，∵∠OCA+∠OAC+∠AOC=180°，∠OBF+∠OFB+∠BOF=180°，又∠AOC=∠BOF，∴∠OCA+∠OAC=∠OBF+∠OFB，即2∠CAO=2∠FOB，∴∠CAO=∠FOB，∴AC∥FB(3)解：在△AEG和△CED中，∵∠GAE=∠DCE AE=CE∠AEG=∠CED ，∴△AEG≌△CED ASA∴AG=CD=12AB，∵AE=CE，∴EG∥CB，∵AC∥FB，∴四边形BCEF是平行四边形，∴BC=FE=AD，∵∠AEG=∠ACD+∠CAD=∠DAE+∠ADE，∴∠ADE=∠ACD，∵∠CAD=∠DAE，∴△ACD∽△ADE，∴EA DA =DA CA，即DA2=EA⋅CA=2EA2，∴DA=2EA，∵AB=AC=2EA，∴AB BC =ABDA=2EA2EA=22=2．【点睛】本题考查了三角形全等的证明，平行线的判定以及利用相似三角形求线段长之比，解题时需要学会将多个小题的结论联系起来，把前面小题的结论用到后面小题的思路中，熟练寻找证明三角形全等或相似所需要的条件是解题的关键．【题型04：旋转相似】13.【典例4】某校数学活动小组探究了如下数学问题：(1)问题发现：如图1，△ABC中，∠BAC=90°，AB=AC．点P是底边BC上一点，连接AP，以AP为腰作等腰Rt△APQ，且∠P AQ=90°，连接CQ、则BP和CQ的数量关系是______；(2)变式探究：如图2，△ABC中，∠BAC=90°，AB=AC．点P是腰AB上一点，连接CP，以CP为底边作等腰Rt△CPQ，连接AQ，判断BP和AQ的数量关系，并说明理由；(3)问题解决：如图3，在正方形ABCD中，点P是边BC上一点，以DP为边作正方形DPEF，点Q是正方形DPEF两条对角线的交点，连接CQ．若正方形DPEF的边长为210，CQ=22，请直接写出正方形ABCD的边长．【答案】(1)BP=CQ(2)BP=2AQ(3)6【分析】(1)根据已知条件利用边角边证明△ABP≌△ACQ，再利用全等三角形的性质即可得到BP和CQ 的数量关系；(2)根据任意等腰直角三角形的直角边与斜边的比是相等的，利用两边长比例且夹角相等的判定定理证明△CBP∽△CAQ，之后再由相似三角形对应边成比例即可得到BP和AQ的数量关系；(3)连接BD，先由正方形的性质判断出△BCD和△PQD都是等腰直角三角形，再利用与第二问同样的方法证出△BDP∽△CDQ，由对应边成比例，依据相似比求出线段BP的长，接着设正方形ABCD的边长为x，运用勾股定理列出方程即可求得答案．【详解】(1)解：∵△APQ是等腰直角三角形，∠P AQ=90°，在△ABC中，∠BAC=90°，AB=AC，∴AP=AQ，∠BAP+∠P AC=∠CAQ+∠P AC，∴∠BAP=∠CAQ．在△ABP和△ACQ中，AB=AC∠BAP=∠CAQ AP=AQ，∴△ABP≌△ACQ(SAS)，∴BP=CQ；(2)解：结论：BP=2AQ，理由如下：∵△CPQ是等腰直角三角形，△ABC中，∠BAC=90°，AB=AC，∴QCPC=ACBC=22，∠ACB=∠QCP=45°．∵∠BCP+∠ACP=∠ACQ+∠ACP=45°，∴∠BCP=∠ACQ，∴△CBP∽△CAQ，∴QCPC=ACBC=AQBP=22，∴BP=2AQ；(3)解：连接BD，如图所示，∵四边形ABCD与四边形DPEF是正方形，DE与PF交于点Q，∴△BCD和△PQD都是等腰直角三角形，∴QDPD=CDBD=22，∠BDC=∠PDQ=45°．∵∠BDP+∠PDC=∠CDQ+∠PDC=45°，∴∠BDP=∠CDQ，∴△BDP∽△CDQ，∴QDPD=CDBD=CQBP=22．∵CQ=22，∴BP=2CQ=4．在Rt△PCD中，CD2+CP2=DP2，设CD=x，则CP=x-4，又∵正方形DPEF的边长为210，∴DP=210，∴x2+(x-4)2=(210)2，解得x1=-2(舍去)，x2=6．∴正方形ABCD的边长为6．【点睛】本题是一道几何综合题，考查了全等三角形，相似三角形的判定和性质，以及正方形和等腰三角形的性质，正确识图并能熟练地掌握几何图形的性质与判定定理进行证明是解题的关键．14.如图1，已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．(1)证明：四边形CEGF是正方形；(2)探究与证明：将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°)，如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；(3)拓展与运用：正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°)，如图3所示，当B，E，F三点在一条直线上时，延长CG交AD于点H，若AG=9，GH=32，求BC的长．【答案】(1)答案见解析；(2)AG=2BE；理由见解析；(3)BC=95 2．【分析】(1)先说明GE⊥BC、GF⊥CD，再结合∠BCD=90°可证四边形CEGF是矩形，再由∠ECG= 45°即可证明；(2)连接CG，证明△ACG∽△BCE，再应用相似三角形的性质解答即可；(3)先证△AHG∽△CHA可得AGAC =GHAH=AHCH，设BC=CD=AD=a，则AC=a，求出AH=23a，DH=13a，CH=103a最后代入即可求得a的值．【详解】(1)∵四边形ABCD是正方形，∴∠BCD=90°，∠BCA=45°，∵GE⊥BC、GF⊥CD，∴∠CEG=∠CFG=∠ECF=90°，∴四边形CEGF是矩形，∠CGE=∠ECG=45°，∴EG=EC，∴四边形CEGF是正方形．(2)结论：AG=2BE；理由：连接CG，由旋转性质知∠BCE=∠ACG=α，在Rt △CEG 和Rt △CBA 中，CE CG=cos45°=22，CB CA =cos45°=22，∴CG CE =CA CB=2，∴△ACG ∽△BCE ，∴AG BE =CA CB=2∴线段AG 与BE 之间的数量关系为AG =2BE ；(3)∵∠CEF =45°，点B 、E 、F 三点共线，∴∠BEC =135°，∵△ACG ∽△BCE ，∴∠AGC =∠BEC =135°，∴∠AGH =∠CAH =45°，∵∠CHA =∠AHG ，∴△AHG ∽△CHA ，∴AG AC =GH AH=AH CH ，设BC =CD =AD =a ，则AC =2a ，由AG AC =GH AH ，得92a =32AH ，∴AH =23a ，则DH =AD -AH =13a ，CH =CD 2+DH 2=103a ，∴AG AC =AH CH ，得 92a =23a 103a ,解得：a =952，即BC =952．【点睛】本题属于四边形综合题，主要考查相似形的判定和性质、正方形的性质等知识点，解题的关键是正确寻找相似三角形解决问题并利用参数构建方程解决问题．【题型05：K 字型相似】15.综合探究如图，在平面直角坐标系中，点O 为原点，□ABCD 的顶点B 、C 在x 轴上，A 在y 轴上，OA =OC =2OB =4，直线y =x +t (-2≤t ≤4)分别与x 轴、y 轴、线段AD 、直线AB 交于点E 、F 、P 、Q ．(1)当t =1时，求证：AP =DP ．(2)探究线段AP 、PQ 之间的数量关系，并说明理由．(3)在x 轴上是否存在点M ，使得∠PMQ =90°，且以点M 、P 、Q 为顶点的三角形与△AOB 相似，若存在，请求出此时t 的值以及点M 的坐标；若不存在，请说明理由．【答案】(1)见解析(2)PQ =22AP(3)t =73时，M 13,0 ；t =23时，M 143,0 ；t =-1时，M -7，0 ．【分析】(1)根据t =1，求出t =1与AD 交点P 的坐标，即可求解；(2)先求出直线AB 的表达式为y =2x +4，再联立直线AB 与直线y =x +t 求出Q (t -4,2t -4)，再求出点P (4-t ,4)，利用坐标系中两点距离公式求出即可PQ =22(t -4)，结合AP =4-t 即可求解；(3)证明△PHM ∽△MIQ ，得到PM QM =AO BO =2或PM QM =BO AO=12，分四种情况画图求解．【详解】(1)证明：由OA =OC =2OB =4知，OC =4，OB =2，则AD =BC =6，则点A 、B 的坐标分别为：(0,4)、(-2,0)，当y =4时，y =x +1=4，则x =3=12AD ，即点P (3,4)，∴AP =DP =3；(2)解：PQ =22AP ，理由：设直线AB 的表达式为：y =kx +b ，将A 0，4 、B -2，0 代入得：4=b 0=-2k +b ，解得：k =2b =4 ．∴直线AB 的表达式为：y =2x +4，联立上式和y =x +t 得y =x +t y =2x +4 ，解得x =t -4y =2t -4 ，即点Q (t -4,2t -4)，同理(1)可得，点P (4-t ,4)，∴PQ =t -4 -4-t 2+2t -4 -4 2=224-t∵AP =4-t ，∴PQ =22AP ；(3)分别过点P 、Q 作PH ⊥x 轴，QI ⊥x 轴，∴∠PHM =∠MIQ =90°，∵∠PMQ =90°，∴∠PMH +∠QMI =90°，∵∠MQI +∠QMI =90°，∴∠PMH =∠MQI ，∴△PHM ∽△MIQ ，∴PH MI =MH QI =PM QM，设点M (x ,0)，由(2)知，点P 、Q 的坐标分别为：(4-t ,4)、(t -4,2t -4)，①若m >0，如图2，则MI =m -(t -4)，MH =4-t -m ，QI =2t -4，当△PMQ ∽△AOB 时，∴PM QM =AO BO=42=2，∴PH MI =MH QI=2．∴PH =2MI ，MH =2QI ，联立方程组：4=2m -(t -4) 4-t -m =2(2t -4) ，解得：m =13t =73∴t =73时，M 13,0 ，②若m >0，MI =m -(t -4)，MH =m -(4-t )，QI =4-2t ，如图3，当△QMP ∽△AOB 时，∴PM QM =BO AO=24=12∴PH MI =MH QI =12∴2PH =MI ，2MH =QI ，联立方程组：2×4=m -(t -4)2m -(4-t ) =4-2t ，解得m =143t =23．∴t =23时，M 143,0 ③若m <0，当△PMQ ∽△AOB 时，如图4，MI =(t -4)-m ，MH =(4-t )-m ，QI =4-2t ，∴PM AO =QM BO ，∴PM QM =AO BO=42=2，∴PH MI =MH QI =2∴PH =2MI ，MH =2QI ，联立方程组：4=2(t -4)-m 4-t -m =2(4-2t )，解得：m =-7t =-1 ∴t =-1，M -7，0④m <0，△QMP ∽△AOB 的情况不存在，综上，t =73时，M 13,0 ；t =23时，M 143,0 ；t =-1时，M -7，0 ．【点睛】本题考查的是一次函数综合运用，涉及到三角形相似、平行四边形的性质等，分类求解是解题的关键．16.如图，边长为10的等边△ABC 中，点D 在边AC 上，且AD =3，将含30°角的直角三角板(∠F =30°)绕直角顶点D 旋转，DE 、DF 分别交边AB 、BC 于P 、Q ，连接PQ ．当EF ∥PQ 时，DQ 长为()A.6B.39C.10D.63【答案】B【分析】证明△ADP ∽△BPQ ，由相似三角形的性质得出AD BP =AP BQ =DP PQ ，求出BP =6，CQ =2，过点Q 作QM ⊥AC 于点M ，由勾股定理可求出答案．【详解】解：∵∠F =30°，∴∠E =60°，∵EF ∥PQ ，∴∠DPQ =∠E =60°，∠DQP =∠F =30°，∴∠APD +∠BPQ =120°，∵△ABC 为等边三角形，∴∠A =∠B =60°，AC =BC =AB =10，∴∠APD +∠ADP =120°，∴∠BPQ =∠ADP ，∴△ADP ∽△BPQ ，∴AD BP =AP BQ =DP PQ，∵∠PDQ =90°，∠DQP =30°，∴PD =12PQ ，∴3 BP =APBQ=12，∴BP=6，∴AP=4，BQ=8，∴CQ=2，过点Q作QM⊥AC于点M，∴CM=12CQ=1，QM=3，∵CD=AC-AD=10-3=7，∴DM=CD-CM=7-1=6，∴DQ=DM2+QM2=62+(3)2=29．故选：B．【点睛】本题考查了勾股定理，等边三角形的性质，相似三角形的判定与性质，直角三角形的性质．先证明△ADP∽△BPQ是解题的关键．17.(1)问题如图1，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=90°时，求证：AD⋅BC=AP ⋅BP．(2)探究若将90°角改为锐角(如图2)，其他条件不变，上述结论还成立吗？说明理由．(3)应用如图3，在△ABC中，AB=22，∠B=45°，以点A为直角顶点作等腰Rt△ADE．点D在BC上，点E在AC上，点F在BC上，且∠EFD=45°，若CE=5，求CD的长．【答案】(1)见解析；(2)成立；理由见解析；(3)5【分析】(1)由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC,即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；(2)由∠DPC=∠A=∠B=α可得∠ADP=∠BPC,即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；(3)证明△ABD∽△DFE,求出DF=4，再证△EFC∽△DEC,可求FC=1,进而解答即可．【详解】解：(1)证明：如图1，∵∠DPC=90°∴∠BPC+∠APD=90°，∵∠A=90°，∴∠ADP+∠APD=90°∴∠APD=∠BPC，又∵∠A=∠B=90°∴△ADP∽△BPC，∴AD:BP=AP:BC∴AD⋅BC=AP⋅BP；(2)结论AD⋅BC=AP⋅BP仍成立；理由：如图2，∵∠BPD=∠DPC+∠BPC，又∵∠BPD=∠A+∠APD，∴∠DPC+∠BPC=∠A+∠APD，∵∠DPC=∠A=α，∴∠BPC=∠APD，又∵∠A=∠B=α，∴△ADP∽△BPC，∴AD:BP=AP:BC∴AD⋅BC=AP⋅BP；(3)∵∠EFD=45°,∴∠B=∠ADE=45°,∴∠BAD=∠EDF,∴△ABD∽△DFE∴AB:DF=AD:DE∵Rt△ADE是等腰直角三角形∴AD:DE=1:2∴AB:DF=1:2∵AB=22∴DF=4∵Rt△ADE是等腰直角三角形∴∠AED=45°∵∠EFD=45°∴∠DEC=∠EFC=180°-45°=135°又∵∠C=∠C∴△DEC∽△EFC∴DC:EC=EC:CF即EC2=FC⋅(4+FC)∵EC=5∴5=FC(4+FC)∴FC=1解得CD=5．【点睛】本题考查相似三角形的综合题，三角形的相似，正切值的求法，能够通过构造45°角将问题转化为一线三角是解题的关键．18.如图，在Rt△ABC中，∠ACB=90°，BCAC =mn，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．(1)探究发现：如图1，若m =n ，点E 在线段AC 上，则DE DF =；(2)数学思考：①如图2，若点E 在线段AC 上，则DE DF =(用含m ，n 的代数式表示)；②当点E 在直线AC 上运动时，①中的结论是否仍然成立？请仅就图3的情形给出证明；(3)拓展应用：若AC =5，BC =25，DF =42，请直接写出CE 的长．【答案】(1)1；n m ；(2)①n m ；②n m ；(3)CE =25或CE =255【分析】(1)先用等量代换判断出∠ADE =∠CDF ，∠A =∠DCB ，得到△ADE ∽△CDF ，再判断出△ADC ∽△CDB 即可；(2)方法和1 一样，先用等量代换判断出∠ADE =∠CDF ，∠A =∠DCB ，得到△ADE ∽△CDF ，再判断出△ADC ∽△CDB 即可；(3)由2 的结论得出△ADE ∽△CDF ，判断出CF =2AE ，求出DE ，再利用勾股定理，计算出即可．【详解】解：1 当m =n 时，即：BC =AC ，∵∠ACB =90°，∴∠A +∠ABC =90°，∵CD ⊥AB ，∴∠DCB +∠ABC =90°，∴∠A =∠DCB ，∵∠FDE =∠ADC =90°，∴∠FDE -∠CDE =∠ADC -∠CDE ，即∠ADE =∠CDF ，∴△ADE ∽△CDF ，∴DE DF =AD DC，∵∠A =∠DCB ，∠ADC =∠BDC =90°，∴△ADC ∽△CDB ，∴AD DC =AC BC=1，∴DE DF =12 ①∵∠ACB =90°，∴∠A +∠ABC =90°，∵CD ⊥AB ，∴∠DCB +∠ABC =90°，∴∠A =∠DCB ，∵∠FDE=∠ADC=90°，∴∠FDE-∠CDE=∠ADC-∠CDE，即∠ADE=∠CDF，∴△ADE∽△CDF，∴DE DF =AD DC，∵∠A=∠DCB，∠ADC=∠BDC=90°，∴△ADC∽△CDB，∴AD DC =ACBC=nm，∴DEDF=nm②成立.如图3，∵∠ACB=90°，∴∠A+∠ABC=90°，又∵CD⊥AB，∴∠DCB+∠ABC=90°，∴∠A=∠DCB，∵∠FDE=∠ADC=90°，∴∠FDE+∠CDE=∠ADC+∠CDE，即∠ADE=∠CDF，∴△ADE∽△CDF，∴DE DF =AD DC，∵∠A=∠DCB，∠ADC=∠BDC=90°，∴△ADC∽△CDB，∴AD DC =ACBC=nm，∴DE DF =n m．3 由2 有，△ADE∽△CDF，∵DE DF =ACBC=12，∴AD CD =AECF=DEDF=12，∴CF=2AE，如图4图5图6，连接EF．在Rt△DEF中，DE=22，DF=42，∴EF=210，①如图4，当E在线段AC上时，在Rt△CEF中，CF=2AE=2AC-CE=25-CE，EF=210，根据勾股定理得，CE2+CF2=EF2，∴CE2+25-CE2=40∴CE=25，或CE=-255(舍)②如图5，当E在AC延长线上时，在Rt△CEF中，CF=2AE=2AC+CE=25+CE，EF=210，根据勾股定理得，CE2+CF2=EF2，∴CE2+25+CE2=40，∴CE=255，或CE=-25(舍)，③如图6，当E在CA延长线上时，在Rt△CEF中，CF=2AE=2CE-AC=2CE-5，EF=210，根据勾股定理得，CE2+CF2=EF2，∴CE2+2CE-52=40，∴CE=25，或CE=-255(舍)，综上：CE=25或CE=25 5．【点睛】本题是三角形综合题，主要考查了三角形相似的性质和判定，勾股定理，判断相似是解决本题的关键，求CE是本题的难点．。

中考复习专题1：相似三角形中的旋转问题配有辅导训练资料含试题解析与参考答案教师版

中考专题：相似三角形与旋转1. 已知，如图1，已知Rt △ABC 中，∠ACB ＝90°，D 、E 分别是AC 、BC 上的点，连DE ，且3AC BCDC EC==，2tan 2B =；（1）如图2，将△CDE 绕C 点旋转，连AD 、BE 交于H ，求证：AD ⊥BE ；（2）如图3，当△CDE 绕C 点旋转过程中，当5CH =时，求2A H ﹣BH 的值；（3）若CD ＝1，当△CDE 绕C 点旋转过程中，直接写出AH 的最大值是．2. 在△ABC 中，CA ＝CB ，∠ACB ＝α（0°＜α＜180°）．点P 是平面内不与A ，C 重合的任意一点，连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接AD ，CP ．点M 是AB 的中点，点N 是AD 的中点．（1）如图1，当α＝60°时，PCMN的值是，直线MN 与直线PC 相交所成的较小角的度数是．（2）如图2，当α＝120°时，请写出的PCMN 值及直线MN 与直线PC 相交所成的较小角的度数，并就图2的情形说明理由．（3）如图3，当α＝90°时，若点E 是CB 的中点，点P 在直线ME 上，请直接写出点B ，P ，D 在同一条直线上时MN PD的值．3. 在△ABC 中，∠ABC ＝120°，线段AC 绕点C 顺时针旋转60°得到线段CD ，连接BD ．（1）如图1，若AB ＝BC ，求证：BD 平分∠ABC ；（2）如图2，若AB ＝2BC ，①求ACBD 的值；②连接AD ，当S △ABC ＝23时，直接写出四边形ABCD 的面积为．4. （1）如图1，在Rt △ABC 中，∠C ＝90°，AC ＝BC ，AP 、BP 分别平分∠CAB 、∠CBA ，过点P作DE ∥AB 交AC 于点D ，交BC 于点E ．①求证：点P 是线段DE 的中点； ②求证：BP 2＝BE •BA ．（2）如图2，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝12，BP 平分∠ABC ，过点P 作DE ∥AB 交AC 于点D ，交BC 于点E ，若点P 为线段DE 的中点，求AD 的长度．5.在△ABC中，AB＝AC，点D在底边BC上，∠EDF的两边分别交AB、AC所在直线于E，F两点，∠EDF＝2∠ABC，BD＝nCD．（1）如图1，若∠ABC＝45°，n＝1，求证：DE＝DF；（2）如图2，求DEDF的值（含n的式子表示）：（3）如图3，连接EF，若tan∠B＝1，EF∥BC，且58EFBC=，直接写出n的值为．6.已知：在▱ABCD中，点E，F分别在AB，AD边上，且∠ECF＝∠B＝α（0°＜α＜90°）（1）如图1，若CF⊥AD，求证：CE CB CF CD=；（2）如图2，若α＝60°，∠AEF＝∠ECB，求证：四边形ABCD是菱形；（3）如图3，若α＝45°，AC⊥EF，EH⊥BC于点H，34CEAD=，直接写出AECH的值．中考专题：相似（一）1. 已知，如图1，已知Rt △ABC 中，∠ACB ＝90°，D 、E 分别是AC 、BC 上的点，连DE ，且3AC BCDC EC==，2tan 2B =；（1）如图2，将△CDE 绕C 点旋转，连AD 、BE 交于H ，求证：AD ⊥BE ；（2）如图3，当△CDE 绕C 点旋转过程中，当5CH =时，求2A H ﹣BH 的值；（3）若CD ＝1，当△CDE 绕C 点旋转过程中，直接写出AH 的最大值是．【解答】（1）证明：如图2中，设BE 交AC 于O ．∵∠ACB ＝∠DCE ＝90°，∴∠ACD ＝∠ECB ， AC BCDC EC =，∴AC CDBC CE =，∴△ACD ∽△BCE ， ∴∠DAC ＝∠EBC ，∵∠AOH ＝∠BOC ，∴∠AHO ＝∠BCO ＝90°，∴AD ⊥BE ．（2）解：如图2中，在HB 上取一点T ，使得HT ＝AH ，连接AT ．在Rt △AHT 中，2tan AH ATH HT ∠==， 2tan ABC ∠=，∴∠ATH ＝∠ABC ， ∵∠ATH +∠HAT ＝90°，∠ABC +∠CAB ＝90°，∴∠HAT ＝∠CAB ，∴∠CAH ＝∠BAT ，∴△AHT ∽△ACB ，∴AT AH AB AC =，∴AH AC AT AB =，∴△CAH ∽△BAT ，∴CH AHBT AT=，2HT AH =，设AH m =，则2HT m =，3AT m ， ∴53m =15BT ∴ （3）解：如图3中，在Rt △AHB 中，∵AH ＝AB •sin ∠ABH ，∴当∠ABH 最大时，AH 的值最大，此时CE ⊥BE ， ∵∠DCE ＝∠CEH ＝∠EHD ＝90°， ∴此时四边形ECDH 是矩形，∴DH ＝EC ，∠ADC ＝∠CDH ＝90°，由题意CD ＝1，，2EC 3AC =， 2DH CE ∴==在Rt ACD ∆中，22312AD AC CD =-=-= 2222AH AD DH ∴=+= 的最大值为2. 在△ABC 中，CA ＝CB ，∠ACB ＝α（0°＜α＜180°）．点P 是平面内不与A ，C 重合的任意一点，连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接AD ，CP ．点M 是AB 的中点，点N 是AD 的中点．（1）如图1，当α＝60°时，PCMN的值是，直线MN 与直线PC 相交所成的较小角的度数是．（2）如图2，当α＝120°时，请写出的PCMN 值及直线MN 与直线PC 相交所成的较小角的度数，并就图2的情形说明理由．（3）如图3，当α＝90°时，若点E 是CB 的中点，点P 在直线ME 上，请直接写出点B ，P ，D 在同一条直线上时MN PD的值．【解答】（1）如图1中，连接PC ，BD ，延长BD 交PC 于K ，交AC 于G ． ∵CA ＝CB ，∠ACB ＝60°，∴△ABC 是等边三角形，∴∠CAB ＝∠PAD ＝60°，AC ＝AB ，∴∠PAC ＝∠DAB ，∵AP ＝AD ，∴△PAC ≌△DAB （SAS ），∴PC ＝BD ，∠ACP ＝∠ABD ， ∵AN ＝ND ，AM ＝BM ，∴BD ＝2MN ，∴PCMN＝21．∵∠CGK ＝∠BGA ，∠GCK ＝∠GBA ，∴∠CKG ＝∠BAG ＝60°，∴BK 与PC 的较小的夹角为60°， ∵MN ∥BK ，∴MN 与PC 较小的夹角为60°．（2）如图设MN 交AC 于F ，延长MN 交PC 于E ．∵CA ＝CB ，PA ＝PD ，∠APD ＝∠ACB ＝120°，∴△PAD ∽△CAB ，∴ABADAC AP =，∵AM ＝MB ，AN ＝ND ，∴AMANAC AP =，∴△ACP ∽△AMN ，∴∠ACP ＝∠AMN ，PCMN ＝23=AC AM∵∠CFE ＝∠AFM ，∴∠FEC ＝∠FAM ＝30°．（3）设MN ＝a ，∵PCMN＝22=AC AM ，∴PC ＝2a ，∵ME 是△ABC 的中位线，∠ACB ＝90°，∴ME 是线段BC 的中垂线， ∴PB ＝PC ＝2a ，∵MN 是△ADB 的中位线，∴DB ＝2MN ＝2a ，如图3﹣1中，当点P 在线段BD 上时，PD ＝DB ﹣PB ＝（2﹣2）a ，∴MN PD＝2﹣2．如图3﹣2中，PD ＝DB +PB ＝（2+2）a ，∴MN PD＝2+2．3. 在△ABC 中，∠ABC ＝120°，线段AC 绕点C 顺时针旋转60°得到线段CD ，连接BD ．（1）如图1，若AB ＝BC ，求证：BD 平分∠ABC ；（2）如图2，若AB ＝2BC ，①求ACBD 的值；②连接AD ，当S △ABC ＝23时，直接写出四边形ABCD 的面积为．【解答】（1）证明：连接AD ，由题意知，∠ACD ＝60°，CA ＝CD ，∴△ACD 是等边三角形，∴CD ＝AD ，又∵AB ＝CB ，BD ＝BD ，∴△ABD ≌△CBD （SSS ），∴∠CBD ＝∠ABD ，∴BD 平分∠ABC ；（2）解：①连接AD ，作等边三角形ACD 的外接圆⊙O ， ∵∠ADC ＝60°，∠ABC ＝120°，∴∠ADC +∠ABC ＝180°，∴点B 在⊙O 上，∵AD ＝CD ，∴⁔AB =⁔CD ，∴∠CBD ＝∠CAD ＝60°，在BD 上截取BM ，使BM ＝BC ，则△BCM 为等边三角形，∴∠CMB ＝60°，∴∠CMD ＝120°＝∠CBA ，又∵CB ＝CM ，∠BAC ＝∠BDC ，∴△CBA ≌△CMD （AAS ），∴MD ＝AB ，设BC ＝BM ＝1，则AB ＝MD ＝2，∴BD ＝3，过点C 作CN ⊥BD 于N ，在Rt △BCN 中，∠CBN ＝60°，∴∠BCN ＝30°， ∴BN ＝21BC ＝21，CN ＝23BC ＝23，∴ND ＝BD ﹣BN ＝25，在Rt △CND 中，CD ＝722=+DN CD ，∴AC ＝7，∴773=ACBD ;②如图3，分别过点B ，D 作AC 的垂线，垂足分别为H ，Q ，设CB ＝1，AB ＝2，CH ＝x ，则由①知，AC ＝7，AH ＝7﹣x ，在Rt △BCH 与Rt △BAH 中，BC 2﹣CH 2＝AB 2﹣AH 2，即1﹣x 2＝22﹣（7﹣x ）2，解得，x ＝772，∴BH ＝721,在Rt △ADQ 中，DQ ＝23AD ＝23×7＝221，∴72=DQ BH∵AC 为△ABC 与△ACD 的公共底，∴72==∆∆DQ BH S SACDABC ，∵S △ABC ＝23，∴S △ACD ＝437，∴S 四边形ABCD ＝23+437＝439，4. （1）如图1，在Rt △ABC 中，∠C ＝90°，AC ＝BC ，AP 、BP 分别平分∠CAB 、∠CBA ，过点P 作DE ∥AB 交AC 于点D ，交BC 于点E ．①求证：点P 是线段DE 的中点； ②求证：BP 2＝BE •BA ．（2）如图2，在Rt △ABC 中，∠C ＝90°，AB ＝13，BC ＝12，BP 平分∠ABC ，过点P 作DE ∥AB 交AC 于点D ，交BC 于点E ，若点P 为线段DE 的中点，求AD 的长度．【解答】（1）①证明：∵BP 平分∠ABC ，∴∠ABP ＝∠CBP ，∵DE ∥AB ，∴∠ABP ＝∠EPB ，∴∠CBP ＝∠EPB ，∴BE ＝PE ，同理可证：DP ＝DA ，∵DE ∥AB ，∴CE CDCB CA=， ∵CA ＝CB ，∴CE ＝CD ，∴BE ＝AD ，∴PE ＝PD ，∴点P 是DE 的中点． ②证明：由①得∠ABP ＝∠EBP ＝∠EPB ＝21∠CBA ， ∵AP 平分∠CAB ，∴∠P AB ＝21∠CAB ， ∵CA ＝CB ，∴∠CBA ＝∠CAB ，∴∠ABP ＝∠EBP ＝∠EPB ＝∠P AB ，∴△ABP ∽△PBE ，∴BP BEBA BP=，∴BP 2＝BA •BE ．（2）过点P 作FG ∥AC 交BC 于F ，交AB 于G ．在Rt △ACB 中，222213125AC AB BC =-=-=，∵FG ∥AC ，∴∠PFE ＝∠C ＝90°，∵PD ∥AG ，∴四边形AGPD 是平行四边形，∴PG ＝AD ， ∵PE ＝PD ，PF ∥CD ，∴EF ＝FC ，∴PF ＝21CD ，由（1）可知BE ＝EP ，设AD ＝PG ＝x ，则CD ＝5﹣x ，PF ＝21（5﹣x ），∵DE ∥AB ，∴CD CE CA CB =，∴512CD CA CE CB ==， 125CE CD ∴=，12(5)5x =-，则6(5)5EF x =-，1212120(5)55BE EP x x ∴==-=，在Rt EFP ∆中，6(5)125sin sin sin 1213(5)5x EF EPF EDC BAC EP x -∠===∠=∠=-，解得6537x =，6537AD ∴=．5.在△ABC中，AB＝AC，点D在底边BC上，∠EDF的两边分别交AB、AC所在直线于E，F两点，∠EDF ＝2∠ABC，BD＝nCD．（1）如图1，若∠ABC＝45°，n＝1，求证：DE＝DF；（2）如图2，求DEDF的值（含n的式子表示）：（3）如图3，连接EF，若tan∠B＝1，EF∥BC，且58EFBC=，直接写出n的值为．【解答】（1）证明：如图1中，连接AD．∵AB＝AC，∴∠ABC＝∠C＝45°，∵BD＝nCD，n＝1，∴BD＝CD，∴AD⊥BC，∠DAC＝∠DAB＝45°，AD＝DB＝DC，∵∠EDF＝2∠ABC＝90°，∴∠BDA＝∠EDF＝90°，∴∠BDE＝∠ADF，∵∠B＝∠DAF，BD＝AD，∴△BDE≌△ADF（SAS），∴DE＝DF．（2）解：在射线B上取一点T，使得DB＝DT．∵DB＝DT，∴∠B＝∠T，∴∠TDC＝∠B+∠T＝2∠B，∵∠EDF＝2∠B，∴∠EDF＝∠TDC，∴∠EDT＝∠DFC，∵∠BAC+2∠B＝180°，∴∠BAC+∠DEF＝180°，∴∠TED+∠AFD＝180°，∵∠DFC+∠AFD＝180°，∴∠TED＝∠DFC，∴△TED∽△FDC，∴DE DT DBn DF DC CD===．（3）如图3中，作ET⊥BC于E，FH⊥BC于H．∵EF∥BC，ET∥FH，∴四边形EFHT是平行四边形，∵∠ETH＝90°，∴四边形EFHT是矩形，∴ET＝FH，EF＝TH，∵EF：BC＝5：8，设EF＝5k，BC＝8k，则TH＝5k，∵tan B＝1，∴∠B＝∠C＝45°，∵∠ETB＝∠FHC＝90°，∴ET＝BT＝FH＝CH＝1.5k，设DT＝x，则DH＝5K﹣x，∵∠EDF＝2∠B＝90°，∠ETD＝∠FHD＝90°，∴∠EDT+∠FDH＝90°，∠TED+∠EDT＝90°，∴∠TED＝∠FDH，∴△ETD∽△DHF，∴ET DTDH FH=，∴1.55 1.5k xk x k=-，∴x2﹣5kx+2.25k2，解得x＝0.5k或4.5k，∴BD＝2k或6k，∴BD：DC＝2k：6k＝1：3或BD：DC＝6k：2k＝3：1．∴n＝3或．6. 已知：在▱ABCD 中，点E ，F 分别在AB ，AD 边上，且∠ECF ＝∠B ＝α（0°＜α＜90°）（1）如图1，若CF ⊥AD ，求证：CE CBCF CD=；（2）如图2，若α＝60°，∠AEF ＝∠ECB ，求证：四边形ABCD 是菱形；（3）如图3，若α＝45°，AC ⊥EF ，EH ⊥BC 于点H ，34CE AD =，直接写出AECH 的值．【解答】（1）证明：如图1中，∵在▱ABCD 中，∠B ＝∠D ，∵∠ECF ＝∠B ＝α，∴∠D ＝∠ECF ＝α，∵CF ⊥AD ，∴∠D +∠DCF ＝90°，∴∠ECF +∠DCF ＝90°，∴EC ⊥CD ， ∵AB ∥CD ，∴CE ⊥AB ，∴∠BEC ＝∠CFD ＝90°，∴∠BCE ∽△DCF ，∴CE CBCF CD=；（2）证明：如图2中，连接AC ，∵四边形ABCD 是平行四边形，∴AD ∥BC ，∠B ＝60°，∴∠BAC ＝120°，∵∠ECF ＝60°，∴∠EAF +∠ECF ＝180°，∴A ，E ，C ，F 四点共圆，∴∠AEF ＝∠ACF ， ∵∠AEF ＝∠BCE ，∴∠ACF ＝∠BCE ，∴∠ACB ＝∠ECF ＝60°，∴△ABC 是等边三角形， ∴AB ＝BC ，∴四边形ABCD 是菱形；（3）解：∵∠ECF ＝∠B ＝45°，∵34CE AD =，∴设CE ＝3m ，BC ＝AD ＝4m ，过C 作CI ⊥BC 交BA 的延长线于I ，交AD 于K ，交EF 于J ，延长HE 交DA 的延长线于L ，则CI ＝BC ＝4m ，作JM ⊥LH 于M ，交BI 于R ，连接AJ ，∵∠ECF ＝∠B ＝45°，∴∠EAF ＝135°，∴C ，E ，A ，F 四点共圆，∴∠CEF ＝∠F AC ， ∵AC ⊥EF ，∴∠EJC ＝∠CAF ，∴∠CEJ ＝∠EJC ，∴CE ＝CJ ，∴AC 垂直平分EJ ，∴AE ＝AJ ，设BH ＝EH ＝n ，CH ＝4m ﹣n ，在Rt △CHE 中，EH 2+CH 2＝CE 2， ∴n 2+（4m ﹣n ）2＝（3m ）2，解得42n ±=，（取42n -=时，结论一样）， 424KL CH m n -∴==-=，42223ME MH HE CJ EH m +-=-=-=-=，2LE LA =，2222KJ LM ME -===，422AK LK AL -=-=-， 2222224222(()22AE AJ AK JK --∴==+=+，解得：3(21)32AE -=-，∴3(21)3322742AE CH --==-。

中考数学专题讲练旋转(解析版)

旋转一．半角模型“半角”旋转模型，经常会出现在等腰直角三角形、正方形中，在一般的等腰三角形中也会有涉及．二．等腰三角形旋转模型等腰三角形的旋转模型比较多，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化，证明的基本思想“SAS”．1．一般等腰三角形的旋转2．等边三角形的旋转3．等腰直角三角形的旋转三．对角互补模型四边形对角互补模型多数题目给出的条件会以四边形或三角形等旋转为载体．四．旋转相似模型共顶点相似的一般三角形模型：如图，图中ABD ACE∆∆∽，得到AB AD BDAC AE CE==，ABD ACE∠=∠，ADB AEC∠=∠，BAD CAE∠=∠，则有ABC ADE∆∆∽．一．考点：1．旋转全等模型；2．旋转相似模型；3．旋转中的轨迹与最值问题；二．重难点：1．这类题的关键是找到题目中所给的特殊条件，结合问题所要证明或者求解的边长角度问题，再去选择是要构造旋转全等还是通过已经得到的旋转全等的性质进一步证明．2．观察图形发现旋转得到的相似；3．通过添加辅助线构造旋转相似或者去挖掘隐含的相似图形．三．易错点：1．在利用旋转构造全等的时候注意辅助线的做法问题；2．构造旋转全等时候一定要有相等边长的条件．3．全等是相似的一个特例，旋转有时候也会出现全等，注意和旋转全等的区别和联系．题模一：旋转与全等例1.1.1已知四边形ABCD中，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E，F．当∠MBN绕B点旋转到AE=CF时（如图1），易证AE+CF=EF；当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE，CF，EF又有怎样的数量关系？请写出你的猜想，不需证明．【答案】图2成立，证明见解析，图3不成立，图3中AE、CF、EF的关系是AE﹣CF=EF【解析】∵AB⊥AD，BC⊥CD，AB=BC，AE=CF，在△ABE和△CBF中，∴△ABE≌△CBF（SAS）；∴∠ABE=∠CBF，BE=BF；∵∠ABC=120°，∠MBN=60°，∴∠ABE=∠CBF=30°，∴AE=12BE，CF=12BF；∵∠MBN=60°，BE=BF，∴△BEF为等边三角形；∴AE+CF=12BE+12BF=BE=EF；图2成立，图3不成立．证明图2．延长DC至点K，使CK=AE，连接BK，在△BAE和△BCK中，则△BAE≌△BCK，∴BE=BK，∠ABE=∠KBC，∵∠FBE=60°，∠ABC=120°，∴∠FBC+∠ABE=60°，∴∠FBC+∠KBC=60°，∴∠KBF=∠FBE=60°，在△KBF和△EBF中，∴△KBF≌△EBF，∴KF=EF，∴KC+CF=EF，即AE+CF=EF．图3不成立，AE、CF、EF的关系是AE﹣CF=EF．例1.1.2（1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD．求证：EF=BE+FD；（2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？（3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=12∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【答案】（1）证明见解析（2）成立（3）EF=BE﹣FD 【解析】（1）延长EB到G，使BG=DF，连接AG．∵∠ABG=∠ABC=∠D=90°，AB=AD，∴△ABG≌△ADF．∴AG=AF，∠1=∠2．∴∠1+∠3=∠2+∠3=∠EAF=12∠BAD．∴∠GAE=∠EAF．又AE=AE，∴△AEG≌△AEF．∴EG=EF．∵EG=BE+BG．∴EF=BE+FD（2）（1）中的结论EF=BE+FD仍然成立．（3）结论EF=BE+FD不成立，应当是EF=BE﹣FD．证明：在BE上截取BG，使BG=DF，连接AG．∵∠B+∠ADC=180°，∠ADF+∠ADC=180°，∴∠B=∠ADF．∵AB=AD，∴△ABG≌△ADF．∴∠BAG=∠DAF，AG=AF．∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=12∠BAD．∴∠GAE=∠EAF．∵AE=AE，∴△AEG≌△AEF．∴EG=EF∵EG=BE﹣BG∴EF=BE﹣FD．例 1.1.3如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；（3）将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．【答案】（1）见解析（2）见解析（3）△ACN仍为等腰直角三角形【解析】（1）证明：如图1，∵EN∥AD，∴∠MAD=∠MNE，∠ADM=∠NEM．∵点M为DE的中点，∴DM=EM．在△ADM和△NEM中，∴△ADM≌△NEM．∴AM=MN．∴M为AN的中点．（2）证明：如图2，∵△BAD和△BCE均为等腰直角三角形，∴AB=AD，CB=CE，∠CBE=∠CEB=45°．∵AD∥NE，∴∠DAE+∠NEA=180°．∵∠DAE=90°，∴∠NEA=90°．∴∠NEC=135°．∵A，B，E三点在同一直线上，∴∠ABC=180°﹣∠CBE=135°．∴∠ABC=∠NEC．∵△ADM≌△NEM（已证），∴AD=NE．∵AD=AB，∴AB=NE．在△ABC和△NEC中，∴△ABC≌△NEC．∴AC=NC，∠ACB=∠NCE．∴∠ACN=∠BCE=90°．∴△ACN为等腰直角三角形．（3）△ACN仍为等腰直角三角形．证明：如图3，延长AB交NE于点F，∵AD∥NE，M为中点，∴易得△ADM≌△NEM，∴AD=NE．∵AD=AB，∴AB=NE．∵AD∥NE，∴AF⊥NE，在四边形BCEF中，∵∠BCE=∠BFE=90°∴∠FBC+∠FEC=360°﹣180°=180°∵∠FBC+∠ABC=180°∴∠ABC=∠FEC在△ABC和△NEC中，∴△ABC≌△NEC．∴AC=NC，∠ACB=∠NCE．∴∠ACN=∠BCE=90°．∴△ACN为等腰直角三角形．例1.1.4如图，△AEF中，∠EAF=45°，AG⊥EF于点G，现将△AEG沿AE折叠得到△AEB，将△AFG沿AF折叠得到△AFD，延长BE和DF相交于点C．（1）求证：四边形ABCD是正方形；（2）连接BD分别交AE、AF于点M、N，将△ABM绕点A逆时针旋转，使AB与AD重合，得到△ADH，试判断线段MN、ND、DH之间的数量关系，并说明理由．（3）若EG=4，GF=6，2，求AG、MN的长．【答案】（1）见解析（2）MN2=ND2+DH2；理由见解析（3）AG=12；2【解析】（1）证明：∵△AEB由△AED翻折而成，∴∠ABE=∠AGE=90°，∠BAE=∠EAG，AB=AG，∵△AFD由△AFG翻折而成，∴∠ADF=∠AGF=90°，∠DAF=∠FAG，AD=AG，∵∠EAG+∠FAG=∠EAF=45°，∴∠ABE=∠AGE=∠BAD=∠ADC=90°，∴四边形ABCD 是矩形，∵AB=AD ，∴四边形ABCD 是正方形；（2）MN 2=ND 2+DH 2，理由：连接NH ，∵△ADH 由△ABM 旋转而成，∴△ABM ≌△ADH ，∴AM=AH ，BM=DH ，∵由（1）∠BAD=90°，AB=AD ，∴∠ADH=∠ABD=45°，∴∠NDH=90°，∴△AMN ≌△AHN ，∴MN=NH ，∴MN 2=ND 2+DH 2；（3）设AG=BC=x ，则EC=x ﹣4，CF=x ﹣6，在Rt △ECF 中，∵CE 2+CF 2=EF 2，即（x ﹣4）2+（x ﹣6）2=100，x 1=12，x 2=﹣2（舍去）∴AG=12，∵AG=AB=AD=12，∠BAD=90°，∴22AB AD +221212+2，∵2，∴MD=BD ﹣2﹣22，设NH=y，在Rt△NHD中，∵NH2=ND2+DH2，即y2=（2y）2+（22，解得2，即2．题模二：旋转与相似例1.2.1如图1，点P在正方形ABCD的对角线AC上，正方形的边长是a，Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N．（1）操作发现：如图2，固定点P，使△PEF绕点P旋转，当PM⊥BC时，四边形PMCN是正方形．填空：①当AP=2PC时，四边形PMCN的边长是________；②当AP=nPC时（n是正实数），四边形PMCN的面积是___________．（2）猜想论证如图3，改变四边形ABCD的形状为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF 的两条直角边PE、PF分别交BC、DC于点M、N，固定点P，使△PEF绕点P旋转，则PMPN=__________．（3）拓展探究如图4，当四边形ABCD满足条件：∠B+∠D=180°，∠EPF=∠BAD时，点P在AC上，PE、PF分别交BC，CD于M、N点，固定P点，使△PEF绕点P旋转，请探究PMPN的值，并说明理由．【答案】（1）①13a②()221an+（2）ab（3）见解析【解析】（1）①如图2，∵PM⊥BC，AB⊥BC ∴△PMC∽△ABC又∵AP=2PC∴PMAB=13，即PMa=13∴PM=13a，即正方形PMCN的边长是13a②当AP=nPC时（n是正实数），PMAB=11n+∴PM=11n+a∴四边形PMCN的面积=（11n+a）2=()221an+（2）如图3，过P作PG⊥BC于G，作PH⊥CD于H，则∠PGM=∠PHN=90°，∠GPH=90°∵Rt△PEF中，∠FPE=90°∴∠GPM=∠HPN∴△PGM∽△PHN由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==∵AB=a，BC=b∴PG PHa b=，即PGPH=ab（3）如图4，过P作PG∥AB，交BC于G，作PH∥AD，交CD于H，则∠HPG=∠DAB ∵∠EPF=∠BAD∴∠EPF=∠GPH，即∠EPH+∠HPN=∠EPH+∠GPM∴∠HPN=∠GPM∵∠B+∠D=180°∴∠PGC+∠PHC=180°又∵∠PHN+∠PHC=180°∴∠PGC=∠PHN∴△PGM∽△PHN由PG∥AB，PH∥AD可得，PG CP PH AB CA AD==即PG AB PH AD=②∴由①②可得，PMPN=ABAD例1.2.2数学活动课上，小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动．操作：使点D落在线段AB的中点处并使DF过点C（如图1），然后将其绕点D顺时针旋转，直至点E落在AC的延长线上时结束操作，在此过程中，线段DE与AC或其延长线交于点K，线段BC与DF相交于点G（如图2，3）．探究1：在图2中，求证：△ADK∽△BGD．探究2：在图2中，求证：KD平分∠AKG．探究3：①在图3中，KD仍平分∠AKG吗？若平分，请加以证明；若不平分，请说明理由．②在以上操作过程中，若设AC=BC=8，KG=x，△DKG的面积为y，请求出y与x的函数关系式，并直接写出x的取值范围．【答案】探究1：见解析；探究2：见解析；探究3：①KD仍平分∠AKG②y=2x，其中≤≤4838x【解析】探究1，∵∠KAD=∠KDG=∠DBG=45°，∴∠KDA+∠BDG=135°．∵∠BDG+∠BGD=135°，∴∠KDA=∠BGD，∴△ADK∽△BGD；探究2，∵△ADK∽△BGD，∵点D是线段AB的中点，∴BD=AD，∵∠KAD=∠KDG=45°，∴△ADK∽△DCK，∴∠AKD=∠DKC，∴KD平分∠AKG．探究3，①KD仍平分∠AKG．理由如下：∵同探究1可得△ADK∽△BGD，同探究2可得，△ADK∽△DGK，∴∠AKD=∠DKG，∴KD仍平分∠AKG；②如图，过点D作DM⊥AC于点M，DN⊥KG于点N，由①知线段KD平分∠AKG，∴DM=DN．∵AC=BC=8，点D是线段AB的中点，∠KAD=45°，∴DM=DN=4．∵KG=x，∴S△DKG=y=12×4x=2x，对于图3的情况同理可得y=2x，综上所示，y=2x，其中38．题模三：旋转中的轨迹与最值问题例1.3.1如图，点P是平行四边形ABCD对角线BD上的动点，点M为AD的中点，已知AD=8，AB=10，∠ABD=45°，把平行四边形ABCD绕着点A按逆时针方向旋转，点P的对应点是点Q，则线段MQ的长度的最大值与最小值的差为．【答案】18﹣2【解析】如图，作AP1⊥BD垂足为P1，∵∠DBA=45°，AB=10，∴∠P1AB=∠DBA=45°，AP1=P12，∵AM=MD=12AD=4，当AP1旋转到与射线AD的重合时（点P1与点E重合），ME就是MQ最小值24，当点P2与B重合时，旋转到与DA的延长线重合时（点P2与点F重合），此时MF就是MQ最大值=AM+AF=14，∴MQ的最大值与最小值的差=14﹣（2﹣4）=18﹣2故答案为18﹣2例 1.3.2如图，菱形ABCD中，AB=2，∠C=60°，我们把菱形ABCD的对称中心O称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为______；经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为______．（结果都保留π）【答案】3231+nπ【解析】∵菱形ABCD中，AB=2，∠C=60°，∴△ABD是等边三角形，BO=DO=1，223AD DO-第一次旋转的弧长6033ππ⨯=∵第一、二次旋转的弧长和60360323ππ⨯⨯=，第三次旋转的弧长为：601 1803ππ⨯=∵3n÷3=n，故经过3n（n为正整数）次这样的操作菱形中心O所经过的路径总长为：n 23π+3π）231+nπ．例1.3.3如图1，点O为正方形ABCD的中心．（1）将线段OE绕点O逆时针方向旋转90︒，点E的对应点为点F，连结EF，AE，BF，请依题意补全图1；（2）根据图1中补全的图形，猜想并证明AE与BF的关系；（3）如图2，点G是OA中点，△EGF是等腰直角三角形，H是EF的中点，90EGF∠=︒，22AB=2GE=，△EGF绕G点逆时针方向旋转α角度，请直接写出旋转过程中BH的最大值．【答案】（1）见解析（2）AE⊥BF（3）25+【解析】（1）正确画出图形；………………1分（2）延长EA 交OF 于点H ，交BF 于点G …2分∵O 为正方形ABCD 的中心，∴OB OA =，∠AOB ＝90……3分∵OE 绕点O 逆时针旋转90角得到OF∴∠AOB ＝∠EOF ＝90∴∠EOA ＝∠FOB ……4分在△EOA 和△FOB 中，∴BF AE =.……5分∴∠OFB +∠FHG =90∴AE ⊥BF ……6分（3）BH 的最大值为25+……8分随练1.1 在ABC ∆中，2AB BC ==，90ABC ∠=︒，BD 为斜边AC 上的中线，将ABD ∆绕点D 顺时针旋转α(0180α︒<<︒)得到EFD ∆，其中点A 的对应点为点E ，点B 的对应点为点F ，BE 与FC 相交于点H .（1）如图1，直接写出BE 与FC 的数量关系：____________;（2）如图2，M 、N 分别为EF 、BC 的中点.求证：MN =__________;（3）连接BF ，CE ，如图3，直接写出在此旋转过程中，线段BF 、CE 与AC 之间的数量关系：____________________________.【答案】（1）BE FC =；（2）22FC ；（3）222BF CE AC +=. 【解析】（1）BE FC =；（2）证明：如图，∵AB BC =，90ABC ∠=︒，BD 为斜边中线，∴12BD AD CD AC ===，BD AC ⊥ ∵EFD ∆是由ABD ∆旋转得到的，∴DE DF DB DC ===，90EDF ADB BDC ∠=∠=∠=︒∴EDF BDF BDC BDF ∠+∠=∠+∠，即BDE FDC ∠=∠，∴BDE FDC ∆∆≌，∴BE FC =且12∠=∠又∵34∠=∠，∴90FHE FDE ∠=∠=︒ ,即BE CF ⊥连接BF ，取BF 中点G ，连接MG 、NG .∵M 为EF 中点，G 为BF 中点，N 为BC 中点又∵EB FC =，BE FC ⊥∴MG NG =，90MGN ∠=︒，∴MGN ∆为等腰直角三角形，∴2MN =. （3）222BF CE AC +=.随练1.2 在菱形ABCD 中，120BAD ∠=︒，4AB =，把一个含60°角的三角板与这个菱形叠合，使三角板的60°角的顶点与点A 重合，两边分别落在AB 、AC 上．将三角板绕点A 按逆时针旋转，设旋转角为α．（1）如图①，当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你通过观察或测量写出图中现有的两组相等线段(菱形的边和对角线除外)．（2）如图②，当60120α︒<<︒时，三角板的两边分别与BC 、CD 的延长线相交于点E 、F ，你在(1)中得到的结论还成立吗?若成立，请你选择一组加以证明；若不成立，请你说明理由．（3）当060α︒<<︒时，三角板的两边分别与菱形的两边BC 、CD 相交于点E 、F ，请你求出这个三角板与这个菱形重合部分的面积．【答案】见解析【解析】（1）BE CF =，AE AF =，CE DF =．写出两组即可．（2）（1）中的结论仍然成立．如图，BE CF =的结论仍然成立．证明如下：∵在菱形ABCD 中，120BAD ∠=︒，又由题意可知，60EAF ∠=︒，∴BAE CAF ∠=∠．在△BAE 和△CAF 中，∴△BAE ≌△CAF ．∴BE CF =．（3）当060α︒<<︒时，三角板与这个菱形重合部分的面积就是四边形AECF 的面积．由题意可证△BAE ≌△CAF ．∴四边形AECF 的面积就是△ABC 的面积．∵4AB =，∴所求图形的面积为43随练1.3如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）（1）如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；（2）如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．【答案】（1）DM=FM，DM⊥FM（2）DM⊥FM，DM=FM【解析】（1）如图2，DM=FM，DM⊥FM，证明：连接DF，NF，∵四边形ABCD和CGEF是正方形，∴AD∥BC，BC∥GE，∴AD∥GE，∴∠DAM=∠NEM，∵M是AE的中点，∴AM=EM，在△MAD与△MEN中，∴△MAD≌△MEN，∴DM=MN，AD=EN，∵AD=CD，∴CD=NE，∵CF=EF，∠DCF=∠DCB=90°，在△DCF与△NEF中，∴△DCF≌△NEF，∴DF=NF，∠CFD=∠EFN，∵∠EFN+∠NFC=90°，∴∠DFC+∠CFN=90°，∴∠DFN=90°，∴DM⊥FM，DM=FM（2）猜想：DM⊥FM，DM=FM，证明如下：如图3，连接DF，NF，连接DF，NF，∵四边形ABCD是正方形，∴AD∥BC，∵点E、B、C在同一条直线上，∴AD∥CN，∴∠ADN=∠MNE，在△MAD与△MEN中，∴△MAD≌△MEN，∴DM=MN，AD=EN，∵AD=CD，∴CD=NE，∵CF=EF，∵∠DCF=90°+45°=135°，∠NEF=180°﹣45°=135°，∴∠DCF=∠NEF，在△DCF与△NEF中，∴△MAD≌△MEN，∴DF=NF，∠CFD=∠EFN，∵∠CFD+∠EFD=90°，∴∠NFE+∠EFD=90°，∴∠DFN=90°，∴DM ⊥FM ，DM=FM ．随练 1.4 已知：在ABC △中，AB AC =，点D 为BC 边的中点，点F 在AB 上，连结DF 并延长到点E ,使BAE BDF ∠=∠，点M 在线段DF 上，且ABE DBM ∠=∠．（1）如图，当45ABC ∠=°时，求证：2AE MD =；（2）如图，当60ABC ∠=°时，则线段AE MD 、之间的数量关系为____________；（3）在（2）的条件下，延长BM 到P ，使MP BM =，连接CP ，若727AB AE ==，，求tan EAB ∠的值．【答案】（1）见解析（2）2AE MD =（33 【解析】该题考查的是四边形综合．（1）如图，连结AD又∵45ABC ∠=°∴cos BD AB ABC =∠即2AB BD =∴△ABE ∽△DBM（2）与（1）类似可知△DBM ∽△ABE ，又60ABC ∠=︒，（3）如图2连结AD 、EP ，∵△ABE ∽△DBM又∵BM MP =∴△BEP 等边三角形∴EM BP ⊥即90BMD ∠=︒在Rt △AEB 中，27AE =7AB =， tan EAB ∠的值为3随练 1.5 在等边ABC ∆的两边AB ，AC 所在直线上分别有两点M N D ，，为ABC ∆外一点，且60MDN ∠=︒，120BDC ∠=︒，BD CD =，探究：当点M N ，分别在直线AB AC ，上移动时，BM NC MN ，，之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系．（1）如图①，当点M N ，在边AB AC ，上，且DM DN =时，BM NC MN ，，之间的数量关系式_________；此时Q L=__________ （2）如图②，当点M N ，在边AB AC ，上，且DM DN ≠时，猜想（1）问的两个结论还成立吗？写出你的猜想并加以证明；（3）如图③，当点M N ，分别在边AB CA ，的延长线上时，若AN x =，则Q =_________（用x L ，表示）【答案】见解析【解析】 (Ⅰ)BM 、NC 、MN 之间的数量关系BM NC MN +=．此时23Q L =． (Ⅱ)猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE BM =，连结DE ．∵BD CD =，且120BDC ∠=︒．又△ABC 是等边三角形，∴90MBD NCD ∠=∠=︒．在△MBD 与△ECD 中，BM CE MBD ECD BD DC =⎧⎪∠=∠⎨⎪=⎩∴△MBD ≌△ECD (SAS)．∴DM DE =，BDM CDE ∠=∠．在△MDN 与△EDN 中，DM DE MDN EDN DN DN =⎧⎪∠=∠⎨⎪=⎩∴△MDN ≌△EDN (SAS)．△AMN 的周长Q AM AN MN =++而等边△ABC 的周长3L AB =(Ⅲ)如图③，当M 、N 分别在AB 、CA 的延长线上时，若AN x =，则223Q x L=+（用x、L表示）．随练1.6（1）正方形ABCD中，对角线AC与BD相交于点O，如图1，请直接猜想并写出AO与CD 之间的数量关系：；（2）如图2，将（1）中的△BOC绕点B逆时针旋转得到△BO1C1，连接AO1，DC1，请猜想线段AO1与DC1的数量关系，并证明你的猜想；（3）如图3，矩形ABCD和Rt△BEF有公共顶点，且∠BEF=90°，∠EBF=∠ABD=30°，则AEDF=______．【答案】（1）AO=2CD．理由如下：∵四边形ABCD为正方形，∴AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=2 CD，故答案为AO=2 CD；（2）∵四边形ABCD为正方形，∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC和△OBC都是等腰直角三角形，∵△BOC绕点B逆时针方向旋转得到△BO1C1，∴∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，∴BC121，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC1∽△BAO1，（3）在R t△EBF中，cos∠EBF=EB FB在R t△ABD中，cos∠ABD=AD BD，∵∠EBF=∠ABD=30°，∵∠EBF+∠FBA=∠ABD+∠FBA，即∠EBA=∠FBD，∴△AEB∽△FBD，故答案为3【解析】（1）根据正方形的性质得AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，由勾股定理得到AO与CD之间的数量关系；（2）如图2根据正方形的性质得AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，得到△ABC和△OBC都是等腰直角三角形，求出AC=2AB BC=2BO，得到BD=2AB，因为△BOC绕点B逆时针方向旋转得到△BO1C1，所以∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，BC1=2BO1，由∠1+∠3=45°，∠2+∠3=45°，得到∠1=∠2，于是得到△BDC1∽△BAO1，求出结论；（3）如图3在R t△ABD中，cos∠ABD=ABBD，在Rt△EBF中，cos∠EBF=EBFB因为∠EBF=∠ABD=30°得到BE ADBF BD=3，再由∠EBF+∠FBA=∠ABD+∠FBA，得到∠EBA=∠FBD，△AEB∽△FBD，由相似的性质得到解．解：（1）AO=2CD．理由如下：如图1，∵四边形ABCD为正方形，∴AO=OC=OD，∠ODC=∠OCD=45°，∠DOC=90°，∴AO=CO=2 CD，故答案为AO=2 CD；（2）如图2，∵四边形ABCD为正方形，∴AB=BC，AC=BD，OB=OC，∠OBC=∠ABO=45°，∠BOC=90°，∴△ABC和△OBC都是等腰直角三角形，∵△BOC绕点B逆时针方向旋转得到△BO1C1，∴∠O1BC1=∠OBC=45°，OB=O1B，BC1=BC，∴BC121，∵∠1+∠3=45°，∠2+∠3=45°，∴∠1=∠2，∴△BDC1∽△BAO1，（3）如图3 在R t△EBF中，cos∠EBF=EB FB在R t△ABD中，cos∠ABD=AD BD，∵∠EBF=∠ABD=30°，∵∠EBF+∠FBA=∠ABD+∠FBA，即∠EBA=∠FBD，∴△AEB∽△FBD，故答案为3．随练1.7如图，正方形OABC的边长为2，以O为圆心，EF为直径的半圆经过点A，连接AE，CF 相交于点P，将正方形OABC从OA与OF重合的位置开始，绕着点O逆时针旋转90°，交点P运动的路径长是______．【答案】2【解析】如图点P运动的路径是以G为圆心的弧EF，在⊙G上取一点H，连接EH、FH．∵四边形AOCB是正方形，∴∠AOC=90°，∴∠AFP=12∠AOC=45°，∵EF是⊙O直径，∴∠EAF=90°，∴∠APF=∠AFP=45°，∴∠H=∠APF=45°，∴∠EGF=2∠H=90°，∵EF=4，GE=GF，∴2，∴EF的长9022π•2．随练1.8已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．【答案】（1）见解析；（2）①∠CMD=135°②2π【解析】（1）如图1中，∵CA=CB，∠ACB=90°，∴∠A=∠ABC=45°，∵△CEF是由△CAD旋转逆时针α得到，α=90°，∴CB与CE重合，∴∠CBE=∠A=45°，∴∠ABF=∠ABC+∠CBF=90°，∵BG=AD=BF，∴∠BGF=∠BFG=45°，∴∠A=∠BGF=45°，∴GF∥AC．（2）①如图2中，∵CA=CE，CD=CF，∴∠CAE=∠CEA，∠CDF=∠CFD，∵∠ACD=∠ECF，∴∠ACE=∠CDF，∵2∠CAE+∠ACE=180°，2∠CDF+∠DCF=180°，∴∠CAE=∠CDF，∴A、D、M、C四点共圆，∴∠CMF=∠CAD=45°，∴∠CMD=180°﹣∠CMF=135°．②如图3中，O是AC中点，连接OD、CM．∵AD=DB，CA=CB，∴CD⊥AB，∴∠ADC=90°，由①可知A、D、M、C四点共圆，∴当α从90°变化到180°时，点M 在以AC 为直径的⊙O 上，运动路径是弧CD ，∵OA=OC ，CD=DA ，∴DO ⊥AC ，∴∠DOC=90°，∴CD ∧的长=901180π=2π． ∴当α从90°变化到180°时，点M 运动的路径长为2π．随练1.9 如图1，点O 是正方形ABCD 两对角线的交点，分别延长OD 到点G ，OC 到点E ，使OG=2OD ，OE=2OC ，然后以OG 、OE 为邻边作正方形OEFG ，连接AG ，DE ．（1）求证：DE ⊥AG ；（2）正方形ABCD 固定，将正方形OEFG 绕点O 逆时针旋转α角（0°＜α＜360°）得到正方形OE ′F ′G ′，如图2．①在旋转过程中，当∠OAG ′是直角时，求α的度数；②若正方形ABCD 的边长为1，在旋转过程中，求AF ′长的最大值和此时α的度数，直接写出结果不必说明理由．【答案】（1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①α=30°；②α=315°．【解析】（1）如图1，延长ED 交AG 于点H ，∵点O 是正方形ABCD 两对角线的交点，∴OA=OD ，OA ⊥OD ，∵OG=OE ，在△AOG 和△DOE 中，∴△AOG ≌△DOE ，∴∠AGO=∠DEO ，∵∠AGO+∠GAO=90°，∴∠GAO+∠DEO=90°，∴∠AHE=90°，即DE ⊥AG ；（2）①在旋转过程中，∠OAG′成为直角有两种情况：（Ⅰ）α由0°增大到90°过程中，当∠OAG′=90°时，∵OA=OD=12OG=12OG′， ∴在Rt △OAG′中，sin ∠AG′O='OA OG =12， ∴∠AG′O=30°，∵OA ⊥OD ，OA ⊥AG′，∴OD ∥AG′，∴∠DOG′=∠AG′O=30°，即α=30°；（Ⅱ）α由90°增大到180°过程中，当∠OAG′=90°时，同理可求∠BOG′=30°，∴α=180°﹣30°=150°．综上所述，当∠OAG′=90°时，α=30°或150°．②如图3，当旋转到A、O、F′在一条直线上时，AF′的长最大，∵正方形ABCD的边长为1，∴2，∵OG=2OD，∴2∴OF′=2，∴2+2，∵∠COE′=45°，∴此时α=315°．作业1如图1，在△ABC中，∠BAC=90°，AB=AC．（1）若点M为AC上的任意一点，过M作MN⊥BC于点N，取BM的中点D，连接AD、DM，求证：AD=DN．（2）如图2，若M为BC上的任意一点，以线段CM为底边作等腰Rt△MCN，此时，取BM的中点D，连接AD、DN，则AD与DN有怎样的数量关系？说明理由．（3）如图3，在（2）的条件下将Rt△MNC绕C点旋转任意角度，连接BM，取BM的中点D，再连接AD、DN，则（2）中的结论仍然成立吗，它们之间又有怎样的位置关系？请说明理由．【答案】（1）见解析；（2）AD=DN；（3）AD=DN，AD⊥DN【解析】（1）证明：解法一：如图1中，延长AD到K，使得DK=AD，连接AN、KN、KM．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KMC=∠BAC=90°，∵AB=AC，∠BAC=90°，∴∠C=45°，∵MN⊥BC，∴∠MNC=90°，∠NMC=45°=∠KMC=∠C，∴MN=NC，在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，即AD=DN．解法二：根据直角三角形斜边中线性质，可知AD=12BM，DN=12BM，由此即可证明．（2）如图2中，结论：AD=DN．理由：延长AD到K，使得DK=AD，连接AN、KN、KM．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KMN=∠B=45°，∵∠NMC=∠NCM=∠ACB=45°∴MN=NC，∠KMN=∠ACN=90°在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，即AD=DN．（3）如图3中，结论：AD=DN，AD⊥DN．理由：延长AD到K，使得DK=AD，连接AN、KN、KM，延长KN交AC于G．在△ADB和△KDM中，∴△ADB≌△KDM，∴AB=KM=AC，∠BAD=∠MKD，∴AB∥KM，∴∠KGC=∠BAC=90°，∴∠ACN+∠NMG=180°，∵∠KMN+∠NMG=180°，∴∠ACN=∠NMK，在△ANC和△KNM中，∴△ANC≌△KNM，∴AN=KN，∠ANC=∠KNM，∴∠KNA=∠MNC=90°∵AD=DK，∴DN=AD=DK，DN⊥AK，即AD=DN．AD⊥DN．作业2已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．【答案】（1）见解析（2）成立（3）见解析【解析】本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质．（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG．（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG=CG；再证出△DMG≌△FNG，得到MG=NG；再证明△AMG≌△ENG，得出AG=EG；最后证出CG=EG．（3）结论依然成立．还知道EG⊥CG．（1）证明：∵四边形ABCD是正方形，∴∠DCF=90°，在Rt△FCD中，∵G为DF的中点，∴CG=12 FD，同理，在Rt△DEF中，EG=12 FD，∴CG=EG．（1）（1）中结论仍然成立，即EG=CG．证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．在△DAG与△DCG中，∵AD=CD，∠ADG=∠CDG，DG=DG，∴△DAG≌△DCG（SAS），∴AG=CG；在△DMG与△FNG中，∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG（ASA），∴MG=NG；∵∠EAM=∠AEN=∠AMN=90°，∴四边形AENM是矩形，在矩形AENM中，AM=EN，在△AMG与△ENG中，∵AM=EN，∠AMG=∠ENG，MG=NG，∴△AMG≌△ENG（SAS），∴AG=EG，∴EG=CG．证法二：延长CG至M，使MG=CG，连接MF，ME，EC，在△DCG与△FMG中，∵FG=DG，∠MGF=∠CGD，MG=CG，∴△DCG≌△FMG．∴MF=CD，∠FMG=∠DCG，∴MF∥CD∥AB，∴EF⊥MF．在Rt△MFE与Rt△CBE中，∵MF=CB，∠MFE=∠EBC，EF=BE，∴△MFE≌△CBE∴∠MEF=∠CEB．∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°，∴△MEC为直角三角形．∵MG=CG，∴EG=12 MC，∴EG=CG．（3）（1）中的结论仍然成立．理由如下：过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB于N．由于G为FD中点，易证△CDG≌△MFG，得到CD=FM，又因为BE=EF，易证∠EFM=∠EBC，则△EFM≌△EBC，∠FEM=∠BEC，EM=EC∵∠FEC+∠BEC=90°，∴∠FEC+∠FEM=90°，即∠MEC=90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG=CG，EG⊥CG．作业3在△ABC中，∠ACB=90°，∠A＜45°，点O为AB中点，一个足够大的三角板的直角顶点与点O重合，一边OE经过点C，另一边OD与AC交于点M．（1）如图1，当∠A=30°时，求证：MC2=AM2+BC2；（2）如图2，当∠A≠30°时，（1）中的结论是否成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由；（3）将三角形ODE绕点O旋转，若直线OD与直线AC相交于点M，直线OE与直线BC相交于点N，连接MN，则MN2=AM2+BN2成立吗？答：____（填“成立”或“不成立”）【答案】（1）见解析；（2）不成立；（3）成立【解析】（1）证明：如图1，过A作AF⊥AC交CO延长线于F，连接MF，∵∠ACB=90°，∴BC∥AF，∴△BOC∽△AOF，∵O为AB中点，∴OA=OB，∴AF=BC，CO=OF，∵∠MOC=90°，∴OM是CF的垂直平分线，∴CM=MF，在Rt△AMF中，由勾股定理得：MF2=AM2+AF2=AM2+BC2，即MC2=AM2+BC2；（2）还成立，理由是：如图2，过A作AF⊥AC交CO延长线于F，连接MF，∵∠ACB=90°，∴BC∥AF，∴△BOC∽△AOF，∵OA=OB，∴AF=BC，CO=OF，∵∠MOC=90°，∴OM是CF的垂直平分线，∴CM=MF，在Rt△AMF中，由勾股定理得：MF2=AM2+AF2=AM2+BC2，即MC2=AM2+BC2；（3）成立．作业4在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．（1）如图1，若四边形ABCD是正方形．请直接写出AC1与BD1的数量关系和位置关系．（2）如图2，若四边形ABCD是菱形，AC=6，BD=8，判断AC1与BD1的数量关系和位置关系，并给出证明；（3）如图3，若四边形ABCD是平行四边形，AC=6，BD=12，连接DD1，设AC1=kBD1，请直接写出k 的值和AC12+（kDD1）2的值．【答案】（1）AC1⊥BD1（2）AC1=34BD1，AC1⊥BD1，理由见解析（3）AC12+（kDD1）2=36【解析】（1）AC1=BD1，AC1⊥BD1；理由：如图1，∵四边形ABCD是正方形，∴OC=OA=OD=OB，AC⊥BD，∴∠AOB=∠COD=90°，∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OC1=OC，OD1=OD，∠COC1=∠DOD1，∴OC1=OD1，∠AOC1=∠BOD1=90°+∠AOD1，在△AOC 1和△BOD 1中1111AO OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩ ，∴△AOC 1≌△BOD 1（SAS ）；∴AC 1=BD 1，∵∠AOB=90°，∴∠OAB+∠ABP+∠OBD 1=90°，∴∠OAB+∠ABP+∠OAC 1=90°，∴∠APB=90°，则AC 1⊥BD 1；故AC 1 与BD 1的数量关系是：AC 1=BD 1；AC 1 与BD 1的位置关系是：AC 1⊥BD 1；（2）AC 1=34BD 1，AC 1⊥BD 1．理由：∵四边形ABCD 是菱形，∴OC=OA=12AC ，OD=OB=12BD ，AC ⊥BD ． ∵△C 1OD 1由△COD 绕点O 旋转得到，∴O C 1=OC ，O D 1=OD ，∠CO C 1=∠DO D 1．∴O C 1=OA ，O D 1=OB ，∠AO C 1=∠BO D 1，∴△AO C 1∽△BOD 1．∴∠O AC 1=∠OB D 1．又∵∠AOB=90°，∴∠O AB+∠ABP+∠OB D 1=90°．∴∠O AB+∠ABP+∠O AC 1=90°．∴∠APB=90°．∴AC 1⊥BD 1．∵△AO C 1∽△BOD 1，即AC 1=34BD 1，AC 1⊥BD 1．（3）如图3，与（2）一样可证明△AOC1∽△BOD1，∴k=12；∵△COD绕点O按逆时针方向旋转得到△C1OD1，∴OD1=OD，而OD=OB，∴OD1=OB=OD，∴△BDD1为直角三角形，在Rt△BDD1中，BD12+DD12=BD2=144，∴（2AC1）2+DD12=144，∴AC12+（kDD1）2=36．作业5在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．（一）尝试探究如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD 上，∠EAF=30°，连接EF．（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF=________度，线段BE、EF、FD之间的数量关系为________．（2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．（二）拓展延伸如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF=30°，BE=1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．【答案】解：（一）（1）：30 ，BE+DF=EF（2）BE﹣DF=EF（二）3【解析】解：（一）（1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′，则∠1=∠2，BE=DE′，AE=AE′，∵∠BAD=60°，∠EAF=30°，∴∠1+∠3=30°，∴∠2+∠3=30°，即∠FAE′=30°∴∠EAF=∠FAE′，在△AEF和△AE′F中，∴△AEF≌△AE′F（SAS），∴EF=E′F，即EF=DF+DE′，∴EF=DF+BE，即线段BE、EF、FD之间的数量关系为BE+DF=EF，故答案为：30，BE+DF=EF；（2）如图3，在BE上截取BG=DF，连接AG，在△ABG和△ADF中，∴△ABG≌△ADF（SAS），∴∠BAG=∠DAF，且AG=AF，∵∠DAF+∠DAE=30°，∴∠BAG+∠DAE=30°，∵∠BAD=60°，∴∠GAE=60°﹣30°=30°，∴∠GAE=∠FAE，在△GAE和△FAE中，∴△GAE≌△FAE（SAS），∴GE=FE，又∵BE﹣BG=GE，BG=DF，∴BE﹣DF=EF，即线段BE、EF、FD之间的数量关系为BE﹣DF=EF；（二）如图4，将△ABE 绕点A 逆时针旋转60°得到△A ′B ′E ′，则AE=AE ′，∠EAE ′=60°，∴△AEE ′是等边三角形，又∵∠EAF=30°，∴AN 平分∠EAF ，∴AN ⊥EE ′，∴直角三角形ANE 中，AN 3AE = ∵在等边△ABC 中，AM ⊥BC ，∴∠BAM=30°， ∴AM 3AB =，且∠BAE+∠EAM=30°，又∵∠MAN+∠EAM=30°，∴∠BAE=∠MAN ，∴△BAE ∽△MAN ， ∴MN AM =BE AB ，即MN 31= ∴3．作业6 探索绕公用顶点的相似多边形的旋转：（1）如图1，已知：等边ABC ∆和ADE ∆，根据__________（指出三角形的全等或相似），可得到CE 与BD 的大小关系为：__________．（2）如图2，正方形ABCD 和正方形AEFG ，求：FCEB 的值；（3）如图3，矩形ABCD 和矩形AEFG ，AB kBC =，AE kEF =，求：FCEB 的值．【答案】（1）全等，相等；（223）21k +．【解析】解：（1）如图1，ABC ∆和ADE ∆都是等边三角形，在AEC ∆和ADB ∆中，AE ADCAE BADAC AB =⎧⎪∠=∠⎨=⎪⎩，AEC ADB ∴∆≅∆，CE BD ∴=；（2）如图2，四边形ABCD 和四边形AEFG 都是正方形，（3）连接FA 、CA ，如图3，四边形ABCD 和四边形AEFG 都是矩形，AB kBC =，AE kEF =，作业7 如图，边长为6的等边三角形ABC 中，E 是对称轴AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针转60°得到FC ，连接DF ．则在点E 运动过程中，DF 的最小值是（）A ． 6B ． 3C ． 2D ． 1.5【答案】D【解析】取线段AC 的中点G ，连接EG ，如图所示．∵△ABC 为等边三角形，且AD 为△ABC 的对称轴，∴CD=CG=12AB=3，∠ACD=60°， ∵∠ECF=60°，∴∠FCD=∠ECG ．在△FCD 和△ECG 中，FC EC FCD ECG DC GC =⎧⎪∠=∠⎨⎪=⎩，∴△FCD ≌△ECG （SAS ），∴DF=GE ．当EG ∥BC 时，EG 最小，∵点G 为AC 的中点，∴此时EG=DF=12CD=32．作业8 已知等边△ABC 边长为2，放置在如图的水平桌面上，将△ABC 水平向右作无滑动翻滚，使△ABC 首次落回开始的位置，则等边△ABC 的中心O 经过的路径长为_________．【答案】433π．【解析】如图，过点C作CD⊥AB于D，则CD一定经过点O，∵CD=32BC=3，∴OC=23CD=233，根据等边三角形的性质，∠BCD=12∠ACB=12×60°=30°，∴每一次翻滚中心O旋转的角度为：180°﹣2×30°=120°，等边三角形翻滚3次翻滚一周，∴点O旋转的角度为：120°×3=360°，∴中心O经过的路径长是：2π•OC=2π×233=433π，故答案为：433π．作业9已知，点O是等边△ABC内的任一点，连接OA，OB，OC．（1）如图1，已知∠AOB=150°，∠BOC=120°，将△BOC绕点C按顺时针方向旋转60°得△ADC．①∠DAO的度数是；②用等式表示线段OA，OB，OC之间的数量关系，并证明；（2）设∠AOB=α，∠BOC=β．①当α，β满足什么关系时，OA+OB+OC有最小值？请在图2中画出符合条件的图形，并说明理由；②若等边△ABC的边长为1，直接写出OA+OB+OC的最小值．【答案】（1）①90°；②OA2+OB2=OC2；证明见解析（2）①α=β=120°，OA+OB+OC有最小值；图形见解析【解析】（1）①∠AOB=150°，∠BOC=120°，∴∠AOC=360°﹣120°﹣150°=90°，。

九年级数学上册重难点相似三角形中的手拉手与十字架模型含解析

相似三角形几何模型（手拉手与十字架模型）第一部分【知识点归纳】【模型一】“手拉手（旋转）”模型图1 图222ADE ABC ABC ACF ADE ∆ ∆∆  →A 绕点旋转如图：∽如图：∽ 以上就是相似三角形中的“手拉手模型”在复杂的图形中可以由这一线索寻找新的相似形，即一转成双，由一得二（由一对相似三角形得第二对相似三角形）。

【模型二】“十字架”模型图3 图41EG AB HF BC⊥==如图3：正方形ABCD 中，EG HF,则有；EG AB HF BC ⊥=如图4：矩形ABCD 中，EG HF,则有. 以上就是矩形中的十字架模型，即矩形中两条互相垂直的线段之比等于矩形的两邻边之比。

第二部分【题型展示与方法点拨】【题型1】三角形中的的“手拉手（旋转）模型”【例1】（23-24九年级上·山西大同·期末）综合与实践-问题情境：如图1，已知在ABC 中，D E ，分别是AB AC ，上的点，且DE BC ∥．（1）操作发现：求证：AB DB =．（2）深入探究：在图1的基础上，将ADE 绕着点A 逆时针旋转一个角度得到图2，连接BD CE ，，那么（1）中的结论是否仍然成立？请判断并说明理由．拓展探究：（3）如图3，当ADE 旋转到点B D E ，，在一条直线上时，BE 与AC 交于点F ，若7BF =，9BE =，求AF CF ⋅的值．【变式1】（23-24九年级上·山西晋中·期中）如图，一副三角板（90C E ∠=∠=°，30B ∠=°，45D ∠=°），AD BC =，顶点A 重合，将ADE 绕其顶点A 旋转，在旋转过程中（不添加辅助线），以下4种位置不存在相似三角形的是（）A ．B ．C ．D ．【变式2】（22-23九年级·上海·假期作业）在ABC 中，CA CB =，在AED △中，DA DE =，点D 、E 分别在CA 、AB 上．（1）如图1，若90ACB ADE ∠=∠=°，则CD 与BE 的数量关系是；（2）若120ACB ADE ∠=∠=°，将AED △绕点A 旋转至如图2所示的位置，则CD 与BE 的数量关系是．【题型2】四边形中的的“手拉手（旋转）模型”【例2】（23-24九年级上·浙江杭州·期末）如图，四边形ABCD 与四边形BEFG 都是正方形，将正方形BEFG 绕点B 按顺时针方向旋转，连接AG ，DF ，CE ．则AG 和CE 的数量关系为；在正方形BEFG 绕点B按顺时针方向旋转的过程中，DFCE的值为．【变式1】（2023·广东广州·一模）如图，正方形ABCD中，等腰直角EBF△绕着B点旋转，BF EF=，90BFE∠=°，则:DE AF=．【变式2】如图，直角梯形ABCD中，∠BCD＝90°，AD∥BC，BC＝CD，E为梯形内一点，且∠BEC＝90°，将△BEC绕C 点旋转90°使BC与DC重合，得到△DCF，连EF交CD于M．已知BC＝5，CF＝3，则DM:MC 的值为（）A．5:3 B．3:5 C．4:3 D．3:4【题型3】正方形中的“十字架模型”【例3】（23-24九年级上·河南郑州·阶段练习）（1）如图1，正方形ABCD中，点P为线段BC上一个动点，若线段MN垂直AP于点E，交线段AB于点M，交线段CD于点N，证明：AP MN=；（2）如图2，正方形ABCD中，点P为线段BC上一动点，若线段MN垂直平分线段AP，分别交AB，AP，BD ，DC 于点M ，E ，F ，N ．求证：EF ME FN =+；【变式1】（23-24九年级上·重庆南岸·期中）如图，在矩形ABCD 中，10AD =，8AB =，点E 为AD 边上一点，将ABE 沿BE 翻折到FBE 处，延长EF 交BC 于点G ，延长BF 交CD 于点H ，且FH CH =，则FG 的长是（）A ．95B ．94C ．45D ．185【变式2】（23-24九年级上·山西太原·期末）如图，在正方形ABCD 中，点E 是DC 边的中点，AE 的垂直平分线分别交AD ，BC 边于点F ，G ，垂足为点H ．若4AB =，则GH 的长为．【题型4】矩形中的“十字架模型”【例4】（23-24九年级上·河南洛阳·期末）小明在学习中发现，当垂直线段出现在四边形中间时，通常有比较简明的结论．下面是他的发现过程，请补充并完成其中的问题．（1）如图1，在正方形ABCD 中，E 为AB 上一点，连接DE ，过点A 作AG DE ⊥于点F ，交BC 于G ，则AG 与DE 的数量关系是：AG ______DE （填“>”“=”“<”号）．(2)①如图2，在矩形ABCD 中，AB nBC M N =，、为AB CD 、上的点，连接MN ，过点D 作DE MN ⊥于点F ，交BC 于E ．小明发现，过M 作MG CD ⊥于点G ，可以得到MN 与DE 的数量关系．这个数量关系是什么？请说明理由；②填空：由①可得，顶点分别在矩形的每一组对边（或延长线）上且互相垂直的两条线段的比等于______； ③应用上述结论解决问题：在Rt ABC △中，9086ACB AC BC ∠°=，=，=，点D 是AB 的中点，连接CD ，过B 作CD 的垂线BE ，交直线AC 于E ，垂足是点F ，直接写出BE 的长度．【变式1】（2024·湖南永州·一模）如图，在矩形ABCD 中，BE AC ⊥于点F ，若1,3BF BC ==，则DE 的长度为（）A ．1B 32C ．32D 332【变式2】（23-24九年级上·河北张家口·阶段练习）如图，在矩形ABCD 中，连接BD ，点E 在AD 上，连接CE ，交BD 于点F ，且DEF DBA ∽ ．（1）BD 与CE 是否垂直？（填“是”或“否”）；（2）若1AB =，30CBD ∠=°，则EF CF的值为．第三部分【中考链接与拓展延伸】1、直通中考【例1】（2021·四川内江·中考真题）如图，矩形ABCD 中，6AB =，8BC =，对角线BD 的垂直平分线EF 交AD 于点E 、交BC 于点F ，则线段EF 的长为．【例2】（2022·湖南娄底·中考真题）如图，已知等腰ABC 的顶角BAC ∠的大小为θ，点D 为边BC 上的动点（与B 、C 不重合），将AD 绕点A 沿顺时针方向旋转θ角度时点D 落在D 处，连接BD ′．给出下列结论：①ACD ABD ′≅△△；②ACB ADD ′ △△；③当BD CD =时，ADD ′ 的面积取得最小值．其中正确的结论有（填结论对应的序号）．2、拓展延伸【例1】（2024·辽宁沈阳·二模）如图1，在Rt ABC △中，90B ∠=︒，4AB =，2BC =，点D ，E 分别是边BC ，AC 的中点，连接.DE 将CDE 绕点C 逆时针方向旋转，记旋转角为α．(1)问题发现：①当0α=°时AE BD =______； ②当180α=°时，AE BD=______． (2)拓展探究：试判断当0360α°<<°时，AE BD的大小有无变化？以下是就图2的情形给出的证明过程，请你补全：∵ECD ACB ∽，EC AC∴=③ ．又∵旋转ECA DCB ∠=∠，∴ECA DCB ∽△△，AE EC BD DC ∴== ． (3)用以上结论解决问题：当CDE 绕点C 逆时针旋转至A ，B ，E 三点在同一条直线上时，请在备用图中画出图形，并写出求线段BD 的长．【例2】（23-24八年级下·江苏苏州·阶段练习）（1）【问题发现】如图①，正方形ABCD ，DEFG ，将正方形DEFG 绕点D 旋转，直线AE 、CG 交于点P ，请直接写出线段AE 与CG 之间的数量关系是______，位置关系是______；（2）【拓展探究】如图2，矩形ABCD ，DEFG ，22AD DE AB DG AD DG ===，，，将矩形DEFG 绕D 旋转；直线AE ,CG 交于点P ，（1）中线段之间的关系还成立吗？若成立，请写出理由；若不成立，请写出线段之间的关系；（3）【解决问题】若2428AD DE AB DG ====，，矩形DEFG 绕D 旋转过程中当点P 与点G 重合时，求线段AE 的长．相似三角形几何模型（手拉手与十字架模型）第一部分【知识点归纳】【模型一】“手拉手（旋转）”模型图1 图222ADE ABC ABC ACF ADE ∆ ∆∆  →A 绕点旋转如图：∽如图：∽ 以上就是相似三角形中的“手拉手模型”在复杂的图形中可以由这一线索寻找新的相似形，即一转成双，由一得二（由一对相似三角形得第二对相似三角形）。

初中数学三角形相似之60°、90°旋转模型讲解、经典例题

60°、90°旋转模型【模型分析】遇60°，旋60°，造等边遇90°，旋90°，造垂遇中点，旋180°，造中心对称遇等腰，旋顶角遇中点，旋180°，造中心对称【经典例题】例1．（2020·武汉市卓刀泉中学八年级月考）如图，已知△ABC中，∠ACB=90°，∠BAC=30°，AB=6，点D为直线AB上一动点，将线段CD绕点C逆时针旋转60°得到线段CE，连接ED、BE，当BE最小时，线段AD的值为（）A．5.5B．6C．7.5D．8【分析】以BC为边作等边△BCF，连接DF，可证△BCE△△FCD，可得BE=DF，则DF△AB 时，DF的长最小，即BE的长最小，即可求解【解析】如图，以BC为边作等边△BCF，连接DF△∠ACB=90°，∠BAC=30°，AB=6△∠ABC=60°，BC=3△将线段CD绕点C逆时针旋转60°得到线段CE△CD=CE，∠DCE=60°△△BCF是等边三角形△CF =BC =BF =3，∠BCF =∠DCE =60° △∠BCE =∠DCF ，且BC =CF ，DC =CE △△BCE △△FCD (SAS ) △ BE = DF△DF △AB 时，DF 的长最小，即BE 的长最小如图，此时作FD AB '⊥△FBD '∠=180°-60°-60°=60°，D F AB '⊥△ 11.52BD BF '== △7.5AD AB BD '=+='故选：C【小结】本题考查了旋转的性质，全等三角形的判定与性质，直角三角形的性质，添加恰当的辅助线构造全等三角形是解题关键．例2．（2021·上海九年级模型练习）平面直角坐标系中，()0,4C，()2,0K ，A 为x 轴上一动点，连接AC ，将AC 绕A 点顺时针旋转90得到AB ，当点A 在x 轴上运动，BK 取最小值时，点B 的坐标为____．【分析】如图，作BH x ⊥轴于点H ，由旋转可知ACO △△BAH ，推出BH OA m ==，4AH OC ==，可得到()4,B m m +，令4x m =+，y m =，可知4y x =-，即可知点B在直线4y x =-的图象上运动，设直线4y x =-交x 轴于点E ，交y 轴于点F ，作KM EF ⊥于点M ，根据垂线段最短可知，当点B 与点M 重合时，BK 的值最小，构建方程组确定交点M 的坐标即可求解【解析】如图，作BH x ⊥轴于点H ，设点A 的坐标为（0，M )()0,4C ，()2,0K∴4OC =，2OK =AC AB =，90AOC CAB AHB ∠=∠=∠=∴90CAO OCA ∠+∠=，90BAH CAO ∠+∠= ∴ACO BAH ∠=∠在ACO △与BAH 中，ACO BAHAOC BHA CA CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ACO △△BAH ()AAS∴BH OA m ==，4AH OC == ∴()4,B m m +令4x m =+，y m =∴4y x =-∴点B 在直线4y x =-上运动设直线4y x =-交x 轴于点E ，交y 轴于点F作KM EF ⊥于点M ，则直线KM 的解析式为：2y x =-+由24y x y x =-+⎧⎨=-⎩，解得：31x y =⎧⎨=-⎩，∴()3,1M -根据垂线段最短可知，当点B 与点M 重合时，BK 的值最小，此时()3,1B -【小结】本题考查了坐标与图形的变化-旋转，全等三角形的判定和性质，一次函数的应用，垂线段最短等知识点，正确找到点B 的运动轨迹是解题的关键．例3．（2021·湖北武汉市·九年级月考）如图，在等腰直角三角形ABC 中，AB =AC ， ∠BAC =90°，O 为BC 的中点，D 为AC 斜下方一点，30,6,ADC CD OD ︒∠===，则AD 的长为______．【分析】连结AO 由等腰直角三角形的性质得AO =CO =OB ，∠AOC =90º，利用旋转变换将三角形△DOC ，逆时针旋转90º得到△EOA ，由性质得AE =CD =6，∠EOD =90º，EO =DO =EA △DC ,，过A 作AF ∥CD ，交ED 于F ，利用平行线的性质∠FED =∠ADC =30º,推出∠EAD =∠EAF +∠F AD =120º,过E 作EG △DA 交延长线于G ，∠EAG =60º利用余角性质∠GEA =30º，在Rt △AGE 中，解直接三角形，AE =6，AG =3，EG =Rt △EOD 中由勾股定理求ED ，在Rt △EGD 中用勾股定理222ED =EG +GD ，构造AD方程(()22214=+3+AD ，解方程即可．【解析】连结AO△在等腰直角三角形ABC 中，AB =AC ， ∠BAC =90°，O 为BC 的中点 △AO =CO =OB ，∠AOC =90º将三角形△DOC ，逆时针旋转90º得到△EOA ，△AE =CD =6，∠EOD =90º，EO =DO =EA △DC , 过A 作AF ∥CD ，交ED 于F ， △∠EAF =90º，∠FED =∠ADC =30º, △∠EAD =∠EAF +∠F AD =90º+30º=120º, 过E 作EG △DA 交延长线于G ， △∠EAG =180º-∠EAD =180º-120º=60º △∠GEA =90º-∠EAG =90º-60º=30º，在Rt △AGE 中，AE =6，AG =11622AE =⨯=3，EG ==在Rt △EOD 中，ED ，在Rt △EGD 中，GD =GA +AD =3+AD ，△222ED =EG +GD ，△(()22214=+3+AD ，△3+AD=13±， △AD =10或-16（舍去），故答案为：10．【小结】本题考查等腰直角三角形的性质，三角形旋转，解直角三角形，勾股定理的应用，掌握等腰直角三角形的性质创造旋转的条件，利用三角形旋转转移线段与角的相等关系，利用解直角三角形求出勾股定理应用的线段的长度，利用勾股定理构造方程是解题关键．【巩固提升】1．（2020·宜兴市实验中学八年级期中）如图，在ABC中，∠ACB＝90°，∠A＝30°，AB＝8，点P是AC上的动点，连接BP，以BP为边作等边BPQ，连接CQ，则点P在运动过程中，线段CQ长度的最小值是（）A．2B．4C D2【分析】如图，取AB的中点E，连接CE，PE．由△QBC△△PBE（SAS），推出QC＝PE，推出当EP△AC时，QC的值最小；【解析】如图，取AB的中点E，连接CE，PE，则AE＝BE＝4．△∠ACB＝90°，∠A＝30°，△∠CBE＝60°，△BE＝AE，△CE＝BE＝AE，△△BCE是等边三角形，△BC＝BE，△∠PBQ＝∠CBE＝60°，△∠QBC＝∠PBE，△QB＝PB，CB＝EB，△△QBC△△PBE（SAS），△QC＝PE，△当EP△AC时，QC的值最小，在Rt△AEP中，△AE＝4，∠A＝30°，△PE＝12AE＝2，△CQ的最小值为2，故选：A ．【小结】本题旋转的性质，考查全等三角形的判定和性质，等边三角形的判定和性质，直角三角形30度角的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题．2．（2020·湖南长沙市·长郡中学八年级期中）如图，ABC ADE DFG ∆∆∆、、均为等边三角形，C E F 、、三点共线，且E 是CF 的中点，下列结论：①ADG EDF ∆≅∆；②AEC ∆为等腰三角形；③=+DF AD GE ；④BAG BCE ∠=∠⑤60GEB ︒∠=，其中正确的个数为（）A ．2B ．3C ．4D ．5【分析】根据等边三角形的性质和判定以及全等三角形的判定和性质证明△ADG △△EDF ，△ABG △△BCE ，然后一一判断即可.【解析】△△ADE 、△DFG ，△ABC 为等边三角形，△DA =DE ，DF =DG ，∠ADE =∠FDG =∠AED =∠ACB =∠DAE =∠BAC =60°， △∠ADG =∠EDF ，∠DAB =∠CAE ， △△ADG △△EDF ，故①正确， △AG =EF ，△AG = EC ,如下图，当D、G、E共线时，显然AG≠AE，AG≠AB△EC≠AE，EC≠AC，∆不是等腰三角形, 故②错误，△AEC△AD+EG=DE+GE＞DG，DG=DF△AD+EG＞DF，故③错误．△△ADG△△EDF，△∠DEF=∠DAG，△∠DEF+∠AED=∠EAC+∠ACE=∠EAC+∠ACB-∠BCE，△∠EAC-∠DEF=∠BCE，△∠BAG=∠DAB-∠DAG=∠EAC-∠DEF，△∠BAG=∠BCE，故④正确，△△ADG△△EDF，△AG=EF=EC,△∠BAG=∠BCE，AB=BC△△ABG△△BCE，△∠ABG=∠EBC，BG=BE,△∠EBG=∠ABC=60︒，△ΔBEG为等边三角形,△∠BEG =60︒，故⑤正确，故选：B．【小结】本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．3．（2020·北京海淀区·人大附中九年级月考）如图，ABC 是等边三角形，3AB =，点E 在AC 上，2AE CE =，点D 在BC 的延长线上，将线段DE 绕点E 逆时针旋转90°，得到线段EF ，连接AF ，若//AF BD ，则AF 的长为______．【分析】如图过点E 作EM AF ⊥于M ，交BD 于N ，解直角三角形求出AM ，EN ，利用全等三角形的性质证明MF =EN ，即可解决问题；【解析】过点E 作EM AF ⊥于M ，交BD 于N△△ABC 是等边三角形△3AB AC BC ===，60ACB ∠=︒ △2AE CE = △2AE =，1EC = △//AF BE△60EAM ACB ∠=∠=︒ △EM AF ⊥ △90AME ∠=︒ △30AEM ∠=︒ △112AM AE == △//AF BD ，EM AF ⊥ △EN BC ⊥△sin 602EN EC =︒=△90EMF END FED ∠=∠=∠=︒△90MFE MEF ∠+∠=︒，90MEF DEN ∠+∠=︒ △ED =EF△()△△EMF DENAAS ≅△MF EN ==△1AF AM MF =+=+【小结】本题主要考查了旋转的性质，等边三角形的性质，特殊角的三角函数值，三角形全等，准确分析计算是解题的关键．4．（2021·四川成都市·八年级期末）已知：等边三角形ABC ，直线l 过点C 且与AB 平行，点D 是直线l 上不与点C 重合的一点，作射线DB ，并将射线DB 绕点D 顺时针转动60︒，与直线AC 交于点E （即60BDE ∠=︒）．（1）如图1，点E 在AC 的延长线上时，过点D 作AC 的平行线与CB 的延长线交于点F ，求证：DE DB =；（2）如图2，2AB =，4CD =，依题意补全图2，试求出DE 的长；（3）当点D 在点C 右侧时，直接写出线段CE 、BC 和CD 之间的数量关系．【分析】（1）过点D 作AC 的平行线与CB 的延长线交于点F ．根据平行线的性质结合等边三角形的判定和性质可得出∠DFB =∠ACB =60°，∠ECD =60°，∠EDC =∠FDB ，CD =DF ．由此即可证出△CDE△△BDF，从而得出DE=DB；（2）分两种情况：①当D在点C右侧时，过点D作AC的平行线与CB的延长线交于点F；②当D在点C左侧时，过点D作BC的平行线与CA于点F，作BH△CD于H．画出图形利用等边三角形的判定和性质、全等三角形的判定和性质分别求解即可；（3）分两种情况考虑：①当点E在AC的延长线上时，过点D作AC的平行线与CB 的延长线交于点F；②当点E在线段AC上时，过点D作AC的平行线与CB交于点F．画出图形利用等边三角形的判定和性质、全等三角形的判定和性质分别求解即可．【解析】（1）如图1，过点D作AC的平行线与CB的延长线交于点F．△△ABC为等边三角形，△∠ACB=∠ABC=60°，△DF∥AC，CD∥AB，△∠DFB=∠ACB=60°，∠DCF=∠ABC=60°，△△CDF是等边三角形，∠ECD=60°，△∠CDF=60°，CD=DF，△∠BDE=60°，△∠EDC+∠CDB=60°，∠FDB+∠CDB=60°，△∠EDC=∠FDB．在△CDE和△BDF中，60ECD BFDCD DFEDC BDF⎧∠=∠=⎪=⎨⎪∠=∠⎩，△△CDE△△BDF（ASA），△DE=DB．（2）分两种情况：①当D在点C右侧时，过点D作AC的平行线与CB的延长线交于点F．如图2所示．由（1）可知，CF=CD=4，CB=AB=2，△BF=2，△BD是等边三角形△CDF的高，=△BD=2△DE=BD=②当D在点C左侧时，过点D作BC的平行线与CA于点F，作BH△CD于H．如图3所示．△△ABC为等边三角形，△∠ACB=∠CAB=60°，△DF∥BC，CD∥AB，△∠DFC=∠ACB=60°，∠DCF=∠CAB=60°，△△CDF是等边三角形，∠DCB=120°，∠DFE=120°，△∠CDF=60°，CD=DF，△∠BDE=60°，△∠EDF+∠FDB=60°，∠FDB+∠CDB=60°，△∠EDF=∠CDB．在△CDB和△EDF中，120BCD EFDCD DFBDC EDF⎧∠=∠=⎪=⎨⎪∠=∠⎩，△△CDB△△EDF（ASA），△DE=DB．在R t△BCH中，∠BCH=60°，∠CBH=30°，CB=AB=2，△CH=1，BH=在R t△BDH中，DH=DC+CH=5，BH=△DB===△DE=，综上，DE的长为（3）分两种情况：①当点E在AC的延长线上时，过点D作AC的平行线与CB的延长线交于点F．如图1所示．由（2）可知，CD=CF，CE=BF，△CD=BC+BF=BC+CE，②当点E在线段AC上时，过点D作AC的平行线与CB交于点F．如图4所示．△△ABC为等边三角形，△∠ACB=∠ABC=60°，△DF∥AC，CD∥AB，△∠DFC=∠ACB=60°，∠DCF=∠ABC=60°，△△CDF是等边三角形，∠CFD=60°，△∠CDF=60°，CD=DF=CF，∠BFD=120°，∠DCE=120°，△∠BDE=60°，△∠EDC+∠EDF=60°，∠FDB+∠EDF=60°，△∠EDC=∠FDB．在△CDE和△BDF中，120 ECD BFDCD DFEDC BDF⎧∠=∠=⎪=⎨⎪∠=∠⎩△△CDE△△BDF（ASA）△CE=BF．△BC=CF+BF=CD+CE．综上所述，当点D在点C右侧时，线段CE、BC和CD之间的数量关系是CD= BC+CE或BC=CD+CE．【小结】本题是三角形综合题，考查了等边三角形的判定及性质，全等三角形的判定与性质，作辅助线构造等边三角形和全等三角形是解题的关键．5．（2019·渠县第三中学八年级月考）如图1，在平面直角坐标系中，直线y=−2x+6交坐标轴于A，B两点，过点C（-6，0）作CD交AB于D，交y轴于点E，且△COE△△BOA．（1）求点B的坐标，线段OA的长；（2）确定直线CD的解析式，求点D的坐标；（3）如图2，点M 是线段CE 上一动点(不与点C ，E 重合)，ON △OM 交AB 于点N ，连接MN ，当△OMN 的面积最小时，请求点M 的坐标和△OMN 的面积．（4）如图3，点M 是直线CD 上一动点，过点M 作x 轴的垂线，交轴于点Q ，连接EQ ，若∠EQM =∠ACD ，求点M 的坐标．【分析】（1）利用x 轴与y 轴的特征求直线y =-2x +6与两轴的交点即可；（2）利用△COE △△BOA ．求出E （0，3）设CD 的解析式为y =kx +b ，将C 、E 代入求出CD解析式，由CD 交AB 于D ，联立解方程组13226y x y x ⎧=+⎪⎨⎪=-+⎩即可；（3）由△COE △△BOA ．推出CO =BO ，∠OCE =∠OBA ，利用同角的余角相等推出∠COM =∠EON ，进而可证△COM △△BON (ASA )，得△MON 为等腰直角三角形，要使△OMN 的面积最小，需OM 最小，此时OM △CE 由△COE 面积桥OC OE 65OM==CE 5即可求出面积最小值，利用△MFO △△COE ，得MF FO 2==635可求MF ，FO 即可；（4）可证△EQO △△CEO 由性质QO OE =OE OC 求出OQ ，当点Q 在x 轴的负半轴上时，Q （32-，0）由点M 在CD 上，当32x =-时求函数值得M 1（32-，94）；当点Q 在x 轴的正半轴上时，Q （32，0）由点M 在CD 上，当32x =时求函数值M 2（32，154），综合得M 的坐标为（32-，94），（32，154）．【解析】（1）当x =0时，y =6，则B （0，6），当y =0时，-2x +6=0，x =3，A (3，0)， OA =3；（2）△△COE △△BOA ， △OE =OA =3，OC =OB =6， △E （0，3），C (-6,0)，设CD 的解析式为y =kx +b ，过C （-6，0）和E （0，3），则360b k b =⎧⎨-+=⎩，解得312b k =⎧⎪⎨=⎪⎩，CD 的解析式为：132y x =+， ∵CD 交AB 于D ，∴13226y x y x ⎧=+⎪⎨⎪=-+⎩，解得65185x y ⎧=⎪⎪⎨⎪=⎪⎩，点D 坐标为D （61855，）；（3）∵△COE ≌△BOA ， △CO =BO ，∠OCE =∠OBA ， △ON △OM ，∠COB =90º，△∠COM +∠MOE =90º,∠MOE +∠EON =90º， △∠COM =∠EON ， △△COM △△BON (ASA )， △OM =ON ，△△MON 为等腰直角三角形， S △MON =211OM ON=OM 22，要使△OMN 的面积最小，需OM 最小，此时OM △CE ，CE由△COE 面积得，11CE OM=OC OE 22，OC OE OM==CE 35，S △MON 最小=221118OM =?=225⎝⎭，过M 作MF △OC 于F ，△∠FMO +∠FOM =90º，∠MCO +∠MOC =90º， △∠FMO =∠MCO ， △∠MFO =∠COE =90º， △△MFO △△COE ，△MF FO OM==OC OE CE即MF FO 2=635， △212MF=6=55⨯，6FO=5， △点M 在第二象限， △M （65-，125）；（4）△MQ △x 轴， △MQ ∥OE ， △∠MQE =∠QEO ， △∠EQM =∠ACD ， △∠QEO =∠OCE ， △∠QOE =∠EOC ， △△EQO △△CEO ，△QO OE= OE OC△OQ=2OE93== OC62当点Q在x轴的负半轴上时，Q（32-，0）由点M在CD上，CD的解析式为：132y x=+当32x=-时1393224y⎛⎫=⨯-+=⎪⎝⎭M1（32-，94）当点Q在x轴的正半轴上时，Q（32，0）由点M在CD上，CD的解析式为：132y x=+当32x=时13153224y⎛⎫=⨯+=⎪⎝⎭M2（32，154），综合得M的坐标为（32-，94），（32，154）．【小结】本题考查直线与两轴的交点，直线解析式，两直线的交点，最小面积，三角形全等的性质，勾股定理，三角形相似，掌握直线与两轴的交点求法，会用待定系数法求直线解析式，会利用解方程组求两直线的交点，会利用点到直线的距离最小求最小面积，利用三角形全等的性质进行线段、角的转化，利用勾股定理求边长，会利用三角形相似的性质解决问题是关键．6．（2020·辽宁沈阳市·九年级其他模拟）在ABC 中，AB AC =，点P 在平面内，连接AP ，并将线段AP 绕A 顺时针方向旋转与BAC ∠相等的角度，得到线段AQ ，连接BQ ．（1）如图，如果点P 是BC 边上任意一点．则线段BQ 和线段PC 的数量关系是__________．（2）如图，如果点P 为平面内任意一点．前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．请仅以图所示的位置关系加以证明（或说明）；（3）如图，在DEF 中，8DE =，60EDF ∠=︒，75DEF ∠=︒，P 是线段EF 上的任意一点，连接DP ，将线段DP 绕点D 顺时针方向旋转60°，得到线段DQ ，连接EQ ．请直接写出线段EQ 长度的最小值．【分析】（1）先判断出∠BAQ =∠CAP ，进而用SAS 判断出△BAQ △△CAP ，即可得出结论；（2）结论BQ =PC 仍然成立，理由同（1）的方法；（3）先构造出△DEQ △△DHP ，得出EQ =HP ，进而判断出要使EQ 最小，当HP △EF （点P 和点M 重合）时，EQ 最小，最后用解直角三角形即可得出结论．【解析】（1）由旋转知：AQ =AP △PAQ BAC ∠=∠△PAQ BAP BAC BAP ∠-∠=∠-∠ △BAQ CAP ∠=∠ △AB AC =△()BAQ CAP SAS ∆≅∆ △BQ CP = 故答案为：相等（2）BQ PC =仍成立，理由如下证明：由旋转知：AQ =AP △PAQ BAC ∠=∠△PAQ BAP BAC BAP ∠-∠=∠-∠ △BAQ CAP ∠=∠ △AB AC =△()BAQ CAP SAS ∆≅∆ △BQ C =Ｐ（3）如图：在DF 上取一点H ，使8DH DE ==，连接ＰＨ，过点Ｈ作HM EF ⊥于Ｍ，由旋转知，DQ DP =，60PDQ ∠=︒，△60EDF ∠=︒，△PDQ EDF ∠=∠，△EDQ HDP ∠=∠，△()DEQ DHP SAS ∆≅∆，△EQ HP =，要使EQ 最小，则有HP 最小，而点H 是定点，点P 是EF 上的动点△当HM EF ⊥（点P 和点M 重合）时，HP 最小即：点P 与点M 重合，EQ 最小，最小值为HM过点E 作EG DF ⊥于G ，在Rt DEG ∆中，8DE =，60EDF ∠=︒△30DEG ∠=︒ △142DG DE ==△EG ==在Rt EGF ∆中，753045FEG DEF DEG ∠=∠-∠=︒-︒=︒△9045F FEG FEG ∠=︒-∠=︒=∠，FG EG ==△4DF DG FG =+=+△484FH DF DH =-=+=在Rt HMF ∆中，45F ∠=︒△)4HM ===即：EQ 的最小值为．【小结】本题考查旋转的性质、最值问题，属于几何变换综合题，掌握全等三角形的证明方法，点到直线的距离等知识为解题关键．。

三角形全等、相似及综合应用模型(6大模型+解题技巧)—2024年中考数学(全国通用)(解析版)

三角形全等、相似及综合应用模型题型解读｜模型构建｜通关试练三角形基础知识部分多以选择或者填空题形式，考察其三边关系、内角和/外角和定理、“三线”基本性质等。

特殊三角形的性质与判定也是考查重点，年年都会考查，最为经典的“手拉手”模型就是以等腰三角形为特征总结的，且等腰三角形单独出题的可能性还是比较大。

直角三角形的出题类型可以是选择填空题这类小题，也可以是各类解答题，以及融合在综合压轴题中，作为问题的几何背景进行拓展延伸。

模型01 与三角形有关的线段应用高（AD）中线（AD）角平分线（AD）中位线（DE）模型02 与三角形有关的角的应用（1）三角形的内角：（1）三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且小于180°．（2）三角形内角和定理：三角形内角和是180°．（3）三角形内角和定理的证明证明方法，不唯一，但其思路都是设法将三角形的三个内角移到一起，组合成一个平角．在转化中借助平行线．（4）三角形内角和定理的应用主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．（2）三角形的外角：（1）三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对．（2）三角形的外角性质：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．（3）若研究的角比较多，要设法利用三角形的外角性质②将它们转化到一个三角形中去．（4）探究角度之间的不等关系，多用外角的性质③，先从最大角开始，观察它是哪个三角形的外角．模型03 三角形全等的判定及应用（1）全等三角形的定义：全等的图形必须满足：（1）形状相同；（2）大小相等能够完全重合的两个三角形叫做全等三角形。

备战中考数学二轮专题归纳提升真题几何模型—三角形中的旋转模型(解析版)

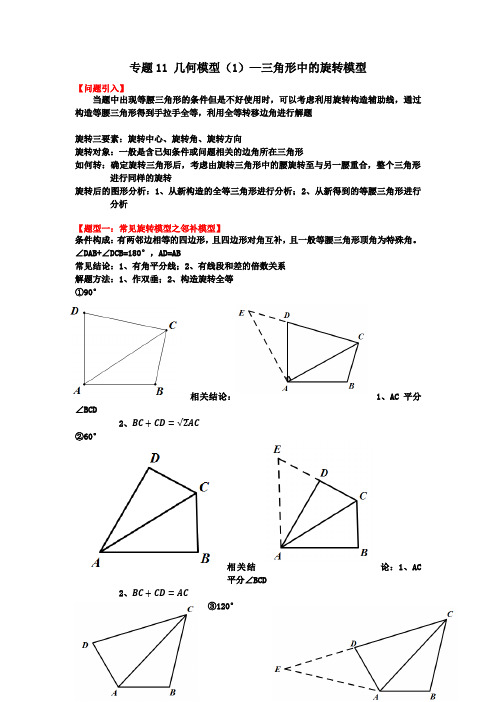
专题11 几何模型（1）—三角形中的旋转模型【问题引入】当题中出现等腰三角形的条件但是不好使用时，可以考虑利用旋转构造辅助线，通过构造等腰三角形得到手拉手全等，利用全等转移边角进行解题旋转三要素：旋转中心、旋转角、旋转方向旋转对象：一般是含已知条件或问题相关的边角所在三角形如何转：确定旋转三角形后，考虑由旋转三角形中的腰旋转至与另一腰重合，整个三角形进行同样的旋转旋转后的图形分析：1、从新构造的全等三角形进行分析；2、从新得到的等腰三角形进行分析【题型一：常见旋转模型之邻补模型】条件构成：有两邻边相等的四边形，且四边形对角互补，且一般等腰三角形顶角为特殊角。

∠DAB+∠DCB=180°，AD=AB常见结论：1、有角平分线；2、有线段和差的倍数关系解题方法：1、作双垂；2、构造旋转全等①90°相关结论：1、AC平分∠BCD2、BC+CD=√2AC②60°相关结论：1、AC平分∠BCD2、BC+CD=AC③120°相关结论：1、AC平分∠BCD2、BC+CD=√3AC补充说明：对角互补、邻边相等、角平分线三个条件知到其中两个就可求另外第三个，辅助线的构造与三角形全等相同，但是全等判定会有差异，需要根据具体情况判断【例】如图，在Rt△ABC和Rt△BCD中，∠BAC＝∠BDC＝90°，BC＝8，AB＝AC，∠CBD＝30°，BD＝4√3，M，N分别在BD，CD上，∠MAN＝45°，则△DMN的周长为_____．【答案】4√3+4．【解析】将△ACN绕点A逆时针旋转，得到△ABE，如图：由旋转得：∠NAE＝90°，AN＝AE，∠ABE＝∠ACD，∠EAB＝∠CAN，∵∠BAC＝∠D＝90°，∴∠ABD+∠ACD＝360°﹣90°﹣90°＝180°，∴∠ABD+∠ABE＝180°，∴E，B，M三点共线，∵∠MAN＝45°，∠BAC＝90°，∴∠EAM＝∠EAB+∠BAM＝∠CAN+∠BAM＝∠BAC﹣∠MAN＝90°﹣45°＝45°，∴∠EAM＝∠MAN，在△AEM和△ANM中，{AE=AN∠EAM=∠NAMAM=AM，∴△AEM≌△ANM（SAS），∴MN＝ME，∴MN＝CN+BM，∵在Rt△BCD中，∠BDC＝90°，∠CBD＝30°，BD＝4√3，CD＝BD×tan∠CBD＝4，∴△DMN的周长为DM+DN+MN＝DM+DN+BM+CN＝BD+DC＝4√3+4，故答案为：4√3+4．【练1】如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________．【答案】3√2【解析】解：将△OBC绕O点旋转90°，∵OB=OA∴点B落在A处，点C落在D处且有OD=OC=3，∠COD=90°，∠OAD=∠OBC，在四边形OACB中∵∠BOA=∠BCA=90°，∴∠OBC+∠OAC=180°，∴∠OAD+∠OAC=180°∴C、A、D三点在同一条直线上，∴△OCD为等要直角三角形，根据勾股定理CD2=OC2+OD2即CD2=32+32=18解得CD=3√2即BC+AC=3√2.【练2】如图，P是等边三角形ABC内一点，将线段BP绕点B逆时针旋转60°得到线段BQ，连接AQ．若PA=4，PB=5，PC=3，则四边形APBQ的面积为_______．【答案】5√34+6【解析】解：如图，连接PQ，由旋转的性质可得，BP=BQ，又∵∠PBQ=60°，∴△BPQ是等边三角形，∴PQ=BP，在等边三角形ABC中，∠CBA=60°，AB=BC，∴∠ABQ=60°-∠ABP∠CBP=60°-∠ABP∴∠ABQ=∠CBP在△ABQ与△CBP中{BQ=BP∠ABQ=∠CBPAB=CB∴△ABQ≌△CBP(SAS)，∴AQ=PC，又∵PA=4，PB=5，PC=3，∴PQ=BP=5，PC=AQ=3，在△APQ中，AQ2=9,AP2=16,PQ2=25，25=16+9，∴由勾股定理的逆定理可知△APQ是直角三角形，∴S 四边形APBQ =S △BPQ +S △APQ =√34×52+12×3×4=5√34+6，故答案为：5√34+6【练3】如图，在△ABC 中，∠ACB =120°，BC >AC ，点E 在BC 上，点D 在AB 上，CE =CA ，连接DE ，180ACB ADE ∠+∠=︒，CH ⊥AB ，垂足为H ．证明：DE AD +=．【答案】见解析【解析】证明：如图，延长BA 到点F ，使AF=DE ，连接CF 、CD ，∵∠ACB+∠ADE=180°∴∠CAD+∠CED=360°－180°=180°∵∠CAD+∠CAF=180°∴∠CAF=∠CED∵AC=EC ，AF=ED∴△AFC ≌△EDC∴CF=CD ，∠ACF=∠ECD∴∠FCD=∠ACF+∠ACD=∠ECD+∠ACD=∠ACB=120°∵CF=CD ，CH ⊥DF∴FH=DH=12DF =12(DE+AD)，∠HCD=12∠FCD=60°∴tan ∠HCD=DH CH =√3∴DH=√3CH∴DE+AD=2DH=2√3CH【题型二：旋转与三角形全等的构造】【例】问题背景：如图①设P 是等边△ABC 内一点，PA ＝6，PB ＝8，PC ＝10，求∠APB 的度数．小君研究这个问题的思路是：将△ACP 绕点A 逆时针旋转60°得到△ABP '，易证：△APP'是等边三角形，△PBP'是直角三角形，所以∠APB＝∠APP'+∠BPP'＝150°．简单应用：（1）如图2，在等腰直角△ABC中，∠ACB＝90°．P为△ABC内一点，且PA ＝5，PB＝3，PC＝2√2，则∠BPC＝°（2）如图3，在等边△ABC中，P为△ABC内一点，且PA＝5，PB＝12，∠APB＝150°，则PC＝．拓展廷伸：①如图4，∠ABC＝∠ADC＝90°，AB＝BC．求证：√2BD＝AD+DC．②若图4中的等腰直角△ABC与Rt△ADC在同侧如图5，若AD＝2，DC＝4，请直接写出BD的长．【答案】（1）135°（2）PC=13；拓展延伸①：证明见解析②：BD=√2【解析】解：简单应用：（1）如图2，∵△ABC是等腰直角三角形，∴∠ACB＝90°，AC＝BC，将△ACP绕点C逆时针旋转90°得到△CBP'，连接PP'，∴BP'＝AP＝5，∠PCP'＝90°，CP'＝CP＝2√2，∴∠CPP'＝∠CP'P＝45°，根据勾股定理得，PP'=√2CP＝4，∵BP'＝5，BP＝3，∴PP'2+BP2＝BP'，∴△BPP'是以BP'为斜边的直角三角形，∴∠BPP'＝90°，∴∠BPC＝∠BPP'+∠CPP'＝135°，（2）如图3，∵△ABC是等边三角形，∴∠BAC＝60°，AC＝AB，将△ACP绕点A逆时针旋转60°得到△ABP'，连接PP'，∴BP'＝CP，AP'＝AP＝5，∠PAP'＝60°，∴△APP'是等边三角形，∴PP'＝AP＝5，∠APP'＝60°，∵∠APB＝150°，∴∠BPP'＝∠APB﹣∠APP'＝90根据勾股定理得，BP'=√BP2+PP′2=13，∴CP＝13，拓展廷伸：①如图4，在△ABC中，∠ABC＝90°，AB＝BC，将△ABD绕点B顺时针旋转90°得到△BCD'，∴BD'＝BD，CD'＝AD，∠BCD'＝∠BAD，∵∠ABC＝∠ADC＝90°，∴∠BAD+∠BCD＝180°，∴∠BCD+∠BCD'＝180°，∴点D'在DC的延长线上，∴DD'＝CD+CD'＝CD+AD，在Rt△DBD'中，DD'=√2BD，∴√2BD＝CD+AD；②如图5，在△ABC中，∠ABC＝90°，AB＝BC，将△CBD绕点B顺时针旋转90°得到△ABD'，∴BD'＝BD，CD＝AD'，∠DBD'＝90°，∠BCD＝∠BAD'，AB与CD的交点记作G，∵∠ADC＝∠ABC＝90°，∴∠DAB+∠AGD＝∠BCD+∠BGC＝180°，∵∠AGD＝∠BGC，∴∠BAD＝∠BCD，∴∠BAD＝∠BAD'，∴点D'在AD的延长线上，∴DD'＝AD'﹣AD＝CD﹣AD＝2，在Rt△BDD'中，BD=√22DD'=√2．【练1】如图，在等边△ABC中，点D为△ABC内的一点，∠ADB＝120°，∠ADC＝90°，将△ABD绕点A逆时针旋转60°得△ACE，连接DE．（1）求证：AD＝DE；（2）求∠DCE的度数；（3）若BD＝1，求AD，CD的长．【答案】（1）见解析（2）90°（3）√3【解析】（1）证明：∵将△ABD绕点A逆时针旋转60°得△ACE∴△ABD≌△ACE，∠BAC＝∠DAE，∴AD＝AE，BD＝CE，∠AEC＝∠ADB＝120°，∵△ABC为等边三角形∴∠BAC＝60°∴∠DAE＝60°∴△ADE为等边三角形，∴AD＝DE，（2）∠ADC＝90°，∠AEC＝120°，∠DAE＝60°∴∠DCE＝360°﹣∠ADC﹣∠AEC﹣∠DAE＝90°，（3）∵△ADE为等边三角形∴∠ADE＝60°∴∠CDE＝∠ADC﹣∠ADE＝30°又∵∠DCE＝90°∴DE＝2CE＝2BD＝2，∴AD＝DE＝2在Rt△DCE中，DC=√DE2−CE2=√22−12=√3．【练2】如图，四边形ABCD中，∠ABC＝∠ADC＝45°，将△BCD绕点C顺时针旋转一定角度后，点B的对应点恰好与点A重合，得到△ACE．（1）请求出旋转角的度数；（2）请判断AE与BD的位置关系，并说明理由；（3）若AD＝2，CD＝3，试求出四边形ABCD的对角线BD的长．【答案】（1）90°（2）证明见解析（3）BD=√22【解析】解：（1）∵将△BCD绕点C顺时针旋转得到△ACE ∴△BCD'≌△ACE∴AC＝BC，又∵∠ABC＝45°，∴∠ABC＝∠BAC＝45°∴∠ACB＝90°故旋转角的度数为90°（2）AE⊥BD．理由如下：在Rt△BCM中，∠BCM＝90°∴∠MBC+∠BMC＝90°∵△BCD'≌△ACE∴∠DBC＝∠EAC即∠MBC＝∠NAM又∵∠BMC＝∠AMN∴∠AMN+∠CAE＝90°∴∠AND＝90°∴AE⊥BD（3）如图，连接DE，由旋转图形的性质可知CD＝CE，BD＝AE，旋转角∠DCE＝90°∴∠EDC＝∠CED＝45°∵CD＝3，∴CE＝3在Rt△DCE中，∠DCE＝90°∴DE=√CD2+CE2=√9+9=3√2∵∠ADC＝45°∴∠ADE＝∠ADC+∠EDC＝90°在Rt△ADE中，∠ADE＝90°∴EA=√AD2+DE2=√18+4=√22∴BD=√22【练3】如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC＞AD．下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC＝EB，∵AD ＝AE，∠DAE＝60°，∴△ADE是等边三角形，∴AD＝DE．在△DBE中，BD+EB＞DE，即：BD+DC＞AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图3，点D是等腰直角三角形△ABC边上的点（点D不与B、C重合）．求证：BD+DC＞√2AD．（2）如果点D运动到等腰直角三角形△ABC外或内时，BD、DC和AD之间又存在怎样的数量关系？直接写出结论．创新应用：（3）已知：如图4，等腰△ABC中，AB＝AC，且∠BAC＝α（α为钝角），D是等腰△ABC外一点，且∠BDC+∠BAC＝180°，BD、DC与AD之间存在怎样的数量关系？写出你的猜想，并证明．【答案】（1）证明见解析（2）BD+DC≥√2AD；（3）猜想：BD+DC＜2AD；证明见解析【解析】解：（1）证明：把△ACD绕点A顺时针旋转90°得到△ABE，连接ED则有△ACD≌△ABE，DC＝EB∵AD＝AE，∠DAE＝90°∴△ADE是等腰直角三角形∴DE=√2AD在△DBE中，BD+EB＞DE，即：BD+DC＞√2AD；（2）把△ABD旋转，使AB与AC AC旋转，得到△ACD′，则BD＝CD′，在△CDD′中，CD+CD′＞DD′，即BD+CD＞DD′，∵△ADD′是钝角三角形，则DD′＞√2AD当D运动到B的位置时，DD′＝BC=√2AD．∴BD+DC≥√2AD；（3）猜想1：BD+DC＜2AD证明：把△ACD绕点A顺时针旋转α，得到△ABE则有△ACD≌△ABE，DC＝EB，∠ACD＝∠ABE∵∠BAC+∠BDC＝180°∴∠ABD+∠ACD＝180°∴∠ABD+∠ABE＝180°即：E、B、D三点共线．∴在△ADE中，AE+AD＞ED，即BD+DC＜2AD．【题型三：旋转与相似三角形的构造】【例】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，给出下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④S△ABF：S四边形CDEF＝2：5，其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】D【解析】解：如图，过D作DM∥BE交AC于N，∵四边形ABCD是矩形，∴AD∥BC，∠ABC＝90°，AD＝BC，∵BE⊥AC于点F，∴∠EAC＝∠ACB，∠ABC＝∠AFE＝90°，∴△AEF∽△CAB，故①正确；∴△AEF ∽△CBF ，∴AE BC ＝AF CF ，∵AE ＝12AD ＝12BC ，∴AF CF ＝12，∴CF ＝2AF ，故②正确，∵DE ∥BM ，BE ∥DM ，∴四边形BMDE 是平行四边形，∴BM ＝DE ＝12BC ，∴BM ＝CM ，∴CN ＝NF ，∵BE ⊥AC 于点F ，DM ∥BE ，∴DN ⊥CF ，∴DF ＝DC ，故③正确；∵△AEF ∽△CBF ，∴EF BF ＝AE BC ＝12，∴S △AEF ＝12S △ABF ，S △ABF ＝16S 矩形ABCD ，∴S △AEF ＝112S 矩形ABCD ，又∵S 四边形CDEF ＝S △ACD ﹣S △AEF ＝12S 矩形ABCD ﹣112S 矩形ABCD ＝512S 矩形ABCD ，∴S △ABF ：S 四边形CDEF ＝2：5，故④正确；【练1】如图，正方形ABCD 的边长为8，线段CE 绕着点C 逆时针方向旋转，且CE =3，连接BE ，以BE 为边作正方形BEFG ，M 为AB FM 的长最小时，tan ∠ECB =______．【答案】13【解析】解：连接BD ，BF ，FD ，如图，∵BD BC =BF BE =√2，∴BD BF =BC BE ，∵∠FBD+∠DBE=45°，∠EBC+∠DBE=45°，∴∠FBD=∠EBC，∴△EBC∽△FBD，∴∠FDB=∠ECB，DFCE =BDBC=√2，∴DF=√2CE=3√2，由题意知：FM、DF、DM三条线段满足FM+DF≥MD，其中DM、DF的值一定，∴当M，F，D三点一线时，FM最小，过点M作MN⊥BD，垂足为G，∵∠MBN=45°，BM=12AB=4，∴MN=BN=2√2，∵MD=√AM2+AD2=√42+82=4√5，∴DG=√MD2−MG2=√(4√5)2−(2√2)2=6√2，∴tan∠ECB=tan∠FDG=MGDG =√26√2=13，故答案为：13．【练2】如图，在△ABC中，AB＝5，D为边AB上－动点，以CD为一边作正方形CDEF，当点D从点B运动到点A时，点E运动的路径长为_________．【答案】5√2【解析】解：如图，作GB⊥BC于B，取GB=BC，当点D与点B重合时，则点E与点G重合，∴∠CBG=90°，∴CG=√2BC，∠GCB=45°，∵四边形CDEF是正方形，∴CE=√2DC，∠ECD=45°，∴∠BCD+∠DCG =∠GCE+∠DCG =45°，∴∠BCD =∠GCE，且CGBC =CEDC=√2，∴△CGE∽△CBD，∴GEBD =CEDC=√2，即GE=√2BD，∵BD=5，∴点E运动的路径长为GE=√2BD=5√2．【练3】在△ABC和△ADE中，BA=BC，DA=DE，且∠ABC=∠ADE=α，点E在△ABC的内部，连接EC，EB，EA和BD，并且∠ACE+∠ABE=90°．（观察猜想）（1）如图①，当α=60°时，线段BD与CE的数量关系为__________，线段EA，EB，EC的数量关系为__________．（探究证明）（2）如图②，当α=90°时，（1）中的结论是否依然成立？若成立，请给出证明，若不成立，请说明理由；（拓展应用）（3）在（2）的条件下，当点E在线段CD上时，若BC=2√5，请直接写出△BDE的面积．【答案】（1）BD=CE，EB2+EC2=EA2；（2）不成立，理由见解析；（3）2【解析】（1）如图①中，∵BA=BC，DA=DE．且∠ABC=∠ADE=60°，∴△ABC，△ADE都是等边三角形，∴AD=AE，AB=AC，∠DAE=∠BAC=60°，∴∠DAB=∠EAC，∴△DAB≌△EAC（SAS），∴BD=EC，∠ABD=∠ACE，∵∠ACE+∠ABE=90°，∴∠ABD+∠ABE=90°，∴∠DBE=90°，∴DE2=BD2+BE2，∵EA=DE，BD=EC，∴EA2=BE2+EC2．故答案为：BD=EC，EA2=EB2+EC2．（2）结论：EA2=EC2+2BE2．理由：如图②中，∵BA =BC ，DA =DE ．且∠ABC =∠ADE =90°， ∴△ABC ，△ADE 都是等腰直角三角形， ∴∠DAE =∠BAC =45°，∴∠DAB =∠EAC ， ∵AD AE =√22，AB AC =√22， ∴AD AE =ABAC ，∴△DAB ∽△EAC ，∴DB EC =AB AC =√22，∠ACE =∠ABD ， ∵∠ACE +∠ABE =90°，∴∠ABD +∠ABE =90°，∴∠DBE =90°，∴DE 2=BD 2+BE 2，∵EA =√2DE ，BD =√22EC ， ∴12EA 2=12EC 2+BE 2，∴EA 2=EC 2+2BE 2．（3）如图③中，∵∠AED =45°，D ，E ，C 共线， ∴∠AEC =135°，∵△ADB ∽△AEC ，∴∠ADB =∠AEC =135°，∵∠ADE =∠DBE =90°，∴∠BDE =∠BED =45°，∴BD =BE ，∴DE =√2BD ，∵EC =√2BD ，∴AD =DE =EC ，设AD =DE =EC =x ，在Rt△ABC中，∵AB=BC=2√5，∴AC=2√10，在Rt△ADC中，∵AD2+DC2=AC2，∴x2+4x2=40，∴x=2√2（负根已经舍弃），∴AD=DE=2√2，∴BD=BE=2，×2×2=2．∴S△BDE=12。

中考数学难点突破与经典模型精讲练相似三角形中的“A”字型相似模型(解析版)

专题09 相似三角形中的“A”字型相似模型【模型展示】非平行A字型∠AED＝∠B∠∠ADE∠∠ACB∠ADAC＝AEAB＝DEBC.非平行A字型∥ACD＝∥B∥∥ADC∥∥ACB∥ADAC＝ACAB＝CDBC.【题型演练】一、单选题1．如图，已知,ADE ABC若:1:3,AD AB ABC的面积为9，则ADE的面积为（）A．1B．2C．3D．9【答案】A 【分析】根据相似三角形的性质得出21=3ADEABC S S ⎛⎫ ⎪⎝⎭，代入求出即可．【详解】解：∥∥ADE∥∥ABC ，AD ：AB ＝1：3，∥21=3ADEABC S S ⎛⎫ ⎪⎝⎭， ∥∥ABC 的面积为9，∥1=99ADES ， ∥S ∥ADE ＝1，故选：A ．【点睛】本题考查了相似三角形的性质定理，能熟记相似三角形的面积比等于相似比的平方是解此题的关键．2．如图，在∥ABC 中，DE ∥BC ，若AE ＝2，EC ＝3，则∥ADE 与∥ABC 的面积之比为（）A ．4：25B ．2：3C ．4：9D ．2：5【答案】A【分析】根据相似三角形的判定定理得到∥ADE ∥∥ABC ，根据相似三角形的面积比等于相似比的平方计算，得到答案．【详解】解：∥AE =2，EC =3，∥AC =AE +EC =5，∥DE ∥BC ，∥∥ADE ∥∥ABC ， ∥2224525ADE ABC S AE S AC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，故选：A ．【点睛】本题考查的是相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．3．如图，在∥ABC 中，∥C=90°，BC=3，D ，E 分别在AB、AC 上，将∥ADE 沿DE 翻折后，点A 落在点A′处，若A′为CE 的中点，则折痕DE 的长为（）A．12B．3C．2D．1【答案】D【详解】试题解析：由题意得：DE∥AC，∥∥DEA=90°，∥∥C=∥DEA，∥∥A=∥A，∥∥AED∥∥ACB,∥DEBC=AEAC,∥A′为CE的中点，∥C A′=E A′，∥C A′=E A′=AE，∥AEAC=DEBC=13，∥DE=1.故选D.4．如图．在∥ABC中，DE∥BC，∥B=∥ACD，则图中相似三角形有（）A．2对B．3对C．4对D．5对【答案】C【分析】根据相似三角形的判定定理即可得到结论．【详解】∥∥B=∥ACD，∥A=∥A，∥∥ACD∥∥ABC，∥DE∥BC，∥∥ADE∥∥ABC，∥∥ACD∥∥ADE，∥DE∥BC，∥∥EDC=∥DCB，∥∥B=∥DCE，∥∥CDE ∥∥BCD ，故共4对，故选：C ．【点睛】本题考查了相似三角形的判定．注意掌握数形结合思想的应用，注意平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似．5．如图，ABC ∆中，8AB =，6AC =，90A ∠=︒，点D 在ABC ∆内，且DB 平分ABC ∠，DC 平分ACB ∠，过点D 作直线PQ ，分别交AB 、AC 于点P 、Q ，若APQ ∆与ABC ∆相似，则线段PQ 的长为（）A ．5B ．356C ．5或356D ．6【答案】B 【分析】分∥APQ∥∥ABC ，∥APQ∥∥ACB 两种情况，结合相似三角形的性质和三角形内切圆求解即可.【详解】解：若∥APQ∥∥ABC ，∥∥APQ=∥ABC ，∥PQ∥BC ，AP AQ PQ AB AC BC==， ∥∥PDB=∥DBC ，∥BD 平分∥ABC ，∥∥PBD=∥CBD ，∥∥PBD =∥PDB ，∥PB=PD ，同理，DQ=CQ ，∥8AB =，6AC =，90A ∠=︒，，设AP=x ，根据AP AQ AB AC=得43AP AB AQ AC ==, ∥AQ=34x ， ∥PB=PD=8-x ，CQ=DQ=6-34x ，∥PQ=PD+QD=7144x-，∥AP PQAB BC，即7144810xx-=，解得：x=143，∥PQ=356；若∥APQ∥∥ACB，则AP AQ PQ AC AB BC==，由题意知：D为∥ABC的内心，设∥ABC的内切圆交AB于M，交AC于N，可知四边形AMDN为正方形，∥∥A=∥AMD=∥AND=∥MDN=90°，∥AM∥DN，AN∥DM，∥∥MPD=∥NDQ，∥MDP=∥NQD，∥∥MPD∥∥NDQ，∥MP MD ND NQ=，∥AB=8，AC=6，BC=10，∥DM=DN=68102+-=2，∥AM=AN=2，设PM=x，则22xNQ =，∥NQ=4x，∥AP AQAC AB=，即42268x x++=，解得：x=32或-2（舍），∥AP=32+2=72， ∥PQ=AP×BC÷AC=72×10÷6=356.综上：PQ 的值为356. 故选B.【点睛】本题考查了相似三角形的判定和性质，三角形内切圆，角平分线的定义，有一定难度，解题的关键是将三角形相似分两种情况讨论.6．如图，在Rt ABC ∆中，90ACB ∠=︒，取AC 的中点D ，连接BD ，点C 关于线段BD 的对称点为点E ，点F 为线段CD 上的一个动点，连接AE 、BD 、BE 、DE ，已知AC =2BC =，103AE =，//BD AE ，当EF BF +的值最小时，则EF BF的值为（）A B C ．109 D ．32【答案】C【分析】设点M 和点B 关于AC 对称，F 为EM 与AC 交点，过点E 作EG∥AC 于G ，过点E 作EN∥BC ，交BC 延长线于点N ，根据题意得出当EF+BF 最小时点F 的位置，再通过平行线的性质得到∥EAG=∥BDC ，从而求出EG 的长，再判定四边形EGCN 为矩形，得到CN ，最后利用∥MFC∥MEN 将EF BF 转化为NC CM求值即可. 【详解】解：当EF+BF 最小时，如图，点M 和点B 关于AC 对称，F 为EM 与AC 交点，过点E 作EG∥AC 于G ，过点E 作EN∥BC ，交BC 延长线于点N ，此时EF+BF 的最小值即为EF+FM ，即EM ，∥AC=D 为AC 中点，BC=2，∥tan∥BDC=BC DC =， ∥AE∥BD ，∥∥EAG=∥BDC ，∥tan∥EAG=EG AG EG=x ，x ，而AE=103，在∥AEG 中，222103x x ⎫⎛⎫+=⎪ ⎪⎪⎝⎭⎝⎭，解之得：x=209或209-（舍），由题意可得：∥N=∥ACB=∥EGC=90°，∥四边形EGCN 为矩形， ∥EG=NC=209， ∥AC∥BC ，EN∥BC ，∥AC∥EN ，∥∥MFC∥MEN ， ∥MC MF CN EF =，则2010299EF EF NC BF FM CM ===÷=，故选C.【点睛】本题考查了平行线的性质，解直角三角形，相似三角形的判定和性质，最短路径问题，矩形的判定和性质，解题的关键是根据平行利用三角函数得到FG 的长.二、填空题7．如图，光源P 在水平横杆AB 的上方，照射横杆AB 得到它在平地上的影子为CD （点P 、A 、C 在一条直线上，点P 、B 、D 在一条直线上），不难发现//AB CD ．已知 1.5AB m =，4.5CD m =，点P 到横杆AB 的距离是1m ，则点P 到地面的距离等于______m ．【答案】3【分析】易得∥P AB ∥∥PCD ，利用相似三角形对应边的比等于对应高的比可得AB 与CD 间的距离．【详解】解：如图，作PF ∥CD 于点F ，∥AB ∥CD ，∥∥P AB ∥∥PCD ，PE ∥AB ，∥∥P AB ∥∥PCD ， ∥AB PE CD PF=，即：1.514.5PF =，解得：PF =3．故答案为：3．【点睛】考查相似三角形的应用；用到的知识点为：相似三角形对应边的比等于对应高的比． 8．如图，矩形 ABCD 中，2AD =，4AB =，AC 为对角线，E 、F 分别为边 AB 、CD 上的动点，且 EF AC ⊥ 于点 M ，连接 AF 、CE ，求AF CE +的最小值是_____．【答案】5【分析】AF 与EC 两条线段不在同一条直线上，只需将两条线段转换在同一条直线上即可，作//CG EF ，且CG EF =，连接AG ，又因点F 是DC 上是一动点，由三角形的边与边关系AF FG AG +≥，只有当点F 在直线AG 上时，AF FG +最小，由平行四边形CEFG 可知FG EC =时，可求AF CE +的最小值【详解】解：如图所示：过点C 作//CG EF ，且CG EF =，连接FG ，设DF x =，则4FC x =-,当点A 、F 、G 三点共线时，AF FG +的最值小，∥//CG EF ，且CG EF =，∥四边形CEFG 是平行四边形；∥//EC FG ，EC FG =，又∥点A 、F 、G 三点共线，∥//AF EC ，又∥四边形ABCD 是矩形，∥//AE DC ，90D ∠=︒，∥四边形AECF 是平行四边形，又∥EF AC ⊥，∥四边形AECF 是菱形，∥4AF FC x ==-，在Rt ADF 中，由勾股定理得：222AD DF AF +=，又∥2AD =，DF x =，则4AF x =-，∥2222(4)x x +=-，解得：32x =， ∥52AF =，在Rt ADC 中，由勾股定理得，2222224AC AD DC =+=+，所以AC =∥AM =又∥//MF CG ，∥AMF ACG ∠=∠，AFM AGC ∠=∠，∥A AMF CG ∽， ∥AM AF AC AG=，52AG=，∥5AG =，又∥AG AF FG =+，FG EC =，∥5AF EC +=，即最小值是5，故答案为：5．【点睛】本题考查了矩形的性质，平行四边形的判定与性质，三角形相似的判定与性质，勾股定理和最短距离问题等知识点，解题的关键是掌握辅助线的作法以及相似三角形的性质与判定．9．如图，正方形ABCD 边长为3，点E 是AD 上一点，且1AE =，连接BE ，过C 作CF BE ⊥，垂足为F ，CF 交对角线BD 于G ，将BCG 沿CG 翻折得到HCG △，CH 交对角线BD 于M ，则HGM S =______．【答案】928【分析】过点G 作GR ∥BC 于R ，过点H 作HN ∥BC 交BD 于N ，由正方形性质可证明：∥ABE ∥∥FCB ，由勾股定理可求BF ，由翻折性质可得∥HGC ∥∥BGC ，进而可证明：∥BHN ∥∥BED ，可求得HN ，再由∥HNM ∥∥CBM ，可求得HGM HGC S S ，再由∥CGR ∥∥CBF 即可求得结论．【详解】解：如图，过点G 作GR BC ⊥于R ，过点H 作HN BC ∥交BD 于N则90BRG CRG ∠=∠=︒，∥CF BE ⊥90BFC ∴∠=︒90CBF BCF ∴∠+∠=︒正方形ABCD90A ABC ∴∠=∠=︒，3AB AD BC ===90ABE CBF ∴∠+∠=︒ABE BCF ∴∠=∠ABE ∴∥FCB在Rt ABE 中，BE ==BF AE BC BE ∴=，即3BF =BF ∴=由翻折知：FH BF =BH =3HC BC ==，HGC ∥BGC //HN BC BHN ∴∥BEDHN BH DE BE ∴=，即2HN = 65HN ∴= HNM ∥CBM 25HM HN MC BC ∴== 27HM HC ∴=， 27HGM HGC SHMS HC ∴==，GR BC ⊥，45CBG ∠=︒BGR ∴是等腰直角三角形，设BR GR x ==，则3CR x =-， CGR ∥CBF13GR BF CR CF ∴==，即133x x =-，解得34x = 34GR ∴= 113932248BCG S BC GR ∴=⨯⨯=⨯⨯= 98HGC S ∴= 229977828HGM HGC S S ∴==⨯=，故答案为：928．【点睛】本题考查了正方形性质，翻折变换的性质，等腰直角三角形性质，勾股定理，全等三角形判定和性质，相似三角形判定和性质，三角形面积等知识点；解题关键是利用平行线证明相似三角形进行转化，有一定难度，属于中考填空压轴题类型．10．如图，在三角形ABC 中，点D 为边BC 的中点，连接AD ，将三角形ABD 沿直线AD 翻折至三角形ABC 平面内，使得B 点与E 点重合，连接CE 、BE ，分别与边AC 交于点H ，与AD 交于点O ，若AH CH =，AB =4OB =，则点A 到线段BC 的距离为__________．【答案】365【分析】如图，过点A 作AT CB ⊥交CB 的延长线于T ．利用勾股定理求出AO ，利用三角形重心的性质求出OD ，再利用勾股定理求出BD ，利用相似三角形的性质求出AT 即可．【详解】解：如图，过点A 作AT CB ⊥交CB 的延长线于T ．由翻折的性质可知，AD 垂直平分线段BE ，90AOB ∠=︒∴，∥AB =4OB =，∥6OA ，∥AH CH =，点D 为边BC 的中点，∴点O 是ABC 的重心，2OA OD ∴=，3OD ∴=，5BD ∴=，BDO ADT ∠=∠，90BOD T ∠=∠=︒，DOB DTA ∴△∽△， ∴OB DB AT AD =， ∴459AT =， 365AT ∴=，故答案为：365．【点睛】本题考查翻折变换，勾股定理的应用，相似三角形的判定和性质以及重心的性质等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．11．如图，在矩形ABCD 中，AB =2，BC =3，点E 是边AB 的中点，连接CE ，将∥BCE 沿CE 折叠得到∥FCE ，CF 与BD 交于点P ，则DP 的长为 ___．【分析】由勾股定理可求出BD 、EC 的长，连接BF 交CE 于点G ，作FH ∥BC 于点H ，PQ ∥BC 于点Q ，根据相似三角形的性质求出BG 的长，再根据面积等式列方程求出FH 的长，再根据相似三角形的性质求出BQ 与CQ 的比，进而求出DP 的长．【详解】解：如图，连接BF 交CE 于点G ，作FH ∥BC 于点H ，PQ ∥BC 于点Q ，∥四边形ABCD 是矩形，∥AB =DC =2，∥ABC =∥BCD =90°，∥BC =3，∥.BD =∥AE =BE =12AB =12×2=1，∥EC =由折叠得，CE 垂直平分BF ，∥∥BGC =∥EBC =90°，∥∥GCB =∥BCE ，∥∥BGC ∥∥EBC ， ∥GB BC BE EC=，∥BC BE GB EC ⋅===∥22BF GB ===CG ==由12BC •FH =12BF •CG 得，12×3FH =12 解得，FH =95； ∥∥CHF =90°，FC =BC =3，∥125CH==；∥PQ∥FH，∥∥CPQ∥∥CFH，∥CQ PQCH FH=，∥1245935CQ CHPQ FH===，∥CQ=43PQ，∥∥BQP=∥BCD=90°，∥PQ∥DC，∥∥BPQ∥∥BDC，∥BQ PQBC DC=，∥32BQ BCPQ DC==，∥BQ=32PQ，∥392483PQBP BQDP CQ PQ===，∥881717DP BD==，．【点睛】本题重点考查矩形的性质、轴对称的性质、相似三角形的判定与性质、勾股定理、二次根式的化简以及用面积等式列方程等知识与方法，解题的关键是正确地作出所需要的辅助线，此题难度较大，计算烦琐，应注意检验所求的结果是否正确．三、解答题12．如图，∥ABD中，∥A＝90°，AB＝6cm，AD＝12cm．某一时刻，动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动；同时，动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动，运动的时间为ts．（1）求t为何值时，∥AMN的面积是∥ABD面积的29；（2）当以点A ，M ，N 为顶点的三角形与∥ABD 相似时，求t 值．【答案】（1）14t =，22t =；（2）t ＝3或245【分析】（1）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，根据三角形的面积公式列出方程可求出答案；（2）分两种情况，由相似三角形的判定列出方程可求出t 的值．【详解】解：（1）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，∥∥AMN 的面积＝12AN •AM ＝12×（12﹣2t ）×t ＝6t ﹣t 2， ∥∥A ＝90°，AB ＝6cm ，AD ＝12cm∥∥ABD 的面积为12AB •AD ＝12×6×12＝36， ∥∥AMN 的面积是∥ABD 面积的29， ∥6t ﹣t 2＝2369⨯， ∥t 2﹣6t +8＝0，解得t 1＝4，t 2＝2，答：经过4秒或2秒，∥AMN 的面积是∥ABD 面积的29；（2）由题意得DN ＝2t （cm ），AN ＝（12﹣2t ）cm ，AM ＝t cm ，若∥AMN ∥∥ABD ，则有AM AN AB AD =，即122612t t -=，解得t ＝3，若∥AMN ∥∥ADB ，则有AM AN AD AB=，即122126t t -=，解得t ＝245，答：当t ＝3或245时，以A 、M 、N 为顶点的三角形与∥ABD 相似．【点睛】本题考查了相似三角形的判定，直角三角形的性质和一元二次方程的应用，正确进行分类讨论是解题的关键．13．在ABC 中，()0AB m m =>，D 为AB 上一点，过D 作DE ∥BC 交AC 于点E ，连接CD ．设21,DCE ABC S S S S ==，求21S S 的取值范围．【答案】21104S S <≤ 【分析】作AG ∥BC 于F 点，交DE 于G 点，设AD =x ，首先结合相似三角形的判定与性质推出DE BC 和GF AF的值，然后结合面积公式进行列式，得出二次函数解析式，最后结合二次函数的性质以及自变量的取值范围进行判断即可．【详解】解：如图所示，作AG ∥BC 于F 点，交DE 于G 点，设AD =x ，∥DE ∥BC ，∥∥ADE ∥∥ABC ， ∥DE AD AG AE x BC AB AF AC m ====， ∥GF m x AF m-=， ∥()2211212DE GF x m x S DE GF x m x S BC AF m m m BC AF --==⨯=⨯=，整理得：22222111124S x m x x S m m m ⎛⎫=-+=--+ ⎪⎝⎭， ∥点D 在AB 上，0m >，∥0x m <<，210m -<， ∥抛物线21S S 的开口向下，且当2m x =时，21S S 取得最大值为14，当0x =和x m =时，均有210S S =，综上分析，21S S 的取值范围是21104S S <≤．【点睛】本题考查相似三角形的判定与性质，二次函数的性质运用等，掌握相似三角形的判定与性质推出相关线段的比例，以及熟练运用二次函数的性质分析是解题关键． 14．Rt ABC 中，90C ∠=︒，20cm AC =，15cm BC =，现有动点P 从点A 出发，沿AC 向点C 方向运动，动点Q 从点C 出发，沿线段CB 也向点B 方向运动，如果点P 的速度是4cm/s ，点Q 的速度是2cm/s ，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为t 秒．（1）求运动时间为多少秒时，P 、Q 两点之间的距离为10cm?（2）若CPQ 的面积为S ，求S 关于t 的函数关系式．（3）当t 为多少时，以点C ，P ，Q 为顶点的三角形与ABC 相似?【答案】（1）3秒或5秒；（2）()22204cm S t t =-；（3）3t =或4011t = 【分析】（1）根据题意得到AP =4t cm ，CQ =2t cm ，AC =20cm ，CP =（20-4t ）cm ，根据三角形的面积公式列方程即可得答案；（2）若运动的时间为t s ，则CP =（20-4t ）cm ，CQ =2t cm ，利用三角形的面积计算公式，即可得出S =20t -4t 2，再结合各线段长度非负，即可得出t 的取值范围；（3）分∥Rt CPQ Rt CAB ∽△△和∥Rt CPQ Rt CBA ∽△△，利用相似三角形得出比例式，建立方程求解，即可得出结论．【详解】（1）解：由运动知，AP =4tcm ，CQ =2t cm ，∥AC =20cm ，∥CP =（20-4t ）cm ，在Rt ∥CPQ 中，222CP CQ PQ +=，即()()222204210t t -+=；∥3t =秒或5t =秒（2）由题意得4AP t =，2CQ t =，则204CP t =-，因此Rt CPQ 的面积为()()2212042204cm 2S t t t t =⨯-⨯=-；（3）分两种情况：∥当Rt CPQ Rt CAB ∽△△时，CP CQ CA CB =，即20422015t t -=，解得3t =； ∥当Rt CPQ Rt CBA ∽△△时，CP CQ CB CA =，即20421520t t -=，解得4011t =．因此3t =或4011t =时，以点C 、P 、Q 为顶点的三角形与ABC 相似．【点睛】本题考查了勾股定理，相似三角形的性质，用方程的思想解决问题是解本题的关键． 15．如图，在∥ABC 中，点D 在边AB 上，点E 、点F 在边AC 上，且DE ∥BC ，AF AE FE EC=．（1）求证：DF ∥BE ；（2）如且AF ＝2，EF ＝4，AB ＝∥ADE ∥∥AEB ．【答案】（1）见详解；（2）见详解【分析】（1）由题意易得AD AE BD EC =，则有AF AD FE BD =，进而问题可求证；（2）由（1）及题意可知12AD AF BD EF ==，然后可得AD =AE AD AB AE ==后问题可求证．【详解】解：（1）∥DE ∥BC ， ∥AD AE BD EC =， ∥AF AE FE EC =， ∥AF AD FE BD =， ∥DF ∥BE ；（2）∥AF ＝2，EF ＝4，∥由（1）可知，12AD AF BD EF ==，AE =6， ∥AB ＝∥13AD AB ==∥AE AD AB AE ==，∥AE AD AB AE == ∥∥A =∥A ，∥∥ADE ∥∥AEB ．【点睛】本题主要考查相似三角形的判定，熟练掌握相似三角形的判定方法是解题的关键．16．矩形ABCD 中，AB ＝CD ＝3cm ，AD ＝BC ＝4cm ，AC 是对角线，动点P 从点A 出发沿AC 方向向点C 匀速运动，速度为1cm/s ；动点Q 从点C 出发沿CD 方向向点D 匀速运动，速度为2cm/s ．过点P 作BC 的垂线段PH ，运动过程中始终保持PH 与BC 互相垂直，连接HQ 交AC 于点O ．若点P 和点Q 同时出发，设运动的时间为t （s ）（0＜t ＜1.5），解答下列问题：（1）求当t 为何值时，四边形PHCQ 为矩形；（2）是否存在一个时刻，使HQ 与AC 互相垂直？如果存在请求出t 值；如果不存在请说明理由；（3）是否存在一个时刻，使矩形ABCD 的面积是四边形PHCQ 面积的7544，如果存在请求出t 值；如果不存在请说明理由．【答案】（1）1513t =；（2）存在，4023t =；（3）存在，1t = 【分析】（1）当四边形PHCQ 为矩形时，PH CQ =，利用相似三角形的性质求出PH ，CH ，构建方程求解即可；（2）证明HCQ ABC ，由相似的性质得出，CH CQAB BC=，由此构建方程求解即可；（3）根据矩形ABCD 的面积是四边形PHCQ 面积的7544，构建方程求解即可．【详解】解：（1）3AB =，4BC =，5AC ∴，由题可得：AP t =，5CP t =-，2CQ t =，四边形ABCD 是矩形，90B ∴∠=︒，PH BC ⊥，90CHP B ∴∠=∠=︒， PCH ACB ∠=∠， PCHACB ∴，PH CH PC AB CB AC ∴==，即5345PH CH t-==， 3(5)5PH t ∴=-，4(5)5CH t =-，当四边形PHCQ 为矩形时，PH CQ =，3(5)25t t ∴-=，解得：1513t =， ∴当1513t =时，四边形PHCQ 为矩形；（2）存在一个时刻，使HQ AC ⊥，当HQ AC ⊥时，90QHC ACB ∠+∠=︒，90BAC ACB ∠+∠=︒，QHC BAC ∴∠=∠，90HCQ B ∠=∠=︒，HCQ ABC ∴，CH CQAB BC∴=，即CH BC AB CQ ⋅=⋅， 4(5)4325t t ∴-⨯=⨯，解得：4023t =，∴当4023t =时，HQ AC ⊥；（3）存在，由题意得：7513434[2(5)](5)44255t t t ⨯=⨯⨯+-⨯-，解得：1t =或137t =（舍去）， ∴当1t =时，矩形ABCD 的面积是四边形PHCQ 面积的7544．【点睛】本题属于四边形综合问题，考查了矩形的性质，相似三角形的判定与性质，掌握相关的知识点是解决本题的关键．17．图，AB GH CD ∥∥，点H 在BC 上，AC 与BD 交于点G ，AB ＝2，CD ＝3，求GH 的长．【答案】65【分析】根据平行线分线段成比例定理，由AB GH ∥，可证∥CGH ∥∥CAB ，由性质得出GH CH AB BC =，由GH CD ∥，可证∥BGH ∥∥BDC ，由性质得出GH BHCD BC=，将两个式子相加，即可求出GH 的长．【详解】解：∥AB CH ∥， ∥∥A =∥HGC ，∥ABC =∥GHC ， ∥∥CGH ∥∥CAB ， ∥GH CHAB BC=， ∥GH CD ∥，∥∥D =∥HGB ，∥DCB =∥GHB ， ∥BGH ∥∥BDC ， ∥GH BHCD BC=， ∥1GH GH CH BHAB CD BC BC+=+=， ∥AB =2，CD =3，∥123GH GH+=，解得：GH =65．【点睛】本题考查了相似三角形的判定和性质，平行线性质，熟练掌握相似三角形的判定和性质是解题的关键．18．一块直角三角形木板的面积为21.5m ，一条直角边AB 为1.5m ，怎样才能把它加工成一个面积最大的正方形桌面？甲、乙两位木匠的加工方法如图所示，请你用学过的知识说明哪位木匠的方法符合要求（加工损耗忽略不计，计算结果中的分数可保留）．【答案】乙木匠的加工方法符合要求．说明见解析．【分析】要求哪位木匠的加工方法符合要求，需要先求出两种加工方式中正方形的边长，边长最大就符合要求；由已知三角形的面积和一条直角边的边长可求出其余两边的边长，根据乙加工方案中的平行关系得到相似三角形，根据相似三角形对应变成比例，可求出正方形的边长；根据甲加工方案中，根据相似三角形的高的比等于边长比，可求出正方形的边长，对比两方案的边长即可知谁符合要求．【详解】解：作BH ∥AC 于H ，交DE 于M ，如图∥1=2ABC S AB BC ⋅△∥2 1.521.5BC ⨯==∥52AC =∥1=2ABC S AC BH ⋅△∥65 BH=又∥DE∥AC∥DE BM AC BH=∥655625xx-=，解得3037x=设正方形的边长为x米，如图乙∥DE∥AB∥DE CD AB CB∥21.52x x-=，解得67x=∥630 737 >∥乙木匠的加工方法符合要求．【点睛】本题考查了相似三角形的判定与性质的实际应用及分析、解决问题的能力，正确理解题意，建立数学模型，把实际问题转化为数学问题是解决本题的关键．19．如图，已知D是BC的中点，M是AD的中点．求:AN NC的值．【答案】12【分析】解法1：过点D作AC的平行线交BN于点H，构造“A”型和“8”型，得出BDH BCN∽和DHM ANM∽，再结合相似三角形的性质和中点的定义即可得出答案；解法2：过点C作AD的平行线交BN的延长线于点H，构造“A”型和“8”型，得出BDM BCH△∽和AMN CHN△∽△，再结合相似三角形的性质和中点的定义即可得出答案；解法3：过点A作BC的平行线交BN的延长线于点H，构造“A”型和“8”型，得出AHM DBM△∽△和AHN CBN△∽△，再结合相似三角形的性质和中点的定义即可得出答案；解法4：过点D作BN的平行线交AC于点H，根据三角形中位线定理得出AN NH CH==，即可得出答案；【详解】解法1：如图2，过点D 作AC 的平行线交BN 于点H ．因为//DH AC ．所以BDH BCN ∽，所以DH BDCN BC=．因为D 为BC 的中点，所以12DH BD CN BC ==．因为//DH AN ，所以DHM ANM ∽，所以DH DMAN AM=．因为M 为AD 的中点，所以1DH DMAN AM==．所以DH AN =，所以12AN CN =．解法2：如图3，过点C 作AD 的平行线交BN 的延长线于点H ．因为//DM CH ，所以BDM BCH △∽，所以DM BDCH BC=．因为D 为BC 的中点，所以12DM BD CH BC ==．因为M 为AD 的中点，所以AM DM =，所以12AM CH =．因为//DM CH ，所以AMN CHN △∽△，所以12AN AM CN CH ==．解法3：如图4，过点A 作BC 的平行线交BN 的延长线于点H ．因为//AH BD ，所以AHM DBM △∽△，所以AH AMBD DM=．因为M 为AD 的中点，所以AM DM =，所以AH BD =．因为//AH BD ，所以AHN CBN △∽△，所以AN AHCN BC=．因为D 为BC 的中点，且AH BD =，所以12AN BD CN BC ==．解法4：如图5，过点D 作BN 的平行线交AC 于点H ．在ADH 中，因为M 为AD 的中点，//MN DH ，所以N 为AH 的中点，即AN NH =．在CBN △中，因为D 为BC 的中点，//DH BN ，所以H 为CN 的中点，即CN HN =，所以AN NH CH ==．所以12AN CN =． 20．如图， ABC 中，中线AD ，BE 交于点F ，//EG BC 交AD 于点G ．（1）求AGGF的值．（2）如果BD =4DF =，请找出与BDA △相似的三角形，并挑出一个进行证明．【答案】（1）3；（2）BDA FGE ∽△△，证明见解析【分析】（1）先证明AGE ADC △∽△，再证明GEF DBF ∽△△，得到2DF GF =，则问题可解；（2）根据题意分别证明BDA FDB ∽△△，BDA FGE ∽△△问题可证．【详解】解：（1）D 是BC 的中点，E 是AC 的中点， BD CD ∴=，AE CE =，//GE BC ， AGE ADC ∴∽△△，12AG GE AE AD CD AC ∴===， AG GD ∴=，2GE CD BD ==， //GE BC ， GEF DBF ∴∽△△，12GE GF BD DF ∴==， 2DF GF ∴=， 3AG DG GF ∴==，3AGGF∴=．（2）当BD =4DF =时，由（1）可得 122GF DF ==，36AG DG GF ===，212AD AG ==，12GE BD == 44BD DF ==AD BD == AD BDBD DF∴=，又BDG ADB ∠=∠，BDA FDB ∴∽△△，3GEGF =AD BD == AD GEBD GF∴=， //GE BC ， ADB EGF ∴∠=∠， BDA FGE ∴∽△△．【点睛】本题考查了相似三角形的性质和判定，解答关键是根据题意选择适当方法证明三角形相似．21．如图，在ABC ∆中，点,E F 分别在,AB AC 上，且AE ABAF AC=．（1）求证：AEFABC ∆∆；（2）若点D 在BC 上，AD 与EF 交于点G ，求证：EG FGBD CD=．【答案】（1）见解析；（2）见解析【分析】（1）直接利用两边成比例且夹角相等的两个三角形相似即可证得结论；（2）根据相似三角形的性质和平行线的判定方法可得EF ∥BC ，于是可得∥AEG ∥∥ABD ，∥AGF ∥∥ADC ，再根据相似三角形的性质即可推出结论．【详解】解：（1）在∥AEF 和∥ABC 中， ∥EAF BAC ∠=∠，AE ABAF AC=， ∥∥AEF ∥∥ABC ；（2）∥∥AEF∥∥ABC，∥∥AEF=∥ABC，∥EF∥BC，∥∥AEG∥∥ABD，∥AGF∥∥ADC，∥EG AGBD AD=,FG AGCD AD=，∥EG FG BD CD=．【点睛】本题考查了相似三角形的判定和性质，属于常考题型，熟练掌握相似三角形的判定和性质是解题关键．22．如图，在平行四边形ABCD中，AD＝AC，∥ADC＝α，点E为射线BA上一动点，且AE＜AB，连接DE，将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H，DE所在直线与射线CA交于点G．（1）如图1，当α＝60°时，求证：∥ADH∥∥CDG；（2）当α≠60°时，∥如图2，连接HG，求证：∥ADC∥∥HDG；∥若AB＝9，BC＝12，AE＝3，请直接写出EG的长．【答案】（1）证明见详解；（2）∥证明见详解；∥EG．【分析】（1）AD＝AC，∥ADC＝60°，可证∥ACD为等边三角形，根据四边形ABCD为平行四边形，可得AB=CD=BC=AD，∥B=∥ADC=60°，AD∥BC，可得∥HAD=∥B=60°=∥GCD，由∥GDH=∥CDA=60°，可证∥HAD =∥CDG，即可证∥ADH∥∥CDG（ASA）；（2）∥根据AD＝AC，∥ADC＝α，可得∥ACD=∥ADC＝α，根据四边形ABCD为平行四边形，可得AD∥BC，可得∥HAD=∥ADC=α=∥GCD，由∥GDH=α=∥ADC，可得∥ADH =∥CDG 即可；∥根据点E的位置分两种情况，当点E在AB上时，过C作CN∥AB于N，过G作GM∥AE于M，根据四边形ABCD为平行四边形，AB∥DC，AB=DC=9，AD=BC=12，可证∥AGE∥∥CGD，得出AG=3，CG=AC-AG=12-3=9，根据等腰三角形三线合一性质可得AN=BN=1922AB=，根据勾股定理CN==GM∥CN，再证∥AMG∥∥ANC，可求1948AM AN==,14GM CN==EM=AE-AM=915388-=，根据勾股定理EG==，当点E在BA延长线上，过C作CN∥AB于N，过G作GM∥AE于M，由AE∥CD，∥GAE∥∥GCD，可求GA=6，由GM∥CN，可证∥GMA∥∥CNA，可得1122GM CN===，11992224AM AN==⨯=，EM=AE-AM=3-9344=，根据勾股定理EG=．【详解】（1）证明：∥AD＝AC，∥ADC＝60°，∥∥ACD为等边三角形，∥四边形ABCD为平行四边形，∥AB=CD=BC=AD，∥B=∥ADC=60°，AD∥BC，∥∥HAD=∥B=60°=∥GCD，∥∥GDH=∥CDA=60°，∥∥HDA+∥ADG=∥CDG+∥ADG=60°，∥∥HDA =∥CDG，在∥ADH和∥CDG中ADH CDGAD CDHAD GCD∠=∠⎧⎪=⎨⎪∠=∠⎩∥ADH∥∥CDG（ASA）；（2）∥证明：∥AD＝AC，∥ADC＝α，∥∥ACD=∥ADC＝α，∥四边形ABCD为平行四边形，∥AD∥BC，∥∥HAD=∥ADC=α=∥GCD，∥∥GDH=α=∥ADC，∥∥ADH+∥ADG=∥CDG+∥ADG=α，∥∥ADH =∥CDG，∥∥ADH∥∥CDG；∥解：当点E在AB上时，过C作CN∥AB于N，过G作GM∥AE于M，∥四边形ABCD为平行四边形，AB∥DC，AB=DC=9，AD=BC=12，∥∥EAG=∥DCG，∥AEG=∥CDG，∥∥AGE∥∥CGD，∥3193 AG AECG CD===，∥3CG AG=，∥AD=AC=12，∥AG+CG=AG+3AG=4AG=12，∥AG=3，∥CG=AC-AG=12-3=9，∥AC=AD=BC，CN∥AB，∥AN=BN=19 22 AB=，在Rt∥BCN中，根据勾股定理CN=∥GM∥CN，∥∥AMG∥∥ANC，∥31124 AM AG GMAN AC CN====，∥1948AM AN==,14GM CN==∥EM=AE-AM=915388-=，在Rt∥MGE中，根据勾股定理EG==，当点E在BA延长线上，过C作CN∥AB于N，过G作GM∥AE于M，∥AE∥CD，∥∥GAE=∥GCD，∥GEA=∥GDC，∥∥GAE∥∥GCD，∥3193 GA EAGC DC===，∥3GC GA=，∥AC=GC-GA=3GA-GA=2GA=12,∥GA=6，∥AC=AD=BC，CN∥AB，∥AN=BN=19 22 AB=，在Rt∥BCN 中，根据勾股定理CN =∥CN ∥AB ， GM ∥AE ， ∥GM∥CN ， ∥∥GMA ∥∥CNA ， ∥61122GA GM AM CA CN AN ====，∥1122GM CN ===11992224AM AN ==⨯=， ∥EM =AE -AM =3-9344=，在Rt∥GME 中，根据勾股定理EG∥综合EG ．【点睛】本题考查图形旋转性质，平行四边形性质，等边三角形判定与性质，三角形全等判定，三角形相似判定与性质，勾股定理，本题难度角度，利用辅助线画出准确图形，掌握以上知识是解题关键．23．已知：矩形ABCD 中，AB ＝9，AD ＝6，点E 在对角线AC 上，且满足AE ＝2EC ，点F 在线段CD 上，作直线FE ，交线段AB 于点M ，交直线BC 于点N ．（1）当CF ＝2时，求线段BN 的长；（2）若设CF ＝x ，∥BNE 的面积为y ，求y 关于x 的函数解析式，并写出自变量的取值范围；（3）试判断∥BME 能不能成为等腰三角形，若能，请直接写出x 的值．【答案】（1）BN＝10；（2）6273xyx-=-，0＜x＜3；2763xyx-=-，3＜x＜4.5；（3）x＝2或32或29 12【分析】（1）由AB CD∥得∥CFE∥∥AME，∥NCF∥∥NBM，进而求得；（2）分为0＜x＜3和3＜x＜4.5两种情形，作EG∥BC于G，根据三角形相似求出EG和BN；（3）分为BM＝BE，EM＝BE，EN＝BM三种，可根据BM＝9﹣2CF求得．【详解】解：（1）如图1，在矩形ABCD中，BC＝AD＝6，AB CD∥，∥∥CFE∥∥AME，∥NCF∥∥NBM，∥1,2CF EC CF NC AM AE BM NB ===,∥AM＝2CF＝4，∥BM＝AB﹣AM＝5，∥265BNBN-=，∥BN＝10；（2）当CF＝BM时，MF BC∥，此时∥BEN不存在，∥CF＝9﹣2CF，∥CF＝3，当点M和B点重合时，AB＝2CF，∥CF＝4.5，∥分为0＜x＜3和3＜x＜4.5，如图2，当0＜x＜3时，作EG∥BC于G，由（1）知，EG＝3，AM＝2CF＝2x，∥BM＝9﹣2x，由CF NCBM NB=得，692x BNx BN-=-，∥1843x BNx-=-，∥y＝12BN EG⋅＝11843 23xx-⋅⨯-＝6273xx--；如图3，当3＜x ＜4.5时，由BN BMCN CF=得， 926BN xBN x-=+∥CN ＝2(92)3x x --， ∥y ＝12(92)323x x -⋅⨯- ＝2763xx --；（3）如图4，∥EG AB ∥， ∥13CG EG CB AB ==， ∥CG ＝13CB ＝2，∥GB ＝CB ﹣CG ＝4， ∥BE ＝5，当BM ＝BE ＝5时， 9﹣2x ＝5， ∥x ＝2，如图5，当EM ＝EB ＝5时，作EH ∥AB 于H ， ∥BM ＝2BH ＝2EG ＝6， ∥9﹣2x ＝6， ∥x =32，如图6，当EM ＝BM 时，作MH ∥BE 于H ，在Rt ∥BMH 中，BH ＝1522BE =，∥MBH ＝cos ∥BEG ＝35EG BE =， ∥BM ＝355252cos 6BH MBH ==∠，∥9﹣2x ＝256， ∥x ＝2912，综上所述：x ＝2或32或2912．【点睛】此题考查相似三角形的判定及性质，锐角三角函数，勾股定理解直角三角形，矩形的性质，正确引出辅助线及掌握分类思想解决问题是解题的关键．24．如图，在平行四边形ABCD 中，90ADB ∠=︒，10cm AB =，8cm AD =，点P 从点D 出发，沿DA 方向匀速运动，速度为2cm/s ；同时，点Q 从点B 出发，沿BC 方向匀速运动，速度为1cm/s .当一个点停止运动，另一个点也停止运动.过点P 作//PE BD 交AB 于点E，连接PQ ，交BD 于点F .设运动时间为()()s 04t t <<.解答下列问题：（1）当t 为___________时，//PQ AB ？（2）连接EQ ，设四边形APQE 的面积为()2cm y ，求y 与t 的函数关系式.（3）当t 为何值时，点E 在线段PQ 的垂直平分线上？（4）若点F 关于AB 的对称点为F'，是否存在某一时刻t ，使得点P ，E ，F'三点共线？若存在，求出t 的值；若不存在，请说明理由.【答案】（1）83；（2）233244y t t =--+；（31；（4）2425．【分析】（1）由题意得，PQ ∥AB ，则四边形P ABQ 是平行四边形，根据平行四边形的性质可得AP =BQ ，即8-2t =t ，解方程即可求解；（2）过点Q 作QH ∥AB 交AB 的延长线于点H ，由勾股定理求出BD =6，证明∥ADB ∥∥BHQ ，根据相似三角形的性质可得QH =35t ，根据平行线分线段成比例定理可得DP BEAD AB =，可得出BE =52t ，根据y =S 四边形APQB -S ∥BEQ 即可求解；（3）先证出∥APE ∥∥ABD ，根据相似三角形的性质可得PE AP DB AD=，可得PE =6-32t ，根据线段垂直平分线的性质得EQ =PE ，由（2）得QH =35t ，可得出BH =45t ，根据勾股定理得出EH 2+HQ 2=EQ 2，列出方程即可求解；（4）连接FF ′交AB 于点N ，由对称及平行线的性质可得∥FEB =∥ABD ，由等角对等边得EF =FB ，则1524BN EN BE t ===，再证∥DPF ∥∥BQF ，可得DF =2BF ，可求出BF =2，然后证明∥BNF ∥∥BDA ，根据相似三角形的性质即可得t 的值．【详解】解：（1）∥四边形ABCD 是平行四边形， ∥AD ∥BC ，若PQ ∥AB ，∥四边形P ABQ 是平行四边形， ∥AP =BQ ，∥8-2t =t ， ∥t =83，∥当t =83时，PQ ∥AB ；故答案为：83；（2）如图，过点Q 作QH ∥AB 交AB 的延长线于点H ，∥∥ADB =90°，∥BD 2=AB 2-AD 2=100-64=36，即BD =6， ∥四边形ABCD 是平行四边形， ∥AD ∥BC ， ∥∥A =∥QBH ，又∥∥ADB =∥BHQ =90°， ∥∥ADB ∥∥BHQ ， ∥BD AB QH BQ =，即610QH t=， ∥35QH t =，∥PE ∥BD ， ∥DP BE AD AB =，即2810t BE=， ∥52BE t =，∥y =S 四边形APQB -S ∥BEQ =211533(82)632422254t t t t t t -+⨯-⨯⨯=--+；（3）如图：∥PE ∥BD ， ∥∥APE =∥ADB ， ∥∥A =∥A ， ∥∥APE ∥∥ADB ， ∥PE AP DB AD =，即8268PE t-=， ∥362PE t =-，∥点E 在线段PQ 的垂直平分线上， ∥EQ =362PE t =-，由（2）得35,52QH t BE t ==，∥BH =∥45335210EH BH BE t t t =+=+=Rt ∥EQH 中，EH 2+HQ 2=EQ 2， ∥2223333()()(6)1052t t t +=-，即t 2+2t -4=0，解得：121,10t t =<（舍去），∥当t 1时，点E 在PQ 的垂直平分线上；（4）连接FF '交AB 于点N ，∥点F 关于AB 的对称点为F ′，∥∥FEB =∥F ′EB ，FN ∥EB ，∥点P ，E ，F ′三点共线，PE ∥AB ，∥∥F ′EB =∥ABD ，∥∥FEB =∥ABD ，∥EF =FB ， ∥15,24BN EN BE t ===， ∥四边形ABCD 是平行四边形，∥AD ∥BC ，∥∥DPF =∥FQB ，∥DFP =∥BFQ ，∥∥DPF ∥∥BQF ， ∥2DF DP BF BQ==， ∥DF =2BF ，∥2BF +BF =6，∥BF =2，∥∥FBN =∥ABD ，∥FNB =∥ADB ，∥∥BNF ∥∥BDA ， ∥BN BD BF AB=， ∥564210t =，解得：t =2425， ∥存在某一时刻t ，使得点P ，E ，F ′三点共线，t 的值为2425．【点睛】本题属于四边形综合题，考查了解直角三角形，相似三角形的判定和性质，平行四边形的性质，多边形的面积等知识，解题的关键是学会利用参数构建方程解决问题． 25．如图1，平行四边形ABCD 的对角线AC ，BD 相交于点O ，CD 边的垂直平分线EH 交BD 于点E ，连接AE ，CE ．（1）过点A 作//AF EC 交BD 于点F ，求证：AF BF =；（2）如图2，将ABE △沿AB 翻折得到'ABE △．∥求证：'//BE CE ；∥若'//AE BC ，1OE =，求CE 的长度．【答案】（1）见解析；（2）∥见解析；∥1【分析】（1）根据题意证明()COE AOF AAS △≌△，即可证明ED BF =，在根据EH 垂直平分CD 可得EC ED =，即可证的结果；（2）∥过点A 作//AF EC 交BD 于点F ，根据（1）中结论，然后证明'//BE AF 即可； ∥求证AEF BCE ∽，则AF EF BE CE=，据此解答即可．【详解】证明：（1）∥四边形ABCD 是平行四边形，∥OA OC =，OB OD =．∥//AF EC ，∥CEO AFO ∠=∠，FAO ECO ∠=∠，∥()COE AOF AAS △≌△，∥CE AF =，OE OF =，∥ED BF =．∥EH 垂直平分CD ，∥EC ED =．∥AF BF =；（2）如图2，过点A 作//AF EC 交BD 于点F ．∥证明：由（1）可知AOF COE ≌，AF BF =，∥ABF BAF ∠=∠，∥将ABE △沿AB 翻折得到'ABE △，∥'ABE ABF ∠=∠，∥'ABE BAF ∠=∠，∥'//BE AF ，又∥//AF CE ，∥'//BE CE ；。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题12 相似三角形中的旋转型相似模型【模型展示】如图，若△ABC∽△ADE，则△ABD∽△ACE.[一、单选题1．如图，正方形ABCD中，点F是BC边上一点，连接AF，以AF为对角线作正方形AEFG，边FG与正方形ABCD的对角线AC相交于点H，连接DG．以下四个结论：①EAB GAD∠=∠；①AFC AGD∆∆∽；①22AE AH AC=⋅；①DG AC⊥．其中正确的个数为（）A．1个B．2个C．3个D．4个【答案】D【分析】①四边形AEFG和四边形ABCD均为正方形，①EAB、①GAD与①BAG的和均为90°，即可证明①EAB与①GAD相等；①由题意易得AD=DC，AG=FG，进而可得AC AF AD AG=，①DAG=①CAF，然后问题可证；①由四边形AEFG和四边形ABCD均为正方形，可求证①HAF①①FAC，则有AF ACAH AF=，然后根据等量关系可求解；①由①及题意知①ADG=①ACF=45°，则问题可求证．【详解】解：①①四边形AEFG和四边形ABCD均为正方形①①EAG=①BAD=90°又①①EAB=90°-①BAG，①GAD=90°-①BAG①①EAB=①GAD①①正确①①四边形AEFG和四边形ABCD均为正方形①AD=DC ，AG=FG，①AC AD =AFAG=即AC AFAD AG= 又①①DAG+①GAC=①FAC+①GAC ①①DAG=①CAF ①AFC AGD ∆∆∽ ①①正确①①四边形AEFG 和四边形ABCD 均为正方形，AF 、AC 为对角线 ①①AFH=①ACF=45° 又①①FAH=①CAF ①①HAF①①FAC ①AF ACAH AF= 即2·AF AC AH =又 ①22AE AH AC =⋅ ①①正确①由①知AFC AGD ∆∆∽又①四边形ABCD 为正方形，为对角线 ①①ADG=①ACF=45°①DG 在正方形另外一条对角线上 ①DG①AC ①①正确故选：D ．【点睛】本题主要考查相似三角形的判定与性质综合运用，同时利用到正方形相关性质，解题关键在于找到需要的相似三角形进而证明．2．如图，在矩形ABCD 中，E 是AD 边的中点，BE ①AC 于点F ，连接DF ，给出下列四个结论：①①AEF ①①CAB ；①CF ＝2AF ；①DF ＝DC ；①S①ABF ：S 四边形CDEF ＝2：5，其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】D【分析】①根据四边形ABCD是矩形，BE①AC，可得①ABC=①AFB=90°，又①BAF=①CAB，于是①AEF①①CAB，故①正确；①根据点E是AD边的中点，以及AD①BC，得出①AEF①①CBF，根据相似三角形对应边成比例，可得CF=2AF，故①正确；①过D作DM①BE交AC于N，得到四边形BMDE是平行四边形，求出BM=DE=12BC，得到CN=NF，根据线段的垂直平分线的性质可得结论，故①正确；①根据①AEF①①CBF得到EF与BF的比值，以及AF与AC的比值，据此求出S①AEF=12S①ABF，S①ABF=16S矩形ABCD，可得S四边形CDEF=S①ACD-S①AEF=512S矩形ABCD，即可得到S四边形CDEF=52S①ABF，故①正确．【详解】如图，过D作DM①BE交AC于N，①四边形ABCD是矩形，①AD①BC，①ABC＝90°，AD＝BC，①BE①AC于点F，①①EAC＝①ACB，①ABC＝①AFE＝90°，①①AEF①①CAB，故①正确；①AD①BC，①①AEF①①CBF，①AEBC ＝AFCF，①AE＝12AD＝12BC，①AFCF ＝12，①CF＝2AF，故①正确，①DE①BM，BE①DM，①四边形BMDE是平行四边形，①BM＝DE＝12BC，①BM＝CM，①CN＝NF，①BE①AC于点F，DM①BE，①DN①CF，①DF＝DC，故①正确；①①AEF①①CBF，①EFBF＝AEBC＝12，①S①AEF＝12S①ABF，S①ABF＝16S矩形ABCD，①S①AEF＝112S矩形ABCD，又①S四边形CDEF＝S①ACD﹣S①AEF＝12S矩形ABCD﹣112S矩形ABCD＝512S矩形ABCD，①S①ABF：S四边形CDEF＝2：5，故①正确；故选D．【点睛】本题考查了相似三角形的判定和性质，矩形的性质，图形面积的计算，正确的作出辅助线是解题的关键．二、填空题3．已知正方形DEFG的顶点F在正方形ABCD的一边AD的延长线上，连结AG，CE交于点H，若3AB=，DE=CH的长为________.【分析】连接EG，与DF交于N，设CD和AH交于M，证明①ANG①ADM，得到DM AD NG AN=，从而求出DM的长，再通过勾股定理算出AM的长，通过证明①ADG①①CDE得到①DAG=①DCE，从而说明①ADM①①CHM，得到AD AMCH CM=，最后算出CH的长.【详解】解：连接EG，与DF交于N，设CD和AH交于M，①①GNA=90°，DN=FN=EN=GN，①①MAD=①GAN，①MDA=①GNA=90°，①①ANG①ADM，①DM ADNG AN=，①DE = ①DF=EG=2, ①DN=NG=1， ①AD=AB=3， ①3131DM =+，解得：DM=34，①MC=94，①①ADM+①MDG=①EDG+①CDG ， ①①ADG=①EDC ，在①ADG 和①CDE 中，AD CD ADG CDE DG DE =⎧⎪∠=∠⎨⎪=⎩， ①①ADG①①CDE （SAS ）， ①①DAG=①DCE ， ①①AMD=①CMH ， ①①ADM=①CHM=90°， ①①ADM①①CHM ， ①AD AMCH CM=，即3494CH=，解得：【点睛】本题考查了全等三角形的判定和性质，相似三角形的判定和性质，正方形的性质，勾股定理，综合性较强，解题的关键是找到合适的全等三角形和相似三角形，通过其性质计算出CH 的长.4．如图，正方形ABCD 的边长为8，线段CE 绕着点C 逆时针方向旋转，且3CE =，连接BE ，以BE 为边作正方形BEFG ，M 为AB 边的中点，当线段FM 的长最小时，tan ECB ∠=______．【答案】13【分析】连接BD ，BF ，FD ，证明①EBC①①FBD ，根据题意，知道M ，F ，D 三点一线时，FM 最小，然后过点M 作MG①BD ，垂足为G ，根据等腰直角三角形的性质、勾股定理分别求出MG 和DG 的长，再根据正切的定义计算即可．【详解】解：连接BD ，BF ，FD ，如图，①BD BFBC BE = ①BD BCBF BE=， ①①FBD+①DBE=45°，①EBC+①DBE=45°， ①①FBD=①EBC ， ①①EBC①①FBD ，①①FDB=①ECB ，DF BDCE BC==由题意知：FM 、DF 、DM 三条线段满足FM+DF≥MD ，其中DM 、DF 的值一定， ①当M ，F ，D 三点一线时，FM 最小，过点M 作MN①BD ，垂足为G ， ①①MBN=45°，BM=12AB=4，①tan tanMG ECB FDG=DG ∠=∠=13，故答案为：13．【点睛】本题考查了正方形的性质，手拉手相似模型，锐角三角函数，勾股定理，三角形面积，线段最值模型，熟练构造相似模型，准确确定线段最小值的条件是解题的关键． 5．如图，在矩形ABCD 中，E 是AD 边的中点，BE ①AC 于点F ，连接DF ，分析下列结论：①①AEF ①①CAB ；①CF ＝2AF ；①DF ＝DC ；①S 四边形CDEF ＝52S △ABF ，其中正确的结论有_______（填正确的序号）【答案】①①①①【分析】根据四边形ABCD 是矩形，BE AC ⊥，可得90ABC AFE ∠=∠=︒，又EAC ACB ∠=∠，于是ΔΔAEF CAB ∽，故①符合题意；根据点E 是AD 边的中点，以及//AD BC ，得出AEF CBF ∆∆∽，根据相似三角形对应边成比例，可得CF 2AF =，故①符合题意；过D 作//DM BE 交AC 于N ，得到四边形BMDE 是平行四边形，求出12BM DE BC ==，得到CN NF =，根据线段的垂直平分线的性质可得结论，故①符合题意；根据AEF CBF ∆∆∽得到EF 与BF 的比值，以及AF 与AC 的比值，据此求出ΔΔ12AEF ABF S S =，Δ16ABF ABCD S S =矩形，可得ΔΔ512ACD AEF ABCD CDEF S S S S =-=矩形四边形，即可得到Δ52ABF CDEF S S =四边形，故①符合题意．【详解】解：如图，过D 作DM BE ∥交AC 于N ，交BC 于M ，四边形ABCD 是矩形，①AD BC ∥，90ABC ∠=︒，AD BC =，EAC ACB ∴∠=∠，BE AC ⊥于点F ，90ABC AFE ∴∠=∠=︒，ΔΔAEF CAB ∴∽，故①符合题意；①,AD BC AD BC =∥，AEF CBF ∴∆∆∽，而E 是AD 的中点，∴12AE AF BC FC ==， ∴12AF CF =， 2CF AF ∴=，故①符合题意；①,DE BM DM BE ∥∥， ∴四边形BMDE 是平行四边形， 12BM DE BC ∴==， BM CM ∴=，CN NF =，BE AC ⊥于点F ，DM BE ∥，DN CF ∴⊥， DN ∴垂直平分CF ， DF DC ∴=，故①符合题意； ΔΔAEF CBF ∽，∴AF FC =12EF AE BF BC ==，ΔΔ12AEF ABF S S ∴=，111236ABFBFCABCABCDS S S S 矩形， Δ112AEF ABCDS S ∴=矩形，又ΔΔ11521212ACD AEF ABCD ABCD ABCD CDEF S S S S S S =-=-=矩形矩形矩形四边形， Δ52ABF CDEF S S ∴=四边形，故①符合题意；故答案①①①①．【点睛】本题属于四边形综合题，主要考查了相似三角形的判定和性质，矩形的性质，图形面积的计算的综合应用，正确作出辅助线是解题的关键．解题时注意，相似三角形的对应边成比例．6．如图，正方形ABCD 中，点F 是BC 边上一点，连接AF ，以AF 为对角线作正方形AEFG ，边FG 与AC 相交于点H ，连接DG ．以下四个结论： ①①EAB ＝①BFE ＝①DAG ； ①①ACF ①①ADG ； ①2AH AC ⋅； ①DG ①AC ．其中正确的是_____．（写出所有正确结论的序号）【答案】①①①【分析】根据正方形的性质可知90B E ∠=∠=︒，有对顶角相等，可证①EAB ＝①BFE ，由90EAG BAD ∠=∠=︒可证①EAB ＝①DAG ，可判断结论①正确；由AC AFAD AG==FAC GAD ∠=∠，两边对应成比例且夹角相等即可得①ACF ①①ADG ，可判断结论①正确；由结论①可知45ACF ADG ∠=∠=︒，可得DG 平分ADC ∠，由正方形可知ACD 是等腰直角三角形，可推出DG ①AC ，结论①正确；利用两组角对应相等的两个三角形相似可得①ACF ①①AFH ，根据相似的性质可得AH AFAF AC=，则2AH AC AF ⋅＝，又有222AF AE ＝，则结论①错误．【详解】解：设AB 与EF 相交于点O ，如图所示，①四边形ABCD 和四边形AEFG 都是正方形， ①90B E ∠=∠=︒，90EAG BAD ∠=∠=︒．又①AOE BOF ∠=∠， ①EAB BFE ∠∠＝．①EAG BAG BAD BAG ∠-∠=∠-∠， ①EAB DAG ∠∠＝， ①EAB BFE DAG ∠∠∠＝＝，故结论①正确；①AC 、AF 是正方形ABCD 和正方形AEFG 的对角线，①AC =，AF =，①AC AFAD AG= 又①45FAG CAD ∠=∠=︒，①FAG GAH CAD GAH ∠-∠=∠-∠，即FAC GAD ∠=∠． ①①ACF ①①ADG ．故结论①正确；由①ACF ①①ADG 可知45ADG ACF ∠=∠=︒， ①DG 平分ADC ∠． ①ACD 是等腰直角三角形， ①DG ①AC ．故结论①正确；①FAC HAF ∠=∠，45ACF AFH ∠=∠=︒， ①①ACF ①①AFH ， ①AH AFAF AC=，①2AH AC AF ⋅＝．①在等腰直角AEF △中，222AF AE ＝，①22AH AC AE ⋅＝，故结论①错误，①正确的结论是①①①，故答案为：①①①．【点睛】本题考查了正方形的性质，相似三角形的判定和性质，等腰直角三角形的判定和性质以及勾股定理，熟练掌握相似三角形的判定定理证明三角形相似是解题的关键． 7．如图，在一个1213⨯的网格中，点,,O A B 都在格点上，8OA AB ==，点P 是线段AB 上的一个动点，连接OP ，将线段OA 沿直线OP 进行翻折，点A 落在点C 处，连接BC ，以BC 为斜边在直线BC 的左侧（或下方）构造等腰直角三角形BDC ，则点P 从A 运动到B 的过程中，线段BC 的长的最小值为____________，线段BD 所扫过的区域内的格点的个数为（不包含所扫过的区域边界上的点）____________．【答案】 8 4【分析】根据OB OC BC -≤仅当C 在OB 上时等号成立，由折叠性质可知OA =OC ，从而求出BC 的最小值；再证明OCB ADB △△，：1，从而得出点D 为半径的圆弧01D D 上运动，由此画出图形即可得出格点的个数．【详解】解：如图，连接OB ，AD ．①8OA AB ==，90OAB ∠=︒①OB =又①OB OC BC -≤仅当C 在OB 上时等号成立，①BC 的最小值OB OC =-，又①8OC OA ==，①BC 的最小值8OB OC =-=，①OAB 和BDC 均为等腰直角三角形，①45OBA CBD ∠=∠=︒，OB BC AB == 又①OBA ABC OBC ∠=∠+∠，DBC ABC ABD ∠∠+∠=，①OBC ABD ∠=∠，①OCB ADB △△，①OC BC AD BD ==2AD ==①如图：点D 为半径的圆弧01D D 上运动，当点P 与点A 重合时，点D 在0D 处，当点P 与点B 重合时，点D 在1D 处，①线段BD 所扫过的区域内的格点的个数为（不包含所扫过的区域边界上的点）4个．故答案为：8-，4．【点睛】本题主要考查了对称变换和旋转相似，解题关键是通过旋转相似证明AD ==，从而得出点D 为半径的圆弧01D D 上运动，再根据画图得出结论．三、解答题8．【问题发现】如图1，在Rt①ABC中，①BAC＝90°，AB＝AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是______，位置关系是______；【探究证明】如图2，在Rt①ABC和Rt①ADE中，①BAC＝①DAE＝90°，AB＝AC，AD＝AE，将①ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；【拓展延伸】如图3，在Rt①BCD中，①BCD＝90°，BC＝2CD＝4，过点C作CA①BD于A．将①ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角①CAE为α（0°＜α＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．【答案】BD＝CE，BD①CE；BD①CE，理由见解析；图见解析，12 5【分析】（1）证明①BAD①①CAE，根据全等三角形的性质解答；（2）连接BD，根据全等三角形的判定和性质以及垂直的定义即可得到结论；（3）如图3，过A作AF①EC，根据相似三角形的判定和性质以及勾股定理即可得到结论．【详解】解：（1）BD＝CE，BD①CE；（2）BD①CE．理由如下：在Rt①ABC和Rt①ADE中，AB＝AC，AD＝AE，①AEC＝45°，①①CAB ＝①DAE＝90°，①①BAD＝①CAE，①①CEA①①BDA，①①BDA＝①AEC＝45°，①①BDE＝①BDA＋①ADE＝90°，①BD①CE．（3）如图所示，过点A作AF①CE，垂足为点F．根据题意可知，Rt①ABC①Rt①AED，①BAC＝①EAD，①AB ACAE AD=，①AB AEAC AD=．①①BAC＝①EAD＝90°，①①BAE＝①CAD，①①BAE①①CAD，①①BEA＝①CDA，①BEC＋①DEA＝①DEA＋90°，①①BEC＝90°，①BE①CE．在旋转前，在Rt①BCD中，①BCD＝90°，BC＝2CD＝4，①BD①AC①BD，①1122BCDS BD AC BD AC=⋅=⋅，①AC①AD=在Rt①ACD中，CD边上的高45AC ADhCD⋅==，旋转后，得45AF h==，1625CE CF====①125BE==．【点睛】本题是几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，等腰三角形的性质等知识点，关键是添加恰当辅助线．9．如图，在正方形ABCD中，点P在对角线BD上，直线AP交CD于E，PF①AE交BC于点F，连接AF交BD于M．(1)判断①APF的形状，并说明理由；(2)连接EF，求EF:PM的值．【答案】(1)①APF是等腰直角三角形，理由见解析(2)EF：PM=2（1）过点P作PG①BC于点G，交AD于点H，根据正方形的性质证明①APH①①PFG，【分析】即可得结论；（2）将①ADE绕点A顺时针旋转90°得到①ABN，利用全等三角形的性质证明①AFN=①AFE，然后证明①APM①①AFE，可得EF：PM=AP：AF，根据①APF是等腰直角三角形，进而可以解决问题．（1）解：①APF是等腰直角三角形，理由如下：如图，过点P作PG①BC于点G，交AD于点H，①GH=CD，①四边形ABCD是正方形，①①ADB=45°，AD=CD，①①PHD=90°，①①HPD=45°，①HD=HP，①AH=GP，①PF ①AE ，①①APF =90°，①①APH +①FPG =90°，①①P AH +①APH =90°，①①P AH =①FPG ，在①APH 和①PFG 中，90PAH FPG AH PG AHP PGF ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ①①APH ①①PFG （ASA ），①AP =FP ，①①APF 是等腰直角三角形；（2）解：如图，将①ADE 绕点A 顺时针旋转90°得到①ABN ，①①ADE =①ABN =90°，①ABC =90°，①①ABC +①ABN =180°，①C ，B ，N 共线，①①EAF =45°，①①NAF =①F AB +①BAN =①F AB +①DAE =45°，①①F AE =①F AN ，在①F AN 和①F AE 中，AF AF FAN FAE AN AE =⎧⎪∠=∠⎨⎪=⎩，①①F AN ①①F AE （SAS ），①①AFN =①AFE ，①①FMB =①AMP ，①MBF =①P AM =45°，①①BFM =①APM ，①①APM =①AFE ，①①APM ①①AFE ，①EF ：PM =AP ：AF ，由（1）知：①APF 是等腰直角三角形，①AF：AP =2①EF ：PM =2．【点睛】本题属于几何综合题，考查正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形或相似三角形解决问题，属于中考题的压轴题．10．某校数学活动小组探究了如下数学问题：(1)问题发现：如图1，ABC 中，90BAC ∠=︒，AB AC =．点P 是底边BC 上一点，连接AP ，以AP 为腰作等腰Rt APQ △，且90PAQ ∠=︒，连接CQ 、则BP 和CQ 的数量关系是______；(2)变式探究：如图2，ABC 中，90BAC ∠=︒，AB AC =．点P 是腰AB 上一点，连接CP ，以CP 为底边作等腰Rt CPQ △，连接AQ ，判断BP 和AQ 的数量关系，并说明理由；(3)问题解决：如图3，在正方形ABCD 中，点P 是边BC 上一点，以DP 为边作正方形DPEF ，点Q 是正方形DPEF 两条对角线的交点，连接CQ ．若正方形DPEF CQ =求正方形ABCD 的边长．【答案】(1)BP CQ =(2)BP =(3)3【分析】（1）根据已知条件利用边角边证明ABP ACQ ≌，再利用全等三角形的性质即可得到BP 和CQ 的数量关系；（2）根据任意等腰直角三角形的直角边与斜边的比是相等的，利用两边长比例且夹角相等的判定定理证明CBP CAQ △∽△，之后再由相似三角形对应边成比例即可得到BP 和AQ 的数量关系；（3）连接BD ，如图（见详解），先由正方形的性质判断出BCD △和PQD △都是等腰直角三角形，再利用与第二问同样的方法证出BDP CDQ △∽△，由对应边成比例，依据相似比求出线段BP 的长，接着设正方形ABCD 的边长为x ，运用勾股定理列出方程即可求得答案．（1）解：①APQ △是等腰直角三角形，90PAQ ∠=︒，在ABC 中，90BAC ∠=︒，AB AC =，①AP AQ =，BAP PAC CAQ PAC ∠+∠=∠+∠，①BAP CAQ ∠=∠．在ABP 和ACQ 中，AB AC BAP CAQ AP AQ =⎧⎪∠=∠⎨⎪=⎩，①()ABP ACQ SAS △≌△，①BP CQ =；（2）解：判断BP =，理由如下：①CPQ 是等腰直角三角形，ABC 中，90BAC ∠=︒，AB AC =，①QC AC PC BC ==45ACB QCP ∠=∠=︒．①45BCP ACP ACQ ACP ∠+∠=∠+∠=︒，①BCP ACQ ∠=∠，①CBP CAQ △∽△，①QC AC AQ PC BC BP ===①BP =；（3）解：连接BD ，如图所示，①四边形ABCD 与四边形DPEF是正方形，DE 与PF 交于点Q ，①BCD △和PQD △都是等腰直角三角形，①22QD CD PD BD ==，45BDC PDQ ∠=∠=︒．①45BDP PDC CDQ PDC ∠+∠=∠+∠=︒，①BDP CDQ ∠=∠，①BDP CDQ △∽△，①22QD CD CQ PD BD BP ===．①2CQ =，①22BP CQ ==．在Rt PCD △中，222CD CP DP +=，设CD x =，则2CP x =-，又①正方形DPEF 的边长为10，①10DP =，①222(2)(10)x x +-=，解得11x =-（舍去），23x =．①正方形ABCD 的边长为3．【点睛】本题是一道几何综合题，考查了全等三角形，相似三角形的判定和性质，以及正方形和等腰三角形的性质，正确识图并能熟练地掌握几何图形的性质与判定定理进行证明是解题的关键．11．［问题发现］(1)如图1，在Rt△ABC 中，AB AC =，90BAC ∠=︒，点D 为BC 的中点，以CD 为一边作正方形CDEF ，点E 与点A 重合，已知ACF BCE ∆∆∽．请直接写出线段BE 与AF 的数量关系；［实验研究］(2)在（1）的条件下，将正方形CDEF 绕点C 旋转至如图2所示的位置，连接BE ，CE ，AF ．请猜想线段BE 和AF 的数量关系，并证明你的结论；［结论运用］(3)在（1）（2）的条件下，若ABC ∆的面积为8，当正方形CDEF 旋转到B ，E ，F 三点共线时，请求出线段AF 的长．【答案】(1)BE = (2)BE =，证明见解析(3)线段AF 的长为2或2【分析】(1)先判断出①ABD 为等腰直角三角形，进而求出AB ，即可得出结论；(2)先利用三角函数得出AC FC BC EC=，证明夹角相等即可得出①ACF ①①BCE ，进而求出结论；(3)分两种情况计算，当点E 在线段BF 上时，先用勾股定理求出EF CF AD ===BF BE =(2)得出结论；当点E 在线段BF 延长线上同前一种情况一样即可得出结论．（1）解：AB AC =，90BAC ∠=︒，45B ACB ∴∠=∠=︒，四边形CDEF 是正方形，EF CF ∴=，90F ∠=︒，45FEC FCE ∴∠=∠=︒，FEC B ∴∠=∠，FCE ACB ∠=∠，点E 与点A 重合，FEC FAC B ∴∠=∠=∠，FCE FCA ACB ∠=∠=∠，AB BE =，ACF BCE ∴∆∆∽；∴AF AC AB BC=，sin sin 45AC B BC ==︒∴AF BE ，BE ∴=；（2）解：BE =．证明：由（1）得，sin sin 45AC B BC ==︒= 四边形CDEF 是正方形，EF CF ∴=，90EFC ∠=︒，45FEC FCE ∴∠=∠=︒，∴sin sin 45FC FEC EC =∠=︒∴AC FC BC EC = 45ACF BCE ACE ∠=∠=︒-∠，ACF BCE ∴∆∆∽，∴AF AC BE BC ==BE ∴=；（3）解：如图1，AB AC =，90BAC ∠=︒，点D 为BC 的中点， 12AD BC ∴=，AD BC ⊥， 2BC AD ∴=，ABC ∆的面积为8， ∴182BC AD ⋅=，28AD ∴=，AD ∴=BC ∴=点E 与点A 重合，四边形CDEF 是正方形，EF CF DE AD ∴====如图2，B 、E 、F 三点共线且点E 在线段BF 上，∠=︒，BFC90∴，BF∴=-=BE BF EF2BE=．∴=∴=；AF2如图3，B、E、F三点共线且点F在线段BE上，则=+=BE BF EFBE=．2∴=，∴=，2AF综上所述，线段AF的长为2或2．【点睛】本题考查了相似三角形的判定和性质，以及等腰直角三角形的性质，正方形性质和旋转性质，分类讨论和画出图形是解决本题的关键．12．如图1，已知点G在正方形ABCD的对角线AC上，GE①BC，垂足为点E，GF①CD，垂足为点F．（1）证明：四边形CEGF是正方形；（2）探究与证明：将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；（3）拓展与运用：正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图3所示，当B，E，F三点在一条直线上时，延长CG交AD于点H，若AG＝9，GH＝BC 的长．【答案】（1）答案见解析；（2）AG；理由见解析；（3）BC．【分析】（1）先说明GE①BC、GF①CD，再结合①BCD=90°可证四边形CEGF是矩形，再由①ECG=45°即可证明；（2）连接CG，证明①ACG①①BCE，再应用相似三角形的性质解答即可；（3）先证①AHG①①CHA可得AG GH AHAC AH CH==，设BC＝CD＝AD＝a，则AC＝a，求出AH＝23a，DH＝13a，CH最后代入即可求得a的值．【详解】（1）①四边形ABCD是正方形，①①BCD＝90°，①BCA＝45°，①GE①BC、GF①CD，①①CEG＝①CFG＝①ECF＝90°，①四边形CEGF是矩形，①CGE＝①ECG＝45°，①EG＝EC，①四边形CEGF是正方形．（2）结论：AG；理由：连接CG，由旋转性质知①BCE＝①ACG＝α，在Rt ①CEG 和Rt ①CBA 中，CE CG ＝cos45°， CB CA ＝cos45°①CG CA CE CB== ①①ACG ①①BCE ，①AG CA BE CB==①线段AG 与BE 之间的数量关系为AGBE ；（3）①①CEF ＝45°，点B 、E 、F 三点共线，①①BEC ＝135°，①①ACG ①①BCE ，①①AGC ＝①BEC ＝135°，①①AGH ＝①CAH ＝45°，①①CHA ＝①AHG ，①①AHG ①①CHA ， ①AG GH AH AC AH CH==，设BC ＝CD ＝AD ＝a ，则ACa ，由AG GH AC AH =9AH =， ①AH ＝23a ，则DH ＝AD ﹣AH ＝13a，CH ==， ①AG AH AC CH =，得29a = 解得：aBC【点睛】本题属于四边形综合题，主要考查相似形的判定和性质、正方形的性质等知识点，解题的关键是正确寻找相似三角形解决问题并利用参数构建方程解决问题．13．如图，ABC 和ADE 是有公共顶点直角三角形，90BAC DAE ∠=∠=︒，点P 为射线BD ，CE 的交点．（1）如图1，若ABC 和ADE 是等腰直角三角形，求证：CP BD ⊥；（2）如图2，若30ADE ABC ∠=∠=︒，问：（1）中的结论是否成立？请说明理由．（3）在（1）的条件下，4AB =，3AD =，若把ADE 绕点A 旋转，当90EAC ∠=︒时，请直接写出PB 的长度【答案】（1）见解析；（2）成立，理由见解析；（3）PB 的长为45或285．【分析】（1）由条件证明①ABD ①①ACE ，即可得①ABD =①ACE ，可得出①BPC =90°，进而得出BD ①CP ；（2）先判断出①ADB ①①AEC ，即可得出结论；(3) 分为点E 在AB 上和点E 在AB 的延长线上两种情况画出图形，然后再证明①PEB ①①AEC ，最后依据相似三角形的性质进行证明即可．【详解】解：（1）证明：如图，①①BAC =①DAE =90°，①①BAE +①CAE =①BAD +①BAE ，即①BAD =①CAE ．①ABC 和ADE 是等腰直角三角形，①AD AE =，AB AC =在①ABD 和①ACE 中，AD AE BAD CAE AB AC ⎧⎪∠∠⎨⎪⎩＝＝＝， ①①ABD ①①ACE （SAS ），①①ABD =①ACE ．①①CAB =90°，①①ACF +①AFC =90°，①①ABP +①BFP =90°．①①BPF =90°，①BD ①CP ；（2）（1）中结论成立，理由：在Rt ①ABC 中，①ABC =30°，①AB ，在Rt ①ADE 中，①ADE =30°，①AD ， ①AD AE AB AC= ①①BAC =①DAE =90°，①①BAD =①CAE ，①①ADB ①①AEC ．①①ABD =①ACE同（1）得CP BD ⊥；（3）解：①ABC 和ADE 是等腰直角三角形，①=3AD AE =，=4AB AC =①当点E 在AB 上时，BE =AC -AE =1．①①EAC =90°，①CE ．同（1）可证①ADB ①①AEC ．①①DBA =①ECA ．①①PEB =①AEC ，①①PEB ①①AEC ． ①PB BE AC CE = ①145PB =． ①PB =45．①当点E 在BA 延长线上时，BE =5．①①EAC =90°，①CE =5．同（1）可证①ADB ①①AEC ．①①DBA =①ECA ．①①BEP =①CEA ，①①PEB ①①AEC ． ①PB BE AC CE =． ①745PB =． ①PB =285．综上所述，PB 的长为45或285．【点睛】此题主要考查的是旋转的性质、等腰三角形的性质、全等三角形的性质和判定、相似三角形的性质和判定，证明得①PEB ①①AEC 是解题的关键．14．一次小组合作探究课上，老师将两个正方形按如图所示的位置摆放（点E 、A 、D 在同一条直线上），发现BE DG =且BE DG ⊥．小组讨论后，提出了下列三个问题，请你帮助解答：（1）将正方形AEFG 绕点A 按逆时针方向旋转（如图1），还能得到BE DG =吗？若能，请给出证明，请说明理由；（2）把背景中的正方形分别改成菱形AEFG 和菱形ABCD ，将菱形AEFG 绕点A 按顺时针方向旋转（如图2），试问当EAG ∠与BAD ∠的大小满足怎样的关系时，BE DG =；（3）把背景中的正方形分别改写成矩形AEFG 和矩形ABCD ，且23AE AB AG AD ==，2AE a =，2AB b =（如图3），连接DE ，BG ．试求22DE BG +的值（用a ，b 表示）．【答案】（1）见解析；（2）当EAG BAD ∠=∠时，BE DG =，理由见解析；（3）221313a b +．【分析】（1）由正方形的性质得出AE AG =，90EAG ∠=︒，AB AD =，90BAD ∠=︒，得出EAB GAD ∠=∠，则可证明()AEB AGD SAS ≌△△，从而可得出结论；（2）由菱形的性质得出AE AG =，AB AD =，则可证明()AEB AGD SAS ≌△△，由全等三角形的性质可得出结论；（3）设BE 与DG 交于Q ，BE 与AG 交于点P ，证明EAB GAD ∽△△，得出EBA GDA ∠=∠，得出GD EB ⊥，连接EG ，BD ，由勾股定理可求出答案．【详解】（1）①四边形AEFG 为正方形，①AE AG =，90EAG ∠=︒，又①四边形ABCD 为正方形，①AB AD =，90BAD ∠=︒，①EAG BAG BAD BAG ∠-∠=∠-∠①EAB GAD ∠=∠，在①AEB 和①AGD 中，AE AG EAB GAD AB AD =⎧⎪∠=∠⎨⎪=⎩，①()AEB AGD SAS ≌△△， ①BE DG =；（2）当EAG BAD ∠=∠时，BE DG =，理由如下：①EAG BAD ∠=∠，①+EAG BAG BAD BAG ∠∠=∠+∠①EAB GAD ∠=∠，又①四边形AEFG 和四边形ABCD 均为菱形，①AE AG =，AB AD =，在①AEB 和①AGD 中，AE AG EAB GAD AB AD =⎧⎪∠=∠⎨⎪=⎩，①()AEB AGD SAS ≌△△， ①BE DG =；（3）设BE 与DG 交于Q ，BE 与AG 交于点P ，由题意知，2AE a =， ①23AE AB AG AD ==，90EAB GDA GAB ∠=∠=︒+∠， ①EAB GAD ∽△△，①EBA GDA ∠=∠，①++90ADB ABD GDA QDB ABD ∠+∠=∠∠∠=︒，①+++90QDB QBD EBA QDB ABD ∠∠=∠∠∠=︒，①GD EB ⊥，连接EG ，BD ，①22ED GB +2222EQ QD GQ QB =+++22EG BD =+， ①23AE AB AG AD ==，2AE a =，2AB b =， ①3AG a =，3AD b =，在Rt ①EAG 中，由勾股定理得：222+EG AE AG =，同理222+BD AB AD =，①22ED GB +()()()()22222323a a b b =+++221313a b =+．【点睛】本题考查了矩形、菱形、正方形的性质，三角形全等的判定与性质，三角形相似的判定与性质，勾股定理等知识，熟练掌握特殊平行四边形的性质是解题的关键．由(3)可得结论：当四边形的对角线相互垂直时，四边形两组对边的平方和相等．15．在①ABC 中，AB ＝AC ，①BAC ＝α，点P 是①ABC 外一点，连接BP ，将线段BP 绕点P 逆时针旋转α得到线段PD ，连接BD ，CD ，AP ．（1）如图1，当α＝60°时，CD AP的值为，直线CD 与 AP 所成的较小角的度数为 °；类比探究：（2）如图2，当α＝90°时，求出CD AP 的值及直线CD 与AP 所成的较小角的度数；拓展应用：（3）如图3，当α＝90°时，点E ，F 分别为AB ，AC 的中点，点P 在线段FE 的延长线上，点A ，D ，P 三点在一条直线上，BD 交PF 于点G ，CD 交AB 于点H . 若CD ＝2BD 的长．【答案】（1）1，60；（2）CD AP，直线CD 与AP 所成的较小角的度数为45°；（3）BD【分析】（1）根据α＝60°时，①ABC 是等边三角形，再证明①PBA①①DBC ，即可求解，再得到直线CD 与 AP 所成的度数；（2）根据等腰直角三角形的性质证明①PBA①①DBC ，再得到CD AP =BC AB ，再根据相似三角形的性质求出直线CD 与 AP 所成的度数；（3）延长CA ，BD 相交于点K ，根据直角三角形斜边上的中线性质及中位线定理证得①BCD ＝①KCD ，由（2）的结论求出AP 的长，再利用在Rt ①PBD 中，设PB ＝PD ＝x ，由勾股定理可得BD ＝AD ，再列出方程即可求出x ，故可得到BD 的长．【详解】（1）①α＝60°，AB ＝AC ，①①ABC 是等边三角形，①AB =CB①将线段BP 绕点P 逆时针旋转α得到线段PD ，①①BDP 是等边三角形，①BP =BD①①PBA =①PBD -①ABD =60°-①ABD ，①DBC =①ABC -①ABD =60°-①ABD ，①①PBA =①DBC①①PBA ①①DBC ，①CD AP=1 如图，延长CD 交AB ，AP 分别于点G ，H ，则①AHC 为直线CD 与AP 所成的较小角， ①①PBA ①△DBC①①P AB =①DCB①①HGA =①BGC①①AHC ＝①ABC ＝60°故答案为：1，60；（2）解：如图，延长CD 交AB ，AP 分别于点M ，N ，则①ANC 为直线CD 与AP 所成的较小角，①AB ＝AC ，①BAC ＝90°，①①ABC ＝45°.在Rt ①ABC 中，AB BC ＝cos①ABC ＝cos45° ①PB ＝PD ，①BPD ＝90°，①①PBD ＝①PDB ＝45°.在Rt ①PBD 中，PB BD ＝cos①PBD ＝cos45°＝2.①AB BC ＝PB BD ，①ABC ＝①PBD . ①①ABC －①ABD ＝①PBD －①ABD .即①PBA ＝①DBC .①①PBA ①①DBC . ①CDAP ＝BC AB ，①P AB ＝①DCB . ①①AMN ＝①CMB ，①①ANC ＝①ABC ＝45°.即CD AP CD 与AP 所成的较小角的度数为45°. (3)延长CA ，BD 相交于点K ，如图.①①APB ＝90°，E 为AB 的中点，①EP ＝EA ＝EB .①①EAP ＝①EP A ，①EBP ＝①EPB.①点E ，F 为AB ，AC 的中点，①PF //BC .①①AFP ＝①ACB ＝①PBD ＝45°.①①BGP ＝①FGK ，①①BPE ＝①K .①①K ＝①EBP ，①①EBP ＝①PEB ，①PEB=①DBC ，①①K ＝①CBD .①CB ＝CK .①①BCD ＝①KCD .由(2)知①ADC ＝①PDB ＝45°，①PBA ①①DBC ，①①P AB ＝①DCB .①①BDC ＝180°－45°－45°＝90°＝①BAC .①①BHD ＝①CHA ，①①DBA ＝①DCA .①①DBA ＝①P AB.①AD ＝BD .由(2)知DC AP ，①AP 1=在Rt ①PBD 中，PB ＝PD ＝x ，由勾股定理可得BD ＝AD .①AD＋PD ＝x x ＝AP ＝1.①x ＝1.①BD【点睛】此题主要考查四边形综合，解题的关键熟知旋转的性质、全等三角形的判定与性质、相似三角形的判定与性质及解直角三角形的方法．16．如图，正方形ABCD ，对角线AC ，BD 相交于O ，Q 为线段DB 上的一点，90MQN ∠=︒，点M 、N 分别在直线BC 、DC 上．（1）如图1，当Q 为线段OD 的中点时，求证：1132DN BM BC +=；（2）如图2，当Q 为线段OB 的中点，点N 在CD 的延长线上时，则线段DN 、BM 、BC 的数量关系为；（3）在（2）的条件下，连接MN ，交AD 、BD 于点E 、F ，若:3:1MB MC =，NQ =求EF 的长．【答案】（1）见解析；（2）BM −13DN =12BC ；（3）EF ．【分析】（1）如图1，过Q 点作QP ①BD 交DC 于P ，然后根据正方形的性质证明①QPN ①①QBM ，就可以得出结论；（2）如图2，过Q 点作QH ①BD 交BC 于H ，通过证明①QHM ①①QDN ，由相似三角形的性质就可以得出结论；（3）由条件设CM =x ，MB =3x ，就用CB =4x ，得出BH =2x ，由（2）相似的性质可以求出MQ 的值，再根据勾股定理就可以求出MN 的值，可以表示出ND ，由①NDE ①①NCM 就可以求出NE ，也可以表示出DE ，最后由①DEF ①①BMF 而求出结论．【详解】解：（1）如图，过Q点作QP①BD交DC于P，①①PQB=90°．①①MQN=90°，①①NQP=①MQB，①四边形ABCD是正方形，①CD=CB，①BDC=①DBC=45°．DO=BO，①①DPQ=45°，DQ=PQ，①①DPQ=①DBC=45°，①①QPN①①QBM，①NP PQ MB QB=，①Q是OD的中点，且PQ①BD，①DO=2DQ，DP=12 DC，①BQ=3DQ，DN+NP=12DC=12BC，①BQ=3PQ，①13 NPMB=，①NP=13 BM，①DN+13BM=12BC；（2）如图，过Q点作QH①BD交BC于H，①①BQH=①DQH=90°，①①BHQ=45°，①①COB=90°，①QH①OC，①Q是OB的中点，①BH=CH=12 BC，①①NQM=90°，①①NQD=①MQH，①①QND+①NQD=45°，①MQH+①QMH=45°，①①QND=①QMH，①①QHM①①QDN，①13 HM QH QMND DQ NQ===，①HM=13 ND，①BM-HM=HB，①BM−13DN=12BC．故答案为：BM−13DN=12BC；（3）①MB：MC=3：1，设CM=x，①MB=3x，①CB=CD=4x，①HB=2x，①HM=x．①HM=13 ND，①ND=3x，①CN=7x，①四边形ABCD是正方形，①ED①BC，①①NDE①①NCM，①DEF①①BMF，①ND DE NE DE EF CN CM NM BM FM ===，，①33 77x DE NEx x NM==，，①DE=37 x，①31737EF x FM ==，①NQ①QM在Rt ①MNQ 中，由勾股定理得：MN = 37=，①NE =，①7EM =，设EF =a ，则FM =7a ，①7a a +=①a =．①EF ．【点睛】本题考查了正方形的性质的运用，相似三角形的判定和性质的运用，勾股定理的运在解答时利用三角形相似的性质求出线段的比是解答本题的关键．17．如图，以ABC 的两边AB 、AC 分别向外作等边ABD △和等边ACE △，BE 与CD 交于点P ，已知3PA =，4PB =，5PC =．（1）求证：ADC ABE ≅；（2）求DPB ∠的度数及BE 的长；（3）若点Q 、R 分别是等边ABD △和等边ACE △的重心（三边中线的交点），连接AQ 、AR 、QR ，作出图象，求QR 的长．【答案】（1）见解析；（2）60°，12；（3）【分析】（1）根据等边三角形的性质得到AD=AB ，AE=AC ，①DAB=①EAC=①AEC=①ACE=60°，得到①DAC=①BAE ，即可证明①ADC①①ABE ；（2）根据全等三角形的性质得到①ADP=①ABP ，设AB ，PD 交于O ，根据三角形的内角和即可得到①DPB=①DAB=60°；在PE 上取点F ，使①PCF=60°，根据全等三角形的性质和等边三角形的性质即可得到结论；（3）过点Q 作QG①AD 于G ，设QG=x ，根据等边三角形的性质得到AQ=2x ，，AB=，证明①ABE①①AQR ，根据相似三角形的性质即可得到结论．【详解】解：（1）①①ABD 和①ACE 都为等边三角形，①AD=AB ，AE=AC ，①DAB=①EAC=①AEC=①ACE=60°，①①DAB+①BAC=①EAC+①BAC ，即①DAC=①BAE ，在①ADC 与①ABE 中，AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩，①①ADC①①ABE （SAS ）；（2）①①ADC①①ABE ；①①ADP=①ABP ，设AB ，PD 交于O ，①①AOD=①POB ，①①DPB=①DAB=60°；如图①，在PE 上取点F ，使①PCF=60°，同（1）可得①APC①①EFC，①EPC=①EAC=60°，①EF=AP=3，①CPF为等边三角形，①BE=PB+PF+FE=4+5+3=12；（3）如图①，过点Q作QG①AD于G，设QG=x，①点Q、R分别是等边①ABD和等边①ACE的重心，①AQ=2x，，AB=，①AQ AR=，①QAR=①QAB+①BAC+①RAC=30°+①BAC+30°=60°+①BAC，AB AE①①QAR=①BAE，①①ABE①①AQR，①QR：BE=AQ：AB，①QR==12【点睛】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，等边三角形的性质，正确的识别图形是解题的关键．18．在矩形ABCD中，:1:2AB BC=，点M为AD的中点，点P为对角线BD的中点，点E、⊥．F分别在边AB、AD上，且PE PF。