(附精选七套模拟卷)上海市杨浦区2019年高一数学下学期期末调研测试模拟试题
(9份试卷汇总)2019-2020学年上海市杨浦区数学高一(上)期末达标检测模拟试题

2019-2020学年高一数学上学期期末试卷一、选择题1.已知函数()f x 是定义在R 上的奇函数,当0x >时,()12log 2,011,1x x f x x x +<<⎧⎪=⎨⎪+≥⎩,若()4f a =-,则a =( )A.14-B.3-C.14-或3 D.14-或3- 2.函数()()2ln 3,(0)33,0x x x x xf x x -+>-⎧⎪=-≤⎨⎪⎩的零点个数为( )A .0B .1C .2D .33.已知α满足sinα>0,tanα<0,化简表达式cos 11sin sin ααα-+-12sin cos αα-为( )A.12sin cos αα-+B.1cos α--C.2sin cos l αα--D.cos 1α-4.已知a r ,b r 都为单位向量,且a r ,b r夹角的余弦值是45,则2(a b -=r r )A .45B .95C .25D .355.已知函数lg(1),0()1lg ,01x x f x x x+≥⎧⎪=⎨<⎪-⎩,且0a b +>,0b c +>,0c a +>,则()()()f a f b f c ++的值( ) A.恒为正 B.恒为负 C.恒为0 D.无法确定 6.等比数列{a n }中,T n 表示前n 项的积,若T 5=1,则( )A .a 1=1B .a 3=1C .a 4=1D .a 5=17.要得到2sin(2)3y x π=-的图像, 需要将函数sin 2y x =的图像( ) A.向左平移23π个单位 B.向右平移23π个单位C.向左平移3π个单位 D.向右平移3π个单位 8.下列函数中,在区间上为增函数的是 A .B .C .D .9.若函数(,且)在上的最大值为4,且函数在上是减函数,则实数的取值范围为( )A .B .C .D .10.函数()()lg 72f x x g x x ==-与图象交点的横坐标所在区间是( ) A .(1,2)B .(2,3)C .(3,4)D .(1,5)11.已知2()sin ()4f x x π=+,若1(lg5),(lg )5a f b f ==,则( )A .0a b +=B .0a b -=C .1a b +=D .1a b -=12.函数22x y x =-的图象大致是()A .B .C .D .二、填空题13.如图,棱长为1(单位:cm )的正方体木块经过适当切割,得到几何体K ,已知几何体K 由两个底面相同的正四棱锥组成,底面ABCD 平行于正方体的下底面,且各顶点...均在正方体的面上,则几何体K 体积的取值范围是________(单位:3cm ).14.数列{}n a 中,若11a =,()112n n n a a n N *++=∈,则()122lim n n a a a →∞+++=L ______; 15.计算22313(8)(272---⨯=_____________. 16.已知,x y 为非零实数,()ππ,42θ∈,且同时满足:①sin cos y x θθ=,② 22103x y xy =+,则cos θ的值等于______. 三、解答题17.某中学的高二(1)班男同学有45名,女同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.(1)求课外兴趣小组中男、女同学的人数;(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;(3)试验结束后,第一次做试验的同学得到的试验数据为68,70,71,72,74,第二次做试验的同学得到的试验数据为69,70,70,72,74 ,请问哪位同学的实验更稳定?并说明理由.18.某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据: 单价x 元99.29.49.69.810销量y 件100 94 93 90 8578y x (2)在(1)的前提下,若该产品的成本是5元/件,问:产品该如何确定单价,可使工厂获得最大利润。
2019杨浦统考高一期末

杨浦区统考高一期末数学试卷2018.06一. 填空题1. 半径为2,圆心角为4π的扇形的面积为 2. 已知(4,3)P -是角α终边上一点,则sin α=3. 若cos()cos 2παα-=,则tan α=4. 函数tan y x =的定义域为5. 若 ABC 的三边长为2、3、4,则 ABC 的最大角的余弦值为6. 函数y =(1)x ≤的反函数为7. 设2log 3a =,则6log 4= (结果用a 表示)8. 设[,]2παπ∈,4sin 5α=,则cos 2α= 9. 方程1sin 3x =,[,]2x ππ∈-的解为 10. 设2()2sin()3f x x πω=-,x ∈R ,实数1x 、2x 满足,对于任意x ∈R ,不等式12()()()f x f x f x ≤≤都成立,若12||x x -的最小值为23π,则正实数ω=二. 选择题11. 设θ∈R ,“sin 0θ=”是“sin20θ=”的( )条件A. 充分不必要B. 必要不充分C. 充要D. 既不充分也不必要 12. 下列函数是奇函数,且值域为实数集R 的是( )A. lg y x =B. lg ||y x =C. tan2y x =D. 3sin 2y x = 13. 已知4cos25θ=,sin 0θ<,则tan θ=( ) A. 2425- B. 247± C. 247 D. 247-14. 函数2sin y x =的图像经由下列变换可以得到函数2sin(2)3y x π=+的图像的是( )A. 先将图像向左平移3π,再将图像上每一点的横坐标变为原来的一半 B. 先将图像上每一点的横坐标变为原来的一半,再将所得图像向左平移3πC. 先将图像向左平移3π,再将图像上每一点的横坐标变为原来的2倍D. 先将图像上每一点的横坐标变为原来的2倍,再将所得图像向左平移3π三. 解答题15. 解方程:222log()log(1)2x x x+=++.16. 已知3(,)4παπ∈,10tan cot3αα+=-.(1)求tanα的值;(2)化简并求sin sin()2sin()cosπααπαα+---的值.17. 已知函数2()sin22cos1f x x x=+-,x∈R,其中集合D为函数的定义域.(1)求函数()f x的最小正周期;(2)用五点法作出函数()f x一个周期内的图像.18. 某小区规划时,计划在周边建造一片扇形绿地,如图所示,已知扇形绿地的半径为50米,圆心角3AOBπ∠=,从绿地的圆弧边界上不同于A、B的一点P处出发铺设两条道路PO和PC(均为直线段),其中PC平行于绿地的边界OB,记POCθ∠=(03πθ<<).(1)当4πθ=时,求所需铺设的道路长;(2)若规划中,绿地边界的OC段也需铺设道路,且道路的铺设费用均为每米100元,当θ变化时,求铺路所需费用的最大值(精确到1元).19. 设3()lgxf xa x-=+,其中常数a∈R,3a≠-.(1)当0a=时,求不等式()0f x>的解;(2)若函数()f x的图像关于原点对称,求实数a的值;(3)当0a=时,求()f x在区间[1,2]上的最大值与最小值的差.参考答案一. 填空题 1.2π2. 35-3. 14. {|,}2x x k k Z ππ≠+∈5. 14-6. 21y x =-(0)x ≤7. 21a +8.9. 1arcsin 3x =或1arcsin 3x π=- 10. 32二. 选择题11. A 12. C 13. D 14. A三. 解答题 15. 4x =. 16.(1)13-;(2)12-.17.(1)())4f x x π=+,T π=;(2)列表描点连线,作图略.18.(1)50+;(2)费用5000)3πθ=+,6πθ=,最大值为10774元. 19.(1)302x <<;(2)3a =;(3)lg 4.。
2019春上海市杨浦区控江中学高一(下)期末数学试卷

2019 春上海市杨浦区控江中学高一(下)期末数学试卷一、选择题(本大题共 4 小题,共 12.0 分)1.已知φ是常数,那么“ tan φ是=2“”等式对任意 x∈R 恒”)成立的(A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既不充分也不必要条件2.已知φ是常数,如果函数y=-5cos( 2x+φ)的图象关于点,中心对称,那么 | φ|的最小值为()A. B. C. D.3.某个命题与正整数n有关,如果当n=k k N+)时命题成立,那么可推得当n=k+1(∈时命题也成立.现已知当 n=7 时该命题不成立,那么可推得()A. 当时该命题不成立B. 当时该命题成立C. 当时该命题不成立D. 当时该命题成立4.已知n N*,实数 x,y 满足关系式,若对于任意给定的n∈N*,当 x 在 [-1,∈+∞x+y的最小值为M n,则=())上变化时,A. B.0 C. D. 1二、填空题(本大题共12 小题,共36.0 分)5.函数 y=arcsin( 2-x)的定义域 ______.6. 函数的最小正周期为______.7.已知数列 { a n } 是等比数列,公比为 q,且 a2?a4?a6 =8, a7=54 ,则 q=______.8. 已知tan α =3=______.,则9.在△ABC 中,角 A,B,C 所对的边为 a,b,c,若 a=4,b=6,c=9,则角 C=______.10.ABC中,角A所对的边为a,若a=2ABC的外接圆半径为2,则A=______.在△,且△11.已知数列{ a n } 满足 a1=5, a+1=2a -3,n∈N*,则数列 { an} 的通项公式为 a =______ .n n n12.n n,( k∈N* ),S n是其前 n 项和,已知数列 { a } 的通项公式为 a =,则 S18=______ .(结果用数字作答)13.已知为等差数列,若<,且它的前项和n有最大值,那么当 S 取得最小正值时, n=______.14.已知无穷等比数列{ a n} 的首项为1,公比为 q,且,则首项aa1的取值范围是 ______.15.在数列∈中, a1=2, S n是其前 n 项和,当 n≥2时,恒有 a n, S n, S n-2成等比数列,则=______.16.设集合 A={2 n|0 ≤n≤ 16, n∈N} ,它共有136 个二元子集,如 {2 0, 21} , {2 1, 22} 等等.记这 136 个二元子集为B1,B2,B3, B136,.设,,∈,定义 S( B1)=|x-y|,则 S(B1) +S( B2) +S( B3)+S( B136)=______ .(结果用数字作答)三、解答题(本大题共 5 小题,共60.0 分),∈.17.在数列 { a n} 中, a1=12 ,a4=3,且满足( 1)求数列 { a n} 的通项公式;( 2)设,∈,求数列{ b n}的前n项和T n.18.设函数,定义域为R.( 1)求函数f( x)的最小正周期,并求出其单调递减区间;( 2)求关于x 的方程的解集.19.已知函数 f( x)=( x-1)2,{ a n } 是公差为 d 的等差数列, { b n} 是公比为 q( q∈R,q≠1)的等比数列.且 a1=f(d-1), a9=f( d+1), b2=f( q-1), b4=f( q+1).( 1)分别求数列 { a n} , { b n} 的通项公式;{ c n ( 2)已知数列 { c n} 满足:∈,求数列}的通项公式.20. 已知常数λ∈R 且λ> -3,在数列∈中,首项a1=λ,S n是其前n项和,且,∈.( 1)设,∈,证明数列 { b n} 是等比数列,并求出 { b n} 的通项公式;( 2)设,∈,证明数列 { c n} 是等差数列,并求出 { c n} 的通项公式;( 3)若当且仅当 n=7时,数列 { S n } 取到最小值,求λ的取值范围.21.已知函数(f x)=sin(ωx+φ()ω>0,0<φ<π)的最小正周期为π,且直线是其图象的一条对称轴.( 1)求函数f( x)的解析式;( 2)在△ABC 中,角 A, B,C 所对的边分别为 a, b, c,且 A<B< C, a=cosB,若 C 角满足 f( C) =-1 ,求 a+b+c 的取值范围;( 3)将函数 y=f( x)的图象向右平移个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的 2 倍后所得到的图象对应的函数记作y=g(x),已知常数λ∈R,n∈N*,且函数 F( x) =f( x) +λg( x)在( 0, nπ)内恰有 2021 个零点,求常数λ与 n 的值.答案和解析1.【答案】C【解析】解: sinx+2cosx=(sinx+cosx),令 =cos φ, =sin φ,则 tan φ =2.sinx+2cosx=sin ( x+φ).∴∴“ tan φ是=2“”等式对任意 x∈R 恒成立”的充要条件.故选: C.sinx+2cosx=(sinx+ cosx),令=cos φ, =sin φ,可得 tan φ =2.即可判断出关系.本题考查了和差公式、同角三角函数基本关系式、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.2.【答案】C【解析】解:函数y=-5cos( 2x+φ)的图象关于点,中心对称,所以 f()=5cos(+φ) =5cos(+φ) =0,即φ=(k∈Z),解得φ=(k∈Z),当k=0时φ=-.所以 | φ|=.故选: C.首先利用余弦形函数的性质得到f()=0,进一步整理得即φ=(k∈Z),最后求出结果.本题考查的知识要点:余弦形函数的性质的应用,函数的对称性的应用,主要考察学生的运算能力和转换能力,属于基础题型.3.【答案】A【解析】解:由题意可知,原命题成立则逆否命题成立,P( n)对 n=7 不成立, P( n)对 n=6 也不成立,否则 n=6 时,由由已知推得n=7 也成立.与当 n=7 时该命题不成立矛盾故选 A.本题考查的知识点是数学归纳法,由归纳法的性质,我们由P( n)对 n=k 成立,则它对 n=k+1 也成立,由此类推,对n> k 的任意整数均成立,结合逆否命题同真同假的原理,当 P( n)对 n=k 不成立时,则它对n=k-1 也不成立,由此类推,对n< k 的任意正整数均不成立,由此不难得到答案.当 P(n)对 n=k 成立,则它对n=k+1 也成立,由此类推,对n> k 的任意整数均成立;结合逆否命题同真同假的原理,当P(n)对 n=k 不成立时,则它对n=k-1 也不成立,由此类推,对n< k 的任意正整数均不成立.4.【答案】A【解析】解:=,当且仅,即时取等号,故,故选: A.由于 x 与 n 之间没有相互约束关系,所以可以先对 n 求极限再对 x 求最值,将问题转化为易于计算的问题.本题的难点在于转化求最值与求极限的顺序,如果直接求解就会很复杂,交换顺序后,就转化为求一个简单的分式极限,与分式函数最值.5.【答案】[1,3]【解析】解:要使y=arcsin ( 2-x)有意义,则 -1≤2-x≤1;∴1≤x≤3;∴原函数的定义域为[1,3].故答案为: [1, 3].可以看出,要使得y=arcsin ( 2-x)有意义,则需满足-1≤2-x≤1,解出 x 的范围即可.考查函数定义域的定义及求法,反正弦函数的定义域.6.【答案】1【解析】解:函数的最小正周期为:T= =1.故答案为: 1.直接利用三角函数的周期公式求解即可.本题考查三角函数的周期的求法,是基本知识的考查.7.【答案】3【解析】解:∵数列 { a n} 是等比数列,公比为q,且 a2?a4?a6=8, a7=54,∴,解得 q=3.故答案为: 3.利用等比数列的通项公式列出方程组,能求出公比.本题考查等比数列的公比的求法,考查等比数列的性质等基础知识,考查运算求解能力,是基础题.8.【答案】【解析】解: tan α=3,则=== .故答案为:.直接利用同角三角函数基本关系式化简表达式为正切函数的形式,代入求解即可.本题考查同角三角函数基本关系式的应用,三角函数化简求值,考查计算能力.9.【答案】π-arccos【解析】解:△ABC 中, a=4, b=6 , c=9,由余弦定理得cosC==-,有 C∈( 0,π),所以 C=π-arccos .故答案为:π-arccos.利用余弦定理求出cosC,再根据反余弦函数求出 C 的值.本题考查了余弦定理和反余弦函数的应用问题,是基础题.10.【答案】,或【解析】解:∵a=2,且△ABC 的外接圆半径为2,∴由正弦定理,可得:,可得 sinA= ,∵A∈( 0,π),∴A= ,或.故答案为:,或.由已知利用正弦定理得sinA= ,结合范围A∈( 0,π),可求 A 的值.本题主要考查了正弦定理在解三角形中的应用,属于基础题.n11.【答案】2 +3.【解析】解:∵a1=5, a n+1=2a n-3,∴a n+1 -3=2( a n-3).又 a1=5,故数列 { a n-3} 是首项为 2,公比为 2 的等比数列.∴a n-3=2 n,∴.故答案为:2n+3.把给出的数列递推式变形,得到数列{ a n-3} 是首项为2,公比为 2 的等比数列,求出等比数列的通项公式后得答案;本题考查了由递推式求数列的通项公式,考查转化思想以及计算能力.12.【答案】727【解析】解: a n=,(k∈N* ),,可得 S18=( a1+a3+ +a17) +(a2+a4+ +a18)8=+ ×9×( 8+40 )=727.故答案为: 727.由数列的分组求和,结合等差数列和等比数列的求和公式,计算可得所求和.本题考查数列的求和方法:分组求和,考查等差数列和等比数列的求和公式,考查运算能力,属于基础题.13.【答案】19【解析】解:∵S n有最大值,∴d< 0则 a10> a11,又<,∴a11<0< a10∴a10+a11< 0,S20=10( a1+a20) =10 ( a10+a11)< 0,S19=19a10> 0又 a1> a2>>a10> 0> a11> a12∴S10>S9>>S2>S1>0,S10>S11>>S19>0>S20>S21又∵S19- S1 =a2+a3+ +a19=9(a10+a11)< 0∴S19为最小正值故答案为: 19要求Sn 取得最小正值时n的值,关键是要找出什么时候a n小于或等于 0,而 a n+1大于 0,由<,我们不难得到 a11< 0< a10,根据等差数列的性质,我们易求出当Sn 取得最小正值时, n 的值.本题考查数列的函数性质,一般的{ a n} 为等差数列,若它的前 n 项和 S n有最小值,则数列的公差 d 小于 0;{ a n} 为等差数列,若它的前n 项和 S n有最大值,则数列的公差 d 大于 0.14.【答案】[2,3)∪(3,4)【解析】解:无穷等比数列 { a n} 的首项为 a1,公比为 q,且,① q=1 时,,解得, a1=2 ;②|q|< 1 时,且 q≠0,可得 -1< q< 0,或 0<q< 1,,,则 a1=3+ q,又 2< 3+q< 3 或 3< 1+q< 4所以首项a1的取值范围是:[2, 3)∪( 3, 4).故答案为: [2, 3)∪( 3, 4).对 q 讨论,① q=1 时,②|q|< 1 时,分别求出极限,解方程或不等式,即可得到范围.本题考查数列的极限运算,注意讨论公比,考查运算能力,属于中档题和易错题.15.【答案】-2【解析】解:数列∈中, a1=2, S n是其前 n 项和,当 n≥2时,恒有 a n,S n,S -2 成等比数列,n可得, n≥2时,,化简可得,{ } 是等差数列,首项为1,公差为 1,所以=1+( n-1) ?1=n,所以 S n= ,当 n≥2时,可得a n ==,a1=2,所以:==-2.故答案为: -2.利用已知条件推出{ } 是等差数列,求出S n,然后求解数列的通项公式,转化求解数列的极限即可.本题考查数列的递推关系式的应用,数列的极限的求法,考查转化首项以及计算能力.16.【答案】1835028【解析】解:由题意可得:S( B1) +S(B2) +S(B3)+S(B136)=( 21-20+22-20++216-20)+(22-21+2 3-21++216-21)++(215-214+2 16-214)+( 216-215)=-16 ×20+-15 ×21++-2 ×214+216-215171621511415=2 ×15+2 - (2+2++2) -( 16+15×2++2×2 +2)=2 17×15+216--( 217-18)=2 17×14+20=1835028 .故答案为: 1835028.由题意可得:S( B1) +S( B2)+S( B3) +S( B136) =( 21 -20+22-20++216-20) + 2131161151416141615(2-2 +2 -2 ++2-2)++(2 -2+2 -2)+( 2-2 ),利用等比数列的求和公式即可得出.本题考查了等比数列的通项公式与求和公式、错位相减法、集合与元素之间的关系,考查了推理能力与计算能力,属于难题.17.【答案】解:(1)数列{ a n}中,满足,∈.所以数列 { a n} 为等差数列.由于 a1=12 ,a4=3,所以公差 d=,故 a n=12-3 ( n-1)=15-3 n.( 2)由于 a n=15-3 n,所以=所以,=.【解析】( 1)首先根据已知条件,判断数列为等差数列,进一步求出数列的通项公式.(2)利用( 1)的通项公式,进一步利用裂项相消法求出数列的和.本题考查的知识要点:数列的通项公式的求法及应用,裂项相消法在数列求和中的应用,主要考察学生的运算能力和转换能力,属于基础题型.18.=【答案】解:( 1)函数+2?( 1-cos2x)=.所以函数 f ( x)的最小正周期为T=π:令( k∈Z),解得(k∈Z),所以单调递减区间为,,.(2)令,即.解得,∈ .【解析】( 1)首先利用三角函数关系式的恒等变换,把函数的关系式变形成正弦型函数,进一步利用整体思想求出函数的最小正周期和单调区间.(2)利用( 1)的结论,进一步利用整体思想求出方程的解集.本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,三角函数的方程的解法,考查了推理能力与计算能力,属于中档题.19.【答案】解:(1)f(x)=(x-1)2,a1=f(d-1),a9=f(d+1),可得 a1=( d-2)2, a9 =d2,则 d=,解得d=-1,a1=9,可得 a n=10- n;由 b2=f( q-1), b4=f( q+1).可得 b2=( q-2)2,b4 =q2,则 q2= =,解得 q=3( 1 舍去), b2=1,则 b n=3n-2;(2)当 n=1 时, b1c1=a1,即 c1=9,解得 c1=27 ;n≥2时, b1 c1+b2c2++b n-1c n-1=a n-1,又 b1c1+b2c2+ +b n c n=a n,两式相减可得 b n c n=a n-a n-1 =d=-1 ,即有 c n=-()n-2. n≥2,综上可得 c n=,.,【解析】(1)运用等差数列和等比数列的通项公式,解方程可得首项和公差、公比,即可得到所求通项公式;(2)求得 n=1 时 c1=27 ;n≥2时,将 n 换为 n-1 相减,可得 c n,注意写出分段形式.本题考查等差数列和等比数列的通项公式的运用,考查方程思想和运算能力,属于基础题.20.1=λS n,∈,【答案】解:( 1)证明:首项 a,是其前 n 项和,且可得 S n=4a n-1+3, n≥2,相减可得 a n+1 =4a n-4a n -1,即有 a n+1-2a n=2( a n-2a n-1),可得 b n=2b n-1,由 a1+a2=4 a1+3,可得 a2=3λ +3, a2-2a1=λ +3,可得 b n=(λ +3) ?2n-1, n∈N* ;( 2)由( 1)可得 a n +1-2a n=(λ +3) ?2n-1,-= ,即为 c n+1-c n=,可得数列 { c n} 是公差为的等差数列,由 c1= = ,可得 c n= +( n-1) = n+, n∈N* ;(3) a1=S1=λ, S n+1 =4a n+3= (λ +3) ?n?2n+(λ-3) ?2n,由 S n+1-S n =(λ +3) ?n?2n+(λ-3) ?2n-(λ +3) ?( n-1) ?2n-1-(λ-3)?2n-1 =2 n-1( 2λ+λn+3n),由题意可得 1≤n≤6时, 2n-1(2λ+λn+3n)< 0 恒成立,即为 -λ>,由=在1≤n≤6递增,可得 -λ>,即λ< - ;又 n≥7时, 2n-1( 2λ+λn+3n)> 0 恒成立,即为 -λ<,由=在n≥7递增,可得 -λ<,即λ>-.综上可得 - <λ<- .【解析】( 1)由原式将 n 换为 n-1,由数列的递推式,相减可得a n+1=4a n-4a n-1,即有a n+1 -2a n=2(a n-2a n-1),再议等比数列的定义和通项公式,可得所求;( 2)由( 1)可得 a n+1-2a n=(λ +3)?2n-1,两边同除以2n+1,结合等差数列的定义和通项公式,可得所求;( 3)求得 S n+1-S n=2n-1( 2λ+λn+3n),由题意可得 1≤n≤6时, 2n-1( 2λ+λn+3 n)< 0 恒成立, n≥7时, 2n -1( 2λ+λn+3 n)> 0 恒成立,运用参数分离和数列的单调性,可得所求范围.本题考查等比数列和等差数列的定义和通项公式,考查构造数列法,以及数列的单调性,考查化简运算能力,属于难题.21.【答案】解:(1)依题意,ω===2 ,2×,+φ=,(k∈Z),即φ=所以 f( x) =sin(ωx+φ) =sin( 2x+ ) =cos2x.(2) f( C) =cos2C=-1 ,所以 C=90°,∴A+B=90 °,∴cosB=sinA,∴a=cosB=sinA,即=1= c,a+b==sinA+sinB=sinA+cosA= sin( A+),∴因为 A< B< C,所以 A∈( 0,),所以A+ ∈(,),∴sin(A+ )∈(1,),所以 a+b=sin( A+ )∈( 1,),所以 a+b+c∈( 2,).(3)依题意,将函数y=f( x)的图象向右平移个单位,得 y=cos2 ( x-) =cos( 2x- )=sin2 x,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的 2 倍得到 y=sinx,∴g( x) =sinx,所以 F( x) =cos2x+λsinx=-2sin 2x+λ sinx+1当λ=0F(x)=cos2x,则F x)在(,nπ时,()内的零点个数为偶数个,F ( x)在(0, nπ)内恰有 2021个零点,为奇数个零点,故λ≠0,所以当 sinx=时 F( x) =0,而≠0,故=±1,即λ =±1,且 n 为奇数.①若λ=1,则 3×=2021 ,解得 n=,不是整数,舍去;②若λ=-1,则 3×+2=2021 ,解得 n=1347 .综上λ=-1, n=1347 .【解析】(1)根据周期为π可得ω=2,再由直线是其图象的一条对称轴可得φ=,即可得到 f ( x)的解析式;(2)(f C)=cos2C=-1 ,所以 C=90°,∴A+B=90°,∴cosB=sinA,∴a=cosB=sin A,即=1= c,再将 a+b 转化为 sinA+sinB=sinA+cosA,合一变形后即可得到 a+b 的范围,进而得到 a+b+c 的范围;( 3)求出(gx)的解析式,得到 F(X),显然λ≠0,有零点个数为奇数个,又 sinx=≠0,则在( 0, 2π)范围内对应 3 个零点,故=±1,的λ =±1,再分情况讨论即可.本题考查了三角函数的图象与性质,考查了三角函数有界性的应用,三角函数的诱导公式,图象变换,函数的零点等,属于难题.第11 页,共 11页。
(3份试卷汇总)2019-2020学年上海市杨浦区高一数学下学期期末达标检测试题

2019-2020学年高一下学期期末数学模拟试卷一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列函数中,既是偶函数,又在()0,π上递增的函数的个数是( ). ①tan y x =;②()cos y x =-;③sin 2y x π⎛⎫=- ⎪⎝⎭;④cos 2y x =向右平移4π后得到的函数. A .0B .1C .2D .32.设n S 为等差数列{}n a 的前n 项和,若4540,a a a <>,则使0n S >成立的最小正整数n 为( ) A .6B .7C .8D .93.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,1cos 9C =,且边2c =,则ABC ∆面积的最大值为( )A .5B .859C .43D .5 4.若线性方程组的增广矩阵是,解为,则的值为( )A .1B .2C .3D .45.数列{}n a 中,12a =,且112(2)n n n n n a a n a a --+=+≥-,则数列()211n a ⎧⎫⎪⎪⎨⎬-⎪⎪⎩⎭前2019项和为( ) A .40362019 B .20191010 C .40372019 D .403920206.已知空间中两点(2,1,4),(4,1,2)A B --,则AB 长为( ) A 11B .112C .211D .3117.已知()2462n f n =++++,则(1)f n +比()f n 多了几项( )A .1B .nC .1n +D .12n -8.已知a,b ∈R ,且0a ≠,若对[]1,2x ∈,不等式2ax b ax b ++-≤恒成立,则22a b a b +--的最大值为( ) A .14B .12C .1D .329.设*n N ∈,则“数列{}n a 为等比数列”是“数列{}n a 满足312n n n n a a a a +++⋅=⋅”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件D .既非充分也非必要条件10.已知直线l 的方程是y =2x +3,则l 关于y =-x 对称的直线方程是( ) A .x -2y +3=0B .x -2y =0C .x -2y -3=0D .2x -y =11.在△ABC 中,c =3,A =75°,B =45°,则△ABC 的外接圆面积为 A .4π B .π C .2π D .4π12.如图,2AB CAOA a OB b OC c ====,,,,下列等式中成立的是( )A .3122c b a =- B .3122c a b =- C .2c a b =-D .2c b a =-二、填空题:本题共4小题13.数列{}()*n a n N ∈满足:135a =,111112,0211,2n n n n n a a a a a ----⎧<<⎪⎪=⎨⎪-≥⎪⎩()2n ≥,则59a =______.14.已知[)0,2ϕπ∈,若方程()sin 3cos 2sin x x x ϕ-=-的解集为R ,则ϕ=__________. 15.设向量,,a b c 满足1a =,||2b =,3c =,0b c ⋅=.若12λ-≤≤,则(1)a b c λλ++-的最大值是________.16.如图所示,隔河可以看到对岸两目标,A B ,但不能到达,现在岸边取相距4km 的两点,C D ,测得,75,4530,45ACB BCD ADC ADB ︒︒︒︒∠=∠=∠=∠=(,,,A B C D 在同一平面内),则两目标,A B 间的距离为_________km .三、解答题:解答应写出文字说明、证明过程或演算步骤。
杨浦区2019届高三期末质量调研数学试卷解析(2021年整理)

杨浦区2019届高三期末质量调研数学试卷解析(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(杨浦区2019届高三期末质量调研数学试卷解析(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为杨浦区2019届高三期末质量调研数学试卷解析(word版可编辑修改)的全部内容。
上海市杨浦区2019届高三期末质量调研数学试卷一、填空题(本大题共12题,1—6每题4分,7—12每题5分,共54分)1.设全集{}=1,2,3,4,5U ,若集合{}3,4,5A =,则U C A =__________。
【答案】{}1,2 【解析】 【分析】利用补集定义直接求解即可.【详解】∵全集{}=1,2,3,4,5U ,集合{}3,4,5A =,∴{1}2U C A ==,, 故答案为{}1,2.【点睛】本题考查补集的求法,是基础题,解题时要认真审题,注意补集定义的合理运用. 2.已知扇形的半径为6,圆心角为3π,则扇形的面积为__________。
【答案】6π 【解析】 【分析】先计算扇形的弧长,再利用扇形的面积公式可求扇形的面积.【详解】根据扇形的弧长公式可得362l ππαr ==⨯=,根据扇形的面积公式可得1126622S lr ππ==⋅⋅=,故答案为6π.【点睛】本题主要考查扇形的弧长与面积公式,正确运用公式是解题的关键,属于基础题. 3.已知双曲线221x y -=,则其两条渐近线的夹角为________。
【答案】2π 【解析】 【分析】先计算渐进线为y x =±,计算其倾斜角,得到答案。
上海杨浦实验学校 高一数学文期末试题含解析
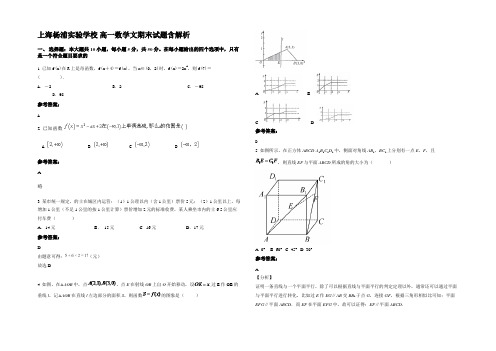
上海杨浦实验学校高一数学文期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知f(x)在R上是奇函数,f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(7)=( ).A.-2 B.2 C.-98D.98参考答案:A2. 已知函数A B C D参考答案:A略3. 某市统一规定,的士在城区内运营:(1)1公理以内(含1公里)票价5元;(2)1公里以上,每增加1公里(不足1公里的按1公里计算)票价增加2元的标准收费,某人乘坐市内的士6.5公里应付车费()A.14元B.15元 C. 16元D.17元参考答案:D由题意可得:(元)故选D.4. 如图,在△AOB中,点,点E在射线OB上自O开始移动,设,过E作OB的垂线l,记△AOB在直线l左边部分的面积S,则函数的图象是()A. B.C. D.参考答案:D5. 如图所示,在正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有一点E,F,且,则直线EF与平面ABCD所成的角的大小为()A. 0°B. 60°C. 45°D. 30°参考答案:A【分析】证明一条直线与一个平面平行,除了可以根据直线与平面平行的判定定理以外,通常还可以通过平面与平面平行进行转化,比如过E作EG∥AB交BB1于点G,连接GF,根据三角形相似比可知:平面EFG∥平面ABCD.而EF在平面EFG中,故可以证得:EF∥平面ABCD.【详解】解:过E作EG∥AB交BB1于点G,连接GF,则,∵B1E=C1F,B1A=C1B,∴.∴FG∥B1C1∥BC.又∵EG∩FG=G,AB∩BC=B,∴平面EFG∥平面ABCD.而EF在平面EFG中,∴EF∥平面ABCD.故答案为:A【点睛】本题主要考查空间直线和平面平行的判定,根据面面平行的性质是解决本题的关键.6. 下列函数中,在区间上是增函数的是()A. B. C. D.参考答案:A略7. 直线x+=0的倾斜角为()A.60°B.90°C.120°D.不存在参考答案:B【考点】I2:直线的倾斜角.【分析】利用直线的倾斜角与斜率的关系即可得出.【解答】解:∵直线x+=0的斜率不存在,∴倾斜角为,即为90°.故选:B.8. 若不等式对满足的所有实数都成立,则实数的取值范围是()A. B.C. D.参考答案:A9. 若为实数,表示不超过的最大整数,则函数在上为()A.奇函数 B.偶函数 C.增函数 D.周期函数参考答案:A略10. 函数的图象必经过点P,则点P的坐标是()A. B. C. D.参考答案:D略二、填空题:本大题共7小题,每小题4分,共28分11. 在中,已知,则该三角形形状为__________.参考答案:略12. 观察下列不等式:,,,,,,由此猜想第个不等式为▲.参考答案:略13. 方程= 的实数解的个数是______________参考答案:402914. 若函数f (x )=|2x ﹣1|﹣m 有两个不同的零点,则实数m 的取值范围是 .参考答案:(0,1)【考点】根的存在性及根的个数判断.【分析】把函数f (x )=|2x﹣1|﹣m 的零点转化为函数y=|2x﹣1|与y=m 的图象交点的横坐标,画出两个函数的图象,数形结合得答案.【解答】解:由f (x )=|2x ﹣1|﹣m=0,得|2x ﹣1|=m , 画出函数y=|2x ﹣1|与y=m 的图象如图,由图可知,要使函数f (x )=|2x﹣1|﹣m 有两个不同的零点,则实数m 的取值范围是(0,1). 故答案为:(0,1).15.如图,中,平面,此图形中有 个直角三角形.参考答案: 4略16. 已知点,,向量,若,则实数的值为 .参考答案:17. 已知两个函数和的定义域和值域都是集合,其定义如下表:则方程的解集为 .参考答案:{3}三、 解答题:本大题共5小题,共72分。
2019学年上海市高一下学期期末考试数学试卷【含答案及解析】
2019学年上海市高一下学期期末考试数学试卷【含答案及解析】姓名____________ 班级_______________ 分数____________一、填空题1. 计算: ------- :—"~*亚4对+ 12. 已知数列;一「为等差数列,•―- ■-,贝V二3. 在等比数列,中,二y - m ,则—的值为4. 已知;;是等差数列,是其前*项和,•,则45. 函数 -■- 在上「一1」.的值域是6. 数列■:中,込一;,,一二,“;一,.一心“ ■-監,贝V :的前2015项和= ----------------------- ----7. 在数列.「中,已知广二」..二1* ,且数列•化+菇是等比数列,则9.函数v = sin —+ cos —在f —hT-"\内的单调递增区间为J7争rr10. 在厶'、、、;、中,已知,贝「1, 的取值范围是11. 在等腰直角 中, ,-一 i ,形,如图所示,若正方形的面积依次为 -.八,则•’•‘12.已知数列{nJ 满足q ・-1勺 >斫.匕灼-他卜严⑷「V*),若数列 ;单调递减,数列;’ 单调递增,则数列罠「;■的通项公式为-=8. 执行右边的程序框图,若 「二、 ,则输出的X1BC 中排列着内接正方(从大到小),其中、选择题) 本题共有2个小题,第1小题4分,第2小题4分.A B.C 的对边分别为 门、氏匸.已知c =C,-EU11 A •C . 钝角三角形D .不能确定14.利用数学归纳法证明“ 1 +灯一小 4-L + /' =■|芒 1、 n e A ) ”,在验1 一证 -,成立时,等号左边是()A .B .C .D .1十亓+打】15.在等差数列打 中, 若且的前•项和有最小值, 则使得 |的最小 值 n 为(A .11B .19C .D16. 有穷数列, CT, , …,- 中的每一项都是一 II , 0 ,1这三个数中的某一个数,若 灯1+ +…+ =425,且 i 一 1 r+・+'+…+■ = 3870 ,则有穷数列■- , ■ ■ ■ ■ ,:: ,中值为0的项数是()A ..■. C B .;门$.1010D . 1030三、 解答题)在 ^中,右,则一宀的形状是()锐角三角形________________ B .直角三角形13. A .(本题满分8分ZU2?C 中,内角 17.在 (1 )求.;,的大小;(2 )若-7.7 ,求 _;;的面积.18. (本题满分8分) 本题共有2个小题,第1小题4分,第2小题4分.已知;[、::|| . ^ ^ 一■; .■'|| — ,■,且函数’图象上的任意两条对称轴之间距离的最小值是—•(1 )求的值;(2)将函数= _■/-,,>>的图像向右平移— 个单位后,得到函数■ = 的图像,6 求函数•的解析式,并求 • 在——-上的最值.19. (本题满分10分) 本题共有2个小题,第1小题4分,第2小题6分已知数列;.:的首项.■ .「 「.(1 )求证:数列;—-J.为等比数列;•%」(2) 记「;-」--[* ,若| ,求最大正整数坏 %6本题共有2个小题,第1小题6分,第2小题6分-公司开拓国际市场,基本形成了市场规模个月(20 14年1月为第一个月)产品的 内销量、出口量和销售总量(销售总量=内销量斗出口量)分别为人 、 和•. (单位:万件),依据销售统计数据发现形成如下营销趋势:.-,■1 T 1Ifl匚-匚广;广叮(其中为常数,卄二严),已知 一万件,• 一 万件,. -万件• (1 )求的值,并写出•-与满足的关系式;(2)证明:逐月递增且控制在2万件内•21. (本题满分14分) 本题共有3个小题,第1小题4分,第2小题5分,第3小题5分•设等比数列..’的前.项的和为 ,公比为,亩戏口 (1 )若 成等差数列,求证:.成等差数列;(2 )若 ..(-为互不相等的正整数)成等差数列,试问数列I 〕中是20. (本题满分12分)在上海自贸区的利好刺激下 自20 14年1月以来的第否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由; (3)若:.为大于的正整数•试问.:中是否存在一项,使得恰好可以表示为该数列中连续两项的和?请说明理由.参考答案及解析第1题【答案】【解析】第2题【答案】【解析】试题分析;由等差数列求和公式£ =即吗十— d 0 = 3 5 ??+戈匕_ x (-2 )/_n = 362 2第3题【答案】 4【解析】--- —Z -- — 一 2 4阳一 1 2试题分析:试题分析:= 102+flj = 1024 =4第4题【答案】-1【解析】第5题【答案】[討]【解析】第6题【答案】1【解析】试题分析:由递推公式应-可得各项依次为12X-1-Z-1J.2,所決周期为d,前6项和 为°,所以电町二珂_込+气+丐+%二“第7题【答案】2 3^-re【解析】试题分折:数列⑺号对第二项込十2-6 ,第三项◎十3二1& ,等比数列公比対3/.心 十 M 二& 3,1~-二心 二 2 3:'-1- n第8题【答案】试题分析;- 1T-CCOE ; A试题分析;s n A【解析】H5:程序执行中的费据变怙尸〃士46 = 2”击.27®二丄十丄L 6<7J 7 = 7,J -—+ —+L +—7<7不成立,输岀 2x3 3><4 2«3 3 如 7«81 】q 丄1 1 1 3二; -- 十 ---- -T [ 十 ---- 二一一一二一 2凉 A4 7^8 2 8 S第9题【答案】【解析】Q r e (~2^r,2^) : 乂亡乂+ 乞214第10题【答案】试题分析:过A 作血)丄EC 于D 」B = 60". C = 2, B[1<1 = 1 0寸、mC 二1』当取=4时 试题分析:严 响吟+遇于三』5血-+ - 匕4丿(35e — /T, —/r I 4 4令三畀 2托714€72'2、增区间为卜寻&・所a sin c 的取值范围是[£i]At【解析】此A 寸=第11题【答案】92【解析】x3 —迸试题分析;设第一个正方形的边长为知贝恼相佩三角册可得= S产4再宙ffilU三角形可得卅丄比L构成4为首项,扌为公比的等比数列,S 4 9■■魚⑶+ S/L ^^)=^-=—=-9第12题【答案】E-L【解析】试题分析;采用列举法得刊=-g =1*理=-3心=5•码=—1血二21L 、然后从数字的变化上找规律,得%广碣二(T厂2” •「①=(外亠%JH為叫卄叽)+L卡@十的)=(—1丫05(Typr+L ±2U2T-1 (-2)^-1 | (-2?-1■■«■-J ■■ 电第13题【答案】【解析】试题分析:由正弦翹里可将迪Ur in诂“血C诗化为R > 丁/nf—十h】一F,7F _LcosC=——; ----- >OAC<-,由已知A,B角的范围不确定,因此形状不能确定2ab2第14题【答案】C【解析】试题分析:n = l时等号左恻卫的最高次数为為所以所边为"卄亍第15题【答案】C【解析】试题分析:M的前斤项和必有最小倩,所以豹列单调递增,且首项巧<o•:加—1二%<0^n>0 且%+知>0.兀二WSjqJ二旧%丸虽二沙匹)二10(佝旳,所以使得\>0的最小1削—--第16题【答案】【解析】试题分析!(巧十1)' +0 +1)]丰他寸1尸+'" + (%手+1)J=3E7OR开得佃+L +d■审”)+2&十碣*L +«;0]j )+2015 = 3870 ”-&+卅4|_ +咗严E0S ・所以7 ,1共W1E硕,刪,值为0啊I页骚是血0天第17题【答案】(1)R = —(2)M 或需【解析】试题分析;⑴ 由关系式刘1^4$)*诚/_£) =wA・结合两角和差的正弦展开式化简可求得8汕的值,得到B角大小£⑵ 由B甬和方疋边利坪余弦定理可求得静边长,结合三角形面积公式S = —^c s-iii *求得面积2试题解析:(1)2&111.4^0£5= SAH A => eos5 -—或虹n 勺兰0(雋)f/. B28 = a2?良卩口' -6^ + S = 0 、二&二2站二4当(? = 2 时,S ——CC sin R 二3 迟;当/T= 4 B寸:S ——crc&in R — 6爲第18题【答案】⑴1⑵sM^ = n ,厭工)碍二运【解析】试题分析;⑴由对称轴的距蛊求得函数周期,进而得到血IB,代入7(0)-0可戒得倂角:从而确JT 7T 定函数解析式,将自变量“亍代入求解的值,⑵由平移规律得到函数y=^W的解析式h 4咖二岳inp■勻,由工的范围得到"■彳的范围,进而结合单调性求得函数最值试题解析:(1) /M=^2sin(^4^+-)_7 = ^ A,■*'- VFsmpx)…'/(彳)-JJsdil 二-14第19题【答案】详见解析(2)99【解析】试西并析:CD证明数列是等比数列需证明数列相邻两项的比值为常数,井且首项不为①本题中通过数列& }的递推公式入手将其变形1冋j⑵借助于(1)的结论求得数列S }的的通项公比进而得到数列]三]的通项公式」结合特点采用分组拥闻W比数列求和公式可得到爲的表达式,解不孝武可求得:值’T ⑴Q土中护亡-1说乜,且Q「“.右I"”⑵由⑴可求得于第20题【答案】(1)应二Lb二"g, g] =2屯档士/ C3详见解析A£【解析】试题分析;(1)依蛊意:口―】=■巾+】=吗+內+占如';将諏1,2;构建方程组丿冃卩可求得S b的値,从而可得為巧芍町满足的关系式』⑵先证明3“為-如/"*6_2卄少2 , 于是供<2 .再用作差法证明久亡弘,从而可得结论;试题解析:Ci)依ffiiS:口“二矗齐十£卄]二“%十口,,、 3 *.\ 0\ —皿】丄诃十5CT*,「*阿+1十H寸一“ ........ ① 又立* —+ t7r卄by jI r j ■■■■u Ji IA -£7+- + ^! -V=- .................. ②解①②得<7=1,6 = -2 2 (2 丿8 2从而口m二2口厂十「(2)由于码T = 2珂厂+口;=一片(臥一2)】十2$2・但碍・1工2・否贝」可推得% =匹=2矛盾・故孝&偽・严2 ,于ftn, < 2 .又旳〒1_码=_*V・2码-q =-斗码(码・2):>0 ,所決為勺卜仇,从而<2 .第21题【答案】(1)详见解析(2)心+].dg.q.] (3)不存在【解析】试题分析:⑴ 根据%%爲成等差数列,q^l,可得2几=2 +耳,化简可得,进而可以证明如.%你成等差数列,(2)根据凡・片$ 51为互不相等的正整数)成等差数列、可得2S#二几4Sr ;化简可得2叩「4珂7‘ ;从而可得%“叶知成尊差数列,即可得出结论,<3)设存在一项①,使得丑・恰好可以表示/该数列中连续两项的和,设冷=6斗%] )可得斤>"} q s'n =1+(?,从而可得结论试题解析:(1)若Z,咼成等差数列,则2S宀览,即2円(1一/;) _ 竹(1-/> | 呵(1-扌)\・q '■ q \-q+ ” …:靳二1 + / ,又2弧- (% +a u) = 2如7 -(a}q9 + qg") = qg°(2/ T -『)=0|.・2<7|g = CT]。
【精选3份合集】上海市杨浦区2019-2020学年高一数学下学期期末达标检测试题
2019-2020学年高一下学期期末数学模拟试卷一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{}n a 的前n 项和n S 满足21n n S a =-.若对任意正整数n 都有10n n S S λ+-<恒成立,则实数λ的取值范围为( ) A .(),1-∞B .12⎛⎫-∞ ⎪⎝⎭,C .13⎛⎫-∞ ⎪⎝⎭,D .14⎛⎫-∞ ⎪⎝⎭,2.函数1lgy x=的大致图像是下列哪个选项( ) A . B .C .D .3.已知函数f :R +→R +满足:对任意三个正数x ,y ,z ,均有f (3xyz xy yz zx ++)3f x f y f z ++=()()().设a ,b ,c 是互不相等的三个正数,则下列结论正确的是( ) A .若a ,b ,c 是等差数列,则f (a ),f (b ),f (c )一定是等差数列 B .若a ,b ,c 是等差数列,则f (1a ),f (1b ),f (1c )一定是等差数列 C .若a ,b ,c 是等比数列,则f (a ),f (b ),f (c )一定是等比数列 D .若a ,b ,c 是等比数列,则f (1a ),f (1b ),f (1c)一定是等比数列 4.定义运算a b ⊗为执行如图所示的程序框图输出的S 值,则式子π2πtancos 43⎛⎫⎛⎫⊗ ⎪ ⎪⎝⎭⎝⎭的值是A .-1B .12 C .1D .325.设b ,c 表示两条直线,α,β表示两个平面,则下列命题正确的是( ) A .若b α⊂,//c α,则//c b B .若b α⊂,//b c ,则//c α C .若c α⊂,αβ⊥,则c β⊥D .若c α⊂,c β⊥,则αβ⊥6.ABC ∆的内角,,A B C 的对边分别为,,a b c ,2221,2b ac AB =+边上的中线长为2,则ABC ∆面积的最大值为( ) A .2B .22C .23D .47.变量,x y 满足2000x y x y x -+≥⎧⎪+≥⎨⎪≤⎩,目标函数2z x y =+,则z 的最小值是( )A .12-B .0C .1D .-18.在直角ABC 中,AB AC ⊥,线段AC 上有一点M ,线段BM 上有一点P ,且::2:1CM AM PB MP ==,若2AB CM ==,则AP BC ⋅=( )A .1B .23-C .143D .239.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若60A =,1b =,3ABC S ∆=,则a 的值为( ) A .4B 13C .2D 2110.将函数sin 23y x π⎛⎫=-⎪⎝⎭的图象向右平移6π个的单位长度,再将所得到的函数图象上所有点的横坐标伸长为原来的2倍(纵坐标不变),则所得到的图象的函数解析式为( ) A .2sin 3y x π⎛⎫=-⎪⎝⎭B .2sin 43y x π⎛⎫=-⎪⎝⎭C.sin2y xπ⎛⎫=-⎪⎝⎭D.sin42y xπ⎛⎫=-⎪⎝⎭11.在ABC∆中,内角A,B,C所对的边分别为a,b,c,若60B=︒,2b ac=,则ABC∆一定是()A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形12.()200000002021tan39cos50cos127cos40cos37,sin56cos56,21tan39a b c-=+=-=+,则,,a b c的大小关系是()A.a b c>>B.b a c>>C.c a b>>D.a c b>>二、填空题:本题共4小题13.102,238的最大公约数是________.14.如图是一个三角形数表,记,1n a,,2n a,…,,n na分别表示第n行从左向右数的第1个数,第2个数,…,第n个数,则当2n≥,*n N∈时,,2n a=______.15.如图,缉私艇在A处发现走私船在方位角45︒且距离为12海里的B处正以每小时10海里的速度沿方位角105︒的方向逃窜,缉私艇立即以每小时14海里的速度追击,则缉私艇追上走私船所需要的时间是__________小时.16.如果()*12nS n n=++⋅⋅⋅+∈N,()*32232,111nnnS SST n nS S S=⨯⨯⋅⋅⋅⨯∈---N≥,则2017T的值为________(用分数形式表示)三、解答题:解答应写出文字说明、证明过程或演算步骤。
2018-2019学年上海市杨浦区控江中学高一(下)期末数学试卷-学生版+解析版(无水印)
2018-2019学年上海市杨浦区控江中学高一(下)期末数学试卷一、填空题1.(3分)函数arcsin(2)y x =-的定义域 .2.(3分)函数2tan()13y x ππ=++的最小正周期为 .3.(3分)已知数列{}n a 是等比数列,公比为q ,且2468a a a =,754a =,则q = .4.(3分)已知tan 3α=,则226cos 3sin cos 3sin cos 2sin αααααα-=- . 5.(3分)在ABC ∆中,角A ,B ,C 所对的边为a ,b ,c ,若4a =,6b =,9c =,则角C = .6.(3分)在ABC ∆中,角A 所对的边为a ,若2a =,且ABC ∆的外接圆半径为2,则A = . 7.(3分)已知数列{}n a 满足15a =,123n n a a +=-,*n N ∈,则数列{}n a 的通项公式为n a = .8.(3分)已知数列{}n a的通项公式为124,2(*),21n n n n ka k N n k -+=⎧⎪=∈⎨=-⎪⎩,n S 是其前n 项和,则18S = .(结果用数字作答) 9.(3分)已知{}1110,1,n n a a n S a <-为等差数列若且它的前项和有最大值,那么当n S 取得最小正值时,n = .10.(3分)已知无穷等比数列{}n a 的首项为1a ,公比为q ,且13lim()1n n qq a →∞+-=,则首项1a 的取值范围是 .11.(3分)在数列{}*()n a n N ∈中,12a =,n S 是其前n 项和,当2n …时,恒有n a ,n S ,2n S -成等比数列,则2lim(1)n n n n a →∞++= .12.(3分)设集合{2|016n A n =剟,}n N ∈,它共有136个二元子集,如0{2,12},1{2,22}⋯等等.记这136个二元子集为1B ,2B ,3B ,136B ⋯,.设{}*,(1136,)i B x y i i N =∈剟,定义1()||S B x y =-,则123136()()()()S B S B S B S B ++⋯+= .(结果用数字作答) 二、选择题13.(3分)已知ϕ是常数,那么“tan 2ϕ=”是“si n 2c o s 5s i n (x x x ϕ+=+等式对任意x R∈恒成立”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件D .既不充分也不必要条件14.(3分)已知ϕ是常数,如果函数5cos(2)y x ϕ=-+的图象关于点4(,0)3π中心对称,那么||ϕ的最小值为( ) A .3πB .4π C .6π D .2π 15.(3分)某个命题与正整数n 有关,如果当()n k k N +=∈时命题成立,那么可推得当1n k =+时命题也成立. 现已知当7n =时该命题不成立,那么可推得( ) A .当6n =时该命题不成立 B .当6n =时该命题成立 C .当8n =时该命题不成立D .当8n =时该命题成立16.(3分)已知*n N ∈,实数x ,y 满足关系式2(2)23n x y nx n +=++,若对于任意给定的*n N ∈,当x 在[1-,)+∞上变化时,x y +的最小值为n M ,则lim (n n M →∞= )A .6B .0C .4D .1三、解答题17.在数列{}n a 中,112a =,43a =,且满足*212,n n n a a a n N +++=∈. (1)求数列{}n a 的通项公式; (2)设*1,(21)n n b n N n a =∈-,求数列{}n b 的前n 项和n T .18.设函数22()2cos(2)4sin 3f x x x π=-+,定义域为R .(1)求函数()f x 的最小正周期,并求出其单调递减区间;(2)求关于x 的方程()2f x =19.已知函数2()(1)f x x =-,{}n a 是公差为d 的等差数列,{}n b 是公比为(,1)q q R q ∈≠的等比数列.且1(1)a f d =-,9(1)a f d =+,2(1)b f q =-,4(1)b f q =+. (1)分别求数列{}n a ,{}n b 的通项公式;(2)已知数列{}n c 满足:*112233()n n n b c b c b c b c a n N +++⋯+=∈,求数列{}n c 的通项公式.20.已知常数R λ∈且3λ>-,在数列{}*()n a n N ∈中,首项1a λ=,n S 是其前n 项和,且*143,n n S a n N +=+∈.(1)设*12,n n n b a a n N +=-∈,证明数列{}n b 是等比数列,并求出{}n b 的通项公式; (2)设*,2n n na c n N=∈,证明数列{}n c 是等差数列,并求出{}n c 的通项公式; (3)若当且仅当7n =时,数列{}n S 取到最小值,求λ的取值范围.21.已知函数()sin()(0f x x ωϕω=+>,0)ϕπ<<的最小正周期为π,且直线2x π=-是其图象的一条对称轴. (1)求函数()f x 的解析式;(2)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且A B C <<,cos a B =,若C 角满足f (C )1=-,求a b c ++的取值范围;(3)将函数()y f x =的图象向右平移4π个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =,已知常数R λ∈,*n N ∈,且函数()()()F x f x g x λ=+在(0,)n π内恰有2021个零点,求常数λ与n 的值.2018-2019学年上海市杨浦区控江中学高一(下)期末数学试卷参考答案与试题解析一、填空题1.(3分)函数arcsin(2)y x =-的定义域 [1,3] . 【解答】解:要使arcsin(2)y x =-有意义,则121x --剟;13x ∴剟;∴原函数的定义域为[1,3].故答案为:[1,3].2.(3分)函数2tan()13y x ππ=++的最小正周期为 1 .【解答】解:函数2tan()13y x ππ=++的最小正周期为:1T ππ==.故答案为:1.3.(3分)已知数列{}n a 是等比数列,公比为q ,且2468a a a =,754a =,则q = 3 . 【解答】解:数列{}n a 是等比数列,公比为q ,且2468a a a =,754a =, ∴3511161854a q a q a q a q ⎧=⎪⎨=⎪⎩,解得3q =. 故答案为:3.4.(3分)已知tan 3α=,则226cos 3sin cos 3sin cos 2sin αααααα-=- 13 . 【解答】解:tan 3α=,则2226cos 3sin cos 63tan 6913sin cos 2sin 3tan 29293tan ααααααααα---===---⨯. 故答案为:13.5.(3分)在ABC ∆中,角A ,B ,C 所对的边为a ,b ,c ,若4a =,6b =,9c =,则角C = 29arccos48π- . 【解答】解:ABC ∆中,4a =,6b =,9c =,由余弦定理得22246929cos 24648C +-==-⨯⨯,有(0,)C π∈,所以29arccos48C π=-. 故答案为:29arccos48π-. 6.(3分)在ABC ∆中,角A 所对的边为a ,若2a =,且ABC ∆的外接圆半径为2,则A = 6π,或56π .【解答】解:2a =,且ABC ∆的外接圆半径为2,∴由正弦定理2sin a R A =,可得:24sin A =,可得1sin 2A =, (0,)A π∈, 6A π∴=,或56π. 故答案为:6π,或56π.7.(3分)已知数列{}n a 满足15a =,123n n a a +=-,*n N ∈,则数列{}n a 的通项公式为n a = 23n +. .【解答】解:15a =,123n n a a +=-, 132(3)n n a a +∴-=-.又15a =,故数列{3}n a -是首项为2,公比为2的等比数列.32n n a ∴-=,∴23n n a =+.故答案为:23n +.8.(3分)已知数列{}n a 的通项公式为124,2(*),21n n n n ka k N n k -+=⎧⎪=∈⎨=-⎪⎩,n S 是其前n 项和,则18S = 727 .(结果用数字作答)【解答】解:124,2(*),21n n n n ka k N n k -+=⎧⎪=∈⎨=-⎪⎩, 可得1813172418()()S a a a a a a =++⋯++++⋯+8(122)(81240)=++⋯++++⋯+91219(840)727122-=+⨯⨯+=-. 故答案为:727.9.(3分)已知{}1110,1,n n a a n S a <-为等差数列若且它的前项和有最大值,那么当n S 取得最小正值时,n = 19 . 【解答】解:n S 有最大值, 0d ∴<则1011a a >, 又11101a a <-, 11100a a ∴<< 10110a a ∴+<,20120101110()10()0S a a a a =+=+<, 1910190S a =>又121011120a a a a a >>⋯>>>>109210S S S S ∴>>⋯>>>,10111920210S S S S S >>⋯>>>>又191231910119()0S S a a a a a -=++⋯+=+< 19S ∴为最小正值故答案为:1910.(3分)已知无穷等比数列{}n a 的首项为1a ,公比为q ,且13lim()1n n qq a →∞+-=,则首项1a 的取值范围是 [2,3)(3⋃,4) .【解答】解:无穷等比数列{}n a 的首项为1a ,公比为q ,且13lim()1n n qq a →∞+-=, ①1q =时,1411a -=,解得,12a =; ②||1q <时,且0q ≠,可得10q -<<,或01q <<,13lim()1n n qq a →∞+-=, 131qa +=,则13a q =+, 又233q <+<或314q <+<所以首项1a 的取值范围是:[2,3)(3⋃,4). 故答案为:[2,3)(3⋃,4).11.(3分)在数列{}*()n a n N ∈中,12a =,n S 是其前n 项和,当2n …时,恒有n a ,n S ,2n S -成等比数列,则2lim(1)n n n n a →∞++= 2- .【解答】解:数列{}*()n a n N ∈中,12a =,n S 是其前n 项和,当2n …时,恒有n a ,n S ,2n S -成等比数列,可得2(2)n n n S a S =-,2n …时,21()(2)n n n n S S S S -=--,化简可得1221n n S S --=, 2{}nS 是等差数列,首项为1,公差为1, 所以21(1)1nn n S =+-=, 所以2n S n=,当2n …时,可得2221(1)n a n n n n -=-=--,12a =, 所以:2222(1)lim(1)lim 2n n n n n n n a n n→∞→∞-++++==--.故答案为:2-.12.(3分)设集合{2|016n A n =剟,}n N ∈,它共有136个二元子集,如0{2,12},1{2,22}⋯等等.记这136个二元子集为1B ,2B ,3B ,136B ⋯,.设{}*,(1136,)i B x y i i N =∈剟,定义1()||S B x y =-,则123136()()()()S B S B S B S B ++⋯+= 1835028 .(结果用数字作答) 【解答】解:由题意可得:123136()()()()S B S B S B S B ++⋯+10201602131161151416141615(222222)(222222)(2222)(22)=-+-+⋯⋯+-+-+-+⋯⋯+-+⋯⋯+-+-+-16215152011416152(21)2(21)2(21)1621522222212121---=-⨯+-⨯+⋯⋯+-⨯+----1716215114152152(222)(16152222)=⨯+-++⋯⋯+-+⨯+⋯⋯+⨯+151716172(21)2152(218)21-=⨯+----1721420=⨯+ 1835028=.故答案为:1835028. 二、选择题13.(3分)已知ϕ是常数,那么“tan 2ϕ=”是“si n 2c o s 5s i n (x x x ϕ+=+等式对任意x R∈恒成立”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件D .既不充分也不必要条件【解答】解:sin 2cos )x x x x +=+,cosϕ=sin ϕ=,则tan 2ϕ=.sin 2cos )x x x ϕ∴+=+.∴ “tan 2ϕ=”是“sin 2cos )x x x ϕ+=+等式对任意x R ∈恒成立”的充要条件.故选:C .14.(3分)已知ϕ是常数,如果函数5cos(2)y x ϕ=-+的图象关于点4(,0)3π中心对称,那么||ϕ的最小值为( )A .3πB .4π C .6π D .2π 【解答】解:函数5cos(2)y x ϕ=-+的图象关于点4(,0)3π中心对称,所以442()5cos(2)5cos()0333f πππϕϕ=+=+=,即2()32k k Z ππϕπ+=+∈,解得()6k k Z πϕπ=-∈,当0k =时6πϕ=-.所以||6πϕ=.故选:C .15.(3分)某个命题与正整数n 有关,如果当()n k k N +=∈时命题成立,那么可推得当1n k =+时命题也成立. 现已知当7n =时该命题不成立,那么可推得( ) A .当6n =时该命题不成立B .当6n =时该命题成立C .当8n =时该命题不成立D .当8n =时该命题成立【解答】解:由题意可知,原命题成立则逆否命题成立, ()P n 对7n =不成立,()P n 对6n =也不成立,否则6n =时,由由已知推得7n =也成立. 与当7n =时该命题不成立矛盾 故选:A .16.(3分)已知*n N ∈,实数x ,y 满足关系式2(2)23n x y nx n +=++,若对于任意给定的*n N ∈,当x 在[1-,)+∞上变化时,x y +的最小值为n M ,则lim (n n M →∞= )A .6B .0C .4D .1【解答】解:22224lim()lim()2(2)666(2)322n n x n x x x y x x x x n x x →∞→∞++=+=+=++-=++++…,当且仅42(2),12x x x +=-+… 即2x 时取等号,故lim 6n n M →∞=,故选:A . 三、解答题17.在数列{}n a 中,112a =,43a =,且满足*212,n n n a a a n N +++=∈. (1)求数列{}n a 的通项公式; (2)设*1,(21)n n b n N n a =∈-,求数列{}n b 的前n 项和n T .【解答】解:(1)数列{}n a 中,满足*212,n n n a a a n N +++=∈.所以数列{}n a 为等差数列. 由于112a =,43a =,所以公差312341d -==--, 故123(1)153n a n n =--=-. (2)由于153n a n =-,所以11111()(21)3(2)62n n b n a n n n n ===--++所以111111(1)63242n T n n =-+-+⋯+-+,1111()4612n n =-+++. 18.设函数22()2cos(2)4sin 3f x x x π=-+,定义域为R .(1)求函数()f x 的最小正周期,并求出其单调递减区间;(2)求关于x 的方程()2f x = 【解答】解:(1)函数22()2cos(2)4sin 2cos22(1cos2))233f x x x x x x x ππ=-+-+-=-+.所以函数()f x 的最小正周期为:T π= 令3222()232k x k k Z πππππ+-+∈剟,解得511()1212k x k k Z ππππ++∈剟, 所以单调递减区间为511[,],1212k k k Z ππππ++=.(2)令)223x π-+=,即1sin(2)32x π-=-.解得(1)(),2126k k x k Z πππ=+--+∈. 19.已知函数2()(1)f x x =-,{}n a 是公差为d 的等差数列,{}n b 是公比为(,1)q q R q ∈≠的等比数列.且1(1)a f d =-,9(1)a f d =+,2(1)b f q =-,4(1)b f q =+. (1)分别求数列{}n a ,{}n b 的通项公式;(2)已知数列{}n c 满足:*112233()n n n b c b c b c b c a n N +++⋯+=∈,求数列{}n c 的通项公式. 【解答】解:(1)2()(1)f x x =-,1(1)a f d =-,9(1)a f d =+, 可得21(2)a d =-,29a d =,则22(2)8d d d --=,解得1d =-,19a =,可得10n a n =-;由2(1)b f q =-,4(1)b f q =+. 可得22(2)b q =-,24b q =, 则22422(2)b q q b q ==-,解得3(1q =舍去),21b =, 则23n n b -=;(2)当1n =时,111b c a =,即1193c =,解得127c =;2n …时,1122111n n n b c b c b c a ---++⋯+=,又1122n n n b c b c b c a ++⋯+=,两式相减可得11n n n n b c a a d -=-==-, 即有21()3n n c -=-.2n …,综上可得227,11(),23n n n c n -=⎧⎪=⎨-⎪⎩….20.已知常数R λ∈且3λ>-,在数列{}*()n a n N ∈中,首项1a λ=,n S 是其前n 项和,且*143,n n S a n N +=+∈.(1)设*12,n n n b a a n N +=-∈,证明数列{}n b 是等比数列,并求出{}n b 的通项公式; (2)设*,2nn n a c n N =∈,证明数列{}n c 是等差数列,并求出{}n c 的通项公式; (3)若当且仅当7n =时,数列{}n S 取到最小值,求λ的取值范围.【解答】解:(1)证明:首项1a λ=,n S 是其前n 项和,且*143,n n S a n N +=+∈,可得143n n S a -=+,2n …,相减可得1144n n n a a a +-=-, 即有1122(2)n n n n a a a a +--=-, 可得12n n b b -=,即有数列{}n b 是公比为2的等比数列;由12143a a a +=+,可得233a λ=+,2123a a λ-=+, 可得1(3)2n n b λ-=+,*n N ∈;(2)由(1)可得112(3)2n n n a a λ-+-=+, 113224n n n n a a λ+++-=, 即为134n n c c λ++-=,可得数列{}n c 是公差为34λ+的等差数列,由1122a c λ==,可得333(1)2444n c n n λλλλ++-=+-=+,*n N ∈; (3)11a S λ==,143(3)2(3)2n n n n S a n λλ+=+=++-, 由111(3)2(3)2(3)(1)2(3)2n n n n n n S S n n λλλλ--+-=++--+---12(23)n n n λλ-=++,由题意可得16n 剟时,12(23)0n n n λλ-++<恒成立, 即为32nnλ->+,由33221n n n =++在16n 剟递增, 可得94λ->,即94λ<-;又7n …时,12(23)0n n n λλ-++>恒成立, 即为32nnλ-<+,由33221n n n =++在7n …递增, 可得219λ-<,即73λ>-. 综上可得7934λ-<<-.21.已知函数()sin()(0f x x ωϕω=+>,0)ϕπ<<的最小正周期为π,且直线2x π=-是其图象的一条对称轴. (1)求函数()f x 的解析式;(2)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且A B C <<,cos a B =,若C 角满足f (C )1=-,求a b c ++的取值范围;(3)将函数()y f x =的图象向右平移4π个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =,已知常数R λ∈,*n N ∈,且函数()()()F x f x g x λ=+在(0,)n π内恰有2021个零点,求常数λ与n 的值. 【解答】解:(1)依题意,222T ππωπ===, 2()22k ππϕπ⨯-+=+,()k Z ∈,即2πϕ=,所以()sin()sin(2)cos22f x x x x πωϕ=+=+=.(2)f (C )cos21C ==-,所以90C =︒, 90A B ∴+=︒,cos sin B A ∴=, cos sin a B A ∴==,即1sin ac A==,sin sin sin cos )114a b a b A B A A A π∴+=+=+=+=+, 因为A B C <<,所以(0,)4A π∈,所以(44A ππ+∈,)2π,sin()(42A π∴+∈,1),所以)(14a b A π+=+∈,所以1)a b c ++∈.(3)依题意,将函数()y f x =的图象向右平移4π个单位,可得: cos2()cos(2)sin 242y x x x ππ=-=-=,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍得到sin y x =, ()sin g x x ∴=,所以2()cos2sin 2sin sin 1F x x x x x λλ=+=-++当0λ=时,()cos2F x x =,则()F x 在(0,)n π内的零点个数为偶数个, ()F x 在(0,)n π内恰有2021个零点,为奇数个零点,故0λ≠,所以当sin x =()0F x =,0≠,1=±,即1λ=±,且n 为奇数.①若1λ=,则13()120212n -⨯+=,解得40433n =,不是整数,舍去; ②若1λ=-,则13()220212n -⨯+=,解得1347n =. 综上1λ=-,1347n =.。
上海杨浦实验学校 高一数学理期末试题含解析
上海杨浦实验学校高一数学理期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 若函数的定义域为,则函数的定义域是A .B.C.D.参考答案:C2. 已知锐角三角形的边长分别为1,3,a,则a的取值范围是()A.(8,10)B.C.D.参考答案:B【分析】根据大边对大角定理知边长为所对的角不是最大角,只需对其他两条边所对的利用余弦定理,即这两角的余弦值为正,可求出的取值范围。
【详解】由题意知,边长为1所对的角不是最大角,则边长为或所对的角为最大角,只需这两个角为锐角即可,则这两个角的余弦值为正数,于此得到,由于,解得,故选:C。
【点睛】本题考查余弦定理的应用,在考查三角形是锐角三角形、直角三角形还是钝角三角形,一般由最大角来决定,并利用余弦定理结合余弦值的符号来进行转化,其关系如下:为锐角;为直角;为钝角.3. 根据表格中的数据,可以断定方程的一个根所在的区间是()A. (-1,0) B.(0,1) C.(1,2) D.(2,3)参考答案:C4. 一个三角形具有以下性质:(1)三边组成一个等差数列;(2)最大角是最小角的2倍.则该三角形三边从小到大的比值为()A.4:5:6 B.3:5:7 C. 4:6:8 D.3:5:6参考答案:A5. 如果对>0,>0,有恒成立,那么实数的取值范围是()A.B.C. D.参考答案:D6. 定义在R上的函数满足当A.335 B.338 C.1678D.2012参考答案:B7. 已知两点M(-2,0),N(2,0),点P满足=12,则点P的轨迹方程为()A. B. C. D.参考答案:B8.A.B.C.D.参考答案:C略9. 函数是定义在R上的减函数,且,则满足的解集为()A .B .C .D .参考答案:C10. 840和1764的最大公约数是()A.84 B.12 C.168 D.252参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. (5分)已知偶函数f(x)对任意x∈R都有f(x+3)=﹣,且当x∈[﹣3,﹣2]时,f(x)=4x,则f=f(6×335+5)=.参考答案:考点:函数奇偶性的性质;函数的值.专题:函数的性质及应用.分析:根据f(x+3)=﹣求出函数的周期,由偶函数的性质、函数的周期性将f转化为f(﹣5),利用恒等式和解析式求出f的值.解答:因为偶函数f(x)满足f(x+3)=﹣,所以f(x+6)=﹣=f(x),则函数f(x)的周期是6,因为当x∈[﹣3,﹣2]时,f(x)=4x,函数f(x)是偶函数,所以f=f(6×335+5)=f(5)=f(﹣5)=﹣=,故答案为:.点评:本题考查利用函数的奇偶性、周期性求函数的值,考查了转化思想,解题的关键是求出函数的周期.12. 设x,y∈R+,且x+4y=40,则lgx+lgy的最大值为.参考答案:2【考点】对数的运算性质.【分析】利用基本不等式的性质、对数的运算性质即可得出.【解答】解:∵x,y∈R+,且x+4y=40,∴40≥,解得xy≤100,当且仅当x=4y=20时取等号.则lgx+lgy=lg(xy)≤2,因此其最大值为2.故答案为:2.【点评】本题考查了基本不等式的性质、对数的运算性质,考查了推理能力与计算能力,属于中档题.13. 计算:________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海市杨浦区2019年高一数学下学期期末调研测试模拟试题一、选择题(本大题共12个小题,每小题3分,共36分). 1. 已知等差数列{}n a ,2816a a +=,41a =,则6a 的值为( ) A .15 B .17 C . 22 D .64 2. 若sin 0tan αα<,且cos tan 0αα⋅<,则角α是( ) A .第一象限 B .第二象限 C .第四象限 D .第三象限 3. 下列命题中正确的是( )A . a b >,c d a c b d >⇒->-B .a ba b c c>⇒> C .22ac bc a b >⇒> D . ac bc a b <⇒< 4. 等差数列{}n a 的前n 项和为n S ,且634S S =,则96SS =( )A .53 B . 23 C. 94D .4 5. 已知不等式250ax x b ++>的解集是{}|23x x <<,则不等式250bx x a -+>的解集是( ) A .1123x x ⎧⎫-<<-⎨⎬⎩⎭ B .1123x x x ⎧⎫<->-⎨⎬⎩⎭或 C. {}32x x x <->-或 D .{}32x x -<<-6. 已知向量m 、n 满足2m =,3n =,17m n -=,则m n +=( ) A .3 BD .97. 在ABC ∆中,若2cos sin sin B A C =,则ABC ∆的形状是( )A . 直角三角形B .等腰三角形 C. 等腰直角三角形 D .等腰或直角三角形8. 实数,x y 满足101010x x y x y -≥⎧⎪+-≥⎨⎪-+≥⎩,则2z x y =-的取值范围是( )A .[]0,2B .[)0,+∞ C. []1,2- D .(],0-∞ 9. 若函数()sin 0,0,2y A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭在一个周期内的图象如图所示,且在y 轴上的截距为,,M N 分别是这段图象的最高点和最低点,则ON 在OM 方向上的投影为( )A. B .D10. 在ABC ∆中,若23C π=,3AB =,则ABC ∆的周长为( ) A . 6sin 33A π⎛⎫++ ⎪⎝⎭ B . 6sin 36A π⎛⎫++ ⎪⎝⎭C.33A π⎛⎫++ ⎪⎝⎭ D.36A π⎛⎫++ ⎪⎝⎭ 11. 设四边形ABCD 为平行四边形,6AB =,4AD =.若点,M N 满足3BM MC =,2DN NC =,则AM NM ⋅=( )A .20B .9 C. 15 D .6 12. 已知0x >,0y >,且211x y+=,若2x y m +>恒成立,则实数m 的取值范围是( ) A . (,6)-∞ B . (],6-∞ C. (],8-∞ D .(),8-∞ 第Ⅱ卷(非选择题)二、填空题(本大题共5分,每小题4分,共20分) 13.sin 240︒= .14. 已知tan 2α=,则 s in cos αα= . 15. 已知函数()sin 23f x x π⎛⎫=+⎪⎝⎭,将其图像向右平移()0ϕϕ>个单位长度后得到函数()g x 的图像,若函数()g x 为奇函数,则ϕ的最小值为 .16. 已知等比数列{}n a 中,13a =,481a =,若数列{}n b 满足3log n n b a =,则数列11n n b b +⎧⎫⎨⎬⎩⎭的 前n 项和n S = .17. 在ABC ∆中,,,a b c 分别为角,,A B C 的对边,若2b ac =,22a c ac bc -=-,则sin cb B= .三、解答题 (共44分.解答应写出文字说明、证明过程或演算步骤.) 18. 已知数列{}n a 的前n 项和n S 满足:21n n S a =-.(1)求数列{}n a 的通项公式;(2)设数列{}n b 满足21n n b a n =+-,求数列n b 的前n 项和n T 19. 已知向量()sin ,cos a x x =,()sin ,sin b x x =,()1,0c =- (1)若3x π=,求向量a 、c 的夹角;(2)若3,84x ππ⎡⎤∈-⎢⎥⎣⎦,求函数()f x a b =⋅的最值以及相应的x 的取值. 20. 在ABC ∆中,角,,A B C 的对边分别为,,a b c,且cos cos CA =. (1)求角A 的值; (2)若6B π∠=,BC边上的中线AM =ABC ∆的面积.21. 已知数列{}n a ,{}n b 满足111a b ==,23a =,n S 为数列{}n a 的前n 项和,且()1-121(2,)n n n S S S n n N *++=+≥∈,又121n n b b +=+对任意n N *∈都成立(1)求数列{}n a 的通项公式;(2)设1n n c b =+,证明{}n c 为等比数列; (3)求数列{}n n a c ⋅的前n 项和n T . 数学参考答案 一、选择题1-5: ADCCA 6-10: ABBDC 11、12:BD 二、填空题13. 2-14. 25 15. 6π16.1n n +17. 3 三、解答题18. 解:(1)当1n =时,1121a a =-,所以113a =, 当2n ≥时,1n n n a S S -=-,即12n n n a a a -=-+,13n n a a -=,113n n a a -=, 所以数列{}n a 是首项为13,公比也为13的等比数列, 所以1111333n nn a -⎛⎫⎛⎫=⋅= ⎪⎪⎝⎭⎝⎭,n N *∈.(2)因为()()121213nn n b n a n ⎛⎫=-+=-+ ⎪⎝⎭231111135(21)3333nn T n ⎛⎫⎛⎫⎛⎫⎛⎤⎛⎫⎛⎫⎛⎫=+++++++-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎥ ⎪ ⎪ ⎪⎝⎦⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭所以()231111(13521)3333nn ⎛⎫⎛⎫⎛⎫⎛⎫=++++-+++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭211123nn ⎛⎫⎛⎫=+- ⎪ ⎪⎪⎝⎭⎝⎭所以数列n b 的前n 项和211123nn T n ⎛⎫⎛⎫=-+ ⎪ ⎪⎪⎝⎭⎝⎭19. 解:(1)31,2a ⎛⎫= ⎪ ⎪⎝⎭,()1,0c =-所以3cos ,a c a c a c ⋅〈〉==-又()0,a c π<<,所以5,6a c π〈〉=(2)()21cos 21sin sin cos sin 222x f x a b x x x x -=⋅=+=+1sin(2)242x π=-+.又384x ππ-≤≤,244x πππ-≤-≤所以1sin 242x π⎛⎫-≤-≤ ⎪⎝⎭所以8x π=-,()f x 的最小值为12, 4x π=,()f x 的最小值为1.20. (1cos cos C A =cos cos CA =,2sin cos cos cos B A C A A C =2sin cos cos cos B A A C C A =+2sin cos cos sin cos )B A A C C A =+()A CB =+=∴cos 2A =,0A π<<,∴6A π=.(2)∵6B π∠=,23C A B ππ=--=,可知ABC ∆为等腰三角形, 在AMC ∆中,由余弦定理,得2222cos120AM AC MC AC MC =+-⋅︒,即2272cos12022b b b b ⎛⎫=+-⨯⨯⨯︒ ⎪⎝⎭,∴2b =,ABC ∆的面积21sin 2S b C ==21. 解:(1)()1121n n n S S S +-+=+,∴()2121n n n S S S +++=+ 两式作差得:212n n n a a a +++=∴当2n ≥时,数列{}n a 是等差数列,首项2a 为3,公差为2,当1n =时成立 ∴()()322211n a n n n =+-=-≥ (2)证明:因为()1121n n b b ++=+ 若1n n c b =+,则12n n c c +=,因为12n nc c += 所以数列{}n c 是以2为公比2为首项的等比数列 (3)因为()212nn n a c n ⋅=-所以11223311n n n n n T a c a c a c a c a c --=+++++()()1231123252232212n n n n -=⋅+⋅+⋅++-+-2n T = ()()234112+32+52++232212n n n n +⋅⋅⋅-+-()123112222222212n n n T n +-=⋅+⋅+⋅++⋅--⋅()16232n n T n +=+-高一下学期期末模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合{}220A x x x =+->,{}2450B x x x =--<,则A B ⋂=( ) A .()1,5 B .()2,1- C .()5,2- D .()2,2- 2.若数列{}n a 中,111,30n n a a a +=+=,则5a =( ) A .27- B .27 C .81- D .813.若直线210x y -+=与直线230ax y +-=平行,则实数a 的值为( ) A .2- B .4- C .2 D .44.若直线y x b =+与圆224230x y x y +-++=有公共点,则实数b 的取值范围是( ) A .[]2,2- B .[]3,1- C .[]4,0- D .[]5,1--5.已知等差数列{}n a 的前n 项和为n S ,若4522,3S a S ==,则{}n a 的公差为( ) A .1- B .1 C .2- D .26.圆()()22213x y -+-=关于直线3560x y ++=对称的圆的方程为( ) A .()()22233x y +++= B .()2213x y -+= C .()()22143x y +++= D .()2233x y ++=7.设,m n 是两条直线,,αβ是两个不同的平面,给出下列条件,其中不能得到αβ⊥的是( ) A .,//,m m n n βα⊂⊥ B .//,//,m m n n αβ⊥ C .,,m n m n αβ⊥⊂⊂ D .,//,//m m n βαβ⊥8.中国古代数学著作《算法统宗》中有这样一个问题,三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了 6天后到达目的地,请问第二天走了多里?”( )A. 113 里B. 107 里C. 96 里D. 87 里9.如图是某几何体的三视图,则该几何体的体积为( )A. 18B. 24C.28D. 3210.若0,0,412a b a b ab >>++=,则ab 的最大值为( ) A .2 B .4 C .6 D .811.若ABC ∆的内角,,A B C 的对边分别为,,a b c ,且1,2b c ==,面积4cos 3S A =,则a =( )ABC12.已知矩形ABCD 的顶点都在球O的球面上,4,AB BC ==O 的表面积为40π,则四棱锥O ABCD -的高为( )AC .1D .2 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知点()()1,2,1,3,4,1A B --,则坐标原点O 到AB 中点的距离为 . 14.若实数,x y 满足不等式组10,240,360,x y x y x y -+≥⎧⎪+-≥⎨⎪+-≤⎩则23z x y =+的最小值为 .15.已知圆锥的底面半径为1,母线长为3,侧面展开图是扇形AOB ,则该扇形圆心角AOB ∠的弧度数为 .16.已知数列{}n a 的前n 项和2n S n =,若122311113979n n a a a a a a ++++=,则n = . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 在四棱锥P ABCD -中,PC ⊥平面,//,ABCD AB DC DC AC ⊥.求证:(1)DC ⊥平面PAC ; (2)平面PAB ⊥平面PAC .18.已知数列{}n a 的前n 项和为n S ,且22,2n S n kn a =-=. (1)求{}n a 的通项公式; (2)求10n n S a -的最小值.19.在ABC ∆中,内角,,A B C 的对边分别是,,a b c ,若3sin sin sin sin 2b B c C a A b C +=-.(1)求sin A 的值;(2)求cos 4B C π⎛⎫++ ⎪⎝⎭的值.20.如图,在四棱锥P ABCD -中,PD ⊥底面ABCD ,底面ABCD 为矩形,E 为PC 的中点,且3,2,4PD AD AB ===.(1)过点A 作一条射线AG ,使得//AG BD ,求证:平面//PAG 平面BDE ; (2)若点F 为线段PC 上一点,且AF BD ⊥,求四棱锥F ABCD -的体积. 21.已知数列{}n a 中,11a =,()12311231,2n n n a a a na a n n Z ++++++=≥∈. (1)求数列{}n a 的通项公式n a ; (2)求数列{}2n n a 的前n 项和n T .22.已知圆心在直线2y x =上的圆C 与直线:4350l x y ++=相切于点01,5x ⎛⎫⎪⎝⎭.(1)求0x 和圆C 的标准方程;(2)若直线y x t =-+与圆交于,A B两点,且AB =,求t 值;(3)若直线m 过()8,2-与圆C 交于()()1122,,,P x y Q x y 两点,且120x x ≠,求证:1211x x +为 定值.试卷答案一、选择题1-5: ADBDB 6-10: CCCCB 11、12:DA 二、填空题19315.23π16. 39三、解答题17.证明:(1)∵PC⊥平面ABCD,DC⊂平面ABCD,∴PC DC⊥,∵,DC AC AC PC C⊥⋂=,,AC PC⊂平面PAC,∴DC⊥平面PAC.(2)∵//AB DC,DC⊥平面PAC,∴AB ⊥平面PAC ,又AB ⊂平面PAB ,∴平面AB ⊥平面PAC .18.解:(1)由3sin sin sin sin 2b B c C a A b C +=-及正弦定理,得22232b c a bc +=-,∴由余弦定理,得2223cos 24b c a A bc +-==-,∴sin A (2)在ABC ∆中,B C A π+=-,∴cos cos cos 444B C A A ππππ⎛⎫⎛⎫⎛⎫++=-+=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3cos cos sin sin 444A A ππ⎛⎛⎫=-+=-+ ⎪ ⎝⎭⎝⎭8=. 20. (1)证明:在矩形ABCD 中,连接AC 和BD 交于点O ,连接OE ,则O 是AC 的中点, ∵E 是PC 的中点,∴OE 是PAC ∆的中位线,则//OE PA , 又OE ⊂平面BDE ,PA ⊄平面BDE ,∴//PA 平面BDE . 又//AG BD ,同理得//AG 平面BDE . ∵PA AG A ⋂=,∴平面//PAG 平面BDE . (2)解:过F //FK PD 交CD 于K , ∵PD ⊥平面ABCD ,∴FK ⊥平面ABCD ,∴FK BD ⊥,∵,AF BD AF FK F ⊥⋂=,,AF FK ⊂平面AFK , ∴BD ⊥平面AFK ,连接AK ,则AK BD ⊥,由ABCD 是矩形,4,2AB AD ==,得1DK =, 由 //FK PD 得FK DK PD CD =,∴94FK =, 又矩形ABCD 的面积为 8,∴198634F ABCD V -=⨯⨯=.21.解:(1)∵()*12311232n n n a a a na a n N ++++++=∈, ∴()()123123122n n na a a n a a n -++++-=≥,两式相减得1122n n n n nna a a ++=-,∴()()1132n n n a n na ++=≥, ∴数列{}n na 从第二项起,是以2为首项,3为公比的等比数列, ∴()2232n n na n -=⋅≥, 故21,1,23,2n n n a n n-=⎧⎪=⎨⋅≥⎪⎩(2)由(1)可知当2n ≥时,2223n n n a n -=⋅.当2n ≥时,0121436323n n T n -=+⋅+⋅++⋅,()121334321323n n n T n n --=+⋅++-⋅+⋅,两式相减得()1113222n n T n n -⎛⎫=+-≥ ⎪⎝⎭. 又∵111T a ==也满足上式,∴()1*11322n n T n n N -⎛⎫=+-∈ ⎪⎝⎭. 22.解:(1)由034505x ++=,得075x =-,过点01,5x ⎛⎫⎪⎝⎭且与l 垂直的直线方程为137545y x ⎛⎫-=+ ⎪⎝⎭,此直线与直线2y x =的交点为()1,2C ,设圆的半径为r ,则2227112955r ⎛⎫⎛⎫=--+-= ⎪ ⎪⎝⎭⎝⎭,∴圆C 的方程为()()22129x y -+-=. (2)圆心()1,2C 到直线y x t =-+的距离d =,由AB ==292d =,∴()23922t -=,∴0t =或6t =.(3)显然直线8x =-与圆C 没有公共点,直线m 的斜率存在,设m 的方程为()28y k x -=+, 将直线m 方程代入圆方程得()()222189x k x -++=,∴()()222211626480k x k x k ++-+-=则21221621k x x k -+=-+,()221222416264811k k x x k k --=-=++,∴1212121114x x x x x x ++==-.高一下学期期末模拟试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
