13.3 全等三角形的判定 能力培优训练(含答案)
人教版八年级数学上册第十二章《全等三角形》判定与性质培优练习(五)

第十二章《全等三角形》判定与性质培优练习(五)1.如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A (n,m),且(m﹣4)2+n2﹣8n=﹣16,过C点作∠ECF分别交线段AB、OB于E、F两点.(1)求A点的坐标;(2)若OF+BE=AB,求证:CF=CE;(3)如图(2),若∠ECF=45°,给出两个结论:OF+AE﹣EF的值不变;OF+AE+EF 的值不变,其中有且只有一个结论正确,请你判断出正确的结论,并加以证明和求出其值.2.如图1,我们定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形.(1)如图2,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=∠AEB.(2)如图3,在非等腰△ABE中,若四边形ABCD仍是互补等对边四边形,试问∠ABD =∠BAC=∠AEB是否仍然成立?若成立,请加以证明;若不成立,请说明理由.43.如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.(1)图①中有对全等三角形,并把它们写出来.(2)求证:G是BD的中点.(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立?如果成立,请予证明.4.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.【探究与发现】(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形【理解与应用】(2)填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是.(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD.5.如图,已知AB∥CD,点E在BC上且BE=CD,AB=CE,EF平分∠AED.(1)求证:△ABE≌△ECD;(2)猜测EF与AD的位置关系,并说明理由;(3)若DF=AE,请判断△AED的形状,并说明理由.6.如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2.(1)求A、B两点的坐标;(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.7.在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.(1)如图1,连接CE,求证:△BCE是等边三角形;(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间的数量关系,并证明.8.如图,在△ABC中,AB=AC,D、A、E在直线m上,∠ADB=∠AEC=∠BAC.(1)求证:DE=DB+EC;(2)若∠BAC=120°,AF平分∠BAC,且AF=AB,连接FD、FE,请判断△DEF的形状,并写出证明过程.9.教学实验:画∠AOB的平分线OC.(1)将一块最够大的三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别于OA,OB交于E,F(如图①).度量PE、PF的长度,PE PF(填>,<,=);(2)将三角尺绕点P旋转(如图②):①PE与PF相等吗?若相等请进行证明,若不相等请说明理由;②若OP=,请直接写出四边形OEPF的面积:.10.(1)如图(1)在△ABC中,∠ACB=2∠B,∠C=90°,AD为∠BAC的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)(2)如图(2)当∠C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.(3)如图(3)当∠ACB≠90°,AD为△ABC的外角∠CAF的平分线,交BC的延长线于点D,则线段AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.参考答案1.解:(1)(m﹣4)2+n2﹣8n=﹣16,即(m﹣4)2+(n﹣4)2=0,则m﹣4=0,n﹣4=0,解得:m=4,n=4.则A的坐标是(4,4);(2)∵AB⊥x轴,AC⊥y轴,A(4,4),∴AB=AC=OC=OB,∠ACO=∠COB=∠ABO=90°,又∵四边形的内角和是360°,∴∠A=90°,∵OF+BE=AB=BE+AE,∴AE=OF,∴在△COF和△CAE中,,∴△COF≌△CAE,得∴CF=CE;(3)结论正确,值为0.证明:在x轴负半轴上取点H,使OH=AE,∵在△ACE和△OCH中,,∴△ACE≌△OCH,∴∠1=∠2,CH=CE,又∵∠EOF=45°,∴∠HCF=45°,∴在△HCF和△ECF中,,∴△HCF≌△ECF,∴HF=EF,∴OF+AE﹣EF=0.2.解:(1)∵AE=BE,∴∠EAB=∠EBA,∵四边形ABCD是互补等对边四边形,∴AD=BC,在△ABD和△BAC中,,∴△ABD≌△BAC(SAS),∴∠ADB=∠BCA,又∵∠ADB+∠BCA=180°,∴∠ADB=∠BCA=90°,在△ABE中,∵∠EAB=∠EBA==90°﹣∠AEB,∴∠ABD=90°﹣∠EAB=90°﹣(90°﹣∠AEB)=∠AEB,同理:∠BAC=∠AEB,∴∠ABD=∠BAC=∠AEB;(2)仍然成立;理由如下:如图③所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,∵四边形ABCD是互补等对边四边形,∴AD=BC,∠ADB+∠BCA=180°,又∠ADB+ADG=180°,∴∠BCA=∠ADC,又∵AG⊥BD,BF⊥AC,∴∠AGD=∠BFC=90°,在△AGD和△BFC中,∴△AGD≌△BFC,∴AG=BF,在△ABG和△BAF中,∴△ABG≌△BAF,∴∠ABD=∠BAC,∵∠ADB+∠BCA=180°,∴∠EDB+∠ECA=180°,∴∠AEB+∠DHC=180°,∵∠DHC+∠BHC=180°,∴∠AEB=∠BHC.∵∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,∴∠ABD=∠BAC=∠AEB.3.解:(1)图①中全等三角形有:△ABF≌△CDE,△ABG≌△CDG,△BFG≌△DEG.故答案是:3;(2)∵AE=CF,∴AF=CE,∴在直角△ABF和直角△CDE中,,∴△ABF≌△CDE,∴BF=DE,在△DEG和△BFG中,,∴△DEG≌△BFG,∴BG=DG,即G是BD的中点;(3)结论仍成立.理由是:)∵AE=CF,∴AF=CE,在直角△ABF和直角△CDE中,,∴△ABF≌△CDE,∴BF=DE,在△DEG和△BFG中,,∴△DEG≌△BFG,∴BG=DG,即G是BD的中点.4.(1)证明:在△ADC与△EDB中,,∴△ADC≌△EDB;故答案为:△ADC≌△EDB;(2)解:如图2,延长EP至点Q,使PQ=PE,连接FQ,在△PDE与△PQF中,,∴△PEP≌△QFP,∴FQ=DE=3,在△EFQ中,EF﹣FQ<QE<EF+FQ,即5﹣3<2x<5+3,∴x的取值范围是1<x<4;故答案为:1<x<4;(3)证明:如图3,延长AD到M,使MD=AD,连接BM,∴AM=2AD,∵AD是△ABC的中线,∴BD=CD,在△BMD与△CAD中,,∴△BMD≌△CAD,∴BM=CA,∠M=∠CAD,∴∠BAC=∠BAM+∠CAD=∠BAM+∠M,∵∠ACB=∠Q+∠CAQ,AB=BC,∵∠ACQ=180°﹣(∠Q+∠CAQ),∠MBA=180°﹣(∠BAM+∠M),∴∠ACQ=∠MBA,∵QC=BC,∴QC=AB,在△ACQ与△MBA中,,∴△ACQ≌△MBA,∴AQ=AM=2AD.5.(1)证明:∵AB∥CD,∴∠B=∠C,在△ABE与△ECD中,,∴△ABE≌△ECD;(2)EF⊥AD,理由:∵△ABE≌△ECD,∴AE=DE,∵EF平分∠AED,∴EF⊥AD;(3)△AED是等边三角形,∵AE=DE,∵EF平分∠AED,∴DF=AD,∵DF=AE,∴AD=AE=DE,∴△AED是等边三角形.6.解:(1)∵a2﹣4a+20=8b﹣b2,∴(a﹣2)2+(b﹣4)2=0,∴a=2,b=4,∴A(0,2),B(4,0);(2)∵AD=OA+OD=8,BC=2OB=8,∴AD=BC,在△CAB与△AMD中,,∴△CAB≌△AMD,∴AC=AM,∠ACO=∠MAD,∵∠ACO+∠CAO=90°,∴∠MAD+∠CAO=∠MAC=90°,∴AC=AM,AC⊥AM;(3)过P作PG⊥y轴于G,在△PGA与△DHN中,,∴△PGA≌△DHN,∴PG=HN,AG=HD,∴AD=GH=8,在△PQG与△NHQ中,,∴△PQG≌△NHQ,∴QG=QH=GH=4,∴S△MQH=×4×2=4.7.(1)证明:∵∠ACB=90°,∠A=30°,∴∠ABC=60°,∵BD是△ABC的角平分线,∴∠DBA=∠ABC=30°,∴∠A=∠DBA,∴AD=BD,∵DE⊥AB,∴AE=BE,∴CE=AB=BE,∴△BCE是等边三角形;(2)证明:∵△BCE与△MNB都是等边三角形,∴BC=BE,BM=BN,∠EBC=∠MBN=60°,∴∠CBM=∠EBN,在△CBM和△EBN中,,∴△CBM≌△EBN(SAS),∴∠BEN=∠BCM=60°,∴∠BEN=∠EBC,∴EN∥BC;(3)解:DQ=AD+DP;理由如下:延长BD至F,使DF=PD,连接PF,如图所示:∵∠PDF=∠BDC=∠A+∠DBA=30°+30°=60°,∴△PDF为等边三角形,∴PF=PD=DF,∠F=60°,∵∠PDQ=90°﹣∠A=60°,∴∠F=∠PDQ=60°,∴∠BDQ=180°﹣∠BDC﹣∠PDQ=60°,∴∠BPQ=∠BDQ=60°,∴∠Q=∠PBF,在△PFB和△PDQ中,,∴△PFB≌△PDQ,∴DQ=BF=BD+DF=BD+DP,∵∠A=∠ABD,∴AD=BD,∴DQ=AD+DP.8.(1)证明:∵∠ADB=∠AEC=∠BAC,∴∠ADB+∠ABD+∠BAD=∠BAD+∠BAC+∠EAC=180°,∴∠ABD=∠EAC,在△ABD与△ACE中,,∴△ABD≌△AEC,∴BD=AE,∵DE=AD+AE,∴DE=DB+EC.(2)结论:△DEF为等边三角形理由:连接BF,CF.∵AF平分∠BAC,∠BAC=120°,∴∠FAB=∠FAC=60°,∵FA=AB=AC,∴△ABF和△ACF均为等边三角形∴BF=AF=AB=AC=CF,∠BAF=∠CAF=∠ABF=60°,∴∠BDA=∠AEC=∠BAC=120°,∴∠DBA+∠DAB=∠CAE+∠DAB=60°,∴∠DBA=∠CAE.在△BAD和△ACE中,,∴△ADB≌△CEA(AAS),∴BD=AE,∠DBA=∠CAE.∵∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE.在△BDF和△AEF中,,∴△DBF≌△EAF(SAS),∴DF=EF,∠BFD=∠AFE,∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,∴△DEF为等边三角形.9.(1)解:PE=PF;故答案为:=;(2)解:①PE=PF;理由如下:把三角尺绕点P顺时针旋转,使三角尺的两条直角边分别与OA,OB垂直于M、N,如图所示:则∠PME=∠PNF=90°,四边形OMPN是矩形∵OP平分∠AOB,∴PM=PN,∴四边形OMPN是正方形,∵∠AOB=∠PME=∠PNF=90°,∴∠MPN=90°,∵∠EPF=90°,∴∠MPE=∠FPN,在△PEM和△PFN中∴△PEM≌△PFN(ASA),∴PE=PF.②由①得:四边形OMPN是正方形,△PEM≌△PFN,∴OM=ON=OP=1,四边形OEPF的面积=正方形OMPN的面积=OM2=1;故答案为:1.10.解:(1)如图1所示,在AB上截取AE=AC,连接DE,∵AD平分∠BAC,∴∠1=∠2.在△ACD和△AED中,,∴△ACD≌△AED(SAS).∴∠AED=∠C=90,CD=ED,又∵∠ACB=2∠B,∠C=90°,∴∠B=45°.∴∠EDB=∠B=45°.∴DE=BE,∴CD=BE.∵AB=AE+BE,∴AB=AC+CD.(2)证明:在AB取一点E使AC=AE,在△ACD和△AED中,,∴△ACD≌△AED,∴∠C=∠AED,CD=DE,又∵∠C=2∠B,∴∠AED=2∠B,∵∠AED是△EDC的外角,∴∠EDB=∠B,∴ED=EB,∴CD=EB,∴AB=AC+CD;(3)AB=CD﹣AC证明:在BA的延长线AF上取一点E,使得AE=AC,连接DE,在△ACD和△AED中,,∴△ACD≌△AED(SAS),∴∠ACD=∠AED,CD=DE,∴∠ACB=∠FED,又∵∠ACB=2∠B,∴∠FED=2∠B,又∵∠FED=∠B+∠EDB,∴∠EDB=∠B,∴DE=BE,∴BE=CD,∴AB=CD﹣AC.。
八年级数学上第13章全等三角形13.3全等三角形的判定4具有特殊位置关系的三角形全等课冀教

精彩一题 1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月11日星期五2022/3/112022/3/112022/3/11
2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/112022/3/112022/3/113/11/2022 3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/112022/3/11March 11, 2022 4、享受阅读快乐,提高生活质量。2022/3/112022/3/112022/3/112022/3/11
解:∵△ABC≌△DEF, ∴∠ABC=∠E=71°,∠A=∠FDE=25°. ∴∠ACB=180°-∠A-∠ABC=84°. ∵CD 为∠ACB 的平分线,∴∠ACD=∠BCD=42°. ∵∠CDB=∠A+∠ACD=∠CDF+∠EDF,∴∠CDF=42°.
9.(2019·四川泸州)如图,AB∥CD,AD 和 BC 相交于点 O, OA=OD. 求证:OB=OC.
第十三章 全等三角形
第3节 命题与证明 第4课时 具有特殊位置关系的三角形
全等
提示:点击 进入习题
1C 2C 3C 4 见习题 5C
6C 7 见习题 8 见习题 9 见习题 10 见习题
答案显示
提示:点击 进入习题
11 见习题
答案显示
1.如图,在△ABC 和△DEF 中,AB=DE,AC=DF,BE=CF,
八上数学同步课时训练13.3.2.1 等边三角形的性质与判定 答案版
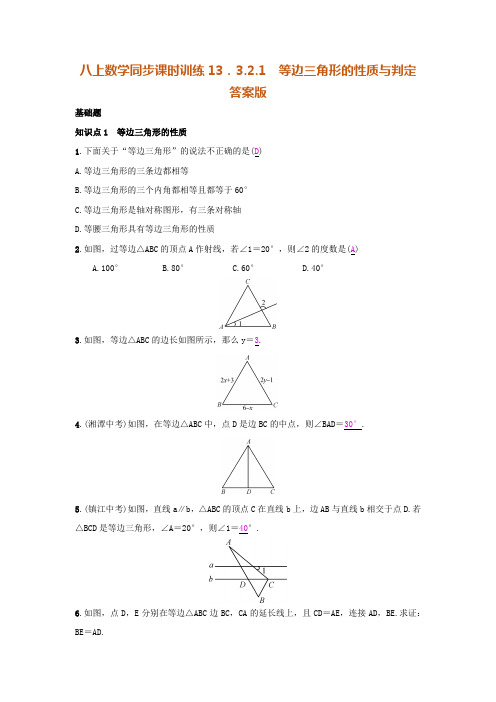
八上数学同步课时训练13.3.2.1 等边三角形的性质与判定答案版基础题知识点1 等边三角形的性质1.下面关于“等边三角形”的说法不正确的是(D)A.等边三角形的三条边都相等B.等边三角形的三个内角都相等且都等于60°C.等边三角形是轴对称图形,有三条对称轴D.等腰三角形具有等边三角形的性质2.如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是(A)A.100°B.80°C.60°D.40°3.如图,等边△ABC的边长如图所示,那么y=3.4.(湘潭中考)如图,在等边△ABC中,点D是边BC的中点,则∠BAD=30°.5.(镇江中考)如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1=40°.6.如图,点D,E分别在等边△ABC边BC,CA的延长线上,且CD=AE,连接AD,BE.求证:BE=AD.证明:∵△ABC 是等边三角形, ∴AB =AC ,∠BAC =∠ACB =60°. ∴∠BAE =∠ACD =120°. 在△BAE 和△ACD 中, ⎩⎪⎨⎪⎧AE =CD ,∠BAE =∠ACD ,AB =CA ,∴△BAE ≌△ACD(SAS). ∴BE =AD.知识点2 等边三角形的判定 7.下列说法中,正确的有(D )①三个内角都相等的三角形是等边三角形;②有两个角等于60°的三角形是等边三角形;③有一个角是60°的等腰三角形是等边三角形;④有两个角相等的等腰三角形是等边三角形.A.0个B.1个C.2个D.3个8.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA =OB =18 cm.若衣架收拢时,∠AOB =60°,如图2,则此时A ,B 两点之间的距离是18cm.9.如图,在△ABC 中,AC =BC ,∠ACB =120°,CE ⊥AB 于点D ,且DE =DC.求证:△CEB 为等边三角形.证明:∵CE ⊥AB ,且DE =DC ,∴BC =BE.∵AC =BC ,∠ACB =120°,CE ⊥AB , ∴∠ECB =12∠ACB =60°.又∵BC =BE ,∴△CEB 为等边三角形.10.(嘉兴中考)如图,在△ABC 中,AB =AC ,D 为AC 的中点,DE ⊥AB ,DF ⊥BC ,垂足分别为E ,F ,且DE =DF.求证:△ABC 是等边三角形.证明:∵AB =AC ,∴∠B =∠C. ∵DE ⊥AB ,DF ⊥BC , ∴∠DEA =∠DFC =90°. ∵D 为AC 的中点, ∴DA =DC , 又∵DE =DF ,∴Rt △ADE ≌Rt △CDF(HL). ∴∠A =∠C. ∴∠A =∠B =∠C. ∴△ABC 是等边三角形. 中档题11.如图,已知△ABC 是等边三角形,点B ,C ,D ,E 在同一直线上,且CG =CD ,DF =DE ,则∠E =(C )A.30°B.20°C.15°D.100°12.如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE相交于点F,则∠DFC=60度.13.【操作探究】如图,在三角形纸片ABC中,∠C=90°,∠B=30°.点D(不与B,C重合)是BC上任意一点.将此三角形纸片按下列方式折叠.若EF的长度为a,则△DEF的周长为3a(用含a的式子表示).14.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.(1)试判定△ODE的形状,并说明你的理由;(2)线段BD,DE,EC三者有什么关系?写出你的判断过程.解:(1)△ODE是等边三角形.理由:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.∵OD∥AB,OE∥AC,∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.∴△ODE是等边三角形.(2)BD=DE=EC.理由:∵OB平分∠ABC,且∠ABC=60°,∴∠ABO=∠OBD=30°.∵OD∥AB,∴∠BOD=∠ABO=30°.∴∠OBD =∠BOD.∴BD =OD.同理,EC =OE. ∵△ODE 是等边三角形,DE =OD =OE. ∴BD =DE =EC. 综合题15.如图1,等边△ABC 中,D 是AB 边上的动点,以CD 为一边,向上作等边△EDC ,连接AE. (1)△DBC 和△EAC 全等吗?请说说你的理由; (2)试说明AE ∥BC 的理由;(3)如图2,将动点D 运动到边BA 的延长线上,所作仍为等边三角形,请问是否仍有AE ∥BC ?证明你的猜想.解:(1)△DBC 和△EAC 全等.理由:∵△ABC ,△EDC 是等边三角形, ∴∠ACB =∠DCE =60°,BC =AC ,DC =EC. ∴∠BCD =∠ACE.在△DBC 和△EAC 中,⎩⎪⎨⎪⎧BC =AC ,∠BCD =∠ACE ,DC =EC ,∴△DBC ≌△EAC(SAS).(2)∵△DBC ≌△EAC ,∴∠EAC =∠B =60°. 又∵∠ACB =60°,∴∠EAC =∠ACB. ∴AE ∥BC. (3)仍有AE ∥BC.证明:∵△ABC ,△EDC 为等边三角形, ∴BC =AC ,DC =CE ,∠BCA =∠DCE =60°. ∴∠BCA +∠ACD =∠DCE +∠ACD , 即∠BCD =∠ACE.在△DBC 和△EAC 中,⎩⎪⎨⎪⎧BC =AC ,∠BCD =∠ACE ,DC =EC ,∴△DBC ≌△EAC(SAS). ∴∠EAC =∠B =60°.又∵∠ACB =60°,∴∠EAC =∠ACB. ∴AE ∥BC.。
人教版 八年级数学 第12章 全等三角形 培优训练 (含答案)

人教版八年级数学第12章全等三角形培优训练一、选择题1. 下列各组的两个图形属于全等图形的是()2. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE相交于点M,则∠DCE等于()A.∠B B.∠A C.∠EMF D.∠AFB3. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PF A的依据是()A.HL B.ASA C.SSS D.SAS4. 根据下列条件,能画出唯一的△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=50°D.∠A=30°,∠B=70°,∠C=80°5. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是()A.点O在点A的南偏东60°方向上B.点B在点A的北偏东30°方向上C.点B在点O的北偏东60°方向上D.点B在点O的北偏东30°方向上6. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是()7. 现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,OA=a,AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点A为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确,小雷的作法错误B.小雷的作法正确,小惠的作法错误C.两人的作法都正确D.两人的作法都错误8. 如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF 于点H.若∠AFB=40°,则∠BCF的度数为()A.40°B.50°C.55°D.60°二、填空题9. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=°.10. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.11. 如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.12. 在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD 的面积之比是________.13. (2019•南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.14. 如图所示,已知AD∥BC,则∠1=∠2,理由是________________;又知AD =CB,AC为公共边,则△ADC≌△CBA,理由是______,则∠DCA=∠BAC,理由是__________________,则AB∥DC,理由是________________________________.15. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.16. 如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC =2,则S△ABC=.三、解答题17. 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20 m,AC=10 m,分别求一串红与鸡冠花两种花草的种植面积.18. 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上.若AD=16,BC=10,求AB的长.19. 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是筝形,其中AB=AD,CB=CD,P是对角线AC上除A,C外的任意一点.求证:∠ABP =∠ADP.20. 如图,已知AP∥BC,∠P AB的平分线与∠CBA的平分线相交于点E,过点E 的直线分别交AP,BC于点D,C.求证:AD+BC=AB.21. (1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.人教版八年级数学第12章全等三角形培优训练-答案一、选择题1. 【答案】A2. 【答案】A[解析] ∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,∴∠DCE=∠B.故选A.3. 【答案】A4. 【答案】C[解析] 对于选项A来说,AB+BC<AC,不能画出△ABC;对于选项B来说,可画出△ABC为锐角三角形或者钝角三角形;对于选项C来说,已知两边及其夹角,△ABC是唯一的;对于选项D来说,△ABC的形状可确定,但大小不确定.5. 【答案】D[解析] 如图,由题意知∠AOD=30°,∠COD=90°,∴∠AOC=120°.由作图可知,OB平分∠AOC,∴∠AOB=∠AOC=60°.∴∠DOB=30°.∴点B在点O的北偏东30°方向上.6. 【答案】C[解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项C中,如图①,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.这两个角所对的边是BE和CF,而已知条件给的是BD=CF=3,故不能判定两个小三角形全等.选项D中,如图②,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.又∵BD=CE=2,∠B=∠C,∴△BDE≌△CEF.故能判定两个小三角形全等.7. 【答案】A[解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.8. 【答案】B[解析] 如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.∵AF平分∠BAC,FZ⊥AE,FW⊥AB,∴FZ=FW.同理FW=FY.∴FZ=FY.又∵FZ⊥AE,FY⊥CB,∴∠FCZ=∠FCY.由∠AFB=40°,易得∠ACB=80°.∴∠ZCY=100°.∴∠BCF=50°.二、填空题9. 【答案】125[解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.10. 【答案】AB =AC11. 【答案】20[解析] 如图,过点D 作射线AF.在△BAD 和△CAD 中,⎩⎨⎧AB =AC ,AD =AD ,BD =CD ,∴△BAD ≌△CAD(SSS). ∴∠BAD =∠CAD ,∠B =∠C.∵∠BDF =∠B +∠BAD ,∠CDF =∠C +∠CAD , ∴∠BDF +∠CDF =∠B +∠BAD +∠C +∠CAD , 即∠BDC =∠B +∠C +∠BAC. ∵∠BAC =80°,∠BDC =120°, ∴∠B =∠C =20°.12. 【答案】4∶3【解析】如解图,过D 作DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,∵AD 是∠BAC 的平分线,∴DE =DF(角平分线上的点到角两边的距离相等),设DE=DF=h,则S△ABDS△ACD =12AB·h12AC·h=43.13. 【答案】70【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,在Rt△ABE和Rt△CBF中,AB CBAE CF=⎧⎨=⎩,∴Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.14. 【答案】两直线平行,内错角相等SAS全等三角形的对应角相等内错角相等,两直线平行15. 【答案】20[解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB =AE+EB=AB.16. 【答案】7[解析] 过点P作PF⊥BC于点F,PG⊥AB于点G ,连接AP.∵△ABC的两条外角平分线BP,CP相交于点P,∴PF=PG=PE=2.∵S△BPC=2,∴BC·2=2,解得BC=2.∵△ABC的周长为11,∴AC+AB=11-2=9.∴S △ABC =S △ACP +S △ABP -S △BPC =AC ·PE+AB ·PG-S △BPC =×9×2-2=7.三、解答题17. 【答案】解:如图,过点D 作DE ⊥AB 于点E ,DF ⊥AC 于点F. ∵AD 是∠BAC 的平分线,∴DE =DF. ∵AB =20 m ,AC =10 m ,∴S △ABC =12×20×10=12×20·DE +12×10·DF ,解得DE =203(m).∴△ACD 的面积=12×10×203=1003(m 2),△ABD 的面积=12×20×203=2003(m 2).故一串红的种植面积为2003 m 2,鸡冠花的种植面积为1003 m 2.18. 【答案】解:∵△ACF ≌△DBE ,∴AC=DB.∴AC-BC=DB-BC ,即AB=CD.∵AD=16,BC=10,∴AB=CD=(AD-BC )=3.19. 【答案】证明:在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,AC =AC ,CB =CD , ∴△ABC ≌△ADC.∴∠BAP =∠DAP.在△BAP 和△DAP 中,⎩⎨⎧AB =AD ,∠BAP =∠DAP ,AP =AP , ∴△BAP ≌△DAP.∴∠ABP =∠ADP.20. 【答案】证明:如图,在AB 上截取AF =AD ,连接EF.∵AE 平分∠PAB ,∴∠DAE =∠FAE.在△DAE 和△FAE 中,⎩⎨⎧AD =AF ,∠DAE =∠FAE ,AE =AE ,∴△DAE ≌△FAE(SAS).∴∠AFE =∠ADE.∵AD ∥BC ,∴∠ADE +∠C =180°.又∵∠AFE +∠EFB =180°,∴∠EFB =∠C.∵BE 平分∠ABC ,∴∠EBF =∠EBC.在△BEF 和△BEC 中,⎩⎨⎧∠EFB =∠C ,∠EBF =∠EBC ,BE =BE ,∴△BEF ≌△BEC(AAS).∴BF =BC.∴AD +BC =AF +BF =AB.21. 【答案】解:(1)证明:∵BD ⊥直线m ,CE ⊥直线m , ∴∠BDA =∠AEC =90°.∴∠BAD +∠ABD =90°.∵∠BAC =90°,∴∠BAD +∠CAE =90°. ∴∠CAE =∠ABD.在△ADB 和△CEA 中,⎩⎨⎧∠ABD =∠CAE ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.(2)成立.证明:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠EAC =180°-α. ∴∠DBA =∠EAC.在△ADB 和△CEA 中,⎩⎨⎧∠DBA =∠EAC ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.。
初中数学冀教版八年级上册第十三章 全等三角形13.3 全等三角形的判定-章节测试习题

章节测试题1.【答题】如图,△ABC≌△BAD,A和B、C和D是对应顶点,如果AB=5,BD =6,AD=4,那么BC等于( )A. 4B. 5C. 6D. 无法确定【答案】A【分析】根据全等三角形对应边相等求解即可.【解答】∵△ABC≌△BAD,A和B、C和D是对应顶点,∴BC与AD是对应线段,∴BC=AD=4.选A.2.【答题】已知如图,△ABC≌△ADE,∠B=30°,∠E=20°,∠BAE=105°,求∠BAC的度数.∠BAC=______°.【答案】130【分析】根据全等三角形的性质,全等三角形对应的角相等,∴∠C=∠E,∠B=∠D,可知∠BAC=180°-∠B-∠C.【解答】解:∵△ABC≌△ADE 且∠B≠∠E,∴∠C=∠E,∠B=∠D;∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣20°=130°.3.【答题】如图,△ABC≌△DEF,若∠A=40°,∠BCA=20°,则∠E=______度.【答案】120【分析】根据全等三角形的性质:对应角相等,来求∠B=∠E;然后在△ABC中根据三角形的内角和来求∠B.【解答】解:在△ABC中,∠A=40°,∠BCA=20°,∴∠B=180°﹣20°﹣40°=120°;又∵△ABC≌△DEF,∴∠B=∠E,∴∠E=120°;故答案为:120°.4.【答题】已知:△ABC≌△A′B′C′,∠A=35°,∠B=75°,则∠C′的度数为______°.【答案】70【分析】根据△ABC≌△A′B′C′,得到∠C=∠C′,根据三角形的内角和定理求出∠C的度数,即可得到答案.【解答】解:∵△ABC≌△A′B′C′,∴∠C=∠C′,∵∠A=35°,∠B=75°,∴∠C=180°﹣∠A﹣∠B,=180°﹣35°﹣75°=70°,∴∠C′=70°.故答案为:70°.5.【答题】如图,若△ABC≌△A1B1C1,且∠A=110°,∠B=40°,则∠C1=______度.【答案】30【分析】本题实际上是全等三角形的性质以及根据三角形内角和等于180°来求角的度数.【解答】解:∵△ABC≌△A1B1C1,∴∠C1=∠C,又∵∠C=180°﹣∠A﹣∠B=180°﹣110°﹣40°=30°,∴∠C1=∠C=30°.故填306.【答题】若△ABC≌△A′B′C′且∠A=35°25′,∠B′=49°45′,则∠C=______°______′.【答案】94,50【分析】全等三角形的对应角相等,三角形内角和等于180°.所以∠C=180°﹣∠A﹣∠B,且∠C1=∠C,∠B=∠B′.【解答】解:∵△ABC≌△A1B1C1,∴∠C1=∠C,∠B=∠B′,又∵∠C=180°﹣∠A﹣∠B=180°﹣∠A﹣∠B′=180°﹣35°25′﹣49°45′=94°50′.7.【答题】如图,△ABC≌△DEF,∠A=80°,∠ABC=60°,则∠F=______度.【答案】40【分析】根据全等三角形的性质求出∠DEF和∠D的度数,在△DEF中,根据三角形的内角和定理求出即可.【解答】解:∵△ABC≌△DEF,∠A=80°,∠ABC=60°,∴∠D=∠A=80°,∠DEF=∠ABC=60°,∵∠F+∠D+∠DEF=180°,∴∠F=40°,故答案为:408.【答题】如图,若△ABC≌△ADE,则BC=______.【答案】DE【分析】根据全等三角形的性质:全等三角形的对应边相等,找出BC的对应边即可.【解答】解:BC=DE,理由是∵△ABC≌△ADE,∴BC=DE.故答案为:DE.9.【答题】如图:△ABC≌△DCB,AB的对应边DC,∠A的对应角是∠D,则BC的对应边是______.【答案】CB【分析】根据全等三角形的性质以及图形可以直接得到答案.【解答】解:∵△ABC≌△DCB,AB的对应边DC,∠A的对应角是∠D,∴BC=CB(全等三角形的对应边相等);故答案是:CB.10.【答题】已知△ABC≌△EFD,若△ABC的周长为26,AB=8,BC=12,则DE=______.【答案】6【分析】根据“全等三角形的对应边相等”的性质进行解答即可.【解答】解:∵△ABC≌△EFD,∴AB=EF,BC=FD,AC=ED;又∵△ABC的周长为26,AB=8,BC=12,∴DE=AC=26﹣AB﹣BC=26﹣8﹣12=6,即DE=6;故答案是:611.【答题】如图,若△ACB≌△AED,且∠B=35°,∠C=48°,则∠EAD=______°.【答案】97【分析】根据全等三角形的对应角相等和三角形的内角和定理即可求得∠EAD的度数.【解答】解:∵∠B=35°,∠C=48°,∴∠CAB=180°﹣35°﹣48°=97°∵△ACB≌△AED,∴∠EAD=∠CAB=97°.故答案为9712.【答题】已知:△ABC≌△A′B′C′,∠A=50°,∠B=70°,则∠C′=______°.【答案】60【分析】根据三角形的内角和定理求出∠C的度数,根据全等三角形的性质求出∠C′=∠C,代入即可.【解答】解:∠C=180°﹣∠B﹣∠A=180°﹣50°﹣70°=60°,∵△ABC≌△A′B′C′,∴∠C′=∠C=60°,故答案为:6013.【答题】如下图所示,△ABD≌△ACE,点B和点C是对应顶点,AB=8,BD=7,AD=6,则BE的长是______.【答案】2【分析】首先根据全等三角形的对应边相等,求出AE的长,根据BE=AB﹣AE,即可求出BE的长.【解答】解:∵△ABD≌△ACE,点B和点C是对应顶点,∴AE=AD=6;∴BE=AB﹣AE=8﹣6=2故BE的长是214.【答题】若△ABC≌△BAD,且AB=4cm,BC=3cm,则AD的长为______cm.【答案】3【分析】首先找准对应边然后根据全等三角形的对应边相等,即可求解.【解答】解:∵△ABC≌△BAD∴AD=BC=3cm.15.【答题】若△OAD≌△OBC,且BC=6cm,则AD=______cm.【答案】6【分析】根据全等三角形的对应边相等得出AD=BC,代入求出即可.【解答】解:∵△OAD≌△OBC,∴AD=BC,∵BC=6cm,∴AD=6cm,故答案为:616.【答题】如图,△ABC≌△ADE,∠EAC=25°,则∠BAD=______°.【答案】25【分析】根据全等三角形对应角相等可以得到∠CAB=∠EAD,然后两个相等的角减去同一个∠EAB即可得到∠CAE=∠BAD,从而得到结论.【解答】解:∵△ABC≌△ADE,∴∠CAB=∠EAD,∴∠CAB﹣∠EAB=∠EAD﹣∠BAD,即:∠BAD=∠EAC=25°,故答案为2517.【答题】如图,DE是ABC中AC边的垂直平分线,若BC=8厘米,AB=10厘米,则EBC的周长为( )厘米A. 16B. 28C. 26D. 18【答案】D【分析】利用线段垂直平分线的性质得AE=CE,再等量代换即可求得三角形的周长.【解答】∵DE是△ABC中AC边的垂直平分线,∴CE=AE,∵△EBC的周长=BE+EC+BC,∴△EBC的周长=BE+AE+BC=AB+BC,∵BC=8cm,AB=10cm,∴△EBC的周长为18cm.选D.18.【答题】如图,AB=DB,BC=BE,要使△AEB≌△DCB,则需添加的条件是( )A. AB=BCB. AE=CDC. AC=CDD. AE=AC【答案】B【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据判定定理逐个判断即可.【解答】只有选项B正确,理由是:在△AEB和△DCB中,,∴△AEB≌△DCB(SSS),选B.19.【答题】如图,,,有交于.在原图形的基础上,要利用“”判定△AOB≌△DOC,还需添加的条件是( )A.B.C.D.【答案】C【分析】因为要用SSS证明,则通过对所给条件的分析可得出AB=CD,OB=OC,从而可判断出所应该添加的条件.【解答】要利用“SSS”判定,只有选项C符合,理由如下:∵AC=BD,若OA=OD,则可得OB=OC,又∵AB=CD,∴可利用SSS证明△AOB≌△DOC,选C.20.【答题】如图,中,,,则由“”可判定( )A. ≌B. ≌C. ≌D. 以上答案都不对【答案】B【分析】要由“SSS”判定,已知AB=AC,EB=EC,观察图形只能是再添加AE=AE,【解答】理由如下:∵AB=AC,EB=EC,AE=AE,∴△ABE≌△ACE,选B.。
中考数学知识点过关培优训练卷:全等三角形的性质与判定(附解析)

中考数学知识点过关培优训练卷: 全等三角形的性质与判定 一.选择题 1.如图,△ABC和△EDC都是等边三角形,连接AE、BE,若AB=BE,∠CAE=20°,则∠BCD的度数是( )
A.25° B.20° C.15° D.10° 2.在等腰直角△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过C作CD⊥BE于D,过A作AT⊥BE于T点,有下列结论:①△AET≌△CDE,②BC=AB+AE,③∠ADB=45°,④BE=AT+TE,其中正确的有( )
A.4个 B.3个 C.2个 D.1个 3.已知△ABC中,∠ABC=45°,AB=7,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为( )
A.25 B. C. D. 4.如图,△ABC是等边三角形,点D、E分别为边BC、AC上的点,且CD=AE,点F是BE和AD的交点,BG⊥AD于G点,已知∠BEC=75°,FG=1,则AB的长为( )
A. B. C. D.3 5.如图,△ABM与△CDM是两个全等的等边三角形,MA⊥MD有下列四个结论:①∠MBC=25°;②∠ADC+∠ABC=180°;③直线MB平分∠DMC;④直线MB垂直平分线段CD.其中正确结论的个数为( )
A.1 B.2 C.3 D.4 6.如图,∠BAC=∠ACD=90°,∠ABC=∠ADC,CE⊥AD,且BE平分∠ABC,则下列结论:①AD=CB;②∠ACE=∠ABC;③∠ECD+∠EBC=∠BEC;④∠CEF=∠CFE;其中正确的是( )
A.①② B.①③④ C.①②④ D.①②③④ 7.如图,在△ABC中,∠ACB=90°,AC=BC,过点B作BE⊥AB于B,D为AB边上一点且AD=BE,连接CD,DE,若CD=2,则DE的长为( )
A.3 B.4 C.4 D.6 8.如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为( )
初中数学冀教版八年级上册第十三章 全等三角形13.3 全等三角形的判定-章节测试习题(2)
章节测试题1.【答题】如图,已知AB=AD给出下列条件:(1)CB=CD (2)∠BAC=∠DAC (3)∠BCA=∠DCA (4)∠B=∠D,若再添一个条件后,能使△ABC≌△ADC的共有( )A. 1个B. 2个C. 3个D. 4个【答案】B【分析】由图形△ABC和△ADC有公共边,结合条件AB=AD,故可再加一组边,和公共边与已知一组边的夹角相等可得全等.【解答】∵在△ABC和△ADC中,AB=AD,AC=AC,∴(1)添加“CB=CD”可由“SSS”判定△ABC≌△ADC;(2)添加“∠BAC=∠DAC”可由“SAS”判定△ABC≌△ADC;(3)添加“∠BCA=∠DCA”不能判定△ABC≌△ADC;(4)添加“∠B=∠D”不能判定△ABC≌△ADC;即4个条件中,添加(1)和(2)能使△ABC≌△ADC.选B.2.【答题】如图,AD平分∠BAC,AB=AC,那么判定△ABD≌△ACD的理由是( )A. SSSB. SASC. ASAD. AAS【答案】B【分析】利用角平分线可得到一组角相等,再加上条件AB=AC,再加公共边,可判定其全等,可得出答案.【解答】∵AD平分∠BAC,∴∠BAD=∠CAD,又∵AB=AC,AD=AD,∴可由“SAS”判定△ABD≌△ACD.选B.3.【答题】已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )A. ∠A与∠D互为余角B. ∠A=∠2C. △ABC≌△CEDD. ∠1=∠2【答案】D【分析】先根据角角边证明△ABC与△CED全等,再根据全等三角形对应边相等,全等三角形的对应角相等的性质对各选项判断后,利用排除法求解.【解答】∵AC⊥CD,∴∠1+∠2=90°,∵∠B=90°,∴∠1+∠A=90°,∴∠A=∠2,在△ABC和△CED中,,∴△ABC≌△CED(AAS),故B、 C选项正确;∵∠2+∠D=90°,∴∠A+∠D=90°,故A选项正确;∵AC⊥CD,∴∠ACD=90°,∠1+∠2=90°,故D选项错误.选D.4.【答题】如图,△ABC≌△CDA,且AD=CB,下列结论错误的是( )A. ∠B=∠DB. ∠CAB=∠ACDC. BC=CDD. AC=CA【答案】C【分析】根据全等三角形的性质进行分析,从而得到答案,做题时要找准对应边,对应角.【解答】∵△ABC≌△CDA,∴∠CAB=∠ACD,CA=AC,∠D=∠B,故A. B. D正确,不符合题意,BC不一定等于CD,C错误,符合题意,选C.5.【答题】如图,FE=BC,DE=AB,∠B=∠E=40°,∠F=70°,则∠A=( )A. 40°B. 50°C. 60°D. 70°【答案】D【分析】根据全等三角形的判定与性质,可得∠C与∠F的关系,根据三角形的内角和定理,可得答案.【解答】∵∠E=40°,∠F=70°,∴∠D =70°,∵FE=BC,DE=AB,∠B=∠E=40°,∴△ABC≌△DEF(SAS)∴∠A=∠D =70°.故选:D .6.【答题】如图,已知E,F是AC上的两点,AE=CF,DF=BE,∠AFD=∠CEB,则下列不成立的是( )A. ∠A=∠CB. AD=CBC. BC=DFD. DF∥BE【答案】C【分析】根据等式的性质,可得AF与CE的关系,根据全等三角形的判定与性质,可得答案.【解答】∵AE=CF(已知),∴AE+EF=EF+CF,∴AF=EC,∵∠AFD=∠CEB,∴△AFD≌△CEB(SAS),∴∠A=∠C,AD=CB,BC=DA,∵∠AFD=∠CEB,∴DF∥BE.选C.7.【答题】如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )A. ∠B=∠CB. ∠AEB=∠ADCC. AE=ADD. BE=DC【答案】C【分析】根据全等三角形的判定与性质,可得答案.【解答】∵AB=AC (已知),∠A=∠A(公共角),∴只需要AE=AD,∴△ABE≌△ACD,选C.8.【题文】如图,已知点B、C、F、E在同一直线上,∠A=∠D,BF=EC,AB//DE,若∠1=80°,求∠BFD的度数;【答案】100°【分析】先根据AAS证明△ABC≌△DEF,得到∠1=∠EFD=80°,再根据邻补角示得∠BFD的度数.【解答】解:∵∠A=∠D,∴∠B=∠E,∵BF=EC,∴BF-CF=EC-CF,即BC=EF,在△ABC和△DEF中∴△ABC≌△DEF(AAS),∴∠1=∠EFD,又∵∠1=80°,∴∠EFD=80°,又∵∠∠EFD+∠BFD=180°,∴∠BFD=100°.9.【题文】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE,BD交于点O;求证:△AEC≌△BED;【答案】见解析【分析】根据全等三角形的判定即可判断△AEC≌△BED;【解答】解:∵AE和BD相交于点O,∴∠AOD=∠BOE.在△AOD和△BOE中,∠A=∠B,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO,∴∠AEC=∠BED.在△AEC和△BED中,∴△AEC≌△BED(ASA).10.【题文】把下面推理过程补充完整,在括号内注明理由:已知:如图,BC//EF,AB=DE,BC=EF,试说明∠C=∠F;解:∵BC//EF(已知)∴∠ABC=∠__________ _________________________在△ABC与△DEF中,∵∴△ABC≌△DEF _______∴∠C=∠F ____________________________【答案】∠E 两直线平行,同位角相等 SAS 全等三角形对应角相等【分析】由于BC∥EF,所以∠ABC=∠DEF的根据是两直线平行,同位角相等,然后再根据已知条件,判定三角形全等,利用全等三角形的性质,求出∠C=∠F.【解答】解:∵BC∥EF(已知),∴∠ABC=∠DEF(两直线平行,同位角相等),在△ABC与△DEF中,AB=DE,∠ABC=∠E,BC=EF,∴△ABC≌△DEF(SAS),∴∠C=∠F(全等三角形的对应角相等).11.【题文】如图,已知,,,,试猜想与的位置关系并说明理由.【答案】.理由见解析【分析】根据SSS证明△ABD≌△ACE,从而得∠BAD=∠CAE,再由∠CAD是公共角,从而可得∠DAE=∠BAC=90°,从而得到AD⊥AE.【解答】解:∵AB⊥AC,∴∠BAC=90°,在△ABD和△ACE中,∴△ABD≌△ACE(SSS),∴∠BAD=∠CAE,∴∠BAD-∠CAD=∠CAE-∠CAD,即∠DAE=∠BAC=90°,∴AD⊥AE.【方法总结】本题考查了全等三角形的判定与性质,得到∠DAE=∠BAC=90°是解题的关键.12.【题文】已知,,那么吗?为什么?那么吗?【答案】∠B=∠D,理由见解析;∠A与∠C不一定相等.【分析】连接AC,证明△ABC≌△ADC,可得∠B=∠D,由已知条件得不到∠A=∠C.【解答】解:连接AC,在△ABC和△ADC中,∴△ABC≌△ADC(SSS),∴∠B=∠D,∠BAC=∠DAC,∠ACB=∠ACD,由已知条件得不到∠BAC=∠ACB,所以不一定能得到∠BAD=∠BCD.13.【题文】如图,点、、、在直线上,不能直接测量,点、在异侧,测得,,;()说明:≌;()指出图中所有平行的线段并说明理由;【答案】(1)说明见解析;(2)AB//DE,AC//DF,理由见解析.【分析】(1)先证明BC=EF,再根据SSS即可证明.(2)结论AB∥DE,AC∥DF,根据全等三角形的性质即可证明.【解答】解:()∵,∴,即,在△ABC和△DEF中,∴≌.(),,理由:∵≌,∴,,∴,.14.【题文】如图,已知,,说出的理由;【答案】见解析【分析】根据边边边判定△ABC与△CDA全等,再根据全等三角形对应角相等的性质即可得.【解答】解:在△ABC和△CDA中,∴△ABC≌△CDA(SSS),∴∠1=∠2.15.【题文】如图,沿AC方向开山修路,为了加快施工进度,要在山的另一边同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD,并延长使DF =BD,过F点作AB的平行线段MF,连接MD,并延长,在其延长线上取一点E,使DE=DM,在E点开工就能使A、C、E成一条直线,请说明其中的道理;【答案】详见解析.【分析】首先根据题意得出△BDE和△FDM全等,从而得出∠BEM=∠DMF,即BE∥MF,最后根据过直线外一点有且只有一条直线与已知直线平行得出答案.【解答】解:∵BD=DF,DE=DM,∠BDE=∠FDM,∴△BDE≌△FDM,∴∠BEM=∠DMF,∴BE∥MF,∵AB∥MF,根据过直线外一点有且只有一条直线与已知直线平行,∴A、C、E在一条直线上.16.【题文】如图,已知:点D是AB上一点,DF交AC于点E,DE=EF,AE=CE;求证:∠B+∠BCF=180°;【答案】详见解析.【分析】首先根据题意得出△ADE和△CFE全等,从而得出∠ADE=∠F,根据平行线的判定定理得出AB∥CF,最后根据平行线的性质定理得出答案.【解答】解:∵DE=FE,∠AED=∠CEF,AE=CE,∴△ADE≌△CFE,∴∠ADE=∠F,∴AB∥CF,∴∠B+∠BCF=180°.17.【题文】已知:线段,,求作:,使,.【答案】答案见解析【分析】首先作进而以B为圆心的长为半径画弧,再以为圆心为半径画弧即可得出的位置.【解答】解:如图所示:△ABC即为所求.18.【题文】如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,点B、C、D在同一条直线上;试说明:∠ADB=∠AEC;【答案】见解析【分析】求出根据SAS证出≌即可.【解答】解:证明:∵△ABC和△ADE都是等腰直角三角形∴AD=AE,AB=AC,又∵∴∠DAB=∠EAC,∵在△ADB和△AEC中,∴△ADB≌△AEC(SAS),∴19.【题文】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.请判断AE与CF的位置关系,并说明理由.【答案】AE⊥CF,理由见解析.【分析】延长AE交FC于点G,先证Rt△ABE≌Rt△CBF,再证∠EAB+∠AFC=90°即可.【解答】解:AE⊥CF,理由如下:如图,延长AE交FC于点G.∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt△ABE和Rt△CBF中,∵AE=CF,AB=CB,∴Rt△ABE≌Rt△CBF(HL),∴∠EAB=∠FCB.∵∠FCB+∠CFB=90°,∴∠EAB+∠AFC=90°,∴∠AGF=90°,∴AE⊥CF.20.【题文】如图所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E,C,A在同一条直线卜,则DE的长就等于A,B之间的距离,请你说明道理.【答案】见解析.【分析】因为AB∥DE,所以∠A=∠E或∠ABC=∠EDC,因为BC=CD,根据AAS证明ΔABC≌ΔEDC,所以AB=ED.从而得证.【解答】由题意并结合图形可以知道BC=CD,∠ACB=∠ECD,又AB∥DE,从而∠A=∠E或∠ABC=∠EDC,故在ΔABC与ΔEDC中,所以ΔABC≌ΔEDC(AAS),所以AB=ED,即测出ED的长后即可知道A,B之间的距离.【方法方法总结】本题目是一道考查三角形全等的说理题目,主要考查了AAS判定.难度一般.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 -
13.3全等三角形的判定
专题一 与全等三角形有关的规律探究
1. 如图,已知AB=AC,D为∠BAC的角平分线上一点,连结BD,CD;如图2,已知AB=AC,D,
E为∠BAC的角平分线上面两点,连结BD,CD,BE,CE;如图3,已知AB=AC,D,E,F为
∠BAC的角平分线上面三点,连结BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中
有全等三角形的对数是________.
2. 如图,在直角△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BE平分∠ABC交CD,AC分别于G,
E,GF∥AC交AB于F,猜想:EF与AB有怎样的位置关系,请说明理由.
3. 如图①,AB=CD,AD=BC.O为AC中点,过O点的直线分别与AD,BC相交于点M,N.
(1)那么∠1与∠2有什么关系?AM,CN有什么关系?请说明理由.
(2)若将过O点的直线旋转至图②③的情况时,其他条件不变,那么(1)中的关系还成立吗?
请说明理由.
- 2 -
专题二 全等三角形与图形变换
4.两个大小不同的等腰直角三角板按如图1所示放置,图2是由它抽象出的几何图形,B,C,E在
同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标
识的字母).
5.如图,在直角△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三
角板如图放置,使三角板斜边的两个端点分别与A,D重合,连结BE,EC.试猜想线段BE和EC
的数量及位置关系,并证明你的猜想.
- 3 -
6.在△ABC中,∠BAC是锐角,AD⊥BC,BE⊥AC,垂足分别为D、E,且DB=DC,AE=BE.
(1)求证:AH=2BD;
(2)若将∠BAC改为钝角,其他条件不变,上述的结论还成立?若成立,请证明;若不成立,请
说明理由.
专题三 利用三角形全等解决实际问题
7. 如图,铁路上A,B两站(视为直线上两点),相距25 km,C,D为铁路同旁的两个村庄(视为
两点),DA⊥AB于A点,CB⊥AB于B点,DA=15 km,CB=10 km,现在要在铁路AB上建一个土特
产产品收购站E,使C,D两村庄到E站的距离相等,求E站应建在离A站多远处,并说明理由.
- 4 -
状元笔记
【知识要点】
1.全等三角形的判定方法
SSS、SAS、ASA、AAS.
2.全等三角形与图形变换
寻找和利用两三角形间的平移或旋转变换关系,能够给命题的证明带来方便.
【温馨提示】
1.全等图形指形状相同,大小相等的两个图形.
2.表示两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
【方法技巧】
选择哪种判定方法,要根据具体已知条件而定:
已知条件 可选择的判定方法
一边一角对应相
等
SAS、AAS、ASA
两角对应相等 ASA、AAS
两边对应相等 SAS、SSS
参考答案
1. (1)2nn 解析:全等三角形依次有1对,3对,6对,…,第n个图形有(1)2nn对.
2.解: EF⊥AB.理由:∵BE平分∠ABC,∴∠CBG=∠FBG.∵GF∥AC,
∴∠A=∠GFB.∵∠A+∠ACD=∠BCG+∠ACD=90°,∴∠A=∠BCG=∠GFB.又∵BG=BG,
∴△FBG≌△CBG,∴BF=BC.∵EB=EB,∠CBE=∠FBE,∴△FBE≌△CBE,∴∠EFB=∠ECB=90°,
∴EF⊥AB.
3.解:(1)∠1=∠2, AM=CN.理由:∵AB=CD,AD=BC,AC=CA,∴△ABC≌△CDA,∴∠DAC=∠BCA.
又∵AO=CO,∠CON=∠AOM,∴△AOM≌△CON. ∴∠1=∠2,AM=CN.
(2)成立,同理可证△AOM≌△CON .
4.解:△BAE≌△CAD,证明:∵∠BAC=∠EAD=90°,∴∠BAC+∠CAE =∠EAD+∠CAE,即
∠BAE=∠CAD.又∵AB=AC,AE=AD,∴△BAE≌△CAD.
5.解:BE=EC,BE⊥EC.
- 5 -
证明:∵AC=2AB, AD=CD,∴AB=AD=CD.∵∠EAD=∠EDA=45°,∴∠EAB=∠EDC=135°.∵EA=ED,
∴△EAB≌△EDC(SAS),∴∠AEB=∠DEC,EB=EC,∴∠BEC=∠AED=90°,∴BE=EC,BE⊥EC.
6.解:(1)证明:如图(1),∵ AD⊥BC,BE⊥AC,∴∠AEH=∠BEC =90°,
∴∠EAH+∠C=∠EBC+∠C=90°,∴∠EAH =∠EBC.又∵AE=BE,∴△AEH≌△BEC,∴AH=BC,
DB=DC,
∴AH=2BD.
(2)如图(2),上述结论成立.同理可证△AEH≌△BEC.
7.解:E站应建在离A站10 km处.理由如下:
在线段AB上截取AE=BC=10 km,又因为AB=25 km,所以BE=AB-AE=25-10=15(km),所以
AD=BE=15 km.在△ADE和△BEC中,,90,,ADBEABAEBC所以△ADE≌△BEC(SAS).所以DE=EC.
