kmp算法next数组构造过程
KMP算法计算next值和nextVal值
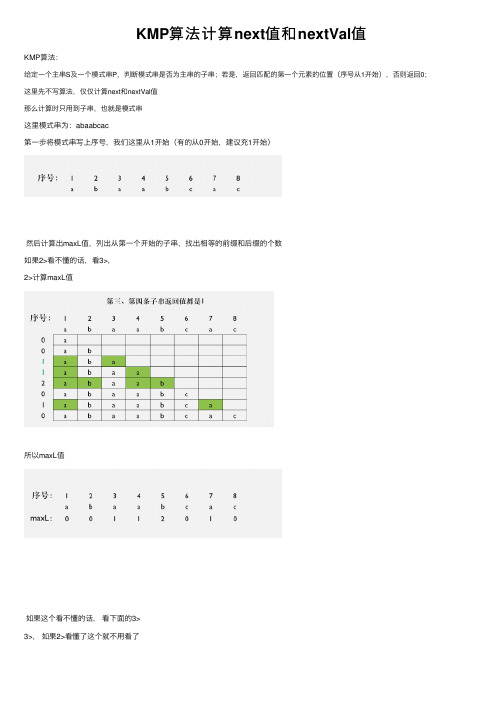
KMP算法计算next值和nextVal值
KMP算法:
给定⼀个主串S及⼀个模式串P,判断模式串是否为主串的⼦串;若是,返回匹配的第⼀个元素的位置(序号从1开始),否则返回0;这⾥先不写算法,仅仅计算next和nextVal值
那么计算时只⽤到⼦串,也就是模式串
这⾥模式串为:abaabcac
第⼀步将模式串写上序号,我们这⾥从1开始(有的从0开始,建议充1开始)
然后计算出maxL值,列出从第⼀个开始的⼦串,找出相等的前缀和后缀的个数
如果2>看不懂的话,看3>,
2>计算maxL值
所以maxL值
如果这个看不懂的话,看下⾯的3>
3>,如果2>看懂了这个就不⽤看了
依次类推4>计算next值
接下来将maxL复制⼀⾏,去掉最后⼀个数,在开头添加⼀个-1,向右平移⼀个格,然后每个值在加1的到next值
5>计算nextVal值,⾸先将第⼀个为0,然后看next和maxL是否相等(先计算不相等的)
当next和maxL不相等时,将next的值填⼊
当next和maxL相等时,填⼊对应序号为next值得nextVal值
所以整个nextVal值为:。
KMP算法以及优化(代码分析以及求解next数组和nextval数组)

KMP算法以及优化(代码分析以及求解next数组和nextval数组)KMP算法以及优化(代码分析以及求解next数组和nextval数组)来了,数据结构及算法的内容来了,这才是我们的专攻,前⾯写的都是开胃⼩菜,本篇⽂章,侧重考研408⽅向,所以保证了你只要看懂了,题⼀定会做,难道这样思想还会不会么?如果只想看next数组以及nextval数组的求解可以直接跳到相应部分,思想总结的很⼲~~⽹上的next数组版本解惑先总结⼀下,⼀般KMP算法的next数组结果有两个版本,我们需要知道为什么会存在这种问题,其实就是前缀和后缀没有匹配的时候next数组为0还是为1,两个版本当然都是对的了,如果next数组为0是的版本,那么对于前缀和后缀的最⼤匹配长度只需要值+1就跟next数组是1的版本⼀样了,其实是因为他们的源代码不⼀样,或者对于模式串的第⼀个下标理解为0或者1,总之这个问题不⽤纠结,懂原理就⾏~~那么此处,我们假定前缀和后缀的最⼤匹配长度为0时,next数组值为1的版本,考研⼀般都是⽤这个版本(如果为0版本,所有的内容-1即可,如你算出next[5]=6,那么-1版本的next[5]就为5,反之亦然)~~其实上⾯的话总结就是⼀句话next[1]=0,j(模式串)数组的第⼀位下标为1,同时,前缀和后缀的最⼤匹配长度+1即为next数组的值,j所代表的的是序号的意思408反⼈类,⼀般数组第⼀位下标为1,关于书本上前⾯链表的学习⼤家就应该有⽬共睹了,书本上好多数组的第⼀位下标为了⽅便我们理解下标为1,想法这样我们更不好理解了,很反⼈类,所以这⾥给出next[1]=0,前缀和后缀的最⼤匹配长度+1的版本讲解前⾔以及问题引出我们先要知道,KMP算法是⽤于字符串匹配的~~例如:⼀个主串"abababcdef"我们想要知道在其中是否包括⼀个模式串"ababc"初代的解决⽅法是,朴素模式匹配算法,也就是我们主串和模式串对⽐,不同主串就往前移⼀位,从下⼀位开始再和模式串对⽐,每次只移动⼀位,这样会很慢,所以就有三位⼤神⼀起搞了个算法,也就是我们现在所称的KMP算法~~代码以及理解源码这⾥给出~~int Index_KMP(SString S,SString T,intt next[]){int i = 1,j = 1;//数组第⼀位下标为1while (i <= S.length && j <= T.length){if (j == 0 || S.ch[i] == T.ch[j]){//数组第⼀位下标为1,0的意思为数组第⼀位的前⾯,此时++1,则指向数组的第⼀位元素++i;++j; //继续⽐较后继字符}elsej = next[j]; //模式串向右移动到第⼏个下标,序号(第⼀位从1开始)}if (j > T.length)return i - T.length; //匹配成功elsereturn 0;}接下来就可以跟我来理解这个代码~~还不会做动图,这⾥就⼿画了~~以上是⼀般情况,那么如何理解j=next[1]=0的时候呢?是的,这就是代码的思路,那么这时我们就知道,核⼼就是要求next数组各个的值,对吧,⼀般也就是考我们next数组的值为多少~~next数组的求解这⾥先需要给出概念,串的前缀以及串的后缀~~串的前缀:包含第⼀个字符,且不包含最后⼀个字符的⼦串串的后缀:包含最后⼀个字符,且不包含第⼀个字符的⼦串当第j个字符匹配失败,由前1~j-1个字符组成的串记为S,则:next[j]=S的最长相等前后缀长度+1与此同时,next[1]=0如,模式串"ababaa"序号J123456模式串a b a b a anext[j]0当第六个字符串匹配失败,那么我们需要在前5个字符组成的串S"ababa"中找最长相等的前后缀长度为多少再+1~~如串S的前缀可以为:"a","ab","aba","abab",前缀只不包括最后⼀位都可串S的后缀可以为:"a","ba","aba","baba",后缀只不包括第⼀位都可所以这⾥最⼤匹配串就是"aba"长度为3,那么我们+1,取4序号J123456模式串a b a b a anext[j]04再⽐如,当第⼆个字符串匹配失败,由前1个字符组成的串S"a"中,我们知道前缀应当没有,后缀应当没有,所以最⼤匹配串应该为0,那么+1就是取1~~其实这⾥我们就能知道⼀个规律了,next[1]⼀定为0(源码所造成),next[2]⼀定为1(必定没有最⼤匹配串造成)~~序号J123456模式串a b a b a anext[j]014再再⽐如,第三个字符串匹配失败,由前两个字符组成的串S"ab"中找最长相等的前后缀长度,之后再+1~~前缀:"a"后缀:"b"所以所以这⾥最⼤匹配串也是没有的长度为0,那么我们+1,取1序号J123456模式串a b a b a anext[j]0114接下来你可以⾃⼰练练4和5的情况~~next[j]011234是不是很简单呢?⾄此,next数组的求法以及kmp代码的理解就ok了~~那么接下来,在了解以上之后,我们想⼀想KMP算法存在的问题~~KMP算法存在的问题如下主串:"abcababaa"模式串:"ababaa"例如这个问题我们很容易能求出next数组序号J123456模式串a b a b a anext[j]011234此时我们是第三个字符串匹配失败,所以我们的next[3]=1,也就是下次就是第⼀个字符"a"和主串中第三个字符"c"对⽐,可是我们刚开始的时候就已经知道模式串的第三个字符"a"和"c"不匹配,那么这⾥不就多了⼀步⽆意义的匹配了么?所以我们就会有kmp算法的⼀个优化了~~KMP算法的优化我们知道,模式串第三个字符"a"不和主串第三个字符"c"不匹配,next数组需要我们的next[3]=1,也就是下次就是第⼀个字符"a"和主串中第三个字符"c"对⽐,之后就是模式串第⼀个字符"a"不和"c"匹配,就是需要变为next[1]=0,那么我们要省去步骤,不就可以直接让next[3]=0么?序号J12345模式串a b a b anext[j]01123nextval[j]00那么怎么省去多余的步骤呢?这就是nextval数组的求法~~nextval的求法以及代码理解先贴出代码for (int j = 2;j <= T.length;j++){if (T.ch[next[j]] == T.ch[j])nextval[j] = nextval[next[j]];elsenextval[j] = next[j];}如序号J123456模式串a b a b a anext[j]011234nextval[j]0⾸先,第⼀次for循环,j=2,当前序号b的next[2]为1,即第⼀个序号所指向的字符a,a!=当前序号b,所以nextval[2]保持不变等于next[2]=1序号J123456模式串a b a b a anext[j]011234nextval[j]01第⼆次for循环,j=3,当前序号a的next[3]为1,即第⼀个序号所指向的字符a,a=当前序号a,所以nextval[3]等于nextval[1]=0序号J123456模式串a b a b a anext[j]011234nextval[j]010第三次for循环,j=4,当前序号b的next[4]为2,即第⼆个序号所指向的字符b,b=当前序号b,所以nextval[4]等于nextval[2]=1序号J123456模式串a b a b a anext[j]011234nextval[j]0101就是这样,你可以练练5和6,这⾥直接给出~~序号J123456模式串a b a b a anext[j]011234nextval[j]010104⾄此nextval数组的求法你也应该会了,那么考研要是考了,那么是不是就等于送分给你呢?⼩练习那么你试着来求⼀下这个模式串的next和nextval数组吧~~next[j]nextval[j]⼩练习的答案序号j12345模式串a a a a b next[j]01234 nextval[j]00004。
字符串的next数组值

在字符串算法中,"next数组"是一个常用于KMP(Knuth-Morris-Pratt)算法的数据结构。
它记录了每个字符之前的模式串的"部分匹配长度"。
具体来说,对于字符串中的每个字符,next数组的值表示到目前为止(包括当前字符),最长的同时也是前缀和后缀的子串的长度。
例如,对于字符串 "ABABC",其next数组为 [0, 0, 1, 2],解释如下:
•对于A,没有前后缀匹配,所以next[0] = 0。
•对于B,同样没有前后缀匹配,所以next[1] = 0。
•对于A,有一个长度为1的前后缀匹配"A",所以next[2] = 1。
•对于B,有一个长度为2的前后缀匹配"AB",所以next[3] = 2。
•对于C,有一个长度为1的前后缀匹配"C",所以next[4] = 0。
这样,当我们在KMP算法中遇到一个字符时,我们可以使用next数组的值来确定下一个应该比较的字符的位置。
KMP算法:next和nextval值计算

KMP算法:next和nextval值计算
KMP算法的next和nextval值计算
先看看next数据值的求解⽅法
例:下标从1开始(若题中给定下标为0开始,把所有值-1即可)
next数组的求解⽅法:根据前⼀个字符next,⼀直循环找到第⼀次匹配成功的下标,并把next=1;如果当前字符与下标1字符都不相同,next 值就为1(初始下标值)
第⼀位为0,第⼆位为1,
第三位:把前⼀个模式串字符b与下标next值所对应的字符⽐较,b 和a不同,next为1(初始下标值)
第四位:前⼀个,c c和a不同,next为1
第五位:a和a相同(下标为1)1+1=2
第六位:b和b相同(下标为2)2+1=3
第七位:a和c不同(下标为3),继续找,c下标为1,a和a相同(下标为1) 1+1=2
nextval数组求解⽅法:根据next数组的值作为下标找到第⼀个不同的字符,把它的下标作为nextval的值;否则继续循环⽐较,直到与第⼀个字符也相同,此时,nextval值为0
第⼀位为0,第⼆位为1,
第三位:(当前下标字符)c与a(next值1作为下标的字符进⾏⽐较),若不同则为初始下标值1
第四位: a和a相同(第⼀个字符),nextval值为0
第五位:b和b(下标为2),相同,继续⽐较,b的next为1,b和下标为1的⽐,即b和a⽐,不同,则nextval值为1
第六位:a和c(下标为3),不同,nextval为下标的值 3
第七位:a和b(下标为2),不同,nextval为下标的值 2
注:如果下标从0开始,只需把所有的next和nextval值-1就是。
关于KMP算法中next数组和nextVal数组求法的整理

关于KMP算法中next数组和nextVal数组求法的整理nextval例如:序号 1 2 3 4 5 6 7 8模式串 a b a a b c a cnext值 0 1 1 2 2 3 1 2next数组的求解⽅法是:第⼀位的next值为0,第⼆位的next值为1,后⾯求解每⼀位的next值时,根据前⼀位进⾏⽐较。
⾸先将前⼀位与其next值对应的内容进⾏⽐较,如果相等,则该位的next值就是前⼀位的next值加上1;如果不等,向前继续寻找next值对应的内容来与前⼀位进⾏⽐较,直到找到某个位上内容的next值对应的内容与前⼀位相等为⽌,则这个位对应的值加上1即为需求的next值;如果找到第⼀位都没有找到与前⼀位相等的内容,那么需求的位上的next值即为1。
看起来很令⼈费解,利⽤上⾯的例⼦具体运算⼀遍。
1.前两位必定为0和1。
2.计算第三位的时候,看第⼆位b的next值,为1,则把b和1对应的a进⾏⽐较,不同,则第三位a的next的值为1,因为⼀直⽐到最前⼀位,都没有发⽣⽐较相同的现象。
3.计算第四位的时候,看第三位a的next值,为1,则把a和1对应的a进⾏⽐较,相同,则第四位a的next的值为第三位a的next值加上1。
为2。
因为是在第三位实现了其next值对应的值与第三位的值相同。
4.计算第五位的时候,看第四位a的next值,为2,则把a和2对应的b进⾏⽐较,不同,则再将b对应的next值1对应的a与第四位的a进⾏⽐较,相同,则第五位的next值为第⼆位b的next值加上1,为2。
因为是在第⼆位实现了其next值对应的值与第四位的值相同。
5.计算第六位的时候,看第五位b的next值,为2,则把b和2对应的b进⾏⽐较,相同,则第六位c的next值为第五位b的next值加上1,为3,因为是在第五位实现了其next值对应的值与第五位相同。
6.计算第七位的时候,看第六位c的next值,为3,则把c和3对应的a进⾏⽐较,不同,则再把第3位a的next值1对应的a与第六位c⽐较,仍然不同,则第七位的next值为1。
kmp算法next函数详解

kmp算法next函数详解KMP算法在介绍KMP算法之前,先介绍⼀下BF算法。
⼀.BF算法BF算法是普通的模式匹配算法,BF算法的思想就是将⽬标串S的第⼀个字符与模式串P的第⼀个字符进⾏匹配,若相等,则继续⽐较S的第⼆个字符和P的第⼆个字符;若不相等,则⽐较S的第⼆个字符和P的第⼀个字符,依次⽐较下去,直到得出最后的匹配结果。
举例说明:S: ababcababaP: ababaBF算法匹配的步骤如下i=0 i=1 i=2 i=3 i=4第⼀趟:a babcababa 第⼆趟:a b abcababa 第三趟:ab a bcababa 第四趟:aba b cababa 第五趟:abab c ababaa baba ab aba ab a ba aba b a abab aj=0 j=1 j=2 j=3 j=4(i和j回溯)i=1 i=2 i=3 i=4 i=3第六趟:a b abcababa 第七趟:ab a bcababa 第⼋趟:aba b cababa 第九趟:abab c ababa 第⼗趟:aba b cababaa baba a baba ab aba ab a ba a babaj=0 j=0 j=1 j=2(i和j回溯) j=0i=4 i=5 i=6 i=7 i=8第⼗⼀趟:abab c ababa 第⼗⼆趟:ababc a baba 第⼗三趟:ababca b aba 第⼗四趟:ababcab a ba 第⼗五趟:ababcaba b aa baba a baba ab aba ab a ba aba b aj=0 j=0 j=1 j=2 j=3i=9第⼗六趟:ababcabab aabab aj=4(匹配成功)代码实现:int BFMatch(char*s,char*p){int i,j;i=0;while(i<strlen(s)){j=0;while(s[i]==p[j]&&j<strlen(p)){i++;j++;}if(j==strlen(p))return i-strlen(p);i=i-j+1; //指针i回溯}return-1;}其实在上⾯的匹配过程中,有很多⽐较是多余的。
kmp算法中模式字符串的nextval数组

在KMP 算法中,模式字符串的next 数组是一个关键部分。
next 数组的作用是存储模式字符串中每个字符的最长相等前缀后缀的长度。
这个数组有助于在匹配过程中跳过尽可能多的字符,从而提高匹配效率。
next 数组的计算方法如下:1. 初始化next 数组为长度为1 的数组,存储第一个字符的长度。
2. 遍历模式字符串的每个字符,对于每个字符,计算其最长前缀后缀的长度。
3. 更新next 数组,将当前字符的最长前缀后缀长度加1,并存储在next 数组中。
以下是一个简单的KMP 算法实现,其中包含next 数组的计算:```pythondef kmp_preprocess(pattern):next = [1] * len(pattern)j = 0for i in range(1, len(pattern)):while j > 0 and pattern[i] != pattern[j]:j = next[j - 1]if pattern[i] == pattern[j]:j += 1next[i] = jreturn nextdef kmp_search(text, pattern):next = kmp_preprocess(pattern)i = 0j = 0while i < len(text):while j > 0 and text[i] != pattern[j]:i += 1if text[i] == pattern[j]:i += 1j += 1if j == len(pattern):return i - jreturn -1text = "我国是一个伟大的国家"pattern = "国家"result = kmp_search(text, pattern)print(result)```在这个例子中,我们首先计算next 数组,然后使用next 数组进行文本匹配。
abaabaab的next数组

abaabaab的next数组是指在字符串abaabaab中,每个前缀的最长相等真前后缀的长度数组。
这个数组在字符串匹配算法中非常重要,它可以帮助我们更快地进行字符串匹配,提高算法的效率。
为了更好地理解abaabaab的next数组,我们首先需要了解字符串匹配算法中的KMP算法。
KMP算法是一种经典的字符串匹配算法,它利用了字符串本身的信息,在匹配过程中尽量减少回溯,以达到提高匹配效率的目的。
在KMP算法中,我们需要先构建出模式串的next数组。
这个next数组其实是一个关于模式串的自身匹配情况的数组,它的定义如下:1. 对于模式串P中的每一个位置i,next[i]的值代表P[0]到P[i]这个子串的最长相等真前后缀的长度。
2. 如果模式串P的长度为n,则next数组的长度也为n。
以abaabaab为例,它的next数组为[0, 0, 1, 1, 2, 3, 4, 5]。
下面我们来详细解释一下这个数组是如何得出的。
1. 我们先来求出每个位置的最长相等真前后缀的长度。
位置0:a,这个位置是一个单字符,自身没有真前后缀,所以长度为0。
位置1:ab,这个位置没有真前后缀,长度为0。
位置2:aba,这个位置的最长相等真前后缀为a,长度为1。
位置3:abaa,这个位置的最长相等真前后缀为a,长度为1。
位置4:abaab,这个位置的最长相等真前后缀为aba,长度为3。
位置5:abaaba,这个位置的最长相等真前后缀为abaab,长度为4。
位置6:abaabaa,这个位置的最长相等真前后缀为abaaba,长度为5。
位置7:abaabaab,这个位置的最长相等真前后缀为abaabaa,长度为5。
经过上面的计算,我们得到了abaabaab的next数组为[0, 0, 1, 1, 2, 3, 4, 5]。
2. 接下来我们来讨论一下如何利用这个next数组来进行字符串匹配。
假设我们现在有一个文本串T和一个模式串P,我们希望在文本串T中找到模式串P的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
kmp算法next数组构造过程
KMP算法的核心部分就是构造next数组,它的作用是在模式
串与目标串不匹配时,快速确定模式串需要移动的位置,从而避免不必要的比较操作。
下面是KMP算法中next数组的构造过程:
1. 首先,创建一个长度与模式串相同的数组next[],用于存储
每个位置的next值。
2. 将next[0]初始化为-1,next[1]初始化为0,这是因为当模式
串只有一个字符时,无法进行移动,所以next[1]为0。
3. 从位置2开始,使用一个指针i遍历整个模式串。
在遍历的
过程中,不断更新next[i]的值。
4. 对于每个位置的next[i],需要判断模式串中位置i之前的子
串的前缀与后缀是否存在重复。
具体操作如下:
- 首先,将next[i-1]的值赋给一个临时变量j,并递归比较j
与i-1位置的字符是否相等。
如果相等,则next[i]的值为j+1;如果不相等,则将next[j]的值再赋给j,重新进行比较。
- 重复上述过程,直到找到一个相等的前缀和后缀,或者不
能再递归比较为止。
5. 当指针i遍历完整个模式串后,next数组的构造过程完成。
这个构造过程的时间复杂度为O(m),其中m是模式串的长度。
通过构造好的next数组,可以快速确定模式串的移动位置,
从而提高匹配效率。
