二维扩散反应方程的三次样条高精度加权隐式差分格式及其多重网格方法_马廷福

合集下载

第五章对流扩散问题(假扩散高阶格式差分方程的求解)

T T u v 0 x y
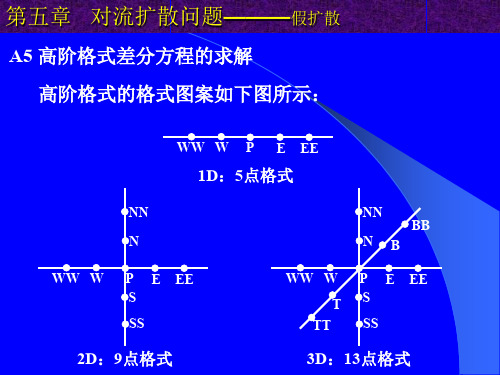
第五章对流扩散问题———假扩散
在P点的控制容积上对上边的 NW 微分方程进行积分，则：
1 6 N 5 w P E NE
u(Te Tw ) v(Tn Ts ) 0
W 2 SW
A 迎风格式
u(Te Tw ) v(Tn Ts ) 0 ue / w 0
n bb a EE n a EE WW WW b
第五章对流扩散问题———假扩散
A5.3 PDMA算法对五对角阵，有没有类似三对角阵TDMA那样的直接求解方法呢？实际上对五对角阵，人们也可以找到相应的直接求解方法，这个方法就是PDMA算法。下边以一维为例来介绍这个算法。
第五章对流扩散问题———假扩散
由此可见，对一维而言，所得到的差分方程不再是可以用TDMA直接求解的三对角矩阵方程，而变成一个五对角阵方程。对二维或三维而言，逐线联立求解的方程组也不再是可以用TDMA直接求解的三对角矩阵方程，也
变成一个五对角阵方程。
那么，针对这样一种五对角方程，通常我们如何来求解它们呢？
假设经过代入后得到的上三角方程为
i Ai i 2 Bi i 1 Ci
*#
问题的关键就变成为：找出系数Ai, Bi与Ci和系数a, b, c, d
, e及f之间的关系。为此，写出i-2点的上三角方程如下：
i 2 Ai 2i Bi 2i 1 Ci 2
****
(****)*(di+ eiBi-2)，有：
(di ei Bi 2 )i 1 Ai 1 (di ei Bi 2 )i 1 Bi 1 (di ei Bi 2 )i Ci 1 (di ei Bi 2 )

结构网格高精度CFD高效隐式求解及众核并行计算

结构网格高精度CFD高效隐式求解及众核并行计算高阶精度格式相比低阶精度格式拥有高分辨率、低色散、低耗散等良好的性质,能够获得更精细的流场结构,对于气动声学、转捩、湍流等复杂流动问题的数值模拟具有重要意义。

大规模多尺度复杂几何外形流动问题的高精度CFD模拟计算开销大、求解耗时长,迫切需要发展与之适应的高效隐式求解方法和并行计算技术。

传统隐式求解方法多是从低精度CFD中发展而来,时间项Jacobian矩阵的离散和线性化精度通常低于二阶,应用到高精度CFD中时,与高阶空间离散格式不匹配,容易出现收敛缓慢、鲁棒性变差等问题。

无矩阵(Jacobian-Free)Newton-Krylov(JFNK)方法巧妙结合了具有超线性收敛性质的Newton类非线性求解方法以及求解大规模稀疏线性方程组的Krylov子空间方法,并可利用传统隐式求解方法作预条件子以提高收敛速度。

JFNK方法采用有限差商近似Jacobian矩阵和向量乘积,避免了Jacobian矩阵的直接计算和存储,这对高精度CFD应用尤其具有吸引力。

相比传统隐式求解方法,预条件JFNK方法更复杂,在CFD中的高效应用依赖于具体算法实现以及针对特定问题的预条件子选择和算法参数优化等,限制了其在高精度CFD模拟中的应用。

当前,高性能众核处理器的兴起以及宽向量处理部件的使用大幅提升了浮点计算性能,但丰富的并行性也对高精度CFD应用的并行性能优化提出了严峻挑战。

在拥有数百并行线程的众核处理器上,传统LU-SGS等具有内在强数据依赖特点的隐式线性求解器(预条件子)的共享存储并行可扩展性严重下降,且难以利用宽向量处理部件,迫切需要在研究新型高效CFD求解算法的同时,发展与众核体系结构适应的并行算法。

本文基于“天河二号”众核超级计算机以及自主发展的高精度加权紧致非线性格式(WCNS),开展结构网格高精度CFD应用高效隐式求解算法及其并行计算研究,并应用于实际的可压缩气动数值模拟中。

空间分数阶扩散方程高精度快速算法及其理论分析

摘要分数阶微积分是一种关于整数阶微积分方程的数学推广, 它研究的是任意阶次的微分与积分的非标准的算子理论及其应用是数学分析的一个重要分支. 近年来, 分数阶微积分以及分数阶微分方程理论在不断发展和完善, 在很多领域它们都已经得到了非常广泛的应用, 例如在物理学,数学和工程学等. 对分数阶微积分以及分数阶微分方程的研究有着十分重要的理论意义和实际的应用价值, 特别是从实际问题中抽象出来的分数阶微分方程成为很多数学工作者的研究热点.众所周知, 分数阶导数使用的范围日益广泛, 但是其数值解的求解过程中仍然存在着弊端, 主要表现为：这些数值计算上的困难本质上都是由于分数阶微分算法的非局部性造成的, 特别是高维问题其存储量和计算代价是难以估量的. 所以对这类问题不管是直接解法还是Krylov子空间迭代法都丧失了其在求解整数阶微分方程方面的优势. 因此, 本文将会提出一种高效快速的解决方法, 本文的主要内容有：第一章, 简要介绍了分数阶扩散方程的背景、研究的意义及国内外研究现状分析.第二章, 介绍了分数阶扩散方程的有关理论知识, 针对一维、二维双侧空间扩散方程, 简要回顾了相关的有限差分格式.第三章, 针对一维分数阶扩散方程的模型, 构造出相应的二次样条离散化格式. 除此以外, 我们用数值实验给出了隐式欧拉格式下的高斯消元法（Gaussian）和双共轭梯度稳定法（Bi-CGSTAB）的数值误差、运算时间和平均迭代次数, 并且通过对比可以看出在相同的剖分下, Bi-CGSTAB法效率优于Gaussian法.第四章, 基于Bi-CGSTAB算法, 通过进一步分析可以得到, 结合快速矩阵--向量乘积和循环预条件之后的快速双共轭梯度稳定法和T. Chan预条件的双共轭梯度稳定法在处理分数阶扩散方程方面的高效性更加显著.第五章, 我们将Fast Bi-CGSTAB, T. Chan preconditioned Fast Bi-CGSTAB应用于二维分数阶扩散方程, 通过数值实验给出了隐式欧拉格式下的Gaussian、Bi-CGSTAB、Fast Bi-CGSTAB、T. Chan preconditioned Fast Bi-CGSTAB这几种方法的数值误差、运算时间和平均迭代次数的对比结果.关键词：空间分数阶扩散方程；高效快速算法；快速矩阵--向量乘积；循环预条件子；数值实验iA High- Accuracy Fast Algorithm for Space FractionalDiffusion Equation and its Theoretical AnalysisChai Xiaochao (Computational Mathematics)Directed by Prof. Fu Hongfei Liu JunAbstractFractional calculus is a mathematical extension of the standard-order integer-order integro-differential equations. It deals with arbitrary order differential and integral non-standard operator theory and its applications. It is an important branch of mathematical analysis. In recent years, the theory of fractional calculus and fractional differential equation has been continuously developed and improved. In many fields, they have been widely used, such as physics, mathematics and engineering. The study of fractional calculus and fractional differential equations has very important theoretical significance and practical application value. In particular, fractional differential equations abstracted from practical problems have become a hot topic for many mathematicians.As we all know, the range of fractional derivatives is increasingly used, but there are still drawbacks in the solution of its numerical solutions, mainly as follows: These numerical calculation difficulties are essentially due to the non-local of the fractional differential algorithm. In particular, for the high-dimensional problem of it difficult to measure the storage and computational costs. Therefore, both the direct solution and the Krylov subspace iteration method for such problems lose their advantages in solving integer differential equations. Therefore, this article will propose an efficient and quick solution. The main contents of this paper are:In the first chapter, the background of the fractional diffusion equation, the significance of the research and the analysis of the research status at home and abroad are briefly introduced.In the second chapter, the theoretical knowledge of fractional diffusion equations is introduced. For the one-dimensional and two-dimensional two-sided spatial diffusion equations, the related finite difference scheme is briefly reviewed.In the third chapter, according to the model of one-dimensional fractional differentialiiequations, a corresponding quadratic spline discretization scheme is constructed. In addition to this, we use numerical experiments to give numerical errors, operation times, and average iteration times for Gaussian elimination and Bi-CGSTAB in the implicit Euler format. In contrast, it can be seen that Bi-CGSTAB is better than Gaussian under the same split.In the fourth chapter, based on the Bi-CGSTAB algorithm, we can obtain the fast quadratic spline configuration method (fast Bi-CGSTAB) combined with the fast matrix-vector product and cyclic precondition, and the secondary of T. Chan preconditioner. The T. Chan preconditioned fast Bi-CGSTAB method is more effective in dealing with the fractional diffusion equation.In the fifth chapter, we apply fast Bi-CGSTAB and T. Chan preconditioned fast Bi-CGSTAB to two-dimensional fractional diffusion equations. Through numerical experiments, Gaussian, Bi-CGSTAB and fast Bi-CGSTAB in implicit Euler format are given. The numerical results of Bi-CGSTAB and T. Chan preconditioned fast Bi-CGSTAB are compared with the numerical error, operation time and average number of iterations.Key words: space fractional diffusion equation; high-accuracy fast algorithm; fast matrix- vector multiplication; circulant preconditioner; numerical experimentiii目录第一章引言 (1)1.1论文研究的背景和意义 (1)1.2国内外研究现状分析 (2)1.3本文结构与框架 (3)第二章基础知识 (4)2.1基本理论 (4)2.2空间分数阶模型有限差分法回顾 (9)2.2.1一维空间分数阶扩散方程 (9)2.2.2一维双侧空间分数阶扩散方程的Grünwald平移型差分格式 (9)2.2.3二维双侧空间分数阶扩散方程WSGD逼近 (11)第三章分数阶扩散方程模型及其二次样条离散化 (13)3.1问题引入 (13)3.2格式构造 (13)3.3数值实验 (16)第四章快速二次样条配置法 (20)4.1算法提出 (20)4.2 快速矩阵--向量乘积 (21)4.3 T.Chan循环预条件子构造 (24)4.4数值实验 (26)第五章二维分数阶扩散方程的逼近 (30)5.1问题引入 (30)5.2格式构造 (30)5.3 循环块矩阵的有效存储 (32)5.4基于张量积的快速矩阵--向量乘积 (34)5.5矩阵的循环块预条件子构造 (37)5.6数值实验 (39)第六章工作内容总结和科研前景展望 (42)参考文献 (43)iv攻读硕士学位期间的科研情况 (46)致谢 (47)v中国石油大学（华东）硕士学位论文第一章引言1.1论文研究的背景和意义随着自然科学和生产技术的不断发展, 分数阶微分方程逐渐成为现代科学技术中分析问题和解决问题的一个强有力的工具. 它主要应用于经济金融保险领域、生物种群的数量结构规律分析、疾病和病虫害的控制与防治、遗传规律的研究领域, 对解决问题起着非常重要的作用. 因此, 分数阶微分方程的研究成为一个极为活跃的研究方向. 其中, 分数阶偏微分方程解的存在性的研究, 是分数阶微分方程的重要研究内容, 它在应用数学领域取得了迅速的发展, 受到广泛的重视.最近几十年中, 分数阶微分方程广泛地应用于很多学科, 像物理学、数学和工程学等.分数阶微积分是一种关于整数阶微积分方程的数学推广, 它研究的是任意阶次的微分与积分的非标准的算子理论及其应用是数学分析的一个重要分支.随着自然界和许多科学领域中大量分数阶问题的出现, 分数阶微积分理论以及分数阶微分方程得到了越来越多的数学家们的肯定, 并吸引了众多科学家和研究学者的关注. 近年来, 分数阶微积分以及分数阶微分方程理论在不断发展和完善, 在很多领域它们都已经得到了非常广泛的应用. 对分数阶微积分以及分数阶微分方程的研究有着十分重要的理论意义和实际的应用价值, 特别是从实际问题中抽象出来的分数阶微分方程成为很多数学工作者的研究热点[1-5].分数阶微积分是传统的微积分的推广和应用是处理任意阶微积分研究及应用的数学分析领域. 在这一领域里, 函数的微分与积分不再局限于整数, 可以是任意的实数或者复数. 分数阶微积分起源于17世纪末, 著名数学家Marquis、Hospital和Leibniz首次提出了分数阶导数的概念. 在随后的一百多年中, 分数阶微积分只有些零星的结果产生,直到1898年, 数学家Lacroix才首次给出了1/2阶导数的结论次使用分数阶算子的是数学家Abel. 1823年, Abel在求解一个积分方程时, 引入了分数阶微积分来表示该方程的解, 但当时对分数阶微积分还没有一个比较合理的定义. 1832年, Liouville提出了分数阶微分的定义, 并用该定义成功解决了势理论问题. 1847年, Riemann对分数阶微积分的定义做了进一步的修正和补充. 之后, Grünwald和Krug这两1第一章引言位科学家统一了Liouville和Riemann分数阶微积分的定义, 给出了目前的研究中最常用的定义之一的Riemann-Liouville分数阶微积分. 以后, 许多科学家也致力于分数阶微积分的完善和改进, 他们在研究不同的课题时, 又提出了许多不同的定义, 例如Caputo 定义Grünwald-Letnikov定义、Weyl-Marchaud定义、Erd´elyi-Kober 定义、Riesz定义等等, 逐渐形成了现有的比较完整的分数阶微积分理论[6-11]. 目前, 研究和应用比较多的两种定义是Caputo定义和Remann-Liouville定义.由于分数阶方程没有精确解, 所以研究它的数值解很有意义, 然而尽管在各类分数阶微分方程数值方法方面的研究工作取得了重大进展, 科研工作者们先后提出了一系列稳定性好、精度高的数值格式, 但分数阶微分方程的数值计算仍然面临着计算量大（大规模问题CPU耗时巨大）和大容量存储（内存耗用非常高）的巨大挑战, 特别是高维问题其计算代价是难以估量的. 因此在前人的研究工作基础上我们找到一种存储量小, 计算量小的一种快速计算方法是很有意义的.1.2国内外研究现状分析在数值计算方面, 国内的郭柏灵院士出版了专著《分数阶偏微分方程及其数值解》[12], 国外的刘发旺[13]教授在分数阶微分方程的应用和数值计算方面都做出了许多开创性的工作. 同时, 相对于分数阶微分方程的应用和数值计算方面, 分数阶微分方程的理论研究相对缓慢, 这是由于分数阶微分算子自身的非局部性使得其研究更复杂, 它并不是整数阶的平行推广, 整数阶微积分里面的许多性质在分数阶微积分里面不再成立,例如函数乘积的求导公式、复合函数求导等. 这给分数阶微分方程的理论分析带来了难度, 但同时也激发了许多科研工作者的兴趣,越来越多的人致力于分数阶微分方程理论和应用问题的研究. 国内著名学者北京应用物理与计算数学研究所郭柏灵院士、北京大学谭文长教授、山东大学徐明瑜教授、河海大学陈文教授、孙洪广教授等等都在分数阶方程的理论和应用方面做出了重要贡献.2004年, Liu、Anh和Turner在文献[12]中以及Meerschaert和Tadjeran在文献[13]首次开启了分数阶偏微分方程数值方法的研究,随后大量优秀的研究工作相继涌现. 其中, 空间分数阶微分方程数值方法方面的研究工作见[14-20]等, 时间分数阶微分方程数值方法方面的研究工作见[21-26]等. 在这一领域, 国外学者如Podlubny、Meerschaert、Tadjeran、Ervin、Roop、沈捷、金邦梯、Turner、Sousa、Murio、Lazarov和Anh等, 国内学者如东南大学的孙志忠教授、上海大学的李常品教授、中科院的唐贻发研究员、厦2中国石油大学（华东）硕士学位论文3门大学的许传炬教授、兰州大学的邓伟华教授、中国石油大学（华东）的付红斐副教授及其团队[40,41]、汕头大学的林福荣教授及其团队等都在各自的具体模型问题上取得了一批优异的成果.1.3本文结构与框架众所周知, 分数阶导数使用的范围日益广泛, 但是由于其无法求得精确解, 故研究其数值解很重要. 事实上, 这些数值计算方面的困难本质上都是由于分数阶微分算法的非局部性造成的, 特别是高维问题其计算代价是难以估量的. 与传统的整数阶导数的局部定义不同, 分数阶导数其定义具有全局性, 因而其数值离散必然会导致一系列满的或稠密的系数矩阵, 这与整数阶导数离散得到稀疏矩阵完全不同. 所以对这类问题不管是直接解法还是Krylov 子空间迭代法都丧失了其在求解整数阶微分方程方面的优势.针对直接解法或Krylov 子空间迭代法等在求解分数阶微分方程方面的缺点和不足,我们期望可以寻求一种克服这些缺点的高效快速算法. 因此, 在本文中将会提出利用矩阵--向量乘法和循环预条件等方法来处理一些实际问题.本文的结构分布如下：第二章：简要介绍本文中将会涉及到的一些基本概念、基本性质、空间一维、二维时空分数阶扩散方程的基本形式和常见的离散格式.第三章：首先, 本文针对一维空间中的双侧分数阶扩散方程, 并且根Grünwald- Letnikov 定义了分数阶导数. 其次, 在时间和空间上采用均匀剖分, 选择一组二次B 样条曲线作为基函数, 从而给出方程的显式、隐式欧拉格式. 最后, 给出了相应的数值实验并对实验结果进行分析, 从而验证该方法的高效性.第四章：基于第三章中得出的QSC-ImE 格式, 结合Toeplitz 矩阵、快速傅里叶变换（FFT ）及循环预条件等方法, 我们进一步提出快速Bi-CGSTAB 方法.第五章：首先, 本文针对二维空间上的双侧分数阶扩散方程, 通过移位的Grünwald 近似估计定义的空间分数阶导数, 得到相应方程的隐式欧拉格式. 其次, 对于系数矩阵1n A +的存储量进行了分析, 并证明了1n A +的存储量为()JK O . 进一步说明了快速 Bi-CGSTAB 方法可以有效降低运算的存储量和计算量并给出了相应的数值试验结果.第六章：对本文所做的工作进行总结, 同时进行前景展望.第二章基础知识4第二章基础知识2.1基本理论本节我们将给出分数阶微分和积分的基本定义和一些重要的性质.）（0>αα阶Riemann-Liouville 分数积分的概念来源于著名的Cauchy 公式⎰∈>--=-+t n n N n t ds s f s t n t f I 010,,0,)()()!1(1:)( 其中N 是正整数集.将上述公式从正整数拓展到一般的正实数,最常用的方法是使用特殊函数Gamma 函数.常见的分数阶导数定义如下：定义2.1[7] 函数R x →+∞),0(:的），（0>∈αααR 阶Riemann-Liouville 分数积分定义为：其中, 等式的右端在(0,)+∞有定义, 其中()Γ是Gamma 函数, 其定义为：,)(01dt t e z z t ⎰∞--=Γ 并且满足迭代关系式)()1(z z z Γ=+Γ. ■ 定义2.2[17] 设1()[,],(,0)f x L a b R ααα∈∈>阶Riemann-Liouville 左、右分数阶导数定义为：其中, α满足n n <≤-α1,n N ∈.特别地, 如果n α=, 则有：定义2.3[7] 设1()[,],(,0)f x L a b R ααα∈∈>的Grünwald -Letnikov 的左、右分数阶导数中国石油大学（华东）硕士学位论文5定义为：其中, []()/M t a h +=-,[]()/M b t h -=-是正整数, ⎪⎪⎭⎫ ⎝⎛-=k g k k αα)1()(, 系数)(αk g 是函数幂级数α)1(z -的系数.,)1()1(0)(0∑∑∞=∞==⎪⎪⎭⎫ ⎝⎛-=-k k k k k k z g z k z ααα所有|z |1≤, 事实上, 它们可以递归地计算：,10=）（αg3,2,1,)11(1)(=+-=-k g k g k k ααα ■ 定义2.4[15] 设1()[,],(,0)f x L a b R ααα∈∈>, 左、右移位的Grünwald 差分算子： ,))((1)(0)(,∑∞=--=k k ph h p k x f g h x f A ααα（2-2） (),01()(())h r k k B f x g f x k r h h ααα∞==+-∑ （2-3）其中p,r 是整数. ■ 引理2.5[7,15,17] 在（2-1）中系数（21≤<α）满足如下性质：⎪⎪⎩⎪⎪⎨⎧≥≤=≥≥≥≥<-==∑∑=∞=)1(,0,0,01,0,10)(0)()(3)(2)(10m g g g g g g m k k k k ααααααα ）（（2-4） ■ 引理2.6[25] 令u D R L u x 21),(+∞-∈α, 它的傅里叶变换属于)(1R L , 定义左、右加权移位的Grünwald 差分算子（WSGD ）如下：第二章基础知识6其中,则有：2,,()()()L h p q x D u x D u x h αα-∞=+O ,2,,()()()Rh p q x D u x D u x h αα∞=+O ,q p q p ≠是整数，且,.由于Riemann-Liouville 分数阶导数在{})1,1(),0,1().(,1,,1,/)(,-=-=-=+=q p n i n a b h ih a x i离散形式如：)()(1)(2110)(h O xu h x u D k i i k kix a +=+-+=∑αααω；)()(1)(2110)(h O xu h x u D k i i N k kib x +=-++-=∑αααω （2-5）其中,⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-++=+=+=-=≥-+===--2,4242,42,42),1,1(),(,1,222,2),0,1(),()(2)()()(1)(1)(0)(0)(1)()()(0)(0k g g g g q p k g g g q p k k k k k k ααααααααααααααωαωαωααωαω （2-6） (1)如果)0,1(),(=q p ：中国石油大学（华东）硕士学位论文7⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<=≥≥≥≥≥-+=<--==∑∑∞==00)()()(4)(3)(02)(22)(1)(0;2,0,0,01,4)4(,0222k mk k k m ααααααααωωωωωαααωααωαω ，（2-7）（2）如果)1,1(),(-=q p ：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥=<=≥≥≥≥≥≥≥≤-+-=>+-+=<+-=+=∑∑∞==00)()()(5)(4)(4)(2)(02)(323)(22)(1)(0;31,0,0,01,06)8)(2(,0844,04242k mk k k m m 或，αααααααααααωωωωωωωααααωαααωααωαω （2-8） ■ 定义2.7[21] Toeplitz 矩阵Toeplitz 矩阵是一个矩阵的每个斜对角, 从左到右是恒定的. 通常, 一个n n ⨯的Toeplitz 矩阵由一个21n -序列{}11--=n n i i t 完全确定. 矩阵() 2,1,,==-j i t j i T i j n 如下：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=--------------0132110323012231011221t t t t t t t t t t t t t t t t t t t t t t t T n n nn n n n n n n n （2-9）■ 定义2.8[22] Circulant 矩阵Circulant 矩阵是一个矩阵中的每个行向量将一个元素旋转到右相对于前面的行向量. 通常, 一个n×n 的Circulant 矩阵由一个n 序列{}10-=n i i c 完全确定. 矩阵 ()mod (,),1,2,,n j i n C i j c i j n -==的具体形式如下：第二章基础知识8⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=---------01321103230122310112210c c c c c c c c c c c c c c c c c c c c c c c C n n n n n n n n n n （2-10）■ 引理2.9 [22,23] 对于具有（2-10）形式的Circulant 矩阵n C 可以分解为1()n n n n C F diag F c F -=.其中01221[,,,,,]T n n c c c c c c --=是Circulant 矩阵n C 的第一列, n F 是n n ⨯离散的Fourier 变换矩阵, 即(,)),,1201n ijlF j l j l n i n π=-≤≤-=由引理2.9可知, 一个Circulant 矩阵显然是Toeplitz 矩阵, 反之并不成立. 然而, 一个n n ⨯Toeplitz 矩阵n T 可以嵌入到一个22n n ⨯的Circulant 矩阵2n C [21,23]⎥⎦⎤⎢⎣⎡=n nn nn T B B T C 2, 其中,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=---------0000121121211121n n n nn n n t t t t t t t t tt t t B. （2-11）■中国石油大学（华东）硕士学位论文92.2空间分数阶模型有限差分法回顾2.2.1一维空间分数阶扩散方程(,)(,)(,)(,)u x y u x t c x t s x t t x αα⎧∂∂=+⎨∂∂⎩. （2-12）其中, (,)0,,0c x t L x R t T ≥≤≤≤≤.定义时间网格尺寸t ∆, 则n t n t =∆, 且满足0n t T ≤≤.同样的, 定义空间网格尺寸0x h ∆=>, 其中, ()/h R L K =-. 令i x L ih =+, 其中0,,i K =, 且i L x R ≤≤. 令n i u 为(,)i n u x t 的近似值, 类似的(,)n i i n c c x t =,(,)n i i n s s x t =.方程（2-12）在时间上的离散格式为：1(,)(,)(,)(,)(,)n n n n n u x t u x t u x t c x t s x t t x αα+-∂=+∆∂.2.2.2一维双侧空间分数阶扩散方程的Grünwald 平移型差分格式对于形如（2-13）的分数阶偏微分方程[26]：0(,)(,)(,)(,)(,)(,),,0(,0)(),,(,)(,)0,0.u x t u x t u x t c x t c x t s x t L x R t Tt x x u x u x L x R u L t u R t t T αααα+-+-⎧∂∂∂=++≤≤≤≤⎪∂∂∂⎪⎪=≤≤⎨⎪⎪⎪==≤≤⎩ （2-13）对于上述左、右分数阶导数可以由定义2.4中的Grünwald 差分算子近似如下：()1((1))()Mkk d f x gf x k h h dx hααα==--+O ∑. （2-14）忽略c 的符号（+,-）可以得到离散格式：1110n n ni nn i i i k i k i k u u c g us t hα++-+=-=+∆∑, 1,2,,1i K =-.令αβh t /∆=整理后得到：t s u g c u g c ug c uni i k n k i k n in i n i n i n i n i∆++++=∑+=+-++1211101)1(βββ. （2-15）其矩阵形式如下：第二章基础知识10n n n tS AU U ∆+=+1 （2-16）其中, 012[,,,,]n n n nn TK U u u u u = , 121[0,,,,,0]n n n n TK S s s s -=.12111013222121112111011(1)(1)1+00010010001+nn n nn nn n n n n K KK K K K K K K K g g g c g c g c g c g c g c A g c g c g c g c g c g βββββββββββ-------+⨯+⎛⎫ ⎪+⎪ ⎪+=⎪⎪ ⎪ ⎪ ⎪⎝⎭ 由此可以看出矩阵A 是非稀疏矩阵, 存储量为(1)/2K K +*. 引理2.10 [22] 系数矩阵的存储量可以降为()K O . 证明：对于系数矩阵A 可以分解为如下形式：102101321212101100000000000:nn nK K K K g g g g g c g g g c A I g g g g g c g I G βββλ---⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪=+*⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=+其中, I 为单位矩阵, 1021032112101000000000K K K g g g g g g g g G g g g g g g --⎛⎫ ⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭1210=0nn nK c c c ββλβ-⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭由定义2.7知, 矩阵G 为Toeplitz 矩阵. 显然, A 分解后存储量降为3K. ■中国石油大学（华东）硕士学位论文112.2.3二维双侧空间分数阶扩散方程WSGD 逼近对于模型12120(,,)((,,)(,,)(,,)(,,))(,,),(,,)[0,](,,0)(,),(,)(,,)(,,),(,,)[0,]a x x b c y y d u x y t K D u x y t K D u x y t K D u x y t tK D u x y t f x y t x y t T u x y u x y x y u x y t x y t x y t T ααββϕ++--∂⎧=++⎪∂⎪⎪++∈Ω⨯⎨⎪=∈Ω⎪=∈∂Ω⨯⎪⎩ (2-17) 其中, 区域ββααd y y c b x x aD D D D d c b a ，和，),,(),(⨯=Ω是2,1≤<βα的Riemann-Liouville 分数阶算子, 0)()(,0)()(,2,1,0,22212221≠+≠+=≥--++-+K K K K i K K i i 并且, 对于边界函数ϕ,如果0),,(,0;0),,(,021=≠=≠++t y b K t y a K ϕϕ则如果则；如果0),,(,0;0),,(,021=≠=≠--t d x K t c x K ϕϕ则如果则. 对于问题（2-17）做剖分：M T N c d h N a b h y y x x /,/)(,/)(=-=-=τ,有,,,τn t jh y ih x n i i === M n N j N i y x ≤≤≤≤≤≤0,0,0；10,2/)(12/1-≤≤+=++M n t t t n n n ；令),,(),,,(2/12/1,,++==n j i n j i n j i n j i t y x f f t y x u u τδ/)(,1.,nj i n j i n j i t u u u -=+,则（2-17）有如下离散形式：)())()()()()()()()((2122/1,,2,1,2,11,21,11,21,1,τδββααββααO f u D K u D K u D K u D K u D K u D K u D K u D K u n j i n j i d y n j i y c n j i b x n j i x a n j i d y n j i y c n j i b x n j i x a n j i t +++++++++=+--+++-+-++++ （2-18）用WSGD 算子：u D u D u D u D qp h R q p h L q p h R q p h Ly y x x ββαα,,,,,,,,,,和. 近似代替u D u D u D u D d y y c b x x aββαα，和，.第二章基础知识12由令1,n i j U +为方程（2-18）的数值解,则可以得到：11212,,,,,,,,,1/21212,,,,,,,,,,1222212222x x y y x x y y n L h p q R h p q L h p q R h p q i jn n L h p qR h p q L h p q R h p q i j i j K K K K D D D D U K K K K D D D D U f ααββααββτττττττττ++--+++--+⎛⎫---- ⎪⎝⎭⎛⎫=+++++ ⎪⎝⎭（2-19）中国石油大学（华东）硕士学位论文13第三章分数阶扩散方程模型及其二次样条离散化3.1问题引入在本节中, 我们考虑以下一维空间中的双侧分数阶扩散方程的二次样条配置（QSC ）方法0(,)(,)(,)(,)(,)(,),0(,0)(),,(,)(,)0,0,u x t u x t u x t a x t a x t s x t L x R t T t x x u x u x L x R u L t u R t t T αααα+-+-⎧∂∂∂=++≤≤≤≤⎪∂∂∂⎪⎪=≤≤⎨⎪⎪⎪==≤≤⎩，（3-1）其中, 方程的空间导数的分数阶满足12α<<, 左右扩散系数满足(,)0,(,)0a x t a x t +->>, (,)s x t 为已知函数. (,)(,),u x t u x t x x αααα+-∂∂∂∂是由[7]中定义的Grünwald-Letnikov 分数阶导数上式中[]x 表示不超过x 的最大整数, ()(1)kkg k αα⎛⎫=- ⎪⎝⎭,k α⎛⎫ ⎪⎝⎭是二项式系数, ()k g α有关性质详见定义2.3和引理2.5.特别地, 当=2α, 分数阶导数即为经典的二阶导数, 模型（3-1）化为经典的扩散方程.3.2格式构造设J 为正整数, 我们考虑空间域的均匀分割{}01=J L x x x R ∆=<<<=第三章分数阶扩散方程模型及其二次样条离散化14其中网格尺寸为B Lx x x J-∆=. 令21([,])j j P x x +为1[,]j j x x +上多项式的集合, 令 {}212,11([,])|([,]),,1,,1,j j P v C LR v P x x j J ∆+=∈∈=-其中1([,])C L R 是[,]L R 上具有连续一阶导数的函数的集合. 此外, 令我们取二次B 样条曲线()2,0,1,,1L j x x x j j J x φφ-⎛⎫=-+=+⎪∆⎝⎭,作为函数空间2,1P ∆的基函数, 定义2,1P ∆为满足齐次Dirichlet 边界条件的二次样条空间, 其维数为J, 它的一组基函数为：{}1101=-,2,,1;.j j J J J j J φφφφφφφφ+==-=-；则方程（3-1）的二次样条近似解可写为：1(,)()(),Jj j j u x t c t x φ∆==∑ （3-3）其中(),1,,j c t j J =为待求函数.将公式（3-3）代入公式（3-1）, 我们可以得到如下方程：11()(,)()()(,)()()(,)J Jj j d d x a x t c t x a x t c t x s x t ααφφφ==+-=++∑∑ （3-4我们取配置点为{}1()/2,1jj j x x j J τ-=+≤≤,将这些点代入方程（3-4）, 从而得到形式如下的二次样条配置方程：中国石油大学（华东）硕士学位论文15其中,0(,)(),(,)(),1,j j i i d Q i j Q i j x i j J d xααααφτφτ+±==∆≤≤, 1()((,),,(,))T J s t s t s t ττ=,{}1()(,),,(,)a J D t diag a t a t ττ±±±=,1()((,),,(,))T J c t c t c t ττ=矢量0Jc R ∈满足000Q c u =, 其中0u 是0()u x 在配置点的插值.方程（3-4）中的空间分数阶导数由下面移位的Grünwald 近似逼近： ()1()[(1)]()ij ik j i k d g k x x d x x ααααφτφτ=±=-∆+O ∆∆∑. （3-6）我们在第三章和第四章中简写()k g α为k g . 方程（3-5）的矩阵0,Q Q α+和Q α-形式如下：051016118161015J JQ ⨯⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭ 01011210102321013234101021232101112320125656056185655555J J J J J J J J J J J J J Jg g g g g g g g g g g g g g g g g Q g g g g g g g g g g g g g g g g g gg g g g g g g αθθθθθθθθθθθθθθ+-----------⨯++⎛⎫⎪++ ⎪ ⎪++ ⎪= ⎪ ⎪++⎪++ ⎪ ⎪+-++⎝⎭第三章分数阶扩散方程模型及其二次样条离散化160122321101123221001123320011223001112001015555565186506565J J J J J J J J J J J J Jg g g g g g g g g g g g g g g g g g g g g g g g g Q g g g g g g g g g g g g g g g g g g αθθθθθθθθθθθθθθ-----------⨯-+++⎛⎫⎪++ ⎪ ⎪++ ⎪= ⎪⎪++⎪++⎪ ⎪++⎝⎭其中, 116j j j j g g g g θ-+=++.方程（3-5）的二次样条配置的显式欧拉方法（QSC-ExE ）可写为：100(()())(),n n a n a n n t Q c Q D t Q D t Q c ts t x ααα+++--∆⎡⎤=+++∆⎢⎥∆⎣⎦（3-7）方程（3-5）的二次样条配置的隐式欧拉方法（QSC-ImE ）可写为：101101(()())().n na n a n n t Q D t Q D t Q c Q c ts t x ααα++++-+-+∆⎡⎤-+=+∆⎢⎥∆⎣⎦（3-8） 3.3数值实验针对3.2节中的离散格式（3-8）, 我们有如下的数值实验：例1 我们考虑如下一个双侧分数阶扩散方程：1.8 1.81.8 1.8(,)(,)(,)(,)(,)(,),02,01u x t u x t u x t a x t a x t s x t x t t x x+-+-∂∂∂=++<<<<∂∂∂ （3-9）其中, 扩散系数为：1.8 1.8(,)(1.2),(,)(1.2)(2)a x t x a x t x +-=Γ=Γ-,方程（3-9）初始条件为22(,0)4(2)u x x x =-, 边界条件为(0,)(2,)0u t u t ==. 其真解为[17,27]给出：22(,)4(2)t u x t e x x -=-.在空间上, 我们使用均匀的网格剖分{}0102J x x x =<<<=, 网格尺寸为中国石油大学（华东）硕士学位论文172x J∆=, 选择配置点 0110,(),2,1,,2j J j x j J τττ+⎧⎫==-∆==⎨⎬⎩⎭在时间上也使用均匀的网格剖分{}0101M τττ=<<<=. 用u ∆表示方程（3-9）的数值解, 所得误差由最大范数衡量：001max max |(,)(,)|j m m M j J u uu j m u t τ∆∞∆≤≤≤≤+-=-其中(,)u j m ∆表示数值解矩阵u ∆的第(,)j m 项, 我们在表3-1中给了隐式欧拉基于高斯消元法（Gaussian ）和Bi-CGSTAB 法的数值误差、CPU 时间和平均迭代次数.表3-1：1.8α=时,一维双侧空间微分方程的运算结果隐式欧拉格式J M 误差计算耗时平均迭代次数Gaussian26 25 2.29e-02 3.32秒 - 27 26 1.14e-02 52.3秒 - 28 27 5.68e-03 13分24秒 - 29 28 2.84e-03 3小时34分44- Bi-CGSTAB26 25 2.29e-02 0.16秒 24 2726 1.14e-02 1.54秒 43.47 28 27 5.68e-03 28.13秒 73.05 29 28 2.84e-03 5分54秒 110.95 210291.42e-031小时32分44156.87由上表可以看出：（1）这两种方法的在J, M 相同时有同样的误差精度；（2）随着J, M 的增加, 无论是Gaussian 法还是Bi-CGSTAB 法, 虽然CPU 耗时都增加了, 但是在J, M 相同时显然Bi-CGSTAB 法的效率更高. 例如, J=29, M=28时, Gaussian 法用时约3.5个小时,而Bi-CGSTAB 法用时仅6分钟.第三章分数阶扩散方程模型及其二次样条离散化18例2 我们考虑如下的左侧分数阶扩散方程：其中, 初始条件(,0)4(1)u x x x =-, 边界条件(0,)(1,)0u t u t ==,方程（3-10）的真解为(,)4(1)t u x t e x x -=-.我们采用和例1相同的时空网格, 用QSC-ImE 方法计算此方程,得到的数值解的误差仍用时空网格上的最大范数来衡量. 表3-2中给出了隐式欧拉基于高斯消元法（Gaussian ）和Bi-CGSTAB 法的数值误差、CPU 时间和平均迭代次数.表3-2： 1.8α=时,一维左侧空间微分方程的运算结果隐式欧拉格式J M 误差运算耗时平均迭代次数Gaussian25 25 2.38e-002 0.51秒 - 26261.25e-0027.15秒-27 27 6.45e-003 1分47秒 - 28 28 3.29e-003 27分29秒 - Bi-CGSTAB25 25 2.38e-002 0.16秒 24.09 2626 1.25e-002 1.15秒 44.05 27 27 6.45e-003 10.93秒 77.46 28 28 3.29e-003 2分18秒 119.55 29291.66e-00321分45秒143.76由上表可以看出：（1）这两种方法的在J, M 相同时有同样的误差精度；（2）随着J, M 的增加, 无论是Gaussian 法还是Bi-CGSTAB 法, 虽然CPU 耗时都增加了, 但是在J, M中国石油大学（华东）硕士学位论文相同时显然Bi-CGSTAB法的效率更高. 例如, J=28, M=28时, Gaussian法用时约半个小时, 而Bi-CGSTAB法用时约2分钟.19第四章快速二次样条配置法20第四章快速二次样条配置法4.1算法提出对于QSC-ImE 方法（3-8）, 我们需要在每个时间步求解一个具有J 维稠密系数矩阵的线性系统, 其存储量为2()J O . 如果我们对每个线性系统使用高斯消元法, 则计算量为3()J O . 如果我们对每个线性系统使用迭代方法, 例如Bi-Conjugate Gradient Stabilized 方法（Bi-CGSTAB ）, 则算法中的矩阵--向量乘积, 其每次迭代的计算量为2()J O . 由于计算迭代次数较多, 我们有必要研究快速算法. 方程（3-8）的预处理Bi-CGSTAB 方法可以表示如下[28]：算法4.1（预处理 Bi-CGSTAB ） for i=1,2,…,(1)1:,Ti i ργγ--=if 10,i ρ-= choose (1)=.i γγ- if i=1()(1),i i p γ-=else()(1)(1)(1)11+(),i i i i i i p p v γβω-----=-endifsolve (),i M p p ∧=1(),i Ti v ργ-中国石油大学（华东）硕士学位论文21(1)(),i i i s v γα-=-if s small enough, choose ()(1),i i i c c p α∧-=+break, solve ,M s s ∧=()(1),i i i i c cp s αω∧∧-=++().i i s t γω=-Check for convergence; continue if necessary. end(1)().n i cc +→=我们可以看出, 上述算法中主要的计算量在于计算如下矩阵--向量乘积：4.2 快速矩阵--向量乘积文献[28-30]提出了一种空间分数阶扩散方程的快速有限差分法, 该方法利用了Toeplitz 矩阵和快速傅里叶变换（FFT ）的特性. 本文中的线性系统也可以通过迭代方法解决.我们可以看到, 矩阵011(()())a n a n t Q D t Q D t Q x ααα+++-+-∆⎡⎤-+⎢⎥∆⎣⎦和向量p ∧,s ∧相乘需要的计算量是2()J O . 所有其他计算只需要()J O 的计算量, 考虑到矩第四章快速二次样条配置法22阵Q α+和Q α-的结构, 我们可以证明该矩阵和向量的乘积所需要最优的计算量为(log )J J O .定理4.1 对于任意的J f R ∈, 矩阵--向量乘积011(()())a n a n t Q D t Q D t Q f x ααα+++-+-∆⎡⎤-+⎢⎥∆⎣⎦的计算量为(log )J J O .证明：矩阵Q α+和Q α-可以分解为：(1)(2),Q Q Q ααα+++=+ (1)(2)Q Q Q ααα---=+其中,0(1)0110,3,,2,1(,)6,1,8,,i j j i g j i Q i j g g j i g j i αθ+-+≥+⎧⎪=+⎪=⎨+=+⎪⎪≤⎩10(2)01,1,1,,(,)(1,),1(,)6,(,)(,),80,i i g g j i J g i j J J Q i j g g i j J J α++--=≤-⎧⎪-=-⎪=⎨--=⎪⎪⎩其他，另外,(1)(1)(1)1(,1)5,(),TJ J Q J g g Q Q ααα+--+=+=010(2)126,(,)(1,1),,(,)(2,1),1(,),2,,80,J i J I g g i j g i j Q i j g g i J j J α--+-+--=⎧⎪-=⎪=⎨--≤≤=⎪⎪⎩其他.可以看到, (1)Q α+是一个J J ⨯的Toeplitz 矩阵, 由引理2.9知它可以嵌入到一个22J J ⨯的循环矩阵2J C 中,(1)2(1)J JJ Q B CB Q αα++⎛⎫= ⎪⎝⎭, 其中中国石油大学（华东）硕士学位论文2311321131110110050050050056000J JJ J JJ J JJ J J J J g g g g g g g g g g g g B g g g g g gg θθθθθθθ--------+⎛⎫⎪+ ⎪ ⎪+ ⎪=⎪⎪⎪+ ⎪⎪+⎝⎭对于任意一个向量2[,0]T T T J f f R =∈2J C f 可以分解为：212222()J J J J J C f F diag F c F f -=其中2J F 是离散傅里叶变换矩阵[30,31], 2J c 是2J C 的第一列向量. 矩阵--向量乘积2J F f 和22JJ F c 可通过FFT 计算得到, 其计算量为(2log(2))J J O .对角阵--向量乘积2(),,J diag v u v R ω∈可用Hadamard 乘积来计算, 其计算量为(2)J O . 通过快速傅里叶逆变换（iFFT ）, 可以在(2log(2))J J O 的计算量下执行12J F f -矩阵--向量乘积运算. 此外, (2)Q α+是一个稀疏矩阵,并且可以在()J O 的计算量下运算(2)Q f α+.我们定义(1)(2)f Q f Q fαα∧++=+.则11()()a n a n D t Q f D t f α∧+++++=可以通过Hadamard 乘积在()J O 的计算量下得到. 同样,(1)(2)1()()a n D t Q f Q f αα-+--+也可以在(2log(2))J J O 的计算量下得到. 另外, 由于0Q 是一个三对角矩阵, 0Q f 可以在存储量为()J O 下完成.最后, 可在计算量为(log )J J O 下运算011(()())a n a n t Q D t Q D t Q f x ααα+++-+-∆⎡⎤-+⎢⎥∆⎣⎦■ 注4.1 Toeplitz 矩阵(1)Q α+和(1)Q α-都有（J + 2）个不同的分量. 稀疏矩阵(2)Q α+和(2)Q α-都有第四章快速二次样条配置法24（J + 1）个非零分量. 连同三对角矩阵1()a n D t ++, 1()a n D t -+和0Q , 故Q α+和Q α-所需的存储量为()J O . 因此, 矩阵所需的存储量也为()J O .注4.2 矩阵Q α+,Q α-和0Q 可以在每次迭代前定义, 但矩阵1()a n D t ++,1()a n D t -+是需要随时间步变化而不断更新的.4.3 T.Chan 循环预条件子构造我们注意到矩阵011(()())a n a n t Q D t Q D t Q x ααα+++-+-∆⎡⎤-+⎢⎥∆⎣⎦在算法4.1中是一个近似Toeplitz 矩阵. 根据广义T. Chan 的循环预条件[30-32], 我们可以对矩阵011(()())a n a n t Q D t Q D t Q x ααα+++-+-∆⎡⎤-+⎢⎥∆⎣⎦进行相应的循环预处理, 步骤如下：Step 1. 取1()a n D t ++,1()a n D t -+对角线元素的均值, 分别为：1111:(,),n J j n j D a t J τ+-+++==∑1111:(,),n Jj n j D a t J τ+---+==∑ （4-1） Step 2. 构造对称三对角矩阵0Q 的广义T. Chan 循环逼近0()F Circ Q , 其中0()F Circ Q 第一列为0,62,1,11,2,,80,3 1.jJ j c J j J J j J -=⎧⎪=-=⎨⎪≤≤-⎩ （4-2）中国石油大学（华东）硕士学位论文25Step 3. 构造矩阵Q α+和Q α-的广义T. Chan 循环逼近+()F Circ Q α和()F Circ Q α-, 其中, +()F Circ Q α和()F Circ Q α-的第一列定义如下：012012111,2121010101(2)(6)410,1,()(6)(5),22,18(6)(5)(2),1,(5)(2)(6)(5),.j j j j j jJ J J J J J J J g g g g g g j J j g g g g g j J c J g g g g g J g j J g g J g g g g j J α-+-+------++-++=⎧⎪-++++≤≤-⎪=⎨+++++-=-⎪⎪++-+++=⎩ （4-3）01201201011,02112312(2)(6)410,1,(2)(6)(5)(5),2,1(2)211,3,8(2)(6)(5),4.J J jJ J J J j J j J j J j J j J g g g g g g j J g g g g g g j c J g g g g j J j g g g g g j J α-----+-+-+-+-+-++-++=⎧⎪-+++++=⎪=⎨-+++=⎪⎪-++++≤≤⎩（4-4）Step 4. 对于011(()())a n a n t Q D t Q D t Q x ααα+++-+-∆⎡⎤-+⎢⎥∆⎣⎦构造广义T. Chan 循环预条件1m F C +, 即1110:()()()n n m FF F F tCCirc Q D Circ Q D Circ Q xααα++--++-+-⎡⎤∆=-+⎢⎥∆⎣⎦（4-5）广义T. Chan 循环预条件1m F C +可以用傅里叶变换矩阵J F 对角化, 即111()m n F J J F J C F diag F c F +-+=.算法4.2 快速预处理循环在每个时间节点n t 上,1. 计算11()n n Fv fft c ++=, 2. 计算111/n n v v ++=,3. 预处理()i M p p ∧=的Bi-CGSTAB 方法计算步骤如下： ()()()i i fft p ω=,1()*n i z v ω+=,()p ifft z ∧=。

——显式差分和隐式差分

边界节点：
A矩阵非零系数减少，同时引入第一类边界，
方程右端项B向量出现非零元素。
AX B
组建A和B矩阵，求解线性方程组得到X
A A(135,135)
X X (135,1)
B B(135,1)
%Matlab 2D clear; clc; figure('color','w');
内部节点：
for j=2:n-1 for i=2:m-1;
a((j-1)*m+i,(j-1)*m+i+1)=1; a((j-1)*m+i,(j-1)*m+i-1)=1; a((j-1)*m+i,j*m+i)=1; a((j-1)*m+i,(j-2)*m+i)=1; a((j-1)*m+i,(j-1)*m+i)=-4; end end
Tair
Tcap
一阶常微分方程的数值解首先对时间和温度进行离散：
dT f (T ,t) dt
利用向前差分形式：
t j t0 jt, Tj T (t j )
dT dt
tt j
Tj1 Tj O(t) t
得到以下的显式差分格式：
Tj1 Tj tf (Tj , t j )
Cui, 2013
Cui, 2013
Cui, 2013
Cui, 2013
总结：
1、有限差分方法给出的数值解的精度取决于所用的差分形式（向前、向后、中心）。
2、偏微分方程的显式有限差分格式通常是有条件稳定的，为了保证得到精确的数值解，最关键的是需要根据稳定性条件选取正确的空间和时间步长。

一种求解对流扩散问题的高精度无网格方法

一种求解对流扩散问题的高精度无网格方法
吴学红;李增耀;马良栋;陶文铨
【期刊名称】《工程热物理学报》
【年(卷),期】2008()9
【摘要】无网格局部Petrov-Galerkin方法是近十年发展起来的一种新的数值计算方法,该疗法在计算区域内布置一些离散的节点,并利用这些节点构建插值函数。

本义以Smith-Hutton问题为例,把该方法的计算结果与有限容积法高阶格式的计算结果进行比较。

研究结果表明:该方法是一种高精度的数值计算方法,能有效地计算高Pe数的流动问题。

【总页数】3页(P1561-1563)
【关键词】无网格法;Petro-Galerkin方法;数值模拟
【作者】吴学红;李增耀;马良栋;陶文铨
【作者单位】西安交通大学动力工程多相流国家重点实验室
【正文语种】中文
【中图分类】TB115
【相关文献】
1.一种新的求解对流扩散边值问题的无网格方法 [J], 童小红;秦新强
2.求解含源项非定常对流扩散问题的移动网格方法 [J], 周琴;杨银
3.求解对流扩散反应方程的一种高精度紧致差分方法 [J], 杨苗苗;葛永斌
4.基于非均匀网格求解非线性对流扩散问题的一种高精度差分格式 [J], 王?;杨志
峰
5.三维稳态对流扩散问题的无网格求解算法研究 [J], 张小华;邓霁恒
因版权原因，仅展示原文概要，查看原文内容请购买。

二维结构化网格CFD LU-SGS时间推进并行算法

二维结构化网格CFD LU-SGS时间推进并行算法*龚春叶1,2,3+，包为民1,2，汤国建2，王玲1，刘杰3，胡庆丰3【摘要】针对二维结构网格CFD（computational fluid dynamics）时间推进LU-SGS（lower-upper symmetric Gauss-Seidel）存在的强数据依赖的特点，提出了波阵面并行算法，设计了相应的数据结构，以及具有更好数据局部性的访存优化方法和分块通信优化方法。

测试结果表明，并行算法可以取得与串行算法完全一致的计算结果，且具有较好的加速效果，在DMP （distributed memory processing）系统下与16个进程相比，64个进程的并行效率达到85.64%，在SMP（symmetric multiprocessing）系统下与16个进程相比，128个进程的并行效率达到83.68%。

【期刊名称】计算机科学与探索【年(卷),期】2013(007)010【总页数】8【关键词】LU-SGS；计算流体动力学（CFD）；结构化网格；并行计算+Corresponding author:E-mail:gongchunye@1 引言计算流体动力学（computational fluid dynamics，CFD）[1-2]是流体力学的一个重要分支，是以理论流体力学与计算技术为基础，对复杂流体进行数值模拟的学科。

近几十年来，随着对流体规律认识的深入和工程应用的需要，CFD 已发展成为一门独立的学科，在航空、航天、汽车、环境工程和船舶等方面得到广泛应用。

在CFD中，首先需要通过有限差分、有限元或者有限体积等离散方法把计算区域离散化为网格，流场的状态由定义在网格节点（或网格单元）上的速度、密度、压力、温度等特征量来表述。

CFD模拟过程主要是对网格上的特征量进行迭代计算，网格数目与计算量直接相关。

当网格数目多时整个计算量非常大，往往需要在高性能计算机上进行大规模并行计算。

ADI(交替方向隐格式)求解二维抛物方程(含matlab程序)

ADI 法求解二维抛物方程学校：中国石油大学（华东）学院：理学院姓名：张道德时间：2013.4.271、ADI 法介绍作为模型，考虑二维热传导方程的边值问题：（3.6.1）,0,,0(,,0)(,)(0,,)(,,)(,0,)(,,)0t xx yy u u u x y l t u x y x y u y t u l y t u x t u x l t ϕ=+<<>⎧⎪=⎨⎪====⎩取空间步长1hM，时间步长0，作两族平行于坐标轴的网线：,,,0,1,,,j k x x jh y y kh j k M =====将区域0,x y l ≤≤分割成2M 个小矩形。

第一个ADI 算法（交替方向隐格式）是Peaceman 和Rachford （1955）提出的。

方法：由第n 层到第n+1层计算分为两步：（1）第一步： 12,12n j k xx yy u +从n->n+，求u 对向后差分,u 向前差分，构造出差分格式为：1(3.6.1)11112222,,1,,1,,1,,1221222,,2-22=21()n n n n n n n n j kj kj kj k j kj k j k j k n n x j k y j k hhhτδδ+++++-+-+-+-+=+uu uuuu u u （+）u u（2）第二步：12,12n j k xx yy u +从n+->n+1，求u 对向前差分,u 向后差分，构造出差分格式为：2(3.6.1)1111111222,,1,,1,,1,,12212212,,2-22=21()n n n n n n n n j kj kj kj k j kj k j k j k n n x j k y j k hh hτδδ++++++++-+-++-+-+=+uu uuuu u u （+）u u其中1211,1,,1,0,1,2,,()22n j k M n n n τ+=-=+=+上表表示在t=t 取值。

分数阶扩散方程的基于隐式龙格-库塔方法的高精度离散方法及快速算法

分数阶扩散方程的基于隐式龙格-库塔方法的高精度离散方法及快速算法分数阶扩散方程是一类常微分方程，其导数的阶数为分数。

对于一维分数阶扩散方程，其一般形式为：∂u(x, t)/∂t = D∂^αu(x, t)/∂x^α，其中0 < α < 1，其中u(x, t)是未知函数，D是扩散系数，α是分数阶指数。

该方程的初始条件为u(x, 0) = f(x)，边界条件为u(0, t) = u(1, t) = 0。

对于离散化方法，我们使用空间网格和时间步长进行离散化。

空间网格上的节点可以用xi = ih表示，其中h是网格步长。

时间离散化可以用tn = nΔt表示，其中Δt是时间步长。

我们的目标是找到一个高精度离散方法，使用隐式龙格-库塔方法进行时间推进，并且具有快速算法。

下面是一个基于隐式龙格-库塔方法的高精度离散方法及其快速算法的步骤：1. 将空间区域[0, 1]等分为N个网格，网格步长为h = 1/N。

建立空间网格点xi = ih，i = 0, 1, 2, ..., N。

2. 初始化时间t = 0，设置时间步长Δt和分数阶指数α。

3. 对于每个时间步n = 1, 2, 3, ..., 进行以下步骤：a. 初始化一个N×N的矩阵A和一个N×1的向量b，令A = I+ DΔt^(1-α)L和b = uⁿ⁻¹，其中I是N×N的单位矩阵，L是一个离散化的二阶导数矩阵。

b. 使用快速算法（例如快速傅里叶变换）解线性方程组Ax = b得到向量x。

c. 根据uⁿ = x更新u的值。

d. 更新时间t = t + Δt。

这个方法的关键在于快速算法的选择。

使用快速傅里叶变换可以将线性方程组的求解复杂度从O(N^3)降低到O(NlogN)，从而实现快速求解。

需要注意的是，在实际应用中，还需要考虑边界条件和初始条件的处理，以及如何选择合适的时间步长Δt和网格步长h，以保证数值稳定性和精度要求。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

摘要：利用二阶微商的三次样条四阶紧致差分逼近公式，推导出两种数值求解二维扩散反应方程的两层９点加权／当 θ＝１该格式在时间和空间方向上分别达到二阶和四阶精度．通过Ｆ隐式紧致差分格式．２时，ｏｕｒｉｅｒ方法讨论／／知，当１格式是无条件稳定的；当０≤ 格式是条件稳定的．为了克服传统迭代法在求解隐格２≤ ２时， θ≤１时， θ＜１式方面的困难，差分方程采用多重网格方法进行求解并将本文格式的结果与Ｐ－Ｒ格式及Ｃ－Ｎ格式下的结果进行比较．数值实验结果验证本文方法的精确性和可靠性及多重网格方法的效率．关键词：扩散反应方程；加权隐式差分格式；高精度；多重网格方法中图分类号：Ｏ２４１．８２文献标识码：Ａ
Ｈｉｈｒｅｃｉｓｉｏｎｗｅｉｈｔｅｄｉｍｌｉｃｉｔｄｉｆｆｅｒｅｎｃｅｆｏｒｍａｔｏｆｔｗｏｄｉｍｅｎｓｉｏｎａｌｄｉｆｆｕｓｉｏｎ－ｐ－－ｇｇｐｒｅａｃｔｉｏｎｅｕａｔｉｏｎｗｉｔｈｃｕｂｉｃｓｌｉｎｅａｎｄｉｔｓｍｕｌｔｉｒｉｄｍｅｔｈｏｄｑｐｇ
ｍｅｔｈｏｄ扩散反应方程是一类描述物理量随时间扩散和自然环境、工程设备衰减规律的抛物型偏微分方程．及生物机体中的许多物理现象．诸如气体的扩散、地下水流、热的传导、充分发展的通道流动等都可归结
１］为扩散反应问题［因此，研究其数值求解方法无疑．
· 兰１４２·
州
理
工
大学学报 Fra bibliotek 第３９卷
４２４４４））其中Ｏ（是无条件稳定的，而Ｏ（ｈ．ｈ τ＋ τ ＋ｈ）４４格式是无条件不稳定的，所以Ｏ（格式不能 τ ＋ｈ）］用于实际计算．文献［采用待定系数法和与差分逼３
，ｏｉｎｔｓｔｗｏｋｉｎｄｓｏｆｗｅｉｈｔｅｄｉｍｌｉｃｉｔｃｏｍａｃｔｄｉｆｆｅｒｅｎｃｅｆｏｒｍａｔｓｗｉｔｈｔｗｏｌｅｖｅｌｓａｎｄｎｉｎｅｗｅｒｅｄｉｆｆｅｒｅｎｃｅｐｇｐｐｄｅｒｉｖｅｄｆｏｒｓｏｌｖｉｎｔｗｏｄｉｍｅｎｓｉｏｎａｌｄｉｆｆｕｓｉｏｎｒｅａｃｔｉｏｎｅｕａｔｉｏｎ．Ｔｈｅｔｗｏｆｏｒｍａｔｓｃｏｕｌｄａｃｈｉｅｖｅｓｅｃｏｎｄｒ－－－ｏ－ｇｑ／ｄｅｒａｃｃｕｒａｃｉｎｔｉｍｅａｎｄｆｏｕｒｔｈｏｒｄｅｒａｃｃｕｒａｃｉｎｓａｃｅｒｅｓｅｃｔｉｖｅｌｗｈｅｎ２．ＢｍｅａｎｓｏｆｔｈｅＦｏｕｒｉｅｒ－ θ＝１ｙｙｐｐｙｙ，／ｉｔｃｏｕｌｄｂｅｃｏｎｃｌｕｄｅｄｔｈａｔｗｈｅｎ１２≤ ｔｈｅｗｏｕｌｄｂｅｕｎｃｏｎｄｉｔｉｏｎａｌｌｓｔａｂｌｅ．Ｗｈｅｎ０≤ ａｎａｌｓｉｓ θ≤１， θ＜ｙｙｙ／，１２ｔｈｅｗｏｕｌｄｂｅｃｏｎｄｉｔｉｏｎａｌｓｔａｂｌｅ．Ｉｎｏｒｄｅｒｔｏｏｖｅｒｃｏｍｅｔｈｅｄｉｆｆｉｃｕｌｔｏｆｃｏｎｖｅｎｔｉｏｎａｌｍｅｔｈｏｄｉｎｓｏｌ－ｙｙ，ｖｉｎｔｈｅｉｍｌｉｃｉｔｆｏｒｍａｔｔｈｅｍｕｌｔｉｒｉｄｍｅｔｈｏｄｗａｓａｄｏｔｅｄｔｏａｃｃｅｌｅｒａｔｅｃｏｎｖｅｒｅｎｃｅｒａｔｅ．ＴｈｅｎｕｍｅｒｉｃａｌｇｐｇｐｇｒｅｓｅｎｔｅｄｒｅｓｕｌｔｆｒｏｍｔｗｏｆｏｒｍａｔｓｗｅｒｅｃｏｍａｒｅｄｗｉｔｈｔｈａｔｆｒｏｍＰａｎｄＣ－Ｎｆｏｒｍａｔｓ．Ｔｈｅｃｏｍａｒｉｓｏｎ－Ｒｐｐｐｒｅｓｕｌｔｒｅｓｅｎｔｅｄｖｅｒｉｆｉｅｄｔｈｅａｃｃｕｒａｃａｎｄｓｔａｂｉｌｉｔｏｆｔｗｏｓｃｈｅｍｅｓａｎｄｔｈｅｅｆｆｉｃｉｅｎｃｏｆｍｕｌｔｉｒｉｄｍｅｔｈｏｄ．ｙｙｐｙｇ
２４４格式的截断误差可分别达到Ｏ（和Ｏ（ τ ＋ｈ） τ＋
具有非常重要的理论意义和实际应用价值．
２０１２０４１９收稿日期：－－，霍英东教育基金会１１０６１０２５）基金项目：国家自然科学基金（）高等院校青年教师基金（１２１１０５，男，宁夏同心人，讲师．１９８１作者简介：马廷福（－）
Ｒｔ－ｕ＝ｅ Φ ）），将式（代入式（将其转化为４１Ｒｔ Φ Φ ＋ｅｆｔ＝Ｄ（ｘｘ＋Φ ｙｙ）
（）４
］式差分格式．文献［基于二阶微商的三次样条四阶４提出了数值求解一维含源纯扩散方程的逼近公式，两层３点加权差分格式，该格式在空间方向上达到／了四阶精度，且当１格式是无条件稳定２≤ θ≤１时，／的，而当０≤ 格式是条件稳定的．文献［将２，５］ θ＜１反应项归并入源汇项并通过指数变换消取反应项的将扩散反应方程转换成扩散方程的形式，然后方法，利用二阶微商的三次样条四阶紧致差分公式，提出了数值求解一维含源纯扩散方程的两种具有无条件
１１２，，ＭＡＴｉｎｆｕＪＩＮＴａｏＧＥＹｏｎｂｉｎ－－ｇｇ
（，，；，１．ＹｉｎｃｈｕａｎＣｏｌｌｅｅＣｈｉｎａＭｉｎｉｎＵｎｉｖｅｒｓｉｔＹｉｎｃｈｕａｎ５００１１，Ｃｈｉｎａ２．ＩｎｓｔｉｔｕｔｅｏｆＡｌｉｅｄＭａｔｈｅｍａｔｉｃｓａｎｄＭｅｃｈａｎｉｃｓＮｉｎｘｉａＵｎｉ７－ｇｇｙｐｐｇ，Ｙ）ｖｅｒｓｉｔｉｎｃｈｕａｎ５００２１，Ｃｈｉｎａ７ｙ
第３９卷第３期２０１３年６月
兰州理工大学学报ＪｏｕｒｎａｌｏｆＬａｎｚｈｏｕＵｎｉｖｅｒｓｉｔｏｆＴｅｃｈｎｏｌｏｙｇｙ
Ｖｏｌ．３９Ｎｏ．３Ｊｕｎ．２０１３
（）１６７３５１９６２０１３０３０１４１０６文章编号：－－－
二维扩散反应方程的三次样条高精度加权隐式差分格式及其多重网格方法
马廷福１，金涛１，葛永斌２
（）１．中国矿业大学银川学院，宁夏银川７５００１１；２．宁夏大学应用数学与力学研究所，宁夏银川７５００２１
：ｄ；ｗ；ｈ；ｍＫｅｗｏｒｄｓｉｆｆｕｓｉｏｎｒｅａｃｔｉｏｎｅｕａｔｉｏｎｅｉｈｔｅｄｉｍｌｉｃｉｔｄｉｆｆｅｒｅｎｃｅｆｏｒｍａｔｉｈａｃｃｕｒａｃｕｌｔｉｒｉｄ－ｑｇｐｇｙｇｙ
近方程的最高阶相容性条件满足相结合的方法，提出了求解一维含源纯扩散方程的两种截断误差分别
３２２３２４））为Ｏ（和Ｏ（的两层３点隐ｈ＋ｈｈ＋ｈ τ＋ τ τ＋ τ
（）５），，（由于式（在整个求解区域内成立，故在（５ｉｉ＋ｊ），（，（，），（，）点上也成立，即１，ｉ－１，ｉｉｊ）ｊ）ｊ＋１ｊ－１Ｒｔ（（（），，，，６＋ｅｆ Φ Φ Φ ｔ）ｉｘｘ）ｉｉｉｊ＝Ｄ［ｊ＋（ｙｙ）ｊ］ｊ
：ＡＡｂｓｔｒａｃｔｌｉｎｓｅｃｏｎｄｄｅｒｉｖａｔｉｖｅａｒｏｘｉｍａｔｉｏｎｆｏｒｍｕｌａｗｉｔｈｃｕｂｉｃｓｌｉｎｅａｎｄｆｏｕｒｔｈｏｒｄｅｒｃｏｍａｃｔ－ｐｐｙｇｐｐｐｐ
Ｒｔ（（＋ｅｆ Φ Φ Φ ｔ）ｉ１，ｘｘ）ｉ１，ｉ１，ｉ１，＋＋＋＋ｊ＝Ｄ［ｊ＋（ｙｙ）ｊ］ｊ（）７Ｒｔ（（，，，，＋ｅｆ Φ Φ Φ ｔ）ｉ１＝Ｄ［ｘｘ）ｉ１＋（ｉ１］ｉ１＋＋＋＋ｊｊｙｙ）ｊｊ（）８Ｒｔ（（ Φ Φ Φ ＋ｅｆｔ）ｉ１，ｘｘ）ｉ１，ｉ１，ｉ１，－－－－ｊ＝Ｄ［ｊ＋（ｙｙ）ｊ］ｊ（）９Ｒｔ（（，，，， Φ Φ Φ ＋ｅｆｔ）ｉ１＝Ｄ［ｘｘ）ｉ１＋（ｉ１］ｉ１＋＋＋＋ｊｊｙｙ）ｊｊ（）１０