13.1.2 定理与证明
合集下载
13.1.2定理与证明

HS八(上) 教学课件
第13章 全等三角形
13.1 命题、定理与证明
2 定理与证明
基本事实与定理
新课讲解
基本事实 :数学中一些命题的正确性是人们在长期 实践中总结出来的,并把它们作为判断其他命题真假 的原始依据,即出发点.这样的真命题视为基本事实. 我们也称它为公理.
1) 直线公理:过两点有且只有一条直线. 2) 线段公理: 两点之间,线段最短. 3) 平行公理:
内错角相等,两直线平行. 同旁内角互补,两直线平行.
8) 平行线的性质定理:
两直线平行,内错角相等. 两直线平行,同旁内角互补.
公理、定理、命题的关系:
新课讲解
命题
真命题 假命题
公理(正确性由实践总结) 定理(正确性通过推理证实)
新课讲解
【思考】(1)一位同学在钻研数学题时发现:
2+1=3, 2×3+1=7, 2×3×5+1=31, 2×3×5×7+1=211,
边形等的内角和,得到一个结论:n边形的内角和等于 (n-2)×180°.这个结论正确吗?是否有一个多边形的
内角和不满足这一规律?
这是一个正确的结论.
新课讲解
【探讨】上面的几个例子说明了什么问题? 通过特殊的事例得到的结论可能正确,也
可能不正确. 【定义】根据条件、定义以及基本事实、定理 等,经过演绎推理,来判断一个命题是否正确, 这样的推理过程叫做证明.
2b
∠1=∠2 ( 已知
)Байду номын сангаас
∴∠3=∠2( 等量代换 )
∴a∥b (同位角相等,两直线平行)
例2.证明:邻补角的平分线互相垂直.
已知:如图,∠AOB、∠BOC互为邻补角,
第13章 全等三角形
13.1 命题、定理与证明
2 定理与证明
基本事实与定理
新课讲解
基本事实 :数学中一些命题的正确性是人们在长期 实践中总结出来的,并把它们作为判断其他命题真假 的原始依据,即出发点.这样的真命题视为基本事实. 我们也称它为公理.
1) 直线公理:过两点有且只有一条直线. 2) 线段公理: 两点之间,线段最短. 3) 平行公理:
内错角相等,两直线平行. 同旁内角互补,两直线平行.
8) 平行线的性质定理:
两直线平行,内错角相等. 两直线平行,同旁内角互补.
公理、定理、命题的关系:
新课讲解
命题
真命题 假命题
公理(正确性由实践总结) 定理(正确性通过推理证实)
新课讲解
【思考】(1)一位同学在钻研数学题时发现:
2+1=3, 2×3+1=7, 2×3×5+1=31, 2×3×5×7+1=211,
边形等的内角和,得到一个结论:n边形的内角和等于 (n-2)×180°.这个结论正确吗?是否有一个多边形的
内角和不满足这一规律?
这是一个正确的结论.
新课讲解
【探讨】上面的几个例子说明了什么问题? 通过特殊的事例得到的结论可能正确,也
可能不正确. 【定义】根据条件、定义以及基本事实、定理 等,经过演绎推理,来判断一个命题是否正确, 这样的推理过程叫做证明.
2b
∠1=∠2 ( 已知
)Байду номын сангаас
∴∠3=∠2( 等量代换 )
∴a∥b (同位角相等,两直线平行)
例2.证明:邻补角的平分线互相垂直.
已知:如图,∠AOB、∠BOC互为邻补角,
华师版八年级数学上册 13.1.2 定理与证明

课程讲授
1 基本事实与定理
基本事实、定理、命题的关系:
命题
真命题 假命题
基本事实(正确性由实践总结) 定理(正确性通过推理证实)
课程讲授
2 命题的证明
证明几何命题的一般步骤: 1.明确命题中的__已__知__和_求__证___; 2.根据题意,_画__出__图__形__,并用数学符号表示已知和 求证; 3.经过分析,找出由已知推出_要__证__的__结__论_的途径, 写出证明过程.
可以从基本事实或其他真命题出发,用逻辑 推理的方法判断它们是正确的,可以作为进一步 判断其他命题真假的依据的真命题叫三角形
13.1 命题、定理与证明
13.1.2 定理与证明
新知导入 课程讲授
随堂练习 课堂小结
知识要点
1.基本事实与定理 2.命题的证明
新知导入
试一试:根据所学知识,完成下列内容.
下列哪些命题是真命题﹖ 1.两点确定一条直线; 2.两点之间,线段最短; 3.过一点有且只有一条直线与已知直线垂直; 4.过直线外一点有且只有一条直线与这条直线平行.
课程讲授
1 基本事实与定理
定义: 数学中,有些命题可以从基本事实或其他真命
题出发,用逻辑推理的方法判断它们是正确的,并且 可以作为进一步判断其他命题真假的依据,这样的真 命题叫做定理.
比如:“内错角相等,两直线平行”这条定理就是在“同 位角相等,两直线平行”这条公理的基础上推理而出的, 它又可以作为判定平行线的依据.
课程讲授
2 命题的证明
例 证明命题:直角三角形的两个锐角互余.
A
已知:如图,在△ABC中,∠C=90°.
求证:∠A+∠B=90°.
证明:∵∠A+∠B+∠C=180°(三角
1312定理与证明华师大八年级上精品PPT课件

演讲人:XXXXXX 时 间:XX年XX月XX日
平行. 两条直线被第三条直线截,如果同位角相等,
那么这两条直线平行.
基本事实与定理
上面的命题是我们七年级中学习的真命题,都是公 认的真命题,这样的真命题我们视为基本事实,并把它 们作为判断其他命题真假的原始依据,即出发点.
有些命题可以从基本事实或其他真命题出发,用逻 辑推理的方法判断它们是正确的,并且可以进一步作为
ab c
d
图中两条线段a与b的长度相等吗? a b
眼睛真的那么可靠?
如何证实一个命题是真命题呢
用我们以前学过 的观察,实验,验 证特例等方法.
能不能根据已 经知道的真命
题证实呢?
那已经知道 的真命题又 是如何证实
的?.
这些方法 往往并不
可靠.
哦……那 可怎么办
思考:1.利用数值实验得到的结果是否可靠呢?
(3)经过分析,找出由已知推出结论的途径, 写出证明过程,并注明依据.
直角三角形的两个锐角互余
A
已知:如图,在直角三角形ABC中,C 90
求证:A B 90
证明:
C
B
A B C 180(三角形的内角和等于180),
又 C 90( 已知),
A B 180-C 90(等式的性质).
(1)一位学生在钻研数学题时发现:
2+1=3,
2×3+1=7,
2×3×5+1=31,
2×3×5×7+1=211.
于是,他根据上面的结果并利用质数表得出结论:从质数 2开始,排在前面的任意多个质数的乘积加1一定是质数。 它的结论正确吗?
计算:2×3×5×7×11+1=
2×3×5×7×11×13+1=
平行. 两条直线被第三条直线截,如果同位角相等,
那么这两条直线平行.
基本事实与定理
上面的命题是我们七年级中学习的真命题,都是公 认的真命题,这样的真命题我们视为基本事实,并把它 们作为判断其他命题真假的原始依据,即出发点.
有些命题可以从基本事实或其他真命题出发,用逻 辑推理的方法判断它们是正确的,并且可以进一步作为
ab c
d
图中两条线段a与b的长度相等吗? a b
眼睛真的那么可靠?
如何证实一个命题是真命题呢
用我们以前学过 的观察,实验,验 证特例等方法.
能不能根据已 经知道的真命
题证实呢?
那已经知道 的真命题又 是如何证实
的?.
这些方法 往往并不
可靠.
哦……那 可怎么办
思考:1.利用数值实验得到的结果是否可靠呢?
(3)经过分析,找出由已知推出结论的途径, 写出证明过程,并注明依据.
直角三角形的两个锐角互余
A
已知:如图,在直角三角形ABC中,C 90
求证:A B 90
证明:
C
B
A B C 180(三角形的内角和等于180),
又 C 90( 已知),
A B 180-C 90(等式的性质).
(1)一位学生在钻研数学题时发现:
2+1=3,
2×3+1=7,
2×3×5+1=31,
2×3×5×7+1=211.
于是,他根据上面的结果并利用质数表得出结论:从质数 2开始,排在前面的任意多个质数的乘积加1一定是质数。 它的结论正确吗?
计算:2×3×5×7×11+1=
2×3×5×7×11×13+1=
§13.1.2定理与证明
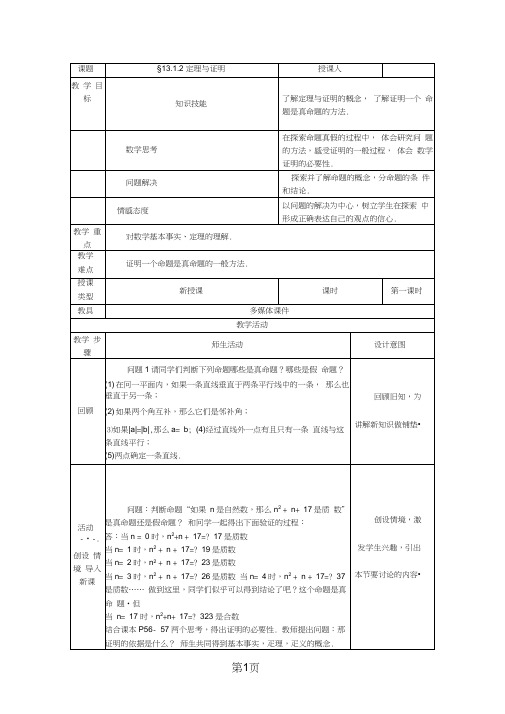
当n=1时,n2+n+17=?19是质数
当n=2时,n2+n+17=?23是质数
当n=3时,n2+n+17=?26是质数 当n=4时,n2+n+17=?37是质数…… 做到这里,同学们似乎可以得到结论了吧?这个命题是真命 题•但
当n=17时,n2+n+17=?323是合数
结合课本P56-57两个思考,得出证明的必要性. 教师提出问题:那证明的依据是什么? 师生共同得到基本事实,疋理,疋义的概念.
第三步:通过分析,找出证明的方法,写出证明过程.
在证明几何命题时,须注意以下几点:
1.明确题目的条件和结论;
2•证明过程中引用的根据(理由)与“定理的证明相同”;
3•证明过程中每一步结果所用的根据必须是取得这一结果的 充分理由;
4•要防止利用未学过的定理来证明学过的命题,避免循环论 证
活动
开放 训练 体现 应用
图13—1—
①DE//BC:②/1= 72;③/B= ZC.
(1)若从这三个条件中任选两个作为题设,另一个作为结论, 组成一个命题,一共能组成几个命题,请你都写出来;
(2)请你就其中的一个真命题给出推理过程.
解:(1)一共能组成2个命题,它们是:题设:①②,结论:
③;题设:①③,结论:②;
⑵情况一题设:①②,结论:③;证明:如图,•••Dቤተ መጻሕፍቲ ባይዱ//BC,
的方法判断它们是正确的,并且可以作为进一步判断其他命题 真假的依据,这样的真命题叫做定理.
归纳:定理的作用不仅在于它揭示了客观事物的本质属性,而
且可以作为进一步确认其他命题真假的依据.
探究证明:根据条件、定义以及基本事实、定理等,经过演绎 推理,来判断一个命题是否正确,这样的推理过程叫做证明 例如图13—1—,有下列三个条件:
当n=2时,n2+n+17=?23是质数
当n=3时,n2+n+17=?26是质数 当n=4时,n2+n+17=?37是质数…… 做到这里,同学们似乎可以得到结论了吧?这个命题是真命 题•但
当n=17时,n2+n+17=?323是合数
结合课本P56-57两个思考,得出证明的必要性. 教师提出问题:那证明的依据是什么? 师生共同得到基本事实,疋理,疋义的概念.
第三步:通过分析,找出证明的方法,写出证明过程.
在证明几何命题时,须注意以下几点:
1.明确题目的条件和结论;
2•证明过程中引用的根据(理由)与“定理的证明相同”;
3•证明过程中每一步结果所用的根据必须是取得这一结果的 充分理由;
4•要防止利用未学过的定理来证明学过的命题,避免循环论 证
活动
开放 训练 体现 应用
图13—1—
①DE//BC:②/1= 72;③/B= ZC.
(1)若从这三个条件中任选两个作为题设,另一个作为结论, 组成一个命题,一共能组成几个命题,请你都写出来;
(2)请你就其中的一个真命题给出推理过程.
解:(1)一共能组成2个命题,它们是:题设:①②,结论:
③;题设:①③,结论:②;
⑵情况一题设:①②,结论:③;证明:如图,•••Dቤተ መጻሕፍቲ ባይዱ//BC,
的方法判断它们是正确的,并且可以作为进一步判断其他命题 真假的依据,这样的真命题叫做定理.
归纳:定理的作用不仅在于它揭示了客观事物的本质属性,而
且可以作为进一步确认其他命题真假的依据.
探究证明:根据条件、定义以及基本事实、定理等,经过演绎 推理,来判断一个命题是否正确,这样的推理过程叫做证明 例如图13—1—,有下列三个条件:
13.1.2 定理与证明 大赛获奖教学课件

足这一规律? 实际上,这是一个正确的结论.
探讨归纳 上面的几个例子说明了什么问题? 通过特殊的事例得到的结论可能正确,也可能不 正确. 定义:根据条件、定义以及基本事实、定理等,经 过演绎推理,来判断一个命题是否正确,这样的推理过
程叫做证明.
典例精析
A
例1 证明命题:直角三角形的两个锐角互余. 已知:如图,在△ABC中,∠C=90°. 求证:∠A+∠B=90°. 证明:∵∠A+∠B+∠C=180°(三角形的内角和等于180°), 又∵∠C=90°(已知), ∴∠A+∠B=180°-∠C=90°(等式的性质). 此命题可以用来作为判断其他命题真假的依据,因此我 们把它也作为定理. 方法归纳:演绎推理是研究数学的一个重要方法.除了基 本事实与已知的定理外,等式与不等式的有关性质以及等量代 换也可以作为推理的依据.
学习目标
1.理解基本事实、定理等概念.(重点) 2.理解证明的概念,并会对真命题进行证明.(难点)
导入新课 问题导入
问题:我们学过的哪些命题是真命题﹖ 1.两点确定一条直线; 2.两点之间,线段最短;
3.过一点有且只有一条直线与已知直线垂直;
4.过直线外一点有且只有一条直线与这条直线平行.
讲授新课
当堂练习
1.证明:邻补角的平分线互相垂直.
已知:如图, ∠AOB +∠BOC = 180°, OE 平分 ∠AOB ,
OF平分∠BOC.
求证:OE⊥OF. 分析:要证明OE⊥OF,只要证明 ∠EOF = 90°, 即 ∠1 +∠2 = 90° 即 A 可. 1 证明:∵OE平分∠AOB, ∴∠1= ∠AOB. ∵OF平分 ∠BOC, ∴∠2= ∴∠1 + ∠2 =
(1)作一条线段等于已知线段; (2)作一个角等于已知角;(3)作已知角的平分线.
探讨归纳 上面的几个例子说明了什么问题? 通过特殊的事例得到的结论可能正确,也可能不 正确. 定义:根据条件、定义以及基本事实、定理等,经 过演绎推理,来判断一个命题是否正确,这样的推理过
程叫做证明.
典例精析
A
例1 证明命题:直角三角形的两个锐角互余. 已知:如图,在△ABC中,∠C=90°. 求证:∠A+∠B=90°. 证明:∵∠A+∠B+∠C=180°(三角形的内角和等于180°), 又∵∠C=90°(已知), ∴∠A+∠B=180°-∠C=90°(等式的性质). 此命题可以用来作为判断其他命题真假的依据,因此我 们把它也作为定理. 方法归纳:演绎推理是研究数学的一个重要方法.除了基 本事实与已知的定理外,等式与不等式的有关性质以及等量代 换也可以作为推理的依据.
学习目标
1.理解基本事实、定理等概念.(重点) 2.理解证明的概念,并会对真命题进行证明.(难点)
导入新课 问题导入
问题:我们学过的哪些命题是真命题﹖ 1.两点确定一条直线; 2.两点之间,线段最短;
3.过一点有且只有一条直线与已知直线垂直;
4.过直线外一点有且只有一条直线与这条直线平行.
讲授新课
当堂练习
1.证明:邻补角的平分线互相垂直.
已知:如图, ∠AOB +∠BOC = 180°, OE 平分 ∠AOB ,
OF平分∠BOC.
求证:OE⊥OF. 分析:要证明OE⊥OF,只要证明 ∠EOF = 90°, 即 ∠1 +∠2 = 90° 即 A 可. 1 证明:∵OE平分∠AOB, ∴∠1= ∠AOB. ∵OF平分 ∠BOC, ∴∠2= ∴∠1 + ∠2 =
(1)作一条线段等于已知线段; (2)作一个角等于已知角;(3)作已知角的平分线.
13.1.2定理与证明

5. 质数个数有多少个? _无__限__个__(有限个或无限个)
思考(1)
2 35711 1 2311 2 3571113 1 30031
一位同学在专研数学题时发现:
21 3
2311是质数
231 7
235 1 31
30031=509×59
2 3 5 7 1 211 30031不是质数
▲真命题的证明过程,必须做到言必有据。
▲证明过程的每一步骤,都应该在后面的括号内写上依据。
公理、定理、命题的关系
真命题
命题
假命题
公理(正确性由实践总结) 定理(正确性通过推理证实)
练习
1.把下列定理改写成“如果……,那么……”的形式,指出 它的条件和结论,并用逻辑推理的方法证明题(1):
(1)同旁内角互补,两直线平行;
思考(3)
我们曾经通过计算四边形、五边形、六边形、七边形
等的内角和,得到一个结论:
n边
形的内角和等于(n-2)×180°。
这个结论正确吗?
正确
是否有一个多边形的内角和不满足这一规律? 没有
体会
通过上面几个例子说明: 通过特殊的事例得到的结论可能正确,也可能不正确. 因此: 通过这种方式得到的结论,还需进一步加以证实。
因为这种证明方法叫做举例法或不完全归纳法, 所以并不包含所有情况,得到的结论不一定正确。
证明的定义
根据已知条件、定义及基本事实、定理等,经过演绎 推理,来判断一个命题是否正确,这样的推理过程叫
做证明。等式或不等式的有关性质及等量代换,也可
以做为推理证明的依据 例如,有了“三角形的内角和等于180°”这条 定理后,我们还可以证明刻画直角三角形的两 个锐角之间的数量关系的命题:
思考(1)
2 35711 1 2311 2 3571113 1 30031
一位同学在专研数学题时发现:
21 3
2311是质数
231 7
235 1 31
30031=509×59
2 3 5 7 1 211 30031不是质数
▲真命题的证明过程,必须做到言必有据。
▲证明过程的每一步骤,都应该在后面的括号内写上依据。
公理、定理、命题的关系
真命题
命题
假命题
公理(正确性由实践总结) 定理(正确性通过推理证实)
练习
1.把下列定理改写成“如果……,那么……”的形式,指出 它的条件和结论,并用逻辑推理的方法证明题(1):
(1)同旁内角互补,两直线平行;
思考(3)
我们曾经通过计算四边形、五边形、六边形、七边形
等的内角和,得到一个结论:
n边
形的内角和等于(n-2)×180°。
这个结论正确吗?
正确
是否有一个多边形的内角和不满足这一规律? 没有
体会
通过上面几个例子说明: 通过特殊的事例得到的结论可能正确,也可能不正确. 因此: 通过这种方式得到的结论,还需进一步加以证实。
因为这种证明方法叫做举例法或不完全归纳法, 所以并不包含所有情况,得到的结论不一定正确。
证明的定义
根据已知条件、定义及基本事实、定理等,经过演绎 推理,来判断一个命题是否正确,这样的推理过程叫
做证明。等式或不等式的有关性质及等量代换,也可
以做为推理证明的依据 例如,有了“三角形的内角和等于180°”这条 定理后,我们还可以证明刻画直角三角形的两 个锐角之间的数量关系的命题:
13.1.2 定理与证明
八年级数学上册(华师版) 第十三章 全等三角形
13.1.2 定理断其他 命题真假的_依__据_,这样的 真命题 叫做定理.
练习1.“同角或等角的补角相等”是( C ) A.定义 B.基本事实 C.定理 D.假命题
2.证明:根据条件、定义以及基本事实、定理等,经过演绎推理,来判 断一个命题是否正确,这样的_推__理_过程叫做证明.
7.如图,AB∥CD,AD∥BC.求证:∠A=∠C.
解:∵AD∥BC,∴∠A+∠B=180°,∵AB∥CD, ∴∠C+∠B=180°,∴∠A=∠C
8.下列命题中:①两点确定一条直线;②同位角相等,两直线平行;③两 点之间,线段最短;④三角形的内角和等于180°.属于基本事实的有( C )
A.1个 B.2个 C.3个 D.4个
2.“两直线平行,同旁内角互补”是一个( B ) A.基本事实 B.定理 C.假命题 D.定义
3.如图,直线a,b与c相交,则下列推理错误的是( D) A.∵∠1=∠3,∴a∥b B.∵a∥b,∴∠2+∠3=180° C.∵∠2=∠4,∴a∥b D.∵a∥b,∴∠2+∠4=180°
4 . 如 图 , AO⊥CO , BO⊥DO , 则 ∠ AOB = ∠ COD , 推 理 的 理 由 是 ( B)
9.如图,AB∥EF,∠C=90°,则α,β和γ的关系是( )C A.α=β+γ B.α+β+γ=180° C.α+β-γ=90° D.β+γ-α=90°
10.如图所示,给出下面的推理: ①∵∠B=∠BEF,∴AB∥EF; ②∵∠B=∠CDE,∴AB∥CD; ③∵∠DCE+∠AEF=180°,∴AB∥CD; ④∵∠A+∠AEF=180°,∴AB∥EF.
解:∵∠ADE=∠B,∴DE∥BC,∴∠1=∠3,∵∠1=∠2, ∴∠2=∠3,∴CD∥FG,∵FG⊥AB,∴CD⊥AB
13.1.2 定理断其他 命题真假的_依__据_,这样的 真命题 叫做定理.
练习1.“同角或等角的补角相等”是( C ) A.定义 B.基本事实 C.定理 D.假命题
2.证明:根据条件、定义以及基本事实、定理等,经过演绎推理,来判 断一个命题是否正确,这样的_推__理_过程叫做证明.
7.如图,AB∥CD,AD∥BC.求证:∠A=∠C.
解:∵AD∥BC,∴∠A+∠B=180°,∵AB∥CD, ∴∠C+∠B=180°,∴∠A=∠C
8.下列命题中:①两点确定一条直线;②同位角相等,两直线平行;③两 点之间,线段最短;④三角形的内角和等于180°.属于基本事实的有( C )
A.1个 B.2个 C.3个 D.4个
2.“两直线平行,同旁内角互补”是一个( B ) A.基本事实 B.定理 C.假命题 D.定义
3.如图,直线a,b与c相交,则下列推理错误的是( D) A.∵∠1=∠3,∴a∥b B.∵a∥b,∴∠2+∠3=180° C.∵∠2=∠4,∴a∥b D.∵a∥b,∴∠2+∠4=180°
4 . 如 图 , AO⊥CO , BO⊥DO , 则 ∠ AOB = ∠ COD , 推 理 的 理 由 是 ( B)
9.如图,AB∥EF,∠C=90°,则α,β和γ的关系是( )C A.α=β+γ B.α+β+γ=180° C.α+β-γ=90° D.β+γ-α=90°
10.如图所示,给出下面的推理: ①∵∠B=∠BEF,∴AB∥EF; ②∵∠B=∠CDE,∴AB∥CD; ③∵∠DCE+∠AEF=180°,∴AB∥CD; ④∵∠A+∠AEF=180°,∴AB∥EF.
解:∵∠ADE=∠B,∴DE∥BC,∴∠1=∠3,∵∠1=∠2, ∴∠2=∠3,∴CD∥FG,∵FG⊥AB,∴CD⊥AB
第13章 13.1 13.1. 2 定理与证明
定理.
2. 经过证明的真命题称为 定理 实是不需要 证明 的真命题.
,而一些基本事
3. 根据条件、定义以及基本事实、定理等,经过演 绎推理,来判断一个命题是否正确,这样的 推理 过程
叫做证明.
知识点 基本事实 1. 下列真命题能作为基本事实的是( C ) A.对顶角相等 B.三角形的内角和是 180° C.过一点有且只有一条直线与已知直线垂直 D.内错角相等,两直线平行
1. 下列真命题中是定理的是( C ) A.两点确定一条直线 B.同位角相等,两直线平行 C.同角(等角)的补角相等 D.两点之间,线段最短
2. 下列说法错误的是( B ) A.命题是判断一件事情的句子 B.基本事实的正确性必须得到证明 C.证明假命题举一个反例即可 D.推理的过程叫做证明
3. 如图,AB∥CD,∠E=37°,∠C=20°,则∠EAB 的度数为( A )
2. “经过两点有且只有一条直线”是( A )
A.基本事实
B.假命题
C.定义
D.以上都不是
3. 下列命题不是基本事实的是( C )
A.两点之间,线段最短
B.过一点有且只有一条直线垂直于已知直线
C.两条平行线被第三条直线所截,内错角相等
D.过直线外一点有且只有一条直线与这条直线平定理是( B ) A.若 a 是整数,则 a 是有理数 B.对顶角相等 C.直线上两点之间的部分叫线段 D.锐角小于直角
7. 如图,比较∠1 与∠2+∠3 的大小,并证明你的 判断.
解:∠1>∠2+∠3. 证明:∵∠1 是△ DEC 的外角, ∴∠1>∠DEC, ∵∠DEC 是△ BEC 的外角, ∴∠DEC=∠2+∠3. ∴∠1>∠2+∠3.
8. 完成下面的证明过程,并在括号内填上理由.
