系统的性能指标 一阶系统的时域分析
02306自动控制理论二

湖北省高等教育自学考试课程考试大纲课程名称:自动控制理论(二)课程代码:02306第一部分课程性质与目标一、课程性质与特点自动控制理论(二)是高等教育自学考试”电气工程及其自动化”专业(专升本)的一门专业课程。
该课程侧重于从理论的角度,系统地阐述自动控制科学和技术领域的基本概念和基本规律,介绍对自动控制系统建模、分析、设计过程中应用的各种原理、思想和方法。
二、课程目标与基本要求通过本课程的学习,应理解和掌握自动控制系统分析的基本方法、理论及应用。
课程内容主要包括以下几个方面:控制系统导论、控制系统的数学模型、线性系统的时域分析法、线性系统的根轨迹法、线性系统的频域分析法、线性系统的校正方法、线性离散系统的分析。
三、与本专业其他课程的关系在学习本课程之前,考生应具有高等数学、电路、信号与线性系统、电子技术等课程的相关知识和理论基础,本课程与后续课程有一定关联。
第二部分考核内容与考核目标第一章控制系统导论一、学习目的与要求通过学习,掌握自动控制系统的基本概念和分类,理解自动控制系统的基本要求。
二、考核知识点与考核目标(一)自动控制的基本原理(重点)1、自动控制技术及其应用(理解),2、自动控制理论(理解),3、反馈控制原理(理解),4、反馈控制系统的基本组成(理解),5、自动控制的基本控制方式(理解)。
(二)自动控制系统示例(一般)1、函数记录仪(识记),2、电阻炉微型计算机温度控制系统(识记),3、锅炉液位控制系统(识记)(三)自动控制系统的分类(次重点)1、线性连续控制系统(理解),2、线性定常离散控制系统(理解),3、非线性控制系统(理解)(四)自动控制系统的基本要求(重点)1、基本要求的提法(理解),2、典型外作用(理解)第2章控制系统的数学模型一、学习目的与要求通过学习,熟悉傅里叶变换与拉普拉斯变换以及控制系统的时域、复数域数学模型,掌握控制系统的结构图与信号流图。
二、考核知识点与考核目标(一)傅里叶变换与拉普拉斯变换(重点)1、傅里叶级数(识记),2、傅里叶积分与傅里叶变换(理解),3、拉普拉斯变换(理解),4、拉普拉斯变换的积分下限(理解),5、拉普拉斯变换定理(理解),6、拉普拉斯变换反变换(理解)。
自动控制原理(3-1)

动态性能指标定义1
hh((tt))
AA
超超调调量量σσ%% ==
AA BB
110000%%
峰峰值值时时间间ttpp BB
上上 升升 时时间间ttrr
调调节节时时间间ttss
tt
动态性能指标定义2 h(t)
调节时间 ts
上升时间tr
t
动态性能指标定义3
h(t)
A
σ%=
A B
100%
B tr tp
一阶系统对典型输入的输出响应
输入信号
输出响应
1(t) 1-e-t/T t≥0
δ(t)
1 et T t 0
T
t
t-T(1-e-t/T) t≥0
1 t2
1 t 2 Tt T 2 (1 et T ) t 0
2
2
由表可见,单位脉冲 响应与单位阶跃响应 的一阶导数、单位斜 坡响应的二阶导数、 单位加速度响应的三 阶导数相等。
自动控制原理
朱亚萍 zhuyp@ 杭州电子科技大学自动化学院
第三章 线性系统的时域分析法
3.1 系统时间响应的性能指标 3.2 一阶系统的暂态响应 3.3 二阶系统的暂态响应 3.4 高阶系统的暂态响应 3.5 线性系统的稳定性分析 3.6 控制系统的稳态误差 3.7 利用MATLAB对控制系统进行时域分析
超调量σ%:指响应的最大偏离量h(tp)与终值 h(∞)的差与终值h(∞)比的百分数,即
% h(tp ) h() 100%
h()
在实际应用中,常用的动态性能指标多为上升 时间tr、调整时间ts和超调量σ%。 用上升时间tr或峰值时间tp评价系统的响应速度; 用超调量σ%评价系统的阻尼程度;
自动控制原理第三章

➢ 0 1 特征根: s1,2 n jn 1 2
Xc (s)
1 s
s2
n2 2ns n2
1 s
s2
s 2n 2ns n2
1
s 2n
s (s n )2 (n 1 2 )2
其阶跃输入下的暂态响应:
xc (t) 1
e nt
1 2
sin(n
1 2 t ) , arctan
WB (s)
X c (s) X r (s)
(1
1 K)s
1
1 Ts 1
式中:T 1 k , 称为时间常数。
3.2.2 单位阶跃响应函数:
X r (s) 1 s
11
Xc
(s)
Ts
1
s
,
xc (t)
L1[ 1 Ts 1
1] s
L1[ 1 s
s
1
1
]
1
t
eT
T
xc (t ) xss xtt
2
1.8
1.6
1.4
1.2
1
0.8
0.6 0.4 0.2
0 0
246
nt
8 10 12
⒊ 当 1时,特征方程有一对相等的负实根,称为临界阻尼
系统,系统的阶跃响应为非振荡过程。
➢当 1 时,
阶跃响应曲线为:
xc
(s)
1 s
s2
n2 2n s
n2
n2 s(s n )2
1 1 n s s n (s n )2
1 )( s
T1
1 T2
)
式中
T1
1 a
n (
1
2
1)
一阶系统瞬态响应

C( s )
1 1 2 Ts 1 s 1 T T 2 s s s 1 T
1 t T
c( t ) t T Te
河海大学机电工程学院
控制工程基础
第三章线性系统的时域分析法
性质: 1)经过足够长的时间 (≥4T),输出增长速率近 似与输入相同; 2)输出相对于输入滞 后时间T;
3)稳态误差=T。
河海大学机电工程学院
控制工程基础
第三章线性系统的时域分析法
线性定常系统的一个性质
对于一阶系统
r( t ) ( t ) r( t ) 1 r( t ) t
R( s ) 1
1 R( s ) s 1 R( s ) 2 s
1 t 1 T c( t ) e T
河海大学机电工程学院
控制工程基础
第三章线性系统的时域分析法
五 Matlab求取瞬态响应
1 t 6
1 15s 1
ct
河海大学机电工程学院
控制工程基础
第三章线性系统的时域分析法
河海大学机电工程学院
控制工程基础
第三章线性系统的时域分析法
例3-1 一阶系统的结构如下图所示。 试求该系统单位阶跃响应的调节时间ts ; 如果要求ts(5%) 0.1(秒),试问系统的反馈系数应取何值?
c( t ) 1 e
1 t T
性质: 1)T 暂态分量 瞬态响应时间 极点距离虚轴 2)T 暂态分量 瞬态响应时间 极点距离虚轴
河海大学机电工程学院
控制工程基础
第三章线性系统的时域分析法
1 t dc( t ) 1 T 1 |t 0 e |t 0 dt T T
第三章 线性系统的时域分析法(第三四五讲)
变号的次数为特征根在s右半平面的个数!
劳斯表出现零行
设系统特征方程为:
s4+5s3+7s2+5s+6=0 劳 斯 表
s4 1 s3 5 1 s2 6 1 s1 0 2 s0 1 7 6 1 5 6 1 这是零行
① 有大小相等符号相反的 特征根时会出现零行 ② 由零行的上一行构成 辅助方程:
或 %
100%
tg
e
100%
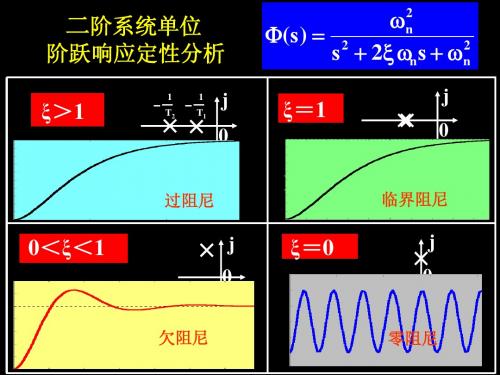
欠阻尼二阶系统动态性能计算
tr d
tr 特征根的虚部
弧度
tp d
tp 特征根的虚部
cos
5%
3.5 ts n
% e
1 2
100%
tg
3.5 ts 特征根的实部
n=[0.05 10]; d=[0.0025 0.5125 2.52 4.01 3]; sys=tf(n,d); step(sys)
第三章 系统的时域性能指标
3.1 系统的时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析
3.4 高阶系统的时域分析
3.5 线性系统的稳定性分析 3.6 线性系统的稳态误差计算
1
t T 2 2
0<ξ<1 s1, 2 n jjn 1 2 ξ=0 0<ξ<1
0
h( t ) 1 ξ=0 e n t 1
2
j 0 0 j
sin(,d jn 欠阻尼t ) s1 2
0 零阻尼 h(t ) 1 cos n t
欠阻尼二阶系统动态性能分析
它们的阶跃响应曲线如图所示,试在同一平面画出3个系统闭环 极点的相对位置,并说明理由。
自动控制原理第3章

12
一阶系统分析
3、单位抛物线响应
y(t)的特点:
y(t)1t2T tT2(1eT t) t0 2
输入与输出之间存在误差为无穷大,这意味着一阶系
统是不能跟踪单位抛物线输入信号的。
4、单位脉冲响应
t
y(t)TeT t0
当 t时, y()0
13
一阶系统分析
对一阶系统典型输入响应的两点说明: 1、输入信号为单位抛物线信号时,输出无法跟踪输入 2、三种响应之间的关系:
38
稳定性分析及代数判据
劳斯判据:
系统稳定的必要条件:特征方程所有系数均为正。
系统稳定的充分条件:特征方程所有系数组成劳斯表,其第 一列元素必须为正。
具体步骤:
1、先求出系统的特征方程
a n S n a n 1 S n 1 a 1 S a n0
注意:
(1) s要降阶排列 (2) 所有系数必须大于0
阶跃响应:
p 2 j1 2 n
Y sss22 n2 n s n2A s1s2 A 2 2 s n s A 3 n
yt 11 12e n t sin 1 2n t
y(t)
ξ=0.3
1
ξ=0.5
20
0
t
二阶系统分析
3、临界阻尼( =1 )
特征根
p1,2 n
阶跃响应:
yt 1 e n t1 n t
42
稳定性分析及代数判据
解:系统闭环特征方程为 s36s25sK0
列劳斯表
s3
1
5
s2
6
K
s 30 K 0
6
s0
K
稳定必须满足
30 K 0 6
自动控制原理及应用课件(第三章)

即 s1,2=- n 临界阻尼情况的单位阶跃响应为
C(s) n2 1 (s n )2 s
设部分分式为
C(s) A1 A2 A3
s s n (s n )2
式中,待定系数分别为A1=1,A2=-1,A3=-n
于是有
C(s) 1 1 n s s n (s n )2
取C(s)的拉普拉斯逆变换,则有
R(s) A0 s2
3.抛物线信号 抛物线信号的数学表达式为
0
r(t)
1 2
A0t
2
(t 0) (t ≥ 0)
式中,A0为常数。
当A0=1时,称为单位抛物线信 号,也称为单位加速度信号。
抛物线信号如图所示,它表示
随时间以等加速度增长的信号。
图3-3 抛物线信号
抛物线信号在零初始条件下的拉普拉斯变换为
R(s) A0 s3
4.脉冲信号 脉冲信号是一个脉宽极短的信号,其数学表达式为
0 t < 0;t >
r
(t
)
A0
0<t <
脉冲信号如图3-4(a)所示,
当A0=1时,若令脉宽 →0,则
称为单位理想脉冲函数,记作
(t),单位脉冲函数如图3-4(
b)所示, (t)函数满足
(t)
0
(t 0) (t 0)
闭环传递函数为 系统特征根为
(s) n2 s2 n2
s1,2 jn
无阻尼情况的单位阶跃响应为
C(s) n2 1 1 s s2 n2 s s s2 n2
取C(s)的拉普拉斯逆变换,则有
c(t) 1 cosnt (t ≥ 0)
系统阶跃响应曲线为等幅振荡,超调量为100%,振荡频率为 自然振荡角频率 n 。由于曲线不收敛,系统处于临界稳定状 态。
【实验报告】一、二阶系统的电子模拟及时域响应测试

实验名称:一二阶系统的电子模拟及时域响应测试课程名称:自动控制原理实验目录(一)实验目的 (3)(二)实验内容 (3)(三)实验设备 (3)(四)实验原理 (3)(五)一阶系统实验结果 (3)(六)一阶系统实验数据记录及分析 (7)(七)二阶系统实验结果记录 (8)(八)二阶系统实验数据记录及分析 (11)(九)实验总结及感想............................................................................错误!未定义书签。
图片目录图片1 一阶模拟运算电路 (3)图片2 二阶模拟运算电路 (3)图片3 T=0.25仿真图形 (4)图片4 T=0.25测试图形 (4)图片5 T=0.5仿真图形 (5)图片6 T=0.5测试图形 (5)图片7 T=1仿真图形 (6)图片8 T=1测试图形 (6)图片9 ζ=0.25s仿真图形 (8)图片10 ζ=0.25s测试图形 (8)图片11 ζ=0.5s仿真图形 (9)图片12 ζ=0.5s测试图形 (9)图片13 ζ=0.8s仿真图形 (10)图片14 ζ=0.8s测试图形 (10)图片15 ζ=1s仿真图形 (11)图片16 ζ=1s测试图形 (11)表格目录表格1 一阶系统实验结果 (7)表格2 二阶系统实验结果 (11)一二阶系统的电子模拟及时域响应测试(一)实验目的1.了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。
2.学习在电子模拟机上建立典型环节系统模型的方法。
3.学习阶跃响应的测试方法。
(二)实验内容1.建立一阶系统的电子模型,观测并记录在不同时间常数T时的跃响应曲线,并测定其过渡过程时间TS。
2.建立二阶系统的电子模型,观测并记录在不同阻尼比ζ时的跃响应曲线,并测定其超调量σ%及过渡过程时间TS。
(三)实验设备HHMN电子模拟机,实验用电脑,数字万用表(四)实验原理一阶系统:在实验中取不同的时间常数T,由模拟运算电路,可得到不同时间常数下阶跃响应曲线及不同的过渡时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 线性系统的时域分析法
分析控制系统的第一步是建立模型,数学模型一旦建立,就可求出已知输入信号作用下系统的输出响应。
第二步分析控制性能,即对系统做定性的分析和定量的计算。
分析有多种方法,主要有时域分析法,频域分析法,根轨迹法等。
第一节 控制系统的性能指标
一、典型输入信号
1.阶跃信号 数学表达式: 拉氏变换:
当R 0=1,称为单位阶跃信号,记为)(t ε。
2.斜坡信号 数学表达式: 拉氏变换:
当v 0=1,称为单位斜坡信号。
3.抛物线(等加速度)信号
数学表达式: 拉氏变换:
当a 0=1,称为单位抛物线函数。
4.脉冲信号 数学表达式:
拉氏变换:
当a 0=1,称为单位抛物线函数。
5.正弦信号 数学表达式: 拉氏变换:
二、系统性能指标:
控制系统的性能指标分为动态性能指标和稳态性能指标。
动态性能指标又分为跟随性能指标和扰动性能指标。
一般讨论的是跟随性能指标,即在给定信号作用下,有系统输出导出的性能指标。
常用的性能指标:
1. 上升时间t r :响应曲线从零开始,第一次上升到稳态值所需的时间。
上升时间越短,⎩⎨⎧≥<=000)(0t R t t r ,,为常数。
,00)(R s R s R =为常量。
,020)(v s v s R =⎩⎨⎧≥<=000)(0t t v t t r ,,为常量。
,030)(a s
a s R =⎪⎩⎪⎨⎧≥<=02100)(20t t a t t r ,,为常量。
,030)(a s a s R =数。
,称为单位理想脉冲函。
若令脉宽时,记为,当,,,0)(10/00)(→=⎩⎨⎧≤≤><=εδεεεt H t H t t t r 22)(ωω+=s A s R ⎩⎨⎧≥<=0sin 00)(t t A t t r ,,ω
响应速度越快 。
2. 峰值时间tp :响应曲线达到过调量的第一个峰值所需要的时间。
3. 调节时间t s :响应曲线达到并永远保持在稳态值的误差范围内,即响应进入并保持在所需的误
差带之内所需的时间。
4. 超调量%σ:指系统输出响应超出稳态值的最大偏离量占稳态值的百分比,即
5. 稳态误差e ss :系统期望值与实际输出的最终稳态值的差值。
第二节 一阶系统的时域分析
一、一阶系统的数学模型
当控制系统的数学模型为一阶微分方程时,称为一阶系统。
如图3-5系统的闭环传递函数:
二、一阶系统的时域响应及性能分析
1. 一阶系统的单位脉冲响应
当输入信号为理想单位脉冲函数时,即R(s)=1,输出量的拉氏变换与系统的传递函数相同,即 则单位脉冲响应为: 2. 一阶系统的单位阶跃响应
设输入 则输出量的拉氏变换: 单位阶跃响应为:
由响应曲线看出,系统响应由零开始按指数规律上升,最后趋于1。
系统没有振荡,也没有超调。
一阶系统的动态性能指标为调节时间。
当t=T 时,c(T)=0.632,这表明响应达到稳态值的63.2%所需的时间。
当t=3T 时,c(t)=0.95,故t s =3T (按%5±误差带)
当t=4T 时,c(t)=0.98,故t s =4T (按%2±误差带)
稳态误差e ss =0。
3. 一阶系统的单位斜坡响应
设输入 则输出量的拉氏变换:
单位斜坡响应为: 为时间常数。
,T TS s R s C s G 1
1)()()(+==01)(≥=-t e T t c T t TS T S T S S TS s R s s C ++-=⋅+==11111)()()(222φt T
t T Te T t e T t t c 11)1()(--+-=--=T s T
Ts s s C 11
11)()(+=+==φ2/1)(s
s R =s s R /1)(=T S T S S TS s R s s C 11111)()()(+-=⋅+==φT t e t c --=1)(%100)()()(%⨯∞∞-=c c t c p σ)1()()()()(11T t T e T Te T t t t r t c t e ---=+--=-=
输入与输出之间的误差为:
则稳态误差T t e t ess =∞→=)(lim 例3-1:一阶系统的结构如图所示,k k 为放大系数,K H 为反馈系数。
若K K =100,K H =0.1。
求系统的调节时间t s (按%5±误差带)。
如果t s =0.1s ,求反馈系数。
解:由结构图得系统的闭环传递函数:
()。
,,得s T t s T s s s s s 3.031.011.0101.01001100
===+=⨯+=Φ。
