【优质课件】高中数学 1.1.2弧度制 新人教A版必修4优秀课件.ppt
合集下载
高中数学 1.1 1.1.2 弧度制课件 新人教A版必修4
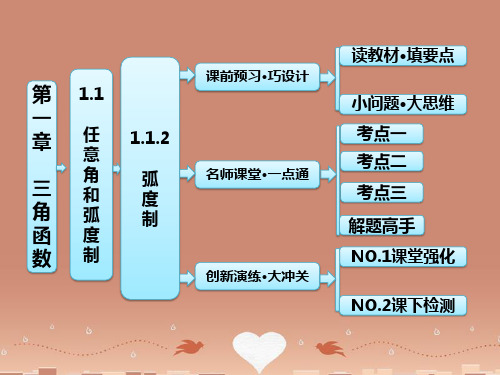
本例条件不变,写出终边在阴影部分(包括边界)的角的集合.
解:终边在阴影部分的角的集合为 π 3π {α|- +2kπ≤α≤ +2kπ,k∈Z}. 6 4
[悟一法] 1.根据已知图形写出区域角的集合的步骤:
(1)仔细观察图形;
(2)写出区域边界作为终边时角的表示; (3)用不等式表示区域范围内的角. 2.注意事项: (1)用不等式表示区域角的范围时,要注意观察角的集合 形式是否能够合并,能合并的一定要合并; (2)对于区域角的书写,一定要看其区域是否跨越x轴的 正方向.若区域跨越x轴的正方向,则前面的角用负角表示, 后面的角用正角表示.
[例 1] 3π π 设 α1=-570° ,α2=750° ,β1= ,β2=- . 5 3
(1)将 α1,α2 用弧度制表示出来,并指出它们各自的终 边所在的象限; (2)将 β1,β2 用角度制表示出来,并在-720° ~0° 范围 内找出与它们终边相同的所有角.
[自主解答] (1)∵180° =π rad, 570π 19π 5π ∴α1=-570° =- =- = -2×2π, 180 6 6 750π 25π π α2=750° = = = +2×2π. 180 6 6 ∴α1 的终边在第二象限,α2 的终边在第一象限.
读教材·填要点
第 一 章 三 角 函 数
1.1
任 意 角 和 弧 度 制 1.1.2 弧 度 制
课前预习·巧设计
小问题·大思维
考点一
名师课堂·一点通
考点二
考点三
解题高手
NO.1课堂强化
创新演练·大冲关
NO.2课下检测
[读教材·填要点] 1.度量角的单位制
单位制 内 容
1 ; 用 度 作为单 角度制 周角的 360 为 1 度角,记作 1°
1.1.2 弧度制 课件(共29张PPT)

栏目 导引
第一章 三角函数
跟踪训练 4.已知扇形面积为25 cm2,当扇形的圆心角为多大时, 扇形的周长取最小值? 解:设扇形的半径是 r,弧长是 l,扇形的周长为 y, 则 y=l+2r.由题意,得12lr=25,则 l=5r0, 故 y=5r0+2r(r>0).利用函数单调性的定义,可以证明 当 0<r≤5,函数 y=5r0+2r 是减函数;
小案例—哪个是你
忙忙叨叨,起早贪黑, 上课认真,笔记认真, 小A 就是成绩不咋地……
好像天天在玩, 上课没事儿还调皮气老师, 笔记有时让人看不懂, 但一考试就挺好…… 小B
栏目 导引
目 录/contents
第一章 三角函数
1. 什么是学习力 2. 高效学习模型 3. 超级记忆法 4. 费曼学习法
栏目 导引
栏目 导引
第一章 三角函数
(2)如图所示,设扇形的半径为 r cm,弧长为 l cm,圆心角为 θ(0<θ<2π), 由 l+2r=20,得 l=20-2r, 由12lr=9,得12(20-2r)r=9, ∴r2-10r+9=0,解得 r1=1,r2=9. 当 r1=1 cm 时,l=18 cm,θ=rl=118=18>2π(舍去). 当 r2=9 cm 时,l=2 cm,θ=rl=29. ∴扇形的圆心角的弧度数为29.
第一章 三角函数
什么是学习力
栏目 导引
第一章 三角函数
什么是学习力-你遇到这些问题了吗
总是 比别人 学得慢
一看就懂 一 做就错
看得懂,但不 会做
总是 比别人学得差 不会举一反三
栏目 导引
第一章 三角函数
什么是学习力-含义
管理知识的能力 (利用现有知识 解决问题)
第一章 三角函数
跟踪训练 4.已知扇形面积为25 cm2,当扇形的圆心角为多大时, 扇形的周长取最小值? 解:设扇形的半径是 r,弧长是 l,扇形的周长为 y, 则 y=l+2r.由题意,得12lr=25,则 l=5r0, 故 y=5r0+2r(r>0).利用函数单调性的定义,可以证明 当 0<r≤5,函数 y=5r0+2r 是减函数;
小案例—哪个是你
忙忙叨叨,起早贪黑, 上课认真,笔记认真, 小A 就是成绩不咋地……
好像天天在玩, 上课没事儿还调皮气老师, 笔记有时让人看不懂, 但一考试就挺好…… 小B
栏目 导引
目 录/contents
第一章 三角函数
1. 什么是学习力 2. 高效学习模型 3. 超级记忆法 4. 费曼学习法
栏目 导引
栏目 导引
第一章 三角函数
(2)如图所示,设扇形的半径为 r cm,弧长为 l cm,圆心角为 θ(0<θ<2π), 由 l+2r=20,得 l=20-2r, 由12lr=9,得12(20-2r)r=9, ∴r2-10r+9=0,解得 r1=1,r2=9. 当 r1=1 cm 时,l=18 cm,θ=rl=118=18>2π(舍去). 当 r2=9 cm 时,l=2 cm,θ=rl=29. ∴扇形的圆心角的弧度数为29.
第一章 三角函数
什么是学习力
栏目 导引
第一章 三角函数
什么是学习力-你遇到这些问题了吗
总是 比别人 学得慢
一看就懂 一 做就错
看得懂,但不 会做
总是 比别人学得差 不会举一反三
栏目 导引
第一章 三角函数
什么是学习力-含义
管理知识的能力 (利用现有知识 解决问题)
2021版高中数学人教A必修4课件:1.1.2 弧度制

M 目标导航 UBIAODAOHANG
Z 知识梳理 HISHI SHULI
题型一 题型二 题型三 题型四
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
易错点 角度与弧度混用致错 【例4】 把角-690°化为2kπ+α(0≤α<2π,k∈Z)的形式为
. 错解:-690°=-720°+30°=-4π+30°. 答案:-4π+30° 错因分析:上述解法中,表示一个角,既用了角度又用了弧度,这种
-10-
Байду номын сангаас 1.1.2 弧度制
M 目标导航 UBIAODAOHANG
Z 知识梳理 HISHI SHULI
题型一 题型二 题型三 题型四
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
-11-
1.1.2 弧度制
M 目标导航 UBIAODAOHANG
Z 知识梳理 HISHI SHULI
(2)如图,已知扇形AOB的圆心角为120°,半径长为6,求弓形ACB的 面积.
-14-
1.1.2 弧度制
M 目标导航 UBIAODAOHANG
Z 知识梳理 HISHI SHULI
题型一 题型二 题型三 题型四
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
-15-
1.1.2 弧度制
Z 知识梳理 HISHI SHULI
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
123
(4)角的概念推广后,在弧度制下,角的集合与实数集R之间建立起 一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度 数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等 于这个实数的角)与它对应.
高中数学必修四1.1.2弧度制课件人教A版

-6-
1.1.2
1 2AOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
(4)角的概念推广后,在弧度制下,角的集合与实数集R之间建立起 一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度 数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等 于这个实数的角)与它对应.
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
3.弧度制与角度制的换算 π (1)角度转化为弧度:360° =2π rad,180° =π rad,1° = rad ≈0.017 180 45 rad. (2)弧度转化为角度:2π rad=360° ,π rad=180° ,1 rad=
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
1.用弧度制表示象限角与终边在坐标轴上的角 剖析:(1)象限角的表示:
角 α 终边所在象限 第一象限 第二象限 第三象限 第四象限 集合 ������ x 2k������ < α < 2k������ + ,������∈Z 2 π ������ 2������π + < ������ < 2������π + π,������∈Z 2 3π ������ 2������π + π < ������ < 2������π + ,������∈Z 2 3π ������ 2������π + < ������ < 2������π + 2π,������∈Z 2
1.1.2
1 2AOHANG
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
(4)角的概念推广后,在弧度制下,角的集合与实数集R之间建立起 一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度 数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等 于这个实数的角)与它对应.
Z 知识梳理
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
3.弧度制与角度制的换算 π (1)角度转化为弧度:360° =2π rad,180° =π rad,1° = rad ≈0.017 180 45 rad. (2)弧度转化为角度:2π rad=360° ,π rad=180° ,1 rad=
HISHI SHULI
Z 重难聚焦
HONGNAN JVJIAO
D典例透析
IANLI TOUXI
1.用弧度制表示象限角与终边在坐标轴上的角 剖析:(1)象限角的表示:
角 α 终边所在象限 第一象限 第二象限 第三象限 第四象限 集合 ������ x 2k������ < α < 2k������ + ,������∈Z 2 π ������ 2������π + < ������ < 2������π + π,������∈Z 2 3π ������ 2������π + π < ������ < 2������π + ,������∈Z 2 3π ������ 2������π + < ������ < 2������π + 2π,������∈Z 2
人教A版高中数学必修四《1.1.2弧度制》ppt课件.ppt
• 20、No man is happy who does not think himself so.——Publilius Syrus认为自己不幸福的人就不会幸福。2020年8月5日星期三11时1分19秒11:01:195 August 2020
• 21、The emperor treats talent as tools, using their strongpoint to his advantage. 君子用人如器,各取所长。上午11时1分19秒上午11时1分11:01:1920.8.5
3
.
1.什么叫1弧度角? 2.“角度制”与“弧度制”的联系与区别; 3.弧长公式与扇形面积公式.
把希望建筑在意欲和心愿上面的人们,二十 次中有十九次都会失望。
——大仲马
• 1、Genius only means hard-working all one's life. (Mendeleyer, Russian Chemist) 天才只意味着终身不懈的努力。20.8.58.5.202011:0311:03:10Aug-2011:03
• •
THE END 8、For man is man and master of his fate.----Tennyson人就是人,是自己命运的主人11:0311:03:108.5.2020Wednesday, August 5, 2020
9、When success comes in the door, it seems, love often goes out the window.-----Joyce Brothers成功来到门前时,爱情往往就走出了窗外。 11:038.5.202011:038.5.202011:0311:03:108.5.202011:038.5.2020
新课标高中数学人教A版必修四全册课件1.1.2弧度制(一)

弧 度
0
6
4
3
2
23
角 度
135o
150o
180o
270o
360o
弧 度
第三十五页,编辑于星期日:十三点 十八分。
特殊角的弧度
角 度
0o
30o
45o
60o
90o 120o
弧 度
0
6
4
3
2
23
角 度
135o
150o
180o
弧 3
度4
270o
360o
第三十六页,编辑于星期日:十三点 十八分。
特殊角的弧度
r ③正角的弧度数是一个正数.
④负角的弧度数是一个负数.
⑤零角的弧度数是零.
⑥角的弧度数的绝对值||=
l. r
第十七页,编辑于星期日:十三点 十八分。
角度与弧度之间的转换
①将角度化为弧度:
第十八页,编辑于星期日:十三点 十八分。
角度与弧度之间的转换
①将角度化为弧度:
第十九页,编辑于星期日:十三点 十八分。
270o
360o
第三十八页,编辑于星期日:十三点 十八分。
特殊角的弧度
角 度
0o
30o
45o
60o
90o 120o
弧 度
0
6
4
3
2
23
角 度
135o
150o
180o
弧 3 5
度4 6
270o
3
2
360o
第三十九页,编辑于星期日:十三点 十八分。
特殊角的弧度
角 度
0o
30o
45o
60o
人教版高中数学必修四弧度制和弧度制与角度制的换算公开课教学课件共18张PPT
当堂检测(限时5分钟,满分10分)
2、
-144o
3、-25º 4、 所求扇形的中心角的弧度数为
小结
圆周角度360
换
算 等价
六十进制 区别
十进制
圆周弧度2
角度制
弧度制
角的度量
三角函数
温故而知新
1、角度制:初中时我们用角度制度量角,1度的角 等于周角的1/360。
周角的 1/360
1°
n° l R
1弧度的概念
如图,把长度等于半径长的圆弧所对的圆心角叫做 1弧度的角,记作1rad,读作1弧度.
探究1:深化弧度的概念
思考1:1弧度圆心角的大小与所在圆的半径的大小 是否有关?为什么?
B’ B l=R
1弧度
1弧度l=r O r R A A’
思考2:如果将半径为r圆的一条半径OA,绕圆心旋转 到OB,若弧AB长为2r,那么∠AOB的大小为多少弧度?
2rad
2r
B
r
A O
思考3:如果半径为r的圆的圆心角α所对的弧长为l, 那么,角α的弧度数的绝对值如何计算?
探究2:角度与弧度的换算
解的?
正角
正实数
零角
零
十进制
负角
负实数
探究3:与扇形有关的公式
思考1:角度制下,扇形的圆心角是n°,则扇形的面积是?
思考2:类比思考1,在弧度制下,若扇形的圆心角是 弧 度,则扇形的面积是?还有其它的表示方法么?
A
r
OS l B
例题讲解
例1 把
解:∵ ∴
化成弧度。
例2 把 化成度。
解:∵ 1rad=
人教版高中数学必修四 弧度制和弧度制与角度 制的换算公开课教学课
【人教版】高中数学必修四第一章《1.1.2弧度制》精品课件
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
(单击进入电子文档)
首
பைடு நூலகம்
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
首
上一页
下一页
末页
结 束
人教A版必修四1.1.2弧度制课件 (共17张PPT)
C
l=2r
2rad
A O
4.角的弧度数的绝对值: l
r
5.
正角 零角 负角 角的弧度数
对应角的
正实数 弧度数 零
负实数 实数集R
二、角度制与弧度制换算:
(1)将角度化为弧度:
360 2 rad 180 rad
1 rad
180
n
n0 _1_8_0__ rad
二、角度制与弧度制换算:
(2)将弧度化为角度:
2 360
180
1rad (180) 57.30 5718'
180n
n _____ 0
特殊角的弧度:
角 度
0o
30o
45o
60o
90o 120o
弧 度
0
6
4
2
323
角 度
135o
150o
180o270o源自360o弧 3 度4
5
6
3 2
2
常规写法:
① 用弧度数表示角时,常常把弧度数
(1)理解弧度制的概念; (2)熟练进行角度制与弧度制的 换算; (3)能应用弧长公式与扇形面积 公式解决有关问题.
角度制:
1.定义:是用“度”作单位来度量角 的单位制叫做角度制.
2.角度制的单位:度、分 规定:周角的 1 为10 ,即周角为3600
360
一、弧度制:
1.定义:是用“弧度”作单位来度量角的 单位制叫做弧度制.
例2:在半径为R的圆中,240º的圆心角
所对的弧长为
,面积为2R2的
扇形的圆心角等于
弧度。
解:(1)240º= 4 ,根据l=αR,得 l 4 R
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)“弧度”与“角度”之间可以相互转化
3.解析弧度制下弧长公式、扇形的面积公式 在弧度制下,弧长公式和扇形的面积公式分别为: l=|α|R,S=12lR=12|α|R2(其中 α 为圆心角的弧度数,R 为扇 形的半径). 要把握好上述公式,需注意以下三个方面: (1)由上述公式可知,由 α、l、R、S 中的两个量可以求出 另外的两个量,即“知二求二”.
弧度制下有关弧长、扇形面积问题 的解(1题)明策确弧略度制下弧长公式 l=|α|r,扇形的面积公式是 S=12
lr=12|α|r2(其中 l 是扇形的弧长,α 是扇形的圆心角). (2)涉及扇形的周长、弧长、圆心角、面积等的计算,关键
是先分析题目已知哪些量求哪些量,然后灵活运用弧长公式、 扇形面积公式直接求解或列方程(组)求解.
角度与弧度的换算
(1)将下列各角化为弧度:①112°30′; ②-315°.
(2)将下列各弧度角化为角度:①-51π2 rad;②139π.
思路点拨:
解:(1)①∵1°=1π80 rad, ∴112°30′=1π80×112.5 rad=58π rad. ②-315°=-315×1π80=-74π. (2)①∵1 rad=1π80°, ∴-51π2 rad=-51π2×1π80°=-75°. ②139π=139π×1π80°=1 140°.
中小学精编教育课件
第一章 三角函数
1.1 任意角和弧度制
1.1.2 弧度制
1.了解角的另外一种度量方法——弧度制.
2.能进行弧度与角度的互化.(重点、难点、 易错点)
3.掌握弧度制中扇形的弧长公式和面积公 式.(重点)
ห้องสมุดไป่ตู้
1.度量角的两种制度 (1)角度制 ①定义:用度作为单位来度量角的单位制. ②1 度的角:周角的3160作为一个单位. (2)弧度制 ①定义:以弧度作为单位来度量角的单位制. ②1 弧度的角:长度等于半___径__长__的弧所对的圆心角.
【即时演练】
-247π 是第________象限的角.
解析:∵-247π=-6π-34π,而-34π 是第三象限的角,
∴-247π 是第三象限的角. 答案:三
感谢各位老师!
祝: 身体健康 万事如意
(2)运用弧度制下的弧长公式及扇形的面积公式明显比角 度制下的公式简单得多,但要注意它的运用前提是 α 为弧度制.
(3)在运用公式时,还应熟练地掌握这两个公式的变形应 用:
①l=|α|R,|α|=Rl ,R=|αl |. ②S=12|α|R2,|α|=2RS2.
弧度制的概念问题
下列说法不正确的是( )
【互动探究】
在本题(1)中,若扇形的周长10 cm改为40 cm,则当它的半径和圆心角各取什么值时,能 使扇形的面积最大?最大面积是多少?
解:设扇形的圆心角为 θ,半径为 r,弧长为 l,面积为 S, 则 l+2r=40,∴l=40-2r.
∴S=12lr=12×(40-2r)r=(20-r)r =-(r-10)2+100. ∴当半径 r=10 cm 时,扇形的面积最大. 这个最大值为 100 cm2,这时 θ=rl=40-120×10=2 rad.
A.“度”与“弧度”是度量角的两种不同的度量单位 B.1 度的角是周角的3160,1 弧度的角是周角的21π C.根据弧度的定义,180°一定等于 π 弧度 D.不论是用角度制还是用弧度制度量角,它们与圆的半 径长短有关
思路点拨: 选项 角―度―制―和―弧―度―制―的―定→义 判断真假
解析:各选项分析如下:
弧长及扇形面积公式的应用问题
(1)已知扇形的周长为10 cm,面积为 4 cm2,求扇形圆心角的弧度数.
(2)已知一扇形的圆心角是72°,半径等于 20 cm,求扇形的面积.
思路点拨:(1) 设出圆心角为θ → 建方程组 →
解方程组得解
(2) 化度为弧度 → 求弧长 → 求扇形面积
解:(1)设扇形圆心角的弧度数为 θ(0<θ<2π),弧长为 l, 半径为 r,
提示:√ 当圆心角一定时,圆心角所对的 弧长与半径成正比,与所取半径无关.
1.用圆心角所对的弧长与半径的比度量圆 心角的合理性
当圆心角一定时,圆心角所对的弧长与半 径成正比,与所取半径无关.
如图,设 α 为 n°(n>0)的角,弧M︵N 和M︵1N1 的长分别为 l 和 l1,点 M 和 M1 到点 O 的距离(即圆的半径)分别为 r(r>0)和 R(R>0).由初中学过的弧长公式可得 l=1n8π0r,l1=n1π8R0,于是rl= Rl1=1n8π0.
2.判一判(判断下列说法的正误) (1)“度”与“弧度”是相同的,都是用来 度量角的单位.( )
提示:× “度”与“弧度”是度量角的 两种不同的度量单位.
(2)1 rad的角和1°的角大小一样.( )
提示:× 1 rad的角比1°的角要大.
(3)用圆心角所对的弧长与半径的比来度量 圆心角是合理的.( )
(2)用角度制和弧度制来度量零角,单位不 同,但数量相同(都是0);用角度制和弧度制度 量任意非零角,单位不同,数量也不同.
(3)牢记180°=π rad,充分利用其进行互 化.
(4)角度的单位不可省略,而弧度的单位 “rad”可以省略.
1.在半径不等的两个圆内,1弧度的圆心 角( )
A.所对的弧长相等 B.所对的弦长相等 C.所对的弦长等于各自半径 D.所对的弧长等于各自半径 解析:1弧度的圆心角是指长度等于半径长 的弧所对的圆心角,所以D正确. 答案:D
2.弧度数的计算 (1)弧度数 ①正角的弧度数是正一数个______. ②负角的弧度数是负一数个______.
0
③零角的弧度数是_l __.
(2)弧度数的计算:|α|=__r__.
如图:
3.角度制与弧度制的换算
1.想一想 角α=5这种表达方式正确吗? 提示:正确.角α=5表示5弧度的角,这里 将“弧度”省去了.
依题意有
l+2r=10,
①
12lr=4.
②
①代入②得 r2-5r+4=0,解得 r1=1,r2=4.
当 r=1 时,l=8(cm),此时 θ=8 rad>2π rad,舍去. 当 r=4 时,l=2(cm),此时 θ=24=12 rad. ∴综上,θ=12. (2)设扇形弧长为 l, ∵72°=72×1π80=25π(rad), ∴l=αR=25π×20=8π(cm). ∴S=12lR=12×8π×20=80π(cm2).
因此用圆心角所对弧长与半径的比来度量这个圆心角是合 理的.
2.有关“角度”与“弧度”概念的理解
(1)定义不同.
区 (2)单位不同.弧度制是以“弧度”为单位,单位可 以省略,而角度制是以“度”为单位,单位不能省
别 略.
(31)弧不度管制以是“十弧进度制”,还而是角以度“制度是”六为十单进位制的角的大小 联 都是一个与圆的半径大小无关的值,仅与圆心角所 系 对的弧与半径的比值有关.
答案:-4π+π6
错解
错因
-3π-56π
在解答过程中,易将-4π 写成-3π,而-3π 不是 2kπ 的形式,不符合做题要求
在解答过程中,易将π6写成 30°的形式,虽然结 -4π+30° 果的数值大小是等同的,但不符合在同一表达
式中角度与弧度不能混用这一原则
【纠错提升】 弧度和角度的书写要求
在解决角度制和弧度制的有关问题时,要 遵循转换的原则,表达的形式要符合基本的原 则和规范性,即在同一个式子中度和弧度不能 混用.
进行角度制与弧度制的互化的策略 以及(1注)原意则:点牢记 180°=π rad,充分利用 1°=1π80 rad 和 1 rad
=1π80°进行换算. (2)方法:设一个角的弧度数为 α,角度数为 n,则
α rad=α·1π80°;n°=n·1π80.
(3)注意点
①用“弧度”为单位度量角时,“弧度” 二字或“rad”可以省略不写.
②用“弧度”为单位度量角时,常常把弧 度数写成多少π的形式,如无特别要求,不必把 π写成小数.
③度化弧度时,应先将分、秒化成度,再 化成弧度.
2.用弧度制表示终边落在x轴上方的角的集 合为________________.
解析:若角α的终边落在x轴上方,则2kπ<α <2kπ+π,k∈Z.
答案:{α|2kπ<α<2kπ+π,k∈Z}
“度”与“弧度”是度量角的两种不同单位,故 A
A 正确
B 因为 1°=336600°,所以 1=22ππ.所以 B 正确
C 由弧度制规定知 π rad=180°,所以 C 正确
角只与弧长和半径的比值有关,与圆的半径无 D
关,故 D 错误
答案:D
角度与弧度的理解与互化
(1)引入弧度制后,角的集合与实数集建立 了一一对应关系.
易错误区系列(二) 用角度与弧度表达角时的误区
把角-690°化为2kπ+α(0≤α<2π, k∈Z)的形式为________.
解析:方法一:-690°=-690×1π80=-263π,
∴-263π=-4π+π6,即-690°=-4π+π6.
方法二:-690°=-2×360°+30°,
∴-690°=-4π+π6.
3.解析弧度制下弧长公式、扇形的面积公式 在弧度制下,弧长公式和扇形的面积公式分别为: l=|α|R,S=12lR=12|α|R2(其中 α 为圆心角的弧度数,R 为扇 形的半径). 要把握好上述公式,需注意以下三个方面: (1)由上述公式可知,由 α、l、R、S 中的两个量可以求出 另外的两个量,即“知二求二”.
弧度制下有关弧长、扇形面积问题 的解(1题)明策确弧略度制下弧长公式 l=|α|r,扇形的面积公式是 S=12
lr=12|α|r2(其中 l 是扇形的弧长,α 是扇形的圆心角). (2)涉及扇形的周长、弧长、圆心角、面积等的计算,关键
是先分析题目已知哪些量求哪些量,然后灵活运用弧长公式、 扇形面积公式直接求解或列方程(组)求解.
角度与弧度的换算
(1)将下列各角化为弧度:①112°30′; ②-315°.
(2)将下列各弧度角化为角度:①-51π2 rad;②139π.
思路点拨:
解:(1)①∵1°=1π80 rad, ∴112°30′=1π80×112.5 rad=58π rad. ②-315°=-315×1π80=-74π. (2)①∵1 rad=1π80°, ∴-51π2 rad=-51π2×1π80°=-75°. ②139π=139π×1π80°=1 140°.
中小学精编教育课件
第一章 三角函数
1.1 任意角和弧度制
1.1.2 弧度制
1.了解角的另外一种度量方法——弧度制.
2.能进行弧度与角度的互化.(重点、难点、 易错点)
3.掌握弧度制中扇形的弧长公式和面积公 式.(重点)
ห้องสมุดไป่ตู้
1.度量角的两种制度 (1)角度制 ①定义:用度作为单位来度量角的单位制. ②1 度的角:周角的3160作为一个单位. (2)弧度制 ①定义:以弧度作为单位来度量角的单位制. ②1 弧度的角:长度等于半___径__长__的弧所对的圆心角.
【即时演练】
-247π 是第________象限的角.
解析:∵-247π=-6π-34π,而-34π 是第三象限的角,
∴-247π 是第三象限的角. 答案:三
感谢各位老师!
祝: 身体健康 万事如意
(2)运用弧度制下的弧长公式及扇形的面积公式明显比角 度制下的公式简单得多,但要注意它的运用前提是 α 为弧度制.
(3)在运用公式时,还应熟练地掌握这两个公式的变形应 用:
①l=|α|R,|α|=Rl ,R=|αl |. ②S=12|α|R2,|α|=2RS2.
弧度制的概念问题
下列说法不正确的是( )
【互动探究】
在本题(1)中,若扇形的周长10 cm改为40 cm,则当它的半径和圆心角各取什么值时,能 使扇形的面积最大?最大面积是多少?
解:设扇形的圆心角为 θ,半径为 r,弧长为 l,面积为 S, 则 l+2r=40,∴l=40-2r.
∴S=12lr=12×(40-2r)r=(20-r)r =-(r-10)2+100. ∴当半径 r=10 cm 时,扇形的面积最大. 这个最大值为 100 cm2,这时 θ=rl=40-120×10=2 rad.
A.“度”与“弧度”是度量角的两种不同的度量单位 B.1 度的角是周角的3160,1 弧度的角是周角的21π C.根据弧度的定义,180°一定等于 π 弧度 D.不论是用角度制还是用弧度制度量角,它们与圆的半 径长短有关
思路点拨: 选项 角―度―制―和―弧―度―制―的―定→义 判断真假
解析:各选项分析如下:
弧长及扇形面积公式的应用问题
(1)已知扇形的周长为10 cm,面积为 4 cm2,求扇形圆心角的弧度数.
(2)已知一扇形的圆心角是72°,半径等于 20 cm,求扇形的面积.
思路点拨:(1) 设出圆心角为θ → 建方程组 →
解方程组得解
(2) 化度为弧度 → 求弧长 → 求扇形面积
解:(1)设扇形圆心角的弧度数为 θ(0<θ<2π),弧长为 l, 半径为 r,
提示:√ 当圆心角一定时,圆心角所对的 弧长与半径成正比,与所取半径无关.
1.用圆心角所对的弧长与半径的比度量圆 心角的合理性
当圆心角一定时,圆心角所对的弧长与半 径成正比,与所取半径无关.
如图,设 α 为 n°(n>0)的角,弧M︵N 和M︵1N1 的长分别为 l 和 l1,点 M 和 M1 到点 O 的距离(即圆的半径)分别为 r(r>0)和 R(R>0).由初中学过的弧长公式可得 l=1n8π0r,l1=n1π8R0,于是rl= Rl1=1n8π0.
2.判一判(判断下列说法的正误) (1)“度”与“弧度”是相同的,都是用来 度量角的单位.( )
提示:× “度”与“弧度”是度量角的 两种不同的度量单位.
(2)1 rad的角和1°的角大小一样.( )
提示:× 1 rad的角比1°的角要大.
(3)用圆心角所对的弧长与半径的比来度量 圆心角是合理的.( )
(2)用角度制和弧度制来度量零角,单位不 同,但数量相同(都是0);用角度制和弧度制度 量任意非零角,单位不同,数量也不同.
(3)牢记180°=π rad,充分利用其进行互 化.
(4)角度的单位不可省略,而弧度的单位 “rad”可以省略.
1.在半径不等的两个圆内,1弧度的圆心 角( )
A.所对的弧长相等 B.所对的弦长相等 C.所对的弦长等于各自半径 D.所对的弧长等于各自半径 解析:1弧度的圆心角是指长度等于半径长 的弧所对的圆心角,所以D正确. 答案:D
2.弧度数的计算 (1)弧度数 ①正角的弧度数是正一数个______. ②负角的弧度数是负一数个______.
0
③零角的弧度数是_l __.
(2)弧度数的计算:|α|=__r__.
如图:
3.角度制与弧度制的换算
1.想一想 角α=5这种表达方式正确吗? 提示:正确.角α=5表示5弧度的角,这里 将“弧度”省去了.
依题意有
l+2r=10,
①
12lr=4.
②
①代入②得 r2-5r+4=0,解得 r1=1,r2=4.
当 r=1 时,l=8(cm),此时 θ=8 rad>2π rad,舍去. 当 r=4 时,l=2(cm),此时 θ=24=12 rad. ∴综上,θ=12. (2)设扇形弧长为 l, ∵72°=72×1π80=25π(rad), ∴l=αR=25π×20=8π(cm). ∴S=12lR=12×8π×20=80π(cm2).
因此用圆心角所对弧长与半径的比来度量这个圆心角是合 理的.
2.有关“角度”与“弧度”概念的理解
(1)定义不同.
区 (2)单位不同.弧度制是以“弧度”为单位,单位可 以省略,而角度制是以“度”为单位,单位不能省
别 略.
(31)弧不度管制以是“十弧进度制”,还而是角以度“制度是”六为十单进位制的角的大小 联 都是一个与圆的半径大小无关的值,仅与圆心角所 系 对的弧与半径的比值有关.
答案:-4π+π6
错解
错因
-3π-56π
在解答过程中,易将-4π 写成-3π,而-3π 不是 2kπ 的形式,不符合做题要求
在解答过程中,易将π6写成 30°的形式,虽然结 -4π+30° 果的数值大小是等同的,但不符合在同一表达
式中角度与弧度不能混用这一原则
【纠错提升】 弧度和角度的书写要求
在解决角度制和弧度制的有关问题时,要 遵循转换的原则,表达的形式要符合基本的原 则和规范性,即在同一个式子中度和弧度不能 混用.
进行角度制与弧度制的互化的策略 以及(1注)原意则:点牢记 180°=π rad,充分利用 1°=1π80 rad 和 1 rad
=1π80°进行换算. (2)方法:设一个角的弧度数为 α,角度数为 n,则
α rad=α·1π80°;n°=n·1π80.
(3)注意点
①用“弧度”为单位度量角时,“弧度” 二字或“rad”可以省略不写.
②用“弧度”为单位度量角时,常常把弧 度数写成多少π的形式,如无特别要求,不必把 π写成小数.
③度化弧度时,应先将分、秒化成度,再 化成弧度.
2.用弧度制表示终边落在x轴上方的角的集 合为________________.
解析:若角α的终边落在x轴上方,则2kπ<α <2kπ+π,k∈Z.
答案:{α|2kπ<α<2kπ+π,k∈Z}
“度”与“弧度”是度量角的两种不同单位,故 A
A 正确
B 因为 1°=336600°,所以 1=22ππ.所以 B 正确
C 由弧度制规定知 π rad=180°,所以 C 正确
角只与弧长和半径的比值有关,与圆的半径无 D
关,故 D 错误
答案:D
角度与弧度的理解与互化
(1)引入弧度制后,角的集合与实数集建立 了一一对应关系.
易错误区系列(二) 用角度与弧度表达角时的误区
把角-690°化为2kπ+α(0≤α<2π, k∈Z)的形式为________.
解析:方法一:-690°=-690×1π80=-263π,
∴-263π=-4π+π6,即-690°=-4π+π6.
方法二:-690°=-2×360°+30°,
∴-690°=-4π+π6.
