高中数学必修五考试题及答案
(完整版)高中数学必修五综合测试题 含答案

.绝密★启用前高中数学必修五综合考试卷第I 卷(选择题)一、单选题1.数列的一个通项公式是( )0,23,45,67⋯A .B . a n =n -1n +1(n ∈N *)a n =n -12n +1(n ∈N *)C .D .a n =2(n -1)2n -1(n ∈N *)a n =2n2n +1(n ∈N *)2.不等式的解集是( )x -12-x ≥0A .B .C .D . [1,2](-∞,1]∪[2,+∞)[1,2)(-∞,1]∪(2,+∞)3.若变量满足 ,则的最小值是( )x,y {x +y ≥0x -y +1≥00≤x ≤1x -3y A .B .C .D . 4-5-314.在实数等比数列{a n }中,a 2,a 6是方程x 2-34x +64=0的两根,则a 4等于( )A . 8B . -8C . ±8D . 以上都不对5.己知数列为正项等比数列,且,则( ){a n }a 1a 3+2a 3a 5+a 5a 7=4a 2+a 6=A . 1B . 2C . 3D . 46.数列前项的和为( )11111,2,3,4,24816n A . B . C .D .2122nn n ++21122n n n +-++2122n n n +-+21122n n n +--+7.若的三边长成公差为的 等差数列,最大角的正弦值为ΔABC a,b,c 232的面积为( )A .B .C .D .1541534213435348.在△ABC 中,已知,则B 等于( )a =2,b =2,A =450A . 30°B . 60°C . 30°或150°D . 60°或120°9.下列命题中正确的是( )A . a >b ⇒ac 2>bc 2B . a >b ⇒a 2>b 2C . a >b ⇒a 3>b 3D . a 2>b 2⇒a >b.10.满足条件,的的个数是 ( )a =4,b =32,A =45∘A . 1个B . 2个C . 无数个D . 不存在11.已知函数满足:则应满足( )f(x)=ax 2-c -4≤f(1)≤-1,-1≤f(2)≤5.f(3)A .B .C .D .-7≤f(3)≤26-4≤f(3)≤15-1≤f(3)≤20-283≤f(3)≤35312.已知数列{a n }是公差为2的等差数列,且成等比数列,则为( )a 1,a 2,a 5a2A . -2B . -3C . 2D . 313.等差数列的前10项和,则等于(){a n }S 10=15a 4+a 7A . 3B . 6C . 9D . 1014.等差数列的前项和分别为,若,则的值为( ){a n },{b n }n S n ,T nS nT n=2n3n +1a 3b 3A .B .C .D . 3547581219第II 卷(非选择题)二、填空题15.已知为等差数列,且-2=-1,=0,则公差={a n }a 7a 4a3d 16.在中,,,面积为,则边长=_________.△ABC A =60∘b =13c 17.已知中,,, ,则面积为_________.ΔABC c =3a =1acosB =bcosA ΔABC 18.若数列的前n 项和,则的通项公式____________{a n }S n =23a n +13{a n }19.直线下方的平面区域用不等式表示为________________.x -4y +9=020.函数的最小值是 _____________.y =x +4x -1(x >1)21.已知,且,则的最小值是______.x ,y ∈R +4x +y =11x +1y三、解答题22.解一元二次不等式(1) (2)-x 2-2x +3>0x 2-3x +5>0.(1)求边上的中线的长;BC AD (2)求△的面积。
(典型题)高中数学必修五第一章《数列》检测题(包含答案解析)

一、选择题1.已知数列{}n a 的前n 项和为n S ,11a =,23a =,且()11222n n nn S S S n +-+=+≥,若()()72n n S a n λλλ-++≥-对任意*n ∈N 都成立,则实数λ的最小值为( ) A .52-B .116C .332D .12.若等差数列{}n a 的前n 项和为n S ,首项10a >,202020210a a +>,202020210a a ⋅<,则满足0n S >成立的最大正整数n 是( ) A .4039B .4040C .4041D .40423.在数列{}n a 中,11a =-,33a =,212n n n a a a ++=-(*n N ∈),则10a =( ) A .10B .17C .21D .354.两个公比均不为1的等比数列{}{},n n a b ,其前.n 项的乘积....分别为,n n A B ,若552a b =,则99A B =( ) A .512B .32C .8D .25.已知数列{}n a 的前n 项和n S 满足21n n S a =-.若对任意正整数n 都有10n n S S λ+-<恒成立,则实数λ的取值范围为( ) A .(),1-∞B .12⎛⎫-∞ ⎪⎝⎭,C .13⎛⎫-∞ ⎪⎝⎭,D .14⎛⎫-∞ ⎪⎝⎭,6.《张丘建算经》是我国北魏时期大数学家丘建所著,约成书于公元466485~年间,其记臷着这么一道题:某女子善于织布,一天比一天织得快,而且每天增加的数量相同. 已知第一天织布5尺,30天其织布390尺,则该女子织布每天增加的尺数(不作近似计算)为( ) A .1629B .1627C .1113D .13297.已知等差数列{}n a 的首项为1a ,公差为d ,其前n 项和为n S ,若直线112y a x m =+与圆()2221x y -+=的两个交点关于直线0x y d +-=对称,则数列1n S ⎧⎫⎨⎬⎩⎭的前10项和为( ) A .1011B .910C .89D .28.记n S 为等比数列{}n a 的前n 项和,若数列{}12n S a -也为等比数列,则43a a =( ).A .2B .1C .32D .129.对于数列{}n a ,定义11233n nn a a a T n-+++=为{}n a 的“最优值”,现已知数列{}n a 的“最优值”3n n T =,记数列{}n a 的前n 项和为n S ,则20202020S=( ) A .2019B .2020C .2021D .202210.已知数列{}n a 的通项公式为211n aa n n n=-+,5a 是数列{}n a 的最小项,则实数a 的取值范围是( ) A .[40,25]--B .[40,0]-C .[25,0]-D .[25,0]-11.已知数列{}n a 满足123n n a a +-=,11a =,3n n b a =+,则10b =( ) A .92B .103C .2048D .102412.已知{}n a 为等比数列,13527a a a =,246278a a a =,以n T 表示{}n a 的前n 项积,则使得n T 达到最大值的n 是( ) A .4B .5C .6D .7二、填空题13.已知数列{}n a 的首项1a m =,其前n 项和为n S ,且满足2123n n S S n n ++=+,若数列{}n a 是递增数列,则实数m 的取值范围是_______. 14.设数列{}n a 是等比数列,公比2q,n S 为{}n a 的前n 项和,记219n nn n S S T a +-=(*n N ∈),则数列{}n T 最大项的值为__________. 15.已知数列{}n a 满足对*,m n N ∀∈,都有m n m n a a a ++=成立,72a π=,函数()f x =2sin 24cos 2xx +,记()n n y f a =,则数列{}n y 的前13项和为______. 16.无穷数列{}n a 满足:只要()*,p q a a p q N=∈,必有11p q aa ++=,则称{}n a 为“和谐递进数列”.已知{}n a 为“和谐递进数列”,且前四项成等比数列,151a a ==,22a =,则2021S =_________.17.在等比数列{}n a 中,2514,2==a a ,则公比q =__________. 18.下图中的一系列正方形图案称为谢尔宾斯基地毯.在图中4个大正方形中,着色的正方形的个数依次构成一个数列{}n a 的前4项,则数列{}n a 的一个通项公式为______.19.已知数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,21nn n b a -=+,且1222n n n S T n ++=+-,则2n T =____.20.已知数列{}n a 的通项公式为()12n n a n =+⋅,若不等式()2235n n n a λ--<-对任意*n N ∈恒成立,则整数λ的最大值为_____.三、解答题21.已知等差数列{}n a 满足()()()()*122312(1)n n a a a a a a n n n N +++++⋅⋅⋅++=+∈. (1)求数列{}n a 的通项公式;(2)求数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和n S .22.已知{}n a 是等差数列,{}n b 是递增的等比数列且前n 和为n S ,112822,10a b a a ==+=,___________.在①2345,,4b b b 成 等差数列,②12n n S λ+=+(λ为常数)这两个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件分别解答,按第一个解答计分). (1)求数列{}n a 和{}n b 的通项公式; (2)求数列{}n n a b +的前n 项和n T . 23.已知数列{}n a 满足112a =,1223241n n n a a n ++-=-,n *∈N . (1)设121n n b a n =+-,求证:数列{}n b 是等比数列; (2)设数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,求证:3n S <,n *∈N .24.已知正项数列{}n a 、{}n b ,记数列{}n a 的前n 项和为n S ,若1143a b +=,21n n S a +=,2211(1)0n n n n nb b b n b ----+=(1)求数列{}n a 、{}n b 的通项公式; (2)求数列{}2n n a b 的前n 项和n T . 25.已知数列{}n a ,11a =,121n n a a +=+.(1)求证数列{}1n a +是等比数列; (2)令()2log 1n n b a =+,求数列21n n b b +⎧⎫⎨⎬⎩⎭的前n 项和n T . 26.已知数列{}n a 满足:12a =,()*112n n n a a n N n ++⎛⎫=∈ ⎪⎝⎭. (1)求数列{}n a 的通项公式; (2)求数列{}n a 的前n 项和n T ;(3)设2nn n b a =,数列{}n b 的前n 项和为n S ,求2n n S S -的最小值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】由n S 与n a 的关系得21nn a =-,则272n maxn λ-⎛⎫≥⎪⎝⎭,设272nn n c -=,利用数列的单调性即可求解. 【详解】解:数列{}n a 的前n 项和为n S ,11a =,23a =,且()11222n n nn S S S n +-+=+≥, 所以112nn n n n S S S S +--=+-,故()122nn n a a n +-=≥,因为1212a a -=,所以()121nn n a a n +-=≥,所以112n n n a a ---=,2122n n n a a ----=,⋯,1212a a -=, 则1211222n n a a --=++⋯+,故11211222121n n n n a --=++⋯+==--, 所以()123122122222221n n n nS n n n +-=+++⋯+-=-=---,所以21nn n S a n -=--,因为()()72n n S a n λλλ-++≥-对任意*n N ∈都成立,所以272nmaxn λ-⎛⎫≥ ⎪⎝⎭. 设272n n n c -=,则111252792222n n n nn n n nc c +++----=-=, 当4n ≤时,1n n c c +>,当5n ≥时,1n n c c +<, 因此1234567c c c c c c c <<⋯<><> 即5332c λ≥=,故λ的最小值为332. 故选:C 【点睛】本题解答的关键利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩求出数列n a 的递推公式,再利用累加法求出na 的通项;2.B解析:B 【分析】由等差数列的10a >,及202020210a a ⋅<得数列是递减的数列,因此可确定202020210,0a a ><,然后利用等差数列的性质求前n 项和,确定和n S 的正负.【详解】∵202020210a a ⋅<,∴2020a 和2021a 异号,又数列{}n a 是等差数列,首项10a >,∴{}n a 是递减的数列,202020210,0a a ><, 由202020210a a +>,所以140404040202020214040()2020()02a a S a a +==+>,14041404120214041()404102a a S a +==<,∴满足0n S >的最大自然数n 为4040. 故选:B . 【点睛】关键点睛:本题求满足0n S >的最大正整数n 的值,关键就是求出100n n S S +><,,时成立的n 的值,解题时应充分利用等差数列下标和的性质求解,属于中档题.3.B解析:B 【分析】根据等式关系得到数列{}n a 为等差数列,求出公差得到其通项公式,最后代值求解即可. 【详解】212n n n a a a ++=-(*n N ∈),212n n n a a a ++∴+=,即数列{}n a 是等差数列, 11a =-,33a =,312a a d ∴=+即312d =-+,则公差2d =,则()11223n a n n =-+-⨯=-(*n N ∈), 所以10210317a =⨯-=. 故选:B . 【点睛】关键点点睛:本题的解题关键是由题中所给关系得出其为等差数列,进而求出通项公式进行计算.4.A解析:A 【分析】直接利用等比数列的性质化简99A B ,再代入552a b =即得解. 【详解】由题得99912919285599129192855()()()2512()()()A a a a a a a a a aB b b b b b b b b b ⋅⋅⋅=====⋅⋅⋅. 故答案为A. 【点睛】(1)本题主要考查等比数列的性质,意在考查学生对该知识的掌握水平和分析推理能力.(2) 等比数列{}n a 中,如果m n p q +=+,则m n p q a a a a =,特殊地,2m p q =+时,则2·m p q a a a =,m a 是p q a a 、的等比中项. 5.C解析:C 【分析】先利用1,1,2n nn S n a S S n =⎧=⎨-≥⎩求出数列{}n a 的通项公式,于是可求出n S ,再利用参变量分离法得到1n n S S λ+<,利用数列的单调性求出数列1n n S S +⎧⎫⎨⎬⎩⎭的最小项的值,可得出实数λ的取值范围. 【详解】当1n =时,1121S a =-,即1121a a =-,得11a =;当2n ≥时,由21n n S a =-,得1121n n S a --=-,两式相减得122n n n a a a -=-,得12n n a a -=,12nn a a -∴=,所以,数列{}n a 为等比数列,且首项为1,公比为2,11122n n n a --∴=⨯=. 12122121n n n n S a -∴=-=⨯-=-,由10n n S S λ+-<,得()()11111112121112221212221n nn n n n n S S λ+++++---<===----,所以,数列1n n S S +⎧⎫⎨⎬⎩⎭单调递增,其最小项为122211213S S -==-,所以,13λ<, 因此,实数λ的取值范围是1,3⎛⎫-∞ ⎪⎝⎭,故选C .【点睛】本题考查利用数列前n 项和求数列的通项,其关系式为1,1,2n nn S n a S S n =⎧=⎨-≥⎩,其次考查了数列不等式与参数的取值范围问题,一般利用参变量分离法转化为数列的最值问题来求解,考查化归与转化问题,属于中等题.6.A解析:A 【解析】由题设可知这是一个等差数列问题,且已知13030,390a S ==,求公差d .由等差数列的知识可得30293053902d ⨯⨯+=,解之得1629d =,应选答案A . 7.A解析:A 【分析】由题意可知,直线112y a x m =+与直线0x y d +-=垂直,且直线0x y d +-=过圆心,可求得1a 和d 的值,然后利用等差数列的求和公式求得n S ,利用裂项法可求得数列1n S ⎧⎫⎨⎬⎩⎭的前10项和. 【详解】 由于直线112y a x m =+与圆()2221x y -+=的两个交点关于直线0x y d +-=对称, 则直线112y a x m =+与直线0x y d +-=垂直,直线0x y d +-=的斜率为1-,则1112a =,可得12a =,且直线0x y d +-=过圆()2221x y -+=的圆心()2,0,则20d -=,可得2d =,()()112212n a a n d n n ∴=+-=+-=,则()()()122122n n n a a n n S n n ++===+,()111111n S n n n n ∴==-++, 因此,数列1n S ⎧⎫⎨⎬⎩⎭的前10项和为1111111110112233410111111⎛⎫⎛⎫⎛⎫⎛⎫-+-+-++-=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:A. 【点睛】本题考查裂项求和,同时也考查了直线与圆的综合问题,以及等差数列求和公式的应用,考查计算能力,属于中等题.8.D解析:D 【分析】分公比是否为1进行讨论,再利用等比数列的前n 项和公式及定义求解即可. 【详解】解:设等比数列{}n a 的公比为q ,当1q =时,()1111222n S a na a n a -=-=-, 则{}12n S a -不为等比数列,舍去, 当1q ≠时,()1111111222111n n n a q a aS a a q a qq q--=-=+----, 为了符合题意,需11201a a q -=-,得12q =,故4312a q a ==. 故选D . 【点睛】本题考查等比数列的前n 项和公式,定义,考查逻辑推理能力以及运算求解能力,属于中档题.9.D解析:D 【分析】 根据11233n nn a a a T n-+++=,且3nn T =,得到112333n n n a a a n -+++=⋅,然后利用数列通项与前n 项和的关系求得21n a n =+,再利用等差数列求和公式求解. 【详解】∵11233n nn a a a T n-+++=,且3nn T =,∴112333n n n a a a n -+++=⋅,当2n ≥时,有()211213313n n n a a a n ---+++⋅=-⋅,两式相减可得:()()1113313213n n n n n a n n n ---⋅=⋅--⋅=+⋅.∴21n a n =+(2n ≥). 当1n =时,13a =适合上式. ∴21n a n =+.则数列{}n a 是以3为首项,以2为公差的等差数列. ∴()202032202012020S 202220202+⨯+⨯==⨯.∴202020222020S =. 故选:D . 【点睛】本题主要考查数列通项与前n 项和的关系以及等差数列的定义和求和公式的应用,属于中档题.10.D解析:D 【分析】由题设得到5n a a ≥恒成立,参变分离后可得实数a 的取值范围. 【详解】由题设有5n a a ≥恒成立, 故21125555a an n n -+≥-+恒成立即()()()5565a n n n n---≥, 当6n ≥时,有()56a n n ≤-恒成立,故0a ≤, 当14n ≤≤时,有()56a n n ≥-恒成立,故25a ≥-, 当5n =时,a R ∈, 故250a -≤≤. 故选:D. 【点睛】本题考查数列的函数性质:最值问题,此类问题可利用函数的单调性来研究,也可以利用恒成立来研究,本题属于较难题.11.C解析:C 【分析】根据题意得到12n n b b +=,计算得到答案. 【详解】123n n a a +-=,()1323n n a a +∴+=+,即12n n b b +=, 14b =,910422048b ∴=⨯=.故选:C . 【点睛】本题考查了根据数列的递推式求通项公式,确定12n n b b +=是解题的关键.12.A解析:A 【分析】先求出首项和公比,得出{}n a 是一个减数列,前4项都大于1,从第五项开始小于1,从而得出结论. 【详解】{}n a 为等比数列,3135327a a a a ==,32464278a a a a ==, 33a ∴=,432a =,4312a q a ∴==,112a =,543·14a a q ==<. 故{}n a 是一个减数列,前4项都大于1,从第五项开始小于1, 以n T 表示{}n a 的前n 项积,则使得n T 达到最大值的n 是4, 故选:A . 【点评】本题主要考查等比数列的性质,属于基础题.二、填空题13.【分析】利用退一作差法求得再求得根据列不等式解不等式求得的取值范围【详解】由可得:两式相减得:两式相减可得:数列是以为公差的等差数列数列是以为公差的等差数列将代入及可得:将代入可得要使得恒成立只需要解析:15,44⎛⎫⎪⎝⎭【分析】利用退一作差法求得114(3)n n a a n +--=≥,再求得234,,a a a ,根据1234a a a a <<<列不等式,解不等式求得m 的取值范围. 【详解】由2123n n S S n n ++=+可得:212(1)3(1)(2)n n S S n n n -+=-+-≥两式相减得:141(2)n n a a n n ++=+≥143(3)n n a a n n -∴+=-≥两式相减可得:114(3)n n a a n +--=≥∴数列2a ,4a ,6a ,...是以4为公差的等差数列,数列3a ,5a ,7a ,...是以4为公差的等差数列,将1n =代入2123n n S S n n ++=+及1a m =可得:252a m =-将2n =代入141(2)n n a a n n ++=+≥可得342a m =+42492a a m =+=-要使得*n N ∀∈,1n n a a +<恒成立 只需要1234a a a a <<<即可524292m m m m ∴<-<+<-解得1544m <<则m 的取值范围是15,44⎛⎫⎪⎝⎭. 故答案为:15,44⎛⎫ ⎪⎝⎭【点睛】本小题主要考查已知n S 求n a ,考查数列的单调性,属于中档题.14.【解析】数列是等比数列公比为的前项和当且仅当时取等号又或时取最大值数列最大项的值为故答案为 解析:3【解析】数列{}n a 是等比数列,公比q 2=,n S 为{}n a 的前n 项和,219()n n n n S S T n N a *+-=∈ ,2111(12)(12)9812129222n nn nn na a T a --⋅---∴==--⋅822n n +≥=, 当且仅当822nn =时取等号, 又,1n N n *∈=或2 时,n T 取最大值19243T =--= .∴ 数列{}n T 最大项的值为3 .故答案为3 .15.【分析】由题意可得为常数可得数列为等差数列求得的图象关于点对称运用等差数列中下标公式和等差中项的性质计算可得所求和【详解】解:对都有成立可令即有为常数可得数列为等差数列函数由可得的图象关于点对称可得 解析:26【分析】由题意可得11n n a a a +-=,为常数,可得数列{}n a 为等差数列,求得()f x 的图象关于点,22π⎛⎫⎪⎝⎭对称,运用等差数列中下标公式和等差中项的性质,计算可得所求和. 【详解】 解:对*,m n ∀∈N ,都有m n m n a a a ++=成立,可令1m =即有11n n a a a +-=,为常数, 可得数列{}n a 为等差数列, 函数2()sin 24cos 2xf x x =+sin 22(1cos )x x =++, 由()()()sin 221cos f x fx x x π+-=++()()()sin 221cos 4x x ππ+-++-=,可得()f x 的图象关于点,22π⎛⎫⎪⎝⎭对称,113212a a a a +=+=6872a a a π=+==,∴()()()()113212f a f a f a f a +=+=()()()6874,2f a f a f a =+==,∴可得数列{}n y 的前13项和为46226⨯+=.故答案为26. 【点睛】本题考查等差数列的性质,以及函数的对称性及运用,化简运算能力,属于中档题.16.7576【分析】根据新定义得数列是周期数列从而易求得【详解】∵成等比数列∴又为和谐递进数列∴…∴数列是周期数列周期为4∴故答案为:7576【点睛】本题考查数列新定义解题关键是由数列新定义性质得出数列解析:7576 【分析】根据新定义得数列是周期数列,从而易求得2021S . 【详解】∵1234,,,a a a a 成等比数列,121,2a a ==,∴344,8a a ==,又15a a =,{}n a 为“和谐递进数列”,∴26a a =,37a a =,48a a =,59a a =,…, ∴数列{}n a 是周期数列,周期为4. ∴2021505(1248)17576S =⨯++++=. 故答案为:7576.【点睛】本题考查数列新定义,解题关键是由数列新定义性质得出数列为周期数列,从而易得结论.17.【分析】本题先用表示再建立方程组解题即可【详解】解:∵是等比数列∴∵∴解得:故答案为:【点睛】本题考查等比数列的基本量法是基础题 解析:12【分析】本题先用1a ,q 表示2a ,5a ,再建立方程组21451412a a q a a q ==⎧⎪⎨==⎪⎩解题即可. 【详解】解:∵ {}n a 是等比数列,∴ 21a a q =,451a a q∵24a =,512a =,∴ 21451412a a q a a q ==⎧⎪⎨==⎪⎩,解得:1812a q =⎧⎪⎨=⎪⎩, 故答案为:12. 【点睛】本题考查等比数列的基本量法,是基础题.18.【分析】根据图象的规律得到前后两项的递推关系然后利用迭代法求通项并利用等比数列求和【详解】由图分析可知依次类推数列是首项为1公比为8的等比数列所以故答案为:【点睛】关键点点睛:本题的关键是迭代法求通解析:817n n a -= 【分析】根据图象的规律,得到前后两项的递推关系,然后利用迭代法求通项,并利用等比数列求和. 【详解】由图分析可知11a =,218181a a =⨯+=+,23281881a a =⨯+=++, 依次类推,1288...1n n n a --=+++,数列{}18n -是首项为1,公比为8的等比数列,所以1881187n n n a --==-, 故答案为:817n n a -=【点睛】关键点点睛:本题的关键是迭代法求通项,重点是得到前后两项的递推关系.19.【解析】所以 解析:22(1)4n n n +++-【解析】1112222n n n n n T S b a b a b a n +-=-+-++-=+-所以222(1)4n n n n n n T T S S T n n +=-++=++-20.4【分析】根据题意等价变形得对任意恒成立再求数列的最大值即可得答案【详解】解:∵∴不等式等价于记∴时即时数列单调递减又∵∴∴即∴整数的最大值为4故答案为:4【点睛】本题考查根据数列不等式恒成立求参数解析:4 【分析】根据题意等价变形得2352nn λ-->对任意*n N ∈恒成立,再求数列232nn n b -=的最大值即可得答案. 【详解】解:∵()102nn a n =+⋅>,∴不等式()2235n n n a λ--<-等价于2352nn λ-->, 记232n nn b -=,112121223462n n n n n b n n b n ++--==--, ∴3n ≥时,11n nb b +<,即3n ≥时数列单调递减, 又∵ 1211,24b b =-=, ∴ ()3max 38n b b ==, ∴358λ->,即337588λ<-=,∴整数λ的最大值为4. 故答案为:4. 【点睛】本题考查根据数列不等式恒成立求参数,考查化归转化思想,是中档题.三、解答题21.(1)21n a n =-;(2)2332n nn S +=-.【分析】(1)利用已知条件列出关于首项与公差的方程组,解方程组即得数列{}n a 的通项公式;(2)先由(1)得到n n n a 2n 122-=,再利用错位相减法求和即可. 【详解】(1)设等差数列{}n a 的公差为d ,由已知得()()121223412a a a a a a +=⎧⎨+++=⎩,即122348a a a a +=⎧⎨+=⎩,所以()()()1111428a a d a d a d ⎧++=⎪⎨+++=⎪⎩,解得112a d =⎧⎨=⎩, 所以21n a n =-. (2)由(1)得n n n a 2n 122-=, 所以1212321223212n n n n n S ---=++⋯++,① 231123212222213n n n n n S +--=++⋯⋯++,② -①②得:21111112132322222222n n n n n n S ++-+⎛⎫=+⨯+⋯+-=- ⎪⎝⎭,所以2332n nn S +=-. 【点睛】易错点睛:用错位相减法求和应注意的问题(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.22.条件选择见解析;(1)n a n =,2n n b =;(2)212222n n n n T +=-++.【分析】选①,(1)列出关于首项与公差、首项与公比的方程组,求出首项与公差、首项与公比,从而求出数列{}n a 和{}n b 的通项公式;(2)由(1)知2nn n a b n +=+,利用分组求和法,结合等差数列与等比数列的求和公式求解即可.选②,(1)列出关于首项与公差的方程组可求出数列{}n a 的通项公式,利用1n n n b S S -=-可求{}n b 的通项公式;(2)由(1)知2n n n a b n +=+,利用分组求和法,结合等差数列与等比数列的求和公式求解即可. 【详解】 选①解:(1)设等差数列{}n a 的公差为d ,1281122,10,2810,1,1a a a a d a d =+=∴+=∴==, 1(1)1n a n n ∴=+-⨯=.由题意知132452,24b b b b ⎛⎫=⋅=+⎪⎝⎭,得324522b b b =+, 设等比数列{}n b 的公比为2222,522q b q b b q ⋅=+,即22520q q -+=,解得2q,或12q =,由数列{}n b 为递增等比数列可知12q =不合题意, 所以{}n b 是一个以2为首项,2为公比的等比数列.1222n n n b -∴=⨯=(2)由(1)知2nn n a b n +=+,()()()()1231222322n n T n ∴=++++++⋯++,()123(123)2222n n T n ∴=+++⋯+++++⋯+, ()212(1)212nn n n T -+∴=+-212222n n n n T +∴=-++.选②解:(1)设等差数列{}n a 的公差为d ,1281122,10,2810,1,1a a a a d a d =+=∴+=∴==, 1(1)1n a n n ∴=+-⨯=.令1n =,则111112,42,2S b S λλλ+=+∴==+=∴=-,122n n S +∴=-当2n ≥时,()()1122222n n n n n n b S S +-=-=---=当1n =时,12b =也满足上式.2n n b =(2)由(1)知2nn n a b n +=+,()()()()1231222322n n T n ∴=++++++⋯++, ()123(123)2222n n T n ∴=+++⋯+++++⋯+, ()212(1)212nn n n T -+∴=+-212222n n n n T +∴=-++.【点睛】方法点睛:利用“分组求和法”求数列前n 项和常见类型有两种:一是通项为两个公比不相等的等比数列的和或差,可以分别用等比数列求和后再相加减;二是通项为一个等差数列和一个等比数列的和或差,可以分别用等差数列求和、等比数列求和后再相加减. 23.(1)证明见解析;(2)证明见解析. 【分析】(1)直接利用定义证明12n n b b +=即得证;(2)分析得到211321n n a -≤⋅-,再利用等比数列求和得证. 【详解】 解:(1)121n n b a n =+-,1223241n n n a a n ++-=-, 则1122123142222222141214121n n n n n n n n b a a a a b n n n n n ++++=+=++=+=+=+-+--, 又11312b a =+=, 所以数列{}n b 是等比数列; (2)由(1)得,1232322n n n b --=⋅=⋅,N n *∈, 213221n n a n -∴=⋅--,N n *∈, 211n -≥,23210n n a -∴≥⋅->,211321n n a -∴≤⋅-, 当2n ≥时,21231111111111222+23312222211112251132112n n n n n S ----⎛⎫- ⎪⎝⎭<++++=+<+=-<-++++⋅-,又11123S a ==<, 综上,3n S <,n *∈N . 【点睛】方法点睛:证明数列不等式常用的方法有:(1)比较法;(2)综合法;(3)分析法;(4)数学归纳法;(5)放缩法;(6)反证法.要根据已知条件灵活选择方法求解. 24.(1)13n n a =,12n n b +=;(2)151144323n n n n T -+=--⋅⋅ 【分析】(1)由1n =求得1a ,再風1b ,然后由11n n n a S S ++=-得到数列{}n a 的递推关系,知其为等比数列,从而得通项公式,由n b 的递推关系得1(1)n n nb n b -=+,用累乘的方法求得n b ;(2)用错位相减法求和n T . 【详解】(1)由题意知:1111221S a a a +=+=,113a =,∴11413b a =-=, ∵1121,21n n n n S a S a +++=+= ∴111333n n n n a a q a +=⇒=⇒= 又∵()[]11(1)0,0n n n n n b b nb n b b --+⋅-+=> ∴121121131(1)122n n n n n n n b b b n n n nb n b b b b b n n ----++=+⇒⋅=⋅⋅⇒=-(1b 也适合), (2)∵123n n n n a b += ∴2323413333n n n T +=++++ 231123133333n n n n T ++=++++ ∴12311111221111219313333333313n n n n n n n T -++⎛⎫- ⎪++⎝⎭=++++-=+-- 11211113633n n n -++⎛⎫=+-- ⎪⎝⎭ ∴151144323n n nn T -+=--⋅⋅. 【点睛】本题考查求等比数列的通项公式,累乘法求通项公式,错位相减法求和.数列求和的常用方法:设数列{}n a 是等差数列,{}n b 是等比数列,(1)公式法:等差数列或等比数列的求和直接应用公式求和; (2)错位相减法:数列{}n n a b 的前n 项和应用错位相减法; (3)裂项相消法;数列1{}n n ka a +(k 为常数,0n a ≠)的前n 项和用裂项相消法; (4)分组(并项)求和法:数列{}n n pa qb +用分组求和法,如果数列中的项出现正负相间等特征时可能用并项求和法;(5)倒序相加法:满足m n m a a A -+=(A 为常数)的数列,需用倒序相加法求和.25.(1)证明见解析;(2)()()235412n n nT n n +=++【分析】(1)利用等比数列的定义变形为()1121n n a a ++=+,证明数列{}1n a +是等比数列;(2)首先求数列{}n b 的通项公式,再利用裂项相消法求和. 【详解】 (1)121n n a a +=+,()1121n n a a +∴+=+,即1121n n a a ++=+,且112a +=, 所以数列{}1n a +是公比为2的等比数列;(2)由(1)可知11222n nn a -+=⋅=, 所以2log 2nn b n ==,()211111222n n b b n n n n +⎛⎫==- ⎪++⎝⎭, 则11111111111...232435112n T n n n n ⎛⎫=-+-+-++-+- ⎪-++⎝⎭111112212n n ⎛⎫=+-- ⎪++⎝⎭()()235412n n n n +=++ 【点睛】关键点点睛:本题第二问考查裂项相消法求和,这样的形式不是连续相消,如果前面剩下两个正数项,那么最后一定剩下两个负数项.26.(1)2nn a n =⋅;(2)()1122n n T n +=-⋅+;(3)12.【分析】(1)利用累乘法可求得数列{}n a 的通项公式; (2)利用错位相减法可求得数列{}n a 的前n 项和n T ;(3)令2n n n c S S =-,分析数列{}n c 的单调性,由此可求得2n n S S -的最小值. 【详解】(1)数列{}n a 满足:12a =,()*112n n n a a n N n ++⎛⎫=∈ ⎪⎝⎭, 则2140a a =>,323202a a =⨯>,,以此类推,对任意的n *∈N ,0n a >,由已知条件可得()121n n n a a n++=, 3211212223222121n n n n a a a na a n a a a n -⨯⨯=⋅⋅⋅⋅=⨯⨯⨯⨯=⋅-; (2)1231222322n n T n =⨯+⨯+⨯++⨯,()23121222122n n n T n n +=⨯+⨯++-⨯+⨯,上式-下式得()()2311121222222212212n n n n n n T n n n +++--=++++-⋅=-⋅=-⋅--,因此,()1122n n T n +=-⋅+;(3)21n n n b a n ==,则111123n S n=++++, 令2n n n c S S =-,则()()()()122122221n n n n n n n n n n c c S S S S S S S S +++++-=---=---()()11111102221121222122n n n n n n n =+-=-=>+++++++,则1n n c c +>, 则数列{}n c 为单调递增数列,所以,数列{}n c 的最小值为12112c S S =-=. 【点睛】方法点睛:数列求和的常用方法:(1)对于等差等比数列,利用公式法直接求和;(2)对于{}n n a b 型数列,其中{}n a 是等差数列,{}n b 是等比数列,利用错位相减法求和;(3)对于{}n n a b +型数列,利用分组求和法;(4)对于11n n a a +⎧⎫⎨⎬⎩⎭型数列,其中{}n a 是公差为()0d d ≠的等差数列,利用裂项相消法求和.。
【人教版】高中数学必修五期末试题(附答案)(1)

一、选择题1.若正数x,y满足21yx+=,则2xy+的最小值为()A.2 B.4 C.6 D.82.已知正数x,y满足1431x y+=+,则x y+的最小值为()A.53B.2 C.73D.63.设变量,x y、满足约束条件236y xx yy x≤⎧⎪+≥⎨⎪≥-⎩,则目标函数2z x y=+的最大值为()A.2 B.3 C.4 D.94.如图,地面四个5G中继站A、B、C、D ,已知()62kmCD=+,30ADB CDB∠=∠=︒,45DCA∠=︒,60ACB∠=︒,则A、B两个中继站的距离是()A.3km B.10km C10km D.62km 5.ABC∆的内角A,B,C的对边分别为a,b,c,已知2b=,6Bπ=,4Cπ,则ABC∆的面积为()A.223+B31C.232D316.设ABC的内角A,B,C的对边分别是a,b,c.已知2cos0b a C-=,()sin3sinA A C=+,则2bca=()A7B14C.23D67.在ABC中,角A,B,C的对边分别为a,b,c,若22tan tanB Cb c=,则ABC的形状为()A.等腰三角形或直角三角形B.等腰直角三角形C.等腰三角形D.直角三角形8.已知实数x ,y 满足2402401x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩,则2x y +的最大值为( )A .2B .8C .11D .139.数列{}n a 的前n 项和为()21n S n n =-(*n ∈N ),若173a a ka +=,则实数k 等于( ) A .2B .3C .269D.25910.已知递增的等差数列{}n a 的前n 项和为n S ,175a a ⋅=,266a a +=,对于n *∈N ,不等式1231111+++⋅⋅⋅+<nM S S S S 恒成立,则整数M 的最小值是( ) A .1B .2C .3D .411.若{}n a 是等比数列,其公比是q ,且546,,a a a -成等差数列,则q 等于( ) A .-1或2B .1或-2C .1或2D .-1或-212.在等比数列{}n a 中,若1234531a a a a a ++++=,2345662a a a a a ++++=,则通项n a 等于( ) A .12n -B .2nC .12n +D .22n -二、填空题13.已知实数x ,y 满足约束条件010x y x y x -≤⎧⎪+≤⎨⎪⎩,则23x y z +=的最大值__________.14.若x >1,y >1,且a b x y xy ==,则a +4b 的最小值为___________. 15.设ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,且3cos 2cos a C c A b ⋅=⋅+,则()tan A C -的最大值为__________.16.在ABC 中,角A ,B ,C 的对边a ,b ,c 为三个连续自然数,且2C A =,则a =_______.17.如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个观测点,C D ,测得15BCD ︒∠=,30CBD ︒∠=,152m CD =,并在C 处测得塔顶A 的仰角为45︒,则塔高AB =______m .18.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若4a =,2c =,60B =︒,则b = ,C = .19.数列{}n a 中,已知22a =,21n n n a a a ++=+,若834a =,则数列{}n a 的前6项和为______.20.在数列{}n a 中,11a =()*1n =∈N ;等比数列{}n b 的前n 项和为2n n S m =-.当n *∈N 时,使得n n b a λ≥恒成立的实数λ的最小值是_________.三、解答题21.已知函数()()()23f x x a x =-+. (1)当72a >-时,解关于x 的不等式()46f x x >+; (2)若关于x 的方程()80f x +=在(–),1∞上有两个不相等实根,求实数a 的取值范围. 22.已知0a >,0b >.(1)求证:()2232a b b a b +≥+;(2)若2a b ab +=,求ab 的最小值.23.在ABC 中a ,b ,c 分别为内角A ,B ,C 所对的边,若()()2sin 2sin sin 2sin sin a A B C b C B c =+++.(1)求A 的大小; (2)求sin sin B C +的最大值.24.ABC 是等边三角形,点D 在边AC 的延长线上,且AD =3CD ,BD,求AD 的值和sin ∠ABD 的值25.在①数列{}n a 为递增的等比数列,且2312a a +=,②数列{}n a 满足122n n S S +-=,③数列{}n a 满足1121222n n n n a a a na -++++=这三个条件中任选一个,补充在下面问题中,再完成解答.问题:设数列{}n a 的前n 项和为n S ,12a =,__________. (1)求数列{}n a 的通项公式; (2)设2221log log n n n b a a +=⋅,求数列{}n b 的前n 项和n T .26.已知等比数列{}n a 的公比3q =,并且满足2a ,318a +,4a 成等差数列. (1)求数列{}n a 的通项公式; (2)设数列{}n b 满足31log n n nb a a =+,记n S 为数列{}n b 的前n 项和,求使2220n S n ->成立的正整数n 的最小值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】 由21y x +=,对2x y +乘以21y x+=,构造均值不等式求最值 .【详解】22242248x y x xy y x y xy ⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪⎝⎭⎝⎭,当且仅当421xy xy y x⎧=⎪⎪⎨⎪+=⎪⎩,即412x y =⎧⎪⎨=⎪⎩时,等号成立,∴min28x y ⎛⎫+= ⎪⎝⎭.故选:D 【点睛】利用基本不等式求最值时,要注意其必须满足的三个条件:“一正、二定、三相等” (1) “一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.如果等号成立的条件满足不了,说明函数在对应区间单调,可以利用单调性求最值或值域.2.B解析:B 【分析】化简114[(1)]()131x y x y x y +=++⨯+-+,再利用基本不等式求解. 【详解】由题得1114(1)1[(1)]31[(1)]()1331x y x y x y x y x y +=++-=++⨯-=++⨯+-+ 1141(5)1(5)123131y x x y y +=++-≥+-=++ 当且仅当1x y ==时取等.所以x y +的最小值为2. 故选:B 【点睛】方法点睛:利用基本不等式求最值时,常用到常量代换,即把所求代数式中的某一常量换成已知中的代数式,再利用基本不等式求解.3.D解析:D 【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域,如图,画出可行域ABC ∆,(2,0)A ,(1,1)B ,(3,3)C , 平移直线2z x y =+,由图可知,直线2z x y =+经过(3,3)C 时 目标函数2z x y =+有最大值,2z x y =+的最大值为9.故选D. 【点睛】本题主要考查线性规划中,利用可行域求目标函数的最值,属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.4.C解析:C 【分析】由正弦定理得求得AC 、BC 长,再由余弦定理得AB 长可得答案. 【详解】由题意可得75DAC ∠=︒,45DBC ∠=︒, 在ADC 中,由正弦定理得()362sin 223sin sin 75CD ADCAC DAC+⨯⋅∠===∠︒, 在BDC 中,由正弦定理得()162sin 231sin 22CD BDC BC DBC+⨯⋅∠===+∠,在ACB △中,由余弦定理得2222cos AB AC BC AC BC ACB =+-⨯⨯⋅∠()()()22123312233112=++-⨯⨯+⨯=,所以10km AB =. 故选:C. 【点睛】本题考查了正弦定理、余弦定理解三角形的应用.5.B解析:B 【解析】试题分析:根据正弦定理,,解得,,并且,所以考点:1.正弦定理;2.面积公式.6.D解析:D 【分析】根据正弦定理把角化边,可得3a b =,进一步得到2cos 3C =,然后根据余弦定理,可得6c b =,最后可得结果.【详解】 在ABC ∆中,sin sin a b A B=,由()sin 3sin()3sin 3sin A A C B B π=+=-=,所以3a b =①,又2cos 0b a C -=②,由①②可知:2cos 3C =,又2222cos 23a b c C ab +-==③,把①代入③化简可得:c =,则()2293bc b a b ==, 故选:D. 【点睛】本题考查正弦定理、余弦定理的综合应用,难点在于将c 用b 表示,当没有具体数据时,可以联想到使用一个参数表示另外两个参数,属于中档题.7.A解析:A 【分析】由三角函数恒等变换的应用,正弦定理化简已知等式可得sin 2sin 2B C =,可得22B C =,或22B C π+=,解得B C =,或2B C π+=,即可判断ABC ∆的形状.【详解】22tan tan B Cb c =, ∴22sin sin cos cos B C b B c C =,由正弦定理可得:22cos cos b cb Bc C=,可得:cos cos b B c C =,可得sin cos sin cos B B C C =,可得:sin 2sin 2B C =,22B C ∴=,或22B C π+=,B C ∴=,或2B C π+=,ABC ∆∴的形状为等腰三角形或直角三角形. 故选:A . 【点睛】本题主要考查了三角函数恒等变换的应用,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.8.C解析:C 【分析】根据条件作出可行域,根据图形可得出答案. 【详解】由实数x ,y 满足2402401x y x y y -+≥⎧⎪+-≤⎨⎪≥-⎩,作出可行域,如图.设2z x y =+,则化为2y x z =-+ 所以z 表示直线2y x z =-+在y 轴上的截距.2401x y y -+=⎧⎨=-⎩可得()6,1A --,2401x y y +-=⎧⎨=-⎩可得()61B -, 根据图形可得,当直线2y x z =-+过点()61B -,时截距最大, 所以2z x y =+的最大值为11. 故选:C【点睛】方法点睛:解决线性规划问题的实质是把代数问题几何化,即数形结合思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意让其斜率与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大值或最小值会在可行域的端点或边界上取得.9.C解析:C 【分析】由已知结合递推公式可求n a ,然后结合等差数列的通项公式即可求解. 【详解】因为()21n S n n =-, 所以111a S ==,当2n ≥时,()()()12112343n n n a S S n n n n n -=-=----=-,111a S ==适合上式,故43n a n =-,因为173a a ka +=, ∴1259k +=, 解可得269k = 故选:C. 【点睛】本题主要考查了由数列前n 项和求数列的通项公式,考查来了运算能力,属于中档题.10.C解析:C 【分析】先求出等差数列的1a 和d ,由等差数列前n 项和公式得n S ,把1nS 拆成两项的差,用裂项相消法求得和12111nS S S +++,在n 变化时,求得M 的范围,得出结论. 【详解】∵{}n a 是等差数列,∴17266a a a a +=+=,由171765a a a a +=⎧⎨=⎩解得1715a a =⎧⎨=⎩或1751a a =⎧⎨=⎩,又{}n a 是递增数列,∴1715a a =⎧⎨=⎩,715127163a a d --===-, 1(1)(1)(2)233n n n n n n n S na d n --+=+=+=, 121113331324(2)n S S S n n +++=+++⨯⨯+3111111112324112n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+- ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦31119311122124212n n n n ⎛⎫⎛⎫=+--=-+ ⎪ ⎪++++⎝⎭⎝⎭94<, 由不等式1231111+++⋅⋅⋅+<n M S S S S 恒成立,得94M ≥,∴最小的整数3M =. 故选:C . 【点睛】本题考查不等式恒成立问题,考查等差数列的性质,等差数列的通项公式和前n 项和公式,裂项相消法求和,本题属于中档题.11.A解析:A 【解析】分析:由546,,a a a -成等差数列可得5642a a a -+=,化简可得()()120q q +-=,解方程求得q 的值. 详解:546,,a a a -成等差数列,所以5642a a a -+=,24442a q a q a ∴-+=,220q q ∴--=,()()120q q ∴+-=,1q ∴=-或2,故选A.点睛:本题考查等差数列的性质,等比数列的通项公式基本量运算,属于简单题. 等比数列基本量的运算是等比数列的一类基本题型,数列中的五个基本量1,,,,,n n a q n a S ,一般可以“知二求三”,通过列方程组所求问题可以迎刃而解,解决此类问题的关键是熟练掌握等比数列的有关性质和公式,并灵活应用.12.A解析:A 【详解】设等比数列{a n }的公比为q ,∵a 1+a 2+a 3+a 4+a 5=31,a 2+a 3+a 4+a 5+a 6=62, ∴q=2,∴a1(1+q+q 2+q 3+q 4)=31, 则a 1=1, 故an=2n−1. 故选A.二、填空题13.【分析】先作出不等式组对应的可行域再通过数形结合求出的最大值即得解【详解】由题得不等式组对应的可行域是如图所示的阴影三角形区域设它表示斜率为纵截距为的直线系要求的最大值即求的最大值当直线经过点时直线 解析:9【分析】先作出不等式组对应的可行域,再通过数形结合求出2x y +的最大值即得解. 【详解】由题得不等式组对应的可行域是如图所示的阴影三角形区域,设12,22m m x y y x =+∴=-+,它表示斜率为12-,纵截距为2m的直线系, 要求23x y z +=的最大值即求m 的最大值.当直线122m y x =-+经过点(0,1)A 时,直线的纵截距2m最大,m 最大. 此时max 022m =+=, 所以23x y z +=的最大值为239=.故答案为:9 【点睛】方法点睛:线性规划问题一般用图解法,其步骤如下: (1)根据题意,设出变量,x y ; (2)列出线性约束条件;(3)确定线性目标函数(,)z f x y =;(4)画出可行域(即各约束条件所示区域的公共区域); (5)利用线性目标函数作平行直线系()(y f x z =为参数);(6)观察图形,找到直线()(y f x z =为参数)在可行域上使z 取得欲求最值的位置,以确定最优解,给出答案。
【苏科版】高中数学必修五期末试题(带答案)(1)
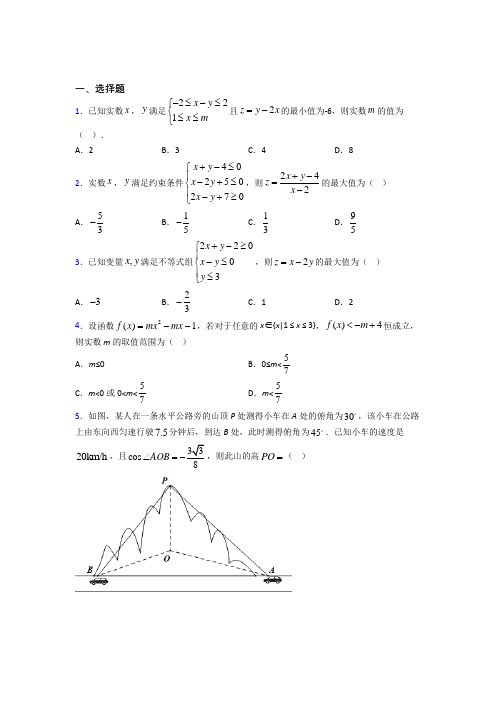
一、选择题1.已知实数x,y满足221x yx m-≤-≤⎧⎨≤≤⎩且2z y x=-的最小值为-6,则实数m的值为().A.2 B.3 C.4 D.82.实数x,y满足约束条件40250270x yx yx y+-≤⎧⎪-+≤⎨⎪-+≥⎩,则242x yzx+-=-的最大值为()A.53-B.15-C.13D.953.已知变量,x y满足不等式组2203x yx yy+-≥⎧⎪-≤⎨⎪≤⎩,则2z x y=-的最大值为()A.3-B.23-C.1 D.24.设函数2()1f x mx mx=--,若对于任意的x∈{x|1 ≤ x ≤ 3},()4f x m<-+恒成立,则实数m的取值范围为()A.m≤0B.0≤m<57C.m<0或0<m<57D.m<575.如图,某人在一条水平公路旁的山顶P处测得小车在A处的俯角为30,该小车在公路上由东向西匀速行驶7.5分钟后,到达B处,此时测得俯角为45.已知小车的速度是20km/h,且33cos AOB∠=-,则此山的高PO=()A .1 kmBCD6.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知2b =,6B π=,4Cπ,则ABC ∆的面积为( ) A.2+B1C.2D17.已知ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,2sin sin sin B A C =,1a cc a+=+,则B = ( ) A .56π B .6π C .3π D .2π 8.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若cos a C ,cos b B ,cos c A 成等差数列,且8a c +=,则AC 边上中线长的最小值是( )A .2B .4C.D.9.已知函数()()f x x R ∈满足()()42f x f x -++=,若函数2xy x =-与()y f x =图象的交点为()()()1122,,,,,,n n x y x y x y ⋯,则()1nii i xy =+=∑( )A .0B .nC .2nD .3n10.已知函数()()31f x x x =-+,数列{}n a 中各项互不相等,记()()()12n n S f a f a f a =+++,给出两个命题:①若等差数列{}n a 满足55S =,则33a =;②若正项等比数列{}n a 满足33S =,则21a <;其中( )A .①是假命题,②是真命题B .①是真命题,②是假命题C .①②都是假命题D .①②都是真命题11.等差数列{}n a 中,10a >,310S S =,则当n S 取最大值时,n 的值为 ( ) A .6B .7C .6或7D .不存在12.已知数列{}n a 满足123n n a a +-=,11a =,3n n b a =+,则10b =( ) A .92B .103C .2048D .1024二、填空题13.正实数,x y 满足1x y +=,则12y x y++的最小值为________. 14.已知实数,x y 满足102801x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩,则3yx +的最大值为_______.15.ABC 中,D 是边BC 上的点,满足90BAD ∠=︒,30DAC ∠=︒,4BD CD =.则sin sin BC=______. 16.设角,,A B C 是ABC ∆的三个内角,已知向量()sin sin ,sin sin m A C B A =+-,()sin sin ,sin n A C B =-,且m n ⊥.则角C 的大小为_____________.17.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,①若sin A >sin B ,则A >B ;②若sin2A =sin2B ,则△ABC 一定为等腰三角形;③若222cos cos cos 1A B C +-=,则△ABC 为直角三角形;④若△ABC 为锐角三角形,则sin A <cos B .以上结论中正确的有____________.(填正确结论的序号)18.已知点(3,A ,O 是坐标原点,点(),P x y的坐标满足0200y x y -≤+≥⎨⎪≥⎪⎩,设z 为OA 在OP 上的投影,则z 的取值范围是__________.19.已知111,2n n a a a +==,若(1)n n n b a n =+-⋅,则数列{}n b 的前10项的和10S =______.20.已知等比数列{a n }的前n 项和为S n ,且133,12n n a S a λ++==,则实数λ的值为_____三、解答题21.已知定义域为R 的函数()22x xb n f x b +=--是奇函数,且指数函数xy b =的图象过点(2,4).(Ⅰ)求()f x 的表达式;(Ⅱ)若方程()23()0f x x f a x ++-+=,(4,)x ∈-+∞恰有2个互异的实数根,求实数a 的取值集合;(Ⅲ)若对任意的[1,1]t ∈-,不等式()22(1)0f t a f at -+-≥恒成立,求实数a 的取值范围.22.已知关于x 的不等式23240x ax -++>. (1)当2a =时,求此不等式的解集;(2)若此不等式的解集为()4,m -,求实数a ,m 的值.23.在①tan 2tan B C =,②22312b a -=,③cos 2cos b C c B =三个条件中任选一个,补充在下面问题中的横线上,并解决该问题.问题:已知ABC ∆的内角,,A B C 及其对边,,a b c ,若2c =,且满足___________.求ABC ∆的面积的最大值(注:如果选择多个条件分别解答,按第一个解答计分)24.在△ABC 中,A =60°,sin B =12,a =3,求三角形中其他边与角的大小. 25.已知等差数列{}n a 的前n 项和为n S ,35a =,636S =.(1)求数列{}n a 的通项公式; (2)记m b 为2log k 在区间(]()*0,m a m N∈中正整数k 的个数,求数列{}mb 的前m 项和.26.在①2na n nb a =⋅,②10nn b a =-,③21n n n b a a +=这三个条件中任选一个,补充在下面问题中,并完成问题的解答.问题:已知数列{}n a 是各项均为正数的等差数列,22a =,且11a +、4a 、8a 成等比数列. (1)求数列{}n a 的通项公式;(2)记_____________,求数列{}n b 的前n 项和n S .【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】 作出不等式组221x y x m-≤-≤⎧⎨≤≤⎩对应的区域,利用数形结合平移直线即可得到结论 .【详解】由题意可作图:当2z y x =-经过点P 时,z 取最小值6, 此时P 符合:2x my x =⎧⎨=-⎩,即(,2)P m m -代入2z y x =-得:m -2-2m =-6,解得m =4 故选:C 【点睛】简单线性规划问题的解题步骤: (1)画出可行域;(2)作出目标函数所表示的某条直线(通常选作过原点的直线),移动此直线并观察此直线经过可行域的哪个(些)点时,函数有最大(小)值; (3)求(写)出最优解和相应的最大(小)值; (4)下结论.2.D解析:D 【分析】首先画出可行域,变形24222x y y z x x +-==+--,利用2yx -的几何意义求z 的最大值.【详解】24222x y yz x x +-==+--设2ym x =-,m 表示可行域内的点和()2,0D 连线的斜率, 4250x y x y +=⎧⎨-+=⎩,解得:1,3x y ==,即()1,3C , 250270x y x y -+=⎧⎨-+=⎩ ,解得:3,1x y =-=,即()3,1B -, 如图,101325BD k -==---,30312CD k -==--,所以m 的取值范围是13,5⎡⎤--⎢⎥⎣⎦,即z 的取值范围是91,5⎡⎤-⎢⎥⎣⎦,z 的最大值是95.故选:D 【点睛】关键点点睛:本题的关键是变形242x y z x +-=-,并理解z 的几何意义,利用数形结合分析问题.3.B解析:B 【分析】画出不等式组表示的区域,将目标函数2z x y =-转化为22x zy =-,表示斜率为12截距为2z-平行直线系,当截距最小时,z 取最大值,由图即可求解. 【详解】解:画出不等式组表示的区域,如图中阴影部分所示:故将目标函数2z x y =-转化为22x z y =-, 表示斜率为12截距为2z -平行直线系, 所以当截距最小时,z 取最大值,由图可知,使得直线22x zy =-经过可行域且截距最小时的解为22,33C ⎛⎫ ⎪⎝⎭, 此时242333max z =-=-. 故选:B 【点睛】本题考查了线性规划的应用,注意将目标函数化成斜截式,从而由截距的最值确定目标函数的最值.4.D解析:D 【分析】将()4f x m <-+恒成立转化为g (x ) = mx 2-mx +m -5 < 0恒成立,分类讨论m 并利用一元二次不等式的解法,求m 的范围 【详解】若对于任意的x ∈{x |1 ≤ x ≤ 3},()4f x m <-+恒成立 即可知:mx 2-mx +m -5 < 0在x ∈{x |1 ≤ x ≤ 3}上恒成立 令g (x )=mx 2-mx +m -5,对称轴为12x = 当m =0时,-5 < 0恒成立当m < 0时,有g (x )开口向下且在[1,3]上单调递减∴在[1,3]上max ()(1)50g x g m ==-<,得m < 5,故有m < 0 当m >0时,有g (x ) 开口向上且在[1,3]上单调递增 ∴在[1,3]上max ()(3)750g x g m ==-<,得507m << 综上,实数m 的取值范围为57m < 故选:D 【点睛】本题考查了一元二次不等式的应用,将不等式恒成立等价转化为一元二次不等式在某一区间内恒成立问题,结合一元二次不等式解法,应用分类讨论的思想求参数范围5.A解析:A 【分析】由题意作图可得60APO ∠=,45BPO ∠=,设PO h =,在Rt POA △,Rt POB 中 求出3AO h =,BO h =,在AOB 中,由余弦定理列方程即可求解.【详解】由题意可知:PO ⊥平面AOB ,903060APO ∠=-=,904545BPO ∠=-=,7.520 2.560AB =⨯=km , 设PO h =,在POA 中,tan AO APO PO ∠=,tan 60AOh=,所以3AO h =, 在POB 中,tan BO BPO PO ∠=,tan 45BOh=,所以BO h =, 在AOB 中,由余弦定理可得:2222cos AB AO BO AO A BO OB =∠+-⨯, 所以()2222.532333h h h h =+-⨯⎛⎫- ⎪ ⎝⎭⨯⎪,即2252544h =,解得:1h =, 所以山的高1PO =, 故选:A.6.B解析:B 【解析】试题分析:根据正弦定理,,解得,,并且,所以考点:1.正弦定理;2.面积公式.7.B解析:B 【分析】根据正弦定理,边角互化可得2b ac =,再根据2221a c a c b c a ac+-+-=,利用余弦定理求角.【详解】∵2sin sin sin B A C =,∴21b ac=,∴2221a c a c b c a ac+-+-==∴cos B =,又()0,πB ∈∴6B π=.故选:B . 【点睛】本题考查正弦定理和余弦定理解不等式,重点考查转化的思想,计算能力,属于基础题型.8.C解析:C 【分析】根据等差中项的性质,结合正弦定理化简可得3B π=,设AC 中点为D ,再利用平面向量的线性运算可得1||||2BD BA BC =+,再平方利用基本不等式求解即可. 【详解】cos a C ,cos b B ,cos c A 成等差数列,2cos cos cos b B a C c A ∴=+,根据正弦定理有2sin cos sin cos sin cos sin()B B A C C A A C =+=+,2sin cos sin B B B ∴=,又sin 0B ≠,1cos 2B ∴=,可得3B π=,设AC 中点为D ,则AC 边上中线长为1||||2BD BA BC =+, 平方可得()()2222221112()444BD BA BC BA BC c a ac a c ac ⎡⎤=++⋅=++=+-⎣⎦ 2221()3()()124416a c a c a c ⎡⎤+≥+-=+=⎢⎥⎣⎦, 当且仅当4a c ==时取等号,故2BD 的最小值为12,即AC 边上中线长的最小值为 故选:C. 【点睛】本题主要考查了正弦定理边角互化的运用,同时也考查了利用基本不等式求最值的问题,同时在处理三角形中线的时候可以用平面向量表示从而简化计算,属于中档题.9.D解析:D 【分析】由题意可得()()f x x R ∈的图像关于点()2,1对称,函数2xy x =-的图像也关于()2,1对称,然后利用对称性以及倒序相加法即可得出答案. 【详解】函数()()f x x R ∈满足()()42f x f x -++=,∴()f x 的图像关于点()2,1对称,而函数2xy x =-的图像也关于()2,1对称, 设123n x x x x >>>>121224n n x x x x -∴+=+==⨯= 121212n n y y y y -+=+==⨯=令121nin i xx x x ==++∑,则111ni n n i x x x x -==++∑,()()()1211124ni n n n i x x x x x x x n -==++++∴+=∑,12ni i x n =∴=∑令121nin i y y yy ==++∑,则111ni n n i y y y y -==++∑,()()()1211122n i n n n i y y y n y y y y -=∴=+++++=∑,1ni i n y =∴=∑()13ni i i x y n =+=∴∑,故选:D 【点睛】本题考查了函数的对称性应用,考查了倒序相加法求和,解题的关键是找出中心对称点,属于中档题.10.A解析:A 【分析】先确定函数()f x 对称性与单调性,再结合等差数列的等距性确定3a ;结合基本不等式将等比数列性质转化到等差数列性质上,解不等式即得结果. 【详解】因为()()()3311(1)1f x x x x x =-+=-+-+,而3y x x =+关于原点对称且在R 上单调递增,所以()f x 关于(1,1)对称且在R 上单调递增, 先证明下面结论:若()g x 为奇函数且在R 上单调递增,{}n a 为等差数列,123g()()()()0n a g a g a g a ++++=,则1230n a a a a ++++=.证明:若1230n a a a a ++++>, 则当n 为偶数时,1211220n n n n a a a a a a -++=+==+> 111()()()()+()0n n n n a a g a g a g a g a g a >-∴>-=-∴>同理21+122()()0,,()+()0n n n g a g a g a g a -+>>,即123g()()()()0n a g a g a g a ++++>与题意矛盾, 当n 为奇数时,1211220n n n a a a a a -++=+==> 类似可得12112()()0,()(),,()0n n n g a g a g a g a g a -++>+>, 即123g()()()()0n a g a g a g a ++++>,与题意矛盾 同理可证1230n a a a a ++++<也不成立,因此1230n a a a a ++++= 再引申结论: 若()f x 为关于(,)a b 函数且在R 上单调递增,{}n a 为等差数列,123()()()()n f a f a f a f a nb ++++=,则123n a a a a na ++++=证明过程只需令()()g x f x a b =+-,再利用上面结论即得.①若等差数列{}n a 满足55S =,即 12345()()()()()5f a f a f a f a f a ++++=,则123453555a a a a a a ++++=∴=, 31a ∴=,故①是假命题,②若正项等比数列{}n a 满足33S =, 即123()()()3f a f a f a ++=因为数列{}n a 中各项互不相等,所以公比不为1,不妨设公比大于1,即123123()()()a a a f a f a f a <<∴<<,因为1322a a a +>=∴2()1f a <,()3222111a a a -+<∴<故②是真命题故选:A【点睛】本题考查函数()f x 对称性与单调性、等差数列性质、基本不等式应用,考查综合分析判断能力,属中档题.11.C解析:C【解析】设等差数列{}n a 的公差为d∵310S S =∴()()113319913922a d a d ⨯-⨯-+=+∴160a d +=∴70a =∵10a >∴当n S 取最大值时,n 的值为6或7故选C12.C解析:C【分析】根据题意得到12n n b b +=,计算得到答案.【详解】123n n a a +-=,()1323n n a a +∴+=+,即12n n b b +=,14b =,910422048b ∴=⨯=.故选:C .【点睛】本题考查了根据数列的递推式求通项公式,确定12n n b b +=是解题的关键.二、填空题13.【分析】根据题中条件由展开后利用基本不等式即可求出结果【详解】因为正实数xy 满足所以当且仅当即时等号成立故答案为:【点睛】易错点睛:利用基本不等式求最值时要注意其必须满足的三个条件:(1)一正二定三 解析:7【分析】 根据题中条件,由1222()2212y x y x y y x x y x y x y++++=+=+++,展开后,利用基本不等式,即可求出结果.【详解】因为正实数x ,y 满足1x y +=,所以1222()221237y x y x y y x x y x y x y ++++=+=+++≥+=, 当且仅当y x x y =,即1212x y ⎧=⎪⎪⎨⎪=⎪⎩时,等号成立. 故答案为:7.【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.14.【分析】根据约束条件画出可行域目标函数可以看成是可行域内的点和的连线的斜率从而找到最大值时的最优解得到最大值【详解】根据约束条件可以画出可行域如下图阴影部分所示目标函数可以看成是可行域内的点和的连线 解析:78【分析】根据约束条件,画出可行域,目标函数可以看成是可行域内的点(),x y 和()3,0-的连线的斜率,从而找到最大值时的最优解,得到最大值.【详解】根据约束条件102801x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩可以画出可行域,如下图阴影部分所示, 目标函数3y x +可以看成是可行域内的点(),x y 和()3,0-的连线的斜率, 因此可得,当在点A 时,斜率最大 联立2801x y x +-=⎧⎨=⎩,得172x y =⎧⎪⎨=⎪⎩即71,2A ⎛⎫⎪⎝⎭所以此时斜率为 ()7072138-=--, 故答案为78.【点睛】本题考查简单线性规划问题,求目标函数为分式的形式,关键是要对分式形式的转化,属于中档题.15.【分析】直接利用三角形的面积建立等量关系进一步利用正弦定理的应用求出结果【详解】解:中D 是边上的点满足所以又因为则则故答案为:【点睛】本题考查了正弦定理三角形面积计算公式及其性质考查了推理能力与计算 解析:12 【分析】 直接利用三角形的面积建立等量关系,进一步利用正弦定理的应用求出结果. 【详解】 解:ABC中,D 是边BC 上的点,满足90BAD ∠=︒,30DAC ∠=︒,4BD CD =,所以1sin 90221sin 302ABD ACD AB AD S AB S ACAC AD ⋅︒==⋅⋅︒△△, 又因为4ABD ACD S BD S CD ==△△,则24AB BD AC CD==, 则sin 1sin 2B AC C AB ==. 故答案为:12.【点睛】本题考查了正弦定理、三角形面积计算公式及其性质,考查了推理能力与计算能力,属于中档题.16.【分析】先利用得到三角正弦之间的关系再根据正余弦定理求出即得角【详解】因为且所以即根据正弦定理得故根据余弦定理知又因为得故答案为:【点睛】本题考查了向量垂直的坐标运算和正余弦定理的应用是常考的综合题 解析:3π【分析】先利用0m n ⋅=得到三角正弦之间的关系,再根据正、余弦定理求出cos C ,即得角C .【详解】因为()sin sin ,sin sin m A C B A =+-,()sin sin ,sin n A C B =-,且m n ⊥ 所以()()()sin sin sin sin sin sin sin 0m n A C A C B A B ⋅=+-+-=即222sin sin sin sin sin A B C A B +-=根据正弦定理得222a b c ab +-= 故根据余弦定理知222cos 122a b c C ab +-==,又因为()0,C π∈ 得3C π= 故答案为:3π. 【点睛】本题考查了向量垂直的坐标运算和正余弦定理的应用,是常考的综合题,属于中档题. 17.①③【分析】结合三角形的性质三角函数的性质及正弦定理对四个结论逐个分析可选出答案【详解】对于①由正弦定理所以由sinA >sinB 可推出则即①正确;对于②取则而△ABC 不是等腰三角形即②错误;对于③则 解析:①③【分析】结合三角形的性质、三角函数的性质及正弦定理,对四个结论逐个分析可选出答案.【详解】对于①,由正弦定理sin sin a b A B =,所以由sin A >sin B ,可推出a b >,则A B >,即①正确;对于②,取15,75A B ︒︒==,则sin 2sin 2A B =,而△ABC 不是等腰三角形,即②错误;对于③,()()()222222cos cos cos 1sin 1sin 1sin 1A B C A B C +-=-+---=, 则222sin sin sin A B C +=,由正弦定理可得222+=a b c ,故△ABC 为直角三角形,即③正确;对于④,若△ABC 为锐角三角形,取80,40A B ︒︒==,此时sin80cos40sin50︒︒︒>=,即sin cos A B >,故④错误.故答案为:①③.【点睛】本题考查真假命题的判断,考查三角函数、解三角形知识,考查学生推理能力与计算求解能力,属于中档题.18.【分析】作出可行域根据投影的定义得数形结合求出的取值范围即求z 的取值范围【详解】作出可行域如图所示∴当时;当时的取值范围是故答案为:【点睛】本题考查简单的线性规划和向量的投影属于中档题解析:[]3,3-【分析】作出可行域.根据投影的定义得23cos z AOP =∠,数形结合求出AOP ∠的取值范围,即求z 的取值范围.【详解】作出可行域,如图所示cos 3OA OPz OA AOP AOP OP ⋅==⋅∠=∠.5,66AOP ππ⎡⎤∠∈⎢⎥⎣⎦,∴当6AOP π∠=时,max 2336z π==;当56AOP π∠=时,min 52336z π==-,z ∴的取值范围是[]3,3-. 故答案为:[]3,3-.【点睛】本题考查简单的线性规划和向量的投影,属于中档题. 19.1028【分析】由题可知为等比数列求出的通项公式即可写出的通项公式利用分组求和法即可求出前10项和【详解】是首项为1公比为2的等比数列则故答案为:1028【点睛】本题考查等比数列的判断以及通项公式的解析:1028【分析】由题可知{}n a 为等比数列,求出{}n a 的通项公式,即可写出{}n b 的通项公式,利用分组求和法即可求出前10项和.【详解】111,2n n a a a +==,{}n a ∴是首项为1,公比为2的等比数列,11122n n n a --∴=⨯=,121n n nb n , 则910124212310S 1011251102812. 故答案为:1028.【点睛】 本题考查等比数列的判断以及通项公式的求法,考查分组求和法求数列的前n 项和,属于基础题.20.【分析】首先利用与的关系式得到求得公比首项和第二项再通过赋值求的值【详解】当时两式相减得即并且数列是等比数列所以当时解得故答案为:【点睛】关键点点睛:本题的关键是利用数列和的关系式求数列的通项解析:34- 【分析】首先利用1n a +与n S 的关系式,得到14n n a a +=,求得公比,首项和第二项,再通过赋值2n =求λ的值.【详解】当2n ≥时,1133n n nn a S a S λλ+-+=⎧⎨+=⎩,两式相减得()1133n n n n n a a S S a +--=-=, 即14n n a a +=,并且数列{}n a 是等比数列,所以4q =,312a =,2133,4a a ∴==, 当2n =时,()321233a S a a λ+==+, 解得34λ=-. 故答案为:34-【点睛】 关键点点睛:本题的关键是利用数列n a 和n S 的关系式,求数列的通项.三、解答题21.(Ⅰ)121()22x x f x +-+=+;(Ⅱ){}40a a -<<;(Ⅲ){}0a a ≥. 【分析】(Ⅰ)先利用已知条件得到b 的值,再利用奇函数得到()00f =,进而得到n 的值,经检验即可得出结果;(Ⅱ)先利用指数函数的单调性判断()f x 的单调性,再利用奇偶性和单调性得到23x x a x +=-,把23x x a x +=-在(4,)x ∈-+∞恰有2个互异的实数根转化为()24f x x x a =+-在(4,)x ∈-+∞恰与x 轴有两个交点,求解即可;(Ⅲ)先利用函数()f x 为R 上的减函数且为奇函数,得到221t a at -≤-,把问题转化为2210t at a +--≤对任意的[1,1]t ∈-恒成立,令()221g t t at a =+--,利用二次函数的图像特点求解即可.【详解】(Ⅰ)由指数函数x y b =的图象过点(2,4),得2b =, 所以2()222x x n f x +=-⋅-, 又()f x 为R 上的奇函数,所以()00f =,得1n =-,经检验,当1n =-时,符合()()f x f x -=-, 所以121()22x x f x +-+=+; (Ⅱ)12111()22221x x x f x +-+==-+++, 因为21x y =+在定义域内单调递增, 则121x y =+在定义域内单调递减, 所以()f x 在定义域内单调递增减,由于()f x 为R 上的奇函数,所以由()23()0f x x f a x ++-+=,可得()()23()f x x f a x f a x +=--+=-, 则23x x a x +=-在(4,)x ∈-+∞恰有2个互异的实数根,即()24f x x x a =+-在(4,)x ∈-+∞恰与x 轴有两个交点, 则()()4000440204f a a a f a ⎧-><⎧⎪⎪∆>⇒>-⇒-<<⎨⎨⎪⎪-<>-⎩⎩, 所以实数a 的取值集合为{}40a a -<<.(Ⅲ)由(Ⅱ)知函数()f x 为R 上的减函数且为奇函数, 由()22(1)0f t a f at -+-≥, 得()()221f t a f at -≥-,所以221t a at -≤-,即2210t at a +--≤对任意的[1,1]t ∈-恒成立,令()221g t t at a =+--, 由题意()()1010g g ⎧-≤⎪⎨≤⎪⎩, 得0a ≥,所以实数a 的取值范围为:{}0a a ≥.【点睛】关键点睛:利用函数的奇偶性求解析式,(Ⅱ)把问题转化为()24f x x x a =+-在(4,)x ∈-+∞恰与x 轴有两个交点的问题;(Ⅲ)把问题转化为2210t at a +--≤对任意的[1,1]t ∈-恒成立是解决本题的关键.22.(1)223x x ⎧⎫-<<⎨⎬⎩⎭;(2)13m =,112a =-. 【分析】(1)当2a =时,不等式为23440x x -++>,即23440x x --<,利用一元二次不等式求解.(2)根据不等式的解集为()4,m -,则由4-,m 为方程23240x ax -++=的两根求解.【详解】(1)当2a =时,不等式为23440x x -++>,所以23440x x --<, 所以()23203x x ⎛⎫+-< ⎪⎝⎭, 解得223x -<<,所以不等式23440x x -++>的解集为223x x ⎧⎫-<<⎨⎬⎩⎭; (2)由已知得4-,m 为方程23240x ax -++=的两根, 则有243a m -+=--且443m -=-, 解得13m =,112a =-. 【点睛】 本题主要考查一元二次不等式的解法以及一元二次不等式与一元二次方程的关系,属于中档题.23.条件选择见解析;最大值为3.【分析】分别选择条件①②③,利用正弦定理和余弦定理,化简得到22312b a -=,再由余弦定理得28cos 2b A b -=,进而求得sin A ,利用面积公式求得ABC S ∆=,即可求解.【详解】选择条件①:因为tan 2tan B C =,所以sin cos 2sin cos B C C B =,根据正弦定理可得cos 2cos b C c B =, 由余弦定理得:222222222a b c a c b b c ab ac+-+-⨯=⨯, 又由2c =,可得22312b a -=, 根据余弦定理得22228cos 22b c a b A bc b+--==,则sin A ===,所以1sin 22ABC S bc A b b ∆==⨯=, 所以当且仅当210b =时,ABC ∆面积取得最大值,最大值为3.选择条件②:因为22312b a -=,由余弦定理得22228cos 22b c a b A hc h+--==,所以sin 2A b ===,1sin 22ABC S bc A b b ∆==⨯=, 所以当且仅当210b =时,ABC ∆面积取得最大值,最大值为3.选择条件③:因为cos 2cos b C c B =,由余弦定理得:222222222a b c a c b b c ab ac+-+-⨯=⨯, 因为2c =,可得22312b a -=,又由余弦定理得:22228cos 22b c a b A bc b+--==,所以sin A ===,1sin 22ABC S bc A b b ∆==⨯=, 所以当且仅当210b =时,ABC ∆面积取得最大值,最大值为3.【点睛】对于解三角形问题的常见解题策略:对于解三角形问题,通常利用正弦定理进行“边转角”寻求角的关系,利用“角转边”寻求边的关系,利用正、余弦定理解三角形问题是高考高频考点,同时注意三角形内角和定理,三角形面积公式在解题中的应用.24.B =30°,90C =,b =c =. 【分析】由三角函数值、三角形内角和性质确定B 、C 的大小,应用正弦定理求,b c 即可.【详解】由1sin 2B =且60A =︒,即0120B <<︒,可知:30B =︒. ∴90C =︒,由正弦定理sin sin sin b c a B C A ==,∴sin 3sin 30sin sin 60a B b A ︒===︒sin 3sin 90sin sin 60a C c A ︒===︒25.(1)21n a n =-;(2)212233m m +-- 【分析】(1)根据等差数列的通项公式和前n 项和公式列出式子求出首项和公差即可求出通项公式;(2)由20log 21m k a m ≤=-<解得2112m k -<≤,即可得出1241m m b -=⨯-,再分组求和即可得出.【详解】(1)设等差数列{}n a 的公差为d , 则3161+25656+362a a d S a d ==⎧⎪⎨⨯==⎪⎩,解得1a 1,d 2, ()11221n a n n ∴=+-⨯=-;(2)由20log 21m k a m ≤=-<,解得2112m k -<≤,m b 为2log k 在区间(]()*0,m a m N ∈中正整数k 的个数,21121241m m m b --∴=-=⨯-,设数列{}m b 的前m 项和为m T ,则()21214221433m m m T m m +-=-=---. 【点睛】本题考查等差数列基本量的计算,解题的关键是求出首项和公差,考查等比数列的求和公式,解题的关键是求出1241m m b -=⨯-.26.(1)n a n =;(2)答案见解析.【分析】(1)设等差数列{}n a 的公差为d ,根据已知条件可得出关于1a 、d 的方程组,解出这两个量的值,利用等差数列的通项公式可求得{}n a 的通项公式;(2)选①,求得2n n b n =⋅,利用错位相减法可求得n S ;选②,求得10,101010,10n n n b n n n -≤⎧=-=⎨->⎩,分10n ≤和10n >两种情况讨论,结合等差数列的求和公式可求得n S ;选③,可得11122n b n n ⎛⎫- ⎪+⎝⎭=,利用裂项相消法可求得n S . 【详解】 (1)因为11a +、4a 、8a 成等比数列,所以()24181a a a =+,设等差数列{}n a 的公差为d ,则0d ≥,则有()()()2111317a d a a d +=++,①又22a =,所以12a d +=,②联立①②解得111a d =⎧⎨=⎩,所以()11n a a n d n =+-=;(2)选①,则2n n b n =⋅,231222322n n S n =⨯+⨯+⨯++⨯()23121222122n n n S n n +=⨯+⨯++-⨯+⨯,上式-下式得()()2311121222222212212n n n n n n S n n n +++--=++++-⨯=-⨯=-⋅--, 化简得()1122n n S n +=-⋅+;选②,则10,101010,10n n n b n n n -≤⎧=-=⎨->⎩, 当10n ≤时,10n b n =-,()()9101922n n n n n S +--==; 当10n >时,()()()()2101109101918098101210+222n n n n n S n -+-⨯-+⎡⎤=++++++++-==⎣⎦. 综上()219,10219180,102n n n n S n n n ⎧-≤⎪⎪=⎨-+⎪>⎪⎩; 选③,则()1111222n b n n n n ⎛⎫==- ⎪++⎝⎭1111111111111213243546112n S n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ()()2111113521212412n n n S n n n n +⎛⎫∴=+--= ⎪++++⎝⎭. 【点睛】方法点睛:数列求和的常用方法:(1)对于等差等比数列,利用公式法直接求和;(2)对于{}n n a b 型数列,其中{}n a 是等差数列,{}n b 是等比数列,利用错位相减法求和;(3)对于{}n n a b +型数列,利用分组求和法;(4)对于11n n a a +⎧⎫⎨⎬⎩⎭型数列,其中{}n a 是公差为()0d d ≠的等差数列,利用裂项相消法求和.。
人教A版高中数学必修五必修五 综合测试题 (第三套).docx

必修五 综合测试题 (第三套)一.选择题:1. 已知等差数列}{n a 中,12497,1,16a a a a 则==+的值是( )A . 15B . 30 C. 31 D. 642. 若全集U=R,集合M ={}24x x >,S =301x xx ⎧-⎫>⎨⎬+⎩⎭,则()U M S I ð=( ) A.{2}x x <- B. {23}x x x <-≥或 C. {3}x x ≥ D. {23}x x -≤<3. 若1+2+22+ (2)>128,n ÎN*,则n 的最小值为( ) A. 6 B. 7 C. 8 D. 9 4. 在ABC V 中,60B =o ,2b ac =,则ABC V 一定是( )A 、等腰三角形B 、等边三角形C 、锐角三角形D 、钝角三角形 5. 若不等式022>++bx ax的解集为⎭⎬⎫⎩⎨⎧<<-3121|x x ,则a -b 值是( )A.-10B.-14C. 10D. 14 6. 在等比数列{a n }中,4S =1,8S =3,则20191817a a a a +++的值是( )A .14B .16C .18D .207.已知12=+y x ,则y x 42+的最小值为( ) A .8 B .6 C .22 D .238. 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第n 个图案中有白色地面砖的块数是( ) A.42n +B.42n -C.24n +D.33n +9. 已知变量y x ,满足⎪⎩⎪⎨⎧≥<+≤+-12553034x y x y x ,目标函数是y x z +=2,则有( )A .3,12min max ==z zB .,12max=z z 无最小值C .z z ,3min=无最大值 D .z 既无最大值,也无最小值10.在R 上定义运算:(1)x y x y ⊗⊗=-,若不等式()()1x a x a -⊗+<对任意实数x 成立,则实数a 的取值范围是( ) A .11a -<< B .02a << C .1322a -<< D .3122a -<< 二填空题: 11. 在数列{}n a 中,11a =,且对于任意正整数n ,都有1n n a a n +=+,则100a =______第1个 第2个 第3个12.在⊿ABC 中,5:4:21sin :sin :sin=C B A ,则角A =13.某校要建造一个容积为83m ,深为2m 的长方体无盖水池,池底和池壁的造价每平方米分别为240元和160元,那么水池的最低总造价为 元。
(必考题)高中数学必修五第二章《解三角形》测试题(含答案解析)(2)

一、选择题1.ABC ∆中,角,,A B C 所对的边分别为,,a b c .若13,3,60a b A ===︒,则边c =( ) A .1B .2C .4D .62.在锐角ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .若22212a b c =+,则tan A 的取值范围是( ) A .)3,⎡+∞⎣ B .()3,+∞C .()2,+∞D .[)2,+∞3.ABC 的内角,,A B C 的对边分别为,,a b c ,分别根据下列条件解三角形,其中有两解的是( )A .2,4,120a b A ===︒B .3,2,45a b A ===︒C . 6,43,60b c C ===︒D .4,3,30b c C ===︒4.已知,,a b c 分别是ABC ∆的三个内角,,A B C 所对的边,若1,3a b ==,B 是,A C 的等差中项,则角C =( ) A .30B .45︒C .60︒D .90︒5.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若cos 2a B c=,21sin sin (2cos )sin 22A B C A -=+,则A =( ) A .6π B .3π C .2π D .23π 6.如图,某船在A 处看见灯塔P 在南偏东15方向,后来船沿南偏东45的方向航行30km 后,到达B 处,看见灯塔P 在船的西偏北15方向,则这时船与灯塔的距离是:A .10kmB .20kmC .3kmD .53km7.在ABC 中,内角,,A B C 所对应的边分别为,,a b c ,若sin 3cos 0b A a B -=,且2b ac =,则a cb+ 的值为( ) A .22B .2C .2D .48.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且BC 边上的高为3a ,则c bb c+的最大值是( ) A .8B .6C .32D .49.ABC 中角A ,B ,C 所对的边分别为a ,b ,c ,已知a ,b ,c 成等差数列,且2C A =,若AC 边上的中线792BD =,则△ABC 的周长为( ) A .15B .14C .16D .1210.在ABC ∆中,30,10B AC =︒=,D 是AB 边上的一点,25CD =,若ACD ∠为锐角,ACD ∆的面积为20,则BC =( ) A .25B .35C .45D .65 11.在ABC 中,若2a =,23b =,30A =︒,则B 等于( ) A .30B .30或150︒C .60︒D .60︒或120︒12.已知ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,2b =,45B =︒,若三角形有两解,则a 的取值范围是( ) A .2a >B .02a <<C .222a <<D .223a <<二、填空题13.在ABC 中,已知1AC =,A ∠的平分线交BC 于D ,且1AD =,2BD =,则ABC 的面积为_________.14.如图,三个全等的三角形ABF ,BCD ,CAE 拼成一个等边三角形ABC ,且DEF 为等边三角形,若2EF AE =,则tan ACE ∠的值为__________.15.如图,在ABC 中,角C 的平分线交AB 于D 且CD AD =.若3AC =,2BC =,则AB =________16.在ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若222a b =,sin 3sin C B =,则cos A =________.17.如图,设A 、B 两点在河的两岸,一测量者在A 的同侧所在的河岸边选定一点C ,测出AC 的距离为50m ,45ACB ∠=︒,105CAB ∠=︒后,就可以计算出A 、B 两点的距离为______18.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,其中23a c ==,,且满足(2)cos cos a c B b C -⋅=⋅,则AB BC ⋅=______.19.在锐角ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对的边,且满足cos 2b aC a-=,则tan A 的取值范围是__. 20.在三角形ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,222a c b ac +-=,3b =2a c +的最大值为______.三、解答题21.如图,在ABC 中,6AB =,3cos 4B =,点D 在BC 边上,4=AD ,ADB ∠为锐角.(1)若62AC =DC 的长度; (2)若2BAD DAC ∠=∠,求sin C 的值.22.在ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若2sin c bC -=tan cos A C -. (1)求角A 的大小;(2)若32b =,2c =,点D 在边BC 上,且2CD DB =,求a 及AD . 23.在ABC 中,内角A 、B 、C 对应的边长分别为a b c 、、,且,,a b c 满足5cos 44cos 5sin sin cos a B b cB A BC -=+.(1)求cos A ;(2)若3a =,求b c +的最大值.24.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知cos cos 12+=A C a c ,且2b =.(1)证明:4+≥a c ;(2)若ABC 的周长为232+S .25.已知ABC 的三个内角A ,B ,C 的对边分别是a ,b ,c ,且cos cos 2cos b C c B a A +=.(1)求角A ;(2)若3a =ABC 的面积为23b c +的值.26.在ABC 中,内角,,A B C 的对边长分别为,,a b c ,已知222a c b -=,且sin cos 3cos sin A C A C = ,求b【参考答案】***试卷处理标记,请不要删除一、选择题1.C 解析:C 【解析】试题分析:2222cos a c b cb A =+-213923cos60c c ⇒=+-⨯⨯︒,即2340c c --=,解得4c =或1c =-(舍去). 考点:余弦定理,正弦定理.2.B解析:B 【分析】根据题中条件,由三角形的余弦定理、正弦定理和两角和的正弦公式,化简可得tan 3tan A B =,再由两角和的正切公式,以及锐角三角形的定义,可得tan 0A >,tan 0C >,解不等式可得所求范围. 【详解】因为22212a b c =+,由余弦定理可得,2222cos a b c bc A =+-,则222212cos 2b c b c bc A +=+-,可得4cos c b A =,由正弦定理可得:sin 4sin cos C B A =,可得sin()sin cos sin cos 4sin cos A B A B B A B A +=+=, 化为3sin cos sin cos B A A B =, 在锐角ABC 中,cos 0A ≠,cos 0B ≠, 则tan 3tan A B =,又21tan tan tan tan 3tan tan()11tan tan 1tan 3A AA B C A B A B A ++=-+=-=---,由tan 0A >,tan 0C >,可得211tan 03A -<,解得tan A >, 故选:B . 【点睛】本题考查三角形的正弦定理和余弦定理的运用,以及两角和的三角函数公式,考查方程思想和化简运算能力,属于中档题.3.D解析:D 【分析】运用正弦定理公式,可以求出另一边的对角正弦值,最后还要根据三角形的特点:“大角对大边”进行合理排除. 【详解】A. 2,4,120a b A ===︒,由,a b <A B ⇒<所以不存在这样的三角形.B. 3,2,45a b A ===︒,由sin sin sin 3a b B A B =⇒=且,a b >所以只有一个角BC. 6,60b c C ===︒中,同理也只有一个三角形.D. 4,3,30b c C ===︒中2sin sin sin 3c b B C B =⇒=此时b c >,所以出现两个角符合题意,即存在两个三角形. 所以选择D 【点睛】在直接用正弦定理求另外一角中,求出 sin θ后,记得一定要去判断是否会出现两个角.4.A解析:A 【详解】由题设可得060B =11sin sin 2A A =⇒=,则030A =或0150A =,但a b A B <⇔<,应选答案A .5.C解析:C 【分析】先利用余弦定理化简条件得sin sin B C =,再利用三角恒等变换即求得B ,C ,再求A 角. 【详解】∵cos 2a B c =,∴22222a c b aac c+-=,解得b c =,∴sin sin B C =. ∵212cos sin sin (2cos )sin 222A AB C A --=+=,易知2cos 0A -≠,∴1sin sin 2B C =,又sin sin B C =,∴sin sin 2B C ==,即4B C π==,∴2A π=.故选:C . 【点睛】本题考查了三角恒等变换与解三角形的综合,属于中档题.6.C解析:C 【分析】在ABP ∆中,利用正弦定理求出BP 得长,即为这时船与灯塔的距离,即可得到答案. 【详解】由题意,可得30PAB PBA ∠=∠=,即30,120AB APB =∠=,在ABP ∆中,利用正弦定理得30sin 30sin120PB ==即这时船与灯塔的距离是km ,故选C . 【点睛】本题主要考查了正弦定理,等腰三角形的判定与性质,以及特殊角的三角函数值的应用,其中熟练掌握正弦定理是解答本题的关键,着重考查了推理与运算能力,属于基础题.7.C解析:C 【分析】利用正弦定理边化角,结合辅助角公式可求得sin 03B π⎛⎫-= ⎪⎝⎭,从而确定3B π=;利用余弦定理构造方程可求得()24+=a c ac ,代入所求式子即可化简得到结果. 【详解】sin cos 0b A B =,()sin sin cos sin sin 2sin sin 03B A A B A B B A B π⎛⎫∴=-=-= ⎪⎝⎭,()0,A π∈,sin 0A ∴≠,sin 03B π⎛⎫∴-= ⎪⎝⎭,又()0,B π∈,3B π∴=.()22222231cos 2222a c ac a cb ac ac B ac ac ac +-+-+-∴====,整理可得:()24+=a c ac ,2a cb+∴====. 故选:C . 【点睛】本题考查解三角形的相关知识,涉及到正弦定理边化角、余弦定理的应用等知识;解决此类问题的关键是能够通过正弦定理,将边的齐次式转化为角的关系,属于常考题型.8.D解析:D 【分析】首先利用面积公式可得:2sin a A =,再利用余弦定理2222cos b c a bc A +=+,两者结合可得22sin 2cos b c A bc A +=+,而22c b b c b c bc++=,即可得c bb c +2cos A A =+,再利用辅助角公式即可求解. 【详解】由已知可得:11sin 226bc A a a =⨯,所以2sin a A =,因为222cos 2b c a A bc+-=,所以2222cos sin 2cos b c a bc A A bc A +=+=+所以222cos 4sin 46c b b c A A A b c bc π+⎛⎫+==+=+≤ ⎪⎝⎭, 所以c bb c +的最大值是4 故选:D 【点睛】本题主要考查了三角形面积公式、余弦定理、以及辅助角公式,属于中档题.9.A解析:A 【分析】由已知结合等差数列的性质及二倍角公式,正弦定理及余弦定理进行化简,即可求得结果. 【详解】由a ,b ,c 成等差数列可知,2b a c =+, 因为2C A =,所以sin sin 22sin cos C A A A ==,由正弦定理及余弦定理可得,22222b c a c a bc+-=⋅,所以2223bc ab ac a =+-, 所以32c a =,54b a =,若AC 边上的中线BD =所以2225379242a a a ⎡⎤⎛⎫⎛⎫+=+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,解可得4a =,5b =,6c =, 故△ABC 的周长为15. 故选:A. 【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有余弦定理,正弦定理,等差数列的条件,以及边角关系,属于简单题目.10.C解析:C先利用面积公式计算出sin ACD ∠,计算出cos ACD ∠,运用余弦定理计算出AD ,利用正弦定理计算出sin A ,在ABC ∆中运用正弦定理求解出BC . 【详解】解:由ACD ∆的面积公式可知,11sin 1025sin 2022ACAD ACD ACD ∠=∠=,可得sin ACD∠=,ACD ∠为锐角,可得cos ACD ∠==在ACD ∆中,21002021025805AD =+-=,即有AD =由sin sin AD CDACD A =∠可得sin sin CD ACD A AD ∠=,由sin sin AC BCB A=可知sin sin 2AC A BC B ===.故选C . 【点睛】本题考查正弦定理与余弦定理在解三角形中的应用,考查方程思想,属于中档题.11.D解析:D 【分析】由正弦定理,求得sin sin bB A a=,再由a b <,且0180B ︒<<︒,即可求解,得到答案. 【详解】由题意,在ABC中,由正弦定理可得sin sin a bA B=, 即sin sin sin 3022b B A a ==︒=, 又由a b <,且0180B ︒<<︒, 所以60B =︒或120B =︒, 故选:D. 【点睛】本题主要考查了正弦定理的应用,其中解答中熟记三角形的正弦定理,准确运算是解答的关键,着重考查了推理与运算能力,属于基础题.12.C解析:C 【分析】直接利用正弦定理计算得到答案.根据正弦定理:sin sin 2a b A B ==sin A =,三角形有两解,故sin 12A <=<,解得2a << 故选:C. 【点睛】本题考查了利用正弦定理解三角形,意在考查学生的计算能力和转化能力.二、填空题13.【分析】设将利用三角形面积公式表示出来可得在中利用余弦定理可得解得即可求出进而可得的值再利用三角形面积公式即可求解【详解】因为平分所以设则因为设所以所以因为所以即在中所以可得解得:所以所以所以故答案【分析】设12BAD CAD BAC θ∠=∠=∠=,AB x =,将BAD CAD ABC S S S +=△△△利用三角形面积公式表示出来,可得1cos 2x xθ+=,在ABD △中,利用余弦定理可得212cos 2x xθ+-=,解得2x =,即可求出cos θ,sin θ,进而可得sin BAC ∠的值,再利用三角形面积公式即可求解. 【详解】因为AD 平分BAC ∠,所以12BAD CAD BAC ∠=∠=∠, 设BAD θ∠=,则CAD θ∠=,2BAC θ∠=, 因为BAD CAD ABC S S S +=△△△,设AB x =, 所以111sin sin sin 2222x x θθθ+=, 所以,sin sin 2sin cos x x θθθθ+=, 因为sin 0θ≠,所以12cos x x θ+=,即1cos 2x xθ+=, 在ABD △中,212cos 2x x θ+-=,所以21122x x x x-+=, 可得220x x --=,解得:2x =,所以3cos cos 4BAD θ∠==,所以sin BAD ∠==,3sin 2sin cos 24BAC θθ∠===,所以1sin 28ABC S AC AB BAC =⋅∠=,【点睛】 关键点点睛:本题解题的关键是将BAD CAD ABC S S S +=△△△用面积公式表示出来可得边角之间的关系,再结合余弦定理即求出边和角即可求面积.14.【分析】首先设中利用正弦定理表示的值【详解】设因为三角形互为全等三角形且是等边三角形所以且在中根据正弦定理有所以所以即故答案为:【点睛】本题主要考查正弦定理三角函数恒等变换属于中档题型【分析】首先设AE x =,CBD ACE θ∠=∠=,CBD 中,CD AE x ==,3BD x =,6060BCE ACE θ∠=-∠=-,利用正弦定理表示tan ACE ∠的值.【详解】设AE x =,22EF AE x ==,因为三角形ABF ,BCD ,CAE 互为全等三角形,且ABC 是等边三角形, 所以CBD ACE θ∠=∠=,CD AE x ==,3BD AF AE EF x ==+=,且6060BCE ACE θ∠=-∠=-,在CDB △中,根据正弦定理有sin sin CD BD CBD BCD=∠∠, 所以()3sin sin 60x x θθ=-,所以()13sin sin 60sin 2θθθθ=-=-,即7sin 2θθ=,sin tan cos θθθ==.【点睛】本题主要考查正弦定理,三角函数恒等变换,属于中档题型.15.【分析】不妨令易知然后在中利用正弦定理求出的值最后在中利用正弦定理可求出的值【详解】解:在中角的平分线交于且设则即整理得所以:结合得即显然是锐角所以再由得:解得故答案为:【点睛】本题考查正弦定理三角【分析】不妨令A α∠=,易知ACD BCD α∠==,3B πα∠=-,然后在ABC 中,利用正弦定理,求出sin α,cos α的值,最后在ABC 中,利用正弦定理,可求出AB 的值.【详解】解:在ABC 中,角C 的平分线交AB 于D ,且CD AD =.设A α∠=,则ACD BCD α∠==,3B πα∠=-, ∴sin sin AC BC B A =∠∠,即32sin(3)sin παα=-, 整理得2sin33sin αα=,所以:2(sin cos2cos sin 2)3sin ααααα+=,结合sin 0α≠得222(2cos 12cos )3αα-+=, 即258cos α=,显然α是锐角,所以cos αα=∴sin 22sin cos ααα==. 再由ABC 得:2sin sin 2AB αα=,∴= 解得10AB .【点睛】本题考查正弦定理,三角恒等变换的知识方法在解题中的作用,属于中档题.16.【分析】由根据正弦定理边化角可得根据余弦定理结合已知联立方程组即可求得角【详解】根据正弦定理:根据余弦定理:又故可联立方程:解得:故答案为:【点睛】本题主要考查了求三角形的一个内角解题关键是掌握由正【分析】由sin C B =,根据正弦定理“边化角”,可得=c ,根据余弦定理2222cos a b c bc A =+-,结合已知联立方程组,即可求得角cos A .【详解】sin C B=,根据正弦定理:sin sinb cB C=,∴=c,根据余弦定理:2222cosa b c bc A=+-,又222a b=,故可联立方程:222222cos2ca b c bc Aa b⎧=⎪=+-⎨⎪=⎩,解得:cos A=..【点睛】本题主要考查了求三角形的一个内角,解题关键是掌握由正弦定理“边化角”的方法和余弦定理公式,考查了分析能力和计算能力,属于中档题.17.【分析】由与求出的度数根据以及的长利用正弦定理即可求出的长【详解】解:在中即则由正弦定理得:故答案为:【点睛】本题考查正弦定理以及特殊角的三角函数值熟练掌握正弦定理是解本题的关键解析:【分析】由ACB∠与BAC∠,求出ABC∠的度数,根据sin ACB∠,sin ABC∠,以及AC的长,利用正弦定理即可求出AB的长.【详解】解:在ABC∆中,50AC m=,45ACB∠=︒,105CAB∠=︒,即30ABC∠=︒,则由正弦定理sin sinAB ACACB ABC=∠∠,得:50sin21sin2AC ACBABABC∠===∠.故答案为:.【点睛】本题考查正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.18.【分析】由题意利用正弦定理边化角求得∠B的值然后结合数量积的定义求解的值即可【详解】根据正弦定理得:故答案为【点睛】本题主要考查正弦定理余弦定理的应用等知识意在考查学生的转化能力和计算求解能力解析:3-【分析】由题意利用正弦定理边化角,求得∠B的值,然后结合数量积的定义求解AB BC⋅的值即可.【详解】()2a c cosB bcosC -=根据正弦定理得:()2sinA sinC cosB sinBcosC -=2sinAcosB sinBcosC sinCcosB =+()2sinAcosB sin B C =+2sinAcosB sinA =12cosB ∴=, 60B ∴=1||2332AB BC AB BC cosB ⎛⎫∴⋅=-⋅=-⨯⨯=- ⎪⎝⎭ 故答案为3-【点睛】本题主要考查正弦定理、余弦定理的应用等知识,意在考查学生的转化能力和计算求解能力.19.【分析】先由余弦定理可将条件整理得到利用正弦定理得到;结合二倍角公式;再由和差化积公式得:代入①整理得;求出和的关系求出角的范围即可求解【详解】解:由余弦定理可知则整理得即由正弦定理可得即①由和差化解析:,1) 【分析】先由余弦定理可将条件整理得到22c a ab -=,利用正弦定理得到22sin sin sin sin C A A B -=;结合二倍角公式1cos21cos2cos2cos2sin sin 222C A A C A B ----==;再由和差化积公式得:cos2cos22sin()sin()A C A C A C -=-+-代入①整理得sin sin()sin()A A C C A =--=-;求出A 和C 的关系,求出角的范围即可求解.【详解】解:由余弦定理可知222cos 2a b c C ab+-=,则22222a b c b a ab a +--=, 整理得2222a b c b ab +-=-,即22c a ab -=,由正弦定理可得,22sin sin sin sin C A A B -=,即1cos21cos2cos2cos2sin sin 222C A A C A B ----==①, 由和差化积公式得:cos2cos22sin()sin()A C A C A C -=-+-代入①得sin()sin()sin sin A C A C A B -+-=;因为sin()sin 0A C B +=≠;sin sin()sin()A A C C A ∴=--=-;在锐角ABC ∆中,C A A -=即2C A =,则3B A C A ππ=--=-, 因为02022032A A A ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩, ∴64A ππ<<,tan A ∴的取值范围是,1);故答案为:,1). 【点睛】 本题主要考查正弦定理、余弦定理以及和差化积公式的应用,特殊角的三角函数值,属于中档题.20.【分析】由余弦定理可求出角再根据正弦定理即可表示出然后利用消元思想和辅助角公式即可求出的最大值【详解】因为所以而∴∵∴∴其中所以的最大值为当时取得故答案为:【点睛】本题主要考查正余弦定理在解三角形中解析:【分析】由余弦定理可求出角B ,再根据正弦定理即可表示出2a c +,然后利用消元思想和辅助角公式,即可求出2a c +的最大值.【详解】因为222a cb ac +-=,所以2221cos 222a c b ac B ac ac +-===,而0B π<<,∴3B π=.∵2sin sin sin sin 3a b c A B C π====,∴2sin ,2sin a A c C ==.∴222sin 4sin 2sin 4sin 4sin 3a c A C A A A A π⎛⎫+=+=+-=+ ⎪⎝⎭()A ϕ=+,其中tan 2ϕ=.所以2a c +的最大值为2A πϕ=-时取得.故答案为:【点睛】 本题主要考查正余弦定理在解三角形中的应用,以及利用三角函数求解三角形中的最值问题,意在考查学生的转化能力和数学运算能力,属于中档题.三、解答题21.(1)7;(2 【分析】(1)分别在△ABD 、△ABC 中,由余弦定理求BD ,BC ,即可求DC 的长度; (2)记DAC ∠θ=,则2BAD θ∠=,在△ABD 中由余弦定理求sin 2θ、sin θ、cos θ,法一:即可求sin3θ、cos3θ,由已知求sin B ,又()sin sin 3C B πθ=--即可求值;法二:由余弦定理求cos BDA ∠,sin BDA ∠,又()sin sin C BDA θ=∠-即可求值.【详解】(1)在△ABD 中,由余弦定理得22223616312co 24s AB BD AD B AB B BD D BD +-⋅⋅=+-==, ∴5BD =或4BD =.当4BD =时,161636cos 0244ADB +-∠=<⨯⨯,则2ADB π∠>,不合题意,舍去; 当5BD =时,162536cos 0245ADB +-∠=>⨯⨯,则2ADB π∠<,符合题意. ∴5BD =. 在△ABC 中,22223672312co 24s AB BC AC B AB B BC C BC +-⋅⋅=+-==, ∴12BC =或3BC =-(舍).∴7DC BC BD =-=.(2)记DAC ∠θ=,则2BAD θ∠=.在△ABD 中,2229cos cos2216AB AD BD BAD AB AD θ+-∠===⋅,∴2θ为锐角,得21cos27sin 232θθ-==,sin 2θ=sin θ=,cos θ=,法一:sin3sin 2cos cos2sin θθθθθ=+=,同理cos3θ=由3cos 4B =知:sin B =,∴()()sin sin 3sin 3sin cos3cos sin3C B B B B πθθθθ=--=+=+法二:2221625361cos 22458AD BD AB BDA AD BD +-+-∠===⋅⨯⨯,sin BDA ∠.∴()sin sin sin cos cos sin C BDA BDA BDA θθθ=∠-=∠-∠=【点睛】关键点点睛:(1)应用余弦定理求三角形的边长,根据边的数量关系求DC ;(2)由余弦定理,利用诱导公式及两角和或差的正弦公式,求角的正弦值即可.22.(1)π4A =;(2)a =3AD =. 【分析】(1()sin sin sin tan cos C B A C A C -=-,再化简计算即可求出cos A =(2)由余弦定理求得a =,求得cos B =3a BD ==,再由余弦定理即可求出AD .【详解】解:(1()sin sin sin tan cos C B A C A C -=-,()()sin sin sin tan cos C A C A C A C -+=-,∴2sin sin cos cos sin sin sin cos cos A C A C A C C A C A--=-,∵sin 0C ≠,∴2sin cos cos A A A+=∴cos 2A =0πA <<,∴π4A =. (2)由余弦定理可得:2222cos 1841210a b c bc A =+-=+-=, ∴a =∵点D 在边BC 上,且2CD DB =,∴33a BD ==,又222cos 2a c b B ac +-==∴222582cos 9AD AB BD AB BD B =+-⋅⋅=,∴3AD =. 【点睛】关键点睛:本题考查正余弦定理的应用,解题的关键是正确利用正弦定理化边为角处理条件,再结合三角恒等变换化简运算.23.(1)45-;(2 【分析】 (1)利用正弦定理边化角,结合两角和的正弦公式、余弦公式,化简整理,即可求得答案.(2)由(1)可得4cos 5A =-,根据余弦定理,可得25()92bc b c ⎡⎤=+-⎣⎦,根据基本不等式,即可求得b c +的最大值.【详解】(1)由题意得5cos cos 4cos 4cos 5sin sin a C B b C c B c A B -=+, 正弦定理边化角得:5sin cos cos 4sin cos 4sin cos 5sin sin sin A C B B C C B C A B -=+,所以5sin (cos cos sin sin )4(sin cos sin cos )A C B C B C B B C -=+,所以5sin cos()4sin()A B C B C +=+,又A B C π++=,所以sin()sin()sin ,cos()cos()cos B C A A B C A A ππ+=-=+=-=-,所以5sin cos 4sin A A A -=,又因为(0,)A π∈,所以sin 0A ≠, 所以4cos 5A =-. (2)由(1)可得4cos 5A =-, 由余弦定理得2222()294cos 225b c a b c bc A bc bc +-+--===-, 所以25()92bc b c ⎡⎤=+-⎣⎦, 由基本不等式可得22b c bc +⎛⎫≤ ⎪⎝⎭,所以225()922b c b c +⎛⎫⎡⎤+-≤ ⎪⎣⎦⎝⎭,解得b c +≤ 当且仅当b c =时等号成立,所以b c +【点睛】解题的关键是熟练掌握正余弦定理、基本不等式等知识,并灵活应用,考查计算化简的能力,属中档题.24.(1)证明见解析;(2)2. 【分析】(1)解法一:用正弦定理化边为角,得到2sin sin sin B A C =,再变成2b ac =,运用基本不等式可证明解法二:用余弦定理化角为边,得到关系式2b ac =,再用基本不等式求解即可. (2)用余弦定理求出3cos 4B =,再用三角形面积公式求解即可. 【详解】(1)解法一:由已知及正弦定理,得cos cos 1sin sin sin A C A C B += 因为cos cos cos sin cos sin sin()sin sin sin sin sin sin sin sin sin +++===A C A C C A A C B A C A C A c A c所以sin 1sin sin sin =B A c B,2sin sin sin B A C =由正弦定理得2b ac =,即4ac =.4a c +≥=. 解法二:由已知及余弦定理,得222221222+-+-+=b c a a b c abc abc ,得24==ac b ,所以4a c +≥=.(2)因为ABC 的周长为2+a c +=因为22222cos ()22cos b a c ac B a c ac ac B =+-⋅=+--⋅又因为4ac =,所以3cos 4B =得sin B =.所以1sin 2sin 2===ABC S ac B B 【点睛】在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注意公式变式的应用.解决三角形问题时,注意角的限制范围.25.(1)π3A =;(2)6. 【分析】(1)由正弦定理把条件cos cos 2cos b C c B a A +=转化为角的关系,再由两角和的正弦公式及诱导公式得A 的关系式,从而可得结论;(2)首先可根据解三角形面积公式得出8bc =,然后根据余弦定理计算出6b c +=.【详解】(1)因为cos cos 2cos b C c B a A +=由正弦定理得,sin cos sin cos 2sin cos B C C B A A +=所以()sin sin 2sin cos B C A A A +==因为0πA <<所以,sin 0A ≠所以1cos 2A =,所以π3A =(2)因为ABC 的面积为所以1sin 2bc A =因为π3A =,所以1πsin 23bc =, 所以8bc =.由余弦定理得,2222cos a b c bc A =+-,因为a =,π3A =, 所以()()2222π122cos 3243b c bc b c bc b c =+-=+-=+-, 所以6b c +=.【点睛】关键点点睛:解题时要注意边角关系的转化.求“角”时,常常把已知转化为角的关系,求“边”时,常常把条件转化为边的关系式,然后再进行转化变形.26.4【分析】根据题意,在ABC 中,因为sin cos 3cos sin A C A C =,由正弦定理及余弦定理可得:2222223,22a b c b c a a c ab bc+-+-⋅=⋅ 化简并整理得:2222()a c b -=,结合已知条件222a c b -=,联立即可得解.【详解】在ABC 中,因为sin cos 3cos sin A C A C =,由正弦定理及余弦定理可得:2222223,22a b c b c a a c ab bc+-+-⋅=⋅ 化简并整理得:2222()a c b -=,又由已知222a c b -=,所以24b b =,解得4b =或0b =,由0b ≠,所以4b =.。
高中数学必修五三角函数知识点+练习题含答案解析(很详细)
高中数学必修五三角函数知识点+练习题含答案解析(很详细)第一部分必修五三角函数知识点整理第一章解三角形1、三角形的性质:①.A+B+C=π,? 222A B C π+=-?sin cos 22A B C += ②.在ABC ?中, a b +>c , a b -<c ; A >B ?sin A >sinB ...........................A >B ?cosA <cosB, a >b ? A >B③.若ABC ?为锐角?,则A B +>2π,B+C >2π,A+C >2π; 22a b +>2c ,22b c +>2a ,2a +2c >2b2、正弦定理与余弦定理:①.(2R 为ABC ?外接圆的直径)2s i n a R A =、2sin b R B =、2sin c R C =sin 2a A R =、 sin 2b B R =、 sin 2c C R= 面积公式:111sin sin sin 222ABC S ab C bc A ac B ?=== ②.余弦定理:2222cos a b c bc A =+-、2222cos b a c ac B =+-、2222cos c a b ab C =+-222cos 2b c a A bc +-=、222cos 2a c b B ac +-=、222cos 2a b c C ab+-= 补充:两角和与差的正弦、余弦和正切公式:⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-;⑶()sin sin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+;⑸()tan tan tan 1tan tan αβαβαβ --=+ ? (()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan 1tan tan αβαβαβ++=- ? (()()tan tan tan 1tan tan αβαβαβ+=+-).二倍角的正弦、余弦和正切公式:⑴sin 22sin cos ααα=.222)cos (sin cos sin 2cos sin 2sin1ααααααα±=±+=±?⑵2222cos2cos sin 2cos 112sin ααααα=-=-=-升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+ ?落幂公式2cos 21cos 2αα+=,21cos 2sin 2αα-=.第二部分必修五练习题含答案解析第一章解三角形1.在△ABC 中,AB =5,BC =6,AC =8,则△ABC 的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .非钝角三角形解析:最大边AC 所对角为B ,则cosB =52+62-822×5×6=-320B>CB .B>A>C C .C>B>AD .C>A>B解析由正弦定理a sinA =b sinB ,∴sinB =bsinA a =32.∵B 为锐角,∴B =60°,则C =90°,故C>B>A. 答案 C3.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( )A .4 2B .4 3C .4 6 D.323解:由A +B +C =180°,可求得A =45°,由正弦定理,得b =asinB sinA =8×sin60°sin45°=8×3222=4 6. 答案 C4.在△ABC 中,AB =5,BC =7,AC =8,则BA →·BC → 的值为( )A .5B .-5C .15D .-15解析在△ABC 中,由余弦定理得:cosB =AB 2+BC 2-AC 22AB ·BC =25+49-642×5×7=17. ∴BA →·BC →=|BA →|·|BC →|cosB =5×7×17=5. 答案 A5.若三角形三边长之比是1:3:2,则其所对角之比是( )A .1:2:3B .1:3:2C .1:2: 3 D.2:3:2解析设三边长分不为a ,3a,2a ,设最大角为A ,则cosA =a 2+3a 2-2a 22·a ·3a =0,∴A =90°.设最小角为B ,则cosB =2a 2+3a 2-a 22·2a ·3a =32,∴B =30°,∴C =60°. 所以三角之比为1:2:3. 答案 A6.在△ABC 中,若a =6,b =9,A =45°,则此三角形有( )A .无解B .一解C .两解D .解的个数别确定解析由b sinB =a sinA ,得sinB =bsinA a =9×226=3 24>1.∴此三角形无解.答案 A7.已知△ABC 的外接圆半径为R ,且2R(sin 2A -sin 2C)=(2a -b)sinB(其中a ,b 分不为A ,B 的对边),这么角C 的大小为( )A .30°B .45°C .60°D .90°解析依照正弦定理,原式可化为2R ? ??a 24R 2-c 24R 2=(2a -b)·b 2R ,∴a 2-c 2=(2a -b)b ,∴a 2+b 2-c 2=2ab ,∴cosC =a 2+b 2-c 22ab =22,∴C =45°. 答案 B8.在△ABC 中,已知sin 2A +sin 2B -sinAsinB =sin 2C ,且满脚ab =4,则该三角形的面积为( )A .1B .2 C. 2 D. 3解析由a sinA =b sinB =c sinC=2R ,又sin 2A +sin 2B -sinAsinB =sin 2C ,可得a 2+b 2-ab =c 2.∴c osC =a 2+b 2-c 22ab =12,∴C =60°,sinC =32. ∴S △ABC =12absinC = 3. 答案 D9.在△ABC 中,A =120°,AB =5,BC =7,则sinB sinC 的值为( ) A.85 B.58 C.53 D.35解析由余弦定理,得 cosA =AB 2+AC 2-BC 22AB ·AC,解得AC =3. 由正弦定理sinB sinC =AC AB =35. 答案 D10.在三角形ABC 中,AB =5,AC =3,BC =7,则∠BAC 的大小为( )A.2π3B.5π6C.3π4D.π3解析由余弦定理,得cos ∠BAC =AB 2+AC 2-BC 22AB ·AC =52+32-722×5×3=-12,∴∠BAC =2π3. 答案 A11.有一长为1 km 的歪坡,它的倾歪角为20°,现要将倾歪角改为10°,则坡底要加长( )A .0.5 kmB .1 kmC .1.5 km D.32km 解析如图,AC =AB ·sin20°=sin20°,BC =AB ·cos20°=cos20°,DC =AC tan10°=2cos 210°,∴DB =DC -BC =2cos 210°-cos20°=1.答案 B12.已知△ABC 中,A ,B ,C 的对边分不为a ,b ,c.若a =c =6+2,且A =75°,则b 为( )A .2B .4+2 3C .4-2 3 D.6- 2解析在△ABC 中,由余弦定理,得a 2=b 2+c 2-2bccosA ,∵a =c ,∴0=b 2-2bccosA =b 2-2b(6+2)cos75°,而cos75°=cos(30°+45°)=cos30°cos45°-sin30°sin45°=22? ????32-12=14(6-2),∴b 2-2b(6+2)cos75°=b 2-2b(6+2)·14(6-2)=b 2-2b =0,解得b =2,或b =0(舍去).故选A. 答案 A 13.在△ABC 中,A =60°,C =45°,b =4,则此三角形的最小边是____________.解析由A +B +C =180°,得B =75°,∴c 为最小边,由正弦定理,知c =bsinC sinB =4sin45°sin75°=4(3-1).答案 4(3-1)14.在△ABC 中,若b =2a ,B =A +60°,则A =________.解析由B =A +60°,得 sinB =sin(A +60°)=12sinA +32cosA. 又由b =2a ,知sinB =2sinA.∴2sinA =12sinA +32cosA. 即32sinA =32cosA.∵cosA ≠0,∴tanA =33.∵0°<A<180°,∴A =30°. 答案30° 15.在△ABC 中,A +C =2B ,BC =5,且△ABC 的面积为103,则B =_______,AB =_______.解析由A +C =2B 及A +B +C =180°,得B =60°.又S =12AB ·BC ·sinB ,∴10 3=12AB ×5×sin60°,∴AB =8. 答案60° 816.在△ABC 中,已知(b +c):(c +a):(a +b)=8:9:10,则sinA :sinB :sinC =________.解析设b +c =8k ,c +a =9k ,a +b =10k ,可得a :b :c =11:9:7.∴sinA :sinB :sinC =11:9:7.答案 11:9:717.在非等腰△ABC 中,角A ,B ,C 所对的边分不为a ,b ,c ,且a 2=b(b +c).(1)求证:A =2B ;(2)若a =XXX ,试推断△ABC 的形状.解 (1)证明:在△ABC 中,∵a 2=b ·(b +c)=b 2+bc ,由余弦定理,得cosB =a 2+c 2-b 22ac =bc +c 22ac =b +c 2a =a 2b =sinA 2sinB ,∴sinA =2sinBcosB =sin2B.则A =2B 或A +2B =π.若A +2B =π,又A +B +C =π,∴B =C.这与已知相矛盾,故A =2B.(2)∵a =XXX ,由a 2=b(b +c),得XXX 2=b 2+bc ,∴c =2b.又a 2+b 2=4b 2=c 2.故△ABC 为直角三角形.18.锐角三角形ABC 中,边a ,b 是方程x 2-23x +2=0的两根,角A ,B 满脚2sin(A +B)-3=0.求:(1)角C 的度数;(2)边c 的长度及△ABC 的面积.解 (1)由2sin(A +B)-3=0,得sin(A +B)=32. ∵△ABC 为锐角三角形,∴A +B =120°,∴∠C =60°.(2)∵a ,b 是方程x 2-23x +2=0的两个根,∴a +b =23,ab =2.∴c 2=a 2+b 2-2abcosC =(a +b)2-3ab =12-6=6.∴c = 6.S △ABC =12absinC =12×2×32=32. 19.已知△ABC 的角A ,B ,C 所对的边分不是a ,b ,c ,设向量m =(a ,b),n =(sinB ,sinA),p =(b -2,a -2).(1)若m ∥n ,求证:△ABC 为等腰三角形;(2)若m ⊥p ,边长c =2,角C =π3,求△ABC 的面积.解 (1)证明:∵m ∥n ,∴asinA =bsinB.由正弦定得知,sinA =a 2R ,sinB =b 2R (其中R 为△ABC 外接圆的半径),代入上式,得a ·a 2R =b ·b 2R,∴a =b.故△ABC 为等腰三角形.(2)∵m ⊥p ,∴m ·p =0,∴a(b -2)+b(a -2)=0,∴a +b =ab.由余弦定理c 2=a 2+b 2-2abcosC 得4=(a+b)2-3ab,即(ab)2-3ab-4=0. 解得ab=4,ab=-1(舍去).∴△ABC的面积S=12absinC=12×4×sinπ3= 3.。
(典型题)高中数学必修五第二章《解三角形》测试题(含答案解析)
一、选择题1.在△ABC 中,若b =2,A =120°,三角形的面积S =AB .C .2D .42.已知ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,且2cos 2b C a c ⋅=+,若3b =,则ABC ∆的外接圆面积为( )A .48π B .12πC .12πD .3π3.在ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,若2224ABCa b c S +-=(其中ABCS表示ABC 的面积),且角A 的平分线交BC 于E ,满足0AE BC ⋅=,则ABC 的形状是( )A .有一个角是30°的等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形4.在ABC 中,,,a b c 分别为三个内角,,A B C 的对边,若cos cos a A b B =,则ABC 一定是( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形5.在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c .已知3a =,(b ∈,且223cos cos a b B b A =+,则cos A 的取值范围为( ).A .133,244⎡⎤⎢⎥⎣⎦ B .133,244⎛⎫⎪⎝⎭ C .13,24⎡⎤⎢⎥⎣⎦D .13,24⎛⎫⎪⎝⎭6.在ABC 中,角A 、B 、C 对边分别为a 、b 、c ,若b =cos 20B B +-=,且sin 2sin C A =,则ABC 的周长是( )A .12+B .C .D .6+7.海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”我国拥有世界上最深的海洋蓝洞,现要测量如图所示的蓝洞的口径A ,B 两点间的距离,在珊瑚群岛上取两点C ,D ,测得80CD =,135ADB ∠=︒,15BDC DCA ∠=∠=︒,120ACB ∠=︒,则A 、B 两点间的距离为( )A .80B .803C .160D .8058.已知△ABC 中,2cos =c b A ,则△ABC 一定是A .等边三角形B .等腰三角形C .直角三角形D .等腰直角三角形9.ABC 中角A ,B ,C 所对的边分别为a ,b ,c ,已知a ,b ,c 成等差数列,且2C A =,若AC 边上的中线792BD =,则△ABC 的周长为( ) A .15B .14C .16D .1210.在ABC ∆中,角A B C ,,的对边分别是a b c ,,,若sin 3cos 0b A a B -=,且三边a b c ,,成等比数列,则2a cb+的值为( ) A .24B .22C .1D .211.如图,测量河对岸的塔高AB 时,选与塔底B 在同一水平面内的两个测点C 与D .现测得15BCD ∠=︒,45BDC ∠=︒,302CD m =,并在点C 测得塔顶A 的仰角为30,则塔高AB 为( )A .302mB .203mC .60mD .20m12.如图,在离地面高400m 的热气球上,观测到山顶C 处的仰角为15,山脚A 处的俯角为45,已知60BAC ∠=,则山的高度BC 为( )A .700mB .640mC .600mD .560m二、填空题13.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,()226b a c =+-,23B π=,则ABC 的面积是______________. 14.如图,点A 是半径为1的半圆O 的直径延长线上的一点,3OA =,B 为半圆上任意一点,以AB 为一边作等边ABC ,则四边形OACB 的面积的最大值为___________.15.锐角ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且()12cos c a B =+,则ba的取值范围是______. 16.在ABC 中,角A 、B 、C 所对的边分别是a 、b 、c ,若8cos 3ABC bc A S =△,则22cos sin 122sin cos B CA A A++-=-________. 17.已知ABC 中,2,2BC AB AC ==,则ABC 面积的最大值为_____ 18.在锐角ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对的边,且满足cos 2b aC a-=,则tan A 的取值范围是__. 19.如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个观测点,C D ,测得15BCD ︒∠=,30CBD ︒∠=,152m CD =,并在C 处测得塔顶A 的仰角为45︒,则塔高AB =______m .20.对于ABC ,有如下命题:①若sin2A =sin2B ,则ABC 为等腰三角形; ②若sin A =cos B ,则ABC 为直角三角形; ③若sin 2A +sin 2B +cos 2C <1,则ABC 为钝角三角形; ④若满足C =6π,c =4,a =x 的三角形有两个,则实数x 的取值范围为(4,8). 其中正确说法的序号是_____.三、解答题21.在①tan 2tan B C =,②22312b a -=,③cos 2cos b C c B =三个条件中任选一个,补充在下面问题中的横线上,并解决该问题.问题:已知ABC ∆的内角,,A B C 及其对边,,a b c ,若2c =,且满足___________.求ABC ∆的面积的最大值(注:如果选择多个条件分别解答,按第一个解答计分)22.ABC 的内角,,A B C 的对边分别为,,a b c .已知222sin sin sin sin sin B A C A C --=.(1)求B ;(2)若3b =,当ABC 的周长最大时,求它的面积. 23.已知ABC 中,51tan 43A π⎫⎛-=⎪⎝⎭. (1)求2sin cos2A A +的值;(2)若ABC 的面积为4,4AB =,求BC 的值. 24.在①π2=+A C ,②5415cos -=c a A ,③ABC 的面积3S =这三个条件中任选两个,补充在下面问题中,然后解答补充完整的题目.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知3b =,且______,______,求c .注:如果选择多个条件分别解答,按第一个解答计分.25.已知ABC 的三个内角A ,B ,C 的对边分别是a ,b ,c ,且cos cos 2cos b C c B a A +=.(1)求角A ;(2)若3a =ABC 的面积为23b c +的值.26.在①()cos cos 3cos 0C A A B +-=,②()cos23cos 1B A C -+=,③cos sin 3b C B a +=这三个条件中任选一个,补充在下面问题中. 问题:在ABC 中,角A 、B 、C 对应的边分别为a 、b 、c ,若1a c +=,___________,求角B 的值和b 的最小值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【解析】12sin1202S c ==⨯︒ ,解得c =2.∴a 2=22+22−2×2×2×cos 120°=12,解得a =,∴24sin 2a R A === , 解得R =2.本题选择C 选项. 2.D解析:D 【分析】 先化简得23B π=,再利用正弦定理求出外接圆的半径,即得ABC ∆的外接圆面积. 【详解】由题得222222a b c b a c ab+-⋅=+,所以22222a b c a ac +-=+, 所以222a b c ac -+=-, 所以12cos ,cosB 2ac B ac =-∴=-, 所以23B π=.,R R∴=所以ABC∆的外接圆面积为=3ππ.故选D【点睛】本题主要考查正弦定理余弦定理解三角形,意在考查学生对这些知识的理解掌握水平和分析推理能力.3.D解析:D【分析】根据角A的平分线交BC于E,满足0AE BC⋅=,得到ABC是等腰三角形,再由2221sin24+-==ABCa b cS ab C,结合余弦定理求解.【详解】因为0AE BC⋅=,所以AE BC⊥,又因为AE是角A的平分线,所以ABC是等腰三角形,又2221sin24+-==ABCa b cS ab C,所以2221sin cos22a b cab C Cab+-==,因为()0,Cπ∈,所以4Cπ,所以ABC是等腰直角三角形,故选:D【点睛】本题主要考查余弦定理,面积公式以及平面向量的数量积,属于中档题.4.D解析:D【分析】根据cos cosa Ab B=,利用正弦定理将边转化为角得到sin cos sin cosA AB B=,然后再利用二倍角的正弦公式化简求解.【详解】因为cos cosa Ab B=,由正弦定理得:sin cos sin cos A A B B =, 所以sin 2sin 2A B =, 所以22A B =或22A B π=-, 即A B =或2A B π+=所以ABC 一定是等腰三角形或直角三角形, 故选:D 【点睛】本题主要正弦定理,二倍角公式的应用,属于中档题.5.B解析:B 【分析】由正弦定理进行边角互化可得9c b=,由余弦定理可得22819cos 18b b A +-=,进而可求出cos A 的范围【详解】因为3a =,223cos cos a b B b A =+,所以22cos cos a ab B b A =+, 所以()22sin sin sin cos sin cos sin sin sin sin A A B B B A B A B B C =+=+=,即29a bc ==,所以9c b=,则22222819cos 218b bc a b A bc +-+-==.因为(b ∈,所以()212,18b ∈,81y x x=+在()12,18上递增, 所以22817545,42b b ⎛⎫+∈ ⎪⎝⎭,则133cos ,244A ⎛⎫∈ ⎪⎝⎭. 故选:B 【点睛】本题考查了正弦定理,考查了余弦定理.解答本题的关键是用b 表示cos A .6.D解析:D 【分析】由已知条件求出角B 的值,利用余弦定理求出a 、c 的值,由此可计算出ABC 的周长. 【详解】cos 2sin 26B B B π⎛⎫+=+= ⎪⎝⎭,sin 16B π⎛⎫∴+= ⎪⎝⎭,0B π<<,7666B πππ∴<+<,则62B ππ+=,3B π∴=,sin 2sin C A =,2c a ∴=,由余弦定理得2222cos b a c ac B =+-,即2312a =, 2a ∴=,24c a ==,因此,ABC 的周长是623a b c ++=+.故选:D. 【点睛】本题考查三角形周长的计算,涉及余弦定理的应用,考查计算能力,属于中等题.7.D解析:D 【分析】如图,BCD △中可得30CBD ∠=︒,再利用正弦定理得802BD =,在ABD △中,由余弦定理,即可得答案; 【详解】如图,BCD △中,80CD =,15BDC ∠=︒,12015135BCD ACB DCA ∠=∠+∠=︒+︒=︒,∴30CBD ∠=︒,由正弦定理得80sin135sin 30BD =︒︒,解得802BD =,ACD △中,80CD =,15DCA ∠=︒,13515150ADC ADB BDC ∠=∠+∠=︒+︒=︒, ∴15CAD ∠=︒,∴==80AD CD , ABD △中,由余弦定理得2222cos AB AD BD AD BD ADB =+-⋅⋅∠2280(802)280802cos135=+-⨯⨯⨯︒2805=⨯,∴805AB =,即A ,B 两点间的距离为805.故选:D. 【点睛】本题考查正余弦定理的运用,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力.8.B解析:B 【解析】试题分析:由2cos =c b A 和正弦定理得sin 2sin cos =C B A ,即sin()2sin cos ,sin cos sin cos A B B A A B B A +==.因sin 0,sin 0A B >>,故,A B 不可能为直角,故tan tan A B =.再由,(0,)A B π∈,故A B =.选B . 考点:本题考查正弦定理、内角和定理、两角和的三角函数公式.点评:综合考查正弦定理、两角和与差的三角公式.三角形中的问题,要特别注意角的范围.9.A解析:A 【分析】由已知结合等差数列的性质及二倍角公式,正弦定理及余弦定理进行化简,即可求得结果. 【详解】由a ,b ,c 成等差数列可知,2b a c =+, 因为2C A =,所以sin sin 22sin cos C A A A ==,由正弦定理及余弦定理可得,22222b c a c a bc+-=⋅,所以2223bc ab ac a =+-, 所以32c a =,54b a =,若AC 边上的中线BD =所以2225379242a a a ⎡⎤⎛⎫⎛⎫+=+⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,解可得4a =,5b =,6c =, 故△ABC 的周长为15. 故选:A. 【点睛】该题考查的是有关解三角形的问题,涉及到的知识点有余弦定理,正弦定理,等差数列的条件,以及边角关系,属于简单题目.10.C解析:C 【分析】先利用正弦定理边角互化思想得出3B π=,再利余弦定理1cos 2B =以及条件2b ac =得出a c =可得出ABC ∆是等边三角形,于此可得出2a cb+的值. 【详解】sin cos 0b A B =,由正弦定理边角互化的思想得sin sin cos 0A B A B =,sin 0A >,sin 0B B ∴=,tan B ∴=,则3B π=.a 、b 、c 成等比数列,则2b ac =,由余弦定理得222221cos 222a cb ac ac B ac ac +-+-===,化简得2220a ac c -+=,a c ∴=,则ABC ∆是等边三角形,12a cb+∴=,故选C . 【点睛】本题考查正弦定理边角互化思想的应用,考查余弦定理的应用,解题时应根据等式结构以及已知元素类型合理选择正弦定理与余弦定理求解,考查计算能力,属于中等题.11.D解析:D 【分析】由正弦定理确定BC 的长,再tan30AB BC 求出AB .【详解】15BCD ∠=︒,45BDC ∠=︒120CBD由正弦定理得:sin120sin 45BC302sin 45203sin120BC3tan 3020320ABBC故选D【点睛】本题是正弦定理的实际应用,关键是利用正弦定理求出BC ,属于基础题.12.C解析:C 【分析】可知ADM ∆为等腰直角三角形,可计算出AM 的长度,在ACM ∆中,利用正弦定理求出AC 的长度,然后在ABC ∆中,利用锐角三角函数求出BC ,即可得出答案. 【详解】根据题意,可得在Rt ADM ∆中,45MAD ∠=,400DM =,所以,sin 45DMAM ==因为在ACM ∆中,451560AMC ∠=+=,180456075,AMC ∠=--=180756045ACM ∠=--=,由正弦定理,得sin sin AM AMCAC ACM∠===∠在Rt ABC ∆中,()sin 600BC AC BAC m =∠==,故选C. 【点睛】本题考查解三角形的实际应用问题,着重考查三角函数的定义、利用正弦定理解三角形等知识,在解题时,要结合三角形已知元素类型合理选择正弦定理和余弦定理解三角形,考查运算求解能力,属于中等题.二、填空题13.【分析】利用余弦定理求出的值再利用三角形的面积公式可求得的面积【详解】由余弦定理可得可得则解得因此的面积是故答案为:【点睛】方法点睛:在解三角形的问题中若已知条件同时含有边和角但不能直接使用正弦定理【分析】利用余弦定理求出ac 的值,再利用三角形的面积公式可求得ABC 的面积. 【详解】由余弦定理可得222222cos b a c ac B a c ac =+-=++,222a c b ac ∴+-=-,()2222626b a c a c ac =+-=++-,可得222260a c b ac +-+-=,则260ac ac --=,解得6ac =,因此,ABC的面积是11sin 62222ABC S ac B ==⨯⨯=△.故答案为:2. 【点睛】方法点睛:在解三角形的问题中,若已知条件同时含有边和角,但不能直接使用正弦定理或余弦定理得到答案,要选择“边化角”或“角化边”,变换原则如下: (1)若式子中含有正弦的齐次式,优先考虑正弦定理“角化边”; (2)若式子中含有a 、b 、c 的齐次式,优先考虑正弦定理“边化角”;(3)若式子中含有余弦的齐次式,优先考虑余弦定理“角化边”; (4)代数式变形或者三角恒等变换前置;(5)含有面积公式的问题,要考虑结合余弦定理求解;(6)同时出现两个自由角(或三个自由角)时,要用到三角形的内角和定理.14.【分析】设表示出的面积及的面积进而表示出四边形的面积并化简所得面积的解析式为正弦函数形式再根据三角函数的有界性进行求解【详解】四边形的面积的面积的面积设则的面积的面积四边形的面积故当即时四边形的面积解析:【分析】设AOB θ∠=,表示出ABC 的面积及OAB 的面积,进而表示出四边形OACB 的面积,并化简所得面积的解析式为正弦函数形式,再根据三角函数的有界性进行求解. 【详解】四边形OACB 的面积OAB =△的面积ABC +△的面积,设AOB θ∠=,2222cos 31214AB OA OB OA OB θθθ∴=+-⋅⋅=+-⨯=-则ABC 的面积213sin 60cos 22AB AC θ=⋅⋅︒=OAB 的面积11sin 1222OA OB θθθ=⋅⋅=⨯=,四边形OACB 的面积3cos 2θθ=13(sin )60)2θθθ=-=-︒,故当6090θ-︒=︒,即150θ=︒时,四边形OACB =故答案为: 【点睛】方法点睛:应用余弦定理一定要熟记两种形式:(1)2222cos a b c bc A =+-;(2)222cos 2b c a A bc+-=,同时还要熟练掌握运用两种形式的条件.另外,在解与三角形、三角函数有关的问题时,还需要记住30,45,60︒︒︒等特殊角的三角函数值,以便在解题中直接应用.15.【分析】利用正弦定理和两角和的正弦公式得出角的关系由为锐角三角形得到角的范围进而利用二倍角公式得出的取值范围【详解】由已知得即为锐角三角形故答案为:【点睛】本题考查正弦定理的应用考查两角和与差的正弦解析:【分析】利用正弦定理和两角和的正弦公式得出角A ,B 的关系,由ABC 为锐角三角形得到角A 的范围,进而利用二倍角公式得出ba的取值范围.【详解】由已知sin sin()sin (12cos )C A B A B =+=+sin cos cos sin sin 2sin cos A B A B A A B ∴+=+得sin()sin B A A -=B A A ∴-=,即2B A =ABC 为锐角三角形 2,322B AC A B A ππππ∴=<=--=-<,cos 64A A ππ∴<<∴∈sin 2sin cos 2cos sin sin b B A A A a A A∴===∈故答案为: 【点睛】本题考查正弦定理的应用,考查两角和与差的正弦公式,考查二倍角公式,属于中档题.16.【分析】由三角形的面积公式结合等式可求得然后利用二倍角余弦公式结合弦化切可求得所求代数式的值【详解】因为所以则故故答案为:【点睛】本题考查利用三角形的面积公式二倍角余弦公式诱导公式以及弦化切求值考查解析:12-【分析】由三角形的面积公式结合等式8cos 3ABC bc A S =△,可求得3tan 4A =,然后利用二倍角余弦公式、结合弦化切可求得所求代数式的值. 【详解】因为881cos sin 332ABC bc A S bc A ==⨯△,所以4cos sin 3A A =,则3tan 4A =,故()()22cos sin 1cos sin sin cos sin cos 22sin cos 2sin cos 2sin cos 2sin cos B CA B C A A A A A A A A A A A A A π++-+++--===---- tan 112tan 12A A -==--. 故答案为:12-.【点睛】 本题考查利用三角形的面积公式、二倍角余弦公式、诱导公式以及弦化切求值,考查计算能力,属于中等题.17.【分析】设则根据面积公式得由余弦定理求得代入化简由三角形三边关系求得由二次函数的性质求得取得最大值【详解】解:设则根据面积公式得由余弦定理可得可得:由三角形三边关系有:且解得:故当时取得最大值故答案解析:43【分析】设AC x =,则2AB x =,根据面积公式得ABC S ∆=,由余弦定理求得cos C 代入化简ABC S ∆=223x <<,由二次函数的性质求得ABC S ∆取得最大值. 【详解】解:设AC x =,则2AB x =,根据面积公式得 1sin sin 12ABC S AC BC C x C x ∆=== 由余弦定理可得2224443cos 44x x x C x x+--==,可得:ABCS ∆==由三角形三边关系有:22x x +>,且22x x +>,解得:223x <<,故当x =时,ABC S ∆取得最大值43, 故答案为:43. 【点睛】本题主要考查余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题,属于中档题.18.【分析】先由余弦定理可将条件整理得到利用正弦定理得到;结合二倍角公式;再由和差化积公式得:代入①整理得;求出和的关系求出角的范围即可求解【详解】解:由余弦定理可知则整理得即由正弦定理可得即①由和差化解析:,1) 【分析】先由余弦定理可将条件整理得到22c a ab -=,利用正弦定理得到22sin sin sin sin C A A B -=;结合二倍角公式1cos21cos2cos2cos2sin sin 222C A A CA B ----==;再由和差化积公式得:cos2cos22sin()sin()A C A C A C -=-+-代入①整理得sin sin()sin()A A C C A =--=-;求出A 和C 的关系,求出角的范围即可求解. 【详解】解:由余弦定理可知222cos 2a b c C ab+-=,则22222a b c b aab a +--=, 整理得2222a b c b ab +-=-,即22c a ab -=, 由正弦定理可得,22sin sin sin sin C A A B -=, 即1cos21cos2cos2cos2sin sin 222C A A CA B ----==①, 由和差化积公式得:cos2cos22sin()sin()A C A C A C -=-+-代入①得 sin()sin()sin sin A C A C A B -+-=;因为sin()sin 0A C B +=≠; sin sin()sin()A A C C A ∴=--=-;在锐角ABC ∆中,C A A -=即2C A =, 则3B A C A ππ=--=-,因为02022032A A A ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩,∴64A ππ<<,tan A ∴的取值范围是,1);故答案为:,1). 【点睛】本题主要考查正弦定理、余弦定理以及和差化积公式的应用,特殊角的三角函数值,属于中档题.19.30【分析】结合图形利用正弦定理与直角三角形的边角关系即可求出塔高AB 的长【详解】在△BCD 中∠BCD =15°∠CBD =30°∴=∴=CB =30×=30;中∠ACB =45°∴塔高AB =BC =30m 故解析:30 【分析】结合图形,利用正弦定理与直角三角形的边角关系,即可求出塔高AB 的长. 【详解】在△BCD 中,∠BCD =15°,∠CBD =30°,CD =,∴sin CD CBD ∠=sin CB CDB ∠,∴sin 30︒=()sin 1801530CB ︒︒︒--, CB =30; Rt ABC △中,∠ACB =45°, ∴塔高AB =BC =30m . 故答案为:30. 【点睛】本题考查了正弦定理和直角三角形的边角关系应用问题,是基础题.20.③④【分析】举出反例可判断①②;由同角三角函数的平方关系正弦定理可得再由余弦定理可判断③;由正弦定理可得再由三角形有两个可得且即可判断④;即可得解【详解】对于①当时满足此时△ABC 不是等腰三角形故①解析:③④ 【分析】举出反例可判断①、②;由同角三角函数的平方关系、正弦定理可得222a b c +<,再由余弦定理可判断③;由正弦定理可得8sin x A =,再由三角形有两个可得566A ππ<<且2A π≠,即可判断④;即可得解.【详解】 对于①,当3A π=,6B π=时,满足sin 2sin 2A B =,此时△ABC 不是等腰三角形,故①错误; 对于②,当23A π=,6B π=时,满足sin cos A B =,此时△ABC 不是直角三角形,故②错误;对于③,∵222sin sin cos 1A B C ++<,∴22222sin sin cos sin cos A B C C C ++<+, ∴222sin sin sin A B C +<,∴根据正弦定理得222a b c +<,∵222cos 02a b c C ab+-=<,()0,C π∈,∴C 为钝角,∴△ABC 为钝角三角形,故③正确;对于④,∵,4,6C c a x π===,∴根据正弦定理得481sin sin 2a c A C ===,∴8sin x A =, 由题意566A ππ<<,且2A π≠,∴1sin 12A <<,∴48x ,即x 的取值范围为(4,8),故④正确.故答案为:③④. 【点睛】本题考查了三角函数及解三角形的综合应用,考查了运算求解能力,合理转化条件是解题关键,属于中档题.三、解答题21.条件选择见解析;最大值为3. 【分析】分别选择条件①②③,利用正弦定理和余弦定理,化简得到22312b a -=,再由余弦定理得28cos 2b A b -=,进而求得sin A ,利用面积公式求得ABCS ∆=,即可求解. 【详解】选择条件①:因为tan 2tan B C =,所以sin cos 2sin cos B C C B =, 根据正弦定理可得cos 2cos b C c B =,由余弦定理得:222222222a b c a c b b c ab ac+-+-⨯=⨯, 又由2c =,可得22312b a -=,根据余弦定理得22228cos 22b c a b A bc b+--==,则sin A ===,所以1sin 22ABCSbc A b b ∆==⨯=, 所以当且仅当210b =时,ABC ∆面积取得最大值,最大值为3. 选择条件②:因为22312b a -=,由余弦定理得22228cos 22b c a b A hc h+--==,所以sin A ===,1sin 22ABC S bc A b b∆==⨯=,所以当且仅当210b =时,ABC ∆面积取得最大值,最大值为3.选择条件③:因为cos 2cos b C c B =,由余弦定理得:222222222a b c a c b b c ab ac+-+-⨯=⨯, 因为2c =,可得22312b a -=,又由余弦定理得:22228cos 22b c a b A bc b+--==,所以sin 2A b===,1sin 2ABCS bc A b ∆===, 所以当且仅当210b =时,ABC ∆面积取得最大值,最大值为3. 【点睛】对于解三角形问题的常见解题策略:对于解三角形问题,通常利用正弦定理进行“边转角”寻求角的关系,利用“角转边”寻求边的关系,利用正、余弦定理解三角形问题是高考高频考点,同时注意三角形内角和定理,三角形面积公式在解题中的应用.22.(1)23B π=;(2)ABC S =△. 【分析】(1)利用正弦定理角化边,整理求得cos B ,由B 的范围可得结果;(2)利用余弦定理和基本不等式可求得当3a c ==时周长最大,由三角形面积公式可求得结果. 【详解】(1)由正弦定理得:222b ac ac --=,2221cos 22a cb B ac +-∴==-,()0,B π∈,23B π∴=; (2)由余弦定理得:()()222222cos 29b a c ac B a c ac ac a c ac =+-=+-+=+-=,()2292a c ac a c +⎛⎫∴=+-≤ ⎪⎝⎭(当且仅当a c =时取等号),6a c ∴+≤,∴当3a c ==时,ABC 取得最大值,此时19sin 2224ABCSac B ==⨯=. 【点睛】方法点睛:求解与边长相关的最值或取值范围类问题通常有两种方法:①利用正弦定理边化角,将所求式子转化为与三角函数值域有关的问题的求解,利用三角恒等变换和三角函数的知识来进行求解;②利用余弦定理构造方程,结合基本不等式求得基本范围;应用此方法时,需注意基本不等式等号成立的条件. 23.(1)45;(2)2. 【分析】(1)首先利用两角差的正切公式求出tan A ,再根据同角三角函数的基本关系及二倍角公式计算可得;(2)由(1)可知,1tan 2A =,即可求出sin A ,cos A ,再利用余弦定理及面积公式计算可得; 【详解】 解:(1)5tan tan 44A A ππ⎫⎫⎛⎛-=-⎪ ⎪⎝⎝⎭⎭1tan 11tan 3A A -==+,解得1tan 2A =,故2222cos sin cos2sin cos AA A A A+=+214tan 15A ==+. (2)由(1)可知,sin 1tan cos 2A A A ==①,且22sin cos 1A A +=②;联立①②,解得sin A =,cos A =.又1sin 42S bc A ==,4c =,可得b = 2222cos 4a b c bc A =+-=,则2a =.即2BC =.24.答案见解析. 【分析】选条件①②.结合3b =,得545cos c a b A -=,进而根据边角互化整理得:cos 45B =,3sin 5B =,再结合π2=+A C ,得π22B C =-,故3cos25C =,进而得sin C =最后利用正弦定理求解.选条件①③.结合已知由面积公式得sin 2a C =,结合π2=+A C ,得π22B C =-,故由正弦定理得sin 3cos sin cos2b A Ca B C==,所以3sin24cos2C C =,再根据π0π2A C <=+<02πC <<,进一步结合同角三角函数关系得3cos25C =,利用二倍角公式得sin C =最后由正弦定理得sin sin b Cc B=选条件②③.结合3b =,得545cos c a b A -=,进而根据边角互化整理得:cos 45B =,再根据面积公式得10ac =,由余弦定理得2225a c +=,联立方程解得c =c =.【详解】解:方案一:选条件①②.因为5415cos -=c a A ,3b =,所以545cos c a b A -=, 由正弦定理得5sin 4sin 5sin cos C A B A -=. 因为()sin sin sin cos cos sin C A B A B A B =+=+, 所以5cos sin 4sin B A A =. 因为sin 0A >, 所以cos 45B =,3sin 5B ==. 因为π2=+A C ,πABC ++=,所以π22B C =-, 所以π3cos 2cos sin 25C B B ⎛⎫=-== ⎪⎝⎭,所以21cos21sin 25C C -==. 因为()0,πC ∈,所以sin C =, 在ABC中,由正弦定理得3sin 53sin 5b Cc B===方案二:选条件①③. 因为1sin 32S ab C ==,3b =,所以sin 2a C =. 因为π2=+A C ,πABC ++=,所以π22B C =-. 在ABC 中,由正弦定理得π3sin sin 3cos 2πsin cos 2sin 22C b A C a B CC ⎛⎫+ ⎪⎝⎭===⎛⎫- ⎪⎝⎭, 所以3sin cos 2cos2C CC=,即3sin24cos2C C =.因为π0π,20π,A C C ⎧<=+<⎪⎨⎪<<⎩所以π02C <<,02πC <<, 所以sin20C >,所以cos20C >.又22sin 2cos 21C C +=,所以3cos25C =, 所以21cos21sin 25C C -==,所以sin C = 在ABC中,由正弦定理得3sin sin sin 53πsin cos 2sin 252b C b C b C c B C C ====⎛⎫- ⎪⎝⎭. 方案三:选条件②③.因为5415cos -=c a A ,3b =,所以545cos c a b A -=,由正弦定理得5sin 4sin 5sin cos C A B A -=,因为()sin sin sin cos cos sin C A B A B A B =+=+,所以5cos sin 4sin B A A =.因为sin 0A >, 所以cos 45B =,3sin 5B ==. 因为1sin 32S ac B ==,所以10ac =.(ⅰ) 在ABC 中,由余弦定理得2222cos b a c ac B =+-,所以2225a c +=.(ⅱ)由(ⅰ)(ⅱ)解得c =c =. 【点睛】试题把设定的方程与三角形内含的方程(三角形的正、余弦定理,三角形内角和定理等)建立联系,从而求得三角形的部分定量关系,体现了理性思维、数学探索等学科素养,考查逻辑思维能力、运算求解能力,是中档题.本题如果选取②5415cos -=c a A ,则需根据3b =将问题转化为545cos c a b A -=,再结合边角互化求解.25.(1)π3A =;(2)6. 【分析】(1)由正弦定理把条件cos cos 2cos b C c B a A +=转化为角的关系,再由两角和的正弦公式及诱导公式得A 的关系式,从而可得结论;(2)首先可根据解三角形面积公式得出8bc =,然后根据余弦定理计算出6b c +=.【详解】(1)因为cos cos 2cos b C c B a A +=由正弦定理得,sin cos sin cos 2sin cos B C C B A A +=所以()sin sin 2sin cos B C A A A +==因为0πA <<所以,sin 0A ≠ 所以1cos 2A =,所以π3A =(2)因为ABC 的面积为所以1sin 2bc A =因为π3A =,所以1πsin 23bc =, 所以8bc =.由余弦定理得,2222cos a b c bc A =+-,因为a =,π3A =, 所以()()2222π122cos 3243b c bc b c bc b c =+-=+-=+-, 所以6b c +=.【点睛】关键点点睛:解题时要注意边角关系的转化.求“角”时,常常把已知转化为角的关系,求“边”时,常常把条件转化为边的关系式,然后再进行转化变形.26.条件选择见解析;3B π=,b 最小值为12. 【分析】选①,利用三角形的内角和定理、诱导公式以及两角和的余弦公式化简得出tan B =结合()0,B π∈可求得B ,再利用余弦定理结合二次函数的基本性质可求得b 的最小值; 选②,利用三角形的内角和定理、诱导公式以及二倍角的余弦公式求出cos B 的值,结合()0,B π∈可求得B ,再利用余弦定理结合二次函数的基本性质可求得b 的最小值; 选③,利用正弦定理边角互化、三角形的内角和定理以及两角和的正弦公式化简可求得tan B =()0,B π∈可求得B ,再利用余弦定理结合二次函数的基本性质可求得b 的最小值.【详解】解:若选择①:在ABC 中,有A B C π++=,则由题可得:()()cos cos cos 0A B A A B π-++-=⎡⎤⎣⎦, ()cos cos cos cos 0A B A B A B -++=,sin sin cos cos cos cos cos 0A B A B A B A B -+-=,sin sin cos A B A B =,又sin 0A ≠,所以sin B B =,则tan B =又()0,B π∈,所以3B π=,因为1a c +=,所以1c a =-,()0,1a ∈.由余弦定理可得:2222cos b a c ac B =+-22a c ac =+-()()2211a a a a =+---2331a a =-+, ()0,1a ∈,又2211324b a ⎛⎫=-+ ⎪⎝⎭, 所以,当12a =时,()2min 14b =,即b 的最小值为12; 若选择②:在ABC 中,有A B C π++=, 则由题可得()222cos 13cos 2cos 3cos 11B B B B π---=+-=, 解得1cos 2B =或cos 2B =-(舍去), 又()0,πB ∈,所以3B π=.(剩下同①)若选择③:由正弦定理可将已知条件转化为sin cos sin sin 3B C C B A +=, ()()sin cos s s in cos in sin sin B C C B A B C B C π=+=-+=+⎡⎤⎣⎦,代入上式得sin sin cos 3C B C B =,又sin 0C ≠,所以sin B B =,tan B =又()0,B π∈,所以3B π=.(剩下同①) 【点睛】方法点睛:在解三角形的问题中,若已知条件同时含有边和角,但不能直接使用正弦定理或余弦定理得到答案,要选择“边化角”或“角化边”,变换原则如下:(1)若式子中含有正弦的齐次式,优先考虑正弦定理“角化边”;(2)若式子中含有a 、b 、c 的齐次式,优先考虑正弦定理“边化角”;(3)若式子中含有余弦的齐次式,优先考虑余弦定理“角化边”;(4)代数式变形或者三角恒等变换前置;(5)含有面积公式的问题,要考虑结合余弦定理求解;(6)同时出现两个自由角(或三个自由角)时,要用到三角形的内角和定理.。
【典型题】高中必修五数学上期末试题附答案(1)
【典型题】高中必修五数学上期末试题附答案(1)一、选择题1.已知点(),M a b 与点()0,1N -在直线3450x y -+=的两侧,给出以下结论:①3450a b -+>;②当0a >时,+a b 有最小值,无最大值;③221a b +>;④当0a >且1a ≠时,11b a +-的取值范围是93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭,正确的个数是( ) A .1B .2C .3D .42.数列{}n a 满足()11nn n a a n ++=-⋅,则数列{}n a 的前20项的和为( ) A .100B .-100C .-110D .1103.正项等比数列中,的等比中项为,令,则( ) A .6B .16C .32D .644.等比数列{}n a 的前n 项和为n S ,若36=2S =18S ,,则105S S 等于( ) A .-3B .5C .33D .-315.已知数列{}n a 的首项110,211n n n a a a a +==++,则20a =( ) A .99B .101C .399D .4016.已知数列{}n a 的前n 项和为n S ,1112n n a S a +=,=, 则n S =( )A .12n -B .13()2n -C .12()3n - D .112n - 7.数列{}{},n n a b 为等差数列,前n 项和分别为,n n S T ,若3n 22n n S T n +=,则77a b =( ) A .4126B .2314C .117 D .1168.在ABC ∆中,,,a b c 是角,,A B C 的对边,2a b =,3cos 5A =,则sinB =( ) A .25B .35C .45 D .859.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,且()cos 4cos a B c b A =-,则cos2A =( ) A .78B .18C .78-D .18-10.已知数列{}n a 满足112,0,2121,1,2n n n n n a a a a a +⎧≤<⎪⎪=⎨⎪-≤<⎪⎩若135a =,则数列的第2018项为( ) A .15B .25C .35D .4511.已知数列{}n a 的前n 项和为n S ,且()*21n n S a n N =-∈,则5a 等于( )A .16-B .16C .31D .3212.已知x 、y 满足约束条件50{03x y x y x -+≥+≥≤,则24z x y =+的最小值是( )A .6-B .5C .10D .10-二、填空题13.已知实数,且,则的最小值为____14.已知数列{}n a 的前n 项和为21nn S =-,则此数列的通项公式为___________.15.已知数列{}n a 中,其中199199a =,11()an n a a -=,那么99100log a =________16.若x ,y 满足约束条件1300x y x y x y -≥-⎧⎪+≤⎪⎨≥⎪⎪≥⎩,则2z x y =-的最大值是__________.17.已知数列{}{}n n a b 、满足ln n n b a =,*n ∈N ,其中{}n b 是等差数列,且431007e a a ⋅=,则121009b b b +++=L ________.18.已知平面四边形ABCD 中,120BAD ∠=︒,60BCD ∠=︒,2AB AD ==,则AC 的最大值为__________.19.若无穷等比数列{}n a 的各项和为2,则首项1a 的取值范围为______. 20.设(32()lg 1f x x x x =++,则对任意实数,a b ,“0a b +≥”是“()()0f a f b +≥”的_________条件.(填“充分不必要”.“必要不充分”.“充要”.“既不充分又不必要”之一)三、解答题21.已知正项等比数列{}n a 满足26S =,314S =. (1)求数列{}n a 的通项公式;(2)若2log n n b a =,已知数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和为n T 证明:1n T <. 22.已知锐角ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c,且满足2sin 1cos A C B =-.(1)若2a =,c =b ; (2)若sin 4B =,a =b . 23.记等差数列{}n a 的前n 项和为n S ,已知2446,10a a S +==. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令2n n n b a =⋅*()n N ∈,求数列{}n b 的前n 项和n T .24.已知在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,sin tan cos sin tan cos b B C b B a A C a A -=-. (1)求证:A B =;(2)若c =3cos 4C =,求ABC ∆的周长.25.设n S 为等差数列{}n a 的前n 项和,公差d ∈N ,25a =,且53545S <<. (1)求{}n a 的通项公式;(2)设数列{}237n S n -的前n 项和为n T ,若m n T T ≤,对n *∈N 恒成立,求m . 26.已知数列{}n a 的首项1122,,1,2,3, (31)n n n a a a n a +===+. (1)证明: 数列11n a ⎧⎫-⎨⎬⎩⎭是等比数列; (2)数列n n a ⎧⎫⎨⎬⎩⎭的前n 项和n S .【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【解析】 【分析】 【详解】∵点M (a ,b )与点N (0,−1)在直线3x −4y +5=0的两侧,∴()()34530450a b -+⨯++<,即3450a b -+<,故①错误; 当0a >时,54a b +>,a +b 即无最小值,也无最大值,故②错误; 设原点到直线3x −4y +5=0的距离为d ,则22513(4)==+-d ,则22a b +>1,故③正确;当0a >且a ≠1时,11b a +-表示点M (a ,b )与P (1,−1)连线的斜率. ∵当0a =,b =54时,51194114b a ++==---,又直线3x −4y +5=0的斜率为34, 故11b a +-的取值范围为93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭,故④正确.∴正确命题的个数是2个. 故选B.点睛:本题是常规的线性规划问题,线性规划问题常出现的形式有:①直线型,转化成斜截式比较截距,要注意z 前面的系数为负时,截距越大,z 值越小;②分式型,其几何意义是已知点与未知点的斜率;③平方型,其几何意义是距离,尤其要注意的是最终结果应该是距离的平方;④绝对值型,转化后其几何意义是点到直线的距离.2.B解析:B 【解析】 【分析】数列{a n }满足1(1)nn n a a n ++=-⋅,可得a 2k ﹣1+a 2k =﹣(2k ﹣1).即可得出.【详解】∵数列{a n }满足1(1)nn n a a n ++=-⋅,∴a 2k ﹣1+a 2k =﹣(2k ﹣1).则数列{a n }的前20项的和=﹣(1+3+……+19)()101192⨯+=-=-100.故选:B . 【点睛】本题考查了数列递推关系、数列分组求和方法,考查了推理能力与计算能力,属于中档题.3.D解析:D 【解析】因为,即,又,所以.本题选择D 选项.4.C解析:C 【解析】 【分析】由等比数列的求和公式结合条件求出公比,再利用等比数列求和公式可求出105S S . 【详解】设等比数列{}n a 的公比为q (公比显然不为1),则()()61636333111119111a q S q q q S qa q q---===+=---,得2q =, 因此,()()101105510555111111233111a q S q q q S q a qq---===+=+=---,故选C. 【点睛】本题考查等比数列基本量计算,利用等比数列求和公式求出其公比,是解本题的关键,一般在求解等比数列问题时,有如下两种方法:(1)基本量法:利用首项和公比列方程组解出这两个基本量,然后利用等比数列的通项公式或求和公式来进行计算;(2)性质法:利用等比数列下标有关的性质进行转化,能起到简化计算的作用.5.C解析:C 【解析】 【分析】 【详解】由1211n n n a a a +=++,可得)211111111n n n n a a a a +++=+++=,,{}+1n a 是以1为公差,以1为首项的等差数列.∴21,1n n a n a n +==-,即220201399a =-=.故选C.6.B解析:B 【解析】 【分析】利用公式1n n n a S S -=-计算得到11323,2n n n n S S S S ++==,得到答案. 【详解】由已知1112n n a S a +==,,1n n n a S S -=- 得()12n n n S S S -=-,即11323,2n n n n S S S S ++==, 而111S a ==,所以13()2n n S -=.故选B. 【点睛】本题考查了数列前N 项和公式的求法,利用公式1n n n a S S -=-是解题的关键.7.A解析:A 【解析】依题意,113713113713132412226132a a a S b b b T +⋅===+⋅.8.A解析:A 【解析】试题分析:由3cos 5A =得,又2a b =,由正弦定理可得sin B =.考点:同角关系式、正弦定理.9.C解析:C 【解析】 【分析】根据题目条件结合三角形的正弦定理以及三角形内角和定理可得sin A ,进而利用二倍角余弦公式得到结果.∵()cos 4cos a B c b A =-. ∴sin A cos B =4sin C cos A ﹣sin B cos A 即sin A cos B +sin B cos A =4cos A sin C ∴sin C =4cos A sin C ∵0<C <π,sin C ≠0. ∴1=4cos A ,即cos A 14=, 那么27cos2218A cos A =-=-. 故选C 【点睛】本题考查了正弦定理及二倍角余弦公式的灵活运用,考查计算能力,属于基础题.10.A解析:A 【解析】 【分析】利用数列递推式求出前几项,可得数列{}n a 是以4为周期的周期数列,即可得出答案. 【详解】1112,0321521,12n n n n n a a a a a a +⎧≤<⎪⎪==⎨⎪-≤<⎪⎩Q , 211215a a =-=,32225a a ==,43425a a ==,5413215a a a =-== ∴数列{}n a 是以4为周期的周期数列,则201845042215a a a ⨯+===. 故选A . 【点睛】本题考查数列的递推公式和周期数列的应用,考查学生分析解决问题的能力,属于中档题.11.B解析:B 【解析】 【分析】令1n =,由11a S =可求出1a 的值,再令2n ≥,由21n n S a =-得出1121n n S a --=-,两式相减可得出数列{}n a 为等比数列,确定出该数列的公比,利用等比数列的通项公式可求出5a 的值.当1n =时,1121S a =-,即1121a a =-,解得11a =;当2n ≥时,由21n n S a =-,得1121n n S a --=-,两式相减得122n n n a a a -=-,得12n n a a -=.所以,数列{}n a 是以1为首项,以2为公比的等比数列,则451216a =⨯=,故选:B. 【点睛】本题考查利用n S 来求通项n a ,一般利用公式11,1,2n nn S n a S S n -=⎧=⎨-≥⎩,同时也要注意等差数列和等比数列定义的应用,考查运算求解能力,属于中等题.12.A解析:A 【解析】 【分析】 【详解】作出不等式50{03x y x y x -+≥+≥≤所表示可行域如图所示,作直线:24l z x y =+,则z 为直线l 在y 轴上截距的4倍, 联立3{x x y =+=,解得3{3x y ==-,结合图象知,当直线l 经过可行域上的点()3,3A -时,直线l 在y 轴上的截距最小, 此时z 取最小值,即()min 23436z =⨯+⨯-=-,故选A.考点:线性规划二、填空题13.3+54【解析】【分析】由a+b=2得出b=2﹣a代入代数式中化简后换元t =2a﹣1得2a=t+1得出1<t<3再代入代数式化简后得出2t6t-(t2+5)然后在分式分子分母中同时除以t利用基本不等解析:【解析】【分析】由a+b=2得出b=2﹣a,代入代数式中,化简后换元t=2a﹣1,得2a=t+1,得出1<t<3,再代入代数式化简后得出,然后在分式分子分母中同时除以t,利用基本不等式即可求出该代数式的最小值.【详解】解:由于a+b=2,且a>b>0,则0<b<1<a<2,所以,,令t=2a﹣1∈(1,3),则2a=t+1,所以,.当且仅当,即当时,等号成立.因此,的最小值为.故答案为:.【点睛】本题考查利用基本不等式求最值,解本题的关键就是对代数式进行化简变形,考查计算能力,属于中等题.14.【解析】【分析】由数列的前项和为得时得出;验证时是否满足即可【详解】当时当时又所以故答案为:【点睛】本题考查了由数列的前项和公式推导通项公式的计算问题;解题时需验证时是否满足是基础题解析:12n n a -=【解析】 【分析】由数列{}n a 的前n 项和为23nn S =-,得2n >时1123n n S --=-,,得出1n n n a S S -=-;验证1n =时11a S =是否满足n a 即可. 【详解】当1n =时,11211a S ==-=, 当2n ≥时,()11121212nn n n n n a S S ---=-=---=,又1121-=,所以12n n a -=. 故答案为:12n n a -=.【点睛】本题考查了由数列{}n a 的前n 项和公式n S 推导通项公式n a 的计算问题;解题时,需验证1n =时11a S =是否满足n a ,是基础题.15.1【解析】【分析】由已知数列递推式可得数列是以为首项以为公比的等比数列然后利用等比数列的通项公式求解【详解】由得则数列是以为首项以为公比的等比数列故答案为:1【点睛】本题考查数列的递推关系等比数列通解析:1 【解析】 【分析】由已知数列递推式可得数列99{log }n a 是以199991991log 9999log a ==为首项,以19999为公比的等比数列,然后利用等比数列的通项公式求解. 【详解】由11()an n a a -=,得991991log log n n a a a -=,∴199991991l 9og log 9nn a a a -==,则数列99{log }n a 是以199991991log 9999log a ==为首项,以19999为公比的等比数列, ∴19999991001log (99)199a =⋅=. 故答案为:1. 【点睛】本题考查数列的递推关系、等比数列通项公式,考查运算求解能力,特别是对复杂式子的理解.16.﹣33【解析】分析:由约束条件作出可行域化目标函数为直线方程的斜截式数形结合得到最优解联立方程组求出最优解的坐标代入目标函数得答案详解:由约束条件作出可行域如图:联立解得化目标函数为直线方程的斜截式 解析:[﹣3,3]【解析】分析:由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.详解:由约束条件作出可行域如图:联立13x y x y -=-+=,解得12x y ==,()1,2B , 化目标函数2z x y =-为直线方程的斜截式22x z y =-. 由图可知,当直线22x z y =-过()1,2B ,直线在y 轴上的截距最大,z 最小,最小值为1223-⨯=-; 当直线22x z y =-过()3,0A 时,直线在y 轴上的截距最小,z 最大,最大值为3203-⨯=. ∴2z x y =-的取值范围为[﹣3,3].故答案为:[﹣3,3].点睛:利用线性规划求最值,一般用图解法求解,其步骤是(1)在平面直角坐标系内作出可行域.(2)考虑目标函数的几何意义,将目标函数进行变形.(3)确定最优解:在可行域内平行移动目标函数变形后的直线,从而确定最优解.(4)求最值:将最优解代入目标函数即可求出最大值或最小值.17.2018【解析】【分析】数列{an}{bn}满足bn =lnann∈N*其中{bn}是等差数列可得bn+1﹣bn =lnan+1﹣lnan =ln 常数t 常数et =q >0因此数列{an}为等比数列由可得a1解析:2018【解析】【分析】数列{a n }、{b n }满足b n =lna n ,n ∈N *,其中{b n }是等差数列,可得b n +1﹣b n =lna n +1﹣lna n =ln 1n na a +=常数t .1n na a +=常数e t =q >0,因此数列{a n }为等比数列.由431007e a a ⋅=, 可得a 1a 1009=a 2a 1008431007a a e =⋅==L .再利用对数运算性质即可得出.【详解】解:数列{a n }、{b n }满足b n =lna n ,n ∈N *,其中{b n }是等差数列,∴b n +1﹣b n =lna n +1﹣lna n =ln 1n na a +=常数t . ∴1n na a +=常数e t =q >0, 因此数列{a n }为等比数列.且431007e a a ⋅=,∴a 1a 1009=a 2a 1008431007a a e =⋅==L .则b 1+b 2+…+b 1009=ln (a 1a 2…a 1009)41009()ln e ==lne 2018=2018.故答案为:2018.【点睛】本题考查了等比数列的通项公式与性质、对数运算性质,考查了推理能力与计算能力,属于中档题.18.4【解析】【分析】由题知:四边形为圆内接四边形的最大值为四边形外接圆的直径由正弦定理即可求出的最大值【详解】因为所以故的最大值为四边形外接圆的直径当为四边形外接圆的直径时得到:又因为所以在中由正弦定 解析:4【解析】【分析】由题知:四边形ABCD 为圆内接四边形,AC 的最大值为四边形外接圆的直径,由正弦定理即可求出AC 的最大值.【详解】因为120BAD ∠=︒,60BCD ∠=︒,所以故AC 的最大值为四边形外接圆的直径.当AC 为四边形外接圆的直径时,得到:90ADC ABC ∠=∠=︒,又因为2AB AD ==,60BCD ∠=︒,所以30ACD ACB ∠=∠=︒.在ABC V 中,由正弦定理得:sin 90sin 30AC AB =︒︒,解得:4AC =. 故答案为:4【点睛】本题主要考查正弦定理得应用,判断四边形ABCD 为圆内接四边形是解题的关键,属于中档题.19.【解析】【分析】首先根据无穷等比数列的各项和为2可以确定其公比满足利用等比数列各项和的公式得到得到分和两种情况求得的取值范围得到结果【详解】因为无穷等比数列的各项和为2所以其公比满足且所以当时当时所 解析:(0,2)(2,4)U .【解析】【分析】首先根据无穷等比数列{}n a 的各项和为2,可以确定其公比满足01q <<,利用等比数列各项和的公式得到121a q=-,得到122a q =-,分01q <<和10q -<<两种情况求得1a 的取值范围,得到结果.【详解】因为无穷等比数列{}n a 的各项和为2,所以其公比q 满足01q <<,且121a q=-, 所以122a q =-,当01q <<时,1(0,2)a ∈,当10q -<<时,1(2,4)a ∈,所以首项1a 的取值范围为(0,2)(2,4)U ,故答案是:(0,2)(2,4)U .【点睛】该题考查的是有关等比数列各项和的问题,涉及到的知识点有等比数列存在各项和的条件,各项和的公式,注意分类讨论,属于简单题目. 20.充要【解析】所以为奇函数又为单调递增函数所以即是的充要条件点睛:充分必要条件的三种判断方法1定义法:直接判断若则若则的真假并注意和图示相结合例如⇒为真则是的充分条件2等价法:利用⇒与非⇒非⇒与非⇒非 解析:充要【解析】33()()lg(()lg(lg10f x f x x x x x +-=++-+-== ,所以()f x 为奇函数,又()f x 为单调递增函数,所以0()()()()()()0a b a b f a f b f a f b f a f b +≥⇔≥-⇔≥-⇔≥-⇔+≥ ,即“0a b +≥”是“()()0f a f b +≥”的充要条件点睛:充分、必要条件的三种判断方法.1.定义法:直接判断“若p 则q ”、“若q 则p ”的真假.并注意和图示相结合,例如“p ⇒q ”为真,则p 是q 的充分条件.2.等价法:利用p ⇒q 与非q ⇒非p ,q ⇒p 与非p ⇒非q ,p ⇔q 与非q ⇔非p 的等价关系,对于条件或结论是否定式的命题,一般运用等价法.3.集合法:若A ⊆B ,则A 是B 的充分条件或B 是A 的必要条件;若A =B ,则A 是B 的充要条件.三、解答题21.(1)2n n a =; (2)见解析.【解析】【分析】(1)由等比数列前n 项和公式求出公比q 和首项1a ,得通项公式;(2)用裂项相消法求出和n T ,可得结论.【详解】(1)设等比数列的首项及公比分别为10a >,0q >,26S =Q ,314S =,显然1q ≠,()()21311611141a q q a q q ⎧-⎪=-⎪∴⎨-⎪=⎪-⎩,解得122a q =⎧⎨=⎩, 2n n a ∴=;(2)证明:由(1)知,n b n =,则11111(1)1n n b b n n n n +==-++, 121n n n T b b b b -∴=++⋯⋯++1111111111223111n n n n n =-+-+⋯⋯+-+-=--++, *n N ∈Q ,1n T ∴<.【点睛】本题考查等比数列的前n 项和与通项公式,考查裂项相消法求数列的和.基本量法是解决等差数列和等比数列的常用方法.裂项相消法、错位相减法、分组(并项)求和法是数列求和的特殊方法,它们针对的是特殊的数列求和.22.(1)b =2)b =【解析】【分析】(12b =,根据已知可求b 的值.(2)利用同角三角函数基本关系式可求cos B,由余弦定理可得2224a c ac =+-g,根据已知可求c ,进而可求b 的值. 【详解】(1)Q 22sin 1cos sin A C B B =-=.∴2b =,2a =Q,c =b ∴=(2)sin 4B =Q,cos 4B ∴=, ∴由余弦定理2222cos b a c ac B =+-2224a c ac =+-⋅,又a =c =b ∴=经检验,b【点睛】本题考查正弦定理,同角三角函数基本关系式,余弦定理在解三角形中的综合应用,考查计算能力和转化思想,属于基础题.23.(1)n a n =(2)1(1)22n n T n +=-⋅+【解析】试题分析:(Ⅰ)因为数列是等差数列,所以根据等差数列的通项公式建立关于首项和公差的方程组11246{434102a d a d +=⨯+=,即可解得11{1a d ==,从而写出通项公式n a n =; (Ⅱ)由题意22n n n nb a n =⋅=⋅,因为是等差数列与等比数列相乘的形式,所以采取错位相减的方法,注意错位相减后利用等比数列前n 项和公式,化简要准确得1(1)22n n T n +=-⋅+.试题解析:(Ⅰ)设等差数列{}n a 的公差为d,由2446,10a a S +==,可得11246{434102a d a d +=⨯+=, 即1123{235a d a d +=+=, 解得11{1a d ==, ∴()111(1)n a a n d n n =+-=+-=, 故所求等差数列{}n a 的通项公式为n a n =(Ⅱ)依题意,22n n n n b a n =⋅=⋅,∴12n n T b b b =+++L231122232(1)22n n n n -=⨯+⨯+⨯++-⋅+⋅L ,又2n T =2341122232(1)22n n n n +⨯+⨯+⨯++-⋅+⋅L ,两式相减得2311(22222)2n n n n T n -+-=+++++-⋅L()1212212nn n +-=-⋅-1(1)22n n +=-⋅-,∴1(1)22n n T n +=-⋅+考点:1、等差数列通项公式;2、等差数列的前n 项和;3、等比数列的前n 项和;4、错位相减法.24.(1)证明见解析;(2).【解析】【分析】(1)利用三角函数恒等变换的应用化简已知等式可求in 0()s A B -=,可得()A B k k Z π-=∈,结合范围A ,(0,)B π∈,即可得证A B =.(2)由(1)可得a b =,进而根据余弦定理可求a b ==ABC ∆的周长.【详解】(1)sin tan cos sin tan cos b B C b B a A C a A -=-Q , ∴sin sin sin sin cos cos cos cos b B C a A C b B a A C C-=-, sin sin cos cos sin sin cos cos b B C b B C a A C a A C ∴-=-,cos()cos()a A C b B C ∴+=+,又A B C π++=Q ,cos cos a B b A ∴-=-,sin cos sin cos A B B A ∴-=-,sin()0A B ∴-=,()A B k k Z π∴-=∈,又A Q ,(0,)B π∈,A B ∴=.(2)Q 由(1)可知A B =,可得a b =,又c =Q 3cos 4C =,∴22222323422a a a a a a+--==⋅, 226a b ∴==,可得a b ==ABC ∆∴的周长a b c ++=【点睛】本题考查三角函数恒等变换的应用、余弦定理在解三角形中的综合应用,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意三角函数求值时,要先写出角的范围.25.(1)31n a n =-;(2)11m =或12m =【解析】【分析】(1)由5335545S a <=<可解得3d =,进而求出1a ,得到31n a n =-;(2)由(1)可求出n S ,进而求出237n S n -,即可求出其前n 项和的最小值,从而得出结论.【详解】(1)()()5325555S a a d d ==+=+Q ,()355545d <∴+<,即24d <<,d ∈N Q ,3d ∴=,则122a a d =-=,故()21331n a n n =+-⨯=-;(2)由(1)知,()()2313122n n n n n S +-+==, 则2237336n S n n n -=-,令2370n S n -≤,解得012n ≤≤,则()1211min n T T T ==,故11m =或12m =.【点睛】本题考查求等差数列的通项公式及其性质的应用,属于中档题.26.(1)证明见解析;(2)24222n n n n n S +++=-. 【解析】试题分析:(1)对121n n n a a a +=+两边取倒数得111111222n n n na a a a ++==+⋅,化简得1111112n n a a +⎛⎫-=- ⎪⎝⎭,所以数列11n a ⎧⎫-⎨⎬⎩⎭是等比数列;(2)由(1)11n a ⎧⎫-⎨⎬⎩⎭是等比数列.,求得1112n n a =+,利用错位相减法和分组求和法求得前n 项和24222n n n n n S +++=-. 试题解析:(1)111211111111,?,1112222n n n n n n n n n a a a a a a a a a +++⎛⎫+=∴==+∴-=- ⎪+⎝⎭Q ,又 11211,132a a =∴-=,∴数列11n a ⎧⎫-⎨⎬⎩⎭是以为12首项,12为公比的等比数列. (2)由(1)知,1111111?222n n n a -+-==,即1112nn a =+,设23123 (2222)n n n T =++++, ① 则2311121...22222n n n n n T +-=++++, ② 由①-②得 21111111111122 (112222222212)nn n n n n n n n n T +++⎛⎫- ⎪⎝⎭=+++-=-=---,11222n n n n T -∴=--. 又()1123...2n n n +++++=.∴数列n n a ⎧⎫⎨⎬⎩⎭的前n 项和()2124222222n n n n n n n n n S +++++=-+=-. 考点:配凑法求通项,错位相减法.。
(典型题)高中数学必修五第三章《不等式》测试卷(含答案解析)(1)
一、选择题1.已知正数x ,y 满足1431x y +=+,则x y +的最小值为( ) A .53B .2C .73D .62.设实数x ,y 满足约束条件21,22,x y x y -≤⎧⎨-≥⎩则x y +的最小值是( )A .2B .-2C .1D .-13.已知a b >,不等式220ax x b ++≥对于一切实数x 恒成立,且0x R ∃∈,使得20020ax x b ++=成立,则22a b a b+-的最小值为( )A .1BC .2D.4.若x 、y 满足约束条件36022x y x y y +-≤⎧⎪+≥⎨⎪≤⎩,则22x y +的最小值为( )A .5B .4C .2D5.已知实数,x y 满足24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩,则32z x y =-的最小值是 ( )A .4B .5C .6D .76.设,x y 满足约束条件321104150250x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩,则z x y =+的最小值为( )A .3B .4C .5D .107.若函数()1xy a a =>的图象与不等式组40,20,1x y y x -≤⎧⎪-≥⎨⎪≤+⎩,表示的区域有公共点,则a 的取值范围为( ) A .[]2,4B.⎤⎦C .(][)1,24,⋃+∞D.([)2,⋃+∞8.已知函数()32f x x ax bx c =+++,且()()()01233f f f <-=-=-≤,则( )A .c 3≤B .3c 6<≤C .6c 9<≤D .c 9>9.设x ,y 满足约束条件261322x y x y y -≤⎧⎪⎪+≥⎨⎪≤⎪⎩,则1z x y =-+的最小值是( )A .1-B .0C .1D .210.在ABC 中,BAC ∠的平分线交BC 于D .若3BAC π∠=,4AB AC +=,则AD 长度的最大值为( ) AB .2C .3D.11.设函数2()1f x mx mx =--,若对于任意的x ∈{x |1 ≤ x ≤ 3},()4f x m <-+恒成立,则实数m 的取值范围为( ) A .m ≤0 B .0≤m <57C .m <0或0<m <57D .m <5712.已知不等式230ax bx a --≥的解集是[]4,1-,则b a 的值为( ) A .-64B .-36C .36D .64二、填空题13.若正实数x 、y 、z ,满足3z x y +=,4z y x +=,则x y x y z++-的最小值为_______.14.已知x ,y 满足不等式组220,10,30x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩,则11x z y -=+,则z 的最大值为________.15.若关于x 的不等式250ax x b -+< 的解集为{|23}x x << ,则+a b 的值是__________.16.若不等式20++≥x mx m 在[1,2]x ∈上恒成立,则实数m 的最小值为________ 17.在下列函数中, ①1y x x=+②1123212y x x x ⎛⎫=++< ⎪-⎝⎭③()2114141x y x x x x ⎛⎫=++> ⎪+⎝⎭ ④22221πsin cos 0,sin cos 2y x x x x x ⎛⎫⎛⎫=+∈ ⎪ ⎪⎝⎭⎝⎭其中最小值为2的函数是__________.18.若关于x 的不等式()0f x <和()0g x <的解集分别为(),a b 和11,b a ⎛⎫⎪⎝⎭,则称这两个不等式为“对偶不等式”.若不等式()2220x x θ-+<和不等式()224sin 210x x θ++<为“对偶不等式”,且,2πθπ⎛⎫∈ ⎪⎝⎭,则θ=______.19.若实数x ,y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则3z x y =-的最小值为__________.20.记等差数列{}n a 的前n 项和为n S ,满足570a a ,1122S =,则7811572a a a a a 的最小值为_________.三、解答题21.2020年受疫情影响,全球经济均受到不同程度的冲击.为稳妥有序地推进复工复产,2月11日晚,郑州市相关政府部门印发了《郑州市关于应对新型冠状病毒肺炎疫情促进经济平稳健康发展的若干举措》的通知,并出台多条举措促进全市经济平稳健康发展.某工厂为拓宽市场,计划生产某种热销产品,经调查,该产品一旦投入市场就能全部售出.若不举行促销活动,该产品的年销售量为28万件,若举行促销活动,年销售量y (单位;万件)与年促销费用()0x x ≥(单位;万元)满足3010(ky k x =-+为常数).已知生产该产品的固定成本为80万元,每生产1万件该产品需要再投入生产成本160万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定成本和生产成本,不包括促销成本). (1)求k 的值,并写出该产品的利润L (单位:万元)与促销费用x (单位:万元)的函数关系﹔ (2)该工厂计划投入促销费用多少万元,才能获得最大利润?22.已知m R ∈,命题p :对任意[]0,1x ∈,不等式2223x m m -≥-恒成立;命题q :存在[]1,1x ∈-,使得m ax ≤成立.(1)若p 为真命题,求m 的取值范围;(2)当1a =时,若p q ∨为真,p q ∧为假,求m 的取值范围. 23.已知()f x 是偶函数,()g x 是奇函数,且2()()2f x g x x x +=+-. (1)求()f x 和()g x 的解析式;(2)设2()33h x mx mx =+-(其中m R ∈),解不等式()()h x g x <.24.已知函数2221,()?23,x ax x af x x ax x a ⎧-+<⎪⎪=⎨⎪+-≥⎪⎩,其中 0a >. (1)若()()01ff =,求a 的值.(2)若函数()f x 的图象在x 轴的上方,求a 的取值范围. 25.已知函数()()21,4f x ax bx a b R =++∈,且()10f -=,对任意实数x ,()0f x ≥成立.(1)求函数()f x 的解析式;(2)若0c ≥,解关于x 的不等式()2131424f x c x x c ⎛⎫⎛⎫>+-++ ⎪ ⎪⎝⎭⎝⎭. 26.某单位计划建造一间背面靠墙的小屋,其地面面积为12m 2,墙面的高度为3m ,经测算,屋顶的造价为5800元,房屋正面每平方米的造价为1200元,房屋侧面每平方米的造价为800元,设房屋正面地面长方形的边长为x m ,房屋背面和地面的费用不计. (1)用含x 的表达式表示出房屋的总造价; (2)当x 为多少时,总造价最低?最低造价是多少?【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】化简114[(1)]()131x y x y x y +=++⨯+-+,再利用基本不等式求解. 【详解】由题得1114(1)1[(1)]31[(1)]()1331x y x y x y x y x y +=++-=++⨯-=++⨯+-+ 1141(5)1(5)123131y x x y y +=++-≥+-=++ 当且仅当1x y ==时取等. 所以x y +的最小值为2. 故选:B 【点睛】方法点睛:利用基本不等式求最值时,常用到常量代换,即把所求代数式中的某一常量换成已知中的代数式,再利用基本不等式求解.2.C解析:C 【分析】先作出约束条件对应的可行域,然后分析目标函数的几何意义,结合图形即可求解. 【详解】作出约束条件2122x y x y -≤⎧⎨-≥⎩所表示的平面区域如图所示:移动直线x y z +=,可知当其过点A 时取得最小值, 解方程组2122x y x y -≤⎧⎨-≥⎩,求得10x y =⎧⎨=⎩,即(1,0)A ,代入求得101=+=z ,所以x y +的最小值是1, 故选:C. 【点睛】方法点睛:该题考查的是有关线性规划的问题,解题方法如下: (1)根据题中所给的约束条件画出可行域; (2)根据目标函数的意义找到最优解; (3)解方程组求得最优解的坐标; (4)代入求得最小值,得到结果.3.D解析:D 【分析】根据条件对于一切实数x 不等式恒成立和0x R ∃∈使得方程成立结合二次不等式、二次方程、二次函数,可得1ab =,将22a b a b+-化成2a b a b -+-,再结合基本不等式求解即可.【详解】解:因为不等式220ax x b ++≥对于一切实数x 恒成立,所以0440a ab >⎧⎨-≤⎩,又因为0x R ∃∈,使得20020ax x b ++=成立,所以440ab -≥,所以440ab -=, 即0,0,1a b ab >>=,所以222()2222a b a b ab a b a b a b a b+-+==-+≥---,当且仅当2a b a b-=-时取得最小值. 故选:D. 【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.4.C解析:C 【分析】由不等式组作出可行域,如图,目标函数22xy +可视为可行域中的点与原点距离的平方,故其最小值应为原点到直线2x y +=的距离平方,根据点到直线的距离公式可得选项. 【详解】由不等式组做出可行域如图,目标函数22xy +可视为可行域内的点与原点距离的平方,故其最小值为原点到直线2x y +=的距离的平方,由点到直线的距离公式可知,原点到直线2x y +=的距离为22d ==,所以所求最小值为2. 故选:C.【点睛】本题主要考查线性规划问题,首先由不等式组作出相应的可行域,作图时,可将不等式0Ax By C ++≥转化为y kx b ≤+(或y kx b ≥+),明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值取法、值域范围.5.C解析:C【分析】由约束条件画出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组得到最优解的坐标,代入目标函数得到答案.【详解】由实数x,y满足2424x yx yy-≥⎧⎪+≤⎨⎪≤⎩得到可行域如图:z=3x﹣2y变形为y=32x﹣2z,由24yx y=⎧⎨-=⎩,解得B(2,0)当此直线经过图中B时,在y轴的截距最大,z最小,所以z的最小值为3×2﹣2×0=6;故选C.【点睛】本题主要考查线性规划中利用可行域求目标函数的最值,求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.6.B解析:B【分析】结合题意画出可行域,然后运用线性规划知识来求解【详解】如图由题意得到可行域,改写目标函数得y x z =-+,当取到点(3,1)A 时得到最小值,即314z =+=故选B 【点睛】本题考查了运用线性规划求解最值问题,一般步骤:画出可行域,改写目标函数,求出最值,需要掌握解题方法7.B解析:B 【分析】由约束条件作出可行域,再由指数函数的图象经过A ,B 两点求得a 值,则答案可求. 【详解】解:由约束条件40,20,1x y y x -⎧⎪-⎨⎪+⎩作出可行域如图:当1x =时,2y a =≤;当4x =时,42y a =≥,则42a ≥故a 的取值范围为42,2⎡⎤⎣⎦.故选:B . 【点睛】本题考查简单的线性规划,考查数形结合的解题思想方法,属于中档题.8.C解析:C 【分析】由()()()123f f f -=-=-可求得a b ,的值,代回不等关系得出c 的取值范围 【详解】由()()()123f f f -=-=-可得184********a b c a b ca b c a b c -+-+=-+-+⎧⎨-+-+=-+-+⎩解得611a b =⎧⎨=⎩则()32611f x x x x c =+++ 所以()16f c -=-,()013f <-≤所以0c 63-≤<,解得6c 9≤<, 故选C . 【点睛】本题主要考查了函数的性质,运用待定系数法求出参量的值,然后结合题意求出取值范围,较为基础.9.C解析:C 【分析】作出约束条件所表示的平面区域,结合图象确定目标函数的最优解,代入求解,即可得到答案. 【详解】作出x ,y 满足约束条件261322x y x y y -≤⎧⎪⎪+≥⎨⎪≤⎪⎩,所对应的可行域,如图所示,目标函数1z x y =-+可化为1y x z =+-,当直线1y x z =+-过点A 时, 此时直线在y 轴上的截距最大值,此时目标函数取得最小值,又由2132y x y =⎧⎪⎨+=⎪⎩,解得(2,2)A , 所以目标函数的最小值为min 2211z =-+=. 故选:C.【点睛】本题主要考查简单线性规划求解目标函数的最值问题.其中解答中正确画出不等式组表示的可行域,利用“一画、二移、三求”,确定目标函数的最优解是解答的关键,着重考查了数形结合思想,及推理与计算能力,属于基础题.10.A解析:A 【分析】根据题意,设,,,AD t AB c AC b ===由三角形面积公式1sin 2S a b θ=⋅⋅可表示出,,ACD ABD ABC ∆∆∆三者之间的关系,进而得边长关系为3,t bc =最后通过基本不等式求得AD 的最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修五测试
一.选择题(本大题共10小题,每小题3分,共30分)
1. 在等比数列中,112
a =
,12
q =
,132
n a =
,则项数n 为 ( )
A. 3
B. 4
C. 5
D. 6
2. 在数列{}n a 中,1a =1,12n n a a +-=,则51a 的值为 ( ) A .99 B .49 C .102 D . 101
3. 已知0x >,函数4y x
x =
+的最小值是 ( )
A .5
B .4
C .8
D .6
4. 不等式20(0)ax bx c a ++<≠的解集为R ,那么 ( ) A. 0,0a <∆< B. 0,0a <∆≤ C. 0,0a >∆≥ D. 0,0a >∆>
5. 在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cos C 等于 ( )
2A.
3
2B .-3
1C .-3
1D .-4
6. 一个等比数列}{n a 的前n 项和为48,前2n 项和为60,则前3n 项和为( ) A 、63 B 、108 C 、75 D 、83 7.设,a R ∈则1a <是
11a >的
A .充分但不必要条件
B .必要但不充分条件
C .充要条件
D .既不充分也不必要条件 8. 命题“若2
2
0a b +=,则,a b 都为零”的逆否命题是 A .若2
20a b +≠,则,a b 都不为零 B .若2
2
0a b +≠,则,a b 不都为零 C .若,a b 都不为零,则2
2
0a b +≠ D .若,a b 不都为零,则2
2
0a b +≠
9.设,x y 满足约束条件12x y y x y +≤⎧⎪
≤⎨⎪≥-⎩
,则3z x y =+的最大值为 ( )
A . 5 B. 3 C. 7 D. -8
10.不等式
21≥-x
x 的解集为 ( )
A. ),1[+∞-
B. )0,1[-
C. ]1,(--∞
D. ),0(]1,(+∞--∞
二、填空题(本题共4小题,每小题3分,共16分)
11.已知命题:,sin 1p x R x ∃∈≥,则p ⌝为________。
12.在A B C ∆中,045,3
B c b ===
,那么A =_____________;
13.已知等差数列{}n a 的前三项为32,1,1++-a a a ,则此数列的通项公式为________ .
14.已知数列{a n }的前n 项和2n S n n =+,那么它的通项公式为a n =_________ 三、解答题 (本大题共5个小题,共44分;解答应写出文字说明、证明过程或演算步骤)
15(8分) 已知等比数列{}n a 中,4
5,106431=+=+a a a a ,求其第4项及前5项和.
16.(8分)在∆ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足(2a-c)cosB=bcosC (1)求角B 的大小; (2)当a=2,c=3时,求∆ABC 的面积.
17.(12分)已知,设命题P : |m -5|≤3;命题Q :函数f (x )=3x 2+2mx +m +
43
有两个不同的零点.求使命题“P 或Q ”为真命题的实数的取值范围.
18.(14分)已知等比数列的各项均为正数,且
.
(I )求数列
的通项公式.
(II )设,求数列的前n 项和.
m R ∈m {}
n a 2
12326
231,9a a a a a +=={}
n a 31323log log log n n
b a a a =+++ 1{}
n
b
19.( 12分)某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万
元。
该公司第n 年需要付出设备的维修和工人工资等费用n a 的信息如下图。
(1)求n a ;
(2)引进这种设备后,第几年后该公司开始获利; (3)这种设备使用多少年,该公司的年平均获利最大?
高中数学必修五测试答案
一.选择题。
题号 1 2 3 4 5 6 7 8 9 10 答案 C D B A D A B C C B
二.填空题。
11. ,sin 1x R x ∀∈<
12. 15o 或75o
13.n a =2n -3 14.n a =2n 三.解答题。
15.解:设公比为q , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄1分
由已知得 ⎪⎩⎪
⎨⎧=
+=+45105
131211q a q a q a a ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 3分 即⎪⎩
⎪
⎨⎧=+=+ 45)1(①
10)1(2
3121 q q a q a ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 5分 ②÷①得 2
1,8
13
=
=q q 即 , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 7分
将2
1=
q 代入①得 81=a , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 8分
②
1)2
1
(83314=⨯==∴q a a , ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 10分
2312
11)21(181)1(5515=
-
⎥⎦
⎤⎢⎣⎡
-⨯=--=q q a s ┄┄┄┄┄┄┄┄┄┄ 12分 16.解:
(1)1 2
2
S acsinB =
=
()()2sin sin cos sin co 2s a c cosB bco C B B C
sC A ∴-=-=
2sin cos sin cos sin cos 2sin cos sin cos sin cos sin()sin A B C B B C
A B C B B C C B A ∴-==+=+=
2cos 11cos 2
B B ∴==
所以角B 是π/3
(2)因为a=2,c=3
,1 2
2
S acsinB =
=
17.(本小题满分12分)已知,设命题P : |m -5|≤3;命题Q :函数f (x )=3x 2
+
2mx +m +4
3有两个不同的零点.求使命题“P 或Q ”为真命题的实数的取值范围.
答案:解:对P : |m -5|≤3,即2≤m ≤8………2分
对Q:由已知得f (x )=3x 2
+2mx +m +430的判别式
Δ=4m 2-12(m +4
3
)=4m 2-12m -16>0, (5)
得m <-1或m >4. ………………………………….8分 所以,要使“P 或Q ”为真命题,只需求其反面,P 假且Q 假, 即………10分 ………11分
实数m 的取值范围是 …………12分
18. 解:(Ⅰ)设数列{an}的公比为q ,由
得
所以
.
由条件可知c>0,故
.
由
得
,所以
.
m R ∈m ⎩⎨⎧≤≤-<>4
128m m m 或∴21<≤-m ∴()[),12,-∞-⋃+∞2
3
26
9a a a =3234
9a a
=2
19q =
13q =
12231
a a +=12231
a a q +=113a =
故数列{an}的通项式为an=. (Ⅱ )
故
所以数列
的前n 项和为
19.解:(1)由题意知,每年的费用是以2为首项,2为公差的等差数列,求得:
12(1)2n a a n n =+-= ┄┄┄┄┄┄┄┄┄┄2分
(2)设纯收入与年数n 的关系为f(n),则: 2
(1)
()21[22]2520252
n n f n n n n n -=-+
⋅-=-- ┄┄┄┄┄┄┄┄┄┄4分
由f(n)>0得n 2-20n+25<0
解得10n 10-<<+ ┄┄┄┄┄┄┄┄┄6分 又因为n N ∈,所以n=2,3,4,……18.即从第2年该公司开始获利 ┄┄┄┄┄┄┄8分 (3)年平均收入为
n
)n (f =20-25(n )202510n
+
≤-⨯= ┄┄┄┄┄┄┄┄┄12分
当且仅当n=5时,年平均收益最大.所以这种设备使用5年,该公司的年平均获利最大。
┄┄┄┄14分
1
3n
31323n
log log ...log n b a a a =+++(12...)(1)2
n n n =-++++=-
1
2112(
)
(1)
1n
b n n n n =-
=--
++1
2
111111112...2((1)(
)...(
))2
231
1
n n b b b n n n +
++=--+-++-
=-
++1{
}
n
b 21n
n -
+。
