高斯投影及换带计算
高斯投影带号计算公式

高斯投影带号计算公式一、引言高斯投影带号是一种用于地图投影的方法,它将地球表面的经纬度坐标转换为平面坐标,以便更方便地绘制地图和进行测量。
高斯投影带号计算公式是用来计算特定经纬度点所在的高斯投影带号的数学公式。
本文将详细介绍高斯投影带号计算公式及其应用。
二、高斯投影带号的定义高斯投影带号是根据地球表面的经线和纬线将地球划分为一系列带状区域的方法。
每个带状区域都有一个唯一的带号,用来表示该区域的位置。
在高斯投影带号系统中,每个带号由一个字母和一个数字组成,字母表示带的纬度范围,数字表示带的经度范围。
三、高斯投影带号计算公式高斯投影带号计算公式可以根据给定的经纬度坐标来计算该点所在的高斯投影带号。
公式如下:带号 = (经度 + 180) / 6 + 1其中,经度是待转换的经度坐标,范围为-180到180度。
带号的取值范围为1到60,表示地球表面的60个高斯投影带。
四、高斯投影带号的应用高斯投影带号广泛应用于地图制作、测量和导航等领域。
通过将地球表面的经纬度坐标转换为高斯投影带号,可以方便地绘制各种比例尺的地图,便于人们进行地理位置的确定和测量。
同时,高斯投影带号还可以用于导航系统中,帮助人们快速准确地定位目标位置。
五、高斯投影带号计算公式的示例为了更好地理解高斯投影带号计算公式的应用,下面举一个例子。
假设某地的经度为120度,根据高斯投影带号计算公式,可以计算出该地点所在的带号为:带号 = (120 + 180) / 6 + 1 = 51因此,该地点所在的高斯投影带号为51。
通过这个带号,可以在地图上快速找到该地点的位置。
六、总结高斯投影带号计算公式是一种将地球表面的经纬度坐标转换为高斯投影带号的数学公式。
它为地图制作、测量和导航等领域提供了便利,使得人们可以更方便地确定地理位置和进行测量。
通过理解和应用高斯投影带号计算公式,可以更好地利用地图和导航系统,提高工作效率和准确性。
坐标换带计算原理
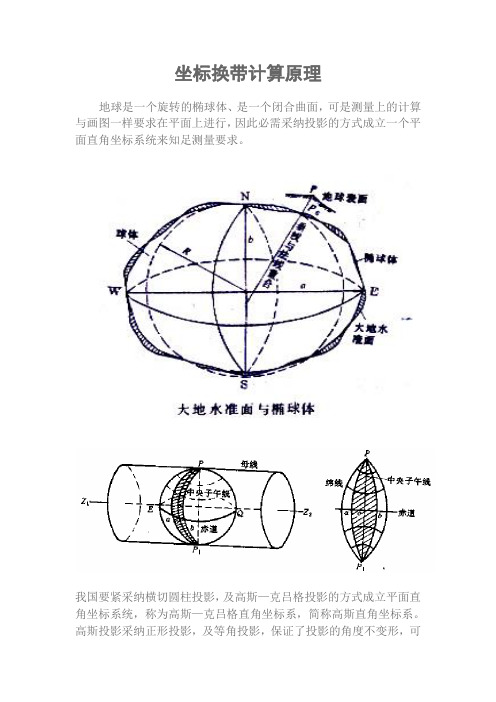
坐标换带计算原理地球是一个旋转的椭球体、是一个闭合曲面,可是测量上的计算与画图一样要求在平面上进行,因此必需采纳投影的方式成立一个平面直角坐标系统来知足测量要求。
我国要紧采纳横切圆柱投影,及高斯—克吕格投影的方式成立平面直角坐标系统,称为高斯—克吕格直角坐标系,简称高斯直角坐标系。
高斯投影采纳正形投影,及等角投影,保证了投影的角度不变形,可是其长度变形较为严峻。
高斯投影平面上的中央子午线投影为直线且长度不变,其余的子午线均为凹向中央子午线的曲线,其长度大于投影前的长度,离中央子午线越远长度变形越大。
为了限制高斯投影的长度变形,必需依据中央子午线进行分带,把投影范围限制在中央子午线东、西双侧必然的狭长带内别离进行。
但这又使得统一的坐标系分割成各带的独立坐标系。
于是,因分带的结果产生了新的矛盾,即在生产建设中提出了各相邻带的相互联系的问题。
那个问题是通过一个带的平面坐标换算到相邻带的平面坐标,简称为“邻带换算”的方式来解决的。
具体来讲,在以下情形下需要进行坐标邻带换算:(1)如图1所示,A、B、一、二、3、4、C、D为位于两个相邻带边缘地域并跨越两个投影带(东、西带)的操纵网。
假设起算点A、B和C、D的起始坐标是按两带别离给出的话,那么为了能在同一带内进行平差计算,必需把西带的A、B点起始坐标换算到东带,或把东带的C、D点的起始坐标换算到西带。
图1(2)在分界子午线周围地域测图时,往往需要用到另一带的三角点作为操纵,因此必需将这些点的坐标换算到同一带中;为了实现两邻带地形图的拼接和利用,位于45′(或′)重叠的三角点需具有相邻带的坐标值,如图2所示。
图2(3)当大比例尺(1:1000或更大)测图时,专门是在工程测量中,要求采纳3°带、°带或任意带,而国家操纵点通常只有6°带坐标,这时就产生了6°带同3°带(或°带、任意带)之间的彼此坐标换算问题。
高斯投影换带计算分解

4、算例
某点P在1954北京坐标系6°带平面直角坐标为:
x1 =3589644.286m,y1 =20679136.438m
求P点在3°第40带的平面坐标 x2 , y2 。
➢ 根据 x1, y1 ,利用高斯反算公计算换算 (B, L) ,得到
3. 根据换带后新的中央子午线经度L0‘ ,计算相应的经差;
4. 由高斯投影正算,求得新的高斯投影坐标 x',y'。
反算公式 正算公式
3、高斯换带的优点
本质: 把椭球面上的大地坐标作为过渡坐标:
平面坐标
大地坐标
平面坐标
这种方法,理论上最简明严密,精度最高,通用性最强。不 仅适用于6°-6°带,3°-3°带以及6°-3°带互相之间的邻带坐标换 算,且适用于任意带之间的坐标换算。
1) 3°带与6°带的中央子午 线重合
如图所示, 3°第41带与6° 带的第21带的中央子午线重 合,中央子午线经度均为 123°。既然中央子午线一致, 坐标系统也就一致。所以, 图中P1点在6°带第21带的坐 标,也就是该点在3°带第41 的坐标。在这种情况下, 6° 带与3°带不存在坐标换带的 计算问题。
邻带方里网: 如图所示:
规定:在一定范围内将邻带的坐标延伸到本带的图幅中。
三、换带的分类
当测区跨不同的投影带时,测图时测区中所有 控制点应采用同一投影带的坐标,位于不同投 影带的点应进行同一坐标系统(同一个椭球) 不同投影带之间的坐标换算:具体情况有以下 几种: 6°带坐标→相邻6°带坐标; 6°带坐标→3°带坐标; 3°带坐标→相邻3°带坐标; 6°带或3°带坐标→任意带坐标;
高斯投影分带计算题

高斯投影分带计算题摘要:1.高斯投影分带计算题的概述2.高斯投影分带的原理3.高斯投影分带计算的方法4.高斯投影分带计算的实例5.总结正文:一、高斯投影分带计算题的概述高斯投影分带计算题是地理信息科学中的一种计算题,主要涉及到高斯克吕格投影的分带计算。
高斯克吕格投影,又称高斯投影,是一种将地球表面的地理坐标(经度和纬度)转换为平面直角坐标的投影方法。
这种投影方法被广泛应用于我国的地图制图、工程测量、导航定位等领域。
二、高斯投影分带的原理高斯投影分带是为了减少投影误差而进行的一种分带计算。
由于地球是一个椭球体,而投影平面是一个平面,因此在进行投影时,会产生一定的投影误差。
高斯投影分带就是将地球表面按照一定的经度间隔划分为多个投影带,每个投影带内的投影误差相对较小。
三、高斯投影分带计算的方法高斯投影分带计算的方法主要包括以下步骤:1.确定投影带的数量:根据需要绘制的地区范围和精度要求,确定投影带的数量。
一般来说,投影带的数量越多,投影误差越小,但计算过程也越复杂。
2.计算每个投影带的经度范围:根据投影带的数量和地球表面的经度范围,计算每个投影带的经度范围。
3.计算每个投影带的横纵坐标转换公式:根据每个投影带的经度范围,使用高斯克吕格投影的公式,计算每个投影带的横纵坐标转换公式。
四、高斯投影分带计算的实例以我国为例,我国常用的高斯投影分带计算方法为6 度分带。
即按照每6 度经度间隔划分为一个投影带,我国共划分为18 个投影带。
每个投影带的横纵坐标转换公式都不同,需要根据具体的经度范围进行计算。
五、总结高斯投影分带计算题是地理信息科学中的一种重要计算题,涉及到高斯克吕格投影的分带计算。
高斯投影3度带计算公式

高斯投影3度带计算公式
高斯投影是一种常用的地图投影方法,广泛应用于地理信息系统和地图制作中。
其中,高斯投影3度带是指将地球划分为每3度经度为一个投影带,每个投影带都有其特定的计算公式。
以下是高斯投影3度带的计算公式。
1.计算中央子午线经度
中央子午线经度可以通过经度除以3再取整得到。
例如,经度120度所在的投影带的中央子午线经度为39度。
2.计算投影坐标系原点
投影坐标系原点的纬度可以通过将纬度分为北纬和南纬两个区间,再通过选择不同的公式计算得到。
北纬区间为0度到84度,南纬区间为0度到80度。
公式如下:
在北纬区间内,原点纬度等于3度带数乘以3度再减去1.5度;
在南纬区间内,原点纬度等于80度减去3度带数乘以3度再减去1.5度。
3.计算投影系数
投影系数是指将经纬度转换为XY平面坐标的转换参数。
根据不同的投影带和纬度区间,投影系数有不同的计算公式。
可以使用以下公式计算投影系数:
投影系数等于扁率乘以半长轴,再乘以纬度差值,再除以360。
4.计算辅助角度
辅助角度可以通过以下公式计算得到:
辅助角度等于经度差值乘以60等于输入经度减去中央子午线经度。
5.计算投影坐标
投影坐标由X和Y两个部分组成,可以通过以下公式计算得到:
X等于投影系数乘以辅助角度的正弦值;
Y等于投影系数乘以辅助角度的余弦值。
这就是高斯投影3度带的计算公式。
通过这些公式,可以将经纬度坐标转换为平面坐标,实现地图投影和测量分析等功能。
高斯投影3度带的计算公式是地图制作和测绘工作中的重要工具,具有广泛的应用前景。
高斯投影换带计算

2) 3°带中央子午线与 6°带分带子午线重合
差;
4. 由高斯投影正算,求得新的高斯投影坐标 x',y'。
反算公式
正算公式
3、高斯换带的优点
本质: 把椭球面上的大地坐标作为过渡坐标: 平面坐标 大地坐标
平面坐标
这种方法,理论上最简明严密,精度最高,通用性最强。不 仅适用于6°-6°带,3°-3°带以及6°-3°带互相之间的邻 带坐标换算,且适用于任意带之间的坐标换算。 虽计算量稍大,但由于计算机的普及和本法的通用性及计 算的高精度,它自然便成为坐标邻带换算中最基本的方法。
1、核心思想
首先将某投影带内已知点的平面坐标(x1, y1), 按高斯投影坐标反算公式求得其在椭球面上的大 地坐标(B, L);然后根据纬度和所需换算的投 影带的中央子午线经度L02,计算该点在新投影 带内的经差l2,再按高斯投影坐标正算公式计算 该点在新投影带内的高斯平面坐标(x2, y2)。 至此,就完成了高斯投影坐标的换带计算问题。
4、算例
某点P在1954北京坐标系6°带平面直角坐标为:
x1 =3589644.286m,y1 =20679136.438m
求P点在3°第40带的平面坐标
x2 , y2 。
( B, L) ,得到
根据 x1 , y1 ,利用高斯反算公计算换算
' '' 。 B 32 24'57.6522'' ,L 1185415.2206
80椭球高斯投影坐标换带计算编程
辽宁工程技术大学大地测量基础综合训练二教学单位测绘与地理科学学院专业测绘工程名称 80椭球高斯投影坐标换带计算编程班级测绘14-1学号学生姓名指导教师王佩贤目录一、高斯投影坐标换带的原理 (3)二、高斯投影坐标换带的目的 (6)三、坐标换带的意义 (8)四、程序设计基础 (8)五、程序界面及源码 (11)六、程序验证 (15)七、软件评价 (15)八、软件使用说明 (16)一、高斯投影坐标换带的原理1.1高斯投影基本概念想象有一个椭圆柱面横套在地球椭球体外面,并与某一条子午线(此子午线称为中央子午线或轴子午线)相切,椭圆柱的中心轴通过椭球体中心,然后用一定投影方法,将中央子午线两侧各一定经差范围内的地区投影到椭圆柱面上,再将此柱面展开即成为投影面。
特点:(1)正形投影(角度不变,a=b:长度比与方向无关);(2)中央子午线投影为纵坐标轴;(3)中央子午线投影后长度不变。
1.2高斯投影邻带换算1.定义:将一个带的高斯平面坐标换算为另一带的高斯平面坐标称为高斯坐标的邻带换算2.内容: 1 )不同六度带和不同三度带之间的化算2 )三度带和六度带之间的化算3.方法: 1 )直接法: 利用相邻两带坐标之间关系式进行坐标互换2 )间接法:通过大地坐标进行高斯正反算互相换算目前广泛采用间接换带计算法,因此下面就此方法作介绍。
如将第一带(东带或西带)的平面坐标换算为第二带(西带或东带)的平面坐标,方法是先根据第一带的平面坐标x,y和中央子午线的经度L。
按高斯投影坐标反算公式求得大地坐标B,L然后根据B,L和第二带的中央子午线经度按高斯投影坐标正算公式求得在第二带中的平面坐标。
由于在换带计算中,把椭球面上的大地坐标作为过渡坐标,因而称为间接换带法。
这种方法理论上是严密的,精度高,而且通用性强,他适用于6°带与6°带,3°带与3°带,6°带与3°带之间的坐标换带。
6高斯投影及其计算
应用大地测量学
第一节 地图投影概念和正形投影性质
应用大地测量学
第一节 地图投影概念和正形投影性质
应用大地测量学
(二)投影变形 角度变形、长度变形和面积变形三种。 (三)投影长度比与变形指标 投影长度比——投影面上无限小线段 ds与椭球面上该线段实际长度 dS之比,以m表示,m=ds/dS。长度变形—— v= m-1 变形指标:主方向上投影长度比a和b叫变形指标。 若a=b,则为等角投影,既投影后长度比不随方向而变化。 若ab=1,则为等面积投影。 椭球面上微分圆: 投影平面上对应为微分椭圆:
第一节 地图投影概念和正形投影性质
应用大地测量学
二、正形投影特性 1、任一点上,投影长度比m为一常数,不随方向而变,仅与点位置有关。 2、投影后角度不变形。又叫保角映射或叫正形投影。条件是在微小范围内成立。
第一节 地图投影概念和正形投影性质
应用大地测量学
三、正形投影的一般条件 正形投影必要和充分的条件是满足柯西—黎曼方程:
y/(km)
10
20
30
40
50
100
150
200
250
300
长度变形m-1
1/810000
1/202000
1/90000
1/50000
1/32000
1/8000
1/3500
1/2000
1/1300
1/900
第二节 高斯投影与国家平面直角坐标系
应用大地测量学
三、高斯投影的分带 为限制长度投影变形,投影分带有6度分带和3度分带两种方法。
应用大地测量学
三、距离改正计算 距离改正——椭球面上大地线长S改换为平面上投影曲线两端点间的弦长D,要加距离改正△S。
高斯投影及换带计算
(距中央子午线132377.620m,距赤道3102467.280m)
不同点: 1、 x,y轴互异。 2、 坐标象限不同。 3、表示直线方向的方位角 定义不同。 相同点: 数学计算公式相同。
工程测量采用3 º带,特殊工程可采用1.5 º带或任意带
按照6º带划分的规定,第1带中央子午线的经度为3º,其余各带中央子午线经度与带号的关系是: L。=6ºN-3º (N为6º带的带号) 例:20带中央子午线的经度为: L。=6º× 20-3º=117 º 按照3º带划分的规定,第1带中央子午线的经度为3º,其余各带中央子午线经度与带号的关系是: L。=3ºn (n为3º带的带号) 例:120带中央子午线的经度为 L。=3º× 120=360 º
N
S
c
中央
子
午线
赤道
高斯投影平面
赤道
中央子午线
1).高斯投影的原理:
高斯投影采用分带投影。将椭球面按一定经差分带,分别进行投影。
2)、高斯投影必须满足:
高斯投影为正形投影, 即等角投影; 中央子午线投影后为直 线,且为投影的对称轴; 中央子午线投影后长度 不变。
3)、高斯投影的特点:
添加标题
若已知某点的经度为L,则该点的6º带的带号N由下式计算:
01
添加标题
若已知某点的经度为L,则该点所在3º带的带号按下式计算:
02
添加标题
(四舍五入)
03
高斯平面直角坐标系的建立:
x轴 — 中央子午线的投影 y轴 — 赤道的投影 原点O — 两轴的交点
O
x
y
高斯投影的邻带坐标换算
(2)计算B点在邻带的经度差为
经度差= 4.7
(3)计算B点在邻带的坐标
换带后x坐标=4078347.2553 换带后y坐标=272139.1392
第三步 C和D点的3度带坐标计算 (1)通过高斯反算C、D点的经纬度
(3)计算C、D点在3度带的坐标
C点 换带后x坐标=4072996.0939 换带后y坐标=40527098.4464
D点 换带后x坐标=4066353.4723 换带后y坐标=38545609.639
第四步 根据四点经度计算经度差
A点经度差=1.565732639521
B点经度差=-3.570440179783
小结
✓高斯投影相邻带的坐标换算产生换带的原因。
产生换带的原因有二: 一、国家只有标准分带坐标,工程建设中用的坐标采用 的是任意度带的; 二、一个测区可能跨几个带,要统一坐标后才能利用。
✓应用高斯投影正、反算公式间接进行换带计算
1、高斯反算得到点的大地坐标 2、计算点新带的经度差 3、高斯正算计算点在新带的坐标
120 5
5、对y的值进行加工 正算公式计算出的自然值+500公里,前面冠以带号
例一 已知某测区四个点平面坐标
A
4074700.925
B
4078073.834
C
4075083.899
D
4069122.263
20763357.427 20236570.978 20690755.754 20277596.488
C点经度差=1.0
D点经度差-3.292195770666
四个点在118度带的坐标
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测绘学院《大地测量学基础》课件
24
高斯平面直角坐标系与数学上的笛卡尔平面直角 坐标系的异同点 :
不同点: 1、 x,y轴互异。 2、 坐标象限不同。 3、表示直线方向的方位角
定义不同。 相同点:
数学计算公式相同。
测绘学院《大地测量学基础》课件
Ⅳx
o
Ⅲ
α Ⅰp
D
y
Ⅱ
x=Dcosα
y=Dsinα
高斯平面直角坐标系
y3
6N
3 f
cos
Bf
1
2t
2 f
2 f
y5
120N
5 f
cos
Bf
5
28t
2 f
24t
4 f
6
2 f
8
2 f
t
2 f
测绘学院《大地测量学基础》课件
30
3、高斯投影坐 标正反算公式的
几何解释 :
①当B=0时x=X=0,y则随l的变化而变化,这就是说,赤道投影为一直线且 为y轴。当l=0时,则y=0,x=X,这就是说,中央子午线投影亦为直线,且为x轴, 其长度与中央子午线长度相等。两轴的交点为坐标原点。
B B f
tf 2M f N f
y2
tf
24M
f
N
3 f
5
3t
2 f
2 f
9
2 f
t
2 f
y4
过所求点P作中央子午线的垂线,
tf
720M
f
N
5 f
y
61
90t
2 f
45t
4 f
y6
该垂线与中央子午线的交点的纬 度,称垂足纬度。其值由子午线 弧长计算公式反算求得。
l y N f cos B f
高斯投影及换带计算
一、高斯投影概述 (正形投影,高斯坐标正反算及换带计算)
二、把椭球面元素归算到高斯投影面 (方向改化,距离改化)
三、各种投影方法概述
测绘学院《大地测量学基础》课件
1
本章提要
本章介绍从椭球面上大地坐标系到平面上 直角坐标系的正形投影过程。研究如何将大地 坐标、大地线长度和方向以及大地方位角等向 平面转化的问题。重点讲述高斯投影的原理和 方法,解决由球面到平面的换算问题,解决相 邻带的坐标坐标换算。
y y p2 = 500000+ p2
=(带号)227559.720m
o
500km
x
xp1
p1
30320825855.565.605m0
m
y
y
p1
p1
(带1号 36)768306.376800.m360m
p1
y
测绘学院《大地测量学基础》课件
23
例:
有一国家控制点的坐标:
x=3102467.280m ,y=19367622.380m,
测绘学院《大地测量学基础》课件
28
自赤道量起的到所求点的子午线弧长
x
X
N
2 2
sin
B cos
B l2
N
24 4
sin
B cos3
B(5 t2
9 2
4 4 )l4
N sin B cos5 B(61 58t2 t4 )l6
720 6
所求点的大地经度与该点所在带 的中央子午线的大地经度之差
y N cos B l N cos3 B(1 t 2 2 )l3
6 3
N
120 5
cos5
B(5
18t 2
t4
14 2
58 2t 2 )l5
t tan B,2 e2 cos2 B
测绘学院《大地测量学基础》课件
29
2、高斯投影坐标反算公式:x,y B,l
满足以下三个条件: ①x坐标轴投影后为中央子午线是投影的对称轴; ② x坐标轴投影后长度不变; ③投影具有正形性质,即正形投影条件。
x F1(L, B) y F2 (L, B)
椭球面是一个凸起的、不可展平的曲面,若将这个曲面上 的元素(比如一段距离、一个角度、一个图形)投影到平 面上,就会和原来的距离、角度、图形呈现差异,这一差 异称作投影的变形
测绘学院《大地测量学基础》课件
4
长度比:
投影面上的边长与原面上的相应长度之比,称为长度比。
在投影平面上任意一块面积与椭球面上相应的面积相等,即面积变形
等于零。
• (3)等距投影
•
定义为沿某一特定方向的距离,投影前后保持不变,即沿着该特定方
向长度比为1。在这种投影图上并不是不存在长度变形,它只是在特定方
向上没有长度变形。
测绘学院《大地测量学基础》课件
6
2)按投影面的形状分类
• (1)方位投影:以平面作为投影面,使平面与球面相切或 相割,将球面上的经纬线投影到平面上而成。
测绘学院《大地测量学基础》课件
14
3)、高斯投影的特点:
x
(1)中央子午线投影后为直
线,且长度不变。
平行圈
(2) 除中央子午线外,其余
子午线的投影均为凹向中央
赤道
O
y
子午线的曲线,并以中央子 子午线
午线为对称轴。投影后有长
度变形。 (3) 赤道线投影后为直线,
但有长度变形。
中央子午线
测绘学院《大地测量学基础》课件
6º带自首子午线开始, 按6º的经差自西向东分成60 个带。
3º带自1.5 º开始,按 3º的经差自西向东分成 120个带。
测绘学院《大地测量学基础》课件
高斯投影带划分 17
6º带与3º带中央子午线之间的关系如图:
3º带的中央子午线与6º带中央子午线及分带子午线重 合,减少了换带计算。
工程测量采用3 º带,特殊工程可采用1.5 º带或任意带
测绘学院《大地测量学基础》课件
27
6.3高斯投影坐标正反算公式(了解)
对于任何一种投影:①坐标对应关系是最主要的;②如果 是正形投影,除了满足正形投影的条件外,还有它本身的 特殊条件。
1、高斯投影坐标正算公式: B,l x,y
高斯投影必须满足以下三个条件: ①中央子午线投影后为直线; ②中央子午线投影后长度不变; ③投影具有正形性质,即正形投影条件。
11
2、高斯投影的基本概念
• 高斯投影是等角横切椭圆柱投影。 • 高斯投影是一种等角投影。它是由德国数学家高斯(Gauss,
1777 ~ 1855)提出,后经德国大地测量学家克吕格(Kruger, 1857~1923)加以补充完善,故又称“高斯—克吕格投影”, 简称“高斯投影”。
测绘学院《大地测量学基础》课件
概念。高斯正算和反算计算;方向改化和距离改化计算; 高斯投影带的换算与应用;工程测量中投影面与投影带的 选择。
测绘学院《大地测量学基础》课件
3
6.1 地图投影概述
1.投影与变形
所谓地图投影,简略说来就是将椭球面各元素(包括坐标、 方向和长度)按一定的数学法则投影到平面上。研究这个 问题的专门学科叫地图投影学。
• (2)圆柱投影:以圆柱面作为投影面,使圆柱面与球面相 切或相割,将球面上的经纬线投影到圆柱面上,然后将圆柱 面展为平面而成。
• (3)圆锥投影:以圆锥面作为投影面,使圆锥面与球面相 切或相割,将球面上的经纬线投影到圆锥面上,然后将圆锥 面展为平面而成。
测绘学院《大地测量学基础》课件
7
测绘学院《大地测量学基础》课件
②当l=常数时(经线),随着B值增加,x值增大,y值减小,这就告诉我们,经 线是凹向中央子午线的曲线,且收敛于两极。又因,即当用-B代替B时,y 值不变,而x值数值相等符号相反,这就说明赤道是投影的对称轴。
③当B=常数时(纬线),随着的l增加,x值和y值都增大,这就是说,纬线是 凸向赤道的曲线。又当用-l代替l时,x值不变,而y值数值相等符号相反, 这就说明,中央子午线是投影对称轴。由于满足正形投影条件,所以经线 和纬线的投影是互相垂直的。
x=Dcosα
y=Dsinα
y
Ⅱ
o
Ⅲ
p
DⅠ
α
x
Ⅳ
笛卡尔坐标系
25
3、椭球面三角系化算到高斯平面
测绘学院《大地测量学基础》课件
26
将椭球面三角系归算到高斯投影面的主要内容是:
➢将起始点的大地坐标B,L归算为高斯平面直角坐标x,y;为了检 核还应进行反算,亦即根据x,y反算B,L。 ➢通过计算该点的子午线收敛角及方向改正,将椭球面上起算边大地 方位角归算到高斯平面上相应边的坐标方位角。 ➢通过计算各方向的曲率改正和方向改正,将椭球面上各三角形内角 归算到高斯平面上的由相应直线组成的三角形内角。 ➢通过计算距离改正,将椭球面上起算边的长度归算到高斯平面上的 直线长度。 ➢当控制网跨越两个相邻投影带,需要进行平面坐标的邻带换算。
测绘学院《大地测量学基础》课件
10
6.2 高斯投影概述(重点)
1、控制测量对地图投影的要求
1)等角投影(又称正形投影)
2)长度和面积变形不大,并能用简单公式计算由变形而引起 的改正数。
3)能很方便地按分带进行,并能按高精度的、简单的、同样 的计算公式和用表把各带联成整体 。
测绘学院《大地测量学基础》课件
L。=3ºn (n为3º带的带号) 例:120带中央子午线的经度为
L。=3º× 120=360 º
测绘学院《大地测量学基础》课件
19
若已知某点的经度为L,则该点的6º 带的带号N由下式计算:
N int( L) 1 6
若已知某点的经度为L,则该点所在
3º带的带号按下式计算:
n
L 3(四舍五入)
测绘学院《大地测量学基础》课件
