DW470-50磁化曲线拟合表
试论磁化曲线的连续可导拟合方法

Q : Q ( )
高 新 技 术
Ch i n a Ne w T e c h n o l o g i e s a n d P r o d u c t s
试论磁 化 曲线 的连 续 可导拟 合 方法
王志 宏
( 哈 尔滨 电机 厂有限责任公 司, 黑龙江 哈 尔滨 1 5 0 0 4 0 )
摘 要: 之 所 以研 究磁 化 曲线的 连续 可导 拟合 方 法 , 主要 是 希 望能 够舍 乎磁 场 的储 能迭代 运 算规 定 。众所 周 知 , 该 曲线有 着 非常独特的非线性特征 , 无法单纯的通过函数来体现 , 结合它的特征 , 指 出了线性插值和二次插值相结合的方法。 分为三段 来拟舍 。结合 其连 接地 方 具有 的约 束现 象, 经 由分析 方程 试 的模 式 来得 到 函数 的相 关数 值 , 确保 了其 是 一直 可导 的。由拟 合 结果给 出了磁导率随磁通密度的函数关 系及其导函数关 系, 进而指 出了详细的拟合运算措施 , 分析 了它的精确性特征。 关 键词 : 磁 化 曲线 ; 连续 可导 ; 拟舍 方 法 中图分 类号 : T Q O 1 6 . 5 + 5 文献 标识 码 : A 对 于铁磁特性 的物体来讲 , 其磁 化曲线 拥 有非常强大 的非线性特 征 , 一般是 无法通 过具 体的函数展示 的。 以前的拟合措施是使 用 分段形式 的差 值措施 , 此措 施有显 著的缺 陷, 即精 确度 不是 很高 , 而且 它 的表 达公 式 很 复杂 , 最主要 的是在连接 的地方是不具 有 可 导特 征的。目 前全新 的措施 是以人工神经 网为前 提的 , 经 由该 网对信 息的分 析 , 切 实 提 升连 接系 数 ,进 而可 以后期 相应 的 函数 值。此措施可以通过公式来体现, 而且精确 性非常好, 不过它的表达很繁琐 , 不容易得 到 。所 以 , 笔者指 出了将线性 以及二次 的差 值融合 到一起 的措施 , 将 曲线划 分为三个 区 域, 而且 经 由约束要 素 , 来 确保 这些分 区 的 连接处是 能稳定 的而且要具有 可导的性 质。 通过 具体 情况 , 我们 发现 , 使用 其来应 对上 述 的拟合 现象 的时 候 ,其 函数非 常的精 准 , 而且精确度好 , 获取 的结果 非常优 秀。 1 磁 化曲线的分段 以1 0 # 钢 为例 , 磁化 曲线一 般可 以分 为 三段 , 如图 1 所示 。
铁磁材料的磁滞回线和基本磁化曲线

铁磁材料的磁滞回线和基本磁化曲线实验讲义铁磁材料按特性分硬磁和软磁两大类,铁磁材料的磁化曲线和磁滞回线,反映该材料的重要特性,也是设计选用材料的重要依据。
一:实验目的:1...认识铁磁材料的磁化规律,比较两种典型铁磁物质的动态磁特性。
2...测定样品的基本磁化特性曲线(B m-H m曲线),并作μ—H曲线。
3...测绘样品在给定条件下的磁滞回线,以及相关的H c,B r,B m,和[H B ]等参数。
二:实验原理:铁磁物质是一种性能特异,在现代科技和国防上用途广泛的材料。
铁,钴,镍及其众多合金以及含铁的氧化物(铁氧体)均属铁磁物质。
其特征是在外磁场作用下能被强烈磁化,磁导率μ 很高。
另一特性是磁滞,即磁场作用停止后,铁磁材料仍保留磁化状态。
图一为铁磁物质的磁感应强度Β与磁场强度HH图一铁磁物质的起始磁化曲线和磁滞回线图中的原点。
表示磁化之前铁磁物质处于磁中性状态,即B=H=O 。
当外磁场H从零开始增加时,磁感应强度B随之缓慢上升,如线段落0a所示;继之B随H迅速增长,如ab段所示;其后,B的增长又趋缓慢;当H值增至Hs 时,B 的值达到Bs ,在S点的B s和H s,通常又称本次磁滞回线的B m和H m。
曲线oabs段称为起始磁化曲线。
当磁场从H s逐渐减少至零时,磁感应强度B并不沿起始磁化曲线恢复到o点,而是沿一条新的曲线sr下降,比较线段os和sr,我们看到:H减小,B也相应减小,但B的变化滞后于H的变化,这个现象称为磁滞,磁滞的明显特征就是当H=0时,B不为0,而保留剩磁B r。
当磁场反向从o逐渐变为-H c时,磁感应强度B=O,这就说明要想消除剩磁,必须施加反向磁场,H c称为矫顽力。
它的大小反映铁磁材料保持剩磁状态的能力,线段rc称为退磁曲线。
图一还表明,当外磁场按H s →0→-H c→-H s→0 → H c→ H s次序变化时,相应的磁感应强度则按闭合曲线srcs’r’c’s变化时,这闭合曲线称为磁滞回线。
铁磁材料的磁滞回线及基本磁化曲线_实验报告

电磁学综合设计性实验报告实验名称:铁磁材料磁滞回线的研究班级:姓名: 学号:同组同学:实验地点:宁夏大学基础物理实验中心实验时间:2014-6-8 指导教师:实验成绩:目录摘要 (2)关键字 (2)实验目的 (2)实验仪器 (2)实验原理 (2)实验内容与步骤 (5)数据记录及处理 (6)误差分析 (9)实验结论 (9)心得体会 (10)参考文献 (10)铁磁材料磁滞回线的研究摘要:铁磁物质是一种性能特异,用途广泛的材料。
其特征是在外磁场作用下能被强烈磁化,故磁导率μ很高。
另一特征是磁滞,即磁化场作用停止后,铁磁质仍保留磁化状态。
研究铁磁材料的特性有着重要的意义,它在传统工业、生物医学中磁应用、军事领域以及考古天文地址采矿界领域都有着广泛的应用。
研究铁磁材料重要的方法是测量和分析磁滞回线和基本磁化曲线。
关键词:铁磁材料;磁滞回线;基本磁化曲线一,实验目的1. 认识铁磁物质的磁化规律,比较两种典型的铁磁物质的动态磁化特性。
2. 测定样品的基本磁化曲线,作μ-H曲线。
3. 测定样品的H D、B r、B S和(H m·B m)等参数。
4. 测绘样品的磁滞回线,估算其磁滞损耗。
二,实验仪器DH4516型磁滞回线实验仪,数字万用表,示波器。
三,实验原理铁磁物质是一种性能特异,用途广泛的材料。
铁、钴、镍及其众多合金以及含铁的氧化物(铁氧体)均属铁磁物质。
其特征是在外磁场作用下能被强烈磁化,故磁导率μ很高。
另一特征是磁滞,即磁化场作用停止后,铁磁质仍保留磁化状态,图1为铁磁物质的磁感应强度B与磁化场强度H之间的关系曲线。
图中的原点O表示磁化之前铁磁物质处于磁中性状态,即B=H=O,当磁场H从零开始增加时,磁感应强度B 随之缓慢上升,如线段oa 所示,继之B 随H 迅速增长,如ab 所示,其后B 的增长又趋缓慢,并当H 增至H S 时,B 到达饱和值B S ,oabs 称为起始磁化曲线。
图1表明,当磁场从H S 逐渐减小至零,磁感应强度B 并不沿起始磁化曲线恢复到“O ”点,而是沿另一条新的曲线SR 下降,比较线段OS 和SR 可知,H 减小B 相应也减小,但B 的变化滞后于H 的变化,这现象称为磁滞,磁滞的明显特征是当H =O 时,B 不为零,而保留剩磁Br 。
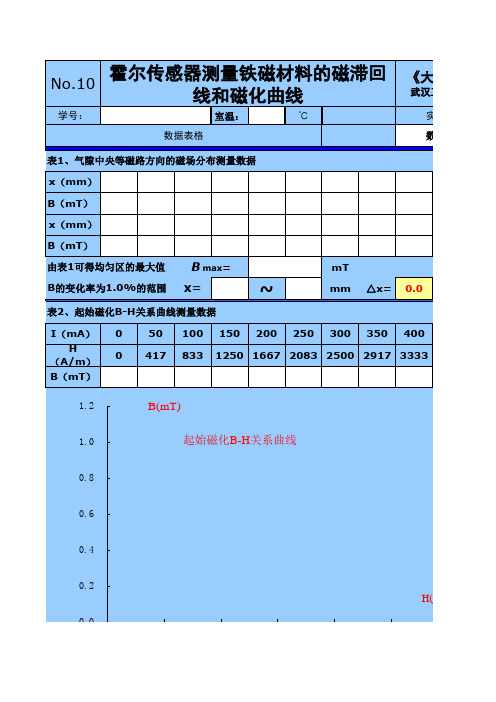
物理实验-霍尔传感器测量铁磁材料的磁滞回线
450 500 550 600 3750 4167 4583 5000
H(A/m)
4000
6000
返回
833.3 416.7 0 -417 -833.3 -1250 -1667 -2083 -2500
0.0 0.0 0.0 0.0 0.0
0.0
0.0
0.0
0.0
-2917 -3333 -3750 -4167 -4583 -5000 -4583 -4167
1000
2000
3000
4000
5000
表3、测模具钢磁滞回线实验数据 (注意:磁场反向时为负值,填写时要带负号)
I(mA)
H (A/m) B(mT)
600 5000
550 4583
500 4167
450 3750
400 3333
350 2917
300 2500
250 2083
200 1667
I(mA) 0 -50 -100 -150 -200 -250 -300 -350 -400
0
B(mT)
50 417
100 150 200 250 300 350 400 833 1250 1667 2083 2500 2917 3333
模具钢磁滞回线
B(mT)
1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
-6000
-4000
-2000
0.0 0
从图中可看出饱和磁感应强度 Bmax=
H (A/m)
0
-417 -833 ### ### ### ### ### ###
B(mT)
I(mA)
H (A/m) B(mT)
磁化曲线和磁滞回线

磁化曲线和磁滞回线磁性材料应用很广,从长用的永久磁铁、变压器铁芯,到录音、录像、计算机存储用的磁带、磁盘等都采用。
磁滞回线和磁化曲线反应了磁性材料磁特性的主要特征。
用示波器法测量铁磁材料的磁特性是磁测量的基本方法之一,它具有直观、方便、迅速以及能够在不同的磁化状态下(交变磁化及脉冲磁化等)测量的优点,适用于一般工厂快速检测和对成品进行分类。
通过实验研究这些性质不仅能掌握用示波器观察磁化曲线和磁滞回线的基本测绘方法,而且能从理论和实际应用上加深对材料磁特性的认识。
〖实验原理〗1. 铁材料的磁滞现象铁磁材料的磁滞现象是反复磁化过程中磁场强度H 与磁感应强度B 之间的关系的特征。
图 7-1 图 7-2将一块未被磁化的铁磁材料放在磁场中进行磁化.当磁场强度H 由零增加时, 磁感应强度B 由零开始增加。
H 继续增加,B 增加缓慢,这个过程的B — H 曲线称为起始磁化曲线,如图7-1中的oa 段所示。
当磁场强度H 减小,B 也跟着减小,但不按起始磁化曲线原路返回,而是沿另一条曲线(图7-1中)ab 段下降,当H 返回到零时,B 不为零,而保留一定的值r B ,即铁磁材料仍处于磁化状态,通常r B 称为磁材料的剩磁。
将磁化场反向,使磁场强度负向增加,当H 达到某一值C H −时,铁磁材料中的磁感应强度才为零,这个磁场强度C H −称为磁材料的矫顽力。
继续增加反向磁场强度,磁感应强度B 反向增加。
如图7-1cd 段所示。
当磁场强度由m H −增加到m H 时,其过程与磁场强度从m H 到m H −过程类似。
这样形成一个闭合的磁滞回线。
C Hm Hm Bm B −m H − C H − r B − r B逐渐增加m H 值,可以得到一系列的逐渐增大的磁滞回线,如图7-2所示。
把原点与每个磁滞回线的顶端a 1,a 2,a 3,a 4…连接起来即得到基本磁化曲线。
如图7-2中oa 段所示。
当H m 增加到一定程度时,磁滞回线两端较平,即.H 增加,B 增加很小,在此时附近铁磁材料处于饱和状态。
铁磁材料磁滞回线和基本磁化曲线的测量

实验26 铁磁材料磁滞回线和基本磁化曲线的测量铁磁性材料分为硬磁材料和软磁材料。
软磁材料的矫顽力小于100A/m ,常用于电机、电力变压器的铁芯和电子仪器中各种频率小型变压器的铁芯。
铁磁材料的磁化过程和退磁过程中磁感应强度和磁场强度是非线性变化的,磁滞回线和基本磁化曲线是反映软磁材料磁性的重要特性曲线。
矫顽力、饱和磁感应强度、剩余磁感应强度、初始磁导率、最大磁导率、磁滞损耗等参数均可以从磁滞回线和基本磁化曲线上获得,这些参数是磁性材料研制、生产和应用的总要依据。
采用直流励磁电流产生磁化场对材料样品反复磁化测出的磁滞回线称为静态磁滞回线;采用交变励磁电流产生磁化场对材料样品反复磁化测出的磁滞回线称为动态磁滞回线。
本实验利用交变励磁电流产生磁场对不同性能的铁磁材料进行磁化,测绘基本磁化曲线和动态磁滞回线。
【实验目的】①了解用示波器显示和观察动态磁滞回线的原理和方法。
②掌握测绘铁磁材料动态磁滞回线和基本磁化曲线的原理和方法,加深对铁磁材料磁化规律的理解。
③学会根据磁滞回线确定矫顽力 、剩余磁感应强度 、饱和磁感应强度 、磁滞损耗等磁化参数。
【实验仪器与用具】FB310型动态磁滞回线实验仪,双踪示波器,导线。
【实验原理】1.磁性材料的磁化特性及磁滞回线研究磁性材料的磁化规律时,一般是通过测量磁化场的磁场强度H 与磁感应强度B 之间的关系来进行的。
铁磁性材料磁化时,它的磁感应强度B 要随磁场强度H 变化而变化。
但是B 与H 之间的函数关系是非常复杂的。
主要特点如下:(1)当磁性材料从未磁化状态(H =0且B =0)开始磁化时,B 随H 的增加而非线性增加由此画出的H B 曲线称为起始磁化曲线,如图3.26.1(O-a )段曲线。
起始磁化曲线大致分为三个阶段,第一阶段曲线平缓,第二阶段曲线较陡,第三阶段曲线又趋于平缓。
最后当H 增大到一定值m H 后,B 增加十分缓慢或基本不再增加,这时磁化达到饱和状态,称为磁饱和。
异步启动永磁同步电动机设计程序

异步启动永磁同步电动机设计程序1.额定数据和技术要求 (1) 额定功率 N P =16kW (2) 相数 m=3(3) 额定线电压 N U =380V (4) 额定频率 f=50Hz (5) 极对数 p=2 (6) 额定效率 N η=93.0% (7) 额定功率因数cos N ϕ=0.93(8) 失步转矩倍数*poN T =1.8(9) 绕组型式 单层交叉,Y 接 (10)额定相电压N U=Nt U(11)额定相电流5510161028.11()cos 3219.39930.93N N N N N P I A mU ηϕ⨯⨯===⨯⨯⨯(12)额定转速6060501500(/min)2N f n r p ⨯=== (13)额定转矩339.54109.541610101.86()1500N N N P T N m n ⨯⨯⨯⨯===•(14)绝缘等级 B 级2.主要尺寸(15)铁芯材料 DW470-50(16)转子磁路结构形式 内置径向W 型 (17)气隙长度 δ=0.065cm (18)定子外径 1D =25.5cm (19)定子内径 1i D =17cm(20)转子外径 ()2122620.06516.87i D D cm δ=-=-⨯= (21)转子内径 2i D =6cm(22)定、转子铁芯长度 12L L ==20.1cm (23)电枢计算长度220.120.06520.23ef a L L cm δ=+=+⨯=()(24)定子槽数 1Q =36(25)定子每极每相槽数 136/(2)==3(60)232q Q mp =⨯⨯相带(26)极距 11 3.1417=13.352()222i D cm pπτ⨯==⨯ (27)硅钢片质量 231()10Fe Fe b Fe m L K D ρ-=+∆⨯237.820.10.93(25.50.5)1098.56()kg -=⨯⨯⨯+⨯=式中,∆——冲剪余量,cm: b L ——1L 和2L 中较大者,cm Fe ρ——铁的密度,3/g cm Fe K ——铁芯叠压系数,0.92~0.95 3.永磁体计算(28) 永磁材料牌号 NTP264H (29) 计算剩磁密度()()20IL 0.1201201175201 1.15 1.0741()100100100100r B r r B t B T α⎡⎤-⎛⎫⎡⎤⎛⎫=+--=+--⨯=⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎣⎦ 式中,20r B ——20C ︒时的剩磁密度,Tr B α——r B 的可逆温度系数,%1K -IL ——r B 的不可逆损失率,% t ——预计工作温度,C ︒ (30) 计算矫顽力()()200.1201201175201875817.25/100100100100r B c c IL H t H kA m α⎡⎤-⎛⎫⎡⎤⎛⎫=+--=+--⨯=⎢⎥ ⎪ ⎪⎢⎥⎝⎭⎣⎦⎝⎭⎣⎦()式中,20c H ——20C ︒时的计算矫顽力,kA/m (31) 相对回复磁导率20373020 1.151.0461041087510r r c B H μμπ--===⨯⨯⨯⨯ 式中,70410/H m μπ-=⨯(32)磁化方向长度 M h =0.53cm(33) 宽度 M b =10.5cm (34) 轴向长度M L =20.1cm(35) 提供每极磁通的截面积 210.520.1211.05()m M M A b L cm ==⨯=(36) 永磁体总质量332102210.520.10.537.410 3.31()m M M M m m pb h L kg ρ--=⨯=⨯⨯⨯⨯⨯⨯=式中,m ρ——永磁体密度,3/g cm 4.定、转子冲片 (37)定子槽形(38)定子槽尺寸 01h =0.08cm 01b =0.38cm 1b =0.72cm 1r =0.49cm 12h =1.6cm1α=30(39)定子齿距 1113.14171.48436i D t cm Q π⨯===() (40) 定子斜槽距离 111 1.484361.405362sk t Q t cm Q p ⨯===++()(41)定子齿宽101121111[2()]3.14[172(0.08 1.6)]220.490.79636i t D h h b r cm Q π++⨯+⨯+=-=-⨯=10111211[2()]3.14[172(0.080.098)]0.720.79436i s t D h h b b cm Q π++⨯+⨯+=-=-=()式中,101110.720.38tan tan 0.098226s b b h cm πα--==⨯=()离齿最狭1/3处齿宽由1211t t b b ≤ 所以12111110.7960.7940.7940.79533t t t t b b b b cm --=+=+=()(42) 定子轭计算高度11101121225.51720.08 1.60.49 2.242323i j D D h h h r cm --⎡⎤⎡⎤=-++=-++⨯=⎢⎥⎢⎥⎣⎦⎣⎦() (43)定子齿磁路计算长度 11120.491.6 1.7633t r h h cm =+=+=() (44) 定子轭磁路计算长度 ()()11125.5 2.249.132442j j L D h cm pππ=-=⨯-=⨯()(45) 定子齿体积3111113620.10.93 1.760.795943.76()t Fe t t V Q L K h b cm ==⨯⨯⨯⨯=(46) 定子轭体积()()311111 3.1420.10.93 2.2425.5 2.243063.87()j Fe j j V L K h D h cm π=-=⨯⨯⨯⨯-=(47) 转子轭计算高度 22216.8760.53 4.905()22i j M D D h h cm --=-=-= (48) 转子轭磁路计算长度 ()()2226 4.905 4.280442i j L D h cm pππ=+=⨯+=⨯()5.绕组计算(49)每槽导体数 s N =12 (50)并联支路数 a =1(51) 并绕根数-线径 111t N d - 2-1.25 212t N d - 3-1.3 式中,1t N 、2t N ——并绕根数11d 、12d ——导线裸线直径,mm (52) 每相绕组串联匝数 11236722231s N Q N ma ⨯===⨯⨯ (53) 槽满率计算槽面积()()22211112220.490.720.491.60.2 1.5672222s r b r A h h cm ππ+⨯+⨯=-+=⨯-+=() 式中,h ——槽楔厚度,cm槽绝缘面积 ()()212120.0352 1.60.490.166i i A C h r cm ππ=+=⨯⨯+⨯=() 式中,i C ——槽绝缘厚度,cm槽有效面积 21.5670.166 1.401ef s i A A A cm =-=-=() 槽满率()()()()222211112122122 1.250.083 1.30.0879.22%1.401s t d t d f ef N N d h N d h S A ⎡⎤⎡⎤+++⨯⨯++⨯+⎣⎦⎣⎦===式中,1d h 、2d h ——对应于11d 、12d 导线的双边绝缘厚度,mm(54) 节距 y=9槽(55) 绕组短距因数 11sin sin122p K πβπ⨯===式中,9133y mq β===⨯ (56) 绕组分布因数 11130sin sin 3220.9598303sin sin 22d q K q αα⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭===⎛⎫⎛⎫⨯ ⎪⎪⎝⎭⎝⎭式中,112p Q πα=(57) 斜槽因数 10.1052sin 2sin 220.99540.105ssk sK απαπ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭===式中,1sks t απτ=(58) 绕组因数 1110.959810.99540.9554dp d p sk K K K K ==⨯⨯=(59) 线圈平均半匝长 ()()'1220.12 1.57.76838.636()av E L L d L cm =++=+⨯+= 式中,d ——绕组直线部分伸出长,一般取1~3cm'0.612.957.758E y L k τ==⨯= k 为系数,单层线圈 ,4极取0.6()()1011121021720.080.098 1.60.490.85212.95222i s y D h h h r cm pπβπτ++++⨯+⨯+++⨯===⨯()式中,0β——与线圈节距有关的系数,对单层同心式线圈或单层交叉式线圈,0β取平均值(60) 线圈端部轴向投影长 '0sin 7.7680.517 4.013d E f L cm α==⨯=()式中,11011120.7220.49sin 0.517220.7220.4920.795t b r b r b α++⨯===+++⨯+⨯(61) 线圈端部平均长 ()()'22 1.57.76818.536E E L d L cm =+=⨯+=()(62) 定子导线质量 22511121211.05104t t Cu Cu s avN d N d m Q N L πρ-+=⨯2252 1.253 1.31.058.9361238.6361010.04()4kg π-⨯+⨯=⨯⨯⨯⨯⨯⨯=式中,Cu ρ——铜的密度,3/g cm 6.磁路计算 (63)极弧系数111.7==0.87513.352pp b ατ=(64)计算极弧系数 144=0.875=0.89113.352660.06510.8751i p p αατδα=++++--(65)气隙磁密波形系数 440.891sinsin1.25522i f K αππππ==⨯= (66)气隙磁通波形系数 22880.891sinsin 0.89720.8912i iK φαπππαπ==⨯=(67)气隙系数 12 1.2051 1.205K K K δδδ==⨯= 式中,()()()()101122101014.40.75 1.4844.40.0650.750.38 1.2054.40.75 1.4844.40.0650.750.380.38t b K t b b δδδ+⨯+⨯===+-⨯+⨯- 2K δ=1(68)空载漏磁系数 0σ=1.3根据转子磁路结构、气隙长度、铁芯长度、永磁体尺寸以及永磁材料性能等因数确定(69)永磁体空载工作点假定值 '0m b =0.838(70)空载主磁通'44000100.838 1.0741211.05100.01461()1.28m r m b B A Wb δφσ--⨯⨯⨯⨯===(71)气隙磁密(72) 440100.01461100.607()0.89113.35220.23i i ef B T L δδφατ⨯⨯===⨯⨯(72)气隙磁位差直轴磁路()()22270220.607100.015 1.2050.06510902.38()410B F K A δδδδδμπ---⨯=+⨯=+⨯⨯=⨯交轴磁路227220.60710 1.2050.06510757.39()410q B F K A δδδδμπ---⨯=⨯=⨯⨯⨯=⨯ 式中,2δ——永磁体沿磁化方向与永磁体槽间的间隙,cm (73)定子齿磁密 11110.607 1.48420.231.225()0.7960.9320.1ef t t Fe B t L B T b K L δ⨯⨯===⨯⨯(74)定子齿磁位差 11122 2.55 1.768.99()t t t F H h A ==⨯⨯=1t H 根据1t B 查附录2硅钢片磁化曲线,A/cm(75)定子轭部磁密440111100.0146110 1.742()2220.10.93 2.24j Fe j B T L K h δφ--⨯⨯===⨯⨯⨯(76)定子轭磁位差1111220.3673.6969.133484.6()j j j F C H L A ==⨯⨯⨯=1j H 根据1j B 查附录2硅钢片磁化曲线,A/cm1C ——定子轭部校正系数,查附图3-1(77)转子轭磁密440222100.01461100.797()2220.10.93 4.905j Fe j B T L K h δφ--⨯⨯===⨯⨯⨯(78)转子轭磁位差2222220.70.957 4.28 5.736()j j j F C H L A ==⨯⨯⨯=2j H 根据2j B 查附录2硅钢片磁化曲线,A/cm2C ——转子轭部校正系数,查附图3-1(79)每对极总磁位差112902.388.99484.6 5.7361401.71()t j j F F FF F A δ=+++=+++=∑(80)磁路齿饱和系数1757.398.991.012757.39q t st qF F K F δδ++===(81)主磁导500.014611.04210()1401.71H Fδδφ-Λ===⨯∑(82)主磁导标幺值 252702102 1.042100.5310 3.9841.046410211.05M r m h A δδλμμπ--Λ⨯⨯⨯⨯⨯===⨯⨯⨯ (83)外磁路总磁导标幺值 0 1.3 3.984 5.179n δλσλ==⨯=(84)漏磁导标幺值()()01 1.31 3.984 1.195σδλσλ=-=-⨯=(85)永磁体空载工作点 0 5.1790.8381615.1791n m n b λλ===++误差:0.83816-0.838=0.00016 0.00016/0.838=0.00019<0.1%(86)气隙磁密基波幅值4401100.01461101.2550.762()0.89113.35220.23f i i ef B K T L δδφατ⨯⨯==⨯=⨯⨯(87)空载反电动势004.44 4.44500.9554720.014610.897200.08()dp E fK N K V δφφ==⨯⨯⨯⨯⨯=7.参数计算(88)定子直流电阻122221112122241.335720.2170.201()1.25 1.31232222av t t L NR d d a N N ρππ⨯⨯==⨯=Ω⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⨯⨯+⨯+⎢⎥⎢⎥ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦式中,ρ——铜线电阻率 (89)漏抗系数()()222720410********.23720.9554100.37792ef dp x f L K N C pπμππ---⨯⨯⨯⨯⨯⨯⨯⨯===(90)定子槽比漏磁导 1111110.38910.951 1.34s U U L L K K λλλ=+=⨯+⨯= 式中,1U K 、1L K ——槽上、下部节距漏抗系数()()131/4311/41U K β=+=⨯+= ()()197/16917/161L K β=+=⨯+=01110101120.0820.0980.3890.380.380.72s U h h b b b λ⨯=+=+=++ 1L λ=0.951(91)定子槽漏抗()111221222320.1 1.1840.37790.18420.230.955436s s x ef dp pmL X C L K Q λ⨯⨯⨯⨯==⨯=Ω⨯⨯ (92)定子谐波漏抗112222313.3520.01280.37790.271()1.2050.0650.9554 1.01d x dp stm sX C K K K δτπδπ⨯⨯==⨯=Ω⨯⨯⨯⨯∑s ∑可查附图3-2(93)定子端部漏抗()1220.6421.2350.6415.1960.470.470.37790.08620.230.9554E yE x ef dp L X C L K τ⎛⎫--⨯⎛⎫==⨯⨯=Ω⎪ ⎪ ⎪⨯⎝⎭⎝⎭(94)定子斜槽漏抗 ()2211 1.4050.50.50.2710.1221.484sk sk d t X X t ⎛⎫⎛⎫==⨯⨯=Ω ⎪ ⎪⎝⎭⎝⎭(95) 定子漏抗 ()11110.1830.2710.0860.1220.663s d E sk X X X X X =+++=+++=Ω (96)直轴电枢磁动势折算系数 110.79681.255ad f K K === (97)交轴电枢磁动势折算系数0.360.28691.255q aq fK K K === q K 由电磁场算出,或取经验值(98)直轴电枢反应电抗()0200.08147.373.75114.05dad dE E X I --===Ω式中,()4.44 4.44500.9554720.010760.897147.36d dp N E fK N K V δφφ==⨯⨯⨯⨯⨯=()4110N mN mN m r b b A B δσφλ-=--⨯⎡⎤⎣⎦()()40.76110.761 1.195211.05 1.0741100.01076Wb -=--⨯⨯⨯⨯=⎡⎤⎣⎦()()'1 5.17910.09230.76115.1791n a mN n f b λλ-⨯-===++'0520.14810.092310 1.30.53817.2510ad a M c F f h H σ===⨯⨯⨯⨯()0.95547214.05350.450.4530.7971520.14812dp dad adK NI F mK A p⨯⨯==⨯⨯⨯=取()/228.1071/214.0535d N I I A ===(99)直轴同步电抗()1 3.7510.663 4.414d ad X X X =+=+=Ω 8.交轴磁化曲线aq q X I -计算(100)设定交轴磁通 aq φ分别取0.60δφ、0.70δφ、0.730δφ、0.750δφ、0.790δφ、0.810δφ、0.830δφ、0.850δφ(101)交轴磁路总磁位差aqF∑(A)以aq φ代替70项中的0δφ,计算第70~80项,所得的F ∑(每对极)即为交轴电枢磁动势aqF∑(102)对应交轴电流 0.9aq q aq dp p F I mK K N=∑(103) 交轴电动势 00aqaq E E δφφ=(104)交轴电枢反应电抗 aq aq qE X I =给定101项中不同的aq φ,重复101~104项,即可得到aq q X I -曲线,见下表9.工作特性计算(105)机械损耗 fw p =160W 可参考同规格感应电动机的机械损耗 (106)设定转矩角θ=45︒(107)假定交轴电流'q I =24.86A (108)交轴电枢反应电抗aq X (Ω)由'q I 查aq q X I -曲线(109)交轴同步电抗 ()1 5.490.663 6.153q aq X X X =+=+=Ω (110)输入功率 ()()22101121sin cos 0.5sin 2N q N N d q d q m P E U X R RU U X X X X R θθθ⎡⎤=⨯-++-⎣⎦+ ()23[200.08219.39 6.153sin 450.201cos 454.414 6.1530.201︒︒=⨯⨯⨯⨯-⨯⨯+ ()220.201219.390.5219.39 4.414 6.153sin(245)]︒+⨯+⨯⨯-⨯⨯=16956.23(W ) (111)直轴电流 ()1021sin cos N q N d d q RU X E U I X X R θθ+-=+()()20.201219.39sin 45 6.153200.08219.39cos 454.414 6.1530.20111.75A ︒︒⨯⨯+⨯-⨯=⨯+=(112)交轴电流 ()1021sin cos d N N q d q X U R E U I X X R θθ--=+()()24.414219.39sin 450.201200.08219.39cos 454.414 6.1530.20124.85A ︒︒⨯⨯-⨯-=⨯+=误差:'q q I I -=24.86-24.85=0.010.01/24.86=0.0004<1%(113)功率因数 cos cos0.357960.9373ϕ== 式中,()/40.427040.35796rad ϕθψπ=-=-=()11.75arctanarctan 0.0.4270424.85d q I rad I ψ=== (114)定子电流()127.49I A ===(115)定子电阻损耗()2211327.490.201413.6Cu p mI R W ==⨯⨯=(116)负载气隙磁通()200.080.015214.44 4.44500.9554720.897dp E Wb fK NK δδφφ===⨯⨯⨯⨯式中,()208.46E V δ===(117)负载气隙磁密()4100.015210.63230.89113.35220.23d i i ef B T L δδφατ⨯===⨯⨯(118)负载定子齿磁密()11111.48420.230.6323 1.27530.7960.9320.1ef t d dt Fe t L B B T b K L δ⨯==⨯=⨯⨯(119)负载定子轭磁密()44111100.0152110 1.8142220.10.93 2.24j dFe j B T L K h δφ⨯⨯===⨯⨯⨯ (120)铁耗()111211 2.5 2.61943.772 3.5753063.88197.0Fe t d t j d j p k p V k p V W =+=⨯⨯+⨯⨯=式中,1t d p 、1j d p ——定子齿及轭单位铁损耗,可由1t d B 和1j d B 查附录2硅钢片损耗曲线1k 、2k ——铁耗修正系数,一般分别取2.5和2(121)杂散损耗()22*33127.29100.0151610187.128.11s sN N N I p p P W I ⎛⎫⎛⎫=⨯=⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭*sN p 可参考实验值或凭经验给定(122)总损耗()413.6197.0160187.1953.7CuFe fw s p pp p p W =+++=+++=∑(123)输出功率 ()2116956.23953.716002.53p p p W =-=-=∑(124)效率 2116002.5310010094.37%16956.23p p η=⨯=⨯= (125)工作特性 给定一系列递增的转矩角θ,分别求出不同转矩角的2p 、η、1I 、cos ϕ等性能,即为电机的工作特性,见下表(126)失步转矩倍数 *max 28.9591.8116pN N P T P ===倍 式中,max P ——最大输出功率,由电机工作特性上求得 (127)永磁体额定负载工作点 ()()'1 5.17910.09950.76115.1791n aN mN n f b λλ-⨯-===++式中,'00.450.4530.79680.95547211.310.0995102 1.3817.250.5310ad dp dNaN c M mK K NI f p H h σ⨯⨯⨯⨯⨯===⨯⨯⨯⨯⨯dN I ——输出额定功率时定子电流的直轴分量(128)电负荷 ()112237228.107241.4/17N i mNI A A m D ππ⨯⨯⨯===⨯(129)电密 112211121222t t I J d d a N N π=⎡⎤⎛⎫⎛⎫+⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦()22227.294.141/1.25 1.312322A mm π==⎡⎤⎛⎫⎛⎫⨯⨯+⨯⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦(130)热负荷11A J =241.4⨯4.141=999.63(()22/A cm mm •) (131)永磁体最大去磁工作点 ()()'1 5.17910.65300.29115.1791n adh mh n f b λλ-⨯-===++式中,'00.450.4530.79680.95547294.840.6530102 1.3817.250.5310ad dp adhadhc M mK K NI f p H h σ⨯⨯⨯⨯⨯===⨯⨯⨯⨯⨯1adh dI =94.84()A ==。
磁性材料磁化曲线和磁滞回线的Matlab绘制与拟合

磁性材料磁化曲线和磁滞回线的Matlab绘制与拟合作者:金华来源:《科技视界》2016年第26期【摘要】利用Matlab软件绘制了由磁滞回线实验仪得到的磁性材料的磁化曲线与磁滞回线,并对相应的图线进行了多项式拟合,计算了磁滞回线面积,具体说明了Matlab软件在大学物理实验数据处理中的应用。
【关键词】Matlab软件;磁化曲线;磁滞回线;大学物理实验0 引言实验数据图线绘制和拟合是大学物理实验数据处理的重要环节。
传统的毫米方格纸绘制图线不够美观工整,容易出错,且只能对数据进行线性拟合。
因而,引入软件绘制实验图线,进行数据拟合,在大学物理实验教学中受到极大重视。
以磁性材料基本特性研究这个实验为例,就有Origin、Mathmatica、Matlab等不同类型的软件被用来讨论实验数据的处理[1-3]。
Matlab 软件具有较强的数值计算和绘图功能。
随着Matlab软件在高校理工课程教学中的普及,在大学物理实验教学中推广Matlab软件进行实验数据处理已经具备了一定的条件。
本文利用Matlab软件讨论磁性材料磁化曲线、磁滞回线的绘制和拟合,来具体说明Matlab软件在大学物理实验教学中的实践与应用。
注意到文献[3]中,利用Matlab软件只绘制了磁化曲线和磁滞回线。
在本文中,我们还将讨论这些图线的拟合,并通过计算拟合的磁滞回线的面积来估算磁滞损耗。
1 实验数据考察磁化曲线和磁滞回线是表征磁性材料物理性质的重要手段。
本文利用FB310A磁滞回线实验仪在不同电压U下通过示波器观察输出的铁磁样品的磁滞回线。
这些磁滞回线的顶点可构成样品的磁化曲线。
具体的实验原理和实验步骤可参见文献[4]。
表1给出了在不同电压下测得的磁滞回线顶点对应的磁场强度H和磁感强度B的数值。
表2 则为最大电压U=3V时磁滞回线上测得的各点的H和B的数值。
2 磁化曲线和磁滞回线的绘制与拟合利用Matlab绘制表1、表2对应的磁化曲线和磁滞回线时,采用plot命令绘制散点图。
