单纯形法例题
单纯形法的矩阵计算例题

1、在使用单纯形法求解线性规划问题时,初始基本可行解通常通过以下哪种方法获得?A. 两阶段法B. 高斯消元法C. 矩阵求逆D. 逐次逼近法(答案)A2、在单纯形表的迭代过程中,当所有检验数均非负时,说明当前解是?A. 无界解B. 无解C. 最优解D. 可行解但非最优(答案)C3、单纯形法中,选择进入基的变量时,通常选择检验数最小的变量,这是?A. 错误的做法B. 正确的做法,但仅当目标函数求最大值时C. 正确的做法,但仅当目标函数求最小值时D. 无论目标函数求最大还是最小,都是正确的做法(答案)B(假设题目中指的是选择绝对值最大的负检验数对应的变量进入基,若求最小值则选择正检验数)4、在单纯形迭代过程中,若出现某个基变量的值为零,而该变量在目标函数中的系数(即检验数)为正,则?A. 该问题无界B. 应立即停止迭代,因为当前解不可行C. 应将该变量从基中换出D. 这种情况不可能发生(答案)C5、单纯形法中,退出基的变量选择通常基于?A. 检验数的大小B. 基变量在约束条件中的系数比值(即比值检验)C. 目标函数中的系数D. 变量的下界或上界(答案)B6、在单纯形迭代过程中,若所有基变量的检验数均为零,则?A. 达到了最优解,且可能存在多个最优解B. 达到了最优解,且唯一C. 问题无解D. 需要进行人工变量调整(答案)A7、单纯形法中,若某个迭代步骤中发现无法找到符合条件的进入基变量(即所有检验数均非负),则?A. 当前解即为最优解B. 问题无解C. 需要引入人工变量继续迭代D. 应检查初始基本可行解的正确性(答案)A8、在构建初始单纯形表时,若目标函数为求最小化,则检验数应如何计算?A. 检验数= 目标函数系数- 约束条件右侧常数与基变量系数的乘积之和B. 检验数= 目标函数系数+ 约束条件右侧常数与基变量系数的乘积之和的相反数C. 检验数= 目标函数系数直接作为检验数D. 检验数= 约束条件左侧系数与目标函数系数的比值(答案)B(简化描述,实际计算中需考虑基变量的当前值和目标函数系数)9、单纯形法中,当某个基变量的值为负时,说明?A. 当前解不可行B. 当前解可能是最优解,但需进一步验证C. 应立即将该变量从基中换出D. 这种情况在正确执行单纯形法时不可能发生(答案)D(在正确执行时,基变量应始终非负)10、在单纯形迭代过程中,若发现某个非基变量的检验数为正,且该变量对应的约束条件为“≤”类型,则?A. 该变量应被选为进入基的变量B. 该变量不能进入基,因为其检验数为正C. 需要检查该变量的上界是否满足约束D. 该问题可能无解(答案)A(在求最大化问题时,正检验数对应的非基变量是潜在的进入基候选)。
求单纯形表中的未知数例题

求单纯形表中的未知数例题以下是一个求解线性规划问题的例题,涉及到单纯形法。
假设有如下线性规划问题:
最大化: 4x + 6y
约束条件:
x + 2y <= 12
x + y <= 8
x, y >= 0
目标函数系数:4 和6。
约束条件的系数分别是:1、2、1 和1。
首先,我们需要构建一个初始单纯形表。
在这个表中,我们有两个基变量和两个非基变量。
基变量的系数是约束条件的系数,而非基变量的系数是目标函数的系数。
初始单纯形表如下:
在这个表中:
B列是基变量的检验数,表示的是当前解是否可行或最优。
非基变量的检验数表示的是当非基变量进入基变量时,目标函数的增加值。
我们将其设置为负无穷,表示这是一个入基变量,其增加量可以被任意大。
最后一行的两个问号表示的是非基变量的值,我们将其设置为待求解的值。
然后,我们开始迭代。
在每一次迭代中,我们都会找到一个入基变量和出基变量,然后更新单纯形表。
这个过程会一直持续到所有的检验数都满足最优性条件(即所有的B列的值都大于等于0)。
单纯形法例题

单纯形法例题1、例1、目标函数 maxz=2+3约束条件:解:首先要将约束条件化为标准形:由此可以看出我们需要加上三个松弛变量,.得到的标准形式为:maxz=2+3+0+0+0然后要将其初始的单纯形表画出来:2 3 0 0 0b0 8 1 2 1 0 0 40 16 4 0 0 1 0 -0 12 0 0 0 1 32 3 0 0 0由初始单纯形表可以看出,为换入变量,而为换出变量;然后根据:=(也就是如果与主元素同行,则用现在的值除以主元素即可得到即将要填入的值,否则,就用现在的值减去与主元素构成矩形的边角上的值的乘积再除以主元素之后的值。
例如:上面的第一行所对应的b值为8-(12*2)/4=2,故填入值应该为2。
而则是由我们根据非基变量的检验数的大小,挑选出最大的那个,作为换入变量,然后用b的值除以该换入变量所在的列的所有值,得到列的值。
2 3 0 0 0b0 2 0 1 0 -1/2 20 16 4 0 0 1 0 43 3 0 1 0 0 1/4 -2 0 0 0 -3/4由于在检验数中仍然存在大于等于0的数,而且P1,P5的坐标中有正分量存在,所以需要继续进行迭代运算。
通过观察可以看出主元素为1,换入变量为,换出变量为,故得到的单纯形表如下:2 3 0 0 0b2 2 1 0 1 0 -1/2 -0 8 0 0 -4 1 43 3 0 1 0 0 1/4 120 0 -2 0 1/4由于检验数中存在正数,且P5和P3中有正分量存在,所以需要继续迭代(换入变量为,换出变量为:得到单纯形表如下:2 3 0 0 0b2 4 1 0 0 1/4 00 4 0 0 -2 1/2 13 2 0 1 1/2 -1/8 00 0 -3/2 -1/8 0此时可以发现检验数中没有大于0的数,表明已经得到了最优解,所以最优解是:(4,2,0,0,4),故目标函数值z=2*4+2*3=142、合理利用线材问题,现在要做100套钢架,每套用长为2.9m,2.1m,和1.5m的钢各一根,已知原料长7.4m,问应如何下料,使用的原材料最省;解:首先我们必须要清楚该问题的需要设立的变量是什么。
运筹学单纯形法的例题

可行域在x1+3x2=7与4x1+2x2=9之下__
3
.
05.07.2020
练习㈠用图解法
5
4 4x1+x2=9
3
2
1 (2.25,0)
0
1
2
3
4
5
6
7
4
.
05.07.2020
练习㈠. 单纯形表
1 31 0 7 4 20 1 9
填入第一个约束的数据.
填入第二个约束的数据.
5
.
05.07.2020
❖至少有一个非基变量的检验数为正,但它的系 数全为非正,则无有限最优解;
❖所有非基变量的检验数全为非正,已有最优解, 但若其中至少有一个的检验数为0,且它的系 数中有2正4 的,则可能有. 无穷多个最优0解5.07.。2020
基变量列中_x_5_换为_x_1_,
改CB列,_-_M__换为_4__.
Excel
17
.
05.07.2020
练习㈢用图解法和单纯形法求 如下线性规划问题的最优解:
Max z =4 x1 + x2 x1 + 3x2 ≥ 7
s.t. 4x1 + 2x2 ≥ 9 x1 , x2 ≥ 0
可行域在直线 x1+3x2=7之上__
s.t. 4x1 + 2x2 -x4+x6=9
基引是进谁两?个这 理x“1里?,x人“2 ,工x-”3 如变,x4何量,x5处”,x6≥0
x5 ,x620
.
05.07.2020
练习㈢.用单纯形法
Max z=4x1+x2+0x3+0x4 -Mx5 –Mx6
15单纯形法(运筹学)

1
2
3
4
X(1)= (2,3) X(2)= (4,2)
全部解: 全部解:X=α
(1) -4 0 1 -2 0
14
15
本问题无界。 本问题无界。 X2
O
X1
Z=0
16
1.5.4 初始基本可行解的求法 (一)、大M法: 一、 法 例1 : maxZ= 6X1 +4X2 2X1 +3X2 ≤ 100 4X1 +2X2 ≤ 120 X1 X1 X2 ≥0
=14
X2 ≥ 22
17
λj <0
8
(3)、 (3)、maxZ=10X1 + 12X2 3X1+4X2 ≤ 6 4X1+ X2 ≤ 2 3X1 +2X2 ≤ 3 X1 , X2 ≥0
9
10
X =(0, 3/2, 0, 1/2, 0)T Zmax=18
退化解
*
11
例:maxZ= -3/4X4+20X5 -1/2X6+6X7 X1+1/4X4 -8X5 -X6+9X7 =0 X2+1/2X4-12X5 -1/2X6+3X7 =0 X3+X6 =1 X1 … X7 ≥0 (P1 P2 P3) → (P4 P2 P3) → (P1 P2 P3) → (P4 P5 P3) → (P6 P5 P3) → (P6 P7 P3) → (P1 P7 P3)
【精品】最优化单纯形法例题讲解

【精品】最优化单纯形法例题讲解最优化单纯形法是一种用于求解线性规划问题的常用方法。
它通过不断迭代调整基变量的取值来寻找使目标函数取得最大(或最小)值的最优解。
下面我们通过一个例题来详细讲解最优化单纯形法的求解过程。
例题:假设有如下线性规划问题:Max Z = 3x1 + 4x2 s.t. 2x1 + x2 ≤ 8 x1 + 2x2 ≤ 6 x1, x2 ≥ 0首先,我们将原问题转化为标准型,即将约束条件全部转化为等式,并引入松弛变量。
将原问题转化为如下形式:Max Z = 3x1 + 4x2 s.t. 2x1 + x2 + x3 = 8 x1 + 2x2 + x4 = 6 x1, x2, x3, x4 ≥ 0接下来,我们构造初始单纯形表。
单纯形表由目标函数系数矩阵、约束条件系数矩阵和右端常数向量组成。
目标函数系数矩阵: 3 4 0 0约束条件系数矩阵: 2 1 1 0 1 2 0 1右端常数向量: 8 6再构造一个松弛变量的列向量,也就是单位矩阵的第一列。
接下来,我们要选择一个入基变量和一个出基变量,通过迭代调整基变量的取值来逼近最优解。
选择入基变量:我们要选择一个非基变量进入基变量集合,使得目标函数系数矩阵中的相应列元素最大(如果是最小化问题,则选择最小的)。
选择出基变量:我们要选择一个基变量出基变量集合,使得约束条件系数矩阵中相应列元素最小的行对应的非基变量列元素大于等于0。
在初始单纯形表中,目标函数系数矩阵中3和4是最大的,所以我们选择x1和x2作为入基变量。
在约束条件系数矩阵中,对于x1,第一行的1最小,所以我们选择第一行的x4作为出基变量;对于x2,第二行的1最小,所以我们选择第二行的x3作为出基变量。
接下来,我们通过计算新的单纯形表来更新基变量的取值。
首先,我们计算新的基变量x1的系数矩阵。
将x1的列除以相应的出基变量的系数(即1),得到新的系数矩阵:1 0 1/2 0 0 1 -1/2 1然后,我们计算新的基变量x2的系数矩阵。
(完整word版)运筹学单纯形法
=0
σj=Cj- Zj
2
-1
1
0
0
0
1
S1
0
0
4
-5
1
-3
0
30
30/4
X1
2
1
-1
2
0
1
0
10
10/-1
S3
0
0
2
-3
0
-1
1
10
10/2
Zj
2
-2
4
0
2
0
Z=Z0=0*30+
2*10+0*10
=20
σj=Cj- Zj
0
1
-3
0
-2
0
2
S1
0
0
0
1
1
-1
-2
10
X1
2
1
0
1/2
0
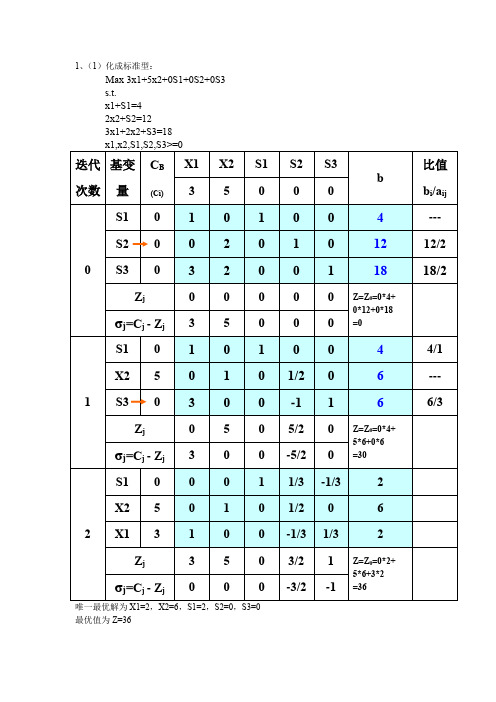
s.t.
5x1+6x2-4x3-4x4+S1=20
3x1-3x2+2x3+8x4+S2=25
4x1-2x2+x3+3x4+S3=10
x1,x2,x3,x4,S1,S2,S3>=0
迭代次数
基变量
CB
(Ci)
X1
X2
X3
X4
S1
S2
S3
b
比值
bi/aij
6
2
10
8
0
0
0
0
S1
0
5
6
-4
-4
1
0
0
20
(参考资料)运筹学单纯形法例题
0
1
0
x4
30
1
[3]
0
σ
(1) j
=cj
− CB
⋅ Pj
3
4
0
30
1
= 10
3
0
0
x3
5
30
[]
3
0
1
1 −
30 × 3 = 18 5
3
4
x2
10
1 3
σ
(2) j
=cj
− CB
⋅ Pj
5 3
3
x1
18
1
4
x2
4
0
σ
(3) j
=cj
− CB
⋅ Pj
1
10 × 3 = 30
1
0
3
0
0
−4
3
3
1
0
−
5
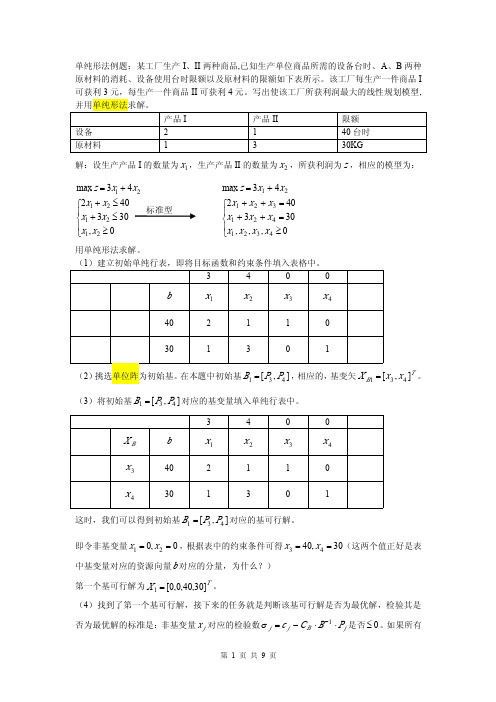
接着看另一行。即第一行,该行的系数表示的是约束条件: 40 = 2x1 + x2 + x3 ①。
我们期待的是:在这个约束条件中, x2 的系数=0, x3 的系数=1。要做到这一点,需要将
①- 1 ×
②’
⇒
30
=
5 3
x1
+
x3
−
1 3
x4
①’,式①’与式①等价。
为实现我们的期待,将约束条件
⎧40 ⎩⎨30
⎧2x1 + x2 + x3 = 40
⎪ ⎨
x1
+
3x2
+
x4
=
30
⎪ ⎩
x1
,
x2 ,
x3 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12 0 [4] 0 0 1 12/4=3 23000
❖ 计算非基变量的检验数
σ1=c1− σ2=c2−
=2−(0×1+0×4+0×0)=2 =3−(0×2+0×0+0×4)=3
填入表1-3的底行对应非基变量处。
(2) 因检验数都大于零,因此继续进行计算; (3) max(σ1,σ2)=max(2,3)=3,对应的变量 x2 进基,
3
x2
3
0 1 0 0 1/4 12
检验数
0 0 -2 0 1/4
重复之前步骤 因为还存在检验数>0,继续进行迭代
(6) 表1-6最后一行的所有检验数都已为负或零。这表示目标函数 值已不可能再增大,于是得到最优解
cj
23 0
00
θ
CB
XB
B﹣1b x1 x2
x3
X4
x5
2
x1
4
1 0 1 1/4 0
计算θ
根据公式求得θ的值,可知θ最小值为3 则它所在行对应的x5出基,x2所在列和x5所在行的交叉处
[4]称为主元素。
(4) 以[4]为主元素进行迭代运算,即初等行变换,使P2变换为(0,0,1)T,在XB 列中将x2 替换x5 ,于是得到新表
cj
2 30 0 0
CB
XB B﹣1b x1 x2 x3 x4 x5 θ
S.T
4x1
x4 16
4x2
x5 12
x j 0 j 1,2, ,5
➢ 根据标准型将有关数字填入表中,得到初始单纯形表
cj
CB
XB
0
x3
0
x40x5 Nhomakorabea检验数
23000
B﹣1b x 1 x 2 x 3 x 4 x 5 θ
8
1 2 1 0 0 8/2=4
16 4 0 0 1 0 -
0
x3
2 [1] 0 1 0 -1/2 2
0
x4
16
4 00 1 04
3
x2
3
检验数
0 1 0 0 1/4 2 0 0 0 -3/4
因为还存在检验数>0,继续进行迭代
cj
2 30 0 0
CB
X1 B﹣1b x1 x2 x3 x4 x5 θ
2
x3
2
1 0 1 0 -1/2
0
x4
8
0 0 -4 1 [2] 4
运筹学演讲之单纯形法
Content
max z 2x1 3x2
x1 2x2 8 4x1 16 4x2 12 x j 0 j 1,2
求其基本可行解和最大目标值
化为标准型:
max z 2x1 3x2 0x3 0x4 0x5
x1 2x2 x3
8
0
x5
4
0 0 -2 1/2 1
3
x2
2
0 1 1/2 -1/8 0
检验数
0 0 -3/2 -1/8 0
X*=X=(4,2,0,0,4)T 目标函数的最大值 z*=14
Thank you !
