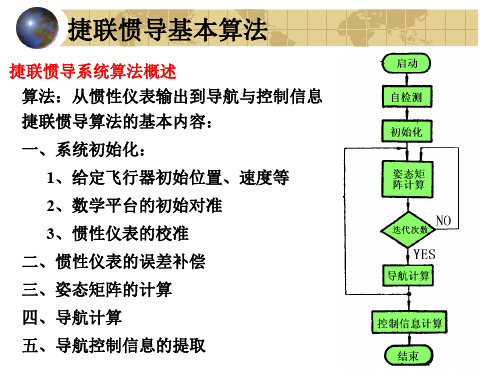
捷联式惯性导航积分算法设计-速度位置计算
捷联惯性导航系统的解算方法

捷联惯性导航系统的解算方法捷联惯性导航系统(Inertial Navigation System,简称INS)是一种利用陀螺仪和加速度计等惯性测量单元测量物体的加速度和角速度,然后通过对这些测量值的积分计算出物体的速度和位置的导航系统。
INS广泛应用于航空航天、无人驾驶车辆和船舶等领域,具有高精度和自主性等特点。
INS的解算方法一般分为初始对准、运动状态估计和航位推算三个主要过程。
初始对准是指在启动导航系统时,通过利用外部辅助传感器(如GPS)或静态校准等方法将惯性传感器的输出与真实姿态和位置进行初次校准。
在初始对准过程中,需要获取传感器的初始偏差和初始姿态,一般采用标定或矩阵运算等方法进行。
运动状态估计是指根据惯性传感器的测量值,使用滤波算法对物体的加速度和角速度进行实时估计。
常用的滤波算法包括卡尔曼滤波、扩展卡尔曼滤波和粒子滤波等。
其中,卡尔曼滤波是一种最优估计算法,通过对观测值和状态进行线性组合,得到对真实状态的最佳估计。
扩展卡尔曼滤波则是基于卡尔曼滤波的非线性扩展,可以应用于非线性INS系统。
粒子滤波是一种利用蒙特卡洛采样技术进行状态估计的方法,适用于非高斯分布的状态估计问题。
航位推算是指根据运动状态估计的结果,对物体的速度和位置进行推算。
INS最基本的航位推算方法是利用加速度值对速度进行积分,然后再对速度进行积分得到位置。
但是,在实际应用中,由于传感器本身存在噪声和漂移等误差,导致航位推算过程会出现积分漂移现象。
为了解决这个问题,通常采用辅助传感器(如GPS)和地图等数据对INS的输出进行校正和修正。
当前,还有一些先进的INS解算方法被提出,如基于深度学习的INS 解算方法。
这些方法利用神经网络等深度学习模型,结合原始传感器数据进行端到端的学习和预测,以实现更高精度的位置和姿态估计。
综上所述,捷联惯性导航系统的解算方法主要包括初始对准、运动状态估计和航位推算三个过程。
其中,运动状态估计过程利用滤波算法对传感器的测量值进行处理,得到物体的加速度和角速度的估计。
惯导速度积分公式

惯导速度积分公式惯导系统,即惯性导航系统,是利用陀螺仪和加速度计来测量和维持方向和位置信息的系统。
当我们考虑一个物体在三维空间中的位置、速度和加速度时,惯导系统可以提供这些信息。
速度积分公式在惯导系统中是非常核心的概念。
这个公式基于以下物理原理:如果一个物体在某个方向上受到一个力的作用,那么这个力会导致物体在该方向上产生加速度,进而改变物体的速度。
具体来说,速度积分公式可以表达为:Δv = F Δt其中,Δv 是速度的变化量,F 是作用在物体上的力,Δt 是时间的变化量。
这个公式告诉我们,一个力在一个时间段内作用在一个物体上,会导致物体的速度在该方向上发生变化。
在惯导系统中,我们通常使用陀螺仪来测量角速度,使用加速度计来测量线性加速度。
通过测量这些数据,我们可以计算出物体的速度和位置信息。
具体来说,如果一个物体在某个时刻的速度为 v,角速度为ω,那么经过Δt 时间后,物体的速度变化量Δv 可以表示为:Δv = v ×ω×Δt其中,“×”表示矢量点乘。
这个公式告诉我们,一个物体在转动时,其速度会发生变化。
这是因为在转动过程中,物体的方向会发生变化,导致其速度的方向发生变化。
另外,我们还可以通过加速度计测量物体在三个轴向上的加速度分量 a_x、a_y、a_z。
如果我们知道物体的初始速度 v 和初始位置 p,那么经过Δt 时间后,物体的位置变化量Δp 可以表示为:Δp = v ×Δt + 1/2 × a ×Δt^2其中,“^2”表示平方,“a”是物体的加速度矢量。
这个公式告诉我们,一个物体在受到力的作用时,其位置会发生变化。
这是因为在力的作用下,物体的速度和加速度都会发生变化。
总之,惯导系统中的速度积分公式是用于计算物体速度和位置变化的关键公式之一。
通过测量陀螺仪和加速度计的数据,我们可以使用这些公式来更新物体的速度和位置信息。
捷联惯导系统算法.ppt
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
捷联惯导算法与组合导航原理讲义

捷联惯导算法与组合导航原理讲义一、捷联惯导算法捷联惯导(Inertial Navigation System,INS)是一种通过测量惯性传感器的运动参数实现导航定位的技术。
惯性导航系统中包括了加速度计和陀螺仪等传感器,通过测量物体的加速度和角速度,可以推算出物体的位置、速度和姿态等信息。
1.1加速度计加速度计是一种测量物体加速度的传感器。
常见的加速度计有基于压电效应的传感器和基于微机电系统(Microelectromechanical System,MEMS)的传感器。
加速度计的原理是通过测量物体受到的惯性力,推算出物体的加速度。
由于加速度是速度对时间的导数,因此通过对加速度的积分操作,可以计算出物体的速度和位移。
1.2陀螺仪陀螺仪是一种测量物体角速度的传感器。
常见的陀螺仪有机械陀螺仪和MEMS陀螺仪等。
陀螺仪的原理是基于角动量守恒定律,通过测量转动惯量的变化,推算出物体的角速度。
与加速度计类似,通过对角速度的积分操作,可以计算物体的姿态。
1.3捷联惯导算法离散时间模型中,位置、速度和姿态等状态变量通过积分加速度和角速度来更新。
由于加速度计和陀螺仪测量结果存在噪声,因此在积分操作时需要加入误差补偿算法来消除误差。
常见的误差补偿算法有零偏校正和比例积分修正等。
连续时间模型中,位置、速度和姿态等状态变量通过微分方程来描述,并通过求解微分方程来更新状态。
由于计算量较大,通常需要使用数值积分方法来求解微分方程。
常见的数值积分方法有欧拉法、中点法和四阶龙格-库塔法等。
二、组合导航原理组合导航是一种融合多种导航技术的导航方式。
常见的组合导航方式有捷联惯导与GPS组合导航。
组合导航通过融合多种导航系统的测量结果,可以提高导航定位的精度和可靠性。
2.1捷联惯导与GPS组合导航捷联惯导与GPS组合导航是一种常见的组合导航方式。
在这种方式下,捷联惯导提供了高频率的惯导数据,可以提供较高的定位精度,但是由于其测量结果累积误差较大,会逐渐偏离真实轨迹。
卫星导航捷联惯性导航系统的建模与设计

卫星导航捷联惯性导航系统的建模与设计导航系统在现代社会中起着不可或缺的作用。
随着卫星导航技术的快速发展,卫星导航捷联惯性导航系统(SGINS)成为一种高精度、高可靠性的导航解决方案。
本文将探讨SGINS的建模与设计方法。
一、SGINS的基本原理卫星导航捷联惯性导航系统是将全球定位系统(GPS)和惯性导航系统(INS)相互融合的一种导航方案。
GPS通过接收卫星发射的定位信号来确定位置,但其精度受环境因素和信号传播延迟的影响。
而INS则通过测量加速度和角速度来估计位置和姿态,但由于积分误差的累积,导航精度会随时间增长而降低。
SGINS利用GPS和INS互补的性质,实现了位置和姿态的精确估计。
二、SGINS的建模方法1. 系统状态估计SGINS的建模首先需要考虑系统状态的估计问题。
系统状态通常包括飞行器的位置、速度和姿态等信息。
可以使用卡尔曼滤波器来处理系统状态的估计问题,通过状态观测和预测来优化估计结果。
同时,还需要根据系统的实际情况选择合适的状态表示和测量模型,以提高估计的准确性。
2. 误差建模SGINS中的误差主要来自于GPS和INS的测量误差,需要进行误差建模和补偿。
对于GPS测量误差,可以通过统计分析和模型辨识来进行建模。
INS测量误差主要包括随机误差和系统误差,可以通过校准和校正来减小。
此外,还需要考虑动态误差和环境因素对误差的影响,例如加速度噪声、温度变化等。
3. 系统动力学建模SGINS的建模还需要考虑系统的动力学特性。
对于飞行器的运动状态,可以利用运动学和动力学方程来描述。
此外,还需要考虑外部扰动和不确定性对系统动力学的影响,以提高系统的稳定性和鲁棒性。
三、SGINS的设计方法1. 系统硬件设计SGINS的设计首先需要选取合适的硬件组件,包括GPS接收器、惯性传感器和计算单元等。
对于GPS接收器,可以选择多系统接收器,以提高定位精度和可用性。
对于惯性传感器,可以选择高精度的加速度计和陀螺仪,以减小测量误差。
惯导精度计算公式

惯导精度计算公式1.定位计算公式:定位计算公式用于计算导航系统的位置和速度。
通常情况下,导航系统会测量三个方向上的加速度(即加速度计),然后通过积分算法来计算导航系统的速度和位置。
速度计算公式:在惯导系统中,速度是通过加速度的积分计算得出的。
通常情况下,速度计算公式如下所示:V(t)=V(t-Δt)+a(t)Δt其中,V(t)表示在t时刻的速度,V(t-Δt)表示在t-Δt时刻的速度,a(t)表示在t时刻的加速度,Δt表示时间间隔。
位置计算公式:在惯导系统中,位置是通过速度的积分计算得出的。
通常情况下,位置计算公式如下所示:P(t)=P(t-Δt)+V(t)Δt其中,P(t)表示在t时刻的位置,P(t-Δt)表示在t-Δt时刻的位置,V(t)表示在t时刻的速度,Δt表示时间间隔。
以上是最基本的速度和位置计算公式,但在实际应用中,还需要考虑一些修正因素,如地球背景力、气动力等,以提高计算的精度。
2.姿态计算公式:姿态计算公式用于计算导航系统的方向和姿态。
姿态通常由三个方向上的角速度(即陀螺仪)测量得出,并通过积分算法计算得到姿态变化。
姿态角计算公式:姿态角度是通过角速度的积分计算得出的。
通常情况下,姿态角计算公式如下所示:θ(t)=θ(t-Δt)+ω(t)Δt其中,θ(t)表示在t时刻的姿态角度,θ(t-Δt)表示在t-Δt时刻的姿态角度,ω(t)表示在t时刻的角速度,Δt表示时间间隔。
3.误差修正公式:惯性导航系统在长时间运行中,由于各种原因,例如器件漂移、传感器误差等,会产生误差。
因此,在进行位置和姿态计算时,需要考虑误差修正的公式。
误差修正公式:误差修正公式通常使用卡尔曼滤波器等方法进行计算,以修正导航系统的误差。
卡尔曼滤波器是一种用于估计系统状态的统计滤波器,通过最小均方误差估计的方法来进行状态估计和修正。
综上所述,惯导精度计算公式包括定位计算公式、姿态计算公式和误差修正公式。
这些公式可以通过测量加速度和角速度的变化,结合积分和滤波算法来计算导航系统的位置、速度和姿态。
捷联惯导

坐标系的定义
1. 地理坐标系(下标为t)—— OXtYtZt :O 取载体质心,Xt 轴指向东,Yt 轴指向北,Zt 轴沿垂线指向天。 2. 导航坐标系(下标为n)—— OX nYnZn :O 取载体质心,Zn与 Zt 重合,Xn 与 Xt,Yn 与 Yt 相差一个游动方
C13
C23
C33
位置速率
p ep
位置速率是由飞行器地速的水平分量引起的,由于平台坐标系与地理坐标系相差 一个游动方位角,
可得:
VVENtt
cos sin
sin cos
VEp VNp
p ep
可写成
p epE
C32 C31
180 ,180
1.求纬度的真值L
L L 反正弦函数的主值域与L的定义域一致,因此:
主
2.求经度的真值
反正切函数的主值域是 90 ,90 与 的定义域不一致,因此需要在 的定义域内确定经度的真值。
由: 主
tan 1
C32 C31
tan 1
cos L sin cos L cos
其中:
.
V ep 平台系相对地球的加速度向量
f 加速度计测量的比力向量
2ie ep V ep 无明显物理意义,又称有害加速度
g 重力加速度向量
整理上式可得:
.
VEp
.
VNp
.
VUp
f
p E
捷联惯导结算原理

0 cos sin , Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角:
(5) 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结:1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系, 加速计的比 力信息直接投影在导航系中,可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出;而捷联式惯导用数学平台取代实体的物理平台,通过求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
捷联惯导积分算法设计 下篇:速度和位置算法Paul G. SavageStrapdown Associates, Inc., Maple Plain, Minnesota 55359摘要:本论文分上下两篇,用于给现代捷联惯导系统的主要软件算法设计提供一个严密的综合方法:将角速率积分成姿态角,将加速度变换或积分成速度以及将速度积分成位置。
该算法是用两速修正法构成的,而两速修正法是具有一定创新程度的新颖算法,是为姿态修正而开发出来的,在姿态修正中,以中速运用精密解析方程去校正积分参数(姿态、速度或位置),其输入是由在参数修正(姿态锥化修正、速度划桨修正以及高分辨率位置螺旋修正)时间间隔内计算运动角速度和加速度的高速算法提供的。
该设计方法考虑了通过捷联系统惯性传感器对角速度或比力加速度所进行的测量以及用于姿态基准和矢量速度积分的导航系旋转问题。
本论文上篇定义了捷联惯导积分函数的总体设计要求,并开发出了用于姿态修正算法的方向余弦法和四元数法;下篇着重讨论速度和位置积分算法的设计。
尽管上下两篇讨论中常常涉及到基本的惯性导航概念,然而本论文提供的材料都假定是为那些熟悉惯性导航的人使用的。
专门用语:12,,A A A =任意坐标系;SF a =定义为由施加的非重力产生的相对于非旋转惯性空间的加速度比力,用加速度计测得;12A A C =将矢量从2A 坐标系投影到1A 坐标系的方向余弦矩阵; I =单位矩阵;A V =列向量,它的各项元素等于矢量V 在坐标系A 的各轴上的投影A V ⨯() =向量AV 的反对称(或交叉积)形式,代表如下矩阵:00ZA YA ZA XA YAXAV V V V V V -⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦其中:XA V ,YA V ,ZA V 是AV 的分量,AV ⨯()与A 系矢量的矩阵乘积等于AV与该矢量的叉积;2A ω1A =2A 坐标系相对于1A 坐标系的角速率,当1A 为惯性系(I 系)时,2A ω1A 是由安装在2A 坐标系上的角速率传感器所测到的角速率。
1 导论捷联惯导系统(INS)一般是由惯性角速率传感器和给INS计算机提供数据的加速度计构成的一个正交三轴系统组成的。
惯性传感器直接安装(捷联)到INS底盘构架上,这与原来采用主动多轴方向架隔离安装组合防止传感器旋转的INS技术形成对比。
INS计算机中进行的主要软件函数运算是将敏感的角速率积分成姿态,将加速度计敏感到的比力加速度变换成导航座标系,将软件模型重力与变换比力相加,计算出整个加速度,并将整个加速度双积分成矢量速度和位置。
INS软件设计过程中的关键因素是开发出能在有动态角速率,比力加速度输入的情况下完美无缺地进行姿态、矢量速度以及位置数字积分函数运算的重复数字算法。
如上篇(参考文献【1】)中讨论的那样,大多数现代捷联INS采用一个基于双速算法的姿态修正算法:高阶修正算法是用来自高速算法的输入以中等重复速率进行的。
中速例行程序可以由精确的封闭型姿态修正运算表示。
高速算法的设计目的在于准确计算出在能校正成系统姿态变化(传统上称为锥化)的各个中速算法修正之间的多轴高频角运动。
原来设想成为简单一阶算法的现今高速姿态算法利用了现代计算机日益增加的吞吐能力,已变成以改善精度为目的的高阶算法(参见参考文献【1】第5—7页和文献【8】的第7节)。
在姿态修正函数演变成现有形式这期间,虽然人们在用于比力加速度转换,矢量速度积分以及位置积分函数的配套捷联INS算法方面同时进行了开发研究,但有关此类研究成果的发表的论文极为少见。
本论文的论题恰是这一主题。
比力变换算法的关键是处理初始传感器数据,进而计算出整个矢量算法修正时间间隔内导航座标中的积分比力增量。
矢量速度的修正是在以前的矢量速度值的基础上增加导航系比力增量(加上用于重力和座标系旋转影响的增量)来实现的。
变换算法的一个关键作用是准确计算出矢量速度更新时间周期内的姿态旋转(也就是捷联加速度计的旋转)。
在一些应用方面,这一目的已经通过使用取中心算法得到实现。
在取中心算法中,比力变换用的姿态数据是在矢量速度修正时间间隔的中心点得到修正的(因此,引入了交错姿态修正/矢量速度修正软件结构)。
变换运算由对矢量速度修正间隔内加速度计比力输入进行积分运算和用矢量修正时间间隔中心点的姿态数据将积分过的比力增量变换成导航系的运算这两种运算组成。
后一~种算法的变种是以两倍矢量修正速度对姿态进行修正,以便得出比力增量变化所需速度修正之间的姿态解。
另一个变种是计算用于比力变换的姿态(作为速度修正时间间隔的起始和末尾姿态解算均值)。
两速算法还可用于动态环境下的比力变换,速度积分(与两速姿态积分算法相类似。
参见参考文献【5】和【8】第7.2节)。
设计高速算法的目的是计算高频角振荡和线性振荡(这些震荡能纠正传统上称之为划桨的系统性速度生成);而中速算法的目的是进行建立在高速算法输入基础上的比力变换。
一般来讲,比力变换/速度积分算法一直没有姿态积分算法在分析上那么复杂,一般只局限于在机动条件下的初阶精度。
实际上,迄今为止尚未见到过有关惯性导航位置积分函数方面的研究专著。
据本文作者所知,现代捷联INS通常产生的位置是一个简单的速度不等边四角形(梯形)积分,其积分速率等于或小于速度修正频率。
对于需要精确位置数据动态环境下的应用而言,如此粗略的位置积分算法是远远不够的。
本文为捷联惯性导航比力变换、速度积分以及位置积分算法等的设计提供了一个综合方法。
所提供的资料是由参考文献【8】第7.2节和第7.3节浓缩而成的(参考文献【5】材料的扩展),着重介绍一套严密的分析方程式和便于计算机文件处理和验证的准确的封闭形式的方程组。
论文中提供的速度和位置算法是采用两速计算格式构建起来的;设计中速算法如50-200HZ的目的是为了使在中速修正时间间隔内,在恒定角速率/比力加速度条件下的运算更为精确;中速算法是由如1—4kHz这样的高速运算提供数据的,这类高速运算在恒定角速率/比力加速度条件下会产生动态偏差[速度算法产生划桨和位置算法产生漩涡(作者术语)]。
本文中还介绍了对积分修正时间间隔内导航座标系旋转进行的严密处理的方法。
本论文的层次结构如下:第2节定义所用座标系。
第3节将上篇姿态算法推导式用作公式化描述两速比力加速度变换/速度积分算法的模式。
第3节把第2节用作以下面两种形式推导位置修正算法的框架,两种形式是建立在不等边四角形基础上的传统形式和两速高分辨率形式。
第5节给出可以参考的推导出的算法一览表。
第6节先围绕本文主题进行一般性讨论,随后介绍如何选择使用于特定用途的算法和如何建立这些算法的运算速率。
第7节是结束语。
最后,认识到下面这一点是十分重要的,即:两速方法的初衷是克服早期计算机技术(1965—75)的吞吐量的局限性,这一局限性随着现代高速计算机技术的不断快速发展而迅速消失。
这就促使业内人士最终回到简单的单速算法结构问题上,正由于单速算法结构较为简单.才使所有算法能以重复速率进行运算,而重复速率又十分之高,能精确求算出多轴高频角速率和比力加速度校正的效果。
本论文所介绍的两速结构和上篇是兼容的,可以压缩成一个单速格式,这在下面算法公式推导的一节中有专门介绍。
2 坐标系座标系是一个由连续编号(或连续字母编序)的三个单元矢量定义的分析抽象阵,三个矢量单元按右手法则彼此正交。
该座标系可以想象为一组三条垂直线(轴)通过一个公共点(原点),单元矢量由该原点沿各自轴线向外发散。
本论文中的座标系原点的实际位置是任意设定的。
某一特定座标系中某矢量的分量(或投影)等于该矢量与座标系各单元矢量的点积。
本文中采用的矢量归类为自由矢量,因而,在对它们进行分析描述时座标系中所取位置上没有孰优孰劣的问题。
坐标系定义如下:1.E 系是用于位置定位因而定义的地球固联座标系。
它的典型定义是它有一个轴与地球极轴平行,其他两轴固连于地球并与赤道平面平行;2.N 系是一个导航座标系,Z 轴与当地地球表面参考位置的垂直向上方向平行,N 系用于将加速度积分为速度并定义E 系内当地垂直角方向;3.L 系是当地水平座标系,与N 系平行,但Z 轴垂直向下,而X 和Y 轴沿N 系的Y 和X 轴。
L 系用于描述捷联传感器座标系方向的基准;4.B 系是捷联惯性传感器座标系(机体系),其轴与标准右手正交传感器输入轴相平行;5.I 系是一个非旋转惯性座标系,用作角旋转测量基准。
为I 系选择的特殊方向在其方向与解析运算有关的章节中进行讨论。
3 速度修正算法本节着重推导用参考文献【1】的方程(16)和(18)积分求解参考文献【1】方程(20)的算法,比力变换项的算法以及将参考文献[1]方程(14)和(15)得出的角速率用于互补(复合向心)加速度项(角速率与速度的乘积):(2)N N L B N N N NL B SF P EN IE v C C a g v ωω=+-+⨯ (1) ()N E T EIE N IE C ωω= (2) ()N N N NEN C ZN ZN ZN F u v u ωρ=⨯+ (3)式中v 是相对于大地的速度.分析定义为E 座标系中从大地中心到INS 的位置矢量的时间导数;P g 是铅垂重力(或重力),对于固定的INS 而言,该重力沿铅垂线沿线。
C F 是一个曲线矩阵(3×3),是一个其元素(3,i )和(i,3)等于零且其余元素绕对角线对称的位置函数。
对于球形大地模型而言,C F 的其余元素是偏离对角线的零.且等于对角线从大地到INS 径向距离的倒数。
对于扁球状大地模型而言,其余的C F 项代表投影到INS 高度的大地表面的本地曲面(参见参考文献【8】中5.3节有关闭环形的表述)。
ZN ρ是NEN ω的垂直分量。
ZN ρ的值的大小取决于所采用的N 系的类型,如漂移方位或自由方位。
设计来确保对于所有大地定位来说NEN ω是非奇异的(见参考文献【8】4.6节和文献【10】第88—89页)。
ZN u 是一个向上沿地垂线(N 系的Z 轴)发散的单元矢量。
方程(1)采用的是方向余弦矩阵变换比力,而不是它的替代形式—参考文献[1]方程(17),四元数变换法,如适用于B 系高度以高度四元数法形式计算那种情况下的四元数变换法。
基于四元数比力变换的速度积分算法可以通过扩展这里提供的结果推导出来。
数字速度积分算法可直接的由方程(1)导出:1/m m N N N L Nm m L SF G Cor v v C v v -=+∆+∆ (4)1/(2)mm m t N N N NN G Cor P EN IE t v g v dt ωω-⎡⎤∆=-+⨯⎣⎦⎰(5) 1mmm t L L BSF B SF t v C a dt -∆=⎰(6)式中m 是数字速度积分算法修正速率计算机周期指数。
