十年(2010-2019)高考数学真题分类汇编(试卷版+解析版):数列
十年高考真题分类汇编(2010-2019) 数学 专题01 集合 解析版

十年高考真题分类汇编(2010—2019)数学专题01 集合1.(2019•全国1•理T1)已知集合M={x|-4<x<2},N={x|x2-x-6<0},则M∩N=( )A.{x|-4<x<3}B.{x|-4<x<-2}C.{x|-2<x<2}D.{x|2<x<3}【答案】C【解析】由题意得N={x|-2<x<3},则M∩N={x|-2<x<2},故选C.2.(2019•全国1•文T2)已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=( )A.{1,6}B.{1,7}C.{6,7}D.{1,6,7}【答案】C【解析】由已知得∁U A={1,6,7},∴B∩∁U A={6,7}.故选C.3.(2019•全国2•理T1)设集合A={x|x2-5x+6>0},B={x|x-1<0},则A∩B=( )A.(-∞,1)B.(-2,1)C.(-3,-1)D.(3,+∞)【答案】A【解析】由题意,得A={x|x<2,或x>3},B={x|x<1},所以A∩B={x|x<1},故选A.4.(2019•全国2•文T1)已知集合A={x|x>-1},B={x|x<2},则A∩B=( )A.(-1,+∞)B.(-∞,2)C.(-1,2)D.⌀【答案】C【解析】由题意,得A∩B=(-1,2),故选C.5.(2019•全国3•T1)已知集合A={-1,0,1,2},B={x|x2≤1},则A∩B=( )A.{-1,0,1}B.{0,1}C.{-1,1}D.{0,1,2}【答案】A【解析】A={-1,0,1,2},B={x|-1≤x≤1},则A∩B={-1,0,1}.故选A.6.(2019•北京•文T1)已知集合A={x|-1<x<2},B={x|x>1},则A∪B=( )A.(-1,1)B.(1,2)C.(-1,+∞)D.(1,+∞)【答案】C【解析】∵A={x|-1<x<2},B={x|x>1},∴A∪B=(-1,+∞),故选C.7.(2019•天津•T1)设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=( )A.{2}B.{2,3}C.{-1,2,3}D.{1,2,3,4}【答案】D【解析】A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.8.(2019•浙江•T1)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则(∁U A)∩B=( )A.{-1}B.{0,1}C.{-1,2,3}D.{-1,0,1,3}【答案】A【解析】∁U A={-1,3},则(∁U A)∩B={-1}.9.(2018•全国1•理T2)已知集合A={x|x2-x-2>0},则∁R A=( )A.{x|-1<x<2}B.{x|-1≤x≤2}C.{x|x<-1}∪{x|x>2}D.{x|x≤-1}∪{x|x≥2}【答案】B【解析】A={x|x<-1或x>2},所以∁R A={x|-1≤x≤2}.10.(2018•全国1•文T1)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B=( )A.{0,2}B.{1,2}C.{0}D.{-2,-1,0,1,2}【答案】A【解析】由交集定义知A∩B={0,2}.11.(2018•全国2•文T2,)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=( )A.{3}B.{5}C.{3,5}D.{1,2,3,4,5,7}【答案】C【解析】集合A、B的公共元素为3,5,故A∩B={3,5}.12.(2018•全国3•T1)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )A.{0}B.{1}C.{1,2}D.{0,1,2}【答案】C【解析】由题意得A={x|x≥1},B={0,1,2},∴A∩B={1,2}.13.(2018•北京•T1)已知集合A={x||x|<2},B={-2,0,1,2},则A∩B=( )A.{0,1}B.{-1,0,1}C.{-2,0,1,2}D.{-1,0,1,2}【答案】A【解析】∵A={x|-2<x<2},B={-2,0,1,2},∴A∩B={0,1}.14.(2018•天津•理T1)设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=( )A.{x|0<x≤1}B.{x|0<x<1}C.{x|1≤x<2}D.{x|0<x<2}【答案】B【解析】∁R B={x|x<1},A∩(∁R B)={x|0<x<1}.故选B.15.(2018•天津•文T1)设集合A={1,2,3,4},B={-1,0,2,3},C={x∈R|-1≤x<2},则(A∪B)∩C=( )A.{-1,1}B.{0,1}C.{-1,0,1}D.{2,3,4}【答案】C【解析】A∪B={-1,0,1,2,3,4}.又C={x∈R|-1≤x<2},∴(A∪B)∩C={-1,0,1}.16.(2018•浙江•T1)已知全集U={1,2,3,4,5},A={1,3},则∁U A=( )A.⌀B.{1,3}C.{2,4,5}D.{1,2,3,4,5}【答案】C【解析】∵A={1,3},U={1,2,3,4,5},∴∁U A={2,4,5},故选C.17.(2018•全国2•理T2,)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )A.9B.8C.5D.4【答案】A【解析】满足条件的元素有(-1,-1),(-1,0),(-1,1),(0,1),(0,0),(0,-1),(1,-1),(1,0),(1,1),共9个。
十年真题(2010-2019)高考数学(理)分类汇编专题04 导数及其应用(新课标Ⅰ卷)(解析版)

专题04导数及其应用历年考题细目表填空题2010 定积分2010年新课标1理科13解答题2019 导数综合问题2019年新课标1理科20解答题2018 导数综合问题2018年新课标1理科21解答题2017 导数综合问题2017年新课标1理科21解答题2016 导数综合问题2016年新课标1理科21解答题2015 导数综合问题2015年新课标1理科21解答题2014 导数综合问题2014年新课标1理科21解答题2013 导数综合问题2013年新课标1理科21解答题2012 导数综合问题2012年新课标1理科21解答题2011 导数综合问题2011年新课标1理科21解答题2010 导数综合问题2010年新课标1理科21历年高考真题汇编1.【2019年新课标1理科05】函数f()在[﹣π,π]的图象大致为()A.B.C.D.【解答】解:∵f(),∈[﹣π,π],∴f(﹣)f(),∴f()为[﹣π,π]上的奇函数,因此排除A;又f(),因此排除B,C;故选:D.2.【2018年新课标1理科05】设函数f()=3+(a﹣1)2+a.若f()为奇函数,则曲线y=f()在点(0,0)处的切线方程为()A.y=﹣2 B.y=﹣C.y=2 D.y=【解答】解:函数f()=3+(a﹣1)2+a,若f()为奇函数,可得a=1,所以函数f()=3+,可得f′()=32+1,曲线y=f()在点(0,0)处的切线的斜率为:1,则曲线y=f()在点(0,0)处的切线方程为:y=.故选:D.3.【2016年新课标1理科07】函数y=22﹣e||在[﹣2,2]的图象大致为()A.B.C.D.【解答】解:∵f()=y=22﹣e||,∴f(﹣)=2(﹣)2﹣e|﹣|=22﹣e||,故函数为偶函数,当=±2时,y=8﹣e2∈(0,1),故排除A,B;当∈[0,2]时,f()=y=22﹣e,∴f′()=4﹣e=0有解,故函数y=22﹣e||在[0,2]不是单调的,故排除C,故选:D.4.【2015年新课标1理科12】设函数f()=e(2﹣1)﹣a+a,其中a<1,若存在唯一的整数0使得f(0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)【解答】解:设g()=e(2﹣1),y=a﹣a,由题意知存在唯一的整数0使得g(0)在直线y=a﹣a的下方,∵g′()=e(2﹣1)+2e=e(2+1),∴当时,g′()<0,当时,g′()>0,∴当时,g()取最小值﹣2,当=0时,g(0)=﹣1,当=1时,g(1)=e>0,直线y=a﹣a恒过定点(1,0)且斜率为a,故﹣a>g(0)=﹣1且g(﹣1)=﹣3e﹣1≥﹣a﹣a,解得a<1故选:D.5.【2014年新课标1理科11】已知函数f()=a3﹣32+1,若f()存在唯一的零点0,且0>0,则实数a 的取值范围是()A.(1,+∞)B.(2,+∞)C.(﹣∞,﹣1)D.(﹣∞,﹣2)【解答】解:∵f()=a3﹣32+1,∴f′()=3a2﹣6=3(a﹣2),f(0)=1;①当a=0时,f()=﹣32+1有两个零点,不成立;②当a>0时,f()=a3﹣32+1在(﹣∞,0)上有零点,故不成立;③当a<0时,f()=a3﹣32+1在(0,+∞)上有且只有一个零点;故f()=a3﹣32+1在(﹣∞,0)上没有零点;而当时,f()=a3﹣32+1在(﹣∞,0)上取得最小值;故f()3•1>0;故a<﹣2;综上所述,实数a的取值范围是(﹣∞,﹣2);故选:D.6.【2012年新课标1理科10】已知函数f(),则y=f()的图象大致为()A.B.C.D.【解答】解:设则g′()∴g()在(﹣1,0)上为增函数,在(0,+∞)上为减函数∴g()<g(0)=0∴f()0得:>0或﹣1<<0均有f()<0排除A,C,又f()中,,能排除D.故选:B.7.【2012年新课标1理科12】设点P在曲线上,点Q在曲线y=ln(2)上,则|PQ|最小值为()A.1﹣ln2 B.C.1+ln2 D.【解答】解:∵函数与函数y=ln(2)互为反函数,图象关于y=对称,函数上的点到直线y=的距离为,设g()(>0),则g′(),由g′()0可得≥ln2,由g′()0可得0<<ln2,∴函数g()在(0,ln2)单调递减,在[ln2,+∞)单调递增,∴当=ln2时,函数g()min=1﹣ln2,,由图象关于y=对称得:|PQ|最小值为.故选:B.8.【2011年新课标1理科09】由曲线y,直线y=﹣2及y轴所围成的图形的面积为()A.B.4 C.D.6【解答】解:联立方程得到两曲线的交点(4,2),因此曲线y,直线y=﹣2及y轴所围成的图形的面积为:S.故选C.9.【2010年新课标1理科03】曲线y在点(﹣1,﹣1)处的切线方程为()A.y=2+1 B.y=2﹣1 C.y=﹣2﹣3 D.y=﹣2﹣2【解答】解:∵y,∴y′,所以=y′|=﹣1=2,得切线的斜率为2,所以=2;所以曲线y=f()在点(﹣1,﹣1)处的切线方程为:y+1=2×(+1),即y=2+1.故选:A.10.【2019年新课标1理科13】曲线y=3(2+)e在点(0,0)处的切线方程为.【解答】解:∵y=3(2+)e,∴y'=3e(2+3+1),∴当=0时,y'=3,∴y=3(2+)e在点(0,0)处的切线斜率=3,∴切线方程为:y=3.故答案为:y=3.11.【2013年新课标1理科16】若函数f()=(1﹣2)(2+a+b)的图象关于直线=﹣2对称,则f()的最大值为.【解答】解:∵函数f()=(1﹣2)(2+a+b)的图象关于直线=﹣2对称,∴f(﹣1)=f(﹣3)=0且f(1)=f(﹣5)=0,即[1﹣(﹣3)2][(﹣3)2+a•(﹣3)+b]=0且[1﹣(﹣5)2][(﹣5)2+a•(﹣5)+b]=0,解之得,因此,f()=(1﹣2)(2+8+15)=﹣4﹣83﹣142+8+15,求导数,得f′()=﹣43﹣242﹣28+8,令f′()=0,得1=﹣2,2=﹣2,3=﹣2,当∈(﹣∞,﹣2)时,f′()>0;当∈(﹣2,﹣2)时,f′()<0;当∈(﹣2,﹣2)时,f′()>0;当∈(﹣2,+∞)时,f′()<0∴f()在区间(﹣∞,﹣2)、(﹣2,﹣2)上是增函数,在区间(﹣2,﹣2)、(﹣2,+∞)上是减函数.又∵f(﹣2)=f(﹣2)=16,∴f()的最大值为16.故答案为:16.12.【2010年新课标1理科13】设y=f()为区间[0,1]上的连续函数,且恒有0≤f()≤1,可以用随机模拟方法近似计算积分,先产生两组(每组N个)区间[0,1]上的均匀随机数1,2,…N和y1,y2,…y N,由此得到N个点(i,y i)(i=1,2,…,N),再数出其中满足y i≤f(i)(i=1,2,…,N)的点数N1,那么由随机模拟方案可得积分的近似值为.【解答】解:由题意可知得,故积分的近似值为.故答案为:.13.【2019年新课标1理科20】已知函数f()=sin﹣ln(1+),f′()为f()的导数.证明:(1)f′()在区间(﹣1,)存在唯一极大值点;(2)f()有且仅有2个零点.【解答】证明:(1)f()的定义域为(﹣1,+∞),f′()=cos,f″()=﹣sin,令g()=﹣sin,则g′()=﹣cos0在(﹣1,)恒成立,∴f″()在(﹣1,)上为减函数,又∵f″(0)=1,f″()=﹣11+1=0,由零点存在定理可知,函数f″()在(﹣1,)上存在唯一的零点0,结合单调性可得,f′()在(﹣1,0)上单调递增,在(0,)上单调递减,可得f′()在区间(﹣1,)存在唯一极大值点;(2)由(1)知,当∈(﹣1,0)时,f′()单调递增,f′()<f′(0)=0,f()单调递减;当∈(0,0)时,f′()单调递增,f′()>f′(0)=0,f()单调递增;由于f′()在(0,)上单调递减,且f′(0)>0,f′()0,由零点存在定理可知,函数f′()在(0,)上存在唯一零点1,结合单调性可知,当∈(0,1)时,f′()单调递减,f′()>f′(1)=0,f()单调递增;当∈()时,f′()单调递减,f′()<f′(1)=0,f()单调递减.当∈(,π)时,cos<0,0,于是f′()=cos0,f()单调递减,其中f ()=1﹣ln(1)>1﹣ln(1)=1﹣ln2.6>1﹣lne=0,f(π)=﹣ln(1+π)<﹣ln3<0.于是可得下表:(﹣1,0)0 (0,1)1()()πf′()﹣0 + 0 ﹣﹣﹣﹣f()减函数0 增函数大于0 减函数大于0 减函数小于0结合单调性可知,函数f()在(﹣1,]上有且只有一个零点0,由函数零点存在性定理可知,f ()在(,π)上有且只有一个零点2,当∈[π,+∞)时,f()=sin﹣ln(1+)<1﹣ln(1+π)<1﹣ln3<0,因此函数f()在[π,+∞)上无零点.综上,f()有且仅有2个零点.14.【2018年新课标1理科21】已知函数f ()+aln.(1)讨论f()的单调性;(2)若f()存在两个极值点1,2,证明:a﹣2.【解答】解:(1)函数的定义域为(0,+∞),函数的导数f ′()1,设g()=2﹣a+1,当a≤0时,g()>0恒成立,即f′()<0恒成立,此时函数f()在(0,+∞)上是减函数,当a>0时,判别式△=a2﹣4,①当0<a≤2时,△≤0,即g()≥0,即f′()≤0恒成立,此时函数f()在(0,+∞)上是减函数,②当a>2时,,f′(),f()的变化如下表:(0,)(,)(,+∞)f′()﹣0 + 0 ﹣f()递减递增递减综上当a≤2时,f()在(0,+∞)上是减函数,当a>2时,在(0,),和(,+∞)上是减函数,则(,)上是增函数.(2)由(1)知a>2,0<1<1<2,12=1,则f(1)﹣f(2)=(2﹣1)(1)+a(ln1﹣ln2)=2(2﹣1)+a(ln1﹣ln2),则2,则问题转为证明1即可,即证明ln1﹣ln2>1﹣2,则ln1﹣ln 1,即ln1+ln1>1,即证2ln1>1在(0,1)上恒成立,设h()=2ln ﹣,(0<<1),其中h(1)=0,求导得h ′()10,则h()在(0,1)上单调递减,∴h()>h(1),即2ln ﹣0,故2ln >,则a﹣2成立.(2)另解:注意到f()=aln=﹣f(),即f()+f()=0,由韦达定理得12=1,1+2=a>2,得0<1<1<2,1,可得f(2)+f()=0,即f(1)+f(2)=0,要证a﹣2,只要证a﹣2,即证2aln2﹣a20,(2>1),构造函数h()=2aln﹣a,(>1),h′()0,∴h()在(1,+∞)上单调递减,∴h()<h(1)=0,∴2aln﹣a0成立,即2aln2﹣a20,(2>1)成立.即a﹣2成立.15.【2017年新课标1理科21】已知函数f()=ae2+(a﹣2)e﹣.(1)讨论f()的单调性;(2)若f()有两个零点,求a的取值范围.【解答】解:(1)由f()=ae2+(a﹣2)e﹣,求导f′()=2ae2+(a﹣2)e﹣1,当a=0时,f′()=﹣2e﹣1<0,∴当∈R,f()单调递减,当a>0时,f′()=(2e+1)(ae﹣1)=2a(e)(e),令f′()=0,解得:=ln,当f′()>0,解得:>ln,当f′()<0,解得:<ln,∴∈(﹣∞,ln)时,f()单调递减,∈(ln,+∞)单调递增;当a<0时,f′()=2a(e)(e)<0,恒成立,∴当∈R,f()单调递减,综上可知:当a≤0时,f()在R单调减函数,当a>0时,f()在(﹣∞,ln)是减函数,在(ln,+∞)是增函数;(2)①若a≤0时,由(1)可知:f()最多有一个零点,当a>0时,f()=ae2+(a﹣2)e﹣,当→﹣∞时,e2→0,e→0,∴当→﹣∞时,f()→+∞,当→∞,e2→+∞,且远远大于e和,∴当→∞,f()→+∞,∴函数有两个零点,f()的最小值小于0即可,由f()在(﹣∞,ln)是减函数,在(ln,+∞)是增函数,∴f()min=f(ln)=a×()+(a﹣2)ln0,∴1ln0,即ln1>0,设t,则g(t)=lnt+t﹣1,(t>0),求导g′(t)1,由g(1)=0,∴t1,解得:0<a<1,∴a的取值范围(0,1).方法二:(1)由f()=ae2+(a﹣2)e﹣,求导f′()=2ae2+(a﹣2)e﹣1,当a=0时,f′()=﹣2e﹣1<0,∴当∈R,f()单调递减,当a>0时,f′()=(2e+1)(ae﹣1)=2a(e)(e),令f′()=0,解得:=﹣lna,当f′()>0,解得:>﹣lna,当f′()<0,解得:<﹣lna,∴∈(﹣∞,﹣lna)时,f()单调递减,∈(﹣lna,+∞)单调递增;当a<0时,f′()=2a(e)(e)<0,恒成立,∴当∈R,f()单调递减,综上可知:当a≤0时,f()在R单调减函数,当a>0时,f()在(﹣∞,﹣lna)是减函数,在(﹣lna,+∞)是增函数;(2)①若a≤0时,由(1)可知:f()最多有一个零点,②当a>0时,由(1)可知:当=﹣lna时,f()取得最小值,f()min=f(﹣lna)=1ln,当a=1,时,f(﹣lna)=0,故f()只有一个零点,当a∈(1,+∞)时,由1ln0,即f(﹣lna)>0,故f()没有零点,当a∈(0,1)时,1ln0,f(﹣lna)<0,由f(﹣2)=ae﹣4+(a﹣2)e﹣2+2>﹣2e﹣2+2>0,故f()在(﹣∞,﹣lna)有一个零点,假设存在正整数n0,满足n0>ln(1),则f(n0)(a a﹣2)﹣n0n0n0>0,由ln(1)>﹣lna,因此在(﹣lna,+∞)有一个零点.∴a的取值范围(0,1).16.【2016年新课标1理科21】已知函数f()=(﹣2)e+a(﹣1)2有两个零点.(Ⅰ)求a的取值范围;(Ⅱ)设1,2是f()的两个零点,证明:1+2<2.【解答】解:(Ⅰ)∵函数f()=(﹣2)e+a(﹣1)2,∴f′()=(﹣1)e+2a(﹣1)=(﹣1)(e+2a),①若a=0,那么f()=0⇔(﹣2)e=0⇔=2,函数f()只有唯一的零点2,不合题意;②若a>0,那么e+2a>0恒成立,当<1时,f′()<0,此时函数为减函数;当>1时,f′()>0,此时函数为增函数;此时当=1时,函数f()取极小值﹣e,由f(2)=a>0,可得:函数f()在>1存在一个零点;当<1时,e<e,﹣2<﹣1<0,∴f()=(﹣2)e+a(﹣1)2>(﹣2)e+a(﹣1)2=a(﹣1)2+e(﹣1)﹣e,令a(﹣1)2+e(﹣1)﹣e=0的两根为t1,t2,且t1<t2,则当<t1,或>t2时,f()>a(﹣1)2+e(﹣1)﹣e>0,故函数f()在<1存在一个零点;即函数f()在R是存在两个零点,满足题意;③若a<0,则ln(﹣2a)<lne=1,当<ln(﹣2a)时,﹣1<ln(﹣2a)﹣1<lne﹣1=0,e+2a<e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)>0恒成立,故f()单调递增,当ln(﹣2a)<<1时,﹣1<0,e+2a>e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)<0恒成立,故f()单调递减,当>1时,﹣1>0,e+2a>e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)>0恒成立,故f()单调递增,故当=ln(﹣2a)时,函数取极大值,由f(ln(﹣2a))=[ln(﹣2a)﹣2](﹣2a)+a[ln(﹣2a)﹣1]2=a{[ln(﹣2a)﹣2]2+1}<0得:函数f()在R上至多存在一个零点,不合题意;④若a,则ln(﹣2a)=1,当<1=ln(﹣2a)时,﹣1<0,e+2a<e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)>0恒成立,故f()单调递增,当>1时,﹣1>0,e+2a>e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)>0恒成立,故f()单调递增,故函数f()在R上单调递增,函数f()在R上至多存在一个零点,不合题意;⑤若a,则ln(﹣2a)>lne=1,当<1时,﹣1<0,e+2a<e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)>0恒成立,故f()单调递增,当1<<ln(﹣2a)时,﹣1>0,e+2a<e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)<0恒成立,故f()单调递减,当>ln(﹣2a)时,﹣1>0,e+2a>e ln(﹣2a)+2a=0,即f′()=(﹣1)(e+2a)>0恒成立,故f()单调递增,故当=1时,函数取极大值,由f(1)=﹣e<0得:函数f()在R上至多存在一个零点,不合题意;综上所述,a的取值范围为(0,+∞)证明:(Ⅱ)∵1,2是f()的两个零点,∴f(1)=f(2)=0,且1≠1,且2≠1,∴﹣a,令g(),则g(1)=g(2)=﹣a,∵g′(),∴当<1时,g′()<0,g()单调递减;当>1时,g′()>0,g()单调递增;设m>0,则g(1+m)﹣g(1﹣m),设h(m),m>0,则h′(m)0恒成立,即h(m)在(0,+∞)上为增函数,h(m)>h(0)=0恒成立,即g(1+m)>g(1﹣m)恒成立,令m=1﹣1>0,则g(1+1﹣1)>g(1﹣1+1)⇔g(2﹣1)>g(1)=g(2)⇔2﹣1>2,即1+2<2.17.【2015年新课标1理科21】已知函数f()=3+a,g()=﹣ln(i)当a为何值时,轴为曲线y=f()的切线;(ii)用min{m,n}表示m,n中的最小值,设函数h()=min{f(),g()}(>0),讨论h()零点的个数.【解答】解:(i)f′()=32+a.设曲线y=f()与轴相切于点P(0,0),则f(0)=0,f′(0)=0,∴,解得,a.因此当a时,轴为曲线y=f()的切线;(ii)当∈(1,+∞)时,g()=﹣ln<0,∴函数h()=min{f(),g()}<0,故h()在∈(1,+∞)时无零点.当=1时,若a,则f(1)=a0,∴h()=min{f(1),g(1)}=g(1)=0,故=1是函数h()的一个零点;若a,则f(1)=a0,∴h()=min{f(1),g(1)}=f(1)<0,故=1不是函数h()的零点;当∈(0,1)时,g()=﹣ln>0,因此只考虑f()在(0,1)内的零点个数即可.①当a≤﹣3或a≥0时,f′()=32+a在(0,1)内无零点,因此f()在区间(0,1)内单调,而f(0),f(1)=a,∴当a≤﹣3时,函数f()在区间(0,1)内有一个零点,当a≥0时,函数f()在区间(0,1)内没有零点.②当﹣3<a<0时,函数f()在内单调递减,在内单调递增,故当时,f()取得最小值.若0,即,则f()在(0,1)内无零点.若0,即a,则f()在(0,1)内有唯一零点.若0,即,由f(0),f(1)=a,∴当时,f()在(0,1)内有两个零点.当﹣3<a时,f()在(0,1)内有一个零点.综上可得:a时,函数h()有一个零点.当时,h()有一个零点;当a或时,h()有两个零点;当时,函数h()有三个零点.18.【2014年新课标1理科21】设函数f()=aeln,曲线y=f()在点(1,f(1))处得切线方程为y=e(﹣1)+2.(Ⅰ)求a、b;(Ⅱ)证明:f()>1.【解答】解:(Ⅰ)函数f()的定义域为(0,+∞),f′(),由题意可得f(1)=2,f′(1)=e,故a=1,b=2;(Ⅱ)由(Ⅰ)知,f()=eln,∵f()>1,∴eln1,∴ln,∴f()>1等价于ln>e﹣,设函数g()=ln,则g′()=1+ln,∴当∈(0,)时,g′()<0;当∈(,+∞)时,g′()>0.故g()在(0,)上单调递减,在(,+∞)上单调递增,从而g()在(0,+∞)上的最小值为g().设函数h()=e﹣,则h′()=e﹣(1﹣).∴当∈(0,1)时,h′()>0;当∈(1,+∞)时,h′()<0,故h()在(0,1)上单调递增,在(1,+∞)上单调递减,从而h()在(0,+∞)上的最大值为h(1).综上,当>0时,g()>h(),即f()>1.19.【2013年新课标1理科21】已知函数f()=2+a+b,g()=e(c+d),若曲线y=f()和曲线y=g()都过点P(0,2),且在点P处有相同的切线y=4+2.(Ⅰ)求a,b,c,d的值;(Ⅱ)若≥﹣2时,f()≤g(),求的取值范围.【解答】解:(Ⅰ)由题意知f(0)=2,g(0)=2,f′(0)=4,g′(0)=4,而f′()=2+a,g′()=e(c+d+c),故b=2,d=2,a=4,d+c=4,从而a=4,b=2,c=2,d=2;(Ⅱ)由(I)知,f()=2+4+2,g()=2e(+1)设F()=g()﹣f()=2e(+1)﹣2﹣4﹣2,则F′()=2e(+2)﹣2﹣4=2(+2)(e﹣1),由题设得F(0)≥0,即≥1,令F′()=0,得1=﹣ln,2=﹣2,①若1≤<e2,则﹣2<1≤0,从而当∈(﹣2,1)时,F′()<0,当∈(1,+∞)时,F′()>0,即F()在(﹣2,1)上减,在(1,+∞)上是增,故F()在[﹣2,+∞)上的最小值为F(1),而F(1)=﹣1(1+2)≥0,≥﹣2时F()≥0,即f()≤g()恒成立.②若=e2,则F′()=2e2(+2)(e﹣e﹣2),从而当∈(﹣2,+∞)时,F′()>0,即F()在(﹣2,+∞)上是增,而F(﹣2)=0,故当≥﹣2时,F()≥0,即f()≤g()恒成立.③若>e2时,F′()>2e2(+2)(e﹣e﹣2),而F(﹣2)=﹣2e﹣2+2<0,所以当>﹣2时,f()≤g()不恒成立,综上,的取值范围是[1,e2].20.【2012年新课标1理科21】已知函数f()满足f()=f′(1)e﹣1﹣f(0)2;(1)求f()的解析式及单调区间;(2)若,求(a+1)b的最大值.【解答】解:(1)f()=f'(1)e﹣1﹣f(0)⇒f'()=f'(1)e﹣1﹣f(0)+令=1得:f(0)=1∴f()=f'(1)e﹣1﹣令=0,得f(0)=f'(1)e﹣1=1解得f'(1)=e故函数的解析式为f()=e﹣令g()=f'()=e﹣1+∴g'()=e+1>0,由此知y=g()在∈R上单调递增当>0时,f'()>f'(0)=0;当<0时,有f'()<f'(0)=0得:函数f()=e﹣的单调递增区间为(0,+∞),单调递减区间为(﹣∞,0)(2)f()(a+1)﹣b≥0得h′()=e﹣(a+1)①当a+1≤0时,h′()>0⇒y=h()在∈R上单调递增,→﹣∞时,h()→﹣∞与h()≥0矛盾②当a+1>0时,h′()>0⇔>ln(a+1),h'()<0⇔<ln(a+1)得:当=ln(a+1)时,h()min=(a+1)﹣(a+1)ln(a+1)﹣b≥0,即(a+1)﹣(a+1)ln(a+1)≥b ∴(a+1)b≤(a+1)2﹣(a+1)2ln(a+1),(a+1>0)令F()=2﹣2ln(>0),则F'()=(1﹣2ln)∴F'()>0⇔0<当时,F()ma即当a时,(a+1)b的最大值为21.【2011年新课标1理科21】已知函数f(),曲线y=f()在点(1,f(1))处的切线方程为+2y﹣3=0.(Ⅰ)求a、b的值;(Ⅱ)如果当>0,且≠1时,f(),求的取值范围.【解答】解:由题意f(1)=1,即切点坐标是(1,1)(Ⅰ)由于直线+2y﹣3=0的斜率为,且过点(1,1),故即解得a=1,b=1.(Ⅱ)由(Ⅰ)知,所以).考虑函数(>0),则.(i)设≤0,由知,当≠1时,h′()<0.而h(1)=0,故当∈(0,1)时,h′()<0,可得;当∈(1,+∞)时,h′()<0,可得h()>0从而当>0,且≠1时,f()﹣()>0,即f().(ii)设0<<1.由于当∈(1,)时,(﹣1)(2+1)+2>0,故h′()>0,而h(1)=0,故当∈(1,)时,h()>0,可得h()<0,与题设矛盾.(iii)设≥1.此时h′()>0,而h(1)=0,故当∈(1,+∞)时,h()>0,可得h()<0,与题设矛盾.综合得,的取值范围为(﹣∞,0].22.【2010年新课标1理科21】设函数f()=e﹣1﹣﹣a2.(1)若a=0,求f()的单调区间;(2)若当≥0时f()≥0,求a的取值范围.【解答】解:(1)a=0时,f()=e﹣1﹣,f′()=e﹣1.当∈(﹣∞,0)时,f'()<0;当∈(0,+∞)时,f'()>0.故f()在(﹣∞,0)单调减少,在(0,+∞)单调增加(II)f′()=e﹣1﹣2a由(I)知e≥1+,当且仅当=0时等号成立.故f′()≥﹣2a=(1﹣2a),从而当1﹣2a≥0,即时,f′()≥0(≥0),而f(0)=0,于是当≥0时,f()≥0.由e >1+(≠0)可得e ﹣>1﹣(≠0). 从而当时,f ′()<e ﹣1+2a (e ﹣﹣1)=e ﹣(e ﹣1)(e ﹣2a ), 故当∈(0,ln 2a )时,f '()<0,而f (0)=0,于是当∈(0,ln 2a )时,f ()<0.综合得a 的取值范围为.考题分析与复习建议本专题考查的知识点为:导数的概念及运算,导数与函数的单调性、极值、最值,导数与函数的综合问题,定积分与微积分基本定理.历年考题主要以选择填空或解答题题型出现,重点考查的知识点为:导数的运算,导数与函数的单调性、极值、最值,导数与函数的综合问题,定积分,预测明年本考点题目会比较稳定.备考方向以知识点导数的运算,导数与函数的单调性、极值、最值,导数与函数的综合问题,定积分为重点较佳. 最新高考模拟试题1.已知函数10()ln ,0x x f x x x x⎧⎪⎪=⎨⎪⎪⎩,<>,若()()F x f x kx =-有3个零点,则k 的取值范围为( ) A .(21e -,0) B .(12e -,0) C .(0,12e ) D .(0,21e) 【答案】C【解析】由题意,函数10()ln ,0x x f x x x x⎧<⎪⎪=⎨⎪>⎪⎩,,要使得函数()()F x f x kx =-在R 上有3个零点,当0x >时,令()()0F x f x kx =-=,可得2ln xk x =,要使得()0F x =有两个实数解,即y k =和()2ln xg x x =有两个交点,又由()312ln xg x x -'=,令12ln 0x -=,可得x =当x ∈时,()0g x '>,则()g x 单调递增;当)x ∈+∞时,()0g x '<,则()g x 单调递减,所以当x =()max 12g x e =,若直线y k =和()2ln xg x x =有两个交点,则1(0,)2k e ∈,当0x <时,y k =和()1g x x =有一个交点,则0k >,综上可得,实数k 的取值范围是1(0,)2e ,故选C.2.已知,(0,)2παβ∈,sin sin 0βααβ->,则下列不等式一定成立的是() A .2παβ+< B .2παβ+= C .αβ< D .αβ>【答案】C【解析】由题意,sin sin βααβ>,sin sin αβαβ∴>,设()sin ,0,2xf x x x π⎛⎫=∈ ⎪⎝⎭,()2cos sin ',0,2x x xf x x x π-⎛⎫∴=∈ ⎪⎝⎭,设()cos sin ,0,2g x x x x x π⎛⎫=-∈ ⎪⎝⎭,()'cos sin cos sin 0g x x x x x x x ∴=--=-<,()g x ∴在0,2π⎛⎫⎪⎝⎭单调递减,且()()00g x g <=,()'0f x ∴<,所以()sin x f x x =在0,2π⎛⎫ ⎪⎝⎭递减, ()()sin sin ,f f αβαβαβ>⇔>Qαβ∴<,故选C.3.已知函数()ln 2f x a x x =-+(a 为大于1的整数),若()y f x =与(())y f f x =的值域相同,则a 的最小值是( )(参考数据:ln20.6931≈,ln3 1.0986≈,ln5 1.6094≈)A .5B .6C .7D .8【答案】A【解析】 '()ln 2()=1a a x f x a x x f x x x-=-+⇒-=,当x a >时,'()0f x <,函数()f x 单调递减,当0x a <<时,'()0f x >,函数()f x 单调递增,故max ()()ln 2f x f a a a a ==-+,又当0,()x f x →→-∞,所以函数()f x 的值域为(,ln 2]a a a -∞-+,令'()ln 2()ln 11ln ,t a a a a t a a a =-+⇒=+-= '1,()0a a Z t a >∈∴>Q 因此()t a 是单调递增函数,因此当2,a a Z ≥∈时,()(2)2ln 20t a t ≥=>,令()ln 2f x a x x n =-+=由上可知:ln 2n a a a ≤-+,(())()y f f x f n ==,由上可知函数(n)f 在0x a <<时,单调递增,在x a >时,单调递减,要想(())()y f f x f n ==的值域为(,ln 2]a a a -∞-+,只需ln 2a a a a ≤-+,即ln 220a a a -+≥,设()ln 22g a a a a =-+,2,a a Z ≥∈,'()ln 1g a a =-,所以当3,a a Z ≥∈时,函数()g a 单调递增,(2)2ln 240,(3)3ln 340g g =-<=-<,(4)4ln 460,(5)5ln 580g g =-<=->,所以a 的最小值是5,故本题选A.4.已知实数a ,b ,c ,d 满足ln 12113a c b d +-==+-,则22()()a c b d -+-的最小值为( )A .8B .4C .2 D【答案】D【解析】 Q ln 12113a cb d +-==+-ln 11ln 1a b a b +∴=⇒=+,2113c d c d -=⇒=+- 可以看成()ln f x x =和()1g x x =+之间的最小值 '1()f x x =Q 当111x x=⇒=时,即点()1,0到直线()1g x x =+的距离最小d ==5.若函数()ln f x x a x =在区间()1,+∞上存在零点,则实数a 的取值范围为( )A .10,2⎛⎫ ⎪⎝⎭B .1,2e ⎛⎫ ⎪⎝⎭C .()0,∞+D .1,2⎛⎫+∞ ⎪⎝⎭ 【答案】D【解析】因为函数()ln f x x a x =,所以()1a f x x '=-=令()22g x x a =,因为()2g x '==,当(1,)x ∈+∞ 时,10,0>>,所以()0g x '>所以()g x 在(1,)+∞上为增函数,则()(1)12g x g a >=-,当120a -≥时,()0g x >,所以()0f x '>,所以()f x 在(1,)+∞上为增函数,则()(1)0f x f >=,所以()f x 在(1,)+∞上没有零点.当120a -<时,即12a >,因为()g x 在(1,)+∞上为增函数,则存在唯一的0(1,)x ∈+∞,使得0()0g x =,且当0(1,)x x ∈时,()0g x <,当0(,)x x ∈+∞时,()0g x >;所以当0(1,)x x ∈时,()0f x '<,()f x 为减函数,当0(,)x x ∈+∞时,()0f x '>,()f x 为增函数,当0x x =时,min 0()()f x f x =,因为0()(1)0f x f <=,当x 趋于+∞时,()f x 趋于+∞,所以在0(,)x x ∈+∞内,()f x 一定存在一个零点. 所以1(,)2a ∈+∞,故答案选D.6.已知函数1()2x a f x e ax x x ⎛⎫=-+- ⎪⎝⎭,若对任意(0,)x ∈+∞,都有()()f x xf x '≥-成立,则实数a 的取值范围是( )A .3,2e ⎛⎤-∞- ⎥⎝⎦B .(,-?C .3,2e 轹÷-+?ê÷ê滕 D .)é-+?êë【答案】D【解析】令2()()(21)x g x xf x x e ax a ==-+-,则()()()g x f x xf x ''=+, 因为对任意(0,)x ∈+∞,都有()()f x xf x '≥-成立,所以()()()0g x f x xf x ''=+≥在(0,)x ∈+∞上恒成立;即()(21)20xg x x e ax '=++≥在(0,)x ∈+∞上恒成立; 即(21)122x x x e a e x x +⎛⎫-≤=+ ⎪⎝⎭在(0,)x ∈+∞上恒成立; 令1()2x h x e x ⎛⎫=+ ⎪⎝⎭,(0,)x ∈+∞, 则22211(21)()2x x x x x h x e e e x x x +-⎛⎫'=-++= ⎪⎝⎭, 由()0h x '=得2210x x +-=,解得1x =-(舍)或12x =, 所以,当102x <<时,22(21)()0x x x h x e x+-'=<,1()2x h x e x ⎛⎫=+ ⎪⎝⎭单调递减; 当12x >时,22(21)()0x x x h x e x+-'=<,1()2x h x e x ⎛⎫=+ ⎪⎝⎭单调递增;所以min 1()2h x h ⎛⎫== ⎪⎝⎭, 因为(21)122x x x e a e x x +⎛⎫-≤=+ ⎪⎝⎭在(0,)x ∈+∞上恒成立,所以只需2a -≤a ≥-故选D7.已知奇函数()f x 是定义在R 上的可导函数,其导函数为()f x ',当0x >时,有()()22f x xf x x '>+,则不等式()()()22018+2018420x f x f +-<+的解集为( )A .(),2016-∞-B .()2016,2012--C .(),2018-∞-D .()2016,0-【答案】A【解析】设()()2g x x f x =, 因为()f x 为R 上奇函数,所以()()()()22g x x f x x f x -=--=-,即()g x 为R 上奇函数对()g x 求导,得()()()2f g f x x x x x '=+'⎡⎤⎣⎦,而当0x >时,有()()220f x xf x x '>+≥ 故0x >时,()0g x '>,即()g x 单调递增,所以()g x 在R 上单调递增不等式()()()22018+2018420x f x f +-<+ ()()()22018+201842x f x f +<--, ()()()22018+201842x f x f +< 即()()20182g x g +<所以20182x +<,解得2016x <-故选A 项.8.已知函数35791131()135791113x x x x x x f x x =+-+-+-+,则使不等式(1)0f x ->成立的x 的最小整数为( )A .-3B .-2C .-1D .0【答案】D【解析】 根据题意,函数35791131()135791113x x x x x x f x x =+-+-+-+,其导数24681012()1f x x x x x x x '=-+-+-+,0x ≠时,()f x '可以看成是1为首项,2x -为公比的等比数列,则有24681012()1f x x x x x x x '=-+-+-+142101x x +=>+, 函数()f x 在R 上为增函数, 又由111111(1)1(1)()()()035791113f -=+-+-+-+->, 35791113222222(2)1(2)035791113f ⎛⎫⎛⎫⎛⎫-=+-+-+-+-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 则函数()f x 在(2,1)--上存在唯一的零点,设其零点为t ,(1)011f x x t x t ->⇒->⇒>+,又由21t -<<-,则110t -<+<,故不等式(1)0f x ->成立的x 的最小整数为0;故选:D .9.直线y ax =是曲线1ln y x =+的切线,则实数a =____.【答案】1【解析】解:∵1ln y x =+,∴1y x'= 设切点为(,1ln )m m +,得切线的斜率为1m ,所以曲线在点(),1ln m m +处的切线方程为:1ln 1()y m x m m --=⨯-. 即:1ln y m x m-= 它过原点,∴ln 0m -=,∴1m =,∴11a m==. 故答案为:1.10.函数()2x f x ae x =-与()21g x x x =--的图象上存在关于x 轴的对称点,则实数a 的取值范围为_________.【答案】1a …【解析】()21g x x x =--关于x 轴对称的函数为()21h x x x =-++,因为函数()2x f x ae x =-与()21g x x x =--的图象上存在关于x 轴的对称点, 所以()2x f x ae x =-与()21h x x x =-++的图象有交点, 方程221x ae x x x -=-++有解,即1x ae x =+有解,0a =时符合题意,0a ≠时转化为()11x e x a=+有解, 即()1,1x y e y x a==+的图象有交点, ()11y x a =+是过定点()1,0-的直线,其斜率为1a, 设()1,1x y e y x a ==+相切时,切点的坐标为(),m m e ,则111mmem a ea⎧=⎪⎪+⎨⎪=⎪⎩,解得1a=,切线斜率为11a=,由图可知,当11a≥,即1a≤且0a≠时,()1,1xy e y xa==+的图象有交点,此时,()2xf x ae x=-与()21h x x x=-++的图象有交点,函数()2xf x ae x=-与()21g x x x=--的图象上存在关于x轴的对称点,综上可得,实数a的取值范围为1a≤,故答案为1a≤.11.已知函数()1xf x e=-,若存在实数,()a b a b<使得()()f a f b=,则2+a b的最大值为________. 【答案】32ln27【解析】作出函数()1xf x e=-图像如下:由题意,令,a b为方程()f x m=的两个根,由图像易得01m<<;由1xe m-=得1xe m=±,解得ln(1)x m=+或ln(1)x m=-,因为a b<,所以ln(1)b m=+,ln(1)a m=-,因此22ln(1)2ln(1)ln(1)(1)a b m m m m+=-++=-+,令232()(1)(1)1g m m m m m m=-+=--++,01m<<,则2()321(31)(1)g m m m m m'=--+=--+,因为01m<<,所以由()0g m'>得13m<<;由()0g m'<得113m<<,即函数()g m在10,3⎛⎫⎪⎝⎭上单调递增;在1,13⎛⎫⎪⎝⎭上单调递减;所以2max11132()1133327g m g ⎛⎫⎛⎫⎛⎫==-+= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭, 因此2+a b 的最大值为32ln 27. 故答案为32ln2712.已知实数a ,b ,c 满足2121a c b c e a b e +--+++≤(e 为自然对数的底数),则22a b +的最小值是_______. 【答案】15【解析】设()(1)xu x e x =-+,则()1xu x e '=-, 所以函数u()的增区间为(0,+),减区间为(-,0), 所以()(0)0u x u ≥=,即e 1x x ≥+;可知21121121a c b c e a c b a e c b +--++++--+=++≥, 当且仅当210a c b c +=--=时取等; 因为2121a c b c e a b e +--+++≤所以2121a c b c e a b e +--+=++,210a c b c +=--=. 所以1,2c a c b +=-=, 解得22222(1)51144245c c a b c c ++=+=++≥,当且仅当15c =时,取等号.故答案为:1513.已知直线x t =与曲线()()()ln 1,xf x xg x e =+=分别交于,M N 两点,则MN 的最小值为________【答案】1. 【解析】令()()()ln(1)th t g t f t e t =-=-+,1'()()()1t h t g t f t e t =-=-+,显然为增函数,且'(0)0h = 所以当(1,0)t ∈-时,'()0,()h t h t <单调递减; 当(1,)t ∈+∞时,'()0,()h t h t >单调递增.所以min ()(0)1h t h ==. 故答案为1.14.曲线cos y a x =在6x π=处的切线l 的斜率为12,则切线l 的方程为_____. 【答案】2306x y π---=【解析】解:曲线cos y a x =,可得'sin y a x =-, 曲线cos y a x =在6x π=处的切线l 的斜率为12, 可得1sin62a π-=, 所以1a =-. 所以切点坐标为:3(,)62π-, 则切线l 的方程为:3126y x π⎛⎫+=- ⎪⎝⎭. 即:2306x y π---=.故答案为:2306x y π---=.15.已知函数22,0,(),0,x x x f x e x ⎧≤=⎨>⎩若方程2[()]f x a =恰有两个不同的实数根12,x x ,则12x x +的最大值是______. 【答案】3ln 22- 【解析】作出()f x 的函数图象如图所示,由()2f x a =⎡⎤⎣⎦,可得()1f x =>, 即1a >,不妨设12x x <,则2212x x e ==(1)t t =>,则12ln x x t ==,12ln x x t ∴+=()ln g t t =,则'()g t =, 当 18t <<时,()'0g t >,()g t 在()1,8上递增; 当8t >时,()'0g t <,()g t 在()8,+∞上递减; 当8t =时,()g t 取得最大值g(8)=ln82=3ln22--, 故答案为3ln 22-.16.已知函数31,0()2,0ax x f x x ax x x -≤⎧=⎨-+->⎩的图象恰好经过三个象限,则实数a 的取值范围______.【答案】0a <或2a > 【解析】(1)当0a <时,()f x 在(,0]-∞上单调递减,又(0)1f =-,所以函数()f x 的图象经过第二、三象限,当0x >时,33(1)2,2()(1)2,02x a x x f x x a x x ⎧---=⎨-++<<⎩…, 所以223(1),2()3(1),,02x a x f x x a x ⎧--=⎨-+<<⎩'…,①若1a -„时,()0f x '>恒成立,又当0x +→时,()2f x →,所以函数()f x 图象在0x >时,经过第一象限,符合题意;②若10a -<<时,()0f x '>在[2,)+∞上恒成立,当02x <<时,令()0f x '=,解13x =,所以()f x在⎛ ⎝上单调递减,在2⎫⎪⎪⎭上单调递增,又(2210f a ⎛=+=> ⎝所以函数()f x 图象在0x >时,经过第一象限,符合题意;(2)当0a =时,()f x 的图象在(,0)-∞上,只经过第三象限,()0f x '>在(0,)+∞上恒成立,所以()f x 的图象在(0,)+∞上,只经过第一象限,故不符合题意;(3)当0a >时,()f x 在(,0)-∞上单调递增,故()f x 的图象在(,0)-∞上只经过第三象限,所以()f x 在(0,)+∞上的最小值min ()0f x <,当02x <<时,令()0f x '=,解得x =2<时,即11a <时,()f x 在(0,)+∞上的最小值为21f ⎛= ⎝,令2102211f a a ⎛=<⇒>∴<< ⎝.211a ⇒≥时,则()f x 在02x <<时,单调递减,当2x ≥时,令()0f x '=,解得x =,21113a <⇒≤<,()f x 在(2,)+∞上单调递增,故()f x 在(0,)+∞上的最小值为(2)82f a =-,令8204a a -<⇒>,所以1113a ≤<;213a ≥⇒≥,()f x 在⎛ ⎝上单调递减,在⎫+∞⎪⎪⎭上单调递增,故()f x 在(0,)+∞上的最小值为2f =,显然20<,故13a ≥;结上所述:0a <或2a >.17.已知函数()||ln (0)f x x a x a =-->. (Ⅰ)讨论()f x 的单调性;(Ⅱ)比较222222ln 2ln 3ln 23n n++⋯+ 与(1)(21)2(1)n n n -++的大小(n N +∈且)2n >,并证明你的结论.【答案】(I )见解析;(II )见解析 【解析】(Ⅰ)函数()f x 可化为ln ,()ln ,0x x a x af x a x x x a --≥⎧=⎨--<<⎩,当0x a <<时,1()10f x x '=--<,从而()f x 在(0,)a 上总是递减的, 当x a ≥时,11()1x f x x x-=-=',此时要考虑a 与1的大小.若1a ≥,则()0f x '≥,故()f x 在[,)a +∞上递增,若01a <<,则当1a x ≤<时,()0f x '<,当1x >时,()0f x '>,故()f x 在[,1)a 上递减, 在(1,)+∞上递增,而()f x 在x a =处连续,所以 当1a ≥时,()f x 在(0,)a 上递减,在[,)a +∞上递增; 当01a <<时,()f x 在(0,1)上递减,在[1,)+∞上递增.(Ⅱ)由(Ⅰ)可知当1a =,1x >时,1ln 0x x -->,即ln 1x x >-,所以ln 11x x x<-.所以 222222ln 2ln 3ln 23n nL +++22211111123n <-+-+-L 222111123n n ⎛⎫=--+++ ⎪⎝⎭L 11112334(1)n n n ⎛⎫<--+++ ⎪⨯⨯+⎝⎭L 11121n n ⎛⎫=--- ⎪+⎝⎭1(1)2(1)n n n -=--+ 2221(1)(21)2(1)2(1)n n n n n n --+-+==++. 18.已知函数()()21ln 2f x x x ax a =++∈R .(1)讨论()f x 的单调性;(2)若12,x x 为()f x 的两个极值点,证明:()()21212+44282f x f x a a x x f +++⎛⎫-> ⎪⎝⎭.【答案】(1)当2a <-时,()f x 在0,2a ⎛⎫-- ⎪ ⎪⎝⎭为增函数,,22a a ⎛⎫--⎪ ⎪⎝⎭减函数,⎫+∞⎪⎪⎝⎭为增函数;当2a ≥-时,()f x 在()0,∞+为增函数.(2)证明见解析.【解析】(1)()f x 的定义域为()0,∞+,()()210x ax f x x x'++=>,对于函数21y x ax =++,①当240a ∆=-≤时,即22a -≤≤时,210x ax ++≥在0x >恒成立.()210x ax f x x++'∴=≥在()0,∞+恒成立,()f x ∴在()0,∞+为增函数;②当∆>0,即2a <-或2a >时,当2a <-时,由()0f x '>,得x <x >,0<<, ()f x ∴在⎛⎫ ⎪ ⎪⎝⎭为增函数,⎛⎫⎪ ⎪⎝⎭减函数,,2a ⎛⎫-++∞⎪ ⎪⎝⎭为增函数, 当2a >时,由()210x ax f x x++'=>在()0,∞+恒成立,()f x ∴在()0,∞+为增函数.综上,当2a <-时,()f x在⎛⎫ ⎪ ⎪⎝⎭为增函数,⎛⎫⎪ ⎪⎝⎭减函数,⎫+∞⎪⎪⎝⎭为增函数; 当2a ≥-时,()f x 在()0,∞+为增函数.(2)由(1)知2a <-,且1212,1x x a x x +=-=, 故()()121222f x f x x x f ++⎛⎫- ⎪⎝⎭()()21222111222121211ln ln 222ln 2222x x x x ax x x ax x x x x a +⎛⎫+++++ ⎪++⎛⎫⎛⎫⎝⎭=--- ⎪ ⎪⎝⎭⎝⎭21ln +228a a ⎛⎫=--- ⎪⎝⎭故只需证明ln 1022a a⎛⎫----> ⎪⎝⎭,令2at =-,故1t >, 原不等式等价于ln 1t t <-对1t >成立, 令1()ln (1),'()0tg t t t g t t-=--=<,所以()ln (1)g t t t =--单调递减,有()ln (1)(1)0g t t t g =--<= 得证.19.已知函数()ln(1)1(1)f x ax x a =+-+…. (Ⅰ)当1a =时,求()f x 的最大值; (Ⅱ)若1()e f x e +„对1,x a ⎛⎫∈-+∞ ⎪⎝⎭恒成立,求实数a 的取值范围. 【答案】(Ⅰ)1;(Ⅱ)[1,e] 【解析】(Ⅰ)当1a =时,()ln(1)1f x x x =+-+,定义域为(1,)-+∞. 1()111xf x x x -'=-=++. 令()0f x '=,得0x =.当(1,0)x ∈-时,()0f x '>,()f x 单调递增, 当(0,)x ∈+∞时,()0f x '<,()f x 单调递减. 所以max ()(0)1f x f ==. (Ⅱ)()11a f x ax '=-+11ax a ax -+-=+,1x a >-.令()0f x '=,得1a x a-=. 当11,a x a a -⎛⎫∈-⎪⎝⎭时,()0f x '>,()f x 单调递增;当1,a x a -⎛⎫∈+∞ ⎪⎝⎭时,()0f x '<,()f x 单调递减,所以max 11()ln a f x f a a a -⎛⎫==+ ⎪⎝⎭. 依题意有11ln e a a e ++„,设1()ln (1)g a a a a =+…, 则22111()0a g a a a a-'=-=…,所以()g a 在[1,)a ∈+∞上单调递增. 又1e 1(e)ln e e e g +=+=,故1e 1ln ea a ++„()(e)g a g ⇔„1e a ⇒剟, 即实数a 的取值范围为[1,e].20.对于函数()y f x =的定义域D ,如果存在区间[],m n D ⊆,同时满足下列条件:①()f x 在()()f x g x +上是单调函数;②当[],x m n ∈时,()f x 的值域为[]2,2m n ,则称区间()()f x g x +是函数()f x 的“单调倍区间”.已知函数()ln 2,0()02,0a x x x f x a a x ->⎧⎪=>≤ (1)若2a =,求()f x 在点()(),e f e 处的切线方程; (2)若函数()f x 存在“单调倍区间”,求a 的取值范围. 【答案】(1)22y x e ⎛⎫=- ⎪⎝⎭;(2)(231,4,2164e e ⎛⎤⎤ ⎦⎥⎝⎦U 【解析】(1)当2a =时,()()2ln 20f x x x x =-> 当0x >时,()22f x x '=-,则:()22f e e'=-,又()22f e e =- ()f x ∴在()(),e f e 处的切线方程为:()()2222y e x e e⎛⎫--=-- ⎪⎝⎭即:22y x e ⎛⎫=- ⎪⎝⎭(2)()ln 2,0()02,0a x x x f x a a x ->⎧⎪=>≤Q ()()2,000ax x f x a x ⎧->⎪⎪∴=>⎨≤' 列表如下:设函数()f x 存在“单调倍区间”是()()f x g x +①当0m n <≤时,由()f x 在(),0-∞上单调递减,则有2222a na m=-=()2n m =-2=12=,代入2222a n a m ==得:12221222a n a m ⎧=-⎪⎪⎨⎪=--⎪⎩要使此关于,m n 的方程组在0m n <≤时有解,则使得2y a =与()21202y x x x =-+≥的图象有两个公共点当14x =时,min 38y =,当0x =时,12y =结合两函数图象,则31282a <≤,即:31164a <≤ 即此时满足()f x 存在“单调倍区间”的a 的取值范围是31,164⎛⎤⎥⎝⎦②当02a m n <<≤时,由()f x 在0,2a ⎛⎫⎪⎝⎭上单调递增,则有 ln 22ln 22a m m m a n n n -=⎧⎨-=⎩即:1ln 41ln 4ma mn a n⎧=⎪⎪⎨⎪=⎪⎩设()ln 4x g x x =,则()21ln 4xg x x-'= 当()0,x e ∈时,()0g x '>,()g x 为增函数 当(),x e ∈+∞时,()0g x '<,()g x 为减函数要使方程1ln 4x a x =有两解,则1y a =与()ln 4x g x x =的图象在0,2a ⎛⎤ ⎥⎝⎦有两个交点结合两函数图象,则()212a e a g g e a⎧>⎪⎪⎨⎛⎫⎪≤< ⎪⎪⎝⎭⎩,即:2ln 122114a e a a a a e ⎧>⎪⎪⎪⎪≤⎨⎪⎪<⎪⎪⎩解得:242e a e <≤即此时满足()f x 存在“在单调倍区间”的a 的取值范围是(24,2e e ⎤⎦③当2a m n <<时,由()f x 在,2a ⎛⎫+∞ ⎪⎝⎭上单调递减,则有ln 22ln 22a m m n a n n m -=⎧⎨-=⎩两式相减得:()ln ln 0a m n -=,此式不成立,即此时()f x 不存在“单调倍区间” 综上,函数()f x 存在“单调倍区间”的a 的取值范围是(231,4,2164e e ⎛⎤⎤ ⎦⎥⎝⎦U 21.已知函数2()(0)4x x a f x e a x ++=⋅≥+. (1)讨论函数()f x 的单调性;(2)当[0,1)b ∈时,设函数22(3)()(2)(2)x e b x g x x x +-+=>-+有最小值()h b ,求()h b 的值域. 【答案】(1)见解析;(2) 21(),24e h b ⎛⎤∈ ⎥⎝⎦【解析】解:(1)()f x 定义域为(,4)(4,)-∞--+∞U ,224(4)4x a x a e x x +⎛⎫-+=+ ⎪++⎝⎭222(4)34(4)x x a x a ex +++++=⋅+.令2(4)340x a x a ++++=,①。
2010-2019十年高考数学真题分类汇编专题08 数列 学生版解析版

22 243 3十年高考真题分类汇编(2010—2019)数学专题 08 数列一、选择题1.(2019·全国 1·理 T9)记 S n 为等差数列{a n }的前 n 项和.已知 S 4=0,a 5=5,则()A.a n =2n-5C.S n =2n 2-8nB.a n =3n-10D.S n =1n 2-2n2.(2019·浙江·T10)设 a,b∈R,数列{a n }满足 a 1=a,a n+1=a n +b,n∈N *,则()A.当 b=1时,a 10>10C.当 b=-2 时,a 10>10B.当 b=1时,a 10>10D.当 b=-4 时,a 10>103.(2018·全国 1·理 T4)记 S n 为等差数列{a n }的前 n 项和,若 3S 3=S 2+S 4,a 1=2,则 a 5=( )A.-12B.-10C.10D.124.(2018·浙江·T10)已知 a 1,a 2,a 3,a 4 成等比数列,且 a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3).若 a 1>1,则()A.a 1<a 3,a 2<a 4B.a 1>a 3,a 2<a 4C.a 1<a 3,a 2>a 4D.a 1>a 3,a 2>a 45.(2018·北京·理 T4 文 T5)“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于 12√2.若第一个单音的频率为 f,则第八个单音的频率为()A. √2fB. √22f C. 12√25fD. 12√27f6.(2017·全国 1·理 T12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动 .这款软件的激活码为下面数学问题的答案 :已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是 20,接下来的两项是 20,21,再接下来的三项是 20,21,22,依此类推.求满足如下条件的最小整数 N:N>100 且该数列的前 N 项和为 2 的整数幂.那么该款软件的激活码是()A.440B.330C.220D.1107.(2017·全国 3·理 T9)等差数列{a n }的首项为 1,公差不为 0.若 a 2,a 3,a 6 成等比数列,则{a n }前 6 项的和为()A.-24B.-3C.3D.88.(2016·全国 1·理 T3)已知等差数列{a n }前 9 项的和为 27,a 10=8,则 a 100=()2B.192C.10D.122D.12D.n (n -1)3B.-13C.19D.-1432 2A.100B.99C.98D.979.(2015·浙江·理 T13)已知{a n }是等差数列,公差 d 不为零,前 n 项和是 S n ,若 a 3,a 4,a 8 成等比数列,则()A.a 1d>0,dS 4>0B.a 1d<0,dS 4<0C.a 1d>0,dS 4<0D.a 1d<0,dS 4>010.(2015·全国 2·文 T5)设 S n 是等差数列{a n }的前 n 项和,若 a 1+a 3+a 5=3,则 S 5=( )A.5B.7C.9D.1111.(2015·全国 1·文 T7)已知{a n }是公差为 1 的等差数列,S n 为{a n }的前 n 项和.若 S 8=4S 4,则 a 10= (A.1712.(2015·全国 2·理 T4)已知等比数列{a n }满足 a 1=3,a 1+a 3+a 5=21,则 a 3+a 5+a 7=()A.21B.42C.63D.8413.(2015·全国 2·文 T9)已知等比数列{a n }满足 a 1=1,a 3a 5=4(a 4-1),则 a 2=()A.2B.1C.18 14.(2014·大纲全国·文 T8)设等比数列{a n }的前 n 项和为 S n .若 S 2=3,S 4=15,则 S 6=()A.31B.32C.63D.6415.(2014·全国 2·文 T5)等差数列{a n }的公差为 2,若 a 2,a 4,a 8 成等比数列,则{a n }的前 n 项和 S n =(A.n(n+1)B.n(n-1)C.n (n+1)216.(2013·全国 2·理 T3)等比数列{a n }的前 n 项和为 S n .已知 S 3=a 2+10a 1,a 5=9,则 a 1=()A.1917.(2013·全国 1·文 T6)设首项为 1,公比为2的等比数列{a n }的前 n 项和为 S n ,则()A.S n =2a n -1B.S n =3a n -2C.S n =4-3a nD.S n =3-2a n18.(2013·全国 1·理 T12)设 A △n B n C n 的三边长分别为 a n ,b n ,c △n , A n B n C n 的面积为 S n ,n=1,2,3,….若b 1>c 1,b 1+c 1=2a 1,a n+1=a n ,b n+1=c n +a n ,c n+1=b n +a n ,则()A.{S n }为递减数列B.{S n }为递增数列C.{S 2n-1}为递增数列,{S 2n }为递减数列))2.(2019·全国3·理 T14)记 S n 为等差数列{a n }的前 n 项和.若 a 1≠0,a 2=3a 1,则S 10= .43 41 S4 4D.{S 2n-1}为递减数列,{S 2n }为递增数列19.(2013·全国 1·理 T7)设等差数列{a n }的前 n 项和为 S n ,若 S m-1=-2,S m =0,S m+1=3,则 m= ( )A.3B.4C.5D.620.(2012·全国·理 T5)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则 a 1+a 10=()A.7B.5C.-5D.-721.(2012·全国·文 T12)数列{a n }满足 a n+1+(-1)n a n =2n-1,则{a n }的前 60 项和为()A.3 690B.3 660C.1 845D.1 830二、填空题1.(2019·全国 3·文 T14)记 S n 为等差数列{a n }的前 n 项和.若 a 3=5,a 7=13,则 S 10=. S 53.(2019·江苏·T8)已知数列{a n }(n∈N *)是等差数列,S n 是其前 n 项和.若 a 2a 5+a 8=0,S 9=27,则 S 8 的值是. 4.(2019·北京·理 T10)设等差数列{a n }的前 n 项和为 S n .若 a 2=-3,S 5=-10,则 a 5= ,S n 的最小值为.5.(2019·全国 1·文 T14)记 S n 为等比数列{a n }的前 n 项和.若 a 1=1,S 3=3,则 S 4=.6.(2019·全国 1·理 T14)记 S n 为等比数列{a n }的前 n 项和.若 a 1=1 , a 2=a 6,则 S 5=________.7.(2018·全国 1·理 T14)记 S n 为数列{a n }的前 n 项和.若 S n =2a n +1,则 S 6=.8.(2018·北京·理 T9)设{a n }是等差数列,且 a 1=3,a 2+a 5=36,则{a n }的通项公式为.9.(2018·上海·T10)设等比数列{a n }的通项公式为 a n =q n-1(n∈N *),前 n 项和为 S n ,若 lim a S n = 2,则 q=.n →∞ n+110.(2018·江苏·T14)已知集合 A={x|x=2n-1,n∈N *},B={x|x=2n ,n∈N *}.将 A∪B 的所有元素从小到大依次排列构成一个数列{a n }.记 S n 为数列{a n }的前 n 项和,则使得 S n >12a n+1 成立的 n 的最小值为 .n11.(2017·全国 2·理 T15)等差数列{a n }的前 n 项和为 S n ,a 3=3,S 4=10,则 ∑ 1 =____________.k=1 k 12.(2017·全国 3·理 T14)设等比数列{a n }满足 a 1+a 2=-1,a 1-a 3=-3,则 a 4=.13.(2017·江苏·理 T9 文 T9)等比数列{a n }的各项均为实数,其前 n 项和为 S n .已知 S 3=7,S 6=63,则 a 8=.14.(2016·浙江·理 T13 文 T13)设数列{a n }的前 n 项和为 S n ,若 S 2=4,a n+1=2S n +1,n∈N *,则 a 1=,S 5= .15.(2016·北京·理 T12)已知{a n }为等差数列,S n 为其前 n 项和.若 a 1=6,a 3+a 5=0,则 S 6= . 16.(2016·全国 1·理 T15)设等比数列{a n }满足 a 1+a 3=10,a 2+a 4=5,则 a 1a 2…a n 的最大值为.17.(2015·全国 1·文 T13)在数列{a n }中,a 1=2,a n+1=2a n ,S n 为{a n }的前 n 项和.若 S n =126,则 n=.18.(2015·湖南·理 T14)设 S n 为等比数列{a n }的前 n 项和,若 a 1=1,且 3S 1,2S 2,S 3 成等差数列,则 a n =.19.(2015·福建·文 T16)若 a,b 是函数 f(x)=x 2-px+q(p>0,q>0)的两个不同的零点,且 a,b,-2 这三个数可适a n =n+1(n∈N ).则数列{ }前 10 项的和为____________.*127.(2014·全国2·文 T16)数列{a n }满足 a n+1=,a 8=2,则 a 1=____________.13 3当排序后成等差数列,也可适当排序后成等比数列,则 p+q 的值等于.20.(2015·江苏·理 T11)设数列{a n }满足 a 1=1,且 a n+1-a n21.(2015·全国 2·理 T16)设 S n 是数列{a n }的前 n 项和,且 a 1=-1,a n+1=S n S n+1,则 S n =.22.(2015·广东·理 T10)在等差数列{a n }中,若 a 3+a 4+a 5+a 6+a 7=25,则 a 2+a 8=.23.(2015·陕西·文 T13)中位数为 1 010 的一组数构成等差数列,其末项为 2 015,则该数列的首项为 .24.(2014·江苏·理 T7)在各项均为正数的等比数列{a n }中,若 a 2=1,a 8=a 6+2a 4,则 a 6 的值是.25.(2014 · 广 东 · 文 T13) 等 比 数 列 {a n } 的 各 项 均 为 正 数 , 且a 1a 5=4, 则log 2a 1+log 2a 2+log 2a 3+log 2a 4+log 2a 5=.26.(2014·安徽·理 T12)数列{a n }是等差数列,若 a 1+1,a 3+3,a 5+5 构成公比为 q 的等比数列,则 q=.1-a n28.(2014·北京·理 T12)若等差数列{a n }满足 a 7+a 8+a 9>0,a 7+a 10<0,则当 n=时,{a n }的前 n 项和最大.29.(2014·天津·理 T11)设{a n }是首项为 a 1,公差为-1 的等差数列,S n 为其前 n 项和.若 S 1,S 2,S 4 成等比数列, 则 a 1 的值为.30.(2013·全国 2·理 T16)等差数列{a n }的前 n 项和为 S n ,已知 S 10=0,S 15=25,则 nS n 的最小值为.31.(2013·辽宁·理 T14)已知等比数列{a n }是递增数列,S n 是{a n }的前 n 项和.若 a 1,a 3 是方程 x 2-5x+4=0 的两 个根,则 S 6=.32.(2013·全国 1·理 T14)若数列{a n }的前 n 项和 S n =2a n +1,则{a n }的通项公式是 a n =.33.(2012·全国·文 T14)等比数列{a n }的前 n 项和为 S n ,若 S 3+3S 2=0,则公比 q=.三、计算题1.(2019·全国 2·文 T18)已知{a n }是各项均为正数的等比数列,a 1=2,a 3=2a 2+16.(1)求{a n }的通项公式;(2)设 b n =log 2a n .求数列{b n }的前 n 项和.2.(2019·全国 2·理 T19)已知数列{a n }和{b n }满足 a 1=1,b 1=0,4a n+1=3a n -b n +4,4b n+1=3b n -a n -4. (1)证明:{a n +b n }是等比数列,{a n -b n }是等差数列; (2)求{a n }和{b n }的通项公式.3.(2019·天津·文 T18)设{a n }是等差数列,{b n }是等比数列,公比大于 0.已知 a 1=b 1=3,b 2=a 3,b 3=4a 2+3. (1)求{a n }和{b n }的通项公式;b k ,n = 2k ,(2)记 c n =√ a n**,n∈N ,证(2)已知数列{bn }(n∈N )满足:b 1=1,* 1 = 2 − 2 ,其中 S n 为数列{b n }的前 n 项和.b n ,n 为偶数,2(2)设数列{c n }满足 c n ={ 1,n 为奇数,求 a 1c 1+a 2c 2+…+a 2n c 2n (n∈N *).24.(2019·天津·理 T19)设{a n }是等差数列,{b n }是等比数列.已知 a 1=4,b 1=6,b 2=2a 2-2,b 3=2a 3+4.(1)求{a n }和{b n }的通项公式;1,2k < n < 2k1 ,(2)设数列{c n }满足 c 1=1,c n ={ 其中 k∈N *.①求数列{a 2n (c 2n -1)}的通项公式; 2n②求∑ a i c i (n∈N *).i=1 5.(2019 · 浙 江 · T 20) 设 等 差 数 列 {a n } 的 前 n 项 和 为 S n ,a 3=4,a 4=S 3. 数 列 {b n } 满 足 : 对 每 个 n ∈N *,S n +b n ,S n+1+b n ,S n+2+b n 成等比数列.(1)求数列{a n },{b n }的通项公式;2b n6.(2019·江苏·T 20)定义首项为 1 且公比为正数的等比数列为“M - 数列”.(1)已知等比数列{a n }(n∈N *)满足:a 2a 4=a 5,a 3-4a 2+4a 1=0,求证:数列{a n }为“M - 数列”;S nb n b n1①求数列{b n }的通项公式;②设 m 为正整数.若存在“M - 数列”{c n }(n∈N *),对任意正整数 k,当 k≤m 时,都有 c k ≤b k ≤c k+1 成立,求 m 的 最大值.7.(2018·北京·文 T15)设{a n }是等差数列,且 a 1=ln 2,a 2+a 3=5ln 2.(1)求{a n }的通项公式; (2)求e a 1e a 2 +…+e a n .8.(2018·上海·T 21)给定无穷数列{a n },若无穷数列{b n }满足:对任意 x∈N *,都有|b n -a n |≤1,则称{b n }与{a n }“接近”.(1)设{a n }是首项为 1,公比为1的等比数列,b n =a n+1+1,n∈N *,判断数列{b n }是否与{a n }接近,并说明理由;(2)设数列{a n }的前四项为 a 1=1,a 2=2,a 3=4,a 4=8,{b n }是一个与{a n }接近的数列,记集合 M={x|x=b i ,i=1,2,3,4},求 M 中元素的个数 m:(3)已知{a n }是公差为 d 的等差数列.若存在数列{b n }满足:{b n }与{a n }接近,且在 b 2-b 1,b 3-b 2,…,b 201-b 200 中至少有 100 个为正数,求 d 的取值范围.9.(2018·江苏·T 20)设{a n }是首项为 a 1,公差为 d 的等差数列,{b n }是首项为 b 1,公比为 q 的等比数列.√ (k+1)(k+2)-2(n∈N *). a(1)设 a 1=0,b 1=1,q=2,若|a n -b n |≤b 1 对 n=1,2,3,4 均成立,求 d 的取值范围;(2)若 a 1=b 1>0,m∈N *,q∈(1, m 2],证明:存在 d∈R,使得|a n -b n |≤b 1 对 n=2,3,…,m+1 均成立,并求 d 的取值 范围(用 b 1,m,q 表示).10.(2018·天津·文 T18)设{a n }是等差数列,其前 n 项和为 S n (n∈N *);{b n }是等比数列,公比大于 0,其前 n 项 和为 T n (n∈N *).已知 b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (1)求 S n 和 T n ;(2)若 S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数 n 的值.11.(2018·天津·理 T18)设{a n }是等比数列,公比大于 0,其前 n 项和为 S n (n∈N *),{b n }是等差数列.已知 a 1=1,a 3=a 2+2,a 4=b 3+b 5,a 5=b 4+2b 6. (1)求{a n }和{b n }的通项公式;(2)设数列{S n }的前 n 项和为 T n (n∈N *), ①求 T n ;nk1②证明 ∑(T k +b k+2)b k 2n+2n+212.(2018·全国 2·理 T17 文 T17)记 S n 为等差数列{a n }的前 n 项和,已知 a 1=-7,S 3=-15.(1)求{a n }的通项公式; (2)求 S n ,并求 S n 的最小值.13.(2018·全国 1·文 T17)已知数列{a n }满足 a 1=1,na n+1=2(n+1)a n .设 b n = n .(1)求 b 1,b 2,b 3;(2)判断数列{b n }是否为等比数列,并说明理由; (3)求{a n }的通项公式.14.(2018·全国 3·理 T17 文 T17)等比数列{a n }中,a 1=1,a 5=4a 3. (1)求{a n }的通项公式;(2)记 S n 为{a n }的前 n 项和,若 S m =63,求 m.15.(2017·全国 1·文 T17)设 S n 为等比数列{a n }的前 n 项和,已知 S 2=2,S 3=-6. (1)求{a n }的通项公式;(2)求 S n ,并判断 S n+1,S n ,S n+2 是否成等差数列.16.(2017 · 全 国 2 · 文 T17) 已 知 等 差 数 列 {a n } 的 前 n 项 和 为 S n , 等 比 数 列 {b n } 的 前 n 项 和 为 T n ,a 1=-1,b 1=1,a 2+b 2=2.(1)若 a +b =5,求{b }的通项公式;(2){bn }为各项非零的等差数列,其前 n 项和为 S n .已知 S 2n+1=b n b n+1,求数列{b n }的前 n 项和 T n .(2)若 T 3=21,求 S 3.17.(2017·全国 3·文 T17)设数列{a n }满足 a 1+3a 2+…+(2n -1)a n =2n. (1)求{a n }的通项公式;(2)求数列{ a n }的前 n 项和.2n+118.(2017·天津·理 T18)已知{a n }为等差数列,前 n 项和为 S n (n∈N *),{b n }是首项为 2 的等比数列,且公比大 于 0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4. (1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b 2n-1}的前 n 项和(n∈N *).19.(2017·山东·理 T19)已知{x n }是各项均为正数的等比数列,且 x 1+x 2=3,x 3-x 2=2. (1)求数列{x n }的通项公式;(2)如图,在平面直角坐标系 xOy 中,依次连接点 P 1(x 1,1),P 2(x 2,2)…P n+1(x n+1,n+1)得到折线 P 1P 2…P n+1,求由该 折线与直线 y=0,x=x 1,x=x n+1 所围成的区域的面积 T n .20.(2017·山东·文 T19)已知{a n }是各项均为正数的等比数列,且 a 1+a 2=6,a 1a 2=a 3.1)求数列{a n }的通项公式;a n21.(2017·天津·文 T18)已知{a n }为等差数列,前 n 项和为 S n (n∈N *),{b n }是首项为 2 的等比数列,且公比大于 0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4. (1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b n }的前 n 项和(n∈N *).22.(2016·全国 2·理 T17)S n 为等差数列{a n }的前 n 项和,且 a 1=1,S 7=28.记 b n =[lg a n ],其中[x]表示不超过 x 的最大整数,如[0.9]=0,[lg 99]=1.(1)求 b 1,b 11,b 101;(2)求数列{b n }的前 1 000 项和.(2)令 c n =(a n +1)(b n +2) ,求数列{c n }的前 n 项和 T n .(1)设 c n =b n+1 − b n 2,n∈N *,求证:数列{c n }是等差数列;(2)设 a 1=d,T n = ∑ (-1)k b k 2d 28.(2016·天津·文 T18)已知{a n }是等比数列,前 n 项和为 S n (n∈N *),且 1 − 133223.(2016·全国 2·文 T17)等差数列{a n }中,a 3+a 4=4,a 5+a 7=6.(1)求{a n }的通项公式;(2)设 b n =[a n ],求数列{b n }的前 10 项和,其中[x]表示不超过 x 的最大整数,如[0.9]=0,[2.6]=2. 24.(2016·浙江·文 T17)设数列{a n }的前 n 项和为 S n .已知 S 2=4,a n+1=2S n +1,n∈N *. (1)求通项公式 a n ;(2)求数列{|a n -n-2|}的前 n 项和.25.(2016·北京·文 T15)已知{a n }是等差数列,{b n }是等比数列,且 b 2=3,b 3=9,a 1=b 1,a 14=b 4. (1)求{a n }的通项公式;(2)设 c n =a n +b n ,求数列{c n }的前 n 项和.26.(2016·山东·理 T18 文 T19)已知数列{a n }的前 n 项和 S n =3n 2+8n,{b n }是等差数列,且 a n =b n +b n+1. (1)求数列{b n }的通项公式;n+1n27.(2016·天津·理 T18)已知{a n }是各项均为正数的等差数列,公差为 d.对任意的 n∈N *,b n 是 a n 和 a n+1 的等比中项.22n n 2,n∈N *,求证: ∑ 1 k1 k1 Tk< 1 .2a 1 a 22 a 3,S 6=63.(1)求{a n }的通项公式;(2)若对任意的 n∈N *,b n 是 log 2a n 和 log 2a n+1 的等差中项,求数列{(-1)n b 2n }的前 2n 项和.29.(2016·全国 1·文 T17)已知{a n }是公差为 3 的等差数列,数列{b n }满足 b 1=1,b 2=1,a n b n+1+b n+1=nb n .(1)求{a n }的通项公式;(2)求{b n }的前 n 项和.30.(2016·全国 3·文 T17)已知各项都为正数的数列{a n }满足 a 1=1, a 2n -(2a n+1-1)a n -2a n+1=0. (1)求 a 2,a 3;(2)求{a n }的通项公式.31.(2016·全国 3·理 T17)已知数列{a n }的前 n 项和 S n =1+λa n ,其中λ≠0. (1)证明{a n }是等比数列,并求其通项公式;(2)若 S 5=31,求λ.(2)设 b n =n+1(2)设S n 为数列{a n }的前 n 项和,b n =,求数列{b n }的前 n 项和 T n .a(2)设 b n = 38.(2015·山东·文 T19)已知数列{a n }是首项为正数的等差数列,数列{ ,求数列{b n }的前 n 项和.,n∈N ,求数列{b n }的前 n 项和.*a n ·a n+1}的前 n 项和为 .n22 2 3132.(2015·北京·文 T16)已知等差数列{a n }满足 a 1+a 2=10,a 4-a 3=2.(1)求{a n }的通项公式;(2)设等比数列{b n }满足 b 2=a 3,b 3=a 7.问:b 6 与数列{a n }的第几项相等?33.(2015·重庆·文 T16)已知等差数列{a n }满足 a 3=2,前 3 项和 S 3=9.(1)求{a n }的通项公式;(2)设等比数列{b n }满足 b 1=a 1,b 4=a 15,求{b n }的前 n 项和 T n . 34.(2015·福建·文 T17)等差数列{a n }中,a 2=4,a 4+a 7=15. (1)求数列{a n }的通项公式;(2)设 b n =2a n -2+n,求 b 1+b 2+b 3+…+b 10 的值.35.(2015·全国 1·理 T17)S n 为数列{a n }的前 n 项和.已知 a n >0,a n +2a n =4S n +3.(1)求{a n }的通项公式;1a n a n+136.(2015·安徽·文 T18)已知数列{a n }是递增的等比数列,且 a 1+a 4=9,a 2a 3=8.(1)求数列{a n }的通项公式;S n S n+137.(2015·天津·理 T18)已知数列{a n }满足 a n+2=qa n (q 为实数,且 q≠1),n∈N *,a 1=1,a 2=2,且 a 2+a 3,a 3+a 4,a 4+a 5 成等差数列.(1)求 q 的值和{a n }的通项公式;l o g 2a 2na 2n -112n+1 (1)求数列{a n }的通项公式;(2)设 b n =(a n +1)·2a n ,求数列{b n }的前 n 项和 T n .39.(2015·浙江·文 T17)已知数列{a n }和{b n }满足 a 1=2,b 1=1,a n+1=2a n (n∈N *),b 1+1b 2+1b 3+…+n b n =b n+1-1(n∈N *).(1)求 a n 与 b n ;(2)记数列{a n b n }的前 n 项和为 T n ,求 T n .40.(2015 · 天 津 · 文 T18) 已 知 {a n } 是 各 项 均 为 正 数 的 等 比 数 列 ,{b n } 是 等 差 数 列 , 且 a 1=b 1=1,b 2+b 3=2a 3,a 5-3b 2=7. (1)求{a n }和{b n }的通项公式;(2)当d>1 时,记 c n =a n,求数列{c n }的前 n 项和 T n .2(2)证明: a 2a nS n =n +n ,n∈N *.(2)设 b n = a n a n+1项和 T n .,求数列{b n }的前 n(2)令b n =(-1)n-1 4n ,求数列{b n }的前 n 项和 T n .(2)设 c n =a n b n ,n∈N *,求数列{c n }的前 n 项和.41.(2015·湖北·文 T19)设等差数列 {a n }的公差为 d,前 n 项和为 S n ,等比数列 {b n }的公比为 q,已知 b 1=a 1,b 2=2,q=d,S 10=100.(1)求数列{a n },{b n }的通项公式;b n42.(2014·全国 2·理 T17)已知数列{a n }满足 a 1=1,a n+1=3a n +1.(1)证明:{a n + 1}是等比数列,并求{a n }的通项公式;1 a 1+ 1 +…+ 1 < 3.243.(2014·福建·文 T17)在等比数列{a n }中,a 2=3,a 5=81.(1)求 a n ;(2)设 b n =log 3a n ,求数列{b n }的前 n 项和 S n .44.(2014·湖南·文 T16)已知数列{a n }的前 n 项和22(1)求数列{a n }的通项公式;(2)设 b n =2a n +(-1)n a n ,求数列{b n }的前 2n 项和.45.(2014·北京·文 T14)已知{a n }是等差数列,满足 a 1=3,a 4=12,数列{b n }满足 b 1=4,b 4=20,且{b n -a n }为等比数 列.(1)求数列{a n }和{b n }的通项公式;(2)求数列{b n }的前 n 项和.46.(2014·大纲全国·理 T18)等差数列{a n }的前 n 项和为 S n .已知 a 1=10,a 2 为整数,且 S n ≤S 4. (1)求{a n }的通项公式;1 47.(2014·山东·理 T19)已知等差数列{a n }的公差为 2,前 n 项和为 S n ,且 S 1,S 2,S 4 成等比数列.(1)求数列{a n }的通项公式;a n a n+148.(2014·全国 1·文 T17)已知{a n }是递增的等差数列,a 2,a 4 是方程 x 2-5x+6=0 的根.(1)求{a n }的通项公式;22a 2n -1a 2n+1 }的前 n3 3- 2(2)求数列{a n }的前 n 项和.49.(2014·安徽·文 T18)数列{a n }满足 a 1=1,na n+1=(n+1)a n +n(n+1),n∈N *.(1)证明:数列{a n }是等差数列;n(2)设 b n =3n ·√a n ,求数列{b n }的前 n 项和 S n .50.(2014·山东·文 T19)在等差数列{a n }中,已知公差 d=2,a 2 是 a 1 与 a 4 的等比中项. (1)求数列{a n }的通项公式;(2)设 b n =a n (n+1),记 T n =-b 1+b 2-b 3+b 4-…+(-1)n b n ,求 T n .51.(2014·大纲全国·文 T17)数列{a n }满足 a 1=1,a 2=2,a n+2=2a n+1-a n +2.(1)设 b n =a n+1-a n ,证明{b n }是等差数列; (2)求{a n }的通项公式.52.(2014·全国 1·理 T17)已知数列{a n }的前 n 项和为 S n ,a 1=1,a n ≠0,a n a n+1=λS n -1,其中λ为常数. (1)证明:a n+2-a n =λ;(2)是否存在λ,使得{a n }为等差数列?并说明理由.53.(2013·全国 2·文 T17)已知等差数列{a n }的公差不为零,a 1=25,且 a 1,a 11,a 13 成等比数列. (1)求{a n }的通项公式; (2)求 a 1+a 4+a 7+…+a 3n-2.54.(2013·全国 1·文 T17)已知等差数列{a n }的前 n 项和 S n 满足 S 3=0,S 5=-5. (1)求{a n }的通项公式;(2)求数列{1项和.55.(2012·湖北·理 T18 文 T20)已知等差数列{a n }前三项的和为-3,前三项的积为 8.(1)求等差数列{a n }的通项公式;(2)若 a 2,a 3,a 1 成等比数列,求数列{|a n |}的前 n 项和.56.(2011·全国·文 T17)已知等比数列{a n }中,a 1=1,公比 q=1.(1)S n 为{a n }的前 n 项和,证明:S n =1 2a n ;(2)设 b n =log 3a 1+log 3a 2+…+log 3a n ,求数列{b n }的通项公式.57.(2011·全国·理 T17)等比数列{a n }的各项均为正数,且 2a 1+3a 2=1,a 3 =9a 2a 6.(1)求数列{a n }的通项公式;(2)设 b n =log 3a 1+log 3a 2+…+log 3a n ,求数列{}的前 n 项和.1 b n58.(2010·全国·理 T17)设数列{a n }满足 a 1=2,a n+1-a n =3·22n-1.(1)求数列{a n }的通项公式;(2)令 b n =na n ,求数列{b n }的前 n 项和 S n .59.(2010·全国·文 T17)设等差数列{a n }满足 a 3=5,a 10=-9, (1)求数列{a n }的通项公式;(2)求数列{a n }的前 n 项和 S n 及使得 S n 最大的序号 n 的值.2解得{ 1 故 a n =2n-5,S n =n 2-4n,故选 A. 2 2 21 2222222232 16 21616 16 × 1 +…>1+4+7>10,故选 A.a 1+a 2+a 3+a 4=a 1(1-q ),a 1+a 2+a 3=a 1(1-q ).十年高考真题分类汇编(2010—2019)数学专题 08 数列一、选择题1.(2019·全国 1·理 T9)记 S n 为等差数列{a n }的前 n 项和.已知 S 4=0,a 5=5,则()A.a n =2n-5C.S n =2n 2-8nB.a n =3n-10D.S n =1n 2-2n【答案】A【解析】由题意可知,{ S 4 = 4a 1 + 4×3 ·d = 0,a 5 = a 1 + 4d = 5,a = -3, d = 2.2.(2019·浙江·T10)设 a,b∈R,数列{a n }满足 a 1=a,a n+1=a n +b,n∈N *,则()A.当 b=1时,a 10>10C.当 b=-2 时,a 10>10B.当 b=4时,a 10>10D.当 b=-4 时,a 10>10【答案】A【解析】当b= 1 时 ,a 2= a 1 + 1 ≥ 1 ,a 3= a 2 + 1 ≥ 4 ,a 4= a 3 + 1 ≥ 17 ≥1,当 n≥4 时,a n+1= a n + 1≥ a n ≥1,则lo g 17 a n+1>2lo g 17 a n ⇒lo g 17 a n+1>2n-1, 则 a n+1≥ ( 17 )1616162n -1(n≥4), 则 a 10≥ ( 17 ) 26 = ( 1+ 16 ) 64=1+ 64 +64×63 2 1623.(2018·全国 1·理 T4)记 S n 为等差数列{a n }的前 n 项和,若 3S 3=S 2+S 4,a 1=2,则 a 5=()A.-12B.-10C.10D.12【答案】B【解析】因为 3S 3=S 2+S 4,所以 3S 3=(S 3-a 3)+(S 3+a 4),即 S 3=a 4-a 3.设公差为 d,则 3a 1+3d=d,又由 a 1=2,得 d=-3,所以 a 5=a 1+4d=-10.4.(2018·浙江·T10)已知 a 1,a 2,a 3,a 4 成等比数列,且 a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3).若 a 1>1,则( )A.a 1<a 3,a 2<a 4B.a 1>a 3,a 2<a 4C.a 1<a 3,a 2>a 4D.a 1>a 3,a 2>a 4【答案】B【解析】设等比数列的公比为 q,则4 3 1-q1-q3 3 a n , 由题意 , an = 12√2(n≥2),所以 {a n } 为等比数列 , 因为 a 1=f,所以为 n,则前 n 组的项数和为n (1n ).第 n 组的和为1-2 =2n -1,前 n 组总共的和为2(1-2 )-n=2n+1-2-n.∵a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3),∴a 1+a 2+a 3=e a 1a2a 3a4,即 a 1(1+q+q 2)=e a 1(1qq2q 3).又 a 1>1,∴q<0.假设 1+q+q 2>1,即 q+q 2>0,解得 q<-1(q>0 舍去).由 a 1>1,可知 a 1(1+q+q 2)>1,∴a 1(1+q+q 2+q 3)>0,即 1+q+q 2+q 3>0,即(1+q)+q 2(1+q)>0,即(1+q)(1+q 2)>0,这与 q<-1 相矛盾.∴1+q+q 2<1,即-1<q<0.∴a 1>a 3,a 2<a 4.5.(2018·北京·理 T4 文 T5)“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于 12√2.若第一个单音的频率为 f,则第八个单音的频率为()A. √2fB. √22f C. 12√25fD. 12√27f【答案】D【解析】设第 n 个单音的频率为a n -1a 8=a 1×(12√2)7= 12√27f,故选 D.6.(2017·全国 1·理 T12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动 .这款软件的激活码为下面数学问题的答案 :已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是 20,接下来的两项是 20,21,再接下来的三项是 20,21,22,依此类推.求满足如下条件的最小整数 N:N>100 且该数列的前 N 项和为 2 的整数幂.那么该款软件的激活码是()A.440B.330C.220D.110【答案】A【解析】设数列的首项为第 1 组,接下来两项为第 2 组,再接下来三项为第 3 组,以此类推,设第 n 组的项数n n2 1-2 1-2由题意,N>100,令n (1n )>100,得 n≥14 且 n∈N *,即 N 出现在第 13 组之后.若要使最小整数 N 满足:N>100 且2前 N 项和为 2 的整数幂,则 S N -S n (1n )应与-2-n 互为相反数,即 2k -1=2+n(k∈N *,n≥14),所以 k=log 2(n+3),解 2得 n=29,k=5.22-a 3 31 3所以 N=29×(1+29 )+5=440,故选 A. 27.(2017·全国 3·理 T9)等差数列{a n }的首项为 1,公差不为 0.若 a 2,a 3,a 6 成等比数列,则{a n }前 6 项的和为( )A.-24B.-3C.3D.8【答案】A【解析】设等差数列的公差为 d,则 d≠0,a 23 =a 2·a 6,即(1+2d)2=(1+d)(1+5d),解得 d=-2,所以 S 6=6×1+6×5×(-2)=-24,故选 A.8.(2016·全国 1·理 T3)已知等差数列{a n }前 9 项的和为 27,a 10=8,则 a 100=()A.100B.99C.98D.97【答案】C【解析】因为 S 9=(a 1 +a9 )×9=27,a 1+a 9=2a 5,所以 a 5=3.又因为 a 10=8,所以 d=a 10-55=1.故 a 100=a 10+(100-10)×1=98.9.(2015·浙江·理 T13)已知{a n }是等差数列,公差 d 不为零,前 n 项和是 S n ,若 a 3,a 4,a 8 成等比数列,则( A.a 1d>0,dS 4>0 B.a 1d<0,dS 4<0 C.a 1d>0,dS 4<0 D.a 1d<0,dS 4>0【答案】B【解析】设{a n }的首项为 a 1,公差为 d,则 a 3=a 1+2d,a 4=a 1+3d,a 8=a 1+7d.∵a 3,a 4,a 8 成等比数列,∴(a 1+3d)2=(a 1+2d)(a 1+7d),即 3a 1d+5d 2=0.∵d≠0,∴a 1d=-5d 2<0,且 a 1=-5d.∵dS 4=4d(a 2+a 4)=2d(2a 1+3d)=-2d 2<0.10.(2015·全国 2·文 T5)设 S n 是等差数列{a n }的前 n 项和,若 a 1+a 3+a 5=3,则 S 5=()A.5B.7C.9D.11【答案】A【解析】由 a 1+a 3+a 5=3 及等差中项,得 3a 3=3,解得 a 3=1.故)2B.192C.10D.12【解析】由题意知a 1+a 3+a 5=1+q 2+q 4=21=7,解得 q 2=2(负值舍去).∴a 3+a 5+a 7=(a 1+a 3+a 5)q 2=21×2=42.a 1 222 2424 2S 5=5(a 1+a 5)=5a 3=5.11.(2015·全国 1·文 T7)已知{a n }是公差为 1 的等差数列,S n 为{a n }的前 n 项和.若 S 8=4S 4,则 a 10= ()A.17【答案】B【解析】∵公差 d=1,S 8=4S 4,∴8(a 1+a 8) = 4×4(a 1+a 4),22即 2a 1+7d=4a 1+6d,解得 a 1=1.∴a 10=a 1+9d=1+9=19.12.(2015·全国 2·理 T4)已知等比数列{a n }满足 a 1=3,a 1+a 3+a 5=21,则 a 3+a 5+a 7=()A.21B.42C.63D.84【答案】B313.(2015·全国 2·文 T9)已知等比数列{a n }满足 a 1=1,a 3a 5=4(a 4-1),则 a 2=()A.2B.1C. 12D.1 8【答案】C【解析】∵a 3a 5=4(a 4-1),∴a 4 =4(a 4-1),解得 a 4=2.又 a 4=a 1q 3,且 a 1=1,∴q=2.∴a 2=a 1q=1.14.(2014·大纲全国·文 T8)设等比数列{a n }的前 n 项和为 S n .若 S 2=3,S 4=15,则 S 6=()A.31B.32C.63D.64【答案】C【 解 析 】 由 等 比 数 列 前 n 项 和 的 性 质 , 得 S 2,S 4-S 2,S 6-S 4 成 等 比 数 列 , 所 以 (S 4-S 2)2=S 2(S 6-S 4), 即(15-3)2=3(S 6-15),解得 S 6=63,故选 C.15.(2014·全国 2·文 T5)等差数列{a n }的公差为 2,若 a 2,a 4,a 8 成等比数列,则{a n }的前 n 项和 S n =( )A.n(n+1)C.n (n+1)2【答案】AB.n(n-1)D.n (n -1)23B.-13C.19D.-1q 4 = 9 = 1.【解析】由 S 3=a 2+10a 1,得 a 1+a 2+a 3=a 2+10a 1,整理得 a 3=9a 1,所以 q 2= 3=9.由 a 5=9,得 a 1= a123=1-2a n【解析】S n =a 1(1-q )1-q=a 1-a n q3 1-2 2 = 5a ,c =3 2 = 7a ,a 2=a 1,b 2=3 1 6 6 2 = 13a , 同理,a 3=a 1,b 3=6 112 2 23 3 2 2 2a 1 a 16√152a 13 a 1612 2a 15 724【解析】∵a 2,a 4,a 8 成等比数列,∴ =a 2·a 8,即(a 1+6)2=(a 1+2)(a 1+14),解得 a 1=2.∴S n =na 1+n (n -1)d=2n+n 2-n=n 2+n=n(n+1).16.(2013·全国 2·理 T3)等比数列{a n }的前 n 项和为 S n .已知 S 3=a 2+10a 1,a 5=9,则 a 1=()A.19【答案】Ca a 5 92 9 17.(2013·全国 1·文 T6)设首项为 1,公比为2的等比数列{a n }的前 n 项和为 S n ,则( )A.S n =2a n -1B.S n =3a n -2C.S n =4-3a nD.S n =3-2a n【答案】Dn3=3-2a n .18.(2013·全国 1·理 T12)设 A △n B n C n 的三边长分别为 a n ,b n ,c △n ,A nB nC n 的面积为 S n ,n=1,2,3,….若b 1>c 1,b 1+c 1=2a 1,a n+1=a n ,b n+1=c n +a n ,c n+1=b n +a n ,则()A.{S n }为递减数列B.{S n }为递增数列C.{S 2n-1}为递增数列,{S 2n }为递减数列D.{S 2n-1}为递减数列,{S 2n }为递增数列 【答案】B【解析】因为 b 1>c 1,不妨设 b 1=4a 1,c 1=2a 1,p=1(a 1+b 1+c 1)=3a 1,则 S 1=√3a 1 · 2 · 6 · 5a 1= 12 a 21;2a +a 4a +a11 1121S 2=√3a 1 · 2 · 2a 1· 3 = √6 a 21;显然 S 2>S 1.7a +a115a +a c 3=6 12 1 = 11a 1,S 3=√3a 1 · 2 · 12 a 1· 12 a 1 = √105 a 21,显然 S 3>S 2.21 联立{a 4a = -8 可解得{a 4 = -2 或 {a 4 = 4,当{a 4 = -2时,q 3=-1, 2当{a 4 = 4时,q 3=-2,同理,有 a 1+a 10=-7. q 319.(2013·全国 1·理 T7)设等差数列{a n }的前 n 项和为 S n ,若 S m-1=-2,S m =0,S m+1=3,则 m= ()A.3B.4C.5D.6【答案】C【解析】∵S m-1=-2,S m =0,S m+1=3,∴a m =S m -S m-1=2,a m+1=S m+1-S m =3. ∴d=a m+1-a m =3-2=1.∵S m =m (a 1+a m ) = m (a 2+2)=0,∴a 1=-2,a m =-2+(m-1)×1=2.∴m=5.20.(2012·全国·理 T5)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则 a 1+a 10=( )A.7B.5C.-5D.-7【答案】D【解析】∵{a n }为等比数列,∴a 5a 6=a 4a 7=-8. a + a = 2, a = 4, a = -2, 4 777a = 4, 7故 a 1+a 10=a 4+a 7q 3=-7;a = -2, 721.(2012·全国·文 T12)数列{a n }满足 a n+1+(-1)n a n =2n-1,则{a n }的前 60 项和为()A.3 690B.3 660C.1 845D.1 830【答案】D【解析】∵a n+1+(-1)n a n =2n-1,∴a 2=1+a 1,a 3=2-a 1,a 4=7-a 1,a 5=a 1,a 6=9+a 1,a 7=2-a 1,a 8=15-a 1,a 9=a 1,a 10=17+a 1,a 11=2-a 1,a 12=23-a 1,…,a 57=a 1,a 58=113+a 1,a 59=2-a 1,a 60=119-a 1,∴a 1+a 2+…+a 60=(a 1+a 2+a 3+a 4)+(a 5+a 6+a 7+a 8)+…+(a 57+a 58+a 59+a 60) =10+26+42+…+234=15×(10+234)=1 830.二、填空题1.(2019·全国 3·文 T14)记 S n 为等差数列{a n }的前 n 项和.若 a 3=5,a 7=13,则 S 10=.【答案】100【解析】设等差数列{a n }的公差为 d,则{a 3 = a 1 + 6d = 13,解得{d 1= 2. 2.(2019·全国 3·理 T14)记 S n 为等差数列{a n }的前 n 项和.若 a 1≠0,a 2=3a 1,则S 10=.2 d=10×1+ 2S 5 =10a 1+10×9d5a 1+ 25.(2019·全国 1·文 T14)记 S n 为等比数列{a n }的前 n 项和.若 a 1=1,S 3= ,则 S 4=.4a = a + 2d = 5, a = 1,71故 S 10=10a 1+10×9 10×9×2=100.S 5【答案】4【解析】设等差数列{a n }的公差为 d.∵a 1≠0,a 2=3a 1, ∴a 1+d=3a 1,即 d=2a 1.∴S 102 5×4d = 100a 1=4. 25a 13.(2019·江苏·T 8)已知数列 {a n }(n ∈N *)是等差数列 ,S n 是其前 n 项和 .若 a 2a 5+a 8=0,S 9=27,则 S 8 的值是.【答案】16【解析】∵{a n }为等差数列,设公差为 d,a 2a 5+a 8=0,S 9=27,∴(a 1 + d )(a 1 + 4d ) + a 1 + 7d = 0,①{9×89a 1 + 2 d = 27,②整理②得 a 1+4d=3,即 a 1=3-4d,③把③代入①解得 d=2,∴a 1=-5. ∴S 8=8a 1+28d=16.4.(2019·北京·理 T10)设等差数列{a n }的前 n 项和为 S n .若 a 2=-3,S 5=-10,则 a 5= ,S n 的最小值为.【答案】0-10【解析】等差数列{a n }中,由 S 5=5a 3=-10,得 a 3=-2,又 a 2=-3,公差 d=a 3-a 2=1,a 5=a 3+2d=0,由等差数列{a n }的性质得当 n≤5 时,a n ≤0,当 n≥6 时,a n 大于 0,所以 S n 的最小值为 S 4 或 S 5,即为-10.3 4【答案】58【解析】设等比数列{a n }的公比为 q.S 3=a 1+a 1q+a 1q 2=1+q+q 2=3,即 q 2+q+1=0.解得 q=-1.42=1--1)1+1 323 32 93 ∴S 5=a 1(1-q )1-q=3(1-3 ) 3 S 6=-1(1-2 )=-63.9.(2018·上海·T10)设等比数列{a n } 的通项公式为a n =q n-1(n ∈N *), 前 n 项和为 S n , 若 lim S n = 1 , 则n →∞ a n+1【解析】由 a n =q n-1,得 a n+1=q n .当 q=1 时,不满足题意;当 q≠1 时,S n =a 1(1-q ) = 1-q .若 0<|q|<1,则 lim 不存在;若|q|>1,则 lim S n = lim = lim1-q = 1,解得 q=3.故 S 4=a 1 (1-q 4) 22 4 = 5. 86.(2019·全国 1·理 T14)记 S n 为等比数列{a n }的前 n 项和.若 a 1=1 , a 4 =a 6,则 S 5=________.【答案】1213【解析】设等比数列{a n }的公比为 q,则 a 4=a 1q 3=1q 3,a 6=a 1q 5=1q 5.∵a 4 =a 6,∴1q 6=1q 5.∵q≠0,∴q=3.5 1 51-3 = 121.7.(2018·全国 1·理 T14)记 S n 为数列{a n }的前 n 项和.若 S n =2a n +1,则 S 6=.【答案】-63【解析】∵S n =2a n +1,①∴S n-1=2a n-1+1(n≥2).②①-②,得 a n =2a n -2a n-1,即 a n =2a n-1(n≥2).又 S 1=2a 1+1,∴a 1=-1.∴{a n }是以-1 为首项,2 为公比的等比数列,则6 1-28.(2018·北京·理 T9)设{a n }是等差数列,且 a 1=3,a 2+a 5=36,则{a n }的通项公式为.【答案】a n =6n-3【解析】∵{a n }为等差数列,设公差为 d, ∴a 2+a 5=2a 1+5d=36.∵a 1=3,∴d=6.∴a n =3+(n-1)×6=6n -3.2q=.【答案】3nn 1-q1-q1-q nn →∞ (1-q )q n1-q n 1 n →∞ a n+1n →∞ (1-q )q nn →∞ (1-q ) · 1 -1)=- 1q n 211.(2017·全国 2·理 T15)等差数列{a n }的前 n 项和为 S n ,a 3=3,S 4=10,则 ∑ 1=____________.a 1,10, d 1.n (n+1)=2(1 - 1 ). 2 22所以 ∑ 1 =2[(1- 1) + (1 - 1)+…+(1 - 1 )]=2(1- 1 ) n2nk1 S k得{ 1 解得{q 1 -2,故 a 4=a 1q 3=-8.744 710.(2018·江苏·T 14)已知集合 A={x|x=2n-1,n∈N *},B={x|x=2n ,n∈N *}.将 A∪B 的所有元素从小到大依次排列构成一个数列{a n }.记 S n 为数列{a n }的前 n 项和,则使得 S n >12a n+1 成立的 n 的最小值为.【答案】27【解析】①若 a n+1=2k (k∈N *),则 S n =21+22+…+2k-1+1+3+…+2k -1=2k -2+(2k-1)2⇒(2k-1)2+2k -2>12·2k .令 2k =t ⇒1t 2+t-2>12t ⇒t(t-44)>8.4∴t≥64⇒k≥6.此时,n=k-1+2k-1=37.②若 a n+1=2k+1(k∈N *),则 S n =21+22+…+2t +1+3+…+2k -1(2t <2k+1,t∈N *), ∴S n =2t+1-2+k 2>12(2k+1)⇒2t+1>-k 2+24k+14. ∴-k 2+24k+14<2t+1<4k+2⇒k(k-20)>12.取 k=21,此时77<2t <43(舍),取 k=22,29<2t <45,t=5,n=5+22=27.2由①②,得 n min =27.n k1 S k【答案】 2nn+1【解析】设等差数列的首项为 a 1,公差为 d,由题意可知{所以 S n =na 1+n (n -1)d=n (1+n ).所以 12 S n n n+1 a 1 + 2d 3,4a 1 + 4×3 d解得{ 1.22 3 n n+1 n+1 n+112.(2017·全国 3·理 T14)设等比数列{a n }满足 a 1+a 2=-1,a 1-a 3=-3,则 a 4=.【答案】-8【解析】设{a n }的公比为 q,则由题意, a (1 + q )-1, a1,a 1(1-q 2) -3,13.(2017·江苏·理 T9 文 T9)等比数列{a n }的各项均为实数,其前 n 项和为 S n .已知 S 3=4,S 6=63,则 a 8=.【答案】32【解析】设该等比数列的公比为 q,则 S 6-S 3=63 − 4=14,即 a 4+a 5+a 6=14.①。
【必刷十年真题】专题07 数列-高考数学(理)(2010-2019)(新课标Ⅰ卷)(原卷版+解析版)
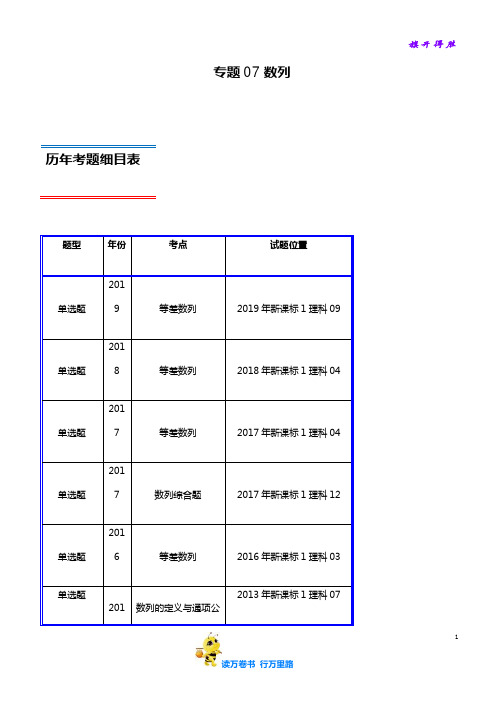
为(
)
A.1 B.2 C.4 D.8
3 读万卷书 行万里路
旗开得胜
4.【2017 年新课标 1 理科 12】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习
数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
已知数列 1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是 20,接下来的两项是
16.已知数列{an} 满足
2(n
+ 1)an
−
nan+1
=
0,
a1
=
4
,则数列
(n
+ 1)
an (
+
2)
的前
n
项和为___________.
17.定义:从数列{an}中抽取 m(m ∈ N, m ≥ 3) 项按其在{an}中的次序排列形成一个新数列{bn} ,则称{bn} 为{an}的子数列;若{bn} 成等差(或等比),则称{bn} 为{an}的等差(或等比)子数列.
20,21,再接下来的三项是 20,21,22,依此类推.求满足如下条件的最小整数 N:N>100 且该数列的
前 N 项和为 2 的整数幂.那么该款软件的激活码是(
)
A.440 B.330 C.220 D.110 5.【2016 年新课标 1 理科 03】已知等差数列{an}前 9 项的和为 27,a10=8,则 a100=( )
5 读万卷书 行万里路
(Ⅱ)是否存在 λ,使得{an}为等差数列?并说明理由.
旗开得胜
16.【2011 年新课标 1 理科 17】等比数列{an}的各项均为正数,且 2a1+3a2=1,a32=9a2a6, (Ⅰ)求数列{an}的通项公式; (Ⅱ)设 bn=log3a1+log3a2+…+log3an,求数列{ }的前 n 项和.
(北京卷)十年真题(2010_2019)高考数学真题分类汇编专题07数列文(含解析)
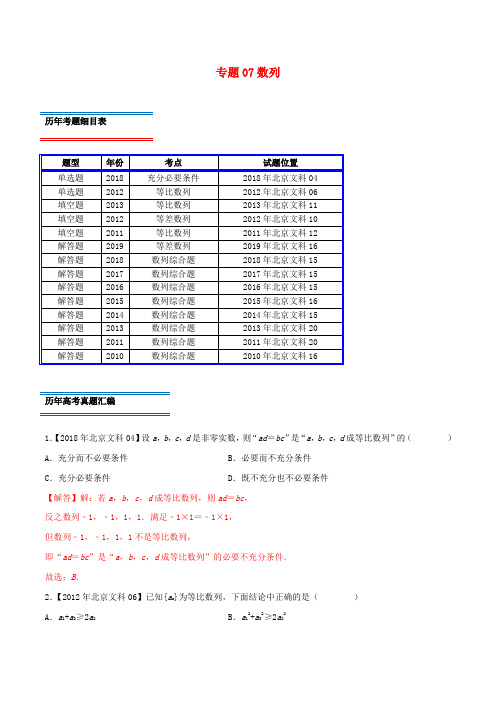
专题07数列历年考题细目表历年高考真题汇编1.【2018年北京文科04】设a,b,c,d是非零实数,则“ad=bc”是“a,b,c,d成等比数列”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:若a,b,c,d成等比数列,则ad=bc,反之数列﹣1,﹣1,1,1.满足﹣1×1=﹣1×1,但数列﹣1,﹣1,1,1不是等比数列,即“ad=bc”是“a,b,c,d成等比数列”的必要不充分条件.故选:B.2.【2012年北京文科06】已知{a n}为等比数列,下面结论中正确的是()A.a1+a3≥2a2B.a12+a32≥2a22C.若a1=a3,则a1=a2D.若a3>a1,则a4>a2【解答】解:设等比数列的公比为q,则a1+a3,当且仅当a2,q同为正时,a1+a3≥2a2成立,故A 不正确;,∴,故B正确;若a1=a3,则a1=a1q2,∴q2=1,∴q=±1,∴a1=a2或a1=﹣a2,故C不正确;若a3>a1,则a1q2>a1,∴a4﹣a2=a1q(q2﹣1),其正负由q的符号确定,故D不正确故选:B.3.【2013年北京文科11】若等比数列{a n}满足a2+a4=20,a3+a5=40,则公比q=;前n项和S n =.【解答】解:设等比数列{a n}的公比为q,∵a2+a4=a2(1+q2)=20①a3+a5=a3(1+q2)=40②∴①②两个式子相除,可得到 2即等比数列的公比q=2,将q=2带入①中可求出a2=4则a1 2∴数列{a n}时首项为2,公比为2的等比数列.∴数列{a n}的前n项和为:S n2n+1﹣2.故答案为:2,2n+1﹣2.4.【2012年北京文科10】已知{a n}为等差数列,S n为其前n项和,若a1,S2=a3,则a2=,S n =.【解答】解:根据{a n}为等差数列,S2=a1+a2=a3a2;∴d=a3﹣a2∴a2 1S n故答案为:1,5.【2011年北京文科12】在等比数列{a n}中,a1,a4=﹣4,则公比q=;a1+a2+…+a n=.【解答】解:q38∴q=﹣2;由a1,q=﹣2,得到:等比数列的前n项和S n=a1+a2+…+a n.故答案为:﹣2;6.【2019年北京文科16】设{a n}是等差数列,a1=﹣10,且a2+10,a3+8,a4+6成等比数列.(Ⅰ)求{a n}的通项公式;(Ⅱ)记{a n}的前n项和为S n,求S n的最小值.【解答】解:(Ⅰ)∵{a n}是等差数列,a1=﹣10,且a2+10,a3+8,a4+6成等比数列.∴(a3+8)2=(a2+10)(a4+6),∴(﹣2+2d)2=d(﹣4+3d),解得d=2,∴a n=a1+(n﹣1)d=﹣10+2n﹣2=2n﹣12.(Ⅱ)由a1=﹣10,d=2,得:S n=﹣10n n2﹣11n=(n)2,∴n=5或n=6时,S n取最小值﹣30.7.【2018年北京文科15】设{a n}是等差数列,且a1=ln2,a2+a3=5ln2.(Ⅰ)求{a n}的通项公式;(Ⅱ)求.【解答】解:(Ⅰ){a n}是等差数列,且a1=ln2,a2+a3=5ln2.可得:2a1+3d=5ln2,可得d=ln2,{a n}的通项公式;a n=a1+(n﹣1)d=nln2,(Ⅱ)2n,∴21+22+23+…+2n2n+1﹣2.8.【2017年北京文科15】已知等差数列{a n}和等比数列{b n}满足a1=b1=1,a2+a4=10,b2b4=a5.(Ⅰ)求{a n}的通项公式;(Ⅱ)求和:b1+b3+b5+…+b2n﹣1.【解答】解:(Ⅰ)等差数列{a n},a1=1,a2+a4=10,可得:1+d+1+3d=10,解得d=2,所以{a n}的通项公式:a n=1+(n﹣1)×2=2n﹣1.(Ⅱ)由(Ⅰ)可得a5=a1+4d=9,等比数列{b n}满足b1=1,b2b4=9.可得b3=3,或﹣3(舍去)(等比数列奇数项符号相同).∴q2=3,{b2n﹣1}是等比数列,公比为3,首项为1.b1+b3+b5+…+b2n﹣1.9.【2016年北京文科15】已知{a n}是等差数列,{b n}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.(1)求{a n}的通项公式;(2)设c n=a n+b n,求数列{c n}的前n项和.【解答】解:(1)设{a n}是公差为d的等差数列,{b n}是公比为q的等比数列,由b2=3,b3=9,可得q3,b n=b2q n﹣2=3•3n﹣2=3n﹣1;即有a1=b1=1,a14=b4=27,则d2,则a n=a1+(n﹣1)d=1+2(n﹣1)=2n﹣1;(2)c n=a n+b n=2n﹣1+3n﹣1,则数列{c n}的前n项和为(1+3+…+(2n﹣1))+(1+3+9+…+3n﹣1)n•2n=n2.10.【2015年北京文科16】已知等差数列{a n}满足a1+a2=10,a4﹣a3=2(1)求{a n}的通项公式;(2)设等比数列{b n}满足b2=a3,b3=a7,问:b6与数列{a n}的第几项相等?【解答】解:(I)设等差数列{a n}的公差为d.∵a4﹣a3=2,所以d=2∵a1+a2=10,所以2a1+d=10∴a1=4,∴a n=4+2(n﹣1)=2n+2(n=1,2,…)(II)设等比数列{b n}的公比为q,∵b2=a3=8,b3=a7=16,∴∴q=2,b1=4∴128,而128=2n+2∴n=63∴b6与数列{a n}中的第63项相等11.【2014年北京文科15】已知{a n}是等差数列,满足a1=3,a4=12,数列{b n}满足b1=4,b4=20,且{b n ﹣a n}为等比数列.(1)求数列{a n}和{b n}的通项公式;(2)求数列{b n}的前n项和.【解答】解:(1)∵{a n}是等差数列,满足a1=3,a4=12,∴3+3d=12,解得d=3,∴a n=3+(n﹣1)×3=3n.设等比数列{b n﹣a n}的公比为q,则q38,∴q=2,∴b n﹣a n=(b1﹣a1)q n﹣1=2n﹣1,∴b n=3n+2n﹣1(n=1,2,…).(2)由(1)知b n=3n+2n﹣1(n=1,2,…).∵数列{a n}的前n项和为n(n+1),数列{2n﹣1}的前n项和为12n﹣1,∴数列{b n}的前n项和为n(n+1)+2n﹣1.12.【2013年北京文科20】给定数列a1,a2,…,a n.对i=1,2,…,n﹣1,该数列前i项的最大值记为A i,后n﹣i项a i+1,a i+2,…,a n的最小值记为B i,d i=A i﹣B i.(Ⅰ)设数列{a n}为3,4,7,1,写出d1,d2,d3的值;(Ⅱ)设a1,a2,…,a n﹣1(n≥4)是公比大于1的等比数列,且a1>0.证明:d1,d2,…,d n﹣1是等比数列;(Ⅲ)设d1,d2,…,d n﹣1是公差大于0的等差数列,且d1>0.证明:a1,a2,…,a n﹣1是等差数列.【解答】解:(Ⅰ)当i=1时,A1=3,B1=1,故d1=A1﹣B1=2,同理可求d2=3,d3=6;(Ⅱ)由a1,a2,…,a n﹣1(n≥4)是公比q大于1的等比数列,且a1>0,则{a n}的通项为:a n=a1q n﹣1,且为单调递增的数列.于是当k=1,2,…n﹣1时,d k=A k﹣B k=a k﹣a k+1,进而当k=2,3,…n﹣1时, q为定值.∴d1,d2,…,d n﹣1是等比数列;(Ⅲ)设d为d1,d2,…,d n﹣1的公差,对1≤i≤n﹣2,因为B i≤B i+1,d>0,所以A i+1=B i+1+d i+1≥B i+d i+d>B i+d i=A i,又因为A i+1=max{A i,a i+1},所以a i+1=A i+1>A i≥a i.从而a1,a2,…,a n﹣1为递增数列.因为A i=a i(i=1,2,…n﹣1),又因为B1=A1﹣d1=a1﹣d1<a1,所以B1<a1<a2<…<a n﹣1,因此a n=B1.所以B1=B2=…=B n﹣1=a n.所以a i=A i=B i+d i=a n+d i,因此对i=1,2,…,n﹣2都有a i+1﹣a i=d i+1﹣d i=d,即a1,a2,…,a n﹣1是等差数列.13.【2011年北京文科20】若数列A n:a1,a2,…,a n(n≥2)满足|a k+1﹣a k|=1(k=1,2,…,n﹣1),则称A n为E数列,记S(A n)=a1+a2+…+a n.(Ⅰ)写出一个E数列A5满足a1=a3=0;(Ⅱ)若a1=12,n=2000,证明:E数列A n是递增数列的充要条件是a n=2011;(Ⅲ)在a1=4的E数列A n中,求使得S(A n)=0成立得n的最小值.【解答】解:(Ⅰ)0,1,0,1,0是一个满足条件的E数列A5(答案不唯一,0,﹣1,0,﹣1,0或0,±1,0,1,2或0,±1,0,﹣1,﹣2或0,±1,0,﹣1,0都满足条件的E数列A5)(Ⅱ)必要性:因为E数列A n是递增数列所以a k+1﹣a k=1(k=1,2, (1999)所以A n是首项为12,公差为1的等差数列.所以a2000=12+(2000﹣1)×1=2011充分性:由于a2000﹣a1999≤1a1999﹣a1998≤1…a2﹣a1≤1,所以a2000﹣a1≤1999,即a2000≤a1+1999又因为a1=12,a2000=2011所以a2000≤a1+1999故a k+1﹣a k=1>0(k=1,2,…,1999),即A n是递增数列.综上所述,结论成立.(Ⅲ)对首项为4的E数列A n,由于a2≥a1﹣1=3a3≥a2﹣1≥2…a8≥a7﹣1≥﹣3…所以a 1+a 2+…+a k >0(k =2,3,…,8),所以对任意的首项为4的E 数列A n ,若S (A n )=0,则必有n ≥9,又a 1=4的E 数列A 9:4,3,2,1,0,﹣1,﹣2,﹣3,﹣4满足S (A 9)=0, 所以n 的最小值是9.14.【2010年北京文科16】已知{a n }为等差数列,且a 3=﹣6,a 6=0. (Ⅰ)求{a n }的通项公式;(Ⅱ)若等比数列{b n }满足b 1=﹣8,b 2=a 1+a 2+a 3,求数列{b n }的前n 项和公式. 【解答】解:(Ⅰ)设等差数列{a n }的公差d . 因为a 3=﹣6,a 6=0所以解得a 1=﹣10,d =2所以a n =﹣10+(n ﹣1)•2=2n ﹣12 (Ⅱ)设等比数列{b n }的公比为q 因为b 2=a 1+a 2+a 3=﹣24,b 1=﹣8, 所以﹣8q =﹣24,即q =3,所以{b n }的前n 项和公式为考题分析与复习建议本专题考查的知识点为:数列的概念与简单表示法,等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.历年考题主要以选择填空或解答题题型出现.重点考查的知识点为:等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项等.预测明年本考点题目会比较稳定,备考方向以知识点等差数列及其前n 项和,等比数列及其前n 项和,数列求和,数列求通项为重点较佳.最新高考模拟试题1.等差数列{}n a ,等比数列{}n b ,满足111a b ==,53a b =,则9a 能取到的最小整数是( ) A .1-B .0C .2D .3【答案】B 【解析】等差数列{}n a 的公差设为d ,等比数列{}n b 的公比设为q ,0q ≠,由111a b ==,53a b =,可得214d q +=,则,可得9a 能取到的最小整数是0. 故选:B .2.中国古代数学名著《九章算术》中有这样一个问題:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马、“马主曰:“我马食半牛,”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟、羊主人说:“我羊所吃的禾苗只有马的一半,”马主人说:“我马所吃的禾苗只有牛的一半,“打算按此比例偿还,他们各应偿还多少?该问题中,1斗为10升,则马主人应偿还( )升粟? A .253B .503C .507D .1007【答案】D 【解析】因为5斗=50升,设羊、马、牛的主人应偿还的量分别为123,,a a a , 由题意可知其构成了公比为2的等比数列,且350S =则,解得1507a =, 所以马主人要偿还的量为:,故选D.3.我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将1,2,…,9填入33⨯的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数21,2,3,,n 填入n n ⨯个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做n 阶幻方.记n 阶幻方的对角线上的数字之和为n N ,如图三阶幻方的315N =,那么 9N 的值为( )A .41B .45C .369D .321【答案】C 【解析】根据题意可知,幻方对角线上的数成等差数列,,,,….故.故选:C4.设数列{}n a 的前n 项和为n S ,且11a =,则数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和是( ) A .290 B .920C .511D .1011【答案】C 【解析】由得,当2n ≥时,,整理得,所以{}n a 是公差为4的等差数列,又11a =,所以,从而,所以,数列13n S n ⎧⎫⎨⎬+⎩⎭的前10项的和.故选C .5.意大利数学家列昂那多·斐波那契以兔子繁殖为例,引入“兔子数列”:,即,此数列在现代物理“准晶体结构”、化学等都有着广泛的应用.若此数列被2整除后的余数构成一个新数列{}n a ,则数列{}n a 的前2019项的和为( ) A .672 B .673C .1346D .2019【答案】C 【解析】 由数列各项除以2的余数, 可得{}n a 为,所以{}n a 是周期为3的周期数列, 一个周期中三项和为1102++=, 因为,所以数列{}n a 的前2019项的和为,故选C.6.已知数列{}n a 是等比数列,数列{}n b 是等差数列,若,,则的值是( )A .1B .2C .2-D .【答案】D 【解析】{}n a 是等比数列6a ∴={}n b 是等差数列673b π∴=本题正确选项:D 7.已知数列{}n a 满足,设数列{}n b 满足:121n n n n b a a ++=,数列{}n b 的前n 项和为nT,若恒成立,则实数λ的取值范围为( )A .1[,)4+∞B .1(,)4+∞C .3[,)8+∞D .3(,)8+∞【答案】D 【解析】 解:数列{}n a 满足,①当2n ≥时,,②①﹣②得:12n a n n=, 故:22n a n =,数列{}n b满足:,则:,由于恒成立,故:,整理得:244n n λ+>+,因为在*n N ∈上单调递减,故当1n =时,所以38λ>. 故选:D .8.已知函数()y f x =的定义域为R ,当0x <时()1f x >,且对任意的实数,x y R ∈,等式成立,若数列{}n a 满足,且()10a f =,则下列结论成立的是( ) A . B . C .D .【答案】A 【解析】由,令0x =,1y =-,则0x <时,()1f x > ()11f ∴-> ()01f ∴= 11a ∴=当0x >时,令y x =-,则,即又()1f x -> ∴当0x >时,令21x x >,则21>0-x x,即()f x ∴在R 上单调递减又令1n =,212a =-;令2n =,32a =-;令3n =,41a = ∴数列{}n a 是以3为周期的周期数列,,,,()f x 在R 上单调递减,,,本题正确选项:A 9.在数列{}n a 中,,则2019a 的值为______.【答案】1 【解析】 因为所以,...,,各式相加,可得,,所以,20191a =,故答案为1. 10.已知正项等比数列{}n a 满足,若存在两项m a ,n a ,使得,则91m n+的最小值为__________. 【答案】2 【解析】正项等比数列{}n a 满足,,整理,得210+2q q -=,又0q >,解得,12q =,存在两项m a ,n a 使得1a ,,整理,得8m n +=,∴,则91m n+的最小值为2. 当且仅当9m n n m=取等号,但此时m ,*n N ∉.又8m n +=, 所以只有当6m =,2n =时,取得最小值是2. 故答案为:211.已知数列{}n a 满足对,都有成立,72a π=,函数()f x =,记()n n y f a =,则数列{}n y 的前13项和为______. 【答案】26 【解析】 解:对,都有成立,可令1m =即有,为常数,可得数列{}n a 为等差数列,函数,由,可得()f x 的图象关于点,22π⎛⎫⎪⎝⎭对称,,∴,∴可得数列{}n y 的前13项和为.故答案为:26.12.已知数列{}n a 的前n 项和为n S ,满足,则n a =_____.【答案】122n +- 【解析】由题意,数列{}n a 满足,则,两式相减可得,即整理得,即,即,当1n =时,1122S a =+,即1122a a =+,解得12a =-, 所以数列{}2n a -表示首项为124a -=-,公比为2的等比数列, 所以,所以122n n a +=-.13.等差数列{}n a 中,410a =且3a ,6a ,10a 成等比数列,数列{}n a 前20项的和20S =____ 【答案】200或330 【解析】设数列{}n a 的公差为d ,则,,由3610,,a a a 成等比数列,得23106a a a =,即,整理得,解得0d =或1d =,当0d =时,;当1d =时,,于是,故答案为200或330.14.已知正项等比数列{}n a 的前n 项和为n S .若,则631S S +取得最小值时,9S 的值为_______.【解析】由,得:q≠1,所以,化简得:,即,即,得32q =,化简得631S S +==,当11311a q q a -=-,即1a =时,631S S +取得最小值,所以=3故答案为:315.设数列{}n a 的前n 项和为n S ,且满足,则5S =____.【答案】3116【解析】 解:,可得1n =时,11a = ,2n ≥时,,又,两式相减可得121n n a -=,即112n n a -⎛⎫= ⎪⎝⎭,上式对1n =也成立,可得数列{}n a 是首项为1,公比为12的等比数列, 可得.故答案为:3116.16.已知数列{}n a 满足,则数列的前n 项和为___________.【答案】2222n n +-+【解析】由,得,所以数列n a n ⎧⎫⎨⎬⎩⎭是以1141a a ==为首项,2为公比的等比数列,于是,所以12n n a n +=⋅,因为,所以的前n 项和2222n n +=-+. 17.定义:从数列{}n a 中抽取项按其在{}n a 中的次序排列形成一个新数列{}n b ,则称{}n b 为{}n a 的子数列;若{}n b 成等差(或等比),则称{}n b 为{}n a 的等差(或等比)子数列. (1)记数列{}n a 的前n 项和为n S ,已知21n n S =-. ①求数列{}n a 的通项公式;②数列{}n a 是否存在等差子数列,若存在,求出等差子数列;若不存在,请说明理由. (2)已知数列{}n a 的通项公式为,证明:{}n a 存在等比子数列.【答案】(1)①12n n a -=;②见解析;(2)见证明【解析】解:(1)①因为21n n S =-,所以当1n =时,,当2n ≥时,,所以.综上可知:12n n a -=.②假设从数列{}n a 中抽3项成等差,则,即,化简得:.因为k l m <<,所以0l k ->,0m k ->,且l k -,m k -都是整数, 所以22l k -⨯为偶数,12m k -+为奇数,所以不成立.因此,数列{}n a 不存在三项等差子数列.若从数列{}n a 中抽项,其前三项必成等差数列,不成立.综上可知,数列{}n a 不存在等差子数列.(2)假设数列{}n a 中存在3项0n a +,0n a k ++,成等比.设0n a b +=,则b Q +∈,故可设qb p=(p 与q 是互质的正整数). 则需满足,即需满足,则需满足.取k q =,则2l k pq =+.此时,.故此时成立.因此数列{}n a 中存在3项0n a +,0n a k ++,成等比,所以数列{}n a 存在等比子数列.18.在等差数列{}n a 中,已知公差2d =,2a 是1a 与4a 的等比中项 (1)求数列{}n a 的通项公式; (2)若数列{}n b 满足,求数列{}n b 的通项公式;(3)令,数列{}n c 的前n 项和为n T .【答案】(1)2n a n =;(2);(3).【解析】(1)因为2a 是1a 与4a 的等比中项,所以,∴数列{}n a 的通项公式为2n a n =. (2)∵①∴②②-①得:,,故。
2010-2019十年高考数学真题分类汇编专题08 数列 学生版+解析版

十年高考真题分类汇编(2010—2019)数学专题08 数列一、选择题1.(2019·全国1·理T9)记S n 为等差数列{a n }的前n 项和.已知S 4=0,a 5=5,则( ) A.a n =2n-5 B.a n =3n-10C.S n =2n 2-8nD.S n =12n 2-2n2.(2019·浙江·T10)设a,b ∈R,数列{a n }满足a 1=a,a n+1=a n 2+b,n ∈N *,则( )A.当b=12时,a 10>10 B.当b=14时,a 10>10 C.当b=-2时,a 10>10D.当b=-4时,a 10>103.(2018·全国1·理T4)记S n 为等差数列{a n }的前n 项和,若3S 3=S 2+S 4,a 1=2,则a 5=( ) A.-12 B.-10 C.10D.124.(2018·浙江·T10)已知a 1,a 2,a 3,a 4成等比数列,且a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3).若a 1>1,则( ) A.a 1<a 3,a 2<a 4 B.a 1>a 3,a 2<a 4 C.a 1<a 3,a 2>a 4 D.a 1>a 3,a 2>a 45.(2018·北京·理T4文T5)“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于√212.若第一个单音的频率为f,则第八个单音的频率为( ) A.√23fB.√223fC.√2512fD.√2712f6.(2017·全国1·理T12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A.440B.330C.220D.1107.(2017·全国3·理T9)等差数列{a n }的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{a n }前6项的和为( ) A.-24 B.-3C.3D.88.(2016·全国1·理T3)已知等差数列{a n }前9项的和为27,a 10=8,则a 100=( )A.100B.99C.98D.979.(2015·浙江·理T13)已知{a n}是等差数列,公差d不为零,前n项和是S n,若a3,a4,a8成等比数列,则( )A.a1d>0,dS4>0B.a1d<0,dS4<0C.a1d>0,dS4<0D.a1d<0,dS4>010.(2015·全国2·文T5)设S n是等差数列{a n}的前n项和,若a1+a3+a5=3,则S5=( )A.5B.7C.9D.1111.(2015·全国1·文T7)已知{a n}是公差为1的等差数列,S n为{a n}的前n项和.若S8=4S4,则a10= ( )A.172B.192C.10D.1212.(2015·全国2·理T4)已知等比数列{a n}满足a1=3,a1+a3+a5=21,则a3+a5+a7=( )A.21B.42C.63D.8413.(2015·全国2·文T9)已知等比数列{a n}满足a1=14,a3a5=4(a4-1),则a2=()A.2B.1C.1D.114.(2014·大纲全国·文T8)设等比数列{a n}的前n项和为S n.若S2=3,S4=15,则S6=( )A.31B.32C.63D.6415.(2014·全国2·文T5)等差数列{a n}的公差为2,若a2,a4,a8成等比数列,则{a n}的前n项和S n=( )A.n(n+1)B.n(n-1)C.n(n+1)2D.n(n-1)216.(2013·全国2·理T3)等比数列{a n}的前n项和为S n.已知S3=a2+10a1,a5=9,则a1=( )A.13B.-13C.19D.-1917.(2013·全国1·文T6)设首项为1,公比为23的等比数列{a n}的前n项和为S n,则( )A.S n=2a n-1B.S n=3a n-2C.S n=4-3a nD.S n=3-2a n18.(2013·全国1·理T12)设△A n B n C n的三边长分别为a n,b n,c n,△A n B n C n的面积为S n,n=1,2,3,….若b1>c1,b1+c1=2a1,a n+1=a n,b n+1=c n+a n2,c n+1=b n+a n2,则()A.{S n}为递减数列B.{S n}为递增数列C.{S2n-1}为递增数列,{S2n}为递减数列D.{S 2n-1}为递减数列,{S 2n }为递增数列19.(2013·全国1·理T7)设等差数列{a n }的前n 项和为S n ,若S m-1=-2,S m =0,S m+1=3,则m= ( ) A.3 B.4 C.5 D.620.(2012·全国·理T5)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=( ) A.7 B.5 C.-5D.-721.(2012·全国·文T12)数列{a n }满足a n+1+(-1)na n =2n-1,则{a n }的前60项和为( ) A.3 690 B.3 660 C.1 845 D.1 830二、填空题1.(2019·全国3·文T14)记S n 为等差数列{a n }的前n 项和.若a 3=5,a 7=13,则S 10= .2.(2019·全国3·理T14)记S n 为等差数列{a n }的前n 项和.若a 1≠0,a 2=3a 1,则S10S 5= .3.(2019·江苏·T8)已知数列{a n }(n ∈N *)是等差数列,S n 是其前n 项和.若a 2a 5+a 8=0,S 9=27,则S 8的值是 . 4.(2019·北京·理T10)设等差数列{a n }的前n 项和为S n .若a 2=-3,S 5=-10,则a 5= ,S n 的最小值为 . 5.(2019·全国1·文T14)记S n 为等比数列{a n }的前n 项和.若a 1=1,S 3=34,则S 4= .6.(2019·全国1·理T14)记S n 为等比数列{a n }的前n 项和.若a 1=13,a 42=a 6,则S 5=________.7.(2018·全国1·理T14)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6= . 8.(2018·北京·理T9)设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为 .9.(2018·上海·T10)设等比数列{a n }的通项公式为a n =q n-1(n ∈N *),前n 项和为S n ,若lim n →∞S n a n+1=12,则q=.10.(2018·江苏·T14)已知集合A={x|x=2n-1,n ∈N *},B={x|x=2n ,n ∈N *}.将A ∪B 的所有元素从小到大依次排列构成一个数列{a n }.记S n 为数列{a n }的前n 项和,则使得S n >12a n+1成立的n 的最小值为 .11.(2017·全国2·理T15)等差数列{a n }的前n 项和为S n ,a 3=3,S 4=10,则∑k=1n1S k =____________.12.(2017·全国3·理T14)设等比数列{a n }满足a 1+a 2=-1,a 1-a 3=-3,则a 4= .13.(2017·江苏·理T9文T9)等比数列{a n }的各项均为实数,其前n 项和为S n .已知S 3=74,S 6=634,则a 8=. 14.(2016·浙江·理T13文T13)设数列{a n }的前n 项和为S n ,若S 2=4,a n+1=2S n +1,n ∈N *,则a 1= ,S 5= . 15.(2016·北京·理T12)已知{a n }为等差数列,S n 为其前n 项和.若a 1=6,a 3+a 5=0,则S 6= . 16.(2016·全国1·理T15)设等比数列{a n }满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为 . 17.(2015·全国1·文T13)在数列{a n }中,a 1=2,a n+1=2a n ,S n 为{a n }的前n 项和.若S n =126,则n= . 18.(2015·湖南·理T14)设S n 为等比数列{a n }的前n 项和,若a 1=1,且3S 1,2S 2,S 3成等差数列,则a n = . 19.(2015·福建·文T16)若a,b 是函数f(x)=x 2-px+q(p>0,q>0)的两个不同的零点,且a,b,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q 的值等于 . 20.(2015·江苏·理T11)设数列{a n }满足a 1=1,且a n+1- a n =n+1(n ∈N *).则数列{1a n}前10项的和为____________.21.(2015·全国2·理T16)设S n 是数列{a n }的前n 项和,且a 1=-1,a n+1=S n S n+1,则S n = . 22.(2015·广东·理T10)在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=25,则a 2+a 8= .23.(2015·陕西·文T13)中位数为1 010的一组数构成等差数列,其末项为2 015,则该数列的首项为 . 24.(2014·江苏·理T7)在各项均为正数的等比数列{a n }中,若a 2=1,a 8=a 6+2a 4,则a 6的值是 . 25.(2014·广东·文T13)等比数列{a n }的各项均为正数,且a 1a 5=4,则log 2a 1+log 2a 2+log 2a 3+log 2a 4+log 2a 5= .26.(2014·安徽·理T12)数列{a n }是等差数列,若a 1+1,a 3+3,a 5+5构成公比为q 的等比数列,则q= . 27.(2014·全国2·文T16)数列{a n }满足a n+1=11-a n,a 8=2,则a 1=____________.28.(2014·北京·理T12)若等差数列{a n }满足a 7+a 8+a 9>0,a 7+a 10<0,则当n= 时,{a n }的前n 项和最大. 29.(2014·天津·理T11)设{a n }是首项为a 1,公差为-1的等差数列,S n 为其前n 项和.若S 1,S 2,S 4成等比数列,则a 1的值为 .30.(2013·全国2·理T16)等差数列{a n }的前n 项和为S n ,已知S 10=0,S 15=25,则nS n 的最小值为 . 31.(2013·辽宁·理T14)已知等比数列{a n }是递增数列,S n 是{a n }的前n 项和.若a 1,a 3是方程x 2-5x+4=0的两个根,则S 6= .32.(2013·全国1·理T14)若数列{a n }的前n 项和S n =23a n +13,则{a n }的通项公式是a n = . 33.(2012·全国·文T14)等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q= . 三、计算题1.(2019·全国2·文T18)已知{a n }是各项均为正数的等比数列,a 1=2,a 3=2a 2+16. (1)求{a n }的通项公式;(2)设b n =log 2a n .求数列{b n }的前n 项和.2.(2019·全国2·理T19)已知数列{a n }和{b n }满足a 1=1,b 1=0,4a n+1=3a n -b n +4,4b n+1=3b n -a n -4. (1)证明:{a n +b n }是等比数列,{a n -b n }是等差数列; (2)求{a n }和{b n }的通项公式.3.(2019·天津·文T18)设{a n }是等差数列,{b n }是等比数列,公比大于0.已知a 1=b 1=3,b 2=a 3,b 3=4a 2+3. (1)求{a n }和{b n }的通项公式;(2)设数列{c n }满足c n ={1,n 为奇数,b n 2,n 为偶数,求a 1c 1+a 2c 2+…+a 2n c 2n (n ∈N *).4.(2019·天津·理T19)设{a n }是等差数列,{b n }是等比数列.已知a 1=4,b 1=6,b 2=2a 2-2,b 3=2a 3+4. (1)求{a n }和{b n }的通项公式;(2)设数列{c n }满足c 1=1,c n ={1,2k <n <2k+1,b k ,n =2k ,其中k ∈N *.①求数列{a 2n (c 2n -1)}的通项公式;②求∑i=12na i c i (n ∈N *).5.(2019·浙江·T 20)设等差数列{a n }的前n 项和为S n ,a 3=4,a 4=S 3.数列{b n }满足:对每个n ∈N *,S n +b n ,S n+1+b n ,S n+2+b n 成等比数列. (1)求数列{a n },{b n }的通项公式; (2)记c n =√a n n,n ∈N *,证明:c 1+c 2+…+c n <2√n ,n ∈N *. 6.(2019·江苏·T 20)定义首项为1且公比为正数的等比数列为“M- 数列”. (1)已知等比数列{a n }(n ∈N *)满足:a 2a 4=a 5,a 3-4a 2+4a 1=0,求证:数列{a n }为“M- 数列”; (2)已知数列{b n }(n ∈N *)满足:b 1=1,1S n=2b n−2b n+1,其中S n 为数列{b n }的前n 项和.①求数列{b n }的通项公式;②设m 为正整数.若存在“M- 数列”{c n }(n ∈N *),对任意正整数k,当k ≤m 时,都有c k ≤b k ≤c k+1成立,求m 的最大值.7.(2018·北京·文T15)设{a n }是等差数列,且a 1=ln 2,a 2+a 3=5ln 2. (1)求{a n }的通项公式; (2)求e a 1+e a 2+…+e a n .8.(2018·上海·T 21)给定无穷数列{a n },若无穷数列{b n }满足:对任意x ∈N *,都有|b n -a n |≤1,则称{b n }与{a n }“接近”.(1)设{a n }是首项为1,公比为12的等比数列,b n =a n+1+1,n ∈N *,判断数列{b n }是否与{a n }接近,并说明理由; (2)设数列{a n }的前四项为a 1=1,a 2=2,a 3=4,a 4=8,{b n }是一个与{a n }接近的数列,记集合M={x|x=b i ,i=1,2,3,4},求M 中元素的个数m:(3)已知{a n }是公差为d 的等差数列.若存在数列{b n }满足:{b n }与{a n }接近,且在b 2-b 1,b 3-b 2,…,b 201-b 200中至少有100个为正数,求d 的取值范围.9.(2018·江苏·T 20)设{a n }是首项为a 1,公差为d 的等差数列,{b n }是首项为b 1,公比为q 的等比数列.(1)设a 1=0,b 1=1,q=2,若|a n -b n |≤b 1对n=1,2,3,4均成立,求d 的取值范围;(2)若a 1=b 1>0,m ∈N *,q ∈(1, √2m],证明:存在d ∈R,使得|a n -b n |≤b 1对n=2,3,…,m+1均成立,并求d 的取值范围(用b 1,m,q 表示).10.(2018·天津·文T18)设{a n }是等差数列,其前n 项和为S n (n ∈N *);{b n }是等比数列,公比大于0,其前n 项和为T n (n ∈N *).已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6. (1)求S n 和T n ;(2)若S n +(T 1+T 2+…+T n )=a n +4b n ,求正整数n 的值.11.(2018·天津·理T18)设{a n }是等比数列,公比大于0,其前n 项和为S n (n ∈N *),{b n }是等差数列.已知a 1=1,a 3=a 2+2,a 4=b 3+b 5,a 5=b 4+2b 6. (1)求{a n }和{b n }的通项公式;(2)设数列{S n }的前n 项和为T n (n ∈N *), ①求T n ;②证明∑k=1n(T k +b k+2)b k(k+1)(k+2)=2n+2n+2-2(n ∈N *). 12.(2018·全国2·理T17文T17)记S n 为等差数列{a n }的前n 项和,已知a 1=-7,S 3=-15. (1)求{a n }的通项公式; (2)求S n ,并求S n 的最小值.13.(2018·全国1·文T17)已知数列{a n }满足a 1=1,na n+1=2(n+1)a n .设b n =an n. (1)求b 1,b 2,b 3;(2)判断数列{b n }是否为等比数列,并说明理由; (3)求{a n }的通项公式.14.(2018·全国3·理T17文T17)等比数列{a n }中,a 1=1,a 5=4a 3. (1)求{a n }的通项公式;(2)记S n 为{a n }的前n 项和,若S m =63,求m.15.(2017·全国1·文T17)设S n 为等比数列{a n }的前n 项和,已知S 2=2,S 3=-6. (1)求{a n }的通项公式;(2)求S n ,并判断S n+1,S n ,S n+2是否成等差数列.16.(2017·全国2·文T17)已知等差数列{a n }的前n 项和为S n ,等比数列{b n }的前n 项和为T n ,a 1=-1,b 1=1,a 2+b 2=2.(1)若a 3+b 3=5,求{b n }的通项公式;(2)若T3=21,求S3.17.(2017·全国3·文T17)设数列{a n}满足a1+3a2+…+(2n-1)a n=2n.(1)求{a n}的通项公式;}的前n项和.(2)求数列{a n2n+118.(2017·天津·理T18)已知{a n}为等差数列,前n项和为S n(n∈N*),{b n}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.(1)求{a n}和{b n}的通项公式;(2)求数列{a2n b2n-1}的前n项和(n∈N*).19.(2017·山东·理T19)已知{x n}是各项均为正数的等比数列,且x1+x2=3,x3-x2=2.(1)求数列{x n}的通项公式;(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P2(x2,2)…P n+1(x n+1,n+1)得到折线P1P2…P n+1,求由该折线与直线y=0,x=x1,x=x n+1所围成的区域的面积T n.20.(2017·山东·文T19)已知{a n}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.1)求数列{a n}的通项公式;}的前n项和T n.(2){b n}为各项非零的等差数列,其前n项和为S n.已知S2n+1=b n b n+1,求数列{b na n21.(2017·天津·文T18)已知{a n}为等差数列,前n项和为S n(n∈N*),{b n}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.(1)求{a n}和{b n}的通项公式;(2)求数列{a2n b n}的前n项和(n∈N*).22.(2016·全国2·理T17)S n为等差数列{a n}的前n项和,且a1=1,S7=28.记b n=[lg a n],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg 99]=1.(1)求b1,b11,b101;(2)求数列{b n}的前1 000项和.23.(2016·全国2·文T17)等差数列{a n }中,a 3+a 4=4,a 5+a 7=6. (1)求{a n }的通项公式;(2)设b n =[a n ],求数列{b n }的前10项和,其中[x]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2. 24.(2016·浙江·文T17)设数列{a n }的前n 项和为S n .已知S 2=4,a n+1=2S n +1,n ∈N *. (1)求通项公式a n ;(2)求数列{|a n -n-2|}的前n 项和.25.(2016·北京·文T15)已知{a n }是等差数列,{b n }是等比数列,且b 2=3,b 3=9,a 1=b 1,a 14=b 4. (1)求{a n }的通项公式;(2)设c n =a n +b n ,求数列{c n }的前n 项和.26.(2016·山东·理T18文T19)已知数列{a n }的前n 项和S n =3n 2+8n,{b n }是等差数列,且a n =b n +b n+1. (1)求数列{b n }的通项公式; (2)令c n =(a n +1)n+1(b n +2)n,求数列{c n }的前n 项和T n .27.(2016·天津·理T18)已知{a n }是各项均为正数的等差数列,公差为d.对任意的n ∈N *,b n 是a n 和a n+1的等比中项.(1)设c n =b n+12−b n 2,n ∈N *,求证:数列{c n }是等差数列;(2)设a 1=d,T n =∑k=12n(-1)kb k 2,n ∈N *,求证:∑k=1n1T k<12d 2.28.(2016·天津·文T18)已知{a n }是等比数列,前n 项和为S n (n ∈N *),且1a 1−1a 2=2a 3,S 6=63.(1)求{a n }的通项公式;(2)若对任意的n ∈N *,b n 是log 2a n 和log 2a n+1的等差中项,求数列{(-1)nb n 2}的前2n 项和.29.(2016·全国1·文T17)已知{a n }是公差为3的等差数列,数列{b n }满足b 1=1,b 2=13,a n b n+1+b n+1=nb n . (1)求{a n }的通项公式; (2)求{b n }的前n 项和.30.(2016·全国3·文T17)已知各项都为正数的数列{a n }满足a 1=1, a n 2-(2a n+1-1)a n -2a n+1=0. (1)求a 2,a 3;(2)求{a n }的通项公式.31.(2016·全国3·理T17)已知数列{a n }的前n 项和S n =1+λa n ,其中λ≠0. (1)证明{a n }是等比数列,并求其通项公式; (2)若S 5=3132,求λ.32.(2015·北京·文T16)已知等差数列{a n }满足a 1+a 2=10,a 4-a 3=2. (1)求{a n }的通项公式;(2)设等比数列{b n }满足b 2=a 3,b 3=a 7.问:b 6与数列{a n }的第几项相等? 33.(2015·重庆·文T16)已知等差数列{a n }满足a 3=2,前3项和S 3=92. (1)求{a n }的通项公式;(2)设等比数列{b n }满足b 1=a 1,b 4=a 15,求{b n }的前n 项和T n . 34.(2015·福建·文T17)等差数列{a n }中,a 2=4,a 4+a 7=15. (1)求数列{a n }的通项公式;(2)设b n =2a n -2+n,求b 1+b 2+b 3+…+b 10的值.35.(2015·全国1·理T17)S n 为数列{a n }的前n 项和.已知a n >0,a n 2+2a n =4S n +3.(1)求{a n }的通项公式;(2)设b n =1a n a n+1,求数列{b n }的前n 项和.36.(2015·安徽·文T18)已知数列{a n }是递增的等比数列,且a 1+a 4=9,a 2a 3=8. (1)求数列{a n }的通项公式;(2)设S n 为数列{a n }的前n 项和,b n =an+1S n S n+1,求数列{b n }的前n 项和T n .37.(2015·天津·理T18)已知数列{a n }满足a n+2=qa n (q 为实数,且q ≠1),n ∈N *,a 1=1,a 2=2,且a 2+a 3,a 3+a 4,a 4+a 5成等差数列.(1)求q 的值和{a n }的通项公式;(2)设b n =log 2a2n a 2n -1,n ∈N *,求数列{b n }的前n 项和.38.(2015·山东·文T19)已知数列{a n }是首项为正数的等差数列,数列{1a n ·a n+1}的前n 项和为n2n+1.(1)求数列{a n }的通项公式;(2)设b n =(a n +1)·2a n ,求数列{b n }的前n 项和T n .39.(2015·浙江·文T17)已知数列{a n }和{b n }满足a 1=2,b 1=1,a n+1=2a n (n ∈N *),b 1+12b 2+13b 3+…+1n b n =b n+1-1(n ∈N *). (1)求a n 与b n ;(2)记数列{a n b n }的前n 项和为T n ,求T n .40.(2015·天津·文T18)已知{a n }是各项均为正数的等比数列,{b n }是等差数列,且a 1=b 1=1,b 2+b 3=2a 3,a 5-3b 2=7. (1)求{a n }和{b n }的通项公式;(2)设c n=a n b n,n∈N*,求数列{c n}的前n项和.41.(2015·湖北·文T19)设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式;(2)当d>1时,记c n=a nb n,求数列{c n}的前n项和T n.42.(2014·全国2·理T17)已知数列{a n}满足a1=1,a n+1=3a n+1.(1)证明:{a n+12}是等比数列,并求{a n}的通项公式;(2)证明:1a1+1a2+…+1a n<32.43.(2014·福建·文T17)在等比数列{a n}中,a2=3,a5=81.(1)求a n;(2)设b n=log3a n,求数列{b n}的前n项和S n.44.(2014·湖南·文T16)已知数列{a n}的前n项和S n=n 2+n,n∈N*.(1)求数列{a n}的通项公式;(2)设b n=2a n+(-1)n a n,求数列{b n}的前2n项和.45.(2014·北京·文T14)已知{a n}是等差数列,满足a1=3,a4=12,数列{b n}满足b1=4,b4=20,且{b n-a n}为等比数列.(1)求数列{a n}和{b n}的通项公式;(2)求数列{b n}的前n项和.46.(2014·大纲全国·理T18)等差数列{a n}的前n项和为S n.已知a1=10,a2为整数,且S n≤S4.(1)求{a n}的通项公式;(2)设b n=1a n a n+1,求数列{b n}的前n项和T n.47.(2014·山东·理T19)已知等差数列{a n}的公差为2,前n项和为S n,且S1,S2,S4成等比数列.(1)求数列{a n}的通项公式;(2)令b n=(-1)n-14na n a n+1,求数列{b n}的前n项和T n.48.(2014·全国1·文T17)已知{a n}是递增的等差数列,a2,a4是方程x2-5x+6=0的根.(1)求{a n}的通项公式;(2)求数列{ann }的前n 项和.49.(2014·安徽·文T18)数列{a n }满足a 1=1,na n+1=(n+1)a n +n(n+1),n ∈N *.(1)证明:数列{an}是等差数列;(2)设b n =3n·√a n ,求数列{b n }的前n 项和S n .50.(2014·山东·文T19)在等差数列{a n }中,已知公差d=2,a 2是a 1与a 4的等比中项. (1)求数列{a n }的通项公式; (2)设b n =a n (n+1)2,记T n =-b 1+b 2-b 3+b 4-…+(-1)nb n ,求T n .51.(2014·大纲全国·文T17)数列{a n }满足a 1=1,a 2=2,a n+2=2a n+1-a n +2. (1)设b n =a n+1-a n ,证明{b n }是等差数列; (2)求{a n }的通项公式.52.(2014·全国1·理T17)已知数列{a n }的前n 项和为S n ,a 1=1,a n ≠0,a n a n+1=λS n -1,其中λ为常数. (1)证明:a n+2-a n =λ;(2)是否存在λ,使得{a n }为等差数列?并说明理由.53.(2013·全国2·文T17)已知等差数列{a n }的公差不为零,a 1=25,且a 1,a 11,a 13成等比数列. (1)求{a n }的通项公式; (2)求a 1+a 4+a 7+…+a 3n-2.54.(2013·全国1·文T17)已知等差数列{a n }的前n 项和S n 满足S 3=0,S 5=-5. (1)求{a n }的通项公式; (2)求数列{1a2n -1a 2n+1}的前n项和.55.(2012·湖北·理T18文T20)已知等差数列{a n }前三项的和为-3,前三项的积为8. (1)求等差数列{a n }的通项公式;(2)若a 2,a 3,a 1成等比数列,求数列{|a n |}的前n 项和. 56.(2011·全国·文T17)已知等比数列{a n }中,a 1=13,公比q=13. (1)S n 为{a n }的前n 项和,证明:S n =1-a n2; (2)设b n =log 3a 1+log 3a 2+…+log 3a n ,求数列{b n }的通项公式.57.(2011·全国·理T17)等比数列{a n }的各项均为正数,且2a 1+3a 2=1,a 32=9a 2a 6.(1)求数列{a n }的通项公式;(2)设b n=log3a1+log3a2+…+log3a n,求数列{1b n}的前n项和. 58.(2010·全国·理T17)设数列{a n}满足a1=2,a n+1-a n=3·22n-1.(1)求数列{a n}的通项公式;(2)令b n=na n,求数列{b n}的前n项和S n.59.(2010·全国·文T17)设等差数列{a n}满足a3=5,a10=-9,(1)求数列{a n}的通项公式;(2)求数列{a n}的前n项和S n及使得S n最大的序号n的值.十年高考真题分类汇编(2010—2019)数学专题08 数列一、选择题1.(2019·全国1·理T9)记S n 为等差数列{a n }的前n 项和.已知S 4=0,a 5=5,则( ) A.a n =2n-5 B.a n =3n-10C.S n =2n 2-8n D.S n =12n 2-2n【答案】A【解析】由题意可知,{S 4=4a 1+4×32·d =0,a 5=a 1+4d =5,解得{a 1=-3,d =2.故a n =2n-5,S n =n 2-4n,故选A.2.(2019·浙江·T10)设a,b ∈R,数列{a n }满足a 1=a,a n+1=a n 2+b,n ∈N *,则( )A.当b=12时,a 10>10 B.当b=14时,a 10>10 C.当b=-2时,a 10>10 D.当b=-4时,a 10>10【答案】A【解析】当b=12时,a 2=a 12+12≥12,a 3=a 22+12≥34,a 4=a 32+12≥1716≥1,当n≥4时,a n+1=a n 2+12≥a n 2≥1,则lo g 1716a n+1>2lo g 1716a n ⇒lo g 1716a n+1>2n-1,则a n+1≥(1716 )2n -1(n≥4),则a 10≥(1716) 26=(1+116)64=1+6416+64×632×1162+…>1+4+7>10,故选A. 3.(2018·全国1·理T4)记S n 为等差数列{a n }的前n 项和,若3S 3=S 2+S 4,a 1=2,则a 5=( ) A.-12 B.-10 C.10 D.12【答案】B【解析】因为3S 3=S 2+S 4,所以3S 3=(S 3-a 3)+(S 3+a 4),即S 3=a 4-a 3.设公差为d,则3a 1+3d=d,又由a 1=2,得d=-3,所以a 5=a 1+4d=-10.4.(2018·浙江·T10)已知a 1,a 2,a 3,a 4成等比数列,且a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3).若a 1>1,则( ) A.a 1<a 3,a 2<a 4 B.a 1>a 3,a 2<a 4 C.a 1<a 3,a 2>a 4 D.a 1>a 3,a 2>a 4 【答案】B【解析】设等比数列的公比为q,则 a 1+a 2+a 3+a 4=a 1(1-q 4)1-q ,a 1+a 2+a 3=a 1(1-q 3)1-q.∵a 1+a 2+a 3+a 4=ln(a 1+a 2+a 3),∴a 1+a 2+a 3=e a 1+a 2+a 3+a 4,即a 1(1+q+q 2)=e a 1(1+q+q2+q 3).又a 1>1,∴q<0.假设1+q+q 2>1,即q+q 2>0,解得q<-1(q>0舍去). 由a 1>1,可知a 1(1+q+q 2)>1, ∴a 1(1+q+q 2+q 3)>0,即1+q+q 2+q 3>0,即(1+q)+q 2(1+q)>0,即(1+q)(1+q 2)>0,这与q<-1相矛盾. ∴1+q+q 2<1,即-1<q<0.∴a 1>a 3,a 2<a 4.5.(2018·北京·理T4文T 5)“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于√212.若第一个单音的频率为f,则第八个单音的频率为( ) A.√23f B.√223fC.√2512fD.√2712f【答案】D【解析】设第n 个单音的频率为a n ,由题意,a na n -1=√212(n≥2),所以{a n }为等比数列,因为a 1=f,所以a 8=a 1×(√212)7=√2712f,故选D.6.(2017·全国1·理T12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是( )A.440B.330C.220D.110 【答案】A【解析】设数列的首项为第1组,接下来两项为第2组,再接下来三项为第3组,以此类推,设第n 组的项数为n,则前n组的项数和为n (1+n )2.第n 组的和为1-2n 1-2=2n -1,前n 组总共的和为2(1-2n )1-2-n=2n+1-2-n.由题意,N>100,令n (1+n )2>100,得n≥14且n ∈N *,即N 出现在第13组之后.若要使最小整数N 满足:N>100且前N 项和为2的整数幂,则S N -S n (1+n )2应与-2-n 互为相反数,即2k-1=2+n(k ∈N *,n≥14),所以k=log 2(n+3),解得n=29,k=5.所以N=29×(1+29)2+5=440,故选A. 7.(2017·全国3·理T9)等差数列{a n }的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{a n }前6项的和为( ) A.-24 B.-3 C.3 D.8【答案】A【解析】设等差数列的公差为d,则d≠0,a 32=a 2·a 6, 即(1+2d)2=(1+d)(1+5d), 解得d=-2,所以S 6=6×1+6×52×(-2)=-24,故选A.8.(2016·全国1·理T3)已知等差数列{a n }前9项的和为27,a 10=8,则a 100=( ) A.100 B.99 C.98 D.97【答案】C 【解析】因为S 9=(a 1+a 9)×9=27,a 1+a 9=2a 5, 所以a 5=3.又因为a 10=8,所以d=a 10-a 510-5=1. 故a 100=a 10+(100-10)×1=98.9.(2015·浙江·理T13)已知{a n }是等差数列,公差d 不为零,前n 项和是S n ,若a 3,a 4,a 8成等比数列,则( ) A.a 1d>0,dS 4>0 B.a 1d<0,dS 4<0 C.a 1d>0,dS 4<0 D.a 1d<0,dS 4>0【答案】B【解析】设{a n }的首项为a 1,公差为d,则a 3=a 1+2d,a 4=a 1+3d,a 8=a 1+7d. ∵a 3,a 4,a 8成等比数列,∴(a 1+3d)2=(a 1+2d)(a 1+7d),即3a 1d+5d 2=0. ∵d≠0,∴a 1d=-53d 2<0,且a 1=-53d. ∵dS 4=4d (a 1+a 4)2=2d(2a 1+3d)=-23d 2<0. 10.(2015·全国2·文T5)设S n 是等差数列{a n }的前n 项和,若a 1+a 3+a 5=3,则S 5=( ) A.5 B.7 C.9 D.11 【答案】A【解析】由a 1+a 3+a 5=3及等差中项,得3a 3=3,解得a 3=1.故S 5=5(a 1+a 5)2=5a 3=5. 11.(2015·全国1·文T7)已知{a n }是公差为1的等差数列,S n 为{a n }的前n 项和.若S 8=4S 4,则a 10= ( ) A.172B.192C.10D.12【答案】B【解析】∵公差d=1,S 8=4S 4, ∴8(a 1+a 8)2=4×4(a 1+a 4)2, 即2a 1+7d=4a 1+6d,解得a 1=12. ∴a 10=a 1+9d=1+9=19.12.(2015·全国2·理T4)已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7=( ) A.21B.42C.63D.84【答案】B 【解析】由题意知a 1+a 3+a 5a 1=1+q 2+q 4=213=7,解得q 2=2(负值舍去).∴a 3+a 5+a 7=(a 1+a 3+a 5)q 2=21×2=42.13.(2015·全国2·文T9)已知等比数列{a n }满足a 1=14,a 3a 5=4(a 4-1),则a 2=( ) A.2 B.1C.12D.18【答案】C【解析】∵a 3a 5=4(a 4-1),∴a 42=4(a 4-1),解得a 4=2.又a 4=a 1q 3,且a 1=14,∴q=2.∴a 2=a 1q=12.14.(2014·大纲全国·文T8)设等比数列{a n }的前n 项和为S n .若S 2=3,S 4=15,则S 6=( ) A.31 B.32 C.63 D.64【答案】C【解析】由等比数列前n 项和的性质,得S 2,S 4-S 2,S 6-S 4成等比数列,所以(S 4-S 2)2=S 2(S 6-S 4),即(15-3)2=3(S 6-15),解得S 6=63,故选C.15.(2014·全国2·文T5)等差数列{a n }的公差为2,若a 2,a 4,a 8成等比数列,则{a n }的前n 项和S n =( ) A.n(n+1) B.n(n-1)C.n (n+1)2D.n (n -1)2【答案】A【解析】∵a 2,a 4,a 8成等比数列, ∴ =a 2·a 8,即(a 1+6)2=(a 1+2)(a 1+14), 解得a 1=2. ∴S n =na 1+n (n -1)2d=2n+n 2-n=n 2+n=n(n+1). 16.(2013·全国2·理T3)等比数列{a n }的前n 项和为S n .已知S 3=a 2+10a 1,a 5=9,则a 1=( ) A.13 B.-13C.19D.-19【答案】C【解析】由S 3=a 2+10a 1,得a 1+a 2+a 3=a 2+10a 1,整理得a 3=9a 1,所以q 2=a 3a 1=9.由a 5=9,得a 1=a 5q 4=992=19.17.(2013·全国1·文T6)设首项为1,公比为2的等比数列{a n }的前n 项和为S n ,则( ) A.S n =2a n -1 B.S n =3a n -2 C.S n =4-3a n D.S n =3-2a n 【答案】D【解析】S n =a 1(1-q n )1-q=a 1-a n q 1-q=1-23a n 1-23=3-2a n .18.(2013·全国1·理T12)设△A n B n C n 的三边长分别为a n ,b n ,c n ,△A n B n C n 的面积为S n ,n=1,2,3,….若 b 1>c 1,b 1+c 1=2a 1,a n+1=a n ,b n+1=c n +a n ,c n+1=b n +an ,则( ) A.{S n }为递减数列 B.{S n }为递增数列C.{S 2n-1}为递增数列,{S 2n }为递减数列D.{S 2n-1}为递减数列,{S 2n }为递增数列 【答案】B【解析】因为b 1>c 1,不妨设b 1=4a 13,c 1=2a 13,p=12(a 1+b 1+c 1)=32a 1,则S 1=√3a 12·a 12·a 16·5a16=√1512a 12; a 2=a 1,b 2=23a 1+a 12=56a 1,c 2=43a 1+a 12=76a 1,S 2=√3a12·a12·2a13·a13=√66a 12;显然S 2>S 1.同理,a 3=a 1,b 3=76a 1+a 12=1312a 1,c 3=56a 1+a 12=1112a 1,S 3=√3a12·a12·512a 1·712a 1=√10524a 12,显然S 3>S 2.19.(2013·全国1·理T7)设等差数列{a n }的前n 项和为S n ,若S m-1=-2,S m =0,S m+1=3,则m= ( ) A.3 B.4 C.5 D.6 【答案】C【解析】∵S m-1=-2,S m =0,S m+1=3, ∴a m =S m -S m-1=2,a m+1=S m+1-S m =3. ∴d=a m+1-a m =3-2=1. ∵S m =m (a 1+a m )2=m (a 1+2)2=0, ∴a 1=-2,a m =-2+(m-1)×1=2.∴m=5.20.(2012·全国·理T5)已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=( ) A.7 B.5 C.-5 D.-7【答案】D【解析】∵{a n }为等比数列,∴a 5a 6=a 4a 7=-8. 联立{a 4+a 7=2,a 4a 7=-8可解得{a 4=4,a 7=-2或{a 4=-2,a 7=4,当{a 4=4,a 7=-2时,q 3=-12, 故a 1+a 10=a4q 3+a 7q 3=-7;当{a 4=-2,a 7=4时,q 3=-2,同理,有a 1+a 10=-7. 21.(2012·全国·文T12)数列{a n }满足a n+1+(-1)na n =2n-1,则{a n }的前60项和为( ) A.3 690 B.3 660 C.1 845 D.1 830【答案】D【解析】∵a n+1+(-1)na n =2n-1, ∴a 2=1+a 1,a 3=2-a 1,a 4=7-a 1,a 5=a 1,a 6=9+a 1,a 7=2-a 1,a 8=15-a 1,a 9=a 1,a 10=17+a 1,a 11=2-a 1,a 12=23-a 1,…,a 57=a 1,a 58=113+a 1,a 59=2-a 1,a 60=119-a 1,∴a 1+a 2+…+a 60=(a 1+a 2+a 3+a 4)+(a 5+a 6+a 7+a 8)+…+(a 57+a 58+a 59+a 60) =10+26+42+…+234=15×(10+234)2=1 830. 二、填空题1.(2019·全国3·文T14)记S n 为等差数列{a n }的前n 项和.若a 3=5,a 7=13,则S 10= . 【答案】100【解析】设等差数列{a n }的公差为d,则{a 3=a 1+2d =5,a 7=a 1+6d =13,解得{a 1=1,d =2. 故S 10=10a 1+10×92d=10×1+10×92×2=100. 2.(2019·全国3·理T14)记S n 为等差数列{a n }的前n 项和.若a 1≠0,a 2=3a 1,则S10S 5= .【答案】4【解析】设等差数列{a n }的公差为d. ∵a 1≠0,a 2=3a 1, ∴a 1+d=3a 1,即d=2a 1.∴S10S 5=10a 1+10×92d5a 1+5×42d=100a 125a 1=4. 3.(2019·江苏·T 8)已知数列{a n }(n ∈N *)是等差数列,S n 是其前n 项和.若a 2a 5+a 8=0,S 9=27,则S 8的值是 . 【答案】16【解析】∵{a n }为等差数列,设公差为d,a 2a 5+a 8=0,S 9=27,∴{(a 1+d )(a 1+4d )+a 1+7d =0,①9a 1+9×82d =27,②整理②得a 1+4d=3,即a 1=3-4d,③ 把③代入①解得d=2,∴a 1=-5. ∴S 8=8a 1+28d=16.4.(2019·北京·理T10)设等差数列{a n }的前n 项和为S n .若a 2=-3,S 5=-10,则a 5= ,S n 的最小值为 . 【答案】0 -10【解析】等差数列{a n }中,由S 5=5a 3=-10,得a 3=-2,又a 2=-3,公差d=a 3-a 2=1,a 5=a 3+2d=0,由等差数列{a n }的性质得当n ≤5时,a n ≤0,当n ≥6时,a n 大于0,所以S n 的最小值为S 4或S 5,即为-10.5.(2019·全国1·文T14)记S n 为等比数列{a n }的前n 项和.若a 1=1,S 3=34,则S 4= . 【答案】58【解析】设等比数列{a n }的公比为q. S 3=a 1+a 1q+a 1q 2=1+q+q 2=34, 即q 2+q+14=0.解得q=-12.故S 4=a 1(1-q 4)=1-(-12)41+12=5.6.(2019·全国1·理T14)记S n 为等比数列{a n }的前n 项和.若a 1=13,a 42=a 6,则S 5=________.【答案】1213【解析】设等比数列{a n }的公比为q, 则a 4=a 1q 3=13q 3,a 6=a 1q 5=13q 5.∵a 42=a 6,∴19q 6=13q 5.∵q≠0,∴q=3.∴S 5=a 1(1-q 5)1-q=13(1-35)1-3=1213. 7.(2018·全国1·理T14)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6= . 【答案】-63【解析】∵S n =2a n +1,① ∴S n-1=2a n-1+1(n ≥2).②①-②,得a n =2a n -2a n-1,即a n =2a n-1(n ≥2).又S 1=2a 1+1,∴a 1=-1.∴{a n }是以-1为首项,2为公比的等比数列,则S 6=-1(1-26)1-2=-63.8.(2018·北京·理T9)设{a n }是等差数列,且a 1=3,a 2+a 5=36,则{a n }的通项公式为 . 【答案】a n =6n-3【解析】∵{a n }为等差数列,设公差为d, ∴a 2+a 5=2a 1+5d=36.∵a 1=3,∴d=6.∴a n =3+(n-1)×6=6n-3.9.(2018·上海·T 10)设等比数列{a n }的通项公式为a n =q n-1(n ∈N *),前n 项和为S n ,若lim n →∞S na n+1=12,则q= . 【答案】3【解析】由a n =q n-1,得a n+1=q n.当q=1时,不满足题意;当q≠1时,S n =a 1(1-q n )1-q=1-q n1-q. 若0<|q|<1,则lim n →∞1-q n(1-q )q n 不存在;若|q|>1,则lim n →∞Sn a n+1=lim n →∞1-q n(1-q )q n =lim n →∞1(1-q )·(1q n -1)=-11-q =12,解得q=3.10.(2018·江苏·T 14)已知集合A={x|x=2n-1,n ∈N *},B={x|x=2n ,n ∈N *}.将A ∪B 的所有元素从小到大依次排列构成一个数列{a n }.记S n 为数列{a n }的前n 项和,则使得S n >12a n+1成立的n 的最小值为 . 【答案】27【解析】①若a n+1=2k(k ∈N *),则S n =21+22+…+2k-1+1+3+ (2)-1=2k-2+(2k-1)2⇒(2k-1)2+2k-2>12·2k. 令2k=t ⇒14t 2+t-2>12t ⇒t(t-44)>8.∴t ≥64⇒k ≥6.此时,n=k-1+2k-1=37. ②若a n+1=2k+1(k ∈N *),则S n =21+22+ (2)+1+3+…+2k-1(2t<2k+1,t ∈N *), ∴S n =2t+1-2+k 2>12(2k+1)⇒2t+1>-k 2+24k+14. ∴-k 2+24k+14<2t+1<4k+2⇒k(k-20)>12.取k=21,此时772<2t <43(舍),取k=22,29<2t<45,t=5,n=5+22=27. 由①②,得n min =27.11.(2017·全国2·理T15)等差数列{a n }的前n 项和为S n ,a 3=3,S 4=10,则∑k=1n1S k=____________.【答案】2nn+1【解析】设等差数列的首项为a 1,公差为d,由题意可知{a 1+2d =3,4a 1+4×32d=10,解得{a 1=1,d =1.所以S n =na 1+n (n -1)2d=n (1+n )2. 所以1S n =2n (n+1)=2(1n -1n+1).所以∑k=1n1S k=2[(1-12)+(12-13)+…+(1n -1n+1)]=2(1-1n+1)=2nn+1. 12.(2017·全国3·理T14)设等比数列{a n }满足a 1+a 2=-1,a 1-a 3=-3,则a 4= . 【答案】-8【解析】设{a n }的公比为q,则由题意, 得{a 1(1+q )=-1,a 1(1-q 2)=-3,解得{a 1=1,q =-2,故a 4=a 1q 3=-8. 13.(2017·江苏·理T9文T9)等比数列{a n }的各项均为实数,其前n 项和为S n .已知S 3=74,S 6=634,则a 8= . 【答案】32【解析】设该等比数列的公比为q,则S 6-S 3=634−74=14,即a 4+a 5+a 6=14.①∵S 3=74,∴a 1+a 2+a 3=74. 由①得(a 1+a 2+a 3)q 3=14,∴q 3=1474=8,即q=2.∴a 1+2a 1+4a 1=7,a 1=1. ∴a 8=a 1·q 7=14×27=32.14.(2016·浙江·理T13文T13)设数列{a n }的前n 项和为S n ,若S 2=4,a n+1=2S n +1,n ∈N *,则a 1= ,S 5= . 【答案】1 121【解析】由题意,可得a 1+a 2=4,a 2=2a 1+1, 所以a 1=1,a 2=3.再由a n+1=2S n +1,a n =2S n-1+1(n ≥2), 两式相减得a n+1-a n =2a n ,即a n+1=3a n (n ≥2).又因为a 2=3a 1,所以数列{a n }是以1为首项,3为公比的等比数列.所以S 5=1-351-3=121. 15.(2016·北京·理T12)已知{a n }为等差数列,S n 为其前n 项和.若a 1=6,a 3+a 5=0,则S 6= . 【答案】6【解析】∵{a n }是等差数列,∴a 3+a 5=2a 4=0.∴a 4=0. ∴a 4-a 1=3d=-6.∴d=-2. ∴S 6=6a 1+15d=6×6+15×(-2)=6.16.(2016·全国1·理T15)设等比数列{a n }满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为 . 【答案】64【解析】由已知a 1+a 3=10,a 2+a 4=a 1q+a 3q=5,两式相除得a 1+a 3q (a 1+a 3)=105=2,解得q=12,a 1=8, 所以a 1a 2…a n =8n·(1)1+2+…+(n -1)=2-12n 2+7n2,函数f(n)=-1n 2+7n的对称轴为n=-722×(-12)=3.5,又n ∈N *,所以当n=3或4时,a 1a 2…a n 取最大值为2-12×32+7×32=26=64.17.(2015·全国1·文T13)在数列{a n }中,a 1=2,a n+1=2a n ,S n 为{a n }的前n 项和.若S n =126,则n= . 【答案】6【解析】∵a n+1=2a n ,即an+1a n=2,∴{a n }是以2为公比的等比数列.。
十年高考数学试卷汇编(10~19年 解答题部分)

全国卷•十年高考(解答题部分)2019年全国统一高考数学试卷(理科)(新课标Ⅰ) (2)2018年全国统一高考数学试卷(理科)(新课标Ⅰ) (6)2017年全国统一高考数学试卷(理科)(新课标Ⅰ) (10)2016年全国统一高考数学试卷(理科)(新课标Ⅰ) (15)2015年全国统一高考数学试卷(理科)(新课标Ⅰ) (20)2014年全国统一高考数学试卷(理科)(新课标Ⅰ) (25)2013年全国统一高考数学试卷(理科)(新课标Ⅰ) (31)2012年全国统一高考数学试卷(理科)(新课标) (36)2011年全国统一高考数学试卷(理科)(新课标) (41)2010年全国统一高考数学试卷(理科)(新课标) (46)2019年全国统一高考数学试卷(理科)(新课标Ⅰ)三、解答题:共60分。
17.(2019•新课标Ⅰ)△ABC的内角A,B,C的对边分别为a,b,c.设(sinB﹣sinC)2=sin2A﹣sinBsin C.(1)求A;(2)若a+b=2c,求sinC.18.(2019•新课标Ⅰ)如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A﹣MA1﹣N的正弦值.19.(2019•新课标Ⅰ)已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.(1)若|AF|+|BF|=4,求l的方程;(2)若=3,求|AB|.20.(2019•新课标Ⅰ)已知函数f(x)=sinx﹣ln(1+x),f′(x)为f(x)的导数.证明:(1)f′(x)在区间(﹣1,)存在唯一极大值点;(2)f(x)有且仅有2个零点.21.(2019•新课标Ⅰ)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得﹣1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得﹣1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.(1)求X的分布列;(2)若甲药、乙药在试验开始时都赋予4分,p i(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,p i=ap i﹣1+bp i+cp i+1(i=1,2,…,7),其中a=P(X=﹣1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.(i)证明:{p i+1﹣p i}(i=0,1,2,…,7)为等比数列;(ii)求p4,并根据p4的值解释这种试验方案的合理性.(二)选考题:共10分。
十年真题(2010_2019)高考数学真题分类汇编专题01集合理(含解析)

专题01集合历年考题细目表历年高考真题汇编1.【2019年新课标1理科01】已知集合M={x|﹣4<x<2},N={x|x2﹣x﹣6<0},则M∩N=()A.{x|﹣4<x<3} B.{x|﹣4<x<﹣2} C.{x|﹣2<x<2} D.{x|2<x<3}【解答】解:∵M={x|﹣4<x<2},N={x|x2﹣x﹣6<0}={x|﹣2<x<3},∴M∩N={x|﹣2<x<2}.故选:C.2.【2018年新课标1理科02】已知集合A={x|x2﹣x﹣2>0},则∁R A=()A.{x|﹣1<x<2} B.{x|﹣1≤x≤2} C.{x|x<﹣1}∪{x|x>2} D.{x|x≤﹣1}∪{x|x≥2} 【解答】解:集合A={x|x2﹣x﹣2>0},可得A={x|x<﹣1或x>2},则:∁R A={x|﹣1≤x≤2}.故选:B.3.【2017年新课标1理科01】已知集合A={x|x<1},B={x|3x<1},则()A.A∩B={x|x<0} B.A∪B=R C.A∪B={x|x>1} D.A∩B=∅【解答】解:∵集合A={x|x<1},B={x|3x<1}={x|x<0},∴A∩B={x|x<0},故A正确,D错误;A∪B={x|x<1},故B和C都错误.故选:A.4.【2016年新课标1理科01】设集合A={x|x2﹣4x+3<0},B={x|2x﹣3>0},则A∩B=()A.(﹣3,)B.(﹣3,)C.(1,)D.(,3)【解答】解:∵集合A={x|x2﹣4x+3<0}=(1,3),B={x|2x﹣3>0}=(,+∞),∴A∩B=(,3),故选:D.5.【2014年新课标1理科01】已知集合A={x|x2﹣2x﹣3≥0},B={x|﹣2≤x<2},则A∩B=()A.[1,2)B.[﹣1,1] C.[﹣1,2)D.[﹣2,﹣1]【解答】解:由A中不等式变形得:(x﹣3)(x+1)≥0,解得:x≥3或x≤﹣1,即A=(﹣∞,﹣1]∪[3,+∞),∵B=[﹣2,2),∴A∩B=[﹣2,﹣1].故选:D.6.【2013年新课标1理科01】已知集合A={x|x2﹣2x>0},B={x|x},则()A.A∩B=∅B.A∪B=R C.B⊆A D.A⊆B【解答】解:∵集合A={x|x2﹣2x>0}={x|x>2或x<0},∴A∩B={x|2<x或x<0},A∪B=R,故选:B.7.【2012年新课标1理科01】已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x﹣y∈A},则B中所含元素的个数为()A.3 B.6 C.8 D.10【解答】解:由题意,x=5时,y=1,2,3,4,x=4时,y=1,2,3,x =3时,y =1,2,x =2时,y =1综上知,B 中的元素个数为10个故选:D .8.【2010年新课标1理科01】已知集合A ={x ∈R ||x |≤2}},,则A ∩B =( ) A .(0,2) B .[0,2] C .{0,2} D .{0,1,2}【解答】解:A ={x ∈R ||x |≤2,}={x ∈R |﹣2≤x ≤2},故A ∩B ={0,1,2}.应选D .考题分析与复习建议本专题考查的知识点为:集合关系及其运算,历年考题主要以选择填空题型出现,重点考查的知识点为:交并补运算,预测明年本考点题目会比较稳定,备考方向以知识点交并补运算为重点较佳.最新高考模拟试题1.若集合{}5|2A x x =-<<,{}|||3B x x =<,则AB =( ) A .{}|32x x -<<B .{}|52x x -<<C .{}|33x x -<<D .{}|53x x -<< 【答案】A【解析】 解:{}{}333||B x x x x =<=-<<,则{}|32A B x x ⋂=-<<,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.(2018·浙江·T10)已知 a1,a2,a3,a4 成等比数列,且 a1+a2+a3+a4=ln(a1+a2+a3).若 a1>1,则( )
A.a1<a3,a2<a4
B.a1>a3,a2<a4
C.a1<a3,a2>a4 D.a1>a3,a2>a4
5.(2018·北京·理 T4 文 T5)“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比
1
A.当 b=2时,a10>10
1
B.当 b=4时,a10>10
C.当 b=-2 时,a10>10
D.当 b=-4 时,a10>10
3.(2018·全国 1·理 T4)记 Sn 为等差数列{an}的前 n 项和,若 3S3=S2+S4,a1=2,则 a5=( )
A.-12 B.-10 C.10 D.12
A.3 B.4 C.5 D.6
20.(2012·全国·理 T5)已知{an}为等比数列,a4+a7=2,a5a6=-8,则 a1+a10=( )
A.7 B.5 C.-5 D.-7
n
21.(2012·全国·文 T12)数列{an}满足 an+1+(-1) an=2n-1,则{an}的前 60 项和为( )
趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列
0
01
012
1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是 2 ,接下来的两项是 2 ,2 ,再接下来的三项是 2 ,2 ,2 ,
依此类推.求满足如下条件的最小整数 N:N>100 且该数列的前 N 项和为 2 的整数幂.那么该款软件的激活码
A.21
B.42 C.63
D.84
1
13.(2015·全国 2·文 T9)已知等比数列{an}满足 a1=4,a3a5=4(a4-1),则 a2=( )
1
1
A.2
B.1
C.2
D.8
14.(2014·大纲全国·文 T8)设等比数列{an}的前 n 项和为 Sn.若 S2=3,S4=15,则 S6=( )
A.3 690
B.3 660
C.1 845 D.1 830
二、填空题
1.(2019·全国 3·文 T14)记 Sn 为等差数列{an}的前 n 项和.若 a3=5,a7=13,则 S10= .
S10
2.(2019·全国 3·理 T14)记 Sn 为等差数列{an}的前 n 项和.若 a1≠0,a2=3a1,则 S5 = .
A.5 B.7 C.9 D.11
11.(2015·全国 1·文 T7)已知{an}是公差为 1 的等差数列,Sn 为{an}的前 n 项和.若 S8=4S4,则 a10= ( )
17
A. 2
19
B. 2
C.10
D.12
12.(2015·全国 2·理 T4)已知等比数列{an}满足 a1=3,a1+a3+a5=21,则 a3+a5+a7=( )
cn+an
bn+an
Hale Waihona Puke b1>c1,b1+c1=2a1,an+1=an,bn+1= 2 ,cn+1= 2 ,则( )
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n-1}为递增数列,{S2n}为递减数列
2
D.{S2n-1}为递减数列,{S2n}为递增数列
19.(2013·全国 1·理 T7)设等差数列{an}的前 n 项和为 Sn,若 Sm-1=-2,Sm=0,Sm+1=3,则 m= ( )
1
1
1
1
A.3
B.-3
C.9
D.-9
2
17.(2013·全国 1·文 T6)设首项为 1,公比为3的等比数列{an}的前 n 项和为 Sn,则( )
A.Sn=2an-1 B.Sn=3an-2
C.Sn=4-3an D.Sn=3-2an
18.(2013·全国 1·理 T12)设△AnBnCn 的三边长分别为 an,bn,cn,△AnBnCn 的面积为 Sn,n=1,2,3,….若
*
3.(2019·江苏·T8)已知数列{an}(n∈N )是等差数列,Sn 是其前 n 项和.若 a2a5+a8=0,S9=27,则 S8 的值
例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从 第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于 √2.若第一个单音的频率为 f,则第
八个单音的频率为( )
A. √2f
B. √2 f
C. √2 f D. √2 f
6.(2017·全国 1·理 T12)几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴
是( )
A.440 B.330
C.220 D.110
7.(2017·全国 3·理 T9)等差数列{an}的首项为 1,公差不为 0.若 a2,a3,a6 成等比数列,则{an}前 6 项的和为 ()
A.-24 B.-3 C.3 D.8
8.(2016·全国 1·理 T3)已知等差数列{an}前 9 项的和为 27,a10=8,则 a100=( )
十年(2010—2019)数学高考真题分类汇编
数列
一、选择题
1.(2019·全国 1·理 T9)记 Sn 为等差数列{an}的前 n 项和.已知 S4=0,a5=5,则( )
A.an=2n-5
B.an=3n-10
2
C.Sn=2n -8n
12
D.Sn=2n -2n
*
2.(2019·浙江·T10)设 a,b∈R,数列{an}满足 a1=a,an+1= +b,n∈N ,则( )
A.31
B.32
C.63 D.64
15.(2014·全国 2·文 T5)等差数列{an}的公差为 2,若 a2,a4,a8 成等比数列,则{an}的前 n 项和 Sn=( )
A.n(n+1)
B.n(n-1)
( +1)
C. 2
( -1)
D. 2
16.(2013·全国 2·理 T3)等比数列{an}的前 n 项和为 Sn.已知 S3=a2+10a1,a5=9,则 a1=( )
1
A.100 B.99 C.98
D.97
9.(2015·浙江·理 T13)已知{an}是等差数列,公差 d 不为零,前 n 项和是 Sn,若 a3,a4,a8成等比数列,则( )
A.a1d>0,dS4>0
B.a1d<0,dS4<0
C.a1d>0,dS4<0
D.a1d<0,dS4>0
10.(2015·全国 2·文 T5)设 Sn 是等差数列{an}的前 n 项和,若 a1+a3+a5=3,则 S5=( )
