第3章电磁解答终稿查
电磁场与电磁波第四版第三章部分答案

电磁场与电磁波第三章无限大导体平板分别置于k = 0和x - d处,板间充满电荷,其体电荷密度为p =-:极板间的电位分别为0和如图所示,求两d级板之间的电位和电场强度。
解:由泊松定理得d2* _ 1dx2电o d3解得二:6«od|在久=0处* * = 0,故B = 0在X二d处,"二%故U。
二-页j亠Ad证明:同轴线单位长度的静电储能$二巴。
式中山为单位长度上的电臼2C|6 c od +荷量,C为单位长度上的电容。
解:由高斯定理可知:故内外导体间的电压为qj Qi h------- d P = ---- ------ ln-则电容为有一半径为a,带电量q的导体球,其球心位于介电常数分别为5和F.汕勺两种介质的分界面上,该分界面为无限大平面。
试求:(1)导体球的电容;(2)总的静电常量解:根据边界条件则Eit = E2t,故有□二E?二日,由于I ■ I _■_ _,所以一- I |_ 1 1;l)iSi I P2S2 = q即 2 n r2 f ]E 十2^r2- Qn qE =-------- ---------------2 n r2( e 1 + e 2)导体球的电位为“(日)二J’Edr二N77:+ 二心电容为「二為=2肌(£ 1亠5)』⑵总的静能量为1I | I在一块厚度为d的导电板上,由两个半径分别为卜汇4的圆弧和夹角为u 的两半径割出的一块扇形体,如图所示。
试求:(1)沿厚度方向的电阻;(2)两圆弧面之间的电阻;(3)沿方向的两电极间的电阻。
设导电板的电导率为。
&解:(1)设沿厚度方向的两电极的电压为f U1则El 二7aUiJ1二晌二〒11 = JiSi =晋-7(ra2一n2)故得到沿厚度方向的电阻为无限长直线电流I 垂直于磁导率分别为「1和叫的两种磁介质的分界 鸟 1辺 应rd (3)设沿 . 一―一 J 厂頁 i'2 u dU 3------- d r… a r ri 1 0 dU 3 r 2 ------ 1 n — a nu 3 a Rj =—= h o din — ri 2dIl a O (r 22 - \'\(2)设内外两圆弧面电极之间的电流为1 [2 I 2 J2肓a rd12比 12 匚2E^dr = -------In 一F LCL rd V] 故两圆弧面之间的电阻为<1K^rd® o 沿d 方向的电阻为1_ (u - jio)l7 _ U 憑_ H _ 五u 叶 心—T ;'=0以z 轴为中心, 为半径做一个圆形回路C,由安培环路定理得其厚度可忽略不计。
人教版物理选修【3-1】第三章《磁场》章末检测(A)及答案

章末检测(A)(90分钟100分)一、选择题(本题10小题,每小题5分,共50分)1.一个质子穿过某一空间而未发生偏转,则( )A.可能存在电场和磁场,它们的方向与质子运动方向相同B.此空间可能有磁场,方向与质子运动速度的方向平行C.此空间可能只有磁场,方向与质子运动速度的方向垂直D.此空间可能有正交的电场和磁场,它们的方向均与质子速度的方向垂直答案ABD解析带正电的质子穿过一空间未偏转,可能不受力,可能受力平衡,也可能受合外力方向与速度方向在同一直线上.2. 两个绝缘导体环AA′、BB′大小相同,环面垂直,环中通有相同大小的恒定电流,如图1所示,则圆心O处磁感应强度的方向为(AA′面水平,BB′面垂直纸面)A.指向左上方B.指向右下方C.竖直向上D.水平向右答案 A3.关于磁感应强度B,下列说法中正确的是( )A.磁场中某点B的大小,跟放在该点的试探电流元的情况有关B.磁场中某点B的方向,跟该点处试探电流元所受磁场力的方向一致C.在磁场中某点试探电流元不受磁场力作用时,该点B值大小为零D.在磁场中磁感线越密集的地方,B值越大答案 D解析磁场中某点的磁感应强度由磁场本身决定,与试探电流元无关.而磁感线可以描述磁感应强度,疏密程度表示大小.4.关于带电粒子在匀强磁场中运动,不考虑其他场力(重力)作用,下列说法正确的是( )A.可能做匀速直线运动B.可能做匀变速直线运动C.可能做匀变速曲线运动D.只能做匀速圆周运动答案 A解析带电粒子在匀强磁场中运动时所受的洛伦兹力跟速度方向与磁场方向的夹角有关,当速度方向与磁场方向平行时,它不受洛伦兹力作用,又不受其他力作用,这时它将做匀速直线运动,故A项正确.因洛伦兹力的方向始终与速度方向垂直,改变速度方向,因而同时也改变洛伦兹力的方向,故洛伦兹力是变力,粒子不可能做匀变速运动,故B、C两项错误.只有当速度方向与磁场方向垂直时,带电粒子才做匀速圆周运动,故D 项中“只能”是不对的.5. 1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图2所示.这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法正确的是( )图2A.离子由加速器的中心附近进入加速器B.离子由加速器的边缘进入加速器C.离子从磁场中获得能量D.离子从电场中获得能量答案 AD解析 本题源于课本而又高于课本,既考查考生对回旋加速器的结构及工作原理的掌握情况,又能综合考查磁场和电场对带电粒子的作用规律.由R =mvqB知,随着被加速离子的速度增大,离子在磁场中做圆周运动的轨道半径逐渐增大,所以离子必须由加速器中心附近进入加速器,A 项正确,B 项错误;离子在电场中被加速,使动能增加;在磁场中洛伦兹力不做功,离子做匀速圆周运动,动能不改变.磁场的作用是改变离子的速度方向,所以C 项错误,D 项正确.6. 如图3所示,一个带负电的油滴以水平向右的速度v 进入一个方向垂直纸面向外的匀强磁场B 后,保持原速度做匀速直线运动,如果使匀强磁场发生变化,则下列判断中正确的是( )图3A .磁场B 减小,油滴动能增加 B .磁场B 增大,油滴机械能不变C .使磁场方向反向,油滴动能减小D .使磁场方向反向后再减小,油滴重力势能减小 答案 ABD解析 带负电的油滴在匀强磁场B 中做匀速直线运动,受坚直向下的重力和竖直向上的洛伦兹力而平衡,当B 减小时,由F =qvB 可知洛伦兹力减小,重力大于洛伦兹力,重力做正功,故油滴动能增加,A 正确;B 增大,洛伦兹力大于重力,重力做负功,而洛伦兹力不做功,故机械能不变,B 正确;磁场反向,洛伦兹力竖直向下,重力做正功,动能增加,重力势能减小,故C 错,D 正确.7.如图4所示为一个质量为m 、电荷量为+q 的圆环,可在水平放置的足够长的粗糙细杆上滑动,细杆处于磁感应强度为B 的匀强磁场中(不计空气阻力).现给圆环向右的初速度v 0,在以后的运动过程中,圆环运动的速度—时间图象可能是下图中的( )图4答案 AD解析 由左手定则可知,圆环所受洛伦兹力竖直向上,如果恰好qv 0B =mg ,圆环与杆间无弹力,不受摩擦力,圆环将以v 0做匀速直线运动,故A 正确;如果qv 0B<mg ,则a =μ mg-qvBm,随着v 的减小,a 增大,直到速度减为零后静止;如果qv 0B>mg ,则a =μ qvB-mgm,随着v 的减小a 也减小,直到qvB =mg ,以后将以剩余的速度做匀速直线运动,故D 正确,B 、C 错误.8. 如图5所示,空间的某一区域内存在着相互垂直的匀强电场和匀强磁场,一个带电粒子以某一初速度由A 点进入这个区域沿直线运动,从C 点离开区域;如果这个区域只有电场则粒子从B 点离开场区;如果这个区域只有磁场,则粒子从D 点离开场区;设粒子在上述3种情况下,从A 到B 点,从A 到C 点和A 到D 点所用的时间分别是t 1、t 2和t 3,比较t 1、t 2和t 3的大小,则有(粒子重力忽略不计)( )图5A .t 1=t 2=t 3B .t 2<t 1<t 3C .t 1=t 2<t 3D .t 1=t 3>t 2 答案 C解析 只有电场时,粒子做类平抛运动,水平方向为匀速直线运动,故t 1=t 2;只有磁场时做匀速圆周运动,速度大小不变,但沿AC 方向的分速度越来越小,故t 3>t 2,综上所述可知,选项C 对.9.如图6所示,a 、b 是一对平行金属板,分别接到直流电源两极上,右边有一挡板,正中间开有一小孔d ,在较大空间范围内存在着匀强磁场,磁感应强度大小为B ,方向垂直纸面向里,在a 、b 两板间还存在着匀强电场E.从两板左侧中点c 处射入一束正离子(不计重力),这些正离子都沿直线运动到右侧,从d 孔射出后分成3束.则下列判断正确的是( )图6A .这三束正离子的速度一定不相同B .这三束正离子的质量一定不相同C .这三束正离子的电荷量一定不相同D .这三束正离子的比荷一定不相同 答案 D解析 本题考查带电粒子在电场、磁场中的运动,速度选择器的知识.带电粒子在金属板中做直线运动,qvB =Eq ,v =EB ,表明带电粒子的速度一定相等,而电荷的带电量、电性、质量、比荷的关系均无法确定;在磁场中R =mvBq,带电粒子运动半径不同,所以比荷一定不同,D 项正确.10.如图7所示,两个半径相同的半圆形轨道分别竖直放置在匀强电场和匀强磁场中.轨道两端在同一高度上,轨道是光滑的,两个相同的带正电小球同时从两轨道左端最高点由静止释放.M 、N 为轨道的最低点,则下列说法正确的是( )图7A .两小球到达轨道最低点的速度v M <v NB .两小球第一次到达轨道最低点时对轨道的压力F M <F NC .小球第一次到达M 点的时间大于小球第一次到达N 点的时间D .在磁场中小球能到达轨道的另一端,在电场中小球不能到达轨道的另一端 答案 D解析 在磁场中运动时,只有重力做正功,在电场中运动时,重力做正功、电场力做负功,由动能定理可知:12mv 2M =mgH 12mv 2N =mgH -qE·d 故v M >v N ,A 、C 不正确.最低点M 时,支持力与重力和洛伦兹力的合力提供向心力,最低点N 时,支持力与重力的合力提供向心力. 因v M >v N ,故压力F M >F N ,B 不正确.在电场中因有电场力做负功,有部分机械能转化为电势能,故小球不能到达轨道的另一端.D 正确. 二、填空题(5+5=10分) 11. 一个电子(电荷量为e ,质量为m)以速率v 从x 轴上某点垂直x 轴进入上方匀强磁场区域,如图8所示,已知上方磁感应强度为B ,且大小为下方匀强磁场磁感应强度的2倍,将从开始到再一次由x 轴进入上方磁场作为一个周期,那么,电子运动一个周期所用的时间是________,电子运动一个周期的平均速度大小为________.图8答案3πm eB 2v3π解析电子一个周期内的运动轨迹如右图所示.由牛顿第二定律及洛伦兹力公式,可知evB =mv 2R ,故圆半径R =mveB,所以上方R 1=mv eB ,T 1=2πm eB ;下方R 2=2mv eB ,T 2=4πm eB .因此电子运动一个周期所用时间是:T =T 12+T 22=πm eB +2πmeB=3πm eB ,在这段时间内位移大小:x =2R 2-2R 1=2×2mv eB -2×mv eB =2mv eB,所以电子运动一个周期的平均速度大小为:v =x T =2mv eB 3πm eB=2v3π.12.(5分)如图9所示,正方形容器处在匀强磁场中,一束电子从a 孔沿a →b 方向垂直射入容器内的匀强磁场中,结果一部分电子从小孔c 竖直射出,一部分电子从小孔d 水平射出,则从c 、d 两孔射出的电子在容器中运动的时间之比t c ∶t d =____________,在容器中运动的加速度大小之比a c ∶a d =__________答案 1∶2 2∶1解析 同一种粒子在同一磁场中运动的周期相同,且t c =14T ,t d =12T ,即t c ∶t d =1∶2.由r =mvqB知,v c ∶v d =r c ∶r d =2∶1,而a c ∶a d =qv c B m ∶qv d Bm=v c ∶v d =2∶1.三、计算题(8+8+12+12=40分)13.如图10所示,在倾角为37°的光滑斜面上有一根长为0.4 m ,质量为6×10-2kg 的通电直导线,电流I =1 A ,方向垂直纸面向外,导线用平行于斜面的轻绳拴住不动,整个装置放在磁感应强度每秒增加0.4 T ,方向竖直向上的磁场中,设t =0时,B =0,则需要多长时间斜面对导线的支持力为零?(g 取10 m/s 2)图10答案5 s解析 斜面对导线的支持力为零时受力分析如右图 由平衡条件得: BIL =mgcot 37°B =mgcot 37°IL=6×10-2×10×0.80.61×0.4T =2 T所需时间t =B ΔB =20.4s =5 s14.电子质量为m ,电荷量为q ,以速度v 0与x 轴成θ角射入磁感应强度为B 的匀强磁场中,最后落在x 轴上的P 点,如图11所示,求:图11(1)OP 的长度;(2)电子由O 点射入到落在P 点所需的时间t.答案 (1)2mv 0Bq sin θ (2)2θmBq解析带电粒子在匀强磁场中做匀速圆周运动,应根据已知条件首先确定圆心的位置,画出运动轨迹,所求距离应和半径R 相联系,所求时间应和粒子转动的圆心角θ、周期T 相联系.(1)过O 点和P 点做速度方向的垂线,两线交点C 即为电子在磁场中做匀速圆周运动的圆心,如右图所示,则可知OP =2R·sin θ①Bqv 0=m v 2R②由①②式可解得:OP =2mv 0Bqsin θ.(2)由图中可知:2θ=ωt ③ 又v 0=ωR ④由③④式可得:t =2θmBq.15.如图12所示,有界匀强磁场的磁感应强度B =2×10-3T ;磁场右边是宽度L =0.2 m 、场强E =40 V/m 、方向向左的匀强电场.一带电粒子电荷量q =-3.2×10-19 C ,质量m =6.4×10-27 kg ,以v =4×104m/s 的速度沿OO′垂直射入磁场,在磁场中偏转后进入右侧的电场,最后从电场右边界射出.求:图12(1)大致画出带电粒子的运动轨迹(画在给出的图中); (2)带电粒子在磁场中运动的轨道半径; (3)带电粒子飞出电场时的动能E k .答案 (1)见解析图 (2)0.4 m (3)7.68×10-18J 解析 (1)轨迹如下图所示.(2)带电粒子在磁场中运动时,由牛顿运动定律,有qvB =m v2R,R =mv qB =6.4×10-27×4×1043.2×10-19×2×10-3 m =0.4 m.(3)E k =EqL +12mv 2=40×3.2×10-19×0.2 J+12×6.4×10-27×(4×104)2 J =7.68×10-18J.16.质量为m ,电荷量为q 的带负电粒子自静止开始,经M 、N 板间的电场加速后,从A 点垂直于磁场边界射入宽度为d 的匀强磁场中,该粒子离开磁场时的位置P 偏离入射方向的距离为L ,如图13所示,已知M 、N 两板间的电压为U ,粒子的重力不计.图13(1)正确画出粒子由静止开始至离开匀强磁场时的轨迹图(用直尺和圆规规范作图); (2)求匀强磁场的磁感应强度B.答案 (1)见解析图 (2)2L L 2+d 2 2mUq解析 (1)作出粒子经电场和磁场的轨迹图,如下图(2)设粒子在M 、N 两板间经电场加速后获得的速度为v , 由动能定理得:qU =12mv 2①粒子进入磁场后做匀速圆周运动,设其半径为r ,则:qvB =m v2r②由几何关系得:r 2=(r -L)2+d 2③ 联立①②③式得:磁感应强度B =2L L 2+d 2 2mUq.。
物理人教选修3-1本章知识结构(第三章磁场)Word版含解析
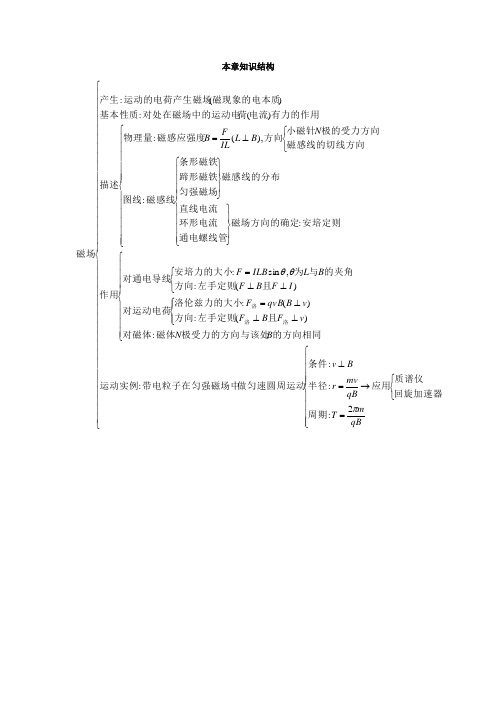
本章知识结构
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎩⎨⎧→=⊥⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⊥⊥⊥=⎩⎨⎧⊥⊥=⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎭⎪⎬⎫⎩⎨⎧⊥=qB m T qB mv r B v B N v F B F v B qvB F I F B F B L ILB F N B L IL F B πθθ2:::::)(:)(:)(:,sin :::),(:)(:)(:周期回旋加速器质谱仪应用半径条件做匀速圆周运动带电粒子在匀强磁场中运动实例的方向相同极受力的方向与该处磁体对磁体且左手定则方向洛伦兹力的大小对运动电荷且左手定则方向的夹角与为安培力的大小对通电导线作用安培定则磁场方向的确定通电螺线管环形电流直线电流磁感线的分布匀强磁场蹄形磁铁条形磁铁磁感线图线磁感线的切线方向极的受力方向小磁针方向磁感应强度物理量描述有力的作用电流荷对处在磁场中的运动电基本性质磁现象的电本质运动的电荷产生磁场
产生磁场洛洛洛。
电磁场理论(柯亨玉)答案第三章静态电磁场.pdf
由B A
得: Az Ay 0 y z
Ax Az 0 z x
Ay x
Ax y
B0
可得一解为: Az Ay 0
还可得另一解为: Ax Az 0
还存在其它解。 两者之差的旋度:
Ax B0 y Ay B0 x
eˆx eˆy eˆz
( Ayeˆy Axeˆx ) (B0 xeˆy B0 yeˆx )
磁失势的引入及方程的推导过程我们以图解的方式表示其中引入的条件是无传导电流的单连通区域如电流是环形分布的磁标势适合的区域只能是挖去环形电流所围成的壳形之后剩下的区域
第三章 静态电磁场
1. 静电场中,电位函数满足的方程及其边界条件 电位函数的引入及其方程的推导过程。我们以图解的方式表示
D
E
x
0 y z
B0 y B0 x 0
3-10. 证明:设线圈中的电流分别为 I1, I 2
线圈 1 对线圈 2 的作用力为
f12
0 4
I
2
dl2
(I1
dl1r12 )
L1 L2
r132
0 I1I2
dl2
(dl1r12 )
4
L1 L2
r132
0 I1I 2
[(dl2 r12 )dl1 (dl1 dl2 )r12 ]
设介质被抽出的一段长为 x , C 便等于无介质部分的电容 C1 与有介质部分的电容
C2 的迭加,即
C
C1
C2
2 0 x ln(b a)
2 (L x) ln(b a)
2 [L ln(b a)
(
0
)x]
则 W V2 C 2
V2 2
2 [L ( ln(b a)
电磁场 第三章 (叶齐政 孙敏 著) 华中科技大学出版社 课后答案

第三章3.3提示,由于静电场中0=×∇E K 放在计算0=×∇F G 若0=×∇F G 则F G可能是电场强度E G ,否则不可能是E G ,即:0=×∇E K 是F G为静电场的必要重要条件。
具体过程;略 3.4解1)P 点的ϕ:()()()()()Vb b b P 86.972ln 4320223,2,222−=−−−×+−××=−=ϕϕ 2)P 点的E G: 由于,k j y x y x i y x x xy kz j yi x E G G G G G G K 20828422222−⎟⎠⎞⎜⎝⎛−+−⎟⎠⎞⎜⎝⎛−−−=∂∂−∂∂−−∂∂−=−∇=ϕϕϕϕ 所以P 点的E G为()k j i p E G GG G 205.715.49−−=3)P 点的D :()()()()3120205.715.491085.8m ck j i p E p D G G G G G −−××==−ε自由电荷密度()⎥⎥⎦⎤⎢⎢⎣⎡−+−−=⎟⎟⎠⎞⎜⎜⎝⎛∂∂+∂∂+∂∂=•∇=•∇=22222000164y x y x y z E y E x E E D z y x εεερG GP 点的为:()()()()()()3112222010526.6262661624mc p −×=⎥⎥⎦⎤⎢⎢⎣⎡−−−+××−−×−=ερ3.5解 提示,空气的击穿场强决定了在金属球表面与空气的交界面上的电场的最大值,另外注意金属导体表面的电场只有法向分量,金属导体球表面上有自由面电荷σ,其中最大值可由导体与介质界面的衔接条件决定()2502020210655.2m cE E E D Max n n Max −×=====εεεσ1)由于面电荷均匀分布特性,可求得金属球上最大的电量()c r ds q s62max max max 10507.74−×=⋅==∫πσσ2)只需要计算长圆柱的单位长度电荷总量()∫−×=⋅⋅==sc r ds q 5max max 110502.212πσσ3)考虑金属球的对称性,可以为金属球上的面电荷在空间产生的电场与同量的处于球心处的点电荷产生的电场等效,金属球表面处的电势最高为()V rq 50maxmax 1005.44×==πεϕ3.6解提示光分析同轴电缆里面的电场强度E G设同轴电缆内外导体沿轴向方向单位强度所带电荷量分到为ττ−+和由高斯定理,电缆中介质的电位移:02r rD G Gπτ=则电场02r rE G G πετ=于是内外导体间的电压120ln 2212121R R Edr r d E l d E U R R R R R R πετ∫∫∫==•=•=G G G G 12ln 2R R U πετ=120ln 2r R R r U r r E G G G ==πετ 显然E正比于1/r故由导体表面上的电场强度最大,即121max 121max lnlnR R R E U R R R U E =⇒=可U 是R1的函数现求U 的极大值 令l RR R R dR dU 211211ln 0=⇒==即可得于是l R E lR R lR E U 2max 222max max ln⋅=⋅=3.7解提示:可利用3。
电磁场与电磁波 第三章答案

x x x 2 ( y h) 2 x 2 ( y h) 2 e x ( y h) ( y h) x 2 ( y h) 2 x 2 ( y h) 2 e y
电场能量密度为
h 2 ( x 4 y 4 h 4 2x 2 h 2 2x 2 y 2 2 y 2 h 2 ) 1 w r E2 l 2 2 r [ x 2 ( y h ) 2 ] 2 [ x 2 ( y h) 2 ] 2
新概念物理教程 电磁学 赵凯华 第二版2版 课后习题答案全解详解
可当作点电荷),求(")! 粒于所受的力;(’)! 粒子的加速度。
解:(")
!
&"
$" + " !#
’" ’’ (’
$ +
%
%& %"" (# %"# !"&%’ ," "+ %)" )$ %"# !"’
%"" %((
(# %"# !"& " &# %"# !"$
)’
%
$ %" (+
%"# !’ %,
’& ,由 " ! ’ 题的结果可知
’"
#
%
" !
!#(
%
!&&+, &)$ ,!
’&
#
%
" !
!#(
%
&+ -& , &
)$ ;
* 点的场强为
[ ] ’
# ’"
!’&
#%
" ! !#
&+ %$ ("
!
" &,
&
%)$
! (
"
" -& ,
&
%)$
[ ( ) ] $%
" ! !#
&+ %$
"
-&$
& %
设两平行线中左边一条带负电右边一条带正电原点取在二者中间场点的坐标为利用书上例题的结果有均匀电场与半径为的半球面的轴线平行试用面积分计算通过此半球面的电通量
电磁场与电磁波(第4版)第3章部分习题参考解答
cos
x)
=
−e− y
cos
x
+
e− y
cos
x
=
0
所以函数 e− y cos x 是 y > 0 空间中可能的电位解;
(3)
∂ (e− 2 sin x cos x) + ∂ (e− 2 sin x cos x) + ∂ (e− 2 sin x cos x)
∂x2
∂y2
∂z 2
= −4e− 2 sin x cos x + 2e− 2 sin x cos x ≠ 0 所以函数 e− 2 sin x cos x 不是 y > 0 空间中的电位解;
+
(L /
2)2
+
L
/
2
⎤ ⎥
2πε0 ⎢⎣
ρ
⎥⎦
=
G −eρ
ρl0 2πε 0
d dρ
[ln(
ρ 2 + (L / 2)2 + L / 2) − ln ρ]
=
G −eρ
ρl0 2πε 0
⎧⎪ ⎨ ⎪⎩[L / 2 +
ρ ρ 2 + (L / 2)2 ]
ρ2
+ (L / 2)2
−
1 ⎫⎪
ρ
⎬ ⎪⎭
=
L/2
ρl0ρdz '
0 2πε0 (ρ 2 + z '2 )3/ 2
=
G eρ
ρl 0 2πε 0 ρ
⎛ ⎜⎜⎝
=
G eρ
ρl 0 4πε 0 ρ
由
G E
=
−∇ϕ
求
G E
,有
电磁场与电磁波(西安交大第三版)第3章课后答案
第3章习题3-1 半径为a 的薄圆盘上电荷面密度为s ρ,绕其圆弧轴线以角频率ω旋转形成电流,求电流面密度。
解:圆盘以角频率ω旋转,圆盘上半径为r 处的速度为r ω,因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中,每立方米体积中大约有28105.8⨯个自由电子。
如果铜线的横截面为210cm ,电流为A 1500。
计算1) 电子的平均漂移速度; 2) 电流密度; 解:2〕电流密度 m A S I J /105.11010150064⨯=⨯==- 1) 电子的平均漂移速度v J ρ= , 3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m Jv /101.11036.1105.14106-⨯=⨯⨯==ρ3-3 一宽度为cm 30传输带上电荷均匀分布,以速度s m /20匀速运动,形成的电流,对应的电流强度为A μ50,计算传输带上的电荷面密度。
解:电流面密度为 m A L I J S /7.1663.050μ=== 因为 v J S S ρ=2/33.8207.166m C v J S S μρ===3-4 如果ρ是运动电荷密度,U是运动电荷的平均运动速度,证明:0=∂∂+∇⋅+⋅∇tU U ρρρ解:如果ρ是运动电荷密度,U是运动电荷的平均运动速度,则电流密度为U Jρ=代入电荷守恒定律t J ∂∂-=⋅∇ρ得 0=∂∂+∇⋅+⋅∇t U U ρρρ 3-5 由m S /1012.17⨯=σ的铁制作的圆锥台,高为m 2,两端面的半径分别为cm 10和cm 12。
求两端面之间的电阻。
解:用两种方法〔1〕⎰⎰===21222)(tan zz z dz S dl R ασπσ)11()(tan 1212z z -=ασπ01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α,m r z 1201.0/12.0tan /21===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R 〔2〕设流过的电流为I ,电流密度为2r IS I J π==电场强度为 2r I J E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上,媒质1的参数为2,/10011==r m S εσ,电流密度的大小为2/50m A ,方向和界面法向的夹角为030;媒质2的参数为4,/1022==r m S εσ。
教科版物理选修3-4学案:第三章 电磁振荡 电磁波 章末整合提升 Word版含解析
章末整合提升一、麦克斯韦电磁场理论1.对麦克斯韦电磁场理论两个基本观点的理解(1)变化的磁场产生电场,可从以下三个方面理解:①稳定的磁场不产生电场②均匀变化的磁场产生恒定的电场③周期性变化的磁场产生同频率的周期性变化的电场(2)变化的电场产生磁场,也可从以下三个方面理解:①恒定的电场不产生磁场②均匀变化的电场产生恒定的磁场③周期性变化的电场产生同频率的周期性变化的磁场2.感应电场方向的判定变化的磁场产生的感应电场的方向,与存在闭合回路时产生的感应电流的方向是相同的.例1关于麦克斯韦的电磁场理论,下列说法正确的是()A.稳定的电场产生稳定的磁场B.均匀变化的电场产生均匀变化的磁场,均匀变化的磁场产生均匀变化的电场C.变化的电场产生的磁场一定是变化的D.振荡的电场周围空间产生的磁场也是振荡的解析麦克斯韦的电磁场理论要点是:变化的磁场(电场)要在周围空间产生电场(磁场),若磁场(电场)的变化是均匀的,产生的电场(磁场)是稳定的,若磁场(电场)的变化是振荡的,产生的电场(磁场)也是振荡的,由此可判定正确答案为D项.答案 D例2一个带正电的粒子在垂直于匀强磁场的平面内做匀速圆周运动,如图1所示.当磁感应强度均匀增大时,此粒子的()图1A.动能不变B.动能增大C.动能减小D.以上情况都可能解析当磁场均匀增强时,根据麦克斯韦电磁场理论,将激起一稳定的电场,带电粒子将受到电场力作用,电场力对带正电的粒子做正功,所以粒子的动能将增大.故正确答案为B.答案 B二、LC回路振荡规律、周期及频率1.LC回路中各量的变化规律电容器上的物理量:电荷量q、电场强度E、电场能E E.振荡线圈上的物理量:振荡电流i、磁感应强度B、磁场能E B.放电过程:q↓—E↓—E E↓―→i↑—B↑—E B↑充电过程:q↑—E↑—E E↑―→i↓—B↓—E B↓充电结束时q、E、E E最大,i、B、E B均为零放电结束时q、E、E E均为零,i、B、E B最大2.电磁振荡的周期和频率(1)周期T=2πLC频率f=12πLC(2)对周期公式T=2πLC的定性分析①L对T的影响:L越大,振荡过程中因自感现象产生的自感电动势就越大,楞次定律中所说的“阻碍”作用也就将越大,从而延缓振荡电流的变化,使振荡周期T变长.②C对T的影响:C越大,振荡过程中无论是充电阶段(将C充至一定电压),还是放电阶段(将一定电压下的电容器C中的电荷量放完),其时间都相应地变长,从而使振荡周期T 变长.例3(多选)为了测量储罐中不导电液体的高度,将与储罐外壳绝缘的两块平行金属板构成的电容器C置于储罐中,电容器可通过开关S与线圈L或电源相连,如图2所示.当开关从a拨到b时,由L与C构成的回路中产生周期T=2πLC的振荡电流.当罐中的液面上升时()图2A.电容器的电容减小B.电容器的电容增大C.LC回路的振荡频率减小D.LC回路的振荡频率增大解析当罐中液面上升时,电容器极板间的介电常数变大,则电容器的电容C增大,根据T=2πLC,可知LC回路的振荡周期T变大,又f=1T,所以振荡频率变小,故选项B、C正确,选项A、D错误.答案BC三、电磁波的传播特点及应用1.电磁波谱无线电波、红外线、可见光、紫外线、伦琴射线(X射线)、γ射线等合起来,便构成了范围非常广阔的电磁波谱.2.各种不同的电磁波既有共性,又有个性(1)共性:它们在本质上都是电磁波,它们的行为服从相同的规律,都满足公式v=fλ,它们在真空中的传播速度都是c=3×108m/s,它们的传播都不需要介质,各波段之间的区别并没有绝对的意义.(2)个性:不同电磁波的频率或波长不同,表现出不同的特性.波长越长越容易产生干涉、衍射现象,波长越短观察干涉、衍射现象越困难.正是这些不同的特性决定了它们不同的用途.例4(多选)下列有关电磁波的说法中正确的是()A.电磁波谱中最难发生衍射的是无线电波B.电磁波谱中最难发生衍射的是γ射线C.频率大于可见光的电磁波表现为沿直线传播D.雷达用的是微波,因为微波传播的直线性好解析波长越长,越容易发生衍射现象,在电磁波中,无线电波波长最长,γ射线的波长最短,故选项A错误,B正确;波长越短,频率越大的电磁波,其衍射现象越不明显,传播的直线性越好,遇到障碍物反射性越好,故C、D正确.答案BCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 静电场的电介质3.2.1 偶极矩为p =l q 的电偶极子,处于场强为的外电场中, p与E的夹角为θ。
(1)若是均匀的,θ为什么值时,电偶极子达到平衡?(2)如果E是不均匀的,电偶极子能否达到平衡? 解: (1)偶极子受的力:F + =F _=qE因而+F =--F故偶极子受合力为零。
偶极子受的力矩 T =p ⨯E即 T=pE sin θ当 T=0时,偶极子达到平衡,∴ pE sin θ =0 p ≠0 E ≠0 ∴θ=0, π θ=0这种平衡是稳定平衡。
θ=π是不稳定平衡。
(2)当E 不是均匀电场时,偶极子除受力矩外还将受一个力(作用在两个点电荷的电场力的合力)。
所以不能达到平衡。
3.2.2 两电偶极子1p 和2p 在同一直线上,所以它们之间距r 比它们自己的线度大的很多。
证明:它们的相互作用力的大小为F=402123r p p πε,力的方向是: 1p 与2p 同方向时互相吸引,反方向时互相排斥。
证: 已知当r>>l 时,偶极子在其延长线上一点的场强:302rpE πε= 当 1p →与2p →同方向时,如图2p →所受的力的大小:+→F =Eq =r lr q p ∧+3201)2(2πε-→F = -q E →=r lr qp ∧--3201)2(2πε∴F →= +→F +-→F =r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =r l r l l r q p ∧⎥⎦⎤⎢⎣⎡---⋅3222322201)2()2(2262πε略去 422l 及 832l 等高级小量。
F →=-r r qlp ∧402146πε= -r rpp ∧402123πε当 1p →与2p →反方向时(如图),同理:F →=r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--323201)2(1)2(12πε =012πεq p ⨯r l r l l r ∧-+32223222)4()2(23略去高级小量得:F →=r r P P ∧42123πε3.2.3 一电偶极子处在外电场中,其电偶极矩为p ql =,其所在处的电场强度为E 。
(1)求电偶极子在该处的电位能,(2)在什么情况下电偶极子的电位能最小?其值是 多少? (3)在什么情况下电偶极子的电位能最大?其值是多少? 解: (1)电位能:W =q +U -q _U =q U ∆ 又由于E →=-ˆU n n∆∆,=∆n cos l θ (θ是l →与E →间夹角) ∴ θcos El n E U -=∆-=∆∴ cos W qEl θ=-= -p E ⋅ (2)当p →与E →一致时,W pE =-.即θ=0时电位能最小。
(3)当p →与E →方向相反时,W pE =. 即θ=π时电位能最大。
3.2.4 一电偶极子,由q=1.0⨯108-(库)的两个异号电荷所组成,这两个电荷相距为l=2.0(厘米),把这电偶极子放在1.0⨯105牛顿/库伦的均匀外场中,试求:(1)作用于电偶极子上最大转矩的多大?(2)偶极子从原来位置(0θ=)转到最大转矩时,外力所作的功是多大? 解:(1)外电场是匀强电场时,偶极子受的力矩为: T=pEsin θ 当时θ=2π时,力矩最大, T=pE qlE ==108-⨯2⨯102-⨯105 =2⨯103- (牛顿∙米)(2)把偶极子从原来的位置(0θ=)转到最大转矩时,外力所做的功:A=⎰20πθTd =⎰20sin πθθd pE =pE =2⨯103-(牛顿∙米)3·4·1 一平行板电容器面积为S ,面板间距离为d ,中间充满均匀电介质,已知当一板上自己电荷为Q 时,整块介质的总偶极矩为p 总, 求电容器中的电场强度。
解:整块介质的总偶极矩为p 总,∴极化强度P =p Sd 总设n 上、n 下是介质上下两面的外法线, =P n =-P n P σ∴∙=-上上,=P n =-P n P σ∙=-下下 自由电荷激发的场强:0000ˆˆAB AB Q E r r S σεε== 极化电荷激发的场强:0000ˆˆˆˆ=-BA AB ABAB P P E r r r r Sd σσεεεε'===-下下总 ∴电容器中电场强度:00001()()AB P Q PE E E r Q S Sd S dεεε'=+=-=-总 3·4·2 一半径为R ,厚度为d 的均匀介质圆板(R>>d )被均匀极化,其极化强度为P ,且平行于板画(如图所示),求极化电荷在圆板中心产生的电场强度。
解:如图所示,在柱坐标系中:cos n P P σϕ'==ϕ是面元法线与极化强度P 为夹角 2204()dsdE R z σπε'=+其中 ds Rd dz ϕ=根据对称性分析,极化电荷在圆板中心产生的电场强度只有y 方向分量(y 轴与P 反方向),2204()y Rd dz dE R z σϕϕπε'=+=22220cos 4()PR d dz R z ϕϕπε+∴22220cos 24()PR E d dz R z ϕϕπε=+⎰⎰=2223022222cos 4()d d PR dz d R z πϕϕπε-+⎰⎰=221220222()4PR d d R R ππε+当R>>d 时,略去高级小量24d 得:00ˆ44PdPd E j R Rπεε==-3.4.3 在图中A 为一块金属,其外部充满均匀介质,其极化率为x ,已知交界面上某点的极化电荷面密度为 ,求该点的自由电荷面密度。
解: 在静点平衡时,利用高斯定理可得,导体外(即介质内)紧靠导体表面一点的场强为: 00000ˆˆE n n n σσσσσεεε''++'===- ˆn '与ˆn 反方向,如图所示,ˆn '是介质表面外法线. 又由于在介质内: 0P E χε=;00PE n σχεχε''∴==000ˆn n σσσχεε''+''∴=- 01(1)(1)σχσσχχ'-+'=-+=3.4.4求一均匀极化的电介质球表面上极化电荷的分布,已知极化强度为P ,如图所示.解: 取球心o 为原点,极轴与P 平行的球坐标,由于轴对称性,表面上任一点A 的极化电荷密度σ'只与θ角有关.这也是A 点外法线n 与P 的夹角,故ˆcos P nP σθ'=∙= 这表明:在右半球σ'为正,左半球σ'为负; 在两半球分界线面上,2πθ=处,0σ'=在0θ=与π处,σ'最大。
3·4·5 图中沿x 轴放置的介质圆柱,地面积为S ,周围是真空,已知介质内个点极化矢量ˆP kxi =(k 为常数) (1)求圆柱两底面上的极化电荷密度aσ'及b σ' ; (2)求出圆柱内体电荷密度ρ'。
解:(1)ˆcos ˆcos 0aa a a bb b b P n P ka P n P kb σπσ'=⋅==-'=⋅==(2)由定义得:()kSdx Skdx Sdx S P P S d P p x dxx s-=-=--=⋅-='+⎰⎰τ 3.4.6平行板电容器充满了极化率为新的均匀电介质,已知充电后金属板极板上的自由电荷面密度为0σ±,求电容器的电容C 与没有电介质时的电容0C 之比。
解:P n P =⋅='ˆσ 极化电荷的场强:00εεσPE ='=' 自由电荷的场强:00εσ=E 0E 与E '反方向,()()x x E E E x E xE E Ex E PE E E E +=+=+=∴-=-=-=-=∴1110000000000εσεεε()x dEd U +==100εσS Q 0σ=()()0011C x dS x U Q C +=+==∴ε 3.4.7一空气平行板电容器,面积S=0.2(2米),d=1.0(厘米),充电后断开电源,其电位差()伏30103⨯=U ,当电介质充满两板间以后,则电压降至1000伏,试计算: (1)原电容0C ;(2)每一个导体板上的电量Q ; (3)放入电介质后的电容C ; (4)两板间的原电场强度0E ; (5)放入电介质后的电场强度E ; (6)电介质每一面上的极化电荷Q '; (7)电介质的相对介电常数r ε[提示00C C =ε]。
解:()()法拉101212001077.1102.01085.81---⨯=⨯⨯==d SC ε ()()库伦710001031.530001077.12--⨯=⨯⨯==U C Q()()法拉10371031.5101031.53--⨯=⨯==U Q C ()()米伏/1031030004520⨯===-dU E ()()米伏/.1010105523===-d U E()E E E '-=060εσ'=-='∴E E E ()()()库伦75512001045.32.010*******.8--⨯=⨯-⨯⨯=-='='SE E S Q εσ()3107.11031.5710100=⨯⨯==--C C r ε3.4.8 两相距为5.0毫米的平行导体板间均匀充满相对介电常数()10.3+==x r r εε的电介质,其介质内的电场强度是610伏/米。
试求: (1)在导体板上的面电荷密度0σ; (2)在电介质面上的极化面电荷密度σ' 解:(1)利用3.4.6题结论: ()dSx C +=10ε又由于Ed SU Q C 0σ==()EdSdSx 001σε=+∴()()251260001065.231058.8101库--⨯=⨯⨯⨯==+=r E x E εεεσ()()()0012652(2)1318.5810101.7710r P x E Eσεεε--'===-=-⨯⨯⨯=⨯库米3.4.9在相对介电常数为()1+=x r r εε的电介质中有一强度为E的均匀电场。
在介质内有一球形空腔。
求球面上的极化电荷在球心产生的电场强度E '。
解:如图所示,在均匀电介质中:()θσεεεcos ˆ100P n P EE x P r -=⋅='-==nˆ是介质表面的外法线即指向球心。
R R ds E d ˆ420πεσ'='根据对称性分析可得,E '只有z 方向分量,⎰⎰⎰⎰-='='='ππθπεθθϕπεθϕθσθ20202202024sin cos 4sin cos d R R P d R d d R E d E s s=3εP =31-r ε E∴ ='E 31-r εE 3.5.1两平行导体板相距5.0毫米,带有等量异号电荷,面密度为20微库/米2,其间有两片电介质,一片厚2.0毫米,r ε=3.0毫米,r ε=4.0。
