平面向量知识点与2013考点精讲(经典)
(完整版)平面向量知识点与考点精(经典)
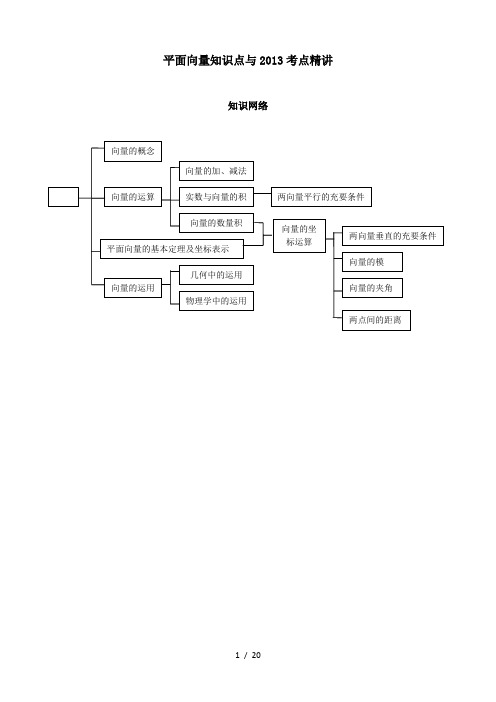
平面向量知识点与2013考点精讲知识网络第1讲 向量的概念与线性运算★ 知 识 梳理 ★1.平面向量的有关概念:(1)向量的定义:既有____大小又有方向_________的量叫做向量.(2)表示方法:用有向线段来表示向量.有向线段的____长度_____表示向量的大小,用_____箭头所指的方向____表示向量的方向.用字母a ,b ,…或用AB ,BC ,…表示.特别提醒:1) 模:向量的长度叫向量的模,记作|a |或|AB |. 2) 零向量:长度为零的向量叫做零向量,记作0;零向量的方向不确定. 3) 单位向量:长度为1个长度单位的向量叫做单位向量.4) 共线向量:方向相同或相反的向量叫共线向量,规定零向量与任何向量共线. 5)相等的向量:长度相等且方向相同的向量叫相等的向量.2.向量的线性运算 1.向量的加法:(1)定义:求两个向量和的运算,叫做向量的加法.如图,已知向量a ,b ,A ,作AB =u u u ra ,BC =u u u rb ,则向量AC 叫做a 与b 的和,记作a+b ,即 a+b AB BC AC =+=u u u r u u u r u u u r特殊情况:abab a+bbaa+b(1)平行四边形法则三角形法则CBDCBabba +ba +AABC C)2()3(对于零向量与任一向量a ,有 a 00+=+ a = a(2)法则:____三角形法则_______,_____平行四边形法则______(3)运算律:____ a +b =b +a ;_______,____(a +b )+c =a +(b +c )._______ 2.向量的减法:(1)定义:求两个向量差的运算,叫做向量的减法. 减法的三角形法则作法:在平面内取一点O , 作OA = a , = b , 则= a - b即a - b 可以表示为从向量b 的终点指向向量a 的终点的向量注意:1)AB表示a-b强调:差向量“箭头”指向被减数2)用“相反向量”定义法作差向量,a-b = a +(-b)显然,此法作图较繁,但最后作图可统一a∥b∥c a - b = a + (-b) a - b3.实数与向量的积:(1)定义:实数λ与向量a的积是一个向量,记作λa,规定:|λa|=|λ||a|.当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0.(2)运算律:λ(μa)=(λμ)a,(λ+μ)a=λa+μa,λ(a+b)=λa+λb.特别提醒:1)向量的加、减及其与实数的积的结果仍是向量。
高考数学平面向量考点及知识点总结解析(理科)

平行且|a|=1,则 a=a0.假命题的个数是
()
A.0
B.1
C.2
D.3
[解析] 向量是既有大小又有方向的量,a 与|a|a0 的模相同,
但方向不一定相同,故①是假命题;若 a 与 a0 平行,则 a 与 a0
的方向有两种情况:一是同向,二是反向,反向时 a=-|a|a0,
故②③也是假命题.综上所述,假命题的个数是 3.
3.如图,设O是正六边形ABCDEF的中心,则图中与 OC 相等 的向量有________.
答案: AB, ED,FO
4.如图,△ABC和△A′B′C′是在各边的
1 3
处相交的两个全等
的等边三角形,设△ABC的边长为a,图中列出了长度均为
a 3
的若干个向量,则
(1)与向量GH 相等的向量有________; (2)与向量GH 共线,且模相等的向量有________; (3)与向量 EA共线,且模相等的向量有________. 解析:向量相等⇔向量方向相同且模相等. 向量共线⇔表示有向线段所在的直线平行或重合. 答案:(1) LB, HC (2) EC, LE , LB,GB, HC (3) EF ,FB, HA, HK , KB
HF
=
1 4
AH ,∴ AH =45 AF , AF = AD+ DF =b+12a,∴ AH =45
b+12a=25a+45b,故选B. 答案:B
4. [考点二] 已知a,b是两个不共线的非零向量,且a与b起点
相同.若a,tb,
1 3
(a+b)三向量的终点在同一直线上,则t
=________.
解析:∵a,tb,
与向量 b 相同,且|aa|=|bb|,所以向量 a 与向量 b 方向相同,故
【全程复习方略】2013版高中数学 (主干知识+典例精析)4.4平面向量的应用课件 理 新人教B版

(
)
②在△ABC中,若 ABBC <0,则△ABC为钝角三角形.(
)
③在四边形ABCD中,边AB与CD为对边,若 AB DC, 则此四边形
为平行四边形.
(
)
【解析】①因为 AB、 共始点A,且 AB∥ AC, 故①正确; AC ②∵ ABBC<0⇔ BABC>0,∴∠B为锐角,不能判断△ABC
利用向量的意义、运算脱去“向量外衣”,导出曲线上点的坐
标之间的关系,从而解决有关距离、斜率、夹角、轨迹、最值 等问题. (2)工具作用:利用 a⊥b ⇔ a·b =0, a∥b ⇔a=λ b (b≠0),可解决 垂直、平行问题.
【例3】已知两点M(-1,0),N(1,0),且点P使
NMNP,PMPN,MPMN 成公差非负的等差数列.
=(5,3b-4y). ∴| PA 3PB|2=25+(3b-4y)2(0≤y≤b), 当y=
3 b时,| PA 3PB|最小,|PA 3PB|min=5. 4
答案:5
【反思·感悟】平面几何问题的向量解法 (1)坐标法 把几何图形放在适当的坐标系中,就赋予了有关点与向量具体的 坐标,这样就能进行相应的代数运算和向量运算,从而使问题得 到解决.
【提醒】向量关系与几何关系并不完全相同,要注意区别, 例如:向量 AB∥ CD 并不能说明直线AB∥CD.
【例1】(2011·天津高考)已知直角梯形ABCD中,AD∥BC,
∠ADC=90°,AD=2,BC=1,P是腰DC上的动点,则|PA 3PB |的最小
的形状,故②不正确; ③∵ AB DC, ∴AB 答案:①√ ②〓
平面向量基本定理及坐标表示知识点讲解+例题讲解(含解析)

平面向量的基本定理及坐标表示一、知识梳理1.平面向量的基本定理如果e 1,e 2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a ,有且只有一对实数λ1,λ2,使a =λ1e 1+λ2e 2.其中,不共线的向量e 1,e 2叫做表示这一平面内所有向量的一组基底. 2.平面向量的正交分解把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 3.平面向量的坐标运算(1)向量加法、减法、数乘运算及向量的模 设a =(x 1,y 1),b =(x 2,y 2),则a +b =(x 1+x 2,y 1+y 2),a -b =(x 1-x 2,y 1-y 2),λa =(λx 1,λy 1),|a |=x 21+y 21.(2)向量坐标的求法①若向量的起点是坐标原点,则终点坐标即为向量的坐标.②设A (x 1,y 1),B (x 2,y 2),则AB →=(x 2-x 1,y 2-y 1),|AB →|=(x 2-x 1)2+(y 2-y 1)2. 4.平面向量共线的坐标表示设a =(x 1,y 1),b =(x 2,y 2),则a ∥b ⇔x 1y 2-x 2y 1=0.小结:1.若a =(x 1,y 1),b =(x 2,y 2)且a =b ,则x 1=x 2且y 1=y2. 2.若a 与b 不共线,λa +μb =0,则λ=μ=0.3.向量的坐标与表示向量的有向线段的起点、终点的相对位置有关系.两个相等的向量,无论起点在什么位置,它们的坐标都是相同的.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”) (1)平面内的任何两个向量都可以作为一组基底.( ) (2)同一向量在不同基底下的表示是相同的.( )(3)设a ,b 是平面内的一组基底,若实数λ1,μ1,λ2,μ2满足λ1a +μ1b =λ2a +μ2b ,则λ1=λ2,μ1=μ2.( )(4)若a =(x 1,y 1),b =(x 2,y 2),则a ∥b 的充要条件可以表示成x 1x 2=y 1y 2.( )解析 (1)共线向量不可以作为基底. (2)同一向量在不同基底下的表示不相同. (4)若b =(0,0),则x 1x 2=y 1y 2无意义.答案 (1)× (2)× (3)√ (4)×2.下列各组向量中,可以作为基底的是( ) A.e 1=(0,0),e 2=(1,-2) B.e 1=(-1,2),e 2=(5,7) C.e 1=(3,5),e 2=(6,10) D.e 1=(2,-3),e 2=⎝ ⎛⎭⎪⎫12,-34解析 两个不共线的非零向量构成一组基底,故选B. 答案 B3.设P 是线段P 1P 2上的一点,若P 1(1,3),P 2(4,0)且P 是线段P 1P 2的一个三等分点(靠近点P 1),则点P 的坐标为( ) A.(2,2)B.(3,-1)C.(2,2)或(3,-1)D.(2,2)或(3,1)解析 由题意得P 1P →=13P 1P 2→且P 1P 2→=(3,-3). 设P (x ,y ),则(x -1,y -3)=(1,-1), ∴x =2,y =2,则点P (2,2). 答案 A4.(2015·全国Ⅰ卷)已知点A (0,1),B (3,2),向量AC →=(-4,-3),则向量BC →=( ) A.(-7,-4) B.(7,4) C.(-1,4)D.(1,4)解析 根据题意得AB→=(3,1),∴BC →=AC →-AB →=(-4,-3)-(3,1)=(-7,-4),故选A. 答案 A5.(2017·山东卷)已知向量a =(2,6),b =(-1,λ),若a ∥b ,则λ=________. 解析 ∵a ∥b ,∴2λ+6=0,解得λ=-3. 答案 -36.(2019·苏州月考)已知▱ABCD 的顶点A (-1,-2),B (3,-1),C (5,6),则顶点D 的坐标为________.解析 设D (x ,y ),则由AB →=DC →,得(4,1)=(5-x ,6-y ),即⎩⎨⎧4=5-x ,1=6-y ,解得⎩⎨⎧x =1,y =5. 答案 (1,5)考点一 平面向量基本定理及其应用【例1】 (1)(2019·衡水中学调研)一直线l 与平行四边形ABCD 中的两边AB ,AD 分别交于点E ,F ,且交其对角线AC 于点M ,若AB →=2AE →,AD →=3AF →,AM →=λAB →-μAC→(λ,μ∈R ),则52μ-λ=( ) A.-12B.1C.32D.-3解析 (1)AM→=λAB →-μAC →=λAB →-μ(AB →+AD →) =(λ-μ)AB→-μAD →=2(λ-μ)AE →-3μAF →.因为E ,M ,F 三点共线,所以2(λ-μ)+(-3μ)=1, 即2λ-5μ=1,∴52μ-λ=-12.(2)(2019·北京海淀区调研)在△ABC 中,D 为三角形所在平面内一点,且AD→=13AB→+12AC →.延长AD 交BC 于E ,若AE →=λAB →+μAC →,则λ-μ的值是________.解析:(2)设AE →=xAD →,∵AD →=13AB →+12AC →, ∴AE→=x 3AB →+x 2AC →. 由于E ,B ,C 三点共线,∴x 3+x 2=1,x =65.根据平面向量基本定理,得λ=x 3,μ=x2.因此λ-μ=x 3-x 2=-x 6=-15.答案 (1)A (2)-15【训练1】 (1)(2019·济南质检)在△ABC 中,AN→=14NC →,若P 是直线BN 上的一点,且满足AP→=mAB →+25AC →,则实数m 的值为( ) A.-4B.-1C.1D.4解析 (1)根据题意设BP →=nBN →(n ∈R ),则AP →=AB →+BP →=AB →+nBN →=AB →+n (AN →-AB→)=AB →+n ⎝ ⎛⎭⎪⎫15AC →-AB →=(1-n )AB →+n 5AC →. 又AP →=mAB →+25AC →,∴⎩⎪⎨⎪⎧1-n =m ,n 5=25,解得⎩⎨⎧n =2,m =-1.(2)在平面直角坐标系中,O 为坐标原点,A ,B ,C 三点满足OC→=23OA →+13OB →,则|AC→||AB →|=________. 解析:(2)因为OC→=23OA →+13OB →,所以OC →-OA →=-13OA →+13OB →=13(OB →-OA →),所以AC →=13AB →,所以|AC →||AB →|=13.考点二 平面向量的坐标运算【例2】 (1)设A (0,1),B (1,3),C (-1,5),D (0,-1),则AB→+AC →等于( )A.-2AD →B.2AD →C.-3AD →D.3AD →(2)向量a ,b ,c 在正方形网格中的位置如图所示,若c =λa +μb (λ,μ∈R ),则λμ=( )A.1B.2C.3D.4解析 (1)由题意得AB →=(1,2),AC →=(-1,4),AD →=(0,-2),所以AB →+AC →=(0,6)=-3(0,-2)=-3AD→.(2)以向量a 和b 的交点为原点建立如图所示的平面直角坐标系(设每个小正方形边长为1),则A (1,-1),B (6,2),C (5,-1),∴a =AO→=(-1,1),b =OB →=(6,2),c =BC →=(-1,-3), ∵c =λa +μb ,∴(-1,-3)=λ(-1,1)+μ(6,2),则⎩⎨⎧-λ+6μ=-1,λ+2μ=-3,解得λ=-2,μ=-12,∴λμ=-2-12=4. 答案 (1)C (2)D【训练2】 (1)已知O 为坐标原点,点C 是线段AB 上一点,且A (1,1),C (2,3),|BC →|=2|AC →|,则向量OB →的坐标是________.解析 (1)由点C 是线段AB 上一点,|BC →|=2|AC →|,得BC →=-2AC →.设点B 为(x ,y ),则(2-x ,3-y )=-2(1,2). 则⎩⎨⎧2-x =-2,3-y =-4,解得⎩⎨⎧x =4,y =7. 所以向量OB→的坐标是(4,7).(2)(2019·天津和平区一模)如图,在直角梯形ABCD 中,AB ∥DC ,AD ⊥DC ,AD =DC =2AB ,E 为AD 的中点,若CA →=λCE →+μDB →(λ,μ∈R ),则λ+μ的值为( )A.65B.85C.2D.83解析:(2)建立如图所示的平面直角坐标系,则D (0,0).不妨设AB =1,则CD =AD =2,所以C (2,0),A (0,2),B (1,2),E (0,1), ∴CA→=(-2,2),CE →=(-2,1),DB →=(1,2), ∵CA→=λCE →+μDB →,∴(-2,2)=λ(-2,1)+μ(1,2), ∴⎩⎨⎧-2λ+μ=-2,λ+2μ=2,解得⎩⎪⎨⎪⎧λ=65,μ=25,则λ+μ=85.答案 (1)(4,7) (2)B考点三 平面向量共线的坐标表示 角度1 利用向量共线求向量或点的坐标【例3-1】 已知点A (4,0),B (4,4),C (2,6),则AC 与OB 的交点P 的坐标为________.解析 法一 由O ,P ,B 三点共线,可设OP →=λOB →=(4λ,4λ),则AP →=OP →-OA →=(4λ-4,4λ).又AC→=OC →-OA →=(-2,6), 由AP→与AC →共线,得(4λ-4)×6-4λ×(-2)=0,解得λ=34,所以OP →=34OB →=(3,3), 所以点P 的坐标为(3,3).法二 设点P (x ,y ),则OP→=(x ,y ),因为OB →=(4,4),且OP →与OB →共线,所以x4=y4,即x =y .又AP→=(x -4,y ),AC →=(-2,6),且AP →与AC →共线, 所以(x -4)×6-y ×(-2)=0,解得x =y =3,所以点P 的坐标为(3,3). 答案 (3,3)角度2 利用向量共线求参数【例3-2】 (1)(2018·全国Ⅲ卷)已知向量a =(1,2),b =(2,-2),c =(1,λ).若c ∥(2a +b ),则λ=________.(2)已知向量a =(2,3),b =(-1,2),若m a +n b 与a -3b 共线,则mn =________. 解析 (1)由题意得2a +b =(4,2),因为c =(1,λ),且c ∥(2a +b ),所以4λ-2=0,即λ=12. (2)由2-1≠32,所以a 与b 不共线, 又a -3b =(2,3)-3(-1,2)=(5,-3)≠0. 那么当m a +n b 与a -3b 共线时, 有m 1=n -3,即得m n =-13.答案 (1)12 (2)-13【训练3】 (1)(2019·北师大附中检测)已知向量a =(1,1),点A (3,0),点B 为直线y =2x 上的一个动点,若AB→∥a ,则点B 的坐标为________.(2)设向量OA →=(1,-2),OB →=(2m ,-1),OC →=(-2n ,0),m ,n ∈R ,O 为坐标原点,若A ,B ,C 三点共线,则m +n 的最大值为( ) A.-3B.-2C.2D.3解析 (1)由题意设B (x ,2x ),则AB→=(x -3,2x ),∵AB →∥a ,∴x -3-2x =0,解得x =-3,∴B (-3,-6).(2)由题意易知,AB →∥AC →,其中AB →=OB →-OA →=(2m -1,1),AC →=OC →-OA →=(-2n -1,2),所以(2m -1)×2=1×(-2n -1),得:2m +1+2n =1. 2m +1+2n ≥22m +n +1,所以2m +n +1≤2-2,即m +n ≤-3. 答案 (1)(-3,-6) (2)A三、课后练习1.如图,在△ABC 中,AD→=23AC →,BP →=13BD →,若AP →=λAB →+μAC →,则λ+μ的值为( )A.89B.49C.83D.43解析 AP→=AB →+BP →=AB →+13BD →=AB →+13(AD →-AB →)=23AB →+13×23AC →=23AB →+29AC →.因为AP →=λAB →+μAC →,所以λ=23,μ=29,则λ+μ=23+29=89. 答案 A2.给定两个长度为1的平面向量OA →和OB →,它们的夹角为90°,如图所示,点C 在以O 为圆心的圆弧AB ︵上运动,若OC →=xOA →+yOB →,其中x ,y ∈R ,则x +y 的最大值是( )A.1B. 2C. 3D.2解析 因为点C 在以O 为圆心的圆弧AB ︵上,所以|OC→|2=|xOA →+yOB →|2=x 2+y 2+2xyOA →·OB →=x 2+y 2,∴x 2+y 2=1,则2xy ≤x 2+y 2=1. 又(x +y )2=x 2+y 2+2xy ≤2, 故x +y 的最大值为 2. 答案 B3.已知|OA→|=1,|OB →|=3,OA →·OB →=0,点C 在∠AOB 内,且OC →与OA →的夹角为30°,设OC→=mOA →+nOB →(m ,n ∈R ),则m n 的值为________.解析 ∵OA→·OB →=0,∴OA →⊥OB →,以OA 为x 轴,OB 为y 轴建立直角坐标系,OA→=(1,0),OB →=(0,3),OC →=mOA →+nOB →=(m ,3n ). ∵tan 30°=3n m =33,∴m =3n ,即mn =3. 答案 34.在△ABC 中,点D 满足BD→=DC →,当点E 在线段AD 上移动时,若AE →=λAB →+μAC→,则t =(λ-1)2+μ2的最小值是________. 解析 因为BD→=DC →,所以AD →=12AB →+12AC →.又AE→=λAB →+μAC →,点E 在线段AD 上移动,所以AE→∥AD →,则12λ=12μ,即λ=μ⎝ ⎛⎭⎪⎫0≤λ≤12. 所以t =(λ-1)2+λ2=2λ2-2λ+1=2⎝ ⎛⎭⎪⎫λ-122+12.当λ=12时,t 的最小值是12. 答案 125.直角△ABC 中,AB =AC =2,D 为AB 边上的点,且AD DB =2,则CD →·CA →=________;若CD→=xCA →+yCB →,则xy =________. 解析 以A 为原点,分别以AB→,AC →的方向为x 轴、y 轴的正方向建立平面直角坐标系,则A (0,0),B (2,0),C (0,2),D ⎝ ⎛⎭⎪⎫43,0,则CD →=⎝ ⎛⎭⎪⎫43,-2,CA →=(0,-2),CB→=(2,-2),则CD →·CA →=⎝ ⎛⎭⎪⎫43,-2·(0,-2)=43×0+(-2)×(-2)=4.由CD→=x CA →+y CB →=x (0,-2)+y (2,-2)=(2y ,-2x -2y )=⎝ ⎛⎭⎪⎫43,-2得⎩⎪⎨⎪⎧2y =43,-2x -2y =-2,解得⎩⎪⎨⎪⎧x =13,y =23,则xy =29.答案 4 29。
(完整版)高中数学平面向量知识点总结

高中数学必修4之平面向量知识点归纳一.向量的基本概念与基本运算1、向量的概念:①向量:既有大小又有方向的量向量不能比较大小,但向量的模可以比较大小.②零向量:长度为0的向量,记为0,其方向是任意的,0与任意向量平行③单位向量:模为1个单位长度的向量④平行向量(共线向量):方向相同或相反的非零向量⑤相等向量:长度相等且方向相同的向量2、向量加法:设,ABa BCb uu u ru uu r r r ,则a +b r =AB BC u u u r u u u r =ACuu u r (1)a a a 00;(2)向量加法满足交换律与结合律;AB BCCDPQQRAR u u u r u u u r u uu r u u u r u u u r u u u rL,但这时必须“首尾相连”.3、向量的减法:①相反向量:与a 长度相等、方向相反的向量,叫做a 的相反向量②向量减法:向量a 加上b 的相反向量叫做a 与b 的差,③作图法:b a可以表示为从b 的终点指向a 的终点的向量(a 、b 有共同起点)4、实数与向量的积:实数λ与向量a 的积是一个向量,记作λa ,它的长度与方向规定如下:(Ⅰ)a a ;(Ⅱ)当0时,λa 的方向与a 的方向相同;当时,λa 的方向与a 的方向相反;当0时,0a,方向是任意的5、两个向量共线定理:向量b 与非零向量a 共线有且只有一个实数,使得b =a6、平面向量的基本定理:如果21,e e 是一个平面内的两个不共线向量,那么对这一平面内的任一向量a ,有且只有一对实数21,使:2211e ea,其中不共线的向量21,e e 叫做表示这一平面内所有向量的一组基底二.平面向量的坐标表示1平面向量的坐标表示:平面内的任一向量a r可表示成axi yj r rr ,记作a r=(x,y)。
2平面向量的坐标运算:(1)若1122,,,ax y bx y rr ,则1212,a bx x y y r r (2)若2211,,,y x B y x A ,则2121,AB x x y y u u u r(3)若a r =(x,y),则a r =(x, y)(4)若1122,,,a x y b x y r r ,则1221//0a b x y x y rr (5)若1122,,,ax y bx y rr ,则1212a bx x y y r r 若ab rr ,则02121y y x x 三.平面向量的数量积1两个向量的数量积:已知两个非零向量a r 与b r,它们的夹角为,则a r ·b r =︱a r︱·︱b r ︱cos 叫做a r与b r 的数量积(或内积)规定00ar r 2向量的投影:︱b r ︱cos =||a b a r r r ∈R ,称为向量b r 在a r方向上的投影投影的绝对值称为射影3数量积的几何意义:a r ·b r 等于a r 的长度与b r 在a r方向上的投影的乘积4向量的模与平方的关系:22||a a a a r r r r 5乘法公式成立:2222a b ab a b a b r r r r r r r r ;2222abaa bb r r r r r r 222aa bbr r r r 6平面向量数量积的运算律:①交换律成立:a bb arr r r ②对实数的结合律成立:a b a b a bRr r r r r r ③分配律成立:abca cb c r r r r r r r ca br r r 特别注意:(1)结合律不成立:ab ca b c r r r r r r ;(2)消去律不成立a ba cr r r r 不能得到bc rr (3)a b r r =0不能得到a r =0r或b r =0r 7两个向量的数量积的坐标运算:已知两个向量1122(,),(,)ax y b x y rr,则a r ·b r=1212x x y y 8向量的夹角:已知两个非零向量a r与b r ,作OA u u u r =a r , OB uuu r =b r ,则∠AOB=(01800)叫做向量a r 与b r 的夹角cos =cos,a b a ba b??r r r r r r =222221212121y x y x y y x x 当且仅当两个非零向量a r 与b r 同方向时,θ=00,当且仅当a r与b r 反方向时θ=1800,同时0r与其它任何非零向量之间不谈夹角这一问题9垂直:如果a r 与b r 的夹角为900则称a r 与b r 垂直,记作a r⊥br 10两个非零向量垂直的充要条件:a ⊥ba ·b =O02121y y x x 平面向量数量积的性质一、选择题1.在△ABC 中,AB =AC ,D ,E 分别是AB ,AC 的中点,则().A .AB 与AC 共线B .DE 与CB 共线C .AD 与AE 相等D .AD 与BD 相等2.下列命题正确的是().A .向量AB 与BA 是两平行向量B .若a ,b 都是单位向量,则a =bC .若AB =DC ,则A ,B ,C ,D 四点构成平行四边形D .两向量相等的充要条件是它们的始点、终点相同3.平面直角坐标系中,O 为坐标原点,已知两点A(3,1),B(-1,3),若点C满足OC =OA +OB ,其中,∈R ,且+=1,则点C 的轨迹方程为().A .3x +2y -11=0B .(x -1)2+(y -1)2=5C .2x -y =0D .x +2y -5=04.已知a 、b 是非零向量且满足(a -2b)⊥a ,(b -2a)⊥b ,则a 与b 的夹角是A .6B .3C .23D .565.已知四边形ABCD 是菱形,点P 在对角线AC 上(不包括端点A ,C ),则AP =A .λ(AB +AD ),λ∈(0,1)B .λ(AB +BC ),λ∈(0,22)C .λ(AB -AD ),λ∈(0,1)D .λ(AB -BC ),λ∈(0,22)6.△ABC 中,D ,E ,F 分别是AB ,BC ,AC 的中点,则DF =().(第1题)A.EF+ED B.EF-DE C.EF+AD D.EF+AF7.若平面向量a与b的夹角为60°,|b|=4,(a+2b)·(a-3b)=-72,则向量a的模为().A.2 B.4 C.6 D.128.点O是三角形ABC所在平面内的一点,满足OA·OB=OB·OC=OC·OA,则点O是△ABC的().A.三个内角的角平分线的交点B.三条边的垂直平分线的交点C.三条中线的交点D.三条高的交点9.在四边形ABCD中,AB=a+2b,BC=-4a-b,DC=-5a-3b,其中a,b不共线,则四边形ABCD为().A.平行四边形B.矩形C.梯形D.菱形10.如图,梯形ABCD中,|AD|=|BC|,EF∥AB∥CD则相等向量是().A.AD与BC B.OA与OBC.AC与BD D.EO与OF二、填空题11.已知向量OA=(k,12),OB=(4,5),OC=(-k,10),且A,B,C三点共线,则k=.12.已知向量a=(x+3,x2-3x-4)与MN相等,其中M(-1,3),N(1,3),则x=.13.已知平面上三点A,B,C满足|AB|=3,|BC|=4,|CA|=5,则AB·BC +BC·CA+CA·AB的值等于.14.给定两个向量a=(3,4),b=(2,-1),且(a+mb)⊥(a-b),则实数m 等于.15.已知A,B,C三点不共线,O是△ABC内的一点,若OA+OB+OC=0,则O是△ABC的.16.设平面内有四边形ABCD和点O,OA=a,OB=b,OC=c, OD=d,若a+c=b+d,则四边形ABCD的形状是.三、解答题17.已知点A(2,3),B(5,4),C(7,10),若点P满足AP=AB+λAC(λ∈R),试求λ为何值时,点P在第三象限内?(第10题)18.如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F,求DF.(第18题)19.如图,在正方形ABCD中,E,F分别为AB,BC的中点,求证:AF⊥DE(利用向量证明).(第19题) 20.已知向量a=(cos θ,sin θ),向量b=(3,-1),则|2a-b|的最大值.一、选择题1.B 解析:如图,AB 与AC ,AD 与AE 不平行,AD 与BD 共线反向.2.A解析:两个单位向量可能方向不同,故B 不对.若AB =DC ,可能A ,B ,C ,D 四点共线,故C 不对.两向量相等的充要条件是大小相等,方向相同,故D 也不对.3.D解析:提示:设OC =(x ,y),OA =(3,1),OB =(-1,3),OA =(3,),OB =(-,3),又OA +OB =(3-,+3),∴(x ,y)=(3-,+3),∴33+=-=y x ,又+=1,由此得到答案为D .4.B解析:∵(a -2b)⊥a ,(b -2a)⊥b ,∴(a -2b)·a =a 2-2a ·b =0,(b -2a)·b =b 2-2a ·b =0,∴a 2=b 2,即|a|=|b|.∴|a|2=2|a||b|cos θ=2|a|2cos θ.解得cos θ=21.∴a 与b 的夹角是3π.5.A解析:由平行四边形法则,AB +AD =AC ,又AB +BC =AC ,由λ的范围和向量数乘的长度,λ∈(0,1).6.D解析:如图,∵AF =DE ,∴DF =DE +EF =EF +AF .7.C解析:由(a +2b)·(a -3b)=-72,得a 2-a ·b -6b 2=-72.而|b|=4,a ·b =|a||b|cos 60°=2|a|,∴|a|2-2|a|-96=-72,解得|a|=6.8.D 解析:由OA ·OB =OB ·OC =OC ·OA ,得OA ·OB =OC ·OA ,即OA ·(OC -OB )=0,故BC ·OA =0,BC ⊥OA ,同理可证AC ⊥OB ,∴O 是△ABC 的三条高的交点.9.C解析:∵AD =AB +BC +D C =-8a -2b =2BC ,∴AD ∥BC 且|AD |≠|BC |.∴四边形ABCD 为梯形.10.D解析:AD 与BC ,AC 与BD ,OA 与OB 方向都不相同,不是相等向量.(第1题)二、填空题11.-32.解析:A ,B ,C 三点共线等价于AB ,BC 共线,AB =OB -OA =(4,5)-(k ,12)=(4-k ,-7),BC =OC -OB =(-k ,10)-(4,5)=(-k -4,5),又A ,B ,C 三点共线,∴5(4-k)=-7(-k -4),∴k =-32.12.-1.解析:∵M(-1,3),N(1,3),∴MN =(2,0),又a =MN ,∴=4-3-2=3+2x x x 解得4=1=-1=-x x x 或∴x =-1.13.-25.解析:思路1:∵AB =3,BC =4,CA =5,∴△ABC 为直角三角形且∠ABC =90°,即AB ⊥BC ,∴AB ·BC =0,∴AB ·BC +BC ·CA +CA ·AB=BC ·CA +CA ·AB =CA ·(BC +AB )=-(CA )2=-2CA =-25.思路2:∵AB =3,BC =4,CA =5,∴∠ABC =90°,∴cos ∠CAB =CAAB =53,cos ∠BCA =CABC=54.根据数积定义,结合图(右图)知AB ·BC =0,BC ·CA =BC ·CA cos ∠ACE =4×5×(-54)=-16,CA ·AB =CA ·AB cos ∠BAD =3×5×(-53)=-9.∴AB ·BC +BC ·CA +CA ·AB =0―16―9=-25.14.323.解析:a +mb =(3+2m ,4-m),a -b =(1,5).∵(a +mb)⊥(a -b),∴ (a +mb)·(a -b)=(3+2m)×1+(4-m)×5=0m =323.15.答案:重心.解析:如图,以OA ,OC 为邻边作□AOCF交AC 于点E ,则OF =OA +OC ,又OA +OC =-OB ,(第15题)D(第13题)∴OF =2OE =-OB .O 是△ABC 的重心.16.答案:平行四边形.解析:∵a +c =b +d ,∴a -b =d -c ,∴BA =CD .∴四边形ABCD 为平行四边形.三、解答题17.λ<-1.解析:设点P 的坐标为(x ,y),则AP =(x ,y)-(2,3)=(x -2,y -3).AB +λAC =(5,4)-(2,3)+λ[(7,10)-(2,3)]=(3,1)+λ(5,7)=(3+5λ,1+7λ).∵AP =AB +λAC ,∴ (x -2,y -3)=(3+5λ,1+7λ).∴713532yx 即7455yx 要使点P 在第三象限内,只需74055解得λ<-1.18.DF =(47,2).解析:∵A(7,8),B(3,5),C (4,3),AB =(-4,-3),AC =(-3,-5).又D 是BC 的中点,∴AD =21(AB +AC )=21(-4-3,-3-5)=21(-7,-8)=(-27,-4).又M ,N 分别是AB ,AC 的中点,∴F 是AD 的中点,∴DF =-FD =-21AD =-21(-27,-4)=(47,2).19.证明:设AB =a ,AD =b ,则AF =a +21b ,ED =b -21a .∴AF ·ED =(a +21b)·(b -21a)=21b 2-21a 2+43a ·b .又AB ⊥AD ,且AB =AD ,∴a 2=b 2,a ·b =0.∴AF ·ED =0,∴AF ⊥ED .本题也可以建平面直角坐标系后进行证明.20.分析:思路1:2a -b =(2cos θ-3,2sin θ+1),∴|2a -b|2=(2cos θ-3)2+(2sin θ+1)2=8+4sin θ-43cos θ.又4sin θ-43cos θ=8(sin θcos3π-cos θsin3π)=8sin(θ-3π),最大值为8,∴|2a -b|2的最大值为16,∴|2a -b|的最大值为4.思路2:将向量2a ,b 平移,使它们的起点与原点重合,则|2a -b|表示2a ,b终点间的距离.|2a|=2,所以2a 的终点是以原点为圆心,2为半径的圆上的动点P ,b 的终点是该圆上的一个定点Q ,由圆的知识可知,|PQ|的最大值为直径的长为4.(第18题)(第19题)。
【全程复习方略】2013版高中数学 (主干知识+典例)4.2平面向量的分解与向量的坐标运算课件 理 新人教B版

①
②
将②代入①得 a d 1 )[c 1 a)] ( (
2
∴ a 4 d 2 c, 代入②
3
3 得 b c 1 )( 4 d 2 c) 4 c 2 d. ( 2 3 3 3 3 ∴ AB 4 d 2 c,AD 4 c 2 d. 3 3 3 3
实数与 向量的 积
向量的 坐标
若a x, y), R,则a (x,y) ( _________
若起点A(x1,y1),终点B(x 2,y 2),则AB
(x 2 x1,y2 y1) ______________
【即时应用】(1)已知 a=(1,1),b =(1,-1),则 a b= .
【解题指南】直接用 c, d 表示 AB 、 有难度,可换一个角度, AD
由 AB , 表示 AN,AM, 进而求 AB,AD. AD
【规范解答】方法一:
设 AB a,AD b.
2.平面向量的正交分解及坐标 (1)正交分解
向量正交分解是把一个向量分解为两个 互相垂直的向量.
(2)平面向量的坐标表示 在直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量
e1 , e2 作为基底,由平面向量基本定理知,该平面内的任一向量
由于 a与数对(a1,a2)是一一对应的,因 a可表示成 a a1e1 a 2e2, 此向量 a的坐标是 (a1,a2),记作 a=(a1,a2) ,其中 a在x轴上的坐 标是a1 ,a 在y轴上的坐标是 a2 .
答案:(1)
1 3
(2)-1
平面向量基本定理及其应用 【方法点睛】 用平面向量基本定理解决问题的一般思路 先选择一组基底,并运用该基底将条件和结论表示成向量的形 式,再通过向量的运算来解决. 【提醒】在基底未给出的情况下,合理地选取基底会给解题带
【全程复习方略】2013版高中数学 (主干知识+典例精析)4.3平面向量的数量积课件 理 新人教B版
【例3】(1)(2011·湖北高考)若向量 a=(1,2),b =(1,-1), 则2 a b 与 a b 的夹角等于 (
1 2 AD AB AC , AE AB AC AB BE , 2 3 1 2 ADBE (AB AC) ( AC AB) 2 3 1 2 1 2 1 AC AB AB AC 3 2 6
量积求平面向量的夹角、模及判断向量的垂直,是重点也是难
点; 2.题型以选择题和填空题为主,与三角函数、解析几何等知识 点交汇则以解答题为主.
1.平面向量的数量积
(1)向量的夹角 非零向量 ①定义:如图,已知两个________ a 和 b ,作 OA=a,OB b,
则向量 a与 b的夹角是_________ ,记作〈 a, b〉. θ 或∠AOB
答案:-140
【反思·感悟】向量的数量积运算是向量之间的一种运算,结 果是一个数量.平面向量的数量积运算类似于多项式的乘法.在 进行数量积运算时,要认清向量的模和夹角,正确地进行数量 积的运算,避免错用公式,如 | ab| | a || b | . ≠
平面向量的垂直问题
【方法点睛】 两向量垂直的判断方法及应用 (1)若a,b为非零向量,则a ⊥b ab =0;若非零向量
a=(x1,y1),b =(x2,y2),则 a⊥b x1x2+y1y2=0.
(2)一对向量垂直与向量所在的直线垂直是一致的,向量的线性
运算与向量的坐标运算是求解向量问题的两大途径. 【提醒】向量垂直问题体现了“形”与“数”的相互转化,可 用来解决几何中的线线垂直问题.
1 3 【例2】已知 a=(- , ), = a b,OB a b, 若△AOB是以O为直 OA 2 2
平面向量综合运用知识点
平面向量综合运用知识点一、知识概述《平面向量综合运用知识点》①基本定义:平面向量啊,就是在一个平面内既有大小又有方向的量。
这么说吧,就像你要描述一个人在操场上跑,只说跑多远不行,还得说往哪个方向跑,这就是向量的直观感觉。
大小就是向量的长度嘛,方向就是它指向哪儿。
②重要程度:在数学学科里特别重要。
很多几何问题、物理问题(像是力的合成啥的)都得靠它来解决。
要是没有平面向量,很多复杂的图形关系和物理真实现象都不好处理。
③前置知识:你得先知道基本的代数运算,像加减乘除这些。
还得了解一些几何的基本概念,比如点线面之类的,因为很多向量的问题都和几何图形有关。
④应用价值:实际应用那就太多了。
在建筑工程里,计算一些力的合成与分解就得用到向量。
比如说想知道一个斜着的梁受到的几个力合起来多大,往哪个方向,用向量就很容易。
还有在导航里,如果说一个飞机的速度是有方向有大小的向量,风的速度也是向量,那求飞机实际飞行方向和速度就得向量的知识。
二、知识体系①知识图谱:平面向量综合运用知识在数学里属于向量这一块内容。
它就像是各个向量知识的集大成者,用到向量的基本运算、向量与几何图形关系这些基础知识。
②关联知识:和三角学、解析几何联系很紧密。
比如向量的方向可以用三角函数表示,在解析几何里很多直线和曲线的关系可以转化成向量关系。
③重难点分析:- 掌握难度:说实话有点难。
因为它是综合运用,需要把好多知识点揉在一起。
- 关键点:要能清楚地把向量问题转化成可计算的形式,不管是用坐标表示也好,还是用几何关系推导也好。
④考点分析:- 在考试中的重要性:非常重要。
数学考试里常常会有和向量综合起来的题目。
- 考查方式:有选择题问向量关系的判断,填空题让你求向量的值,还有大题综合几何和向量让你证明或者求值。
三、详细讲解【理论概念类】①概念辨析:- 向量加法的平行四边形法则和三角形法则。
平行四边形法则就是把两个向量当成平行四边形的相邻两边,那它们的和向量就是这个平行四边形的对角线(同一起点)。
平面向量十个需要牢记的重点知识
平面向量十个需要牢记的重点知识1.向量的概念:既有大小又有方向的量叫向量,有二个要素:大小、方向.①用有向线段表示;2.向量的表示方法:②用字母a 、b等表示;③平面向量的坐标表示:分别取与x 轴、y 轴方向相同的两个单位向量i 、j作为基底。
任作一个向量a,由平面向量基本定理知,有且只有一对实数x 、y ,使得a xi yj =+ ,),(y x 叫做向量a 的(直角)坐标,记作(,)a x y =,其中x 叫做a 在x 轴上的坐标,y 叫做a 在y 轴上的坐标, 特别地,i (1,0)=,j (0,1)=,0(0,0)= 。
22a x y=+ ;若),(11y x A ,),(22y x B ,则()1212,y y x x AB --=,222121()()AB x x y y =-+-3.零向量、单位向量:①长度为0的向量叫零向量,记为0;②长度为1个单位长度的向量,叫单位向量.(注:||a a 就是单位向量)①方向相同或相反的非零向量叫平行向量;4.平行向量:②我们规定0 与任一向量平行.向量a 、b 、c 平行,记作a ∥b ∥c.③共线向量与平行向量关系:平行向量就是共线向量.5.相等向量:长度相等且方向相同的向量叫相等向量.6.向量的加法、减法:①求两个向量和的运算,叫做向量的加法。
向量加法的三角形法则和平行四边形法则。
②向量的减法向量a 加上的b 相反向量,叫做a 与b 的差。
即:a -b = a+ (-b );差向量的意义: OA = a , OB =b , 则BA =a - b③平面向量的坐标运算:若11(,)a x y = ,22(,)b x y = ,则a b + ),(2121y y x x ++=,a b - ),(2121y y x x --=,(,)a x y λλλ=。
④向量加法的交换律:a +b =b +a ;向量加法的结合律:(a +b ) +c =a + (b +c )7.实数与向量的积:实数λ与向量a 的积是一个向量,记作:λa(1)|λa|=|λ||a|;(2)λ>0时λa 与a方向相同;λ<0时λa 与a方向相反;λ=0时λa=0;(3)运算定律 λ(μa)=(λμ)a ,(λ+μ)a =λa +μa ,λ(a +b )=λa+λb8.向量共线定理:向量b 与非零向量a共线(也是平行)的充要条件是:有且只有一个非零实数λ,使b =λa 。
(完整版)平面向量重要基础知识点
平面向量重要知识点1、向量有关概念:(1)向量的概念:既有大小又有方向的量,向量是可以平移的,(2)零向量:长度为0的向量叫零向量,记作:,注意零向量的方向是任意的;(3)单位向量:长度为一个单位长度的向量叫做单位向量(与AB u u u r 共线的单位向量是||AB AB ±u u u r u u u r ); (4)相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性;(5)平行向量(也叫共线向量):方向相同或相反的非零向量a 、b 叫做平行向量,记作:∥,规定零向量和任何向量平行。
提醒平行向量无传递性!(因为有0r )2.平面向量的基本定理:如果e 1和e 2是同一平面内的两个不共线向量,那么对该平面内的任一向量a ,有且只有一对实数1λ、2λ,使a =1λe 1+2λe 2。
3、实数与向量的积:实数λ与向量a 的积是一个向量,记作λa :当λ>0时,λa 的方向与a 的方向相同,当λ<0时,λa 的方向与a 的方向相反4、平面向量的数量积:(1)两个向量的夹角:(2)平面向量的数量积:规定:零向量与任一向量的数量积是0注意数量积是一个实数,不再是一个向量。
(3)b 在a 上的投影为||cos b θr ,它是一个实数,但不一定大于0。
(4)a •b 的几何意义:数量积•等于的模||a r 与在上的投影的积。
(5)向量数量积的性质:设两个非零向量,,其夹角为θ,则:①0a b a b ⊥⇔•=r r r r ;②当a ,b 同向时,a •b =a b r r ,特别地,22,a a a a a =•==r r r r r ;当a 与b 反向时,•=-a b r r ;当θ为锐角时,•>0,且 a b r r 、不同向,0a b ⋅>r r 是θ为锐角的必要非充分条件;当θ为钝角时,•<0,且 a b r r 、不反向,0a b ⋅<r r 是θ为钝角的必要非充分条件; ③非零向量,夹角θ的计算公式:cos a b a bθ•=r r r r ;④||||||a b a b •≤r r r r 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面向量知识点与2013考点精讲知识网络第1讲 向量的概念与线性运算★ 知 识 梳理 ★1.平面向量的有关概念:(1)向量的定义:既有____大小又有方向_________的量叫做向量.(2)表示方法:用有向线段来表示向量.有向线段的____长度_____表示向量的大小,用_____箭头所指的方向____表示向量的方向.用字母a ,b ,…或用AB ,BC ,…表示.特别提醒:1) 模:向量的长度叫向量的模,记作|a |或|AB |. 2) 零向量:长度为零的向量叫做零向量,记作0;零向量的方向不确定. 3) 单位向量:长度为1个长度单位的向量叫做单位向量.4) 共线向量:方向相同或相反的向量叫共线向量,规定零向量与任何向量共线. 5)相等的向量:长度相等且方向相同的向量叫相等的向量.2.向量的线性运算 1.向量的加法:(1)定义:求两个向量和的运算,叫做向量的加法.如图,已知向量a ,b ,A ,作AB =a ,BC =b ,则向量AC 叫做a 与b 的和,记作a+b ,即 a+b AB BC AC =+=特殊情况:abab a+bbaa+b(1)平行四边形法则三角形法则CBDCBab ba +AAB)2()3(对于零向量与任一向量a ,有 a 00+=+ a = a(2)法则:____三角形法则_______,_____平行四边形法则______(3)运算律:____ a +b =b +a ;_______,____(a +b )+c =a +(b +c )._______ 2.向量的减法:(1)定义:求两个向量差的运算,叫做向量的减法. 减法的三角形法则作法:在平面内取一点O , 作OA = a , OB = b , 则BA = a - b即a-b可以表示为从向量b的终点指向向量a的终点的向量注意:1)AB表示a-b强调:差向量“箭头”指向被减数2)用“相反向量”定义法作差向量,a-b = a +(-b)显然,此法作图较繁,但最后作图可统一a∥b∥c a - b = a + (-b) a - b3.实数与向量的积:(1)定义:实数λ与向量a的积是一个向量,记作λa,规定:|λa|=|λ||a|.当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa=0.(2)运算律:λ(μa)=(λμ)a,(λ+μ)a=λa+μa,λ(a+b)=λa+λb.特别提醒:1)向量的加、减及其与实数的积的结果仍是向量。
2)重要定理:向量共线定理:向量b与非零向量a共线的充要条件是有且仅有一个实数λ,使得b=λa,即b∥a⇔b=λa(a≠0).向量★重难点突破★1.重点:理解向量及与向量相关的概念,掌握向量的几何表示,掌握向量的加法与减法,会正确运用三角形法则、平行四边形法则.2.难点:掌握向量加法的交换律、结合律,并会用它们进行向量化简与计算.3.重难点:.问题1: 相等向量与平行向量的区别答案:向量平行是向量相等的必要条件。
问题2:向量平行(共线)与直线平行(共线)有区别答案:直线平行不包括共线(即重合),而向量平行则包括共线(重合)的情况。
问题3:对于两个向量平行的充要条件:a∥b⇔a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.问题4;向量与有向线段的区别:(1)向量是自由向量,只有大小和方向两个要素;与起点无关:只要大小和方向相同,则这两个向量就是相同的向量;(2)有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段【新题导练】 题型1. 概念判析[例1]判断下列各命题是否正确(1)零向量没有方向 (2)b a ==则 (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =,c b =,则c a=;(7)若b a r r //,c b//,则c a // (8)若四边形ABCD 是平行四边形,则DA BC CD B ==,A (9) b a =的充要条件是||||b a=且b a //;[解题思路]:正确理解向量的有关概念,以概念为判断依据,或通过举反例说明。
解析:解:(1) 不正确,零向量方向任意, (2) 不正确,说明模相等,还有方向 (3) 不正确,单位向量的模为1,方向很多 (4) 不正确,有向线段是向量的一种表示形式 (5)正确, (6)正确,向量相等有传递性 (7)不正确,因若0=b ,则不共线的向量c a ,也有0//a,c //0。
(8) 不正确, 如图DA BC CD B ≠=,A (9)不正确,当b a //,且方向相反时,即使||||b a=,也不能得到b a=;【名师指引】对于有关向量基本概念的考查,可以从概念的特征入手,也可以从通过举出反例而排除或否定相关命题。
考点一: 向量及与向量相关的基本概念1.【2012高考浙江文7】设a ,b 是两个非零向量。
A.若|a+b|=|a|-|b|,则a ⊥b B.若a ⊥b ,则|a+b|=|a|-|b|C.若|a+b|=|a|-|b|,则存在实数λ,使得b=λaD.若存在实数λ,使得b=λa ,则|a+b|=|a|-|b| 【答案】C【命题意图】本题考查的是平面向量,主要考查向量加法运算,向量的共线含义,向量的垂直关系。
【解析】利用排除法可得选项C 是正确的,∵|a +b |=|a |-|b |,则a ,b 共线,即存在实数λ,使得a =λb .如选项A :|a +b |=|a |-|b |时,a ,b 可为异向的共线向量;选项B :若a ⊥b ,由正方形得|a +b |=|a |-|b |不成立;选项D :若存在实数λ,使得a =λb ,a ,b 可为同向的共线向量,此时显然|a +b |=|a |-|b |不成立.2.【2012高考四川文7】设a 、b 都是非零向量,下列四个条件中,使||||a ba b =成立的充分条件是( )A 、||||a b =且//a b B 、a b =- C 、//a b D 、2a b =【答案】D[解析]若使||||a ba b = 成立,则方向相同,与b a 选项中只有D 能保证,故选D.[点评]本题考查的是向量相等条件⇔模相等且方向相同.学习向量知识时需注意易考易错零向量,其模为0且方向任意.考点二: 向量的加、减法【指引】掌握向量加减的定义及向量加法的交换律、结合律等基础知识.在求解时需将杂乱的向量运算式有序化处理,必要时也可化减为加,减低出错律. 题型2: 结合图型考查向量加、减法3. (2009)在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=,则PBC ∆与ABC ∆的面积之比是( )A .13B .12C .23D .34[解题思路]: 本题中的已知向量都集中体现在三角形中.为此,可充分利用向量加减法的三角形法则实施求解.【解析】由PA PB PC AB ++= ,得PA PB BA PC +++=0,即2PC AP =,所以点P 是CA 边上的第二个三等分点,如图所示.故23PBC ABCS BC PC S BC AC∆∆⋅==⋅.【名师指引】三角形中两边对应向量已知,可求第三边所对应的向量.值得注意的是,向量的方向不能搞错.当向量运算转化成代数式运算时,其运算过程可仿照多项式的加减运算进行.4.如图,在ΔABC 中,D 、E 为边AB 的两个三等分点,CA → =3a ,CB → =2b ,求CD → ,CE → . 解析: AB → =AC → +CB →= -3a +2b ,因D 、E 为AB →的两个三等分点,故AD → =31AB → =-a +32b =DE →,CD → =CA → +AD →=3a -a +32b =2a +32b ,CE → =CD → +DE →=2a +32b -a +32b=a +34b .考点三: 向量数乘运算及其几何意义 题型1: 三点共线问题[例4] 设21,e e 是不共线的向量,已知向量2121212,3,2e e CD e e CB e k e AB -=+=+=,若A,B,D 三点共线,求k 的值ABDE[解题思路]:证明存在实数λ,使得BD ABλ=解析:214e e CB CD BD -=-=, 使BD AB λ=)4(22121e e e k e -=+∴λ 得84,2-=⇒-==k k λλ【指引】1、逆向应用向量加法运算法则,使得本题的这种证法比其他证法更简便,值得一提的是,一个向量拆成两个向量的和,一定要强化目标意识. 2、这是一个重要结论,要牢记。
题型2: 用向量法解决几何问题基础巩固训练1. 判断下列命题是否正确,并说明理由: (1)共线向量一定在同一条直线上。
( ) (2)所有的单位向量都相等。
( ) (3)向量→→b a 与共线,→→c b 与共线,则→→c a 与共线。
( ) (4)向量→→b a 与共线,则→→b //a( ) (5)向量→→CD //AB ,则CD //AB 。
()(6)平行四边形两对边所在的向量一定是相等向量。
( )2. 在四边形ABCD 中,“AB →=2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件3.已知向量12112b ,a , ,0l l l R l =+=∈≠λλ,若向量b a和共线,则下列关系一定成立的是( )A 、0=λB 、02 =lC 、12 // l lD 、02 =l 或0=λABCD4..D 、E 、F 分别是△ABC 的BC 、CA 、AB 上的中点,且a BC =, b CA =,给出下列命题,其中正确命题的个数是( )①b a AD --=21 ②b a BE 21+=③b a CF 2121+-= ④0=++CF BE ADA 、1B 、2C 、3D 、45.已知:2121212CD ,BC ),(3e e e e e e AB +=-=+=,则下列关系一定成立的是( ) A 、A ,B ,C 三点共线 B 、A ,B ,D 三点共线 C 、C ,A ,D 三点共线 D 、B ,C ,D 三点共线 6.若||||OA OB OA OB +=- 则向量,OA OB的关系是( ) A .平行 B .重合 C .垂直 D .不确定综合拔高训练7.如图,已知,,3AB a AC b BD DC === ,用,a b 表示AD,则AD = ( )A .34a b +B .1344a b +C .1144a b +D .3144a b +答案:B解析:33()44AD AB BD AB BC AB AC AB =+=+=+-= 1344a b +8.已知a +b =213e e +,a -b =212e e -,用1e 、2e 表示a= 。
