07蓝青提前批招生(数学)
诸暨市2007年重点中学提前招生考试试卷
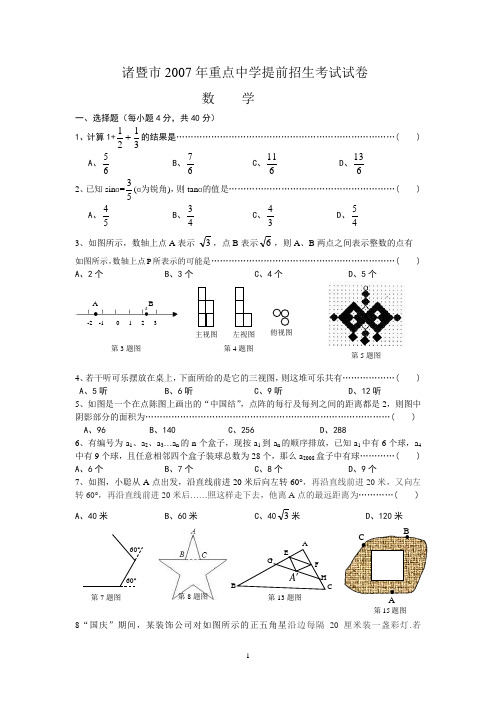
诸暨市2007年重点中学提前招生考试试卷数 学一、选择题(每小题4分,共40分)1、计算1+3121+的结果是…………………………………………………………………( ) A 、65 B 、67 C 、611 D 、6132、已知sin ɑ=53(ɑ为锐角),则tan ɑ的值是…………………………………………………( )A 、54B 、43C 、34D 、453、如图所示,数轴上点A 表示-3,点B 表示6,则A 、B 两点之间表示整数的点有如图所示,数轴上点P 所表示的可能是………………………………………………………( )A 、2个B 、3个C 、4个D 、5个4、若干听可乐摆放在桌上,下面所给的是它的三视图,则这堆可乐共有………………( ) A 、5听 B 、6听 C 、9听 D 、12听5、如图是一个在点陈图上画出的“中国结”,点阵的每行及每列之间的距离都是2,则图中阴影部分的面积为…………………………………………………………………………( ) A 、96 B 、140 C 、256 D 、2886、有编号为a 1、a 2、a 3…a n 的n 个盒子,现按a 1到a n 的顺序排放,已知a 1中有6个球,a 4中有9个球,且任意相邻四个盒子装球总数为28个,那么a 2008盒子中有球…………( ) A 、6个 B 、7个 C 、8个 D 、9个 7、如图,小聪从A 点出发,沿直线前进20米后向左转60°,再沿直线前进20米,又向左转60°,再沿直线前进20米后……照这样走下去,他离A 点的最远距离为…………( ) A 、40米 B 、60米 C 、403米 D 、120米8“国庆”期间,某装饰公司对如图所示的正五角星沿边每隔20厘米装一盏彩灯.若第5题图-2 -1 0 1 2 3B A ∙第3题图 主视图 左视图 俯视图 第4题图60°60° 第7题图 第8题图 C第13题图 第15题图BC=(5-1)米,则需安装彩灯………………………………………………………………( ) A 、100盏 B 、101盏 C 、102盏 D 、110盏9、已知a.b.c 为实数,且b+c = 6-4a+3a ²,c-b=4-4a+a ²,求a 、b 、c 之间的大小关系为( ) A 、b a c B 、a c b C 、c a b D 、c b a 10、函数y=kx+b(其中k 、b 为正整数,且k ≥2),当自变量x 取不同整数值时,某同学算得y 的对应值分别为39,71,83,116,171,182,237,358.但实际上这些y 值中有一个值是错误的,你认为这个错误的y 值应是……………………………………………………( ) A 、358 B 、182 C 、171 D 、71 二、填空题(每小题5分,共30分) 11、因式分解5x 2-20= 。
2020-2021学年浙江省宁波市鄞州区蓝青学校七年级(下)期末数学试卷(含答案)

2020-2021学年浙江省宁波市鄞州区蓝青学校七年级(下)期末数学试卷一、选择题(共10小题,每小题3分,总共30分)1.(3分)下列多项式乘法中,不能进行平方差计算的是()A.(x+y)(﹣x﹣y)B.(2a+b)(2a﹣b)C.(﹣3x﹣y)(﹣y+3x)D.(a2+b)(a2﹣b)2.(3分)下列由左边到右边的变形中,是因式分解的是()A.x2﹣4x+4=(x﹣2)2B.x2﹣1=x(x﹣)C.x2﹣4+3x=(x+2)(x﹣2)+3xD.(x+2)(x﹣2)=x2﹣43.(3分)不改变分式的值,把它的分子与分母中各项的系数化为整数,其结果正确的是()A.B.C.D.4.(3分)《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有x个人,该物品价格是y元,则下列方程组正确的是()A.B.C.D.5.(3分)如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,DE交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有()A.②③B.①②③C.①③④D.①②③④6.(3分)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长()A.3条B.4条C.5条D.6条7.(3分)如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲和乙B.乙和丙C.只有乙D.只有丙8.(3分)要使分式(﹣)÷的值是负整数,则整数a应取的数为()A.1和2 B.2和3 C.a>1 D.a>29.(3分)一只船有一个漏洞,水以均匀速度进入船内.发现漏洞时,船内已经进入了一些水,如果以12个人淘水,3h可以淘完,如果以5个人淘水,10h才能淘完.现在要想在2h内淘完,需要()人.A.17 B.18 C.20 D.2110.(3分)已知abc=1,a+b+c=2,a2+b2+c2=3,则的值为()A.﹣1 B.C.2 D.二、填空题(共8小题,每小题4分,总共32分)11.(4分)已知a=35555,b=44444,c=53333,用“<”将a,b,c连接起来:.12.(4分)一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分组.13.(4分)如图所示,E,F分别是ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=12cm2,S△BQC=22cm2,则阴影部分的面积为cm2.14.(4分)若方程组的解是,则方程组的解是x =,y=.15.(4分)如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF的度数是.16.(4分)若关于x的方程=﹣1的解为正数,则a的取值范围是.17.(4分)已知724﹣1可被40至50之间的两个整数整除,这两个整数是.18.(4分)若x、y、z满足3x+7y+z=1和4x+10y+z=2001,则分式的值为.三、解答题(共7小题,总共38分)19.(3分)若(x﹣3)(x+m)=x2+nx﹣15,求的值.20.(3分)已知(n﹣2020)2+(2021﹣n)2=3,求(n﹣2020)(2021﹣n)的值.21.(3分)已知多项式2x4﹣3x3+ax2+7x+b含有因式x2+x﹣2,求的值.22.(3分)若2x+3y﹣4z+1=0,求9x•27y÷81z的值.23.(10分)如图,已知AM∥BN,∠A=58°,点P是射线AM上一动点(与点A不重合),BC.BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是度;②∵AM∥BN,∴∠ACB=∠.(2)求∠CBD的度数.(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是.(直接写出结果)24.(8分)已知x,y都是有理数,且满足方程=0,求x﹣y 的值.25.(8分)如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,(1)求∠BFC的度数.(2)求证:BC=BE+CD.2020-2021学年浙江省宁波市鄞州区蓝青学校七年级(下)期末数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,总共30分)1.(3分)下列多项式乘法中,不能进行平方差计算的是()A.(x+y)(﹣x﹣y)B.(2a+b)(2a﹣b)C.(﹣3x﹣y)(﹣y+3x)D.(a2+b)(a2﹣b)【解答】解:平方差公式的使用条件:两个代数式相乘,其中两项相同,两项互为相反数.不具备这两个条件的只有:(x+y)(﹣x﹣y).故选:A.2.(3分)下列由左边到右边的变形中,是因式分解的是()A.x2﹣4x+4=(x﹣2)2B.x2﹣1=x(x﹣)C.x2﹣4+3x=(x+2)(x﹣2)+3xD.(x+2)(x﹣2)=x2﹣4【解答】解:A.x2﹣4x+4=(x﹣2)2,是因式分解,故本选项符合题意;B.x2﹣1=x(x﹣),是分式,所以不是因式分解,故本选项不符合题意;C.x2﹣4+3x=(x+2)(x﹣2)+3x,等式的右边不是几个整式的积的形式,不是因式分解,故本选项不符合题意;D.(x+2)(x﹣2)=x2﹣4,是整式乘法,不是因式分解,故本选项不符合题意;故选:A.3.(3分)不改变分式的值,把它的分子与分母中各项的系数化为整数,其结果正确的是()A.B.C.D.【解答】解:原式=,故选:C.4.(3分)《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有x个人,该物品价格是y元,则下列方程组正确的是()A.B.C.D.【解答】解:若设有x人,物品价值y元,根据题意,可列方程组为,故选:C.5.(3分)如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,DE交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有()A.②③B.①②③C.①③④D.①②③④【解答】解:∵△DEF的是直角三角形ABC沿着斜边AC的方向平移后得到的,且A.D.C.F 四点在同一条直线上,∴BE∥AC,AB∥DE,BC=EF,BE=CF,故③正确;由图形的平移知,ED∥AB,AC∥BE,∴∠EDC=∠A,∠EDC=∠BED,∴∠A=∠BED,故①正确;∵BG=4,∴AD=BE>BG,∴△ABC平移的距离>4,故②错误;∵EF=10,∴CG=BC﹣BG=EF﹣BG=10﹣4=6,∵△BEG的面积等于4,∴BG•GE=4,∴GE=2,∴四边形GCFE的面积=(6+10)×2=16,故④正确;故选:C.6.(3分)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长()A.3条B.4条C.5条D.6条【解答】解:如图:若要知道该图形周长,至少需要知道4条线段的长:BC.AB,IJ,EF,∵BC=AL+KJ+IH+GF+DE,AB=LK+KK′=LK+CC′,IJ=HG+GG′=HG+C′D′,EF=DD′,∴只要知道BC.AB,IJ,EF4条线段的长,就能知道该图形周长.故选:B.7.(3分)如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是()A.甲和乙B.乙和丙C.只有乙D.只有丙【解答】解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;图乙符合SAS定理,即图乙和△ABC全等;图丙符合AAS定理,即图丙和△ABC全等;故选:B.8.(3分)要使分式(﹣)÷的值是负整数,则整数a应取的数为()A.1和2 B.2和3 C.a>1 D.a>2【解答】解:原式=[﹣]•(a﹣1)=a+1﹣=﹣,∵分式的值为负整数,∴a﹣1=1或a﹣1=2,则a=2和3.故选:B.9.(3分)一只船有一个漏洞,水以均匀速度进入船内.发现漏洞时,船内已经进入了一些水,如果以12个人淘水,3h可以淘完,如果以5个人淘水,10h才能淘完.现在要想在2h内淘完,需要()人.A.17 B.18 C.20 D.21【解答】解:设水流入的速度为y,原来有水z,一人的淘水速度为x,需要w人,根据题意得:,(2)﹣(1)得:y=2x,代入(1)得:z=30x,把z=30x,y=2x代入(3)得:w=17(人).所以要想在2小时内淘完,需要17人.故选:A.10.(3分)已知abc=1,a+b+c=2,a2+b2+c2=3,则的值为()A.﹣1 B.C.2 D.【解答】解:由a+b+c=2,两边平方,得a2+b2+c2+2ab+2bc+2ac=4,将已知代入,得ab+bc+ac=;由a+b+c=2得:c﹣1=1﹣a﹣b,∴ab+c﹣1=ab+1﹣a﹣b=(a﹣1)(b﹣1),同理,得bc+a﹣1=(b﹣1)(c﹣1),ca+b﹣1=(c﹣1)(a﹣1),∴原式=++=====﹣.故选:D.二.填空题(共8小题,每小题4分,总共32分)11.(4分)已知a=35555,b=44444,c=53333,用“<”将a,b,c连接起来:c<a<b.【解答】解:∵a=35555,b=44444,c=53333,∴a=31111×5=(35)1111=2431111,b=41111×4=(44)1111=2561111,c=51111×3=(53)1111=1251111,∵1251111<2431111<2561111,∴c<a<b,故答案为:c<a<b.12.(4分)一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分10组.【解答】解:在样本数据中最大值为141,最小值为50,它们的差是141﹣50=91,已知组距为10,那么由于=9.1,故可以分成10组.故答案为:10.13.(4分)如图所示,E,F分别是ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=12cm2,S△BQC=22cm2,则阴影部分的面积为34cm2.【解答】解:连接E.F两点,∵四边形ABCD是平行四边形,∴AB∥CD,∴△EFC的FC边上的高与△BCF的FC边上的高相等,∴S△EFC=S△BCF,∴S△EFQ=S△BCQ,同理:S△EFD=S△ADF,∴S△EFP=S△ADP,∵S△APD=12cm2,S△BQC=22cm2,∴S四边形EPFQ=34cm2,故阴影部分的面积为34cm2.故答案为:34.14.(4分)若方程组的解是,则方程组的解是x=﹣1,y=﹣3.【解答】解:把代入方程组得,,所以c1﹣c2=2(a1﹣a2),c1﹣2a1=3,方程组,①﹣②得,(a1﹣a2)x=a1﹣a2﹣(c1﹣c2),所以(a1﹣a2)x=﹣(a1﹣a2),因此x=﹣1,把x=﹣1代入方程组中的方程①得,﹣a1+y=a1﹣c1,所以y=2a1﹣c1=﹣(c1﹣2a1)=﹣3,故答案为:﹣1,﹣3.15.(4分)如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF的度数是20°.【解答】解:∵AD∥BC,∴设∠DEF=∠EFB=α,图2中,∠GFC=∠BGD=∠AEG=180°﹣2∠EFG=180°﹣2α,图3中,∠CFE=∠GFC﹣∠EFG=180°﹣2α﹣α=120.解得α=20.即∠DEF=20°,故答案为:20°.16.(4分)若关于x的方程=﹣1的解为正数,则a的取值范围是a<2且a≠﹣4.【解答】解:去分母得,2x+a=﹣x+2解得x=∵分母x﹣2≠0即x≠2∴≠2解得,a≠﹣4又∵x>0∴解得,a<2则a的取值范围是a<2且a≠﹣4.17.(4分)已知724﹣1可被40至50之间的两个整数整除,这两个整数是48,43.【解答】解:724﹣1=(712+1)(712﹣1)=(712+1)(76+1)(76﹣1)=(712+1)(76+1)(73+1)(73﹣1)=(712+1)(76+1)(7+1)(72﹣7×1+1)(7﹣1)(72+7×1+1)=(712+1)(76+1)×8×43×6×57=(712+1)(76+1)×48×43×57,∵724﹣1可被40至50之间的两个整数整除,∴这两个整数是48,43.故答案为:48,43.18.(4分)若x、y、z满足3x+7y+z=1和4x+10y+z=2001,则分式的值为﹣3999.【解答】解:由x、y、z满足3x+7y+z=1和4x+10y+z=2001,得出:,解得:,∴=,==﹣3999.故答案为:﹣3999.三.解答题(共7小题,总共38分)19.(3分)若(x﹣3)(x+m)=x2+nx﹣15,求的值.【解答】解:(x﹣3)(x+m)=x2+(m﹣3)x﹣3m=x2+nx﹣15,则解得:.=.20.(3分)已知(n﹣2020)2+(2021﹣n)2=3,求(n﹣2020)(2021﹣n)的值.【解答】解:令n﹣2020=a,2021﹣n=b,根据题意得:a2+b2=3,a+b=1,∴原式=ab===﹣1.21.(3分)已知多项式2x4﹣3x3+ax2+7x+b含有因式x2+x﹣2,求的值.【解答】解:∵x2+x﹣2=(x+2)(x﹣1),∴2x4﹣3x3+ax2+7x+b能被(x+2)(x﹣1)整除,设商是A.则2x4﹣3x3+ax2+7x+b=A(x+2)(x﹣1),则x=﹣2和x=1时,右边都等于0,所以左边也等于0.当x=﹣2时,2x4﹣3x3+ax2+7x+b=32+24+4a﹣14+b=4a+b+42=0 ①当x=1时,2x4﹣3x3+ax2+7x+b=2﹣3+a+7+b=a+b+6=0 ②①﹣②,得3a+36=0,∴a=﹣12,∴b=﹣6﹣a=6.∴==﹣2.22.(3分)若2x+3y﹣4z+1=0,求9x•27y÷81z的值.【解答】解:∵2x+3y﹣4z+1=0,∴2x+3y﹣4z=﹣1,∴9x•27y÷81z=32x×33y÷34z=32x+3y﹣4z=3﹣1=.23.(10分)如图,已知AM∥BN,∠A=58°,点P是射线AM上一动点(与点A不重合),BC.BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是122度;②∵AM∥BN,∴∠ACB=∠CBN.(2)求∠CBD的度数.(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是30.5°.(直接写出结果)【解答】解:(1)①∵AM∥BN,∠A=58°,∴∠A+∠ABN=180°,∴∠ABN=122°;②∵AM∥BN,∴∠ACB=∠CBN;(2)∵AM∥BN,∴∠ABN+∠A=180°,∴∠ABN=180°﹣58°=122°,∴∠ABP+∠PBN=122°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=122°,∴∠CBD=∠CBP+∠DBP=61°;(3)不变,∠APB:∠ADB=2:1.∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM∥BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,由(1)可知∠ABN=122°,∠CBD=61°,∴∠ABC+∠DBN=61°,∴∠ABC=30.5°.故答案为:122,CBN;30.5°.24.(8分)已知x,y都是有理数,且满足方程=0,求x﹣y 的值.【解答】解:原方程变形为:x+y﹣4+y﹣π=0.∵x,y都是有理数.∴,解得:.∴x﹣y=4﹣2=2.25.(8分)如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,(1)求∠BFC的度数.(2)求证:BC=BE+CD.【解答】解:(1)在△ABC中,∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,∵∠ABC,∠ACB的平分线BE,CD相交于点F,∴∠FBC=∠ABC,∠FCB=∠ACB,∴∠FBC+∠FCB=(∠ABC+∠ACB)=×120°=60°,在△BCF中,∠BFC=180°﹣(∠FBC+∠FCB)=180°﹣60°=120°.(2)证明:在BC上取一点O,使得BO=BE,∵∠A=60°,BD.CE是△ABC的角平分线,∴∠BFC=120°,∴∠BFE=∠CFD=60°,在△BFE和△BFO中,,∴△BFE≌△BFO,(SAS)∴∠BFO=∠BFE=60°,∴∠CFO=∠BFC﹣∠BFO=60°,在△OCF和△DCF中,,∴△OCF≌△DCF(ASA),∴CO=CD,∵BC=BO+CO,∴BC=BE+CD.。
浙江省宁波市宁海2023-2024学年高一提前招生考试数学试卷含答案

2024年浙江省宁波市宁海创新班提前招生数学试卷(答案在最后)一、选择题(48分)1.若二次函数()2231y mx m m x m =--+-的图象经过点(),a b 、(),a b -,则m 的值为()A.0B.3C.1D.0或3【答案】B【解析】【分析】由于函数图象关于y 轴对称,则函数的解析式形式应该是2y ax k =+型,由此求得问题的答案.【详解】∵二次函数()2231y mx m m x m =--+-的图象经过点(),a b 、(),a b -,∴函数图象关于y 轴对称,∴函数的解析式形式应该是2y ax k =+型,∴()230m m --=,解得:0m =或3m =,∴二次函数的二次系数不能为0,∴3m =.故选:B.2.小明同学在计算出8个数的平均数后,不小心将这个数也混到数据中了,那么重新计算这些新数据后一定不变的量是()A.平均数B.中位数C.众数D.方差【答案】A【解析】【分析】由平均数的定义可得答案.【详解】小明同学在计算出8个数的平均数后,不小心将这个数也混到数据中了,那么重新计算这些新数据后一定不变的量是平均数,故选:A.3.已知直线11324y x =+上横、纵坐标都是整数的点的个数是()A.0个B.1个C.不少于2个但有限个D.无数个【答案】A【解析】【分析】由直线11324y x =+,可得4213y x +=,分析整数性以及奇偶性即可得得解.【详解】由直线11324y x =+可得2413x y +=,如果直线11324y x =+上存在横、纵坐标都是整数的点,即x ,y 都是整数,可知4y ,2x 都是偶数,则24x y +为偶数,这与13为奇数矛盾,所以直线11324y x =+上不存在横、纵坐标都是整数的点.故选:A.4.如图四边形ABCD 与BEFG 是并列放在一起的两个正方形,O 是BF 与EG 的交点.如果正方形ABCD 的面积是9,2CG =,则DEO 的面积为()A.1B.94C.4D.254【答案】D【解析】【分析】连接BD ,根据正方形的面积可得3BC =,从而可得5BG =,进而可得正方形BEFG 的面积25=,然后根据正方形的性质可得45ABD BEG ∠=∠=°,从而可得BD EG ∥,然后利用平行线间的距离处处相等可得:DOE 的面积BOE = 的面积14=正方形BEFG 的面积,即可解答.【详解】连接BD ,因为正方形ABCD 的面积是9,则3BC =,且2CG =,则325BG BC CG =+=+=,可得正方形BEFG 的面积为25,又因为四边形ABCD 和四边形BEFG 都是正方形,则45ABD BEG ∠=∠=°,可知BD EG ∥,所以DOE 的面积12544DOE BOE BEFG S S S ===V △.故选:D.5.将正三角形、正方形、正五边形按如图所示的方式摆放,其中正方形和正五边形的下底边是水平共线的,如果150∠=︒,那么2∠=()A.30︒B.34︒C.36︒D.40︒【答案】B【解析】【分析】根据正三角形的内角等于60︒,150∠=︒得()180170DET GEF ∠=︒-∠+∠=︒,根据正五边形的内角等于108︒,得18072TSA RST ∠=-∠=°°,再根据正方形的内角等于90︒得9018STA TSA ∠=-∠=°°,进而得()18054ETD STA STP ∠=︒-∠+∠=︒,然后由三角形的内角和定理得()18056EDT DET ETD ∠=︒-∠+∠=︒,最后再根据2180EDT CDA ∠+∠+∠=°可得出2∠的度数.【详解】如下图所示:EFG △为正三角形,60GEF ∴∠=︒,1180DET GEF ∠+∠+∠= °,150∠=︒,()()1801180605070DET GEF ∴∠=︒-∠+∠=︒-︒+︒=︒,五边形PQRST 为正五边形,108RST STP ∴∠=∠=°,180********TSA RST ∴∠=-∠=-=°°°°,四边形ABCD 为正方形,90DAB CDA ∴∠=∠=︒,90SAT ∴∠=°,90TSA STA ∴∠+∠=°,90907218STA TSA ∴∠=-∠=-=°°°°,180STA STP ETD ∠+∠+∠= °,()()1801801810854ETD STA STP ∴∠=︒-∠+∠=︒-︒+︒=︒,()()180180705456EDT DET ETD ∴∠=︒-∠+∠=︒-︒+︒=︒,2180EDT CDA ∠+∠+∠= °,()()2180180569034EDT CDA ∴∠=︒-∠+∠=︒-︒+︒=︒.故选:B.6.若实数x 12x -=--,则x 应满足的条件是()A .0x ≥或1x ≤- B.0x ≤ C.10x -≤≤ D.1x ≥-【答案】C【解析】【分析】分1x <-、10x -≤≤和0x >三种情况,结合根式分析求解即可.【详解】当1x <-时,则10x x <+<,()1112x x x ⎡⎤=---+=<--⎣⎦,不合题意;当10x -≤≤时,则10x +≥,()112x x x =--+=--,符合题意;当0x >时,则01x x <<+,()1112x x x =-+=->--,不合题意;综上所述:x 应满足的条件是10x -≤≤.故选:C.7.如图ABC 的三条高相交于点G ,CH 是角平分线,已知=45ABC ∠︒,60ACD ∠=︒,则图中的等腰三角形共有()个.A.5B.6C.7D.8【答案】D【解析】【分析】根据条件和等腰三角形的判定分别找出等腰三角形即可.【详解】①AD BC ⊥ ,=45ABC ∠︒,ABD ∴ 是等腰三角形;②CF AB ⊥ ,=45ABC ∠︒,BCF ∴ 是等腰三角形;③60ACB ∠=︒ ,906030CBE ∴∠=︒-︒=︒,CH 是角平分线,1302BCH ACH ACB ∴∠=∠=∠=°,CBI ICB ∴∠=∠,BCI ∴△是等腰三角形;④60ACB ∠=︒ ,906030CAD ∴∠=︒-︒=︒,30ACJ CAJ ∴∠=∠=°,ACJ ∴ 是等腰三角形;⑤604515ACF ∠=-= °°°,901575CAF ∴∠=-=°°°,453075AHC ABC BCH ∴∠=∠+∠=+=°°°,75CAH CHA ∴∠=∠=°,ACH ∴△是等腰三角形;⑥45GCD DGC ∠=∠= °,CDG ∴ 是等腰三角形;⑦303060GIJ EBC HCB ∠=∠+∠=+= °°°,903060GJI CJD ∠=∠=-=°°°,60GIJ GJ ∴∠=∠=°,GIJ ∴△是等腰三角形;⑧AFG 是等腰三角形:综上分析,图中等腰三角形共有8个:ABD △、BCF △、BCI 、ACJ 、ACH 、CDG 、GIJ 、AFG .故选:D.8.如图,O 截ABC 的三条边所得的弦长相等,若80A ∠=︒,则BOC ∠的度数为()A.125︒B.120︒C.130︒D.115︒【答案】C【解析】【分析】过点O 作OE AB ⊥于E ,OD BC ⊥于D ,OF AC ⊥于F ,根据心角、弧、弦的关系定理得到OD OE OF ==,根据角平分线的判定定理、三角形内角和定理计算,得到答案.【详解】解:过点O 作OE AB ⊥于E ,OD BC ⊥于D ,OF AC ⊥于F ,80A ∠=︒ ,18080100ABC ACB ∴∠+∠=︒-︒=︒,由题意得,HG PQ MN ==,OD OE OF ∴==,OE AB ⊥ ,OD BC ⊥,OF AC ⊥,OB ∴平分ABC ∠,OC 平分ACB ∠,12OBC ABC ∴∠=∠,12OCB ACB ∠=∠,()1502OBC OCB ABC ACB ∴∠+∠=⨯∠+∠=︒,18050130BOC ∴∠=︒-︒=︒,故选:C .9.如图,在Rt ABC △纸片中,90ACB ∠=︒,4AC =,3BC =,点D ,E 分别在AB ,AC 上,连结DE ,将ADE V 沿DE 翻折,使点A 的对应点F 落在BC 的延长线上,若FD 平分EFB ∠,则AD 的长为()A.259 B.258 C.157 D.207【答案】D【解析】【分析】由翻折得出AD DF =,A DFE ∠=∠,再根据FD 平分EFB ∠,得出DFH A ∠=∠,然后借助相似列出方程即可.【详解】作//DH AC ,交BC 于H ,结合题设有DH BC ⊥,在Rt ABC △纸片中,90ACB ∠=︒,由勾股定理得:5AB ==,将ADE V 沿DE 翻折得DEF ,则AD DF =,A DFE ∠=∠,又因为FD 平分EFB ∠,则DFE DFH ∠=∠,可得DFH A ∠=∠,在Rt DHF △中,3sin sin 5DFH A ∠=∠=,设3DH x =,则5DF x =,55BD x =-,因为BDH BAC ∽,则BD DH AB AC =,即55354x x -=,解得47x =,所以2075AD x ==.故选:D.10.如图,在平面直角坐标系中,矩形ABCD 的边BC 在x 轴上,点D 的坐标为()2,6-,反比例函数()0k y x x =<经过点D ,若AC 的延长线交y 轴于点E ,连接BE ,则BCE 的面积为()A.3B.5C.6D.7【答案】C【解析】【分析】依据点D 的坐标为()2,6-,即可得出2CO =,6AB =,进而得到12CO AB ⨯=,再根据线段成比例可得BCE 的面积.【详解】因为点D 的坐标为()2,6-,且CD CO ⊥,则2CO =,6CD AB ==,可得12CO AB ⨯=,又因为AB ∥OE ,则BC AB OC EO =,可得12BC EO AB CO ⋅=⋅=,所以BCE 的面积162BCE BC O S E =⨯⨯=△.故选:C.11.如图,正方形ABCD 的边长是3,BP CQ =,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ DP ⊥;②2OA OE OP =⋅;③AOD OECF S S = 四边形;④当1BP =时,1an 136t OAE ∠=,其中正确结论的个数是()A.1B.2C.3D.4【答案】C【解析】【分析】由四边形ABCD 是正方形,得到AD BC =,90DAB ABC ∠=∠=︒,根据全等三角形的性质得到P Q ∠=∠,根据余角的性质得到AQ DP ⊥;故①正确;根据相似三角形的性质得到2AO OD OP =⋅,由OD OE ≠,得到2OA OE OP ≠⋅;故②错误;根据全等三角形的性质得到CF BE =,DF CE =,于是得到ADF DFO DCE DOF S S S S -=-△△△△,即AOD OECF S S = 四边形;故③正确;根据相似三角形的性质得到34BE =,求得134QE =,135QO =,3920OE =,由三角函数的定义即可得到结论.【详解】因为四边形ABCD 是正方形,AD BC ∴=,90DAB ABC ∠=∠=︒,BP CQ = ,AP =BQ ∴,在DAP 与ABQ 中,AD AB DAP ABQ AP BQ =⎧⎪∠=∠⎨⎪=⎩.DAP ABQ ∴△≌△,P Q ∴∠=∠,90Q QAB ∠+∠=︒ ,90P QAB ∴∠+∠=︒,90AOP ∴∠=︒,AQ DP ∴⊥;故①正确;90DOA AOP ∠=∠=︒ ,90ADO P ADO DAO ∠+∠=∠+∠=︒,DAO P ∴∠=∠,DAO APO ∴△∽△,AO OP OD OA∴=,2AO OD OP ∴=⋅,AE AB > ,AE AD ∴>,OD OE ∴≠,2OA OE OP ∴≠⋅;故②错误;在CQF △与BPE 中FCQ EBP Q P CQ BP ∠=∠⎧⎪∠=∠⎨⎪=⎩,CQF BPE ∴△≌△,CF BE ∴=,DF CE ∴=,在ADF △与DCE △中,AD CD ADC DCE DF CE =⎧⎪∠=∠⎨⎪=⎩ADF DCE ∴V V ≌,ADF DFO DCE DOF S S S S ∴-=-△△△△,即AOD OECF S S = 四边形;故③正确;1BP = ,3AB =,4AP ∴=,PBE PAD △∽△,43PB PA EB DA ∴==,34BE ∴=,134QE ∴=,QOE PAD △∽△,1345QO OE QE PA AD PD ===,135QO ∴=,3920OE =,1255AO QO ∴=-=,13tan OA 16OE OAE ∴∠==,故④正确,故选:C.【点睛】关键点点睛:熟练掌握相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,三角函数的定义是解题的关键.12.在Rt ABC △中,90BAC ∠=︒,6AB =,8AC =,点P 是ABC 所在平面内一点,则222PA PB PC ++取得最小值时,下列结论正确的是()A.点P 是ABC 三边垂直平分线的交点B.点P 是ABC 三条内角平分线的交点C.点P 是ABC 三条高的交点D.点P 是ABC 三条中线的交点【答案】D 【解析】【分析】作辅助线,设AD PE x ==,AE DP y ==,则()22222820033233AP CP BP x y ⎛⎫++=-+-+ ⎪⎝⎭,可知当83x =,2y =时,222AP CP BP ++的值最小,进而分析点P 的位置.【详解】过P 作PD AC ⊥于D ,过P 作PE AB ⊥于E ,延长CP 交AB 于M ,延长BP 交AC 于N ,如图:因为90A ∠=︒,PD AC ⊥,PE AB ⊥,可知四边形AEPD 是矩形,设AD PE x ==,AE DP y ==,在Rt AEP △中,可得222AP x y =+,在Rt CDP △中,可得()2228CP x y =-+,在Rt BEP 中,可得()2226BP x y =+-,则()()22222222286AP CP BP x y x y x y ++=++-+++-22316312100x x y y =-+-+()22820033233x y ⎛⎫=-+-+ ⎪⎝⎭,可知当且仅当832x y ⎧=⎪⎨⎪=⎩时,222AP CP BP ++的值最小,此时83AD PE ==,2AE PD ==,又因为90A ∠=︒,PD AC ⊥,可知PD AB ∥,则AM AC PD CD=,即81623AM =,解得3AM =,可知12AM AB =,即M 是AB 的中点,同理可得12AN AC =,N 为AC 中点,所以P 是ABC 三条中线的交点.故选:D.二、填空题(24分)13.已知a 是一元二次方程210x x --=的一个解,则代数式221a a a a--+的值是______.【答案】2【解析】【分析】由题意可得210a a --=,结合题意整理即可得解.【详解】因为a 是一元二次方程210x x --=的一个解,则210a a --=,显然0a ≠,可得2211,1a a a a--==,所以2212a a a a--+=.故答案为:2.14.如图,正八边形ABCDEFGH 中,GFB ∠=______.【答案】3π8【解析】【分析】利用外接圆被各个顶点平分确定圆心角,再随之确定圆周角.【详解】如图,正八边形存在外接圆,且各个顶点将圆周平分为八段弧,而整个圆对应的圆心角是2π,所以包含三段单位弧段的 GB对应的圆心角33π2π84GOB ∠=⋅=,从而其对应的圆周角13π28GFB GOB ∠=∠=.故答案为:3π8.15.二次函数2y ax bx c =++的图象如图所示,则不等式()()2220a x b x c -+-+<的解集为______.【答案】()(),35,-∞⋃+∞【解析】【分析】先根据图象确定2x -的取值范围,再确定x 的取值范围.【详解】根据图象,原不等式等价于()()2,13,x -∈-∞+∞ ,即()(),35,x ∈-∞+∞ .故答案为:()(),35,-∞⋃+∞.16.有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点G 正好在书架边框上,每本书的厚度为5cm ,高度为20cm ,书架宽为40cm ,则FI 的长______.【答案】4017##6217【解析】【分析】设CFE θ∠=,则20cos ,5sin CF FI θθ==,结合题意分析可得sin 44cos θθ=-,与22sin cos 1θθ+=联立运算求解即可.【详解】由题意可知:20cm,20cm,5cm BC EF FG ===,设CFE θ∠=,则FGI θ∠=,20cos ,5sin CF FI θθ==,由题意可知:2020cos 5sin 40BC CF FI θθ++=++=,整理得sin 44cos θθ=-,联立方程22sin 44cos sin cos 1θθθθ=-⎧⎨+=⎩,消去sin θ整理得217cos 32cos 150θθ-+=,即()()17cos 15cos 10θθ--=,解得15cos 17θ=或cos 1θ=(舍去),所以8sin 17θ=,405sin 17FI θ==.故答案为:4017.17.如图,已知四边形ABCD 是平行四边形,将边AD 绕点D 逆时针旋转60︒得到DE ,线段DE 交边BC于点F ,连接BE .若165C E ∠+∠=︒,2BE =,CD =,则线段BC 的长为______.【答案】【解析】【分析】先证明135EBA ∠=︒,然后通过构造等腰直角三角形的方法求得AE ,即可随之确定BC .【详解】如图,过A 作直线BE 的垂线,交直线BE 于点G ,则90BGA ∠=︒.同时,连接AE .由已知有DE DA =,60EDA ∠=︒,故ADE V 是等边三角形,且60CFD EFB ∠=∠=︒.所以()180180360606024016575CDF EBF C CFD E EFB C E ∠+∠=︒-∠-∠+︒-∠-∠=︒-︒-︒-∠+∠=︒-︒=︒.从而7560135EBA EBF FBA EBF CDA EBF CDF FDA ∠=∠+∠=∠+∠=∠+∠+∠=︒+︒=︒.由于180********GBA EBA ∠=︒-∠=︒-︒=︒,而90BGA ∠=︒,故BGA △是等腰直角三角形,AB 为斜边.由已知有2BE =,AB CD ==,故42BG AG AB ===,所以426EG BG BE =+=+=,从而BC AD AE =====故答案为:【点睛】关键点点睛:本题的关键在于利用已知条件的同时构造等腰直角三角形,方可使用勾股定理解决问题.18.如图,等腰直角ABC 的斜边AB 下方有一动点D ,90ADB ∠=︒,BE 平分ABD ∠交CD 于点E ,则CECD的最小值是______.【答案】2【解析】【分析】设ABD ϕ∠=,先用平面几何方法及正弦定理求得πsin4πsin 4CECDϕ=⎛⎫+ ⎪⎝⎭,再求最小值.【详解】设ABD ϕ∠=,则2ABE ϕ∠=,π0,2ϕ⎛⎫∈ ⎪⎝⎭.由于πππ22ACB ADB ∠+∠=+=,故,,,A B C D 四点共圆,从而π4CDB CAB ∠=∠=.所以πsin sin 4πsin sin 4CBD CD CB CB CDB ϕ⎛⎫+ ⎪∠⎝⎭=⋅=⋅∠,()πsin sin sin 42πsin sin sin 42CBE CBE CE CB CB CB CB CEB CDB DBE ϕϕ⎛⎫+ ⎪∠∠⎝⎭=⋅=⋅=⋅∠∠+∠⎛⎫+ ⎪⎝⎭.这就得到πsin π4sinπ42sin 4CECDϕ=≥=⎛⎫+ ⎪⎝⎭.当π4ϕ=时,ππsin sin44ππ2sin sin 24CE CD ϕ===⎛⎫+ ⎪⎝⎭.所以CE CD的最小值是2.故答案为:2.【点睛】关键点点睛:本题的关键在于使用正弦定理确定CECD的表达式,再求出最小值.三、解答题(48分)19.已知实数,a b 满足1a b +=,222a b +=,求a b -的值.【解析】【分析】先由已知条件证明()23a b -=,再确定a b -的可能值.【详解】由于()()()()()()22222222212224a b a b a b a ab baab b a b -+=-++=-++++=+=,故()23a b -=.所以a b -=或a b -=.当132a =,12b -=时,有1a b +=,222a b +=,此时a b -=;当132a -=,132b +=时,有1a b +=,222a b +=,此时a b -=.所以a b -的所有可能值为.20.今年6月份,永州市某中学开展“六城同创”知识竞赛活动,赛后,随机抽取了部分参赛学生的成绩,按得分划为A ,B ,C ,D 四个等级,A :90100S <≤,B :8090S <≤,C :7080S <≤,D :70S ≤,并绘制了如图两幅不完整的统计图,请结合图中所给信息,解答下列问题:(1)请把条形统计图补充完整.(2)扇形统计图中m =______,n =______,B 等级所占扇形的圆心角度数为______.(3)该校准备从上述获得A 等级的四名学生中选取两人参加永州市举行的“六城同创”知识竞赛,已知这四人中有两名男生(用1A ,2A 表示),两名女生(用1B ,2B 表示),请利用树状图法或列表法,求恰好抽到1名男生和1名女生的概率.【答案】(1)统计图见详解(2)15;5;252︒(3)23【解析】【分析】(1)根据题意求总人数和C 等级人数,进而可得统计图;(2)根据题意结合人数关系求,m n ,再根据比例取圆心角;(3)作出树状图或列表,结合相应数据求概率.【小问1详解】由题意可得:总人数为2870%40÷=,则C 等级的人数为4042826---=,据此补全统计图,如图所示:【小问2详解】由题意可得:62%100%15%,%100%5%4040m n =⨯==⨯=,即15,5m n ==,所以B 等级所占扇形的圆心角度数为70%360252⨯︒=︒.【小问3详解】树状图如下:列表如下:1A 2A 1B 2B 1A ╱×√√2A ×╱√√1B √√╱×2B √√×╱所以恰好抽到1名男生和1名女生的概率82123P ==.21.定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.根据以上定义,解决下列问题:(1)如图1,正方形ABCD 中,E 是CD 上的点,将BCE 绕B 点旋转,使BC 与BA 重合,此时点E 的对应点F 在DA 的延长线上,则四边形BEDF 为“直等补”四边形,为什么?(2)如图2,已知四边形ABCD 是“直等补”四边形,5AB BC ==,1CD =,AD AB >,点B 到直线AD 的距离为BE .①求BE 的长;②若,M N 分别是,AB AD 边上的动点,求MNC 周长的最小值.【答案】(1)理由见解析(2)①4②【解析】【分析】(1)使用旋转前后的三角形全等即可得到结论;(2)①构造,AD BC 的交点,并使用相似三角形理论;②构造C 关于直线,AB AD 的对称点,然后利用两点之间线段最短即可.【小问1详解】此时有BCE 全等于BAF △,故90FBE ABC ABF CBE ABC ∠=∠+∠-∠=∠=︒,且BE BF =.从而BE BF =,90FBE ∠=︒,且9090180FBE FDE ∠+∠=︒+︒=︒.所以四边形BEDF 为“直等补”四边形.【小问2详解】如图,延长,AD BC ,设它们交于点F .①由已知有90ABC ADC ∠=∠=︒,故AC ==7AD ===.由于90CDF ABF ∠=∠=︒,CFD AFB ∠=∠,故CDF 相似于ABF △,所以15DF CF CD BF AF AB ===.而1111247115552525AD AF DF AF BF AF BC CF AF AF AF ==-=-=--=--=-,故253AF =.由于90AEB ABF ∠=∠=︒,BAE FAB ∠=∠,故ABE 相似于AFB △,所以AE ABAB AF=.故2253253AB AE AF===,所以4BE ===.②由于734DE AD AE =-=-=,故BD ===.设C 关于直线,AB AD 的对称点分别是,C C ''',则,B D 分别是,CC CC '''的中点,所以2C C BD '''=.从而根据对称性有2CM MN NC C M MN NC C C BD ''''''++=++≥==当,M N 分别为,AB AD 各自与线段C C '''的交点时,等号成立.所以MNC的周长的最小值是【点睛】关键点点睛:小问2的①亦可通过15CF AF AF ====解出253AF =或254AF =,再由24125AD AF =-和5AD AB >=得到254AF >,从而推知253AF =.22.已知在平面直角坐标系中,直线13:34=+l y x 交坐标轴于A 、B 两点,直线2:l y kx b =+交坐标轴于C 、D 两点,已知点()2,0C ,()0,6D .(1)设1l 与2l 交于点E ,试判断ACE △的形状,并说明理由;(2)点P 、Q 在ACE △的边上,且满足OPC 与OPQ △全等(点Q 异于点C ),直接写出点Q 的坐标.【答案】(1)ACE △为等腰三角形,理由见详解(2)点Q 在坐标为86,55⎛⎫ ⎪⎝⎭,412,55⎛⎫-⎪⎝⎭,(2,0)-,418,55⎛⎫ ⎪⎝⎭【解析】【分析】(1)代入点C ,D 求得直线2:36l y x =-+,进而可得到点E 的坐标为418,55⎛⎫ ⎪⎝⎭,分别求出AE ,,AC CE ,从而可判断出ACE △为等腰三角形;(2)分①P 、Q 在CE 上;②P 在CE 上,Q 在AE 上;③P 在AE 上,Q 在CE 上;④P 在AC 上,Q 与点E 重合四种情况结合图形求解即可.【小问1详解】ACE △为等腰三角形,理由如下:对于直线13:34=+l y x ,令0x =,可得3y =,令0y =,可得4x =-,即()()4,0,0,3A B -;将点()2,0C ,()0,6D 代入直线2:l y kx b =+,可得206k b b +=⎧⎨=⎩,解得36k b =-⎧⎨=⎩,则直线2:36l y x =-+,联立方程33436y x y x ⎧=+⎪⎨⎪=-+⎩,解得45185x y ⎧=⎪⎪⎨⎪=⎪⎩,即418,55E ⎛⎫ ⎪⎝⎭,可得6,,65AE CE AC =====,即AE AC CE =≠,所以ACE △为等腰三角形.【小问2详解】①当P 、Q 在CE 上时,如图1,此时OPC OPQ ≅,则2OQ OC ==,设(3),6Q m m -+,又因为(2,0)C ,则()222362m m +-+=,解得85m =或2m =(舍去),所以86,55Q ⎛⎫ ⎪⎝⎭;②P 在CE 上,Q 在AE 上时,如图2,此时OPC POQ ≅V V ,则,2POC OPQ PQ OC ==∠=∠,可知PQ OC ∥,设3,34Q n n ⎛⎫+ ⎪⎝⎭,则32,34P n n ⎛⎫++ ⎪⎝⎭,代入36y x =-+得()333264n n +=-++,解得45n =-,所以412,55Q ⎛⎫- ⎪⎝⎭;③P 在AE 上,Q 在CE 上时,如图3,此时OPC OPQ ≅ ,则2OQ OC ==,可知(2,0)Q -;④P 在AC 上,Q 与点E 重合时,如图4,此时OPC POQ ≅V V ,则2,PQ OC POC OPQ ∠∠===,可得AOD APO =∠∠,AP PQ AO OC AC AE +=+==,所以Q 与点E 重合,即418,55Q ⎛⎫ ⎪⎝⎭;综上所述:点Q 在坐标为86,55⎛⎫ ⎪⎝⎭,412,55⎛⎫- ⎪⎝⎭,(2,0)-,418,55⎛⎫ ⎪⎝⎭.23.如图,在平面直角坐标系中,抛物线2y ax bx c =++经过()3,0A 、()1,0B -、()0,3C .(1)求抛物线的函数表达式;(2)点D 是线段BC 上一动点,点D 关于AC 、AB 的对称点分别为点M 、N ,连接MN 交线段AC 、AB 于E 、F .求MF NE ⋅最小值;(3)在(2)的条件下请直接写出线段MN 的取值范围.【答案】(1)223y x x =-++(2)725(3)12565MN ≤≤【解析】【分析】(1)将,,A B C 三点代入解析式解得,,a b c ,即可得函数表达式;(2)分析可知:MAN △为等腰直角三角形,且AEN FAM :△△,进而可得2MF NE AD ⋅=,可知当且仅当AD BC ⊥时,AD 取到最小值,运算求解即可;(3)结合(2)可知:5AD ≤≤,且MN =,即可得结果【小问1详解】因为抛物线2y ax bx c =++经过()3,0A 、()1,0B -、()0,3C ,则93003a b c a b c c ++=⎧⎪-+=⎨⎪=⎩,解得123a b c =-⎧⎪=⎨⎪=⎩,所以抛物线的函数表达式为223y x x =-++.【小问2详解】连接AD,由题意可知:3,1OC OA OB ===,则45,4,CAO BC AB AC ∠=︒===由对称可知:,,AM AD AN MAC CAD BAD BAN ==∠=∠∠=∠,则()2290MAN MAC CAD BAD BAN CAD BAD CAO ∠=∠+∠+∠+∠=∠+∠=∠=︒,可知MAN △为等腰直角三角形,则45AMN ANM ∠=∠=︒,即AMN ANM EAO ∠=∠=∠,又因为AEN AMN MAE EAO MAE MAF ∠=∠+∠=∠+∠=∠,可知AEN FAM :△△,则NA NE MF MA=,可得2MF NE NA MA AD ⋅=⋅=,当且仅当AD BC ⊥时,AD 取到最小值,即MF NE ⋅最小值,此时5OC AB AD BC ⋅==,所以MF NE ⋅最小值为2725AD =.【小问3详解】由(2)可知4,AB AC ==,且AD的最小值为5,可知5AD ≤≤,且MAN △为等腰直角三角形,则MN ==,所以65MN ≤≤.24.如图,在矩形ABCD 中,4cm AD =,3cm DC =,对角线AC 、BD 相交于点O ,动点P 、Q 分别从点C 、A 同时出发,运动速度均为1cm/s ,点P 沿C O B →→运动.到点B 停止,点Q 沿A D C →→运动,到点C 停止.连接,,AP AQ PQ ,设APQ △的面积为()2cmy (这里规定:线段是面积为0的几何图形),点Q 的运动时间为x (s ).(1)当PQ CD ∥时,求x 的值;(2)当572x ≤≤时,求y 与x 之间的函数关系式;(3)直接写出在整个运动过程中,使AQ PQ =的所有x 的值.【答案】(1)209(2)2235,41022128,45556,57x x y x x x x ⎧≤≤⎪⎪⎪=-+<≤⎨⎪<≤⎪⎪⎩(3)2511,4,132【解析】【分析】(1)计算,P Q 到直线AB 的距离,由已知条件得到方程,再求解即可;(2)对不同的情况分类讨论计算三角形的面积;(3)对不同的情况分类讨论,列出相应的方程,再解出即可.【小问1详解】先大致将情况分为以下四种:当502x ≤≤时,点P 在OC 上,点Q 在AD 上;当542x ≤≤时,点P 在OB 上,点Q 在AD 上;当45x ≤≤时,点P 在OB 上,点Q 在DC 上;当57x ≤≤时,点P 停止在点B 处,点Q 在DC 上.由于点P 到直线AB 的距离为4max 4,05x ⎧⎫-⎨⎬⎩⎭,点Q 到直线AB 的距离为{}min ,4x ,故{}4max 4,0min ,405x x ⎧⎫-=≠⎨⎬⎩⎭,由4max 4,005x ⎧⎫-≠⎨⎬⎩⎭知4405x ->,故{}44min ,45x x -=.直接验证即知0x ≠,从而由{}4min ,4445x x =-<知4x <,故445x x =-,得209x =.【小问2详解】当542x ≤≤时,有AQ x =,而点P 在OB 上,点P 到直线AB 的距离为445x -,故点P 到直线AD 的距离为35x ,所以21332510y x x x =⋅⋅=;当45x ≤≤时,点Q 在DC 上,4DQ x =-,而点P 在OB 上,点P 到直线AB 的距离为445x -,故点P 到直线AD 的距离为35x ,所以()()21343121244421482555555y x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫=⋅---=---=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭;当57x ≤≤时,点Q 在DC 上,4DQ x =-,而点P 停止在点B 处,故13462y =⋅⋅=.综上,所求的函数关系式为2235,41022128,45556,57x x y x x x x ⎧≤≤⎪⎪⎪=-+<≤⎨⎪<≤⎪⎪⎩.【小问3详解】当502x ≤≤时,点P 在OC 上,点Q 在AD 上.若AQ PQ =,则85AP AQ =,即855x x -=,解得2513x =;当542x ≤≤时,点P 在OB 上,点Q 在AD 上.此时点P 到直线AB 的距离为445x -,点P 到直线AD 的距离为35x .若AQ PQ =,则x =,解得4x =;当45x ≤≤时,点P 在OB 上,点Q 在DC 上.此时4DQ x =-,点P 到直线AB 的距离为445x -,点P 到直线AD 的距离为35x .若AQ PQ ==4x =;当57x ≤≤时,点P 停止在点B 处,点Q 在DC 上.此时4DQ x =-,若AQ PQ =,则Q 是CD 的中点,从而342x -=,得112x =.综上,满足条件的x 的所有可能取值是2511,4,132.【点睛】关键点点睛:本题的关键在于不同情况的分类讨论,较为繁琐,需要细心才能不重不漏.。
宁波中考 重点高中提前批录取数学试卷

宁波市重点中学提前招生数学试卷1.已知关于x 的方程mx+2=2(m —x)的解满足|x-21 |-1=0,则m 的值是 ( ) A.10或52 B.10或-52 c.-10或52 D.-10或522.设直角三角形的三边长分别为a 、b 、c ,若c-b=b-a>O ,则 ( )A.1/2B.1/3C.1/4D.1/53.某工厂第二季度的产值比第一季度的产值增长了x %,第三季度的产值又比第二季度的产值增长了x %,则第三季度的产值比第一季度的产值增长了 ( )A.2x %B. 1+2x % C(1+x %)x % D.(2+x %)x %4.甲从一个鱼摊上买了三条鱼,平均每条a 元,又从另—个鱼摊上买了两条鱼,平均每条b 元,后来他又以每条元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( )A .a>b b .a<b C. a=b D.与a 和b 的大小无关5.若D 是△ABC 的边AB 上的一点,么ADC=么BCA,AC=6,DB=5,△ABC 的面积是S ,则△BCD 的面积是 ( ) A.S 53 B. S 74 C .S 95 D .S 1166.如图,AE ⊥AB 且AE=AB ,BC ⊥CD 且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是( )A .50 B.62 C .65 D .687.如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a ,右图轮子上方的箭头指着的数字为b ,数对(a ,b)所有可能的个数为n ,其中a+b 恰为偶数的不同数对的参数为m ,则m/n 等于 ( )A .21B .61C .125D .438.如图,甲、乙两动点分别从正方形ABCD 的顶点,A 、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2000次相遇在边 ( )A .AB 上 B.BC 上 C .CD 上D .DA 上9.已知2+x a 与2-x b 和等于442-x x ,则a= ,b=10.如图,AD 是△ABC 的中线,E 是AD 上的一点,且AE=31AD ,CE 交AB 于点F .若AF=1.2cm ,则AB= cm11.在梯形ABCD 中,AB ∥CD,AC .BD 相交于点O ,若AC=5,BD=12,中位线长为213,△AOB 的面积为S 1,△COD 的面积为S 2,则21S S +=12.已知矩形A的边长分别为a和b,如果总有另一矩形B,使得矩形B与矩形A的周长之比与面积之比都等于k,则k的最小值为.13.如图,AB∥EF∥CD,已知 AC+BD=240,BC=100,EC+ED=192,求CF.14.已知x、y均为实数,且满足xy+x+y=17,x2y+xy2=66,求x4+x3y+x2y2+xy3+y4的值.15.将数字1,2,3,4,5,6,7,8分别填写到八边形ABCDEFGH的8个顶点上,并且以S1,S2,…,S8分别表示(A,B,C),(B,C,D),…,(H,A,B)8组相邻的三个顶点上的数字之和.(1)试给出一个填法,使得S1,S2,…,S8都大于或等于12;(2)请证明任何填法均不可能使得S1,S2,…,S8都大于或等于13.宁波市重点中学提前招生数学试卷1.A 2.C 3.D 4.A 5.C 6.A 7.C 8.A9.2;2 10.6 11.30 12.2)(4b a ab15.(1)不难验证,如图所示填法满足.s1,s2,…s8都大于或等于12.(2)显然,每个顶点出现在全部8组3个相邻顶点组的3个组中,所以有s1+S2+…+S8= (1+2+3+…+8)·3=108.如果每组三数之和都大于或等于13,因13·8=104,所以至多有108-104=4个组的三数之和大于13.由此我们可得如下结论:(1)相邻两组三数之和一定不相等.设前一组为(i ,j ,k),后一组为(j ,k ,l).若有i+j+k=j+k+l ,则l=i ,这不符合填写要求;(2)每组三数之和都小于或等于14.因若有一组三数之和大于或等于15,则至多还有另外两个组,其三数之和大于13,余下5个组三数之和等于13,必有相邻的两组相等,这和上述结论(1)不符.因此,相邻两组三数之和必然为13或14.不妨假定1填在B 点上,A 点所填为i ,C 点所填为j .(1)若S1=i+1+J=13,则.s2=1+j+l=14,S3=j+l+k=13,因J>1,这是不可能的.(2)若sl=i+1+j=14,则S2=1+j+(i-1)=13,S=j+(i-1)+2:14,s4=(i-1)+2+(j-1)=13,这时S5=14,只能是S=2+(j-1)+i ,i 重复出现:所以不可能有使得每组三数之和均大于或等于13的填法.。
2020-2021学年浙江省宁波市鄞州区蓝青学校七年级(下)期末数学试卷(附答案详解)

2020-2021学年浙江省宁波市鄞州区蓝青学校七年级(下)期末数学试卷一、选择题(本大题共10小题,共30.0分)1. 下列多项式乘法中,不能进行平方差计算的是( )A. (x +y)(−x −y)B. (2a +b)(2a −b)C. (−3x −y)(−y +3x)D. (a 2+b)(a 2−b)2. 下列由左边到右边的变形中,是因式分解的是( )A. x 2−4x +4=(x −2)2B. x 2−1=x(x −1x ) C. x 2−4+3x =(x +2)(x −2)+3xD. (x +2)(x −2)=x 2−43. 不改变分式1.3x−12x−0.7y 的值,把它的分子与分母中各项的系数化为整数,其结果正确的是( )A. 13x−12x−7yB.13x−102x−7yC. 13x−1020x−7yD. 13x−120x−7y4. 《九章算术》是中国古代第一部数学专著,书中有这样一题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价格是多少?设共有x 个人,该物品价格是y 元,则下列方程组正确的是( )A. {8x +3=y7x −4=yB. {8y +3=x7y −4=xC. {8x −3=y7x +4=yD. {8y −3=x7y +4=x5. 如图,将直角△ABC 沿斜边AC 的方向平移到△DEF 的位置,DE 交BC 于点G ,BG =4,EF =10,△BEG 的面积为4,下列结论:①∠A =∠BED ;②△ABC 平移的距离是4;③BE =CF ;④四边形GCFE 的面积为16,正确的有( )A. ②③B. ①②③C. ①③④D. ①②③④6. 如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )A. 3条B. 4条C. 5条D. 6条7. 如图,已知△ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是( )A. 甲和乙B. 乙和丙C. 只有乙D. 只有丙8. 要使分式(a+1a−1−a 2+1a 2−2a+1)÷1a−1的值是负整数,则a 应取的数为( ) A. 1和2 B. 2和3 C. a >1 D. a >29. 一只船有一个漏洞,水以均匀速度进入船内.发现漏洞时船内已经进入了一些水,如果以12个人淘水,3小时可以淘完,如果以5个人淘水,10小时才能淘完.现在要想在2小时内淘完,需要( )人.A. 17B. 18C. 20D. 2110. 已知abc =1,a +b +c =2,a 2+b 2+c 2=3,则1ab+c−1+1bc+a−1+1ca+b−1的值为( )A. −1B. −12C. 2D. −23二、填空题(本大题共8小题,共32.0分)11. 已知a =35555,b =44444,c =53333,用“<”将a ,b ,c 连接起来:______ . 12. 一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分______组.13. 如图所示,E ,F 分别是ABCD 的边AB ,CD 上的点,AF 与DE 相交于点P ,BF 与CE 相交于点Q ,若S △APD =12cm 2,S △BQC =22cm 2,则阴影部分的面积为______ cm 2.14. 若方程组{a 1x +y =c 1a 2x +y =c 2的解是{x =2y =3,则方程组{a 1x +y =a 1−c 1a 2x +y =a 2−c 2的解是x =______,y =______.15.如图,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3,若图3中∠CFE=120°,则图1中的∠DEF=______.=−1的解为正数,则a的取值范围是______.16.若关于x的方程2x+ax−217.已知724−1可被40至50之间的两个整数整除,这两个整数是______ .18.若x、y、z满足3x+7y+z=1和4x+10y+z=2001,则分式2000x+2000y+2000z的x+3y 值为______.三、计算题(本大题共1小题,共3.0分)19.若(x−3)(x+m)=x2+nx−15,求n2−m2的值.8n+5四、解答题(本大题共6小题,共35.0分)20.已知(n−2020)2+(2021−n)2=3,求(n−2020)(2021−n)的值.21.已知多项式2x4−3x3+ax2+7x+b含有因式x2+x−2,求a的值.b22.若2x+3y−4z+1=0,求9x⋅27y÷81z的值.23.如图,已知AM//BN,∠A=58°,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是______ 度;②∵AM//BN,∴∠ACB=∠______ .(2)求∠CBD的度数.(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是______ .(直接写出结果)24.已知x,y都是有理数,且满足方程(12+13)x+(13+π2)y−4−π=0,求x−y的值.25.如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,(1)求∠BFC的度数.(2)求证:BC=BE+CD.答案和解析1.【答案】A【解析】解:平方差公式的使用条件:两个代数式相乘,其中两项相同,两项互为相反数.不具备这两个条件的只有:(x+y)(−x−y).故选:A.平方差公式的使用条件:两个代数式相乘,其中两项相同,两项互为相反数即可判断.本题考查平方差公式的使用条件,理解使用条件是求解本题的关键.2.【答案】A【解析】解:A、x2−4x+4=(x−2)2,是因式分解,故本选项符合题意;B、x2−1=x(x−1x ),1x是分式,所以不是因式分解,故本选项不符合题意;C、x2−4+3x=(x+2)(x−2)+3x,等式的右边不是几个整式的积的形式,不是因式分解,故本选项不符合题意;D、(x+2)(x−2)=x2−4,是整式乘法,不是因式分解,故本选项不符合题意;故选:A.根据因式分解的定义逐个判断即可.本题考查了因式分解的定义,能熟记因式分解的定义的内容是解此题的关键,注意:把一个多项式化成几个整式的积的形式,叫因式分解.3.【答案】C【解析】解:原式=13x−1020x−7y,故选:C.根据分式的基本性质即可求出答案.本题考查分式的基本性质,解题的关键熟练运用分式的基本性质,本题属于基础题型.4.【答案】C【解析】解:若设有x 人,物品价值y 元,根据题意,可列方程组为{8x −3=y7x +4=y ,故选:C .根据“8×人数−3=物品价值、物品价值=7×人数+4”可得方程组.本题主要考查由实际问题抽象出二元一次方程组,由实际问题列方程组是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的相等关系.5.【答案】C【解析】解:∵△DEF 的是直角三角形ABC 沿着斜边AC 的方向平移后得到的,且A 、D 、C 、F 四点在同一条直线上,∴BE//AC ,AB//DE ,BC =EF ,BE =CF ,故③正确; ∴四边形ABED 是平行四边形, ∴∠A =∠BED ,故①正确; ∵BG =4, ∴AD =BE >BG ,∴△ABC 平移的距离>4,故②正确; ∵EF =10,∴CG =BC −BG =EF −BG =10−4=6, ∵△BEG 的面积等于4, ∴12BG ⋅GE =4, ∴GE =2,∴四边形GCFE 的面积=12(6+10)×2=16,故④正确; 故选:C .由平移的性质得到BE//AC ,AB//DE ,BC =EF ,BE =CF ,故③正确;根据平行四边形的性质得到∠A =∠BED ,故①正确;根据直角三角形斜边大于直角边得到△ABC 平移的距离>4,故②错误;根据三角形的面积公式得到GE =2,根据梯形的面积公式得到四边形GCFE 的面积=12(6+10)×2=16,故④正确.本题考查了平移的性质,面积的计算,平行四边形的判定和性质,正确的识别图形是解题的关键.6.【答案】B【解析】解:如图:若要知道该图形周长,至少需要知道4条线段的长:BC、AB,IJ,EF,∵BC=AL+KJ+IH+GF+DE,AB=LK+KK′=LK+CC′,IJ=HG+GG′=HG+ C′D′,EF=DD′,∴只要知道BC、AB,IJ,EF4条线段的长,就能知道该图形周长.故选:B.根据题意,结合图形,通过平移构成矩形,据此判断即可.此题考查了生活中的平移现象,此题的本质可理解为将线段平移构成矩形.7.【答案】B【解析】解:图甲不符合三角形全等的判定定理,即图甲和△ABC不全等;图乙符合SAS定理,即图乙和△ABC全等;图丙符合AAS定理,即图丙和△ABC全等;故选:B.全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理逐个判断即可.本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.8.【答案】B【解析】解:原式=[a+1a−1−a2+1(a−1)2]⋅(a−1)=a+1−a2+1a−1=−2a−1,∵分式的值为负整数,∴a−1=1或a−1=2,则a=2和3.故选:B.原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,利用乘法分配律计算得到最简结果,由分式的值是负整数,即可求出a 的值.此题考查了分式的化简求值,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式.9.【答案】A【解析】解:设水流入的速度为y ,原来有水z ,一人的淘水速度为x ,需要w 人,根据题意得:{3y +z =3×12x(1)10y +z =10×5x(2)2y +z =2⋅wx(3), (2)−(1)得: y =2x , 代入(1)得: z =30x ,把z =30x ,y =2x 代入(3)得: w =17(人).答:要想在2小时内淘完,需要17人.设水流入的速度为y ,原来有水z ,一人的淘水速度为x ,需要w 人,根据流入的水+原来的水=人淘出的水,列出方程组求解.本题通过列出方程组求解,关键是找到等量关系为:流入的水+原来的水=人淘出的水.10.【答案】D【解析】解:由a +b +c =2,两边平方, 得a 2+b 2+c 2+2ab +2bc +2ac =4, 将已知代入,得ab +bc +ac =12; 由a +b +c =2得:c −1=1−a −b ,∴ab +c −1=ab +1−a −b =(a −1)(b −1), 同理,得bc +a −1=(b −1)(c −1), ca +b −1=(c −1)(a −1),∴原式=1(a−1)(b−1)+1(b−1)(c−1)+1(c−1)(a−1) =c−1+a−1+b−1(a−1)(b−1)(c−1)=−1(ab−a−b+1)(c−1)=−1abc−ac−bc+c−ab+a+b−1=−11−12+2−1=−23.故选:D .由a +b +c =2,a 2+b 2+c 2=3,利用两个等式之间的平方关系得出ab +bc +ac =12;再根据已知条件将各分母因式分解,通分,代入已知条件即可.本题考查了分式的化简其中计算,解题时,充分运用已知条件变形,使分式能化简通分,得出结果.11.【答案】c <a <b【解析】解:∵a =35555,b =44444,c =53333, ∴a =31111×5=(35)1111=2431111, b =41111×4=(44)1111=2561111, c =51111×3=(53)1111=1251111, ∵1251111<2431111<2561111, ∴c <a <b ,故答案为:c <a <b .将a ,b ,c 转化成同指数的幂再进行比较即可得解.此题考查了幂的乘方与积的乘方,将a ,b ,c 转化成同指数的幂再进行比较是解题的关键.12.【答案】10【解析】解:在样本数据中最大值为141,最小值为50,它们的差是141−50=91,已知组距为10,那么由于9110=9.1,故可以分成10组. 故答案为:10.根据组数=(最大值−最小值)÷组距计算,注意小数部分要进位.本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.13.【答案】34【解析】解:连接E 、F 两点,∵四边形ABCD 是平行四边形,∴AB//CD ,∴△EFC 的FC 边上的高与△BCF 的FC 边上的高相等,∴S △EFC =S △BCF ,∴S △EFQ =S △BCQ ,同理:S △EFD =S △ADF ,∴S △EFP =S △ADP ,∵S △APD =12cm 2,S △BQC =22cm 2,∴S 四边形EPFQ =34cm 2,故阴影部分的面积为34cm 2.故答案为:34.连接E 、F 两点,由三角形的面积公式我们可以推出S △EFC =S △BCQ ,S △EFD =S △ADF ,所以S △EFG =S △BCQ ,S △EFP =S △ADP ,因此可以推出阴影部分的面积就是S △APD +S △BQC . 本题主要考查平行四边形的性质,三角形的面积,解题的关键在于求出各三角形之间的面积关系.14.【答案】−1 −3【解析】解:把{x =2y =3代入方程组{a 1x +y =c 1a 2x +y =c 2得, {2a 1+3=c 12a 2+3=c 2, 所以c 1−c 2=2(a 1−a 2),c 1−2a 1=3,方程组{a 1x +y =a 1−c 1①a 2x +y =a 2−c 2②,①−②得,(a 1−a 2)x =a 1−a 2−(c 1−c 2), 所以(a 1−a 2)x =−(a 1−a 2),因此x =−1,把x =−1代入方程组{a 1x +y =a 1−c 1①a 2x +y =a 2−c 2②中的方程①得,−a 1+y =a 1−c 1,所以y =2a 1−c 1=−(c 1−2a 1)=−3,故答案为:−1,−3.把{x =2y =3代入方程组{a 1x +y =c 1a 2x +y =c 2可求出c 1−c 2=2(a 1−a 2),c 1−2a 1=3,再根据方程组{a 1x +y =a 1−c 1①a 2x +y =a 2−c 2②,即可求出x 、y 的值. 本题考查二元一次方程组及其解法,掌握方程组的解法是解决问题的关键,解二元一次方程组的基本思想是消元.15.【答案】20°【解析】解:∵AD//BC ,∴设∠DEF =∠EFB =a ,图2中,∠GFC =∠BGD =∠AEG =180°−2∠EFG =180°−2a ,图3中,∠CFE =∠GFC −∠EFG =180°−2a −a =120°.解得a =20°.即∠DEF =20°,故答案为:20°.先根据平行线的性质,设∠DEF =∠EFB =a ,图2中根据图形折叠的性质得出∠AEF 的度数,再由平行线的性质得出∠GFC ,图3中根据∠CFE =∠GFC −∠EFG 即可列方程求得a 的值.本题考查图形的翻折变换以及平行线的性质,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.16.【答案】a <2且a ≠−4【解析】解:去分母得,2x +a =−x +2解得x =2−a 3∵分母x −2≠0即x ≠2∴2−a 3≠2 解得,a ≠−4又∵x >0∴2−a 3>0 解得,a <2则a 的取值范围是a <2且a ≠−4.先解关于x 的分式方程,求得x 的值,然后再依据“解是正数”建立不等式求a 的取值范围.本题考查了分式方程无解的条件,是需要识记的内容.并且在解方程去分母的过程中,一定要注意分数线起到括号的作用,并且要注意没有分母的项不要漏乘.17.【答案】48,43【解析】解:724−1=(712+1)(712−1)=(712+1)(76+1)(76−1)=(712+1)(76+)(73+1)(73−1)=(712+1)(76+1)(7+1)(72−7×1+1)(7−1)(72+7×1+1)=(712+1)(76+1)×8×43×6×57=(712+1)(76+1)×48×43×57,∵724−1可被40至50之间的两个整数整除,∴这两个整数是48,43.故答案为:48,43.利用平方差公式,对已知的多项式进行因式分解即可得出结论.本题主要考查了因式分解的应用.利用因式分解将多项式分解因式可以得到它含有的整式.18.【答案】−3999【解析】解:由x 、y 、z 满足3x +7y +z =1和4x +10y +z =2001,得出:{2(x +3y)+(x +y +z)=13(x +3y)+(x +y +z)=2001,解得:{x +3y =2000x +y +z =−3999, ∴2000x+2000y+2000z x+3y =2000(x+y+z)x+3y , =2000×(−3999)2000=−3999.故答案为:−3999.分式2000x+2000y+2000z x+3y =2000(x+y+z)x+3y ,视x +3y 与x +y +z 为两个整体,对方程组进行整体改造后即可得出答案.本题考查了分式的化简求值与三元一次方程组的应用,难度较大,关键是视x +3y 与x +y +z 为两个整体,对方程组进行整体改造.19.【答案】解:(x −3)(x +m)=x 2+(m −3)x −3m=x 2+nx −15,则{m −3=n −3m =−15解得:{m =5n =2. n 2−m 28n+5=22−528×2+5=−1.【解析】首先把)(x −3)(x +m)利用多项式的乘法公式展开,然后根据多项式相等的条件:对应项的系数相同即可得到m 、n 的值,从而求解.本题考查了多项式的乘法法则以及多项式相等的条件,理解多项式的乘法法则是关键.20.【答案】解:令n −2020=a ,2021−n =b ,根据题意得:a 2+b 2=3,a +b =1,∴原式=ab=(a+b)2−(a 2+b 2)2 =1−32=−1.【解析】利用完全平方公式和整体代入,用多项式乘多项式法则求解即可.这道题考查的是完全平方公式和多项式乘多项式,熟记完全平方公式和多项式乘多项式法则是解题的基础.21.【答案】解:∵x2+x−2=(x+2)(x−1),∴2x4−3x3+ax2+7x+b能被(x+2)(x−1)整除,设商是A.则2x4−3x3+ax2+7x+b=A(x+2)(x−1),则x=−2和x=1时,右边都等于0,所以左边也等于0.当x=−2时,2x4−3x3+ax2+7x+b=32+24+4a−14+b=4a+b+42= 0①当x=1时,2x4−3x3+ax2+7x+b=2−3+a+7+b=a+b+6=0②①−②,得3a+36=0,∴a=−12,∴b=−6−a=6.∴ab =−126=−2.【解析】由于x2+x−2=(x+2)(x−1),而多项式2x4−3x3+ax2+7x+b能被x2+ x−2整除,则2x4−3x3+ax2+7x+b能被(x+2)(x−1)整除.运用待定系数法,可设商是A,则2x4−3x3+ax2+7x+b=A(x+2)(x−1),则x=−2和x=1时,2x4−3x3+ax2+7x+b=0,分别代入,得到关于a、b的二元一次方程组,解此方程组,求出a、b的值,进而得到ab的值.本题主要考查了待定系数法在因式分解中的应用,注意因式的特点,灵活解决问题.22.【答案】解:∵若2x+3y−4z+1=0,∴2x+3y−4z=−1,∴9x⋅27y÷81z=32x×33y÷34z=32x+3y−4z=3−1=13.【解析】由2x+3y−4z+1=0可得2x+3y−4z=−1,再根据同底数幂的乘除法以及幂的乘方运算法则求解即可.本题考查了同底数幂的乘除法以及幂的乘方,掌握相关运算法则是解答本题的关键.23.【答案】122 CBN30.5°【解析】解:(1)①∵AM//BN,∠A=58°,∴∠A+∠ABN=180°,∴∠ABN=122°;②∵AM//BN,∴∠ACB=∠CBN;(2)∵AM//BN,∴∠ABN+∠A=180°,∴∠ABN=180°−58°=122°,∴∠ABP+∠PBN=122°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=122°,∴∠CBD=∠CBP+∠DBP=61°;(3)不变,∠APB:∠ADB=2:1.∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM//BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,由(1)可知∠ABN=122°,∠CBD=61°,∴∠ABC+∠DBN=61°,∴∠ABC=30.5°.故答案为:122,CBN;30.5°.(1)由平行线的性质:两直线平行同旁内角互补和内错角相等可得;(2)由(1)知∠ABP +∠PBN =122°,再根据角平分线的定义知∠ABP =2∠CBP 、∠PBN =2∠DBP ,可得2∠CBP +2∠DBP =122°,即∠CBD =∠CBP +∠DBP =61°;(3)由AM//BN 得∠APB =∠PBN 、∠ADB =∠DBN ,根据BD 平分∠PBN 知∠PBN =2∠DBN ,从而可得∠APB :∠ADB =2:1;(4)由AM//BN 得∠ACB =∠CBN ,当∠ACB =∠ABD 时有∠CBN =∠ABD ,得∠ABC +∠CBD =∠CBD +∠DBN ,即∠ABC =∠DBN ,根据∠ABN =122°,∠CBD =61°可得答案.本题主要考查平行线的性质和角平分线的定义,熟练掌握平行线的性质是解题的关键.24.【答案】解:原方程变形为:56x +13y −4+π2y −π=0.∵x ,y 都是有理数.∴{π2y −π=056x +13y −4=0,解得:{y =2x =4. ∴x −y =4−2=2.【解析】先将原式变形为56x +13y +π2y −4−π=0,由x ,y 都是有理数可以得出π2y −π=0,56x +13y −4=0,这样就可以求出x 、y 、的值,从而可以求出其解.本题考查了有理数和无理数的概念及有理数和无理数的运算及关系的运用,在解答时巧妙运用有理数、无理数的和为0,则有理数、无理数分别为0求解.25.【答案】(1)解:在△ABC 中,∠ABC +∠ACB =180°−∠A =180°−60°=120°, ∵∠ABC ,∠ACB 的平分线BD ,CE 相交于点F ,∴∠FBC =12∠ABC ,∠FCB =12∠ACB ,∴∠FBC +∠FCB =12(∠ABC +∠ACB)=12×120°=60°,在△BCF 中,∠BFC =180°−(∠FBC +∠FCB)=180°−60°=120°.(2)证明:在BC 上取一点O ,使得BO =BE ,∵∠A=60°,BD、CE是△ABC的角平分线,∴∠BFC=120°,∴∠BFE=∠CFD=60°,在△BFE和△BFO中,{BF=BF∠FBE=∠FBO BE=BO,∴△BFE≌△BFO,(SAS)∴∠BFO=∠BFE=60°,∴∠CFO=∠BFC−∠BFO=60°,在△OCF和△DCF中,{∠CFO=∠CFD=60°CF=CF∠FCO=∠FCD,∴△OCF≌△DCF(ASA),∴CO=CD,∵BC=BO+CO,∴BC=BE+CD.【解析】(1)根据三角形的内角和等于180°列式求出∠ABC+∠ACB,再根据角平分线的定义求出∠FBC+∠FCB,然后利用三角形的内角和等于180°列式计算即可得解.(2)在BC上取一点O使得BO=BE,易证∠BFE=∠CFD=60°,即可证明△BFE≌△BFO,可得∠BFO=∠BFE=60°,即可证明△OCF≌△DCF,可得CO=CD,根据BC=BO+ OC即可证明.本题考查了全等三角形的判定和性质、三角形的内角和定理,角平分线的定义,解题的关键是学会添加辅助线构造全等三角形解决问题,属于中考常考题型.。
初中数学精品试题:鄞州中学提前招生数学试卷-

鄞州中学提前招生数学试卷(本卷考试时间80分钟,满分120分)一、填空题(把答案填在题中横线上,每小题7分,共70分)1、已知a 、b 满足a 2-2a -1=0,b 2-2b -1=0,且a ≠b ,则a b +ba +1= . 2、△ABC 的周长是24,M 是AB 的中点,MC =MA =5,则△ABC 的面积是 .3、要使关于x 的方程21++x x -1-x x =22-+x x m 的解为负数,则m 的取值范围是 . 4、已知:41(b -c )2=(a -b )(c -a ),且a ≠0,则ac b 4+= . 5、如图,E 、F 分别在AD 、BC 上,EFCD 是正方形,且矩形ABCD ∽矩形AEFB ,则AB ∶BC 的值是 .6、设x 、y 、z 满足关系式x -1=21+y=32-z ,则x 2+y 2+z 2的最小值为. 7、如图,在△ABC 中,D 、E 是BC 的三等分点,M 是AC 的中点, BM交AD 、AE 于G 、H 则BG ∶GH ∶HM = . 8、如图3×3的正方形的每一条方格内的字母都代表某个数,已 知其每行、每列以及两条对角线上三角形个数之和都相等,若a =4,d =19,i =22,那么b = ,h = .9、在矩形ABCD 中,AB =6cm ,BC =8cm ,若将矩形折叠,使B点与D 点重合,如图所示,则折痕EF 的长为 .10、如图,已知ABCD 是一个半径为R 的圆内接四边形,AB =12, CD =6,分别延长AB 和DC ,它们相交于点P ,且BP =8,∠APD =600,则R = . 二、解答题(本大题共4小题,共50分,解答应写出文字说明、证明过程或演算步骤)11、如图,在直角坐标系内有两个点A (-1,-1),B (2,3)-MA 最大,求M 点的坐标,并说明理由.(10分)第7题 第10题 第8题 第11题12、分别求所有的实数k,使得关于x的方程kx2+(kx+1)x+(k-1)=0(1)有实根(2)都是整数根(12分)13、如图,设△ABC是直角三角形,点D在斜边BC上,BD=4DC,已知圆过点C且与AC相交于F,与AB相切于AB的中点G. 求证:AD⊥BF. (14分)14、我国是水资源比较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市用水收费方法是:水费=基本费+超额费+损耗。
蓝青中学初三试卷数学答案
一、选择题(每题5分,共50分)1. 若a > b,则下列哪个不等式成立?A. a + 2 > b + 2B. a - 2 < b - 2C. a - 2 > b - 2D. a + 2 < b + 2答案:A2. 已知等腰三角形底边长为8,腰长为10,那么这个三角形的周长是:A. 26B. 28C. 30D. 32答案:B3. 下列哪个函数是奇函数?A. y = x^2B. y = |x|C. y = x^3D. y = x^4答案:C4. 若a、b、c、d为等差数列,且a + b + c + d = 24,那么a + c的值为:A. 12B. 14C. 16答案:A5. 下列哪个图形是正方形?A. 对角线相等的矩形B. 对角线互相垂直的菱形C. 对角线相等的平行四边形D. 对角线互相平分的四边形答案:B6. 已知一元二次方程x^2 - 5x + 6 = 0,则方程的解为:A. x = 2, x = 3B. x = 2, x = 4C. x = 3, x = 2D. x = 4, x = 3答案:A7. 下列哪个函数是反比例函数?A. y = 2xB. y = x^2C. y = 1/xD. y = x + 1答案:C8. 已知等腰三角形的底边长为8,腰长为10,那么这个三角形的面积是:A. 40B. 50D. 80答案:B9. 若一个数的平方根是2,那么这个数是:A. 4B. -4C. 16D. -16答案:A10. 下列哪个方程的解集是空集?A. x + 2 = 0B. 2x + 1 = 0C. 3x + 2 = 0D. 4x + 3 = 0答案:C二、填空题(每题5分,共50分)11. 若a = 3,b = 5,那么a^2 + b^2的值是______。
答案:3412. 已知一个等差数列的首项为2,公差为3,那么第10项是______。
答案:3113. 函数y = 2x + 1的图像是一条______。
山东省青岛市市南区青岛大学附属中学2024-2025学年七年级上学期小升初分班考试数学试题(含答案)
2024级入学教育数学(考试时间:90分钟;满分:100分)友情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!请将答案全部写在答题纸上一、基础题(共35分)(一)填空题(每空1分,共22分)1.我国某次人口普查结果公布,全国总人口为1443497378人。
把横线上的数改写成用“万”作单位,省略“万”后面的尾数是( )万。
2.一个三角形三个内角的度数比是1∶2∶3,这个三角形是()三角形。
3.观察下图,将涂色部分的面积与整个图形的面积关系分别用分数乘法、最简整数比、百分数表示出来。
4.如图的梯形是由一张长方形纸片折叠而成的。
这个梯形的面积是( )平方厘米。
(单位:cm )5.一堆煤,运走一部分,还剩,运走的与剩下的比为( )。
(填分数)6.一个圆柱体木块,底面直径是6厘米,高是3厘米,它的表面积是()平方厘米。
把它削成一个最大的圆锥,应削去()立方厘米。
(取3)7.3.2升=( )毫升 1.5公顷=( )平方米。
8.丁丁的身高是1.2米,妈妈的身高是1.6米,周末母子俩拍照合影,照片中妈妈的身高是8厘米,则这幅照片是把人按( )的比缩小了,照片中的丁丁应该()厘米。
9.已知(x 、y 均为非0自然数),那么x 和y 最大公因数是( ),x 和y 成( )比例。
10.鞋的尺码是指鞋内底的长度,通常用“码”或“厘米”作单位,它们之间的关系可以用来表示(y 表示码数,x 表示厘米数)。
丽丽买了一双内底长度是23厘米的鞋,她买的是( )码的鞋;爸爸买了一双41码的鞋,他的鞋内底长( )厘米。
11.某省于2021年实行新高考“”方案。
“3”是指语文数学外语三门学科为必考科目,“1”是3()( )( )%4⨯==25π40.5x y =210y x =-312++指考生在物理和历史两门学科里面必须选一科,“2”是指考生在剩下的化学、生物、思想政治、地理四门学科中选择两科。
这样,新高考方案中最多出现( )种考试科目组。
2024-2025学年广西南宁三十七中七年级(上)入学数学试卷(一)+答案解析
2024-2025学年广西南宁三十七中七年级(上)入学数学试卷(一)一、选择题:本题共4小题,每小题2分,共8分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.在一条线段中间另有6个点,则这8个点可以构成线段.A.15B.21C.28D.362.大圆的直径是小圆直径的3倍,小圆面积与大圆面积的比是()A.1:9B.9:1C.1:3D.3:13.把8个边长都是3厘米的正方形,一个接一个地拼成长方形,这个长方形的周长是()A.24厘米B.48厘米C.54厘米D.64厘米4.密封的纸盒里有60粒大小相同的珠子,每15粒是同一种颜色,为保证一次能取出3粒颜色相同的珠子,至少要取出粒.A.6B.9C.12D.18二、填空题:本题共14小题,每小题2分,共28分。
5.一个数的2倍加上4,再乘4,再除以4得74,这个数是______.6.时=______时______分;3公顷9平方米=______公顷.7.把:化成最简整数比是______,比值是______.8.……个7相乘,积的个位数是______.9.如果在81个零件中混杂一个重量轻的次品,最少称______次才能把次品挑出来.10.计算:______.11.已知一串有规律的数:,,,,,…那么这串数的第9个数是______.12.如图,在长方形ABCD中,厘米,厘米,四边形EFHG的面积是3平方厘米,阴影部分的面积和是______平方厘米.13.甲、乙两个同学分别在长方形围墙外的两角.如果他们同时开始绕着围墙逆时针方向跑,甲每秒跑5米,乙每秒跑4米,那么甲最少要跑______秒才能看到乙.14.工程队修一段公路原计划每天修千米,15天完成,实际每天多修千米,可提前______天修完.15.把浓度为的600毫升酒精稀释成浓度为的消毒酒精,需要加入蒸馏水______毫升.16.甲、乙两种水性笔共90支,已知甲种笔每支5元,乙种笔每支4元,两种笔的总钱数相等甲种笔有______支,乙种笔有______支.17.某班有学生36人,骑自行车和打篮球每个人至少会一项,结果的学生会骑自行车,有的学生两样都会,会打篮球的有______人.18.A、B两船,分别从甲、乙两港同时向对方港口开出,经过6小时后,两船相遇,相遇后两船继续向前行驶,A船又经4小时到达乙港,B船又经______小时到达甲港.三、解答题:本题共9小题,共64分。
2007年台山市高中提前招生数学模拟题(含答案)
2007 年台山市高中提早招生数学模拟试题一、选择题(此题有12 小题,每题 3 分,共 36 分,请选出各题中一个切合题意的正确选项,不选、多项选择、错选,均不给分)1.以下计算正确的选项是()A 、 2 a2·a32a 6B、(3a2)39a 6C、a6 a 2a3D、(a2)3 a 6 2.抛物线y(a8)2 2 的极点坐标是()A 、(2, 8)B、( 8,2)C、(— 8, 2)D、(— 8,— 2)3.已知圆锥的底面半径为9 ㎝,母线长为30 ㎝,则圆锥的侧面积为()A、270π cm2B、360π cm2C、450π cm 2D、540π cm2 4.如图,已知 AB ∥CD , AB=CD,AE=FD,则图中的全等三角形有()A、1对B、2 对C、3 对D、4对5.现有 2008 年奥运会福娃卡片20 张,其B中贝贝 6 张,京京 5 张,欢欢 4 张,迎迎 3 张,AFD E妮妮 2 张,每张卡片大小、质地平均相同,将画有福娃的一面朝下反扣在桌子上,从中随机C (第4题图)抽取一张,抽到京京的概率是()1B、311A 、10C、D、10456.假如一个定值电阻R 两头所加电压为 5 伏时,经过它的电流为 1 安培,那么经过这一电阻的电流 I 随它的两头电压U 变化的图像是()A C7.如图是 5× 5 的正方形络,以点 D、 E 为两个极点作位置不一样的格点三角形,使所作的格点三角形与△ABC全等,B 这样的格点三角形最多能够画出()D EA、2个B、4 个C、6 个D、8 个(第 7题图)8. 如 ,已知△ ABC 的六个元素, 以下甲、乙、丙三个三角形中和△ABC 全等的 形是 ( )Ba50 c50 a72甲乙 丙C 58725050AbacaA 、甲乙B、甲丙C 、乙丙D 、乙9.如 ,∠ ACB = 60○,半径 2 的⊙ 0 切 BC 于点 C ,若将⊙ O 在 CB 上向右 , 当到⊙ O 与 CA 也相切 , 心 O 移 的水平距离 ()A 、 2πB、4πC 、23 D 、4HADAOEGC (第9题图)BB F C( 第11题图)10.如 ,是用4 个全等的直角三角形与 1 个小正方形 嵌而成的正方形 案,已知大正方形面 49,小正方形面 4,若用 X 、 Y 表示直角三角形的两直角 ( x >y ),察 案,指出以下关系式中不正确的选项是 ( )A 、 x 2+ y 2= 49B 、 x - y = 2C 、 2xy + 4= 49D 、 x + yY = 1311.如 ,正方形ABCD1, E 、F 、 G 、 H 分 各 上的点,且 AE=BF=CG=DH, 小 正方形 EFGH 的面 Y ,AE X , Y 对于 X 的函数 象大概是()12.先作半径2的 的内接正方形,接着作上述内接正方形的内切 ,再作上述内切2的内接正方形,⋯, 按以上 律作出的第7 个 的内接正方形的()A 、( 2 )6B、( 2 )7C、(2)6D、( 2)722二、填空题(第小题 4 分,共 24 分)O13.我们知道, 1 纳米 =10—9米,一栽花粉直径为35000 纳米,那么这ACB栽花粉的直径用科学记数法可记为米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
07蓝青学校初三数学竞赛试题
一、填空题:(每小题5分) 1、已知直线y =-
2
1
x -3,则此直线关于y 轴对称的直线为 . 2、计算:12003200220012000+⨯⨯⨯
3、如图一,已知点M (p ,q )在抛物线y 以M 为圆心的圆与x
轴交于A 、B 两点的横坐标是关于x 的方程x 2-2px 根,则弦AB 的长等于 .
4、已知实数x 、y 满足x 2+2y =3,y 2且x ≠y ,则:
y x +x
y
的值是 . 5、若y =2x -3+134-x ,则y 的最小值是 . 6、木匠师傅要用一块三夹板(矩形,尺寸如图二)
做一个圆桌的桌面,如果直接锯下一个圆,则半径 太小,于是就锯下两个一样大的半圆,拼成一个圆, 这样做成的桌面半径最大是 .
7、已知:凸n 边形的n 个内角与一个外角的和是20000, 则n = .
8、设:a 、b 、c 均为非零实数,并且ab =2(a +b ),bc =3(b +c ),ca =4(c +a ),则
b
ac
= . 二、选择题(每小题5分)
1、某旅社有100张床位,每床每晚收费10元时,客床可全部租出;若每床每晚收费提高2元,则减少10张床位租出;若每床每晚收费再提高2元,则再减少10张床位租出.以每次提高2元的这种方法变化下去,为了投资少而获利大,每床每晚收费应提高( ) (A )4元或6元 (B )4元 (C )6元 (D )8元
2、已知Rt △ABC 和Rt △A 'B 'D 中,AC =A 'C ',AD =1,∠B =∠D =900,∠C +∠C '
=600,BC =2,则:这两个三角形面积的和是( )
(A )3 (B )
2
33 (C )23 (D )不能确定
3、已知a 、b 满足3a +5│b │=7,(a ≥0),则s =2a -3│b │的取值范围为( )
(A )-
321<s <314 (B )-521≤s ≤314 (C )-19
21≤s ≤1914
(D )以上都不对
4、如图三,以△ABC 的三边为边在BC 的同侧作正△BCE 、 正△ABF 和正△ACD ,已知BC =3,高AH =1,则五边 形BCDEF 的面积是( ) (A )3+493 (B )3+2
9
3 (C )6 (D )3398+
(图一)
2
三、综合题(每小题15分,共60分) 1、设:s =
2
211111⨯+⨯+
+3
31
2211⨯+⨯+
+4
41
3311⨯+⨯+
+……+2003
20031
2002200211⨯+⨯+
求与s 最接近的整数.
2、对于方程(1+a )x 4+x 3-(3a +2)x 2-4a =0,
求证:①对于任何实数a 都有一个确定的实数是它的解,求出这个实数解.
②存在一实数x ,使得不论a 为任何实数,x 都不是这个方程的解.
3、如图四,∠CAB =∠ABD =900,AB =AC +BD ,AD 交
于P ,作⊙P 与AB 相切.
试问:以AB 为直径作出的⊙O 与⊙P 请作出判断并加以证明.
4、如图五,已知P 为直径是2的⊙O 内的一定点,且 PO =2
2
,线段AB 为过点P 的任一弦,且它所对 的圆心角∠AOB =2θ,分别过A 和B 作⊙O 的切
线交于C ,设点P 到AC ,BC 的距离分别是a 、b . (1)求证:a 、b 是方程2x 2-(2A bs i n θ)x +s i n 2
θ=0 (2)问θ为多少时,点P 恰好在线段OC 上?
(3)设:y =a 2+b 2,求其最小值及线段AB 、圆心角、∠AOB 的变化范围?
(图四) (图五)。
