“зx∈R,ax 2-2ax+3≤0”是命题吗?
高考数学集合与常用逻辑用语
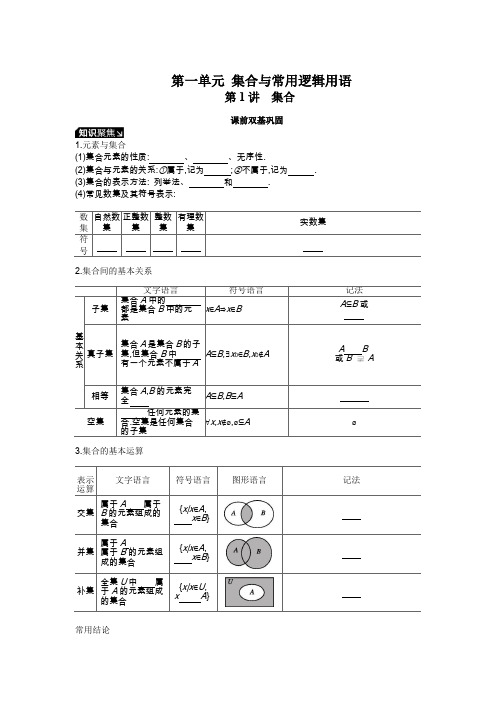
第一单元集合与常用逻辑用语第1讲集合课前双基巩固1.元素与集合(1)集合元素的性质:、、无序性.(2)集合与元素的关系:①属于,记为;②不属于,记为.(3)集合的表示方法: 列举法、和.(4)常见数集及其符号表示:2.集合间的基本关系A B或B A 3.集合的基本运算}}常用结论(1)非常规性表示常用数集:如{x|x=2(n-1),n∈Z}为偶数集,{x|x=4n±1,n∈Z}为奇数集等.(2)①一个集合的真子集必是其子集,一个集合的子集不一定是其真子集;②任何一个集合是它本身的子集;③对于集合A,B,C,若A⊆B,B⊆C,则A⊆C(真子集也满足);④若A⊆B,则有A=⌀和A≠⌀两种可能.(3)集合子集的个数:集合A中有n个元素,则集合A有2n个子集、2n-1个真子集、2n-1个非空子集、2n-2个非空真子集.(4)①并集的性质:A∪⌀=A;A∪A=A;A∪B=B∪A;A∪B=A⇔B⊆A;②交集的性质:A∩⌀=⌀;A∩A=A;A∩B=B∩A;A∩B=A⇔A⊆B;③补集的性质:A∪(∁U A)=U;A∩(∁U A)=⌀;∁U(∁U A)=A;∁U(A∪B)=(∁U A)∩(∁U B);∁U(A∩B)=(∁U A)∪(∁U B).题组一常识题1.[教材改编]已知集合A={-1,0,1,2},B={-1,1,2,5},则集合A∩B所含元素之和为.2.[教材改编]已知集合A={a,b},若A∪B={a,b,c},则满足条件的集合B有个.3.[教材改编]设全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则(∁U A)∪B= .4.[教材改编]已知集合A={-1,1},B={a,a2+2}.若A∩B={1},则实数a的值为.题组二常错题◆索引:忽视集合元素的性质致错;对集合的表示方法理解不到位致错;忘记空集的情况导致出错;集合运算中端点取值致错;对子集的概念理解不到位致错.5.已知集合A={1,3,},B={1,m},若B⊆A,则m= .6.已知集合A={x|y=log2(x+1)},集合B=y y=,x>0,则A∩B= .7.已知集合M={x|x-a=0},N={x|ax-1=0},若M∩N=N,则实数a的值是.8.设集合A={x||x-a|<1,x∈R},B={x|1<x<5,x∈R},若A B,则a的取值范围为.9.已知集合A={x|x2-3x+2=0,x∈R},B={x|0<x<5,x∈N},则满足条件A⊆C⊆B的集合C的个数为.课堂考点探究探究点一集合的含义与表示1 (1)设集合A={x∈Z||x|≤2},B={y|y=x2+1,x∈A},则B中的元素有 ()A.5个B.4个C.3个D.无数个(2)设集合A={-4,2a-1,a2},B={9,a-5,1-a},且A,B中有唯一的公共元素9,则实数a的值为.[总结反思] (1)研究集合问题时,首先要明确构成集合的元素是什么,即弄清该集合是数集、点集,还是其他集合,然后再看集合的构成元素满足的限制条件是什么,从而准确把握集合的意义.(2)依据元素与集合的关系确定参数时,往往要对集合中含参数的元素取值情况进行分类讨论,并要注意检验集合中的元素是否满足互异性.式题(1)设集合A={-1,0,2},集合B={-x|x∈A且2-x∉A},则B=()A.{1}B.{-2}C.{-1,-2}D.{-1,0}(2)已知集合A={x|x=3k-1,k∈Z},则下列表示正确的是()A.-1∉AB.-11∈AC.3k2-1∈AD.-34∉A探究点二集合间的基本关系2 (1)[2017·江西八校联考]集合M=x x=+1,n∈Z,N=y y=m+,m∈Z,则两集合M,N 的关系为()A.M∩N=⌀B.M=NC.M⊆ND.N⊆M(2)[2017·大庆三模]已知集合A={y|0≤y<a,y∈N},B={x|x2-2x-3≤0,x∈N},若A⫋B,则满足条件的正整数a所构成集合的子集的个数为()A.2B.4C.8D.16[总结反思] (1)判断两集合之间的关系的方法:当两集合不含参数时,可直接利用数轴、图示法进行判断;当集合中含有参数时,需要对满足条件的参数进行分类讨论或采用列举法.(2)要确定非空集合A的子集的个数,需先确定集合A中的元素的个数,再求解.不要忽略任何非空集合是它自身的子集.(3)根据集合间的关系求参数值(或取值范围)的关键是将条件转化为元素或区间端点间的关系,进而转化为参数所满足的关系,常用数轴、图示法来解决这类问题.式题(1)[2017·长沙一中月考]已知集合A={x|x2-2x≤0},B={x|x≤a},若A⊆B,则实数a的取值范围是()A.a≥2B.a>2C.a<0D.a≤0(2)[2017·临川一中模拟]若集合A∪B=B∩C,则对于集合A,B,C的关系,下列表示正确的是()A.A⊆B⊆CB.C⊆B⊆AC.B⊆C⊆AD.B⊆A⊆C探究点三集合的基本运算考向1集合的运算3 (1)[2017·保定二模]设集合P={3,log2a},Q={a,b},若P∩Q={0},则P∪Q=()A.{3,0}B.{3,0,2}C.{3,0,1}D.{3,0,1,2}(2)已知集合A={(x,y)|y=x+1,0≤x≤1},集合B={(x,y)|y=2x,0≤x≤10},则集合A∩B= ()A.{1,2}B.{x=1,y=2}C.{(1,2)}D.{x=1,x=2}(3)[2017·河西五市二模]已知全集U=R,集合A={x|y=lg(x-1)},B={y|y=},则A∩(∁B)=()UA.[1,2]B.[1,2)C.(1,2]D.(1,2)[总结反思] 解决集合的基本运算问题一般应注意以下几点:(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决运算问题的前提.(2)对集合化简.有些集合是可以化简的,如果先化简再研究其关系并进行运算,可使问题变得简单明了,易于解决.(3)注意数形结合思想的应用.集合运算常用的数形结合形式有数轴和Venn图.考向2利用集合运算求参数4 (1)[2017·邯郸二模]已知集合A={x∈Z|x2-4x-5<0},B={x|4x>2m},若A∩B有三个元素,则实数m的取值范围是()A.[3,6)B.[1,2)C.[2,4)D.(2,4](2)[2017·泰安二模]设全集U=R,集合A={x|x>1},集合B={x|x>p},若(∁U A)∩B=⌀,则p应该满足的条件是()A.p>1B.p≥1C.p<1D.p≤1[总结反思] 根据集合运算结果求参数,主要有以下两种形式:(1)用列举法表示的集合,直接依据交、并、补的定义求解,重点注意公共元素;(2)由描述法表示的集合,一般先要对集合化简,再依据数轴确定集合的运算情况,特别要注意端点值的情况.考向3集合语言的运用5 设P和Q是两个集合,定义集合P-Q={x|x∈P且x∉Q},如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于()A.{x|0<x<1}B.{x|0<x≤1}C.{x|1≤x<2}D.{x|0≤x<2}[总结反思] 解决集合新定义问题,应做到:(1)准确转化.解决新定义问题时,一定要读懂新定义的本质含义,紧扣题目所给定义,结合题目的要求进行恰当转化,切忌同已有概念或定义相混淆.(2)方法选取.对于新定义问题,可恰当选用特例法、筛选法、一般逻辑推理等方法,并结合集合的相关性质求解.强化演练1.【考向1】[2017·资阳二模]设全集U=R,集合A={x|(x+1)(x-3)<0},B={x|x-1≥0},则图1-1-1中阴影部分所表示的集合为()图1-1-1A.{x|x≤-1或x≥3}B.{x|x<1或x≥3}C.{x|x≤1}D.{x|x≤-1}2.【考向1】[2017·汕头三模]已知集合A={x∈N|x<3},B={x|x=a-b,a∈A,b∈A},则A∩B=()A.{1,2}B.{-2,-1,0,1,2}C.{1}D.{0,1,2}3.【考向2】[2017·天津静海一中二模]设集合A={-1,1,2},B={a+1,a2-2},若A∩B={-1,2},则a 的值为()A.-2或-1B.0或1C.-2或1D.0或-24.【考向2】[2017·厦门一中模拟]已知集合A={x|x<a},B={x|x2-3x+2<0},若A∩B=B,则实数a 的取值范围是()A.a≤1B.a<1C.a≥2D.a>25.【考向3】若数集A={a1,a2,…,a n}(1≤a1<a2<…<a n,n≥2)具有性质P:对任意的i,j(1≤i≤j≤n),a i a j 与两数中至少有一个属于A,则称集合A为“权集”.则()A.{1,3,4}为“权集”B.{1,2,3,6}为“权集”C.“权集”中元素可以有0D.“权集”中一定有元素1第2讲命题及其关系、充分条件与必要条件课前双击巩固1.命题(1)命题概念:在数学中把用语言、符号或式子表达的,能够判断的陈述句叫作命题.其中的语句叫作真命题,的语句叫作假命题.(2)四种命题及其相互关系图1-2-1注:若两个命题互为逆否命题,则它们有相同的真假性.2.充分条件、必要条件与充要条件(1)如果p⇒q,则p是q的条件;(2)如果q⇒p,则p是q的条件;(3)如果既有p⇒q又有q⇒p,记作p⇔q,则p是q的条件.常用结论1.充要条件的两个结论(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r的充分不必要条件;(2)若p是q的充分不必要条件,则q是p的充分不必要条件.2.充分、必要条件与集合的关系使p成立的对象构成的集合为A,使q成立的对象构成的集合为BB⊆AA BB A题组一常识题1.[教材改编]对于下列语句:①垂直于同一直线的两条直线必平行吗?②作△ABC∽△A'B'C';③x2+2x-3<0;④四边形的内角和是360°.其中是命题的是.(填序号)2.[教材改编]下面有4个命题:①集合N中最小的数是1;②若-a不属于N,则a属于N;③若a ∈N,b∈N,则a+b的最小值为2;④x2+1=2x的解可表示为.其中真命题的个数为.3.[教材改编]命题“若整数a不能被2整除,则a是奇数”的逆否命题是.4.[教材改编]已知集合M={x|1<x<a},N={x|1<x<3},则“a=3”是“M⊆N”的条件. 题组二常错题◆索引:命题的条件与结论不明确;含有大前提的命题的否命题易出现否定大前提的情况;真、假命题的推理考虑不全面;对充分必要条件判断错误.5.命题“若a2+b2=0,a,b∈R,则a=b=0”的逆否命题是.6.已知命题“∀a,b∈R,若ab>0,则a>0”,则它的否命题是.7.若命题“ax2-2ax-3≤0成立”是真命题,则实数a的取值范围是.8.已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q的条件.课堂考点探究探究点一四种命题及其相互关系1 (1)已知命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,命题γ:如果x≥5,那么x≥3.关于这三个命题之间的关系,下列三种说法正确的是()①命题α是命题β的否命题,且命题γ是命题β的逆命题;②命题α是命题β的逆命题,且命题γ是命题β的否命题;③命题β是命题α的否命题,且命题γ是命题α的逆否命题.A.①③B.②C.②③D.①②③(2) 给出以下五个命题:①“若x+y=0,则x,y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若q≤-1,则x2+x+q=0有实根”的逆否命题;④若ab是正整数,则a,b都是正整数;⑤若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递减.其中为真命题的是.(写出所有真命题的序号)[总结反思] (1)写一个命题的其他三种命题时,需注意:①对于不是“若p,则q”形式的命题,需先改写;②若命题有大前提,写其他三种命题时需保留大前提.(2)判断一个命题为真命题,要给出推理证明;判断一个命题是假命题,只需举出反例.(3)当一个命题不易直接判断真假时,根据“互为逆否的命题同真同假”的结论,可转化为判断与其等价的命题的真假.式题(1)命题“若a,b,c成等比数列,则b2=ac”的逆否命题是()A.若a,b,c成等比数列,则b2≠acB.若a,b,c不成等比数列,则b2≠acC.若b2=ac,则a,b,c成等比数列D.若b2≠ac,则a,b,c不成等比数列(2)[2017·枣庄二模]已知命题“若x>1,则2x<3x”,则在它的逆命题、否命题、逆否命题中,真命题的个数是()A.0B.1C.2D.3探究点二充分﹑必要条件的判断2 (1)[2017·北京卷]设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·n<0”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(2)[2017·天津卷]设θ∈R,则“θ-<”是“sin θ<”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件[总结反思] 充要条件的三种判断方法:(1)定义法.根据p⇒q,q⇒p进行判断.(2)集合法.根据p,q成立时对应的集合之间的包含关系进行判断.(3)等价转化法.根据一个命题与其逆否命题的等价性,把要判断的命题转化为其逆否命题进行判断,这个方法特别适合以否定形式给出的问题,如“xy≠1”是“x≠1或y≠1”的何种条件,即可转化为判断“x=1且y=1”是“xy=1”的何种条件.式题(1)对任意的实数x,若[x]表示不超过x的最大整数,则“-1<x-y<1”是“[x]=[y]”的() A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(2)[2017·衡水一模]设p:<1,q:log2x<0,则p是q的 ()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件探究点三充分、必要条件的应用3 (1)[2017·湖北新联考四联]若“x>2m2-3”是“-1<x<4”的必要不充分条件,则实数m的取值范围是()A.[-1,1]B.[-1,0]C.[1,2]D.[-1,2](2)已知条件p:≤-1,条件q:x2+x<a2-a,且q的一个充分不必要条件是p,则a的取值范-围是()A.--B.C.[-1,2]D.-∪[2,+∞)[总结反思] (1)求解充分、必要条件的应用问题时,一般是把充分、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(组)求解.(2)求解参数的取值范围时,一定要注意对区间端点值进行检验,尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现错误.式题(1)[2017·武汉三模]下面四个条件中,使a>b成立的必要而不充分条件是() A.a-1>b B.a+1>bC.|a|>|b|D.a3>b3(2)“直线x-y-k=0与圆(x-1)2+y2=2有两个不同的交点”的一个充分不必要条件可以是()A.-1≤k<3B.-1≤k≤3C.0<k<3D.k<-1或k>3第3讲简单的逻辑联结词、全称量词与存在量词课前双击巩固1.简单的逻辑联结词命题中的、、叫作逻辑联结词,用符号分别表示为、、.2.全称量词与存在量词(1)短语“对所有的”“对任意一个”在逻辑中通常叫作,用符号“”表示.(2)短语“存在一个”“至少有一个”在逻辑中通常叫作,用符号“”表示.(3)含有一个量词的命题的否定:全称命题p:∀x∈M,p(x),它的否定是.特称命题q:∃x0∈M,q(x0),它的否定是.常用结论1.否命题是把原命题的条件与结论都否定,命题的否定只需否定命题的结论.2.用“并集”的概念来理解“或”,用“交集”的概念来理解“且”,用“补集”的概念来理解“非”.3.记忆口诀:(1)“p或q”,有真则真;(2)“p且q”,有假则假;(3)“非p”,真假相反.4.命题p∧q的否定是p∨q;命题p∨q的否定是p∧q.题组一常识题1.[教材改编]给出下列命题:①函数y=ln x是减函数;②2是方程x+2=0的根又是方程x-2=0的根;③28是5的倍数或是7的倍数.其中是“p或q”形式的命题的是.(填序号)2.[教材改编]p∨q是真命题,q是真命题,则p是(填“真”或“假”)命题.3.已知命题p:∃x0∈R,+x0-1<0,则命题p是.4.[教材改编]命题“有的四边形是平行四边形”的否定是.题组二常错题◆索引:全称命题或特称命题的否定出错;不会利用真值表判断命题的真假;复合命题的否定中出现逻辑联结词错误;考查命题真假时忽视对参数的讨论.5.[教材改编]命题“所有奇数的立方都是奇数”的否定是.6.已知命题p:所有有理数都是实数,命题q:正数的对数都是负数.则下列命题中为真命题的是.(填序号)①p∨q;②p∧q;③p∧q;④p∨q.7.已知命题:若ab=0,则a=0或b=0,则其否命题为.8.已知命题“∀x∈R,ax2+4x+1>0”是假命题,则实数a的取值范围是.课堂考点探究探究点一含逻辑联结词的命题及真假1 在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为()A.p∨qB.p∨qC.p∧qD.p∨q(2)给出下列两个命题:命题p:若在边长为1的正方形ABCD内任取一点M,则|MA|≤1的概率为.命题q:若函数f(x)=x+,则f(x)在区间1,上的最小值为4.那么,下列命题为真命题的是()A.p∧qB.pC.p∧qD.p∧q[总结反思] 判断含有逻辑联结词的命题真假的一般步骤:(1)判断复合命题的结构;(2)判断构成这个命题的每个简单命题的真假;(3)依据“或”:一真即真,“且”:一假即假,“非”:真假相反,作出判断即可.式题(1)[2017·惠州调研]设命题p:若定义域为R的函数f(x)不是偶函数,则∀x∈R,f(-x)≠f(x),命题q:f(x)=x|x|在(-∞,0)上是减函数,在(0,+∞)上是增函数.则下列判断错误..的是() A.p为假B.q为真C.p∨q为真D.p∧q为假(2)已知命题p:若x>y,则-x<-y,命题q:若x<y,则x>y2.给出命题:①p∧q;②p∨q;③p∧q;④p ∨q.其中为真命题的是()A.①③B.①④C.②③D.②④探究点二全称命题与特称命题2 (1)[2017·陕西师大附中二模]若命题p:对任意的x∈R,都有x3-x2+1<0,则p为()A.不存在x0∈R,使得-+1<0B.存在x0∈R,使得-+1<0C.对任意的x∈R,都有x3-x2+1≥0D.存在x0∈R,使得-+1≥0(2)下列命题中为假命题的是()A.∃α,β∈R,sin(α+β)=sin α+sin βB.∀φ∈R,函数f(x)=sin(2x+φ)都不是偶函数C.∃x0∈R,+a+bx0+c=0(a,b,c∈R且为常数)D.∀a>0,函数f(x)=(ln x)2+ln x-a有零点[总结反思] 全称命题与特称命题的真假判断及其否定:∀x∈M,p(x)式题[2017·山东师大附中二模]已知f(x)=e x-x,g(x)=ln x+x+1,命题p:∀x∈R,f(x)>0,命题q:∃x0∈(0,+∞),g(x0)=0,则下列说法正确的是()A.p是真命题,p:∃x0∈R,f(x0)<0B.p是假命题,p:∃x0∈R,f(x0)≤0C.q是真命题,q:∀x∈(0,+∞),g(x)≠0D.q是假命题,q:∀x∈(0,+∞),g(x)≠0探究点三根据命题的真假求参数的取值范围3 (1)[2017·南充一模]设p:∃x0∈1,,g(x0)=log2(t+2x0-2)有意义,若p为假命题,则t 的取值范围为.(2)[2017·湖南十三校二联]已知命题p:函数f(x)=2ax2-x-1(a≠0)在(0,1)内恰有一个零点; 命题q:函数y=x2-a在(0,+∞)上是减函数.若p且q为真命题,则实数a的取值范围是. [总结反思] 根据命题真假求参数的方法步骤:(1)根据题目条件,推出每一个命题的真假(有时不一定只有一种情况);(2)求出每个命题是真命题时参数的取值范围;(3)根据每个命题的真假情况,求出参数的取值范围.式题(1)[2018·衡水中学模拟]已知命题p:∃x0∈R,+ax0+a<0,若p是真命题,则实数a 的取值范围为()A.[0,4]B.(0,4)C.(-∞,0)∪(4,+∞)D.(-∞,0]∪[4,+∞)(2)[2017·太原二模]若命题“∀x∈(0,+∞),x+≥m”是假命题,则实数m的取值范围是.。
第1章 第3节 不等关系与一元二次不等式2023届高三一轮复习数学精品备课(新高考人教A版2019)

命题点3 给定参数范围的恒成立问题 [例3-3] 已知a∈[-1,1],不等式x2+(a-4)x+4 -2a>0恒成立,则x的取值范围是(_-__∞__,__1_).∪(3,+∞)
►规律方法
形如f(x)≥0(f(x)≤0)恒成立问题的求解策略 (1)对x∈R的不等式确定参数的范围时,结合二次函 数的图象,利用判别式来求解. (2)对x∈[a,b]的不等式确定参数的范围时,①根据 函数的单调性,求其最值,让最值大于等于或小于等于
A.ac<bc
B.abc<bac
C.alogbc<blogac
D.logac<logbc
C
(2)解关于x的不等式ax2-2≥2x-ax(a∈ R).
B
(2)求不等式12x2-ax>a2(a∈ R)的解集.
►考向三 一元二次不等式恒成立问题[多维探究]
命题点1 在R上的恒成立问题
第三节 不等关系与一元二次不等式
基础知识·自主回顾
知识梳理
a<b
a<b
b<a
> a+c>b+d
>
<
>
>
>
{x|x<x1或x>x2}
{x|x≠x1}
{x|x1<x<x2}
∅
教材拓展
基础自测
√
× √
×
C
A
◇考题再现
4.已知集合A={x|x2-2x-15<0},B={x|x≥e},则
A∪B=( C ) A.[e,5)
1.比较法是不等式性质证
明的理论依据,是不等式 1.“三个二次”的
证明的主要方法之一,比 关系是解一元二
四川省成都2022-2023学年高三下学期二诊复习(文科)数学试题含答案

成都高2023届二诊复习卷(三)(答案在最后)数学试题(文科)一、单选题1.已知集合{}{}3|11,,log 1A y y x x B x x ==--∈=R ∣ ,则R A B = ð()A .{}1xx -∣ B .{3}x x <∣C .{}13x x -∣ D .{13}xx -<∣ 2.若复数z 满足||2,3z z z z -=⋅=,则2z 的实部为()A .2-B .1-C .1D .23.已知函数()y f x =的图像在点()()33P f ,处的切线方程是27y x =-+,则()()33f f '-=()A .2-B .2C .3-D .34.命题p :“2R,240x ax ax ∃∈+-≥”为假命题,则a 的取值范围是()A .40a -<£B .40a -≤<C .30a -≤≤D .40a -≤≤5.已知向量(),3a m m =+ ,()4,b m = ,则“6m =”是“a 与b共线”的().A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.我国古代数学家僧一行应用“九服晷影算法”在《大衍历》中建立了晷影长1与太阳天顶距()0180θθ︒≤≤︒的对应数表,这是世界数学史上较早的一张正切函数表,根据三角学知识可知,晷影长度l 等于表高h 与太阳天顶距θ正切值的乘积,即tan l h θ=.对同一“表高”两次测量,第一次和第二次太阳天顶距分别为,αβ,且1tan()3αβ-=,若第二次的“晷影长”与“表高”相等,则第一次的“晷影长”是“表高”的()A .1倍B .2倍C .3倍D .4倍7.在平面直角坐标系xOy 中,已知点()0,0O ,点()0,8A ,点M 满足5MA MO =,又点M 在曲线224y x x =-++上,则MO =()A .5B .22C .25D .108.若2021log 2022a =,2022log 2023b =,20222021c =,20232022d =,则a ,b ,c ,d 中最大的是()A .a B .b C .c D .d9.十八世纪早期,英国数学家泰勒发现了公式357sin 3!5!7!=-+-++ x x x x x ()()211121!n n x n ---+- ,(其中x R ∈,*n ∈N ,n !=1×2×3×…×n ,0!=1),现用上述公式求()()11111112!4!6!22!n n --+-++-+- 的值,下列选项中与该值最接近的是()A .sin 30B .sin 33C .sin 36D .sin3910.如图,边长为2的正方形ABCD 中,点E ,F 分别是边AB ,BC 的中点,将△AED ,△EBF ,△FCD 分别沿DE ,EF ,FD 折起,使A ,B ,C 三点重合于点A ′,若四面体A ′EFD 的四个顶点在同一个球面上,则该球的半径为()A .2B .62C .112D .5211.若双曲线2222:1x y C a b-=()0,0a b >>的一条渐近线被圆()2224x y ++=所截得的弦长为2,则C 的离心率为()A .233B .2C .3D .212.已知2π3是函数()()()sin 20πf x x ϕϕ=+<<的一个零点,则下列选项不正确的为()A .()f x 在区间5π0,12⎛⎫ ⎪⎝⎭单调递减B .()f x 在区间π11π,1212⎛⎫- ⎪⎝⎭只有一个极值点C .直线7π6x =是曲线()y f x =的对称轴D.直线y x =是曲线()y f x =的切线二、填空题13.已知在ABC 中,角,,A B C 所对边分别为a b c ,,,满足2cos 2b A a c +=,且b =2a c -的取值范围为______.14.已知边长为2的菱形ABCD 中,点F 为BD 上一动点,点E 满足22,3BE EC AE BD =⋅=- ,则AF EF⋅ 的最小值为______.15.如图,多面体ABCDEF 中,面ABCD 为正方形,DE ⊥平面ABCD ,CF ∥DE ,且AB=DE=2,CF=1,G 为棱BC 的中点,H 为棱DE 上的动点,有下列结论:①当H 为DE 的中点时,GH ∥平面ABE ;②存在点H ,使得GH ⊥AE ;③三棱锥B −GHF 的体积为定值;④三棱锥E −BCF 的外接球的表面积为14π.其中正确的结论序号为________.(填写所有正确结论的序号)16.在数列{}n a 中给定1a ,且函数()()311sin 213n n f x x a x a x +=-+++的导函数有唯一的零点,函数()()()8sin πcos πg x x x x =+-且()()()12918g a g a g a ++⋅⋅⋅+=.则5a =______.三、解答题17.已知等差数列{}n a 的前三项的和为-9,前三项的积为-15.(1)求等差数列{}n a 的通项公式;(2)若{}n a 为递增数列,求数列{}n a 的前n 项和Sn .18.某食品研究员正在对一种过期食品中菌落数目进行统计,为检测该种过期食品的腐败程度,研究员现对若干份过期不同天数的该种食品样本进行检测,并且对样本的菌落数目逐一统计,得到如下数据:过期天数x (单位:天)12345菌落数目y (单位:千个)0.30.30.50.9 1.0(1)请用线性回归模型拟合y 与x 的关系;(2)实验数据表明,该种食品在未添加防腐剂的条件下(其余条件相同),短期内(7天内)菌落数目y (单位:千个)与过期天数x (单位:天)应满足关系:0.01e 0.5x y =+.(i )判断该样本是否添加防腐剂;(ii )简要分析过期7天内防腐剂发挥的效果.附:()()()121ˆˆˆ,niii nii x x y y ba y bx x x ==--==--∑∑.19.如图,在四棱锥P ABCD -中,底面ABCD 是等腰梯形,,22AB CD AB CD AD ==∥,平面PAB ⊥平面ABCD ,且PAB 是正三角形,,M N 分别是,AD PC 的中点.(1)证明:MN平面PAB ;(2)若4PC =,求三棱锥N PAB -的体积.20.如图所示,已知椭圆22:163x y C +=与直线:163x y l +=.点P 在直线l 上,由点P 引椭圆C 的两条切线PA 、PB ,A 、B 为切点,O 是坐标原点.(1)若点P 为直线l 与y 轴的交点,求PAB 的面积S ;(2)若OD AB ⊥,D 为垂足,求证:存在定点Q ,使得DQ 为定值.21.已知函数2()e ,2xmx f x m =-∈R .(1)讨论()f x 极值点的个数;(2)若()f x 有两个极值点12,x x ,且12x x <,证明:()()122e f x f x m +<-.22.在直角坐标系xOy 中,曲线C的参数方程为22114t x ty t ⎧=+-⎪⎪⎨⎪=-⎪⎩(0t >,t 为参数).(1)求曲线C 的直角坐标方程;(2)已知直线:10l x y --=与x 轴的交点为F ,且曲线C 与直线l 交于A 、B 两点,求||||FA FB ⋅的值.23.已知()|1||3|f x x x =-+-.(1)求()3f x ≤的解集;(2)已知2(2)1()a x f x -+≥在[3,)+∞上恒成立,求实数a 的取值范围.参考答案:1.D【分析】由题意可得{|1}A y y =≥-,{|3}B x x =≥,R {|3}B x x =<ð,再根据交集的定义求解即可.【详解】解:因为{}|11,{|1}A y y x x y y ==--∈=≥-R ,{}3log 1{|3}B x x x x =≥=≥∣,所以{|3}B x x =<R ð,所以(){|1}{|3}{|13}A B x x x x x x ⋂=≥-⋂<=-≤<R ð.故选:D.2.C【分析】设复数i,(,R)z x y x y =+∈,则i z x y =-,故根据||2,3z z z z -=⋅=可求得222,1x y ==,结合复数的乘方运算,可求得答案.【详解】设复数i,(,R)z x y x y =+∈,则i z x y =-,则由||2,3z z z z -=⋅=可得|2i |2y =且223x y +=,解得222,1x y ==,故2222(i)2i x y x y x z y =+=-+,其实部为22211x y -=-=.故选:C.3.D【分析】利用导数的几何意义求出()3f 和()3f ',即可求得.【详解】函数()f x 的图像在点()()33P f ,处的切线的斜率就是在该点处的导数,即()3f '就是切线27y x =-+的斜率,所以()32f '=-.又()32371f =-⨯+=,所以()()()33123f f -=--='.故选:D4.A【分析】存在命题为假命题,则其否定是全称命题且为真命题,写出命题的否定,由不等式的性质可得结论.【详解】命题2:R,240p x ax ax ∃∈+-≥为假命题,即命题2:R,240p x ax ax ⌝∀∈+-<为真命题.首先,0a =时,4<0-恒成立,符合题意;其次0a ≠时,则a<0且2(2)160a a ∆=+<,即40a -<<,综上可知,-4<0a ≤故选:A 5.A【分析】根据给定条件,求出a 与b共线的充要条件,再利用充分条件、必要条件的定义判断作答.【详解】向量(),3a m m =+,()4,b m = ,则2//4(3)0a b m m ⇔-+= ,解得2m =-或6m =,所以“6m =”是“a 与b共线”的充分不必要条件.故选:A6.B【分析】根据给定条件,可得tan 1β=,再利用和角的正切公式计算作答.【详解】依题意,tan 1β=,则11tan()tan 3tan tan[()]211tan()tan 13αββααββαββ+-+=-+===--⋅-,所以第一次的“晷影长”是“表高”的2倍.故选:B 7.B【分析】先判断出点M 两个圆的公共点,求出()2,2M ,进而求出MO .【详解】设(),M x y .因为点()0,0O ,点()0,8A,且MA MO =,()22220x y ++=.而点M 在曲线y =y =平方后,整理为一个圆()2215x y -+=,所以曲线y =()2215x y -+=在x 轴上方部分.则两个圆的公共弦为两圆的方程相减,整理得:260x y +-=.所以(),M x y 满足260y x y ⎧⎪=⎨+-=⎪⎩,解得:22y x =⎧⎨=⎩.即()2,2M .所以MO ==故选:B 8.C【分析】先将a ,b ,c ,d 变换为:202111log 12021a ⎛⎫=++ ⎪⎝⎭,202211log 12022b ⎛⎫=++ ⎪⎝⎭,20221120212021c ==+,20231120222022d ==+,得到c d >,构造函数()()2022log 1g x x x =-+,()()2021log 1x x x ϕ=-+,()0,1x ∈,结合导数和作差法得到d b >,c a >,从而得出a ,b ,c ,d 中最大值.【详解】因为20212021202120221log 2022log 20211log 120212021a ⎛⎫⎛⎫==⨯=++ ⎪ ⎪⎝⎭⎝⎭,20222022202220231log 2023log 20221log 120222022b ⎛⎫⎛⎫==⨯=++ ⎪ ⎪⎝⎭⎝⎭,20221120212021c ==+,20231120222022d ==+,所以c d >;20222022111111log 1log 12022202220222022d b ⎡⎤⎛⎫⎛⎫⎛⎫-=+-++=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,设()()2022log 1g x x x =-+,()0,1x ∈,则()()111ln 2022g x x '=-+,当01x <<时,()0g x '>,所以()g x 在()0,1上单调递增,则()102022g g ⎛⎫> ⎪⎝⎭,即202211log 1020222022⎛⎫-+> ⎪⎝⎭,所以0d b ->,即d b >;20212021111111log 1log 12021202120212021c a ⎡⎤⎛⎫⎛⎫⎛⎫-=+-++=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,设()()2021log 1x x x ϕ=-+,()0,1x ∈,则()()111ln 2021x x ϕ'=-+,当01x <<时,()0x ϕ'>,所以()x ϕ在()0,1上单调递增,则()102021ϕϕ⎛⎫> ⎪⎝⎭,即202111log 1020212021⎛⎫-+> ⎪⎝⎭,所以0c a ->,即c a >;综上:c d b >>,c a >,即a ,b ,c ,d 中最大的是c .故选:C.9.B【分析】求出(sin )'x 后代入1x =得cos1=sin 12π⎛⎫- ⎪⎝⎭可得答案,即18090π︒⎛⎫- ⎪⎝⎭ 与33 最接近.【详解】()()246221'(sin )cos 112!4!6!22!n n x x x x x x n --==-+-++-+- 所以cos1=111111(1)2!4!6!(22)!n n --+-++-+- =sin 12π⎛⎫- ⎪⎝⎭=sin 18090π⎛⎫- ⎪⎝⎭ ,由于18090π⎛⎫- ⎪⎝⎭ 与33 最接近,故选:B【分析】把棱锥扩展为正四棱柱,求出正四棱柱的外接球的半径就是三棱锥的外接球的半径.【详解】易知四面体A EFD '的三条侧棱,,A E A F A D '''两两垂直,且1,1,2A E A F A D '''===,把四面体A EFD '补成从顶点A ′出发的三条棱长分别为1,1,2的一个长方体,则长方体的外接球即为四面体A EFD '的外接球,球的半径为6,2R =故选:B.【点睛】本题考查几何体的折叠问题,几何体的外接球的半径的求法,考查空间想象能力.11.D【解析】由双曲线的方程可得一条渐近线方程,根据圆的方程得圆心和半径,运用点到直线的距离公式和弦长公式,可得a,b 的关系,即可求解.【详解】不妨设双曲线2222:1x y C a b-=()0,0a b >>的一条渐近线为0bx ay -=,圆()2224x y ++=的圆心为()2,0-,半径2r =,则圆心到渐近线的距离为2bd c==所以弦长2=,化简得:2243b c =,即()22243c a c -=,解得2c a =所以2ce a==.故选:D【点睛】本题主要考查了双曲线的标准方程,双曲线的简单几何性质,圆的标准方程,考查方程思想和运算能力,属于中档题型.12.ABD【分析】先利用函数的零点解出ϕ,再根据整体代换思想结合正弦函数的图象和性质判断ABC ,利用导数的几何意义判断D.【详解】由题意得2π4πsin 033f ϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以4ππ3k ϕ+=,Z k ∈,即4π3k πϕ=-+,Z k ∈,又0πϕ<<,所以2k =时,2π3ϕ=,故()2πsin 23f x x ⎛⎫=+ ⎪⎝⎭,选项A :当5π0,12x ⎛⎫∈ ⎪⎝⎭时,2π2π3π2,332x ⎛⎫+∈ ⎪⎝⎭,由正弦函数sin y u =图象可得()y f x =在50,12π⎛⎫⎪⎝⎭上单调递减,正确;选项B :当11,1212x ππ⎛⎫∈- ⎪⎝⎭时,2ππ5π2,322x ⎛⎫+∈ ⎪⎝⎭,由正弦函数sin y u =图象可得()y f x =只有1个极值点,由2π3π232x +=,解得512x π=,即512x π=为函数的唯一极值点,正确;选项C ,当7π6x =时,2π23π3x +=,07π6f ⎛⎫= ⎪⎝⎭,故直线7π6x =不是对称轴,错误;选项D ,由2π2cos 213y x '⎛⎫=+=- ⎪⎝⎭得2π1cos 232x ⎛⎫+=- ⎪⎝⎭,所以2π2π22π33x k +=+或22π22π33x k π+=-+,Z k ∈,解得πx k =或ππ3x k =+,Z k ∈,所以函数()y f x =在点0,2⎛⎫ ⎪ ⎪⎝⎭处的切线斜率为2π2cos 013k ⎛⎫=+=- ⎪⎝⎭,切线方程为()02y x -=--即32y x =-,正确;故选:ABD 13.(-【分析】根据已知利用正弦定理边化角结合两角和的正弦公式可得π3B =,从而可表示出2a c -的表达式,利用辅助角公式化简结合三角函数的性质,即可求得答案.【详解】由题意在ABC 中,满足2cos 2b A a c +=,即2sin cos sin 2sin 2sin()B A A C A B +==+,即sin 2sin cos A A B =,而(0,π),sin 0A A ∈∴≠,故1cos 2B =,又π(0,π),3B B ∈∴=,则sin 4sin sin b A a AB ==,同理4sin c C =,故)22πsin 4sin s 8s 8in 4in(3a c A C A A -=-=--π6sin 6A A A =-=-,又2ππππ(0,),(,)3662A A ∈∴-∈-,故π1sin ,162A ⎛⎫⎛⎫-∈- ⎪ ⎪⎝⎭⎝⎭,则(2a c -∈-,故答案为:(-14.7336-【分析】由22,3BE EC AE BD =⋅=- ,根据向量的线性运算以及数量积的运算律,可求得∠DAB =π3;以菱形对角线交点为原点,对角线所在直线为坐标轴建立平面直角坐标系,利用坐标表示出AF EF ⋅,得到关于t 的二次函数,求得二次函数最小值即为所求.【详解】由题意知:2=3BE BC,设=DAB θ∠,所以()()22222333AE BD AB BE AD AB AB AD AB BC BC AB ⋅=+⋅-=⋅-+-⋅=-故()22214cos 444cos cos 3332θθθ-+⨯-⨯=-⇒=由于()0,πθ∈,所以π=3θ,以AC 与BD 交点为原点,AC 为x 轴,BD 为y 轴建立如图所示的直角坐标系,所以A (﹣3,0),C (3,0),D (0,1),B (0,﹣1),E (231,33-),设F (0,t ),则AF =(3,t ),EF =23133,t ⎛⎫-+ ⎪ ⎪⎝⎭,所以2117323636AF EF t t t ⎛⎫⎛⎫⋅=-++=+- ⎪ ⎪⎝⎭⎝⎭ 当t =16-时,AF EF ⋅ 取最小值7336-,故答案为:7336-15.①③④【分析】根据线面平行的判定定理,以及线线垂直的判定,结合棱锥体积的计算公式,以及棱锥外接球半径的求解,对每一项进行逐一求解和分析即可.【详解】对①:当H 为DE 的中点时,取EA 中点为M ,连接,MH MB ,如下所示:因为,H M 分别为,ED EA 的中点,故可得MH //AD ,12MH AD =,根据已知条件可知:BG //1,2AD BG AD =,故MH //,BG MH BG =,故四边形HMBG 为平行四边形,则HG //MB ,又MB ⊂面,ABE HG ⊄面ABE ,故HG //面ABE ,故①正确;对②:因为ED ⊥面,,ABCD DA DC ⊂面ABCD ,故,DE DA DE DC ⊥⊥,又四边形ABCD 为矩形,故DA DC ⊥,则,,DE DA DC 两两垂直,以D 为坐标原点,建立空间直角坐标系如下所示:则()()()2,0,0,0,0,2,1,2,0A E G ,设()0,0,H m ,[]0,2m ∈,若GH ⊥AE ,则()()1,2,2,0,20GH AE m ⋅=--⋅-=,即220m +=,解得1m =-,不满足题意,故②错误;对③:B GFH H BGF V V --=,因为,,B F G 均为定点,故BGF S 为定值,又DE //,CF CF ⊂面,BGF DE ⊄面BGF ,故DE //面BGF ,又点H 在DE 上运动,故点H 到面BGF 的距离是定值,故三棱锥B GFH -的体积为定值,则③正确;对④:取△EFC 的外心为1O ,过1O 作平面EFC 的垂线1O N ,则三棱锥B EFC -的外接球的球心O 一定在1O N 上因为1OO ⊥面EFC ,FC ⊥面,ABCD CB ⊂面ABCD ,则CF CB ⊥,又CB CD ⊥,,,CF CD C CF CD ⋂=⊂面EFCD ,故CB ⊥面EFCD ,又BC ⊥面EFC ,则1OO //CB ,故1,OO BC 在同一个平面,则过O 作OP BC ⊥,连接,OB OC 如图所示.在△EFC 中,容易知5,2,1EF EC FC ===,则由余弦定理可得5cos 25EFC ∠=-25sin EFC ∠=,则由正弦定理可得1102sin 2EC O C OP EFC ===∠;设三棱锥E FCB -的外接球半径为R ,则OC OB R ==,在△OBP 中,OB R =,102OP =,又22211522222BP PC OO OC O C R =-=-=-=-故由勾股定理可知:222OB OP BP =+,即22255544222R R R =++---解得:272R =,则该棱锥外接球的表面积2414S R ππ==,故④正确.故答案为:①③④.【点睛】本题考查线面平行的证明,线线垂直的判定,以及三棱锥体积的计算和外接球半径的求解,属综合困难题.16.14##0.25【分析】利用导数的定义和对称性可得12n n a a +-=,利用辅助角公式对()g x 化简,构造新函数,利用导数判断新函数的单调性并结合夹逼原理即可求解.【详解】因为()21cos 2n n f x x a x a +'=-++有唯一的零点,()f x '为偶函数,所以()00f '=,即12n n a a +-=,*N n ∈,所以数列{}n a 为公差为2的等差数列,又因为()228sinπcosπ82ππg x x x x x x x ⎫=+-=⎪⎪⎭11188π2444x x x x ⎛⎫⎛⎫⎛⎫=-=--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,令()8h t t t =,则()h t 为奇函数,因为()80h t t '=>,所以()h t 在R 上单调递增,由题意得()()()1292220g a g a g a -+-+⋅⋅⋅+-=⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦,因为数列{}n a 是公差不为0的等差数列,其中129a a a <<⋅⋅⋅<,则129111444a a a -<-<⋅⋅⋅<-,假设1911044a a ⎛⎫⎛⎫-+-> ⎪ ⎝⎭⎝⎭,1919191111110444444a a h a h a h a h a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫->--⇒->--⇒-+-> ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,因为1928371651111111112444444444a a a a a a a a a ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-=-+-=-+-=-+-=- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭所以1291110444h a h a h a ⎛⎫⎛⎫⎛⎫-+-+⋅⋅⋅+-> ⎪ ⎪⎝⎭⎝⎭⎝⎭,假设1911044a a ⎛⎫⎛⎫-+-< ⎪ ⎝⎭⎝⎭,同理可得1291110444h a h a h a ⎛⎫⎛⎫⎛⎫-+-+⋅⋅⋅+-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,综上,19195111104424a a a a a ⎛⎫⎛⎫-+-=⇒+=⇒= ⎪ ⎪⎝⎭⎝⎭,故答案为:1417.(1)an =-2n +1或an =2n -7;(2)Sn =226,3618,4n n n n n n ⎧-+≤⎨-+≥⎩.【解析】(1)设等差数列{}n a 的公差为d ,由等差数列{}n a 前三项的和为9-,前三项的积为15-,利用等差数列的通项公式列出方程组,求公差和首项,由此能求出等差数列{}n a 的通项公式.(2)由(1)得an =2n -7,知|an |=72,327,4n n n n -≤⎧⎨-≥⎩,分类讨论,结合等差数列的求和公式能求出数列{||}n a 的前n 项和为n S .【详解】(1)设公差为d ,则依题意得a 2=-3,则a 1=-3-d ,a 3=-3+d ,所以(-3-d )(-3)(-3+d )=-15,得d 2=4,d =±2,所以an =-2n +1或an =2n -7.(2)由题意得an =2n -7,所以|an |=72,327,4n n n n -≤⎧⎨-≥⎩,①n ≤3时,Sn =-(a 1+a 2+…+an )=()5722n n +-⨯=6n -n 2;②n ≥4时,Sn =-a 1-a 2-a 3+a 4+…+an =-2(a 1+a 2+a 3)+(a 1+a 2+…+an )=18-6n +n 2.综上,数列{|an |}的前n 项和Sn =226,3618,4n n n n n n ⎧-+≤⎨-+≥⎩.【点睛】本题考查等差数列的通项公式和前n 项和公式的求法,解题时要认真审题,注意分类讨论思想的合理运用.易错点是求等差数列通项公式时容易丢解.18.(1)ˆ0.2yx =(2)(i )该样本添加了防腐剂;(ii )抑制食品产生菌落,且效果越来越好.【分析】(1)根据线性回归方程的求法根据已知即可得出答案;(2)(i )根据回归方程过样本中心列式即可判断;(ii )根据所给关系得出未添加防腐剂的条件下的各天的菌落数目,与已知添加防腐剂的条件下的各天的菌落数目对比,即可总结得出答案.【详解】(1)由题意可得:1234535x ++++==,0.30.30.50.910.65y ++++==,且522222211234555ii x ==++++=∑,5110.320.330.540.95111i i i x y ==⨯+⨯+⨯+⨯+⨯=∑,所以()()()551552221121511530.6ˆ0.255553i ii ii iii ii x x y y bx xyx y xx x ====---⨯⨯===--=-⨯-∑∑∑∑,则ˆˆ0.60.230ay bx =-=-⨯=,所以回归直线方程为ˆ0.2yx =(2)(i )0.01e 0.5x y ≠+,则样本不满足未添加防腐剂的条件,即该样本添加了防腐剂;(ii )根据该种食品在未添加防腐剂的条件下应满足关系:0.01e 0.5x y =+,可得10.01e 0.50.5+≈,20.01e 0.50.6+≈,30.01e 0.50.7+≈,40.01e 0.5 1.0+≈,50.01e 0.5 2.0+≈,即过期天数x (单位:天)12345添加防腐剂菌落数目y (单位:千个)0.30.30.50.9 1.0未添加防腐剂菌落数目y (单位:千个)0.50.50.7 1.0 2.0则过期7天内防腐剂让其菌落数目小于未添加防腐剂,且差距越来越大,即过期7天内防腐剂发挥的效果为抑制食品产生菌落,且效果越来越好.19.(1)证明见解析(2)2【分析】(1)取BC 的中点E ,连接,EM EN ,易证EM 平面PAB ,EN 平面PAB ,再利用面面平行的判定定理证明;(2)取AB 的中点O ,连接,PO CO ,根据PAB 是正三角形,得到PO AB ⊥,再由平面PAB ⊥平面ABCD ,得到PO ⊥平面ABCD ,在Rt POC △中,由222PO OC PC +=,求得2224AB CD AD BC ====,方法一:由60BAD ∠= ,求得点M 到AB 的距离,由MN 平面PAB ,得到点N 到平面PAB 的距离,再由体积公式求解;方法二:连接AC ,由60ABC ∠= ,得到点C 到AB 的距离,再根据N 为CP 的中点得到三棱锥N PAB -的高为三棱锥C PAB -高的12,然后由体积公式求解.【详解】(1)证明:如图所示:取BC 的中点E ,连接,EM EN .因为底面ABCD 是等腰梯形,AB CD ,又,M E 分别是,AD BC 的中点,所以EM AB ∥.又因为EM ⊄平面,PAB AB ⊂平面PAB ,所以EM 平面PAB .因为N 是PC 的中点,所以EN PB ∥.又因为EN ⊄平面,PAB PB ⊂平面PAB ,所以EN 平面PAB .因为EM ⊂平面,MNE EN ⊂平面,MNE EM EN E ⋂=,所以平面MNE 平面PAB .因为MN ⊂平面MNE ,所以MN 平面PAB .(2)如图所示:取AB 的中点O ,连接,PO CO .由已知得OA CD ∥且OA CD =,所以四边形OADC 是平行四边形,所以OC AD ∥,且OC AD =.因为PAB 是正三角形,所以PO AB ⊥,因为平面PAB ⊥平面ABCD ,平面PAB ⋂平面ABCD AB =,所以PO ⊥平面ABCD ,又OC ⊂平面ABCD ,所以PO OC ⊥.设2222AB CD AD BC a ====,则3PO a =.在Rt POC △中,由222PO OC PC +=,即222)4a +=,解得2a =,即2224AB CD AD BC ====.方法一:由题意可得60BAD ∠= ,点M 到AB 的距离,1sin60sin6022h AM AD ===,即点M 到平面PAB又MN 平面PAB ,所以点N 到平面PAB所以11142332N PAB PAB V S h -=⋅⋅=⨯⨯⨯= .方法二:连接AC ,由题意得,60ABC ∠= ,所以点C 到AB 的距离为sin60d BC = .因为N 为CP 的中点,所以三棱锥N PAB -的高为三棱锥C PAB -高的12,所以1122N PAB C PAB P ABC V V V ---==.所以11111142223232N PAB P ABC ABC V V S OP --==⨯⨯⨯=⨯⨯⨯= .20.(1)4;(2)证明见解析.【分析】(1)可得点()0,3P ,设切线方程为3y kx =+,将切线方程与椭圆方程联立,由判别式为零可求得k 的值,可知PA PB ⊥,求出两切点的坐标,可得出PA 、PB ,利用三角形的面积公式可求得结果;(2)设()11,A x y 、()22,B x y ,可得出切线PA 、PB 的方程,设点(),P m n ,求出直线AB 的方程,可得出直线AB 过定点T ,由OD AB ⊥结合直角三角形的几何性质可得出结论.【详解】(1)解:由题意知()0,3P ,过点P 与椭圆相切的直线斜率存在,设切线方程为3y kx =+,联立22326y kx x y =+⎧⎨+=⎩,可得()222112120k x kx +++=,(*)由()()22214448214810k k k ∆=-+=-=,可得1k =±,即切线方程为3y x =±+,所以,PA PB ⊥,将1k =代入方程(*)可得2440x x ++=,可得2x =-,此时1y =,不妨设点()2,1A -,同理可得点()2,1B ,PA PB ===因此,142S PA PB =⋅=.(2)证明:先证明出椭圆22163x y +=在其上一点()0,Mx y 处的切线方程为0163x x y y +=,因为点()00,M x y 在椭圆22163x y +=上,则220026x y +=,联立0022163163x x y yx y ⎧+=⎪⎪⎨⎪+=⎪⎩,消去y 可得()222200002103633x y x x x y +-+-=,整理得220020x x x x -+=,即()200x x -=,解得0x x =,因此,椭圆22163x y +=在其上一点()0,Mx y 处的切线方程为0163x x y y +=.设()11,A x y 、()22,B x y ,则切线PA 的方程为11163x x y y +=,切线PB 的方程为22163x x y y+=.设(),P m n ,则1122163163mx ny mx ny ⎧+=⎪⎪⎨⎪+=⎪⎩,所以,点A 、B 的坐标满足方程260mx ny +-=,所以,直线AB 的方程为260mx ny +-=,因为点(),P m n 在直线163xy+=上,则26m n +=,则26n m =-,所以,直线AB 的方程可表示为()660mx m y +--=,即()()610m x y y -+-=,由010x y y -=⎧⎨-=⎩,可得11x y =⎧⎨=⎩,故直线AB 过定点()1,1T ,因为OD AB ⊥,所以,点D 在以OT 为直径的圆上,当点Q 为线段OT的中点时,122DQ OT ==,此时点Q 的坐标为11,22⎛⎫ ⎪⎝⎭.故存在点11,22Q ⎛⎫ ⎪⎝⎭,使得DQ.【点睛】方法点睛:求解直线过定点问题常用方法如下:(1)“特殊探路,一般证明”:即先通过特殊情况确定定点,再转化为有方向、有目的的一般性证明;(2)“一般推理,特殊求解”:即设出定点坐标,根据题设条件选择参数,建立一个直线系或曲线的方程,再根据参数的任意性得到一个关于定点坐标的方程组,以这个方程组的解为坐标的点即为所求点;(3)求证直线过定点()00,x y ,常利用直线的点斜式方程()00y y k x x -=-或截距式y kx b =+来证明.21.(1)见解析(2)见解析【分析】(1)分类讨论导函数e ()x f x x m x ⎛⎫'=- ⎪⎝⎭的实数根即可求解极值点,(2)构造函数()()(2),(0,1)F x g x g x x =--∈和2e ()(3)e e,(0,1)xxxG x x x x-=-+-∈,通过判断函数的单调性,求解最值,当导数正负不好确定的时候,需要构造新的函数,不断的通过求导判断单调性.【详解】(1)2()e 2xmx f x =-,则()e x f x mx '=-,0x = 显然不是()f x '的零点,e (),x f x x m x '⎛⎫∴=- ⎪⎝⎭令e ()=x g x x ,则2e (1)()-'=x x g x x ,()g x ∴在(,0)-∞单调递减,在(0,1)单调递减,在(1,)+∞单调递增.当0x <时,()0g x <,当0x >时,()0g x >,且()(1)e g x g ==极小值(,0)m ∴∈-∞时,e =xm x只有一个实数根,所以此时()f x 有1个极值点,[)0,e m ∈时,e =xm x没有实数根,故()f x 有0个极值点,当e m =时,e=x m x,有一个实数根1x =,但1x =不是极值点,故此时()f x 没有极值点,(e,)m ∈+∞时,e =xm x有两个不相等的实数根,故()f x 有2个极值点.(2)由(1)知,(e,)m ∈+∞,且()()121201,,()x x g x g x m g x <<<==在(0,1)单调递减,在(1,)+∞单调递增,先证:122x x +>,即证:212x x >-,1201x x <<< 121x ∴->即证:()()212g x g x >-.即证:()()112g x g x >-.令()()(2),(0,1)F x g x g x x =--∈,即证:(0,1),()0x F x ∀∈>,2'22e e ()(1)()(2)x xF x x x x -=---令2(1,2)t x =-∈则x t <令2e ()h =λλλ,则4)(e (2)h '⋅⋅-=λλλλλ,则()h λ在(0,2)λ∈单调递减()()(2)h x h t h x ∴>=-,()0F x '∴<,即()F x 在(0,1)x ∈单调递减,()(1)0F x F ∴>=,证毕.再证:()()122e f x f x m +<-,1201x x <<< ,且122x x +>1122x x x ∴<-<.()f x 在()10,x 单调递增,在()12,x x 单调递减,在()2,x +∞单调递增,()()122f x f x ∴->.即证:()()1122e f x f x m +-<-,又11e x m x = ,即证:()()()11121111e 23e e2e x x x f x f x m x x -+-+=-+-<.令2e ()(3)e e,(0,1)xx xG x x x x-=-+-∈,()23222222e 21e e (1)()(2)e eexx x xxxx x x x G x x x x '--+-+--∴=---=.令()23222()e21e xp x xx x x =-+-+-,()2322()e 2212e x p x x x x x '∴=-+++-,令()()q x p x '=()2322()2e 22322e x x q x x x ∴=-+--'-,令()()r x q x '=()232()2e 41027x x x x r x ∴=-'+--令32()41027,(0,1)m x x x x x =+--∈,2()12202m x x x '∴=+-,11(0,1),()x m x ∴∃∈在()110,x 单调递减,在()11,1x 单调递增.(0)7,(1)5m m =-= ,12(0,1)x ∴∃∈,当()120,x x ∈时,()()0,r x q x >''单调递增;当()12,1x x ∈时,()()0,r x q x <''单调递减.()()2042e 0,10q q '<'=-= ,13(0,1),()x p x '∴∃∈在()130,x 单调递减,在()13,1x 单调递增.(0)10,(1)0p p ''=>= ,14(0,1),()x p x ∴∃∈在()140,x 单调递增,在()14,1x 单调递减.(0)1,(1)0p p == ,()0p x ∴>,()0G x '∴>,()G x ∴在(0,)x x ∈单调递增,()(1)2e G x G ∴<=,所以原命题得证.【点睛】本题考查了导数的综合运用,利用导数求单调性时,如果求导后的正负不容易辨别,往往可以将导函数的一部分抽离出来,构造新的函数,利用导数研究其单调性,进而可判断原函数的单调性.在证明不等式时,常采用两种思路:求直接求最值和等价转化.无论是那种方式,都要敢于构造函数,构造有效的函数往往是解题的关键.22.(1)212y x =(2)24【分析】(1)根据曲线C的参数方程为22114txty⎧=+-⎪⎪⎨⎪=⎪⎩t>,t为参数),由y=两边平方求解;(2)易知直线的参数方程为()122xty⎧=+⎪⎪⎨⎪=⎪⎩'''为参数,代入212y x=,利用参数的几何意义求解.【详解】(1)解:因为曲线C的参数方程为22114txtyt⎧=+-⎪⎪⎨⎪=-⎪⎩(0t>,t为参数),所以由y=2221121124ty xt⎛⎫=+-=⎪⎝⎭,而2211104txt=+-≥=,当且仅当2214tt=,即t=时,等号成立,所以曲线C的直角坐标方程212y x=;(2)易知直线:10l x y--=与x轴的交点为()1,0F,直线的参数方程为()12xty⎧=+⎪⎪⎨⎪=⎪⎩'''为参数,代入212y x=得2240t''--=,设A,B两点对应的参数分别为12,t t'',则1224t t''⋅=-,所以12||||24FA FB t t''⋅==.23.(1)17[,]22;(2)[1,)+∞.【分析】(1)把函数()f x化成分段函数,再分段解不等式作答.(2)根据给定条件,分离参数并构造函数,求出函数最大值作答.【详解】(1)依题意,24,1()2,1324,3x x f x x x x -+≤⎧⎪=<<⎨⎪-≥⎩,不等式()3f x ≤化为:1243x x ≤⎧⎨-+≤⎩或1323x <<⎧⎨≤⎩或3243x x ≥⎧⎨-≤⎩,解得112x ≤≤或13x <<或732x ≤≤,即有1722x ≤≤,所以()3f x ≤的解集为17[,]22.(2)依题意,[3,)x ∀∈+∞,22225(2)1()(2)124(2)x a x f x a x x a x --+≥⇔-+≥-⇔≥-,21x -≥,1012x <≤-,于是2222252(2)1121(1)11(2)(2)(2)22x x x x x x x ---==-+=--+≤-----,当且仅当3x =时取等号,则1a ≥,所以实数a 的取值范围是[1,)+∞.24.设a ,b 为实数,且1a >,函数()2R ()x f x a bx e x =-+∈(1)求函数()f x 的单调区间;(2)若对任意22b e >,函数()f x 有两个不同的零点,求a 的取值范围;(3)当a e =时,证明:对任意4b e >,函数()f x 有两个不同的零点()1221,,x x x x >,满足2212ln 2b b e x x e b>+.(注: 2.71828e =⋅⋅⋅是自然对数的底数)25.已知()()()2ln ln f x ax x x x x =+--有三个不同零点1x ,2x ,3x ,且123.<<x x x (1)求实数a 的范围;(2)求证:3121232.ln ln ln x x xx x x ++>26.已知函数()()2ln ,2ln 2a f x ax x g x x x =+=+.(1)若()()f x g x ≥,求a 的取值范围;(2)记()f x 的零点为12,x x (12x x <),()g x 的极值点为0x ,证明:1024e x x x >.27.已知函数()e nxf x x nx =-(*n ∈N 且2n ≥)的图象与x 轴交于P ,Q 两点,且点P 在点Q 的左侧.(1)求点P 处的切线方程()y g x =,并证明:0x ≥时,()()f x g x ≥.(2)若关于x 的方程()f x t =(t 为实数)有两个正实根12,x x ,证明:122ln ln t nx x n n n-<+.28.已知()2e sin =-+xf x ax x .其中a R ∈,e 2.71828≈为自然对数的底数.(1)设曲线()y f x =在点()()0,0f 处的切线为l ,若l 与两坐标轴所围成的三角形的面积为12,求实数a 的值.(2)若*a N ∈,当0x ≥时,()0f x ≥恒成立时,求a 的最大值.29.已知函数()1e 2x f x x =+.(1)求函数()f x 在[]22-,上的最值;(2)若()()321e 3x g x f x x kx =-+-,当0k ≥时,判断函数()g x 的零点个数.30.已知抛物线()2:20C x py p =>的焦点为F ,且F 与圆22:(4)1M x y ++=上点的距离的最小值为4.(1)求p ;(2)若点P 在M 上,,PA PB 是C 的两条切线,,A B 是切点,求PAB 面积的最大值.24.(1)0b ≤时,()f x 在R 上单调递增;0b >时,函数的单调减区间为,log ln a b a ⎛⎫-∞ ⎪⎝⎭,单调增区间为log ,ln ab a ⎛⎫+∞ ⎪⎝⎭;(2)(21,e ⎤⎦;(3)证明见解析.【分析】(1)首先求得导函数的解析式,然后分类讨论即可确定函数的单调性;(2)将原问题进行等价转化,然后构造新函数,利用导函数研究函数的性质并进行放缩即可确定实数a 的取值范围;(3)方法一:结合(2)的结论将原问题进行等价变形,然后利用分析法即可证得题中的结论成立.【详解】(1)2(),()ln x x f x b f a x e a x a b '==+--,①若0b ≤,则()ln 0x f x a a b '=-≥,所以()f x 在R 上单调递增;②若0b >,当,log ln a b x a ⎛⎫∈-∞ ⎝⎭时,()()'0,f x f x <单调递减,当log ,ln ab x a ⎛⎫∈+∞ ⎪⎝⎭时,()()'0,f x f x >单调递增.综上可得,0b ≤时,()f x 在R 上单调递增;0b >时,函数的单调减区间为,log ln a b a ⎛⎫-∞ ⎪⎝⎭,单调增区间为log ,ln ab a ⎛⎫+∞ ⎪⎝⎭.(2)()f x 有2个不同零点20x a bx e ⇔-+=有2个不同解ln 20x a e bx e ⇔-+=有2个不同的解,令ln t x a =,则220,0ln ln t tb b e e e e t a a tt +-+=⇒=>,记()22222(1)(),()t t t t e t e e e e e t e g t g t t t t'⋅-++--===,记2()(1),()(1)10t t t t h t e t e h t e t e e t '=--=-+⋅=⋅>,又(2)0h =,所以(0,2)t ∈时,()0,(2,)h t t ∞<∈+时,()0h t >,则()g t 在(0,2)单调递减,(2,)+∞单调递增,22(2),ln ln b bg e a a e∴>=∴<,22222,ln ,21bb e a a e e>∴>∴≤⇒<≤ .即实数a 的取值范围是(21,e ⎤⎦.(3)[方法一]【最优解】:2,()x a e f x e bx e ==-+有2个不同零点,则2x e e bx +=,故函数的零点一定为正数.由(2)可知有2个不同零点,记较大者为2x ,较小者为1x ,1222412x x e e e e b e x x ++==>,注意到函数2x e e y x+=在区间()0,2上单调递减,在区间()2,+∞上单调递增,故122x x <<,又由5245e ee +<知25x >,122211122x e e e e b x x x b+=<⇒<,要证2212ln 2b b e x x e b >+,只需22ln e x b b>+,222222x x e e e b x x +=<且关于b 的函数()2ln e g b b b =+在4b e >上单调递增,所以只需证()22222222ln 52x x e x e x x x e >+>,只需证2222222ln ln 02x x x e x e e x e-->,只需证2ln ln 202x e xx e-->,242e < ,只需证4()ln ln 2x x h x x e =--在5x >时为正,由于()11()44410x x xh x xe e e x xx '---+-+-==>,故函数()h x 单调递增,又54520(5)ln 5l 20n 2ln 02h e e =--=->,故4()ln ln 2xxh x x e =--在5x >时为正,从而题中的不等式得证.[方法二]:分析+放缩法2e,()e e x a f x bx ==-+有2个不同零点12,x x ,不妨设12x x <,由()e x f x b '=-得12ln x b x <<(其中ln 4b >).且()()12221122e e 0,e e 0x x f x bx f x bx =-+==-+=.要证2212ln e 2e >+b b x x b,只需证2212ln e 2e b b bx bx ->,即证212ln e 2e x b b bx >,只需证212ln ln 2e b b x bx ⎛⎫> ⎪⎝⎭.又22c 222e e e 0bf b ⎛⎫=-< ⎪⎝⎭,所以212e x b<,即1212e bx <.所以只需证2ln(ln )x b b >.而ln 4b >,所以ln b b b >,又ln(ln )ln b b b >,所以只需证(ln(ln ))0f b b <.所以2242(ln(ln ))ln ln(ln )e lnln e e ln4e 0f b b b b b b b b b =-+=-+<-+<,原命题得证.[方法三]:若e a =且4e >b ,则满足21e a <≤且2e 2b >,由(Ⅱ)知()f x 有两个零点()1212,x x x x <且120ln x b x <<<.又2(2)2e 20f b =-<,故进一步有1202ln x b x <<<<.由()()120f x f x ==可得121e e x bx +=且222e e x bx =-,从而()212222121222ln e ln ln e e e e 2e 2e 2e x x b b b b b b x x bx bx b >+⇔->⇔>+..因为102x <<,所以122e e 21e x +<,故只需证22222e e ln e ln ln x b b bx b b x b b>⇔->⇔>+.又因为()f x 在区间(ln ,)b +∞内单调递增,故只需证()22e ln 0f b f x b ⎛⎫+<= ⎪⎝⎭,即2e ln 0e b b b ⎛⎫-< ⎪ ⎪⎝⎭,注意4e >b 时有2e e 4ln e bb <<<,故不等式成立.【整体点评】本题第二、三问均涉及利用导数研究函数零点问题,其中第三问难度更大,涉及到三种不同的处理方法,方法一:直接分析零点212e x b<,将要证明的不等式消元,代换为关于b 的函数,再利用零点反代法,换为关于2x 的不等式,移项作差构造函数,利用导数分析范围.方法二:通过分析放缩,找到使得结论成立的充分条件,方法比较冒险!方法三:利用两次零点反代法,将不等式化简,再利用函数的单调性,转化为2e ln f b b ⎛⎫+ ⎪⎝⎭与0比较大小,代入函数放缩得到结论.25.(1)()2e e 11e e 1-+-(,(2)答案见解析【分析】(1)先利用参变量分离法,可得ln ln x x a x x x =--,然后构造函数ln ()ln x xh x x x x=--,判断()h x 单调性,然后作出函数的大致图像,确定a 的范围即可;(2)由(1)知,12301e x x x <<<<<,可设ln ()xu x x =,则1()1h x u u=--,然后利用导数确定()u x 的图像,由根的分布情况及111ln x u x =,32223ln ln x x u x x ==运算可得结果.【详解】(1)解:令()0f x =,得2ln (0)ln x ax x x x x+=>-,∴ln ln x x a x x x =--.设ln ()ln x xh x x x x=--,221ln (1)1ln ()(ln )x x x x x h x x x x ----=--'2222(1ln )(ln )(ln )x x x x x x x ⎡⎤---⎣⎦=-22222(1ln )2ln (ln )ln (1ln )(2ln )(ln )(ln )x x x x x x x x x x x x x x ⎡⎤----⎣⎦==--设()2ln x x x ϕ=-,121()2x x x x ϕ'-=-=,易知()x ϕ在102⎛⎫⎪⎝⎭,单调递减,在12⎛⎫+∞ ⎪⎝⎭单调递增,∴min 11()()1ln 1ln 2022x ϕϕ==-=+,∴()2ln 0x x x ϕ=->,则由()0h x '=,得1x =或e x =,令()0h x '>,解得()1,e x ∈;令()0h x '<,解得()()01e,x ∞∈⋃+,()h x ∴在()01,单调递减,在()1,e 单调递增,在()e,+∞单调递减,()h x ∴有极小值()11h =,有极大值()()2e 1e e 1e e 1e e e 1h -+=-=--,又1ln ()ln 1xh x x x x=--,当0x +→时,ln 1ln =⋅→-∞x x x x ,()∴→+∞h x ,当x →+∞时,ln 0xx→,∴()1h x →,()h x ∴的图像如下:由图可知,要使()f x 有3个不同零点,即()h x a =有3个不同零点,实数a 的取值范围为()2e e 11,e e 1⎛⎫-+ ⎪ ⎪-⎝⎭.(2)由(1)知,12301e x x x <<<<<,令ln ()xu u x x ==,则1()1h x u u=--,21ln xu x -=',故当()0,e x ∈时,()u x 单调递增;当()e,x ∈+∞时,()u x 单调递减.且0x +→时,u ∞→-;()10u =;x →+∞时,0u →;()()max1e .eu x u ==所以ln ()xu x x=的图像如下:由11u a u-=-,得1(1)(1)u u a u --=-,即2(1)10u a u a +-+-=,由根的分布知:2(1)10u a u a +-+-=有两根1u ,2u ,且1210eu u <<<,由图①②知,111ln x u x =,32223ln ln x x u x x ==,又121211u u au u a +=-⎧⎨=-⎩,∴1212u u u u +=,∴12111u u +=,∴3121231211212ln ln ln x x x x x x u u u ++=+=-,又10<u ,∴110u ->,故3121232ln ln ln x x x x x x ++>.【点睛】本题考查利用导数研究函数的零点,利用导数证明不等式,考查逻辑思维能力和运算求解能力,属于难题.导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.26.(1)44ln2,12ln2∞+⎡⎫+⎪⎢+⎣⎭(2)证明见解析【分析】(1)构造函数()()()h x f x g x =-,然后分类讨论,即可得到a 的取值范围(2)()f x 和()g x 分别求导,求出()g x 的极值点0x 的关系式,()f x 单调区间,()f x 零点所在区间,即可证明.【详解】(1)记()()()21ln 202a h x f x g x x ax x ⎛⎫=-=-+-≥ ⎪⎝⎭,①当2a ≤时,取102h ⎛⎫< ⎪⎝⎭,不符条件;②当2a >时,()()221122122a a x ax ax x h x xx⎛⎫--+-+-⎪⎝⎭==',令()0,()0h x h x ''<>,∴()h x 在10,2⎛⎫⎪⎝⎭单调递减,在1,2⎛⎫+∞ ⎪⎝⎭单调递增,所以11ln210224a a h ⎛⎫⎛⎫=-+-≥ ⎪ ⎪⎝⎭⎝⎭,即44ln212ln2a +≥+,则a 的取值范围为44ln2,12ln2∞+⎡⎫+⎪⎢+⎣⎭;(2)∵()22ag x x='+,令()0g x '=,则00,4e e 4ax x a =-=-,。
【高考总动员】高考数学大一轮复习 第1章 第2节 命题及其关系、充分条件与必要条件课时提升练 文 新

课时提升练(二)命题及其关系、充分条件与必要条件一、选择题1.(2023·东北四市联考)以下命题中真命题是( )A.“a>b”是“a2>b2”的充分条件B.“a>b”是“a2>b2”的必要条件C.“a>b”是“ac2>bc2”的必要条件D.“a>b”是“|a|>|b|”的充要条件【解析】C中,当c2=0时,由a>b ac2>bc2;反过来,由ac2>bc2⇒a>b,故“a>b”是“ac2>bc2”的必要条件.【答案】 C2.命题“假设a,b,c成等比数列,那么b2=ac”的逆否命题是( )A.“假设a,b,c成等比数列,那么b2≠ac”B.“假设a,b,c不成等比数列,那么b2≠ac”C.“假设b2=ac,那么a,b,c成等比数列”D.“假设b2≠ac,那么a,b,c不成等比数列”【解析】根据原命题与其逆否命题的关系知,命题“假设a,b,c成等比数列,那么b2=ac”的逆否命题为“假设b2≠ac,那么a,b,c不成等比数列”.【答案】 D3.(2023·长沙模拟)设A,B为两个互不相同的集合,命题p:x∈A∩B,命题q:x∈A 或x∈B,那么┑q是┑p的( )A.充分必要条件B.充分不必要条件C.必要不充分条件D.既不充分又不必要条件【解析】由题意p⇒q,故┑q⇒┑p;而q p,故┑p┑q,所以┑q是┑p的充分不必要条件.【答案】 B4.有以下四个命题:①“假设x+y=0,那么x,y互为相反数”的逆否命题;②“全等三角形的面积相等”的否命题;③“假设q≤1,那么x2+2x+q=0有实根”的逆否命题;④“不等边三角形的三个内角相等”的逆命题.其中的真命题为( )A.①②B.②③C.①③D.③④【解析】“假设x+y=0,那么x,y互为相反数”为真命题,那么逆否命题也为真;“全等三角形的面积相等”的否命题为“不全等三角形的面积不相等”,该否命题为假命题;假设q≤1⇒4-4q≥0,即Δ=4-4q≥0,那么x2+2x+q=0有实根,所以原命题为真命题,故其逆否命题也为真;“不等边三角形的三个内角相等”的逆命题为“三个内角相等的三角形是不等边三角形”,该逆命题为假命题.应选C.【答案】 C5.(2023·重庆模拟)假设p是q的必要条件,s是q的充分条件,那么以下推理一定正确的选项是( )A.┑p⇔┑s B.p⇔sC.┑p⇒┑s D.┑s⇒┑p【解析】由题意得q⇒p,且s⇒q,故s⇒p,所以┑p⇒┑s.【答案】 C6.(2023·深圳高级中学高三月考)命题:①假设“p且q”为假命题,那么p,q均为假命题;②命题“假设x≥2且y≥3,那么x+y≥5”的否命题为“假设x<2且y<3,那么x+y<5”;③在△ABC中,“A>45°”是“sin A>22”的充要条件;④命题“∃x0∈R,使得e x0≤0”是真命题.其中正确命题的个数是( )A.3 B.2C.1 D.0【解析】假设“p且q”为假命题,那么p,q至少有一个为假命题,①错;②中命题的否命题为:“假设x<2或y<3,那么x+y<5”,②错;③中当A=150°时,sin A<22,③错;由指数函数的性质,可知∀x∈R,e x>0,故④错.【答案】 D7.(2023·天津高考)设a,b∈R,那么“a>b”是“a|a|>b|b|”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件【解析】当b<0时,显然有a>b⇔a|a|>b|b|;当b=0时,显然有a>b⇔a|a|>b|b|;当b>0时,a>b有|a|>|b|,所以a>b⇔a|a|>b|b|.综上可知a>b⇔a|a|>b|b|,应选C.【答案】 C8.(2023·甘肃诊断)以下选项中,p是q的必要不充分条件的是( ) A.p:x=1,q:x2=xB.p:A∩B=A,q:∁U B⊆∁U AC.p:x>a2+b2,q:x>2abD.p:a+c>b+d,q:a>b且c>d【解析】A中,x=1⇒x2=x,x2=x⇒x=0或x=1 x=1,故p是q的充分不必要条件;B中,由A∩B=A得A⊆B,所以∁U B⊆∁U A.反之,假设∁U B⊆∁U A,那么A⊆B,那么A∩B =A,故p是q的充要条件;C中,因为a2+b2≥2ab,由x>a2+b2得x>2ab.反之不成立,如a=0,b=2,x=1,那么有x>2ab,但x=1<4=a2+b2,故p是q的充分不必要条件;D中,取a=-1,b=1,c=0,d=-3,满足a+c>b+d,但a<b,c>d.反之,由同向不等式可加性得a>b,c>d⇒a+c>b+d,故p是q的必要不充分条件.综上所述,应选D.【答案】 D9.(2023·福建高考)直线l :y =kx +1与圆O :x 2+y 2=1相交于A ,B 两点,那么“k =1”是“△OAB 的面积为12”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分又不必要条件【解析】 将直线l 的方程化为一般式得kx -y +1=0,所以圆O :x 2+y 2=1的圆心到该直线的距离d =1k 2+1.又弦长为21-1k 2+1=2|k |k 2+1,所以S △OAB =12·1k 2+1·2|k |k 2+1=|k |k 2+1=12,解得k =±1.因此可知“k =1”是“△OAB 的面积为12”的充分而不必要条件,应选A.【答案】 A10.已知集合A ={x |x >5},集合B ={x |x >a },假设命题“x ∈A ”是命题“x ∈B ”的充分不必要条件,那么实数a 的取值范围是( )A .a <5B .a ≤5C .a >5D .a ≥5【解析】 由题意可知A B ,又A ={x |x >5},B ={x |x >a },如下图,由图可知a <5.【答案】 A11.(2023·上海高考)钱大姐常说“廉价没好货”,她这句话的意思是:“不廉价”是“好货”的( )A .充分条件B .必要条件C .充分必要条件D .既非充分也非必要条件【解析】 根据等价命题,廉价⇒没好货,等价于,好货⇒不廉价,应选B. 【答案】 B12.(2023·湖北高考)设U 为全集,A ,B 是集合,那么“存在集合C 使得A ⊆C ,B ⊆∁U C ”是“A ∩B =∅”的( )A .充分而不必要的条件B .必要而不充分的条件C .充要条件D .既不充分也不必要的条件【解析】 假设存在集合C 使得A ⊆C ,B ⊆∁U C ,那么可以推出A ∩B =∅;假设A ∩B =∅,由Venn 图(如图)可知,存在A =C ,同时满足A ⊆C ,B ⊆∁U C .故“存在集合C 使得A ⊆C ,B ⊆∁U C ”是“A ∩B =∅”的充要条件. 【答案】 C 二、填空题13.已知集合A ={1,a },B ={1,2,3},那么“a =3”是“A ⊆B ”的________条件. 【解析】 a =3⇒A ⊆B ,A ⊆B ⇒a =2或3,因此“a =3”是“A ⊆B ”的充分不必要条件. 【答案】 充分不必要14.在命题p 的四种形式(原命题、逆命题、否命题、逆否命题)中,真命题的个数记为f (p ),已知命题p :“假设两条直线l 1:a 1x +b 1y +c 1=0,l 2:a 2x +b 2y +c 2=0平行,那么a 1b 2-a 2b 1=0”.那么f (p )=________.【解析】 命题p 为真命题,其逆否命题也为真命题;命题p 的逆命题为假命题,其否命题也为假命题.【答案】 215.假设命题“ax 2-2ax -3>0不成立”是真命题,那么实数a 的取值范围是________. 【解析】 由题意得,ax 2-2ax -3≤0,当a =0时,有-3≤0,成立;当a ≠0时,需满足⎩⎪⎨⎪⎧a <0,Δ=4a 2+12a ≤0,即-3≤a <0,综上知-3≤a ≤0.【答案】 [-3,0]16.已知命题p :⎩⎪⎨⎪⎧x +2≥0,x -10≤0,命题q :1-m ≤x ≤1+m ,m >0,假设q 是p 的必要而不充分条件,那么m 的取值范围为________.【解析】 命题p :-2≤x ≤10,由q 是p 的必要不充分条件知, {x |-2≤x ≤10}{x |1-m ≤x ≤1+m ,m >0},∴⎩⎪⎨⎪⎧m >01-m ≤-21+m >10或⎩⎪⎨⎪⎧m >01-m <-21+m ≥10,∴m ≥9,即m 的取值范围是[9,+∞). 【答案】 [9,+∞)。
2019-2020学年江西省高三(上)第一次大联考数学试卷2(含答案解析)

2019-2020学年江西省⾼三(上)第⼀次⼤联考数学试卷2(含答案解析)2019-2020学年江西省⾼三(上)第⼀次⼤联考数学试卷2⼀、选择题(本⼤题共12⼩题,共60.0分)1. 已知集合A ={x|y =lg(1?x)},B ={y|y =2x +1},则( )A. A ∩B ={x|x <0}B. A ∪B =RC. A ∪B ={x|x >1}D. A ∩B =? 2. 已知集合M ={x|?2x +1>0},N ={x|x 12 B. a <12 C. a ≤12 D. a ≥12 3. 下列命题中的真命题是( )A. 2>5B. (?1)2<0C. 12≥5D. a 2<04. 函数f(x)=x 2?2ax +3在区间[2,3]上是单调函数,则a 的取值范围是( )A. a ≤2或a ≥3B. 2≤a ≤3C. a ≤2D. a ≥35. 函数y =lnx 2的图像可能是( )A. B.C. D.6. 设函数f (x ?2)=2x +5,则f (2)=( )A. 11B. 13C. 15D. 97. 如果log 12x x >1D. x >y >1 8. 已知x ,y ∈R ,则“x +y ≤1”是“x ≤12且y ≤12”的( )A. 充分且不必要条件B. 必要且不充分条件C. 充分且必要条件D. 不充分也不必要条件 9. 已知函数f(x)=2lnx +x 22+(5?m)x 在(4,5)上单调递增,则实数m 的取值范围是( )A. (?∞,5+2√2]B. (?∞,192)C. (?∞,5+2√2)D. (?∞,192] 10. 已知函数f(x)是定义在上的偶函数,且当x ≤0时,f(x)=log 2(1?x).若f(a 2?1)<1,则实数a 的取值范围是( )A. (?√2,0)∪(0,√2)B. (?√2,√2)C. (?1,0)∪(0,1)D. (?1,1)11. 函数f(x)={1?x 2(x <1)2?x (x ≥1),f[f(?4)]=( ) A. 12 B. 18 C. 2 D. 812.已知函数f(x)=lnx?(a+1)x,若关于x的不等式f(x)>0恰有3个整数解,则这3个整数解为()A. 1,2,3B. 2,3,4C. 3,4,5D. 4,5,6⼆、填空题(本⼤题共4⼩题,共20.0分)13.函数f(x)=1xlnx的单调递增区间是______ .14.曲线f(x)=2?xe x在点(0,2)处的切线⽅程为______ .15.命题“?x∈[?1,1],x2?3x+1<0”的否定是______.16.函数的最⼤值为______,此时x=__________________.三、解答题(本⼤题共6⼩题,共70.0分)17.已知:命题p:和是⽅程的两个实根,且不等式对任意实数m∈[?1,1]恒成⽴;命题q:函数的定义域为R.若命题p是假命题,命题q是真命题,求a的取值范围.18.已知函数f(x)=a?b2x+1(a,b为常数)是奇函数,且f(1)=13.(1)求实数a,b的值;(2)若函数g(x)=(4x?1)f(x)?k有两个不同零点,求实数k的取值范围;19.已知函数f(x)=e x?x2+a,x∈R的图象在点x=0处的切线为y=bx.(1)求函数f(x)的解析式;(2)若f(x)>kx对任意的x>0恒成⽴,求实数k的取值范围.20.已知函数f(x)=x2?2ax+2,x∈[?2,3].(1)当a=?2时,求函数f(x)的最⼤值和最⼩值.(2)求y=f(x)在区间[?2,3]上的最⼩值.21.已知函数f(x)=xlnx+ax+b在(1,f(1))处的切线为2x?2y?1=0.(1)求实数a,b的值;(2)求f(x)的单调区间.+ln(1+x)22.设函数f(x)=11+x(1)求函数f(x)的单调区间;x2+1.(2)证明:当x∈(0,1)时,f(x)<(1?ln2)x3+12-------- 答案与解析 --------1.答案:D解析:解:∵集合A ={x|y =lg(1?x)}={x|x <1},B ={y|y =2x +1}={y|y >1},∴A ∩B =?.故选:D .先分别求出集合A 和B ,利⽤交集定义能求出结果.本题考查交集的求法,考查交集、并集、不等式性质等基础知识,考查运算求解能⼒,考查函数与⽅程思想,是基础题.2.答案:D解析:解:M ={x|?2x +1>0}={x|x <12},∵M ?N ,由数轴得∴a ≥12.故选:D .化简集合M ,利⽤数轴求解.本题考查了集合的包含关系,属于基础题.3.答案:C解析:解:∵2>5为假命题;(?1)2=1<0为假命题;12≥5为真命题a 2≥0恒成⽴,a 2<0为假命题;故选C根据实数⼤⼩的关系,可以判断A ,C 的真假,根据实数平⽅具有⾮负性,可以判断B ,D 的真假,进⽽得到答案.本题考查的知识点是命题的真假判断与应⽤,是对真假命题定义的直接考查,属于基础题,认真解答,属于送分题.4.答案:A解析:解:∵函数f(x)=x 2?2ax +3的图象是开⼝⽅向向上,且以x =a 为对称轴的抛物线故函数f(x)=x 2?2ax +3在区间(?∞,a]为减函数,在区间[a,+∞)上为增函数,若函数f(x)=x 2?2ax +3在区间[2,3]上为单调函数,则a ≤2,或a ≥3,故答案为:a ≤2或a ≥3.故选:A .由已知中函数的解析式f(x)=x 2?2ax +3,根据⼆次函数的图象和性质,判断出函数f(x)=x 2?2ax +3在区间(?∞,a]为减函数,在区间[a,+∞)上为增函数,由函数f(x)=x 2?2ax +3在区间[2,3上为单调函数,可得区间在对称轴的同⼀侧,进⽽构造关于a的不等式,解不等式即可得到实数a 的取值范围.本题考查的知识点是⼆次函数的性质,其中根据函数f(x)=x2?2ax+3在区间[2,3]上为单调函数,判断出区间在对称轴的同⼀侧,进⽽构造关于a的不等式是解答本题的关键.5.答案:B解析:【分析】本题主要考查函数的图像.【解答】解:因为函数为偶函数,图像关于y轴对称,故排除C,D⼜函数y=lnx2在(0,+∞)上为增函数,故排除A,故选B.6.答案:B解析:【分析】本题主要考查函数的基本概念,是基础题.令x=4,代⼊解析式即可求值.【解答】解:因为f(x?2)=2x+5,令x=4,所以f(2)=f(4?2)=2×4+5=13.故选B.7.答案:D解析:【分析】本题主要考查了对数函数的单调性.利⽤底数⼩于1时,对数函数为减函数得出x,y,1的⼤⼩关系.【解答】解:log12x2y<0=log121,因为为减函数,则x>y>1.故选D.8.答案:B解析:【分析】本题主要考查充分条件和必要条件的判断,结合不等式的关系是解决本题的关键,属于简单题.根据不等式的关系,结合充分条件和必要条件的定义进⾏解答即可.【解答】解:若x≤12且y≤12”,则x+y≤12+12=1成⽴,即必要性成⽴,当x=1,y=0时,满⾜x+y≤1,但x≤12且y≤12不成⽴,即充分性不成⽴,则“x+y≤1”是“x≤12且y≤12”必要不充分条件,故选:B.9.答案:D解析:解:函数在(4,5)上单调递增,∴f′(x)=2x+x+5?m≥0,化为:m≤2x+x+5,⽽g(x)=2x+x+5在(4,5)上单调递增,∴g(x)>g(4)=192.∴m≤192.则实数m的取值范围是(?∞,192].故选:D.函数f(x)=2lnx+x22+(5?m)x在(4,5)上单调递增,f′(x)≥0,化为:m≤2x+x+5,⽽g(x)=2x+x+5在(4,5)上单调递增,即可得出最⼩值.本题考查了利⽤导数研究函数的单调性极值与最值、分离参数法,考查了推理能⼒与计算能⼒,属于中档题.10.答案:A解析:【分析】本题考查函数的奇偶性、函数的单调性,⼀元⼆次不等式的解法,属于中档题.当x≤0时,f(x)=log2(1?x)为减函数,结合偶函数f(x)满⾜f(?1)=1,可得答案.。
数学课件(新教材人教A版强基版)第一章集合常用逻辑用语不等式15一元二次方程不等式

命题点2 在给定区间上恒成立问题 例4 已知函数f(x)=mx2-mx-1.若对于x∈[1,3],f(x)<5-m恒成立,则 实数m的取值范围为__-__∞__,__67___.
要使f(x)<-m+5在x∈[1,3]上恒成立,
即 mx-122+34m-6<0 在 x∈[1,3]上恒成立. 方法一 令 g(x)=mx-122+34m-6,x∈[1,3]. 当m>0时,g(x)在[1,3]上单调递增, 所以g(x)max=g(3),即7m-6<0, 所以 m<67,所以 0<m<67;
a<0的解集为
√A.x-1<x<21
B.xx<-1或x>12
C.{x|-2<x<1}
D.{x|x<-2或x>1}
1 2 3 4 5 6 7 8 9 10 11 12 13 14
因为不等式ax2+bx+2>0的解集为{x|-1<x<2},
所以ax2+bx+2=0的两根为-1,2,且a<0,
即-1+2=-ba,(-1)×2=2a, 解得a=-1,b=1,
取值范围是
A.{a|a<-22}
√C.{a|-2<a≤2}
D.{a|a<2}
因为不等式(a-2)x2+2(a-2)x-4≥0的解集为∅, 所以不等式(a-2)x2+2(a-2)x-4<0的解集为R. 当a-2=0,即a=2时,-4<0,符合题意; 当a-2≠0,即a≠2时, 需满足Δa-=2[2<0a,-2]2+4×4×a-2<0, 解得-2<a<2. 综上,实数a的取值范围是{a|-2<a≤2}.
1.4.3含有一个量词的命题的否定(李用2)
假 假
(2) ㄱq:存在一个正方形不是矩形;
例题
例2 :写出下列全称命题的否定:
(1)p:所有能被3整除的整数都是奇数;
(2)p:每一个四边形的四个顶点共圆;
(3)p:对任意x∈Z, x² 的个位数字不等于3.
答:(1)ㄱp:存在一个能被3整除的整数不是奇数;
(2)ㄱp:存在一个四边形,它的四个顶点不共圆; (3)ㄱp: ∃x0∈Z, x0² 的个位数字等于3.
探究二:特称命题的否定
课本25页:写出下列命题的否定:
(1)有些实数的绝对值是正数;
(2)有些平行四边形是菱形;
(3) ∃x0∈R, x0² +1<0.
这些命题和它们的否定在形式上
有什么变化?
以上三个命题都是特称命题,即具有形式 “∃x ∈M, p(x )”其中命题(1)的否定是“不 存在一个实数,它的绝对值是正数”,也就是说,
解析: (1)为全称命题. (2)为特称命题. (3)不是命题. (4)为全称命题. (5)为特称命题.
将下列命题用量词符号“∀”或“∃”表 示,并判断真假. (1)实数的平方是非负数; (2)整数中1最小; (3) 方程 ax2 + 2x + 1 = 0(a<1) 至少存在一个负根; (4)对于某些实数x,有2x+1>0; (5)若直线l垂直于平面α内任一直线,则l⊥α.
[解题过程]
π (1)特称命题. α=2时, tan α 不存在, 所以,
特称命题“有一个实数 α,tan α 无意义”是真命题. (2)不是命题. (3)含有全称量词,所以该命题是全称命题,又任何一个 圆的圆心到切线的距离都等于半径, 所以,全称命题“所有圆的圆心到其切线的距离都等于 半径”是真命题.
高三数学复习(理):第2讲 命题及其关系、充分条件与必要条件
第2讲命题及其关系、充分条件与必要条件[学生用书P5]1.命题用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.2.四种命题及其关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题,它们有相同的真假性;②两个命题为互逆命题或互否命题,它们的真假性没有关系.3.充分条件、必要条件与充要条件的概念若p⇒q,则p是q的充分条件,q是p的必要条件p是q的充分不必要条件p⇒q且q⇒/pp是q的必要不充分条件p⇒/q且q⇒pp是q的充要条件p⇔qp是q的既不充分也不必要条件p⇒/q且q⇒/p1.充要条件的两个结论(1)若p是q的充分不必要条件,q是r的充分不必要条件,则p是r的充分不必要条件.(2)若p是q的充分不必要条件,则﹁q是﹁p的充分不必要条件.2.一些常见词语及其否定词语是都是都不是等于大于否定不是不都是至少一个是不等于不大于一、思考辨析判断正误(正确的打“√”,错误的打“×”)(1)“x2+2x-3<0”是命题.()(2)命题“若p,则q”的否命题是“若p,则﹁q”.()(3)若原命题为真,则这个命题的否命题、逆命题、逆否命题中至少有一个为真.()(4)当q是p的必要条件时,p是q的充分条件.()(5)q不是p的必要条件时,“p⇒/q”成立.()答案:(1)×(2)×(3)√(4)√(5)√二、易错纠偏常见误区|K(1)命题的条件与结论不明确;(2)含有大前提的命题的否命题易出现否定大前提的情况;(3)对充分必要条件判断错误.1.命题“若a2+b2=0,a,b∈R,则a=b=0”的逆否命题是________.答案:若a≠0或b≠0,a,b∈R,则a2+b2≠02.已知命题“对任意a,b∈R,若ab>0,则a>0”,则它的否命题是________.答案:对任意a,b∈R,若ab≤0,则a≤03.已知p:a<0,q:a2>a,则﹁p是﹁q的________条件(填:充分不必要、必要不充分、充要、既不充分也不必要).解析:﹁p:a≥0;﹁q:a2≤a,即0≤a≤1,故﹁p是﹁q的必要不充分条件.答案:必要不充分[学生用书P5]四种命题的相互关系及真假判断(自主练透)1.命题“若x2<1,则-1<x<1”的逆否命题是()A.若x2≥1,则x≥1或x≤-1B.若-1<x<1,则x2<1C.若x>1或x<-1,则x2>1D.若x≥1或x≤-1,则x2≥1解析:选D.命题的形式是“若p,则q”,由逆否命题的知识,可知其逆否命题是“若﹁q,则﹁p”的形式,所以“若x2<1,则-1<x<1”的逆否命题是“若x≥1或x≤-1,则x2≥1”.2.有以下命题:①“若xy=1,则x,y互为倒数”的逆命题;②“面积相等的两个三角形全等”的否命题;③“若m≤1,则x2-2x+m=0有实数解”的逆否命题;④“若A∩B=B,则A⊆B”的逆否命题.其中真命题是()A.①②B.②③C.④D.①②③解析:选D.①原命题的逆命题为“若x,y互为倒数,则xy=1”,是真命题;②原命题的否命题为“面积不相等的两个三角形不全等”,是真命题;③若m≤1,Δ=4-4m≥0,所以原命题是真命题,故其逆否命题也是真命题;④由A∩B =B,得B⊆A,所以原命题是假命题,故其逆否命题也是假命题,故①②③正确.3.已知集合P =⎩⎨⎧⎭⎬⎫x |x =k +12,k ∈Z ,Q =⎩⎨⎧⎭⎬⎫x |x =k 2,k ∈Z ,记原命题:“x ∈P ,则x ∈Q ”,那么,在原命题及其逆命题、否命题、逆否命题中,真命题的个数是( ) A .0B .1C .2D .4 解析:选 C.因为P =⎩⎨⎧⎭⎬⎫x |x =k +12,k ∈Z =⎩⎨⎧⎭⎬⎫x |x =2k +12,k ∈Z ,Q =⎩⎨⎧⎭⎬⎫x |x =k 2,k ∈Z , 所以P Q ,所以原命题“x ∈P ,则x ∈Q ”为真命题,则原命题的逆否命题也为真命题.原命题的逆命题“x ∈Q ,则x ∈P ”为假命题,则原命题的否命题为假命题,所以真命题的个数为2.(1)写一个命题的其他三种命题时需关注2点①对于不是“若p ,则q ”形式的命题,需先改写;②若命题有大前提,写其他三种命题时需保留大前提.[提醒] 四种命题的关系具有相对性,一旦一个命题定为原命题,相应的也就有了它的“逆命题”“否命题”“逆否命题”.(2)判断命题真假的2种方法①直接判断:判断一个命题为真命题,要给出严格的推理证明;说明一个命题是假命题,只需举出一个反例即可;②间接判断:当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.充分条件、必要条件的判断(师生共研)(1)(2020·高考天津卷)设a∈R,则“a>1”是“a2>a”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件(2)已知p:x=2,q:x-2=2-x,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解析】(1)由a2>a得a>1或a<0,反之,由a>1得a2>a,则“a>1”是“a2>a”的充分不必要条件,故选A.(2)当x-2=2-x时,两边平方可得(x-2)2=2-x,即(x-2)(x-1)=0,解得x1=2,x2=1.当x=1时,-1=1,不成立,故舍去,则x=2,所以p是q 的充要条件,故选C.【答案】(1)A(2)C判断充要条件的3种常用方法(1)定义法:直接判断若p,则q、若q,则p的真假.(2)等价法:利用A⇒B与﹁B⇒﹁A,B⇒A与﹁A⇒﹁B,A⇔B与﹁B⇔﹁A 的等价关系,对于条件或结论是否定式的命题,一般运用等价法.(3)利用集合间的包含关系判断:若A⊆B,则A是B的充分条件或B是A 的必要条件;若A=B,则A是B的充要条件.[提醒]判断充要条件时需注意3点(1)要分清条件与结论分别是什么.(2)要从充分性、必要性两个方面进行判断.(3)直接判断比较困难时,可举出反例说明.1.(2021·南充市第一次适应性考试)“A=60°”是“cos A=12”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选A.A=60°⇒cos A=12,cos A=12⇒A=±60°+k·360°,k∈Z,所以“A=60°”是“cos A=12”的充分不必要条件.2.(2021·广东省七校联考)已知命题p:2x<2y,命题q:log2x<log2y,则命题p是命题q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选B.由题意可得p:x<y,q:0<x<y,故p是q的必要不充分条件,选B.3.王安石在《游褒禅山记》中写道“世之奇伟、瑰怪,非常之观,常在于险远,而人之所罕至焉,故非有志者不能至也”,请问“有志”是到达“奇伟、瑰怪,非常之观”的()A.充要条件B.既不充分也不必要条件C.充分不必要条件D.必要不充分条件解析:选D.由“非有志者不能至也”,可得能够到达“奇伟、瑰怪,非常之观”的必须有志,而有志者未必到达“奇伟、瑰怪,非常之观”,故“有志”是到达“奇伟、瑰怪,非常之观”的必要不充分条件.充分条件、必要条件的探求及应用(典例迁移)(1)设集合A ={x |x >-1},B ={x |x ≥1},则“x ∈A 且x ∉B ”成立的充要条件是( )A .-1<x ≤1B .x ≤1C .x >-1D .-1<x <1(2)已知P ={x |x 2-8x -20≤0},非空集合S ={x |1-m ≤x ≤1+m }.若“x ∈P ”是“x ∈S ”的必要条件,则m 的取值范围为________.【解析】 (1)因为集合A ={x |x >-1},B ={x |x ≥1},又因为“x ∈A 且x ∉B ”,所以-1<x <1;又当-1<x <1时,满足x ∈A 且x ∉B ,所以“x ∈A 且x ∉B ”成立的充要条件是“-1<x <1”.故选D.(2)由x 2-8x -20≤0,得-2≤x ≤10,所以P ={x |-2≤x ≤10},由x ∈P 是x ∈S 的必要条件,知S ⊆P .则⎩⎪⎨⎪⎧1-m ≤1+m ,1-m ≥-2,1+m ≤10,所以0≤m ≤3.所以当0≤m ≤3时,“x ∈P ”是“x ∈S ”的必要条件,即所求m 的取值范围是[0,3].【答案】 (1)D (2)[0,3]【迁移探究】 (变问法)本例(2)条件不变,若“x ∈﹁P ”是“x ∈﹁S ”的必要不充分条件,求实数m 的取值范围.解:由例题知P ={x |-2≤x ≤10},因为“x ∈﹁P ”是“x ∈﹁S ”的必要不充分条件,所以P ⇒S 且S ⇒P .所以[-2,10][1-m ,1+m ].所以⎩⎪⎨⎪⎧1-m ≤-2,1+m >10或⎩⎪⎨⎪⎧1-m <-2,1+m ≥10.所以m ≥9,即m 的取值范围是[9,+∞).根据充要条件求解参数范围的方法及注意事项(1)解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(组)求解.(2)求解参数的取值范围时,一定要注意区间端点值的检验,尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.1.(2021·东北三校第一次联考)下列说法中正确的是( )A .若“a >b ”是“a >c ”的充分条件,则b ≥cB .若“a >b ”是“a >c ”的充分条件,则b ≤cC .若“a >b ”是“a >c ”的充要条件,则b >cD .若“a <b ”是“a >c ”的必要条件,则b <c解析:选A.令A ={a |a >b },B ={a |a >c },C ={a |a <b }.若“a >b ”是“a >c ”的充分条件,则有A ⊆B ,则b ≥c ,故选项A 正确,选项B 错误;若“a >b ”是“a >c ”的充要条件,则有A =B ,则b =c ,故选项C 错误;若“a <b ”是“a >c ”的必要条件,则有B ⊆C ,这是不可能的,故选项D 错误.故选A.2.命题“∀x ∈[1,3],x 2-a ≤0”为真命题的一个充分不必要条件是( )A .a ≥9B .a ≤9C .a ≥10D .a ≤10解析:选C.命题∀x ∈[1,3],x 2-a ≤0⇔∀x ∈[1,3],x 2≤a ⇔9≤a .则“a ≥10”是“命题∀x ∈[1,3],x 2-a ≤0”为真命题的一个充分不必要条件.故选C.3.若“x 2-x -6>0”是“x >a ”的必要不充分条件,则a 的最小值为________.解析:由x 2-x -6>0,解得x <-2或x >3.因为“x 2-x -6>0”是“x >a ”的必要不充分条件,所以{x |x >a }是{x |x <-2或x >3}的真子集,即a ≥3,故a 的最小值为3. 答案: 3[学生用书P7]思想方法系列1 等价转化思想在充要条件中的应用等价转化思想就是对原问题换一个方式、换一个角度、换一个观点加以考虑,把要解决的问题通过某种转化,再转化,化归为一类已经解决或比较容易解决的问题,从而使问题得到圆满解决的思维方式.已知条件p :|x -4|≤6,条件q :(x -1)2-m 2≤0(m >0).若﹁p 是﹁q 的充分不必要条件,则m 的取值范围为______.【解析】 条件p :-2≤x ≤10,条件q :1-m ≤x ≤1+m ,又﹁p 是﹁q 的充分不必要条件,则q 是p 的充分不必要条件.故有⎩⎪⎨⎪⎧m >0,1-m ≥-21+m ≤10,,所以0<m ≤3.【答案】 (0,3]本例涉及参数问题,直接解决较为困难,先用等价转化思想,将复杂、生疏的问题化归为简单、熟悉的问题来解决.一般地,在涉及字母参数的取值范围的充分、必要条件问题中,常常要利用集合的包含、相等关系来考虑,这是解此类问题的关键.1.如果x ,y 是实数,那么“x ≠y ”是“cos x ≠cos y ”的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件解析:选C.方法一:设集合A={(x,y)|x≠y},B={(x,y)|cos x≠cos y},则A的补集C={(x,y)|x=y},B的补集D={(x,y)|cos x=cos y},显然C D,所以B A,于是“x≠y”是“cos x≠cos y”的必要不充分条件.方法二(等价转化法):因为x=y⇒cos x=cos y,而cos x=cos y⇒/x=y,所以“cos x=cos y”是“x=y”的必要不充分条件,故“x≠y”是“cos x≠cos y”的必要不充分条件.2.王昌龄的《从军行》中两句诗为“黄沙百战穿金甲,不破楼兰终不还”,其中后一句中“攻破楼兰”是“返回家乡”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选B.“攻破楼兰”不一定“返回家乡”,但“返回家乡”一定是“攻破楼兰”,故“攻破楼兰”是“返回家乡”的必要不充分条件.故选B.[学生用书P357(单独成册)][A级基础练]1.已知命题p:“正数a的平方不等于0”,命题q:“若a不是正数,则它的平方等于0”,则q是p的()A.逆命题B.否命题C.逆否命题D.否定解析:选B.命题p:“正数a的平方不等于0”可写成“若a是正数,则它的平方不等于0”,从而q是p的否命题.2.“若x,y∈R,x2+y2=0,则x,y全为0”的逆否命题是()A.若x,y∈R,x,y全不为0,则x2+y2≠0B.若x,y∈R,x,y不全为0,则x2+y2=0C.若x,y∈R,x,y不全为0,则x2+y2≠0D.若x,y∈R,x,y全为0,则x2+y2≠0解析:选C.依题意得,原命题的题设为若x2+y2=0,结论为x,y全为0.逆否命题:若x,y不全为0,则x2+y2≠0,故选C.3.下列命题:①“若a≤b,则a<b”的否命题;②“若a=1,则ax2-x+3≥0的解集为R”的逆否命题;③“周长相同的圆面积相等”的逆命题;④“若2x为有理数,则x为无理数”的逆否命题.其中真命题的序号为()A.②④B.①②③C.②③④D.①③④解析:选B.对于①,逆命题为真,故否命题为真;对于②,原命题为真,故逆否命题为真;对于③,“面积相等的圆周长相同”为真;对于④,“若2x为有理数,则x为0或无理数”,故原命题为假,逆否命题为假.故选B.4.(2021·西安五校联考)“ln(x+1)<0”是“x2+2x<0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选A.由ln(x+1)<0得0<x+1<1,-1<x<0,由x2+2x<0得-2<x<0,所以“ln(x+1)<0”是“x2+2x<0”的充分不必要条件,故选A.5.(2021·开封市第一次模拟考试)若a,b是非零向量,则“a·b>0”是“a 与b的夹角为锐角”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件解析:选B.因为a,b为非零向量,a·b>0,所以由向量数量积的定义知,a 与b的夹角为锐角或a与b方向相同;反之,若a与b的夹角为锐角,由向量数量积的定义知,a·b>0成立.故“a·b>0”是“a与b的夹角为锐角”的必要不充分条件.故选B.6.使a>0,b>0成立的一个必要不充分条件是()A.a+b>0 B.a-b>0C.ab>1 D.ab>1解析:选A.因为a>0,b>0⇒a+b>0,反之不成立,而由a>0,b>0不能推出a-b>0,ab>1,ab>1,故选A.7.已知p:m=-1,q:直线x-y=0与直线x+m2y=0互相垂直,则p是q的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选A.由题意得,直线x+m2y=0的斜率是-1,所以-1m2=-1,m=±1.所以p是q的充分不必要条件.故选A.8.(2021·六校联盟第二次联考)若a>0,b>0,则“a+b≤8”是“ab≤16”的()A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件解析:选B.a>0,b>0,8≥a+b≥2ab,故4≥ab,ab≤16,所以a+b≤8可以推出ab≤16.若a=2,b=8,则a+b=2+8=10,所以ab≤16推不出a+b≤8.9.“(x+1)(y-2)=0”是“x=-1且y=2”的________条件.解析:因为(x+1)(y-2)=0,所以x=-1或y=2,所以(x+1)(y-2)=0⇒/x =-1且y=2,x=-1且y=2⇒(x+1)(y-2)=0,所以是必要不充分条件.答案:必要不充分10.条件p:x>a,条件q:x≥2.(1)若p是q的充分不必要条件,则a的取值范围是________;(2)若p 是q 的必要不充分条件,则a 的取值范围是________.解析:设A ={x |x >a },B ={x |x ≥2},(1)因为p 是q 的充分不必要条件,所以A B ,所以a ≥2.(2)因为p 是q 的必要不充分条件,所以B A ,所以a <2.答案:(1)a ≥2 (2)a <211.若命题“ax 2-2ax -3>0不成立”是真命题,则实数a 的取值范围是________.解析:由题意知ax 2-2ax -3≤0恒成立,当a =0时,-3≤0成立;当a ≠0时,得⎩⎪⎨⎪⎧a <0,Δ=4a 2+12a ≤0, 解得-3≤a <0,故-3≤a ≤0.答案:[-3,0]12.给出下列说法:①“若x +y =π2,则sin x =cos y ”的逆命题是假命题;②在△ABC 中,“sin B >sin C ”是“B >C ”的充要条件是真命题;③“a =1”是“直线x -ay =0与直线x +ay =0互相垂直”的充要条件; ④命题“若x <-1,则x 2-2x -3>0”的否命题为“若x ≥-1,则x 2-2x -3≤0”.以上说法中正确的是________.(填序号)解析:对于①,“若x +y =π2,则sin x =cos y ”的逆命题是“若sin x =cos y ,则x +y =π2”,当x =0,y =3π2时,有sin x =cos y 成立,但x +y =3π2,故逆命题为假命题,①正确;对于②,在△ABC 中,由正弦定理得sin B >sin C ⇔b >c ⇔B >C ,②正确;对于③,“a=±1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件,故③错误;对于④,根据否命题的定义知④正确.答案:①②④[B级综合练]13.若a,b都是正整数,则a+b>ab成立的充要条件是()A.a=b=1 B.a,b至少有一个为1C.a=b=2 D.a>1且b>1解析:选B.因为a+b>ab,所以(a-1)(b-1)<1.因为a,b∈N*,所以(a-1)(b-1)∈N,所以(a-1)(b-1)=0,所以a=1或b=1.故选B.14.已知条件p:x2+2x-3>0;条件q:x>a,且﹁q的一个充分不必要条件是﹁p,则a的取值范围是________.解析:由x2+2x-3>0,得x<-3或x>1,由﹁q的一个充分不必要条件是﹁p,可知﹁p是﹁q的充分不必要条件,等价于q是p的充分不必要条件,故a≥1.答案:[1,+∞)[C级提升练]15.A,B,C三个学生参加了一次考试,A,B的得分均为70分,C的得分为65分.已知命题p:若及格分低于70分,则A,B,C都没有及格.则下列四个命题中为p的逆否命题的是()A.若及格分不低于70分,则A,B,C都及格B.若A,B,C都及格,则及格分不低于70分C.若A,B,C至少有一人及格,则及格分不低于70分D.若A,B,C至少有一人及格,则及格分高于70分解析:选C.根据原命题与它的逆否命题之间的关系知,命题p的逆否命题是若A,B,C至少有一人及格,则及格分不低于70分.故选C.16.能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是________.解析:这是一道开放性试题,答案不唯一,只要满足f(x)>f(0)对任意的x∈(0,2]都成立,且函数f(x)在[0,2]上不是增函数即可.如f(x)=sin x,答案不唯一.答案:f(x)=sin x(答案不唯一)。
2020年高考数学复习题:二次函数与幂函数
二次函数与幂函数[基础训练]1.在同一直角坐标系中,函数f(x)=x a(x>0),g(x)=log a x的图象可能是()答案:D解析:因为a>0,所以f(x)=x a在(0,+∞)上为增函数,故A错.在B中,由f(x)的图象知a>1,由g(x)的图象知0<a<1,矛盾,故B错.在C中,由f(x)的图象知0<a<1,由g(x)的图象知a>1,矛盾,故C错.在D中,由f(x)的图象知0<a<1,由g(x)的图象知0<a<1,相符,故选D.2.[2019上海模拟]如图是函数y=x mn(m,n∈N*,m,n互质)的图象,则下列结论正确的是()A.m,n是奇数,且m<nB.m是偶数,n是奇数,且m>nC .m 是偶数,n 是奇数,且m <nD .m 是奇数,n 是偶数,且m >n答案:C 解析:由图象可知函数y =x m n 为偶函数,∴m 是偶数,又m ,n 互质,n ∈N *,∴n 是奇数.又∵图象在第一象限是上凸的,∴m n <1,即m <n .故选C.3.[2019广东佛山模拟]已知实数m ,n ∈{1,2,3,4},若m ≠n ,则函数f (x )=|m -n |x n m 为幂函数且为偶函数的概率为( )A.12B.14C.16D.23答案:B 解析:函数f (x )=|m -n |x n m 为幂函数且为偶函数,则|m -n |=1,且n 为偶数,∴(m ,n )的可能情况有(1,2),(3,2),(3,4).又实数m ,n ∈{1,2,3,4},∴(m ,n )的所有可能情况有(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),共12种情况.∴函数f (x )=|m -n |x n m 为幂函数且为偶函数的概率为312=14.故选B.4.[2019湖南长沙统一模拟]已知函数f (x )=x 12,则( )A .∃x 0∈R ,使得f (x )<0B .∀x >0,f (x )>0C .∃x 1,x 2∈[0,+∞),使得f (x 1)-f (x 2)x 1-x 2<0D .∀x 1∈[0,+∞),∃x 2∈[0,+∞),使得f (x 1)>f (x 2) 答案:B 解析:由题意得f (x )=x ,函数的定义域为[0,+∞),函数的值域为[0,+∞),并且函数是单调递增函数.所以A 不成立,根据单调性可知C 也不成立.而D 中,当x 1=0时,不存在x 2∈[0,+∞),使得f (x 1)>f (x 2),所以D 不成立.故选B.5.若函数f (x )=x 2-2x +m 在[3,+∞)上的最小值为1,则实数m 的值为 ( )A .-3B .-2C .-1D .1答案:B 解析:函数f (x )=x 2-2x +m =(x -1)2+m -1的图象如图所示.由图象知在[3,+∞)上,f (x )min =f (3)=32-2×3+m =1,得m =-2.6.[2019湖南株洲联考]函数y =ax 2+bx 与y =log|b a |x (ab ≠0,|a |≠|b |)在同一直角坐标系中的图象可能是( )答案:D 解析:对于A ,B 两图,⎪⎪⎪⎪⎪⎪b a >1,而ax 2+bx =0的两根分别为0和-b a ,且两根之和为-b a ,由图知0<-b a <1,得-1<b a <0,矛盾;对于C ,D 两图,0<⎪⎪⎪⎪⎪⎪b a <1,在C 图中两根之和-b a <-1,即b a >1,矛盾,C 错.故选D.7.已知函数f (x )=ax 2+bx +c ,且a >b >c ,a +b +c =0,则( )A .∀x ∈(0,1),都有f (x )>0B .∀x ∈(0,1),都有f (x )<0C .∃x 0∈(0,1),使f (x 0)=0D .∃x 0(0,1),使f (x 0)>0答案:B 解析:由a >b >c ,a +b +c =0可知a >0,c <0,抛物线开口向上,因为f (0)=c <0,f (1)=a +b +c =0,即1是方程ax 2+bx +c =0的一个根,所以∀x ∈(0,1),都有f (x )<0.故选B.8.[2019广东汕头一模]命题“ax 2-2ax +3>0恒成立”是假命题,则实数a 的取值范围是( )A .(-∞,0)∪[3,+∞)B .(-∞,0]∪[3,+∞)C .(-∞,0)∪(3,+∞)D .(0,3)答案:A 解析:若ax 2-2ax +3>0恒成立,则a =0或⎩⎪⎨⎪⎧ a >0,Δ=4a 2-12a <0,可得0≤a <3,故当命题“ax 2-2ax +3>0恒成立”是假命题时,a <0或a ≥3.9.[2019福建龙海期末]若幂函数y =(m 2-3m +3)·xm 2-m -2 的图象不经过坐标原点,则实数m =________.答案:1或2 解析:由题意得m 2-3m +3=1,解得m =1或m =2.当m =1时,y =x -2,图象不过原点, 当m =2时,y =x 0,图象不过原点,故m =1或2.10.[2019山西一模]已知函数f (x )=x 2-m 是定义在区间[-3-m ,m 2-m ]上的奇函数,则f (m )=________.答案:-1 解析:由题意得m 2-m =3+m ,即m 2-2m -3=0,∴m =3或m =-1.当m =3时,f (x )=x -1,[-3-m ,m 2-m ]为[-6,6], f (x )在x =0处无意义,故舍去.当m =-1时,f (x )=x 3,[-3-m ,m 2-m ]为[-2,2],满足题意,∴f (m )=f (-1)=(-1)3=-1.11.已知函数f (x )=x 2+2ax +3,若y =f (x )在区间[-4,6]上是单调函数,则实数a 的取值范围为________.答案:(-∞,-6]∪[4,+∞) 解析:函数f (x )=x 2+2ax +3的图象的对称轴为直线x =-2a 2=-a ,要使f (x )在[-4,6]上为单调函数,只需-a ≤-4或-a ≥6,解得a ≥4或a ≤-6.12.[2019重庆二模]已知函数f (x )=x 2-2ax +5(a >1).(1)若f (x )的定义域和值域均是[1,a ],求实数a 的值;(2)若对任意的x 1,x 2∈[1,a +1],总有|f (x 1)-f (x 2)|≤4,求实数a 的取值范围.解:(1)∵f (x )=(x -a )2+5-a 2(a >1),∴f (x )在[1,a ]上为减函数.又∵f (x )的定义域和值域均是[1,a ],∴⎩⎪⎨⎪⎧ f (1)=a ,f (a )=1,即⎩⎪⎨⎪⎧ 1-2a +5=a ,a 2-2a 2+5=1,解得a =2.(2)对任意的x 1,x 2∈[1,a +1],总有|f (x 1)-f (x 2)|≤4,即f (x )max -f (x )min ≤4.若a ≥2,则a ∈[1,a +1],且(a +1)-a ≤a -1.∴f (x )max =f (1)=6-2a ,f (x )min =f (a )=5-a 2,∴f (x )max -f (x )min =6-2a -(5-a 2)≤4,解得-1≤a ≤3,又a ≥2,∴2≤a ≤3.若1<a <2,则a ∈[1,a +1],且a -1<(a +1)-a .∴x ∈[1,a +1]时,f (x )max =f (a +1)=6-a 2,f (x )min =f (a )=5-a 2,f (x )max -f (x )min =(6-a 2)-(5-a 2)=1,∴f (x )max -f (x )min ≤4成立.综上,a 的取值范围是(1,3].[强化训练]1.已知函数f (x )=x 2+1的定义域为[a ,b ](a <b ),值域为[1,5],则在平面直角坐标系内,点(a ,b )的运动轨迹与两坐标轴围成的图形的面积为( )A .8B .6C .4D .2 答案:C 解析:二次函数f (x )=x 2+1,开口向上,顶点为(0,1), 且当x =±2时,y =5.根据二次函数的图象特点,f (x )在[a ,b ]上的最大值一定是在端点处取得.∴要使f (x )在[a ,b ]上的值域为[1,5],则f (a )=5,f (b )≤5或f (b )=5,f (a )≤5,且0∈[a ,b ], ∴a =-2,0≤b ≤2或者b =2,-2≤a ≤0.∴点(a ,b )的运动轨迹与两坐标轴围成的图形是一个边长为2的正方形,面积为4.2.已知函数f (x )=ax 2-2x +2,若对一切x ∈⎣⎢⎡⎦⎥⎤12,2,f (x )>0都成立,则实数a 的取值范围为( )A.⎣⎢⎡⎭⎪⎫12,+∞B.⎝ ⎛⎭⎪⎫12,+∞ C .[-4,+∞) D .(-4,+∞)答案:B 解析:由题意f (x )>0对一切x ∈⎣⎢⎡⎦⎥⎤12,2都成立, 分离参数得a >2x -2x 2对一切x ∈⎣⎢⎡⎦⎥⎤12,2都成立, 即只需满足a 大于函数y =2x -2x 2⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤12,2的最大值即可. ∵y =2x -2x 2=-2x 2+2x =-2⎝ ⎛⎭⎪⎫1x -122+12,x ∈⎣⎢⎡⎦⎥⎤12,2, ∴y =2x -2x 2的最大值为12.∴a >12.故选B.3.[2019山东烟台模拟]定义在R 上的奇函数f (x )在(0,+∞)上是增函数,则使得f (x )>f (x 2-2x +2)成立的x 的取值范围是( )A .(1,2)B .(-∞,1)∪(2,+∞)C .(-∞,1)D .(2,+∞) 答案:A 解析:因为f (x )是R 上的奇函数且在(0,+∞)上是增函数.则函数f (x )在(-∞,0)上也是增函数,故函数在R 上为增函数,f (x )>f (x 2-2x +2)⇒x >x 2-2x +2⇒x 2-3x +2<0,解得1<x <2,即x 的取值范围是(1,2).故选A.4.[2019河北保定模拟]对于任意a ∈[-1,1],函数f (x )=x 2+(a -4)x +4-2a 的值总大于0,则x 的取值范围是( )A .{x |1<x <3}B .{x |x <1或x >3}C .{x |1<x <2}D .{x |x <1或x >2} 答案:B 解析:由题意知,关于a 的一次函数y =a (x -2)+x 2-4x +4的值大于0在a ∈[-1,1]上恒成立,只需⎩⎪⎨⎪⎧ (-1)×(x -2)+x 2-4x +4>0,1×(x -2)+x 2-4x +4>0,解得⎩⎪⎨⎪⎧ x >3或x <2,x >2或x <1,即x <1或x >3,故选B.5.[2019江西吉安模拟]不等式2x 2-axy +3y 2≥0对于任意x ∈[1,2]及y ∈[1,3]恒成立,则实数a 的取值范围是( )A .(-∞,22]B .(-∞,26]C .(-∞,5] D.⎝ ⎛⎦⎥⎤-∞,92 答案:B 解析:∵2x 2-axy +3y 2≥0,∴2x 2-axy +3y 2x 2≥0,即3⎝ ⎛⎭⎪⎫y x 2-a ⎝ ⎛⎭⎪⎫y x +2≥0, ∵x ∈[1,2],y ∈[1,3],∴12≤y x ≤3.设t =y x ,t ∈⎣⎢⎡⎦⎥⎤12,3,g (t )=3t 2-at +2, 则g (t )≥0在区间⎣⎢⎡⎦⎥⎤12,3恒成立, ∴g (t )min ≥0.函数g (t )的对称轴为t =a 6,当a 6≤12,即a ≤3时,g (t )在⎣⎢⎡⎦⎥⎤12,3上单调递增, ∴g (t )min =g ⎝ ⎛⎭⎪⎫12=34-a 2+2≥0, 解得a ≤112,∴a ≤3;当a 6≥3,即a ≥18时,g (t )在⎣⎢⎡⎦⎥⎤12,3上单调递减, ∴g (t )min =g (3)=27-3a +2≥0,解得a ≤293,∴a 不存在;当12<a 6<3,即3<a <18时,g (t )在⎣⎢⎡⎦⎥⎤12,3上先减后增, ∴g (t )min =g ⎝ ⎛⎭⎪⎫a 6=24-a 212≥0,解得-26≤a ≤26,∴3<a ≤2 6.综上所述,a ≤2 6.故选B.6.[2019湖北荆州模拟]二次函数f (x )满足f (x +2)=f (-x +2),又f (0)=3,f (2)=1,若在[0,m ]上有最大值3,最小值1,则m 的取值范围是 ( )A .(0,+∞)B .[2,+∞)C .(0,2]D .[2,4] 答案:D 解析:∵二次函数f (x )满足f (2+x )=f (2-x ), ∴其图象的对称轴是x =2,又f (0)=3,∴f (4)=3,又f (2)<f (0),∴f (x )的图象开口向上,∵f (0)=3,f (2)=1,f (4)=3,f (x )在[0,m ]上的最大值为3,最小值为1,∴由二次函数的性质知2≤m ≤4.故选D.7.[2019河南南阳模拟]设函数f (x )=mx 2-mx -1,若对于x ∈[1,3],f (x )<-m +4恒成立,则实数m 的取值范围为( )A .(-∞,0]B.⎣⎢⎡⎭⎪⎫0,57 C .(-∞,0)∪⎝ ⎛⎭⎪⎫0,57 D.⎝ ⎛⎭⎪⎫-∞,57 答案:D 解析:由题意,f (x )<-m +4对于x ∈[1,3]恒成立,即m (x 2-x +1)<5对于x ∈[1,3]恒成立.∵当x ∈[1,3]时,x 2-x +1∈[1,7],∴不等式f (x )<-m +4等价于m <5x 2-x +1. ∵当x =3时,5x 2-x +1取最小值57, ∴若要不等式m <5x 2-x +1对于x ∈[1,3]恒成立, 则必须满足m <57,因此,实数m 的取值范围为⎝ ⎛⎭⎪⎫-∞,57,故选D.8.[2019河北保定一模]已知函数f (x )既是二次函数又是幂函数,函数g (x )是R 上的奇函数,函数h (x )=g (x )f (x )+1+1,则h (2 018)+h (2 017)+h (2 016)+…+h (1)+h (0)+h (-1)+…+h (-2 016)+h (-2 017)+h (-2 018)=( )A .0B .2 018C .4 036D .4 037答案:D 解析:函数f (x )既是二次函数又是幂函数, ∴f (x )=x 2,∴f (x )+1为R 上的偶函数,又函数g (x )是R 上的奇函数,h (x )=g (x )f (x )+1+1, ∴h (x )+h (-x )=⎣⎢⎢⎡⎦⎥⎥⎤g (x )f (x )+1+1+⎣⎢⎢⎡⎦⎥⎥⎤g (-x )f (-x )+1+1=⎣⎢⎢⎡⎦⎥⎥⎤g (x )f (x )+1+-g (x )f (x )+1+2=2, ∴h (2 018)+h (2 017)+h (2 016)+…+h (1)+h (0)+h (-1)+…+h (-2 016)+h (-2 017)+h (-2 018)=[h (2 018)+h (-2 018)]+[h (2 017)+h (-2 017)]+…+[h (1)+h (-1)]+h (0)=2+2+…+2+1=2×2 018+1=4 037.故选D.9.[2019湖南祁阳二模]已知幂函数f (x )=(m -1)2xm 2-4m +2在(0,+∞)上单调递增,函数g (x )=2x -k .(1)求m 的值;(2)当x ∈[1,2)时,记f (x ),g (x )的值域分别为集合A ,B ,设p :x ∈A ,q :x ∈B ,若p 是q 成立的必要条件,求实数k 的取值范围.解:(1)依题意,得(m -1)2=1⇒m =0或m =2,当m =2时,f (x )=x -2在(0,+∞)上单调递减,与题设矛盾,舍去,所以m =0.(2)由(1),得f (x )=x 2,当x ∈[1,2)时,f (x )∈[1,4),即A =[1,4), 当x ∈[1,2)时,g (x )∈[2-k,4-k ),即B =[2-k,4-k ),因为p 是q 成立的必要条件,则B ⊆A ,则⎩⎪⎨⎪⎧ 2-k ≥1,4-k ≤4,即⎩⎪⎨⎪⎧ k ≤1,k ≥0,得0≤k ≤1.10.设函数f (x )=x 2+ax +b (a ,b ∈R ).(1)当b =a 24+1时,求函数f (x )在[-1,1]上的最小值g (a )的表达式;(2)已知函数f (x )在[-1,1]上存在零点,0≤b -2a ≤1,求b 的取值范围.解:(1)当b =a 24+1时,f (x )=⎝ ⎛⎭⎪⎫x +a 22+1,故对称轴为直线x =-a 2.当a <-2时,g (a )=f (1)=a 24+a +2.当-2≤a ≤2时,g (a )=f ⎝ ⎛⎭⎪⎫-a 2=1. 当a >2时,g (a )=f (-1)=a 24-a +2.综上,g (a )=⎩⎪⎨⎪⎧ a 24+a +2,a <-2,1,-2≤a ≤2,a 24-a +2,a >2.(2)设s ,t 为方程f (x )=0的解,且-1≤t ≤1,则⎩⎪⎨⎪⎧ s +t =-a ,st =b ,由于0≤b -2a ≤1,因此-2t t +2≤s ≤1-2t t +2(-1≤t ≤1). 当0≤t ≤1时,-2t 2t +2≤st ≤t -2t 2t +2. 由于-23≤-2t 2t +2≤0和-13≤t -2t 2t +2≤9-45, 所以-23≤b ≤9-4 5.当-1≤t<0时,t-2t2t+2≤st≤-2t2t+2,由于-2≤-2t2t+2<0和-3≤t-2t2t+2<0,所以-3≤b<0.故b的取值范围是[-3,9-45].。
高考一轮复习第1章集合与常用逻辑用语第2讲命题及其关系充分条件与必要条件
第二讲命题及其关系、充分条件与必要条件知识梳理·双基自测知识点一命题及四种命题之间的关系1.命题用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.2.四种命题及其关系(1)四种命题间的相互关系(2)四种命题的真假关系①若两个命题互为逆否命题,则它们有相同的真假性;②两个命题为互逆命题或互否命题,它们的真假性没有关系.知识点二充分条件与必要条件若p⇒q,则p是q的充分条件,q是p的必要条件p是q的充分不必要条件p⇒q且qpp是q的必要不充分条件pq且q⇒pp是q的充要条件p⇔qp是q的既不充分又不必要条件pq且qp重要结论1.若A={x|p(x)},B={x|q(x)},则(1)若A⊆B,则p是q的充分条件;(2)若A⊇B,则p是q的必要条件;(3)若A=B,则p是q的充要条件;(4)若A B,则p是q的充分不必要条件;(5)若A B,则p是q的必要不充分条件;(6)若A B且AB,则p是q的既不充分也不必要条件.2.充分条件与必要条件的两个特征:(1)对称性:若p是q的充分条件,则q是p的必要条件,即“p⇒q”⇔“q⇐p”.(2)传递性:若p 是q 的充分(必要)条件,q 是r 的充分(必要)条件,则p 是r 的充分(必要)条件,即“p ⇒q 且q ⇒r ”⇒“p ⇒r ”(“p ⇐q 且q ⇐r ”⇒“p ⇐r ”).注意:不能将“若p ,则q”与“p ⇒q ”混为一谈,只有“若p ,则q”为真命题时,才有“p ⇒q ”,即“p ⇒q ”⇔“若p ,则q”为真命题.双基自测题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)语句x 2-3x +2=0是命题.( × )(2)命题“三角形的内角和是180°”的否命题是“三角形的内角和不是180°”.( × ) (3)已知集合A ,B ,则A∪B=A∩B 的充要条件是A =B .( √ ) (4)“α=β”是“tan α=tan β”的充分不必要条件.( × ) (5)“若p 不成立,则q 不成立”等价于“若q 成立,则p 成立”.( √ )[解析] (4)当α=β=π2时,tan α、tan β都无意义.因此不能推出tan α=tan β,当tan α=tan β时,α=β+k π,k∈Z,不一定α=β,因此是既不充分也不必要条件.题组二 走进教材2.(选修2-1P 8T3改编)下列命题是真命题的是( A ) A .矩形的对角线相等 B .若a>b ,c>d ,则ac>bd C .若整数a 是素数,则a 是奇数 D .命题“若x 2>0,则x>1”的逆否命题3.(选修2-1P 10T4改编)x 2-3x +2≠0是x≠1的充分不必要条件. [解析] x =1是x 2-3x +2=0的充分不必要条件. 题组三 走向高考4.(2020·天津,2,5分)设a∈R,则“a>1”是“a 2>a ”的( A ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件[解析] 易知a>1⇒a 2>a ,而a 2>a ⇒a<0或a>1,所以“a>1”是“a 2>a ”的充分不必要条件. 5.(2015·山东,5分)设m∈R,命题“若m>0,则方程x 2+x -m =0有实根”的逆否命题是( D ) A .若方程x 2+x -m =0有实根,则m>0 B .若方程x 2+x -m =0有实根,则m≤0 C .若方程x 2+x -m =0没有实根,则m>0 D .若方程x 2+x -m =0没有实根,则m≤0 [解析] 由原命题和逆否命题的关系可知D 正确.6.(2018·北京,5分)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是f(x)=sin_x(答案不唯一).[解析]这是一道开放性试题,答案不唯一,只要满足f(x)>f(0)对任意的x∈(0,2]都成立,且函数f(x)在[0,2]上不是增函数即可.如f(x)=sin x,答案不唯一.考点突破·互动探究KAO DIAN TU PO HU DONG TAN JIU考点一命题及其关系——自主练透例1 (1)(2021·新高考八省联考)关于x的方程x2+ax+b=0,有下列四个命题:甲:x=1是该方程的根;乙:x=3是该方程的根;丙:该方程两根之和为2;丁:该方程两根异号.如果只有一个假命题,则该命题是( A )A.甲B.乙C.丙D.丁(2)(2021·长春模拟)已知命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,则命题α是命题β的( A )A.否命题B.逆命题C.逆否命题D.否定形式(3)(多选题)下列命题为真命题的是( CD )A.“若a2<b2,则a<b”的否命题B.“全等三角形面积相等”的逆命题C.“若a>1,则ax2-2ax+a+3>0的解集为R”的逆否命题D.“若3x(x≠0)为有理数,则x为无理数”的逆否命题(4)命题“若a+b=0,则a,b中最多有一个大于零”的否定形式为若a+b=0,则a,b都大于零,否命题为若a+b≠0,则a,b都大于零.[解析](1)若乙、丙、丁正确,显然x1=-1,x2=3,两根异号,x1+x2=2,故甲错,因此选A.(2)命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,则命题α是命题β的否命题.(3)对于A ,否命题为“若a 2≥b 2,则a≥b”,为假命题;对于B ,逆命题为“面积相等的三角形是全等三角形”,是假命题;对于C ,当a>1时,Δ=-12a<0,原命题正确,从而其逆否命题正确,故C 正确;对于D ,原命题正确,因此该命题的逆否命题也正确,D 正确.故选C 、D .(4)否定形式:若a +b =0,则a ,b 都大于零.否命题:若a +b ≠0,则a ,b 都大于零. 名师点拨 MING SHI DIAN BO(1)由原命题写出其他三种命题,关键要分清原命题的条件和结论,如果命题不是“若p ,则q”的形式,应先改写成“若p ,则q”的形式;如果命题有大前提,写其他三种命题时需保留大前提不变.(2)判断一个命题为真命题,要给出严格的推理证明;判断一个命题为假命题,只需举出反例. (3)根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.考点二 充分必要条件考向1 充分条件与必要条件的判断——师生共研 方法1:定义法判断例2 ( 2020·北京,9,4分)已知α,β∈R,则“存在k∈Z 使得α=k π+(-1)kβ”是“sinα=sin β”的( C )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件[解析] (1)充分性:已知存在k∈Z 使得α=k π+(-1)kβ,(ⅰ)若k 为奇数,则k =2n +1,n∈Z,此时α=(2n +1)π-β,n∈Z,sin α=sin(2n π+π-β)=sin(π-β)=sin β;(ⅱ)若k 为偶数,则k =2n ,n∈Z,此时α=2n π+β,n∈Z,sin α=sin(2n π+β)=sin β. 由(ⅰ)(ⅱ)知,充分性成立.(2)必要性:若sin α=sin β成立,则角α与β的终边重合或角α与β的终边关于y 轴对称,即α=β+2m π或α+β=2m π+π,m∈Z,即存在k∈Z 使得α=k π+(-1)kβ,必要性也成立,故选C . 方法2:集合法判断例3 (2020·天津一中高三月考)设x∈R,则“|x-1|<4”是“x -52-x >0”的( B )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件[解析] 解绝对值不等式可得-4<x -1<4,即-3<x<5, 将分式不等式变形可得x -5x -2<0,解得2<x<5,因为(2,5)(-3,5),所以“|x-1|<4”是“x -52-x >0”的必要而不充分条件.方法3 等价转化法判断例4 (1)给定两个条件p ,q ,若¬ p 是q 的必要不充分条件,则p 是¬q 的( A ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件(2)“已知命题p :cos α≠12,命题q :α≠π3”,则命题p 是命题q 的( A )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件[解析] (1)因为¬ p 是q 的必要不充分条件,则q ⇒¬ p ,但¬pq ,其逆否命题为p ⇒¬q ,但¬qp ,所以p 是¬q 的充分不必要条件.(2) ¬p :cos α=12,¬q :α=π3,显然¬q ⇒¬p ,¬p ¬q ,∴¬q 是¬p 的充分不必要条件,从而p 是q 的充分不必要条件,故选A .另解:若cos α≠12,则α≠2kπ±π3(k∈Z),则α也必然不等于π3,故p ⇒q ;若α≠π3,但α=-π3时,依然有cos α=12,故q p.所以p 是q 的充分不必要条件.故选A . 名师点拨 MING SHI DIAN BO有关充要条件的判断常用的方法(1)根据定义判断:①弄清条件p 和结论q 分别是什么;②尝试p ⇒q ,q ⇒p.若p ⇒q ,则p 是q 的充分条件;若q ⇒p ,则p 是q 的必要条件;若p ⇒q ,qp ,则p 是q 的充分不必要条件;若pq ,q ⇒p ,则p 是q 的必要不充分条件;若p ⇒q ,q ⇒p ,则p 是q 的充要条件.(2)利用集合判断 记法 A ={x|p(x)},B ={x|q(x)} 关系 ABBAA =BAB 且BA结论p 是q 的充分不必要条件p 是q 的必要不充分条件p 是q 的充要条件p 是q 的既不充分也不必要条件断¬q 是¬p 的什么条件.〔变式训练1〕(1)指出下列各组中,p 是q 的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答).①非空集合A ,B 中,p :x∈(A∪B),q :x∈B;②已知x ,y∈R,p :(x -1)2+(y -2)2=0,q :(x -1)(y -2)=0; ③在△ABC 中,p :A =B ,q :sin A =sin B ; ④对于实数x ,y ,p :x +y≠8,q :x≠2或y≠6.(2)(2020·天津部分区期末)设x∈R,则“x 2-2x<0”是“|x-1|<2”的( A ) A .充分不必要条件 B .充要条件C .必要不充分条件D .既不充分也不必要条件[解析] (1)①显然x∈(A∪B)不一定有x∈B,但x∈B 一定有x∈(A∪B),所以p 是q 的必要不充分条件.②条件p :x =1且y =2,条件q :x =1或y =2,所以p ⇒q 但qp ,故p 是q 的充分不必要条件. ③在△ABC 中,A =B ⇒sin A =sin B ;反之,若sin A =sin B ,因为A 与B 不可能互补(三角形三个内角之和为180°),所以只有A =B ,故p 是q 的充要条件.④易知¬p :x +y =8,¬q :x =2且y =6,显然¬q ⇒¬p ,但¬p ¬q ,所以¬q 是¬p 的充分不必要条件,根据原命题和逆否命题的等价性知,p 是q 的充分不必要条件.(2)解不等式x 2-2x<0得0<x<2,解不等式|x -1|<2得-1<x<3,所以“x 2-2x<0”是“|x-1|<2”的充分不必要条件.故选A .考向2 充要条件的应用——多维探究 角度1 充要条件的探究例 5 (多选题)下列函数中,满足“x 1+x 2=0”是“f(x 1)+f(x 2)=0”的充要条件的是( BC )A .f(x)=tan xB .f(x)=3x -3-xC .f(x)=x 3D .f(x)=log 3|x|[解析] 因为f(x)=tan x 是奇函数,所以x 1+x 2=0⇒f(x 1)+f(x 2)=0,但f ⎝ ⎛⎭⎪⎫π4+f ⎝ ⎛⎭⎪⎫3π4=0时,π4+3π4≠0,不符合要求,所以A 不符合题意;因为f(x)=3x -3-x 和f(x)=x 3均为单调递增的奇函数,所以满足“x 1+x 2=0”是“f(x 1)+f(x 2)=0”的充要条件,符合题意;对于选项D ,由f(x)=log 3|x|的图象易知不符合题意,故选BC .注:满足条件的函数是奇函数且单调. 角度2 利用充要条件求参数的值或取值范围例6 已知P ={x|x 2-8x -20≤0},非空集合S ={x|1-m ≤x ≤1+m}.若x ∈P 是x∈S 的必要条件,则m 的取值范围是[0,3].[解析] 由x 2-8x -20≤0,得-2≤x≤10, 所以P ={x|-2≤x≤10},由x∈P 是x∈S 的必要条件,知S ⊆P.则⎩⎪⎨⎪⎧1-m≤1+m ,1-m≥-2,1+m≤10,所以0≤m≤3. 所以当0≤m≤3时,x∈P 是x∈S 的必要条件,即所求m 的取值范围是[0,3].[引申1]若本例将条件“若x∈P 是x∈S 的必要条件”改为“若x∈P 是x∈S 的必要不充分条件”,则m 的取值范围是[0,3].[解析] 解法一:由(1)若x∈P 是x∈S 的必要条件,则0≤m ≤3,当m =0时,S ={1},不充分;当m =3时,S ={x|-2≤x≤4}也不充分,故m 的取值范围为[0,3].解法二:若x∈P 是x∈S 的必要且充分条件,则P =S ,即⎩⎪⎨⎪⎧1-m =-2,1+m =10⇒m 无解,∴m 的取值范围是[0,3].[引申2]若本例将条件“若x∈P 是x∈S 的必要条件”变为“若非P 是非S 的必要不充分条件”,其他条件不变,则m 的取值范围是[9,+∞).[解析] 由(1)知P ={x|-2≤x≤10), ∵非P 是非S 的必要不充分条件, ∴S 是P 的必要不充分条件,∴P ⇒S 且SP. ∴[-2,10] [1-m ,1+m].∴⎩⎪⎨⎪⎧1-m≤-2,1+m>10或⎩⎪⎨⎪⎧1-m<-2,1+m≥10. ∴m ≥9,即m 的取值范围是[9,+∞). 名师点拨 MING SHI DIAN BO充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.(2)一定要注意端点值的取舍,处理不当容易出现漏解或增解的现象.(3)注意区别以下两种不同说法:①p 是q 的充分不必要条件,是指p ⇒q 但qp ;②p 的充分不必要条件是q ,是指q ⇒p 但pq.(4)注意下列条件的等价转化:①p 是q 的什么条件等价于¬q 是¬p 的什么条件,②p 是¬q 的什么条件等价于q 是¬ p 的什么条件.〔变式训练2〕(1)(角度1)(多选题)(2020·江西赣州十四县市高三上期中改编)角A ,B 是△ABC 的两个内角.下列四个条件下,“A>B”的充要条件是( ABD )A .sin A>sinB B .cos A<cos BC .tan A>tan BD .cos 2A<cos 2B(2)(角度2)(2021·山东省实验中学高三诊断)已知p :x≥k,q :(x +1)(2-x)<0.如果p 是q 的充分不必要条件,那么实数k 的取值范围是( B )A .[2,+∞)B .(2,+∞)C .[1,+∞)D .(-∞,-1][解析] (1)当A>B 时,根据“大边对大角”可知,a>b ,由于a sin A =bsin B ,所以sin A>sin B ,则A 是“A>B”的充要条件;由于0<B<A<π,余弦函数y =cos x 在区间(0,π)内单调递减,所以cos A<cosB ,则B 是“A>B”的充要条件;当A>B 时,若A 为钝角,B 为锐角,则tan A<0<tan B ,则C 不是“A>B”的充要条件;当cos 2A<cos 2B ,即1-sin 2A<1-sin 2B ,所以sin 2A>sin 2B ,所以D 是“A>B”的充要条件;故选A 、B 、D .(2)由q :(x +1)(2-x)<0,可知q :x<-1或x>2.因为p 是q 的充分不必要条件,所以x≥k ⇒x<-1或x>2,即[k ,+∞)是(-∞,-1)∪(2,+∞)的真子集,故k>2.故选B .名师讲坛·素养提升MING SHI JIANG TAN SU YANG TI SHENG抽象命题间充要条件的判定例7 已知p 是r 的充分不必要条件,q 是r 的充分条件,s 是r 的必要条件,q 是s 的必要条件,现有下列命题:①r 是q 的充要条件;②p 是q 的充分不必要条件;③r 是q 的必要不充分条件;④¬p 是¬s 的必要不充分条件;⑤r 是s 的充分不必要条件,则正确命题的序号是( B )A .①④⑤B .①②④C .②③⑤D .②④⑤[分析] 本题涉及命题较多,关系复杂,因此采用“图解法”.[解析] 由题意得p,显然q ⇒r 且r ⇒s ⇒q ,即q ⇔r ,①正确;p ⇒r ⇒s ⇒q 且qp ,②正确;r⇔q ,③错误;由p ⇒s 知¬ s ⇒¬ p ,但sp ,∴¬ p ¬ s ,④正确;r ⇔s ,⑤错误.故选B .名师点拨 MING SHI DIAN BO命题较多、关系复杂时,画出各命题间关系图求解,简洁直观,一目了然. 〔变式训练3〕若p 是r 的必要不充分条件,q 是r 的充分条件,则p 是q 的必要不充分条件. [解析] 由题意可知q ⇒rp ,∴p 是q 的必要不充分条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
34 福建中学数学 2012年第4期
标与方程系数之间的关系.所以无需解方程,直接 利用根与系数的关系就可以求出.j}的值,即 上’. ,' ’,, 1 半= =2,解得k=一1或k= 1,经检验知 三 K k=一1满足题目要求,解答完毕,学生们脸上露出了 满意的笑容.是呀,“忍一时风平浪静,退一步海阔 天空”,没想到妇孺皆知的道理也可以用到数学学习 中.所以说,有时候教师的几句话却能带给学生不 一样的情感和人格教育,让我想起了赞科夫的一句 话,“教学法一旦触及学生的情绪和意志领域、触及 精神需求,这种教学法就会发挥高度有效地作用”, 所以教师要重视在教学过程中开发学生的积极情感 因素. 案例2在学习了“系统抽样”后,笔者设计这 样的作业:估计一下我们年段经常做家务、偶尔做 家务、从不做家务,家长要求才做家务的同学分布 情况.做完这个作业,学生就会认识到应该尊重和 孝敬父母,主动承担家务的责任.在学习了 用样
本估计总体 后,笔者设计这样的家庭作业:“如果
在刷牙时不关水龙头会浪费5杯水,那么一个班级
一
天会浪费多少水,进而估算整个学校浪费多少水”,
在估算中不仅培养了数感,而且用数字教育了同学
要节约用水的意识.这些都是数学老师对德育举手
之劳的贡献,无需更多语言,只需将其无声无息、
隐而不露地渗透在教学中,便可收到不错的效果.
总之,在数学教学中,教师应该结合生活实际,
抓住典型事例,教给学生思考方法,结合学生思想
实际和知识的接受能力,点点滴滴,有机渗透,潜
移默化,让学生真正体会到数学学习的趣味性和实
用性,只要教师做到“渗透有心,渗透得法”,就可以
达到德育、智育的双重教育目的,达到“随风潜入夜,
润物细无声”的境界.
“3x∈R,ax 一2ax+3 o’’是命题吗?
袁守义 江苏省常州市第一中学(213003)
前不久,笔者所在的年级备课组统一布置的作
业上有这样一道填空题:若命题“3x R, ax 一2ax+3 0”是假命题,则实数a的取值范围 是——. 大多数学生和教师都认同以下的解法(不妨叫方 法1)和结果. 解问题“若命题‘3x∈R,ax 一2ax+3 0’是假 命题,求实数a的取值范围”,等价于“已知不等式 ax 一2ax+3>0对任意X∈R恒成立,求实数a的取 值范围”. 于是有 =0或{ 2 ) 一12口<0, 从而得到结果为:0≤a<3. 但是每个班级中也有一部分学生给出的结果为 a∈R,问其理由,几乎得到同样的解释(方法2): 取X=2,此时得到3 0,而“3≤0”显然是一假命题, 也就是说,不管a取什么实数,总存在实数x=2, 使命题ax 一2ax+3 0为假命题,所以a∈R. 碰到这样的问题,有些教师感到无法解释,最 后认为此题本身有问题,理由是不等式“ax 一2ax+3 0”中有两个变量,从而不能判断“3x∈R,ax 一2ax +3 0”的真假,所以“3x∈R,ax 一2ax+3 0”不是
命题,既然不是命题,又何来“假命题”之说,所以题
目有问题.题目有问题,结果多样化也就不足为奇
了.
这样的解释显然不能让大多数学生满意.我们
知道,能够判断真假的语句叫命题.在数学中,含
有变量的语句一般不是命题,如“X>3”、“X 一2x一
3<0”、“X+2y=0”等都不是命题,因为无法判断它
们的真假,这些语句习惯上被称为开语句.虽然开
语句不是命题,但在开语句前面加上约束变量的量
词,那么就成为一个命题了,如“3x∈R,X 一2x一3
<0”是真命题,而“Vx∈R, 一2x一3≥0”是假命题.
在本题中,由于不等式“ax 一2ax+3≤0”中有两
个变量,从而只约束一个变量依然不能判断“3x∈R,
ax 一2ax+3 0”的真假,所以若问“3x∈R,
ax 一2ax+3≤0”是否为命题时,答案应是唯一的一
它不是命题.
但笔者认为,在本题中, 和a两个量不都是变
量,其中a是常数.我们可以这样理解,比如当a=1
2012年第4期 福建中学数学 35
时,“3x∈R,ax 一2ax+3 0”就成为“3x∈R, 一
2 +3 0”,它显然是一个命题,而且是一个假命题; 再比如当口=3时,“3x∈R, 一2ax+3 0”就成为 “3x∈R, 3x 一6x+3 0”,即“3x∈R,X 一2x+1 0”,它显然也是一个命题,而且是真命题.所以 本题的本意就是要求常数a的取值范围,使“3x∈R, ax 一2ax+3≤0”成为命题,而且是假命题,或者说, 当“3x∈R,似 一2ax+3 0”是命题而且是假命题 时,求实数a的取值范围.而“3x∈R,ax 一2ax+3 ≤0”为假命题与它的否定“Vx∈R,似 一2ax+3>0” 是真命题等价,所以方法l的解法和结果是正确的. 那么,方法2又错在哪里呢?首先我们可以用上 面的例子来说明方法2的结果是错的,若结果是 a∈R,则说明当 取任何实数时,“3x∈R,ax 一2ax +3≤0”恒为假命题.但当日=3时,“3x∈R,似 一 2ax+3 0”却为真命题.事实上,方法2中取X=2时 得到3 0,虽然“3 0”是一个假命题,但这只能说 明不论a为何实数,“3x∈R,ax 一2ax+3>0”恒为 真命题,而不能说明“3x∈R,ax 一2ax+3 0”恒为 假命题,因为这两个命题之间不是互为否定的关系. 说到这里,笔者又联想到“利用真值表求参变量
范围”的一类题,比如以下两例:
例1已知命题P:方程X +mx+1:0有两个不等
的负实根,命题q:方程4 +4(m一2)x+1=0无实根.
若p或q为真,P且口为假,求实数m的取值范
围.
例2已知P:X 一2x一3>0,q:X 一4<0.若P或
g为真,P且g为假,求实数X的取值范围.
两个例题的形式也值得关注,由于不知m的取
值情况而无法判断“方程x +mx+1=0有两个不等的
负实根”的真假,所以它显然不是命题,而“X。一2x一3
>0”是典型的开语句,所以它也不是命题.但我们
同样可以将例1中的m和例2中的X视着常数,这样
随着常数m和X给定的值的变化,“方程X + +1=0
有两个不等的负实根”和“X 一2x一3>0”就可以判断
真假,因而它们就是命题了.
长方体与四面体包含关系的妙用
李志红 徐彩刚
江西省樟树中学(33 1200)
长方体是立体几何中的基本几何体,其结构对
称,各元素之间存在着相等、平行、垂直等关系,
是研究线面关系、特殊几何体的一个重要载体.某
些四面体可以看成是“寄居”在长方体内.如三组对棱
分别相等的四面体、直角四面体(即一个顶点处的
三条棱两两垂直)都可以看成是长方体的寄居体;
正四面体也可以看成是正方体的寄居体.
构造长方体解有关四面体问题,能把复杂的位
置、度量关系简化成典型的位置、度量关系,从整
体上把握局部问题,思路更清晰,手段更灵活,使
问题轻松获解.本文拟例说之.
例1(2011年高考江西卷・理21)
(1)如图,对于任意给定的
四面体4 ,找出依次排列的
四个相互平行的 -, z, ,54,叠
使得4∈5i(i=1,2,3,4),且其中
每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面
, , ,a4,其中每相邻两个平面间的距离为1,
若一个正四面体4 的四个顶点满足:
4∈ (i=1,2,3,4),求该正四面体4 的体积.
该题是考卷最后一题,满分l4分,平均得分0.14
分,只有很少的同学得了不高的分,多数考生无从
下手.
分析如果第--d,题将此正四面体置于一个正
方体中,问题就会更好处理:
(1)将直线4 三等分,其中另两个分点依次
为A , ,连结 , ,作平行于 ,
的平面,分别过 , ,即为 , .同理,
过点4, 作平面 , 即可的出结论.
(2)现将此正四面体4 置于一个正方体
ABCD—AIBIQDl中,巨, 分别是AlB1,cl 的中
点, DID和阳 F是两个平行平面,若其距离为
