离散数学命题练习题
《离散数学》试题及答案

《离散数学》试题及答案一、选择题(每题5分,共25分)1. 设集合A={1,2,3,4,5},B={2,4,6,8,10},则A∩B的结果是()A. {1,2,3,4,5}B. {2,4}C. {1,3,5}D. {1,2,3,4,5,6,8,10}答案:B2. 下列关系中,哪个是等价关系?()A. ≤B. ≠C. |D. ≠答案:A3. 设图G有5个顶点,每两个顶点之间都有一条边相连,则图G的边数是()A. 5B. 10C. 15D. 20答案:C4. 下列哪一个图是欧拉图?()A. 无向图B. 有向图C. 树D. 环答案:D5. 下列哪一个命题是正确的?()A. 若p→q为真,则p为真B. 若p∧q为假,则p为假C. 若p∨q为真,则q为真D. 若p→q为假,则p为假答案:B二、填空题(每题5分,共25分)1. 设集合A={a,b,c,d},B={c,d,e},则A-B=________。
答案:{a,b}2. 设p是命题“今天是晴天”,q是命题“我去公园玩”,则命题“如果今天不是晴天,那么我不去公园玩”可以表示为________。
答案:¬p→¬q3. 设图G有n个顶点,e条边,则图G的度数之和为________。
答案:2e4. 一个连通图至少有________个顶点。
答案:25. 设图G的邻接矩阵为A,则A的转置矩阵表示________。
答案:图G的转置图三、判断题(每题5分,共25分)1. 离散数学是研究离散结构的数学分支。
()答案:正确2. 两个集合的笛卡尔积是这两个集合的直积。
()答案:正确3. 有向图中,顶点u和顶点v之间的长度为2的路径是指路径上有3条边。
()答案:错误4. 树是一种无向图。
()答案:正确5. 哈夫曼编码是一种贪心算法。
()答案:正确四、应用题(每题25分,共50分)1. 设集合A={1,2,3,4,5},B={2,4,6,8,10},C={3,6,9,12,15},求A∪(B∩C)。
离散数学练习题2 答案
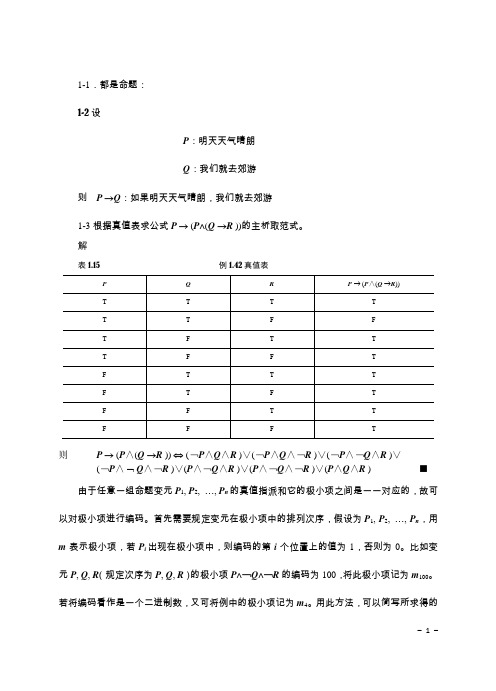
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
命题逻辑练习题

《离散数学》命题逻辑部分练习题一、选择题1.下列句子中,( )是命题。
A .2是常数。
B .这朵花多好看呀!C .请把门关上!D .下午有会吗?2.令p : 今天下雪了,q :路滑,r :他迟到了。
则命题“下雪路滑,他迟到了” 可符号化为( )。
A. p q r ∧→ B. p q r ∨→ C. p q r ∧∧ D. p q r ∨↔3.令:p 今天下雪了,:q 路滑,则命题“虽然今天下雪了,但是路不滑”可符号化为( )。
A. p q ∧⌝ B. p q ∧ C. p q ∨⌝D. p q →⌝4.设()P x :x 是鸟,()Q x :x 会飞,命题“有的鸟不会飞”可符号化为( )。
A. ()(()())x P x Q x ⌝∀→B. ()(()x P x ⌝∀∧())Q xC. ()(()())x P x Q x ⌝∃→D. ()(()x P x ⌝∃∧())Q x 5.设()F x :x 是人,()G x :x 犯错误,命题“没有不犯错误的人”符号化为( )。
A .(()())x F x G x ∀∧B . (()())x F x G x ⌝∃→⌝C .(()())x F x G x ⌝∃∧D . (()())x F x G x ⌝∃∧⌝ 6.下列命题公式不是永真式的是( )。
A. ()p q p →→B. ()p q p →→C. ()p q p ⌝∨→D. ()p q p →∨ 7.下列式子为矛盾式的是( )。
A .()p p q ∨∧B .p p ∨⌝C .p p ∧⌝D . ()p q p q ⌝∨⇔⌝∧⌝ 8.命题:“所有马都比某些牛跑得快” 的符号化公式为( )。
假设:H(x ):x 是马;C(x ):x 是牛;F(x,y ):x 跑得比y 快。
A. ()(()()(()(,)))x H x y C y F x y ∀∧∃∧B. ()(()()(()(,)))x H x y C y F x y ∀→∃→C. ()(()()(()(,)))x H x y C y F x y ∀→∃∧D. ()()(()(()(,)))y x H x C y F x y ∃∀→→二、计算题(仅给出部分题目的解题思路,未给出答案自己完成)1. 已知命题公式()()p q p r ⌝→→∧ (1)构造真值表(2)求出公式的主析取范式(2)()()p q p r ⌝→→∧0157()()()()p q r p q r p q r p q r m m m m ⇔⌝∧⌝∧⌝∨∧∧⌝∨∧⌝∧∨∧∧⇔∨∨∨2.已知命题公式()()p q p r ∨→⌝∨ (1)构造真值表;(2)用等值演算法求公式的主析取范式。
离散数学练习题库

离散数学练习题库1. 集合论- 1.1 列出集合{1, 2, 3}的所有子集。
- 1.2 计算集合A={1, 2, 3}和集合B={2, 3, 4}的并集、交集和差集。
- 1.3 证明集合{a, b, c}的幂集包含2^3个元素。
2. 逻辑- 2.1 将命题p:“今天是周一”和q:“明天是周二”转化为逻辑表达式,并判断它们的逻辑关系。
- 2.2 写出命题“如果今天是周一,那么明天是周二”的逆命题、否命题和逆否命题。
- 2.3 证明德摩根定律:(A∪B)' = A'∩B' 和(A∩B)' = A'∪B'。
3. 函数- 3.1 定义函数f: {1, 2, 3} → {a, b, c},使得f(1) = a,f(2) = b,f(3) = c,并画出其函数图。
- 3.2 判断函数f(x) = x^2是否为单射函数、满射函数或双射函数。
- 3.3 找出函数f(x) = x^2 + 1的值域。
4. 关系和图- 4.1 定义关系R在集合{1, 2, 3, 4}上,使得R = {(1, 2), (2, 3), (3, 4)},并判断R是否为等价关系。
- 4.2 画出集合{1, 2, 3}上的完全图,并标记边。
- 4.3 证明图的邻接矩阵的转置等于其自身的转置。
5. 组合数学- 5.1 计算5个元素的集合中,选取3个元素的所有可能组合数。
- 5.2 计算从8个不同的球中选取3个球的排列数。
- 5.3 证明二项式系数的性质:C(n, k) = C(n, n-k)。
6. 代数结构- 6.1 定义一个群(G, *),其中G={1, 2, 3},*为模3加法,并找出群的单位元。
- 6.2 判断集合{1, 2, 3}在乘法下是否构成环。
- 6.3 找出所有满足a^2 = e(其中e为群的单位元)的元素a,对于群(G, *)。
7. 归纳和递归- 7.1 使用数学归纳法证明对于所有自然数n,1 + 2 + ... + n = n(n+1)/2。
离散数学的练习题

离散数学的练习题1. 集合论基础- 定义一个集合A,包含元素{1, 2, 3},并求出A的子集数量。
- 给定集合B={2, 4, 6}和集合C={4, 5, 6},计算B∩C(B与C的交集)。
- 集合D={1, 3, 5}和集合E={0, 2, 4},求D∪E(D与E的并集)。
2. 逻辑运算- 写出命题p和q的逻辑表达式,其中p为“今天是星期三”,q为“明天是星期五”。
- 计算复合命题“p且非q”的真值表。
- 给定命题r和s,其中r为“x > 0”,s为“x < 0”,求r∨s(r或s)的真值表。
3. 函数- 定义一个函数f: {1, 2, 3} → {a, b, c},满足f(1) = a,f(2) = b,f(3) = c,并画出函数的映射图。
- 给定函数g: {a, b} → {1, 2},其中g(a) = 1,g(b) = 2,判断g是否为单射(一对一函数)。
- 定义一个函数h: {x | x是偶数} → {x | x是奇数},满足h(x) = x + 1,并判断h是否为满射(到上函数)。
4. 关系和矩阵表示- 给定集合F={1, 2, 3},定义一个关系R在F上,使得R={(1, 2), (2, 3), (3, 1)},并用矩阵表示R。
- 判断关系R是否为自反的、对称的和传递的。
- 给定集合G={a, b, c},定义一个关系S在G上,使得S={(a,b), (b, c), (c, a)},并判断S是否为等价关系。
5. 图论基础- 画出一个包含5个顶点的无向图,并标记顶点为A, B, C, D, E,其中边为AB, BC, CD, DE。
- 给定一个有向图,包含顶点{1, 2, 3, 4}和边{(1, 2), (2, 3), (3, 4), (4, 1)},判断该图是否有环。
- 定义一个图H,包含顶点{p, q, r, s}和边{(p, q), (q, r), (r, s), (s, p)},并找出H的所有生成树。
应用离散数学命题逻辑逻辑门电路题库试卷习题及答案

§1.6 逻辑门电路习题1.61.用非门、与门和或门构造产生下列输出的电路。
(1)y x +(2)x y x )(+ (3)z y x xyz +(4)))((z y z x ++解: (1)(2)x(3)(4)xyx +xy x )(+zy x xyz +))((z y z x ++2.试设计一个电路来实现五个人的少数服从多数的表决系统。
解:设A、B、C、D、E分别表示五个人表决,S表示表决结果,根据少数服从多数的原则,共有如下几种情况S=1.A B C D E S0 0 1 1 1 10 1 0 1 1 10 1 1 0 1 10 1 1 1 0 11 0 0 1 1 11 0 1 0 1 11 0 1 1 0 11 1 0 0 1 11 1 0 1 0 11 1 1 0 0 10 1 1 1 1 11 0 1 1 1 11 1 0 1 1 11 1 1 0 1 11 1 1 1 0 11 1 1 1 1 1得S=(⌝A∧⌝B∧C∧D∧E)∨(⌝A∧B∧⌝C∧D∧E)∨(⌝A∧B∧C∧⌝D∧E)∨(⌝A ∧B∧C∧D∧⌝E)∨(A∧⌝B∧⌝C∧D∧E)∨(A∧⌝B∧C∧⌝D∧E)∨(A∧⌝B∧C∧D ∧⌝E)∨∨(A∧B∧⌝C∧⌝D∧E)∨(A∧B∧⌝C∧D∧⌝E)∨(A∧B∧C∧⌝D∧⌝E)∨(⌝A∧B∧C∧D∧E)∨(A∧⌝B∧C∧D∧E)∨(A∧B∧⌝C∧D∧E)∨(A∧B∧C∧⌝D ∧E)∨(A∧B∧C∧D∧⌝E)∨(A∧B∧C∧D∧E)=(A∧B∧(C∨D∨E))∨(((⌝A∧B)∨(A∧⌝B))∧(E∧((⌝C∧D)∨(C∧⌝D)))∨(((⌝A∧B)∨(A∧⌝B))∧(C∧D))=(A∧B∧(C∨D∨E))∨(((⌝A∧B)∨(A ∧⌝B))∧((E∧((⌝C∧D)∨(C∧⌝D))∨(C∧D))=(A∧B∧(C∨D∨E))∨((⌝A ∨⌝B)∧(A∨B)∧(C∨D)∧(C∨E)∧(D∨E))据此得到组合逻辑电路图如下:3.试设计一个由四个开关控制的电灯混合控制器,使得当电灯在打开时,按动任意一个开关都可关闭它,在电灯关闭时,按动任意一个开关都可打开它。
离散数学章练习题及答案
离散数学章练习题及答案离散数学练习题第⼀章⼀.填空1. 公式(p q) ( p q )的成真赋值为01 ;102. 设p, r 为真命题,q, s 为假命题,则复合命题(p q) ( r s) 的真值为03. 公式(p q)与(p q) (p q )共同的成真赋值为01;104. 设A为任意的公式,B为重⾔式,则A B 的类型为重⾔式5.设p, q 均为命题,在不能同时为真条件下,p与q的排斥也可以写成p与q的相容或。
⼆.将下列命题符合化1. 7 不是⽆理数是不对的。
解:( p) ,其中p: 7 是⽆理数;或p,其中p: 7 是⽆理数。
2. ⼩刘既不怕吃苦,⼜很爱钻研。
解:p q, 其中 p: ⼩刘怕吃苦,q:⼩刘很爱钻研3. 只有不怕困难,才能战胜困难。
解:q p ,其中p: 怕困难,q: 战胜困难或p q ,其中p: 怕困难,q: 战胜困难4. 只要别⼈有困难,⽼王就帮助别⼈,除⾮困难解决了。
解:r (p q),其中p: 别⼈有困难,q: ⽼王帮助别⼈,r: 困难解决了或:( r p) q ,其中p: 别⼈有困难,q: ⽼王帮助别⼈,r: 困难解决了5. 整数n是整数当且仅当n 能被2 整除。
解:p q,其中p: 整数n是偶数,q: 整数n能被2整除三、求复合命题的真值P:2能整除5,q :旧⾦⼭是美国的⾸都,r :在中国⼀年分四季1. ((p q) r) (r (p q))2. (( q p) (r p)) (( p q) r解:p, q 为假命题,r 为真命题1. ((p q) r) (r (p q)) 的真值为02. (( q p) (r p)) (( p q) r 的真值为1四、判断推理是否正确设y 2x 为实数,推理如下:若y在x=0可导,则y在x=0连续。
y 在x=0连续,所以y在x=0可导。
解:y 2x,x为实数,令p: y在x=0可导,q: y 在x=0连续。
P为假命题,q为真命题,推理符号化为:(p q) q p,由p,q 得真值可知,推理的真值为0,所以推理不正确。
离散数学命题逻辑习题答案
二年级叙事作文:枪战达人_350字
我们想去后院走走,没想到刚出门就看到后院玩的那些人,他们问我和朋友:“你们和我们玩会儿呗?”我思考了一会,回答:“行啊!走。
”
到达了后院,他站在大石头边宣布:“规则:四人一队,一人两把武器,开始玩吧!”刚开始,我被投票选为队长,随后我下令:“前进,进入掩体,让对方不能发现我们!”因为和我们的掩体最近的只有一棵树,所以我又命令一个人:“在右边观察‘战场’上的一举一动!”
战场上,激战已经非常激烈,可我们一动不动,没有参与。
直到共五队只剩三队时,我大喊:“冲啊!”把其他两个队一举歼灭了。
枪战结束了,我们欢呼:“终于胜利了!”第二名在一边唠叨:“你们不是也损失了两个。
”第三名嘀咕:“你们肯定了。
”
就这样,枪战在我们的欢声笑语中结束了。
离散数学6章理解练习知识题及答案解析
离散数学练习题第一章一.填空1.公式)()(q p q p ∧⌝∨⌝∧的成真赋值为 01;102.设p, r 为真命题,q, s 为假命题,则复合命题)()(s r q p →⌝↔→的真值为 03.公式)()()(q p q p q p ∧∨⌝∧↔⌝与共同的成真赋值为 01;104.设A 为任意的公式,B 为重言式,则B A ∨的类型为 重言式5.设p, q 均为命题,在 不能同时为真 条件下,p 与q 的排斥也可以写成p 与q 的相容或。
二.将下列命题符合化 1.7不是无理数是不对的。
解:)(p ⌝⌝,其中p: 7是无理数; 或p ,其中p: 7是无理数。
2.小刘既不怕吃苦,又很爱钻研。
解:其中,q p ∧⌝p: 小刘怕吃苦,q :小刘很爱钻研3.只有不怕困难,才能战胜困难。
解:p q ⌝→,其中p: 怕困难,q: 战胜困难或q p ⌝→,其中p: 怕困难, q: 战胜困难4.只要别人有困难,老王就帮助别人,除非困难解决了。
解:)(q p r →→⌝,其中p: 别人有困难,q:老王帮助别人 ,r: 困难解决了 或:q p r →∧⌝)(,其中p:别人有困难,q: 老王帮助别人,r: 困难解决了5.整数n 是整数当且仅当n 能被2整除。
解:q p ↔,其中p: 整数n 是偶数,q: 整数n 能被2整除三、求复合命题的真值P :2能整除5, q :旧金山是美国的首都, r :在中国一年分四季 1. ))(())((q p r r q p ∧→∧→∨2.r q p p r p q ∧⌝∧⌝∨∨→→⌝)(())()(( 解:p, q 为假命题,r 为真命题1.))(())((q p r r q p ∧→∧→∨的真值为02. r q p p r p q ∧⌝∧⌝∨∨→→⌝)(())()((的真值为1四、判断推理是否正确 设x y 2=为实数,推理如下:若y 在x=0可导,则y 在x=0连续。
y 在x=0连续,所以y 在x=0可导。
