面板数据讲义20091124
面板数据分析PPT课件

相同(都是1),t 却因截面(时点)不同而异。可见时点固定效应 模型中的截距项t 包括了那些随不同截面(时点)变化,但不随个 体变化的难以观测的变量的影响。t 是一个随机变量。
以家庭消费性支出与可支配收入关系为例,“全国零售物价指数” 就是这样的一个变量。对于不同时点,这是一个变化的量,但是对 于不同省份(个体),这是一个不变化的量。
变换上式: yi = + X i ' +( i - + i ), i = 1, 2, …, N
称作平均数模型。对上式应用 OLS 估计,则参数估计量称作平均数 OLS 估 计量。此条件下的样本容量为 N,(T=1)。
如果 X i 与( i - + i )相互独立,和的平均数 OLS 估计量是一致估计量。
yit = + Xit ' +it, i = 1, 2, …, N; t = 1, 2, …, T 如果模型是正确设定的,且解释变量与误差项不相关,即 Cov(Xit,it) = 0。 那么无论是 N,还是 T,模型参数的混合最小二乘估计量都具有 一致性。 对于经济序列每个个体 i 及其误差项来说通常是序列相关的。NT 个相关 观测值要比 NT 个相互独立的观测值包含的信息少。从而导致误差项的标 准差常常被低估,估计量的精度被虚假夸大。
为误差项(标量),满足通常假定条件。Xit 为 k 1 阶回归变量列
向量(包括 k 个回归变量),为 k 1 阶回归系数列向量,则称此
模型为时点固定效应模型。
第8页/共30页
2.2.2 时点固定效应模型(time fixed effects model)
设定时点固定效应模型的原因。假定有面板数据模型
面板数据讲义

面板数据模型与应用1.面板数据定义panel data的中译:面板数据、桌面数据、平行数据、纵列数据、时间序列截面数据、混合数据(pool data)、固定调查对象数据。
面板数据定义(1)面板数据定义为相同截面上的个体在不同时点的重复观测数据。
(2)称为纵向(longitudinal)变量序列(个体)的多次测量。
面板数据从横截面(cross section)看,是由若干个体(entity, unit, individual)在某一时点构成的截面观测值,从纵剖面(longitudinal section)看每个个体都是一个时间序列。
1图1 N=7,T=50的面板数据示意图2面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, Ti对应面板数据中不同个体。
N表示面板数据中含有N个个体。
t对应面板数据中不同时点。
T表示时间序列的最大长度。
若固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;若固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列(个体)。
2. 面板数据模型面板数据模型是利用面板数据构建的模型。
面板数据系一组个体在一段时间内的观测值形成的数据集,这里“个体”可以是个人、家庭、企业、行业、地区3或国家(Baltagi,2008)。
1966年,Balestra & Nerlove发表了第一篇利用面板数据模型研究天然气需求估计的论文,此后,面板数据模型这一新的计量分析方法在理论和应用上得到迅速发展,已形成现代计量经济学的一个相对独立的分支。
面板数据模型由于同时使用了截面数据(cross-sectional data)和时间序列数据(time series data),因而可以控制个体的异质性,识别、测量单纯使用这两种数据无法估计的效应;并且具有包含更多的信息、更大的变异和自由度、变量间的共线性也更弱的特性,可得到更精确的参数估计(Hsiao,2003、2008)。
面板数据分析方法 ppt课件

it i t uit
i 1,2, N t 1,2,T
面板数据:多个观测对象的时间序列数据所组 成的样本数据。
i 反映不随时间变化的个体上的差异性,
被称为个体效应
t 反映不随个体变化的时间上的差异性,
被称为时间效应。
ppt课件 33
第二节 面板数据的模型形式
11,000 10,000 9,000 8,000 7,000 6,000 5,000 4,000 3,000 IP 2,000 3,000 5,000 7,000 9,000 11,000 13,000 CP_1996 CP_1997 CP_1998 CP_1999 CP_2000 CP_2001 CP_2002
安徽 北京 福建 河北 黑龙江 吉林 江苏 江西 辽宁 内蒙古 山东 上海 山西 天津 浙江
14000 12000 10000 8000 6000 4000 2000 0 1996 1997 1998 1999 2000 2001
浙江 山西 山东 辽宁 江苏
山西
14000 12000 10000 8000 6000 4000 2000
ppt课件
16
二、面板数据的分类
2.微观面板数据与宏观面板数据 微观面板数据一般指一段时期内不同个体或者家庭 的调查数据,其数据中往往个体单位较多,即 N较大( 通常均为几百或上千)而时期数 T较短(最短为两个时 期,最长一般不超过20个时期)。
ppt课件
17
二、面板数据的分类
2.微观面板数据与宏观面板数据 宏观面板数据通常为一段时间内不同国家或地区的 数据集合,其个体单位数量N不大(一般为7-200)而时 期数T较长(一般为20-60年)。
面板数据模型ppt课件

精选课件
计量经济学,面板数据模型,3王0 少平
六、动态面板-IV估计
IV估计量求解:如果只选择 Y i ,t 2 作为 Yi,t 1 的工具变量, 正交的约束条件:
E(Yi,t2it ) 0
基于一个给定的样本,通过求解:
1
N Ti t
Y i,t 2ˆ it N 1 Ti
Y i,t 2 (Y it ˆY i,t 1 ) 0
▪ OLS估计量:
▪
有偏的,非一致的。
▪ 本质问题:
▪
个体效应(或时间效应)的内生性。
▪ 其BLUE是最小二乘虚拟变量(LSDV)法。
精选课件
计量经济学,面板数据模型,1王5 少平
四、静态面板-固定效应LSDV估计
LSDV估计方法:
基本思想:
通过虚拟变量把个体效应(和时间效应)从误差
项中分离出来,使分离后剩余的误差项与解释变量不
协方差矩阵估计量。
精选课件
计量经济学,面板数据模型,2王3 少平
五、Hausman检验
若随机效应为真时,豪斯曼检验统计量:
H~2(K)
自由度K为模型中解释变量(不包括截距项)的个数。
精选课件
计量经济学,面板数据模型,2王4 少平
六、动态面板数据模型
▪ 动态面板模型:解释变量中包含被解释变量的滞后 项。
(11)
▪ 为解决虚拟变量的完全多重共线性,可直接估计模型:
Y it1 * D 1 N * D N 1 X it u it
(12)
如果 u it 是经典误差项,可以直接对(12)进行OLS估计。并 且
ˆ0
1 N
N i1
ˆi*
ˆi
ˆi*
1 N
第一讲 面板数据
第一讲面板数据因家庭调查得到的面板数据越来越多,面板数据的计量分析可以说是过去三十年社会应用研究领域所取得的最重要的进展。
-Fitzgerald, Gottschalk和Moffitt(1998, P252)第一讲介绍的内容面板数据面板数据的优点与缺陷扩展的面板数据面板数据“面板数据”一词指的是一部分家庭、国家或企业等在一段时期内的观测值所构成的集合。
这样的数据可以通过在一段时期内对一些家庭或个体进行跟踪调查来获得。
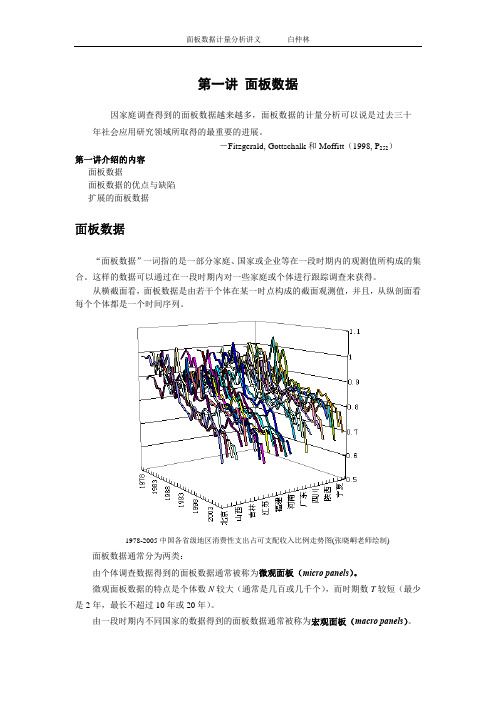
从横截面看,面板数据是由若干个体在某一时点构成的截面观测值,并且,从纵剖面看每个个体都是一个时间序列。
1978-2005中国各省级地区消费性支出占可支配收入比例走势图(张晓峒老师绘制)面板数据通常分为两类:由个体调查数据得到的面板数据通常被称为微观面板(micro panels)。
微观面板数据的特点是个体数N较大(通常是几百或几千个),而时期数T较短(最少是2年,最长不超过10年或20年)。
由一段时期内不同国家的数据得到的面板数据通常被称为宏观面板(macro panels)。
这类数据一般具有适度规模的个体N (从7到100或200不等,如七国集团,OECD ,欧盟,发达国家或发展中国家),时期数T 一般在20年到60年之间。
因数据结构上的区别,微观面板和宏观面板要求使用不同的计量方法。
样本容量的区别微观面板必须研究T 固定而N 较大时的渐近特性,而宏观面板的渐近特性则是指T 和N 都较大时的情况。
平稳性对于宏观面板,当时间序列较长时需要考虑数据的非平稳问题,如单位根、结构突变以及协整等;而微观面板不需要处理非平稳问题,特别是每个家庭或个体的时期数T 较短时。
个体相关性在处理宏观面板时必须考虑国家之间的相关性,而在微观面板中,如果个体是随机抽样产生,则个体之间不大可能存在相关性,因此不需要考虑此问题。
为什么使用面板数据?它们的优点和局限性1 面板数据的优点使用面板数据具有下列一些好处:(1)可以控制个体异质性面板数据能反映个体、企业、州或国家之间存在的异质性,即时间上和空间上的异质效应。
《面板数据分析》课件

面板数据分析的步骤
1
数据描述
对数据进行描述性统计,确定数据在时间和个体方面的特征。
2
ห้องสมุดไป่ตู้
分类讨论
分析不同情况下个体间行为的差异和影响因素,如何影响个体行为的内部因素和外部 环境。
3
建模和估计
根据分类讨论的结论,运用面板数据模型建立样本分布,通过极大似然法和广义矩估 计法进行参数估计。
4
结果解释
对估计的结果进行解释,如何分析因素对个体行为的影响和相关关系等。
生产领域
跟踪生产的进度和效果,寻找 提高生产效率的方法。
总结和展望
总结
面板数据分析是一种高通量数据分析方法,通 过对个体间微观差异的捕捉和分析,提高了分 析数据的精确性,研究结果更具有真实性和普 遍性。
展望
随着数据分析和研究技术的不断发展,面板数 据分析将进一步被广泛接受和使用,为各行各 业的发展与创新提供支持。
《面板数据分析》PPT课 件
欢迎各位来到《面板数据分析》课件。本课程将向大家介绍如何运用面板数 据分析各种数据,并运用不同的分析方法提升数据的价值。
面板数据的定义和特点
什么是面板数据?
面板数据指的是在一定时间内,对相同个体做重复观测所得到的数据。
面板数据的特点
相对于横截面数据和时间序列数据,面板数据能够更精确地反映个体间的差异和发展。
面板数据模型的建立
线性回归模型
用于研究数值型因变量和数值 型自变量之间的关系。
逻辑回归模型
用于研究分类因变量和数值型 自变量之间的关系。
混合效应模型
考虑组间差异和个体内部差异, 更为精确地分析面板数据的特 点。
面板数据分析的常用方法
1 固定效应模型
面板数据模型经典PPT
该模型假设个体和时间特定效应是固定的,不会随着解释变量的变化 而变化。
03
固定效应模型可以通过固定效应估计量来估计变量的影响,该估计量 不受个体和时间特定效应的影响。
04
固定效应模型可以通过各种方法进行估计,包括最小二乘法、广义最 小二乘法、工具变量法和随机效应法等。
随机效应模型
01 02 03 04
面板数据模型经典
• 面板数据模型概述 • 面板数据模型的类型 • 面板数据模型的估计方法 • 面板数据模型的检验与诊断 • 面板数据模型的应用案例
01
面板数据模型概述
定义与特点
定义
面板数据模型是一种统计分析方法, 用于分析时间序列和截面数据的混合 数据集。
特点
能够同时考虑时间和个体效应对因变 量的影响,提供更全面的分析视角, 有助于揭示数据背后的复杂关系。
面板数据模型的适用场景
01
面板数据模型适用于分析长时间跨度下多个个体或 经济实体的数据,如国家、地区或公司等。
02
当需要探究时间趋势和个体差异对因变量的影响时, 面板数据模型是理想的选择。
03
在经济学、社会学、生物学等领域,面板数据模型 被广泛应用于实证研究。
面板数据模型与其他模型的比较
01
与时间序列模型相 比
其他领域的应用案例
总结词
除了上述领域外,面板数据模型还广泛应用 于金融、环境科学、医学和交通等领域,为 各领域的科学研究和实践提供了重要的方法 和工具。
详细描述
在金融领域,面板数据模型被用于股票价格 、收益率和风险评估等方面;在环境科学领 域,面板数据模型被用于研究气候变化、环 境污染和生态平衡等方面;在医学领域,面 板数据模型被用于疾病诊断、治疗方法和药 物研发等方面;在交通领域,面板数据模型 被用于交通流量、交通规划和交通安全等方
第7章 面板数据模型课件
面板数据的优点
(1)可以控制个体异质性 可以克服未观测到的异质性(unobserved heterogeneity)这种遗漏变量问题。这个异质性是指在面 板数据样本期间内取值恒定的某些遗漏变量。 (2)面板数据模型容易避免多重共线性问题 • 面板数据具有更多的信息; • 面板数据具有更大的变异; • 面板数据的变量间更弱的共线性; • 面板数据模型具有更大的自由度以及更高的效率。 (3)与纯横截面数据或时间序列数据相比,面板数据模型 允许构建并检验更复杂的行为模型。
例 1 表 1 中展示的数据就是一个面板数据的例子。 表 1 华东地区各省市 GDP 历史数据 1995 1996 1997 1998 2462.57 2902.20 3360.21 3688.20 上海 江苏 浙江 安徽 福建 江西 5155.25 3524.79 2003.66 2191.27 1244.04 6004.21 4146.06 2339.25 2583.83 1517.26 6680.34 4638.24 2669.95 3000.36 1715.18 7199.95 4987.50 2805.45 3286.56 1851.98
yit yi ( X it X i ) +随机误差项
其中, y i 和 X i 代表各自变量个体的均值。 上式中,OLS 估计量主要利用的是个体变量对其均值偏离的信 息,随机误差项也仅反映对其个体均值的偏离波动,这是该估计 量被称为组内估计量的原因。
第二步,估计参数α 。由于已经得到了β 的估计值,所以α 的估 计就变得比较简单。
ˆ ) ˆ ( D D ) 1 D (Y X w
ˆ ˆ 其实就是用自变量和解释变量的个体均值和 w 按下列模型计
算出的误差项:
计量经济学-詹姆斯斯托克-第9章-面板数据的处理ppt课件
35
.
FatalityRate v. BeerTax:
36
.
问题
在上述模型中,如果超过两期,即T>2, 怎么处理呢?
37
.
面板数据模型的一般理论
在模型的设定上,分为两大类: (一)“固定效应”模型; (二)“随机效应”模型;
38
.
(一) 固定效应的回归 Fixed Effects Regression
2
.
面板数据,简而言之是时间序列和截面数据的混合。 严格地讲是对一组个体(如居民、国家、公司等)连 续观察多期得到的资料。所以很多时候我们也称其为 “追踪资料”。近年来,由于面板数据资料的获得变 得相对容易,使其应用范围也不断扩大。
3
.
当描述截面数据时,我们用下标表示个体,如Yi表示 变量Y的第i个个体。当描述面板数据时,我们需要其 他符号同时表示个体和时期。为此我们采用双下标而 不是单下标,其中第一个下标i表示个体,第二个下 标t表示观测时间。
23
.
案例二:
啤酒税与交通死亡率
啤酒税与交通死亡率会是什么关系?
24
.
U.S. traffic death data for 1982:
$1982
较高的啤酒税,会导致更多的交通死亡吗?
25
.
U.S. traffic death data for 1988
较高的啤酒税,会导致更多的交通死亡吗?
16000
15000
14000
13000
INC
12000
11000
10000
9000
8000 10000
15000
20000
25000
计量经济学面板数据模型讲义
计量经济学面板数据模型讲义1.面板数据定义。
时间序列数据或截面数据都是一维数据。
例如时间序列数据是变量按时间失掉的数据;截面数据是变量在截面空间上的数据。
面板数据〔panel data〕也称时间序列截面数据〔time series and cross section data〕或混合数据〔pool data〕。
面板数据是同时在时间和截面空间上取得的二维数据。
面板数据表示图见图1。
面板数据从横截面〔cross section〕上看,是由假定干集体〔entity, unit, individual〕在某一时辰构成的截面观测值,从纵剖面〔longitudinal section〕上看是一个时间序列。
面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, TN表示面板数据中含有N个集体。
T表示时间序列的最大长度。
假定固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;假定固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列〔集体〕。
图1 N=7,T=50的面板数据表示图例如1990-2000年30个省份的农业总产值数据。
固定在某一年份上,它是由30个农业总产总值数字组成的截面数据;固定在某一省份上,它是由11年农业总产值数据组成的一个时间序列。
面板数据由30个集体组成。
共有330个观测值。
关于面板数据y i t, i = 1, 2, …, N; t = 1, 2, …, T来说,假设从横截面上看,每个变量都有观测值,从纵剖面上看,每一期都有观测值,那么称此面板数据为平衡面板数据〔balanced panel data〕。
假定在面板数据中丧失假定干个观测值,那么称此面板数据为非平衡面板数据〔unbalanced panel data〕。
留意:EViwes 3.1、4.1、5.0既允许用平衡面板数据也允许用非平衡面板数据估量模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面板数据模型与应用1.面板数据定义panel data的中译:面板数据、桌面数据、平行数据、纵列数据、时间序列截面数据、混合数据(pool data)、固定调查对象数据。
面板数据定义(1)面板数据定义为相同截面上的个体在不同时点的重复观测数据。
(2)称为纵向(longitudinal)变量序列(个体)的多次测量。
面板数据从横截面(cross section)看,是由若干个体(entity, unit, individual)在某一时点构成的截面观测值,从纵剖面(longitudinal section)看每个个体都是一个时间序列。
1图12面板数据用双下标变量表示。
例如y i t, i = 1, 2, …, N; t = 1, 2, …, Ti对应面板数据中不同个体。
N表示面板数据中含有N个个体。
t对应面板数据中不同时点。
T表示时间序列的最大长度。
若固定t不变,y i ., ( i = 1, 2, …, N)是横截面上的N个随机变量;若固定i不变,y. t, (t = 1, 2, …, T)是纵剖面上的一个时间序列(个体)。
例1:1996-2002年中国东北、华北、华东15个省级地区的居民家庭固定价格的人均消费(CP)和人均收入(IP)数据见5panel02.wf1。
数据是7年的,每一年都有15个数据,共105组(个)观测值。
3人均消费和收入两个面板数据都是平衡(balance)面板数据,各有15个时间序列数据。
人均消费和收入的面板数据从纵剖面观察分别见图2和图3。
从横截面观察分别见图4和图5。
横截面数据散点图的表现与观测值顺序有关。
图4和图5中人均消费和收入观测值顺序是按地区名的汉语拼音字母顺序排序的。
图2 15个省级地区的人均消费序列(纵剖面)图3 15个省级地区的人均收入序列452000400060008000100001200014000246810121420004000600080001000012000140002468101214图4 7个时点人均消费横截面数据(含15个地区) 图5 7个时点人均收入横截面数据(含15个地区) (每条连线数据表示同一年度15个地区的消费值) (每条连线数据表示同一年度15个地区的收入值)用CP 表示消费,IP 表示收入。
AH, BJ, FJ, HB, HLJ, JL, JS, JX, LN, NMG , SD, SH, SX, TJ, ZJ 分别表示安徽省、北京市、福建省、河北省、黑龙江省、吉林省、江苏省、江西省、辽宁省、内蒙古自治区、山东省、上海市、山西省、天津市、浙江省。
图6 人均消费对收入的面板数据散点图(15个时间序列叠加)67200040006000800010000120002000400060008000100001200014000IP(1996-2002)C P1996C P1997C P1998C P1999C P2000C P2001C P2002图7 人均消费对收入的面板数据散点图(7个截面叠加)8图8 北京和内蒙古1996-2002年消费对收入散点图 图9 1996和2002年15个地区的消费对收入散点图2.面板数据模型分类用面板数据建立的模型通常有3种,即混合回归模型、固定效应回归模型和随机效应回归模型。
2.1 混合回归模型(Pooled model)。
如果一个面板数据模型定义为,y it = α+X it 'β+εit, i = 1, 2, …, N; t = 1, 2, …, T(1)其中y it为被回归变量(标量),α表示截距项,X it为k⨯1阶回归变量列向量(包括k个回归量),β为k⨯1阶回归系数列向量,εit为误差项(标量)。
则称此模型为混合回归模型。
混合回归模型的特点是无论对任何个体和截面,回归系数α和β都相同。
如果模型是正确设定的,解释变量与误差项不相关,即Cov(X it,εit) = 0。
那么无论是N→∞,还是T→∞,模型参数的混合最小二乘估计量(Pooled OLS)都是一致估计量。
92.2 固定效应回归模型(fixed effects regression model)。
固定效应模型分为3种类型,即个体固定效应回归模型、时点固定效应回归模型和个体时点双固定效应回归模型。
下面分别介绍。
2.2.1个体固定效应回归模型(entity fixed effects regression model)如果一个面板数据模型定义为,y it = αi+X it 'β +εit, i = 1, 2, …, N; t = 1, 2, …, T(2)其中αi是随机变量,表示对于i个个体有i个不同的截距项,且其变化与X it有关系;y it为被回归变量(标量),εit为误差项(标量),X it为k⨯1阶回归变量列向量(包括k个回归量),β为k⨯1阶回归系数列向量,对于不同个体回归系数相同,则称此模型为个体固定效应回归模型。
αi作为随机变量描述不同个体建立的模型间的差异。
因为αi是不可观测的,且与可观测的解释变量X it的变化相联系,所以称(2)式为个体固定效应回归模1011型。
个体固定效应回归模型也可以表示为y it = α1 + α2 D 2 + … +αN D N + X it 'β +εit , t = 1, 2, …, T (3) 其中D i =⎩⎨⎧= 其他,,个个体如果属于第,...,,,021N i i , 设定个体固定效应回归模型的原因如下。
假定有面板数据模型y it = β0 + β1 x it +β2 z i +εit , i = 1, 2, …, N ; t = 1, 2, …, T (4) 其中β0为常数,不随时间、截面变化;z i 表示随个体变化,但不随时间变化的难以观测的变量。
上述模型可以被解释为含有N 个截距,即每个个体都对应一个不同截距的模型。
令αi = β0 +β2 z i ,于是(4)式变为y it = αi+β1 x it +εit, i = 1, 2, …, N; t = 1, 2, …, T(5)这正是个体固定效应回归模型形式。
对于每个个体回归函数的斜率相同(都是β1),截距αi却因个体不同而变化。
可见个体固定效应回归模型中的截距项αi中包括了那些随个体变化,但不随时间变化的难以观测的变量的影响。
αi是一个随机变量。
以案例1为例,省家庭平均人口数就是这样的一个变量。
对于短期面板来说,这是一个基本不随时间变化的量,但是对于不同的省份,这个变量的值是不同的。
以案例1为例(file:panel02)得到的个体固定效应模型估计结果如下:12图10 个体固定效应回归模型的估计结果132.2.2 时点固定效应回归模型(time fixed effects regression model)如果一个面板数据模型定义为,y it = γt+X it 'β+εit, i = 1, 2, …, N(6)其中γt是模型截距项,随机变量,表示对于T个截面有T个不同的截距项,且其变化与X it有关系;y it为被回归变量(标量),εit为误差项(标量),满足通常假定条件。
X it为k⨯1阶回归变量列向量(包括k个回归变量),β为k⨯1阶回归系数列向量,则称此模型为时点固定效应回归模型。
时点固定效应回归模型也可以加入虚拟变量表示为y it = γ1 + γ2W2 + … +γ T W T + X it 'β+εit, i = 1, 2, …, N; t = 1, 2, …, T(7)其中1415W t =⎩⎨⎧= 。
,个截面其他个截面)(,;,...,,t t T t 不属于第如果属于第021 设定时点固定效应回归模型的原因。
假定有面板数据模型y it = β0 + β1 x it +β2 z t +εit , i = 1, 2, …, N ; t = 1, 2, …, T (8) 其中β0为常数,不随时间、截面变化;z t 表示随不同截面(时点)变化,但不随个体变化的难以观测的变量。
上述模型可以被解释为含有T 个截距,即每个截面都对应一个不同截距的模型。
令γt = β0 +β2 z t ,于是(8)式变为 y it = γt + β1 x it +εit , i = 1, 2, …, N ; t = 1, 2, …, T (9) 这正是时点固定效应回归模型形式。
对于每个截面,回归函数的斜率相同(都是β1),γt 却因截面(时点)不同而异。
可见时点固定效应回归模型中的截距项γt 包括了那些随不同截面(时点)变化,但不随个体变化的难以观测的变量的影响。
t是一个随机变量。
以案例1为例,“全国零售物价指数”就是这样的一个变量。
对于不同时点,这是一个变化的量,但是对于不同省份(个体),这是一个不变化的量。
16图11 172.2.3 个体时点双固定效应回归模型(time and entity fixed effects regression model)如果一个面板数据模型定义为,y it = αi+γt+X it 'β+εit, i = 1, 2, …, N; t = 1, 2, …, T(11)其中y it为被回归变量(标量);αi是随机变量,表示对于N个个体有N个不同的截距项,且其变化与X it有关系;γt是随机变量,表示对于T个截面(时点)有T 个不同的截距项,且其变化与X it有关系;X it为k⨯1阶回归变量列向量(包括k 个回归量);β为k⨯1阶回归系数列向量;εit为误差项(标量)满足通常假定(εit⎢X it,αi,γt) = 0;则称此模型为个体时点固定效应回归模型。
个体时点固定效应回归模型还可以表示为,y it = α1+α2D2 +…+αN D N+γ2W2 +…+γ T W T + X it 'β+εit, t = 1, 2, …, (12)1819其中D i =⎩⎨⎧= 其他,,个个体如果属于第,...,,,021N i i , (13)W t =⎩⎨⎧= 。
,个截面其他个截面)(,;,...,,t t T t 不属于第如果属于第021 (14) 如果模型形式是正确设定的,并且满足模型通常的假定条件,对模型(12)进行混合OLS 估计,全部参数估计量都是不一致的。
正如个体固定效应回归模型可以得到一致的、甚至有效的估计量一样,一些计算方法也可以使个体时点双固定效应回归模型得到更有效的参数估计量。
以例1为例得到的截面、时点固定效应模型估计结果如下:回归系数为0.67,这与个体固定效应回归模型给出的估计结果0.70基本一致。
20在上述三种固定效应回归模型中,个体固定效应回归模型最为常用。
