自动控制原理C作业(第二章)答案
自动控制理论第二章习题答案
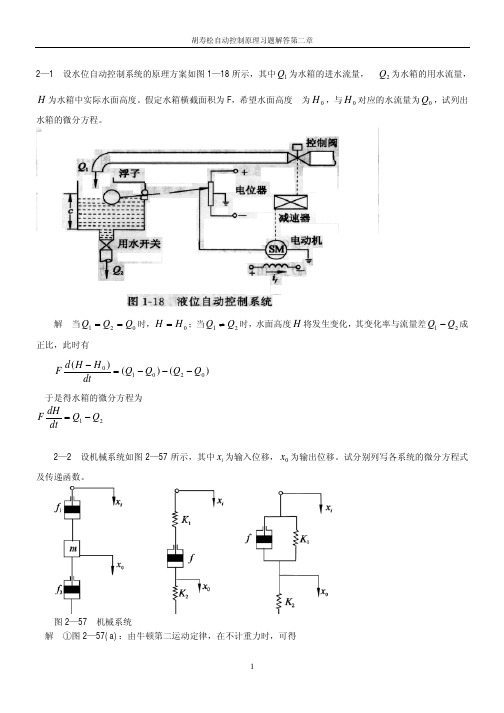
式中 K 为比例常数, P 为阀门前后的压差。若流量 Q 与压差 P 在其平衡点 (Q0 , P0 ) 附近作微小变化,试导出线性化
方程。 解:
设正常工作点为 A,这时 Q0 = K P0
在该点附近用泰勒级数展开近似为:
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 Q − Q0 = K1 (P − P0 )
其中 K1
= dQ dP P=P0
=
1K 2
1 P0
2-7 设弹簧特性由下式描述:
F = 12.65 y1.1
其中,是弹簧力;是变形位移。若弹簧在变形位移附近作微小变化,试推导的线性化方程。 解:
设正常工作点为 A,这时 F0
=
12.65
y1.1 0
在该点附近用泰勒级数展开近似为:
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解:(a):利用运算阻抗法得: Z1
=
R1
//
1 C1s
=
R1 C1s
R1
+
1 C1s
=
R1 = R1 R1C1s + 1 T1s + 1
Z2
=
R2
+
1 C2s
(C2
+
2C1 )
du0 dt
+ u0 R
=
C1C2 R
d 2ui dt 2
自动控制原理_王万良(课后答案2
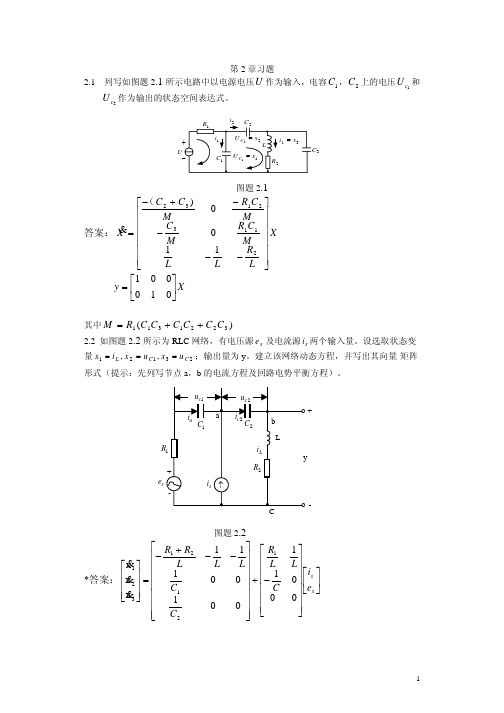
第2章习题2.1 列写如图题2.1所示电路中以电源电压U 作为输入,电容1C ,2C 上的电压1c U 和2c U 作为输出的状态空间表达式。
图题2.1答案:X L R LL M C R M C M C R M C C X ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−−+−=211321321100)(& X y ⎥⎦⎤⎢⎣⎡=010001其中)(3221311C C C C C C R M ++=2.2 如图题2.2所示为RLC 网络,有电压源s e 及电流源s i 两个输入量。
设选取状态变量23121,,C C L u x u x i x ===;输出量为y 。
建立该网络动态方程,并写出其向量-矩阵形式(提示:先列写节点a ,b 的电流方程及回路电势平衡方程)。
图题2.2*答案:⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−+⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡−−+−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡s s e i C L L R C C L L L RR 0001100100111x x x 12121321&&&U 3+-se[]111−−−=R y ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x +[]⎥⎦⎤⎢⎣⎡s s e i R 11 2.3 列写图题2.3所示RLC 网络的微分方程。
其中,r u 为输入变量,c u 为输出变量图题2.3答案:r c cc u u dt du RC dtu d LC =++22 2.4 列写图题2.4所示RLC 网络的微分方程,其中r u 为输入变量,c u 为输出变量。
图题2.4答案:r c cc uu dt du R L dtu d LC =++22 2.5 图题2.5所示为一弹簧—质量—阻尼器系统,列写外力)(t F 与质量块位移)(t y 之间)(t图题2.5答案:)()()()(22t f t ky dt t dy f dtt y d m =++ 2.6 列写图题2.6所示电路的微分方程,并确定系统的传递函数,其中r u 为输入变量,cu 为输出变量。
自动控制原理C作业(第二章)答案
4 3
0.1
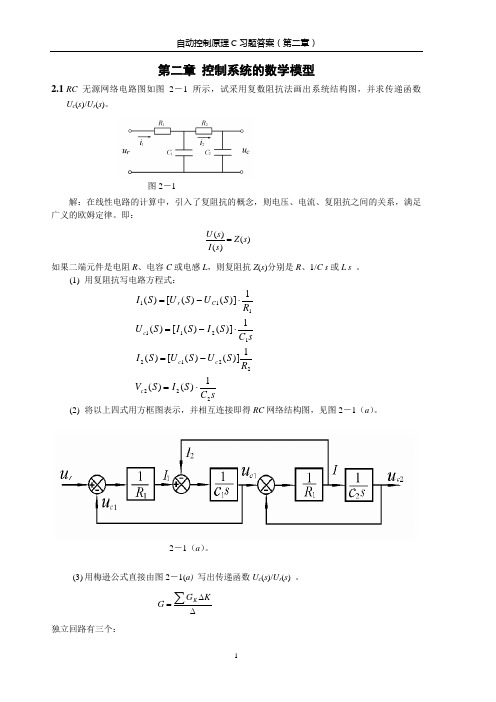
图 3-1 二阶控制系统的单位阶跃响应
解 在单位阶跃作用下响应的稳态值为 3,故此系统的增益不是 1,而是 3。系统模型为
(s)
s2
3
2 n
2n s
2 n
然后由响应的 p % 、 t p 及相应公式,即可换算出 、 n 。
p%
c(t p ) c() c()
4
3
3
33%
t p 0.1(s)
P1 G1G2
1 1
P2 G2G4
2 1
因此,传递函数为
C(s) P11 P2 2
R(s)
G2G1 G4G2 1 G1G2G3
3
自动控制原理 C 习题答案(第二章)
2.4 用梅森公式求系统传递函数。
R(S)
-
_
+ G1(s)
- _
G2(s)
+ C(S)
+
图 2-4 解: 单独回路 5 个,即
L1
1 R
1 C1S
1 R1C1S
11
1
L2
R2
C2S
R2C2 S
L3
1 C1S
1 R2
1 R2C1S
回路相互不接触的情况只有 L1 和 L2 两个回路。则
L12
L1L2
1 R1C1R2C2S 2
由上式可写出特征式为:
1
( L1
L2
L3 )
L1 L2
1
1 R1C1S
1 R2C2 S
1 R2C1S
1 R1C1R2C2S 2
益 K1 和速度反馈系数 Kt 。同时,确定在此 K1 和 Kt 数值下系统的延迟时间、上升时间和调节时间。
自动控制原理第二章习题答案详解
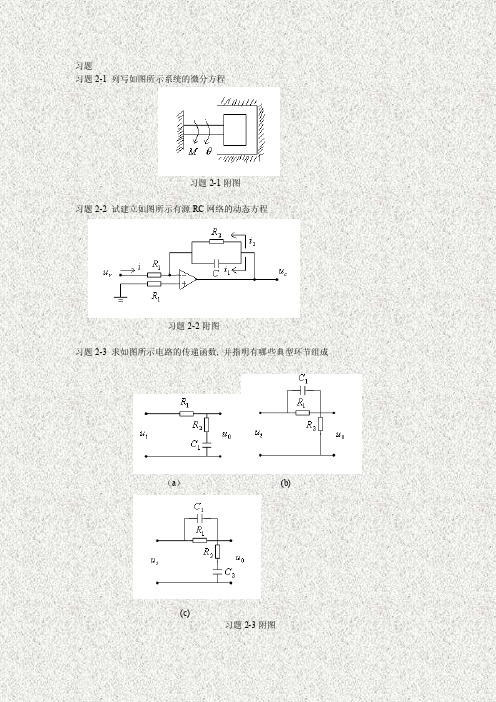
习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成(a)(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图(a)图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。
),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。
习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。
图(a )图(b)习题2-8附图习题2-9 求如下各图的传递函数(a)(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图(a )(b)(c)(d)习题2-10附图习题答案习题2-1答案:解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案:解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案: 解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节,惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节,惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节,二阶振荡环节组成。
胡寿松自控习题答案 第二章习题解答

(2)
iC 2
=
uC1
+ iC1R R
K 2 x0 = f (x& − x&0 )
消去中间变量 x,可得系统微分方程
f (K1
+
K
2
)
dx0 dt
+
K1K2 x0
=
K1 f
dxi dt
对上式取拉氏变换,并计及初始条件为零,得系统传递函数为
X 0 (s) =
fK1s
X i (s) f (K1 + K2 )s + K1K2
③图 2—57(c):以 x0 的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:
u0
= (iC
+ iR1 )R2
=
C
duC dt
+
uC R1
R2
=
C
d
(ui −
dt
u0
)
+
ui
− u0 R1
R2
整理得:
CR2
du0 dt
+ C
R2 R1
+ 1u0
= CR2
dui dt
+C
R2 R1ui − u0 = uC1 (1)
iC1
=
C1
duC1 dt
K
=
1
K2
( f1 s + 1)( f 2 s + 1) + f1
K 1
K2
K2
所以图 2-58(a)的电网络与(b)的机械系统有相同的数学模型。 2—4 试分别列写图 2-59 中个无源网络的微分方程式。
解:(a) :列写电压平衡方程:
自动控制原理作业题(后附答案)

自动控制原理作业题(后附答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII自动控制原理作业题第一章基本概念一、简答题1 简述自动控制的基本概念2 简述自动控制系统的基本组成3 简述控制系统的基本控制过程4 简述自动控制系统的基本分类5 试比较开环控制和闭环控制的特点6 简述自动控制系统的性能评价指标二、分析计算题1 液位自动控制系统如图所示。
试分析该系统工作原理,画出系统原理框图,指出被控对象、被控参量和控制量2 发动机电压调节系统如图所示,试分析其工作原理,画出系统原理框图,指出其特点。
3液面控制系统如图所示。
试分析该系统的工作原理,指出系统中的干扰量、被控制量及被控制对象,并画出系统的方框图。
4控制系统如图所示。
简述该系统的工作原理,说明该系统的给定值、被控制量和干扰量,并画出该系统的方块图。
图1-7发电机-电动机调速系统操纵电位计发电机伺服电机减速器负载Θr给定值Ur 前置放大器功放执行元件被控量Wm这是一个开环控制的例子+E-EUr操纵电位计R1R2R3R4放大器直流发电机伺服电机Wd Wm发电机-电动机调速系统减速器负载5火炮随动控制系统如图所示。
简述该系统的工作原理,并画出该系统的原理框图。
第二章 线性控制系统的数学模型一、简答题1 简述建立控制系统数学模型的方法及其数学表示形式2 简述建立微分方程的步骤3 简述传递函数的基本概念及其特点4 给出组成控制系统典型基本环节二、分析计算题1 有源电网络如图所示,输入量为)(1t u ,输出量为)(2t u ,试确定该电网络的传递函数2 电枢控制式直流电动机原理图如图所示,输入量为)(1t e ,输出量为)(t o θ,试确定其微分方程。
图中,电动机电枢输入电压;电动机输出转角;电枢绕组的电阻;电枢绕组的电感;流过电枢绕组的电流;电动机感应电势;电动机转矩;电动机及负载这和到电动机轴上的转动惯量;电动机及负载这和到电动机轴上的粘性摩擦系数。
自动控制原理课后习题答案第二章
解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
自动控制原理第二章课后习题答案(免费)
⾃动控制原理第⼆章课后习题答案(免费)⾃动控制原理第⼆章课后习题答案(免费)离散系统作业注明:*为选做题2-1 试求下列函数的Z 变换(1)()E z L =();n e t a = 解:01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ (2) ();at e t e -= 解:12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值:(1)112();(1)Tz E z z --=-解: 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- (2)2()(0.8)(0.1)z E z z z =--。
解:211(1)()(1)()0(0.8)(0.1)lim lim lim t z z z z f t z E z z z →∞→→-=-==--2-3* 已知()(())E z L e t =,试证明下列关系成⽴:(1)[()][];n z L a e t E a=证明:()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ (2)()[()];dE z L te t TzT dz=-为采样周期。
证明:11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以:()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。
自动控制原理课后习题答案
R1R2C1C2d2du22(tt)(R1C1R2C2R1C2)dd2u(tt)u2(t) v(t)
R1C1ddV (tt)V(t)
输入
(b) 以电压u3(t)为输出量,列写微分方程为:
u1(t)
C1
R1 R2
C2
R1R2C 1C2d2d u32(tt)(R1C 1R2C2)dd3u (t)t(R1C21)u3(t)
y=x3+x4=G2x2+G4x2=(G2+G4)G1x1
y=(G2+G4)G1x1
G(s)=Y(s)/U(s)=(G2+G4)G1/(1+G3G2G1)
作业:2.59题 把图2.75改画为信号流图,并用Mason公式求u到y传递函数
方框图
u(S)
__
G1(s)
G5(s)
—
y(S)
G2(s)
—
G3(s)
essfls i0m se(s)1K K21K2
(b)当r(t)=1(t),f(t)=1(t)时的ess。 解:求输入误差传递函数,直接代数计算法:
根据电路定律写出单体微分方程式(2.2.2)和 (2.2.3)。把特征受控量uc(t)选作输出量,依 据式(2.2.2)和(2.2.3),消除中间量i(t) , 则可得到输入输出微分方程(2.2.4)。
3、利用Laplace变换求出传递函数
R
L
+
+
u(t) i(t)
输入
_
+ uc(t) _
y
输出
_
U(t)Ld dtiR i uC
自动控制原理课后习题答案
第二章作业 概念题:传递函数定义:
单输入输出线性定常系统的传递函数,定义为零初始条件下,系统输出 量的拉氏变换像函数与输入量的拉氏变换像函数之比。
黄家英自动控制原理第二版第二章习题答案
(2)欲使图B2.18(a)系统的输出Y(s)不受扰动D(s)的影响
G 3G 4 G1G 2G 3G 4 H1 G 3G 5 H 2 Y(s) D(s) 1 G 1G 2 H1 G 2G 3 H 2 G1G 5 H 3 G1G 2G 3G 4 H 3 Y(s) D(s) G 3G 4 G1G 2G 3G 4 H1 G 3G 5 H 2 1 G1G 2 H1 G 2G 3 H 2 G1G 5 H 3 G1G 2G 3G 4 H 3
2
6 s
代入初值整理 2s 2 12s 6 Y(s) 3 s 5s 2 6s
部分分式展开 4 5 1 Y(s) s3 s2 s
y(t ) 4e3t 5e2t 1 , t 0
B2.9 已知控制系统的微分方程(或微分方程组)为
式中r(t)为输入量,y(t)为输出量,z1(t)、z2(t)和z3(t) 为中间变量,τ 、β 、K1和K2均为常数。 试求:(a)各系统的传递函数Y(s)/R(s);(b)各系统含 有哪些典型环节?
R
E - G1
G1 -
G5
D
Y
G2
H2 H3
G3
G4
H1 G2 R E - G1 G1 G2 G5 D(s) G3 G4 Y
H2
H3
G5 R E - G1
-
1 1 G 1G 2 H 1
G2 G3
H2 H3
G4
Y
G5 G 2G 3
R
E - G1
-
1 1 G 1G 2 H 1
G2 G3 H2 H3
闭环传递函数为 0.5 s 3 + 0.5 s 2 + s + 1 s 3 + 3.5 s 2 - 0.5 s + 1 s 3 + s 2 + 2s + 2 3 2s + 7 s 2 - s + 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章控制系统的数学模型2.1RC无源网络电路图如图2-1所示,试采用复数阻抗法画出系统结构图,并求传递函数U c(s)/U r(s)。
图2-1解:在线性电路的计算中,引入了复阻抗的概念,则电压、电流、复阻抗之间的关系,满足广义的欧姆定律。
即:)()()(sZsIsU=如果二端元件是电阻R、电容C或电感L,则复阻抗Z(s)分别是R、1/C s或L s。
(1)用复阻抗写电路方程式:sCSISVRSUSUSIsCSISISURSUSUSIccccCr222221212111111)()(1)]()([)(1)]()([)(1)]()([)(⋅=-=⋅-=⋅-=(2)将以上四式用方框图表示,并相互连接即得RC网络结构图,见图2-1(a)。
2-1(a)。
(3)用梅逊公式直接由图2-1(a)写出传递函数U c(s)/U r(s) 。
∆∆=∑KGG K独立回路有三个:SC R S C R L 1111111-=⋅-=SC R S C R L 22222111-=⋅-=回路相互不接触的情况只有L 1和L 2两个回路。
则2221121121S C R C R L L L == 由上式可写出特征式为:222111222112132111111)(1S C R C R S C R S C R S C R L L L L L ++++=+++-=∆通向前路只有一条221212*********SC C R R S C R S C R G =⋅⋅⋅=由于G 1与所有回路L 1,L 2, L 3都有公共支路,属于相互有接触,则余子式为Δ1=1代入梅逊公式得传递函数1)(111111121221122121222111222112221111++++=++++=∆∆=s C R C R C R s C C R R s C R C R s C R s C R s C R s C R C R G G2-2 已知系统结构图如图2-2所示,试用化简法求传递函数C (s )/R (s )。
图2-2解:(1)首先将含有G 2的前向通路上的分支点前移,移到下面的回环之外。
如图2-2(a )所示。
(2)将反馈环和并连部分用代数方法化简,得图2-2(b )。
(3)最后将两个方框串联相乘得图2-2(c )。
SC R R S C L 12213111-=⋅-=图2-2 系统结构图的简化2.3化简动态结构图,求C(s)/R(s)图2-3解: 单独回路1个,即3211G G G L -=两个互不接触的回路没有 于是,得特征式为3211 1G G G L a +=-=∆∑从输入R 到输出C 的前向通路共有2条,其前向通路传递函数以及余因子式分别为211G G P = 11=∆422G G P = 12=∆因此,传递函数为∆∆+∆=2211)()(P P s R s C32124121G G G G G G G ++=2.4 用梅森公式求系统传递函数。
图2-4解: 单独回路5个,即11G L -=212G G L =23G L -=214G G L -=215G G L -=两个互不接触的回路没有于是,得特征式为21211 1G G G G L a+++=-=∆∑从输入R 到输出C 的前向通路共有4条,其前向通路总增益以及余因子式分别为11G P = 11=∆ 22G P = 12=∆ 213G G P = 13=∆214G G P -= 14=∆因此,传递函数为∆∆+∆+∆+∆=44332211)()(P P P Ps R s C 2121211G G G G G G ++++=2-5 试简化图2-5中的系统结构图,并求传递函数C(s)/R(s )和C(s)/N(s)。
图2-5解: 仅考虑输入R (S )作用系统时,单独回路2个,即211G G L -=1212H G G L -=两个互不接触的回路没有,于是,得特征式为121211 1H G G G G L a++=-=∆∑从输入R 到输出C 的前向通路共有1条,其前向通路总增益以及余因子式分别为211G G P = 11=∆因此,传递函数为∆∆=11)()(P s R s C 12121211H G G G G G G ++=仅考虑输入N (S )作用系统时,单独回路2个,即211G G L -=1212H G G L -=两个互不接触的回路没有,于是,得特征式为121211 1H G G G G L a++=-=∆∑从输入N 到输出C 的前向通路共有2条,其前向通路总增益以及余因子式分别为11-=P 12111H G G +=∆ 322G G P = 12=∆因此,传递函数为∆∆+∆=2211)()(P P s N s C 12121322111H G G G G G G H G G ++-+-=2-6用梅逊增益公式求传递函数C(s)/R(s)和E(s)/R(s)。
图2-6解:C(s)/R(s):单独回路3个,即111H G L -=232H G L -=213213H H G G G L -=1L 2L 两个互不接触的回路,于是,得特征式为21312132123111 1H H G G H H G G G H G H G L L L cb a ++++=+-=∆∑∑从输入R 到输出C 的前向通路共有1条,其前向通路总增益以及余因子式分别为3211G G G P = 11=∆432G G P = +=∆1211H G因此,传递函数为∆∆+∆=2211)()(P P s R s C 213121321231111433211)1(H H G G H H G G G H G H G H G G G G G G ++++++=E(s)/R(s):单独回路3个,即111H G L -=232H G L -=213213H H G G G L -=1L 2L 两个互不接触的回路,于是,得特征式为21312132123111 1H H G G H H G G G H G H G L L L cb a ++++=+-=∆∑∑从输入R 到输出E 的前向通路共有2条,其前向通路总增益以及余因子式分别为11=P 2311H G +=∆21432H H G G P -= 12=∆因此,传递函数为∆∆+∆=2211)()(P P s R s E213121321231121432311H H G G H H G G G H G H G H H G G H G ++++-+=第三章 线性系统的时域分析法3-1 设二阶控制系统的单位阶跃响应曲线如图3-1所示。
试确定系统的传递函数。
图3-1 二阶控制系统的单位阶跃响应解 在单位阶跃作用下响应的稳态值为3,故此系统的增益不是1,而是3。
系统模型为22223)(nn ns s s ωξωωφ++=然后由响应的%p σ、p t 及相应公式,即可换算出ξ、n ω。
%33334)()()(%=-=∞∞-=c c t c p p σ 1.0=p t (s )由公式得%33%21/==--ξπξσe p1.012=-=ξωπn p t换算求解得: 33.0=ξ、 2.33=n ω34 0.1110222330623)(2222++=++=s s s s s n n n n ωξωωφ3-2 设系统如图3-2所示。
如果要求系统的超调量等于%15,峰值时间等于0.8s ,试确定增益K 1和速度反馈系数K t 。
同时,确定在此K 1和K t 数值下系统的延迟时间、上升时间和调节时间。
图3-2解 由图示得闭环特征方程为0)1(112=+++K s K K s t即21n K ω=,nnt t K ωωξ212+=由已知条件8.0115.0%21/2=-===--t n p p t e t tξωπσξπξ解得1588.4,517.0-==s n t ωξ于是05.211=K 178.0211==-K K nt t ωξs t nt t d 297.02.06.012=++=ωξξst tn t tn r 538.01arccos 122=--=--=ξωξπξωβπR (s )C (s )1+K t sK/s(s+1)s t nt s 476.15.3==ωξ3-3 已知系统特征方程式为0516188234=++++s s s s 试用劳斯判据判断系统的稳定情况。
解 劳斯表为4s 1 18 5 3s 8 16 0 2s168161188=⨯-⨯ 580158=⨯-⨯1s 5.1316581616=⨯-⨯ 00s 55.1301655.13=⨯-⨯由于特征方程式中所有系数均为正值,且劳斯行列表左端第一列的所有项均具有正号,满足系统稳定的充分和必要条件,所以系统是稳定的。
3-4 已知系统特征方程为053222345=+++++s s s s s 试判断系统稳定性。
解 本例是应用劳斯判据判断系统稳定性的一种特殊情况。
如果在劳斯行列表中某一行的第一列项等于零,但其余各项不等于零或没有,这时可用一个很小的正数ε来代替为零的一项,从而可使劳斯行列表继续算下去。
劳斯行列式为5s 1 2 3 4s 1 2 5 3s 0≈ε 2- 2sεε22+ 51s 225442+---εεε0s 5由劳斯行列表可见,第三行第一列系数为零,可用一个很小的正数ε来代替;第四行第一列系数为(2ε+2/ε,当ε趋于零时为正数;第五行第一列系数为(-4ε-4-5ε2)/(2ε+2),当ε趋于零时为2-。
由于第一列变号两次,故有两个根在右半s 平面,所以系统是不稳定的。
3.5解;在求解系统的稳态误差前必须判定系统是否稳定;系统特征方程为05055.11.023=+++s s s 由劳斯判据判断 劳斯行列式为3s 1.0 5 2s 5.1 501s 350s 50由于特征方程式中所有系数均为正值,且劳斯行列表左端第一列的所有项均具有正号,满足系统稳定的充分和必要条件,所以系统是稳定的。
)12.0)(11.0(10)5)(11.0(50)(++=++=s s s s s s s G 可知v=1,K=10当 ,当I ∞=∞++=+++= 型系统,01k k k k e a v p ss βγβαt t r 2)(=222)(tt t r ++=2.0102== == k k e vssββ I ∞=∞++=+++=型系统,10201avpss k k k e γβα第五章 线性系统的频域分析法5.1已知系统的开环传函)12.0)(12(10)()(++=s s s s H s G ,用奈氏判据(画出奈氏曲线)判别闭环系统的稳定性。
解:(1) 确定起点和终点1,2)(0=⋅-=∠→νπνωωνj k 初始相角为,故初始相角为-90°, ∞→→0)(ωνωj k 模值为终点: 0)(=∞→-ωωm n j k 模值为,0027090)()(-=⋅--=∠∞→-m n j kmn ωω终止相角为 (2) 求幅相曲线与负实轴的交点)4.01(2.210)(22ωωωω-+-=j j G ,P=0,N-=1, N+=0,R=2(N+-N-)=-2,Z=P-2N=2 由奈氏判据知,闭环系统是不稳定的。
