九上数学《同步练习》§2.8圆锥的侧面积
九年级数学上册2.8圆锥的侧面积圆锥的侧面展开图,计算圆锥的侧面积和全面积素材苏科版(new)

圆锥的侧面展开图,计算圆锥的侧面积和全面积难易度:★★★★关键词:圆锥的侧面积、全面积答案:圆锥的侧面展开图是扇形,其侧面积就是展开图扇形的面积,全面积就是侧面积与底面圆面积的和。
【举一反三】如图,圆锥的底面半径为3cm,母线长5cm,则它的侧面积为.典题:如果圆锥的底面圆周长为20,侧面展开后所得扇形的圆心角为1200,则该圆锥的侧面积是。
(结果保留)思路导引:圆锥的侧面展开图是扇形,求侧面积实际是求扇形的面积,求扇形面积除需知道圆心角外还需知道扇形的半径,由底面圆周长可得扇形的半径。
标准答案:尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
九年级数学上册2.8圆锥的侧面积圆锥的侧面积和全面积的计算素材苏科版(new)

圆锥的侧面积和全面积的计算如图,我们把圆锥底面圆周上任意一点与圆锥顶点的连线叫做圆锥的母线。
连结顶点与底面圆心的线段叫做圆锥的高.如图,沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长.圆锥的侧面积就是弧长为圆锥底面的周长、半径为圆锥的一条母线的长的扇形面积,而圆锥的全面积就是它的侧面积与它的底面积的和.研究圆锥的侧面积和全面积,必须先研究其侧面展开图。
圆锥的侧面展形图是扇形,这个扇形的半径是圆锥的母线长,弧长是圆锥底面圆的周长。
如图,设圆锥的母线长为l,底面半径为r,则圆锥的侧面积就转为其展开图扇形的面积,是122r l rlππ⋅⋅=;圆锥的全面积是侧面积与底面积的和,是2rl rππ+。
另外,知道扇形的半径和弧长,还可以求得扇形的圆心角.例1 底面半径为r,高为h的圆柱的侧面积和全面积分别是多少?SB【研析】:如图,沿着圆柱的母线,把一个圆柱的侧面展开,得到一个矩形,这个矩形的一边等于圆柱的高,即圆柱的母线长,另一边是底面圆的周长,所以圆柱的侧面积就等于底面圆的周长乘以圆柱的高,而圆柱的全面积就是它的侧面积与它的底面积(两个等圆)的和.解 圆柱的侧面积为S 侧=2π rh .圆柱的全面积为S =S 侧+2S 圆=2π rh +2π r 2.例2 如图,如果圆锥的底面圆的半径是8,母线长是15,那么这个圆锥侧面展开图的扇形的圆心角的度数是 .【研析】由圆锥的底面圆的半径是8,可以求出底面圆的周长,也就是扇形CAB 的弧长,再利用弧长公式2360180n n rl r ππ=⋅=即可求扇形的圆心角的度数。
解:∵圆锥底面圆的半径是8 ∴BC l r C ==⋅=ππ162 ∵母线长为15∵180Rn l BC ⌒π=∴1801516⋅=ππn 192=n例3 如图已知圆锥的底面半径r =10cm ,母线长为40cm. (1)求它的侧面展开图的圆心角和表面积;(2)若一只甲虫从A 点出发沿着圆锥侧面绕行到母线SA 的中点B ,它所走的最短路程是多少?AO BC图23-49【研析】(1)把圆锥的侧面沿母线SA展开,如图则⌒AA'的长为2πr=20π,SA=40所以20π=40 180 nπ⋅所以n=90°所以圆锥的侧面展开图的圆心角是90°S表面=S侧+S底=29040360π⋅+π·102=500π(cm2)(2)由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路程是线段AB的长在Rt△ASB中,∠ASB=90°,SA=40,SB=20所以AB=22SA+SB=205cm答:圆锥的侧面展开图的圆心角是90°,圆锥的表面积是500π,甲虫所走的最短路程.点评在解决有关圆锥的问题时,明确圆锥侧面展开图的实质,明确各元素之间的对应关系,以及母线、高线、底面半径的关系是解题的关键。
九年级数学上册 2.8 圆锥的侧面积 例说圆锥及其侧面展开图素材 (新版)苏科版

例说圆锥及其侧面展开图我们在解决圆锥的有关计算问题时,常常将其转化为平面图形,再利用平面图形的有关知识来解决。
如图,圆锥的底面半径r ,圆锥母线ι,圆锥的高h ,构成直角三角形,从而有ι2=r 2+h 2。
圆锥的底面直径AB 与圆锥母线SA 、SB 构成等腰△SAB ,等腰△SAB 又称圆锥的轴截面。
圆锥的侧面展开图是一个以圆锥的底面周长2πr 为弧长,以圆锥母线ι为半径的扇形,从而根据扇形面积公式得S 侧=360n πι2或S 侧=21·2πr·ι=πr ι。
圆锥的全面积是指侧面积与底面积的和,公式为S 全=πr ι+πr 2。
上述四个公式共有5个量:ι、h 、r 、n 、S 侧,由于每个公式中只有三个量,从而只要知道其中的两个量,就可以将另外三个量利用方程或方程组求出来。
我们经常要用到“四个公式”和“三个图形”的相关性质解决有关圆锥问题。
例1、如图1已知扇形AOB 的半径为6cm ,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为( )A 、24πcmB 、26πcmC 、29πcmD 、212πcm分析:因为是用扇形围成一个圆锥,则围成的圆锥的侧面积就是这个扇形的面积。
解:所以圆锥的侧面积是360120×πr 2=12π, 所以选D 。
例2、(2009年江汉油田)现有30%圆周的一个扇形彩纸片,该扇形的半径为40cm ,小红同学为了在“六一”儿童节联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作成一个底面半径为10cm 的圆锥形纸帽(接缝处不重叠),那么剪去的扇形纸片的圆心角为( )A 、9° B、18° C、63° D、72°分析:因为是用剩下扇形纸片围成的圆锥形纸帽,所以剩下扇形纸片就是圆锥形纸帽的侧面展开图,根据圆锥的底面周长与圆锥的侧面展开图的弧长相等,求出剩下扇形纸片的圆心角即可。
(含答案)九年级数学苏科版上册课时练第2单元《2.8 圆锥的侧面积》(1)

20. 在城市规划建设中,某超市需要拆迁.爆破时,导火索的燃烧速度为每秒 0.9 cm,点导火索的人 需在爆破前跑到离爆破点 120 m 以外的安全区域.这个导火索的长度为 18 cm,那么点导火索的 人以 6.5 m/s 的速度往外跑是否安全?
21. 如图,以 △
的一边
∠ = ,∠ = .
为直径的半圆与边 , 分别交于点 , ,且 = ,设
∴ ∠ = 2∠ .
∵ 是 ⊙ 的直径, ∴ ∠ = 90∘, ∴ ∠ + = ∠ + = 90∘, ∴ 90∘ − = 2 90∘ − , ∴ = 2 − 90∘.
的取值范围为 45∘ < < 90∘.
(2) 作 ⊥ ,垂足为点 ,则 = ,
∴
=
1 2
,
∵ ∠ = + 90∘ −
∴ =,
= 2 − 90∘ + 90∘ −
Rt △ ABC 绕直线
旋转一周得到的圆锥的底面周长为 2π × 8 = 16π,表面积
2
=
1 2
×
16π
×
ห้องสมุดไป่ตู้
10 = 80π, ∴ 1: 2 = 3: 4.
请问安安的解法正确吗?如果不正确,请说明理由.
24. 如图,从一个半径为 1 m 的圆形铁皮中剪出一个圆心角为 90∘ 的扇形,并将剪下来的扇形围成 一个圆锥,求该圆锥的底面圆的半径.
B. 3 cm 或 8 cm
C. 3 cm
D. 8 cm
6. 已知圆锥的底面半径为 4 cm,母线长为 6 cm,则它的侧面展开图的面积等于
A.24 cm2
B.48 cm2
C.24π cm2
D.12π cm2
2022-2023学年苏科版九年级数学上册《圆锥的侧面积》填空专项练习题(含答案)
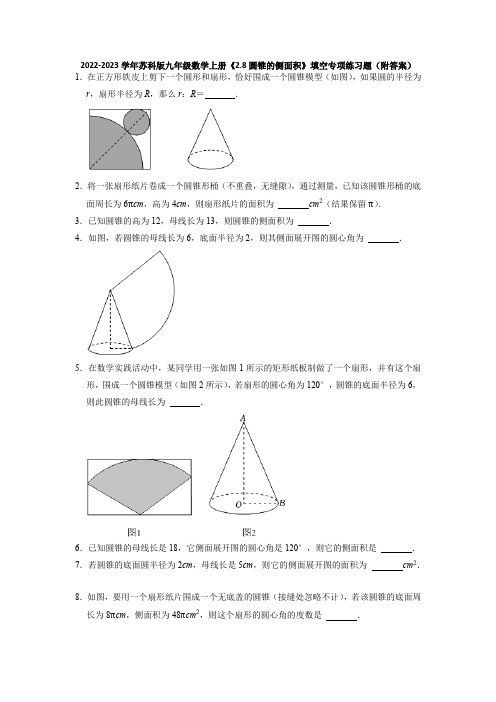
2022-2023学年苏科版九年级数学上册《2.8圆锥的侧面积》填空专项练习题(附答案)1.在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型(如图),如果圆的半径为r,扇形半径为R,那么r:R=.2.将一张扇形纸片卷成一个圆锥形桶(不重叠,无缝隙),通过测量,已知该圆锥形桶的底面周长为6πcm,高为4cm,则扇形纸片的面积为cm2(结果保留π).3.已知圆锥的高为12,母线长为13,则圆锥的侧面积为.4.如图,若圆锥的母线长为6,底面半径为2,则其侧面展开图的圆心角为.5.在数学实践活动中,某同学用一张如图1所示的矩形纸板制做了一个扇形,并有这个扇形,围成一个圆锥模型(如图2所示),若扇形的圆心角为120°,圆锥的底面半径为6,则此圆锥的母线长为.6.已知圆锥的母线长是18,它侧面展开图的圆心角是120°,则它的侧面积是.7.若圆锥的底面圆半径为2cm,母线长是5cm,则它的侧面展开图的面积为cm2.8.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面周长为8πcm,侧面积为48πcm2,则这个扇形的圆心角的度数是.9.用圆心角为120°,弧长为4π的扇形围成一个圆锥的侧面,则所围成的圆锥的高为.10.小丽在手工制作课上,用面积为120πcm2,半径为20cm的扇形卡纸,围成一个圆锥侧面,则这个圆锥的底面半径为cm.11.如图,圆锥的母线长AB=12cm,底面圆的直径BC=10cm,则该圆锥的侧面积等于cm2.(结果用含π的式子表示)12.如图,用圆心角为120°,半径为3cm的扇形纸片卷成一个圆锥形无底纸帽,则这个纸帽的高是cm.13.如图,圆锥的高AO=4,底面圆半径为3,则AC=,圆锥的侧面积为.14.如图,在一个边长为4cm的正方形里作一个扇形,再将这个扇形剪下卷成一个圆锥的侧面,则这个圆锥的底面圆的半径为cm.15.如图(1)所示的瓶子中盛满了水,如果将这个瓶子中的水全部倒入图(2)所示的杯子中,那么一共需要个这样的杯子?(单位:cm)16.圆锥的母线长为5cm,高为4cm,则该圆锥侧面展开图扇形的圆心角为°.17.已知圆锥的高为8cm,母线长为10cm,则其侧面展开图的面积为.18.若一个圆锥的母线长为5cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径为cm.19.如图,△ABC中,∠C=90°,∠B=60°,AC=3,以AC为轴旋转一周得到一个圆锥,则该圆锥的侧面积为.20.已知Rt△ABC,∠C=90°,AB=5cm,AC=4cm,将此三角形绕AC旋转一周所形成的圆锥的侧面积是.参考答案1.解:因为扇形的弧长等于圆锥底面周长,所以2πR=2πr,所以R=2r所以r:R=1:4;故答案为:1:4.2.解:设圆锥的底面圆的半径为rcm,根据题意得2πr=6π,解得r=3,所以圆锥的母线长为=5(cm),所以圆锥的侧面积为×6π×5=15π(cm2),即扇形纸片的面积为15πcm2.故答案为:15π.3.解:由勾股定理得,圆锥的底面半径==5,∴圆锥的底面周长=10π,∴圆锥的侧面积=×10π×13=65π,故答案为:65π.4.解:设圆锥的侧面展开图的圆心角为n°,根据题意得2π×2=,解得n=120,所以侧面展开图的圆心角为120°.故答案为:120°.5.解:设此圆锥的母线长为l,根据题意得2π×6=,解得l=18,即此圆锥的母线长为18.故答案为:18.6.解:根据题意得圆锥的侧面积==108π.故答案为:108π.7.解:根据题意,圆锥的侧面展开图的面积=×2π×2×5=10π(cm2).故答案为:10π.8.解:设圆锥的母线长为lcm,扇形的圆心角为n°,∵圆锥的底面圆周长为8πcm,∴圆锥的侧面展开图扇形的弧长为8πcm,由题意得:×8π×l=48π,解得:l=12,则=8π,解得,n=162,即扇形的圆心角为120°,故答案为:120°.9.解:设圆锥的底面圆的半径为r,则2πr=4π,解得r=2;设圆锥的母线长为l,则=4π,解得l=6,所以圆锥的高==4.故答案为:4.10.解:∵S=l•R,∴•l•20=120π,解得l=12π,设圆锥的底面半径为rcm,∴2π•r=12π,∴r=6.故答案为:6.11.解:根据题意该圆锥的侧面积=×10π×12=60π(cm2).故答案为:60π.12.解:设这个圆锥的底面圆的半径为rcm,根据题意得2πr=,解得r=1,即这个圆锥的底面圆的半径为1cm,所以这个纸帽的高为=2(cm).故答案为:2.13.解:在Rt△AOC中,AC===5,根据题意,圆锥的侧面积=×2π×3×5=15π.故答案为:5;15π.14.解:设圆锥的底面圆的半径为rcm,根据题意得=2πr,解得r=1,故答案为:1.15.解:瓶子中大圆柱的容积为V大=πa2H(cm3),瓶子中小圆柱容积V小=a2h(cm3),杯子得容积为V杯子=π()2×8=a2(cm3),则所需杯子个数为(πa2H+a2h)÷a2=2H+h.故答案为:(2H+h).16.解:圆锥的底面圆的半径为:=3(cm),设圆锥侧面展开图的圆心角为n°,则2π×3=,∴n=216,∴圆锥侧面展开图的圆心角为216°,故答案为:216.17.解:圆锥的高为8cm,母线长为10cm,由勾股定理得,底面半径=6cm,侧面展开图的面积=πrl=π×6×10=60πcm2.故答案为:60πcm2.18.解:圆锥侧面展开图扇形的弧长为:=,设圆锥的底面半径为r,则2πr=,∴r=cm.故答案为:.19.解:∵∠C=90°,∠B=60°,AC=3,∴BC==,AB=2BC=2,根据题意,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积=×2π××2=6π.故答案为:6π.20.解:∵∠C=90°,AB=5cm,AC=4cm,∴BC==3cm,根据题意,△ABC绕AC所在直线旋转一周,所形成的圆锥侧面积=×2π×3×5=15π(cm2).故答案为:15πcm2.。
九年级数学上册2.8圆锥的侧面积课堂学习检测题一(新版)苏科版

第二章第八节圆锥的面积1.已知圆锥的底面半径为1 cm,母线长为3 c m,则圆锥的侧面积是( )A. 6 cm2 B. 3π cm2 C. 6π cm2 D.cm22.如图,圆锥的底面半径r 为6cm,高h 为8cm,则圆锥的侧面积为()A. B. C. D.3.如图是一个圆锥的主视图,则这个圆锥的全面积是( )A.12π B.15π C.21π D.24π4.如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是()m.A.. 5 C..5.如图,圆锥的底面半径为3,母线长为6,则侧面积为A. B. C. D.6.已知一个圆锥的底面半径为3 cm,母线长为10 cm,则这个圆锥的侧面积为 ( )A. 15π cm2 B. 30π cm2C. 60π cm2 D.27.若圆锥的母线长为4cm,底面半径为3cm,则圆锥的侧面展开图的面积是_______cm2.8.已知圆锥的底面直径是8cm,母线长是5cm,其侧面积是_____cm2(结果保留π).9.圆锥的底面积为25π,母线长为13 cm,这个圆锥的底面圆的半径为________ cm,高为________ cm,侧面积为________ cm2.10.若圆锥的底面圆的半径为2cm,母线长为8cm,则这个圆锥侧面展开图的面积为_____cm2.11.用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,则这个圆锥的底面半径是_______。
12.如图,粮仓的顶部是锥形,这个圆锥底面周长为32m,母线长7m,为防雨,需要在粮仓顶部铺上油毡,则共需油毡______m2.13.已知:如图,观察图形回答下面的问题:(1)此图形的名称为________.(2)请你与同伴一起做一个这样的物体,并把它沿AS剪开,铺在桌面上,则它的侧面展开图是一个________.(3)如果点C是SA的中点,在A处有一只蜗牛,在C处恰好有蜗牛想吃的食品,但它又不能直接沿AC爬到C处,只能沿此立体图形的表面爬行,你能在侧面展开图中画出蜗牛爬行的最短路线吗?(4)SA的长为10,侧面展开图的圆心角为90°,请你求出蜗牛爬行的最短路程.14.如图,有一直径是米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形A BC,则:(1)AB的长为多少米?(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面半径为多少米?15.如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形.(1)求这个扇形的面积(结果保留π);(2)用此扇形围成一个圆锥的侧面,求该圆锥的底面半径.16.如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D。
苏科版数学九年级上册-2.8 圆锥的侧面积 同步课件
1.圆锥的侧面展开图是扇形 A
2.母线的长=其侧面展开图扇
形的半径
BO
C
3. 底 面 周 长 = 侧 面 展 开 图 扇 形的弧长
,解得R=6r,
因为圆锥的全面积为28π,
所以πr2+ •2πr•R=28π,
即πr2+ •2πr•6r=28π,解得r=2,
所以圆锥的侧面积= •2πr•6r=6π•22=24π.
S 侧 =πrl
(r表示圆锥底面的半径, l 表示圆锥的母线长 ) 圆锥的侧面积与底面积的和叫做圆锥的全 面积(或表面积).
l
将一个圆锥的侧面沿它的一条母线剪开铺平, 思考圆锥中的各元素与它的侧面展开图中的各 元素之间的关系
R A
BO
C
圆锥母线的长=侧面展开图扇形的半径
底面周长=侧面展开图扇形的弧长 S
A Or B
A
1.如何求圆锥的侧面积?
BO
C
2.如何求圆锥的全面积?
例 用铁皮制作圆锥形容器盖,其尺寸要求如图所示, 求所需铁皮的面积S(精确到1 cm2).
圆锥的侧面积
说说你对圆锥的一些认识。 圆锥的侧面展开图是__扇__形____ 要得此图,我们该如何展开? 扇形的弧长和面积如何计算?
我们把连接圆锥的顶点S和底面圆上任一 点的连线SA,SB 等叫做圆锥的母线
圆锥的高
母线 A
连接顶点S与底面圆的圆心O的线段叫 做圆锥的高
S
思考圆锥的母线和圆锥的高
ቤተ መጻሕፍቲ ባይዱ
解:圆锥形容器盖的底面圆周长为 2 40 80
制作圆锥形容器盖所需铁皮面积
S 1 80 50 6280.
2
度第一学期苏科版九年级数学上册_2.8_圆锥的侧面积_同步课堂检测题
度第一学期苏科版九年级数学上册_22.8 圆锥的正面积同步课堂检测题考试总分: 100 分考试时间:90 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题〔共 10 小题,每题 3 分,共 30 分〕1.一个圆锥的底面半径为3,正面展开图是半圆,那么圆锥的正面积是〔〕A.9nB.18nC.27nD.39n2.圆柱的底面半径为2cm,高为5cm,那么圆柱的正面积是〔〕A.20cm2B.20πcm2C.10πcm2D.5πcm23.底面半径R,高为ℎ的圆柱与底面半径为r,高为ℎ的圆柱的体积的比是9:25,那么R:r等于〔〕A.9:25B.25:9C.3:5D.5:34.圆锥底面圆的半径为1cm,母线长为6cm,那么圆锥正面展开图的圆心角是〔〕A.30∘B.60∘C.90∘D.120∘5.圆锥的底面半径为3,母线长为4,那么圆锥的正面积等于〔〕A.15πB.14πC.13πD.12π6.如图是一个圆柱形木块,四边形ABB1A1是经边它的轴的剖面,设四边形ABB1A1的面积为S,圆柱的正面积为S侧,那么S与S侧的关系是〔〕A.S=13S侧B.S=2S侧πC.S=S侧πD.不能确定7.如图,矩形ABCD中,AB=1,BC=2,把矩形ABCD绕AB所在直线旋转一周所得圆柱的正面积为〔〕A.10πB.4πC.2πD.28.小明预备在毕业晚会上扮演戏剧需制造一顶圆锥形小丑帽,现有一张边长为30cm的正方形纸片,如下图,沿虚线剪上去后,制形成的小丑帽的正面积为〔〕〔接缝出疏忽不计〕A.15πcm2B.90πcm2C.225πcm2D.450πcm29.如图是某几何体的三视图及相关数据,那么该几何体的片面积是〔〕A.15πB.24πC.20πD.10π10.假设圆柱的底面半径为1.高为3,那么圆柱正面展开图的面积为〔〕A.6πB.12πC.3πD.3二、填空题〔共 10 小题,每题 3 分,共 30 分〕11.一个圆锥和一个圆柱,它们的底面半径相等,高也相等,且圆锥的轴截面是正三角形.那么圆柱与圆锥的正面积之比为________.12.一个圆锥的母线长为6cm,高为√35cm,那么它的底面圆的半径为________,它的正面展开图的圆心角等于________度.13.一个底面直径是40cm,母线长为60cm的圆锥的正面展开图的圆心角的度数为________.14.圆柱的底面半径为2cm,高为5cm,那么圆柱的正面积是________cm2.〔结果保管π〕15.一个底面为正方形的直棱柱的正面展开图是一个边长为8的正方形,那么它的外表积为________.16.圆锥的正面展开图是一个半圆,那么母线与高的夹角是________.17.用一个半径为6的扇形作一个圆锥的正面,这个圆锥的底面画圆的半径为2,那么这个扇形的圆心角为________.18.矩形ABCD的一边AB=10cm,另一边AD=3cm,假定以直线AB为轴旋转一周,那么所失掉的圆柱的正面积是________cm2.19.假定圆锥的底面半径为1cm,高为√3cm,那么它的外表积为________.20.扇形的圆心角为120∘,面积为300πcm2,假定用该扇形围成一个圆锥,那么该圆锥底面圆的半径为________cm.三、解答题〔共 5 小题,每题 8 分,共 40 分〕21.圆锥形烟囱帽的母线长为100cm,高为38.7cm.求这个烟囱帽的面积〔π取3.14,结果保管2个有效数字〕.22.矩形的周长为30厘米,矩形绕着它的一条边旋转构成一个圆柱,矩形的长、宽各为多少时,旋转构成的圆柱的正面积最大?正面积的最大值是多少?23.如图,一个直角三角形纸板,其两条直角边长区分为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板构成如下图的旋转体.请你帮小明推算出这个旋转体的片面积.(π取3.14)24.以下图是一纸杯,它的母线AC和EF延伸后构成的平面图形是圆锥.该圆锥的正面展开图形是扇形OAB.经测量,纸杯上启齿圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的外表积.〔面积计算结果用π表示〕.25.如下图的粮仓可以看成圆柱体与圆锥体的组合体,其底面半径为6米,高为4米,下方圆柱高为3米.(1)求该粮仓的容积;(2)求上方圆锥的正面积.〔计算结果保管根号〕答案1.B2.B3.C4.B5.D6.C7.B8.C9.B10.A11.√3:112.1cm6013.120∘14.20π15.7216.30∘17.120∘18.60π19.3πcm220.1021.解:圆锥的底面圆的半径=√1002−38.72≈92.208,所以这个烟囱帽的面积=12×100×2π×92.208≈2.9×104(cm).22.解:设矩形的一边是acm,那么另一条边是(15−a)cm.那么圆柱的正面积=2πa(15−a)=−2πa2+30πa,那么a=7.5时,圆柱的正面积最大,即112.5π.故矩形的长和宽都是7.5cm时,所构成的圆柱的正面积最大,即为112.5πcm2.23.解:设AC=8cm,BC=6cm.∴AB=√AC2+BC2=10cm,作CD⊥AB,垂足为D.∴BC2=BD⋅AB,∴BD=BC2AB =3610=185,CD=2−BD2=245,∴S=π⋅CD⋅AC+π⋅CD⋅BC=π⋅CD⋅(AC+BC)=3.14×245×14≈211.0cm2.24.解:由题意可知:BA^=6π,CD^=4π,设∠AOB=n,AO=R,那么CO= R−8,由弧长公式得:nπR180=6π,nπ(R−8)180=4π,∴{6×180=nR4×180=nR−8n,解得:n=45,R=24,故扇形OAB的圆心角是45度.∵R=24,R−8=16,∴S扇形OCD =12×4π×16=32π(cm2),S扇形OAB =12×6π×24=72π(cm2),纸杯正面积=S扇形OAB−S扇形OCD=72π−32π=40π(cm2),纸杯底面积=π⋅22=4π(cm2)纸杯外表积=40π+4π=44π(cm2).25.解:(1)体积V=π×62×3+13×π×62×(4−3)=108π+12π=120π;(2)圆锥的母线长为l=√62+12=√37,所以圆锥的正面积为s=π×6×√37=6√37π.。
苏教版九年级数学上册第二章 2.8 圆锥的侧面积 练习题(含答案解析)
2.8圆锥的侧面积一、选择题(本大题共8小题,每小题3分,共24分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020春•锡山区期中)已知圆锥的底面半径为4cm,母线长为5cm,则圆锥的侧面积是()A.20cm2B.20πcm2C.10cm2D.10πcm2 2.(2020•通州区一模)若用半径为6,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为()A.1 B.2 C.3 D.4 3.(2020•宜兴市一模)圆锥的底面半径为1,母线长为3,则该圆锥侧面积为()A.3 B.6πC.3πD.6 4.(2020•张家港市模拟)如图,粮仓的顶部是圆锥形状,这个圆锥底面的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是()A.540π元B.360π元C.180π元D.90π元5.(2019秋•海州区校级期末)如图,如果从半径为6cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径是()A.2cm B.4cm C.6cm D.8cm6.(2019秋•新吴区期末)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的全面积是()A.65πcm2B.90πcm2C.130πcm2D.155πcm2 7.(2019秋•江都区期末)若将半径为24cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为()A.3cm B.6cm C.12cm D.24cm 8.(2020•迎江区校级模拟)如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于()A.9πB.12πC.15πD.20π二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在横线上)9.(2020•连云港)用一个圆心角为90°,半径为20cm的扇形纸片围成一个圆锥的侧面,这个圆锥的底面圆半径为cm.10.(2020•无锡)已知圆锥的底面半径为1cm,高为cm,则它的侧面展开图的面积为=cm2.11.(2020•邗江区二模)圆锥的母线长为4cm,侧面积为8πcm2,圆锥的底面圆的半径为cm.12.(2020•吴中区二模)已知圆锥的侧面积为10πcm2,母线长为5cm,则该圆锥的底面半径为cm.13.(2020•徐州模拟)若一个圆锥的母线长为6cm,它的侧面展开图是半圆,则这个圆锥的底面半径为cm.14.(2020•江都区二模)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=4,扇形的圆心角θ=120°,则该圆锥母线l的长为.15.(2020•扬中市模拟)已知圆锥的底面圆半径为cm,高为cm,则圆锥的侧面积是cm2.16.(2020•徐州模拟)如图,圆锥底面半径为r,母线长为6,其侧面展开图是圆心角为180°的扇形,则r的值为.三、解答题(本大题共4小题,共52分.解答时应写出文字说明、证明过程或演算步骤)17.(2019秋•五峰县期末)如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:(1)求出围成的圆锥的侧面积为多少?(2)求出该圆锥的底面半径是多少?18.(2019秋•东海县期中)如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(﹣4,4)、C(﹣6,2),请在网格图中进行如下操作:(1)若该圆弧所在圆的圆心为D点,则D点坐标为;(2)连接AD、CD,则圆D的半径长为(结果保留根号).∠ADC的度数为°;(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长(结果保留根号)19.(2019秋•淮安区期中)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;20.(2019•邵阳)如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.答案解析一、选择题(本大题共8小题,每小题3分,共24分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020春•锡山区期中)已知圆锥的底面半径为4cm,母线长为5cm,则圆锥的侧面积是()A.20cm2B.20πcm2C.10cm2D.10πcm2【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算即可.【解析】这个圆锥的侧面积2π×4×5=20π(cm2).故选:B.2.(2020•通州区一模)若用半径为6,圆心角为120°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为()A.1 B.2 C.3 D.4【分析】根据弧长公式求出扇形弧长,根据圆的周长公式计算,得到答案.【解析】扇形的弧长4π,∴圆锥的底面圆的周长=4π,∴圆锥的底面圆半径2,故选:B.3.(2020•宜兴市一模)圆锥的底面半径为1,母线长为3,则该圆锥侧面积为()A.3 B.6πC.3πD.6【分析】根据扇形面积公式求出圆锥侧面积.【解析】圆锥的底面周长=2π×1=2π,即圆锥的侧面展开图扇形的弧长为2π,则圆锥侧面积2π×3=3π,故选:C.4.(2020•张家港市模拟)如图,粮仓的顶部是圆锥形状,这个圆锥底面的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是()A.540π元B.360π元C.180π元D.90π元【分析】圆锥的侧面积=底面周长×母线长÷2.算出侧面积后乘以单价即可.【解析】底面半径为3m,则底面周长=6π,侧面面积6π×6=18π(m2).所需要的费用=18π×10=180π(元),故选:C.5.(2019秋•海州区校级期末)如图,如果从半径为6cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面半径是()A.2cm B.4cm C.6cm D.8cm【分析】易求得扇形的弧长,除以2π即为圆锥的底面半径.【解析】扇形的弧长为:8πcm,圆锥的底面半径为:8π÷2π=4cm,故选:B.6.(2019秋•新吴区期末)已知圆锥的底面半径为5cm,母线长为13cm,则这个圆锥的全面积是()A.65πcm2B.90πcm2C.130πcm2D.155πcm2【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算扇形的侧面积,然后计算扇形的底面积,从而求得答案.【解析】这个圆锥的侧面积2π×5×13=65π(cm2).底面积为:52×π=25π(cm2),所以全面积为65π+25π=90π(cm2).故选:B.7.(2019秋•江都区期末)若将半径为24cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为()A.3cm B.6cm C.12cm D.24cm【分析】易得圆锥的母线长为12cm,以及圆锥的侧面展开图的弧长,也就是圆锥的底面周长,除以2π即为圆锥的底面半径.【解析】圆锥的侧面展开图的弧长为2π×24÷2=24π(cm),∴圆锥的底面半径为24π÷2π=12(cm),故选:C.8.(2020•迎江区校级模拟)如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于()A.9πB.12πC.15πD.20π【分析】由勾股定理易得圆锥的底面半径长,那么圆锥的侧面积2π×底面半径×母线长,把相应数值代入即可求解.【解析】∵AC=4,BC=5,∴由勾股定理得:AB=3∴底面的周长是:6π∴圆锥的侧面积等6π×5=15π,故选:C.二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在横线上)9.(2020•连云港)用一个圆心角为90°,半径为20cm的扇形纸片围成一个圆锥的侧面,这个圆锥的底面圆半径为5cm.【分析】设这个圆锥的底面圆半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr,然后解关于r的方程即可.【解析】设这个圆锥的底面圆半径为r,根据题意得2πr,解得r=5(cm).故答案为:5.10.(2020•无锡)已知圆锥的底面半径为1cm,高为cm,则它的侧面展开图的面积为=2πcm2.【分析】先利用勾股定理求出圆锥的母线l的长,再利用圆锥的侧面积公式:S侧=πrl 计算即可.【解析】根据题意可知,圆锥的底面半径r=1cm,高h cm,∴圆锥的母线l2,∴S侧=πrl=π×1×2=2π(cm2).故答案为:2π.11.(2020•邗江区二模)圆锥的母线长为4cm,侧面积为8πcm2,圆锥的底面圆的半径为2 cm.【分析】根据扇形面积公式S lr计算即可.【解析】设圆锥的底面圆的半径为rcm,则圆锥的底面周长为2πrcm,∴圆锥的侧面展开图扇形的弧长为2πrcm,由题意得,2πr×4=8π,解得,r=2,故答案为:2.12.(2020•吴中区二模)已知圆锥的侧面积为10πcm2,母线长为5cm,则该圆锥的底面半径为2cm.【分析】根据圆锥的侧面积和圆锥的母线长求得圆锥的弧长,利用圆锥的侧面展开扇形的弧长等于圆锥的底面周长求得圆锥的底面半径即可.【解析】∵圆锥的母线长是5cm,侧面积是10πcm2,∴圆锥的侧面展开扇形的弧长为:l4π,∵锥的侧面展开扇形的弧长等于圆锥的底面周长,∴r2cm.故答案为:2.13.(2020•徐州模拟)若一个圆锥的母线长为6cm,它的侧面展开图是半圆,则这个圆锥的底面半径为3cm.【分析】由于圆锥的母线长为6cm,侧面展开图是圆心角为180°扇形,设圆锥底面半径为rcm,那么圆锥底面圆周长为2πrcm,所以侧面展开图的弧长为2πrcm,然后利用扇形的面积公式即可得到关于r的方程,解方程即可求解.【解析】设圆锥底面半径为rcm,那么圆锥底面圆周长为2πrcm,所以侧面展开图的弧长为2πrcm,S圆锥侧面积2πr×6,解得:r=3,故答案为:3.14.(2020•江都区二模)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=4,扇形的圆心角θ=120°,则该圆锥母线l的长为12.【分析】由于圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.则利用弧长公式得到2π×4,然后解方程即.【解析】根据题意得2π×4,解得l=12.故答案为12.15.(2020•扬中市模拟)已知圆锥的底面圆半径为cm,高为cm,则圆锥的侧面积是πcm2.【分析】先利用勾股定理计算出圆锥的母线长,然后根据扇形的面积公式计算这个圆锥的侧面积.【解析】这个圆锥的母线长6,所以这个圆锥的侧面积2π6π(cm2).故答案为π.16.(2020•徐州模拟)如图,圆锥底面半径为r,母线长为6,其侧面展开图是圆心角为180°的扇形,则r的值为3.【分析】根据底面圆周长=扇形的弧长,构建方程即可解决问题.【解析】由题意:2πr,解得r=3,故答案为:3.三、解答题(本大题共4小题,共52分.解答时应写出文字说明、证明过程或演算步骤)17.(2019秋•五峰县期末)如图所示,已知扇形AOB的半径为6cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:(1)求出围成的圆锥的侧面积为多少?(2)求出该圆锥的底面半径是多少?【分析】(1)根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算;(2)根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式计算.【解析】(1)圆锥的侧面积12π(cm2);(2)该圆锥的底面半径为r,根据题意得2πr,解得r=2.即圆锥的底面半径为2cm.18.(2019秋•东海县期中)如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(﹣4,4)、C(﹣6,2),请在网格图中进行如下操作:(1)若该圆弧所在圆的圆心为D点,则D点坐标为(﹣2,0);(2)连接AD、CD,则圆D的半径长为2(结果保留根号).∠ADC的度数为90°;(3)若扇形ADC是一个圆锥的侧面展开图,求该圆锥的底面圆的半径长(结果保留根号)【分析】(1)根据线段垂直平分线的性质得出D点位置,结合图形得到点D的坐标;(2)利用点的坐标结合勾股定理得出⊙D的半径长,根据勾股定理的逆定理∠ADC的度数;(3)利用圆锥的底面圆的周长等于侧面展开图的扇形弧长即可得出答案.【解析】(1)分别作AB、BC的垂直平分线,两直线交于点D,则点D即为该圆弧所在圆的圆心,由图形可知,点D的坐标为(﹣2,0),故答案为:(﹣2,0);(2)圆D的半径长2,AC2,AD2+CD2=20+20=40,AC2=40,则AD2+CD2=AC2,∴∠ADC=90°,故答案为:2;90;(3)设圆锥的底面圆的半径长为r,则2πr,解得,r.19.(2019秋•淮安区期中)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;【分析】(1)易得底面半径为6m,直接利用圆的周长公式求得底面圆的周长即可;(2)利用勾股定理求得母线的长,然后求得圆锥的侧面积即可.【解析】(1)2π×6=12π.(2)∵∠C=90°,AC=6,BC=8,∴AB10,所以以直线AC为轴,把△ABC旋转一周,得到的圆锥的侧面积10×2π×8=80π;20.(2019•邵阳)如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧EF,交AB于点E,交AC于点F.(1)求由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积;(2)将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高h.【分析】(1)利用等腰三角形的性质得到AD⊥BC,BD=CD,则可计算出BD=6,然后利用扇形的面积公式,利用由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC﹣S扇形EAF进行计算;(2)设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr,解得r =2,然后利用勾股定理计算这个圆锥的高h.【解析】∵在等腰△ABC中,∠BAC=120°,∴∠B=30°,∵AD是∠BAC的角平分线,∴AD⊥BC,BD=CD,∴BD AD=6,∴BC=2BD=12,∴由弧EF及线段FC、CB、BE围成图形(图中阴影部分)的面积=S△ABC﹣S扇形EAF6×123612π;(2)设圆锥的底面圆的半径为r,根据题意得2πr,解得r=2,这个圆锥的高h4.。
苏科版九年级数学上册 第二章 对称图形-圆 2.8 圆锥的侧面积 同步测试题(无答案)
2.8 圆锥的侧面积同步测试题(满分120分;时间:120分钟)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!题号一二三总分得分一、选择题(本题共计9小题,每题 3 分,共计27分,)1. 若圆柱的底面半径为,母线长为,则这个圆柱的侧面积为()A. B. C. D.2. 若圆柱的底面半径为,高为,则圆柱的表面积为()A. B. C. D.3. 已知圆柱的底面半径为,高为,则圆柱的侧面积是()A. B. C. D.4. 一个圆锥底面直径为,母线为,则它的侧面积为()C. D.A.B.5. 如果圆柱的底面直径为,母线长为,那么圆柱的侧面展开图的面积等于()A. B. C. D.6. 如果圆锥的侧面积为,它的母线长为,那么此圆锥的底面半径的长等于()C. D.A.B.7. 已知某圆锥的底面半径为,母线长,则它的侧面展开图的面积为()A. B. C. D.8. 如果圆柱的母线长为,底面半径为,那么这个圆柱的侧面积是()A. B. C. D.9. 把长和宽分别为和的矩形纸片卷成一个圆柱状,则这个圆柱的底面半径为()A. B.C. D.或二、填空题(本题共计10 小题,每题 3 分,共计30分,)10. 已知一个圆锥的侧面展开图是一个半径为的半圆,则该圆锥的底面半径等于________.11. 蛋糕店制作两种高度相同的圆柱形蛋糕,一种半径是,一种半径是,如果半径是的蛋糕能够个人吃,半径是的蛋糕能够________个人吃.12. 圆锥的底面直径为,母线长为,则圆锥的侧面积是________.13 已知一个圆柱底面半径增加,它的侧面积就增加,若它的底面周长增加,则它的侧面积增加________.14. 已知圆锥的侧面积为,母线长为,则圆锥底面半径为________.15. 已知一个直角三角形的两条直角边的长分别为和,以它的直角边所在直线为轴旋转一周,所得圆锥的全面积是________.16 用一张面积为的正方形硬纸片围成一个圆柱的侧面,这个圆柱的底面直径是________(精确到).17 若一个圆锥的侧面展开图是半径为的半圆形,则这个圆锥的底面半径是________.18. 将半径为的半圆围成一个圆锥,其底面与侧面面积之比为________.19. 矩形中,,,则以该矩形的一边为轴旋转一周而所得到的圆柱的表面积为________.三、解答题(本题共计 6 小题,共计63分,)20. 如图,一个圆锥的侧面展开图是的扇形.(1)求圆锥的母线长与底面半径之比;(2)若底面半径,求圆锥的高及侧面积(结果保留).21. 一个圆柱形容器的内半径为厘米,里面盛有一定高度的水,将一个长厘米,宽厘米的长方体金属块完全淹没,结果容器内的水升高了厘米(没有溢出),问这个金属块的高是多少厘米?的取值22 圣诞节马上就要到了,中山市某制衣厂打算生产圆锥形圣诞帽出售,设计该圣诞帽底面周长为,高为,那么制作一顶这样的圣诞帽至少需要多少材料?(结果保留和根号)23 如图,蒙古包可以近似地看作由圆锥和圆柱组成的,现想用毛毡搭建底面积为,高为,外围高为的蒙古包,求至少需要多少平方米的毛毡?(结果保留)24. 如图,圆柱的体积.其中,为圆柱的底而积,为圆柱的高.(1)当圆柱底面的半径扩大为原来的倍而高不变时,变化后圆柱的体积是原来的多少倍;(2)当圆柱的底面积扩大为原来的倍,而体积不变时,变化后圆柱的高是原来的几分之一.25 在数学课上,张老师布置了一道课外作业题:要求同学利用正方形纸片制作一个圆锥的模型,(1)甲同学认为按如图剪下其中的扇形和小圆,就可以一个做侧面,一个做底面,做成一个圆锥模型.(2)乙同学认为按如图剪下其中的扇形和小圆,就可以一个做侧面,一个做底面,做成一个圆锥模型.已知正方形的边长为,请你就甲、乙两位同学的观点谈谈你的看法,如果你认为不对,请说明理由,如果你认为正确,请求出扇形的底面半径和母线长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宝应县柳堡镇中心初级中学 吕坤林
1
九上数学《同步练习》§2.7弧长及扇形的面积
隨堂练习
1.已知圆锥底面半径是4,母线长是9,它的侧面积是______。
2.如图,扇形OAB的圆心角是1200,半径是30用它
做成一个圆锥的侧面,这个圆锥的底面半径O/C
是_______,高OO/是______。
3.已知圆锥的底面半径是2,母线长是4,这个圆锥
的侧面展开的扇形圆心角是________。
4.已知扇形的圆心角为1500,弧长为20π,用它围成一个圆锥伯侧面,这个圆锥的侧面积
为_____。
5.一个圆锥的母线和底面圆的直径都等于20,这个圆锥的高是______。
6.已知圆锥形模具的母线长和底面圆的周长均是10cm,这个模具的侧面积是_______。
7.一个矩形纸片的长8cm,宽为6cm,用它围成一个圆柱的侧面,所得圆柱的底面圆的半
径是_____。
8.如图,Rt△ABC的两条直角边分别为3cm和4cm,以斜边所在直线为轴旋转1周得到一
个几何体,求该几何体的表面积。
宝应县柳堡镇中心初级中学 吕坤林
2
课后复习
9.用半径为4、面积为24π的扇形围成一个圆锥的侧面,该圆锥的底面半径为______0。
10.如图,一个圆锥的高为33 cm,侧面展开图是半圆,求:
(1)圆锥的母线长与底面半径之比;
(2)圆锥的侧面积(结果保留π)
拓展延伸
11.小明要制作一个圆锥模具,操作规则:在一张边长为16cm的正方形纸片上剪出一个扇
形和圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面。他首先设计了如图所
示的方案一,发现这种方案不可行,于是调整了扇形和圆的半径,设计了如图所示的
方案二。
(1)请说明方案一不可行的理由;
(2)判断方案二是否可行。若可行,请确定圆锥的母线长及其底面圆半径;若不可行,
请说明理由。
